Lifetime Considerations for Electrospray Thrusters
Abstract
1. Introduction
2. Materials and Methods
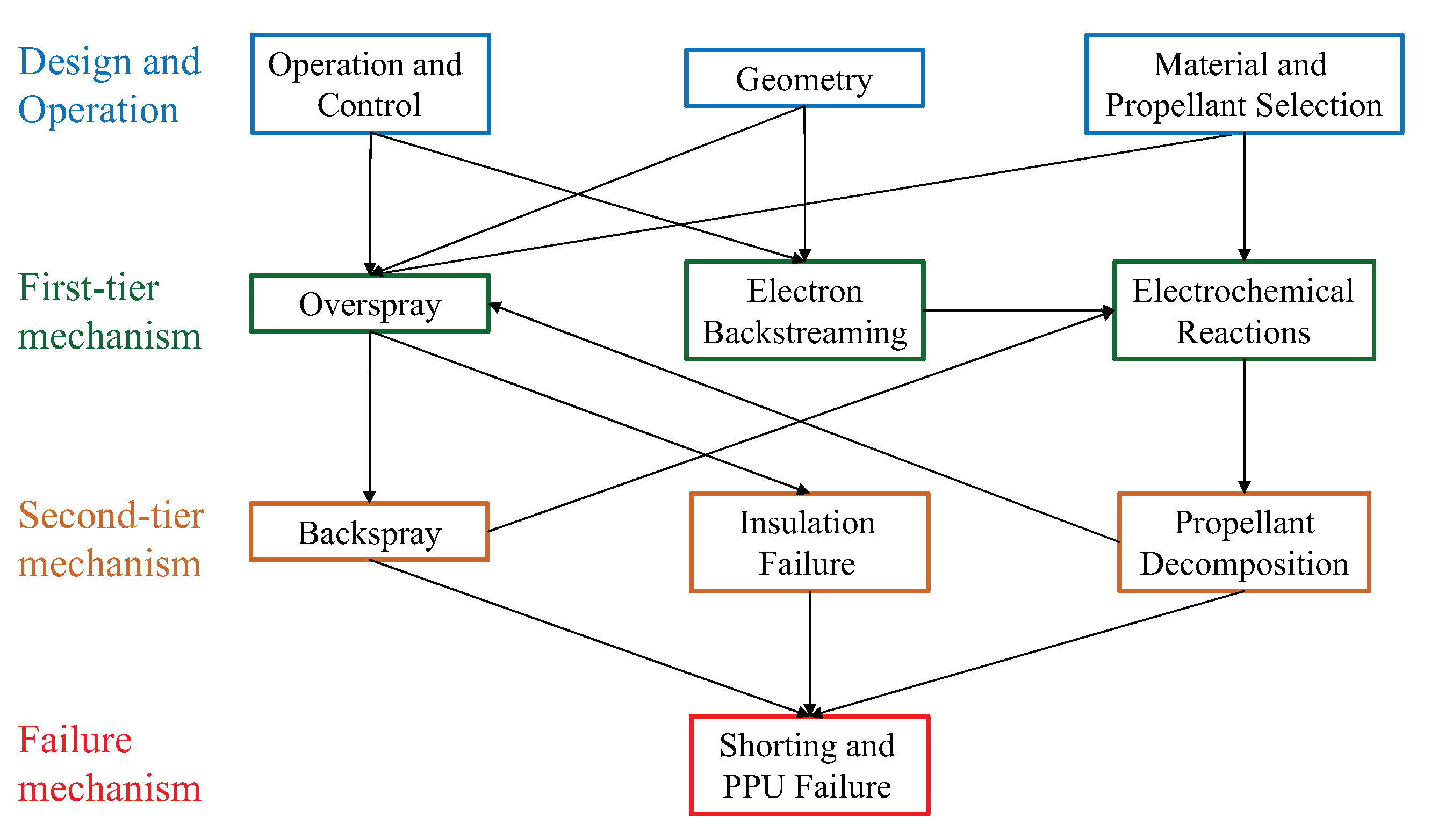
2.1. Lifetime Limiting Mechanisms
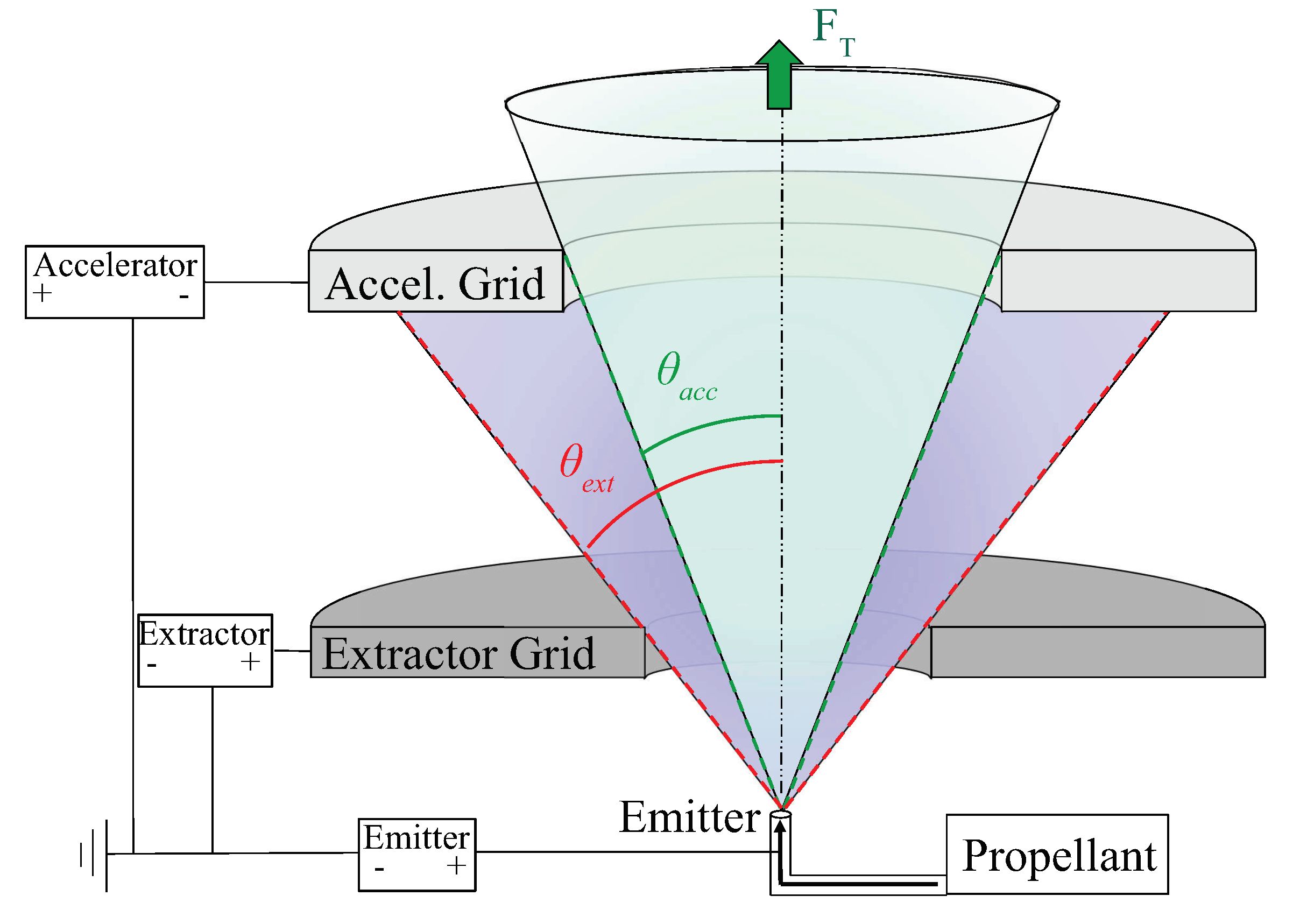
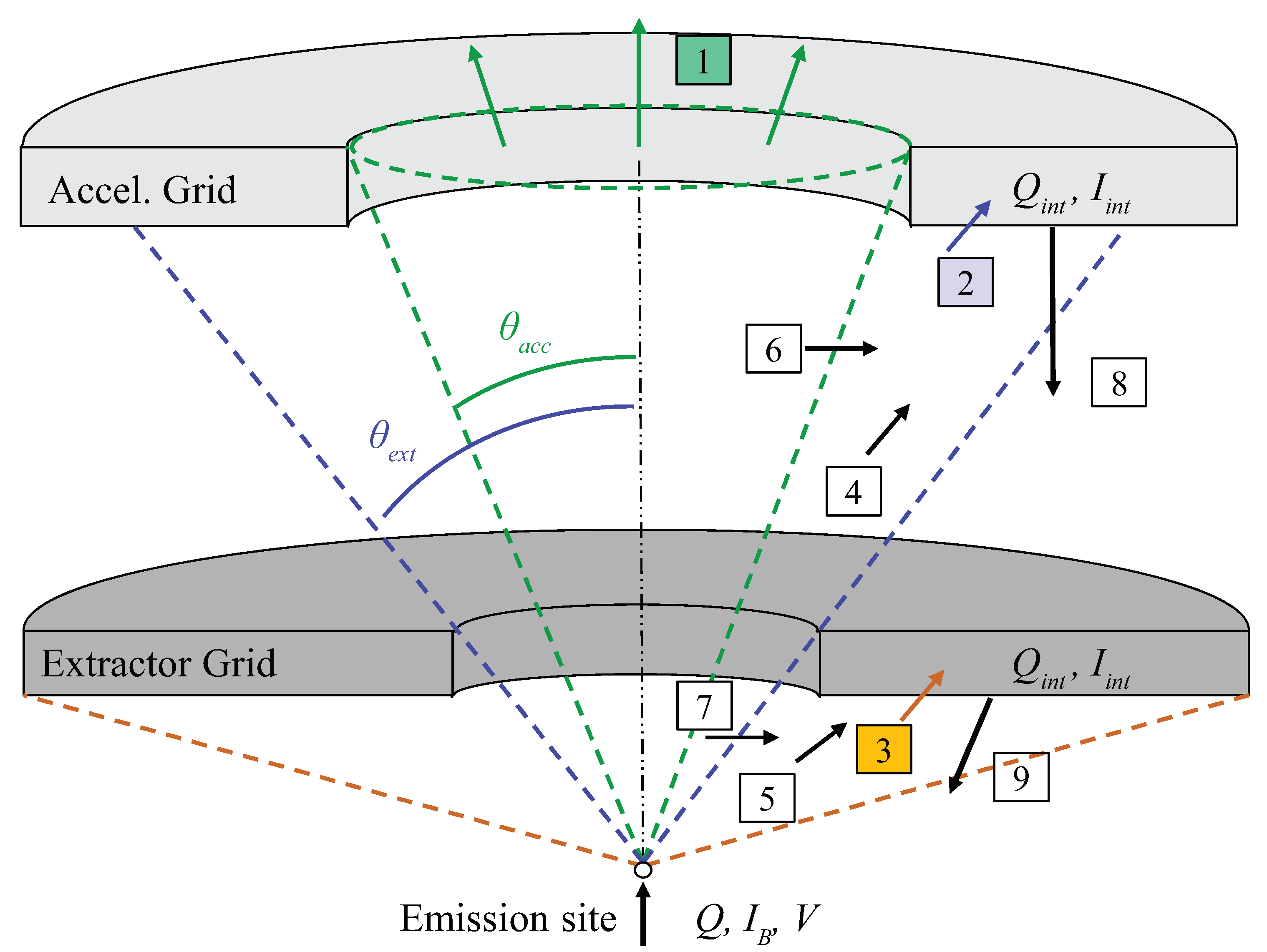
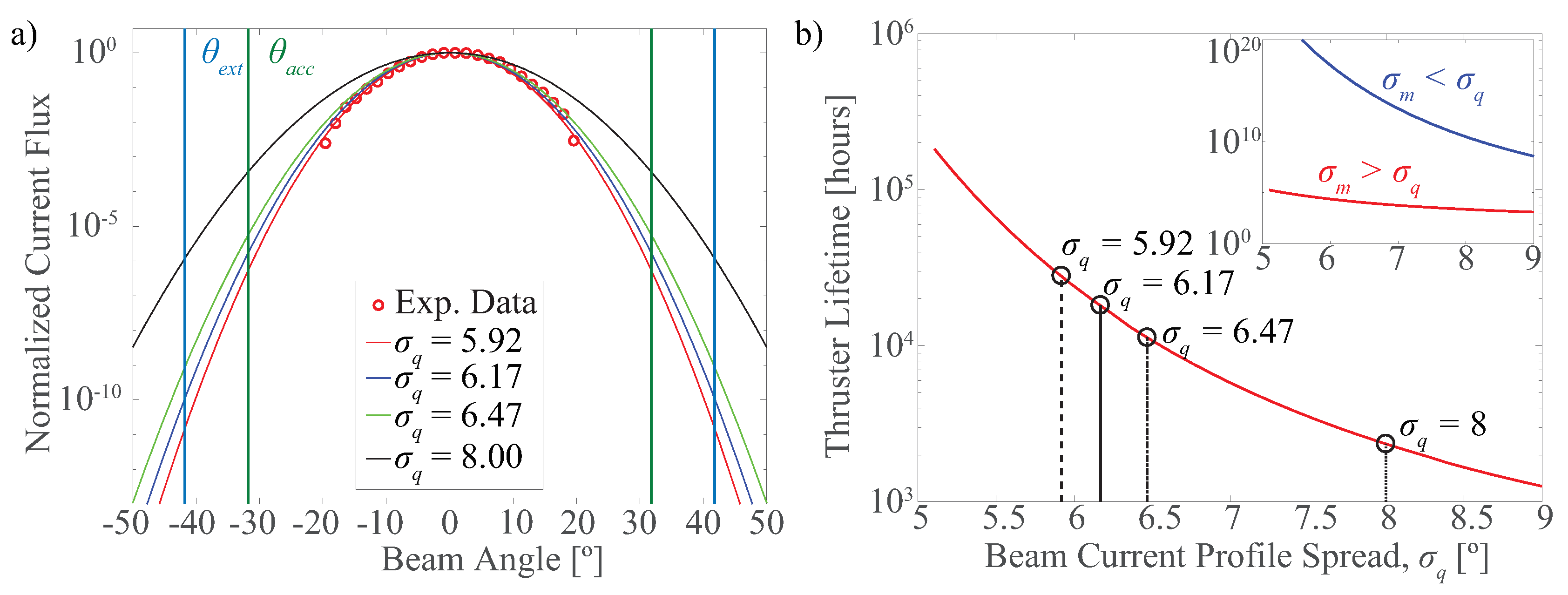
2.2. Overspray
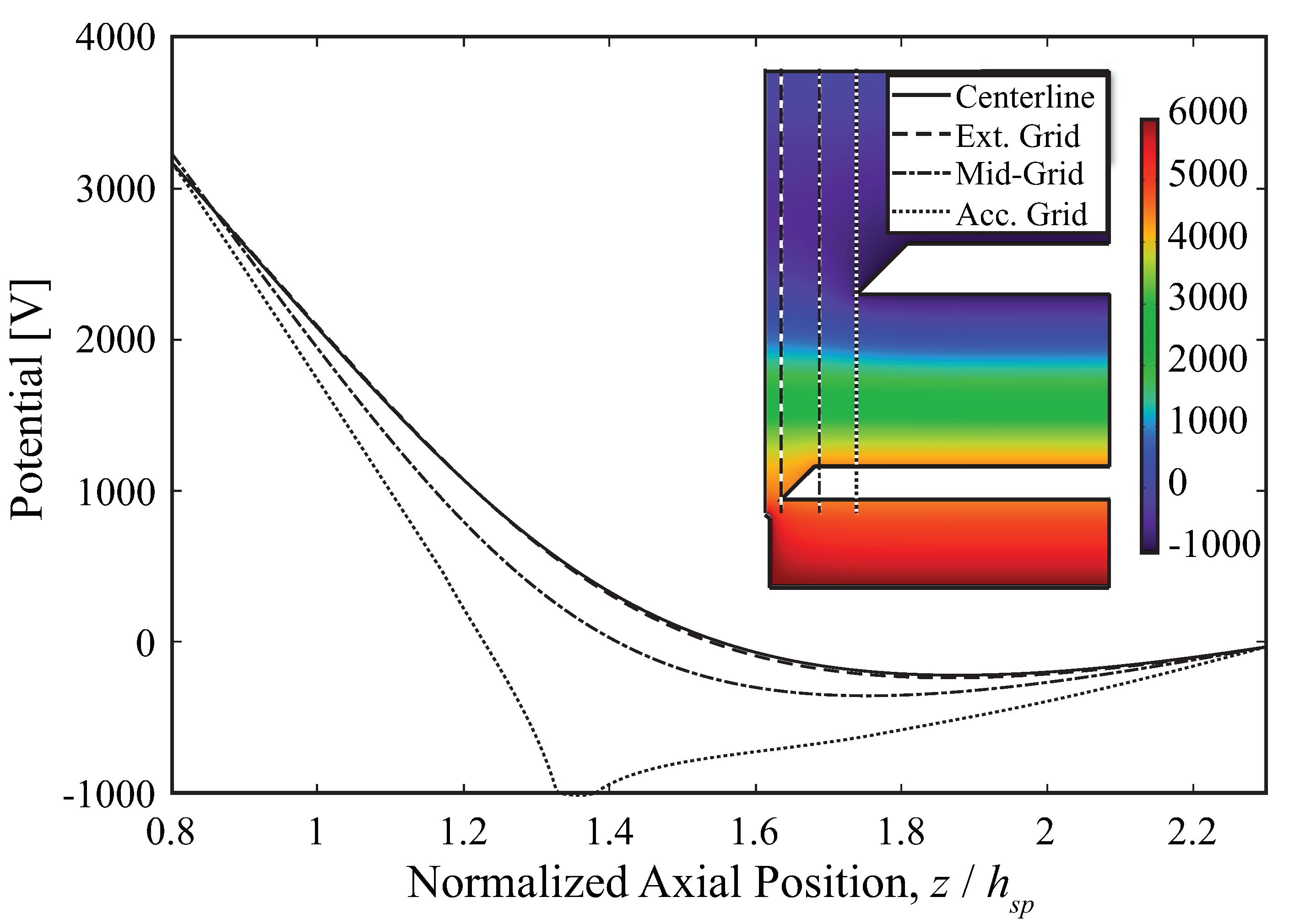
2.3. Electron Backstreaming
3. Results and Discussion
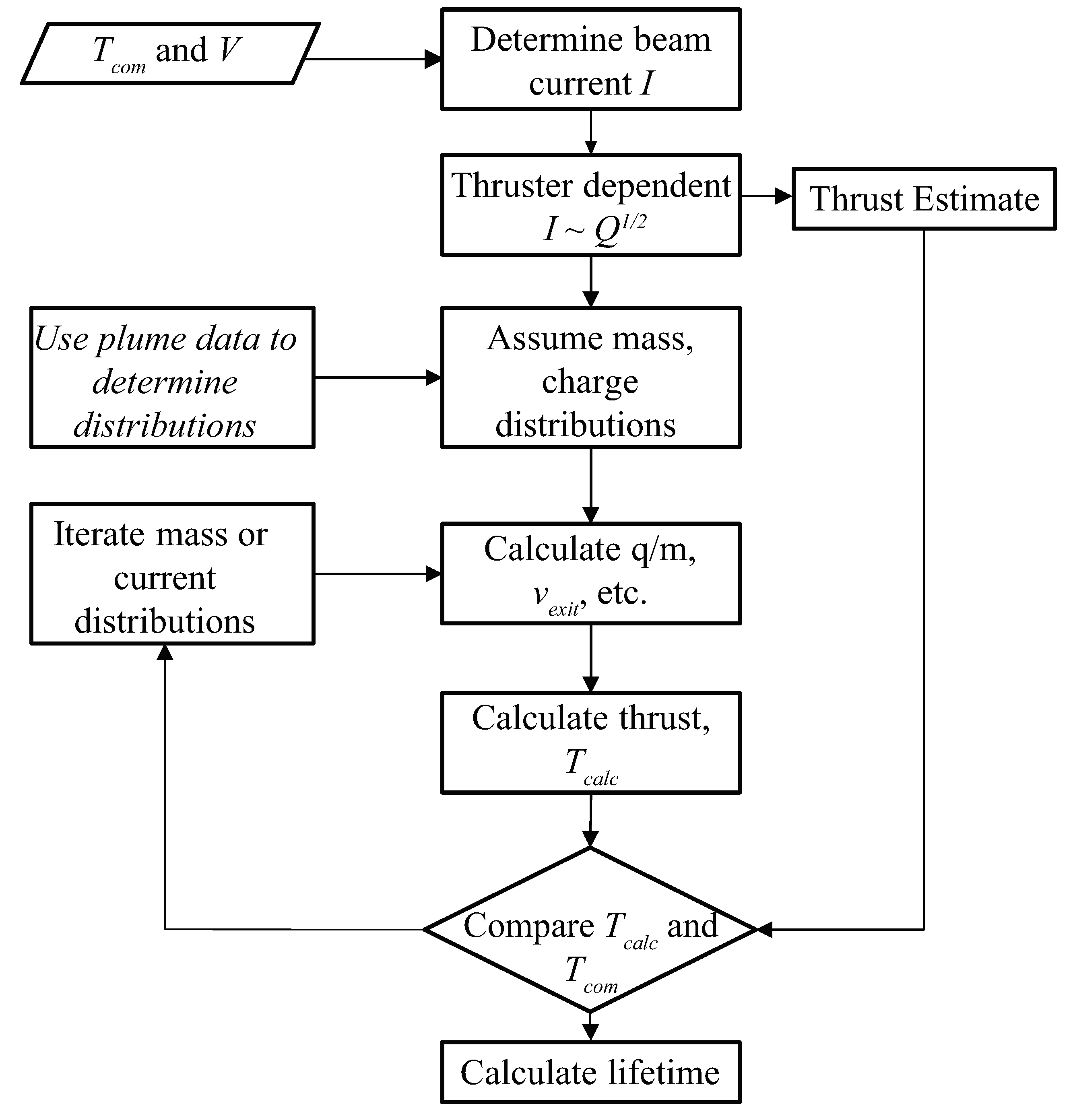
3.1. Overspray
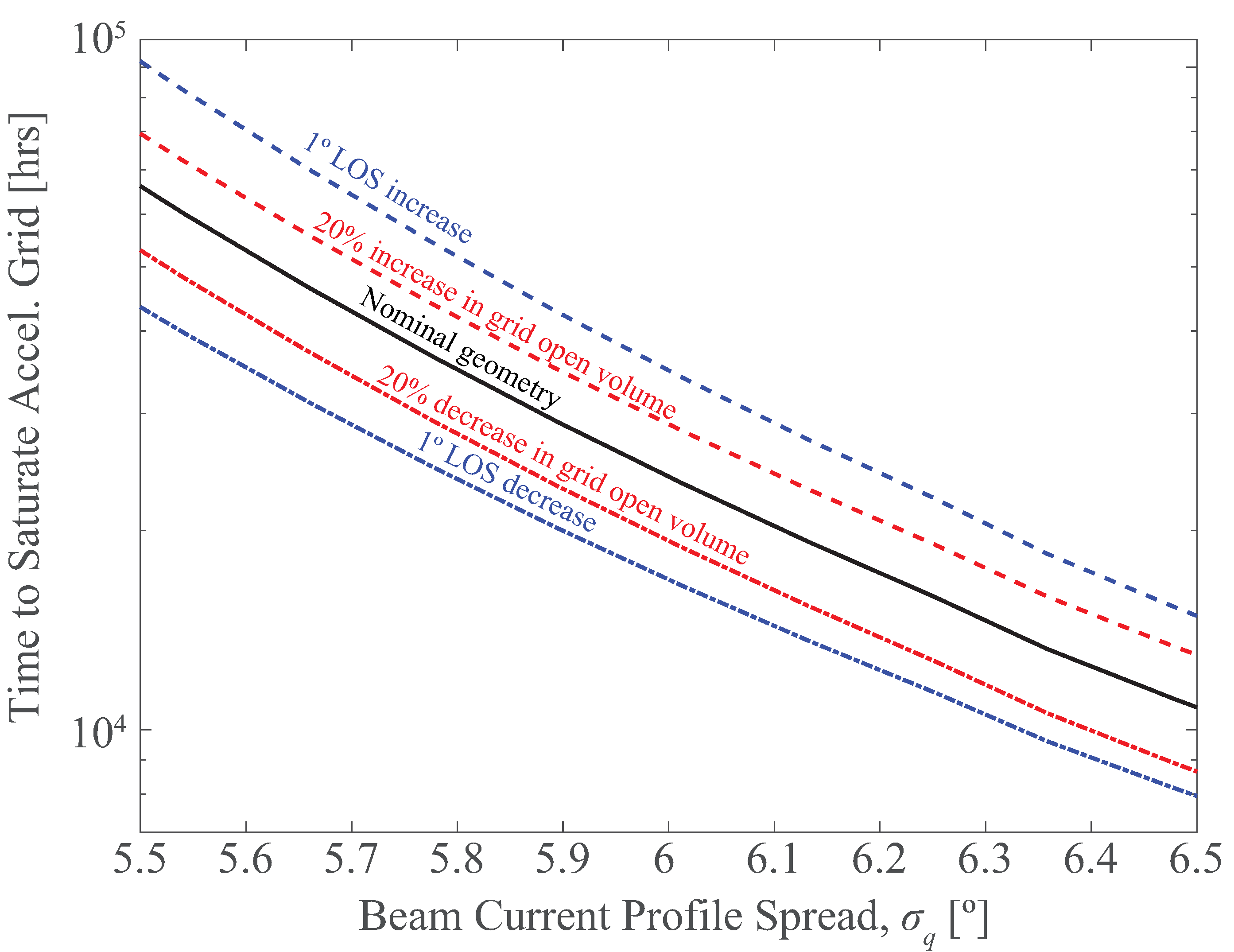
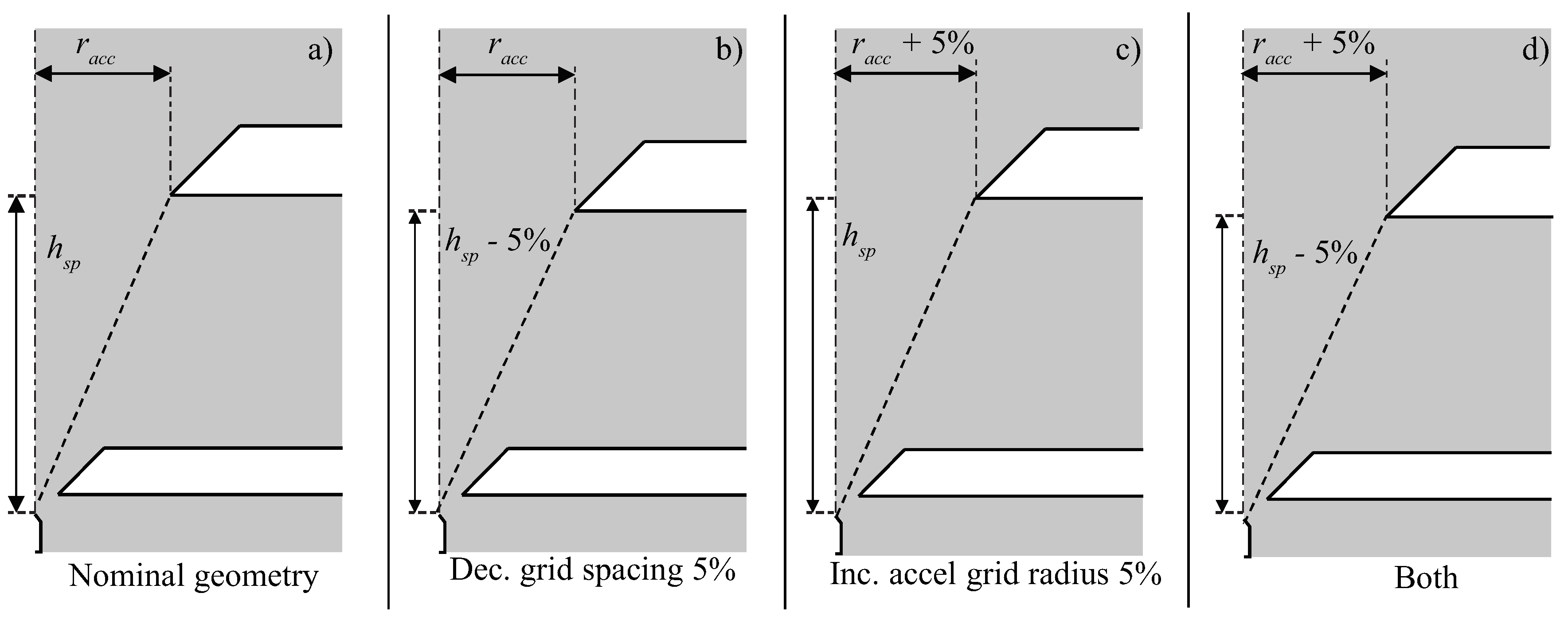
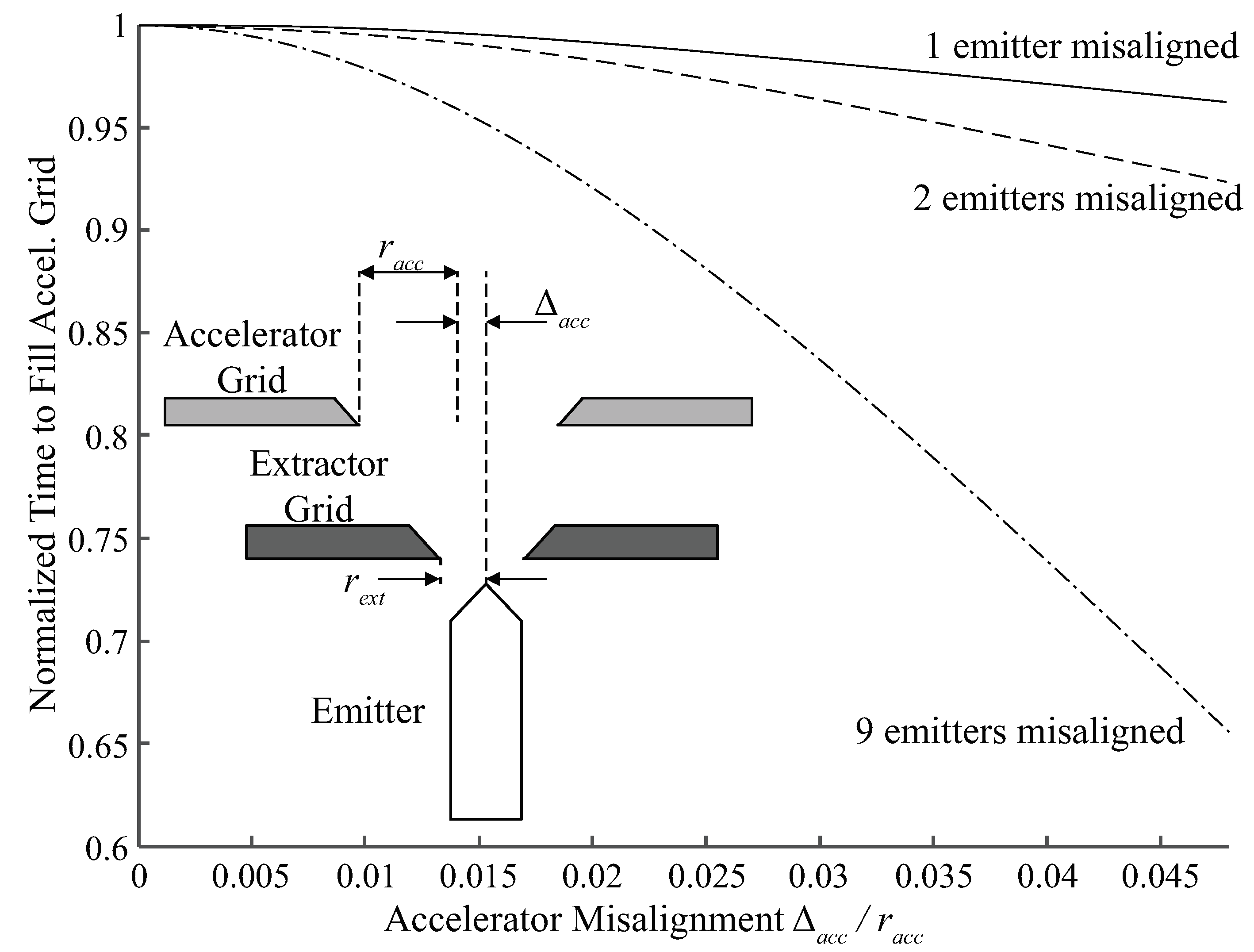
3.2. Misalignment and Tolerances
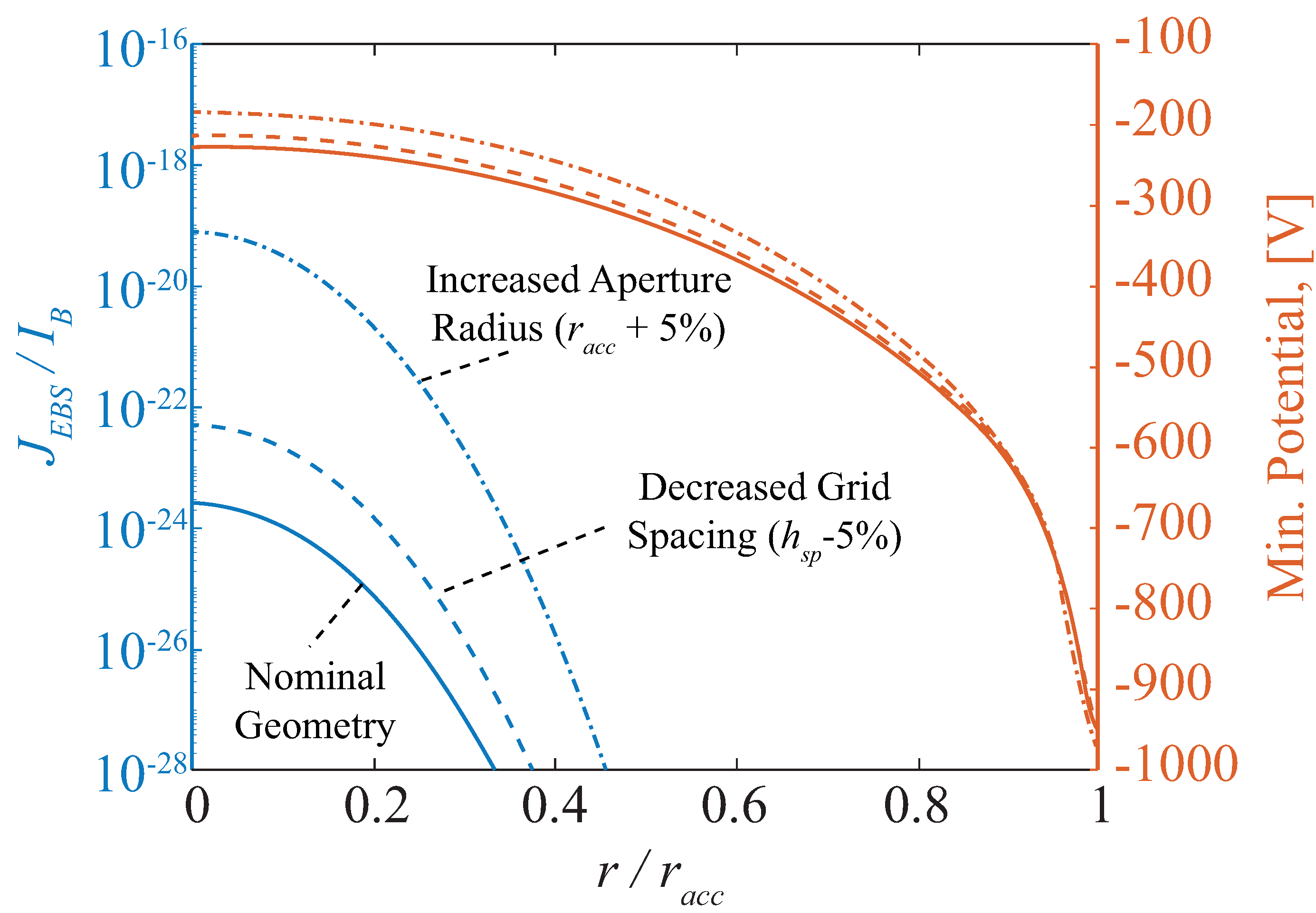
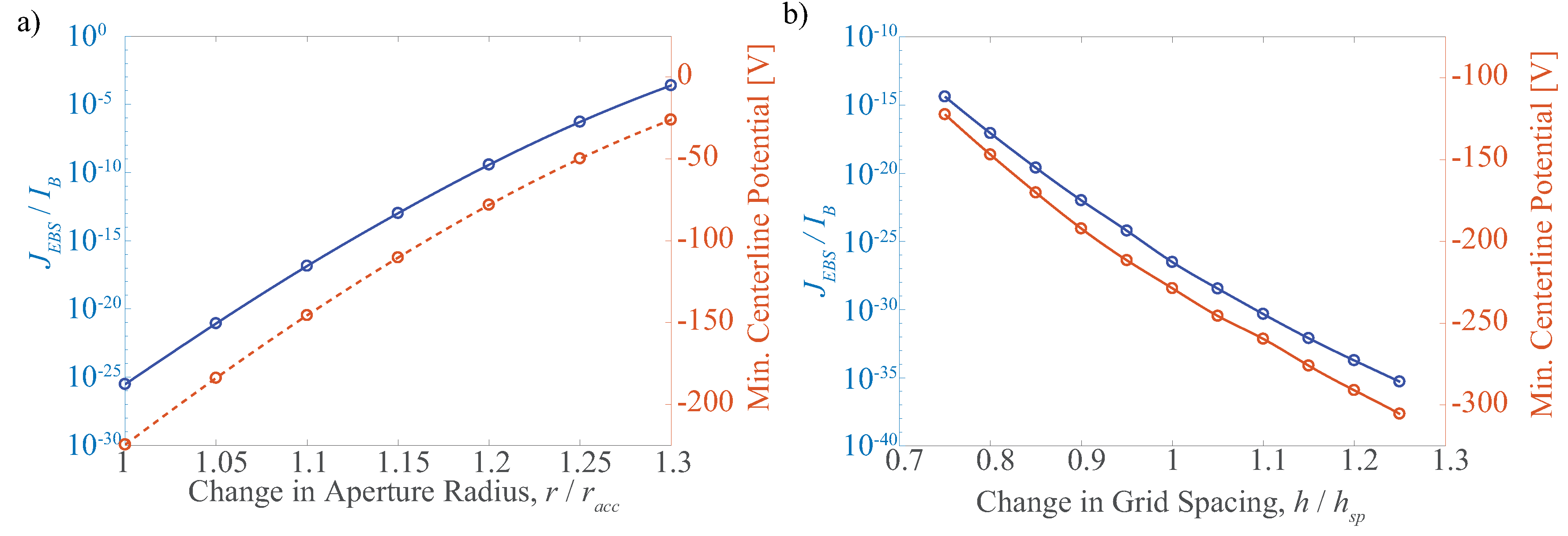
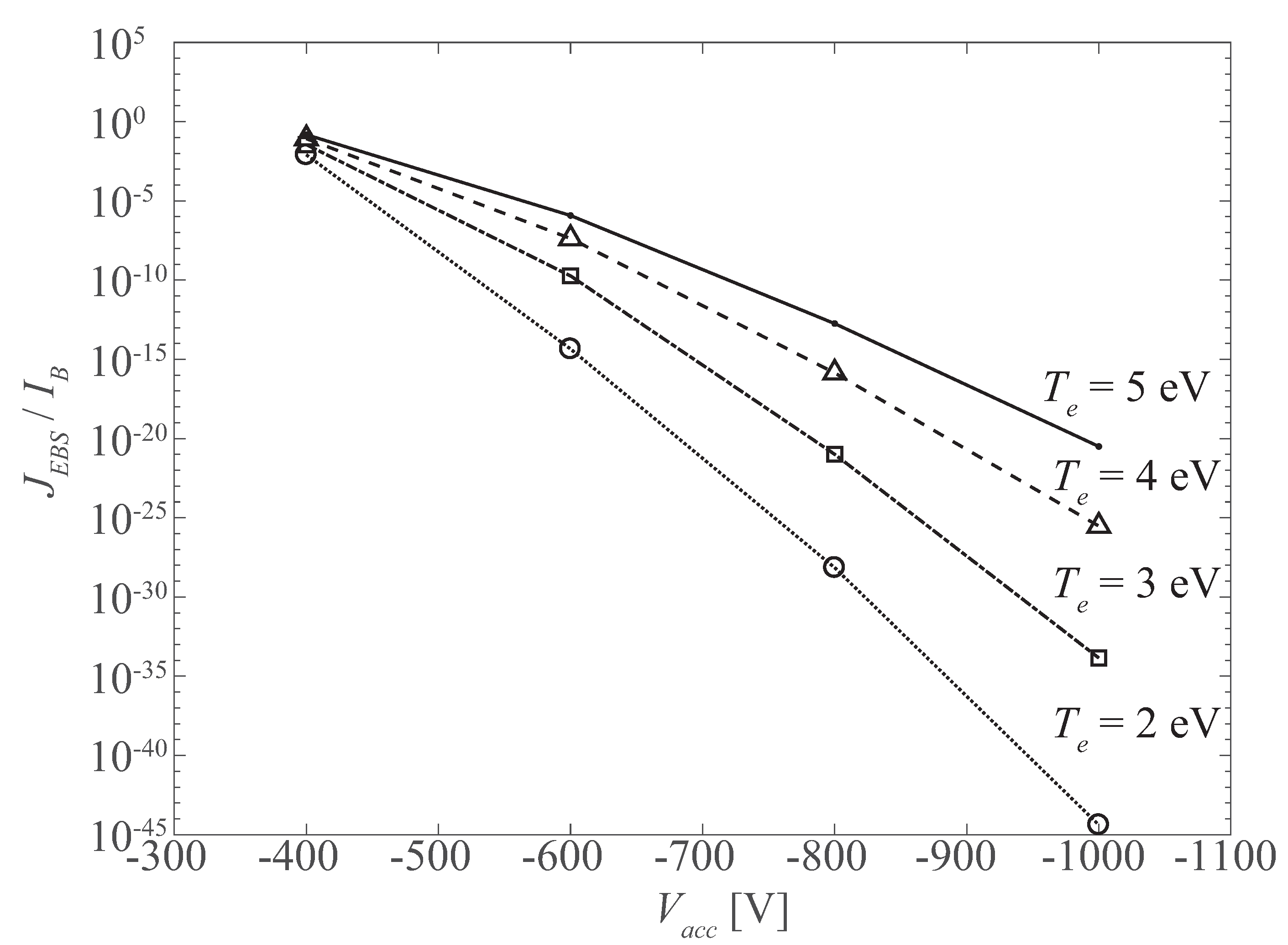
3.3. Electron Backstreaming
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Blandino, J.J.; Martinez-Baquero, N.; Demetriou, M.A.; Gatsonis, N.A.; Paschalidis, N. Feasibility for Orbital Life Extension of a CubeSat in the Lower Thermosphere. J. Spacecr. Rocket. 2016, 53, 864–875. [Google Scholar] [CrossRef]
- NASA. NASA Technology Roadmaps, TA 2: In-Space Propulsion Technologies; 2.2.1.5 Electrospray Propulsion; Technical Report; National Aeronautics and Space Administration: Washington, DC, USA, 2015.
- Marrese-Reading, C.; Anderson, J.R.; Jung-Kubiak, C.; Greer, F.; Rouhi, N.; Wilson, D.; White, V.; Dickie, M.; Mueller, R.; Singh, V.; et al. Silicon Emitter Needle and Array Design for Indium Electrospray Arrays for Spacecraft Propulsion. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; pp. 1–14. [Google Scholar] [CrossRef]
- Marrese-Reading, C.; Anderson, J.R.; Jung-Kubiak, C.; Polk, J.; Singh, V.; Yee, K.; White, V.; Wilson, D.; Bruneau, P.; Rouhi, N.; et al. Microfluidic Electrospray Propulsion (MEP) Thruster Performance with Microfabricated Emitter Arrays for Indium Propellant. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; pp. 1–15. [Google Scholar]
- Tajmar, M.; Genovese, A.; Steiger, W. Indium field emission electric propulsion microthruster experimental characterization. J. Propuls. Power 2004, 20, 211–218. [Google Scholar] [CrossRef]
- Hruby, V.; Spence, D.; Demmons, N.; Roy, T.; Ehrbar, E.; Zwahlen, J.; Martin, R.; Ziemer, J.; Connolly, W.; Rhodes, S.; et al. ST7-DRS colloid thruster system development and performance summary. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; pp. 1–32. [Google Scholar] [CrossRef]
- Demmons, N.R.; Lamarre, N.; Ziemer, J.K.; Parker, M.; Spence, D. Electrospray Thruster Propellant Feedsystem for a Gravity Wave Observatory Missions. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016; pp. 1–16. [Google Scholar] [CrossRef]
- Ziemer, J.K. Performance of Electrospray Thrusters. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009; pp. 1–13. [Google Scholar]
- Ziemer, J.; Marrese-Reading, C.; Dunn, C.; Romero-Wolf, A.; Cutler, C.; Javidnia, S.; Li, T.; Li, I.; Franklin, G.; Barela, P.; et al. Colloid microthruster flight performance results from space technology 7 disturbance reduction system. In Proceedings of the 35th International Electric Propulsion Conference, Atlanta, GA, USA, 8–12 October 2017; pp. 1–17. [Google Scholar]
- Amaro-Seoane, P.; Audley, H.; Babak, S.; Baker, J.; Barausse, E.; Bender, P.; Berti, E.; Binetruy, P.; Born, M.; Bortoluzzi, D. Laser interferometer space antenna. arXiv 2017, arXiv:1702.00786. [Google Scholar]
- Ziemer, J.K.; Randolph, T.M.; Gamero-Castaño, M.; Hruby, V.; Connolly, W.; Demmons, N.; Ehrbar, E.; Martin, R.; Roy, T.; Spence, D.; et al. Flight hardware development of colloid microthruster technology for the space technology 7 and LISA missions. In Proceedings of the 30th International Electric Propulsion Conference, Florence, Italy, 17–20 September 2007; pp. 1–13. [Google Scholar]
- Ziemer, J.K.; Randolph, T.; Hruby, V.; Spence, D.; Demmons, N.; Roy, T.; Connolly, W.; Ehrbar, E.; Zwahlen, J.; Martin, R. Colloid Microthrust Propulsion for the Space Technology 7 (ST7) and LISA Missions. In AIP Conference Proceedings; American Institute of Physics: College Park, MD, USA, 2006; Volume 873, pp. 548–555. [Google Scholar] [CrossRef]
- Thuppul, A.; Wright, P.; Wirz, R.E. Lifetime Considerations and Estimation for Electrospray Thrusters. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; p. 4652. [Google Scholar]
- Demmons, N.; Martin, R.; Hruby, V.; Roy, T.; Spence, D.; Ehrbar, E.; Zwahlen, J. Electrospray Device. U.S. Patent 7,932,492, 26 April 2011. [Google Scholar]
- Courtney, D.G.; Shea, H. Influences of porous reservoir Laplace pressure on emissions from passively fed ionic liquid electrospray sources. Appl. Phys. Lett. 2015, 107, 103504. [Google Scholar] [CrossRef]
- Terhune, K.J.; King, L.B.; He, K.; Cumings, J. Radiation-induced solidification of ionic liquid under extreme electric field. Nanotechnology 2016, 27, 375701. [Google Scholar] [CrossRef]
- Brikner, N.; Lozano, P.C. The role of upstream distal electrodes in mitigating electrochemical degradation of ionic liquid ion sources. Appl. Phys. Lett. 2012, 101, 193504. [Google Scholar] [CrossRef]
- Lozano, P.; Martínez-Sánchez, M. Ionic liquid ion sources: Suppression of electrochemical reactions using voltage alternation. J. Colloid Interface Sci. 2004, 280, 149–154. [Google Scholar] [CrossRef]
- Wright, P.L.; Thuppul, A.; Wirz, R.E. Life-Limiting Emission Modes for Electrospray Thrusters. In Proceedings of the 54th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 9–11 July 2018; pp. 1–9. [Google Scholar] [CrossRef]
- Rosell-Llompart, J.; Grifoll, J.; Loscertales, I.G. Electrosprays in the cone-jet mode: From Taylor cone formation to spray development. J. Aerosol Sci. 2018. [Google Scholar] [CrossRef]
- Barrios-Collado, C.; Vidal-de Miguel, G.; Sinues, P.M.L. Numerical modeling and experimental validation of a universal secondary electrospray ionization source for mass spectrometric gas analysis in real-time. Sens. Actuators B Chem. 2016, 223, 217–225. [Google Scholar] [CrossRef]
- Lozano, P.; Martínez-Sánchez, M. Studies on the Ion-Droplet Mixed Regime in Colloid Thrusters. Ph.D. Thesis, Department of Aeronautics and Astronautics, Massachusetts Institute of Technology, Cambridge, MA, USA, 2003. [Google Scholar]
- Konermann, L.; Metwally, H.; McAllister, R.G.; Popa, V. How to run molecular dynamics simulations on electrospray droplets and gas phase proteins: Basic guidelines and selected applications. Methods 2018, 144, 104–112. [Google Scholar] [CrossRef]
- Borner, A.; Li, Z.; Levin, D.A. Prediction of fundamental properties of ionic liquid electrospray thrusters using molecular dynamics. J. Phys. Chem. B 2013, 117, 6768–6781. [Google Scholar] [CrossRef] [PubMed]
- Mehta, N.A.; Levin, D.A. Electrospray molecular dynamics simulations using an octree-based Coulomb interaction method. Phys. Rev. E 2019, 99, 033302. [Google Scholar] [CrossRef] [PubMed]
- Daily, J.W.; Micci, M.M. Ionic velocities in an ionic liquid under high electric fields using all-atom and coarse-grained force field molecular dynamics. J. Chem. Phys. 2009, 131, 094501. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.Y.; Micci, M.M. Molecular dynamics simulations of a liquid gallium electrospray thruster. J. Propuls. Power 2013, 29, 899–905. [Google Scholar] [CrossRef]
- Gamero-Castano, M.; Fernandez De La Mora, J. Direct measurement of ion evaporation kinetics from electrified liquid surfaces. J. Chem. Phys. 2000, 113, 815–832. [Google Scholar] [CrossRef]
- Gamero-Castaño, M. The structure of electrospray beams in vacuum. J. Fluid Mech. 2008, 604, 339. [Google Scholar] [CrossRef]
- Grifoll, J.; Rosell-Llompart, J. Continuous droplets’ charge method for the Lagrangian simulation of electrostatic sprays. J. Electr. 2014, 72, 357–364. [Google Scholar] [CrossRef]
- Davis, M.; Collins, A.L.; Wirz, R.E. Electrospray Plume Evolution Via Discrete Simulations. In Proceedings of the 36th International Electric Propulsion Conference, IEPC-2019, Vienna, Austria, 15–20 September 2019; Volume 590. [Google Scholar]
- Gamero-Castaño, M. Characterization of the electrosprays of 1-ethyl-3-methylimidazolium bis (trifluoromethylsulfonyl) imide in vacuum. Phys. Fluids 2008, 20, 032103. [Google Scholar] [CrossRef]
- Demmons, N.; Hruby, V.; Spence, D.; Roy, T.; Ehrbar, E.; Zwahlen, J.; Martin, R.; Ziemer, J.; Randolph, T. ST7-DRS mission colloid thruster development. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; pp. 1–18. [Google Scholar] [CrossRef]
- Thuppul, A.; Collins, A.L.; Wright, P.L.; Uchizono, N.M.; Wirz, R.E. Spatially-Resolved Mass Flux and Current Measurements of Electrospray Plumes. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019; pp. 1–10. [Google Scholar]
- De La Mora, J.F.; Loscertales, I.G. The current emitted by highly conducting Taylor cones. J. Fluid Mech. 1994, 260, 155–184. [Google Scholar] [CrossRef]
- Fernández de La Mora, J. The fluid dynamics of Taylor cones. Ann. Rev. Fluid Mech. 2007, 39, 217–243. [Google Scholar] [CrossRef]
- Demmons, N.R.; Hruby, V.J.; Courtney, D.; Ziemer, J.K.; Marrese-Reading, C. Ground and On-Orbit Thruster Performance Comparison for the Lisa Pathfinder Colloid MicroNewton Thrusters. In Proceedings of the 2018 Joint Propulsion Conference, Cincinnati, OH, USA, 9–11 July 2018; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2018; pp. 1–15. [Google Scholar] [CrossRef]
- Courtney, D.G.; Dandavino, S.; Shea, H. Comparing direct and indirect thrust measurements from passively fed ionic electrospray thrusters. J. Propuls. Power 2015, 32, 392–407. [Google Scholar] [CrossRef]
- Wirz, R.E.; Katz, I.; Goebel, D.M.; Anderson, J.R. Electron Backstreaming Determination for Ion Thrusters. J. Propuls. Power 2011, 27, 206–210. [Google Scholar] [CrossRef]
- Ryan, C.; Daykin-Iliopoulos, A.; Stark, J.; Salaverri, A.; Vargas, E.; Rangsten, P.; Dandavino, S.; Ataman, C.; Chakraborty, S.; Courtney, D.; et al. Experimental progress towards the MicroThrust MEMS electrospray electric propulsion system. In Proceedings of the 33rd International Electric Propulstion Conference, Washington, DC, USA, 6–10 October 2013. [Google Scholar]
- Prince, B.D.; Fritz, B.A.; Chiu, Y.H. Ionic liquids in electrospray propulsion systems. In Ionic Liquids: Science and Applications; ACS Publications: Washington, DC, USA, 2012; pp. 27–49. [Google Scholar] [CrossRef]
- Miller, S.W.; Prince, B.D.; Bemish, R.J.; Rovey, J.L. Electrospray of 1-Butyl-3-Methylimidazolium Dicyanamide Under Variable Flow Rate Operations. J. Propuls. Power 2014, 30, 1701–1710. [Google Scholar] [CrossRef]
- Ma, C.; Ryan, C.N. The Design and Characterization of a Porous-emitter Electrospray Thruster (PET-100) for Interplanetary CubeSats. In Proceedings of the 7th Interplanetary CubeSat Workshop, Paris, France, 29–30 May 2018. [Google Scholar]
- Collins, A.L.; Thuppul, A.; Wright, P.L.; Uchizono, N.M.; Huh, H.; Davis, M.J.; Ziemer, J.K.; Demmons, N.R.; Wirz, R.E. Assessment of Grid Impingement for Electrospray Thruster Lifetime. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019; pp. 1–17. [Google Scholar]
- Thompson, J.W.; Eschelbach, J.W.; Wilburn, R.T.; Jorgenson, J.W. Investigation of electrospray ionization and electrostatic focusing devices using a three-dimensional electrospray current density profiler. J. Am. Soc. Mass Spectrom. 2005, 16, 312–323. [Google Scholar] [CrossRef] [PubMed]
- Chandrupatla, T.R. Quality and Reliability in Engineering; Cambridge University Press: New York, NY, USA, 2009; Volume 2. [Google Scholar]

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Thuppul, A.; Wright, P.L.; Collins, A.L.; Ziemer, J.K.; Wirz, R.E. Lifetime Considerations for Electrospray Thrusters. Aerospace 2020, 7, 108. https://doi.org/10.3390/aerospace7080108
Thuppul A, Wright PL, Collins AL, Ziemer JK, Wirz RE. Lifetime Considerations for Electrospray Thrusters. Aerospace. 2020; 7(8):108. https://doi.org/10.3390/aerospace7080108
Chicago/Turabian StyleThuppul, Anirudh, Peter L. Wright, Adam L. Collins, John K. Ziemer, and Richard E. Wirz. 2020. "Lifetime Considerations for Electrospray Thrusters" Aerospace 7, no. 8: 108. https://doi.org/10.3390/aerospace7080108
APA StyleThuppul, A., Wright, P. L., Collins, A. L., Ziemer, J. K., & Wirz, R. E. (2020). Lifetime Considerations for Electrospray Thrusters. Aerospace, 7(8), 108. https://doi.org/10.3390/aerospace7080108





