State-of-the-Art and Advancement Paths for Inductive Pulsed Plasma Thrusters
Abstract
1. Introduction
2. Review of Inductive Pulsed Plasma Thrusters
2.1. Open Magnetic Flux Thrusters
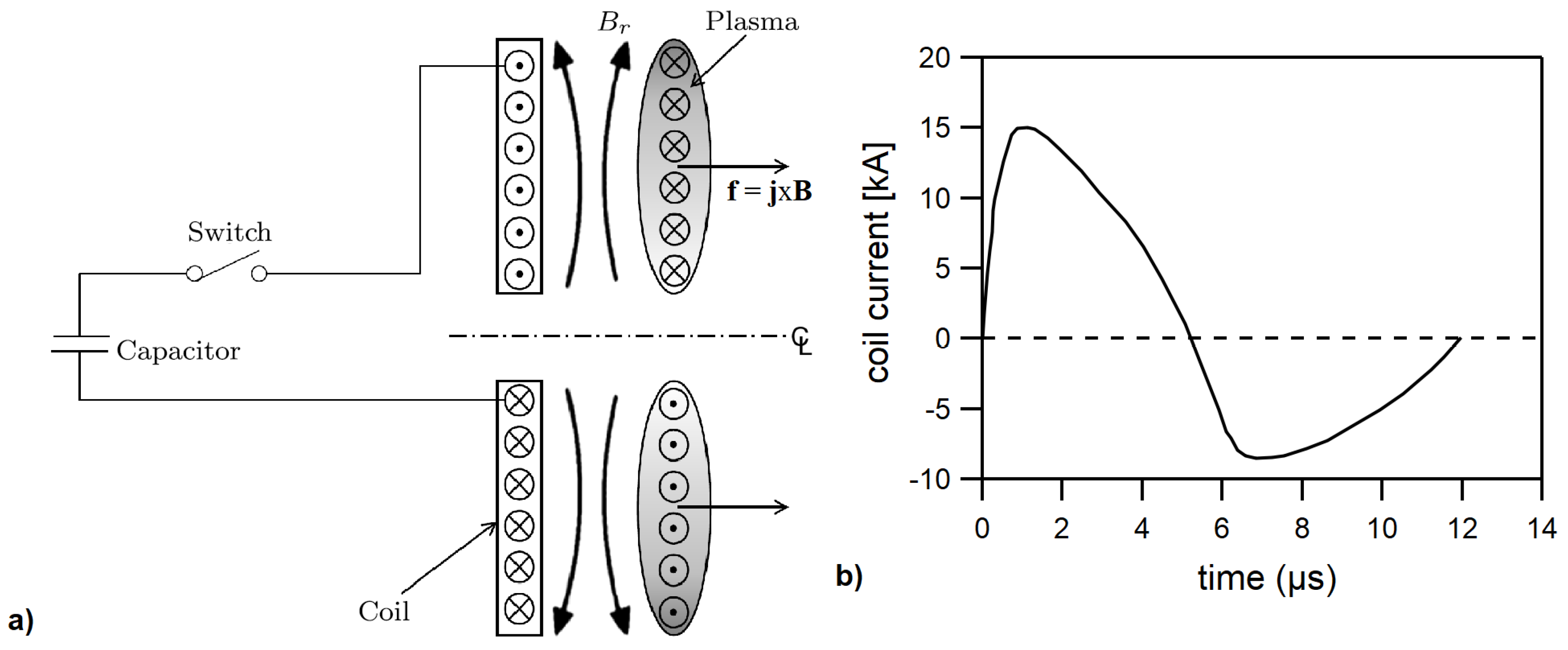
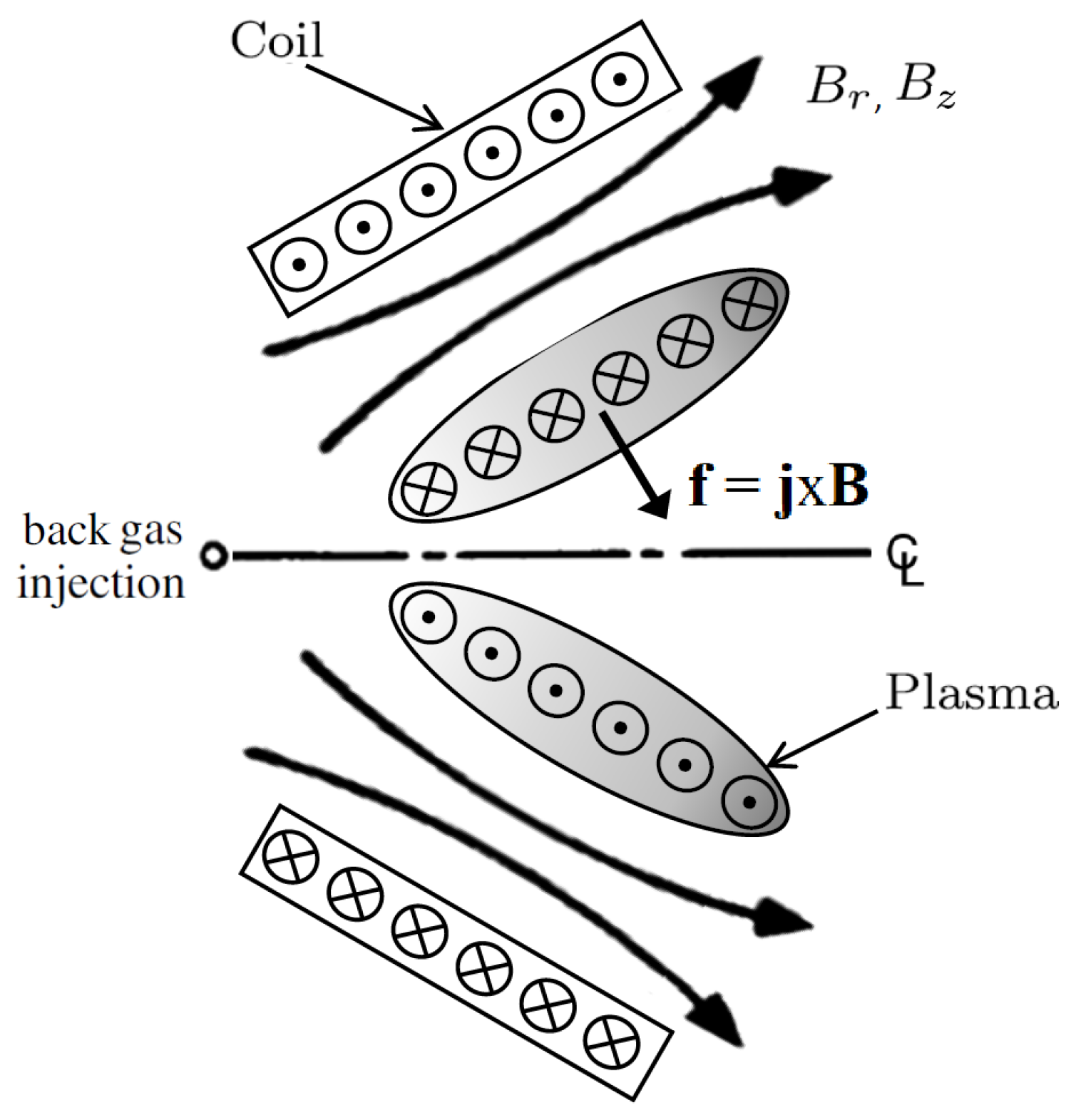
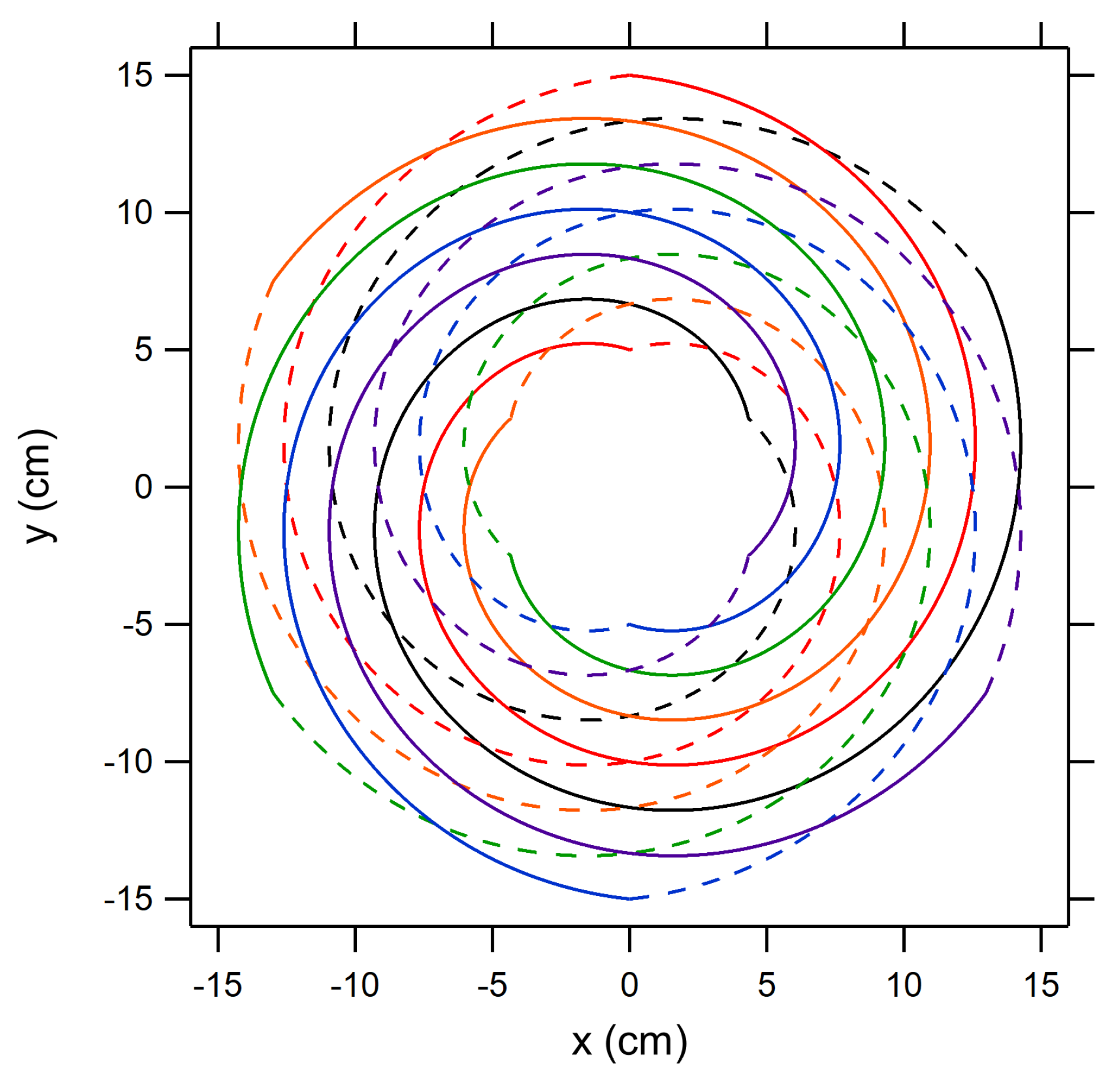
2.1.1. Planar Thrusters
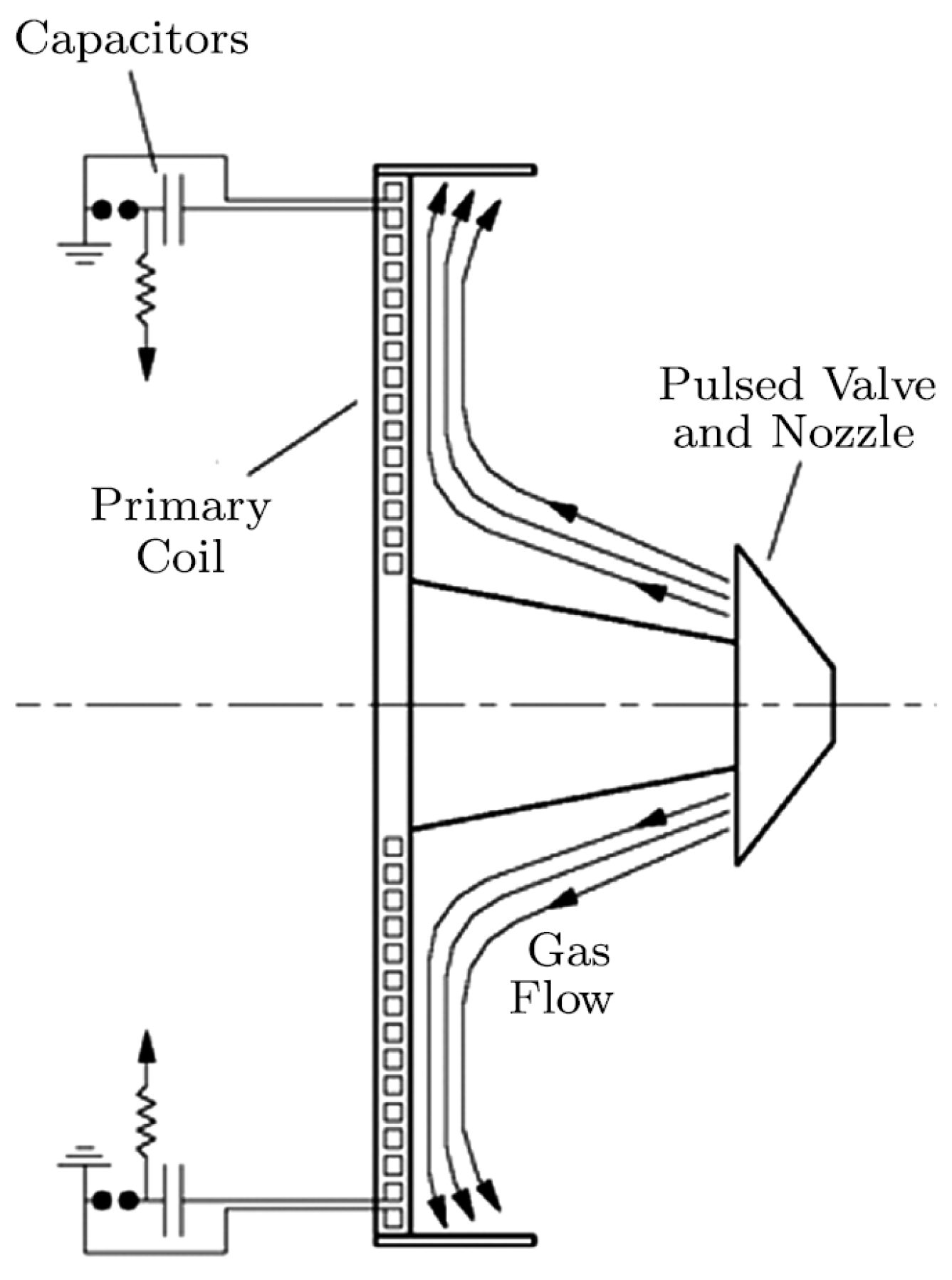
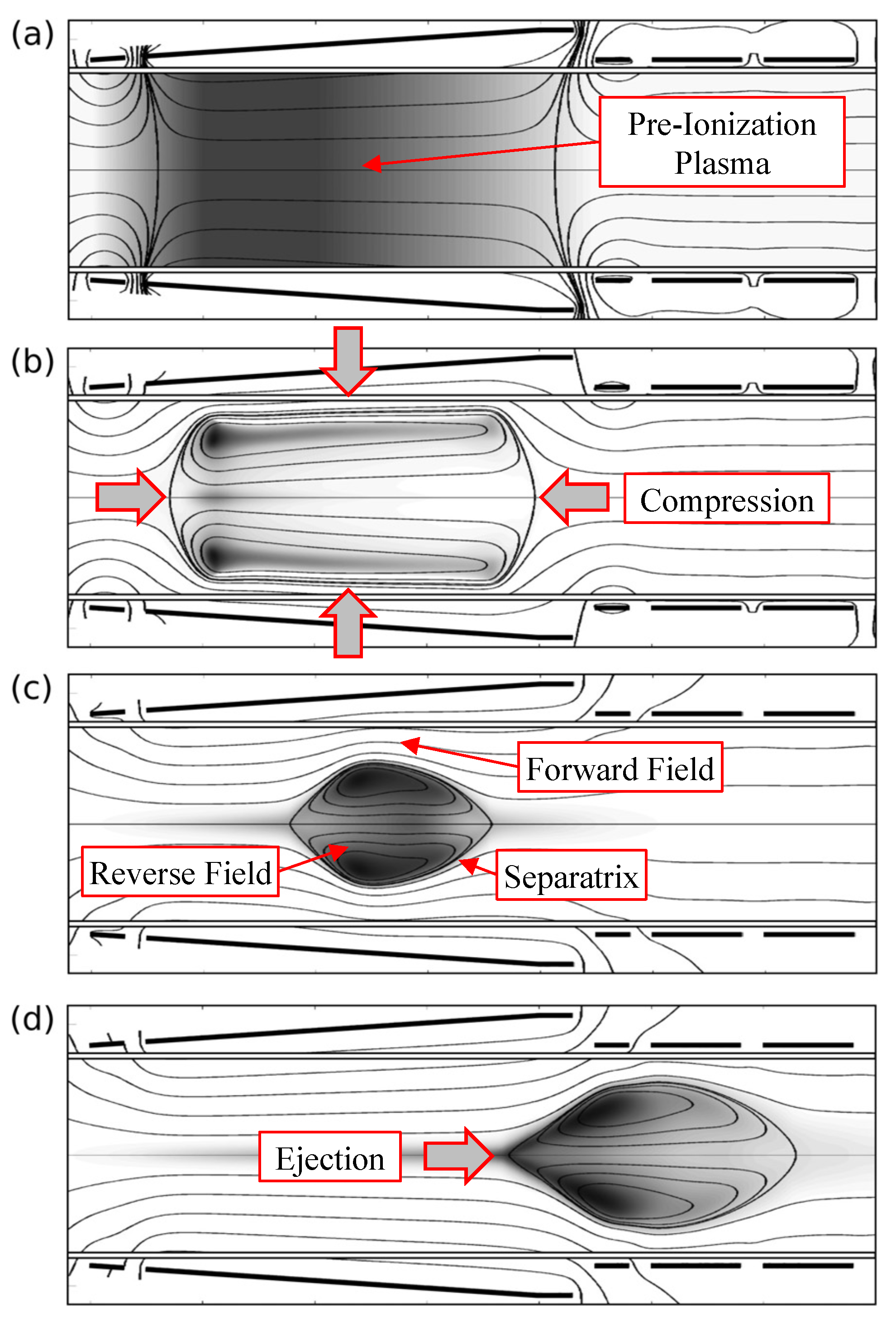
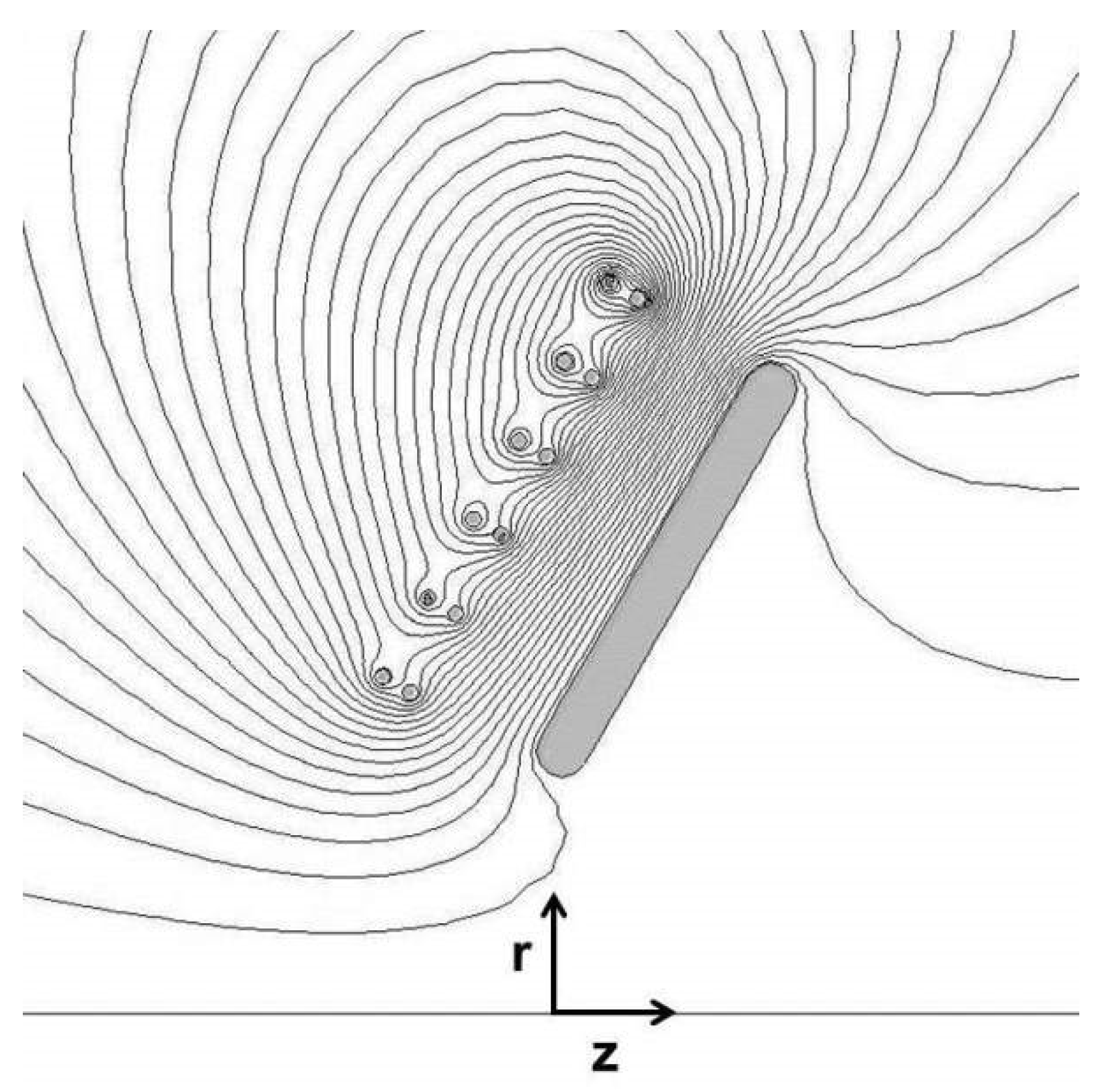
2.1.2. Conical Theta-Pinch Thrusters
2.2. Closed Magnetic Flux Thrusters
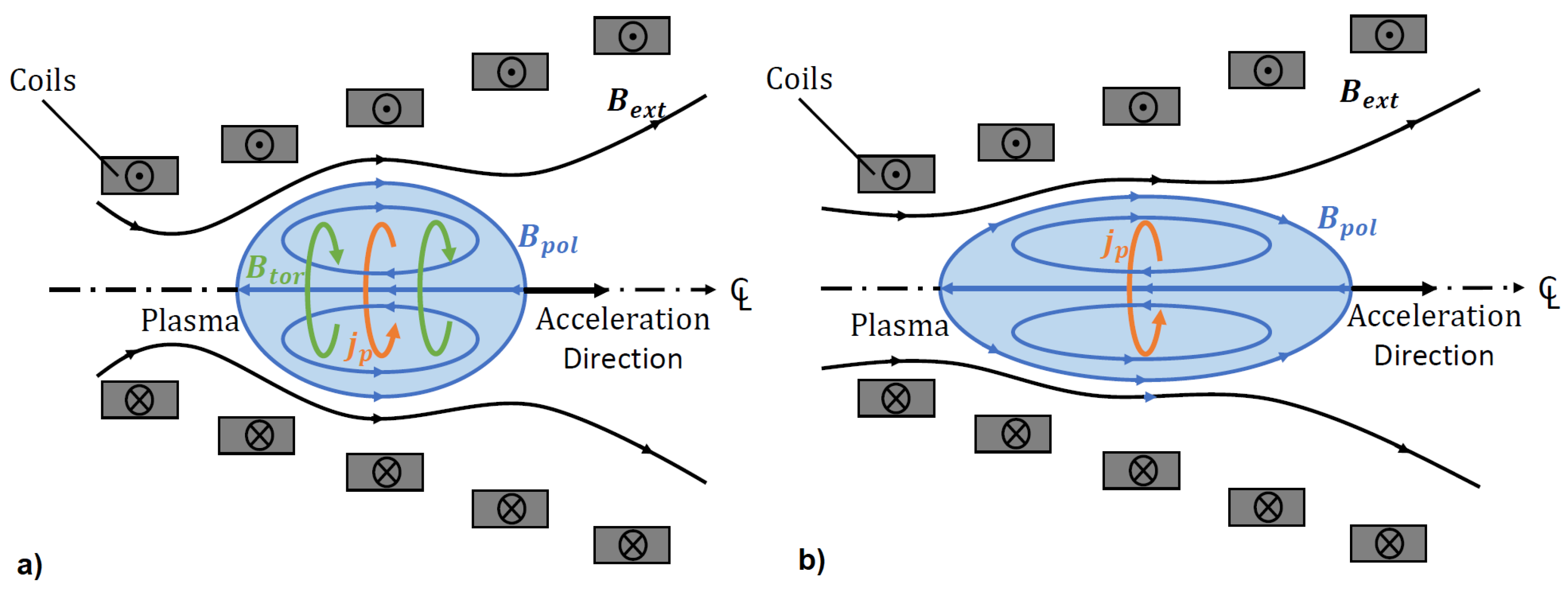
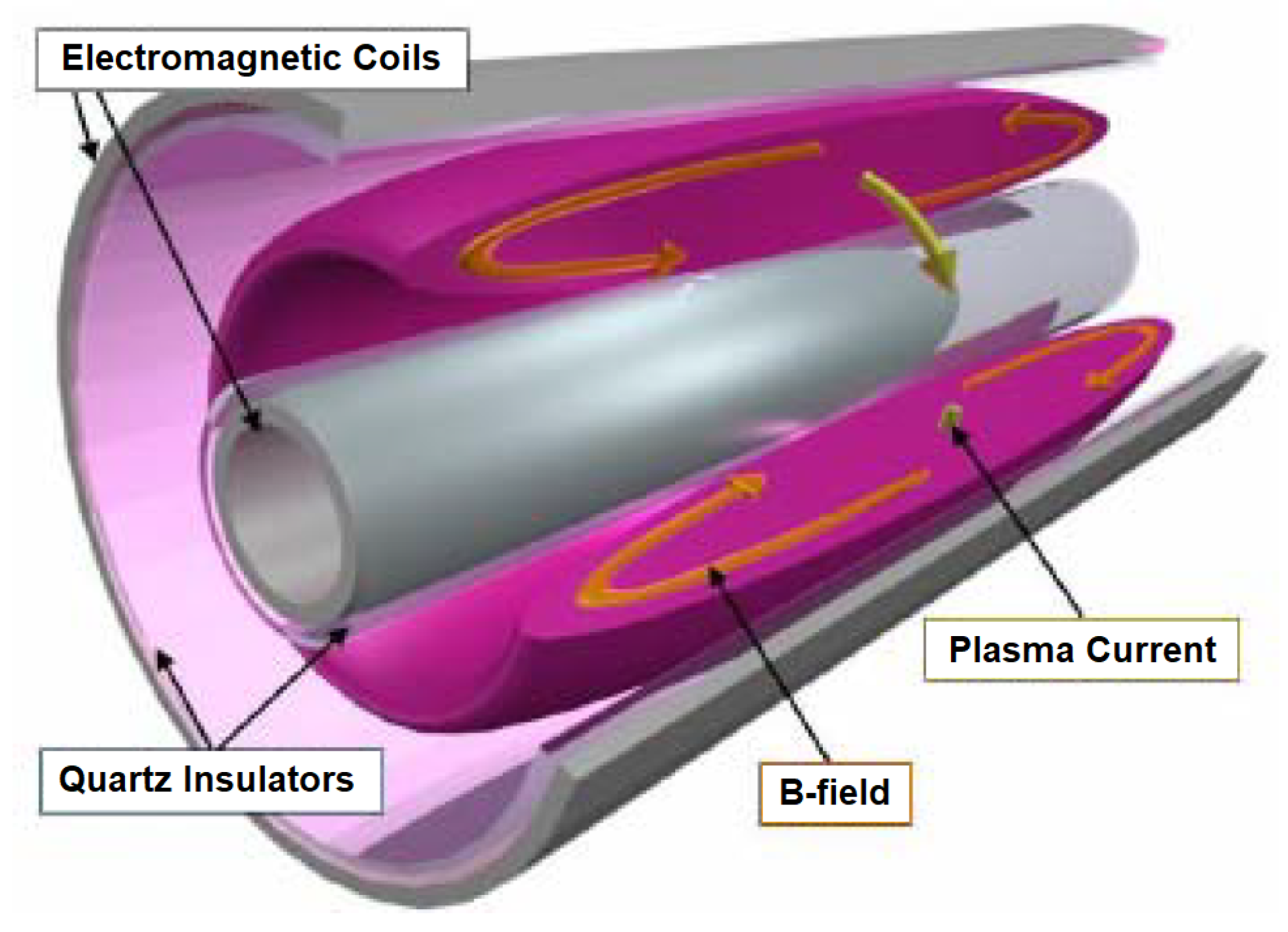
2.2.1. Field-Reversed Theta-Pinch FRCs
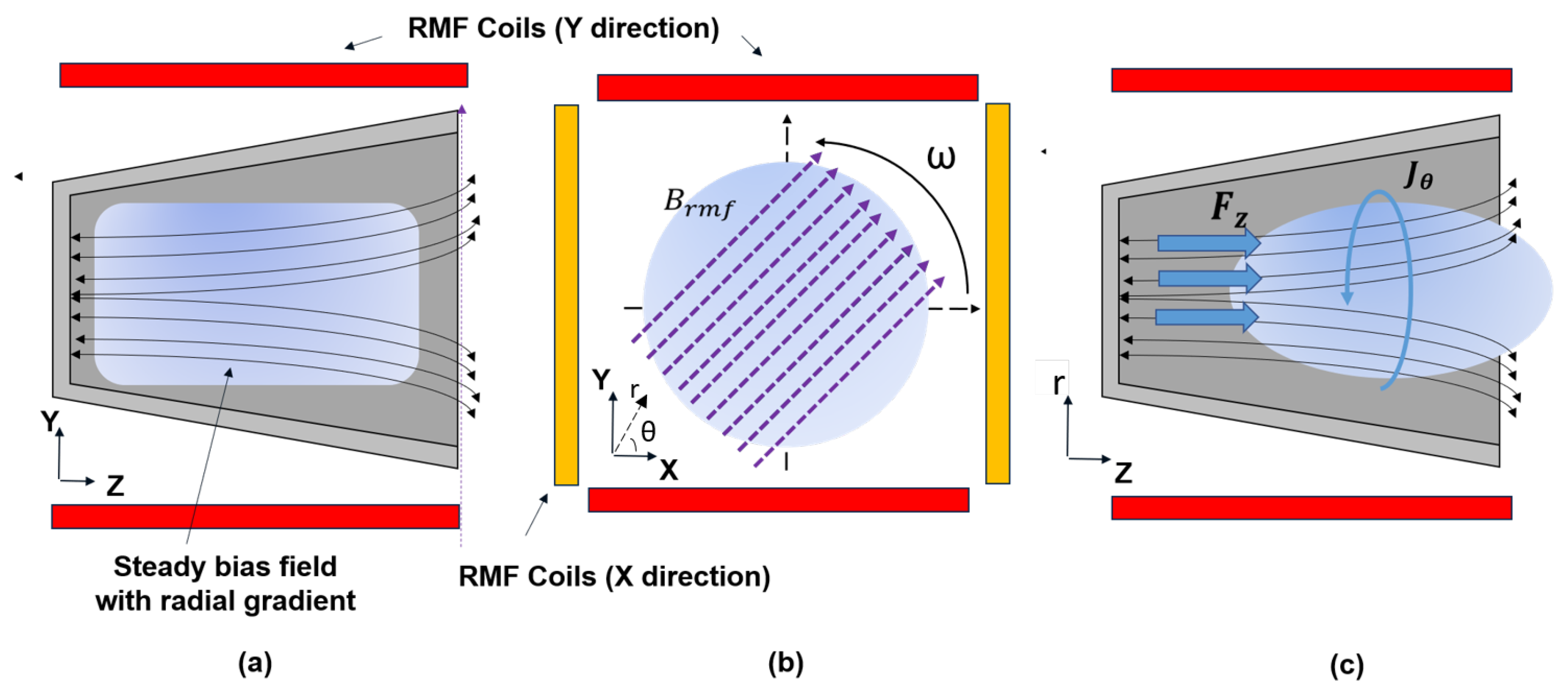
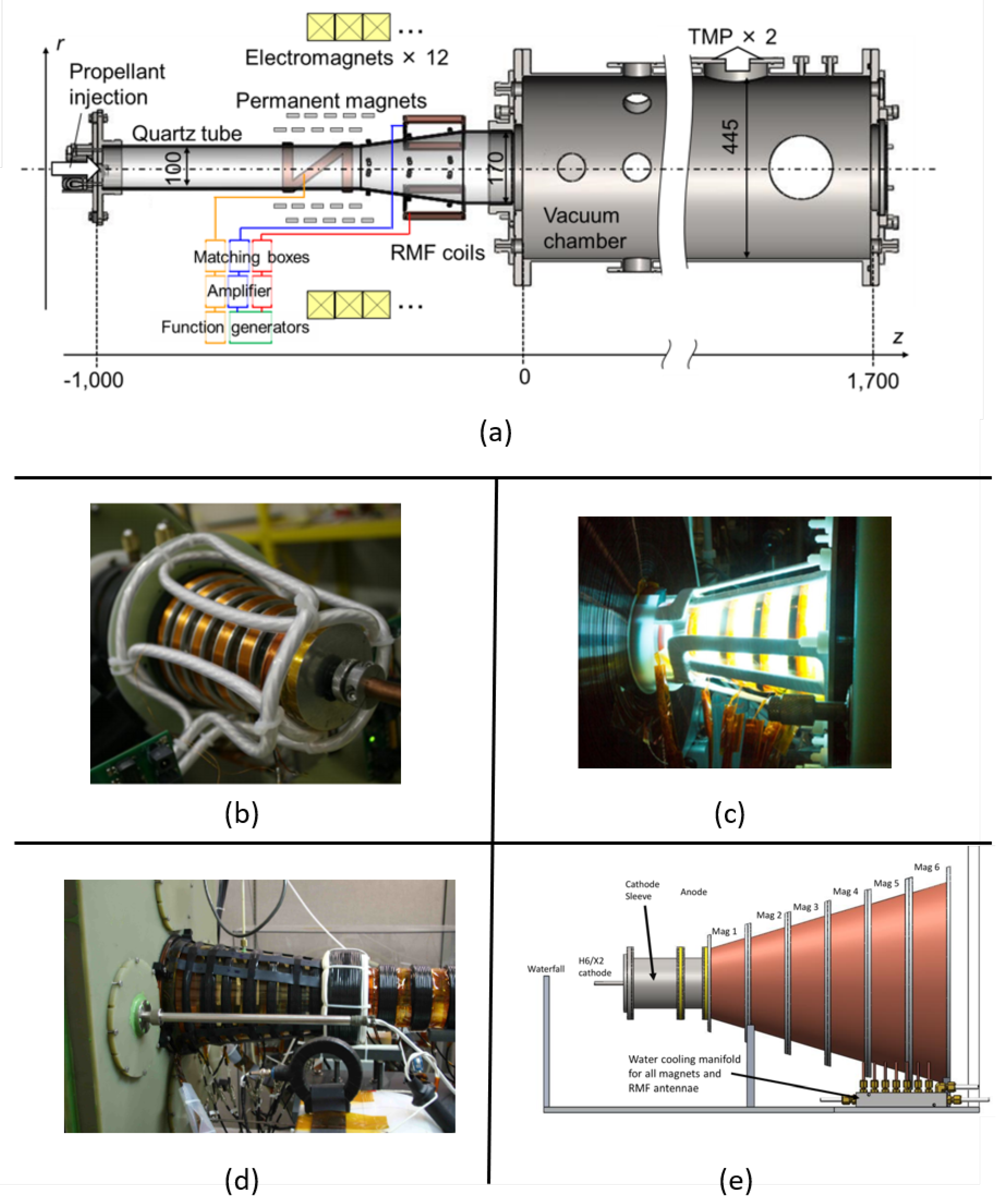
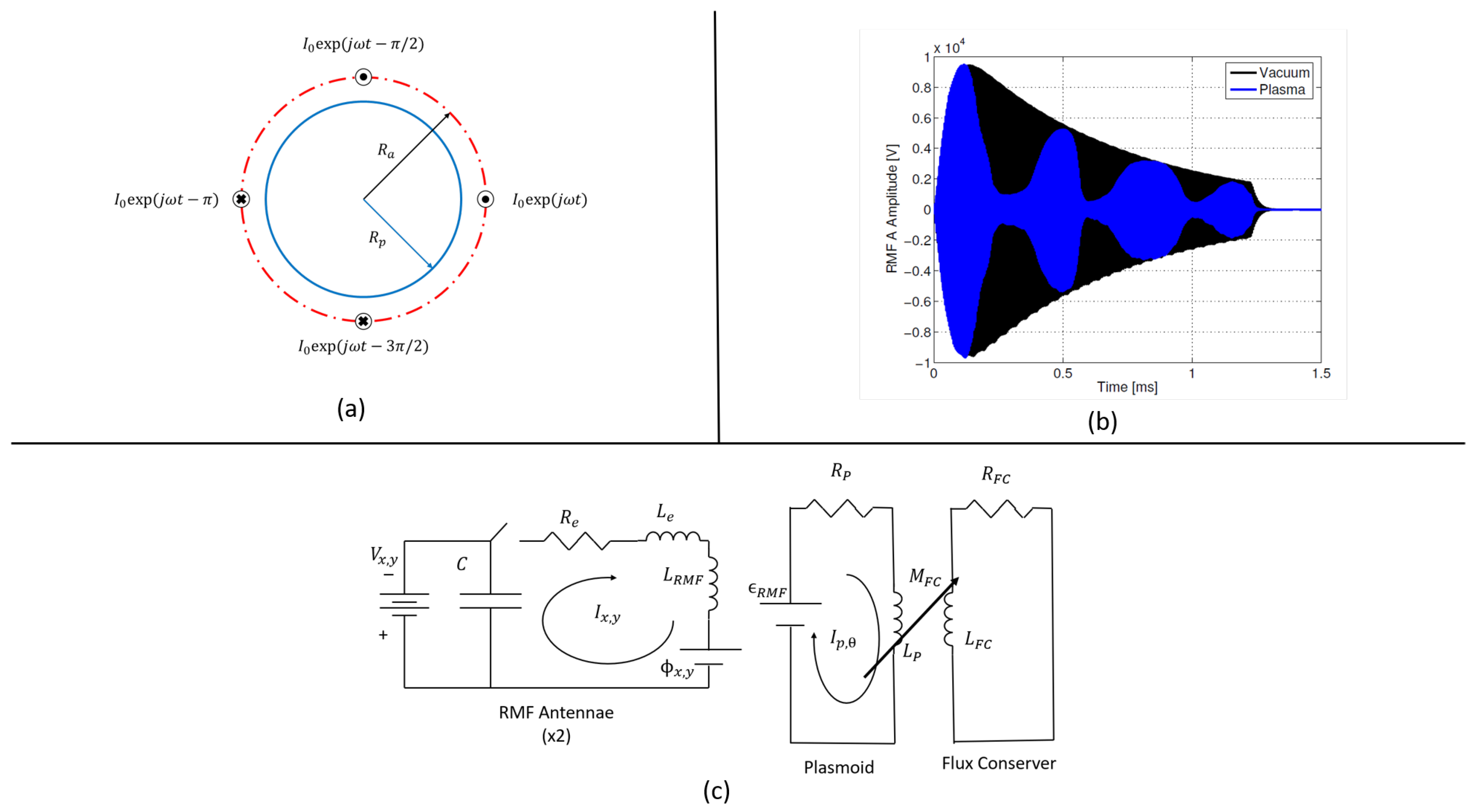
2.2.2. Rotating Magnetic Field FRC Thrusters
Principle of Operation
Review of RMF-FRC Test Articles
Technical Obstacles to Testing
2.2.3. Annular FRC Thrusters
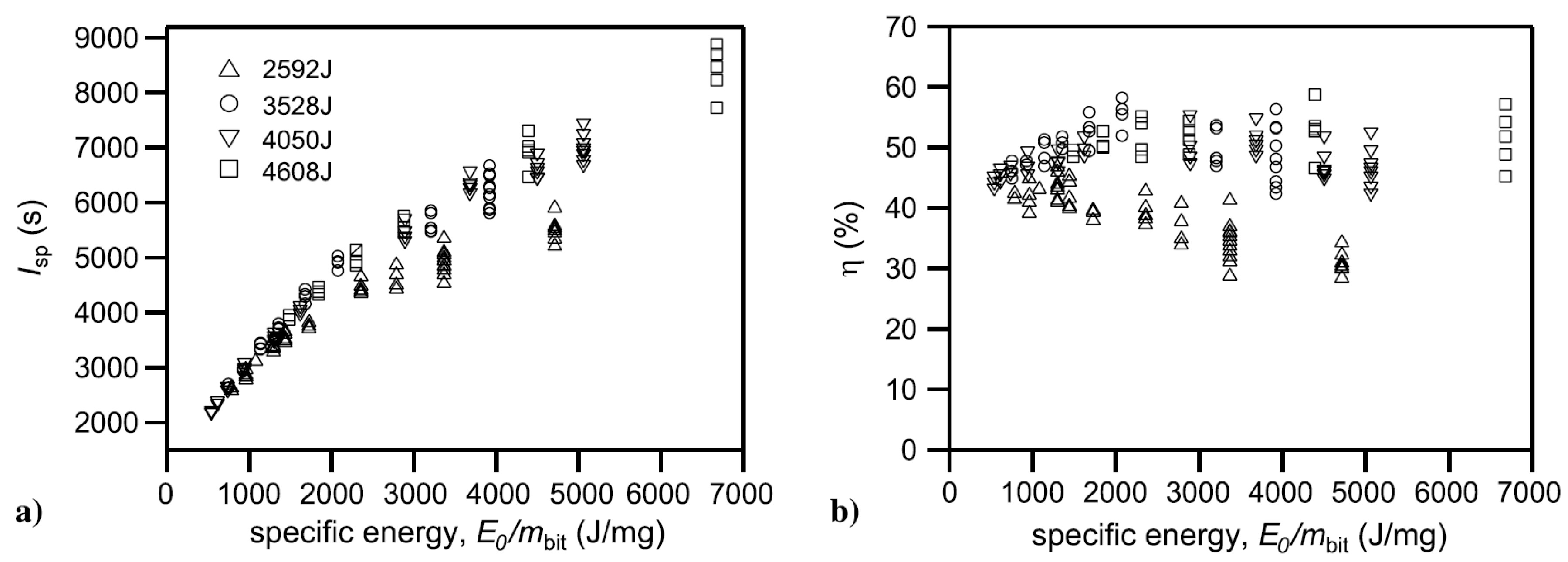
2.3. Summary of Experimental Data
3. Review of Modeling Techniques
3.1. Open Magnetic Flux Thrusters
3.1.1. Planar Thruster Modeling
3.1.2. Conical Theta-Pinch Thruster Modeling
3.2. Closed Magnetic Flux Thrusters
3.2.1. Thruster Scaling Laws
Efficiency from Energy Conservation
Performance Metrics from Asymptotic Analysis of Equivalent Circuits
Challenges in Deriving Scaling Laws
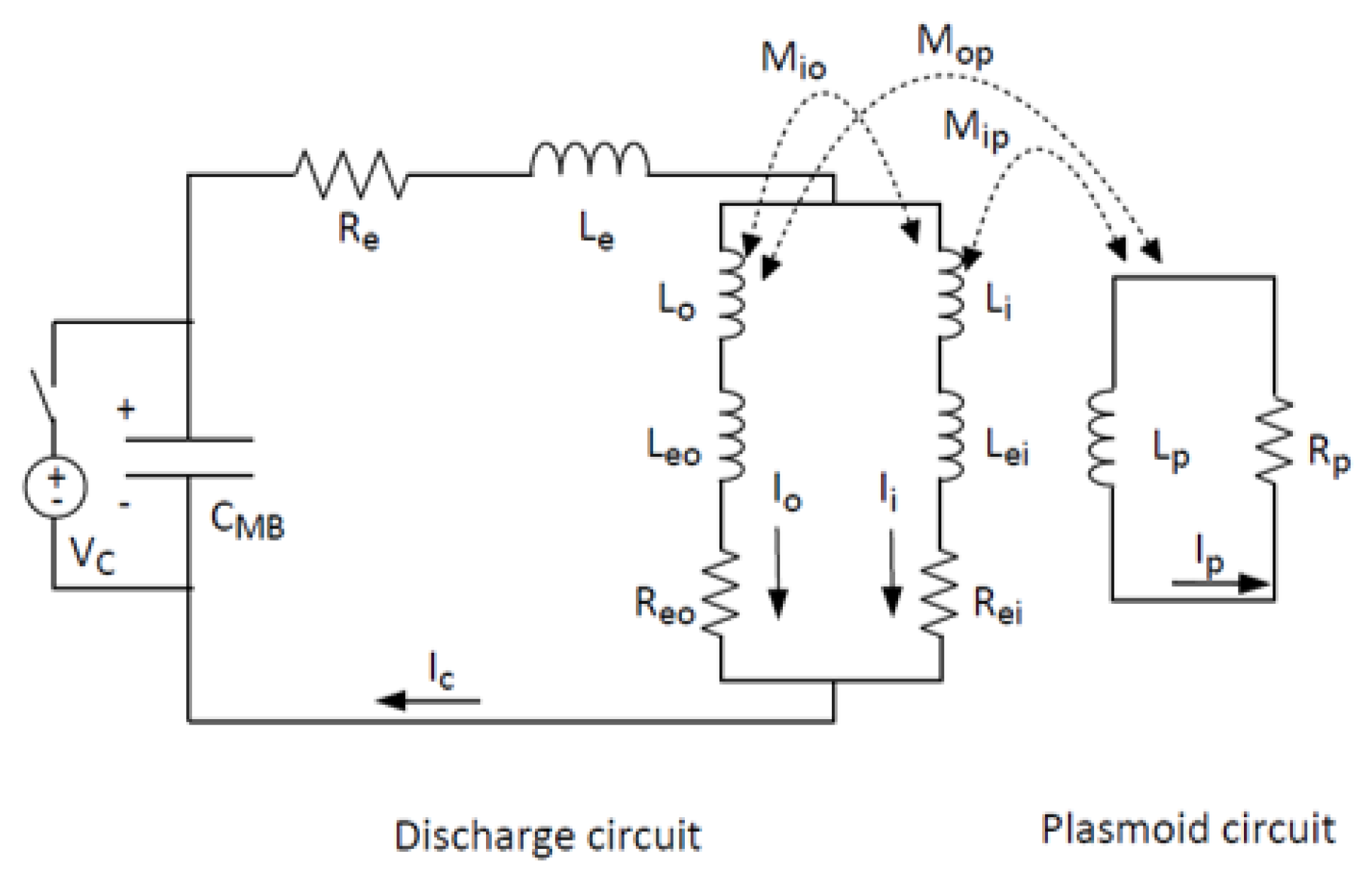
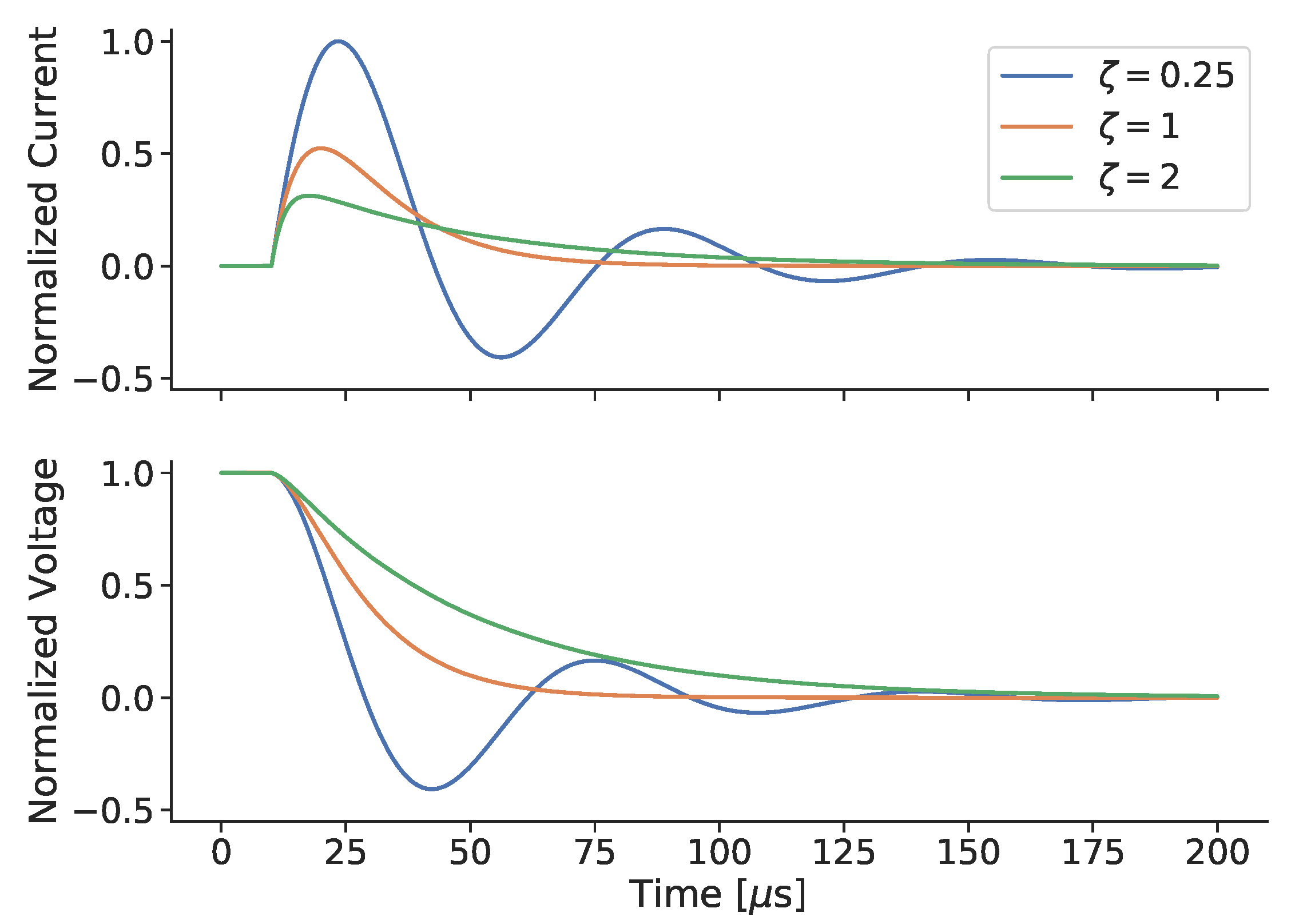
3.2.2. Equivalent Circuit Models
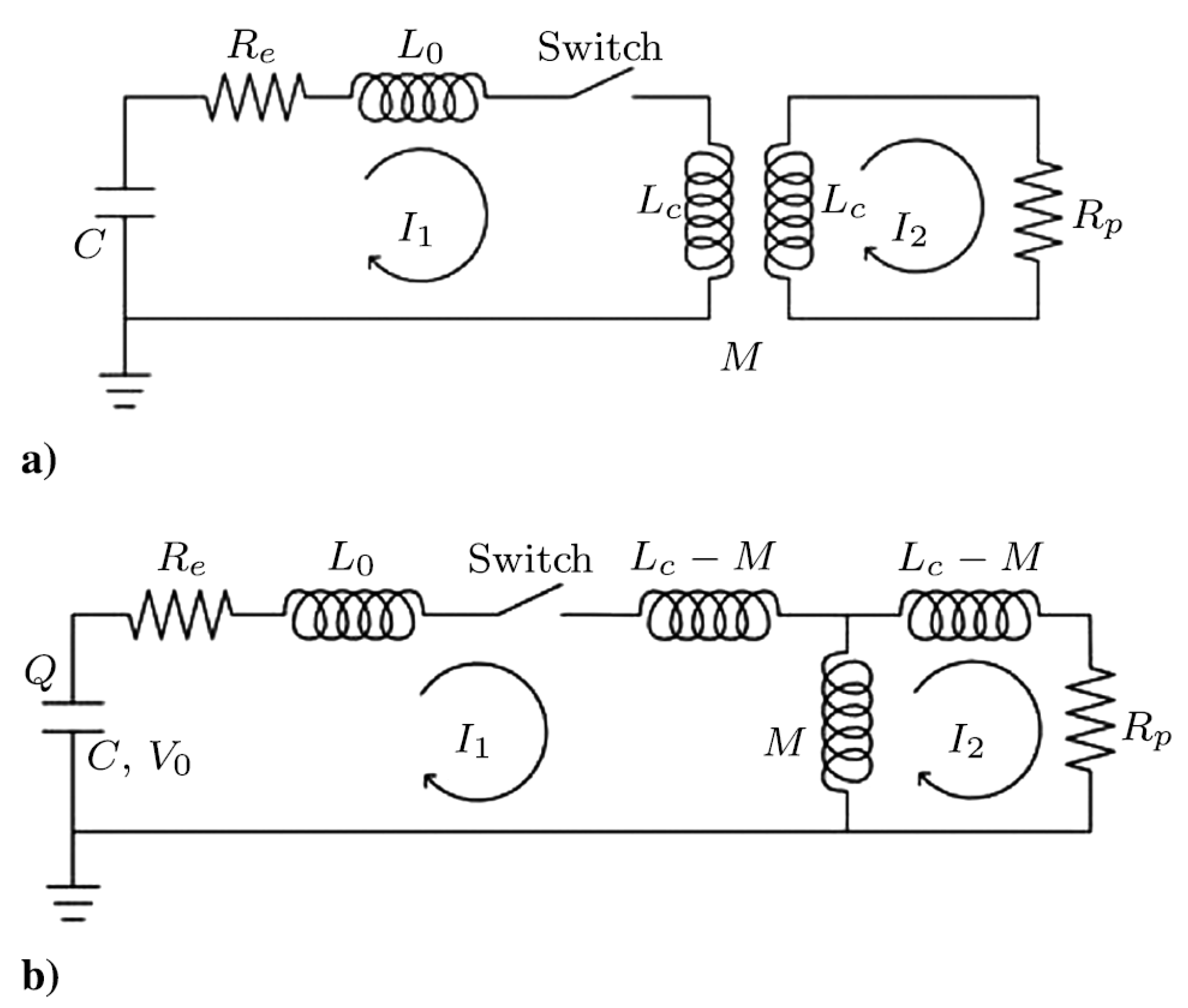
Equivalent Circuit Model for a Stationary Plasmoid
Calibrated Equivalent Circuit Model to Estimate Energy Deposition in FRC
Circuit Model for Second Stage Acceleration of an FRC Plasmoid
Equivalent Circuit Model for FRC Translation including RMF Coils
Equivalent Circuit Model for Annular FRC Translation
Challenges with Equivalent Circuit Modeling
3.2.3. High-Fidelity Models
Magnetohydrodynamic (MHD) Fluid Models
Two-Fluid Models
Kinetic Models
High Fidelity Modeling Challenges
4. Review of Major Subsystems
4.1. Power
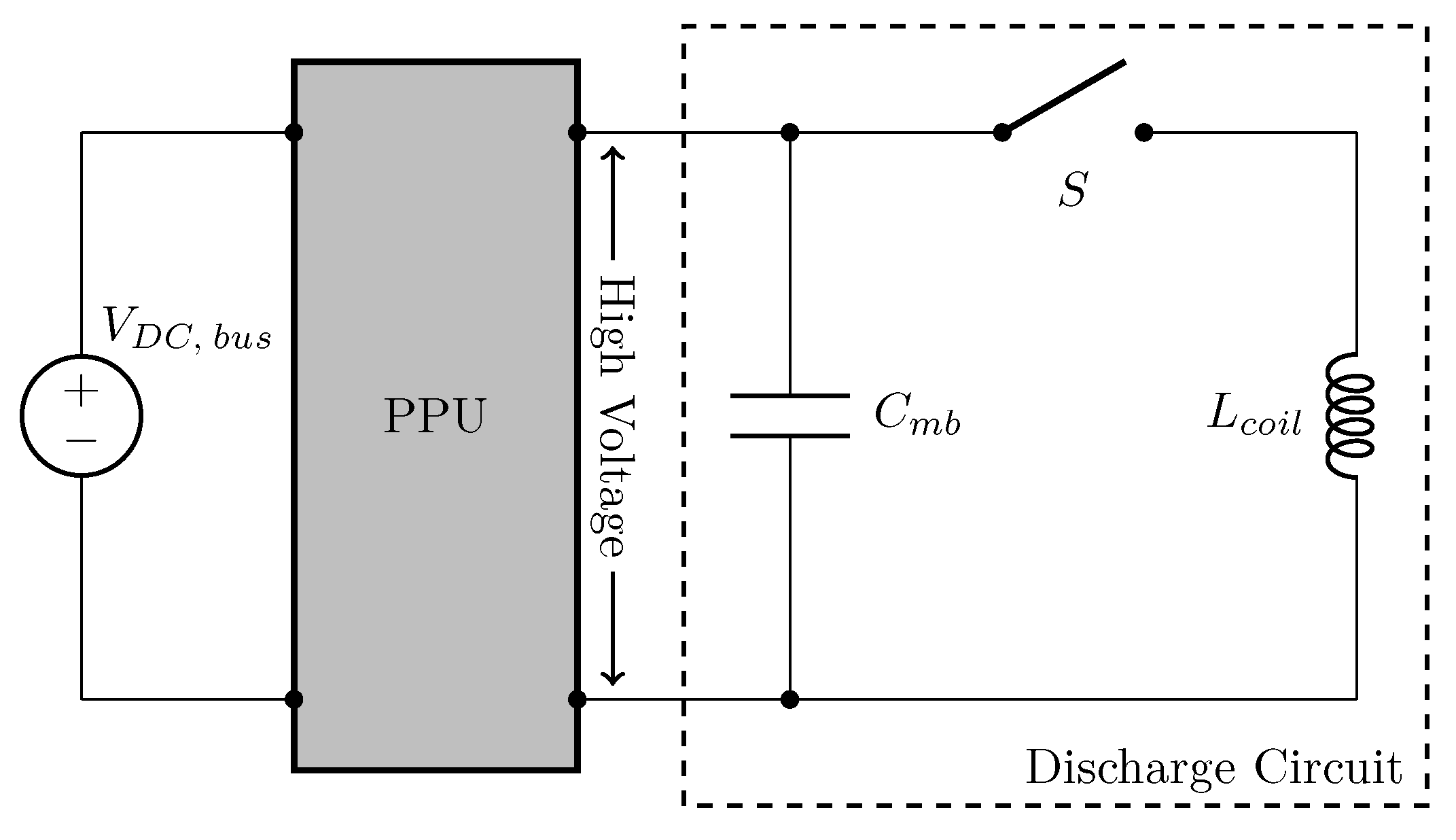
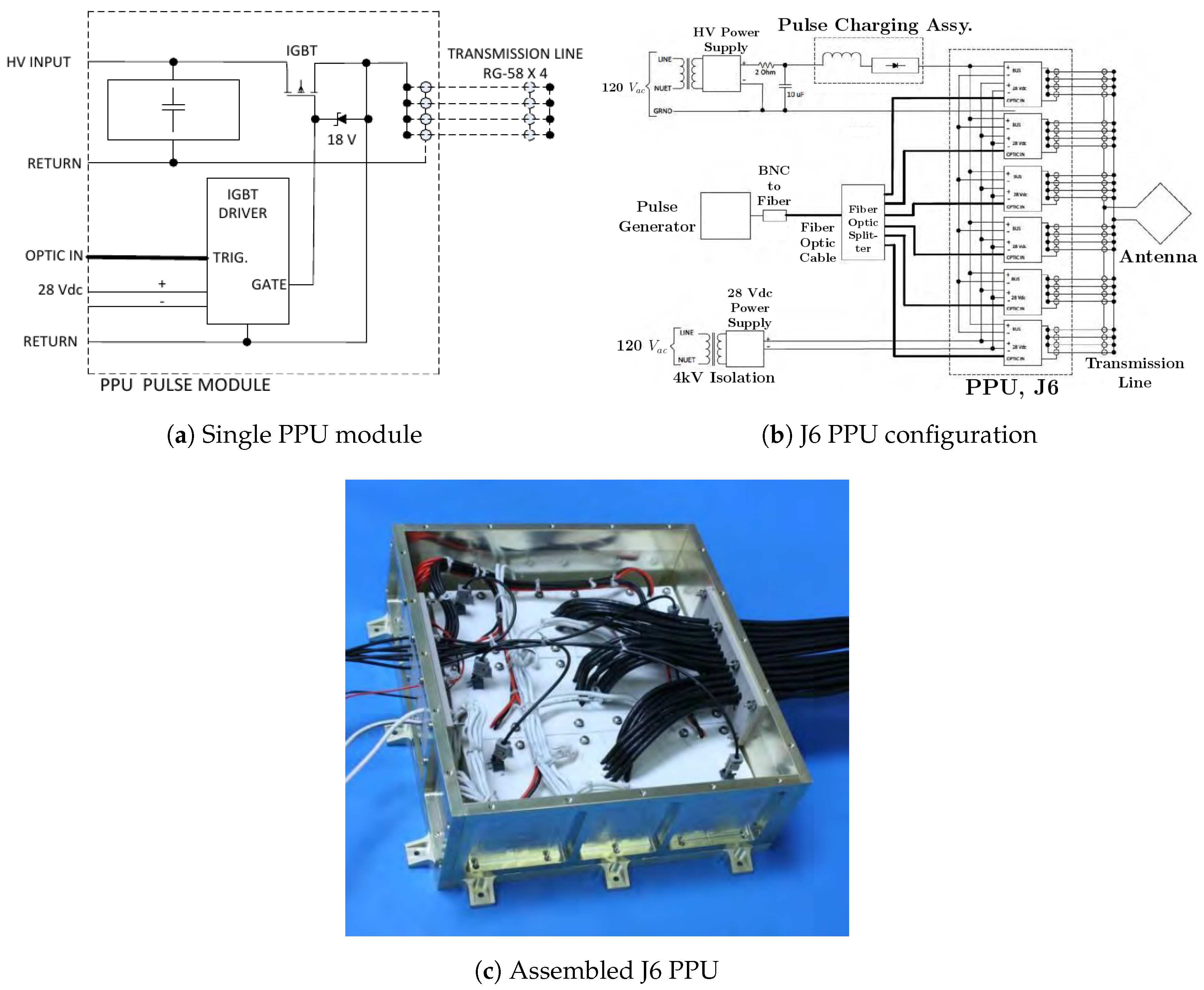
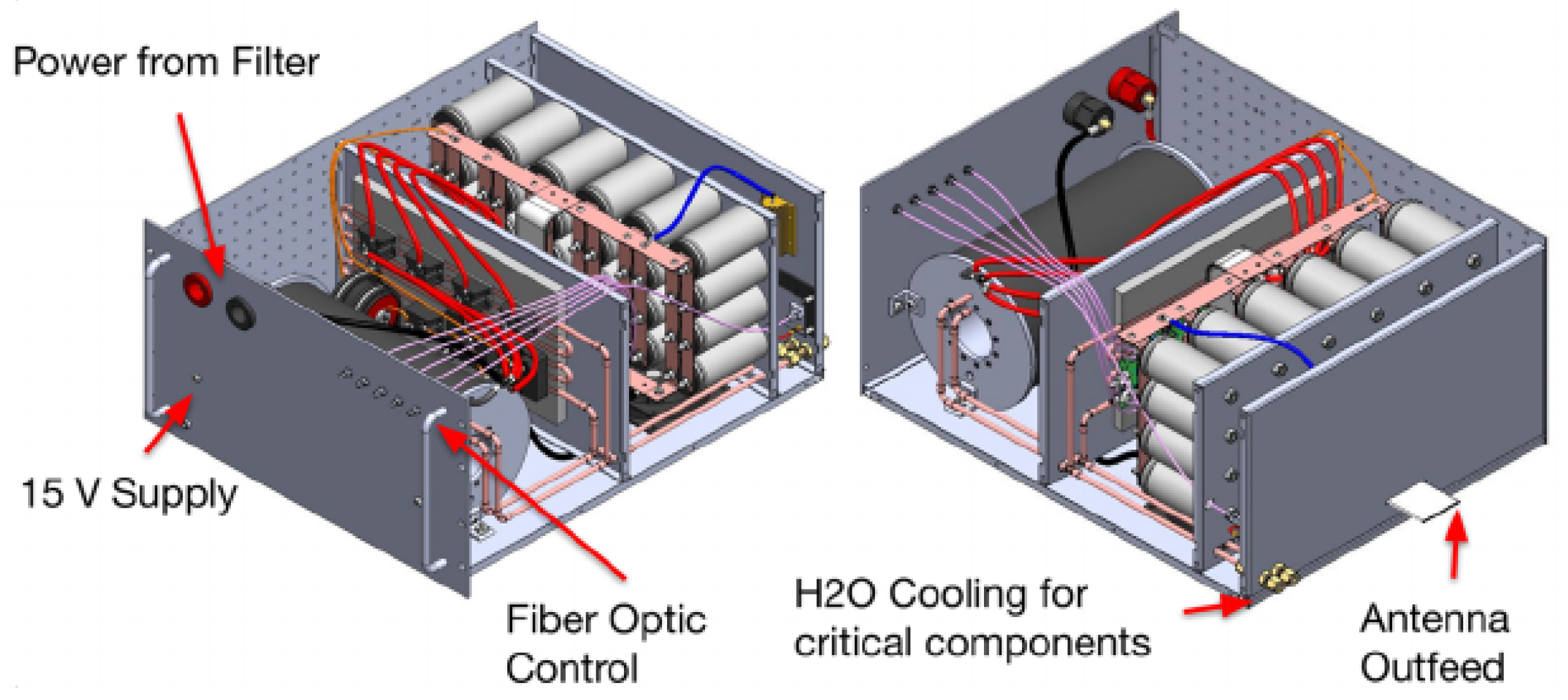
4.1.1. Power Processing Units
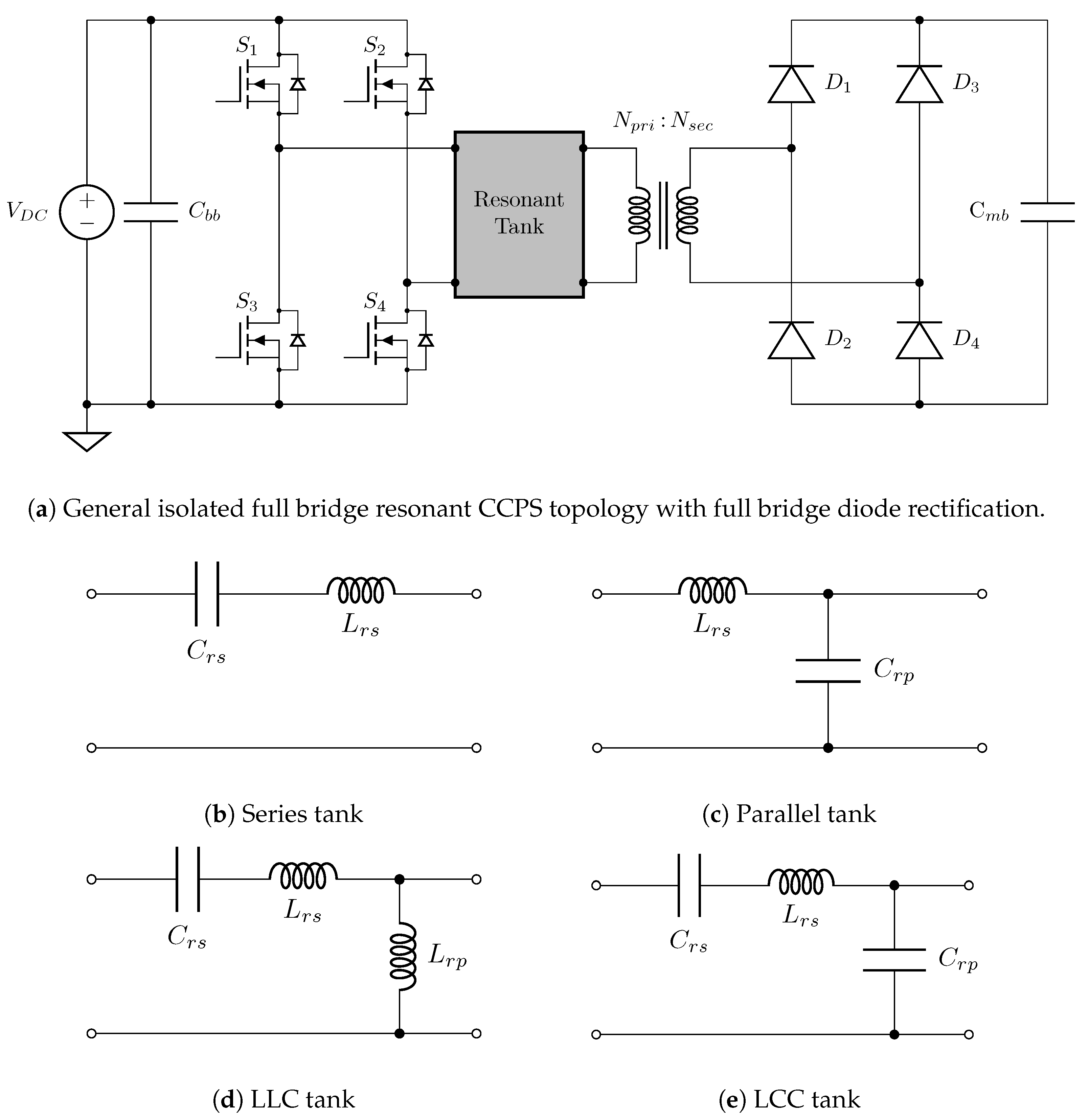
EMPT and ELF Thruster PPU
UM RMF-FRC PPU
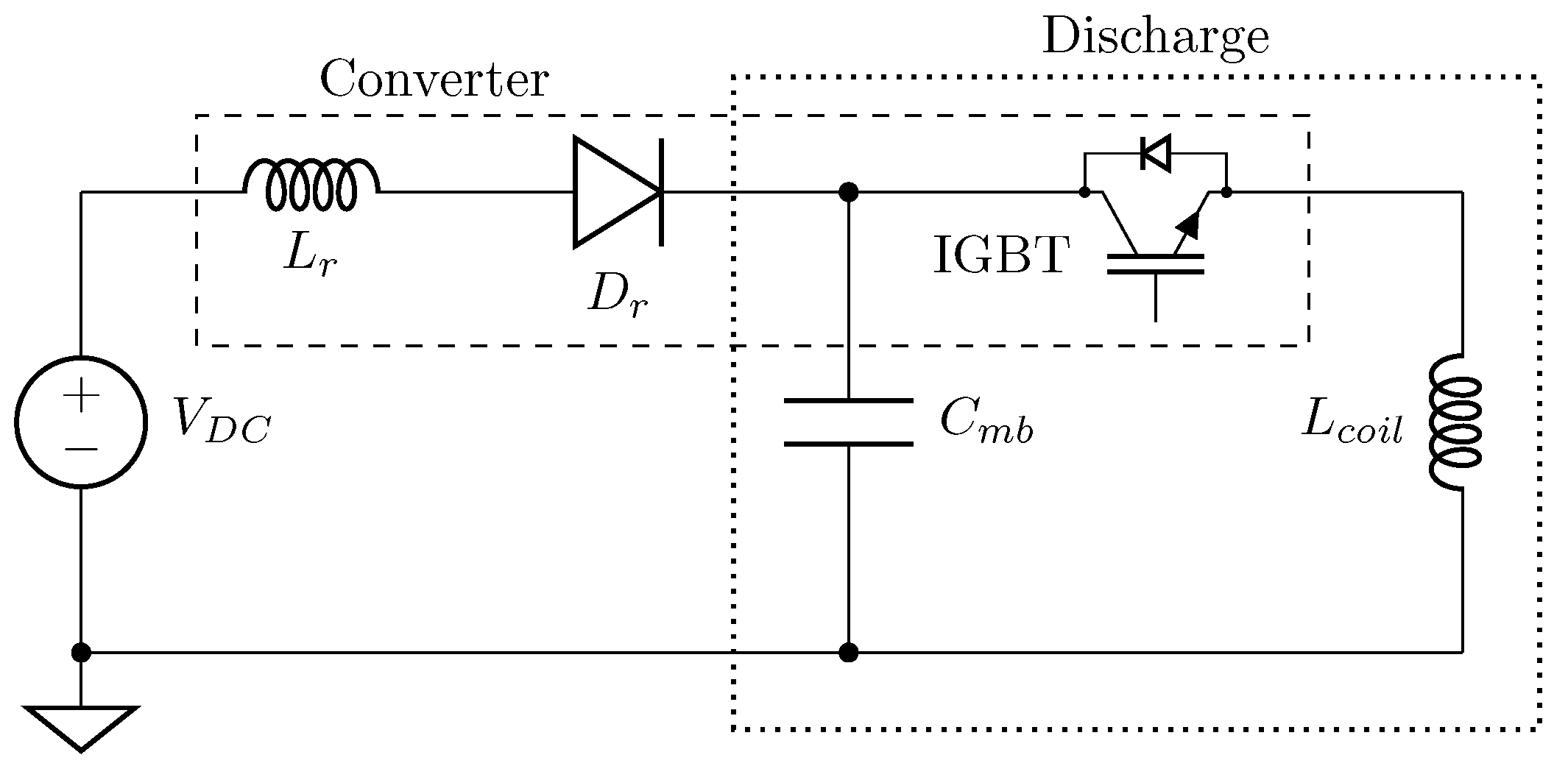
4.1.2. Discharge Circuit
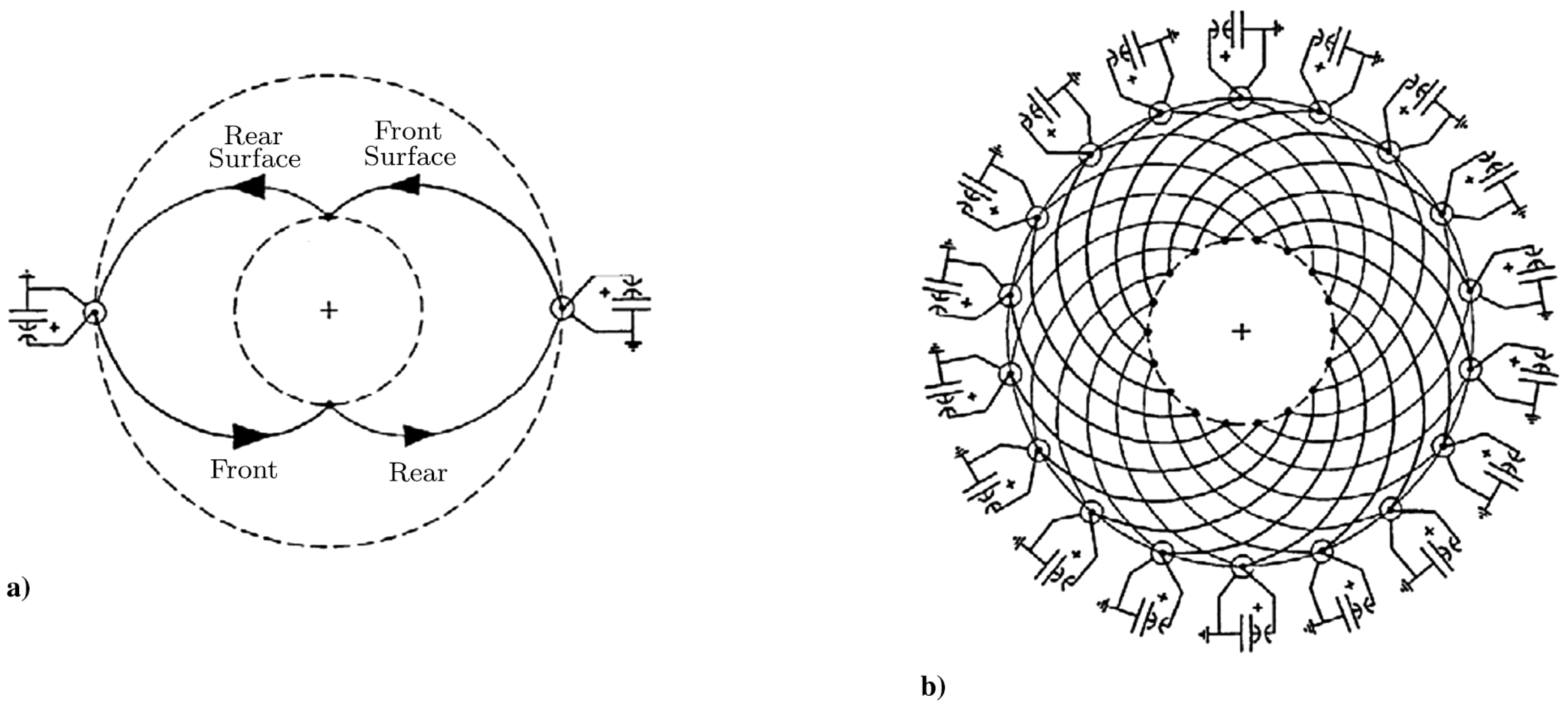
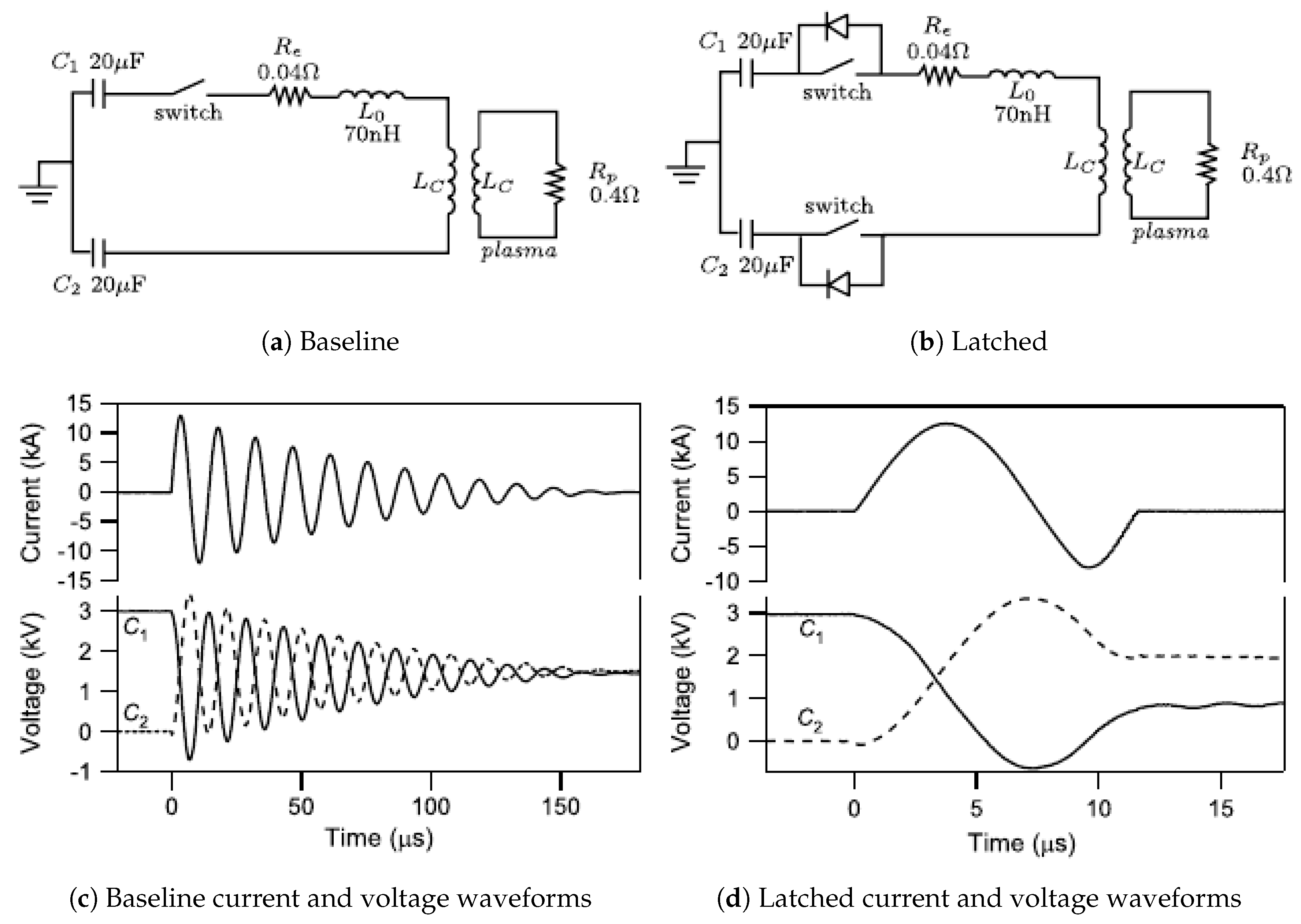
Discharge Circuit Topologies
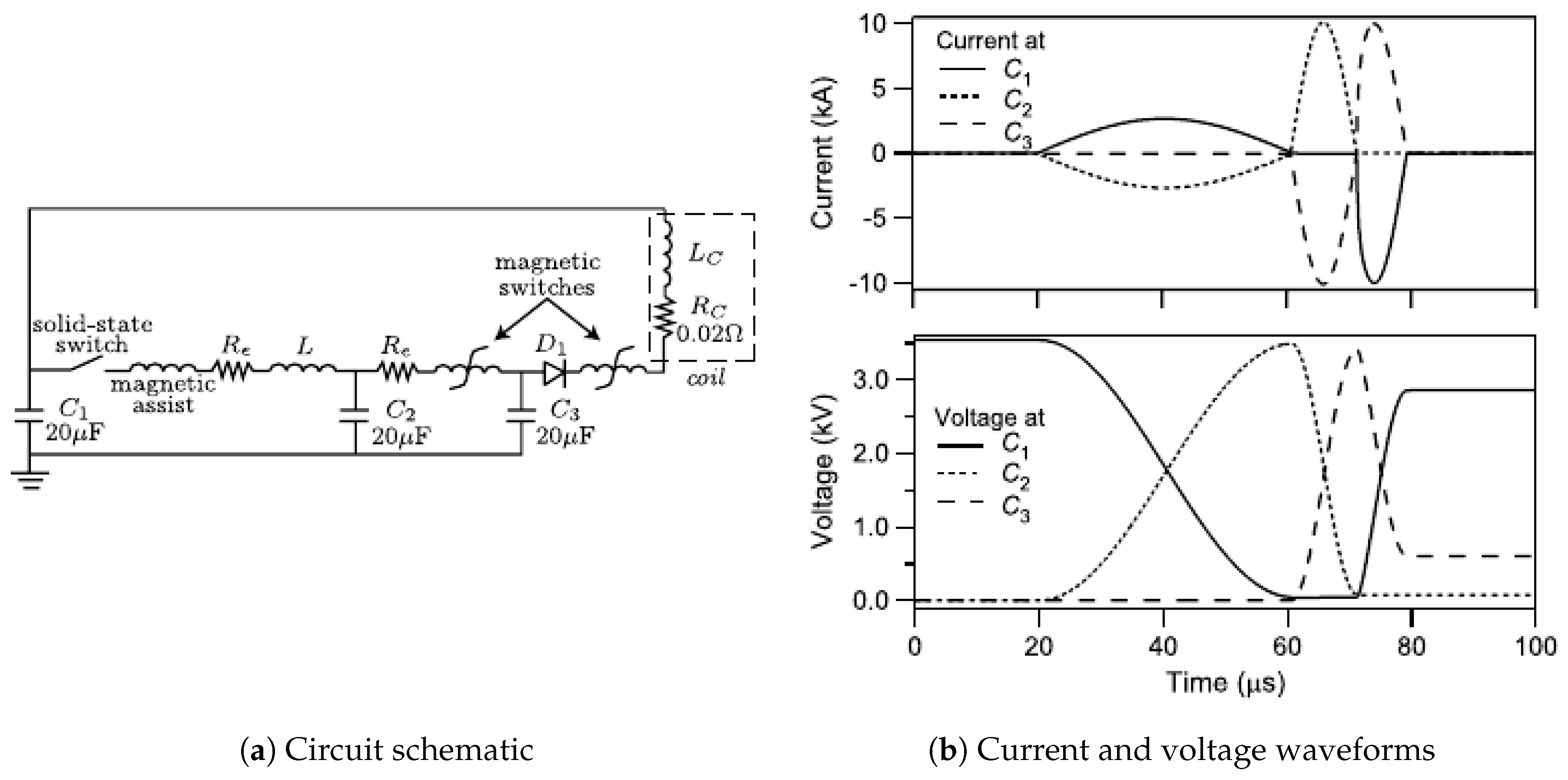
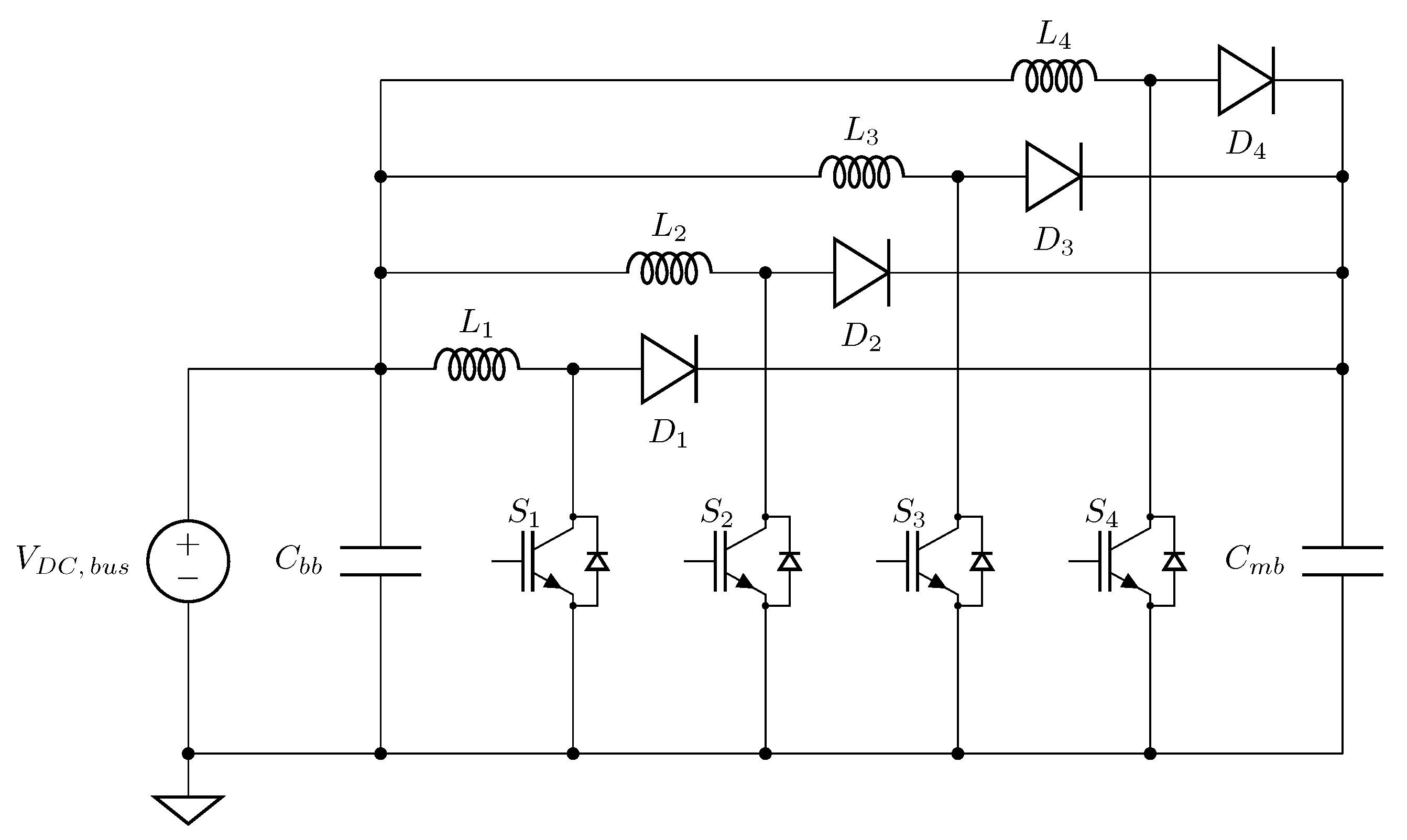
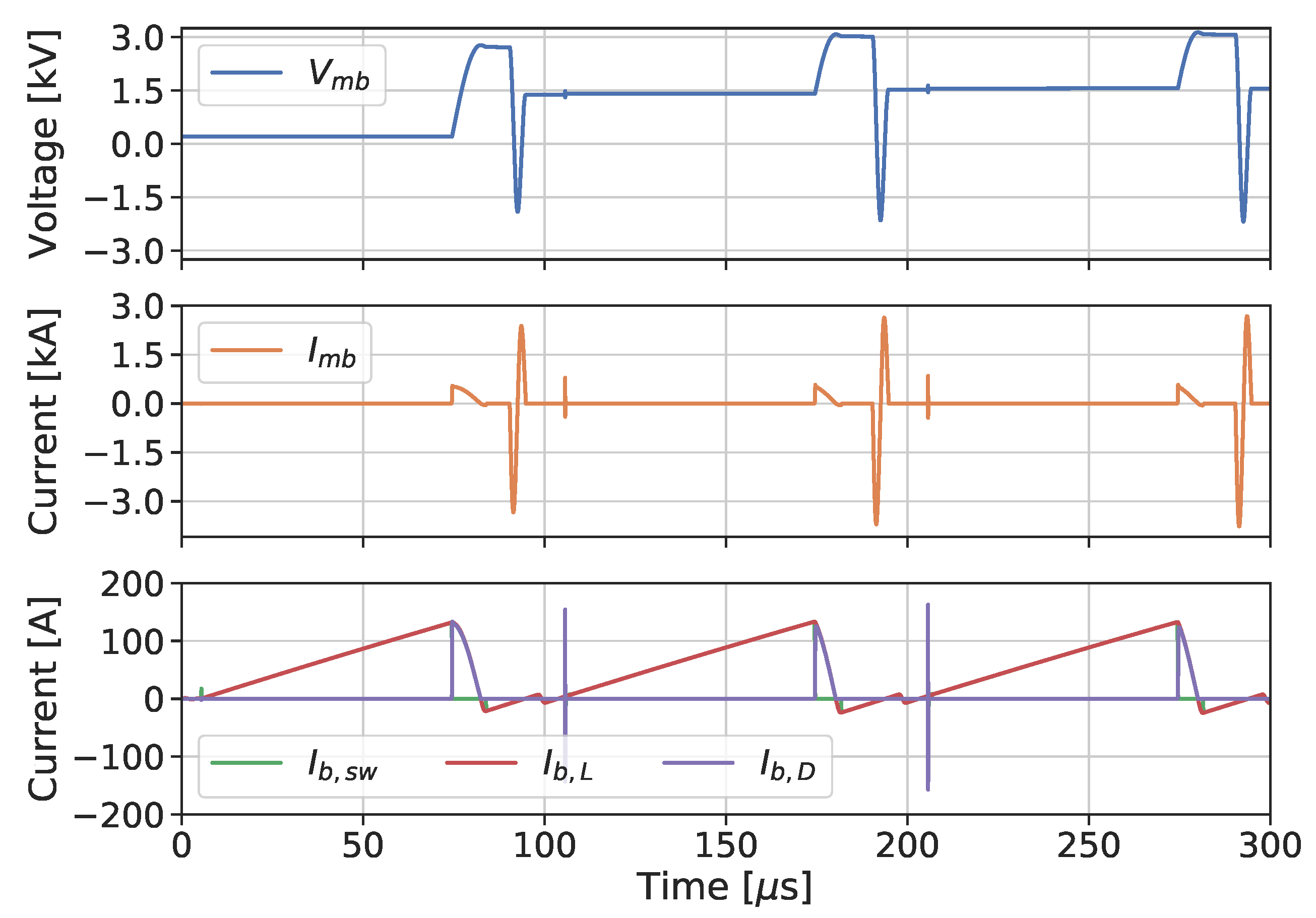
Inductive Energy Recapture
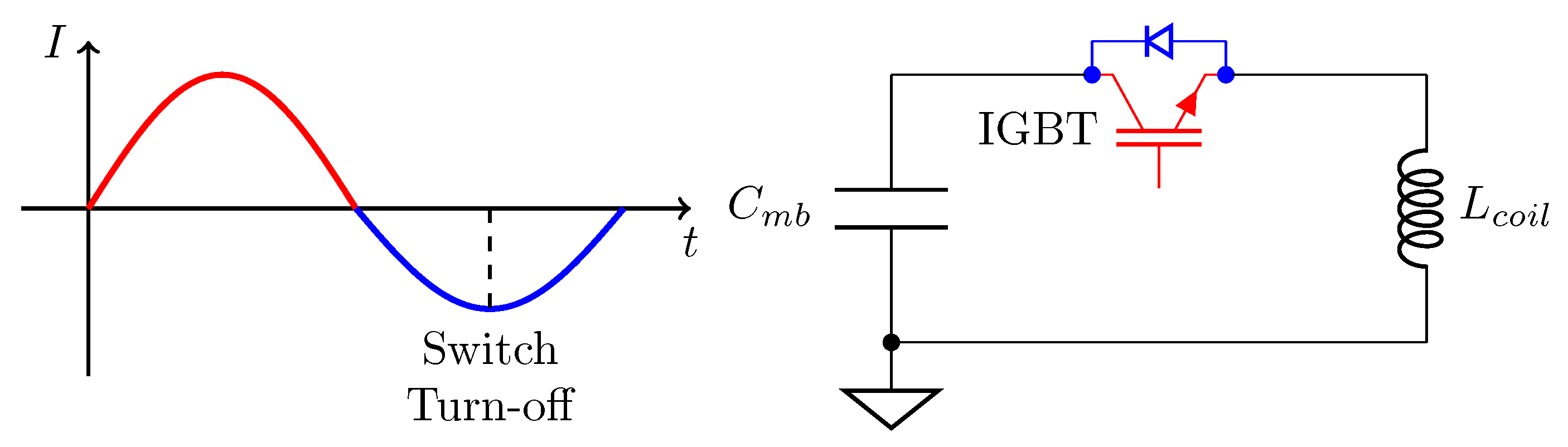
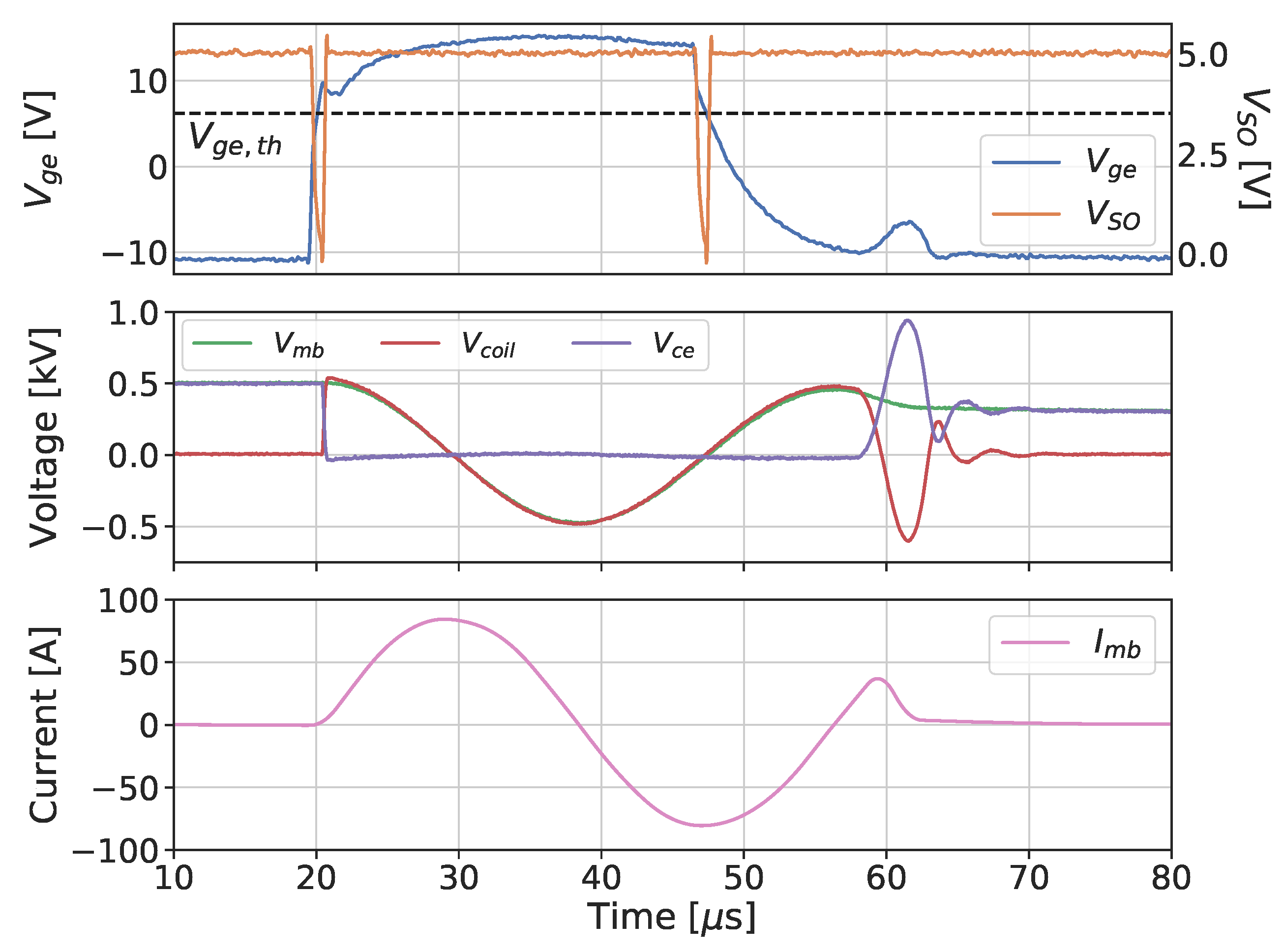
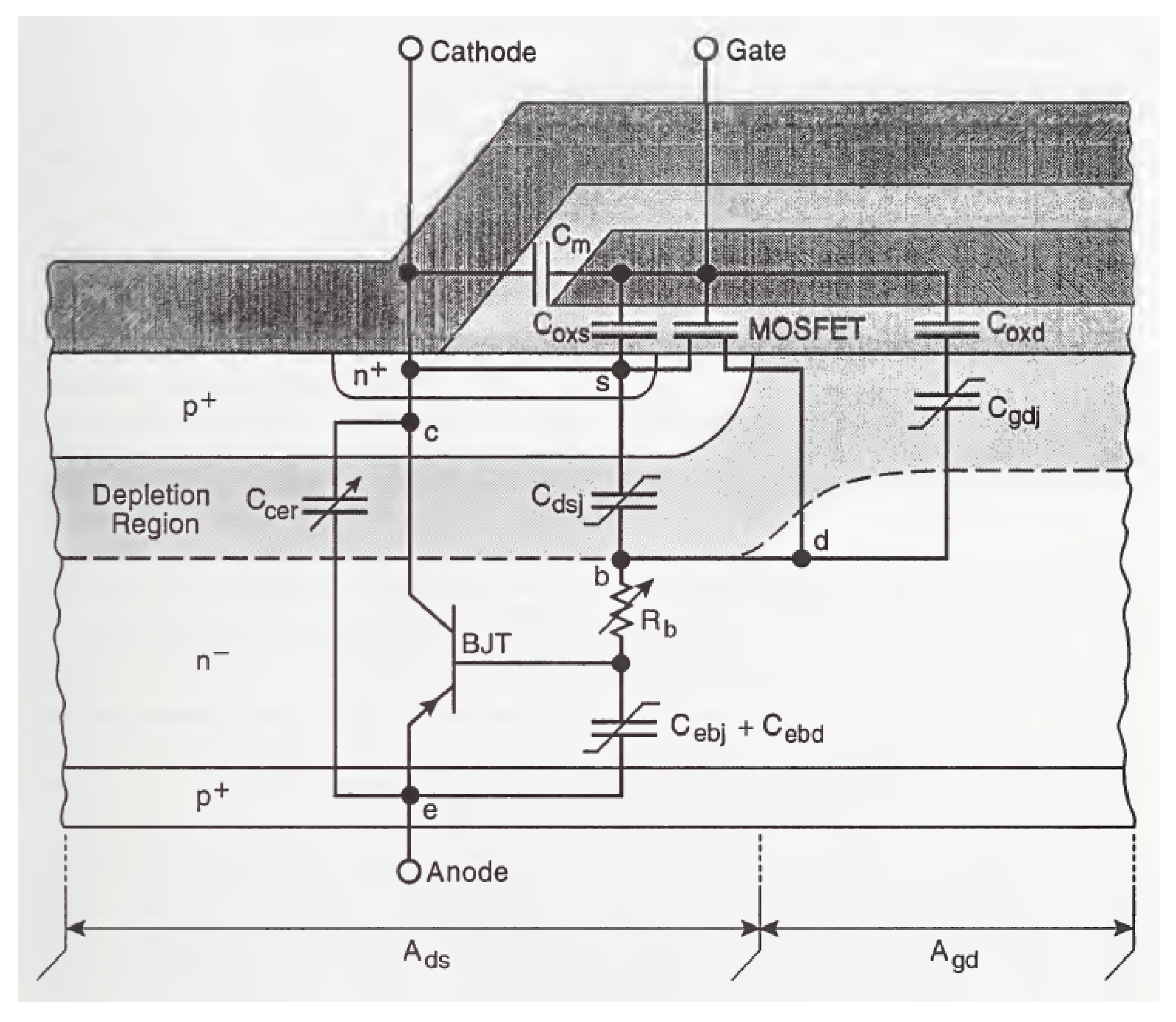
Switches
Capacitors
4.2. Drive Coil
4.3. Propellant Management and Injection
4.4. Preionization
4.5. Cooling
4.6. External Fields
5. Advancement Paths: Modeling
5.1. Formation Physics
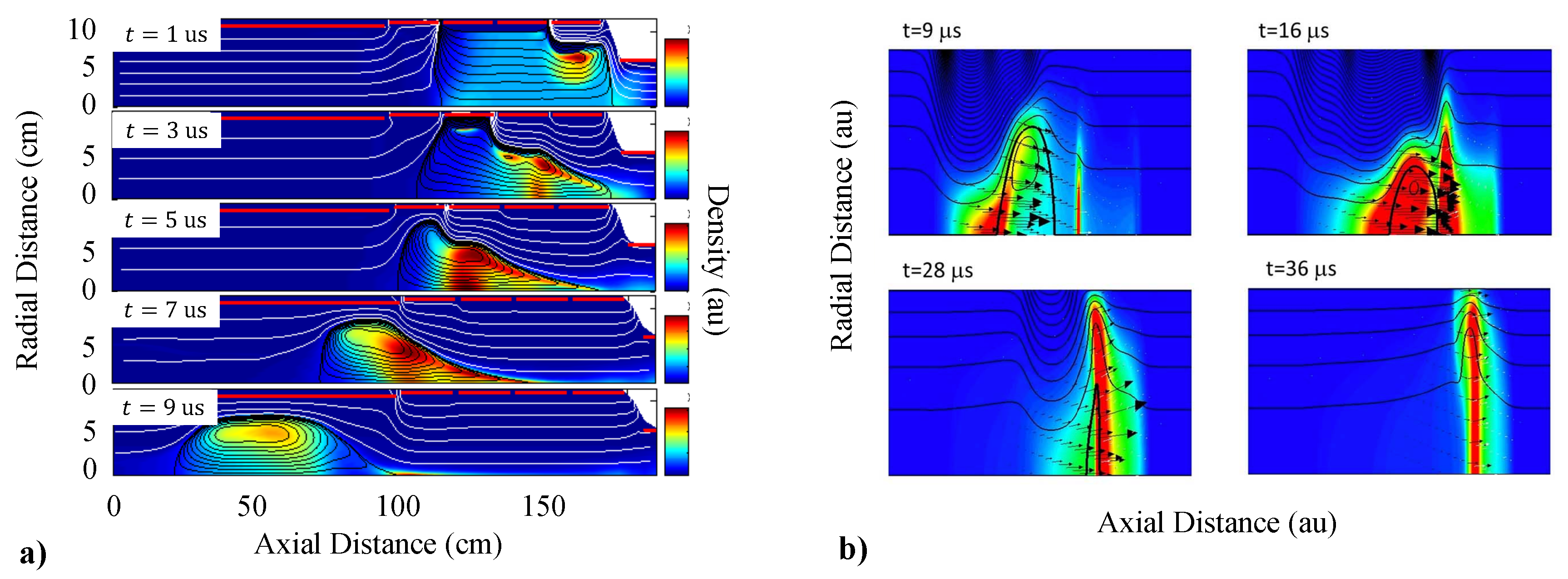
5.1.1. IPPT Current Sheet Formation
Key Physics and Requirements for Current Sheet Formation
Current Sheet Formation Scaling to Lower Energy per Pulse
Propellant Mass and Energy Loss during Current Sheet Formation
Current Sheet Stability on Formation and Acceleration Timescales
5.1.2. FRC Formation
Key Physics and Requirements for FRC formation at Low Discharge Energy
Propellant Mass and Energy Losses During FRC Formation
5.2. Acceleration Physics
5.2.1. Identification and Scaling of Dominant Acceleration Mechanisms
5.2.2. Influence of Changing Plasma Geometry on Inductive Acceleration
5.3. Molecular Propellant Physics
5.3.1. Influence of Plasma Chemistry on the Design and Scaling of IPPTs
5.3.2. Importance of Recombination in the Presence of Large Temperature Gradients
5.4. Effects of Asymmetric Charge Exchange Reactions
6. Advancement Paths: Major Subsystems
6.1. Power
6.1.1. Discharge Circuit
Discharge Circuit Topology
Inductive Energy Recapture
Capacitors
Switches
IPPT PPUs
6.1.2. Circuit Modeling
6.2. Propellant Injection
6.3. Preionization
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jahn, R.G. Physics of Electric Propulsion; McGraw-Hill: New York, NY, USA, 1968. [Google Scholar]
- Lovberg, R.H.; Hayworth, B.R.; Gooding, T. The Use of a Coaxial Plasma Gun for Plasma Propulsion; Technical Report TR AE62-0678; Convair/General Dynamics: San Diego, CA, USA, 1962.
- Dailey, C.L.; Lovberg, R.H. The PIT MkV Pulsed Inductive Thruster; Technical Report NASA CR 191155; TRW Space & Technology Group: Redondo Beach, CA, USA, 1993. [Google Scholar]
- Hallock, A.K.; Martin, A.K.; Polzin, K.A.; Kimberlin, A.C.; Eskridge, R.H. Single- and Repetitive-Pulse Conical Theta-Pinch Inductive Pulsed Plasma Thruster Performance. IEEE Trans. Plasma Sci. 2015, 43, 433–443. [Google Scholar] [CrossRef]
- Kirtley, D.; Gallimore, A.D.; Haas, J.; Reilly, M. High density magnetized toroid formation and translation within XOCOT: An annular field reversed configuration plasma concept. In Proceedings of the 30th International Electric Propulsion Conference, Florence, Italy, 17–20 September 2007. IEPC Paper 2007-041. [Google Scholar]
- Martin, A.; Eskridge, R.; Lee, M.; Koelfgen, S.; Fimognari, P. The plasmoid thruster experiment (PTX). In Proceedings of the 46th APS Division of Plasma Physics Meeting, Savannah, GA, USA, 15–19 November 2004. Paper RM2.007. [Google Scholar]
- Polzin, K.A. Comprehensive review of planar pulsed inductive plasma thruster research and technology. J. Propuls. Power 2011, 27, 513–531. [Google Scholar] [CrossRef]
- Tuszewski, M. Field Reversed Configurations. Nucl. Fusion 1988, 28, 2033–2092. [Google Scholar] [CrossRef]
- Hrbud, I.; LaPointe, M.; Vondra, R.; Dailey, C.L.; Lovberg, R. Status of pulsed inductive thruster research. AIP Conf. Proc. 2002, 608, 627–632. [Google Scholar] [CrossRef]
- Lovberg, R.H.; Dailey, C.L. A PIT Primer; Technical Report TR 005; RLD Associates: Lebanon, PA, USA, 1994. [Google Scholar]
- Dailey, C.L. Pulsed Electromagnetic Thruster; Technical Report AFRPL-TR-71-107; TRW Systems Group: Redondo Beach, CA, USA, 1971. [Google Scholar]
- Dailey, C.L.; Davis, H.A. Pulsed Plasma Propulsion Technology; Technical Report AFRPL-TR-73-81; TRW Systems Group: Redondo Beach, CA, USA, 1973. [Google Scholar]
- Lovberg, R.H.; Dailey, C.L. Large Inductive Thruster Performance Measurement. AIAA J. 1982, 20, 971–977. [Google Scholar] [CrossRef]
- Dailey, C.L.; Lovberg, R.H. Pulsed Inductive Thruster Component Technology; Technical Report AFAL-TR-87-012; TRW Space and Technology Group: Redondo Beach, CA, USA, 1987. [Google Scholar]
- Choueiri, E.Y.; Polzin, K.A. Faraday acceleration with radio-frequency assisted discharge. J. Propuls. Power 2006, 22, 611–619. [Google Scholar] [CrossRef]
- Polzin, K.A. Faraday Accelerator With Radio-Frequency Assisted Discharge (FARAD). Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2006. Thesis Number 3147-T. [Google Scholar]
- Polzin, K.A.; Rose, M.F.; Miller, R. Laboratory-Model Integrated System FARAD Thruster. In Proceedings of the 44th AIAA/SAE/ASME/ASEE Joint Propulsion Conference, Hartford, CT, USA, 21–23 July 2008. AIAA Paper 2008-4821. [Google Scholar] [CrossRef]
- Martin, A.K.; Dominguez, A.; Eskridge, R.H.; Polzin, K.A.; Riley, D.P.; Perdue, K.A. Design and Testing of a Small Inductive Pulsed Plasma Thruster. In Proceedings of the 34th International Electric Propulsion Conference, Kobe-Hyogo, Japan, 4–10 July 2015. IEPC Paper 2015-50. [Google Scholar]
- Polzin, K.A.; Martin, A.K.; Eskridge, R.H.; Kimberlin, A.C.; Addona, B.M.; Devineni, A.P.; Dugal-Whitehead, N.R.; Hallock, A.K. Summary of the 2012 Inductive Pulsed Plasma Thruster Development and Testing Program; Technical Report NASA/TP-2013-217488; NASA-Marshall Space Flight Center: Huntsville, AL, USA, 2013.
- Steinhauer, L.C. Review of field-reversed configurations. Phys. Plasmas 2011, 18, 070501. [Google Scholar] [CrossRef]
- Barnes, D.C.; Seyler, C.E.; Anderson, D.V. Compact torus theory: MHD equilibrium and stability. In Proceedings of the US-Japan Joint Symposium on Compact Toruses and Energetic Particle Injection, Princeton, NJ, USA, 11–14 December 1979. [Google Scholar]
- Tuszewski, M.; Gupta, D.; Gupta, S.; Onofri, M.; Osin, D.; Deng, B.H.; Dettrick, S.A.; Hubbard, K.; Gota, H.; TAE Team. Equilibrium properties of hybrid field reversed configurations. Phys. Plasmas 2017, 24, 012502. [Google Scholar] [CrossRef]
- Guo, H.; Binderbauer, M.; Tajima, T.; Milroy, R.D.; Steinhauer, L.C.; Yang, X.; Garate, E.G.; Gota, H.; Korepanov, S.; Necas, A.; et al. Achieving a long-lived high-beta plasma state by energetic beam injection. Nat. Commun. 2015, 6, 6897. [Google Scholar] [CrossRef]
- Slough, J.; Votroubek, G.; Pihl, C. Creation of a high-temperature plasma through merging and compression of supersonic field reversed configuration plasmoids. Nucl. Fusion 2011, 51, 053008. [Google Scholar] [CrossRef]
- Gota, H.; Binderbauer, M.; Tajima, T.; Putvinski, S.; Tuszewski, M.; Deng, B.; Dettrick, S.; Gupta, D.; Korepanov, S.; Magee, R.; et al. Formation of hot, stable, long-lived field-reversed configuration plasmas on the C-2W device. Nucl. Fusion 2019, 59, 112009. [Google Scholar] [CrossRef]
- Rosenbluth, M.N.; Bussac, M.N. MHD stability of Spheromak. Nucl. Fusion 1979, 19, 489–498. [Google Scholar] [CrossRef]
- Armstrong, W.T.; Linford, R.K.; Lipson, J.; Platts, D.A.; Sherwood, E.G. Field-reversed experiments (FRX) on compact toroids. Phys. Fluids 1981, 24, 2068–2089. [Google Scholar] [CrossRef]
- Rej, D.J.; Armstrong, W.T.; Chrien, R.E.; Klingner, P.L.; Linford, R.K.; McKenna, K.F.; Sherwood, E.G.; Siemon, R.E.; Tuszewski, M.; Milroy, R.D. Experimental studies of field-reversed configuration translation. Phys. Fluids 1986, 29, 852–862. [Google Scholar] [CrossRef]
- Weber, T.; Intrator, T.; Smith, R. Plasma-gun-assisted field-reversed configuration formation in a conical θ-pinch. Phys. Plasmas 2015, 22, 042518. [Google Scholar] [CrossRef]
- Koelfgen, S.; Eskridge, R.; Lee, M.; Martin, A.; Hawk, C.; Fimognari, P. Magnetic and Langmuir probe measurements on the plasmoid thruster experiment (PTX). In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. AIAA Paper 2004-4094. [Google Scholar] [CrossRef]
- Fimognari, P.J.; Cassibry, J.T.; Ims, K.E. Effects of Pre-ionization and Bias Field on Plasmoid Formation and Acceleration. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Cincinnati, OH, USA, 8–11 July 2007. AIAA Paper 2007-5262. [Google Scholar] [CrossRef]
- Weber, B.V.; Hinshelwood, D.D. He–Ne interferometer for density measurements in plasma opening switch experiments. Rev. Sci. Instrum. 1992, 63, 5199–5201. [Google Scholar] [CrossRef]
- Markusic, T.E. Current Sheet Canting in Pulsed Electromagnetic Accelerators. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2002. Thesis Number 3102-T. [Google Scholar]
- Berkery, J.W. Current Sheet Mass Leakage in a Pulsed Plasma Accelerator. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2005. Thesis Number 3144-T. [Google Scholar]
- Fimognari, P.J., III. A Magnetic and Interferometric Study of a Plasma Formed in a Conical-Theta-Pinch. Ph.D. Thesis, University of Alabama in Huntsville, Huntsville, AL, USA, 2007. [Google Scholar]
- Eskridge, R.H.; Fimognari, P.J.; Martin, A.K.; Lee, M.H. Design and Construction of the PT-1 Prototype Plasmoid Thruster. AIP Conf. Proc. 2006, 813, 474–483. [Google Scholar] [CrossRef]
- Slough, J.; Votroubek, G. Magnetically accelerated plasmoid (MAP) propulsion. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. AIAA Paper 2004-4654. [Google Scholar] [CrossRef]
- Pahl, R.; Rovey, J. Pre-ionization plasma in an FRC test article. In Proceedings of the 50th AIAA Aerospace Sciences Meeting, Nashville, TN, USA, 9–12 July 2012. AIAA Paper 2012-194. [Google Scholar] [CrossRef][Green Version]
- Pahl, R.A.; Rovey, J.L. Effects of DC Preionization Voltage and Radial Location on Pulsed Inductive Plasma Formation. IEEE Trans. Plasma Sci. 2015, 43, 3883–3888. [Google Scholar] [CrossRef]
- Hoffman, A.L.; Guo, H.Y.; Slough, J.T.; Tobin, S.J.; Schrank, L.S.; Reass, W.A.; Wurden, G.A. The TCS Rotating Magnetic Field FRC Current-Drive Experiment. Fusion Sci. Technol. 2002, 41, 92–106. [Google Scholar] [CrossRef]
- Blevin, H.A.; Thonemann, P.C. Plasma confinement using an alternating magnetic field. In Conference on Plasma Physics and Controlled Nuclear Fusion Research; Nuclear Fusion Supplement, Part 1; International Atomic Energy Agency: Vienna, Austria, 1962; pp. 55–60. [Google Scholar]
- Slough, J.; Kirtley, D.; Weber, T. Pulsed plasmoid propulsion: The ELF thruster. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. IEPC Paper 2009-265. [Google Scholar]
- Woods, J.M.; Sercel, C.L.; Gill, T.M.; Viges, E.; Jorns, B.A. Data-Driven Approach to Modeling and Development of a 30 kW Field-reversed Configuration Thruster. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 September 2019. IEPC Paper 2019-717. [Google Scholar]
- Weber, T.E.; Slough, J.T.; Kirtley, D. The electrodeless Lorentz force (ELF) thruster experimental facility. Rev. Sci. Instrum. 2012, 83, 113509. [Google Scholar] [CrossRef]
- Furukawa, T.; Takizawa, K.; Kuwahara, D.; Shinohara, S. Electrodeless plasma acceleration system using rotating magnetic field method. AIP Adv. 2017, 7, 115204. [Google Scholar] [CrossRef]
- Furukawa, T.; Shimura, K.; Hachisu, K.; Shinohara, S.; Yamamura, S.; Kuwahara, D. Electrodeless Helicon Plasma Thruster Employing Additional Electromagnetic Acceleration Methods. In Proceedings of the 36th International Electric Propulsion Conference, Vienna, Austria, 15–20 July 2019. IEPC Paper 2019-A-198. [Google Scholar]
- Kirtley, D.; Slough, J.; Pfaff, M.; Pihl, C. Steady operation of an electromagnetic plasmoid thruster. In Proceedings of the 5th Joint Army-Navy-NASA-Air Force (JANNAF) Spacecraft Propulsion Subcommittee Meeting, Huntsville, AL, USA, 2011. [Google Scholar]
- Justin, K.; Martin, R.; Sousa, E.M. High Fidelity Modeling of Field-Reversed Configuration (FRC) Thrusters; Technical Report AFRL-RQ-ED-TR-2017-0002; Air Force Research Laboratory: Edwards AFB, CA, USA, 2017. [Google Scholar]
- Li, G. Time-Resolved Emission Spectroscopy of Field Reversed Configuration Thruster; Technical Report AFRL-RQ-ED-VG-2016-276; Air Force Research Laboratory: Edwards AFB, CA, USA, 2016. [Google Scholar]
- Schmidt, G.; Jacobson, D.; Patterson, M.; Ganapathi, G.; Brophy, J.; Hofer, R. Electric Propulsion Research and Development at NASA. In Proceedings of the Space Propulsion Conference, Seville, Spain, 16–18 May 2018. Paper SP2018 00389. [Google Scholar]
- Weber, T. The Electrodeless Lorentz Force Thruster Experiment. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2010. [Google Scholar]
- Wong, A.R.; Toftul, A.; Polzin, K.A.; Pearson, J.B. Non-contact thrust stand calibration method for repetitively pulsed electric thrusters. Rev. Sci. Instrum. 2012, 83, 025103. [Google Scholar] [CrossRef] [PubMed]
- Brown, D.L.; Beal, B.E.; Haas, J.M. Air Force Research laboratory High Power Electric Propulsion Technology Development. In Proceedings of the IEEE Aerospace Conference, Big Sky, MT, USA, 6–13 March 2010. IEEEAC Paper 1549. [Google Scholar]
- Hill, C.S. Translation Studies on an Annular Field Reversed Configuration Device for Space Propulsion. Ph.D. Thesis, Michigan Technological University, Houghton, MI, USA, 2012. [Google Scholar]
- Phillips, J. Proposal to Produce Large Compact Toroids; Technical Report LA-8711-P; Los Alamos National Laboratory: Los Alamos, NM, USA, 1981.
- Alidieres, M.; Aymar, R.; Jourdan, P.; Koechlin, F.; Samain, A. Acceleration d’un plasma dans une configuration de striction. Plasma Phys. 1967, 9, 73–83. [Google Scholar] [CrossRef]
- Kirtley, D.E. Study of the Synchronous Operation of an Annular Field Reversed Configuration Device. Ph.D. Thesis, University of Michigan, Ann Arbor, MI, USA, 2008. [Google Scholar]
- Kirtley, D.; Pancotti, A.; Slough, J.; Pihl, C. Steady operation of an FRC thruster on Martian atmosphere and liquid water propellants. In Proceedings of the 48th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Atlanta, GA, USA, 30 July–1 August 2012. AIAA Paper 2012-4071. [Google Scholar] [CrossRef]
- Martin, A.K.; Eskridge, R.H. Electrical coupling efficiency of inductive plasma accelerators. J. Phys. D Appl. Phys. 2005, 38, 4168–4179. [Google Scholar] [CrossRef]
- Polzin, K.A.; Choueiri, E.Y. Performance optimization criteria for pulsed inductive plasma acceleration. IEEE Trans. Plasma Sci. 2006, 34, 945–953. [Google Scholar] [CrossRef]
- Polzin, K.A. Scaling and systems considerations in pulsed inductive plasma thrusters. IEEE Trans. Plasma Sci. 2008, 36, 2189–2198. [Google Scholar] [CrossRef]
- Polzin, K.A.; Reneau, J.P. Effect of Conductive Walls on the Performance of a Pulsed Inductive Thruster. IEEE Trans. Plasma Sci. 2009, 37, 359–364. [Google Scholar] [CrossRef]
- Polzin, K.A. Pulsed Inductive Plasma Acceleration: Optimization. In Encyclopedia of Plasma Technology; Shohet, J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 1191–1200. [Google Scholar]
- Polzin, K.A.; Sankaran, K.; Ritchie, A.G.; Reneau, J.P. Inductive pulsed plasma thruster model with time-evolution of energy and state properties. J. Phys. D Appl. Phys. 2013, 46. [Google Scholar] [CrossRef]
- Mikellides, P.G.; Neilly, C. Modeling and Performance Analysis of the Pulsed Inductive Thruster. J. Propuls. Power 2007, 23, 51–58. [Google Scholar] [CrossRef]
- Mikellides, P.G.; Ratnayake, N. Modeling of the Pulsed Inductive Thruster Operating on Ammonia propellant. J. Propuls. Power 2007, 23, 854–862. [Google Scholar] [CrossRef]
- Mikellides, P.G.; Villarreal, J.K. High Energy Pulsed Inductive Thruster Modeling Operating with Ammonia Propellant. J. Appl. Phys. 2007, 102, 103301. [Google Scholar] [CrossRef]
- Allison, D.L.; Mikellides, P.G. A High-Temperature, Thermal Non-Equilibrium Equation of State for Ammonia. Int. J. Thermophys. 2006, 27, 794–819. [Google Scholar] [CrossRef]
- Mikellides, P.; Villarreal, J. Numerical Modeling of a Low Energy Pulsed Inductive Thruster. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008. AIAA Paper 2008-4726. [Google Scholar] [CrossRef]
- Che, B.X.; Cheng, M.S.; Li, X.K.; Guo, D.W. Physical mechanisms and factors influencing inductive pulsed plasma thruster performance: A numerical study using an extended magnetohydrodynamic model. J. Phys. D Appl. Phys. 2018, 51, 365202. [Google Scholar] [CrossRef]
- Hallock, A.K. Effect of Inductive Coil Geometry on the Operating Characteristics of a Pulsed Inductive Plasma Accelerator. Ph.D. Thesis, Princeton University, Princeton, NJ, USA, 2012. Thesis Number 3252-T. [Google Scholar]
- Martin, A.K. Performance scaling of inductive pulsed plasma thrusters with coil angle and pulse rate. J. Phys. D Appl. Phys. 2016, 49, 025201. [Google Scholar] [CrossRef]
- Polzin, K.; Rose, M.F.; Miller, R.; Best, S.; Owens, T.; Dankanich, J. Design of a low-energy FARAD thruster. In Proceedings of the 43rd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Cincinnati, OH, USA, 8–11 July 2007. AIAA Paper 2007-5257. [Google Scholar] [CrossRef][Green Version]
- Woods, J.M.; Jorns, B.A.; Gallimore, A.D. Circuit Modeling of Rotating Magnetic Field Field-reversed Configuration Thrusters. In Proceedings of the AIAA Propulsion and Energy Forum, Cincinnati, OH, USA, 9–11 July 2018. AIAA paper 2018-4911. [Google Scholar] [CrossRef]
- Hugrass, W.N.; Okada, T.; Ohnishi, M. Plasma-circuit Interactions in Rotating Magnetic Field Current Drive. Plasma Phys. Control. Fusion 2008, 50, 055008. [Google Scholar] [CrossRef]
- Little, J.; Cornella, B.; Pancotti, A.; Kirtley, D. Scaling of FRC Thrusters with Neutral Entrainment. In Proceedings of the 8th Joint Army-Navy-NASA-Air Force (JANNAF) Spacecraft Propulsion Subcommittee Meeting, Phoenix, AZ, USA, 5–8 December 2016. [Google Scholar]
- Ji, H.; Yamada, M.; Kulsrud, R.; Pomphrey, N.; Himura, H. Studies of Global Stability of Field-Reversed Configuration Plasmas Using a Rigid Body Model. Phys. Plasmas 1998, 5, 3685–3693. [Google Scholar] [CrossRef]
- Niemela, C.S.; King, L.B. Numerical Optimization of an Annular Field Reversed Configuration Translation Experiment. In Proceedings of the 31st International Electric Propulsion Conference, Ann Arbor, MI, USA, 20–24 September 2009. IEPC paper 2009-008. [Google Scholar]
- Milroy, R.D.; Brackbill, J.U. Numerical studies of a field-reversed theta-pinch plasma. Phys. Fluids 1982, 25, 775–783. [Google Scholar] [CrossRef]
- Slough, J. Multi-megawatt propulsion based on a compact toroid thruster. In Proceedings of the 29th International Electric Propulsion Conference, Princeton, NJ, USA, 31 October–4 November 2005. IEPC paper 2005-296. [Google Scholar]
- Meier, E.T. Modeling Plasmas with Strong Anisotropy, Neutral Fluid Effects, and Open Boundaries. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2011. [Google Scholar]
- Milroy, R.D. A numerical study of rotating magnetic fields as a current drive for field reversed configurations. Phys. Plasmas 1999, 6, 2771–2780. [Google Scholar] [CrossRef]
- Brackbill, J.; Cambier, J.L.; Gimelshein, N.E.; Gimelshein, S.F. Numerical analysis of neutral entrainment effect on field-reversed configuration thruster efficiency. J. Propuls. Power 2014, 30, 1450–1458. [Google Scholar] [CrossRef]
- Patel, M.R. Spacecraft Power Systems; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Kirtley, D.; Pihl, J.; Pihl, C. Development of a steady operating pulsed power system for FRC and inductive thrusters. In Proceedings of the 33rd International Electric Propulsion Conference, Washington, DC, USA, 6–10 October 2013. IEPC Paper 2013-361. [Google Scholar]
- Kirtley, D.; Pihl, J.; Bernhard, B.; Goff, J. Development, Vibration, and Thermal Characterization of a Steady Operating Pulsed Power System for FRC Thrusters; Technical Report AFRL-RQ-ED-TP-2015-139; Air Force Research Laboratory: Edwards AFB, CA, USA, 2015. [Google Scholar]
- Polzin, K.A.; Rose, M.F.; Miller, R. Operational Characteristics of a Low-Energy FARAD Thruster. In Proceedings of the 44th AIAA/SAE/ASME/ASEE Joint Propulsion Conference, Hartford, CT, USA, 21–23 July 2008. AIAA Paper 2008-5011. [Google Scholar] [CrossRef][Green Version]
- Pancotti, A.P.; Little, J.M.; Neuhoff, J.S.; Cornella, B.M.; Kirtley, D.E.; Slough, J.T. Electrodeless Lorentz Force (ELF) Thruster for ISRU and Sample Return Mission. In Proceedings of the 34th International Electric Propulsion Conference, Kobe-Hyogo, Japan, 4–10 July 2015. IEPC Paper 2015-67. [Google Scholar]
- Owens, T.L. A pulse-compression-ring circuit for high-efficiency electric propulsion. Rev. Sci. Instrum. 2008, 79, 034701. [Google Scholar] [CrossRef] [PubMed]
- Bernardes, J.; Merryman, S. Parameter analysis of a single stage induction mass driver. In Proceedings of the 5th IEEE International Pulsed Power Conference, Washington, DC, USA, 10–12 June 1985; IEEE Paper PI-27. pp. 552–555. [Google Scholar]
- Toftul, A.; Polzin, K.A.; Martin, A.K.; Hudgins, J.L. Testing of Diode-Clamping in an Inductive Pulsed Plasma Thruster Circuit. In Proceedings of the 50th AIAA/ASME/SAE/ASEE Joint Propulsion Conference, Cleveland, OH, USA, 28–30 July 2014. AIAA Paper 2014–3503. [Google Scholar] [CrossRef][Green Version]
- Poylio, J.H.; Russell, D.; Goldstein, W.; Jackson, B.; Lovberg, R.H.; Dailey, C.L. Pulsed inductive thruster: Flight-scale proof of concept demonstrator. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. AIAA Paper 2004-3640. [Google Scholar] [CrossRef]
- Raines, T. Propellant Mass Scaling and Decoupling and Improved Plasma Coupling in a Pulsed Inductive Thruster. Master’s Thesis, Arizona State University, Tempe, AZ, USA, 2018. [Google Scholar]
- Frisbee, R.H. Evaluation of High-Power Solar Electric Propulsion Using Advanced Ion, Hall, MPD, and PIT Thrusters for Lunar and Mars Cargo Missions. In Proceedings of the 42nd AIAA/SAE/ASME/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. AIAA Paper 2006-4465. [Google Scholar] [CrossRef]
- Burkhardt, W.M.; Crapuchettes, J.M.; Addona, B.M.; Polzin, K.A. Development of Long-Lifetime Pulsed Gas Valves for Pulsed Electric Thrusters. In Proceedings of the 51st AIAA/SAE/ASEE Joint Propulsion Conference & Exhibit, Orlando, FL, USA, 27–29 July 2015. AIAA Paper 2015-4187. [Google Scholar] [CrossRef]
- Burkhardt, W. Fast Acting Control Valve; Technical Report, NASA SBIR Phase 2 Contract NNX15CM11C; WASK Engineering, Inc.: Cameron Park, CA, USA, 2017. [Google Scholar]
- Dailey, C.L.; Lovberg, R.H. Current sheet structure in an inductive-impulsive plasma accelerator. AIAA J. 1972, 10, 125–129. [Google Scholar] [CrossRef]
- Hallock, A.; Choueiri, E.; Polzin, K. Current sheet formation in a conical theta pinch faraday accelerator with radio-frequency assisted discharge. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Hartford, CT, USA, 21–23 July 2008; p. 5201. [Google Scholar] [CrossRef]
- Milroy, R.D.; Brackbill, J.U. Toroidal magnetic field generation during compact toroid formation in a field-reversed theta pinch and a conical theta pinch. Phys. Fluids 1986, 29, 1184–1195. [Google Scholar] [CrossRef]
- Milroy, R.D.; Kim, C.C.; Sovinec, C.R. Extended magnetohydrodynamic simulations of field reversed configuration formation and sustainment with rotating magnetic field current drive. Phys. Plasmas 2010, 17, 062502. [Google Scholar] [CrossRef]
- Choueiri, E. Scaling of thrust in self-field magnetoplasmadynamic thrusters. J. Propuls. Power 1998, 14, 744–753. [Google Scholar] [CrossRef]
- Takahashi, K.; Lafleur, T.; Charles, C.; Alexander, P.; Boswell, R.W. Electron diamagnetic effect on axial force in an expanding plasma: Experiments and theory. Phys. Rev. Lett. 2011, 107, 235001. [Google Scholar] [CrossRef] [PubMed]
- Sheppard, A.J.; Little, J. Scaling laws for electrodeless plasma propulsion with water vapor propellant. Plasma Sources Sci. Technol. 2020, 29, 045007. [Google Scholar] [CrossRef]
- Florescu-Mitchell, A.I.; Mitchell, J.B.A. Dissociative recombination. Phys. Rep. 2006, 430, 277–374. [Google Scholar] [CrossRef]
- Rapp, D.; Francis, W.E. Charge exchange between gaseous ions and atoms. J. Chem. Phys. 1962, 37, 2631–2645. [Google Scholar] [CrossRef]
- Singh, R.; Cooper, J.A.; Melloch, M.R.; Chow, T.P.; Palmour, J.W. SiC power Schottky and PiN diodes. IEEE Trans. Electron Devices 2002, 49, 665–672. [Google Scholar] [CrossRef]
- Morisette, D.T.; Cooper, J.A. Theoretical comparison of SiC PiN and Schottky diodes based on power dissipation considerations. IEEE Trans. Electron Devices 2002, 49, 1657–1664. [Google Scholar] [CrossRef]
- Benson, S.W.; Frus, J.R. Advanced pulsed plasma thruster electrical components. In Proceedings of the 37th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Salt Lake City, UT, USA, 8–11 July 2001. AIAA Paper 2001-3894. [Google Scholar] [CrossRef]
- Celem Power Capacitors. Conduction-Cooled Capacitor; CPRI 300; Celem Power Capacitors: Jerusalem, Israel, 2015. [Google Scholar]
- Yang, S.; Xiang, D.; Bryant, A.; Mawby, P.; Ran, L.; Tavner, P. Condition monitoring for device reliability in power electronic converters: A review. IEEE Trans. Power Electron. 2010, 25, 2734–2752. [Google Scholar] [CrossRef]
- Hudgins, J.L.; De Doncker, R.W. Power semiconductor devices: For variable speed drives. IEEE Ind. Appl. Mag. 2012, 18, 18–25. [Google Scholar] [CrossRef]
- Gao, B.; Morgan, A.J.; Xu, Y.; Zhao, X.; Hopkins, D.C. 6.0 kV, 100 A, 175 kHz super cascade power module for medium voltage, high power applications. In Proceedings of the IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, USA, 4–8 March 2018; pp. 1288–1293. [Google Scholar] [CrossRef]
- Millan, J.; Godignon, P.; Perpiñà, X.; Pérez-Tomás, A.; Rebollo, J. A survey of wide bandgap power semiconductor devices. IEEE Trans. Power Electron. 2013, 29, 2155–2163. [Google Scholar] [CrossRef]
- Casady, J.B.; Johnson, R.W. Status of silicon carbide (SiC) as a wide-bandgap semiconductor for high-temperature applications: A review. Solid-State Electron. 1996, 39, 1409–1422. [Google Scholar] [CrossRef]
- Boomer, K.; Lauenstein, J.M.; Hammoud, A. Body of Knowledge for Silicon Carbide Power Electronics; Technical Report; NASA Electronic Parts and Packaging (NEPP) Program, Office of Safety and Mission Assurance: Washington, DC, USA, 2016.
- Hefner, A.R., Jr. INSTANT—IGBT Network Simulation and Transient ANalysis Tool; Spec. Publ. 400-88; National Institute of Standards and Technology: Washington, DC, USA, 1992.
- Perez, S.; Kotecha, R.M.; Rashid, A.U.; Hossain, M.M.; Vrotsos, T.; Francis, A.M.; Mantooth, A.H.; Santi, E.; Hudgins, J.L. A datasheet driven unified Si/SiC compact IGBT model for N-channel and P-channel devices. IEEE Trans. Power Electron. 2018, 34, 8329–8341. [Google Scholar] [CrossRef]
- Hefner, A.R.; Diebolt, D.M. An experimentally verified IGBT model implemented in the Saber circuit simulator. IEEE Trans. Power Electron. 1994, 9, 532–542. [Google Scholar] [CrossRef]
- Mudholkar, M.; Ahmed, S.; Ericson, M.N.; Frank, S.S.; Britton, C.L.; Mantooth, H.A. Datasheet driven silicon carbide power MOSFET model. IEEE Trans. Power Electron. 2013, 29, 2220–2228. [Google Scholar] [CrossRef]
- Tan, C.M.; Tseng, K.J. Using power diode models for circuit simulations—A comprehensive review. IEEE Trans. Ind. Electron. 1999, 46, 637–645. [Google Scholar] [CrossRef]



| Experiment | [s] | [mN-s] | [%] | [T] | [kV] | [kA] | |
|---|---|---|---|---|---|---|---|
| PIT MK Va (open flux) [3] | 2000–7000 | 50–120 | 40–55 | 0.55 | 30–32 ** | 135 *** | |
| CTP-IPPT (open flux) [4] | 1000–4500 | 0.1–1 | <6 | * | 5 | 18 | |
| MSFC-IPPT (open flux) [18] | * | * | * | * | 3 | 7.4 | |
| PTX (closed flux) [35] | * | * | * | 0.5 | * | 35 | 50 |
| PT-1 (closed flux) [36] | * | * | * | 0.1 | * | 3 | 14 |
| 1 kW EMPT (closed flux) [47] | * | * | * | 0.03 | ∼0.5 | 1.3 | 1 |
| 50 J/pulse ELF (closed flux) [51] | * | 0.4 | * | 0.04 | ∼0.5 | 10 | * |
| 30 kW ELF (closed flux) [58] | * | * | * | 0.01 | ∼0.5 | 3 | 3 |
| Thruster | |||||||
|---|---|---|---|---|---|---|---|
| [F] | [nH] | [nH] | [kV] | [kA] | [kV/s] | [kA/s] | |
| PIT MK Va [3,65] | 9 | 680 | 60 | 30 | 135 | 11 | 270 |
| FARAD [17,87] | 20 | 810 | 70 | 3.1 | 10* | 1.2 | 45 |
| MSFC IPPT [18] | 10 | 705 | 336 | 3 | 7 | 0.7 | 2 |
| ELF-160 [88] * | 1.32 | 325 | ** | 3.4 | 7 | 5 | 10 |
| Parameter | Thyristor/SCR | IGBT | MOSFET |
|---|---|---|---|
| Switching Speed | Slowest | Intermediate | Fastest |
| Current | Highest | Intermediate | Lowest |
| Breakdown Voltage | Highest | Intermediate | Lowest |
| Control Type | Current | Voltage | Voltage |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Polzin, K.; Martin, A.; Little, J.; Promislow, C.; Jorns, B.; Woods, J. State-of-the-Art and Advancement Paths for Inductive Pulsed Plasma Thrusters. Aerospace 2020, 7, 105. https://doi.org/10.3390/aerospace7080105
Polzin K, Martin A, Little J, Promislow C, Jorns B, Woods J. State-of-the-Art and Advancement Paths for Inductive Pulsed Plasma Thrusters. Aerospace. 2020; 7(8):105. https://doi.org/10.3390/aerospace7080105
Chicago/Turabian StylePolzin, Kurt, Adam Martin, Justin Little, Curtis Promislow, Benjamin Jorns, and Joshua Woods. 2020. "State-of-the-Art and Advancement Paths for Inductive Pulsed Plasma Thrusters" Aerospace 7, no. 8: 105. https://doi.org/10.3390/aerospace7080105
APA StylePolzin, K., Martin, A., Little, J., Promislow, C., Jorns, B., & Woods, J. (2020). State-of-the-Art and Advancement Paths for Inductive Pulsed Plasma Thrusters. Aerospace, 7(8), 105. https://doi.org/10.3390/aerospace7080105






