Predicting Rotor Heat Transfer Using the Viscous Blade Element Momentum Theory and Unsteady Vortex Lattice Method
Abstract
:1. Introduction
2. Methodology
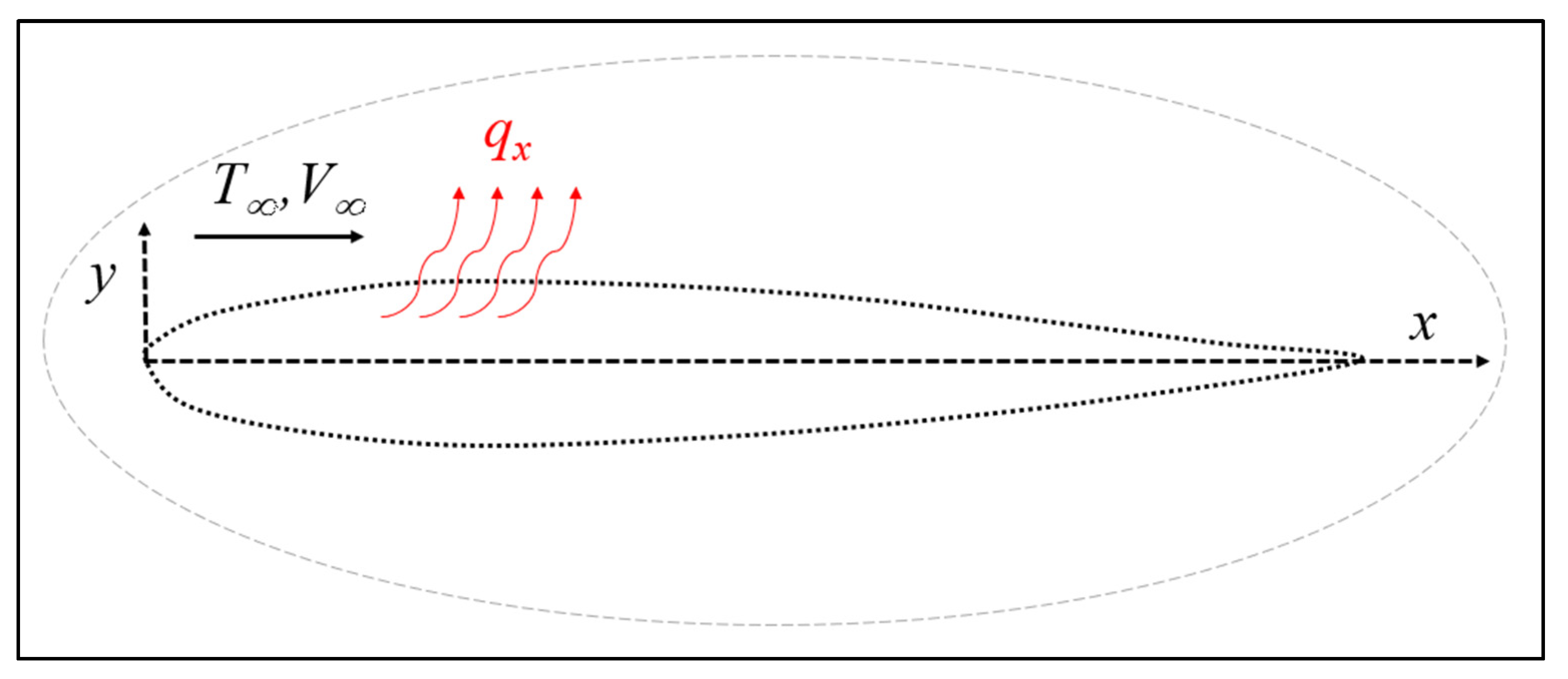
2.1. CFD Heat Transfer Simulations
2.1.1. Airfoil Average Heat Transfer Correlation
2.1.2. CFD Simulations Details
2.1.3. Convective Heat Transfer
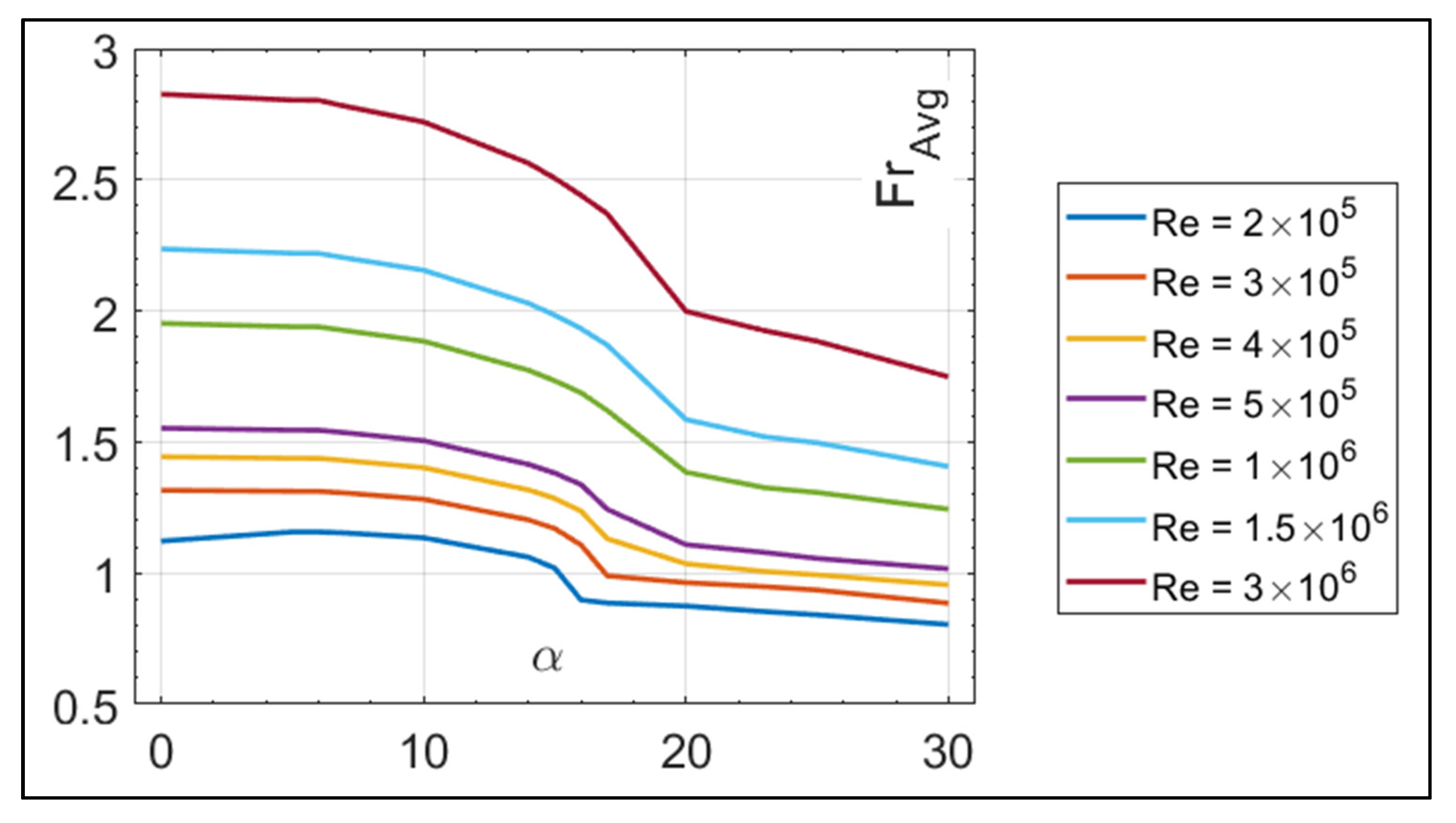
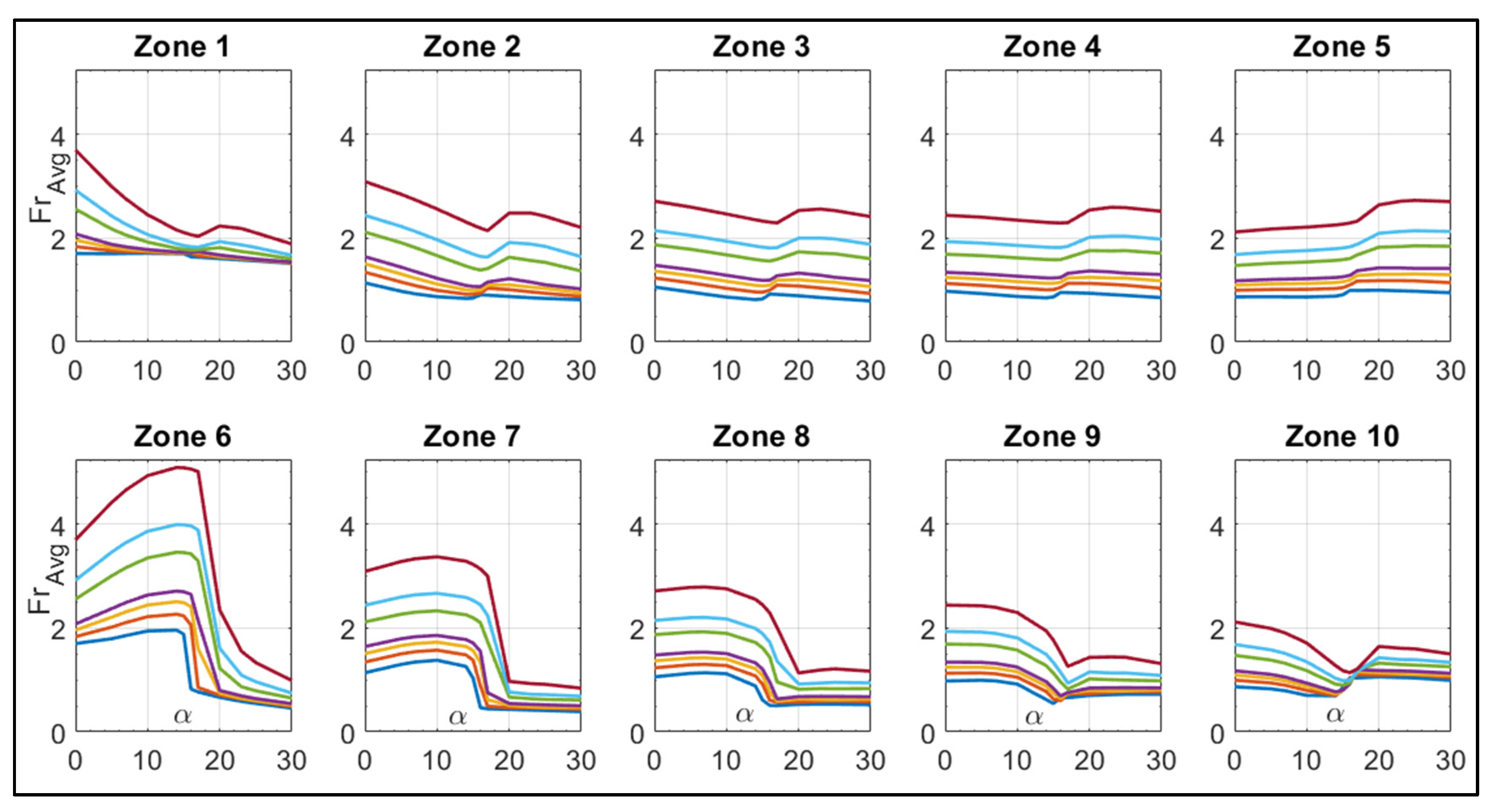
2.1.4. Zone with Maximum Fr
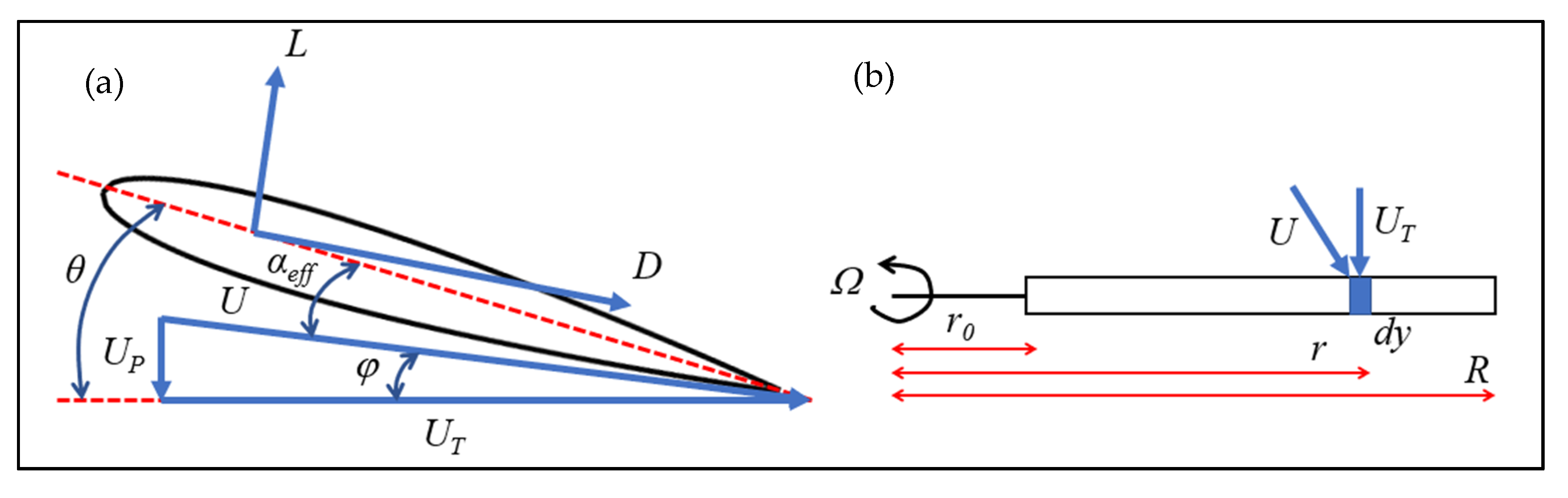
2.2. BEMT-RHT
2.3. UVLM-RHT
2.3.1. Discretization and Grid Construction
2.3.2. Induced Velocities Calculation
2.3.3. Vortex Strength and Forces Calculation
2.3.4. Slow Start Method
2.3.5. Modified Viscous-Heat Transfer Coupling Algorithm
- Calculate αeff at each blade section .
- Find CL-visc by interpolating αeff in the CFD viscous database
- Check
- Adjust αeff in the first step by the found Δαvisc
- Repeat until |CL-inv − CL-visc| < ε
2.3.6. Complete UVLM-RHT Solution Procedure
3. Results
3.1. CFD Heat Transfer Results
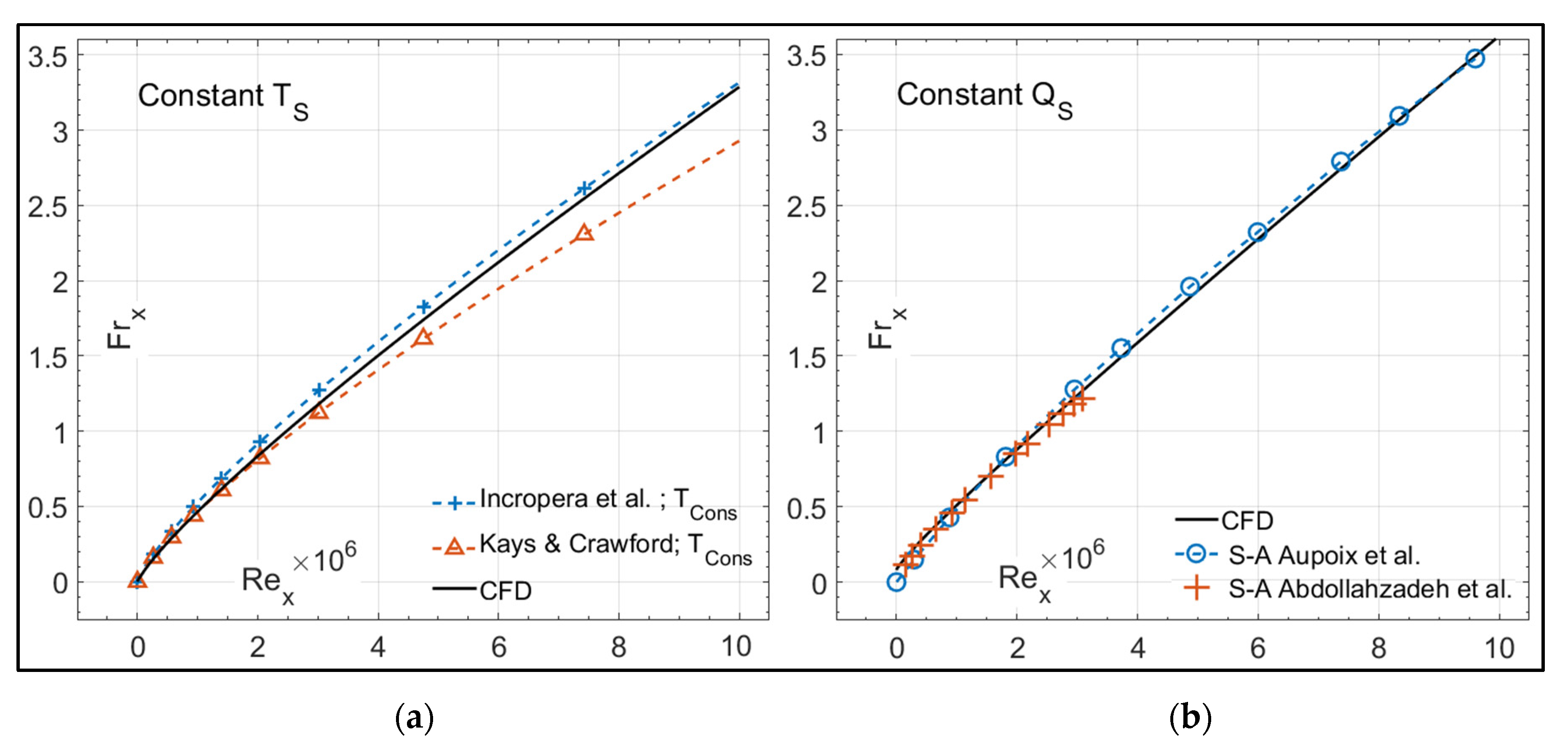
3.1.1. Flat Plate Verification Test Case
3.1.2. Average Frossling Number Correlation
3.1.3. Maximum Frossling Number Correlation
3.2. Validation of Implemented BEMT and UVLM
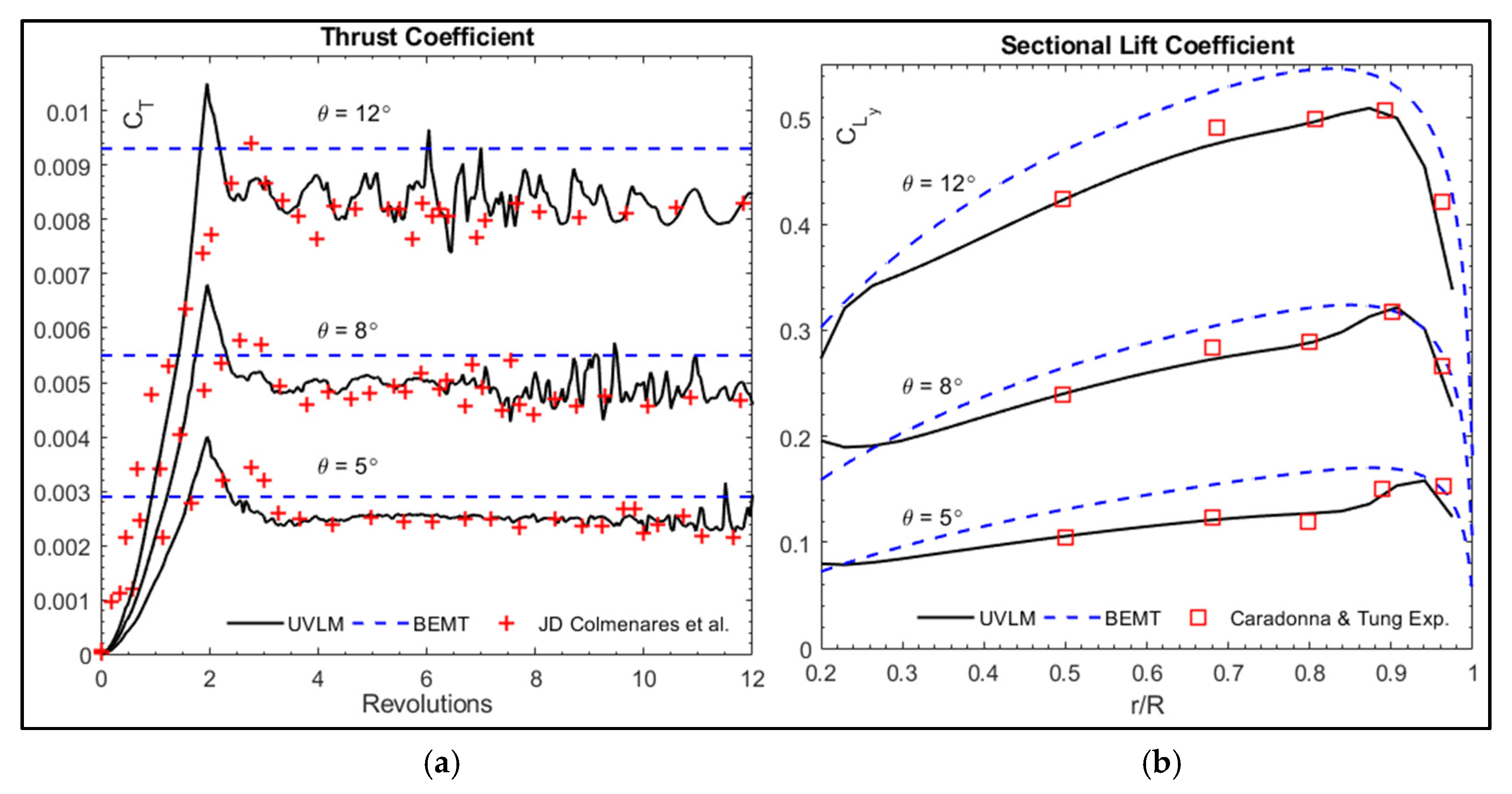
3.2.1. Two-Blade Hovering Rotor
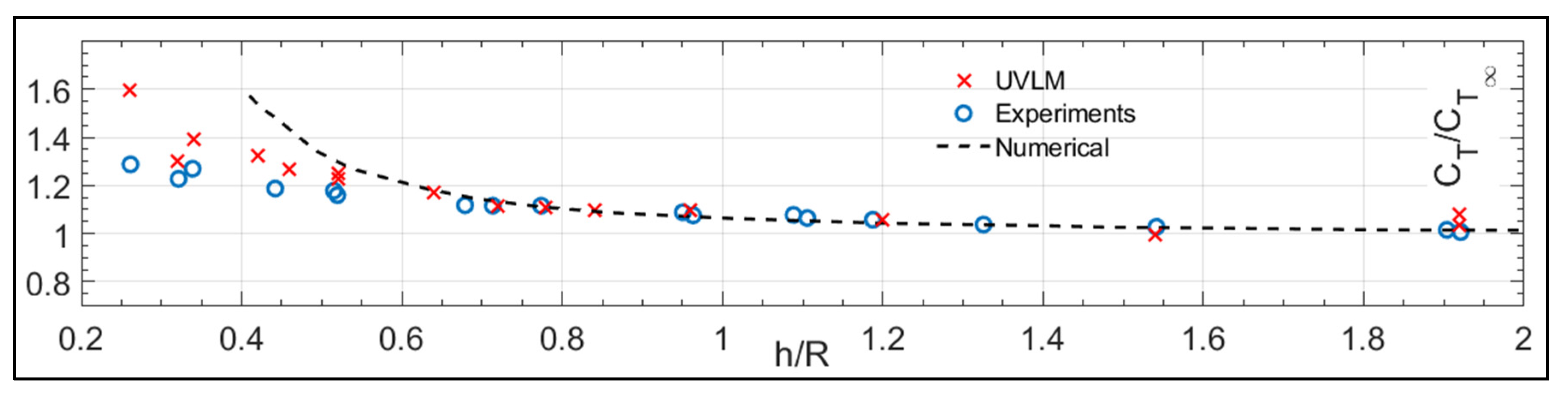
3.2.2. Four-Blade Hovering Rotor in Ground Effect
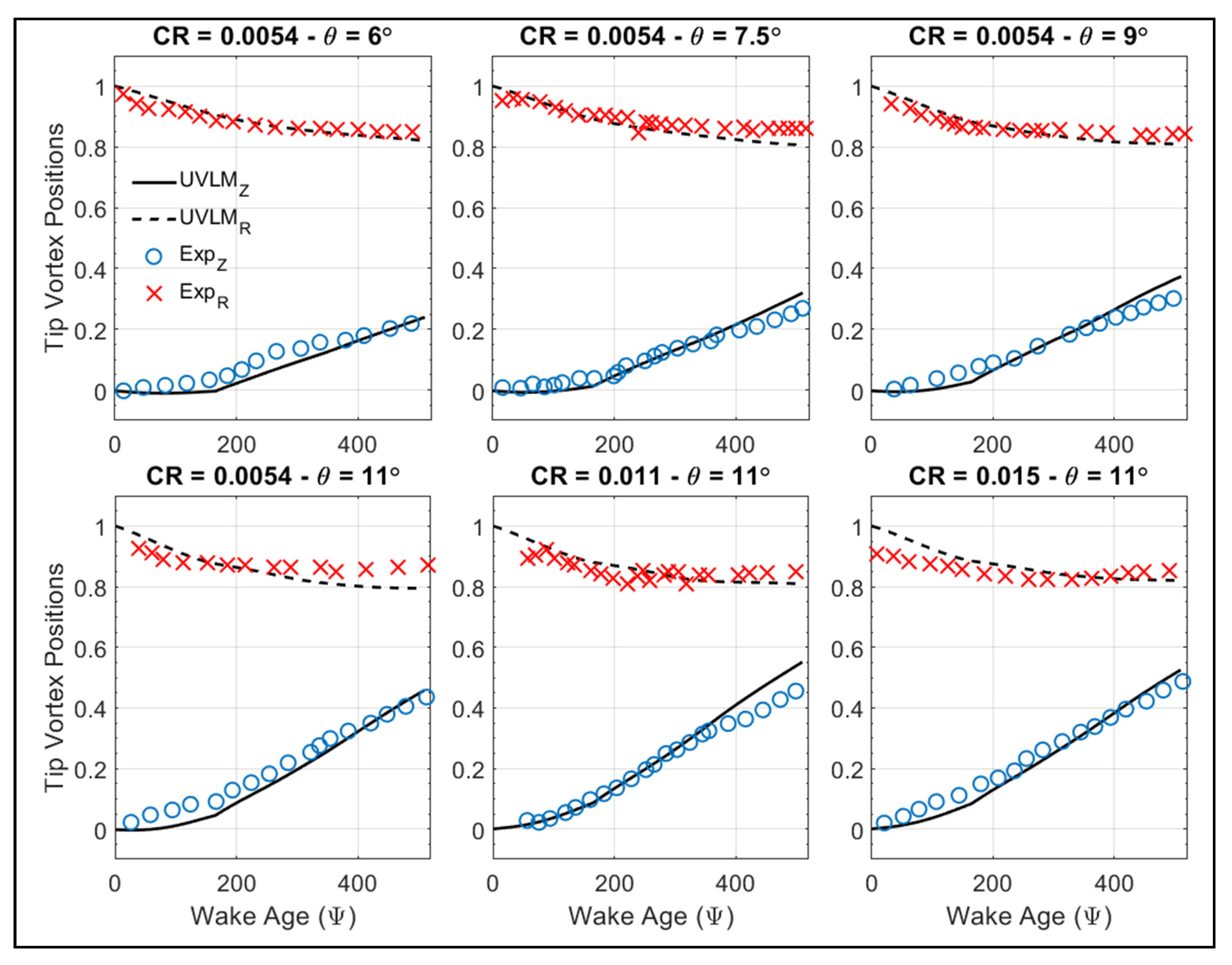
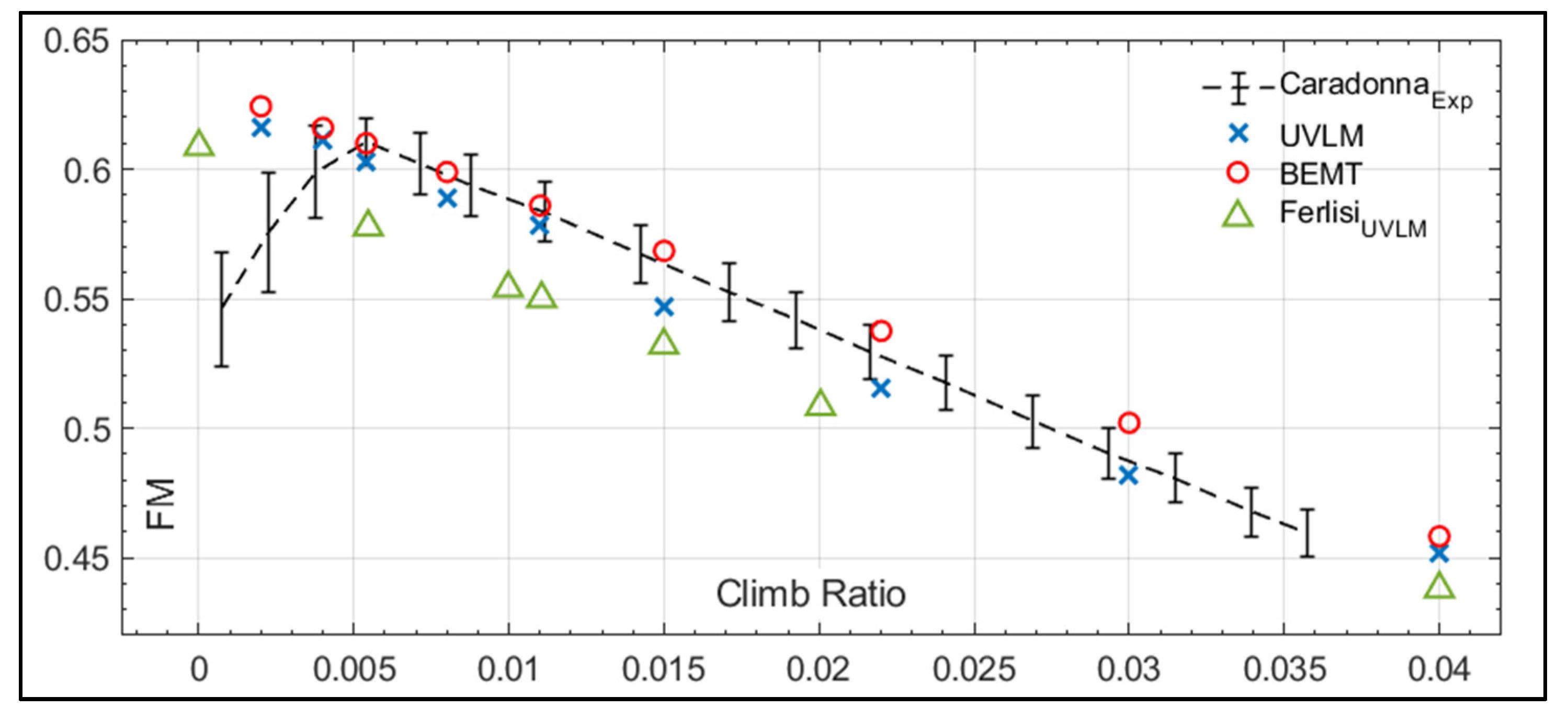
3.2.3. Two-Blade Rotor in Axial Flight
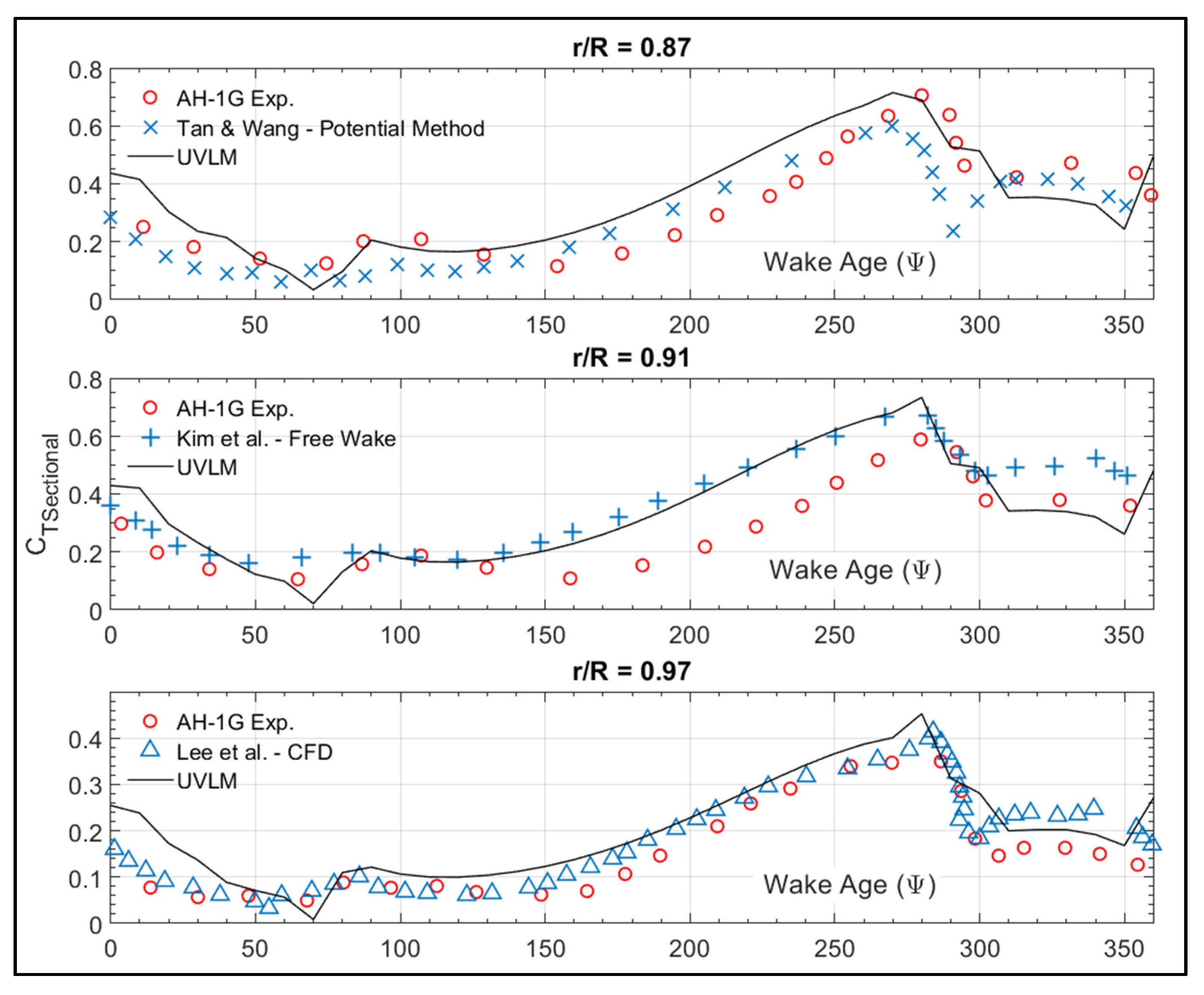
3.2.4. Two-Blade Rotor in Forward Flight
3.3. Rotor Heat Transfer Results
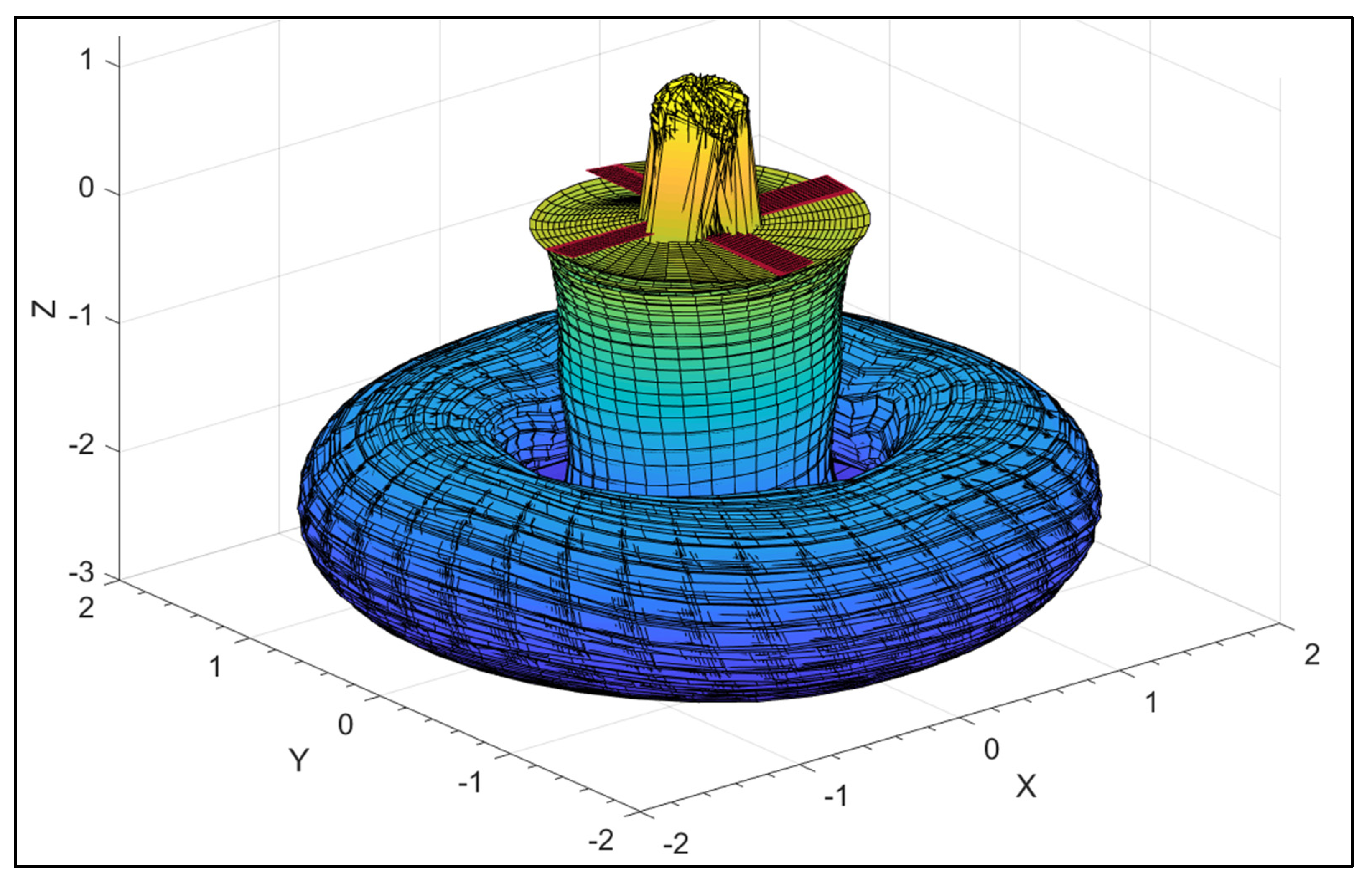
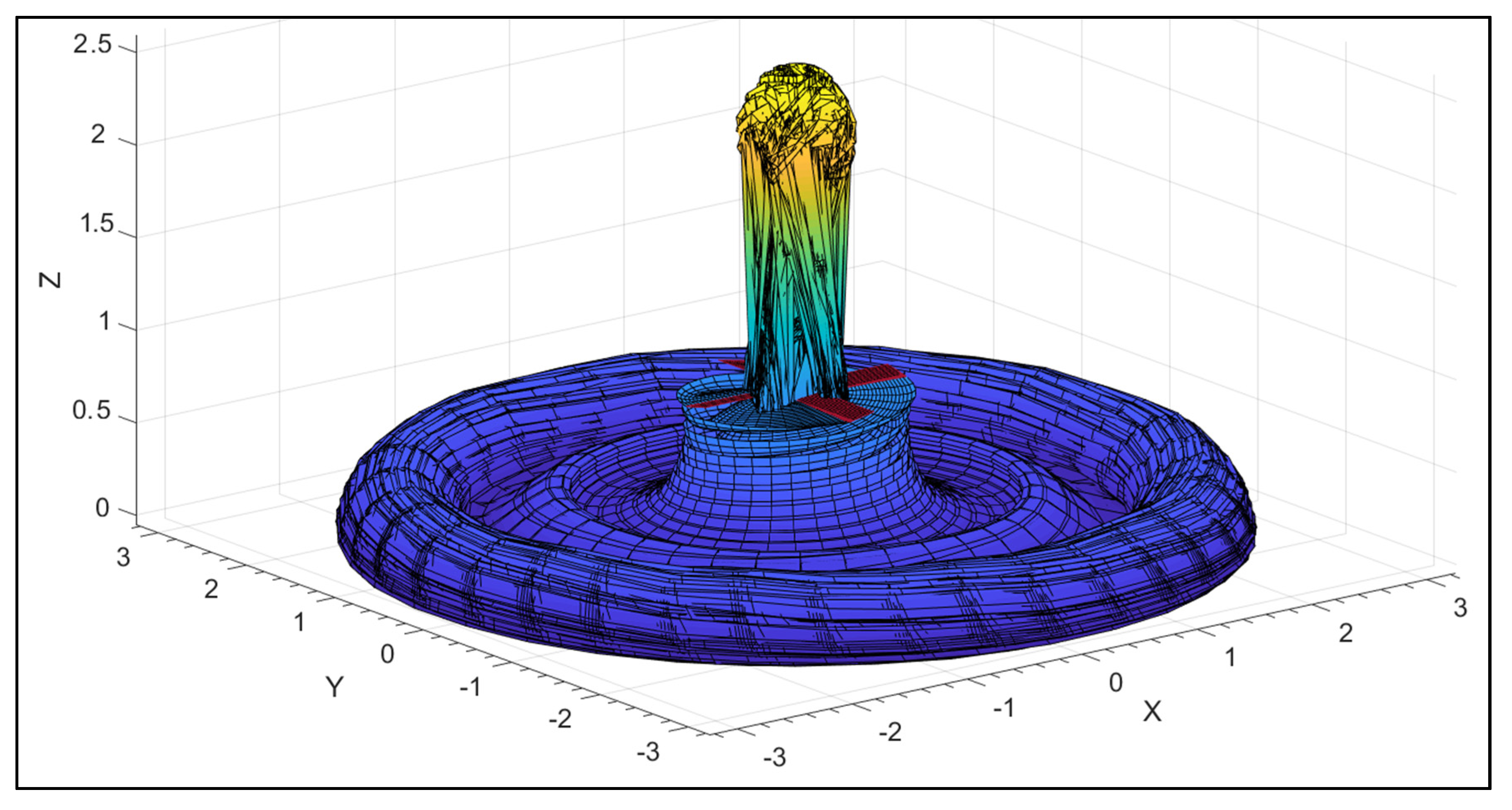
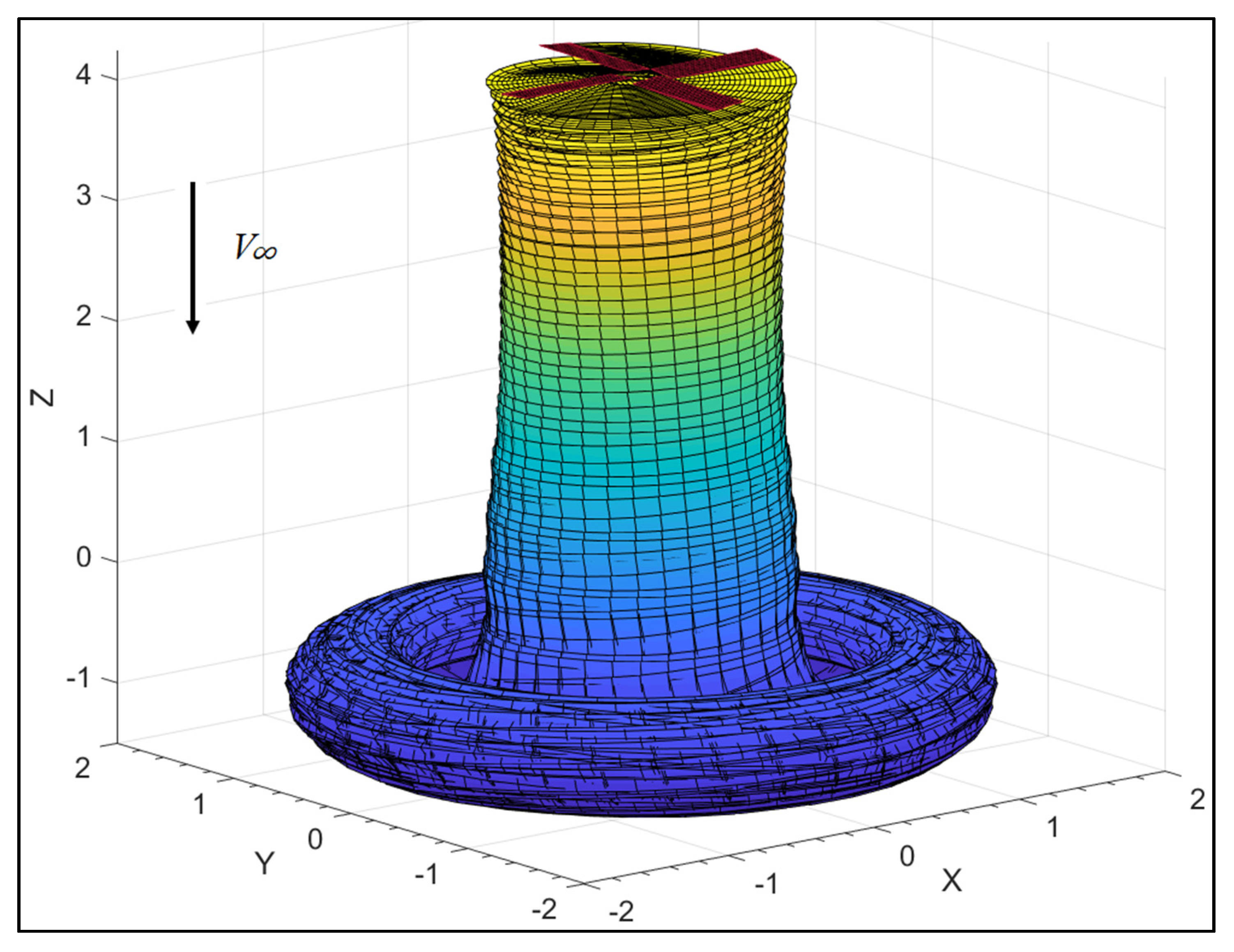
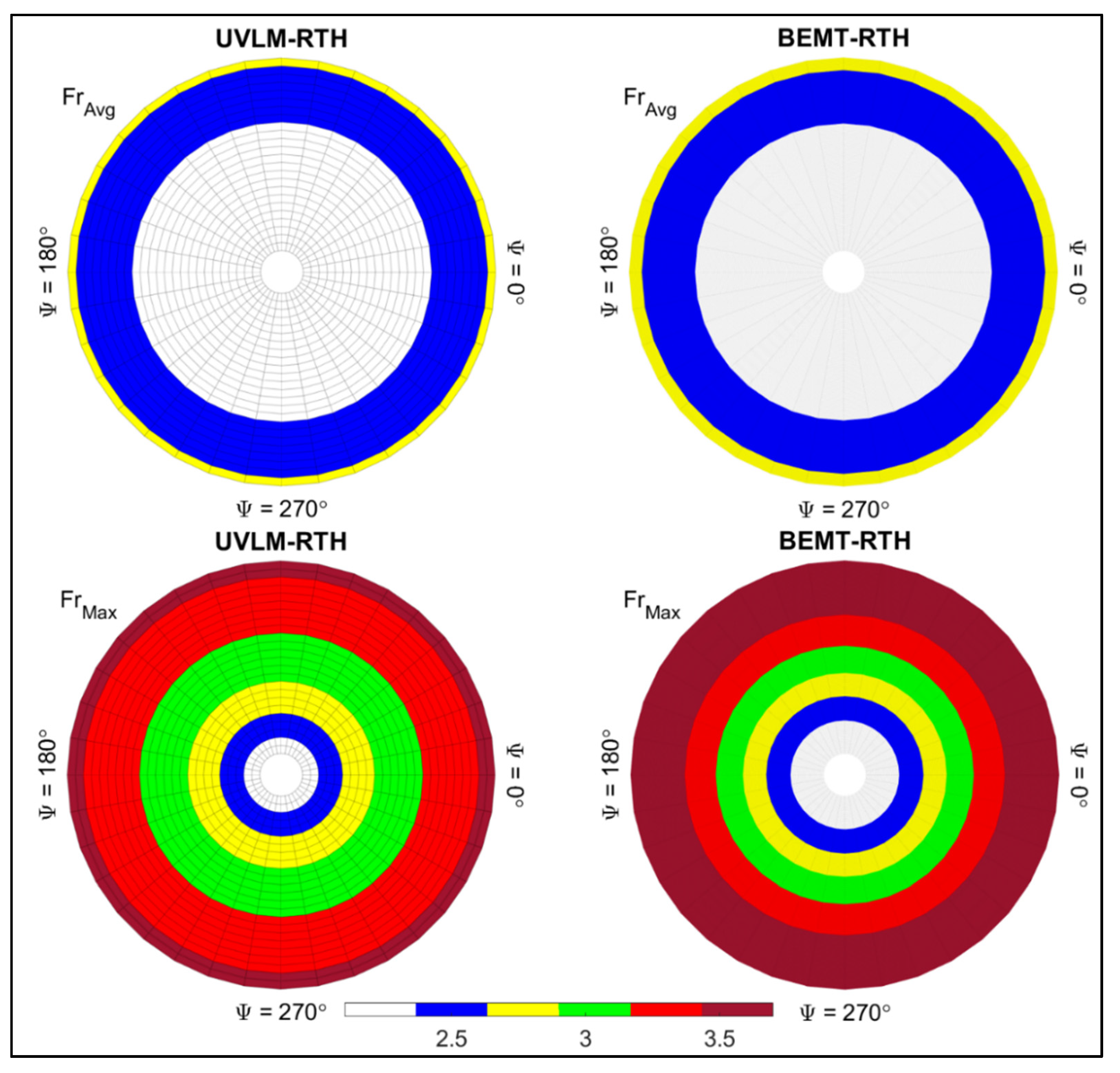
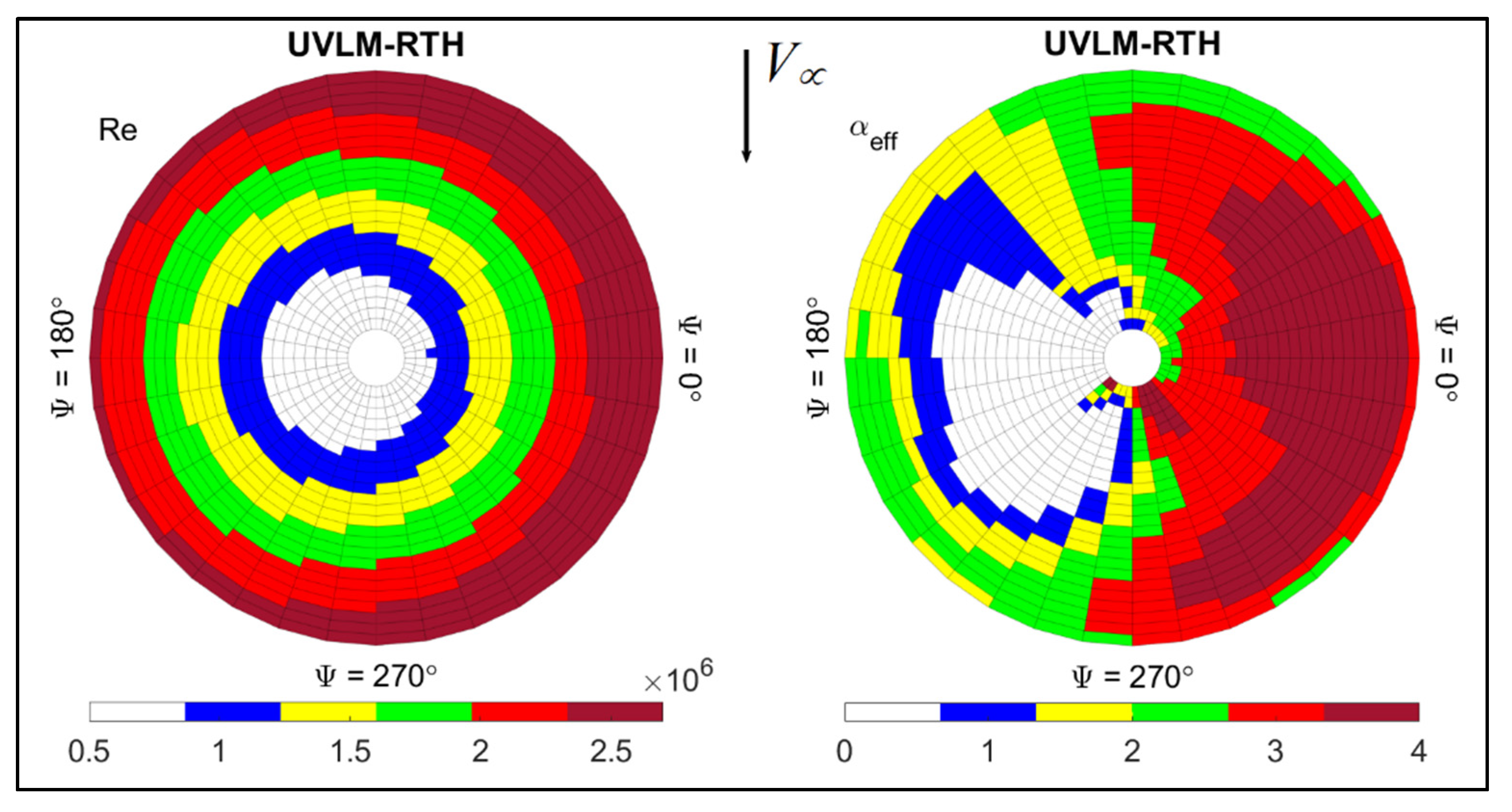
3.3.1. Hover Out of Ground Effect (OGE)
3.3.2. Hover in Ground Effect (IGE)
3.3.3. Axial Flight
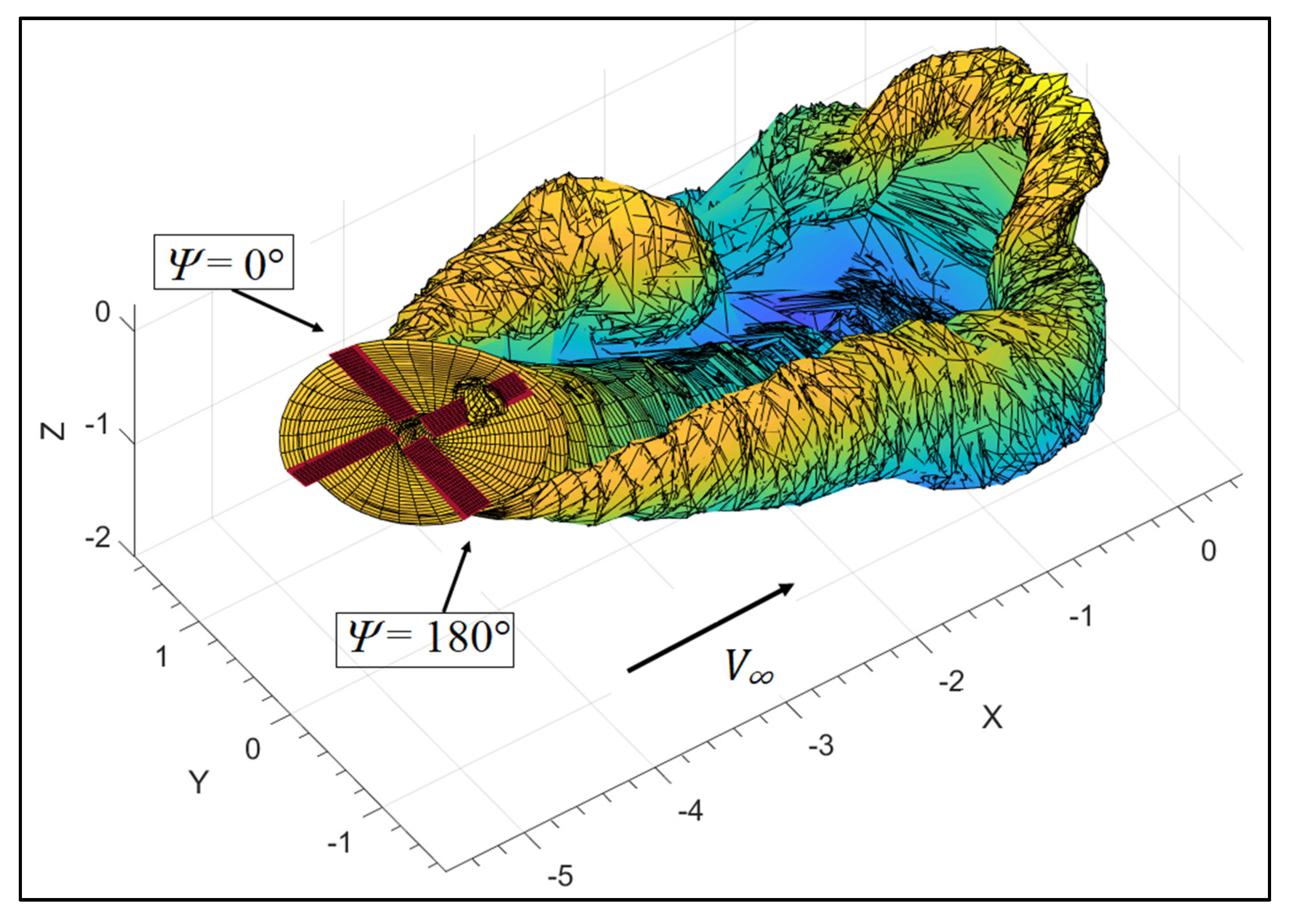
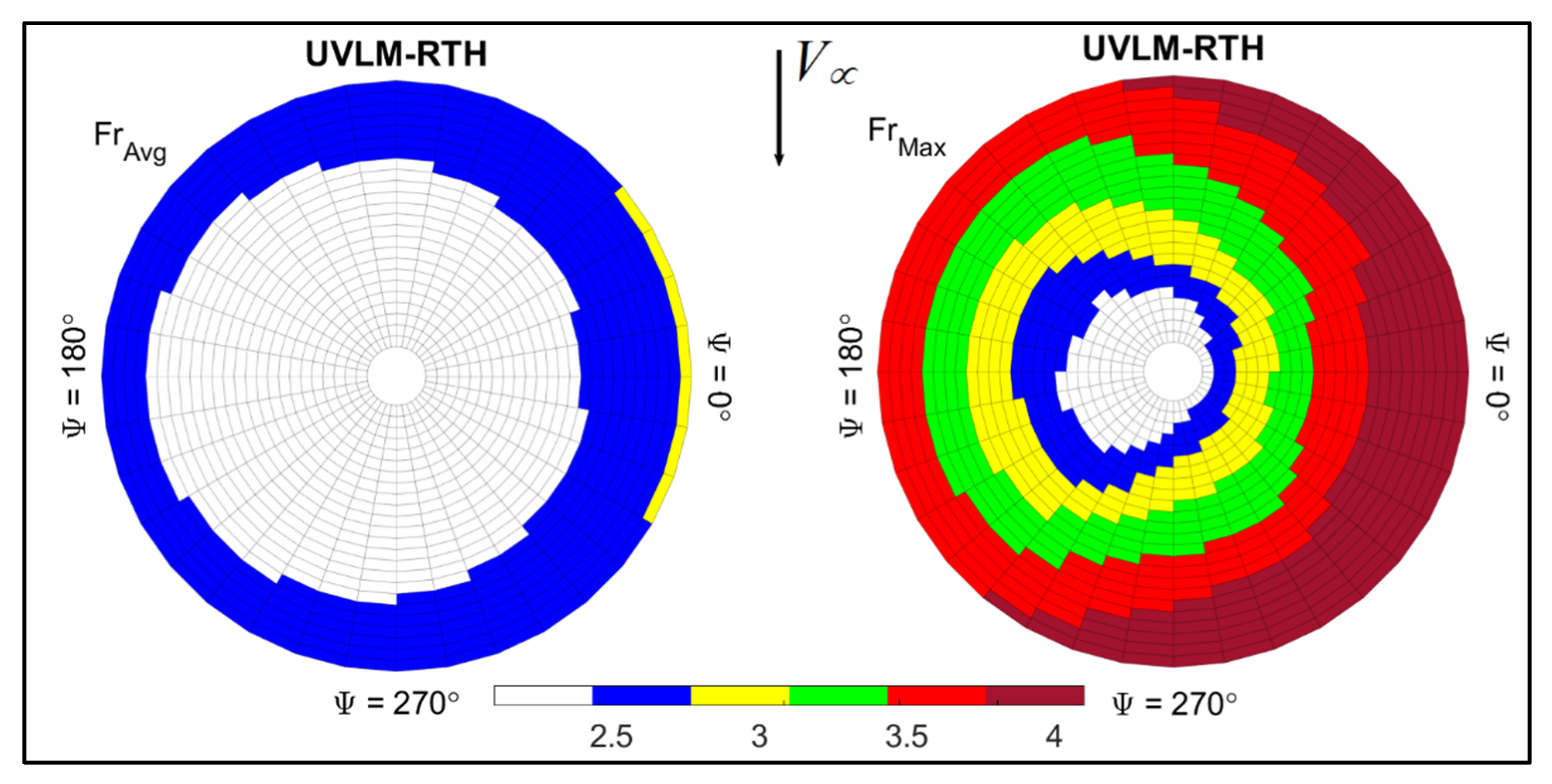
3.3.4. Forward Flight
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Guidelines for Aircraft Ground Icing Operations, 3rd ed.; Transport Canada: Ottawa, ON, Canada, 2018.
- Helicopter Flying Handbook; Branch, A.T.S. (Ed.) United States Department of Transportation—Federal Aviation Administration: Washington, DC, USA, 2012.
- Reid, T.; Baruzzi, G.S.; Habashi, W.G. FENSAP-ICE: Unsteady conjugate heat transfer simulation of electrothermal de-icing. J. Aircr. 2012, 49, 1101–1109. [Google Scholar] [CrossRef]
- Pourbagian, M.; Habashi, W.G. Parametric analysis of energy requirements of in-flight ice protection systems. In Proceedings of the 20th Annual conference of the CFD society of Canada, Canmore, AB, Canada, 9–11 May 2012. [Google Scholar]
- Hannat, R.; Morency, F. Numerical validation of conjugate heat transfer method for anti-/de-icing piccolo system. J. Aircr. 2014, 51, 104–116. [Google Scholar] [CrossRef]
- Mu, Z.; Lin, G.; Shen, X.; Bu, X.; Zhou, Y. Numerical simulation of unsteady conjugate heat transfer of electrothermal deicing process. Int. J. Aerosp. Eng. 2018, 2018, 5362541. [Google Scholar] [CrossRef]
- Gallay, S.; Laurendeau, E. Nonlinear generalized lifting-line coupling algorithms for pre/poststall flows. AIAA J. 2015, 53, 1784–1792. [Google Scholar] [CrossRef]
- Van Dam, C. The aerodynamic design of multi-element high-lift systems for transport airplanes. Prog. Aerosp. Sci. 2002, 38, 101–144. [Google Scholar] [CrossRef] [Green Version]
- Gallay, S.; Laurendeau, E. Preliminary-design aerodynamic model for complex configurations using lifting-line coupling algorithm. J. Aircr. 2016, 53, 1145–1159. [Google Scholar] [CrossRef]
- Parenteau, M.; Plante, F.; Laurendeau, E.; Costes, M. Unsteady Coupling Algorithm for Lifting-Line Methods. In Proceedings of the 55th Aerospace Sciences Meeting, Grapevine, TX, USA, 9–13 January 2017; p. 0951. [Google Scholar]
- Parenteau, M.; Sermeus, K.; Laurendeau, E. VLM Coupled with 2.5 D RANS Sectional Data for High-Lift Design. In Proceedings of the 55th Aerospace Sciences Meeting, Kissimmee, FL, USA, 8–12 January 2018; p. 1049. [Google Scholar]
- Bourgault-Cote, S.; Parenteau, M.; Laurendeau, E. Quasi-3D multi-layer ice accretion model using a Vortex Lattice Method combined with 2.5 D RANS solutions. In Proceedings of the 54rd 3AF International Conference on Applied Aerodynamics, Paris, France, 25–27 March 2019. [Google Scholar]
- Edmunds, M.; Malki, R.; Williams, A.; Masters, I.; Croft, T. Aspects of tidal stream turbine modelling in the natural environment using a coupled BEM–CFD model. Int. J. Mar. Energy 2014, 7, 20–42. [Google Scholar] [CrossRef] [Green Version]
- Masters, I.; Malki, R.; Williams, A.J.; Croft, T.N. The influence of flow acceleration on tidal stream turbine wake dynamics: A numerical study using a coupled BEM–CFD model. Appl. Math. Model. 2013, 37, 7905–7918. [Google Scholar] [CrossRef]
- Sun, Z.; Chen, J.; Shen, W.Z.; Zhu, W.J. Improved blade element momentum theory for wind turbine aerodynamic computations. Renew. Energy 2016, 96, 824–831. [Google Scholar] [CrossRef]
- Olczak, A.; Stallard, T.; Feng, T.; Stansby, P. Comparison of a RANS blade element model for tidal turbine arrays with laboratory scale measurements of wake velocity and rotor thrust. J. Fluids Struct. 2016, 64, 87–106. [Google Scholar] [CrossRef]
- Colmenares, J.D.; López, O.D.; Preidikman, S. Computational study of a transverse rotor aircraft in hover using the unsteady vortex lattice method. Math. Probl. Eng. 2015, 2015, 478457. [Google Scholar] [CrossRef] [Green Version]
- Chung, K.H.; Kim, J.W.; Ryu, K.W.; Lee, K.T.; Lee, D.J. Sound generation and radiation from rotor tip-vortex pairing phenomenon. Am. Inst. Aeronaut. Astronaut. 2006, 44, 1181–1187. [Google Scholar] [CrossRef]
- Ferlisi, C. Rotor Wake Modelling Using the Vortex-Lattice Method. Master’s Thesis, École Polytechnique de Montréal, Montréal, QC, Canada, 2018. [Google Scholar]
- Pérez, A.M.; Lopez, O.; Poroseva, S.V. Free-Vortex Wake and CFD Simulation of a Small Rotor for a Quadcopter at Hover. In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019; p. 0597. [Google Scholar]
- Bhagwat, M.J.; Leishman, J.G. Generalized viscous vortex model for application to free-vortex wake and aeroacoustic calculations. In Proceedings of the Paper presented at the 58th Annual Forum Proceedings- American Helicopter Society, Montreal, QC, Canada, 11–13 June 2002. [Google Scholar]
- Poinsatte, P.E. Heat Transfer Measurements from a NACA 0012 Airfoil in Flight and in the NASA Lewis Icing Research Tunnel. Master’s Thesis, University of Toledo, Toledo, OH, USA, 1990. [Google Scholar]
- Poinsatte, P.E.; Newton, J.E.; De Witt, K.J.; Van Fossen, G.J. Heat transfer measurements from a smooth NACA 0012 airfoil. J. Aircr. 1991, 28, 892–898. [Google Scholar] [CrossRef]
- Henry, R.C.; Guffond, D.; Garnier, F.; Bouveret, A. Heat transfer coefficient measurement on iced airfoil in small icing wind tunnel. J. Thermophys. Heat Transf. 2000, 14, 348–354. [Google Scholar] [CrossRef]
- Wang, X.; Bibeau, E.; Naterer, G. Experimental correlation of forced convection heat transfer from a NACA airfoil. Exp. Therm. Fluid Sci. 2007, 31, 1073–1082. [Google Scholar] [CrossRef]
- Wang, X.; Naterer, G.; Bibeau, E. Convective heat transfer from a NACA airfoil at varying angles of attack. J. Thermophys. Heat Transf. 2008, 22, 457–463. [Google Scholar] [CrossRef]
- Li, G.; Gutmark, E.J.; Ruggeri, R.T.; Mabe, J. Heat Transfer and Pressure Measurements on a Thick Airfoil. J. Aircr. 2009, 46, 2130–2138. [Google Scholar] [CrossRef]
- Incropera, F.P.; Lavine, A.S.; Bergman, T.L.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]
- Abdollahzadeh, M.; Esmaeilpour, M.; Vizinho, R.; Younesi, A.; Pàscoa, J. Assessment of RANS turbulence models for numerical study of laminar-turbulent transition in convection heat transfer. Int. J. Heat Mass Transf. 2017, 115, 1288–1308. [Google Scholar] [CrossRef]
- Rumsey, C.; Smith, B.; Huang, G. 2D Finite Flat Plate Validation Case. Available online: https://turbmodels.larc.nasa.gov/finiteflatplatenumerics_val.html (accessed on 1 August 2019).
- Rumsey, C.; Smith, B.; Huang, G. 2D NACA 0012 Airfoil Validation Case. Available online: https://turbmodels.larc.nasa.gov/naca0012_val.html (accessed on 1 August 2019).
- Kays, W.M. Convective Heat and Mass Transfer; Tata McGraw-Hill Education: New York, NY, USA, 2012. [Google Scholar]
- Leishman, G.J. Principles of Helicopter Aerodynamics with CD Extra; Cambridge University Press: New York, NY, USA, 2006. [Google Scholar]
- Katz, J.; Plotkin, A. Low Speed Aerodynamics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2001; Volume 13. [Google Scholar]
- Leishman, J.G.; Bhagwat, M.J.; Bagai, A. Free-vortex filament methods for the analysis of helicopter rotor wakes. J. Aircr. 2002, 39, 759–775. [Google Scholar] [CrossRef]
- Glauert, H. The effect of compressibility on the lift of an aerofoil. Proc. R. Soc. 1928, 118, 113–119. [Google Scholar]
- Aupoix, B.; Spalart, P. Extensions of the Spalart–Allmaras turbulence model to account for wall roughness. Int. J. Heat Fluid Flow 2003, 24, 454–462. [Google Scholar] [CrossRef]
- Samad, A.; Morency, F.; Volat, C. A Numerical Model of the Blade Element Momentum Method for Rotating Airfoils with Heat Transfer Calculation. In Proceedings of the Joint Thermophysics and Heat Transfer Conference, Atlanta, GA, USA, 25–29 June 2018; p. 4077. [Google Scholar]
- Caradonna, F.X.; Tung, C. Experimental and analytical studies of a model helicopter rotor in hover. In Proceedings of the 6th European Rotorcraft and Powered Lift Aircraft Forum, Bristol, UK, 16–19 September 1980. [Google Scholar]
- Light, J.S. Tip vortex geometry of a hovering helicopter rotor in ground effect. J. Am. Helicopter Soc. 1993, 38, 34–42. [Google Scholar] [CrossRef]
- Cheeseman, I.; Bennett, W. The Effect of Ground on a Helicopter Rotor in Forward Flight; Ministry of Supply: London, UK, 1955. [Google Scholar]
- Caradonna, F. Performance measurement and wake characteristics of a model rotor in axial flight. J. Am. Helicopter Soc. 1999, 44, 101–108. [Google Scholar] [CrossRef]
- Cross, J.L. Tip Aerodynamics and Acoustics Test: A Report and Data Survey; NASA Ames Research Center: Moffett Field, CA, USA, 1988. [Google Scholar]
- Tan, J.; Wang, H. Panel/full-span free-wake coupled method for unsteady aerodynamics of helicopter rotor blade. Chin. J. Aeronaut. 2013, 26, 535–543. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.W.; Park, S.H.; Yu, Y.H. Euler and Navier-Stokes simulations of helicopter rotor blade in forward flight using an overlapped grid solver. In Proceedings of the 19th AIAA Computational Fluid Dynamics, San Antonio, TX, USA, 22–25 June 2009; p. 4268. [Google Scholar]
- Lee, J.B.; Yee, K.J.; Oh, S.J.; Kim, D.H. Development of an unsteady aerodynamic analysis module for rotor comprehensive analysis code. Int. J. Aeronaut. Space Sci. 2009, 10, 23–33. [Google Scholar] [CrossRef] [Green Version]
- Gennaretti, M.; Bernardini, G.; Serafini, J.; Romani, G. Rotorcraft comprehensive code assessment for blade–vortex interaction conditions. Aerosp. Sci. Technol. 2018, 80, 232–246. [Google Scholar] [CrossRef]





| Without CFD Database | With CFD Database | ||
|---|---|---|---|
| BEMT | 1 | Guess a value for λ | |
| 2 | Calculate tip loss factor F | ||
| 3 | Calculate αeff and φ (Equations (2) and (3)) | ||
| 4 | Redo until convergence (|λ i+1−λ i| = 10−5) | ||
| Aerodynamic Coefficients | 5 | Obtain CL-inv and CD-inv by a correlation | Obtain CL-visc and CD-visc from viscous database by interpolating αeff |
| Thrust and torque | 6 | Calculate incremental dCT, dCPi and dCPo, Output CT, CP and CQ | |
| Heat transfer | 7 | For every Re and αeff at every r, calculate Fr | |
| Step | Task | |
|---|---|---|
| UVLM | 1 | Blade camber line geometry and flight path kinematics |
| 2 | Blade influence coefficients matrix A | |
| 3 | Form the right-hand side matrix RHS | |
| 4 | Solve RHS to obtain Γ | |
| 5 | Pressure and forces calculation (CT, CLy, …) | |
| 6 | Wake rollup | |
| Heat transfer | 7 | Viscous coupling algorithm (Re, CL-visc, and αeff) |
| 8 | For every Re and αeff at every collocation point, calculate Fr |
| Constant Surface Temperature TS | Constant Surface Heat Flux QS |
|---|---|
| [32] | S-A CFD data, Aupoix et al. [37] |
| [28] | S-A CFD data, Abdollahzadeh et al. [29] |
| UVLM | BEMT | Ferlisi | Colmenares et al. | Caradonna and Tung | |
|---|---|---|---|---|---|
| θ = 5° | 0.00243 | 0.00290 | 0.00237 | 0.00221 | 0.00213 |
| θ = 8° | 0.00477 | 0.00540 | 0.00460 | 0.00467 | 0.00459 |
| θ = 12° | 0.00794 | 0.00910 | 0.00824 | 0.00821 | 0.00796 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samad, A.; Tagawa, G.B.S.; Morency, F.; Volat, C. Predicting Rotor Heat Transfer Using the Viscous Blade Element Momentum Theory and Unsteady Vortex Lattice Method. Aerospace 2020, 7, 90. https://doi.org/10.3390/aerospace7070090
Samad A, Tagawa GBS, Morency F, Volat C. Predicting Rotor Heat Transfer Using the Viscous Blade Element Momentum Theory and Unsteady Vortex Lattice Method. Aerospace. 2020; 7(7):90. https://doi.org/10.3390/aerospace7070090
Chicago/Turabian StyleSamad, Abdallah, Gitsuzo B. S. Tagawa, François Morency, and Christophe Volat. 2020. "Predicting Rotor Heat Transfer Using the Viscous Blade Element Momentum Theory and Unsteady Vortex Lattice Method" Aerospace 7, no. 7: 90. https://doi.org/10.3390/aerospace7070090
APA StyleSamad, A., Tagawa, G. B. S., Morency, F., & Volat, C. (2020). Predicting Rotor Heat Transfer Using the Viscous Blade Element Momentum Theory and Unsteady Vortex Lattice Method. Aerospace, 7(7), 90. https://doi.org/10.3390/aerospace7070090







