Unsteady Lift Prediction with a Higher-Order Potential Flow Method
Abstract
1. Introduction
1.1. Motivation
1.2. Background on Unsteady Lift Prediction
2. Method
3. Results
3.1. Panel and Time-Step Size Constraint
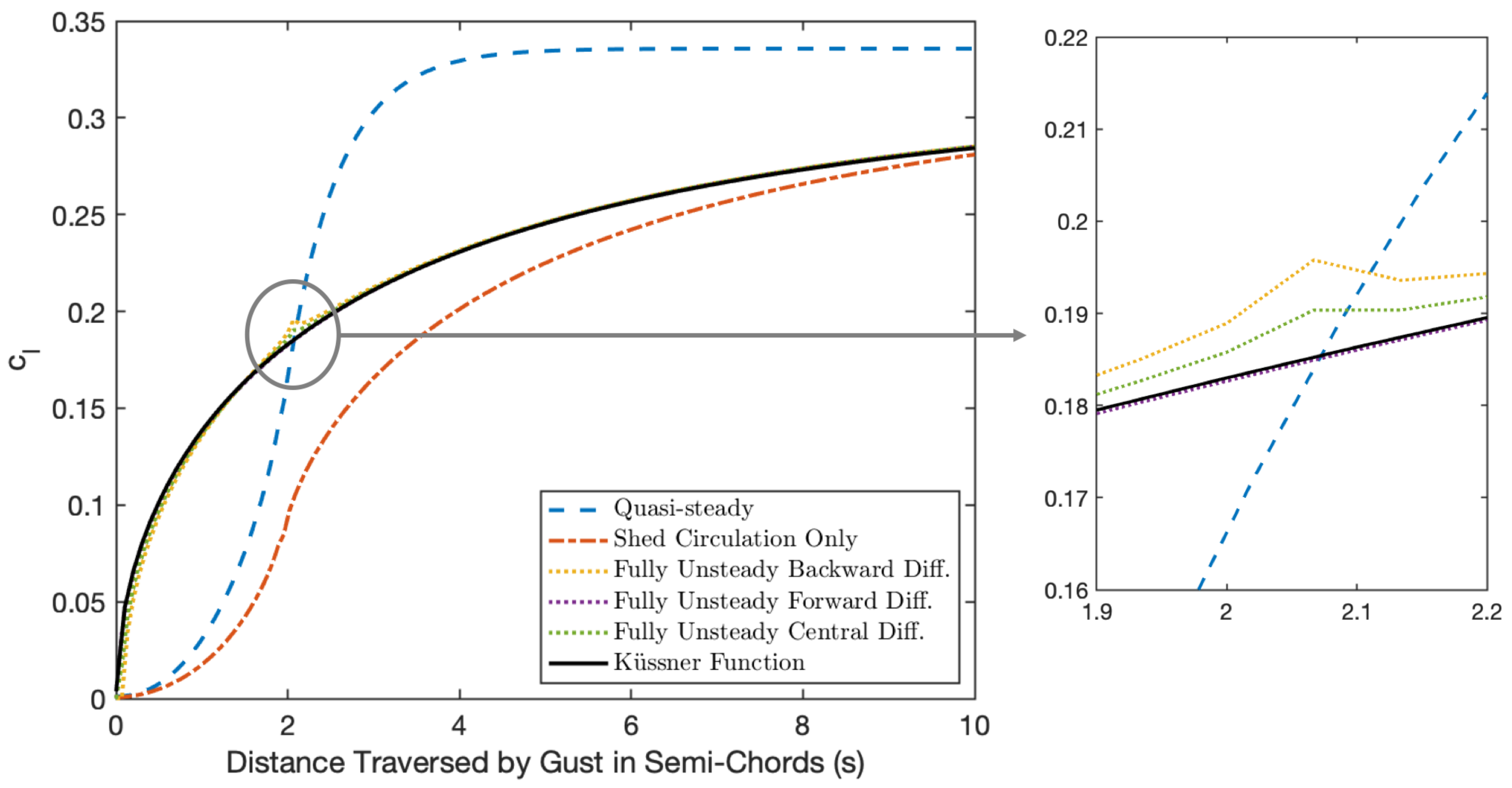
3.2. Sharp-Edged Gust Verification
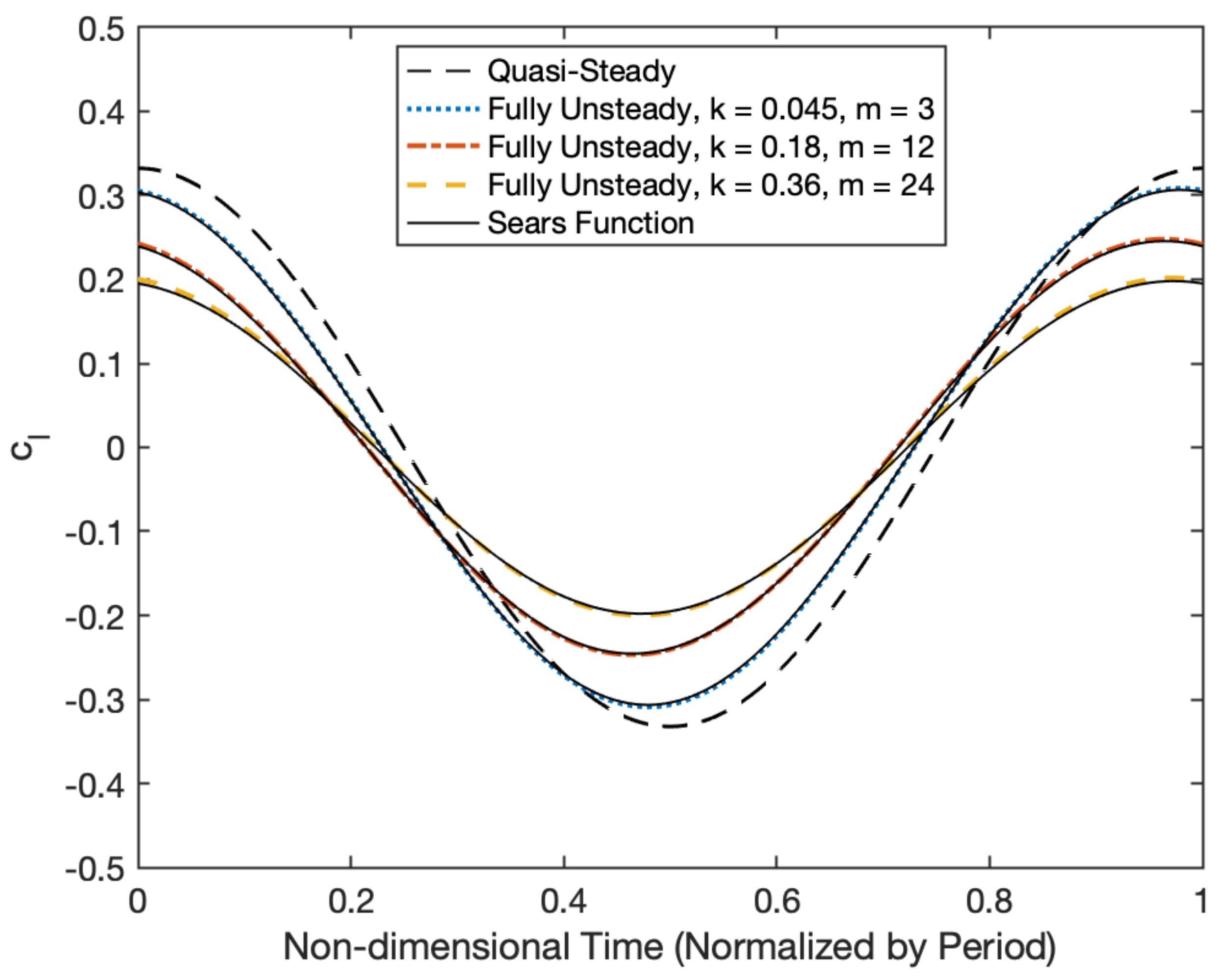
3.3. Sinusoidal Gust Verification
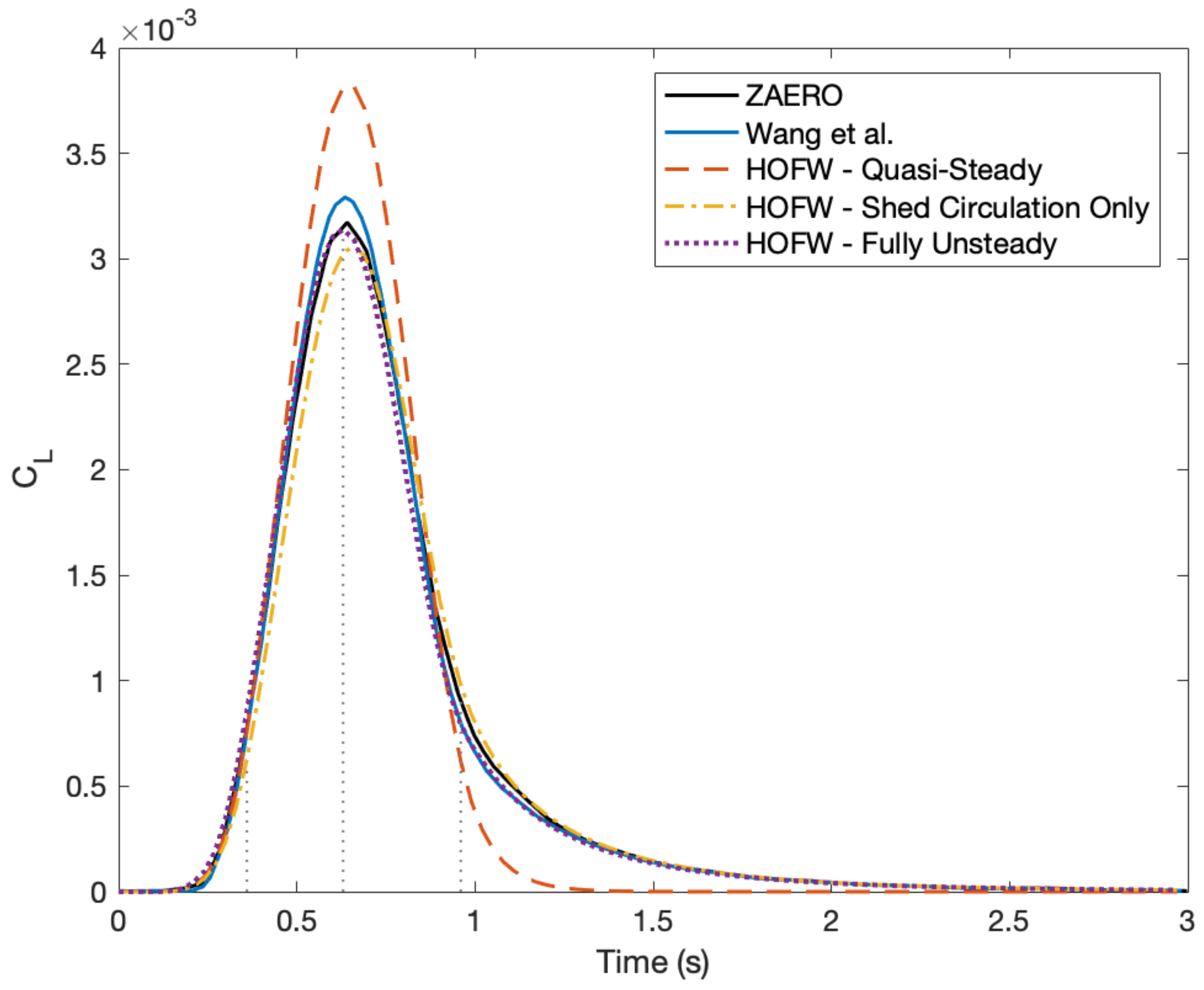
3.4. Finite Wing Comparison
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| Circulation coefficients | |
| c | Wing chord |
| Two-dimensional lift coefficient | |
| Three-dimensional lift coefficient | |
| Theodorsen function | |
| D | Propeller diameter |
| Distributed vorticity element | |
| Higher-order fixed-wake | |
| k | Reduced frequency |
| m | Number of lifting lines |
| n | Number of spanwise panels |
| q | Freestream dynamic pressure |
| s | Semi-chord of wing or airfoil () |
| Sears function | |
| Unit vector aligned with lifting line | |
| Surface DVE | |
| u,v,w | Components of the velocity in the global reference frame |
| Velocity vector | |
| Freestream velocity vector | |
| Magnitude of the vertical gust | |
| Ratio of the distance traversed by a wing in a time-step to the length of a surface DVE | |
| Vorticity | |
| Circulation | |
| Coordinate in DVE reference frame orthogonal to and | |
| Spanwise coordinate in the DVE reference frame | |
| Streamwise coordinate in the DVE reference frame | |
| Air density | |
| Frequency of oscillations in unsteady flow |
References
- Bramesfeld, G. A Higher Order Vortex-Lattice Method with a Force-Free Wake. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2006. [Google Scholar]
- Bramesfeld, G.; Maughmer, M.D. Relaxed-Wake Vortex-Lattice Method Using Distributed Vorticity Elements. J. Aircr. 2008, 45, 560–568. [Google Scholar] [CrossRef]
- Cole, J. A Higher-Order Free-Wake Method for Aerodynamic Performance Prediction of Propeller-Wing Systems. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2016. [Google Scholar]
- Cole, J.A.; Maughmer, M.D.; Kinzel, M.; Bramesfeld, G. Higher-Order Free-Wake Method for Propeller–Wing Systems. J. Aircr. 2019, 56, 150–165. [Google Scholar] [CrossRef]
- Leishman, J. Principles of Helicopter Aerodynamics; Cambridge University Press: Cambridge, UK, 2006. [Google Scholar]
- Katz, J.; Plotkin, A. Low-Speed Aerodynamics, 2nd ed.; Cambridge University Press: Cambridge, UK, 2001. [Google Scholar]
- Drela, M. Flight Vehicle Aerodynamics; The MIT Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Drela, M. Integrated Simulation Model for Preliminary Aerodynamic, Structural, and Control-Law Design of Aircraft; AIAA Paper 99-1394; AIAA: Reston, VA, USA, 1999. [Google Scholar] [CrossRef]
- Simpson, R.J.S.; Palacios, R.; Murua, J. Induced-Drag Calculations in the Unsteady Vortex Lattice Method. AIAA J. 2013, 51, 1775–1779. [Google Scholar] [CrossRef]
- Leishman, J. Subsonic Unsteady Aerodynamics Caused by Gusts Using the Indicial Method. J. Aircr. 1996, 33, 869–879. [Google Scholar] [CrossRef]
- Saberi, H.; Khoshlahjeh, M.; Ormiston, R.; Rutkowski, M. Overview of RCAS and Application to Advanced Rotorcraft Problems. In Proceedings of the AHS 4th Decennial Specialist’s Conference on Aeromechanics. American Helicopter Society International, San Francisco, CA, USA, 21–23 January 2004. [Google Scholar]
- Johnson, W. A General Free Wake Geometry Calculation For Wings and Rotors. In Proceedings of the AHS 51st Annual Forum Proceedings, Forum, TX, USA, 9–11 May 1995; American Helicopter Society: Fairfax, VA, USA, 1995. [Google Scholar]
- Johnson, W. Rotorcraft aerodynamics models for a comprehensive analysis. In Proceedings of the AHS 54th Annual Forum Proceedings, Washington, DC, USA, 20–22 May 1998; American Helicopter Society: Fairfax, VA, USA, 1998; Volume 54, pp. 71–94. [Google Scholar]
- Wagner, H. Über die Entstehung des dynamischen Auftriebes von Tragflügeln. ZAMM J. Appl. Math. Mech./Z. Für Angew. Math. Und Mech. 1925, 5, 17–35. [Google Scholar] [CrossRef]
- Kitson, R.; Lupp, C.A.; Cesnik, C.E.S. Modeling and Simulation of Flexible Jet Transport Aircraft with High-Aspect-Ratio Wings; AIAA Paper 2016-2046; AIAA: Reston, VA, USA, 2016. [Google Scholar] [CrossRef]
- Simpson, R.; Palacios, R. Numerical Aspects of Nonlinear Flexible Aircraft Flight Dynamics Modeling; AIAA Paper 2013-1634; AIAA: Reston, VA, USA, 2013. [Google Scholar] [CrossRef][Green Version]
- von Karman, T.; Sears, W. Airfoil Theory for Non-Uniform Motion. J. Aeronaut. Sci. 1938, 5, 379–390. [Google Scholar] [CrossRef]
- Bisplinghoff, R.; Ashley, H.; Halfman, R. Aeroelasticity; Dover Publications, Inc.: Mineola, NY, USA, 1996. [Google Scholar]
- Kayran, A. Küssner’s Function in the Sharp-Edged Gust Problem - A Correction. J. Aircr. 2006, 43, 1596–1598. [Google Scholar] [CrossRef]
- Wang, Z.; Chen, P.C.; Liu, D.; Mook, D. Nonlinear Aeroelastic Analysis for A HALE Wing Including Effects of Gust and Flow Separation. In Proceedings of the 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, Palm Springs, CA, USA, 4–7 May 2007. [Google Scholar]
- Goland, M. The flutter of a uniform cantilever wing. J. Appl. Mech. 1945, 12, A197–A208. [Google Scholar]
- ZONA. ZAERO; ZONA Technology Inc.: Scottsdale, AZ, USA, 2003. [Google Scholar]
Sample Availability: The potential flow method is available from the authors. |



© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cole, J.A.; Maughmer, M.D.; Bramesfeld, G.; Melville, M.; Kinzel, M. Unsteady Lift Prediction with a Higher-Order Potential Flow Method. Aerospace 2020, 7, 60. https://doi.org/10.3390/aerospace7050060
Cole JA, Maughmer MD, Bramesfeld G, Melville M, Kinzel M. Unsteady Lift Prediction with a Higher-Order Potential Flow Method. Aerospace. 2020; 7(5):60. https://doi.org/10.3390/aerospace7050060
Chicago/Turabian StyleCole, Julia A., Mark D. Maughmer, Goetz Bramesfeld, Michael Melville, and Michael Kinzel. 2020. "Unsteady Lift Prediction with a Higher-Order Potential Flow Method" Aerospace 7, no. 5: 60. https://doi.org/10.3390/aerospace7050060
APA StyleCole, J. A., Maughmer, M. D., Bramesfeld, G., Melville, M., & Kinzel, M. (2020). Unsteady Lift Prediction with a Higher-Order Potential Flow Method. Aerospace, 7(5), 60. https://doi.org/10.3390/aerospace7050060





