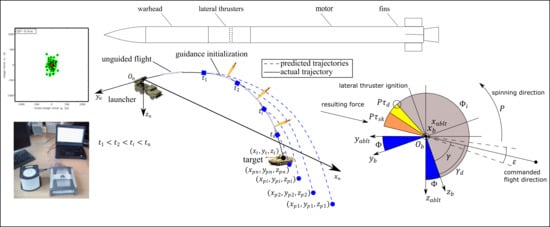
Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters
Abstract
1. Introduction
2. Materials and Methods
2.1. The Test Platform
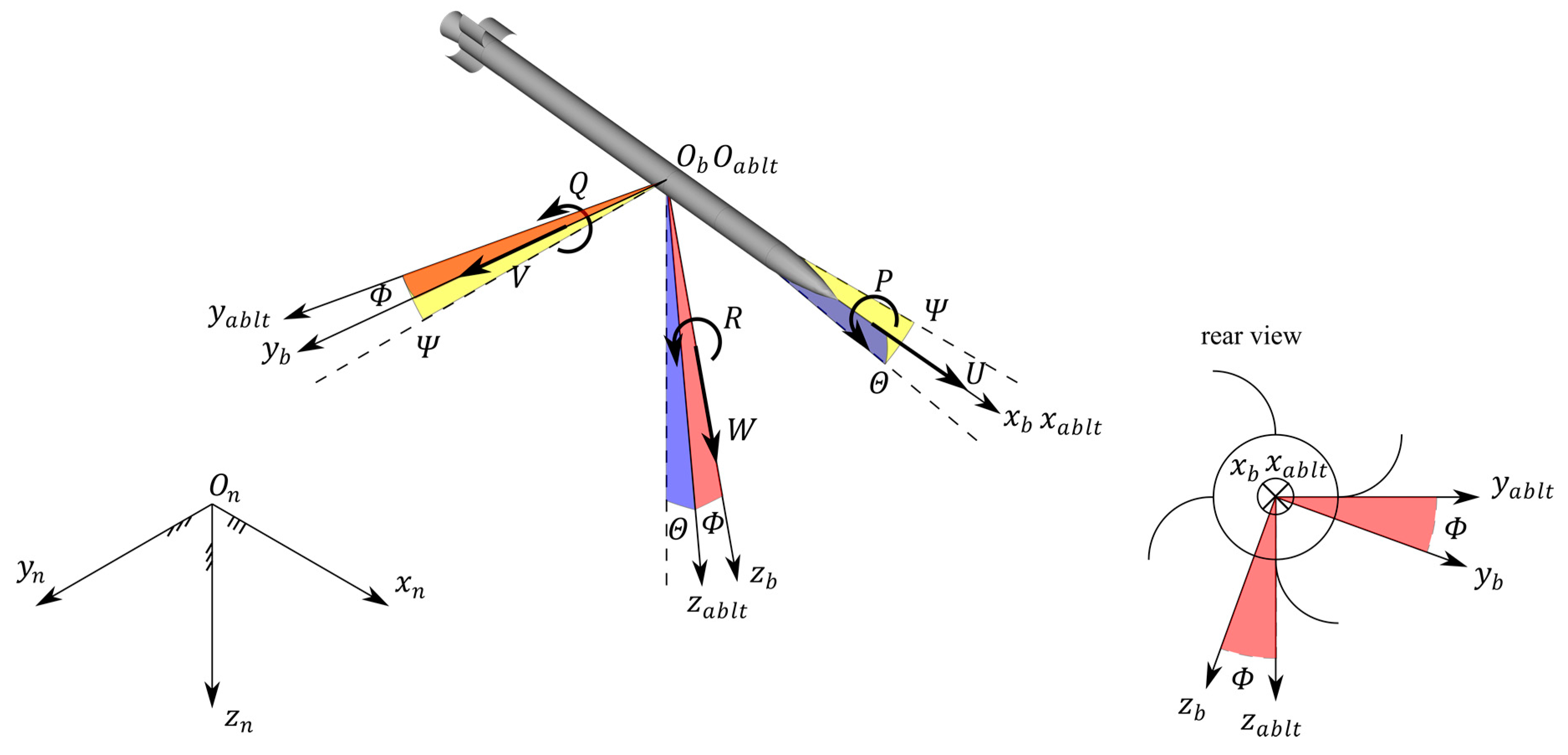
2.2. Projectile Mathematical Model
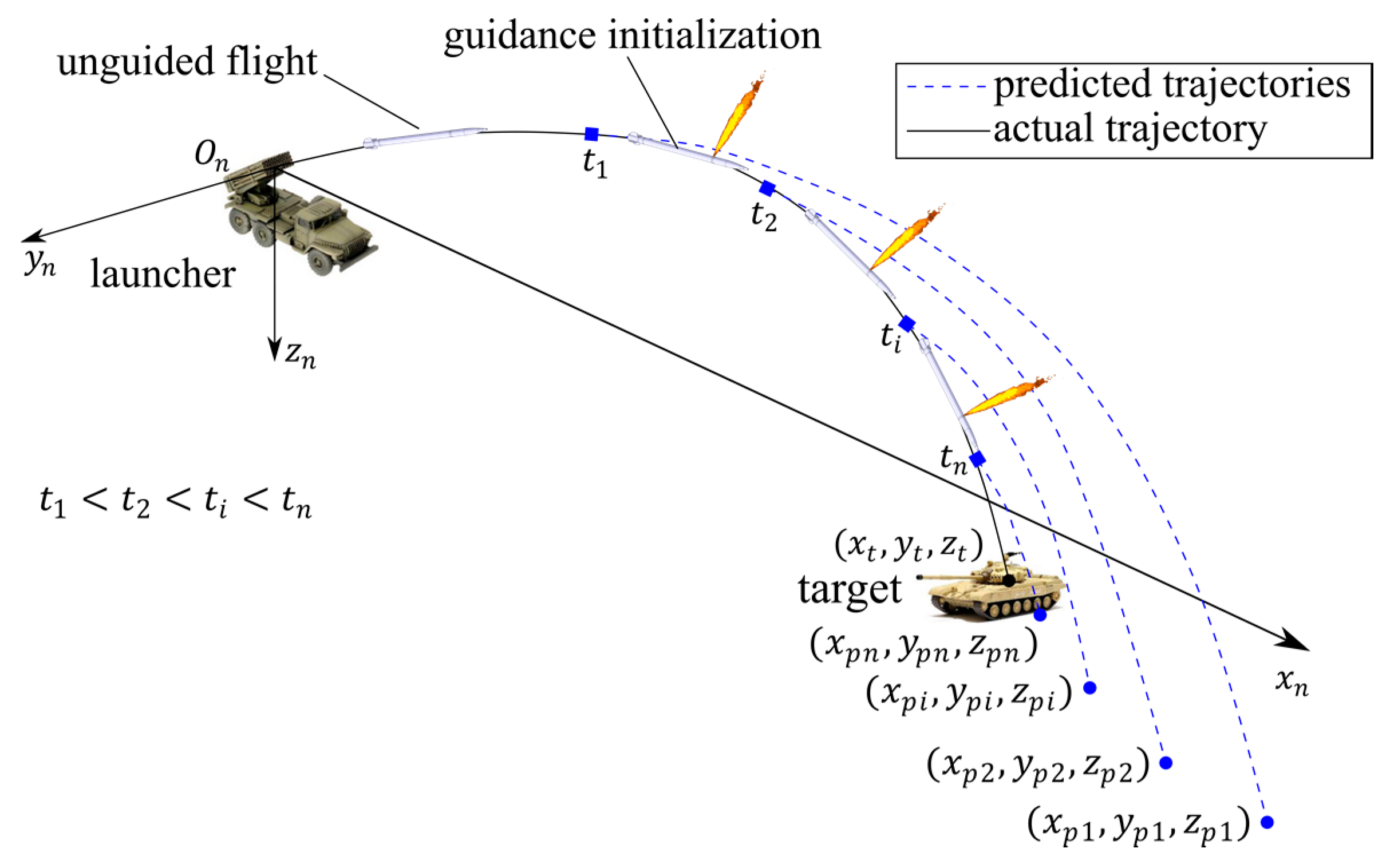
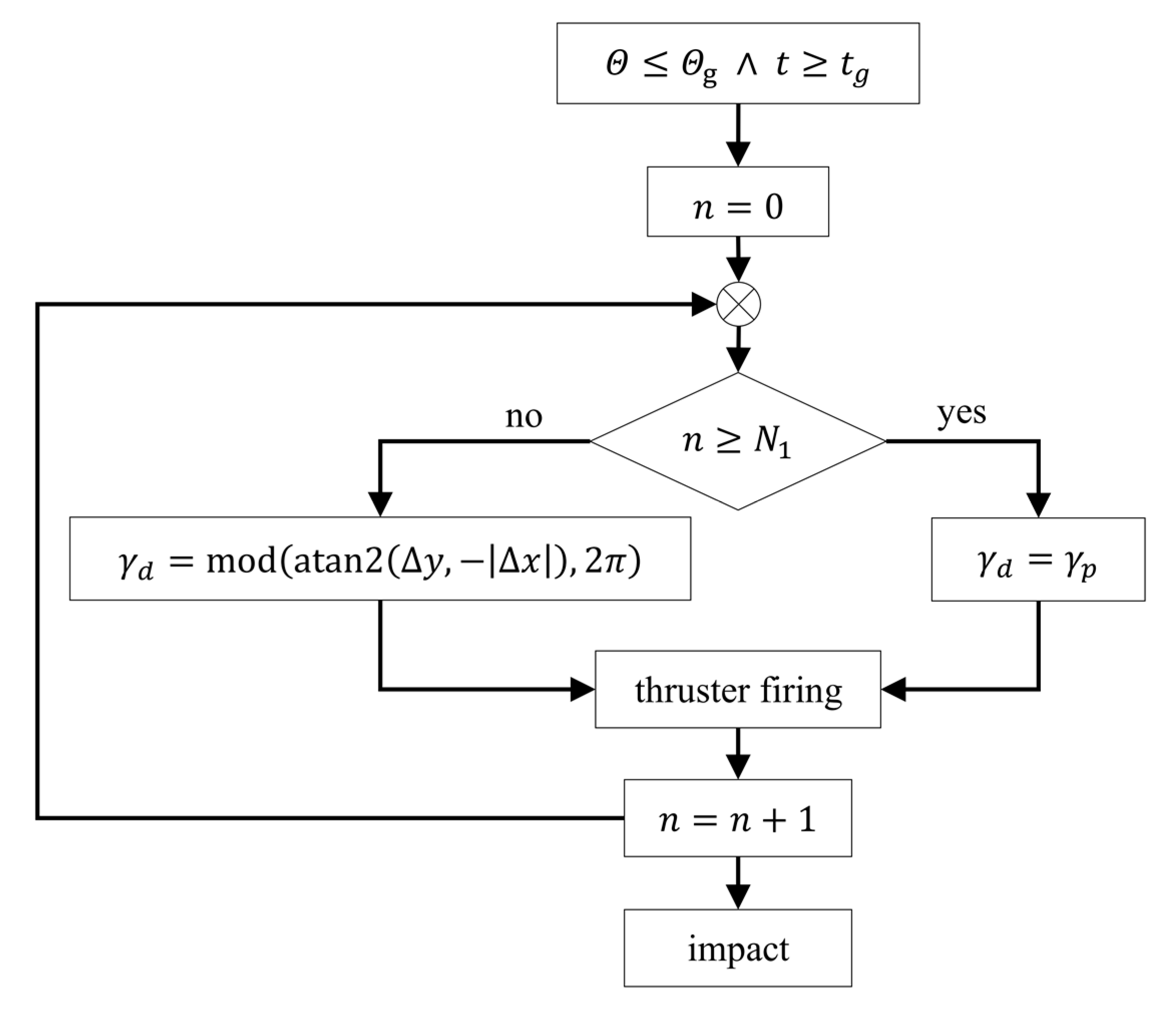
2.3. Combined Prediction and Trajectory Shaping Guidance
- The thruster has not been consumed already
- The difference between the actual time and the last motor firing is bigger than some thresholdwhere is a function of air density and was calculated as . It means that at low elevation angles , but at high launch angles . The projectile altitude is estimated in real time with the onboard navigation system.
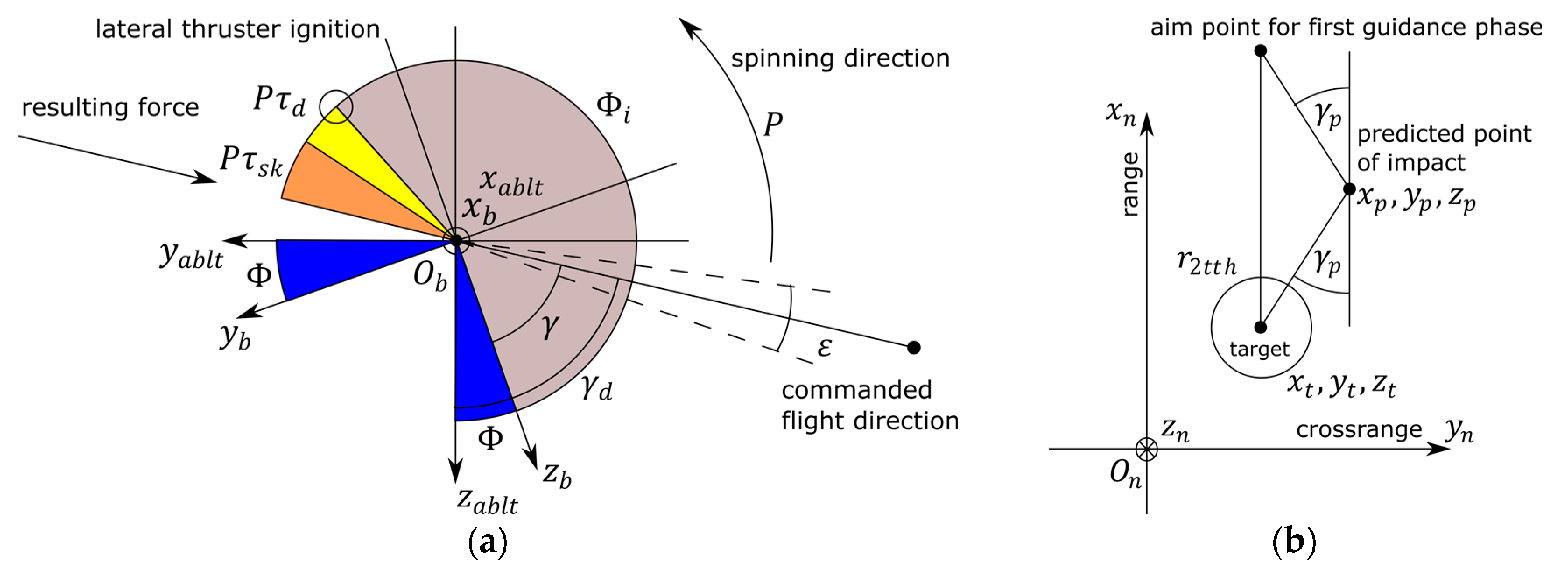
- The thruster is fired when the projectile is at a proper angular orientation (Figure 4a)where is the angle defining the desired flight direction, is the angular location of the -th thruster, is projectile roll rate and is calculated as:where is operation time of the lateral rocket motor. is the angle threshold which defines the directional accuracy and should be as small as possible. In (15), is subtracted from other quantities because the control force must be generated at the opposite side of the projectile fuselage than the commanded flight direction.
- The consumption of lateral thrusters takes place only when the shell pitch angle is smaller or equal than the desired threshold and the flight time is larger thanAdditionally, the miss distance magnitude between the target and predicted point of impact was calculated as [31]:
- The thrusters might be fired only when .
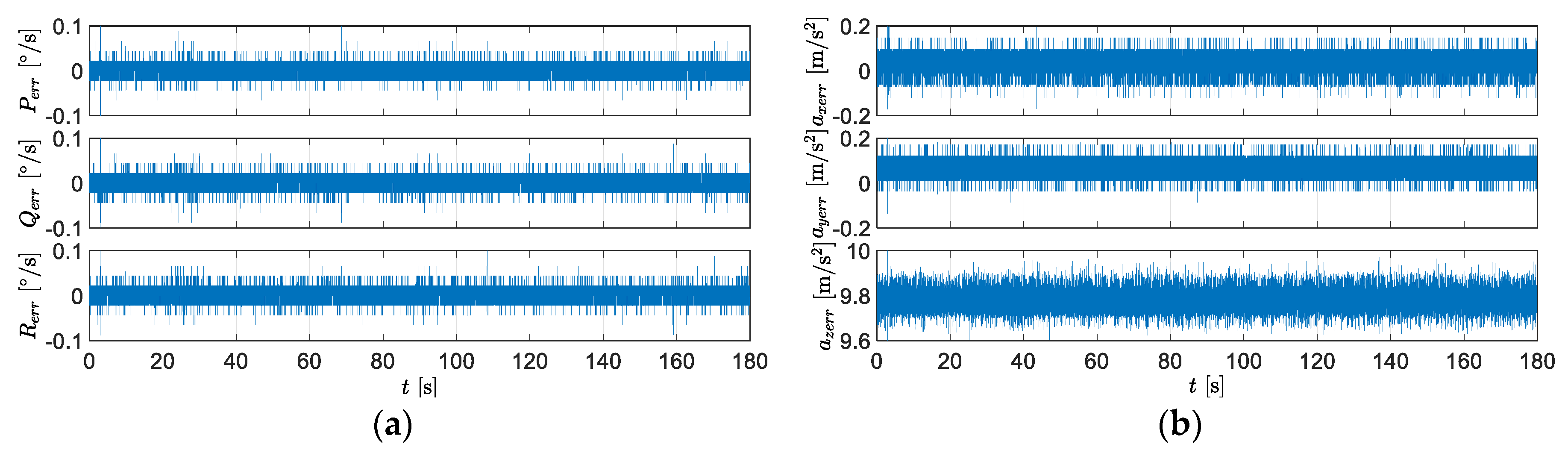
2.4. Inertial Navigation System Noise
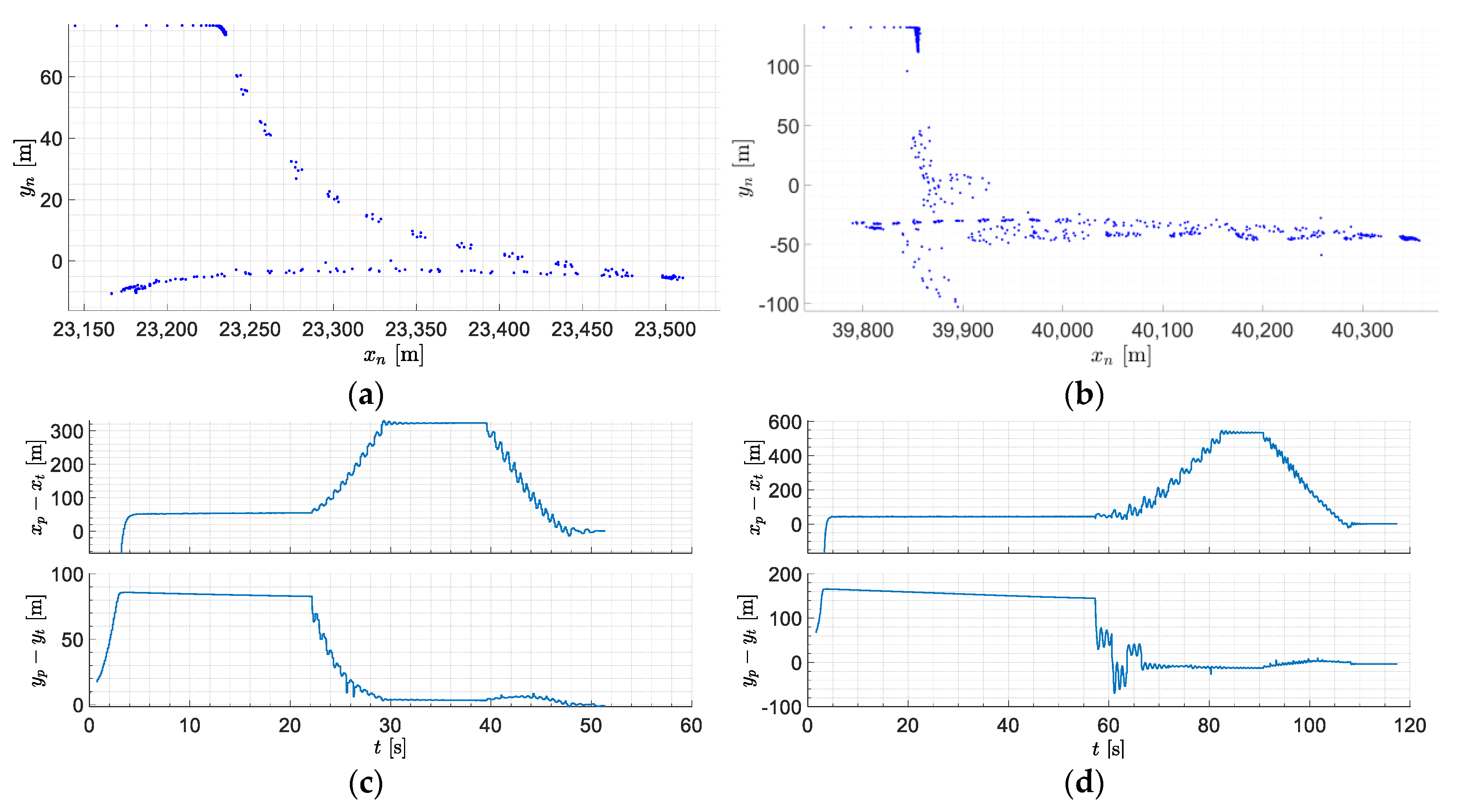
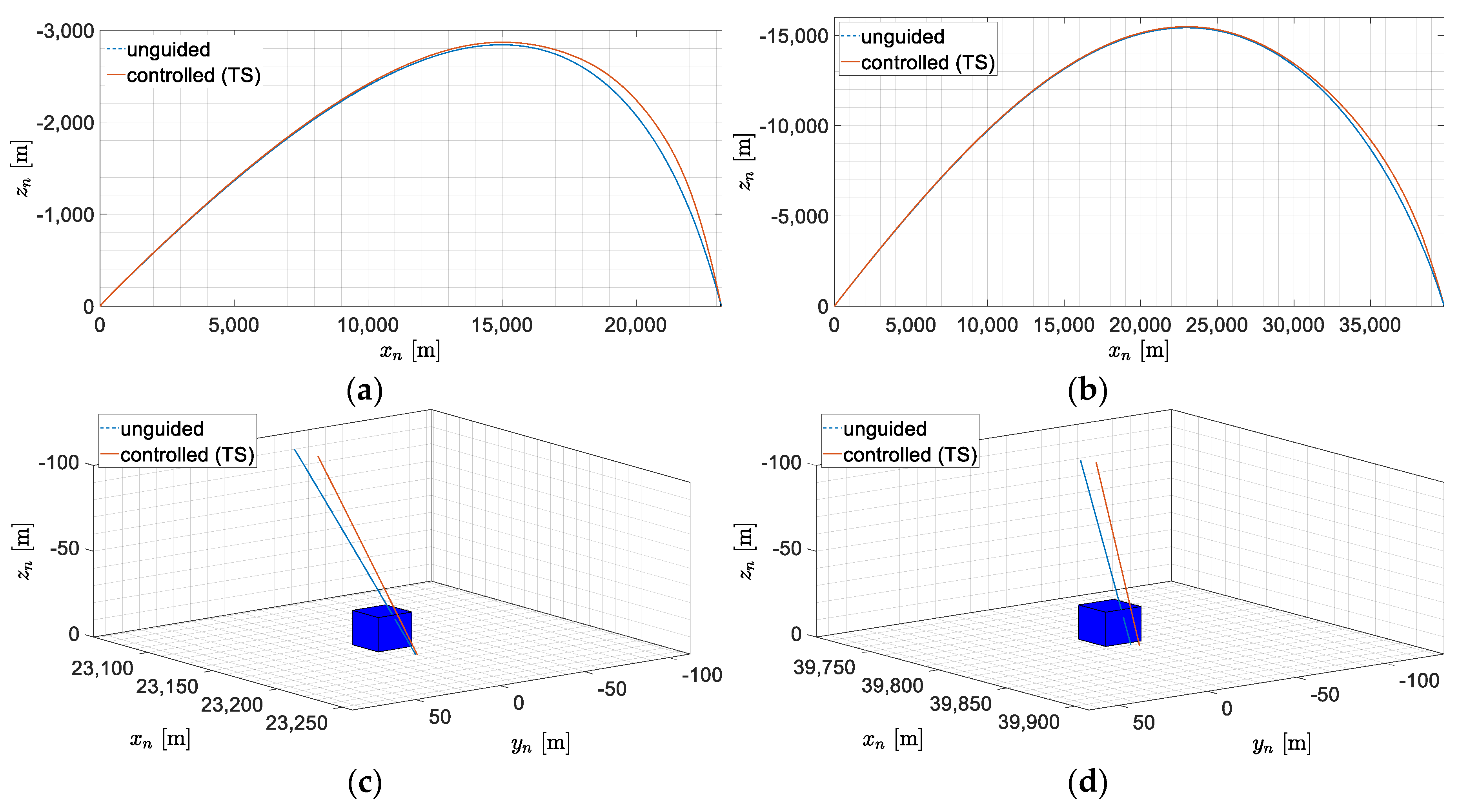
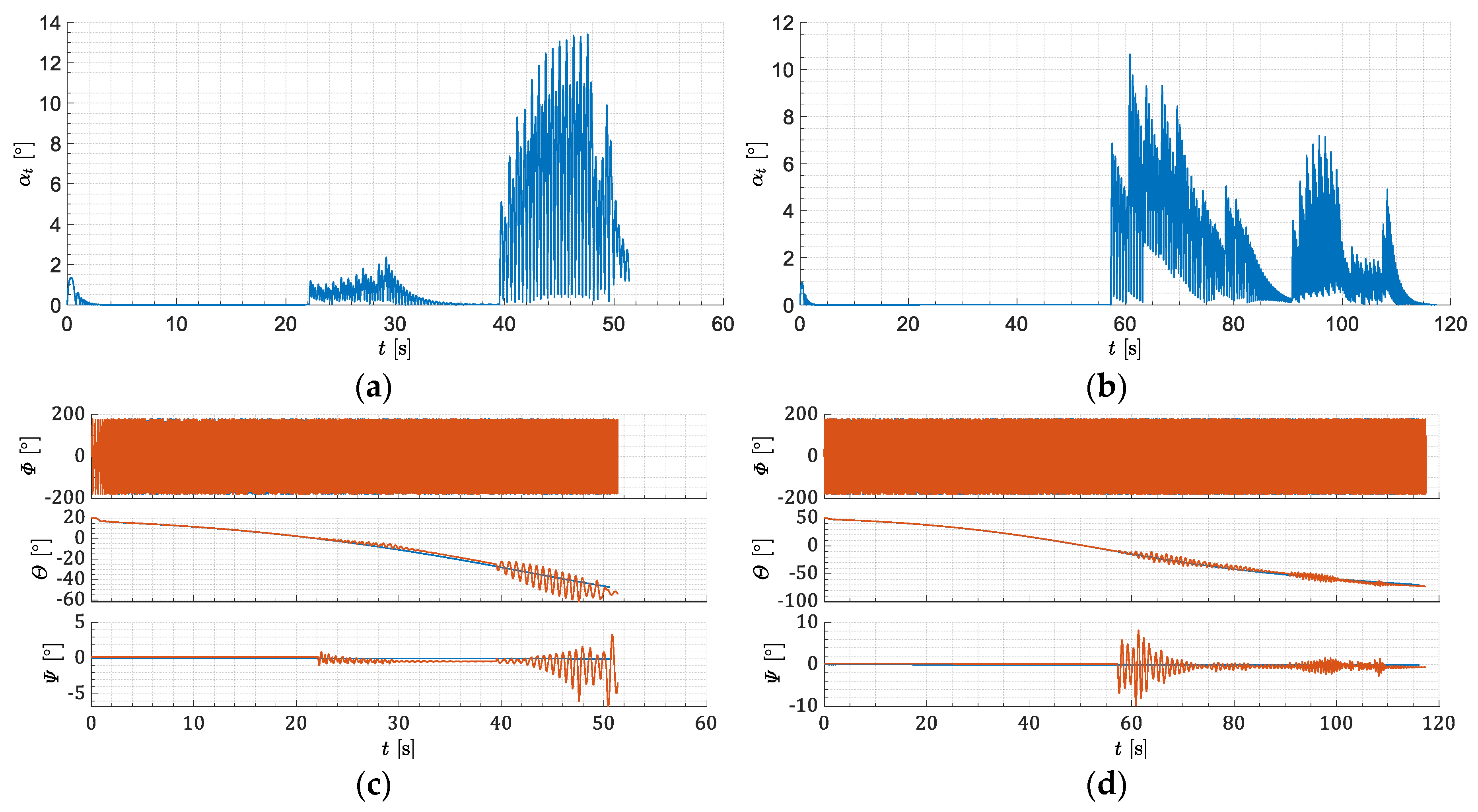
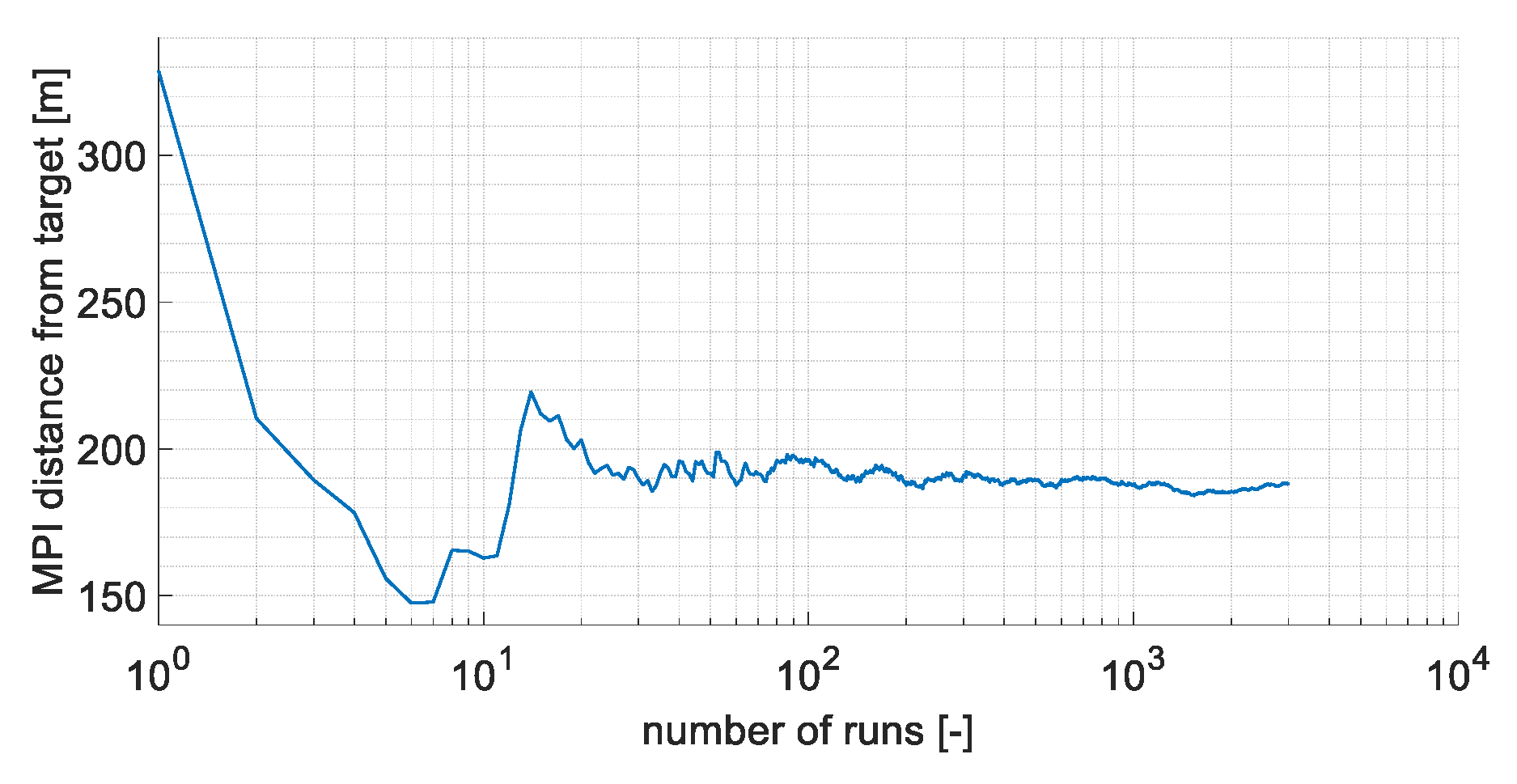
3. Results
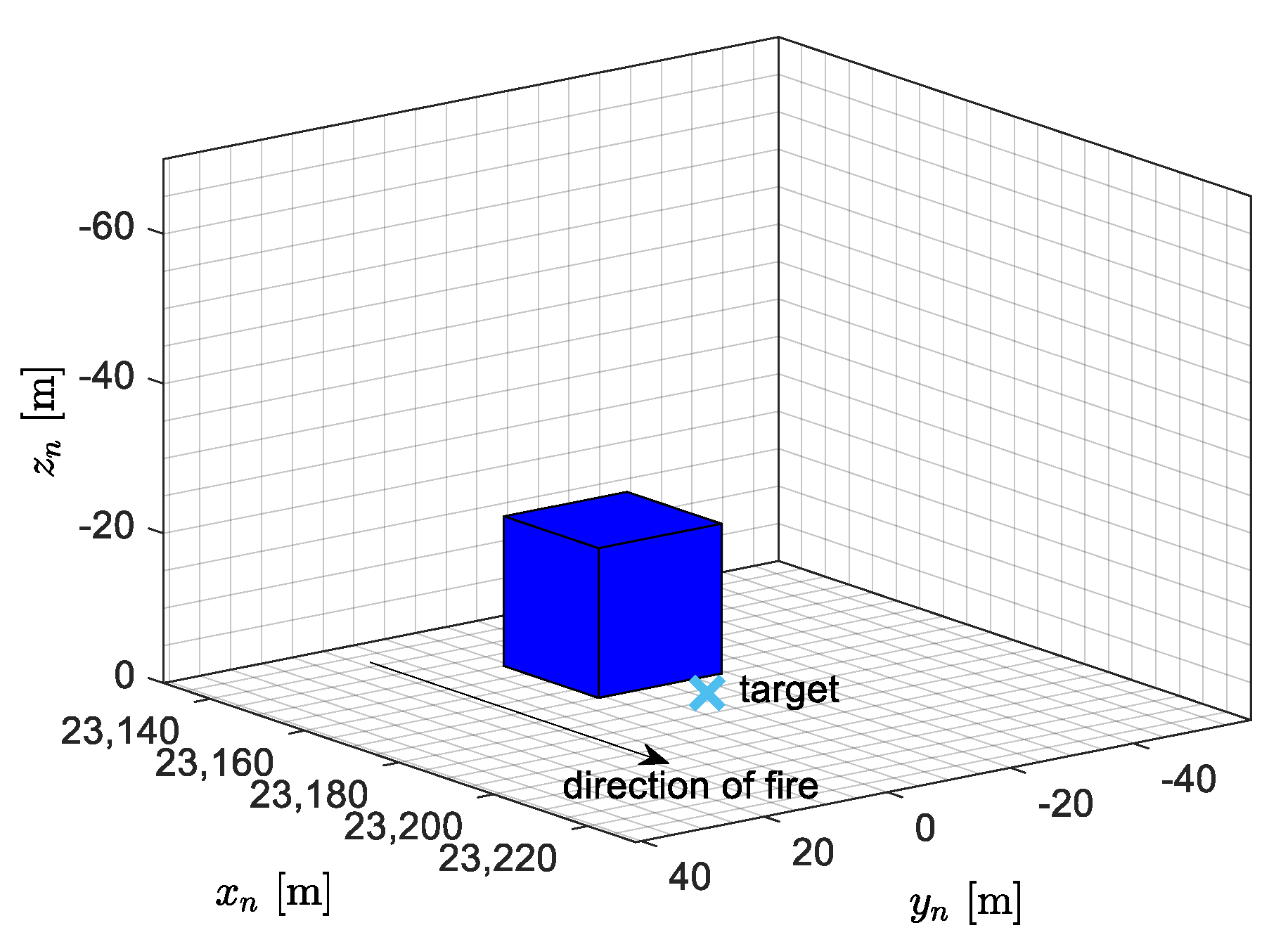
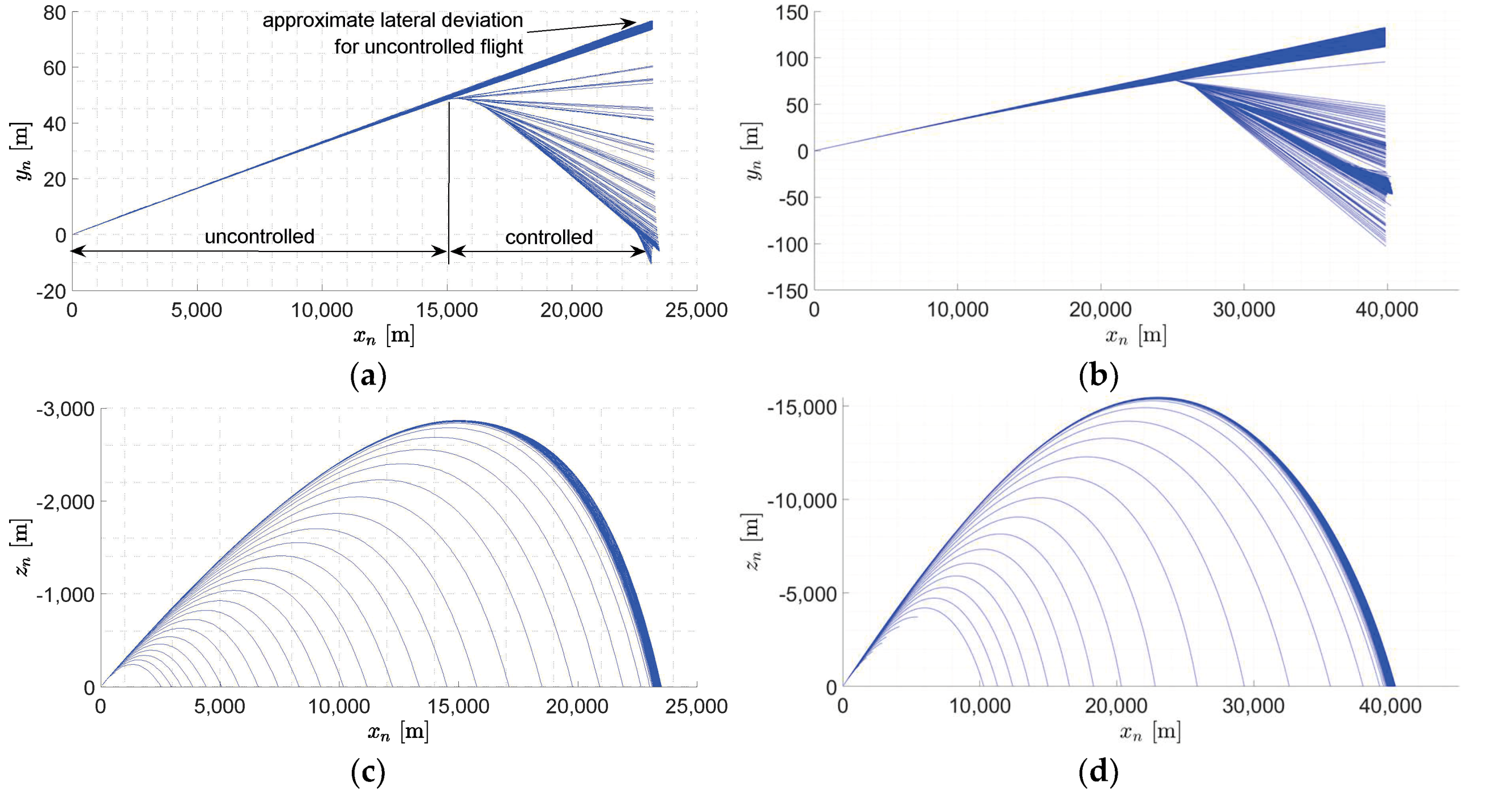
3.1. Algorithm Test
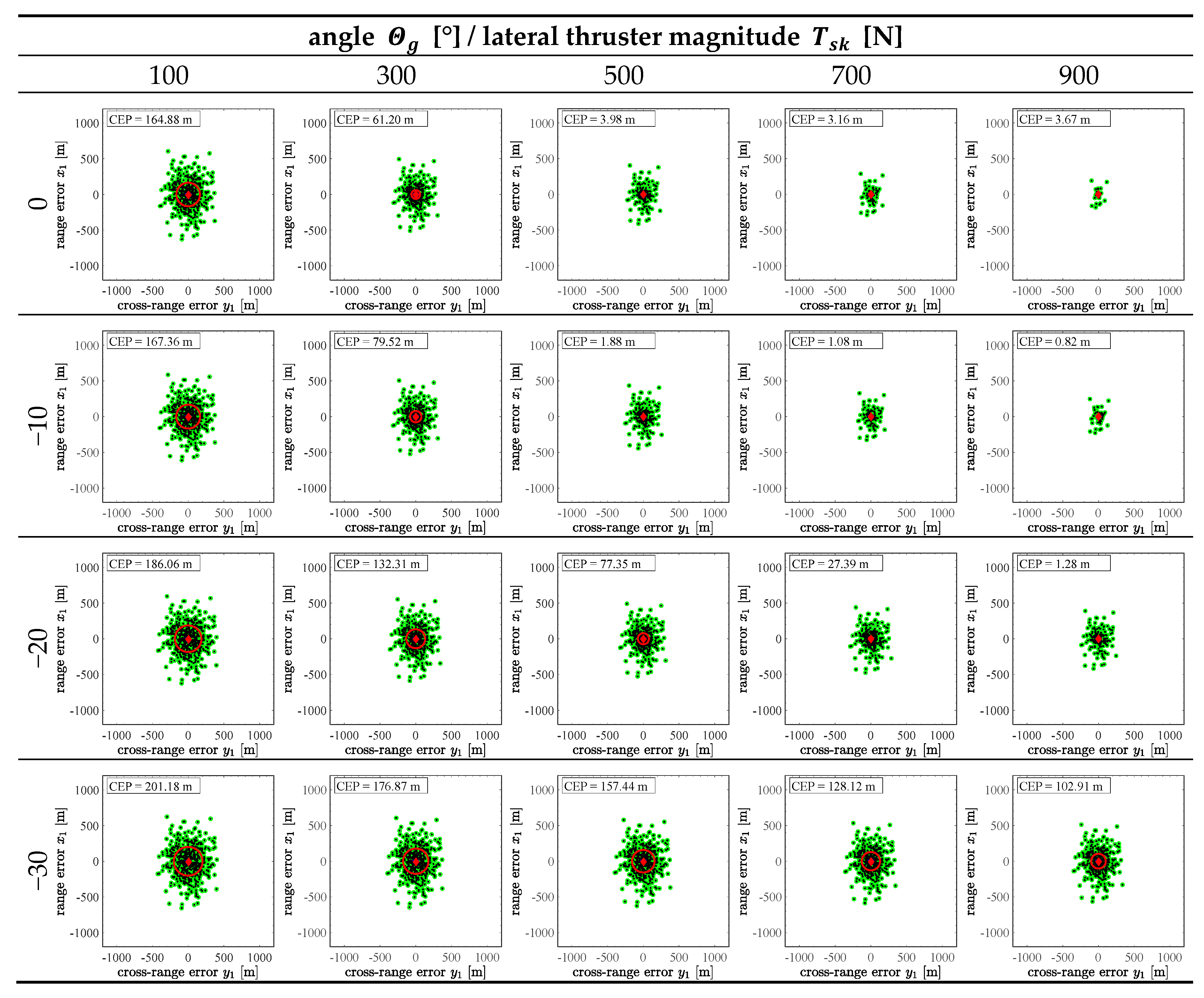
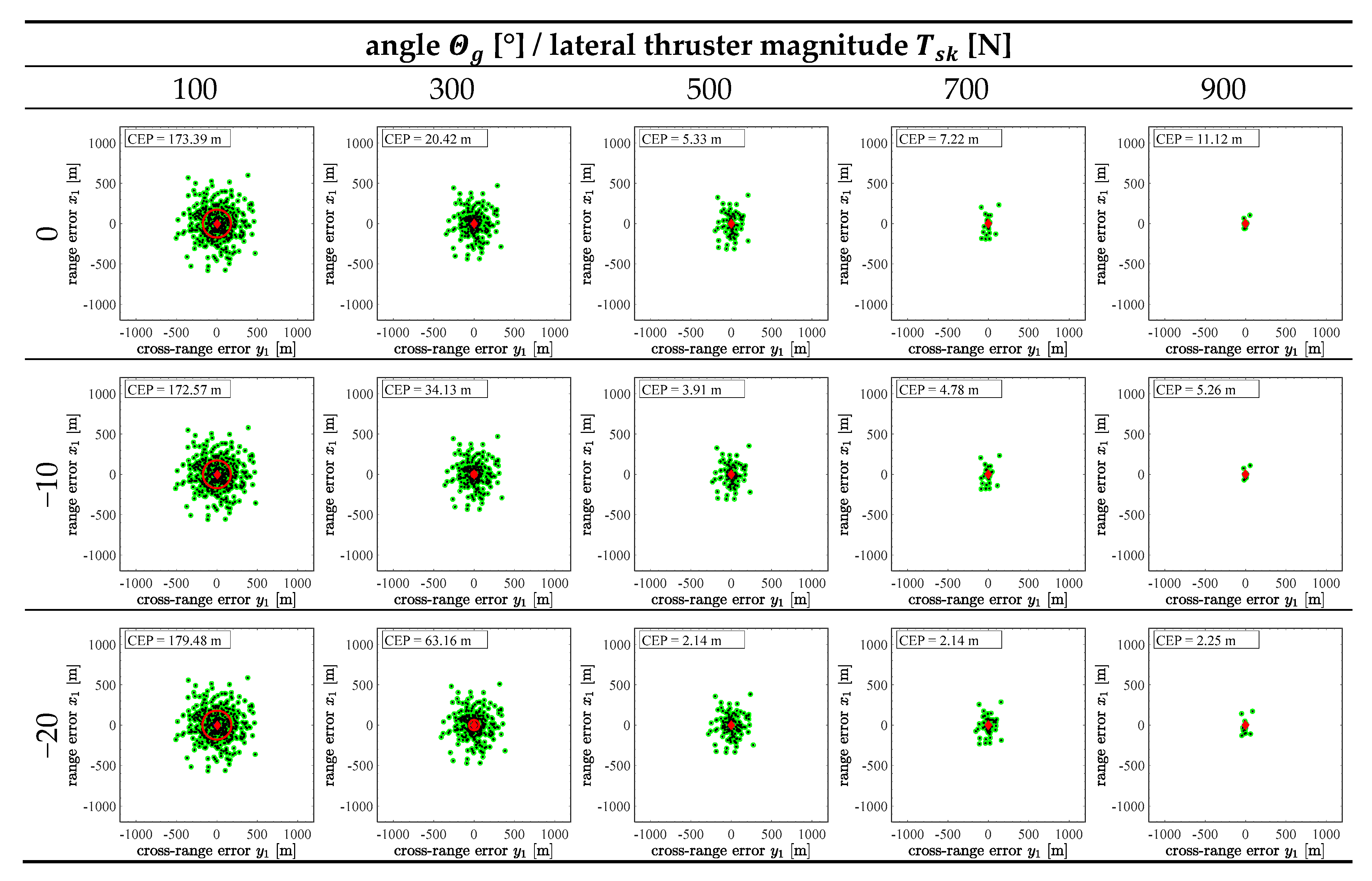
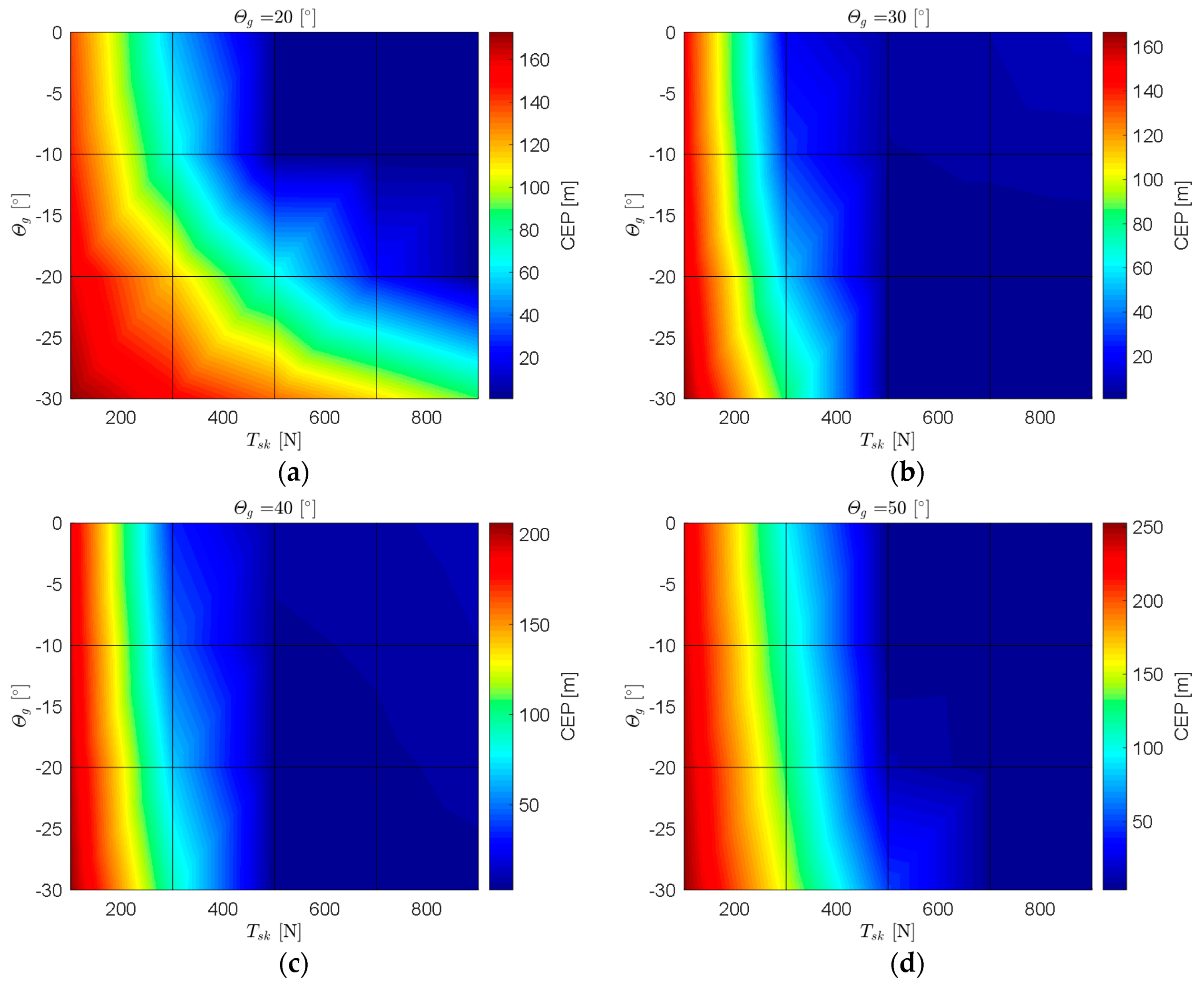
3.2. Sensitivity Analysis
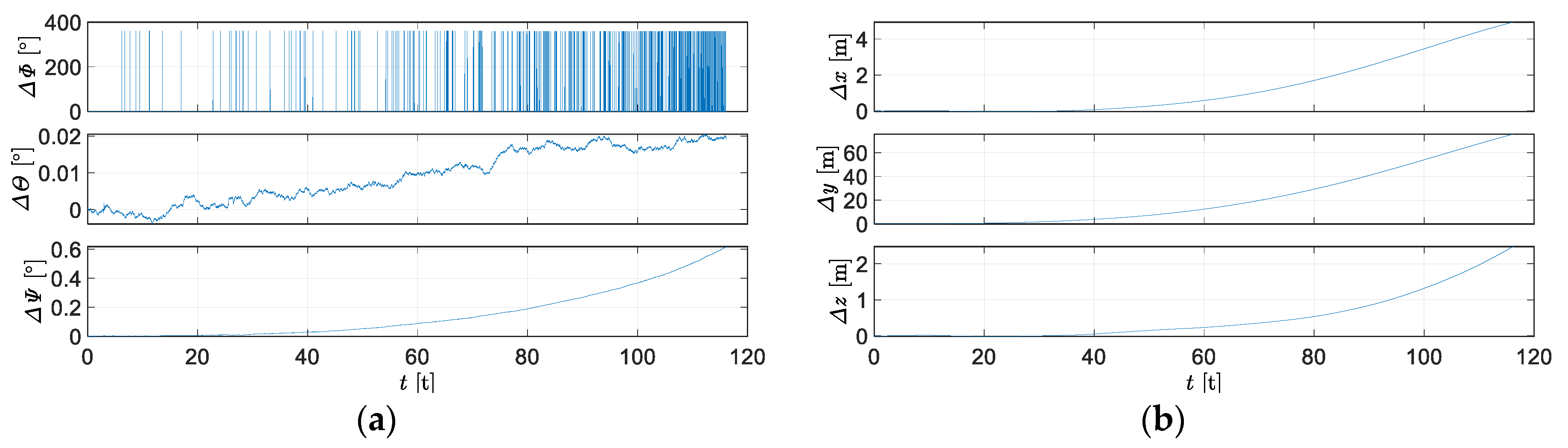
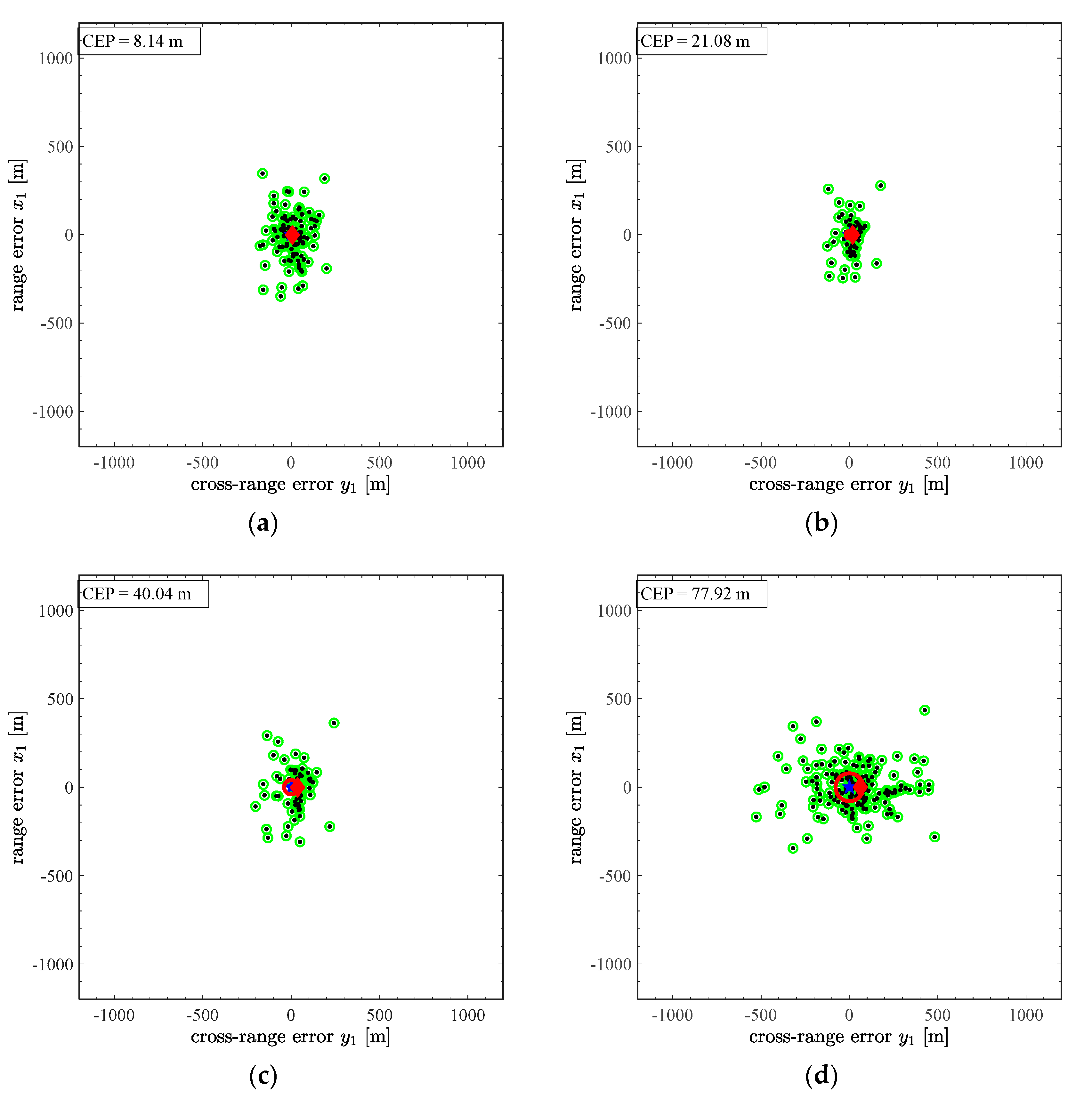
3.3. INS Errors Influence on the Guidance Process
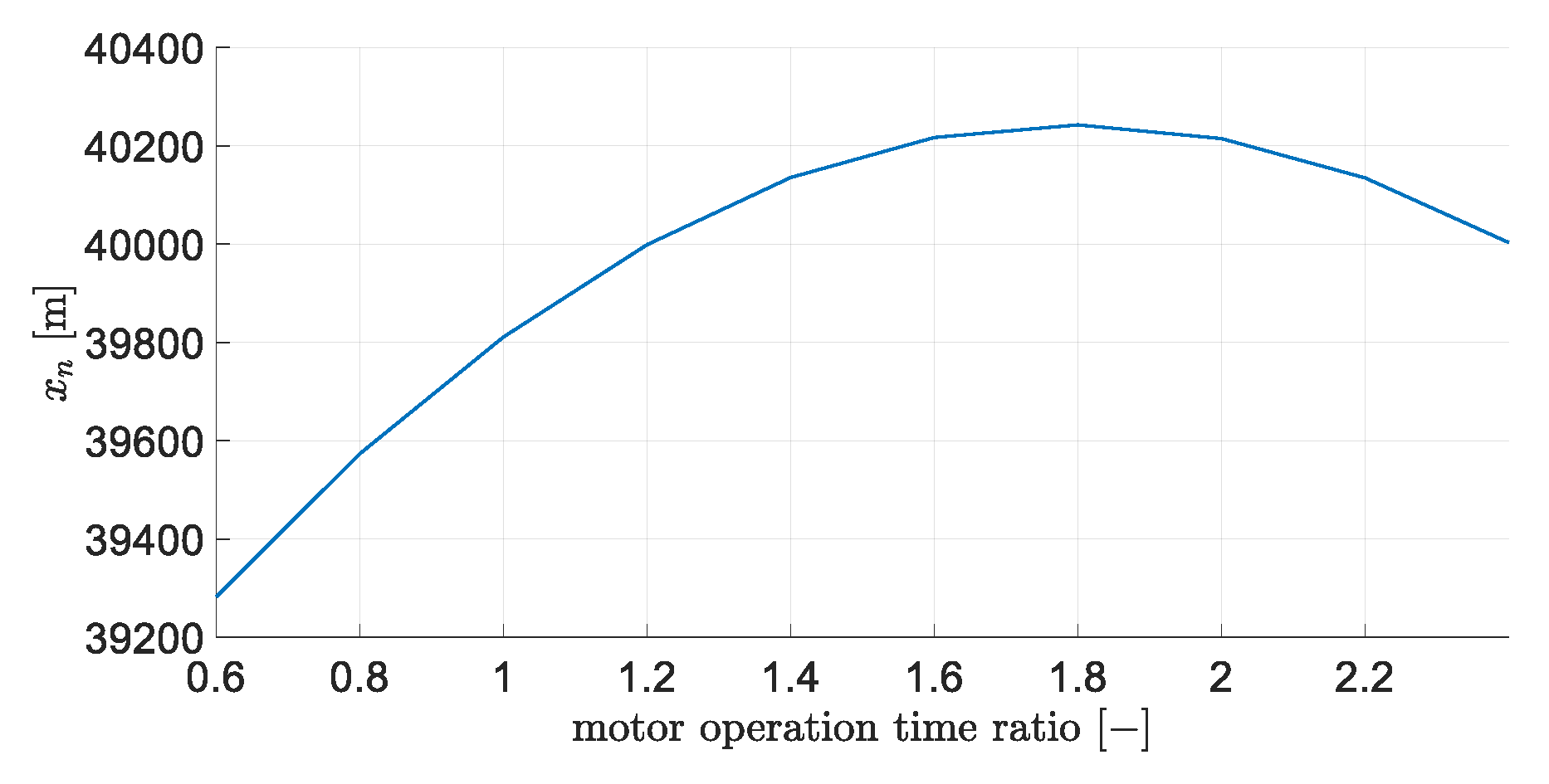
3.4. Main Motor Thrust Curve Optimization
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Latin Symbols | |
| axial, side and normal force aerodynamic coefficients, [-] | |
| rolling, pitching and yawing moment coefficients, [-] | |
| rolling, pitching and yawing damping moments coefficients, [-] | |
| drag force coefficient, [-] | |
| projectile diameter, [m] | |
| forces, [N] | |
| gravity acceleration, [m/s2] | |
| number of the thruster, [-] | |
| inertia matrix, [kgm2] | |
| projectile initial moments of inertia before main motor burnout, [kgm2] | |
| projectile initial moments of inertia after main motor burnout, [kgm2] | |
| projectile mass, [kg] | |
| projectile initial mass, [kg] | |
| projectile mass after main motor burnout, [kg] | |
| moments, [Nm] | |
| number of already fired thrusters, [-] | |
| number of the lateral thrusters, [-] | |
| number of thrusters used in the first guidance phase, [-] | |
| roll rate, [°/s] | |
| pitch rate, [°/s] | |
| miss distance, [m] | |
| miss distance threshold, [m] | |
| yaw rate, [°/s] | |
| projectile cross section area, [m2] | |
| time, [s] | |
| guidance initialization time, [s] | |
| operation time of the single lateral thruster, [s] | |
| minimum time between two consecutive firings, [s] | |
| time of the previous thruster firing, [s] | |
| lateral thruster thrust amplitude, [N] | |
| main motor thrust, [N] | |
| projectile velocities in body fixed frame, [m/s] | |
| total flight velocity, [m/s] | |
| non-rotating frame | |
| center of mass position before main motor burnout (from the projectile base), [m] | |
| center of mass location after main motor burnout (from the projectile base), [m] | |
| lateral thrusters position (from projectile base), [m] | |
| coordinates of the projectile center of mass in reference frame, [m] | |
| predicted impact point of the projectile in reference frame, [m] | |
| target location in reference frame, [m] | |
| range and cross-range errors, [] | |
| Greek Symbols | |
| total angle of attack, [°] | |
| desired flight direction in body fixed frame , [°] | |
| commanded flight direction in non-rolling body fixed frame , [°] | |
| miss distance phase in target plane, [°] | |
| range and cross-range miss distance, [m] | |
| angular tolerance of lateral thruster firing, [°] | |
| pitch angle, [°] | |
| pitch angle threshold for first guidance phase, [°] | |
| pitch angle threshold for second guidance phase, [°] | |
| main motor thrust misalignment pitch angle, [°] | |
| mean value | |
| air density, [kg/m3] | |
| standard deviation | |
| roll angle, [°] | |
| angular location of the -th lateral thruster, [°] | |
| yaw angle, [°] | |
| main motor thrust misalignment yaw angle, [°] | |
| minimum allowed time between two consecutive firings, [s] | |
| igniter delay, [s] | |
| lateral thruster delay, [s] | |
| Abbreviations | |
| CEP | Circular Error Probable [m] |
| DoF | Degree of Freedom |
| GPU | Graphic Processing Unit |
| G&C | Guidance and Control |
| IMU | Inertial Measurement Unit |
| INS | Inertial Navigation System |
| IPP | Impact Point Prediction |
| MPI | Mean Point of Impact |
| TT | Trajectory Tracking |
| TS | Trajectory Shaping |
References
- Saghafi, F.; Khalilidelshad, M. A Monte Carlo Dispersion Analysis of a Rocket Flight Simulation Software. In Proceedings of the 17th European Simulation Multiconference, Nottingham, UK, 9–11 June 2003. [Google Scholar]
- Al-Garni, A.Z.; Kassem, A.H.; Abdallah, A.M. Aerodynamic-Shape Optimization of Supersonic-Missiles Using Monte-Carlo. Int. Rev. Aerosp. Eng. 2016, 4, 7–15. [Google Scholar]
- Mihailescu, C.; Radulescu, M.; Coman, F. The Analysis of Dispersion for Trajectories of Fire-extinguishing Rocket. Recent Advances in Fluid Mechanics and Heat & Mass Transfer. In Proceedings of the 9th IASME/WSEAS International Conference on Fluid Mechanics & Aerodynamics (FMA ′11), Florence, Italy, 23–25 August 2011; pp. 135–140. [Google Scholar]
- Ilg, M.; Rogers, J.; Costello, M. Projectile Monte-Carlo Trajectory Analysis Using a Graphics Processing Unit. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Portland, Oregon, USA, 8–11 August 2011. [Google Scholar] [CrossRef]
- Ilg, M. Guidance, Navigation, and Control System Simulations via Graphics Processor Unit; Army Research Laboratory: Aberdeen Proving Ground, MD, USA, 2011. [Google Scholar]
- Ilg, M. Multi-Core Computing Cluster for Safety Fan Analysis of Guided Projectiles; Army Research Laboratory: Aberdeen Proving Ground, MD, USA, 2011. [Google Scholar] [CrossRef]
- Pavković, B. Research of Projectile Trajectory Correction Methods in Function of Their Range and Precision Enhancement. Ph.D. Thesis, University of Belgrade, Belgrade, Serbia, 2012. [Google Scholar]
- Pavković, B.; Pavić, M.; Ćuk, D. Frequency-Modulated Pulse-Jet Control of an Artillery Rocket. J. Spacecr. Rockets 2012, 49, 286–294. [Google Scholar] [CrossRef]
- Pavković, B.; Pavić, M.; Ćuk, D. Enhancing the Precision of Artillery Rockets Using Pulsejet Control Systems with Active Damping. Sci. Tech. Rev. 2012, 62, 10–19. [Google Scholar]
- Pavić, M.; Pavković, B.; Mandić, S.; Zivković, S.; Ćuk, D. Pulse-frequency modulated guidance laws for a mortar missile with a pulse jet control mechanism. Aeronaut. J. 2015, 119, 389–405. [Google Scholar] [CrossRef]
- Drescher, T.; Kreuzer, W.; Nielson, J. Rocket Trajectory Correction using Strap-on GPS Guided Thrusters. In Proceedings of the IEEE 1998 Position Location and Navigation Symposium (Cat. No.98CH36153), Palm Springs, CA, USA, 20–23 April 1996. [Google Scholar] [CrossRef]
- Guo, Q.-W.; Song, W.-D.; Gao, M.; Fang, D. Advanced Guidance Law Design for Trajectory-Corrected Rockets with Canards under Single Channel Control. Eng. Lett. 2016, 24, 469–477. [Google Scholar]
- Sahu, J.; Fresconi, F. Flight Behaviors of a Complex Projectile using a Coupled CFD-based Simulation Technique: Closed-loop Control. In Proceedings of the 34th AIAA Applied Aerodynamics Conference, Washington, DC, USA, 13–17 June 2016. [Google Scholar] [CrossRef]
- Zhang, Y.; Gao, M.; Yang, S.; Fang, D. Optimization of Trajectory Correction Scheme for Guided Mortar Projectiles. Int. J. Aerosp. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Guo, Q.-W.; Song, W.-D.; Wang, Y.; Lu, Z.-C. Guidance Law Design for a Class of Dual-Spin Mortars. Int. J. Aerosp. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Gamble, A.; Jenkins, P. Low Cost Guidance for the Multiple Launch Rocket System (MLRS) Artillery Rocket. IEEE Aerosp. Electron. Syst. Mag. 2001, 16, 33–39. [Google Scholar] [CrossRef]
- Fresconi, F. Control mechanism strategies for spin-stabilized projectiles. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2010, 224, 979–991. [Google Scholar] [CrossRef]
- Lichota, P.; Jacewicz, M.; Szulczyk, J. Spinning gasodynamic projectile system identification experiment design. Aircr. Eng. Aerosp. Technol. 2020, 92, 452–459. [Google Scholar] [CrossRef]
- Burchett, B. Prediction of Swerving Motion of a Dual-Spin Projectile With Lateral Pulsejets in Atmospheric Flight. Math. Comput. Model. 2002, 35, 821–834. [Google Scholar] [CrossRef]
- Frost, G.; Costello, M. Stability and Control of a Projectile with an Internal Rotating Disk. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Austin, TX, USA, 11–14 August 2003. [Google Scholar] [CrossRef]
- Elsaadany, A.; Wen-jun, Y. Accurate Trajectory Prediction for Typical Artillery Projectile. In Proceedings of the 33rd Chinese Control Conference, Nanjing, China, 28–30 July 2014; pp. 6368–6374. [Google Scholar] [CrossRef]
- IMI Systems. Available online: http://www.imisystems.com/wp-content/uploads/2017/01/ACCULAR-1.pdf (accessed on 23 March 2020).
- State Kyiv Design Bereau “LUCH”. Available online: http://www.luch.kiev.ua/en/catalogue-of-product (accessed on 21 March 2020).
- Gao, M.J.; Zhang, Y.; Yang, S.; Fang, D.Y. Trajectory Correction Capability Modeling of the Guided Projectiles with Impulse Thrusters. Eng. Lett. 2016, 24, 11–18. [Google Scholar]
- Corriveau, D.; Berner, C.; Fleck, V. Trajectory Correction Using Impulse Thrusters for Conventional Artillery Projectiles. In Proceedings of the 23rd International Symposium on Ballistics: Ballistics 2007, Tarragona, Spain, 16–20 April 2007; pp. 639–646. [Google Scholar]
- Robinson, J.; Berefelt, F. On Guidance and Control for Guided Artillery Projectiles, Part 1: General Considerations; FOI Swedish Defence Research Agency: Stockholm, Sweden, 2011.
- Gagnon, E.; Lauzon, M. Course Correction Fuze Concept Analysis for In-Service 155 mm Spin-Stabilized Gunnery Projectiles. In Proceedings of the AIAA Guidance, Navigation and Control Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Jitpraphai, T.; Costello, M. Dispersion Reduction of a Direct-Fire Rocket Using Lateral Pulse Jets. J. Spacecr. Rockets 2001, 38, 929–936. [Google Scholar] [CrossRef]
- Gupta, S.; Saxena, S.; Singhal, A.; Ghosh, A. Trajectory Correction Flight Control System using Pulsejet on an Artillery Rocket. Def. Sci. J. 2008, 58, 15–33. [Google Scholar] [CrossRef]
- Jitpraphai, T.; Burchett, B.; Costello, M. A Comparison of Different Guidance Schemes for a Direct Fire Rocket With a Pulse Jet Control Mechanism. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Guidance, Navigation, and Control and Co-located Conferences, Montreal, QC, Canada, 6–9 August 2001. [Google Scholar] [CrossRef][Green Version]
- Burchett, B.; Costello, M. Model Predictive Lateral Pulse Jet Control of an Atmospheric Rocket. J. Guid. Control Dyn. 2002, 25, 860–867. [Google Scholar] [CrossRef]
- Gross, M.; Costello, M. Impact point model predictive control of a spin-stabilized projectile with instability protection. In Proceedings of the AIAA Atmospheric Flight Mechanics (AFM) Conference, Boston, MA, USA, 19–22 August 2013. [Google Scholar] [CrossRef]
- Rogers, J. Stochastic Model Predictive Control for Guided Projectiles Under Impact Area Constraints. J. Dyn. Syst. Meas. Control 2015, 137. [Google Scholar] [CrossRef]
- Tian, Z.K.; Yang, S.C.; Feng, D.L.; Yao, Y.Z. Modeling and Simulation of impact point prediction algorithm. Appl. Mech. Mater. 2013, 347, 438–442. [Google Scholar] [CrossRef]
- Fresconi, F.; Ilg, M. Model Predictive Control of Agile Projectiles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar] [CrossRef]
- Park, W.; Yun, J.; Ryoo, C.-K.; Kim, Y. Guidance Law for a Modern Munition. In Proceedings of the International Conference on Control, Automation and Systems 2010, Gyeonggi-do, Korea, 27–30 October 2010. [Google Scholar] [CrossRef]
- Slegers, N. Model Predictive Control of a Low Speed Munition. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Hilton Head, SC, USA, 20–23 August 2007. [Google Scholar] [CrossRef]
- Slegers, N. Predictive Control of a Munition Using Low-Speed Linear Theory. J. Guid. Control Dyn. 2008, 31, 768–775. [Google Scholar] [CrossRef]
- Fresconi, F.; Cooper, G.; Costello, M. Practical Assessment of Real-Time Impact Point Estimators for Smart Weapons. J. Aerosp. Eng. 2011, 24, 1–11. [Google Scholar] [CrossRef][Green Version]
- Fairfax, L.D.; Vasile, J.D.; Strohm, L.; Fresconi, F. Trajectory Shaping for Quasi-Equilibrium Glide in Guided Munitions. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar] [CrossRef]
- Pamadi, K.; Ohlmeyer, E. Evaluation of Two Guidance Laws for Controlling the Impact Flight Path Angle of a Naval Gun Launched Spinning Projectile. In Proceedings of the AIAA Guidance, Navigation, and Control Conference and Exhibit, Keystone, CO, USA, 21–24 August 2006. [Google Scholar] [CrossRef]
- Corriveau, D.; Wey, P.; Berner, C. Analytical Model Development and Impulse Thrusters Pairing Guidelines for Trajectory Corrections of Spin-Stabilized Projectiles. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Corriveau, D.; Wey, P.; Berner, C. Thrusters Pairing Guidelines for Trajectory Corrections of Projectiles. J. Guid. Control Dyn. 2011, 34, 1120–1128. [Google Scholar] [CrossRef]
- National Aeronautics and Space Administration. U.S. Standard Atmosphere, 1976; National Aeronautics and Space Administration: Washington, DC, USA, 1976.
- Burchett, B. Predictive Optimal Pulse–jet Control for Symmetric Projectiles. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, AIAA SciTech Forum, National Harbor, MD, USA, 13–17 January 2014. [Google Scholar] [CrossRef]
- Lichota, P.; Szulczyk, J.; Tischler, M.B.; Berger, T. Frequency Responses Identification from Multi-Axis Maneuver with Simultaneous Multisine Inputs. J. Guid. Control Dyn. 2019, 42, 2550–2556. [Google Scholar] [CrossRef]
- Baranowski, L. Equations of Motion of A Spin-Stabilized Projectile for Flight Stability Testing. J. Theor. Appl. Mech. 2013, 51, 235–246. [Google Scholar]
- Burchett, B.T. Genetic Algorithm Optimization of Hydra Pulse Jet Controller. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference and Exhibit, Honolulu, HI, USA, 18–21 August 2008. [Google Scholar] [CrossRef]
- Gao, M.; Zhang, Y.; Yang, S. Firing Control Optimization of Impulse Thrusters for Trajectory Correction Projectiles. Int. J. Aerosp. Eng. 2015, 2015. [Google Scholar] [CrossRef]
- Fresconi, F. Guidance and Control of a Projectile with Reduced Sensor and Actuator Requirements. J. Guid. Control Dyn. 2011, 34. [Google Scholar] [CrossRef]
- Liu, F.; Su, Z.; Zhao, H.; Li, Q.; Li, C. Attitude Measurement for High-Spinning Projectile with a Hollow MEMS IMU Consisting of Multiple Accelerometers and Gyros. Sensors 2019, 19, 1799. [Google Scholar] [CrossRef] [PubMed]
- Matsumoto, M.; Nishimura, T. Mersenne twister: A 623-dimensionally equidistributed uniform pseudo-random number generator. ACM Trans. Model. Comput. Simul. 1998, 8, 3–30. [Google Scholar] [CrossRef]
- Driels, M. Weaponeering: Conventional Weapon System Effectiveness; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2013. [Google Scholar]


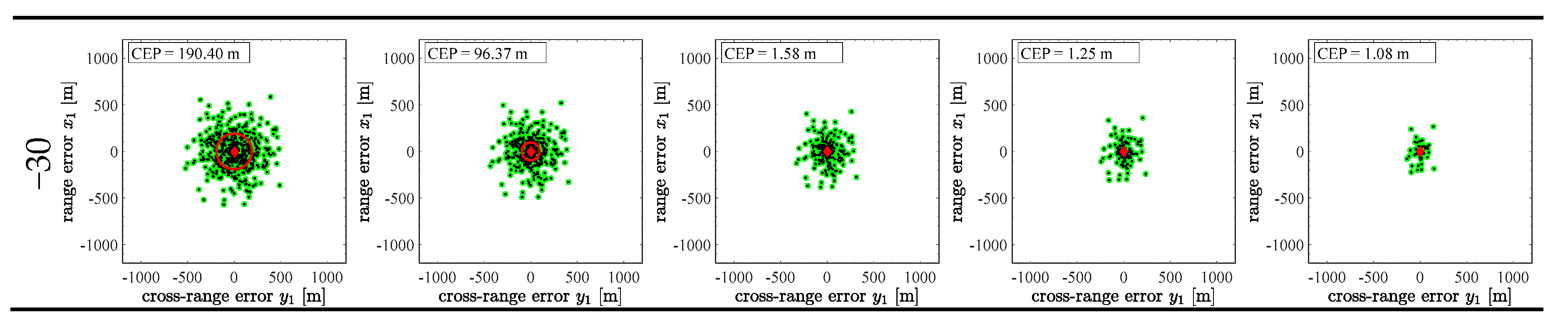
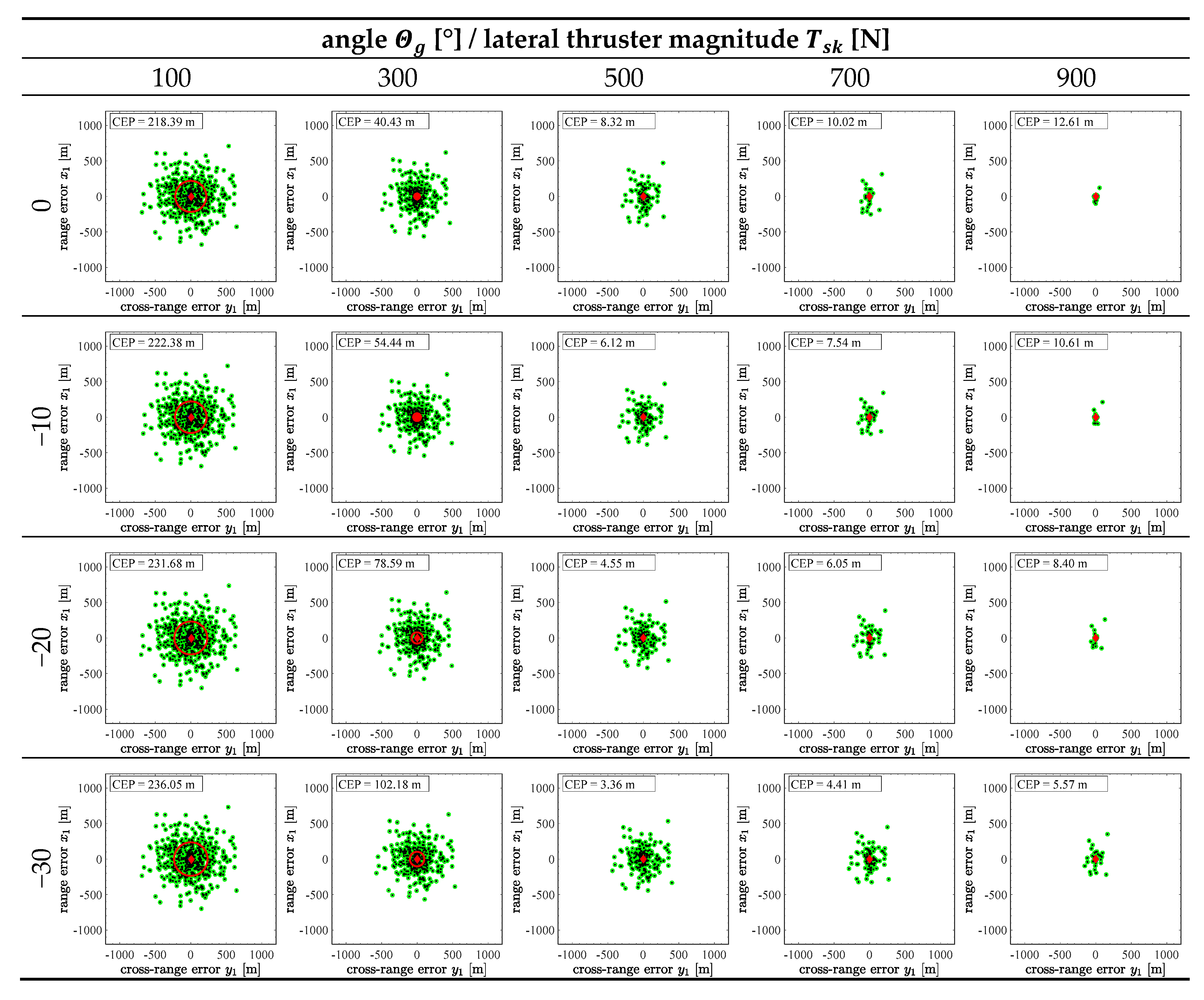
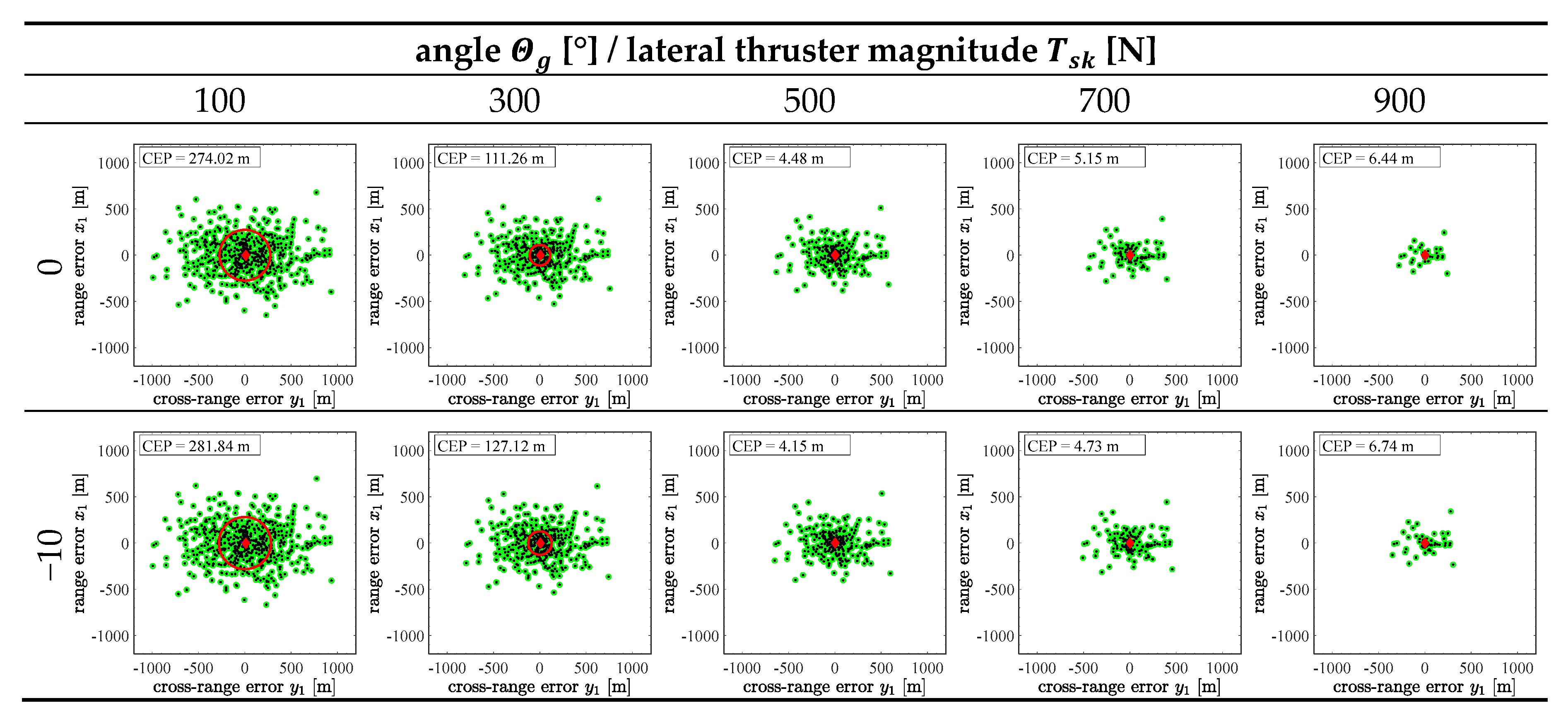
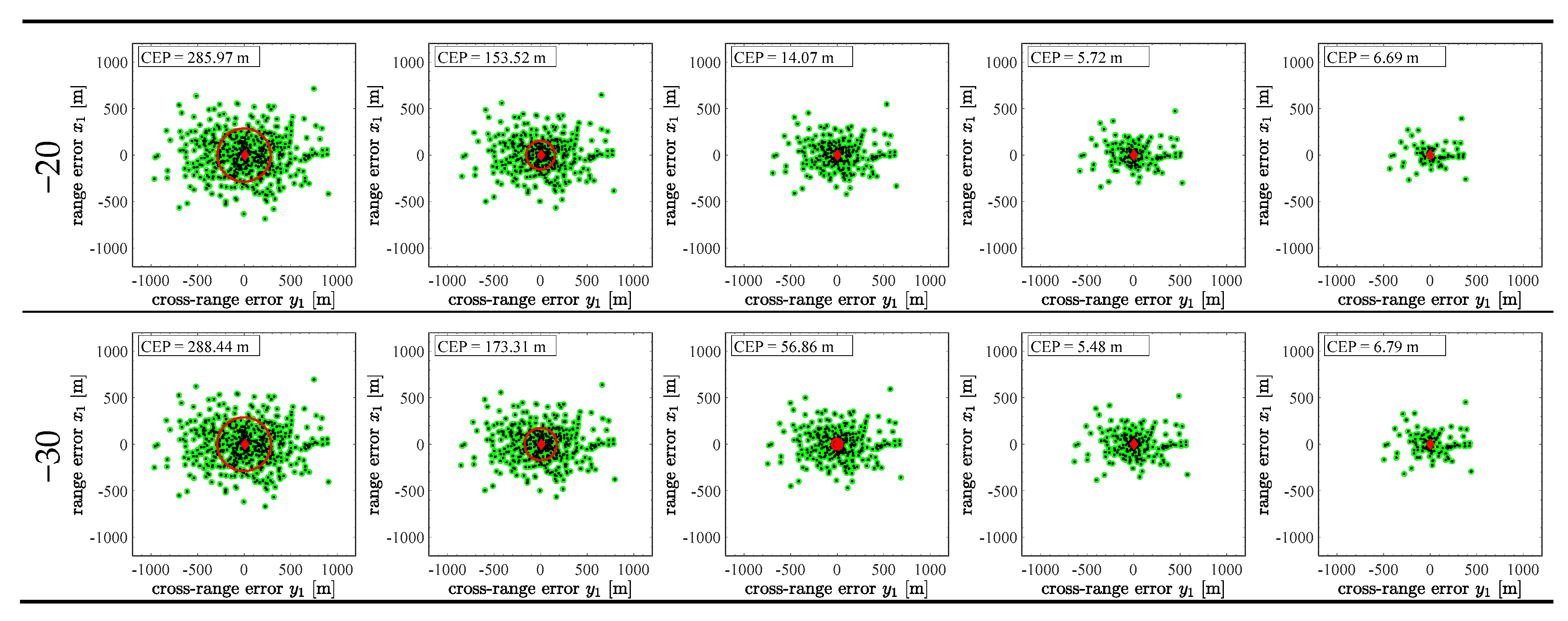
| No. | Parameter | Unit | ||
|---|---|---|---|---|
| 1. | 110 | 0.1 | kg | |
| 2. | 66 | 0.1 | kg | |
| 3. | 0.5 | 0.03 | kgm2 | |
| 4. | 0.4 | 0.03 | kgm2 | |
| 5. | 38 | 2 | m/s | |
| 6. | 0 | 1 | m/s | |
| 7. | −1.7 | 1 | m/s | |
| 8. | 0 | 10 | °/s | |
| 9. | −7.5 | 1 | °/s | |
| 10. | 0 | 1 | °/s | |
| 11. | 0 | 5 | ° | |
| 12. | 20/30/40/50 * | 0.2 | ° | |
| 13. | 0 | 0.1 | ° | |
| 14. | 0 | 0.1 | ° | |
| 15. | 0 | 0.1 | ° | |
| 16. | - | 1 | % | |
| 17. | - | 0.7 | % | |
| 18. | - | 1 | % | |
| 19. | - | 0.8 | % | |
| 20. | - | 0.5 | % |
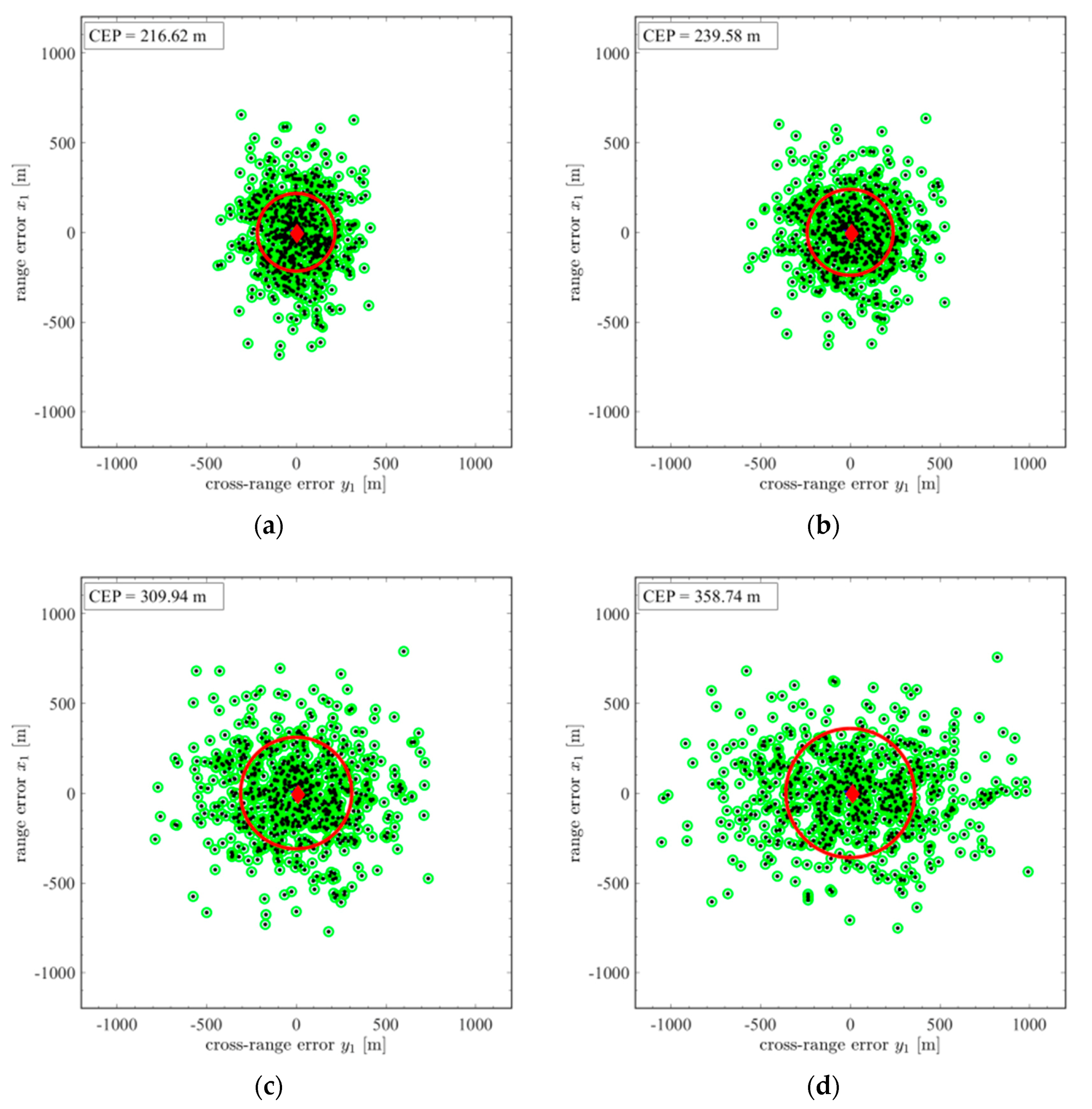
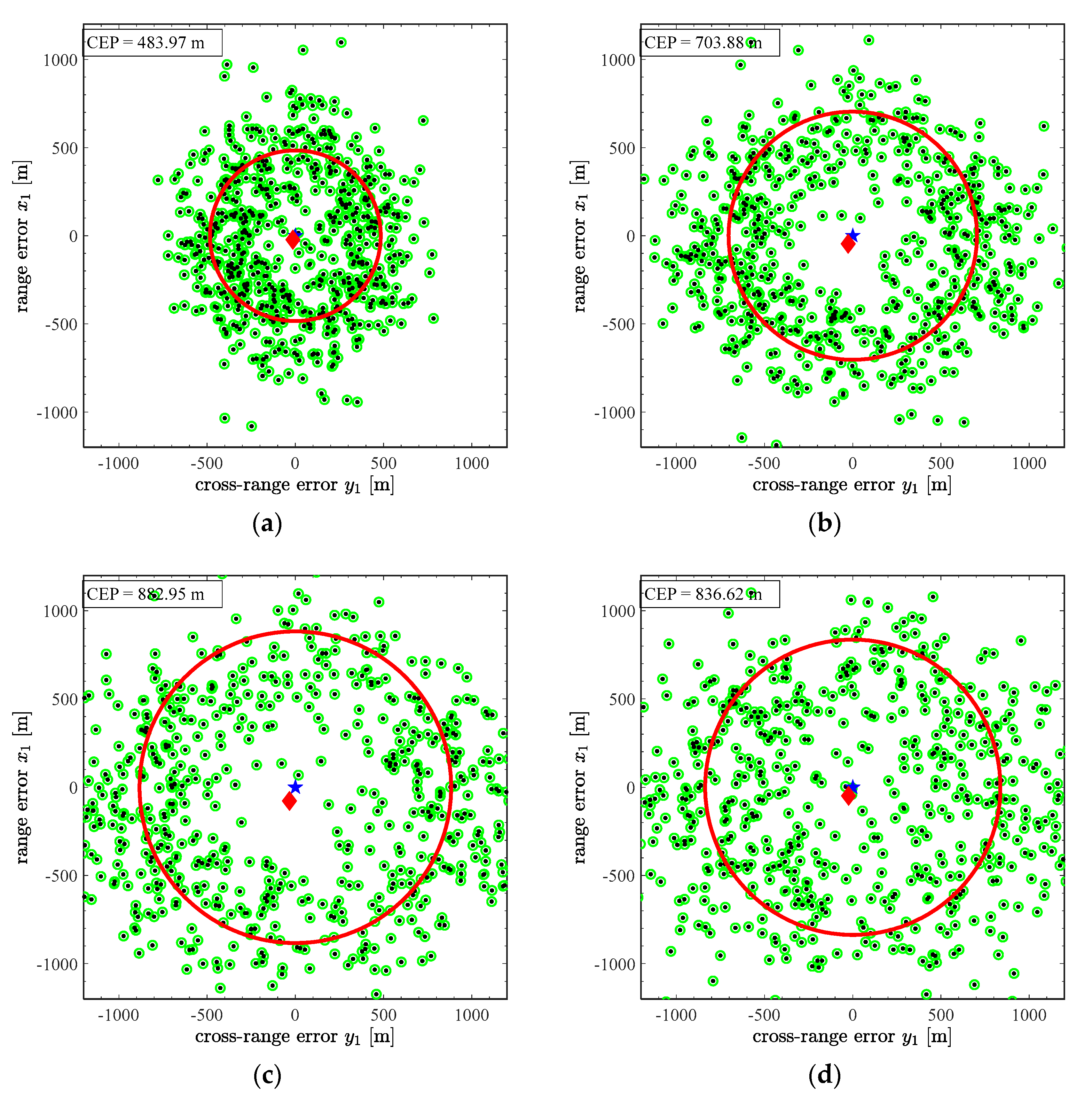
| Simulation Scenario | Ballistic Flight | Controlled (without INS Noise) | Controlled (with INS Noise) |
|---|---|---|---|
| Launch Angle [°] | CEP [m] | ||
| 20 | 216.62 | 3.16 | 8.14 |
| 30 | 239.58 | 7.22 | 21.08 |
| 40 | 309.94 | 10.02 | 40.04 |
| 50 | 358.74 | 5.15 | 77.92 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Głębocki, R.; Jacewicz, M. Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters. Aerospace 2020, 7, 61. https://doi.org/10.3390/aerospace7050061
Głębocki R, Jacewicz M. Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters. Aerospace. 2020; 7(5):61. https://doi.org/10.3390/aerospace7050061
Chicago/Turabian StyleGłębocki, Robert, and Mariusz Jacewicz. 2020. "Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters" Aerospace 7, no. 5: 61. https://doi.org/10.3390/aerospace7050061
APA StyleGłębocki, R., & Jacewicz, M. (2020). Parametric Study of Guidance of a 160-mm Projectile Steered with Lateral Thrusters. Aerospace, 7(5), 61. https://doi.org/10.3390/aerospace7050061