1. Introduction
Northern regions around the globe experiment yearly, during the winter, numerous freezing and frozen precipitations. Those precipitations seriously affect the transportation systems. More specifically, aerial transports, such as aircraft, that cannot take off if only a slight layer of frost covers their critical parts, i.e., wings, tails, and fuselage. Avoiding contaminants removal from the aircraft, may lead to a thrust reduction and an increase in the drag that may cause, in the worst case, a crash causing inevitably numerous fatalities [
1]. Aircraft AMS1424 deicing [
2] and AMS1428 anti-icing [
3] fluids are generally used during the winter to remove and to prevent contaminants accumulations over the aircraft while on the ground. Anti-icing fluids have been developed to protect the aircraft for a limited period of time. It mainly depends on environmental conditions including, but not exclusively, the nature of icy precipitation, the outside air temperature (OAT), and the precipitation intensity.
In order to be qualified and approved by the governmental instances, the different fluids used currently had passed through several endurance and acceptance tests. Those tests cover from the stability, the compatibility, and the environmental information to the endurance of the product under freezing and frozen contaminants. All the tests are included in the Society of Automotive Engineering (SAE) documents [
2,
3,
4,
5,
6].
All the endurance tests have in common that the endurance times have to be determined visually by a technician. The failure criterion depends only on the technician’s visual inspection of the plate, since it requires identifying frozen contaminants and mentally calculating the proportion of the test plate that they occupy. This visual inspection has been selected following the actual practice in the industry that after the deicing the aircraft should be inspected visually and manually to ensure that frozen contaminants are completely removed. However, this assessment is subjective and depends on several factors. All of these factors could introduce variability in the endurance time determined by the same person who would repeat the test several times. In addition, different people might determine different endurance times for the same trial. Similarly, the need for permanent supervision makes the procedure tedious since the test can last up to 12 h.
Extended research has been performed by Transport Canada and Federal Aviation Administration to detect the ice and frost deposition on aircraft surface to support the ground operations using remote on-ground ice detection systems (ROGIDS) [
7,
8]. ROGIDS principally uses near-infrared multi-spectrum detection systems to identify different phases (liquid or solid), like ice and water, over aircraft surface and validate when the ice is removed [
9]. Numerous ground-based ice detections systems (GIDS) have been developed and tested over the past years. It may help to detect the ice formation during the precipitation; however, it does not give the percentage of coverage.
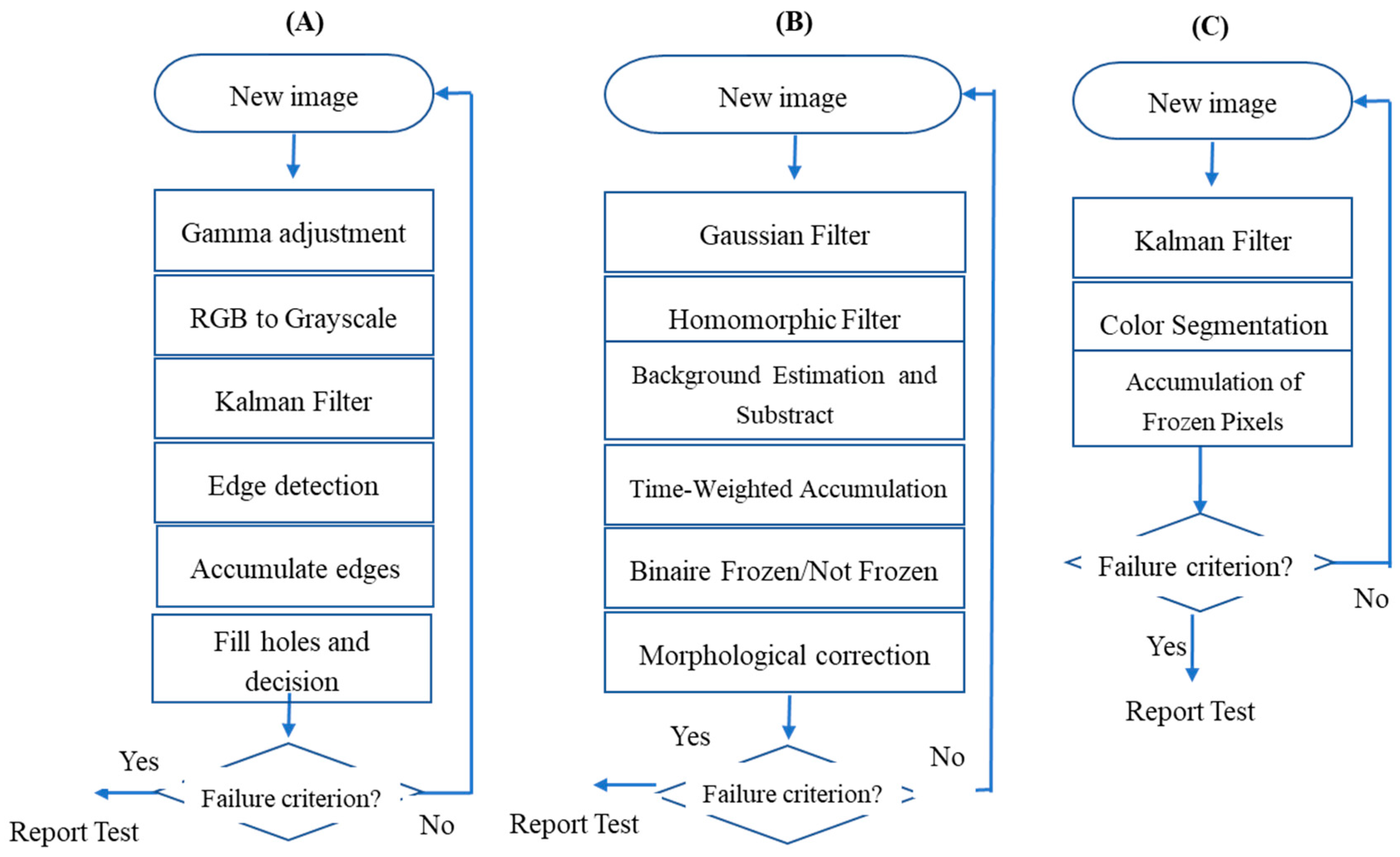
This paper proposed help-decision computer-assisted automated methods to determine the endurance time by image analysis, with the goal of minimizing human error resulting from visual inspection and helping in the interpretation of fluid failure.
4. Results and Discussion
In order to validate the algorithms presented in the previous sections, 14 different tests have been performed and recorded in the three conditions: 2 WSET, 6 LZR, and 6 SNW. The duration times obtained by the algorithms have been compared to two different duration determinations: By the technicians during the test and by the average of three technicians using the same images as the algorithms. The results are presented in
Table 1 and in
Figure 6. Two different limits have been selected, the first using the standard deviation and if the standard deviation was too low, an arbitrary limit of 5% of difference has been selected for the comparison.
The first two tests compared are the WS1 and the WS2. When comparing the time determined by the algorithm and by the average of three technicians using the images, there was non-significant difference. However, the algorithm does not determine the same duration as the one determined during the tests, giving time 63% higher than the technicians in the case of WS2.
The second algorithm developed, for LZR, has been tested in six different tests: LZR1, LZR2, LZR3, LZR4, LZR6, and LZR7. In two cases, the algorithm does not meet the failure criterium, so the time of the last image has been considered the failure duration. In the case of the LZR004, the ice front covered 29%, slightly under the failure criteria. When the deviation standard is considered, there is no significant difference between the algorithm and the duration determined by the three technicians using the images for only two tests: LZR1 and LZR7. By applying the second criteria, the algorithm remains valid for LZR2, LZR4, and LZR6. The results brought by the algorithm are more significant for this type of test. It is also interesting to see that the algorithm fits with the duration determined during the tests for two tests LZR6 and LZR7; but has a considerably higher percentage difference.
The third algorithm developed for the indoor snow test has been tested under six different tests: SNW1, SNW2, SNW3, SNW4, SNW5, and SNW6. In one case, SNW4, the algorithm does not meet the failure criterium, so the time of the last image has been considered the failure duration. In the case of the SNW4, the white snow covered 29%, slightly under the failure criteria. When the standard deviation is considered, there is no significant difference between the algorithm and the duration determined by the three technicians using the images for only three tests: SNW1, SNW5, and SNW6. By applying the second criteria, the SNW2 test also fits with both the algorithm and the average of the technicians. However, the percentage difference is too high for two tests: SNW4 and SNW5. By comparing the time determined during the test only the SNW2 meets the algorithm.
From the results presented, it is clear that the algorithms meet the average duration determined by the technician using the images: The duration fit in 11 tests out of 14, so 79% of success. However, the algorithms do not fit with the duration determined during the tests: 3 tests fit out of 14, only 20% of success.
The most important cause of error is the reflection of light on the test plate. When these reflections are static, a homomorphic filter has helped to significantly reduce this problem. However, in the case of snow tests, the device for dispersing snow moves over the test plate while reflecting light. These reflections are very intense and white and change their position constantly. Not only must the algorithm not detect these reflections as white snow it tries to detect, but they also make a significant part of the plate inaccessible for a time since completely white. This cause of error is probably responsible for the fact that the only two failures in determining the endurance time of the algorithm compared to the technicians who used the photos are snow tests.
Another cause of error arises from the use of the Kalman filter. It is necessary to filter the images because of precipitation falling on the plate that should not be detected as ice. The Kalman filter is particularly effective in eliminating these sudden noises. However, an undesirable consequence of its use is when ice front progresses rapidly. During the first moments of this progression, the filter interprets sudden change as noise. The algorithm then takes a little more time before the quickly appearing iced part is detected and computed.
There is also a significant difference between the endurance time determined by the technician present during the test and that determined by the technicians using the images. In fact, in order to determine whether the images allow a correct interpretation of reality, it would be relevant to verify during the test if, for the same technician, the visual inspection of the plate gives the same endurance time as with the images. On the one hand, the camera is closer to the test plate than the technician present, which could facilitate the detection of ice. On the other hand, the images contain artifacts that could interfere with the detection of ice and thus give the advantage to the technician present during the test.
Without doing more research, it is difficult to know which of the endurance times, between the determined one, in presence by a single technician, and the one determined with the images by three technicians, is the closest to reality. However, it can be seen that the algorithms give results equivalent to the human for most of the tests if only the images are used. So, if there is a difference between the determined endurance times in relation to those determined with the images is explained by a problem with them, it is possible to believe that by improving their quality, the developed algorithms would help to determine endurance times equivalent to those of technicians present during the tests.
In addition, the results show that, in general, using the same images, different technicians determine different endurance times. For example, a 21-min difference in endurance time is observed for test WS1. These discrepancies are to be expected since, on the one hand, the visual evaluation of the frosted parts is subjective and, on the other hand, the zone of failure (for WSET) or the percentage of iced areas (for LZR and SNW) must be mentally valued by the technicians.
What limits the automated determination of endurance time is significantly the ability to obtain good quality images. First, the camera placed in the climate chamber is exposed to precipitation, which randomly obstructs the lens. In addition, the camera should be placed far enough from the plate as to not interfere with the test and cannot be orthogonal to the test due to the experimental setup. Moreover, the results obtained show a significant difference between the endurance times obtained by a technician present during the tests and those obtained by technicians who used the images of these tests. It will be necessary to determine if this difference is caused by the quality of the photos and, if it is the case, to improve the quality of these until finding the same endurance time in the presence as with the images.
Also, the experimental data used for the verification of the algorithms are the same as those used for their elaboration. Although the endurance times were not known beforehand, it would be relevant to validate the endurance times obtained by these algorithms using other experimental data. Indeed, it should be verified that the algorithms give results comparable to those of a human for other tests for which the experimental conditions vary (light, cameras, fluid, etc.) in order to verify that the parameters are not over-adjusted. Even though, the purpose of the algorithms is to determine the endurance time, it would be relevant to verify that they identify the same iced parts on the test plate as the technicians. Indeed, in this research work, the performance of algorithms for the detection of frost has not been evaluated. To do this, each technician could identify the areas he considers iced on the image of the moment of failure. Subsequently, images summarizing all the photos of the technicians would be created. These would be divided into three classes of areas: The areas they all consider as iced, the areas they all consider as un-iced and the areas that some consider iced and others not at the time of failure.
In order to evaluate the performance of the algorithms proposed for automated ice detection, the areas considered iced by the technicians would be compared to the iced/non-iced binary images produced by the algorithm. The percentage of ice detected by the software and by at least one of the technicians would be calculated. Then, the percentage of ice not detected by the software but identified by all the technicians would be given. Finally, the percentage of false positives, that is to say ice detected by the software but by none of the technicians would be presented. This method would verify that the algorithms give valid endurance times because they detect the frost correctly.