Abstract
Components of aeronautical gas turbines are increasingly being constructed from two layers, including a pressure containing skin, which is then protected by a thermal tile. Between them, pedestals and/or other heat transfer enhancing features are often employed. This results in air admission ports through the dual skin having a step feature at the inlet. Experimental data have been captured for stepped ports with a cross flow approach, which show a marked increase of 20% to 25% in discharge coefficient due to inlet step sizes typical of combustion chamber configurations. In this respect, the step behaves in a fashion comparable to ports with inlet chamfering or radiusing; the discharge coefficient is increased as a result of a reduction in the size of the vena contracta brought about by changes to the flow at inlet to the port. Radiused and chamfered ports have been the subject of previous studies, and empirical correlations exist to predict their discharge coefficient as used in many one-dimensional flow network tools. A method to predict the discharge coefficient change due to a step is suggested: converting the effect of the step into an equivalent radius to diameter ratio available in existing correlation approaches. An additional factor of eccentricity between the hole in the two skins is also considered. Eccentricity is shown to reduce discharge coefficient by up to 10% for some configurations, which is more pronounced at higher port mass flow ingestion fraction.
1. Introduction
Ports for metering gas flow are used extensively in gas turbines, for example, in the internal air system, for blade cooling, and for combustor walls (and of course, there are many none gas turbine related examples). Despite an increased use of CFD in the design stages of combustors, good quality experimental data on discharge coefficients is still essential for validating and determining flow splits between the numerous ports. This is true in the initial design stage where one-dimensional flow network calculations are most appropriate, because these methods rely heavily on empirical correlations, and also in complex networks where hundreds of flow paths are possible. Rubini [1] describes such a network methodology for combustor preliminary design and these methods continue to be used. With more complex cooling strategies in cooling tiles or turbine blades, similar approaches are used in cooling circuits, such as within turbine blades as in Kukutla and Prasad [2], for example, where several hundred discharge coefficients are required to determine the network flow solution. Even in the detailed design phases, the CFD model requires at least some validation because air admission ports present their own difficulties to performing accurate predictions with a wide range of flow scales that require capturing. This is particularly true when sharp edges are present that result in significant separation and vena contracta formation. Moreover, the ports are often at a small scale compared with typical CFD grid cell sizes when full systems are modelled, and thus require significant grid distortion or local refinement to accurately define them. This is even worse if port inlet features such as radiusing, chamfering, or—as considered here—sharp steps are present, which are usually another order of magnitude smaller in scale than the port itself. The predicted discharge coefficient, Cd, is also found to be sensitive to approach flow conditions that may not be well predicted or may be only crudely defined as a boundary condition to the calculation, as discussed by McGuirk and Spencer [3].
Improving engine efficiency requires reducing parasitic losses. Cooling tiles have thus become desirable in modern engine combustors because they require less air for wall cooling than conventional cooling methods such as z-rings, as outlined in the literature [4]. This has led to a two-skin combustor wall construction shown schematically in Figure 1, see the work of [5] for an example of a patent application of this nature. The outer ‘cold’ skin provides the structural integrity of the combustor. The inner ‘hot’ skin, or ‘cooling tile’ provides the thermal barrier and wall cooling mechanisms between the flame and the cold skin. A primary air admission port thus must penetrate two skins. The outer skin hole is made larger than the inner skin hole to account for manufacturing and assembly tolerances, as well as differential thermal expansion. Without this provision, an inadvertent reduction in open area could result as the layers become misaligned—leading to a reduction in required flow rate. Of more concern could be the regions of hot gas recirculation behind the resulting ‘fence’ that could occur, leading to premature failure of the cooling tile.
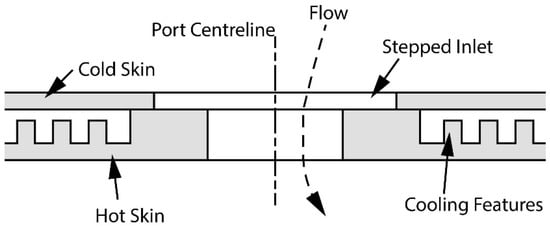
Figure 1.
Cross-section through typical two skin air admission port.
Cold skin thickness for a combustor liner tends to be of the order 1 mm and the cooling tile effective thickness can be around 5 times this value. Much of the hot skin thickness is the result of the pedestals and similar features usually employed between the two skins, but a ‘boss’ feature provides a sealing land between the port flow and the cooling feature flow paths. The outer skin hole is typically larger than the inner skin hole by at least a similar magnitude as the cold skin thickness. A chute at exit from the cooling tile may be required to direct the resulting jet in a desired direction, typically these are half a port diameter in length. With typical port diameters of 10 to 25 mm in size using such construction, the main geometric parameter ranges of the port of interest in this study can be determined. Described here as stepped inlets, they could also be called shallow counterbore holes.
It is well known that small features at the inlet of a port can have a large effect on the discharge coefficient of a port. Ports with inlet radiusing have been the focus of many studies (for example, [6,7]), and it is found that as the inlet radius is increased, as is the discharge coefficient. The rate of increase is large initially, but the coefficient asymptotes towards a value close to 1 as the inlet radius exceeds the port diameter. These findings have been codified as empirical correlations, such as McGreehan and Schotsch [8] and, more recently, Feseker et al. [9]. Chamfered ports are also investigated in the works of [6,7], but there are few other examples. It is found for a given chamfering angle that a significant increase in discharge coefficient is achieved very quickly with chamfer depth to port diameter ratio of only 0.08. Beyond this depth to diameter ratio, little or no further increase in Cd is found. The discharge coefficient of chamfered ports is found to be less sensitive to the flow conditions than radiused ports. Empirical correlation for chamfer effects have been presented in the literature [9] for holes that have a chamfer angle of 45°, but otherwise empirical relationships are not available for chamfering because of the limited data available to calibrate them. Naturally, the increase in discharge coefficient brought about by chamfering is dependent upon the chamfer angle with a maximum found at a chamfer angle of around 30°. Once a given depth of chamfer is achieved, the discharge coefficient is found to be fairly insensitive to chamfer depth [6] and chamfer tooling mis-alignment [10], making them attractive because of the lower manufacturing tolerances required to produce them.
Other parameters, such as port length to diameter ratio, Reynolds number, and proximity to other ports, also influence the discharge coefficient. These effects have been the subject of previous research and several empirical correlations exist, but are not investigated in detail here. Interdependence between the port inlet shape and these other parameters is found to be small, provided that the inlet feature is small compared with the port diameter and length. The first of these criteria is easily met within the context of this work, with step sizes typically being an order of magnitude smaller than that of the port diameter. Port length could be important in terms of the reattachment of flow within the port. Separation of the flow from a sharp-edged port takes around half a port diameter to reattach. Once this occurs, pressure recovery within the port leads to an increase in the discharge coefficient. With inlet shaping, the resulting increase in discharge coefficient implies a reduction in the size of flow separation at inlet, thus reattachment will occur much sooner. For the stepped ports described without chutes, it is probable that the flow is marginally reattached and further comment will be given on this.
All these geometrical and crossflow effects on discharge coefficient discussed above have been summarized by various empirical correlations. Notable ones and those relevant here are McGreehan and Schotsch [7], Chin et al. [11], Adkins and Gueroui [12], and more recently Fesker et al. [9], which allow prediction (within typical experimental uncertainty) of a port discharge coefficient to be determined. Each uses a different methodology and base flow parameters and each has their own limits of applicability. The effect of stepped inlets on discharge coefficients is currently not reported in open literature and not included in any available correlation methodology. It is thus difficult to predict combustor pressure loss without an indication of their effect. Indeed, a recent full-scale test of a combustor with stepped ports performed very differently than expected because sharp-edged port discharge coefficients had been assumed. Without hindsight, this is perhaps a reasonable assumption. The combustor total pressure loss was close to 20% lower than its design value and had weaker jet penetration than required.
The objective of this work is thus to test stepped holes with crossflow feed for port ingestion fractions of 30% to 100% (i.e., annulus bleed ratios, α, 0–70%). This will include investigating the effect of changing the port diameter to feed annulus height and step angle, for example. Benchmarking the stepped port against plain port data is useful to determine the influence of the step and provide validation of the experimental techniques. An initial indication of how to include the effect of the inlet step on the Cd can then be made.
These tests do not consider the effects of compressibility or explore full ranges of geometrical parameters that are already well captured by existing Cd correlations (such as length to diameter ratio (L/D), for example). Instead, only two or three values of other main parameters are studied to ensure stepped port behavior is consistent with these existing correlations and exhibits no significant coupling between the step feature geometry and other parameters.
2. Materials and Methods
A water flow rig has been used for most measurements in which a single row of multiple ports is fed by an annular crossflow and the jets issue into a crossflow, as in a combustor, this also allows for a bleed flow stream, where the port only receives a fraction of the approaching cross flow. Flow through the ports are at supercritical jet Reynolds numbers above which it is found that there is little variation in Cd, quoted in various works to be between 1.8 × 104 and 3.5 × 104 [13,14]. Reynolds number variation in Cd has been tested in this work in the range 5 × 104 to 2 × 105, which has agreed with these previous works and all results presented are for jet Reynolds numbers above 5 × 104. Results from both rigs agree with previous studies, within experimental uncertainty. Other numerous parameters affecting discharge coefficients have been studied previously and several empirical correlations exist to describe each of their behaviors.
2.1. Water Flow Facility
The test rig is an isothermal, vertically flowing, constant head, water flow rig. Figure 2 shows a schematic of the rig, and it is described in detail in McGuirk and Spencer [15]. The test section has two inlet flows and two outlet flows that can be controlled by two return flow valves and one inlet valve to provide a range of jet Reynolds numbers, jet to downstream cross flow ratios, and annulus bypass flow ratios independently. Setting these three parameters effectively defines the mass flows through each path of the test section.
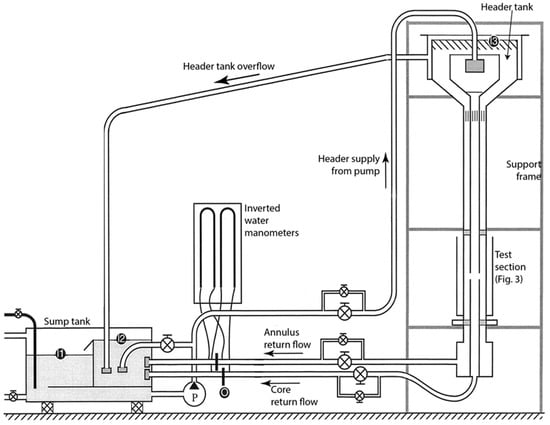
Figure 2.
Water flow rig: constant head closed circuit system.
The working section shown in Figure 3 is comprised of two circular 600-mm long pipes, the inner one being held concentric with the outer at each end via a set of six NACA 0015 struts. The inner pipe contains the ports approximately half way along its length. Wall static pressure tappings were positioned 70 mm upstream of the ports on the inner and outer surface of the liner to monitor the wall static pressure drop.
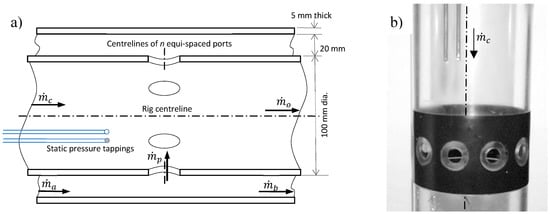
Figure 3.
Waterflow test section. (a) schematic and (b) photo of inner liner with stepped ports.
The liner pressure tappings are seen in Figure 3 embedded in the Perspex wall of the inner liner, which has been removed from the test rig in the right-hand photograph. The tapping location was positioned upstream to avoid regions of recirculation within the core pipe induced when low internal crossflow to jet velocities are used. It has previously been investigated if the jet to downstream crossflow velocity ratio has any effect on discharge coefficients and findings have shown the effect to be less than 1%, provided the measurement of liner pressure drop is not influenced by the tapping location. The inner liner can be rotated, and this had no effect on the pressure measurements, giving confidence in the axisymmetric nature of the approach flows. More details on these aspects can be found in Spencer [16]. Using water as an essentially incompressible media implies the findings can be equated to port behavior in air at low pressure ratios. The behavior of compressibility is well captured by existing discharge coefficient correlations through compressibility corrections, for example, in the works of [7,9,11], and is thus not considered further.
2.2. Airflow Facility
Shown in Figure 4 is the open circuit air flow rig that was used to compliment the main body of work. In the final results section, a short study is presented on axis-symmetric flow through ports with stepped inlets, and compares this with ports of similar chamfered dimensions. A centrifugal fan draws air through the stepped port by creating a low-pressure region behind it. A bypass flow is allowed into the fan to ensure the fan operates in a stable, non-stalled condition that would occur otherwise. The stepped port is fed by a 2.5-m long, 90-mm internal diameter pipe downstream of a 30-mm diameter venturi meter, which measures the mass flow through the stepped port. Static pressure ports are positioned 50 mm upstream downstream of the stepped port to determine the pressure drop across it. Equipment, methods of instrumentation, and data reduction are all in line with simplified versions of what is presented for the water flow results.
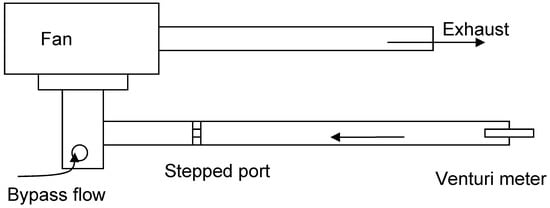
Figure 4.
Airflow rig schematic: axisymmetric testing.
2.3. Instrumentation
It was important to know actual port mass flow and port pressure drops to determine the port discharge coefficient. Temperature is recorded to determine viscosity for Reynolds number and density of water is taken as a 1000 kg/m3.
Three types of instrumentation were used for this study: orifice plates were used to measure the flow rates exiting the test section (core and annulus), a 1D laser Doppler anemometer was used to measure the velocity profiles entering the test section (again, core, and annulus), and finally a pressure transducer was used to measure the liner pressure drop. With these measurements, the discharge coefficient could be calculated, as will be described in the next section. These devices are described in a little detail below and summarized in Table 1, but for a fuller description, refer to Spencer [16].

Table 1.
Measurement uncertainty of key parameters.
Orifice plates were used to measure the return flow from the annulus and core passages of the test section. Designed and made to BS 1042, the uncertainty in the orifice plate’s Cd obtained from the Stolz equation was always below 2.0% (refer to the standard for further details). The pressure drop across each plate was monitored using an inverted water manometer connected to D and D/2 static pressure tappings. Typically, each return mass flow rate could be measured to better than ±2.5% over the flow conditions used for these tests. This has been verified by checking the measured outlet mass flows against the mass flows obtained by integrating the Laser Doppler Anemometer (LDA) determined diametral velocity profiles through the annulus and core of a blank test section (i.e., with no ports).
A 1D LDA system was used to measure the axial velocity profiles 150 mm upstream of the ports in both the annulus and core inflow streams. By assuming the flow at inlet is axis-symmetric, the mass flow rate into the core and annulus may be obtained by integration of the measured axial velocity profiles. Within the core, the assumption of axis-symmetry has been shown to be good. However, in the annulus, a circumferential variation is found because of the six struts used to hold the liner concentric to the outer casing. It has been established that the effect of the wakes is that the actual mass flow rate is about 2% lower than if axis-symmetry is assumed. Only three mass flow rates are required to specify the flow split through the rig, as if the two exit and one of the inlet mass flow rates are known, then by mass continuity, the unknown inlet mass flow may be calculated. Because the annulus inlet mass flow rate was determined to have the highest error associated with its measurement, it was decided to use this purely as a check on the mass flow balance through the test section. It was considered acceptable if the inferred and measured annulus inlet mass flows agreed to within 3%. Considering the other three mass flows were measured to within 2.5%, this could be considered a stringent condition, however, all measurements reported were within this limit. Subsequent calculations requiring knowledge of the annulus mass flow rate used the value inferred from the other three measured values for consistency.
2.4. Data Reduction
Discharge coefficient is evaluated here by dividing the actual mass flow passing through the ports by the ideal mass flow, defined as follows:
and the port to annulus inlet mass flow ratio, α, calculated via the following:
noting that the annulus inlet mass flow is not used in any calculation to keep the uncertainty associated with Cd and α minimised for the current experimental setup. Inputs to this calculation were the inlet axial velocity profiles, the exit orifice plate pressure drops, and the pressure transducer voltage. Calibration coefficients for each of these then allows the respective inlet, exit, and ideal mass flow rates to be calculated in kg/s.
Direct comparison was made between the inferred and measured value of annulus inlet mass flow rate of around 1% to 2% was found, which was typical of most tests, and for all measurements, the accepted maximum difference between measured and calculated annulus inlet mass flow rate was 3%, as previously stated.
Uncertainties were determined from the contributions from the individual measured value uncertainties for all measured conditions. In combining the sources of uncertainty, the overall absolute uncertainty in the discharge coefficient of 4% is calculated with 95% confidence for conditions with α > 0.5. This is typical of most measurements though, with the highest annulus bleed ratios (i.e., low α, of less than 0.4), the uncertainty rises to around 6% because of compounding the effect of port mass flow being derived from the decreasing difference of two mass flows. Taking into account only the systematic errors indicates that the repeatability of a typical test should be within 2.5%. The level of scatter within data supports these findings.
The port pressure ratio of the airflow tests was typically around 1.02 to obtain sufficiently high Reynolds numbers, but stay comfortably within an incompressible regime that has been assumed within the analysis. Peak through port velocities of the order 50 m/s were obtained. Again, Cd is defined as the actual to ideal mass flow ratio and assuming constant density locally and using the calibrated venturi meter (Cd,v = 0.994) as the reference (actual mass flow), the port Cd was calculated using the following:
Airflow rig results are also at sufficiently high Reynolds numbers (the Cd is quoted as an average of the tests over the range 6 × 104 and 3 × 105) and uncertainty analysis shows the Cd is reported at better than 3% with 95% certainty.
2.5. Test Configurations
Several test sections were used for this study, one with plain sharp edged (s = 0, or no step) circular port inlets for reference purposes, and the rest were representative of stepped ports, either full scale ports or two-thirds scale (based on a nominal port diameter, D, of 18 mm). A typical test section as shown in Figure 4 for the water flow rig will have several of these ports with a curvature in the through page direction as a result of the walls through which the port passes being cylindrical.
The dimensions of each test port can be seen parametrically in Figure 5. This figure shows a cross section through the centreline of one port. It is clear to see how the step is formed by the two joined walls with holes of slightly differing diameters. A dimension not shown in Figure 5 is the hole pitch spacing, Z, for the waterflow measurements. This is the distance between port centres measured around the circumference—which will decrease as the number of ports increases. As shown in Figure 3, the outer radius of the liner (outer wall) was fixed at 50 mm, and the annulus height, H, was 20 mm, giving an outer annulus diameter of 70 mm. Some plain port validation work also included annulus heights of 5 mm.
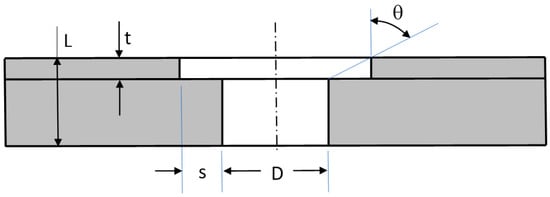
Figure 5.
Parametric stepped port definition.
Plain port measurement configurations are used to verify the measurement set taken and to benchmark against both Cd correlation methods and the stepped port results are listed in Table 2. Stepped port configurations are given in Table 3. The 12-mm diameter stepped ports are able to closely match all of the important geometric ratios found typically on an engine. Four step length, s, (hence four angles, θ) are considered for the 12 mm ports (cases A to D). At around two-thirds scale, it would be difficult to manufacture a test section with accurate eccentricity between the cold skin and tile ports. Approximately full-scale ports (diameter 18 mm) were thus employed to explore the effect of eccentricity in three directions, in which the outer sleeve could be moved relative to the inner ring to create the eccentricity (cases ε1, ε2, and ε3 have the cold skin upstream, downstream, and to one side of the smaller port, respectively). These are benchmarked against case E, which had no eccentricity but otherwise matched all other geometric parameters. To compare the effects of the step inlet to inlet chamfering, some airflow tests were also performed for single ports in axisymmetric flow with a range of step inlet angles comparable to the chamfering angles that had been considered in previous studies [6]. These are reported separately at the end of the results section.

Table 2.
Plain port test configurations, waterflow rig with crossflow.

Table 3.
Stepped port test configurations, waterflow rig with crossflow.
The port Reynolds number determines the port velocity for both the water flow and air flow tests, and hence for a given port size, also the port mass flow. This fully defines the airflow test condition. Two additional parameters are required to determine the crossflow conditions. (1) The proportion of the annulus inlet flow that is ingested by the port, α. This, combined with the absolute port mass flow, sets both the annulus inlet and outlet mass flow rates. The area ratio of the port to the annulus, β, then determines the annulus approach velocity. (2) Similarly, the core inlet mass flow is determined by the port to cross flow velocity ratio, Vp/Vc. Discharge coefficients are known to be insensitive to this parameter and no correlations feature in Cd as a result. In these tests, the port jet to cross flow velocity ratio was kept in the range 2 < Vp/Vc < 5. Experience on the facility used here has shown no measurable change in Cd in this range. However, exceeding a value of 5 for Vp/Vc can cause problems because the jet impingement becomes very strong and forms a recirculation large enough to give unsteady pressure measurements in the core, and was thus avoided. These flow conditions are summarized in Table 4. Readers interested in further details, such as the approach flow velocity profiles, may see references [3,16].

Table 4.
Range of flow conditions tested.
3. Results
3.1. Plain Port
A collection of discharge coefficient data measured for plain ports (including repeat tests) is shown in Figure 6. Two configurations (with the lowest H/D values) show variability of Cd at high α, which is thought to be because of the formation of an unsteady vortex over a variable number of the ports at this high ingestion fraction with low port to annulus area ratio. Otherwise, the scatter of the measured Cd is generally reasonable and within ±3% as expected from the uncertainty analysis.
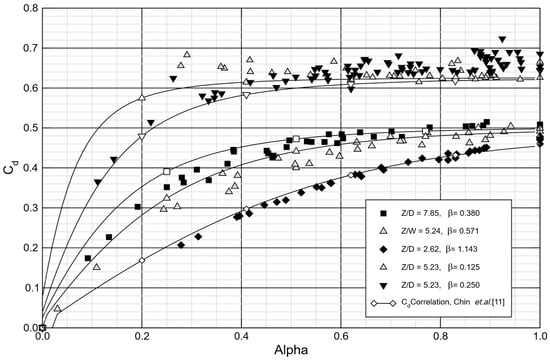
Figure 6.
Plain port Cd Variation with alpha, experimental data and empirical correlation.
Values of Cd predicted by the correlation of Chin et al. [11] for the plain circular port configurations are also shown in Figure 6 by the solid lines (the configuration they have been calculated for is indicated by unfilled versions of the respective symbol for the experimental data). The correlation has been further modified to also consider the L/D of the ports using the method outlined by McGreehan and Schotsch [8].
Reasonable but not perfect agreement between the correlations and the measurements can be seen. Two main factors are suspected to account for the discrepancy. Firstly, in the range 0 < L/D < 1, the Cd of a port is very sensitive to the port’s length. Significant scatter can be seen in the measured Cd’s of different workers in this range because of the L/D sensitivity (Lichtarowicz [13]). This effect could be further compounded by the crossflow inducing non-axisymmetric flow. Secondly, and more important to consider here, is that from experience, some doubt may be cast on Cd correlations as the annulus height is reduced in comparison to the port diameter. For the plain port geometry, this ratio, H/D, was 1.0, and it has been seen for this geometry that unsteady through-port vortices can be formed at high α (Spencer [16]). The higher levels of scatter in the measurements for α > 0.9 seen in Figure 7 are thought to be caused by these vortices. To avoid this problem in the subsequent stepped port measurements, it was decided to scale the ports so that H/D (and all other geometrical ratios) were higher and more representative of the engine configuration. This was indeed seen to reduce scatter in subsequent data.
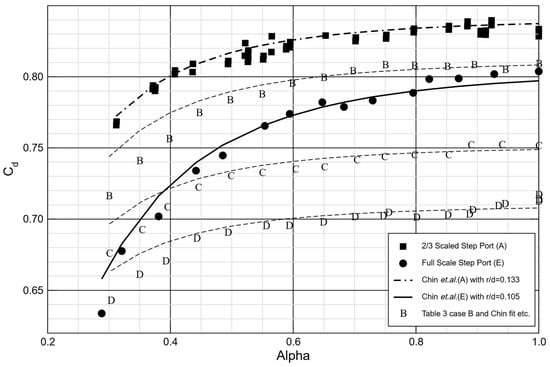
Figure 7.
Stepped port Cd for cases A to E. Chin et al. [11] correlation best fit by adjusting r/D.
3.2. Stepped Ports, with Crossflow
Variation of Cd with alpha is shown in Figure 7 for stepped inlet port configurations A to E. Cases A and E are highlighted with filled symbols, cases B, C, and D use the respective character to indicate measurement points. Each set has a best fit correlation line plotted through it. It can be seen that there is a significant increase in Cd compared with the plain ports of the previous section. Here, the discharge coefficients reach up to 0.83 at high alpha compared with around 0.62 to 0.64 for plain ports. Principally, this significant increase is because the size of the vena contracta has been increased by the presence of the step, which in turn has increased the coefficient of contraction. With no empirical data available for stepped ports, correlations for its effect are not available. Here, the correlation of Chin et al. [11] is fitted to the data, with modifications for L/D as described earlier using McGreehan and Schotsch [8] for plain ports. An additional correction is added by increasing r/D also using the method of the authors of [8] until the correlation best fits the experimental data available here, see Appendix A. In total, five step configurations with varying step angles are considered and this process has been repeated for each. At lower values of alpha, it can be seen that the correlation appears to increasingly overpredict the discharge coefficient. This suggests that the directionality of the flow can be important to the discharge coefficient, as might be expected, but stepped port Cd appears to fall more rapidly compared with expectation from this correlation with reducing α at lower values (α < 0.5).
The effective r/D determined for the five cases above is conveniently summarized in Figure 8. Here, the value of r/D that produces the best correlation fit to the test configuration is plotted against step angle for each of cases A to E. For typically employed step angles of around 60°, it would appear that an effective inlet radiusing of r/D of 0.1 could be used in existing correlation techniques to reproduce the equivalent change in Cd. To predict Cd for stepped ports in the range 50 < θ < 90°, a linear distribution maybe acceptable as indicated.
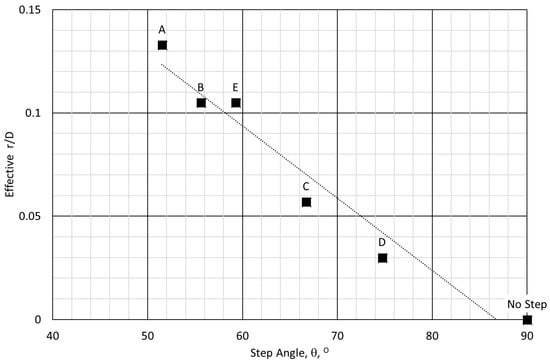
Figure 8.
Effective r/D value to produce best fit correlation with varying step angle.
3.3. Stepped Ports, Eccentricity
It was seen in the previous section that with inlet step features, the variation in Cd with alpha was not well captured by empirical correlations at low α, suggesting a different flow direction sensitivity of stepped ports compared with plain or radiused ports. As a result, it was considered sensible to investigate if eccentricity of the holes in the hot and cold skins had an effect. A single magnitude of eccentricity was considered of ε/D = 0.083, but in three directions, as indicated in the bottom right of Figure 9. The correlation of the work of [11] did not fit this data very well in variation with α, therefore, to compare the change in Cd between the configurations, a best fit quadratic was fitted to the measured data. The percentage difference between these smoothed curves and the datum (concentric) case is then shown in Figure 10.
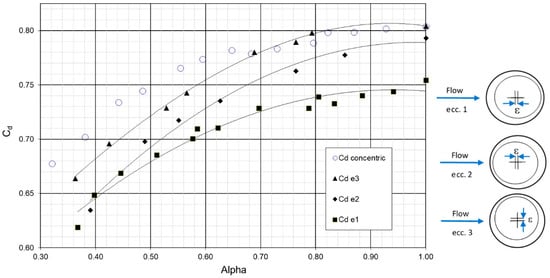
Figure 9.
Affect of step concentricity with main port on discharge coefficient.
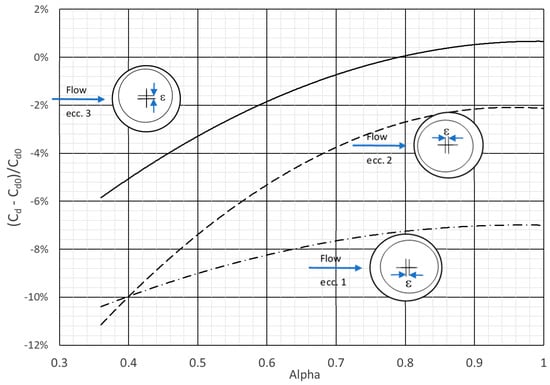
Figure 10.
Sensitivity of change in Cd with alpha for eccentric cases ε1, ε2, and ε3.
Moving the cold skin upstream has the largest effect on Cd, reducing by 7% to 10% across the range of α considered. At high port mass ingestion (α), moving the cold skin downstream has a reduced effect, from −7% (ecc.1) down to −2% (ecc.2) at α = 1.0. At lower α, both eccentricity directions have a similar effect of a 10% reduction. Sideways eccentricity does not appear to be too detrimental to Cd at high α, but Cd is reduced by 5% at α = 0.4. These figures should be seen in the context of a systematic uncertainty in Cd of around 2.5%, relevant when considering ratios to the concentric datum case Cd0.
Cooling tiles are often constructed using additive manufacturing techniques to allow complex features to be introduced. One approach to avoid eccentricity effects outlined above would be to introduce a raised feature to eliminate the effects of the step. This is sketched in Figure 11 with the inclusion of an inlet chamfer to help increase the discharge coefficient and help jet directionality.
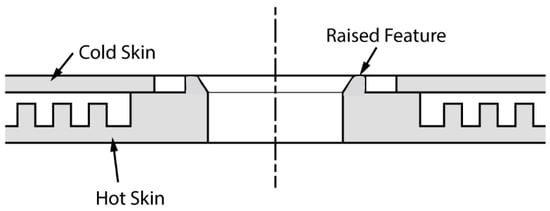
Figure 11.
Method to avoid inlet step effects on discharge coefficient.
3.4. Axisymmetric Stepped Ports, Low Step Angles
To compliment the work described so far, a study was undertaken to compare the effect of a step inlet feature to a chamfer of similar size. The step angle range, shown in Table 5, was chosen to align with values typically used when chamfering ports where previous data exists, e.g., [6]. Common chamfering angles are 45° due to ease of tooling, or 30° as it is known that this value produces the highest Cd value, which the results here have confirmed. The Cd of chamfered ports is maximised once their depth exceeds ~0.08D, beyond this value, increasing the size of the chamfer has little effect. Thus, in Figure 12, the high Cd values of just above 0.95 at a chamfer angle of 30° are constant with t/D.

Table 5.
Axis-symmetric chamfered and stepped port flow testing configurations, airflow rig.
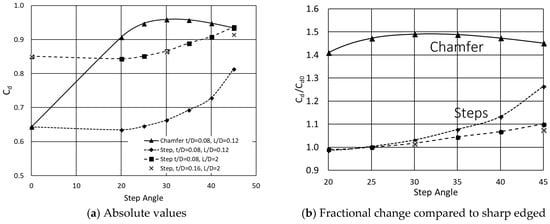
Figure 12.
Stepped inlet and chamfered inlet comparison for a range of step/chamfer angles.
As the step angle increases from a sharp edge (0°) to 45°, a steady increase in Cd is seen for L/D of both 0.12 and 0.2. The shorter port sees a larger percentage increase than the longer port (~25% cf. ~10%) in discharge coefficient compared with the sharp-edged ports (Cd0), and the maximum value in this range occurs at 45°. Insensitivity to increased step height of t/D = 0.16 for an L/D of 2.0 is also seen for two points that map closely to the t/D = 0.08 curve. It would appear the Cd is increased using stepped inlets, with the peak value (at θ = 45°) being about half of the increase obtained by chamfering at θ = 30°. However, it does appear from this and the previous sections that there is limited sensitivity of Cd to step height, as is the case for chamfer depth.
The differences in increase of Cd in cases in Figure 12 highlight some coupling between L/D and t/D that exist for short ports (low L/D). Coupling of this nature is compensated for in Cd correlations for inlet radiusing. Radiusing, unlike chamfering and stepped inlets, continues to increase Cd to values very close to 1.0, which is obtained once r/D is ~0.82. Thus, the data in Figure 12 can also be presented in the form of an equivalent r/D value by best fitting a correlation to the data using the best r/D to replicate the measured value. In this way, the t/D to L/D coupling can be deconvolved by the empirical data that has trained correlations, where here, we use McGreehan and Schotsch [8] approach as briefly outlined in Appendix A.
Stepped inlet results of the effective r/D for the axisymmetric and crossflow cases are brought together in in Figure 13 and compared with the chamfered port evidence. These data compactly indicate the best way to implement the effect of stepped ports in Cd correlation based on the evidence from this study. Provided t/D > 0.07 and t < 0.75L, the effective r/D in existing correlations can be chosen from Figure 13 for the appropriate value of step angle. This should provide a Cd estimate within typical measurement accuracy.
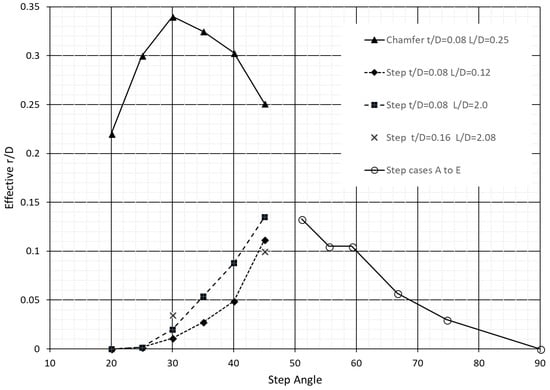
Figure 13.
Effective r/D for all stepped inlet cases and chamfered inlet comparison.
The 50–90° portion of the curve in Figure 13 was determined first, and it was anticipated that a peak would appear at around 30° comparable to chamfering, but perhaps with a lower peak value. This motivated the axisymmetric study, which was conducted at a later point. It can be seen that the evidence suggests a peak Cd increase in the 45–50° region with an equivalent r/D of around 0.15, with step angles below ~25° and above ~80–85°, the step has no discernable effect on Cd.
4. Conclusions
A range of port configurations with stepped inlets have been tested with and without approach cross flow. Discharge coefficients have been measured and compared to plain port benchmark tests for validation purposes.
Stepped inlets at entrance to ports produce a significant increase of the port discharge coefficient.
For a stepped port geometry similar to a typical engine combustor primary port, an increase in Cd of 25% over the equivalent sharp-edged port was found (L/D = 0.25, t/D = 0.08).
To include the effect of the step in empirical correlations, an equivalent r/D factor may be used. The equivalent r/D depends primarily on the port step angle (arctan of ratio of step length to height). Step height to diameter ratios in the range 0.06 to 0.2 had an insignificant effect on discharge coefficient in comparison compared with step angle, and is compensated for in existing correlations.
Eccentricity of the two diameters that define the stepped port is a significant factor influencing the overall discharge coefficient. Cd was reduced by up to 10% for the orientations of eccentricity tested and approach flow directionality behavior was changed compared with concentric inlet features.
Step angles of around 45° to 50° appear to produce the highest Cd, though further work is required to verify this because this value fell between the two testing configurations.
Funding
This research was funded in part by Rolls Royce plc.
Conflicts of Interest
The author declares no conflict of interest.
Nomenclature
| Symbol | |
| A | Area |
| Cd | Discharge Coefficient |
| Mass flow rate | |
| p | Static pressure |
| q | Dynamic pressure |
| V | Velocity |
| α | Port ingestion fraction |
| β | Port to annulus area ratio |
| ρ | Density |
| Subscript | |
| a | Annulus inflow |
| b | Bleed (Annulus outflow) |
| c | Core inflow |
| o | Core outflow |
| p | Port |
| v | Venturi |
| :l | Length corrected value |
| :r | Radius corrected value |
| 0 | Base value (no inlet step) |
| Symbols for the geometrical descriptions of ports are defined in Figure 5 and Table 2, Table 3 and Table 4. | |
Appendix A
The correlations of Chin et al. [11] have been fitted to the experimental data presented in this paper in most figures associated with the crossflow approach cases. This correlation accounts for crossflow effects, compressibility, and annulus to port area ratios, among other parameters. Interested readers may refer to this paper for further details of the full correlation. To compensate for length to diameter ratio (L/D) and effective radius to diameter ratio (r/D), the method of McGreehan and Schotsch [8] has been used. Here, the baseline (sharp edged, thin port) discharge coefficient (Cd0) is corrected for inlet radiusing via the following:
where
A similar relationship is available for L/D effects:
where
When both L/D and r/D effects are taken into account, compensation is made by reducing the effective L/D by the r/D value used, and making a cross compensation for Cd:r, not explained fully here for brevity. These formulae have been used to calculate an effective r/D that best matches the stepped or chamfered port behavior. ‘r/D’ in the f equation has thus been changed to minimize the rms error in fitting the correlation of the literature [11] (taken as the baseline ‘Cd0’ value) to the data for cross flow cases. For axis-symmetric flow, Cd0 has been taken to be the sharp-edged value (no step/no chamfer case) for the same L/D port. ‘r/D’ has then been changed to obtain the best fit to experimental values of Cd.
References
- Stuttaford, P.J.; Rubini, P.A. Preliminary Gas Turbine Design Using a Network Approach. ASME J. Eng. Gas Turbines Power 1997, 119, 546–552. [Google Scholar] [CrossRef]
- Kukutla, P.R.K.; Prasad, B.V.S.S.S. Network analysis of a coolant flow performance for the combined impingement and film cooled first-stage of high pressure gas turbine nozzle guide vane. Proc. Inst. Mech. Eng. Part G 2018. [Google Scholar] [CrossRef]
- McGuirk, J.J.; Spencer, A. Coupled and Uncoupled CFD Prediction of the Characteristics of Jets from Combustor Air Admission Ports. ASME J. Eng. Gas Turbines Power 2001, 123, 327–332. [Google Scholar] [CrossRef]
- Lefebvre, A.H. Gas Turbine Combustion, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2008; ISBN 9781420086058. [Google Scholar]
- Pidcock, A.; Close, D. Double Wall Combustor Tile Arrangement. U.S. Patent 2003/0145604 A1, 7 August 2003. [Google Scholar]
- Hay, N.; Spencer, A. Discharge Coefficients of Cooling Holes with Radiused and Chamfered Inlets. J. Turbomach. 1992, 114, 701–706. [Google Scholar] [CrossRef]
- Dittmann, M.; Dullenkopf, K.; Wittig, S. Discharge Coefficient of Rotating Short Orifices with Radiused and Chamfered Inlets; ASME Paper No. GT2003-38314; ASME: New York, NY, USA, 2003. [Google Scholar]
- McGreehan, W.F.; Schotsch, M.J. Flow Characteristics of Long Orifices with Rotation and Corner Radiusing. ASME J. Turbomach. 1988, 110, 213–217. [Google Scholar] [CrossRef]
- Feseker, D.; Kinell, M.; Neef, M. Experimental Study on Pressure Losses in Circular Orifices with Inlet Cross Flow. ASME J. Turbomach. 2018, 140. [Google Scholar] [CrossRef]
- Chernukha, P.; Spencer, A.; Colwill, J.A. The Effect of Manufacturing Tolerances on the Performance of Gas Turbine Air System Metering Holes with Chamfered Inlets. In Proceedings of the ASME Turbo Expo 2018: Turbomachinery Technical Conference and Exposition, Oslo, Norway, 11–15 June 2018. [Google Scholar]
- Chin, J.; Shi, X.; Zhou, K. Analysis and Experimental Study on the Discharge Coefficient of Liner Holes. Int. J. Turbo Jet Engines 1993, 10, 97–106. [Google Scholar] [CrossRef]
- Adkins, R.C.; Gueroui, D.D. An Improved Method for Accurate Prediction of Mass Flows through Combustor Liner Holes. ASME J. Eng. Gas Turbines Power 1986, 108, 491–497. [Google Scholar] [CrossRef]
- Lichtarowicz, A.; Duggins, R.K.; Markland, E. Discharge Coefficients for Incompressible Non-Cavitating Flow through Long Orifices. J. Mech. Eng. Sci. 1965, 7, 210–219. [Google Scholar] [CrossRef]
- Deckker, B.E.L.; Chang, Y.F. An Investigation of Steady Compressible Flow through Thick Orifices. Proc. Inst. Mech. Eng. 1965, 180, 312–323. [Google Scholar] [CrossRef]
- Spencer, A.; McGuirk, J.J. LDA Measurements of Feed Annulus Effects on Combustor Liner Port Flows. ASME J. Fluids Eng. 2001, 123, 219–227. [Google Scholar] [CrossRef]
- Spencer, A. Gas Turbine Combustor Port Flows. Ph.D. Thesis, Loughborough University, Loughborough, UK, 1998. [Google Scholar]
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).