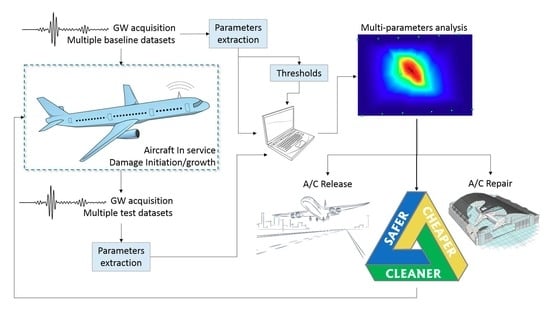
Damage Localization in Composite Structures Using a Guided Waves Based Multi-Parameter Approach
Abstract
1. Introduction
2. Materials and Methods
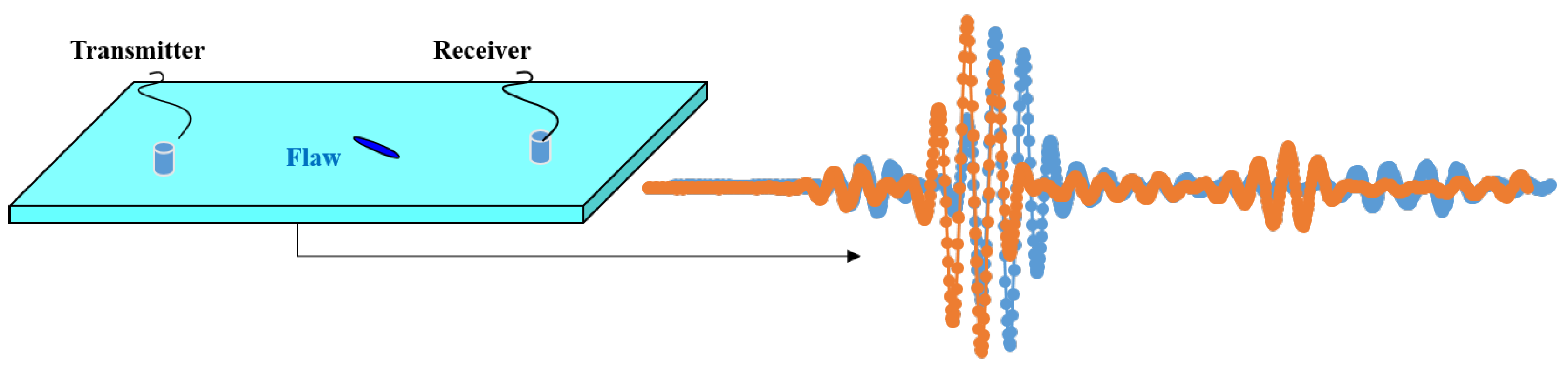
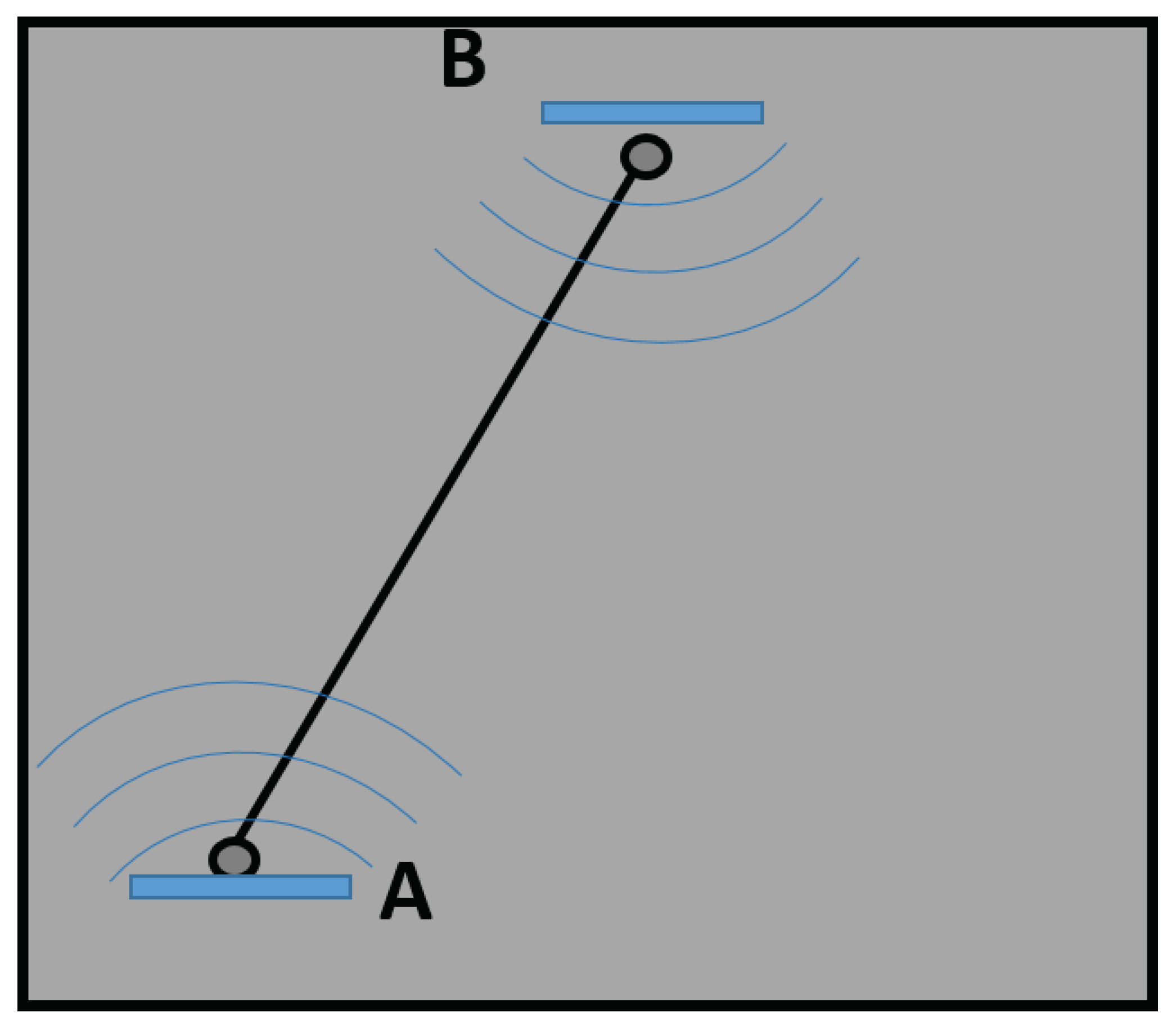
2.1. Flaw Detection Using Direct Propagating Waves
- data acquisition, where the guided waves are recorded during aircraft parking according to the interrogation mode and stored for analysis;
- data processing, which deals with the analysis of stored data to extract features possibly affected by the damage (signal response);
- decision-making process, where the minimum metric associated to a damage with a reasonable confidence is established; and
- damage reconstruction, which deals with all algorithms aimed at a certain diagnosis, no matter what is the level of the estimation.
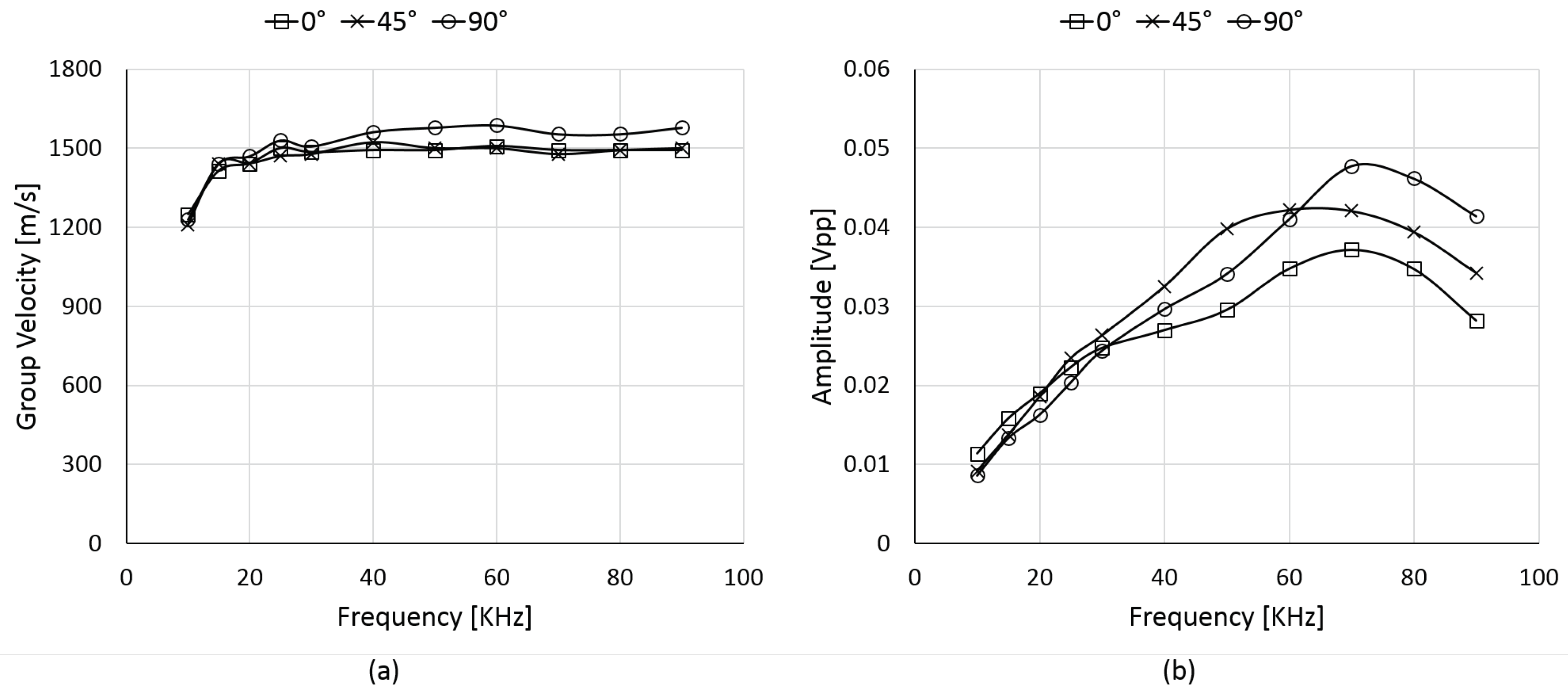
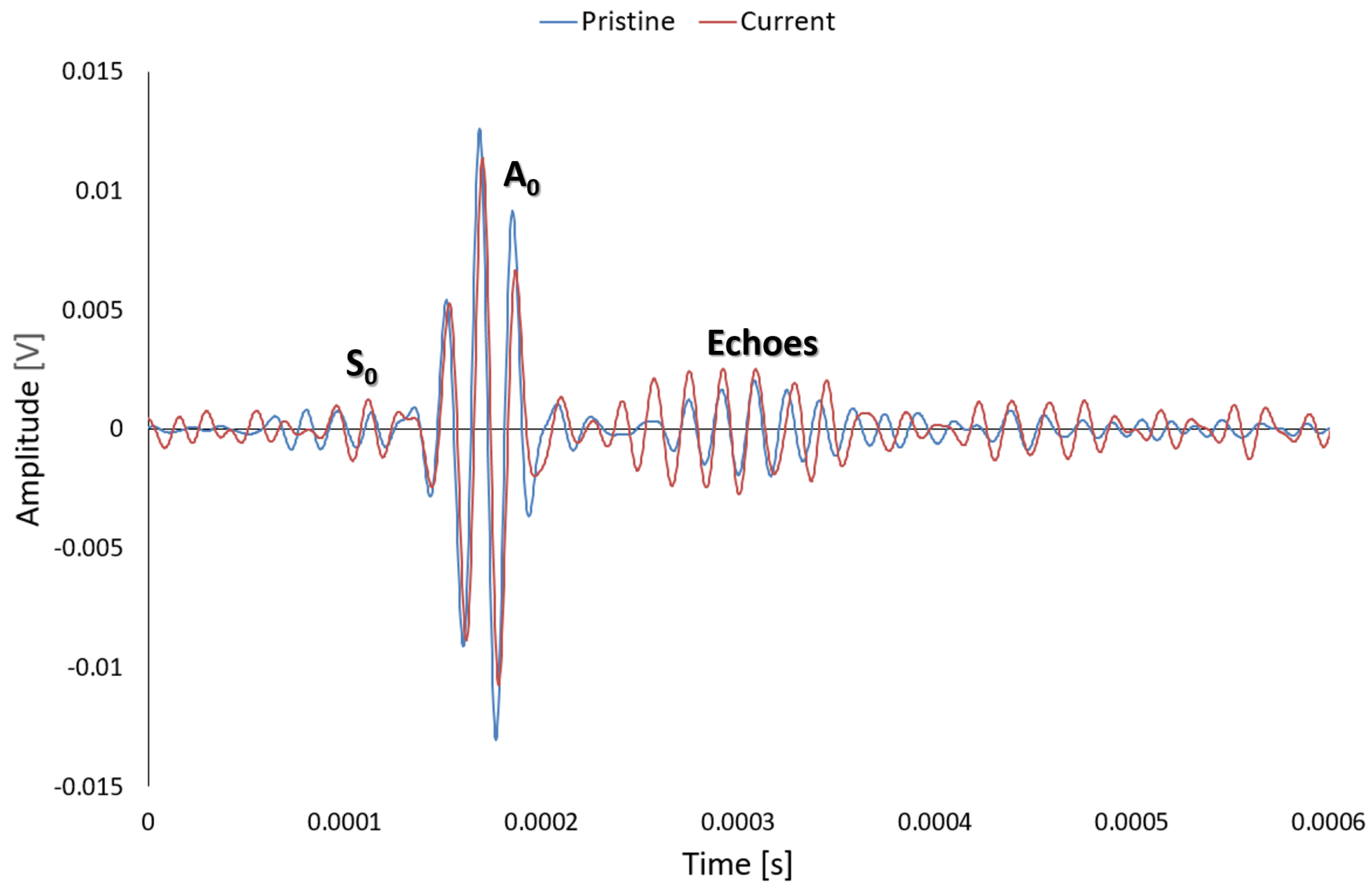
2.2. Ultrasonic Metrics
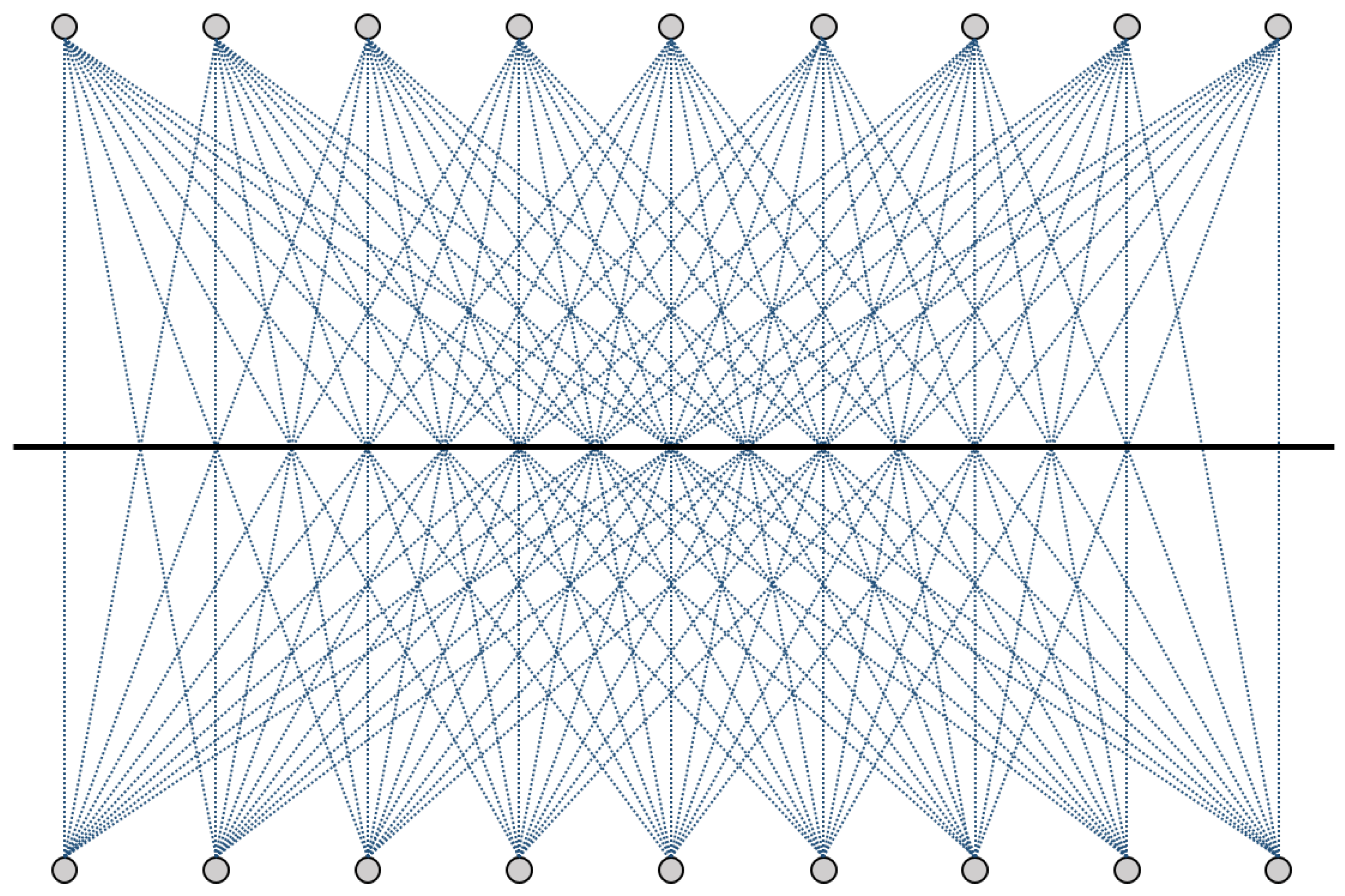
2.3. Multi-Path Reconstruction Principles
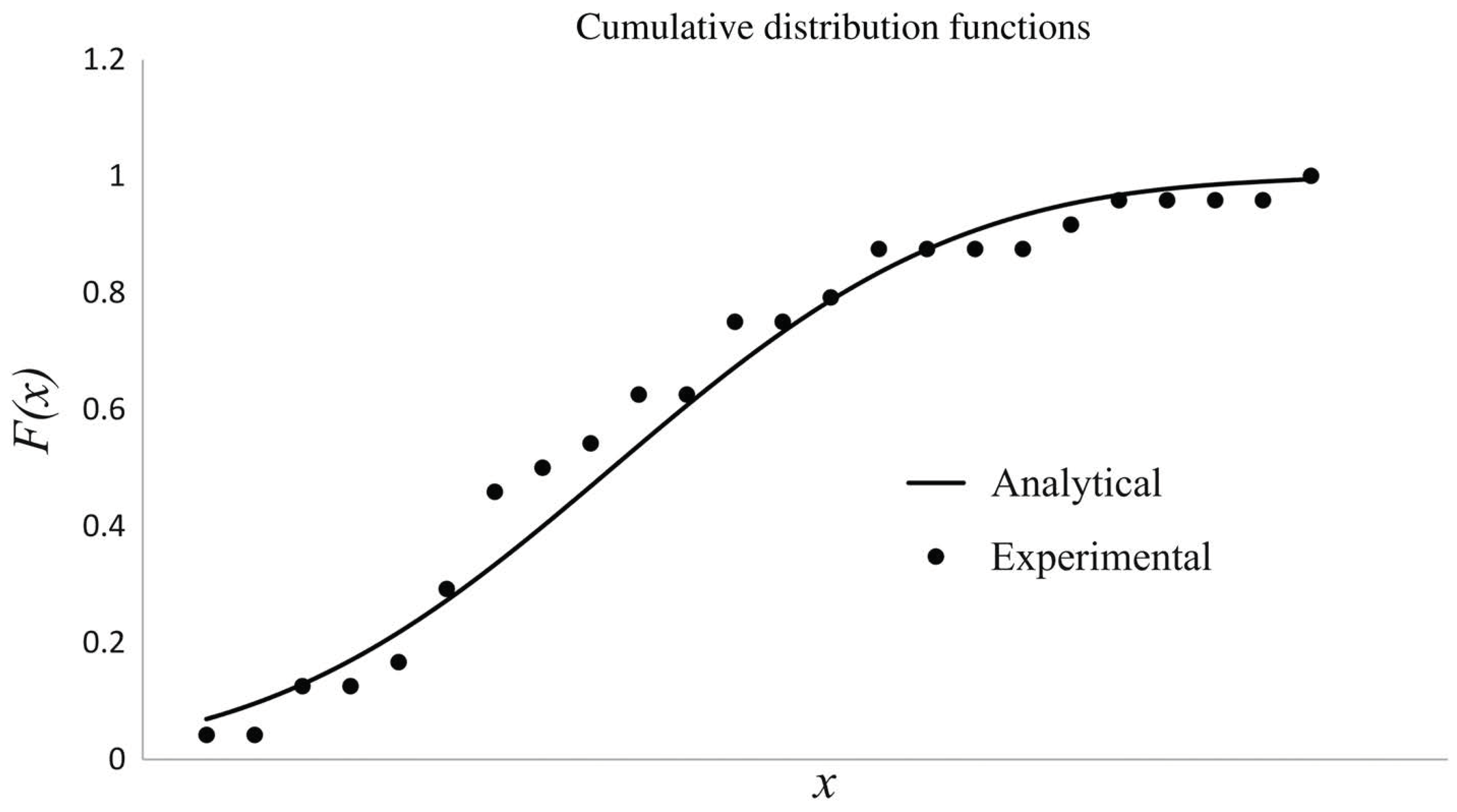
2.4. Decision-Making Approach
2.5. Reconstruction Algorithm
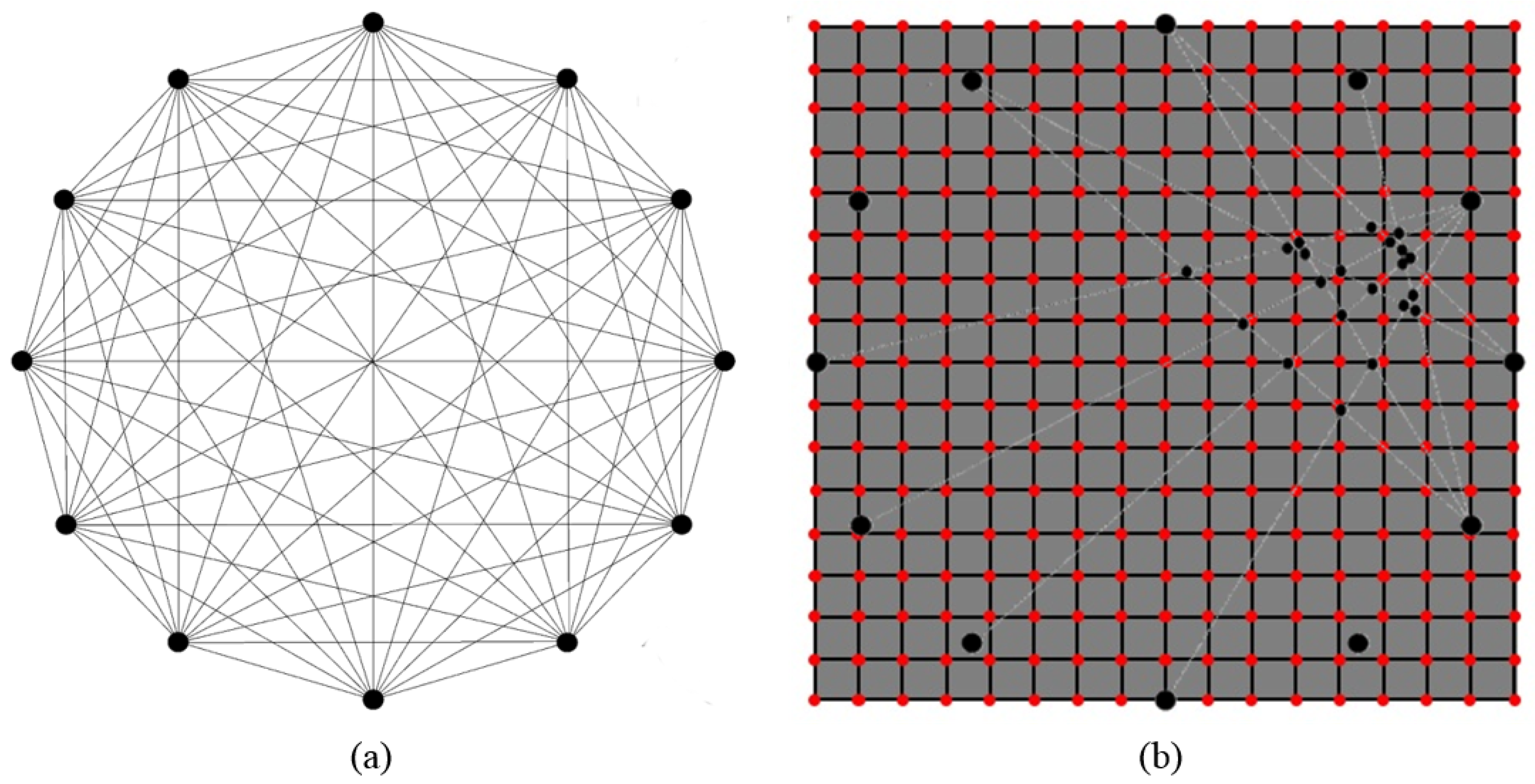
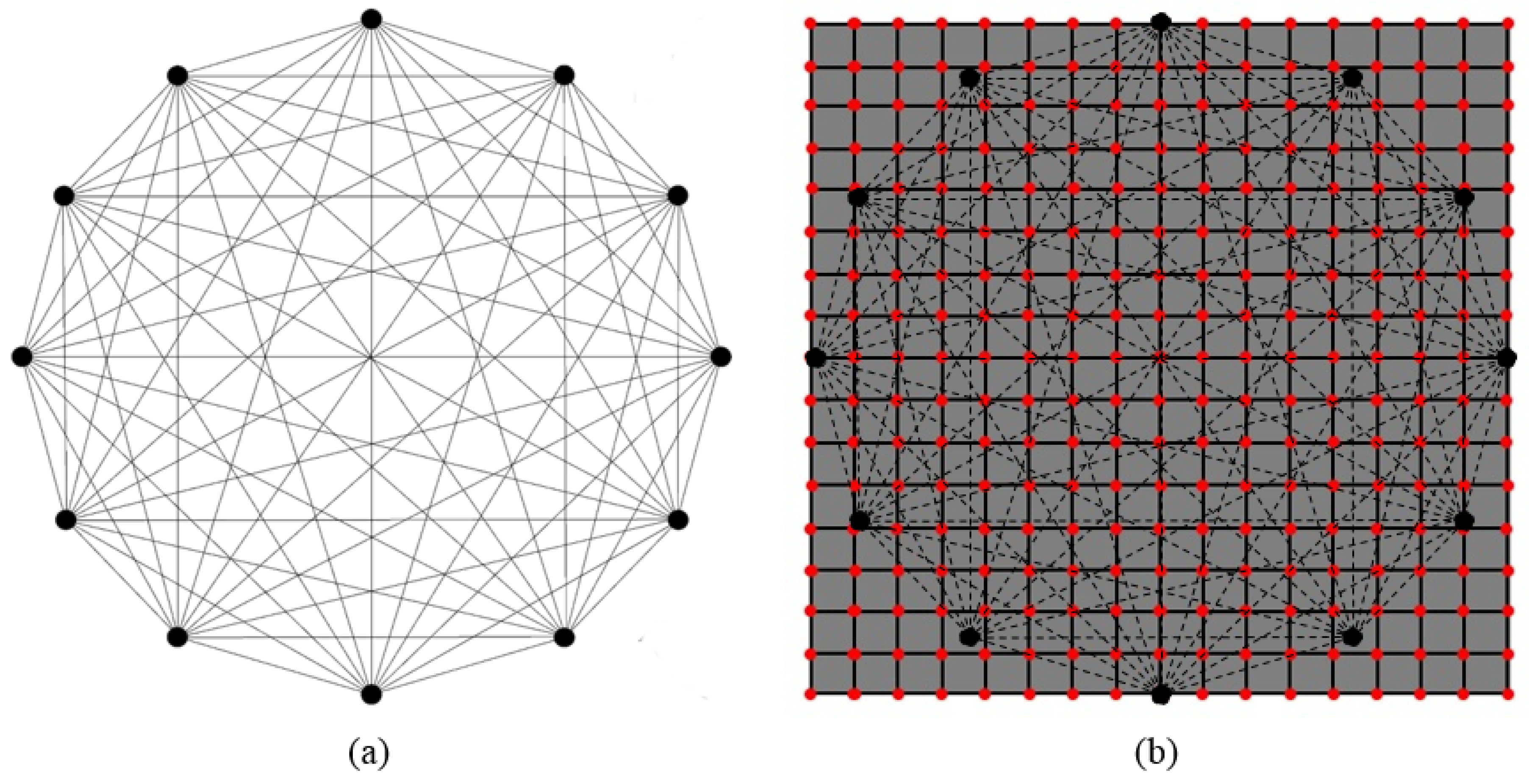
- mesh-based approaches, where SHM data are directly obtained on the structural mesh (i.e., the SHM mesh corresponds to the structural mesh [18]); and
- meshless approaches, where the SHM data are obtained in points not previously known and interpolated on the structural mesh (i.e., the SHM mesh does not match with the structural mesh [47]).
- discrete approach;
- spatial interpolation; and
- nodal density.
- The damage risk is estimated on the area enclosed by the sensors which are employed to set boundary conditions for the interpolation.
- The data below the threshold do not affect the interpolation because are censured by the decision-making approach.
- Every isolated path which is not intersecting at least another path does not affect the localization.
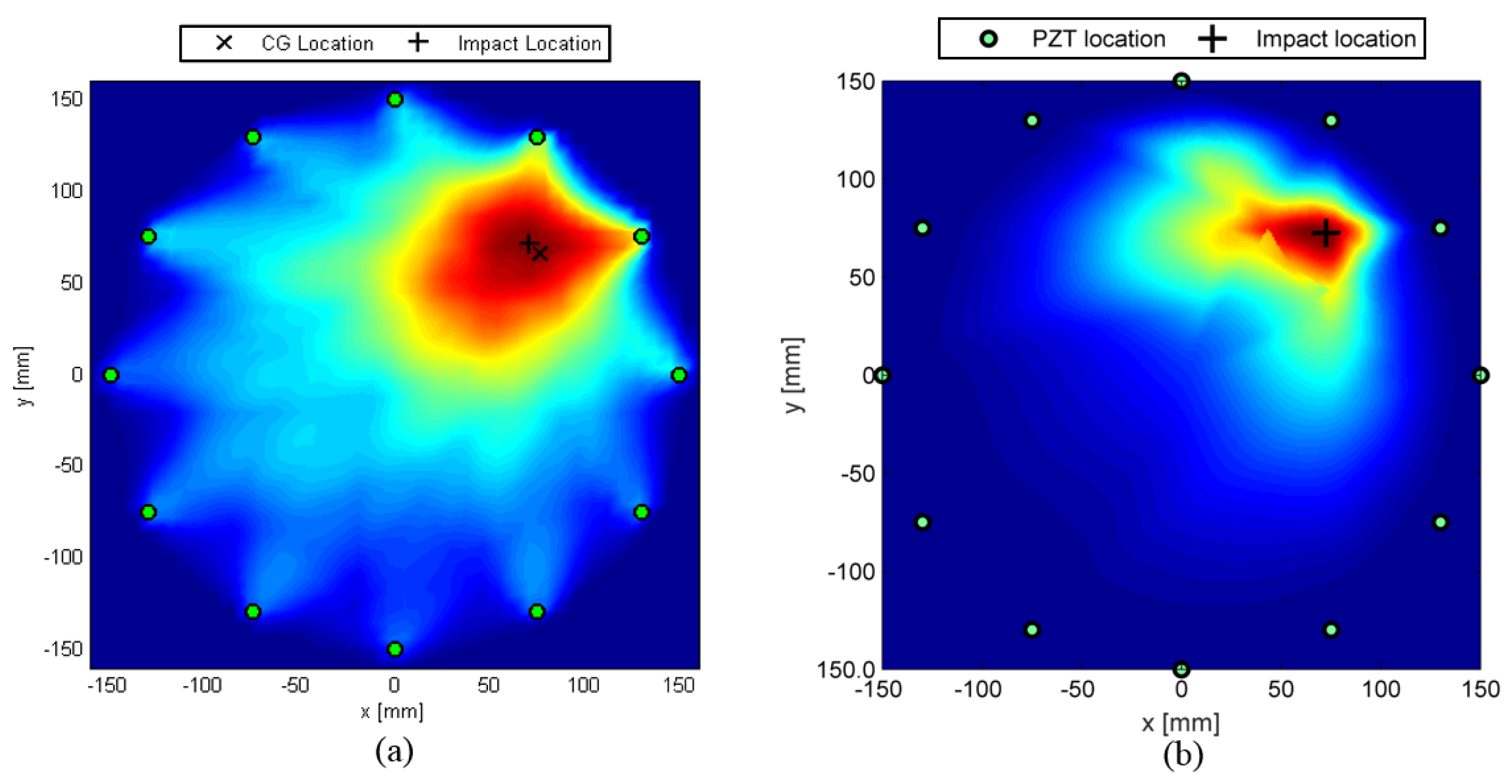
- The peak of smoothed function returns the damage position whose coordinates are used to estimate the impact location.
3. Results
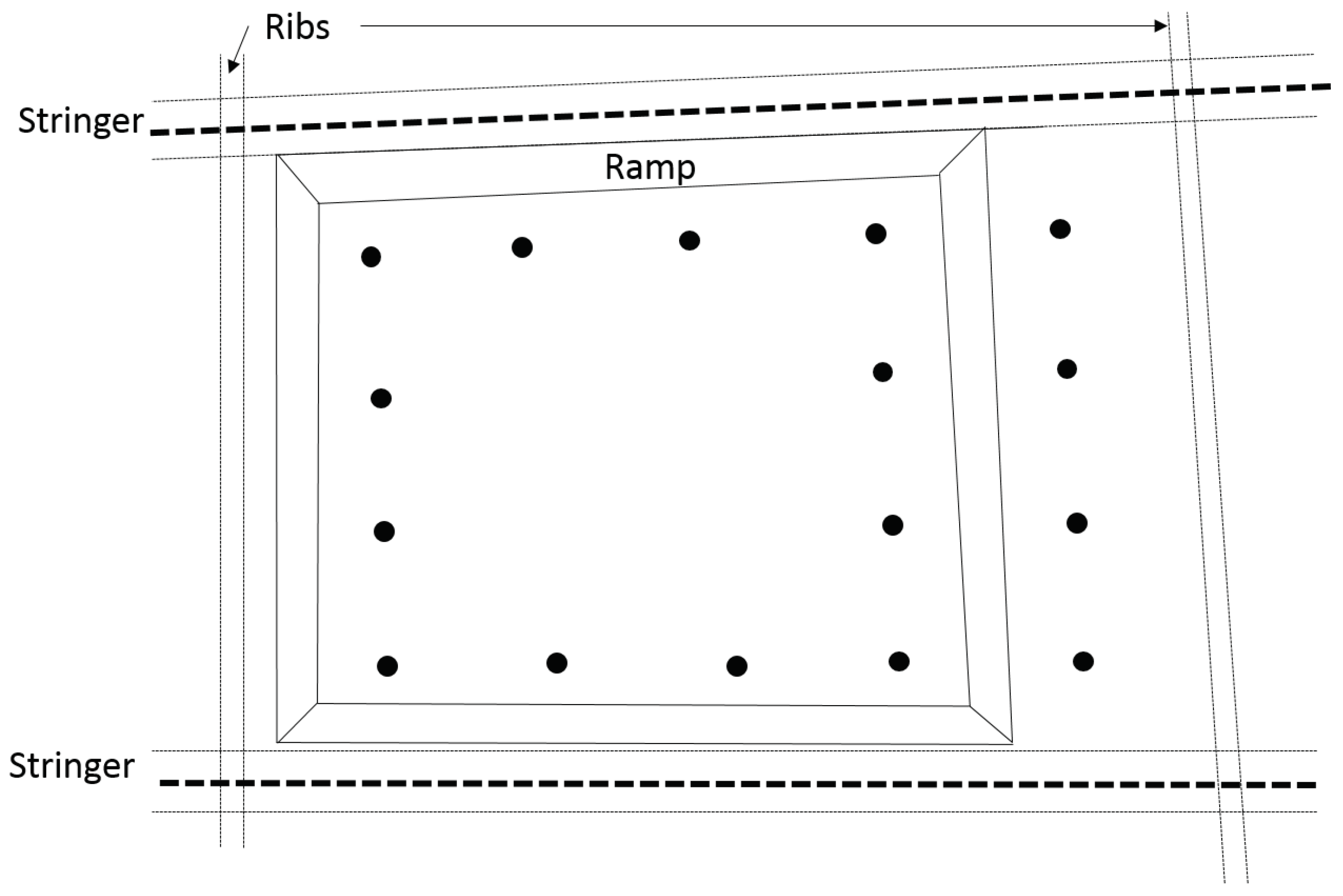
3.1. Setup
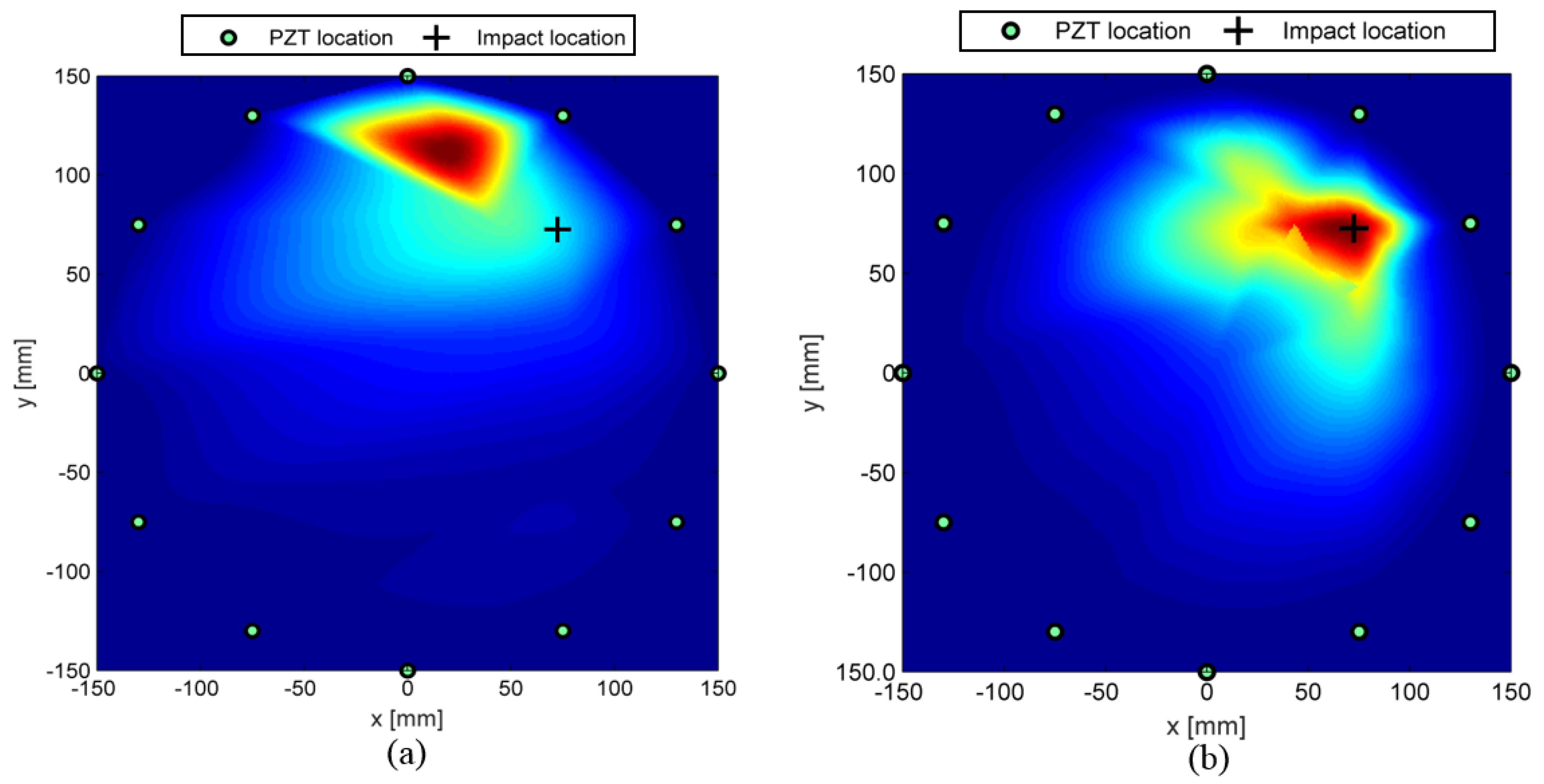
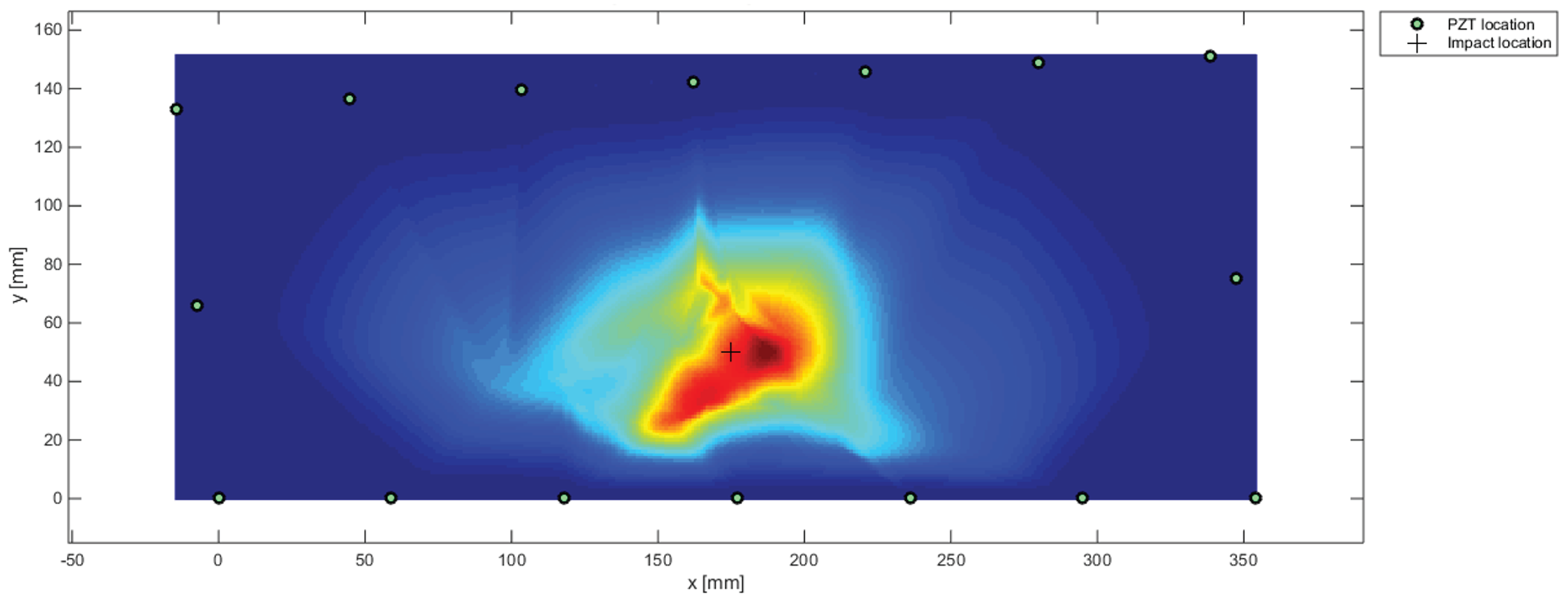
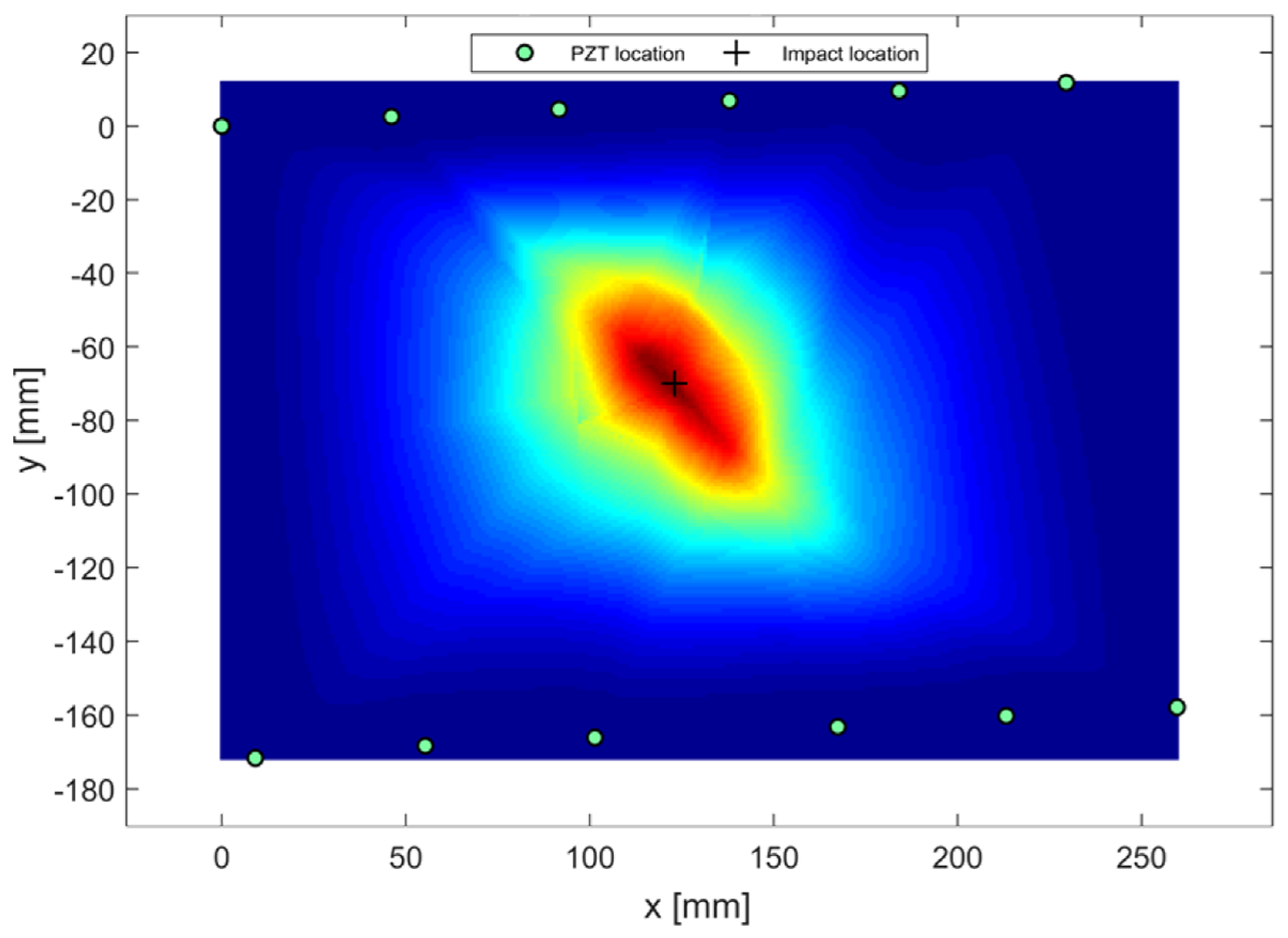
3.2. Validation of Multi-Parameter Analysis
- Phantom damages: Several spots in the image may suggest damage where no failure is present. This event happens when few nodes in the SHM mesh are emerging far from the damage due to the intersection of most affected paths among those selected. The high DI level associated to those paths induces a high risk to a single node which is indeed far from damage location.
- Feature sensitivity: Due to the complex behavior of wave propagation and the statistical decision-making approach, a few paths that should be affected by the damage show a response suggesting no change in the structure. Otherwise, relevant changes in signal response can be detected even when no such a damage affects the correspondent line of sight. This happens especially when time of flight associated with low dispersivity of mode is adopted to detect changes in the waveguide.
- (i) weighting procedure according to Equation (12) for each parameter extracted from traveling waves and selected by decision-making step;
- (ii) interpolation of damage according to each feature on the structural mesh (single parameter approach);
- (iii) normalization of data obtained on that mesh; and
- (iv) data fusion for the multi-parameter representation of damage.
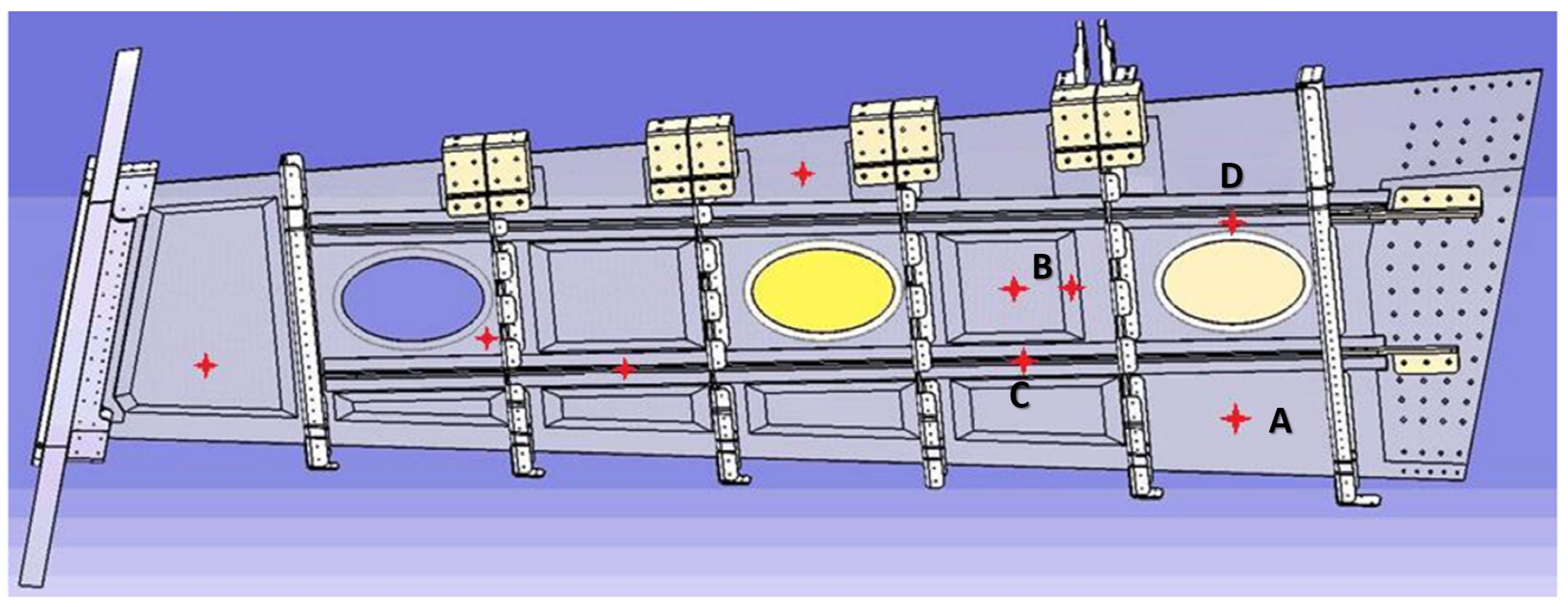
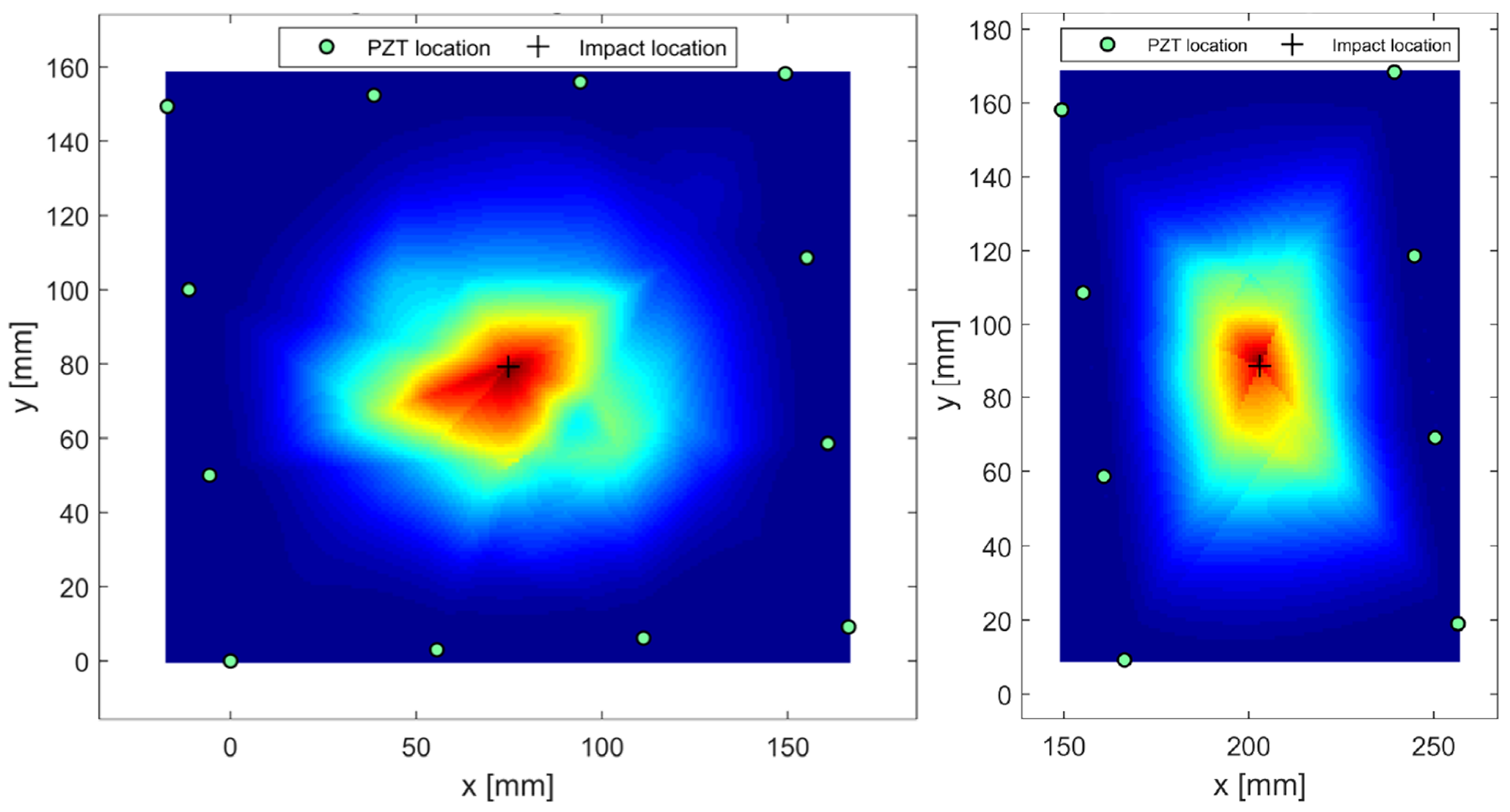
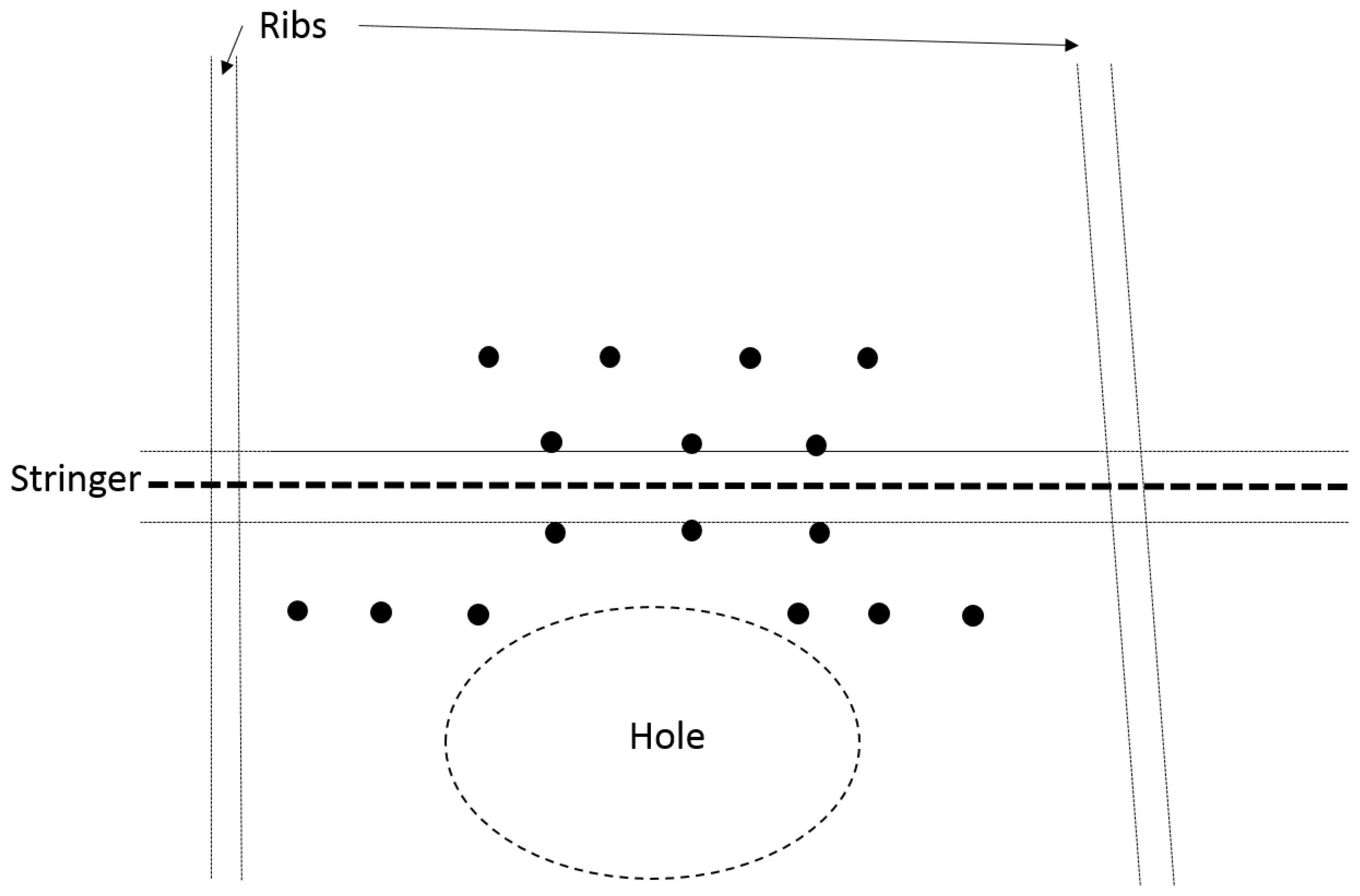
3.3. Delamination Detection in Complex Structures
- 60 J for 6.4 mm thickness;
- 90 J for 8.3 mm thickness; and
- 100–110 J for 10 mm thickness.
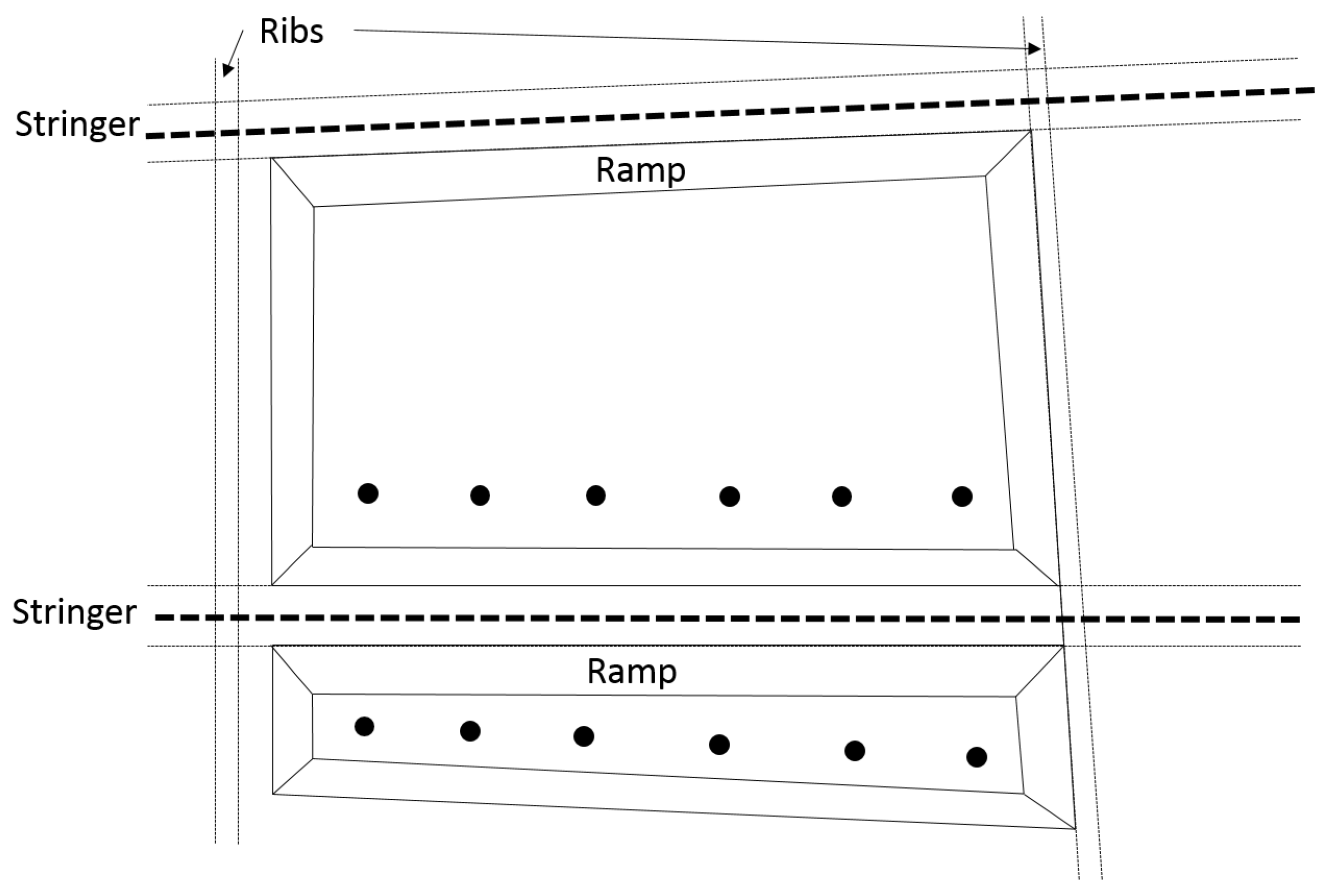
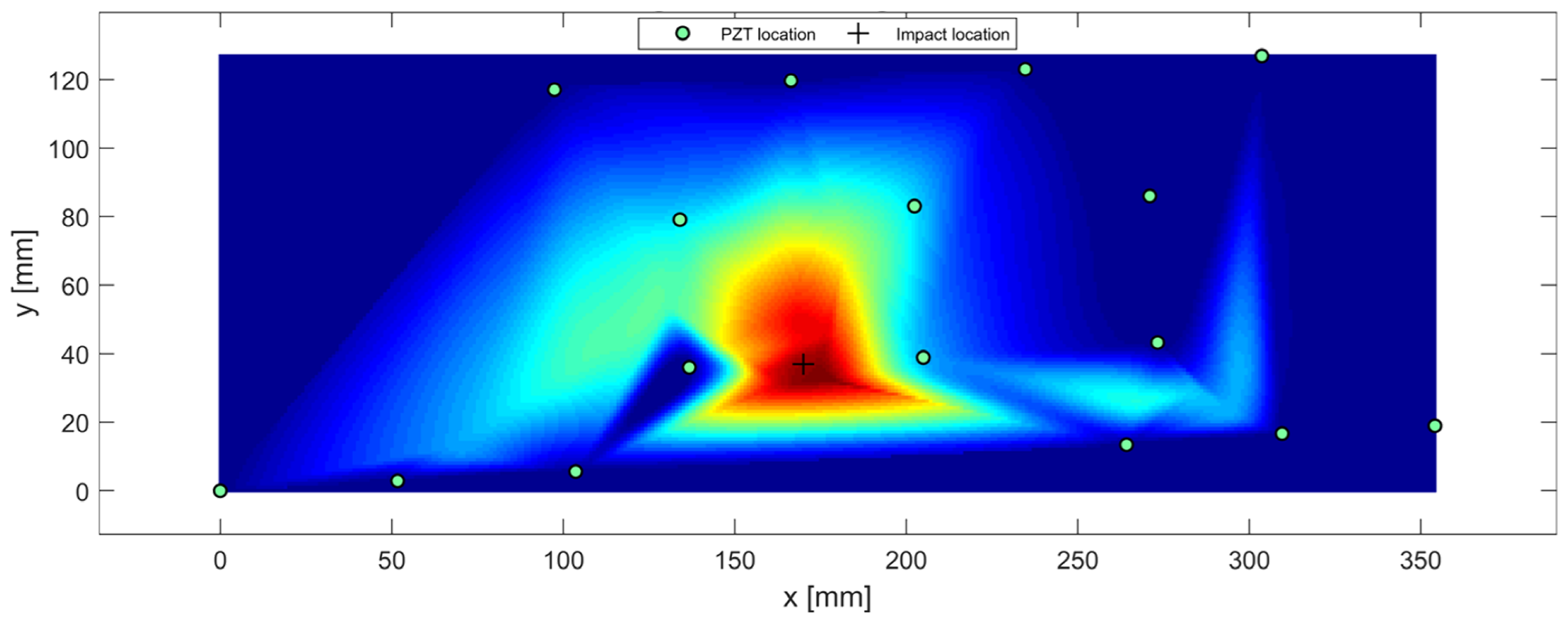
3.4. Disbonding Detection in Complex Structures
4. Discussion and Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| SHM | Structural Health Monitoring |
| NDT | Non destructive Testing |
| GW | Guided Wave |
| PZT | Lead zirconate titanate (piezoelectric material) |
| POD | Probability of detection |
| PFA | Probability of false alarm |
References
- Jones, R. Mechanics Of Composite Materials; Materials scIence And Engineering Series; Taylor & Francis: Abingdon, UK, 1998. [Google Scholar]
- Megson, T. Aircraft Structures for Engineering Students, 5th ed.; Butterworth-Heinemann: Boston, MA, USA, 2013. [Google Scholar]
- Maio, L.; Monaco, E.; Ricci, F.; Lecce, L. Simulation of low velocity impact on composite laminates with progressive failure analysis. Compos. Struct. 2013, 103, 75–85. [Google Scholar] [CrossRef]
- USA Department of Defense. MIL-HDBK 17-3F: Composite Materials Handbook; Department of Defense Handbook: Washington, DC, USA, 2002.
- USA Department of Defense. JSSG-2006, Aircraft Structures; Department of Defense Joint Service Specification Guide: Washington, DC, USA, 1998.
- US Department of Transportation—Federal Aviation Administration. AC No: 20-107B. Composite Aircraft Structure; US Department of Transportation—Federal Aviation Administration: Washington, DC, USA, 2009.
- Cot, L.; Wang, Y.; Bes, C.; Gogu, C. Scheduled and SHM structural airframe maintenance applications using a new probabilistic model. In Proceedings of the 7th European Workshop on Structural Health Monitoring, EWSHM 2014—2nd European Conference of the Prognostics and Health Management (PHM) Society, Nantes, France, 8–11 July 2014; pp. 2306–2313. [Google Scholar]
- Clean Sky 1 GRA—Green Regional Aircraft. Available online: http://www.cleansky.eu/green-regional-aircraft-gra (accessed on 16 September 2018).
- Wolcken, P.C.; Papadopoulos, M. SARISTU—Smart Intelligent Aircraft Structures; Springer: Berlin, Germany, 2015. [Google Scholar]
- Clean Sky 2 RA—Regional Aircraft. Available online: http://www.cleansky.eu/regional-aircraft (accessed on 16 September 2018).
- Giurgiutiu, V. Structural Health Monitoring with Piezoelectric Wafer Active Sensors, 2nd ed.; Academic Press: Oxford, UK, 2014. [Google Scholar]
- Viktorov, I. Rayleigh and Lamb Waves: Physical Theory and Applications; Ultrasonic Technology; Springer: New York, NY, USA, 1967. [Google Scholar]
- Maio, L.; Memmolo, V.; Ricci, F.; Boffa, N.; Monaco, E. Investigation on fundamental modes of guided waves propagating in symmetric and nonsymmetric composite laminates. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2017, 231, 2988–3000. [Google Scholar] [CrossRef]
- Abrate, S. Impact on Composite Structures; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar] [CrossRef]
- Memmolo, V.; Pasquino, N.; Ricci, F. Experimental characterization of a damage detection and localization system for composite structures. Measurement 2018, 129, 381–388. [Google Scholar] [CrossRef]
- Hay, T.R.; Royer, R.L.; Gao, H.; Zhao, X.; Rose, J.L. A comparison of embedded sensor Lamb wave ultrasonic tomography approaches for material loss detection. Smart Mater. Struct. 2006, 15, 946. [Google Scholar] [CrossRef]
- Testoni, N.; De Marchi, L.; Marzani, A. Detection and characterization of delaminations in composite plates via air-coupled probes and warped-domain filtering. Compos. Struct. 2016, 153, 773–781. [Google Scholar] [CrossRef]
- Zhao, X.; Royer, R.L.; Owens, S.E.; Rose, J.L. Ultrasonic Lamb wave tomography in structural health monitoring. Smart Mater. Struct. 2011, 20, 105002. [Google Scholar] [CrossRef]
- De Marchi, L.; Marzani, A.; Moll, J.; Kudela, P.; Radzieński, M.; Ostachowicz, W. A pulse coding and decoding strategy to perform Lamb wave inspections using simultaneously multiple actuators. Mech. Syst. Signal Process. 2017, 91, 111–121. [Google Scholar] [CrossRef]
- Michaels, J.E.; Michaels, T.E. Guided wave signal processing and image fusion for in situ damage localization in plates. Wave Mot. 2007, 44, 482–492. [Google Scholar] [CrossRef]
- Croxford, A.J.; Moll, J.; Wilcox, P.D.; Michaels, J.E. Efficient temperature compensation strategies for guided wave structural health monitoring. Ultrasonics 2010, 50, 517–528. [Google Scholar] [CrossRef] [PubMed]
- US Department of Defence. MIL-HDBK No: 1823A. Non Destructive Evaluation System Reliability Assessment; US Department of Defence: Washington, DC, USA, 2009.
- Janapati, V.; Kopsaftopoulos, F.; Li, F.; Lee, S.; Chang, F.K. Damage detection sensitivity characterization of acousto-ultrasound-based structural health monitoring techniques. Struct. Health Monit. 2016, 15, 143–161. [Google Scholar] [CrossRef]
- Worden, K.; Allen, D.W.; Sohn, H.; Farrar, C.R. Damage detection in mechanical structures using extreme value statistics. In Smart Structures and Materials 2002: Modeling, Signal Processing, and Control; International Society for Optics and Photonics: Bellingham, WA, USA, 2002; Volume 4693, pp. 289–299. [Google Scholar]
- Monaco, E.; Memmolo, V.; Ricci, F.; Boffa, N.; Maio, L. Guided waves based SHM systems for composites structural elements: Statistical analyses finalized at probability of detection definition and assessment. In Proceedings of the SPIE—The International Society for Optical Engineering, San Diego, CA, USA, 8–12 March 2015; Volume 9438. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.; Hunter, N.; Worden, K. Structural health monitoring using statistical pattern recognition techniques. J. Dyn. Syst. Meas. Control 2001, 133, 706–711. [Google Scholar] [CrossRef]
- Cottone, G.; Gollwitzer, S.; Heckenberger, U.; Straub, D. Reliability-oriented optimization of replacement strategies for monitored composite panels for aircraft structures. In Proceedings of the 9th International Workshop on Structural Health Monitoring: A Roadmap to Intelligent, Stanford, CA, USA, 10–13 September 2013; Volume 2, pp. 2728–2735. [Google Scholar]
- Gianneo, A.; Carboni, M.; Giglio, M. Feasibility study of a multi-parameter probability of detection formulation for a Lamb waves based structural health monitoring approach to light alloy aeronautical plates. Struct. Health Monit. 2017, 16, 225–249. [Google Scholar] [CrossRef]
- Maio, L.; Ricci, F.; Memmolo, V.; Monaco, E.; Boffa, N. Application of laser Doppler vibrometry for ultrasonic velocity assessment in a composite panel with defect. Compos. Struct. 2018, 184, 1030–1039. [Google Scholar] [CrossRef]
- Maio, L.; Memmolo, V.; Ricci, F.; Boffa, N.; Monaco, E.; Pecora, R. Ultrasonic wave propagation in composite laminates by numerical simulation. Compos. Struct. 2016, 121. [Google Scholar] [CrossRef]
- Staszewski, W.; Boller, C.; Tomlinson, G. Health Monitoring of Aerospace Structures: Smart Sensor Technologies and Signal Processing; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Memmolo, V.; Ricci, F.; Maio, L.; Boffa, N.; Monaco, E. Model assisted probability of detection for a guided waves based SHM technique. In Proceedings of the SPIE—The International Society for Optical Engineering, Las Vegas, NV, USA, 20–24 March 2016; Volume 9805. [Google Scholar] [CrossRef]
- Cremer, L.; Heckl, M.; Petersson, B.A.T. Structure-Borne Sound: Structural Vibrations and Sound Radiation at Audio Frequencies; Springer: Berlin, Germany, 2005. [Google Scholar]
- Harris, F.J. On the use of windows for harmonic analysis with the discrete Fourier transform. Proc. IEEE 1978, 66, 51–83. [Google Scholar] [CrossRef]
- Auld, B. Acoustic Fields and Waves in Solids; Ripol Classic: Moscow, Russia, 1975. [Google Scholar]
- Oppenheim, A.; Verghese, G. Signals, Systems and Inference, Global Edition; Pearson Education: London, UK, 2016. [Google Scholar]
- Memmolo, V.; Maio, L.; Boffa, N.D.; Monaco, E.; Ricci, F. Damage detection tomography based on guided waves in composite structures using a distributed sensor network. Opt. Eng. 2015, 55, 011007. [Google Scholar] [CrossRef]
- Memmolo, V.; Boffa, N.; Maio, L.; Monaco, E.; Ricci, F.; Pasquino, N. Experimental characterization of a composite structures health monitoring methodology. In Proceedings of the 3rd IEEE International Workshop on Metrology for Aerospace, MetroAeroSpace, Florence, Italy, 22–23 June 2016. [Google Scholar] [CrossRef]
- Worden, K.; Manson, G.; Fieller, N. Damage detection using oulier analysis. J. Sound Vib. 2000, 229, 647–667. [Google Scholar] [CrossRef]
- Fugate, M.; Sohn, H.; Farrar, C. Vibration-based damage detection using statistical process control. Mech. Syst. Signal Process. 2001, 15, 707–721. [Google Scholar] [CrossRef]
- Sohn, H.; Czarnecki, J.A.; Farrar, C.R. Structural health monitoring using statistical process control. J. Struct. Eng. 2000, 126, 1356–1363. [Google Scholar] [CrossRef]
- Bornn, L.; Farrar, C.R.; Park, G.; Farinholt, K. Structural health monitoring with autoregressive support vector machines. J. Vib. Acoust. 2009, 131, 021004. [Google Scholar] [CrossRef]
- Farrar, C.; Worden, K. Structural Health Monitoring: A Machine Learning Perspective; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Laboratory, L.A.N.; States, U. A Comparison Study of Modal Parameter Confidence Intervals Computed Using the Monte Carlo and Bootstrap Techniques; Department of Energy, Office of the Assistant Secretary, Management and Administration: Washington, DC, USA, 1998.
- Hazewinkel, M. Encyclopaedia of Mathematics: Volume 3 Heaps and Semi-Heaps—Moments, Method of (in Probability Theory); Encyclopaedia of Mathematics; Springer: New York, NY, USA, 2013. [Google Scholar]
- Mitra, M.; Gopalakrishnan, S. Guided wave based structural health monitoring: A review. Smart Mater. Struct. 2016, 25, 053001. [Google Scholar] [CrossRef]
- Moll, J.; Schulte, R.; Hartmann, B.; Fritzen, C.P.; Nelles, O. Multi-site damage localization in anisotropic plate-like structures using an active guided wave structural health monitoring system. Smart Mater. Struct. 2010, 19. [Google Scholar] [CrossRef]
- Ricci, F.; Monaco, E.; Maio, L.; Boffa, N.; Mal, A. Guided waves in a stiffened composite laminate with a delamination. Struct. Health Monit. 2016, 15, 351–358. [Google Scholar] [CrossRef]
- Memmolo, V.; Ricci, F.; Boffa, N.; Maio, L.; Monaco, E. Structural health monitoring in composites based on probabilistic reconstruction techniques. Procedia Eng. 2016, 167, 48–55. [Google Scholar] [CrossRef]
- Memmolo, V.; Park, Y.; Lilov, M.; Monaco, E.; Ricci, F. Preliminary acousto-ultrasonic investigation for multi-parameter transducer self-diagnostic system in composites. Compos. Struct. 2018, 202, 1229–1238. [Google Scholar] [CrossRef]
- Mueller, I.; Fritzen, C.P. Inspection of piezoceramic transducers used for structural health monitoring. Materials 2017, 10, 71. [Google Scholar] [CrossRef] [PubMed]



| Properties | Biaxial | Uniaxial | 5Harness |
|---|---|---|---|
| [kg/m] | 1790 | 1790 | 1770 |
| [MPa] | 81,000 | 152,000 | 158,420 |
| [MPa] | 81,000 | 8800 | 8800 |
| [MPa] | 8800 | 8800 | 8800 |
| [MPa] | 4100 | 4100 | 3600 |
| 0.31 | 0.31 | 0.31 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Memmolo, V.; Boffa, N.D.; Maio, L.; Monaco, E.; Ricci, F. Damage Localization in Composite Structures Using a Guided Waves Based Multi-Parameter Approach. Aerospace 2018, 5, 111. https://doi.org/10.3390/aerospace5040111
Memmolo V, Boffa ND, Maio L, Monaco E, Ricci F. Damage Localization in Composite Structures Using a Guided Waves Based Multi-Parameter Approach. Aerospace. 2018; 5(4):111. https://doi.org/10.3390/aerospace5040111
Chicago/Turabian StyleMemmolo, Vittorio, Natalino D. Boffa, Leandro Maio, Ernesto Monaco, and Fabrizio Ricci. 2018. "Damage Localization in Composite Structures Using a Guided Waves Based Multi-Parameter Approach" Aerospace 5, no. 4: 111. https://doi.org/10.3390/aerospace5040111
APA StyleMemmolo, V., Boffa, N. D., Maio, L., Monaco, E., & Ricci, F. (2018). Damage Localization in Composite Structures Using a Guided Waves Based Multi-Parameter Approach. Aerospace, 5(4), 111. https://doi.org/10.3390/aerospace5040111