Robust Optimization of Airplane Passenger Seating Assignments

Abstract

We present a method that reduces the time it takes to complete the passenger boarding of an airplane. In particular, we describe a two-stage mixed integer programming (MIP) approach, which assigns passengers to seats on an airplane based on the number of bags they carry aboard the plane. The first stage is an MIP that assigns passengers to seats to minimize the time to complete the boarding of the plane. The second-stage MIP also determines seating assignments, while constraining the total boarding time to that determined by the stage-one MIP and maximizing weighted slack times to provide a more robust assignment. Numerical results show that this two-stage approach results in lower average boarding times than the one-stage approach, when the time it takes passengers to walk and sit in their seats is random. Experiments indicate that the magnitude of the improvement is not very sensitive to variations in the slack time weights.

1. Introduction

Delays in airplane takeoffs cost $29 billion annually [1]. The costs of these delays have been estimated from $30 to $250 per minute [2]. The time to board passengers can contribute to these delays [3,4,5]. A number of researchers have created and investigated methods that board passengers by groups, with the group assignment depending upon their seat assignment [6,7,8,9,10,11,12,13,14]. For instance, Van den Briel et al. [12] shows that it is effective to board the passengers who will be sitting in window seats before the passengers who will sit in middle seats and to board the passengers who will sit in aisle seats last. This approach eliminates delays caused by seated passengers leaving their seats to make room for other passengers to sit down. A number of researchers have recently used stochastic simulation [15,16,17,18,19,20,21,22] and field tests [23,24,25,26,27] to compare the performance of boarding strategies. Schultz [28] estimates the improved boarding performance resulting from a “slip seat” configuration that enables aisle seats to temporarily move closer to the windows, thereby extending the aisle width, permitting passengers to pass others waiting ahead of them in the aisle.

Steffen [29] improves on the boarding by group approach by determining the optimal sequence in which passengers should board a fully loaded single-aisle plane based upon their assigned seats. In this sequence, a passenger sitting in a window seat in the back row of the plane will be the first to board. The second passenger to board will be sitting in a window seat two rows in front of the previously boarded passenger, and so on. The passengers continue boarding in a sequence based on their seating assignments in every other row (back to front): Window seats first, then middle seats, and, finally, those sitting in the seats adjacent to the aisle. The final passenger to board sits in an aisle seat in the first row of the plane. This method works well [2,30], assuming that passengers can board in a predetermined sequence; however, Steffen [29] assumes that passengers are assigned to seats randomly and independently of the luggage volumes they carry aboard the plane. Milne and Kelly [31] extend Steffen’s work [29] by assigning passengers to seats so that their carry-on luggage is distributed approximately uniformly throughout the plane. Once those passengers have been assigned to their seats, they board the plane in the sequence determined by Steffen [29]. The method of Milne and Kelly [31] results in a faster time to complete the boarding of the plane than when carry-on luggage is not aligned with the seat assignment [31]. Further improvement results from Milne and Salari [32], who use a mixed integer program (MIP) to assign passengers to seats based on the quantities of their carry-on luggage. Milne and Kelly [31], as well as Milne and Salari [32], assume that after passengers have been assigned to seats, they board the plane according to the Steffen [29] sequence. The MIP proposed by Milne and Salari [31] minimizes the time to complete the boarding of the plane and results in a faster boarding time than that using the method of Milne and Kelly [31].

Milne and Salari [32] assume average passenger walking and sitting times. In reality, these times vary from passenger to passenger because some passengers are more agile than others. Milne and Salari [32] acknowledge that there are many optimal solutions that minimize the time to complete boarding when passenger walking and sitting times are deterministic.

In this paper, we propose a two-stage method that determines a seating assignment that is more likely than Milne and Salari [32], which results in a faster time to board, when considering the uncertainty of the walking, luggage storing and sitting times of passengers. In the first stage, the proposed method solves the MIP of Milne and Salari [32] to determine the minimum time to complete boarding using average walking and sitting times. In the second stage, an MIP determines a seating assignment that maximizes weighted slack times, while constraining the time to complete boarding to that determined in the first stage. The two-stage method results in a reduction of the total time it takes to complete the boarding of the airplane, when compared with the previous one-stage method of Milne and Salari [32].

The remainder of the paper is organized as follows. Section 2 introduces terminology. Section 3 describes the proposed two-stage method. Section 4 contains numerical results. Section 5 provides a brief conclusion that summarizes the work and mentions two additional research opportunities.

2. Nomenclature

We introduce terminology that is consistent with Milne and Salari [32], except when new terminology is introduced because of the stage-two MIP.

2.1. Indexes

c 

combination of luggage carried by the three passengers sitting in a particular row and on particular side of the plane. For example, one combination would have the aisle seat, middle seat and window seat passengers carrying one, zero, and two bags respectively.

i 

increment of slack time

p 

passenger that boards. The $p$th passenger boards after $p$−1 passengers have boarded.

p′ 

passenger to board the plane prior to passenger $p$

r 

row of the plane

s 

side of the plane

2.2. Sets

C 

set of possible luggage combinations for a single side of a single row = {1, …, 27} (there are 27 combinations because there are 3 × 3 × 3 possible luggage assignments with three passengers each carrying 0, 1 or 2 bags)

I 

set of increments of possible slack times = {1, …, 15}

P 

set of passengers to board the plane = {1, …, 120}

R 

set of rows on the plane = {1, …, 20}

S 

set of sides on the plane = {left, right}

2.3. Parameters

• $Nbin$: Number of bags already in the overhead bin prior to a particular passenger storing his or her bags
• $Npassenger$: Number of bags a particular passenger needs to store in the overhead bin
• $Rewar{d}_{pri}$: Stage-two objective function coefficient, representing the reward per unit of slack time in increment $i$ for passenger $p$ clearing row $r$. A passenger is considered to have cleared a row when the passenger has completely departed from it (either by completing a move into the next row or by sitting down)
• $Bas{e}_{pri}$: Stage-two value of the objective function coefficient ($Rewar{d}_{pri}$) for the base (first) scenario tested
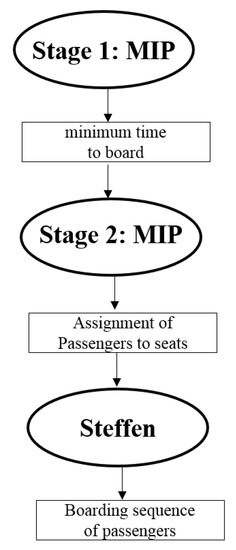
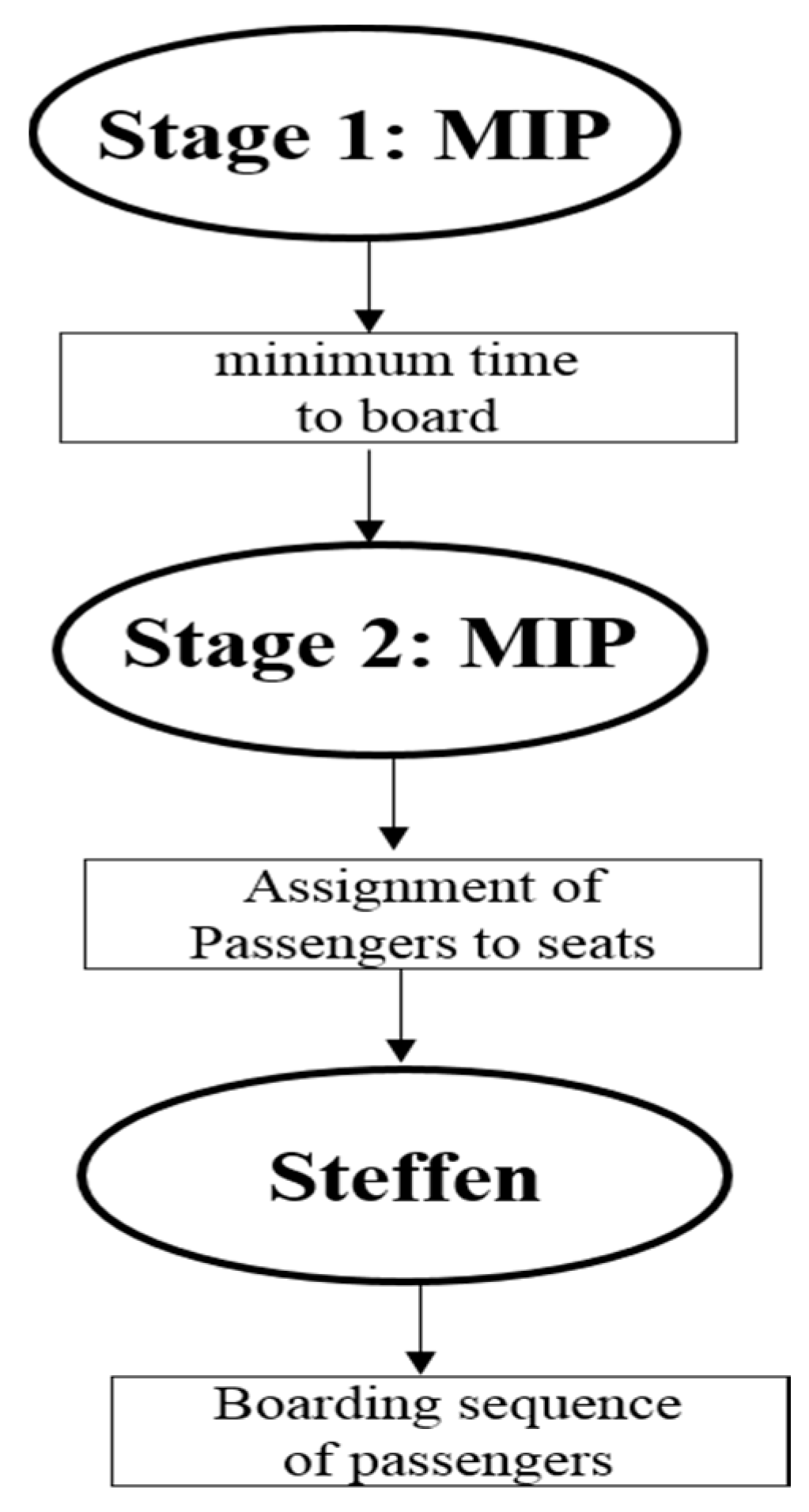
• $ro{w}_p$: Row in which passenger $p$ will be seated (this is predetermined according to the Steffen [29] sequence of boarding the plane)
• $sid{e}_p$: Side of the plane in which passenger $p$ will be seated (this is predetermined according to the Steffen [29] sequence of boarding the plane)
• TimeToCompleteBoardingFromFirstMIP: Optimal time to complete boarding of the plane, as determined by the stage-one MIP; this is a parameter of the stage-two MIP
• $Trow$: Time it takes a passenger to walk from one row to the next row (if unimpeded)
• $Tsit$: Time it takes a passenger to sit after storing luggage
• $Tstor{e}_{pc}$: Time for passenger p to store luggage, in the event that luggage combination c is chosen for the row and side of the plane in which this passenger is seated.

2.4. Decision Variables

• $C_{rsc}$: Binary variable, indicating whether the combination of luggage chosen for side s of the plane in row r corresponds to combination c (=1 if the combination of luggage $c$ is chosen for row r and side s; 0 otherwise)
• $ClearRo{w}_{pr}$: Time at which passenger p has cleared (exited) the aisle of row r (defined for all $p\in P$ and $r\le ro{w}_p$; and assumed for notational convenience to be to zero when $r>ro{w}_p$)
• $Slac{k}_{pri}$: Slack time of increment i for passenger p clearing (exiting) the aisle of row r. (Slack time represents additional time—beyond the average times—that the passenger could take without delaying the completion of boarding)
• TimeToCompleteBoarding: Time at which the final passenger to be seated has been seated.

3. Proposed Method

We make the same airplane and passenger movement assumptions as Milne and Salari [32]. Passengers board a single aisle plane containing 20 rows of 6 passenger seats each, with a total of 120 passenger seats. There is a window, middle and aisle seat on each side of the aisle in each row. Once boarding has completed, every seat will contain a passenger. Once seats have been assigned to passengers, they board the plane in the Steffen [29] sequence. Consequently, our focus is on the assignment of passengers to seats based on the amount of carry-on luggage they have. A passenger boarding the plane will carry zero, one, or two bags of luggage, and their carry-on luggage volumes are assumed to be known in advance. We support this assumption by noting that some airlines charge fees for carry-on luggage and charge less if the passengers specify their carry-on luggage before boarding [32].

Continuing with the same assumptions of Milne and Salari [32], the first passenger begins entering the first row at time zero. To allow for passenger personal space and comfort, we assume that a passenger in the aisle consumes the aisle space of an entire row and that a passenger does not enter a row until it has been completely cleared of other passengers. Once a passenger has completely entered the row of his or her seat, the passenger will store any carry-on luggage in the overhead bin above the seat and then sit down. The overhead bin space is assumed to be unlimited, but with the assumption that the time to store luggage increases with the number of bags being stored by the passenger (Npassenger) and the number of bags already in the overhead bin (Nbin), as indicated in Equation (1), which was developed in Audenaert et al. [33] and used by Milne and Kelly [31], as well as by Milne and Salari [32]. See Milne and Salari [32] for further details on our passenger flow and luggage storing assumptions.

$$Tstore=\left(\frac{\left(Nbin+Npassenger\right)Npassenger}{2}\right)Trow$$

(1)

The proposed method and its context are illustrated in Figure 1. The stage-one MIP is identical to the MIP described in Milne and Salari [32] and determines an assignment of passengers to seats that minimizes the total time to complete the boarding of the plane. The stage-two MIP determines a more robust assignment of passengers to seats on the plane, while ensuring that the resulting time to board is not more than the minimum time to board that was determined by the stage-one MIP. Once the passengers have been assigned to seats by the stage-two MIP, they board the plane in the sequence determined by the Steffen [29] method.

There are many optimal solutions to the stage-one MIP [32]. In other words, there are many equally good assignments of passengers to seats that minimize the time to complete boarding of the airplane when uncertainty is not considered. The stage-two MIP selects one of the many optimal solutions to the stage-one MIP formulation that tends to be robust to the variability of the walking, luggage storing, and sitting times of passengers. This is because the stage-two MIP maximizes a weighted average of passenger slack times.

We first describe the stage-one MIP that minimizes the time to complete boarding as follows.

$$\mathrm{Minimize}TimeToCompleteBoarding$$

(2)

Subject to

$$TimeToCompleteBoarding\ge ClearRo{w}_{pr}\forall p\in P,r\in R:r=ro{w}_p$$

(3)

$${\displaystyle \sum _{c\in C}{C}_{rsc}}=1\forall r\in R,s\in S$$

(4)

$${\displaystyle \sum _{r\in R}{\displaystyle \sum _{s\in S}{\displaystyle \sum _{c\in C}{Y}_{cb}}}}{C}_{rsc}=NumPassengersWithBbag{s}_b\forall b\in B$$

(5)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{pr-1}+Trow\forall p\in P,r<ro{w}_p$$

(6)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{p^{\prime }r}+2Trow\forall p^{\prime }<p,p\in P,r<ro{w}_p$$

(7)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{p^{\prime }r+1}+Trow\forall p^{\prime }<p,p\in P,r<ro{w}_p$$

(8)

$$ClearRo{w}_{pro{w}_p}\ge ClearRo{w}_{pro{w}_p-1}+Tsit+{\displaystyle \sum _{c\in C}Tstor{e}_{pc}}{C}_{ro{w}_{p}sid{e}_{p}c}\forall p\in P$$

(9)

$$ClearRo{w}_{pro{w}_p}\ge ClearRo{w}_{p^{\prime }ro{w}_p}+Trow+Tsit+{\displaystyle \sum _{c\in C}Tstor{e}_{pc}}{C}_{ro{w}_{p}sid{e}_{p}c}\forall p^{\prime }<p,p\in P$$

(10)

The objective function (2) minimizes the time to complete the boarding of the airplane. Constraint (3) ensures that boarding has not concluded until all rows have been cleared of passengers (who are by then seated). Constraint (4) ensures that exactly one combination of luggage is assigned for the three passengers sitting in the aisle, middle, and window seats on each side of each row of the plane. Constraint (5) ensures that the total number of passengers carrying a specified number of bags aboard the plane equals the total number of passengers assigned to seats. Constraints (6) through (10) control passenger flow by ensuring that a passenger cannot begin to enter a row until he/she is at the beginning of that row (6) nor until that row has been cleared of all passengers who have previously boarded (7). The Equations (9) and (10) further ensure that a passenger cannot leave (clear) a row until the passenger has stored any luggage and sat down, or moved into the subsequent row (6)–(8). These Equations, (2) through (10), are the same as in Milne and Salari [32]. Deterministic times (constant parameters) are used in the MIP for the walking ($Trow$), storing ($Tstor{e}_{pc}$), and sitting ($Tsit$) durations, as described in the Numerical Results section below.

Below we describe the formulation of the stage-two MIP, wherein we boldface those elements that are new to the stage-two MIP and are not included in the stage-one MIP. None of these additional boldface elements of the stage-two MIP are included in Milne and Salari [32], which has only one MIP, the stage-one MIP. In particular, the objective function (11) is completely new, as are Equations (20) and (21). The inclusion of the slack variables ($Slac{k}_{pri}$) are new to the stage-two MIP and are not included in [32].

$$Maximizeweightedslacktimes={\displaystyle \sum _{\mathit{p}\in \mathit{P}}{\displaystyle \sum _{\begin{array}{l}\mathit{r}\in \mathit{R}\\ \mathit{s}.\mathit{t}.,\mathit{r}<{\mathit{row}}_{\mathit{p}}\end{array}}{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Reward}}_{\mathit{pri}}{\mathit{Slack}}_{\mathit{pri}}}}}$$

(11)

Subject to

$$TimeToCompleteBoarding\ge ClearRo{w}_{pr}\forall p\in P,r\in R:r=ro{w}_p$$

(12)

$${\displaystyle \sum _{c\in C}{C}_{rsc}}=1\forall r\in R,s\in S$$

(13)

$${\displaystyle \sum _{r\in R}{\displaystyle \sum _{s\in S}{\displaystyle \sum _{c\in C}{Y}_{cb}}}}{C}_{rsc}=NumPassengersWithBbag{s}_b\forall b\in B$$

(14)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{pr-1}+Trow+{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Slack}}_{\mathit{pri}}}\forall p\in P,r<ro{w}_p$$

(15)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{p^{\prime }r}+2Trow+{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Slack}}_{\mathit{pri}}}\forall p^{\prime }<p,p\in P,r<ro{w}_p$$

(16)

$$ClearRo{w}_{pr}\ge ClearRo{w}_{p^{\prime }r+1}+Trow+{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Slack}}_{\mathit{pri}}}\forall p^{\prime }<p,p\in P,r<ro{w}_p$$

(17)

$$ClearRo{w}_{pro{w}_p}\ge ClearRo{w}_{pro{w}_p-1}+Tsit+{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Slack}}_{\mathit{pri}}}+{\displaystyle \sum _{c\in C}Tstor{e}_{pc}}{C}_{ro{w}_{p}sid{e}_{p}c}\forall p\in P$$

(18)

$$\begin{array}{l}ClearRo{w}_{pro{w}_p}\ge ClearRo{w}_{p^{\prime }ro{w}_p}+Trow+Tsit+{\displaystyle \sum _{\mathit{i}\in \mathit{I}}{\mathit{Slack}}_{\mathit{pri}}}+\\ {\displaystyle \sum _{c\in C}Tstor{e}_{pc}}{C}_{ro{w}_{p}sid{e}_{p}c}\forall p^{\prime }<p,p\in P\end{array}$$

(19)

$${\mathit{Slack}}_{\mathit{pri}}\le 0.1\forall p\in P,r\in R,i\in I$$

(20)

$$\mathit{TimeToCompleteBoarding}\le \mathit{TimeToCompleteBoardingFromFirstMIP}+\mathit{0.001}$$

(21)

The objective function (11) of the stage-two MIP maximizes an aggregation of weighted slack times. The objective function coefficients ($Rewar{d}_{pri}$) are described further below, after we first summarize the core Equations of the stage-two MIP. Slack times ($Slac{k}_{pri}$) can be viewed as time buffers that protect against variations in the walking ($Trow$), storing ($Tstor{e}_{pc}$), and sitting ($Tsit$) times of the passengers. Constraints (15) through (19) keep track of these slack times ($Slac{k}_{pri}$) as a function of the decision variables that control the seating of passengers, while the objective function (11) rewards positive values of those slack variables. In other respects, Constraints (12) through (19) have the same purpose and function as the corresponding Constraints (3) through (10) of the stage-one MIP, explained earlier.

Constraint (20) is incorporated in the stage-two MIP to limit the size of each increment of slack time. The value of 0.10 is somewhat arbitrary. We conducted experiments with moderately different values to 0.10 and found no meaningful differences in the results.

To ensure that the time to complete the boarding of the plane (TimeToCompleteBoarding) in the stage-two MIP solution is not more than the optimal time to complete boarding, which was determined by the stage-one MIP (TimeToCompleteBoardingFromFirstMIP), we include Constraint (21) in the stage-two MIP. This ensures that the resulting solution of the stage-two MIP is one of the optimal solutions for the stage-one MIP problem formulation. Constraint (21) includes a tiny positive number (0.001 s) to avoid computational difficulties.

Of the many optimal solutions of the stage-one MIP, some of these solutions have more aggregate slack times than others and—perhaps more important—the distribution of these slack times across the passengers and rows differs. The proposed method is based on our conjecture that the optimal solutions that are more robust against uncertain variations are those that tend to have slack times spread broadly across the different passengers and rows of the plane. Because each passenger has uncertain variations in walking, luggage storing and sitting times, having at least a little slack for many passengers may lead to a time to complete boarding that is lower than that resulting from having a lot of slack for only a few passengers. The objective function coefficients ($Rewar{d}_{pri}$) associated with the slack variables are segregated into i increments for each passenger ($p$) and row ($r$). This segregation of the slack variables allows us to assign objective function weights ($Rewar{d}_{pri}$) that reflect the diminishing marginal value of the slack time for a passenger and row by setting:

$$Rewar{d}_{pri}>Rewar{d}_{pri+1}\forall i\in I\backslash i=\left|I\right|$$

(22)

For example, the reward weight (objective coefficient) for the first increment of slack should be greater than the reward weight for the second increment. This encourages the solver to prefer a solution that assigns slack to the first increment rather than to the second increment. By preferring the first increments of slack to later increments, the diminishing marginal values of slack are modeled.

The values of the reward weights vary from one test scenario to another. In all scenarios, these objective function coefficients are a function of the base reward weight ($Bas{e}_{pri}$) shown in

Table 1. Objective function reward per unit of slack for the base case scenario. For p = 1 to 120 and r = 1 to 20 as a function of increment i.

i	Basepri
1	8000
2	4000
3	2000
4	1000
5	500
6	250
7	125
8	64
9	32
10	16
11	8
12	4
13	2
14	1
15	0.5

. In particular, for the first scenario, the reward weight is set to be the same as the base weight, as indicated in (23).

$$Rewar{d}_{pri}=Bas{e}_{pri}\forall p\in P,r\in R,i\in I$$

(23)

To summarize the proposed method, consistent with Figure 1, the stage-one MIP determines an assignment of passengers to seats that minimizes the total time to complete the boarding of the plane. The stage-two MIP determines a more robust assignment of passengers to seats on the plane (by rewarding slack times), while ensuring that the resulting time to board is not more than the minimum time to board that was determined by the stage-one MIP. Once the passengers have been assigned to seats by the stage-two MIP, they board the plane in the sequence determined by the Steffen [29] method.

4. Numerical Results

We conducted numerical tests using the General Algebraic Modeling System (GAMS) for the algebraic modeling and stochastic simulation capabilities, while invoking the IBM CPLEX optimization software (as a subroutine within GAMS) for the optimization solving. We used the default parameter settings for CPLEX, except with a zero-tolerance gap. The experiments were conducted on a personal computer (Intel Core i7-6700 3.4 GHz with 16 GB of RAM).

Four scenarios were tested, with each scenario using a particular set of values for the slack reward weights ($Rewar{d}_{pri}$), as summarized in

Table 2. Objective function reward per unit of slack as a function of base reward for tested scenarios.

Scenario.	Rewardpri For p = 1 to 110 For r = 1 to 20 For i = 1 to 15	Rewardpri For p = 111 to 120 For r = 1 to 20 For i = 1 to 15
1	Basepri	Basepri
2	Basepri	10 × Basepri
3	Basepri × p	Basepri × p
4	Basepri/p	Basepri/p

. Scenario 1 uses the base reward coefficients ($Rewar{d}_{pri}=Bas{e}_{pri}$), where the slack times of all passengers are weighted equally. Scenario 2 examines a conjecture that the final ten passengers to board may have a larger than normal impact on the total boarding time. This is because those final ten passengers will sit (almost) simultaneously when passengers board in the Steffen [29] sequence and when all passengers are (nearly) identical with respect to the time it takes them to move and store luggage; in a deterministic environment, with identical passengers, the boarding is complete when the last of the ten passengers has sat down. Consequently, in Scenario 2, those final ten passengers to board (111 to 120) have reward weights that are more (ten times more) than those of the passengers who previously boarded for the same increment i. Scenarios 3 and 4 provide greater (and lesser) slack reward weights ($Rewar{d}_{pri}$) to the later (and earlier) passengers to board the plane by multiplying (dividing) the base weight ($Bas{e}_{pri}$) by $p$.

We used stochastic simulation to test the proposed method (with two MIPs) versus the single-MIP method of Milne and Salari [32] with a performance measure of average time to board. The results are shown in the remaining tables (

Table 3. Improvement for the proposed method scenarios versus the previous method ¹.

Probability Passenger Carries			Av. #Bags	% Improvement in Average Time to Board
0 Bags	1 Bag	2 Bags		Scen 1	Scen 2	Scen 3	Scen 4
10%	30%	60%	180	0.31	0.26	0.27	0.33
10%	40%	50%	168	0.27	0.33	0.24	0.26
10%	50%	40%	156	0.21	0.28	0.20	0.20
10%	60%	30%	144	0.19	0.24	0.16	0.18
20%	50%	30%	132	0.23	0.27	0.21	0.22
30%	50%	20%	108	0.11	0.13	0.11	0.11
40%	40%	20%	96	0.12	0.13	0.12	0.12
50%	40%	10%	72	0.03	0.04	0.03	0.03
60%	30%	10%	60	0.07	0.07	0.07	0.07
70%	20%	10%	48	0.17	0.17	0.17	0.17
			Average	0.17	0.19	0.16	0.17

¹ Please refer to the section entitled “Supplementary Materials” to regenerate the results presented in this table and the following tables.

,

Table 4. %Improvement for the proposed method with respect to the two scenarios, varying the number of replications.

Probability Passenger Carries			Av. #Bags	%Improvement in Average Time to Board
				200 Replications		10,000 Replications
0 Bags	1 Bag	2 Bags		Scen 1	Scen 2	Scen 1	Scen 2
10%	30%	60%	180	0.31	0.26	0.34	0.13
10%	50%	40%	156	0.21	0.28	0.23	0.28

,

Table 5. Frequency of the proposed method doing better, worse or the same as the previous method in scenario 1.

Probability Passenger Carries			Av. #Bags	Frequency of the Fast Time to Board
0 Bags	1 Bag	2 Bags		Proposed	Previous	Same
10%	30%	60%	180	128	22	50
10%	40%	50%	168	126	22	52
10%	50%	40%	156	109	28	63
10%	60%	30%	144	101	26	73
20%	50%	30%	132	135	6	59
30%	50%	20%	108	80	0	120
40%	40%	20%	96	78	0	122
50%	40%	10%	72	51	0	149
60%	30%	10%	60	58	0	142
70%	20%	10%	48	100	0	100

and

Table 6. Frequency of the proposed method doing better, worse or the same as the previous method in scenario 2.

Probability Passenger Carries			Av. #Bags	Frequency of the Fast Time to Board
0 Bags	1 Bag	2 Bags		Proposed	Previous	Same
10%	30%	60%	180	121	31	49
10%	40%	50%	168	131	11	58
10%	50%	40%	156	124	17	59
10%	60%	30%	144	112	18	70
20%	50%	30%	132	129	4	67
30%	50%	20%	108	75	0	125
40%	40%	20%	96	80	0	120
50%	40%	10%	72	43	0	157
60%	30%	10%	60	58	0	142
70%	20%	10%	48	103	0	97

), where the proposed two-stage approach is referred to as the “proposed method scenarios,” and the results of using Milne and Salari [32] are referred to as, “previous method.” In all three of the MIPs (one stage from Milne and Salari [32] and two stages of the proposed method), we use average times for $Trow$(2.4 s) and Tsit (8 s) in the formulations. Similarly, the formulations use the value of $Tstor{e}_{pc}$, determined using the average value of $Trow$, the luggage combination (c) used, and Equation (1). These are the same times as used by Milne and Kelly [31], as well as by Milne and Salari [32].

The tests assume there are 20 rows on the plane, with each row of the plane consisting of 6 passengers for a total of 120 passengers. Each row of Table 3 was created by conducting 200 replications for each scenario (and for the previous method) using stochastic simulation. For each replication, each of the 120 passengers carried a number of bags, randomly generated from a multinomial probability distribution, with parameter values corresponding to the left three columns of Table 3. The table’s average number of bags column is the theoretically expected number of bags, obtained by multiplying the Table 3 probabilities by the corresponding number of bags and the 120 passengers. For instance, with 10%, 30% and 60% of the 120 passengers, expected to carry, on average, zero, one, and two bags, respectively, 180 (= 30% × 1 × 120 + 60% × 2 × 120) bags are expected to be carried aboard the plane, according to the theoretical average. Depending on the random number of bags generated for the replications, the actual number of bags may differ—due to randomness—from the theoretical average shown in the table’s average number of bags column.

For each replication corresponding to a row of Table 3, a row to row time (Trow) is randomly generated for each passenger from a triangular probability distribution, with 1.8, 2.4 and 3.0 s as the min, mode and max parameters, respectively, which is consistent with [13,31,32,33]. Because we assume that passengers who walk quickly are also able to sit down quickly, like Milne and Kelly [31], we calculate a passenger’s time to sit ($Tsit$) by multiplying 3.33 by the passenger’s randomly generated value of $Trow$. Similarly, we calculate the passenger’s time to store luggage ($Tstor{e}_{pc}$) based upon the passenger’s randomly generated $Trow$ and using Equation (1). Our assumptions for generating random passenger times are the same as those of Milne and Kelly [31].

For each replication, an assignment of luggage to seats is conducted using average passenger times, the proposed method scenarios and the previous method [32]. The resulting luggage seat assignments are then used to calculate the time to complete boarding when using the randomly generated passenger times and the Steffen [29] sequence of boarding. These boarding times are averaged for each scenario (and for the prior method) for each average number of bags case in Table 3. For a given row of Table 3, the percentage improvement in the average time to board, using the proposed method, is calculated using Equation (24).

$$\%improvement=\left(\frac{AV\_proposed-AV\_prior}{AV\_prior}\right)\times 100$$

(24)

where AV_proposed = average time to complete boarding using the proposed method and AV_prior = average time to complete boarding using the prior method of [32].

These percentage improvements are shown in the final four columns of Table 3. For instance, when the average number of bags is 180, Scenario 1 averaged a 0.31% improvement in the average time to complete boarding, and Scenario 4 resulted in a 0.33% average improvement. The final column of Table 3 shows the average percentage improvement in the time to board using the proposed method, instead of the previous method. As indicated in Table 3, the proposed method provides an improved average performance in all cases and scenarios tested. The largest improvement in each row is gray-shaded, with all four scenarios performing about the same for the two cases of luggage near the bottom of the table.

The same set of 120 randomly generated passenger walking times for the 200 replications (120 × 200 = 24,000 randomly generated walking times in total), corresponding to a row of Table 3, was used in testing both the proposed and previous methods. Thus, neither method scenario outperforms the other due to having a faster or slower set of passengers. When comparing one row of Table 3 with another row of the same table, the results were determined using different random number seeds, so any comparison of the performance in one row of a table versus another could stem—at least partially—from one row having a faster (or slower) set of passengers than another row. For instance, the average $Trow$ of the 48 bags case was 2.41 s, which is slower than the average $Trow$ (2.39 s) of the 60 bags case. Consequently, the slower passenger times of the 48 bags case may be the reason for why its average boarding time was more than that of the 60 bags case.

Because all these scenarios have a similar performance when averaged over the ten cases, we wondered whether the tiny differences may have stemmed from randomness. We conducted additional tests (with 10,000 replications) for Scenario 1 and Scenario 2 for two of the cases. As illustrated in Table 4, the ranking performance of the scenarios was the same, with Scenario 1 providing the better performance for the 180 bags case and Scenario 2 providing the better performance for the 156 bags case—regardless of whether 200 or 10,000 replications were generated.

Further insight into how randomness affects the relative performance of the proposed method versus the previous method, using slack reward weights for Scenarios 1 and 2 as examples, is provided in Table 5 and Table 6, respectively. The proposed method performs better than the previous method more often than the reverse for each row of Table 5 and Table 6. For example, in the 180 bags case in Table 5 (with Scenario 1), the proposed method had the fastest time to board 128 times (i.e., a frequency of 128 times) out of the 200 replications, 22 times when the proposed method had a higher time to board, and 50 times when the proposed and previous methods resulted in the same time to board (128 + 22 + 50 = 200, which is the number of replications). For the lower luggage volume cases of Table 5 and Table 6, the previous method never had a faster time to board than the proposed method.

The average time (in seconds) to complete the boarding of the airplane, when using Scenario 2 reward penalties, for the previous method and the proposed method, where 200 replications are randomly generated for each row of the table, is shown in

Table 7. Boarding time for the proposed method versus the previous method (scenario 2), varying #rows.

Probability Passenger Carries			Average Time to Complete Boarding
0 Bags	1 Bag	2 Bags	16-Rows Previous	16-Rows Proposed	26-Rows Previous	26-Rows Proposed
10%	30%	60%	542.32	540.34	827.89	826.45
10%	40%	50%	540.78	539.41	827.8	826.47
10%	50%	40%	539.75	538.66	827.87	826.55
10%	60%	30%	539.4	538.61	827.44	826.59
20%	50%	30%	534.27	533.08	824.37	823.03
30%	50%	20%	533.4	532.03	811.6	810.66
40%	40%	20%	533.56	531.96	824.11	823
50%	40%	10%	532.55	531.9	823.36	823
60%	30%	10%	533.01	531.91	824.13	823
70%	20%	10%	533.22	531.95	823.98	823

; these results are shown for a plane with 16 rows and a plane with 26 rows, with other passenger flow assumptions remaining the same as before. We note that the Boeing 737 Max 8 (7M8) configuration has 26 rows for Economy passengers, with three economy passengers on each side of a single aisle. As with the 20 rows experiments, the proposed method results in a consistently faster average time to board than the previous method, when 16 rows and 26 rows are used.

5. Conclusions

In summary, the proposed two-stage method (with weighted slack times) provides more robust solutions—and superior average boarding time performance—than the method of Milne and Salari [32]. While there are many optimal solutions to the deterministic optimization problem of the stage-one MIP, we use the stage-two MIP to identify one of those optimal solutions that is likely to perform well when passenger walking, luggage storing and sitting durations are uncertain. Numerical results indicate that the two-stage approach is superior and not especially sensitive to variations in the objective function coefficients used to weight the slack times. When generalized, this approach—of using a second stage deterministic optimization to select one of the best solutions of a first stage optimization problem—has the potential to be applied to other optimization problems to create robust solutions.

Additional research opportunities include the investigation of the optimal boarding of passengers when passengers express seating preferences (e.g., prefer an aisle or window seat) and groups of passengers (e.g., families) who prefer to sit together. Such work can build upon and extend the earlier concepts and models of [29,30,31,32], as well as the present paper.