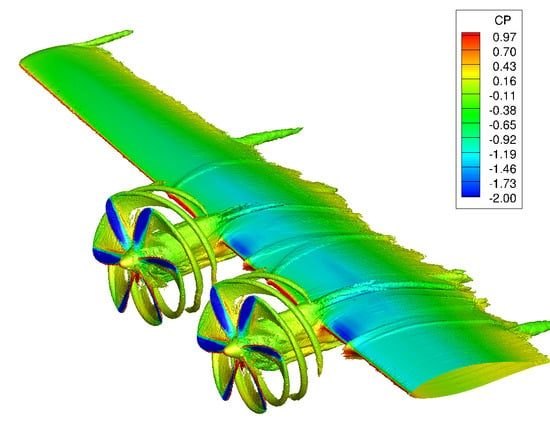
Computational Study of Propeller–Wing Aerodynamic Interaction
Abstract
:1. Introduction
2. CFD Solver
3. Propeller Performance
4. Test Cases
5. Results and Discussion
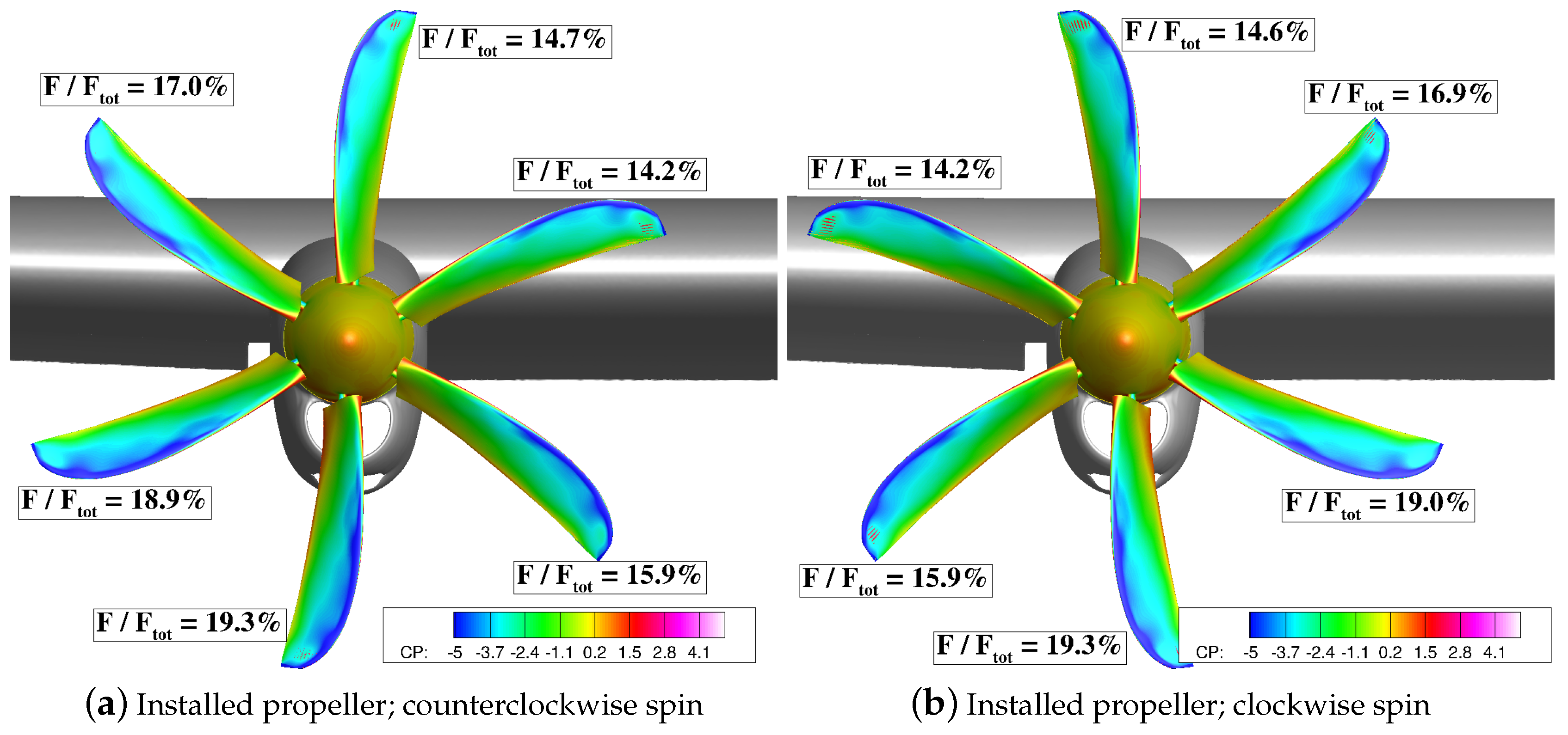
5.1. Propeller Performance
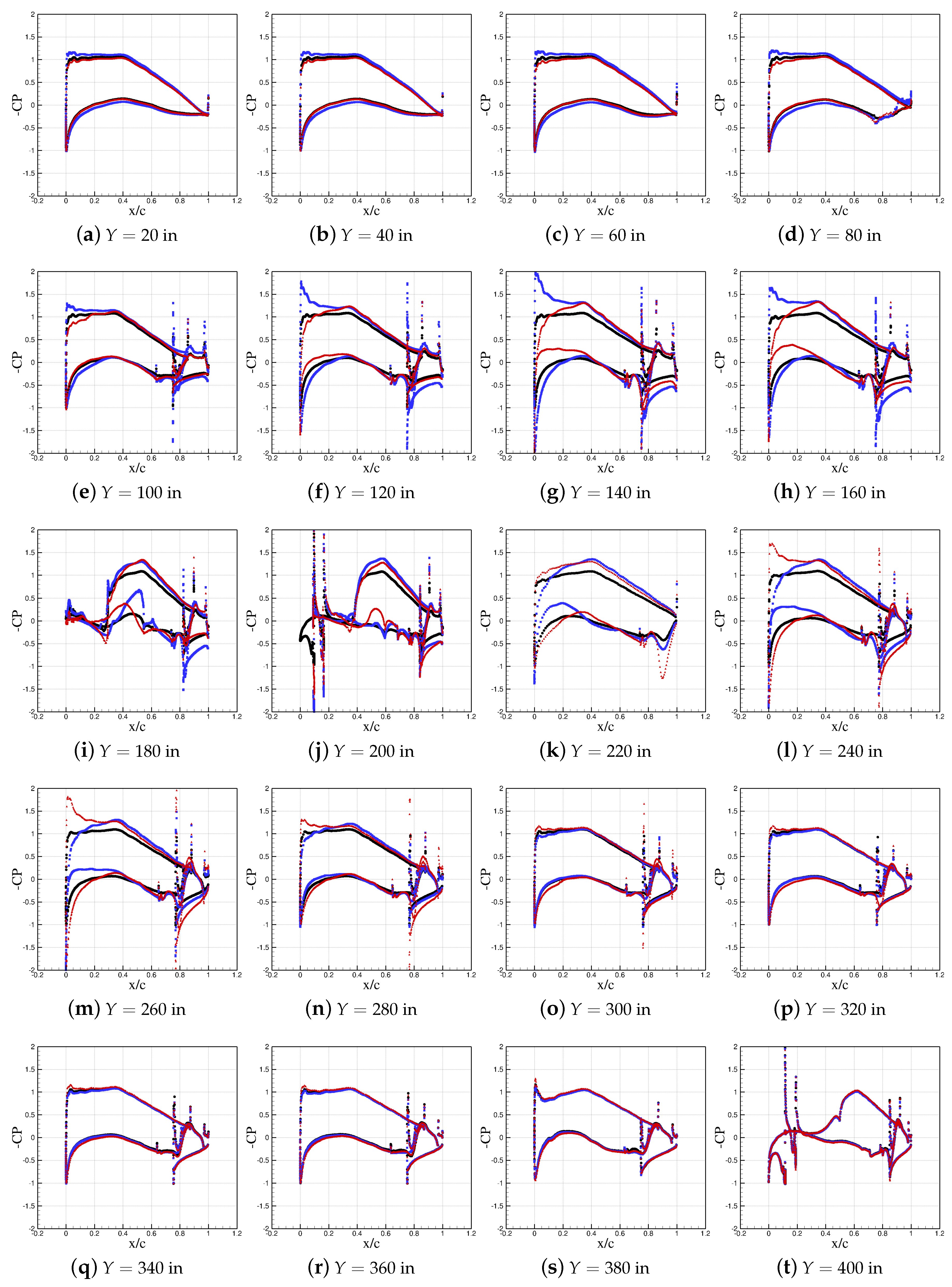
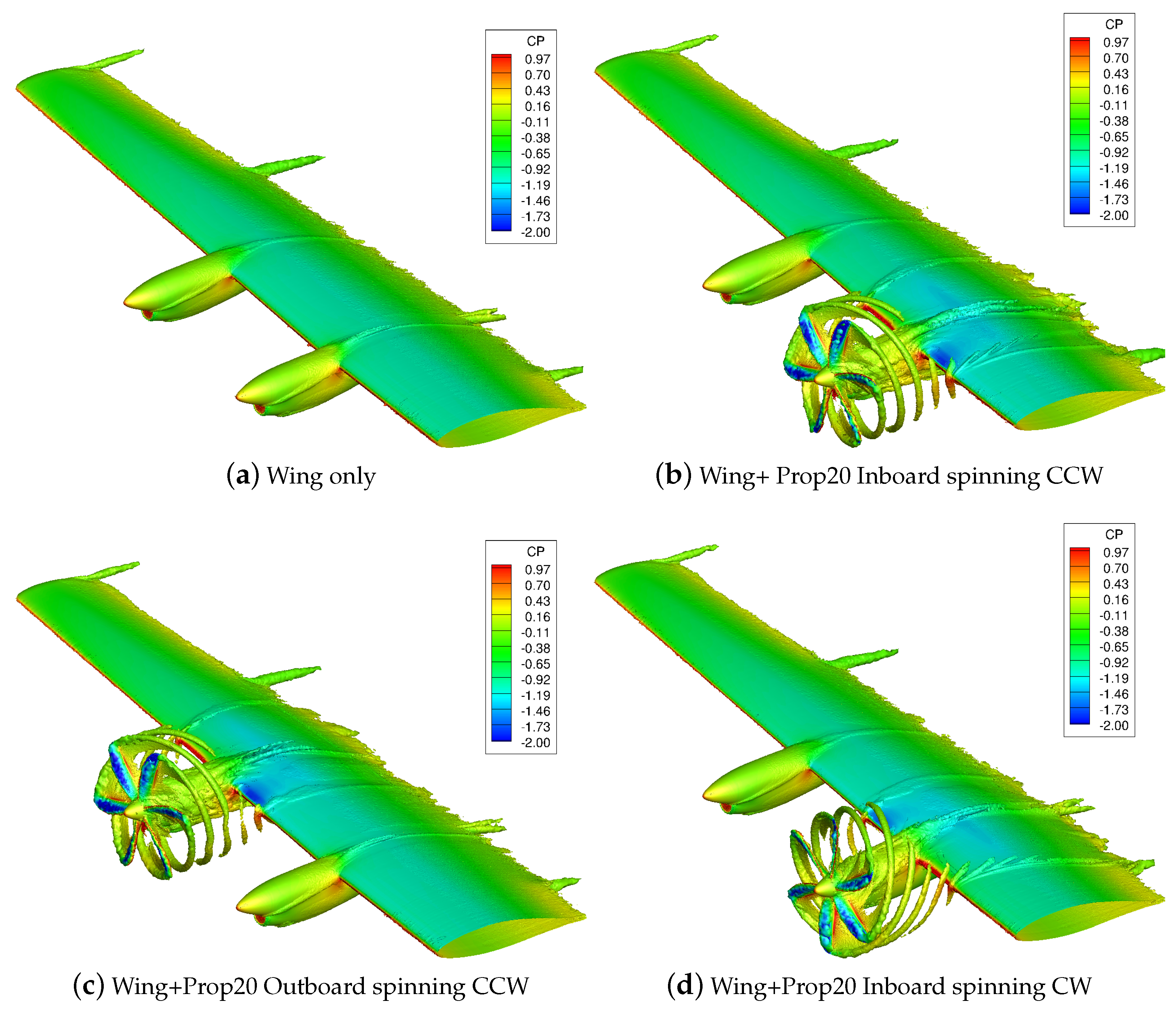
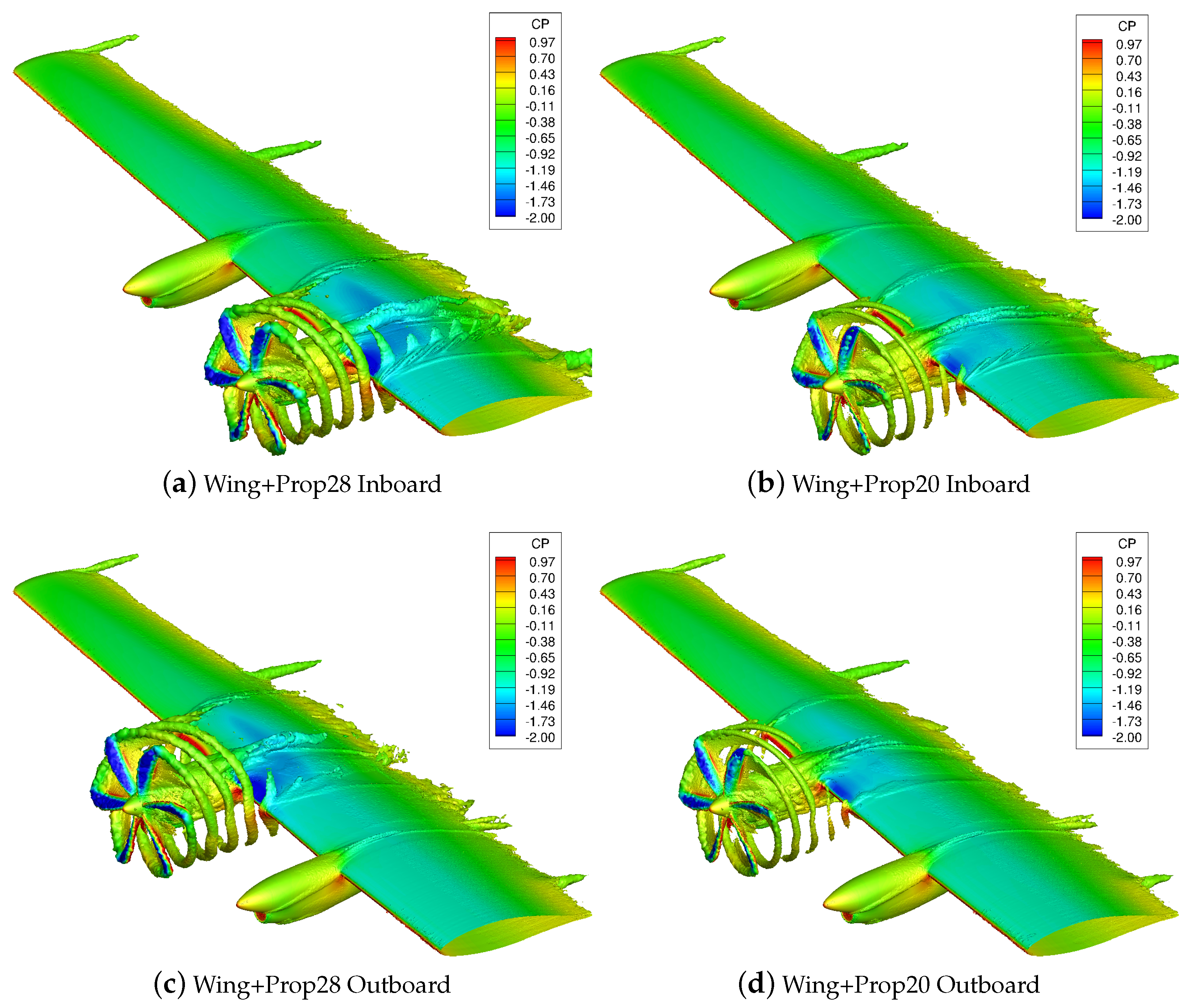
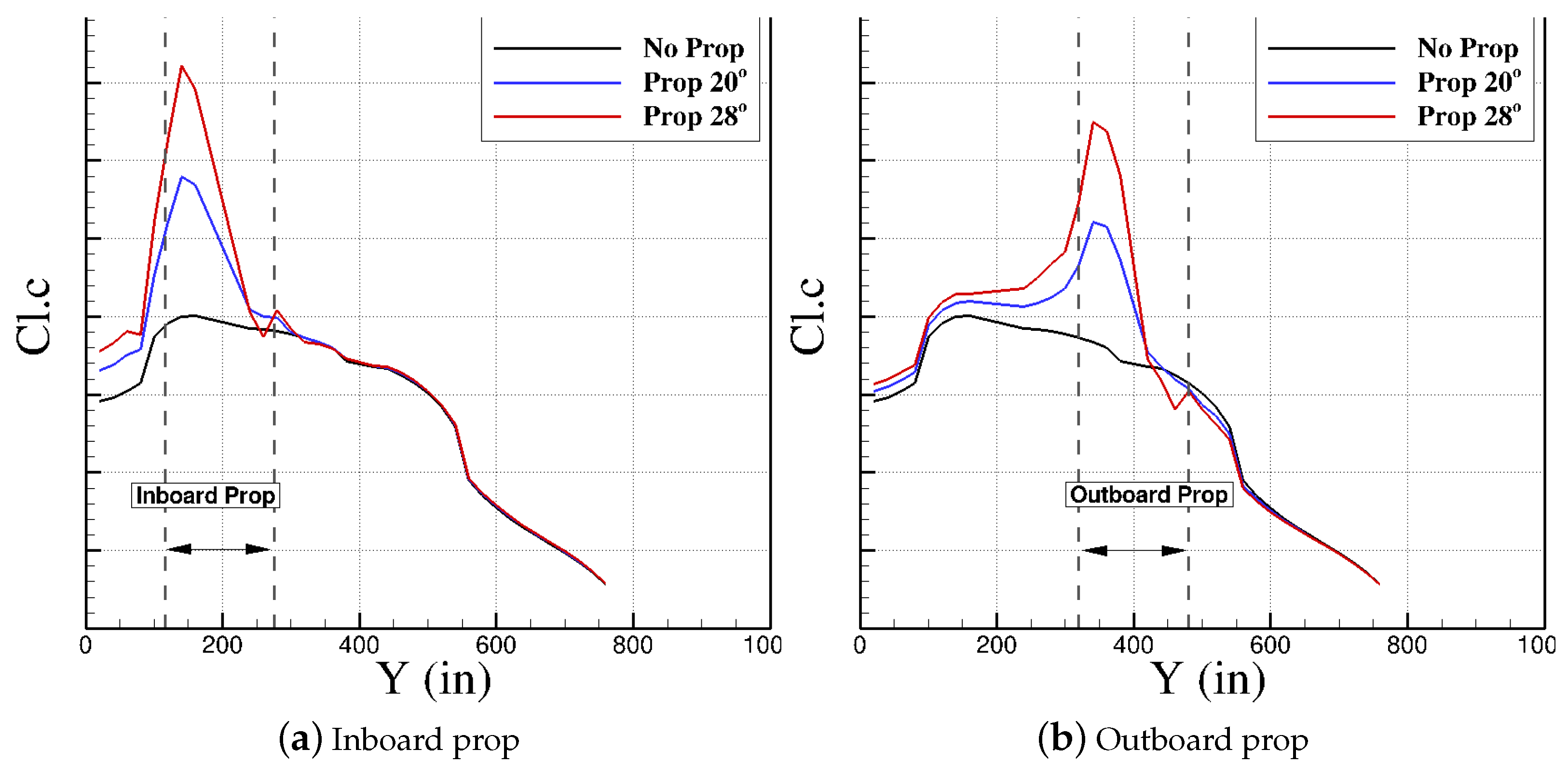
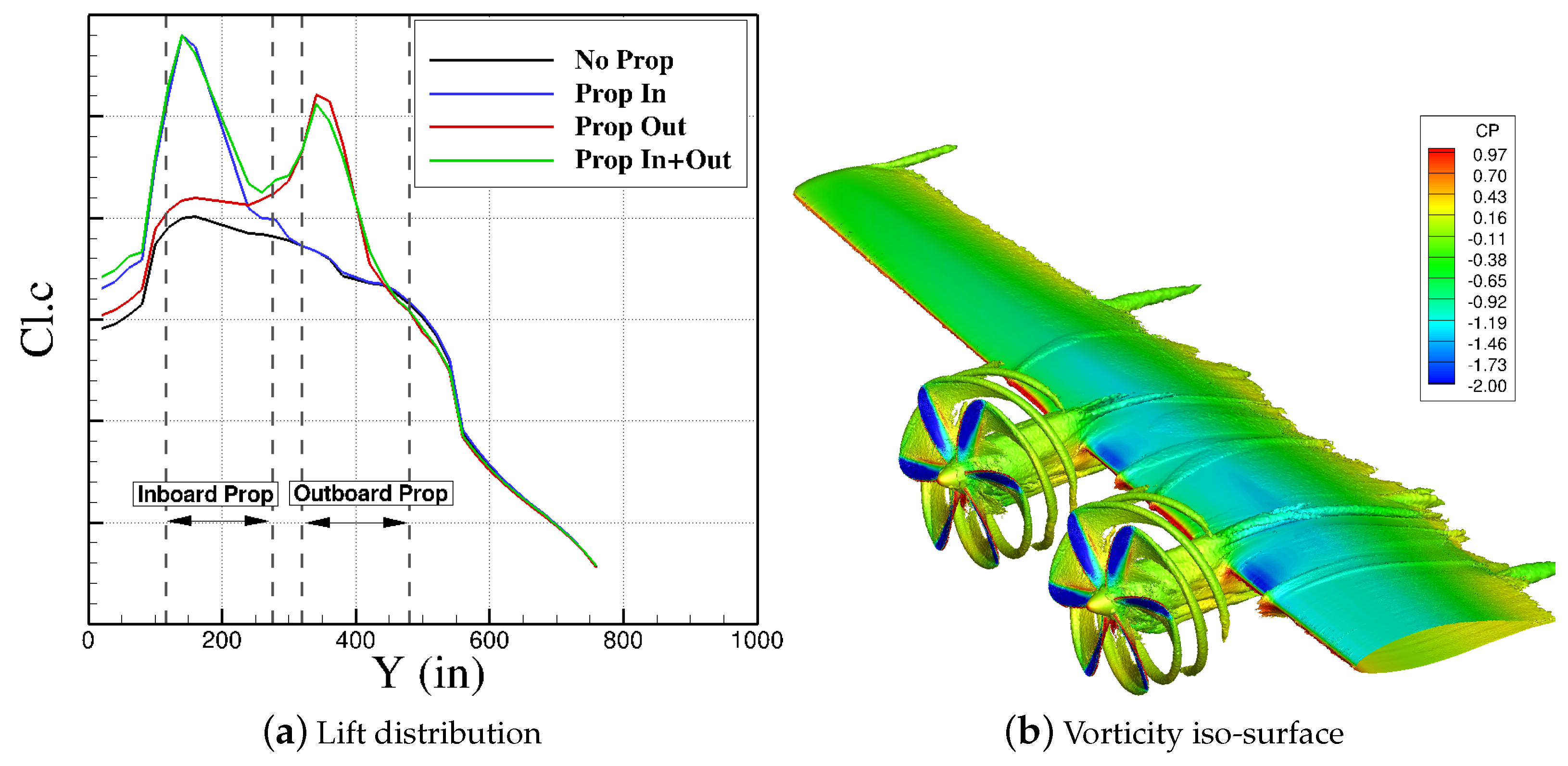
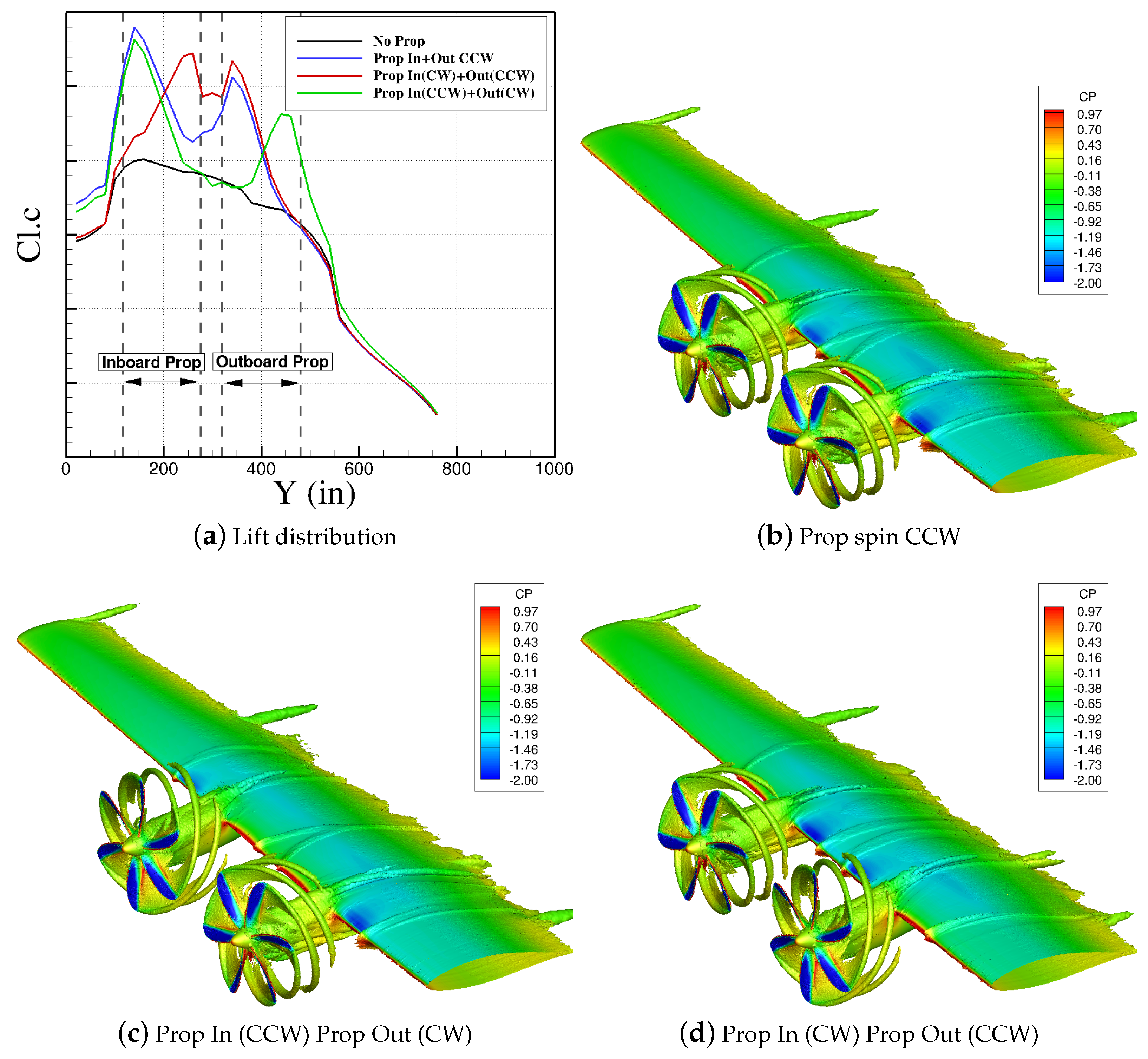
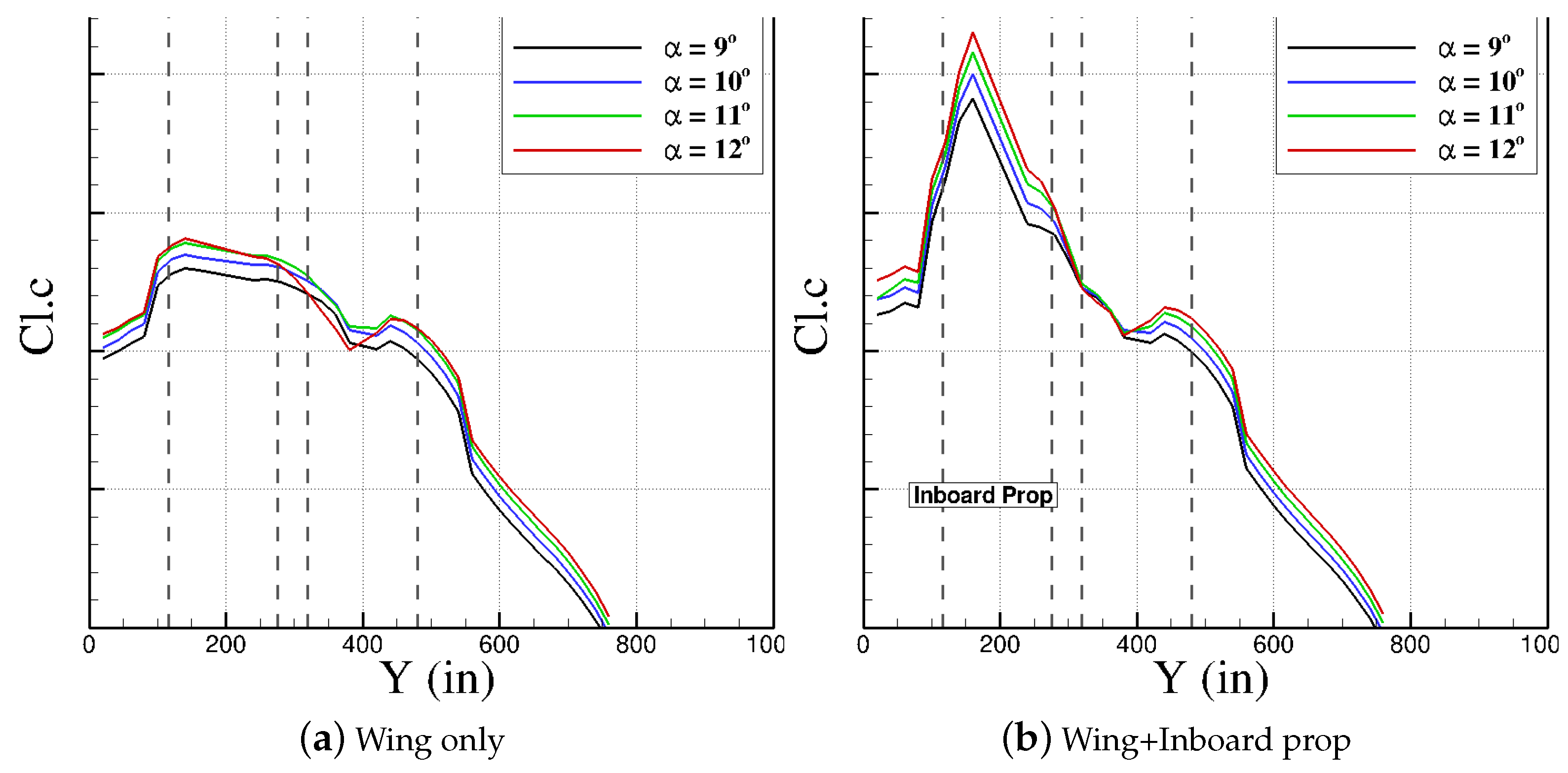
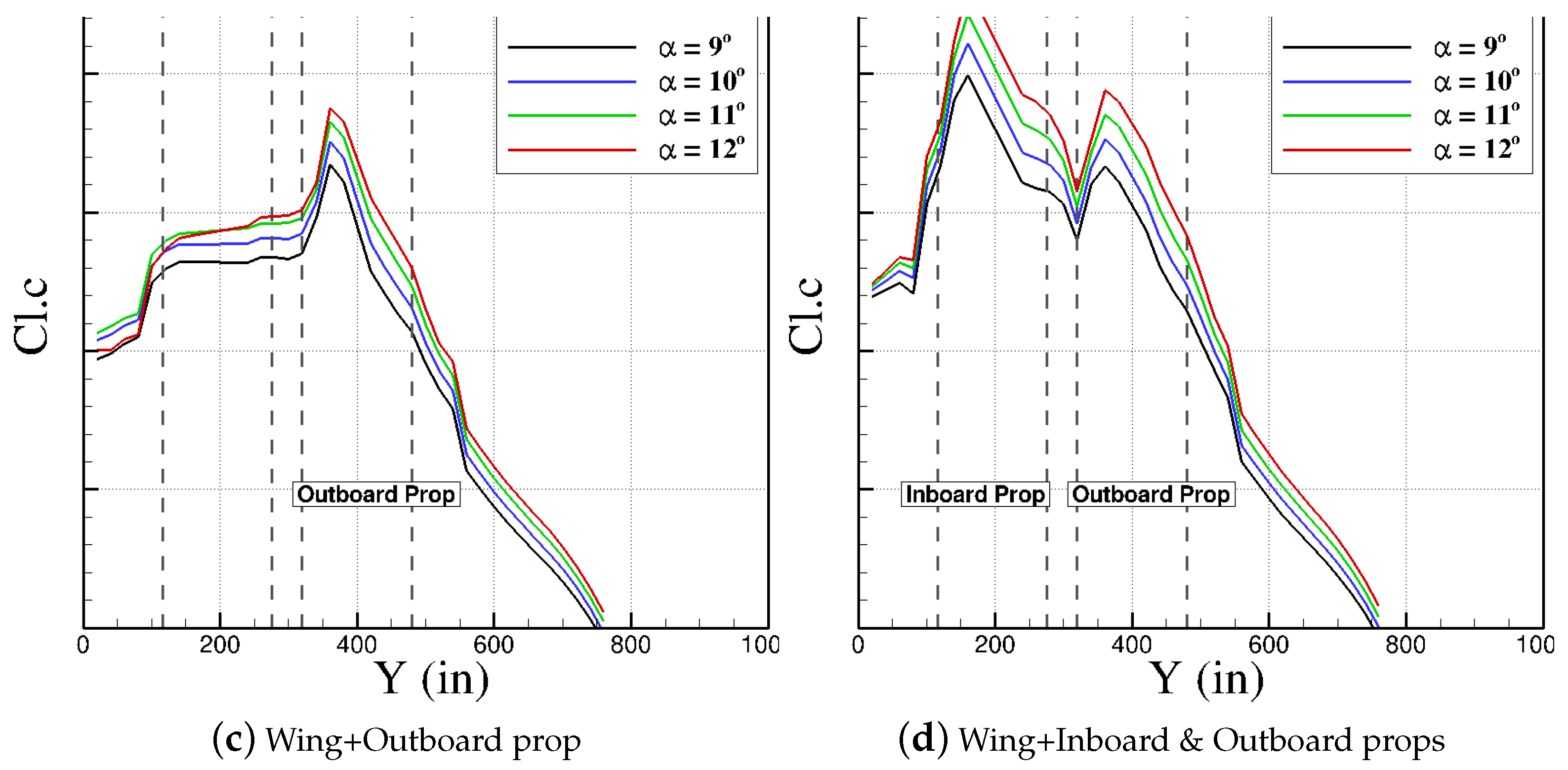
5.2. Wing/Propeller Aerodynamic Interaction
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| a | acoustic speed, m·s |
| CFD | computational fluid dynamics |
| pressure coefficient, | |
| CREATE | Computational Research and Engineering Acquisition Tools and Environments |
| CCW | counterclockwise |
| CW | clockwise |
| D | propeller diameter, m |
| DDES | delayed detached eddy simulation |
| F | thrust force, N |
| M | Mach number, V/a |
| p | static pressure, N/m |
| free-stream pressure, N/m | |
| free-stream dynamic pressure, N/m | |
| SARC | Spalart–Allmaras with rotational and curvature correction |
| RANS | Reynolds Averaged Navier–Stokes |
| t | time, s |
| VZLU | Czech aerospace research center |
| free-stream velocity, m·s | |
| x,y,z | grid coordinates, m |
| Greek | |
| angle of attack, deg | |
| blade angle, deg |
References
- Froude, R.E. On the Part Played in Propulsion by Differences of Fluid Pressure. Trans. Inst. Nav. Archit. 1889, 30, 390. [Google Scholar]
- Rankin, W.J. On the Mechanical Principles of the Action of Propellers. Trans. Inst. Nav. Archit. 1865, 6, 13–39. [Google Scholar]
- Westmoreland, W.S.; Tramel, R.W.; Barber, J. Modeling Propeller Flow-Fields Using CFD. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. AIAA Paper 2008-0402. [Google Scholar]
- Stuermer, A. Unsteady CFD Simulations of Propeller Installation Effects. In Proceedings of the 42nd AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Sacramento, CA, USA, 9–12 July 2006. AIAA Paper 2006-4969. [Google Scholar]
- Shafer, T.; Green, B.; Hallissy, B.; Hine, D. Advanced Navy Applications Using CREATETM-AV Kestrel. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA Paper 2014-0418. [Google Scholar]
- McDaniel, D.; Nichols, R.; Klepper, J. Unstructured Sliding Interface Boundaries in Kestrel. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-1299. [Google Scholar]
- Steij, R.; Barakos, G. Sliding Mesh Algorithm for CFD Analysis of Helicopter Rotor–Fuselage Aerodynamics. Int. J. Numer. Methods Fluids 2008, 58, 527–549. [Google Scholar] [CrossRef]
- Ghoreyshi, M.; Bergeron, K.; Lofthouse, A.J. Numerical Simulation of Wake Flowfield Behind the C-130 with Cargo Ramp Open. J. Aircr. 2017, 55, 1103–1121. [Google Scholar] [CrossRef]
- Bergeron, K.; Ghoreyshi, M.; Jirasek, A. Simulation of C-130 H/J Troop Doors and Cargo Ramp Flow Fields. Aerosp. Sci. Technol. 2018, 72, 525–541. [Google Scholar] [CrossRef]
- Bergeron, K.; Ghoreyshi, M.; Jirasek, A.; Aref, P.; Lofthouse, A.J. Computational Modeling of C-130 H/J Propellers and Airdrop Configurations. In Proceedings of the 35th AIAA Applied Aerodynamics Conference, Denver, CO, USA, 5–9 June 2017. AIAA Paper 2017-3574. [Google Scholar]
- Roth, G.L.; Morton, S.A.; Brooks, G.P. Integrating CREATE-AV Products DaVinci and Kestrel: Experiences and Lessons Learned. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012. AIAA Paper 2012-1063. [Google Scholar]
- Morton, S.A.; McDaniel, D.R. A Fixed-Wing Aircraft Simulation Tool for Improving DoD Acquisition Efficiency. Comput. Sci. Eng. 2016, 18, 25–31. [Google Scholar] [CrossRef]
- Morton, S.A.; McDaniel, D.R.; Sears, D.R.; Tillman, B.; Tuckey, T.R. Kestrel: A Fixed Wing Virtual Aircraft Product of the CREATE Program. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FO, USA, 4–7 January 2009. AIAA Paper 2009-0338. [Google Scholar]
- McDaniel, D.; Nichols, R.; Eymann, T.; Starr, R.; Morton, S. Accuracy and Performance Improvements to Kestrel’s Near-Body Flow Solver. In Proceedings of the 54th AIAA Aerospace Sciences Meeting, San Diego, CA, USA, 4–8 January 2016. AIAA Paper 2016-1051. [Google Scholar]
- Godunov, S.K. A Difference Scheme for Numerical Computation of Discontinuous Solution of Hydrodynamic Equations. Sbornik Math. 1959, 47, 271–306. [Google Scholar]
- Tramel, R.; Nichols, R.; Buning, P. Addition of Improved Shock-Capturing Schemes to OVERFLOW 2.1. In Proceedings of the 19th AIAA Computational Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. AIAA Paper 2009-3988. [Google Scholar]
- Spalart, P.R.; Allmaras, S.R. A One Equation Turbulence Model for Aerodynamic Flows. In Proceedings of the 30th Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 1992. AIAA Paper 1992-0439. [Google Scholar]
- Spalart, P.R.; Schur, M. On the Sensitisation of Turbulence Models to Rotation and Curvature. Aerosp. Sci. Technol. 1997, 1, 297–302. [Google Scholar] [CrossRef]
- Menter, F. Eddy Viscosity Transport Equations and Their Relation to the k-ε Model. ASME J. Fluids Eng. 1997, 119, 876–884. [Google Scholar] [CrossRef]
- Spalart, P.R.; Jou, W.H.; Strelets, M.; Allmaras, S.R. Comments on the Feasibility of LES for Wings, and on a Hybrid RANS/LES Approach. In Proceedings of the 1st AFSOR International Conference on DNS/LES, Ruston, LA, USA, 4–8 August 1997; Greyden Press: Columbus, OH, USA, 1997; pp. 137–147. [Google Scholar]
- Ferraro, G.; Kipouros, T.; Savill, A.M.; Rampurawala, A.; Agostinelli, A. Propeller–Wing Interaction Prediction for Early Design. In Proceedings of the 52nd Aerospace Sciences Meeting, National Harbor, MD, USA, 13–17 January 2014. AIAA Paper 2014-0564. [Google Scholar]
- Stuermer, A.; Rakowitz, M. Unsteady Simulation of a Transport Aircraft Propeller Using MEGAFLOW; RTO-MP-AVT-123 Technical Report; Meeting Proceedings RTO-MP-AVT-123, Paper 7; RTO: Neuilly-sur-Seine, France, 2015. [Google Scholar]
- Swatton, P. Principles of Flight for Pilots; Aerospace Series; Wiley: Hoboken, NJ, USA, 2011. [Google Scholar]
- Mikolowsky, W. A Short History of the C-130 Hercules. In Proceedings of the AIAA International Air and Space Symposium and Exposition: The Next 100 Years, Dayton, OH, USA, 14–17 July 2003. AIAA Paper 2003-2746. [Google Scholar]
- Thom, A.; Duraisamy, K. Computational Investigation of Unsteadiness in Propeller Wake–Wing Interactions. J. Aircr. 2013, 50, 985–988. [Google Scholar] [CrossRef]
- Veldhuis, L.M. Review of Propeller–Wing Aerodynamic Interference. In Proceedings of the 24th International Congress of the Aeronautical Sciences, Yokohama, Japan, 29 August–3 September 2004. [Google Scholar]
- Computational Research and Engineering Acquisition Tools And Environments (CREATE), Eglin AFB, FL 32542. In Kestrel User Guide, Version 6.0; High Performance Computing Modernization Program: Lorton, VA, USA, 2015.
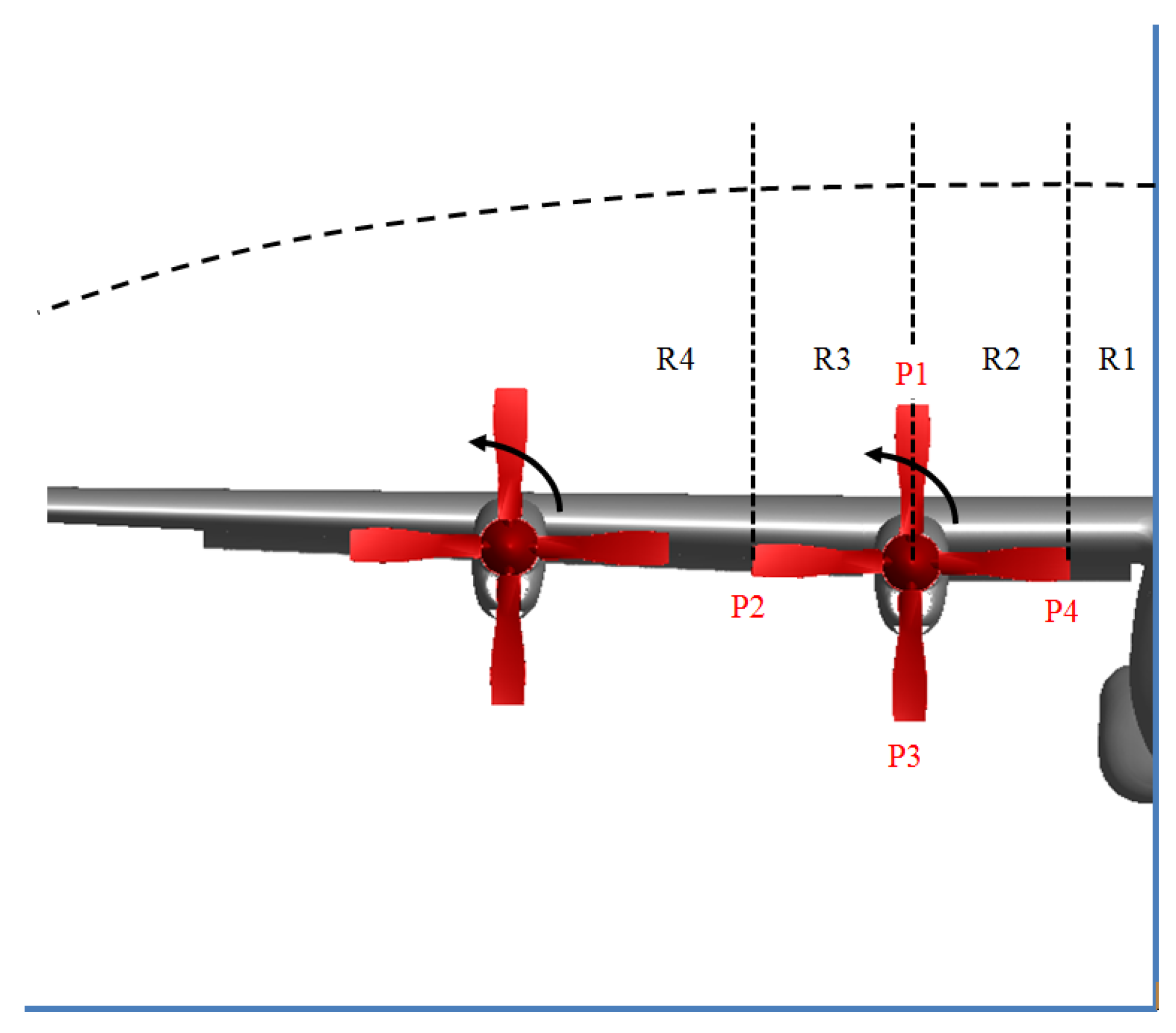

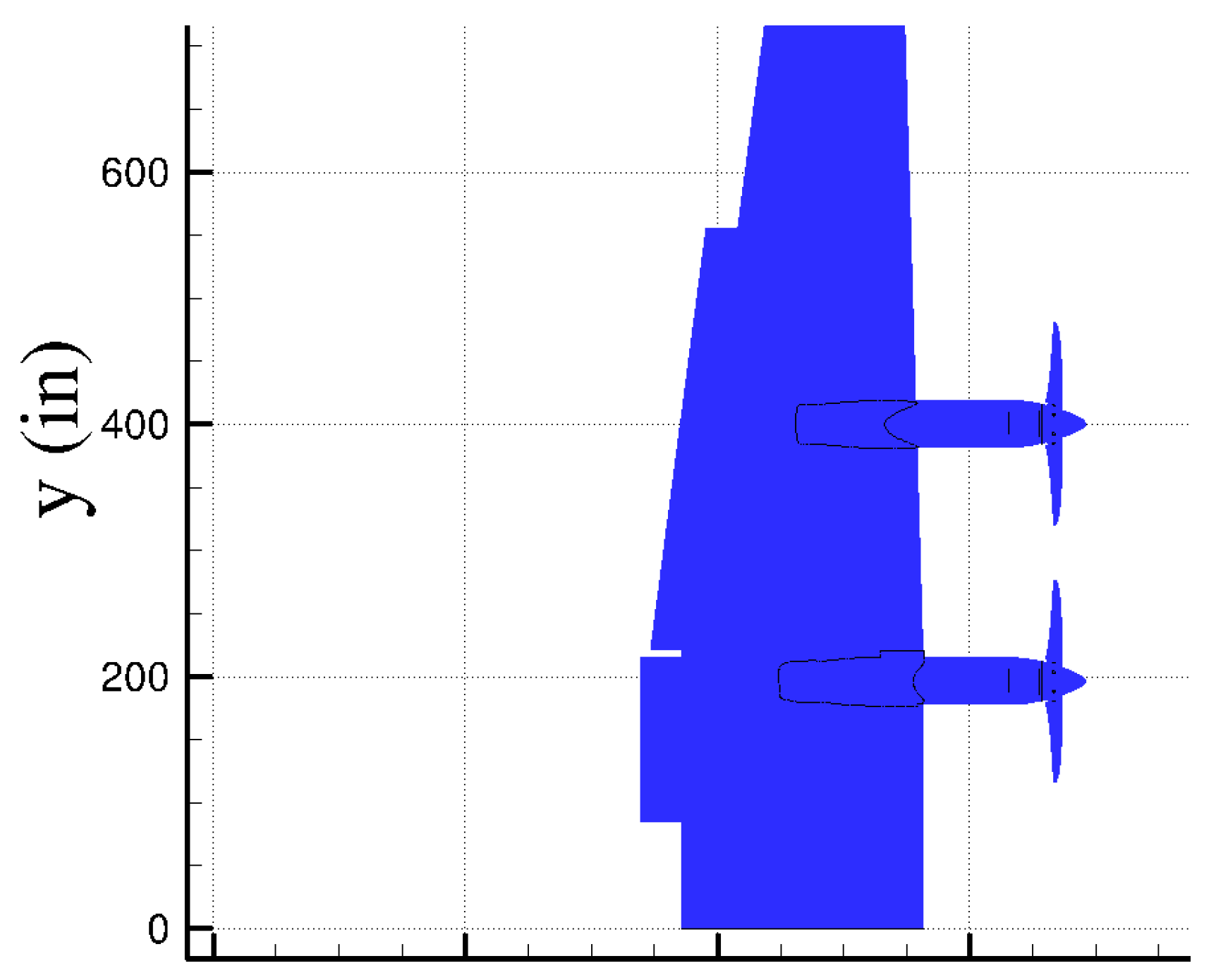
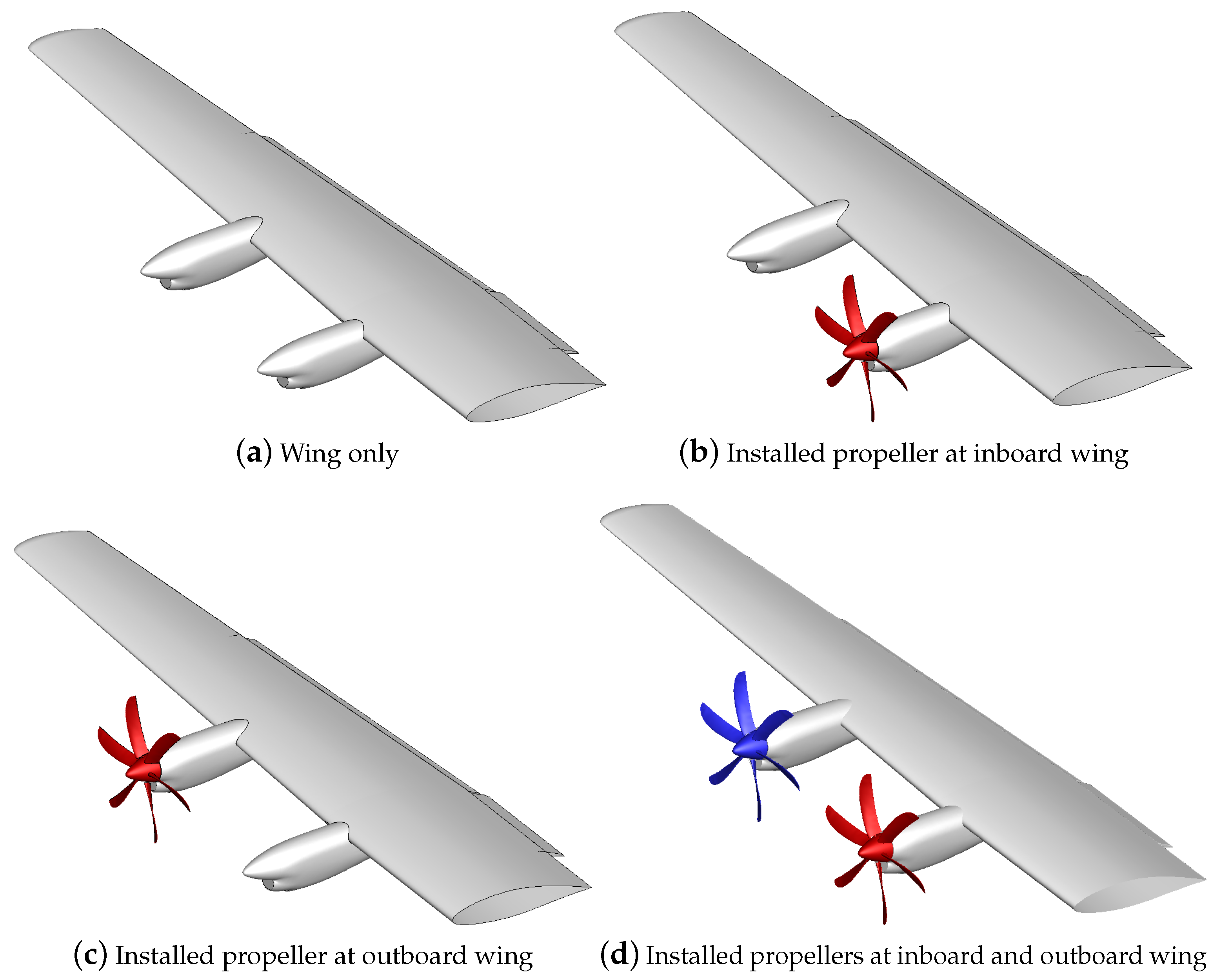




| Simulation Cases | Inboard Propeller | Outboard Propeller | Angle of Attack (deg) | Blade Angle (deg) |
|---|---|---|---|---|
| Case 1 | CCW | [0, 9, 10, 11, 12] | [20, 28] | |
| Case 2 | CW | 20 | ||
| Case 2 | CCW | [0, 9, 10, 11, 12] | [20, 28] | |
| Case 4 | CCW | CCW | [0, 9, 10, 11, 12] | 20 |
| Case 5 | CW | CCW | [0, 9, 10, 11, 12] | 20 |
| Case 6 | CCW | CW | [0, 9, 10, 11, 12] | 20 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aref, P.; Ghoreyshi, M.; Jirasek, A.; Satchell, M.J.; Bergeron, K. Computational Study of Propeller–Wing Aerodynamic Interaction. Aerospace 2018, 5, 79. https://doi.org/10.3390/aerospace5030079
Aref P, Ghoreyshi M, Jirasek A, Satchell MJ, Bergeron K. Computational Study of Propeller–Wing Aerodynamic Interaction. Aerospace. 2018; 5(3):79. https://doi.org/10.3390/aerospace5030079
Chicago/Turabian StyleAref, Pooneh, Mehdi Ghoreyshi, Adam Jirasek, Matthew J. Satchell, and Keith Bergeron. 2018. "Computational Study of Propeller–Wing Aerodynamic Interaction" Aerospace 5, no. 3: 79. https://doi.org/10.3390/aerospace5030079
APA StyleAref, P., Ghoreyshi, M., Jirasek, A., Satchell, M. J., & Bergeron, K. (2018). Computational Study of Propeller–Wing Aerodynamic Interaction. Aerospace, 5(3), 79. https://doi.org/10.3390/aerospace5030079