Abstract
Over the last decades quaternions have become a crucial and very successful tool for attitude representation in robotics and aerospace. However, there is a major problem that is continuously causing trouble in practice when it comes to exchanging formulas or implementations: there are two quaternion multiplications commonly in use, Hamilton’s multiplication and its flipped version, which is often associated with NASA’s Jet Propulsion Laboratory. This paper explains the underlying problem for the popular passive world-to-body usage of rotation quaternions, and promotes an alternative solution compatible with Hamilton’s multiplication. Furthermore, it argues for discontinuing the flipped multiplication. Additionally, it provides recipes for efficiently detecting relevant conventions and migrating formulas or algorithms between them.
1. Introduction
“The quaternion [1] is one of the most important representations of the attitude in spacecraft attitude estimation and control.” With these words Malcolm D. Shuster opened his introduction of [2], ‘The nature of the quaternion’ (in 2008). It details on a conventional shift from Hamilton’s original quaternion multiplication, ⊙ (Hamilton used the symbol · instead. See also Section 2), to its flipped version, ⊗, Shuster had successfully advocated for in the 1990s—in particular with the very influential [1]. For example, the well known JPL-convention chooses ⊗ but it also includes other conventional decisions [3]. Shuster called ⊗ the natural multiplication, and called the ⊙ traditional. We will refer to the former as Shuster’s multiplication and to the latter as Hamilton’s multiplication, because we consider ‘natural’ too biased and because Shuster’s labels are generally rather unknown. Back then, the goal of the introduction was to prevent confusion and mistakes when dealing with chains of rotations (compositions) motivated by the application of spacecraft attitude estimation and control [2]. However, the introduced conventional split from other fields (e.g., mathematics, physics, or computer graphics/visualization) caused a great deal of confusion and is a source for mistakes in practice (see Section 1.2). Therefore, in this paper, we advocate to undo this split and return to only using Hamilton’s original multiplication. At the same time, we show how an alternative approach can be used to solve the original problem addressed in [1].
1.1. Original Problem and Shuster’s Solution
The historical problem with Hamilton’s multiplication only appeared in connection with an arguably arbitrary, specific convention on how to assign direction cosine matrices (DCM; equivalent in value to a corresponding coordinate transformation matrix between oriented orthonormal bases), to unit length quaternions. When using this assignment, as in [1], the product of two quaternions, , would correspond to the product of the two corresponding DCMs, but with reversed order:
i.e., the mapping, , was not a homomorphism but an antihomomorphism, which is generally more uncommon and confusing and therefore more error-prone. Introducing ⊗ is Shuster’s solution to this problem [1]:
1.2. The Problem Today with Shuster’s Solution
Since its introduction, a great fraction of spacecraft literature has adopted ⊗ [2]. On the other hand, virtually the entire rest of the scientific community dealing with quaternions is apparently not following, and partially not even aware of this transition in the spacecraft community, as we will show in Section 5. Having two different quaternion multiplications in use comes at a significant and ongoing cost: formulas and implementations need translation or adaptation, let alone the fact that one must first identify which multiplication is used in a given formula or algorithm. The latter can be particularly tedious if the authors are not aware of the two possibilities and hence do not mention which one they use (as a small self experiment, the reader in doubt is invited to try to figure out which quaternion multiplication the popular c++ template library for linear algebra, Eigen, is using). If a reader is unaware of the split, the discovery that two different quaternion multiplications are in use, and that in fact ‘the other’ was employed, might be made only after several failures.
The troubles may be little per subject but they are continuously affecting a significant number of scientists and engineers, causing delays in the best case. This accumulated cost is particularly large for interdisciplinary domains such as robotics that lean on publications from both conventional worlds, for instance aerospace and computer vision. In fact, in robotics, there are several recent publications for each of the two multiplications (see Section 5). It is also a pressing matter because the effort to correct becomes larger with every new implementation or publication using a convention different from what the community will agree on eventually.
1.3. Contribution
Given this current situation, it is an interesting question whether the proposed switch was necessary or at least the best of all available options. Motivated by this question, this work provides the following contributions (an extended version of this paper with in-depth arguments, derivations, proofs, and more additional material can be found in [4]):
- give an overview over the two quaternion multiplications and their consequences for representing ;
- identify the problem with commonly using both;
- promote and explain a neglected alternative solution;
- demonstrate that this alternative yields a more formal similarity to corresponding formulas using matrices;
- advocate to discontinue Shuster’s multiplication;
- provide recipes to detect and migrate between quaternion multiplication conventions.
To the best of our knowledge, this is the first work explicitly addressing the ambiguity of quaternion multiplication as a problem and proposing a potential solution.
1.4. Outline
We start with introducing our notation in Section 2 and important background information in Section 3. Next, we propose an alternative solution to the original problem in Section 4. In Section 5, we summarize relevant contributions on quaternion multiplication related conventions, and tabulate their popularity in recent or influential publications. Then we argue for discontinuing Shuster’s multiplication in Section 6. Lastly, we provide recipes for detecting and migrating rotation quaternion related conventions in Section 7.
2. Notation
In this section, we introduce our nonstandard notation. An outline of the entire notation can be found in the nomenclature on page 13.
Regarding quaternion notation this paper has two major challenges: First, we must distinguish two different quaternion multiplications and consequentially two different quaternion structures having most of their structure in common. Second, we do not want to load most readers with a representation of quaternions different from what they are used to (for instance, by assuming the real part to be the first component of a real quadruple instead of its last component). We approach these challenges purely axiomatically by assuming to be only a four-dimensional -vector space of quaternions with inner product and an orthonormal standard basis . Pairing with Hamilton’s quaternion multiplication, ⊙, yields Hamilton’s quaternions, , a skew field (also division ring), with multiplicative identity 1 and additional defining relations:
We use ⊙ instead of Hamilton’s original · in this paper to better contrast ⊗ while at the same time stressing the symmetry. For documents using Hamilton’s multiplication only, we recommend using the plain · or the default operator (omitted symbol), because they are the default multiplication symbols (for quaternions) in mathematics, which should not be needlessly questioned as the standardizing authority.
Pairing instead with Shuster’s quaternion multiplication, ⊗, the flipped version of ⊙, yields Shuster’s quaternions, , a similar skew field, but with slightly different additional relations:
The real and imaginary coordinates/components of a quaternion we denote with and , respectively. The right-inverse of , mapping an imaginary coordinate triple into a purely imaginary quaternion we denote with . The quaternion conjugation of q we denote with .
3. Background: Duality of Rotation Representations
Physical rotations are conceptually rather unambiguous. However, when it comes to describing them, there are two popular ways to do so. The active way is to describe what happens to the rotated body’s points from a fixed world frame’s perspective. The passive way is to describe how coordinates of fixed world points change from the perspective of the rotated body frame (the two ways are also distinguished as alibi for active and alias for passive). The passive way comes in two flavours, world-to-body (PWTB) and body-to-world (PBTW). The first describes the change from before rotation to after and the second from after to before. The names stem from assuming that body and world frame are initially aligned (Alternative: local to global vs. global to local as in [3]). We call these options the usage of the mathematical model to describe the physical rotation (In [3], the authors use “function” for active vs. passive without flavours). Mathematically, the described actions on the observed points have identical properties in all three cases matching precisely the actions of the special orthogonal group (SO) (this paper only deals with ). However, because, given the same physical rotation, PWTB describes the inverse compared to PBTW, they yield mutually inverse group elements. Despite being conceptually very different, the active usage always yields the same group element as PBTW. Consequentially, we will often not distinguish these two.The crucial consequence is that, while every parametrization of the SO can be employed for all usages, switching usage from or to PWTB corresponds to an inversion. The main target audience of this paper are those who favour the PWTB usage because the problem represented by Equation (1) is exclusive for the PWTB usage.
4. The Proposed Alternative Solution
The alternative solution for the original problem represented by Equation (1) we suggest is the use of a different correspondence rule, . Explicit forms for and would only detract from our argument here, but can be found in Section 6.4.2. Assuming we keep fixed how rotation matrices represent rotations, this new correspondence inverts the corresponding quaternion. It also yields the desired homomorphy from quaternions to rotation matrices together with ⊙ and the usual matrix multiplication:
This suggestion might falsely give the negative impression of an ‘additional’ inversion. In fact, it could equally well be that for the ‘wrong’ (inverted) quaternions were chosen. And our observations in Section 6.4.3 support this interpretation. Please note that both solutions yield the usual way to apply the rotation represented by a quaternion (this fact is actually equivalent to both being homomorphic; see also Example 5 in Section 7.2.2):
5. Literature Review
5.1. Literature on or Introducing Relevant Conventions
5.1.1. Aerospace
According to [5], Shuster’s multiplication, ⊗, was introduced in [6]. According to [7], it was later proposed as a standard in [8]. Unfortunately, the exact details are impossible for us to reconstruct as NASA has never published [8]. In [9], the authors derive a homomorphic composition rule for the Euler (symmetric) parameter (ESP; usually treated as equal to the rotation quaternion components), effectively equal to ⊗, and infer a required conjugation from ESP to Hamilton’s quaternions. In Section 4, we propose the same quaternion values but with different derivations.
In [2], the author describes the transition from Hamilton’s ⊙ to Shuster’s ⊗ for spacecraft attitude estimation and control literature, citing [1] as probably, more than any other work, responsible for the conventional shift. In [1], ⊗ is indeed derived as necessity given some requirements, of which one was the correspondence . At the same time, Shuster already speculated why mathematicians had no reason to reform the quaternions: “The concern of pure mathematics is not in representing physical reality efficiently but in exploring mathematical structures … As engineers, our interest is in ‘im-pure’ mathematics, contaminated by the needs of practical application.” A major struggle with the quaternion conventions within NASA that led to a conventional switch from the Space Shuttle program (STS) to the (American) International Space Station (ISS) software standard is reported in [10]. According to the author both conventions use PWTB quaternions, but with mutually inverse values. Hence, one must use (ISS) and one (STS). Both use Hamilton’s multiplication, yielding an antihomomorphic quaternion-to-matrix conversion for ISS. Apparently, this drawback was preferred over using ⊗, which would yield the homomorphic convention from [1]. The author compares these two conventions with a third convention that he calls Robotics, which uses PBTW quaternions. Neither [1] nor [2] are mentioned in [10] despite their apparent relevance. Similarly, the problem of antihomomorphy is entirely left out. The only easily accessible reference for quaternions in [10,11] uses Hamilton’s multiplication and also does not mention Shuster’s work. Sadly, its reference for the STS quaternions, [12], is not publicly available. Therefore, we cannot verify the impression that the STS quaternions are exactly what we are proposing in Section 4. If this is the case, something in the line of the argument quoted in [10] must have been the reason to abandon the STS quaternion convention: “Define the application’s fundamental quaternion with no negative signs.” (It is referring to the conversion from rotation vector to quaternion; see Section 6.1.3.) Again, this is impossible for us to verify due to NASA’s lack of publications on the matter. For the same reason, we neither know the foundation of the quoted rule nor how it translates to other circumstances.
The Navigation and Ancillary Information Facility (NAIF), a sub-organization of NASA’s Jet Propulsion Laboratory (JPL), uses Hamilton’s multiplication and everywhere in their primary software suite called SPICE [13]. The authors use the short terms SPICE quaternions, using ⊙, and Engineering quaternions, using ⊗, and describe the first as “Invented by Sir William Rowan Hamilton; Frequently used in mathematics and physics textbooks” and the second as “Widely used in aerospace engineering applications” (e.g., cspice/qxq_c).
In [14] (pp. 37, 38), both multiplications are introduced, but the authors focus on ⊗ because it “has proven to be more useful in attitude analysis”, while being aware of the trouble with quaternion conventions: “Care must be taken to thoroughly understand the conventions embodied in any quaternion equation that one chooses to reference.”
5.1.2. Robotics
In [3], the author proposes a classification of rotation quaternion-related conventions based on four binary choices leading to “12 different combinations” (only 12 instead of 16 because one binary choice, body-to-world vs. world-to-body is only distinguished in the passive case). The author also points out two most commonly used conventions, one using Shuster’s and one using Hamilton’s multiplication, which the author calls JPL-convention and Hamilton-convention, respectively. He chooses to use the latter because it “coincides with many software libraries of widespread use in robotics, such as Eigen, ROS, Google Ceres, and with a vast amount of literature on Kalman filtering for attitude estimation using IMUs ([15,16,17,18,19], and many others).” We discourage the usage of the name Hamilton-convention, because only one decision of the four is associated with the name Hamilton, namely the multiplication (or algebra as it is called in [3]) and there are many very different conventions using this multiplication. The conversions between rotation vector, matrix, and quaternion are not among the four choices. Instead, they are consequences and are only presented for the chosen convention (for quaternion, matrix, and vector) and not for the other possible quaternion conventions. Since the chosen convention includes PBTW (passive + local-to-global) as two further choices, the problem represented by Equation (1) is circumvented and not discussed as a potential problem for other combinations of the four choices (antihomomorphy occurs only when combining ⊙ with PWTB usage of quaternions; see Section 3).
5.2. Popularity in Influential and Recent Literature
In Table 1, we group publications, which are recently dealing with rotation quaternions, by (i) which quaternion multiplication is used, (ii) the type of publication, and (iii) the scientific community. Of course, this is merely a small selection of corresponding publications in the respective fields. Within these constraints the table shows that all relevant online general purpose or mathematical encyclopedias, which we could find, use Hamilton’s multiplication (without mentioning any alternatives)—and so do all major software packages. Most of them also use precisely the quaternion-to-matrix mapping we suggest as part of an alternative solution to Equation (1) in Section 4. The only scientific communities we could find using Shuster’s multiplication are those of aerospace and robotics. Both seem to be divided to this day, including even NASA itself and its substructure JPL. Please note that only [9] (from 1986) and probably [12] (from 1975; not publicly available; only indirect and incomplete knowledge through [10]) combines ⊙ with the PWTB usage and homomorphic quaternion-to-matrix conversion. All other users of this multiplication either accept the antihomomorphy or use PBTW or active quaternions (indicated in the table by the non-B flags in parentheses). The frequent use of PWTB (all except such with -, a, or w-flag) indicates that this is not due to a general lack of popularity or usefulness of the PWTB usage. To the contrary, it can be considered state of the art in aerospace (only two, from 1987 and 2004 and with little influence, do differently among our 17 samples). Additionally, it was used for the Space Shuttle program and is still used on the International Space Station [10]. We believe that precisely this popularity of PWTB together with a lack of examples or understanding how to combines with ⊙ still poses an unsolved problem for many who prefer or only know ⊙. The alternative solution we propose in Section 4 solves this problem and unlocks PWTB for all proponents of ⊙ without leading to an error-prone antihomomorphism.

Table 1.
Popularity of the two multiplications .
6. Rationale against Shuster’s Multiplication
6.1. Overview
First of all, it is important to emphasize that the question of which quaternion multiplication to use should be considered a pragmatic question. Conceptually, there is no problem with any of the two multiplications nor with having both commonly used. Having said that, our main argument is as follows.
6.1.1. Both Multiplications Are Equally Capable and Interchangeable for Every Application
As we explain in Section 6.2, one multiplication is as good as the other in terms of applicability—importantly also when representing 3D rotations.
6.1.2. One of the Two Multiplications Should Be Discontinued
Having two quaternion multiplications in formulas and software comes at a significant and ongoing cost (see Section 1.2 and Section 5), and does not provide benefits (see Section 6.1.1). It is also not necessary to accept or maintain everything that is consistent and sound, as we explain in Section 6.3. Hence, we should discontinue one multiplication, i.e., at least avoid using it in future educative material, books, and software libraries.
6.1.3. Hamilton’s Multiplication Is Preferable
Hamilton’s multiplication is predominant over all existing publications. This is because (i) it is about 150 years older and (ii) Shuster’s multiplication has not spread to mathematics or theoretical physics and probably never will. The latter arises from the fact that both disciplines have very different needs that typically do not even lead to the original problem expressed in Equation (1) as already observed in [1]. To the best of our knowledge, Shuster’s multiplication only spread from aerospace to parts of robotics, which has similar needs and is strongly influenced by aerospace literature. Additionally, Hamilton’s multiplication is used by the vast majority of current software (see Table 1). These observations make it extremely difficult to discontinue Hamilton’s multiplication instead. Even more so, pure mathematics should be almost impossible to influence in that respect because it is against the very nature of mathematics to change such a definition without an inner-mathematical reason. Additionally, as we show in Section 6.4.2, Hamilton’s multiplication has its benefits over Shuster’s from a formal point of view. These benefits make it less error-prone if combined with , which is at least as old and well-known as ( is usually referred to as the Euler–Rodrigues formula). It is typically used whenever rotations are represented actively or PBTW (see Section 3). Because of that, is also already predominant among existing software implementations (see Table 1).
Employing also for the very popular PWTB usage, as we suggest, has a consequence that one could consider its biggest drawback: It introduces the comparatively rarely seen passive quaternion (see Table 2, Figure 1), and thus induces an unusual conversion from an active rotation vector, : . Eventually, the original problem, expressed by Equation (1) leaves two options besides not solving it: (i) introducing an unusual quaternion multiplication (Shuster’s solution) and (ii) introducing an unusual conversion from the active rotation vector to the (passive) rotation quaternion (used, e.g., in [9]). Having only these two options is probably the very difficulty behind the overall struggle and what prevented a standardization so far (see Section 5). Our position, in favour of (ii), emerges from rephrasing the question equivalently: What should be specific for the PWTB usage of quaternions when compared to the active usage, their multiplication, or the conversion to the active rotation vector? (There is good reason to call the usual rotation vector active. However, it is not required here. Our argument works as well for a neutral rotation vector notion.) It reveals an immediate argument for (ii) the conversion from the active rotation vector to the PWTB quaternion should even be expected to be different from its conversion to an active quaternion (compare also Section 3). An argument against (i) is that the multiplication is used much more often, because conversions are merely interface operations and usually do not appear where the heavy lifting is done. Additionally, if we have to choose the multiplication depending on the usage of quaternions to represent rotations, which multiplication is right for other applications? Furthermore, it is very unusual and therefore unexpected that a fundamental algebraic operation such as multiplication is a matter of dispute and convention, while it is quite common for representations. Finally, the very same question for rotation matrices was answered historically: there is no flipped matrix multiplication in regular use. Instead, it is fully accepted that there is an active and a passive rotation matrix which relate differently to an active rotation vector. Why not accept the exact same for rotation quaternions when employing them for exactly the same purpose?

Table 2.
Comparing homomorphic QM-conventions.
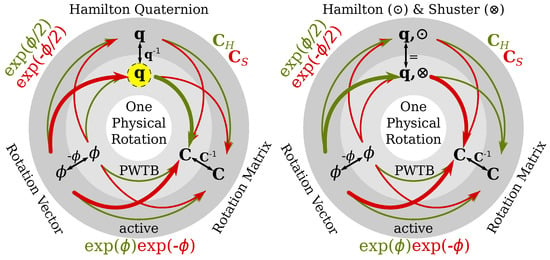
Figure 1.
Active (or passive body-to-world; outer ring) and passive world-to-body (=:PWTB; inner ring) representations of a single physical rotation with the three common parametrizations: rotation matrix, C, rotation vector , and rotation quaternion q. Their mutual conversions are represented by arrows pointing to the codomain of the associated expression/function name (nearby and the same color). On the left, Hamilton multiplication only: Black arrows represent conversion between active and PWTB usage while keeping the parametrization, green arrows represent conversion between different parametrizations while keeping the usage, and red arrows represent additional switching of the usage. The bold arrows constitute the homomorphic convention suggested in this paper. It is suitable for everybody preferring PWTB for q and C. The rare users of PWTB rotation vectors would instead entirely remain in the inner circle. Clinging to the green conversion from the common active to q even if q is intended to be employed PWTB, as done in [1] leads to the situation on the right, using Shuster’s multiplication for quaternions used passively. The colors are kept for conversion functions that also appear on the left (all except the identity conversion between Hamilton and Shuster quaternions). This conventional branch neglects the option of the highlighted inverted q (on the left) and thus requires the flipped multiplication, ⊗, and inevitably breaks the symmetry between C and q on the right compared to the left, i.e., there is no coloring of conversion functions that achieves the same level of symmetry.
6.2. Equal Capability Argument
In this section, we provide support for Section 6.1.1 by arguing why both multiplications are equally capable. The migration recipes in Section 7.2 show that any algorithm or formula can be migrated between the two multiplications in very simple steps: just introduce quaternion conjugation at some places and exchange all multiplications. This already shows that both multiplications can provide the same service to the user (writer, reader, or programmer), as the migration concepts work in both directions.
The question remains whether one implementation could be computationally more efficient than the other. However, one should easily be convinced that the extra cost for some additional conjugations is negligible for most use cases since it only involves scalar negations. Furthermore, for very performance-critical parts of an implementation, the negations can almost always be statically merged into other operations or eliminated through algebraic simplification.
6.3. Why Consistency Is Not Enough
One could counter argue against Section 6.1.2 that what ever is mathematically sound and consistent should or even must be accepted out of principle. However, this is a disastrous position, because when taken to the extreme that would mean that every publication should be allowed to introduce or refer to its own version of mathematics or even use its own private language! However, the immense power and usefulness of mathematics and language comes not only from its consistency but very much from how much it is shared. Especially as engineers or scientists, we benefit from the effort put into standardization and unification by, e.g., mathematicians on a daily basis. It is only due to this effort that we can readily use answers from a mathematical software or encyclopedia. It would work even better if we all cared more about standardization. For example, imagine engineers chose freely, albeit in a consistent manner, between the standard matrix product and its flipped version in their implementations and publications. What pain and massive economic drawback would this little additional freedom cause? Every paper would need to introduce its matrix multiplication before using it—just as it is now with quaternions. We are not in that situation only because there is an accepted standard matrix product and it is treated as such.
When it comes to representation of 3D rotations, we are used to having many conventions and this might reinforce this false idea that we must accept any consistent convention. In this case, one of the underlying reasons is that there are in fact conventional options that have benefits and drawbacks given an application, such as the usage (see Section 3), and others that do not. It is important to distinguish these two cases. The position of this paper is that the quaternion multiplication is of the second type.
In summary, we should not adopt the simplistic position from above. Instead, we must invest in the assessment for every consistent convention candidate whether it is unnecessary or useful and worth its additional (future) cost. And unfortunately, sometimes we must even do that for a convention that is already widely used.
6.4. Formal Differences
In this section, we are going to investigate the formal differences of the two alternative solutions to the original problem expressed in Equation (1) to support parts of Section 6.1.3. Please note that this does not contradict our observation of equal capability in Section 6.2, because neither similarity nor symmetry affect the practical capability of a mathematical tool. Instead, it affects mostly the probability of human error when dealing with the tool. This can be a strong argument, too. In fact, it is the very type of argument with which [1] justifies the introduction of Shuster’s multiplication.
We start without any assumptions about how unit quaternions and proper orthogonal matrices are conceptually used for modeling rotations (for instance, active/passive/DCM matrices) and only focus on how quaternions are converted to matrices. This conversion must be at least implicitly determined by all consistent rotation conventions involving rotation matrices and rotation quaternions. The benefit is that our abstract observations automatically apply to all such conventions. In particular, the C in and no longer stands for the direction cosine matrix, but for any rotation matrix concept.
6.4.1. QM-Conventions
We call a convention that determines a specific conversion, , and a particular quaternion multiplication, ⋆, a QM-convention and represent it with (). In this way, many common conventions collapse to a single representative. However, this is an intended abstraction. The ignored details do not impact the following analysis, i.e., it holds equally for all conventions collapsing to a given representative. We call a QM-convention homomorphic iff the multiplication order is preserved when switching between quaternions and matrices, as in Equation (3), antihomomorphic iff the order flips, as in Equation (1), and inconsistent otherwise. There are only four options for consistent QM-conventions, namely all pairs in . It seems commonly accepted that a homomorphy is preferable and less error-prone reducing the good candidates to the two homomorphic QM-conventions, and , with their homomorphy given in Equations (3) and (2), respectively.
6.4.2. Formal Comparison Independent of the Usage
In Table 2, we compare the two homomorphic conventions. Here denotes a rotation vector in . The convention-factors (both active and PBTW are represented by 1 and both PWTB and DCM by ) encode the usage of rotation matrices () and rotation vectors (). The usage of the quaternion follows from given the chosen and is identical to for homomorphic QM-conventions. We’ll look deeper into their effect in Section 6.4.3. The indices A and B for the angular velocities, , indicate differences stemming from frame assignments for and the usage of C. Depending on these choices one of the two formulas is correct assuming another convention factor, is suitably chosen. To spell out further details would require the introduction of frames and physical meaning for the involved rotations. Leaving out these details instead stresses the independence of our similarity arguments.
The neutral differences are highlighted in blue. Green vs. red highlights the benefits of in terms of more similarity between corresponding rotation matrix and quaternion equations. The table clearly shows that yields more formal similarity with the rotation matrices when related to rotation vectors or angular velocities: The alternative, , introduces a difference in sign for the expressions involving or (− instead of +) compared to the matrix cases. This difference in similarity with the corresponding rotation matrix formula does not depend on the interpretation/usage (encoded in , , ) but only on the choice of the homomorphic QM-convention.
Table 2 also indicates that additionally flipping the cross product (negating the ) would change the similarity argument in favour of . In fact, it seems probable that this lack of formal similarity was one reason to introduce the matrix valued operator in ([1], p. 445). Unfortunately, this is hard to verify because it was introduced only on the grounds that this “matrix turns out to be more convenient overall”. In [2], this matrix was abandoned again.
6.4.3. Formal Comparison Distinguishing Active and Passive Usage
A further symmetry aspect in favour of Hamilton’s multiplication becomes apparent if we compare both active and passive usage of matrices and quaternions (see Section 3). This yields Table 3, again using the factor to encode the usage of a given rotation vector . In contrast to Table 2, which assumes an arbitrary but single usage for rotation matrices and quaternions, it compares both usages (corresponding values in Columns 2 and 3). Each row corresponds to a rotation representation: rotation matrix and three different flavours of rotation quaternions, each yielding homomorphic conversion to the rotation matrix in row 1. The table shows that neither using Shuster’s multiplication for the passive and Hamilton’s for active usage (Row 3), nor a full switch to Shuster’s multiplication (Row 4) can yield the same level of form-similarity, when compared to the rotation matrices, as our proposed option, using ⊙ in all cases (Row 2). Similarity flaws are marked in red vs. green. A graphical illustration of the the comparison between the pure Hamilton and the mixed multiplication scenarios is depicted in Figure 1.

Table 3.
Active vs. passive usage given a rotation vector .
7. Recipes
In this section, we give some practical advice to (a) identify QM-conventions and (b) migrate between them.
7.1. How to Detect Which QM-Convention Is Used
QM-conventions are fully determined by two binary choices: the quaternion-to-matrix map, C, and the quaternion multiplication, ⋆. These choices can be ascertained as follows:
7.1.1. For the Quaternion Multiplication
One of the easiest ways is to find out the result of the product . If the result is k, then ; otherwise it is and .
7.1.2. The Quaternion-to-Matrix and Matrix-to-Quaternion Conversions
The quaternion-to-matrix conversion can be identified by applying it to a suitable test quaternion, e.g., . It holds that and . This test can also be performed on a matrix-to-quaternion conversion. It maps to if is used and to in case of .
7.2. Migrating from one QM-Convention to Another
There are several efficient ways to migrate a tool (e.g., formulas, proofs, publications or algorithms and implementations) between QM-conventions, where migration shall refer to a transformation after which the tool does exactly the same job but with all quaternions going in or out being compatible with the target convention. We introduce two powerful migration procedures, translate and interface, that are applicable to all types of tools. Both procedures migrate between the two homomorphic QM-conventions. (To migrate a non homomorphic QM-convention first replace all multiplications with the other and flip their arguments. This is an equivalence transformation yielding a tool using a homomorphic convention.) It can be very helpful to first decompose a tool into smaller sub-tools and migrate each with the most advantageous procedure.
7.2.1. The Two Migration Procedures
For both procedures, a successive mathematical simplification step is recommended.
Translate
Replace all quaternion constants, , within the tool with their conjugated value, , and all quaternion multiplications with their flipped version ().
Interface
Conjugate all quaternion valued in- and outputs of the tool (also suggested in [13]). Components of a partial quaternion (i.e., not constituting a complete quaternion) going in or out should be treated as plain real numbers.
7.2.2. Examples
Next, we provide some examples:
- translates into , which simplifies to . Interfacing it would not change it since it has no inputs and only a logic output.
- interfaces into . When translating it, its implicit dependence on constants must be respected: The right hand side of translates into .
- could be first decomposed in , and . The first translates into (the variable q is an input and no constant). The second interfaces into . Putting these together yields the expected .
- interfaces into . Hence, the matrix part of the QM-convention is indeed migrated. translates into the same, , because must use coordinates with respect to a basis (constants) for its input and , because (compare 2).
- could be first decomposed in , interfacing into , and translating into , where the minus comes from translating constants in . Putting these together yields the expected result: .
7.2.3. Correctness of the Migration Recipes
A question remains as to why these two migration concepts work. Unfortunately, being intuitively convinced of their correctness is much easier than proving them. Formal proofs are far beyond this paper. A rather detailed sketch can be found in our extended version [4]. Here, we only provide proof ideas:
Interfacing
The interfacing strategy must yield a corresponding tool, i.e., having the same input–output behavior except for quaternion inputs and outputs, which are conjugated, because we can interface it twice and yield the same tool as before (conjugation and identity are self-inverse). From this, it follows immediately that the interfacing is loss and error-free. The correspondence follows the interfacing itself, which is designed to achieve corresponding input–output behavior.
Translation
The translation strategy must yield a corresponding tool essentially because it represents precisely the application of an isomorphism, namely quaternion conjugation, between the isomorphic algebraic structures and . Since this isomorphism also does not alter the real numbers embedded in (as the linear span of ), the input–output behavior is affected precisely as hoped. This can be seen as follows: First, there is no other way to exchange information with the ‘quaternion world’ than through quaternions or real numbers because the axiomatic properties do not provide any other possibility. Second, all quaternions get conjugated and real numbers remain the same if we apply conjugation to all constants and inputs, which corresponds to using the translated tool with the target convention.
8. Conclusions
In this paper, we suggested an alternative solution to the antihomomorphy problem that led to the introduction of the flipped quaternion multiplication. We further proposed to discontinue its use in favour of Hamilton’s original definition combined with the suggested alternative solution. To argue for this we gave evidence of the cost of maintaining two multiplications and showed that for principal reasons there cannot be any significant capability benefit in using the flipped multiplication for theory or algorithms. Additionally, we demonstrated that the formal similarity between matrices and quaternions, when related to angular velocity or rotation vectors, is in favour of the Hamiltonian multiplication independently of any other conventional decision as long as the definition of the cross product is not additionally questioned. Furthermore, we provided recipes for how to migrate formulas and algorithms from one quaternion multiplication to the other as well as how to detect which convention is used in a given context.
Author Contributions
Conceptualization: H.S.; investigation: H.S.; project administration: J.N.; supervision: I.G., S.W., R.S., and J.N.; writing—original draft: H.S., I.G., M.B., S.W., and J.N.
Funding
The research leading to these results has received funding from the ARL within the BAA W911NF-12-R-0011 under grant agreement W911NF-16-2-0112.
Acknowledgments
The authors are grateful to Michael Burri and Anne-Katrin Schlegel for very helpful comments.
Nomenclature
| implicitly identified | |
| cross product | |
| : | |
| , gafterf | |
| inner product (also called scalar or dot product) | |
| 4D Euclidean -vector space of quaternions (without quaternion-multiplication) | |
| orthonormal standard basis for | |
| , unit length quaternions | |
| ⊙ | Hamilton’s quaternion multiplication, i.e. |
| ⊗ | Shuster’s flipped quaternion multiplication [1]: |
| , imaginary components of q | |
| (shorthand) | |
| , real component ofq | |
| , conjugation | |
References
- Shuster, M.D. Survey of attitude representations. J. Astronaut. Sci. 1993, 41, 439–517. [Google Scholar]
- Shuster, M.D. The nature of the quaternion. J. Astronaut. Sci. 2008, 56, 359–373. [Google Scholar] [CrossRef]
- Sola, J. Quaternion Kinematics for the Error-State KF; Technical Report; LAAS-CNRS: Toulouse, France, 2012. [Google Scholar]
- Sommer, H.; Gilitschenski, I.; Bloesch, M.; Weiss, S.M.; Siegwart, R.; Nieto, J. Why and How to Avoid the Flipped Quaternion Multiplication. arXiv 2018, arXiv:1801.07478. [Google Scholar]
- Crassidis, J.L. Sigma-point Kalman filtering for integrated GPS and inertial navigation. IEEE Trans. Aerosp. Electron. Syst. 2006, 42, 750–756. [Google Scholar] [CrossRef]
- Lefferts, E.J.; Markley, F.L.; Shuster, M.D. Kalman filtering for spacecraft attitude estimation. JGCD 1982, 5, 417–429. [Google Scholar]
- Trawny, N.; Roumeliotis, S.I. Indirect Kalman Filter for 3D Attitude Estimation; Technical Report 2005-002; University of Minnesota, Department of Computer Science and Engineering: Minneapolis, MN, USA, 2005. [Google Scholar]
- Breckenridge, W.G. Quaternions—Proposed Standard Conventions; Technical Report JPL-IOM-343-79-1199; NASA: Washington, DC, USA, 1999.
- Junkins, J.L.; Turner, J.D. Optimal Spacecraft Rotational Maneuvers; Elsevier: New York, NY, USA, 1986; Volume 3. [Google Scholar]
- Yazell, D. Origins of the unusual space shuttle quaternion definition. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including The New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009; Volume 66. [Google Scholar]
- Stevens, B.; Lewis, F. Aircraft Control and Simulation; Wiley: Hoboken, NJ, USA, 2003. [Google Scholar]
- Carroll, J. The Notation and Use of Quaternions for Shuttle Ascent Steering; Charles Stark Draper Laboratory Memo: SSV10C-75-47; Charles Stark Draper Laboratory: Cambridge, MA, USA, 1975. [Google Scholar]
- Naif, N. Quaternions White Paper; 2003; Technical Report NAIF; JPL: Pasadena, CA, USA, 2003. [Google Scholar]
- Markley, F.; Crassidis, J. Fundamentals of Spacecraft Attitude Determination and Control; Space Technology Library, Springer: New York, NY, USA, 2014. [Google Scholar]
- Chou, J.C.K. Quaternion kinematic and dynamic differential equations. IEEE TRA 1992, 8, 53–64. [Google Scholar] [CrossRef]
- Kuipers, J. Quaternions and Rotation Sequences: A Primer with Applications to Orbits, Aerospace, and Virtual Reality; Mathematical Sciences Series; Princeton University Press: Princeton, NJ, USA, 1999. [Google Scholar]
- Piniés, P.; Lupton, T.; Sukkarieh, S.; Tardós, J.D. Inertial aiding of inverse depth SLAM using a monocular camera. In Proceedings of the 2007 IEEE ICRA, Rome, Italy, 10–14 April 2007; pp. 2797–2802. [Google Scholar]
- Roussillon, C.; Gonzalez, A.; Solà, J.; Codol, J.-M.; Mansard, N.; Lacroix, S.; Devy, M. RT-SLAM: A Generic and Real-Time Visual SLAM Implementation; Lecture Notes in Computer Science; Springer: Berlin, Germany, 2011; pp. 31–40. [Google Scholar]
- Martinelli, A. Vision and IMU data fusion: Closed-form solutions for attitude, speed, absolute scale, and bias determination. IEEE Trans. Robot. 2012, 28, 44–60. [Google Scholar] [CrossRef]
- Hazewinkel, M. Encyclopedia of Mathematics: Volume 6: Subject Index—Author Index; Springer Science & Business Media: Berlin, Germany, 2013. [Google Scholar]
- Gowers, T.; Barrow-Green, J.; Leader, I. The Princeton Companion to Mathematics; Princeton University Press: Princeton, NJ, USA, 2010. [Google Scholar]
- Lengyel, E. Mathematics for 3D Game Programming and Computer Graphics; Cengage Learning: Boston, MA, USA, 2012. [Google Scholar]
- Rodman, L. Topics in Quaternion Linear Algebra; Princeton University Press: Princeton, NJ, USA, 2014. [Google Scholar]
- Battin, R. An Introduction to the Mathematics and Methods of Astrodynamics; AIAA Education Series; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 1987. [Google Scholar]
- Shivarama, R.; Fahrenthold, E.P. Hamilton’s equations with Euler parameters for rigid body dynamics modeling. JDSMC 2004, 126, 124–130. [Google Scholar] [CrossRef]
- Bacon, B.J. Quaternion-based control architecture for determining controllability/maneuverability limits. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Minneapolis, MN, USA, 13–16 August 2012. [Google Scholar]
- Crassidis, J.L.; Markley, F.L.; Cheng, Y. Survey of nonlinear attitude estimation methods. JGCD 2007, 30, 12–28. [Google Scholar] [CrossRef]
- Barfoot, T.D.; Forbes, J.R.; Furgale, P.T. Pose Estimation using Linearized Rotations and Quaternion Algebra. Acta Astronaut. 2011, 68, 101–112. [Google Scholar] [CrossRef]
- Ainscough, T.; Zanetti, R.; Christian, J.; Spanos, P.D. Q-method extended Kalman filter. JGCD 2014, 38, 752–760. [Google Scholar] [CrossRef]
- Queen, S.Z. A Kalman Filter for Mass Property and Thrust Identification of the Spin-Stabilized Magnetospheric Multiscale Formation. In Proceedings of the 25th International Symposium on Space Flight Dynamics, Munich, Germany, 19–23 October 2015; NTRS: Chicago, IL, USA, 2015. [Google Scholar]
- Galante, J.M.; Van Eepoel, J.; D’Souza, C.; Patrick, B. Fast Kalman Filtering for Relative Spacecraft Position and Attitude Estimation for the Raven ISS Hosted Payload. In Proceedings of the 39th AAS Guidance and Control Conference, Breckenridge, CO, USA, 5–10 February 2016; NTRS: Chicago, IL, USA, 2016. [Google Scholar]
- McCabe, J.S.; Brown, A.J.; DeMars, K.J.; Carson, J.M., III. Comparison of Factorization-Based Filtering for Landing Navigation. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, Grapevine, TX, 9–13 January 2017; NTRS: Chicago, IL, USA, 2017. [Google Scholar]
- Pervin, E.; Webb, J.A. Quaternions in Computer Vision and Robotics; Technical Report; Carnegie Mellon University: Pittsburgh, PA, USA, 1982. [Google Scholar]
- Murray, R.M.; Li, Z.; Sastry, S.S.; Sastry, S.S. A Mathematical Introduction to Robotic Manipulation; CRC Press: Boca Raton, FL, USA, 1994. [Google Scholar]
- Fresk, E.; Nikolakopoulos, G. Full quaternion based attitude control for a quadrotor. In Proceedings of the 2013 ECC, Zurich, Switzerland, 17–19 July 2013; pp. 17–19. [Google Scholar]
- Diebel, J. Representing attitude: Euler angles, unit quaternions, and rotation vectors. Matrix 2006, 58, 1–35. [Google Scholar]
- Li, M.; Mourikis, A.I. Improving the accuracy of EKF-based visual-inertial odometry. In Proceedings of the ICRA 2012, Saint Paul, MN, USA, 14–18 May 2012; pp. 828–835. [Google Scholar]
- Li, M.; Yu, H.; Zheng, X.; Mourikis, A.I. High-fidelity sensor modeling and self-calibration in vision-aided inertial navigation. In Proceedings of the 2014 IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 29 September 2014; pp. 409–416. [Google Scholar]
- Schwab, A.L. Quaternions, Finite Rotation and Euler Parameters; Technical Report; Delft University of Technology: Delft, The Netherlands, 2002. [Google Scholar]
- Schwab, A.L.; Meijaard, J. How to draw Euler angles and utilize Euler parameters. In Proceedings of the IDETC/CIE 2006 ASME 2006 International Design Engineering Technical Conferences & Computers and Information in Engineering Conference, Philadelphi, PA, USA, 10–13 September 2006; pp. 10–13. [Google Scholar]
- Holm, D. Geometric Mechanics: Part II: Rotating, Translating and Rolling; Imperial College Press: London, UK, 2008. [Google Scholar]
- Heard, W. Rigid Body Mechanics: Mathematics, Physics and Applications; Physics Textbook; Wiley: Hoboken, NJ, USA, 2008. [Google Scholar]
- Flügge, S. Principles of Classical Mechanics and Field Theory/Prinzipien der Klassischen Mechanik und Feldtheorie; Encyclopedia of Physics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mason, M.T. Mechanics of Robotic Manipulation; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Bonnable, S.; Martin, P.; Salaün, E. Invariant Extended Kalman Filter: Theory and application to a velocity-aided attitude estimation problem. In Proceedings of the 48h IEEE Conference on Decision and Control (CDC) Held Jointly with 2009 28th Chinese Control Conference, Shanghai, China, 15–18 December 2009; pp. 1297–1304. [Google Scholar]
- Gui, H.; Vukovich, G. Finite-time angular velocity observers for rigid-body attitude tracking with bounded inputs. Int. J. Robust Nonlinear Control 2016. [Google Scholar] [CrossRef]
- Mukundan, R. Quaternions: From classical mechanics to computer graphics, and beyond. In Proceedings of the 7th Asian Technology Conference in Mathematics, Melaka, Malaysia, 17–21 December 2002; pp. 97–105. [Google Scholar]
- Shoemake, K. Quaternion calculus and fast animation, computer animation: 3-D motion specification and control. In Proceedings of the SIGGRAPH’87, Anaheim, CA, USA, 27–31 July 1987. [Google Scholar]
- Hanson, A.J. Visualizing quaternions. In Proceedings of the ACM SIGGRAPH 2005 Courses, Los Angeles, CA, USA, 31 July–4 August 2005; p. 1. [Google Scholar]
- Vince, J. Quaternions for Computer Graphics; Springer: London, UK, 2011. [Google Scholar]
- Kolaman, A.; Yadid-Pecht, O. Quaternion Structural Similarity: A New Quality Index for Color Images. IEEE Trans. Image Process. 2012, 21, 1526–1536. [Google Scholar] [CrossRef] [PubMed]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).