Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD)
Abstract
1. Introduction
2. Configuration
3. Numerical Methods
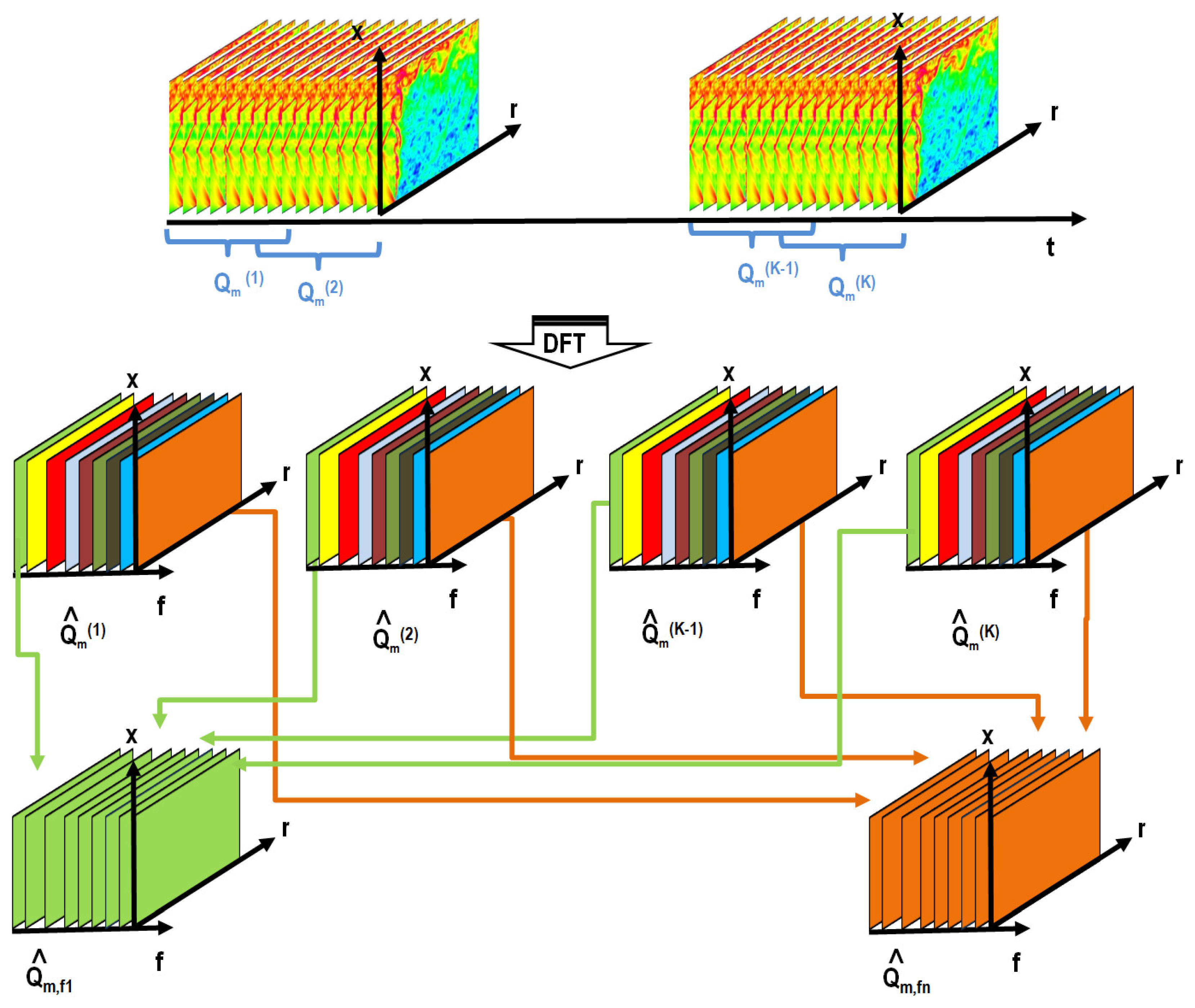
4. Spectral Proper Orthogonal Decomposition (SPOD)
5. Results
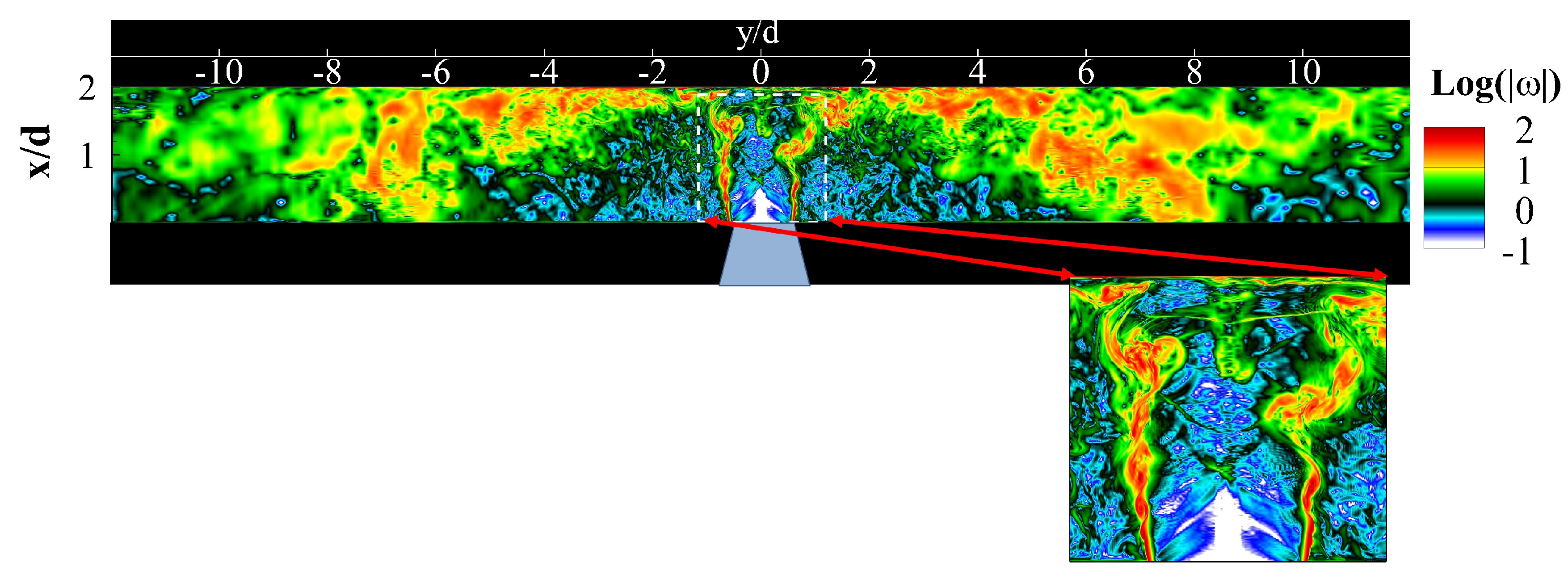
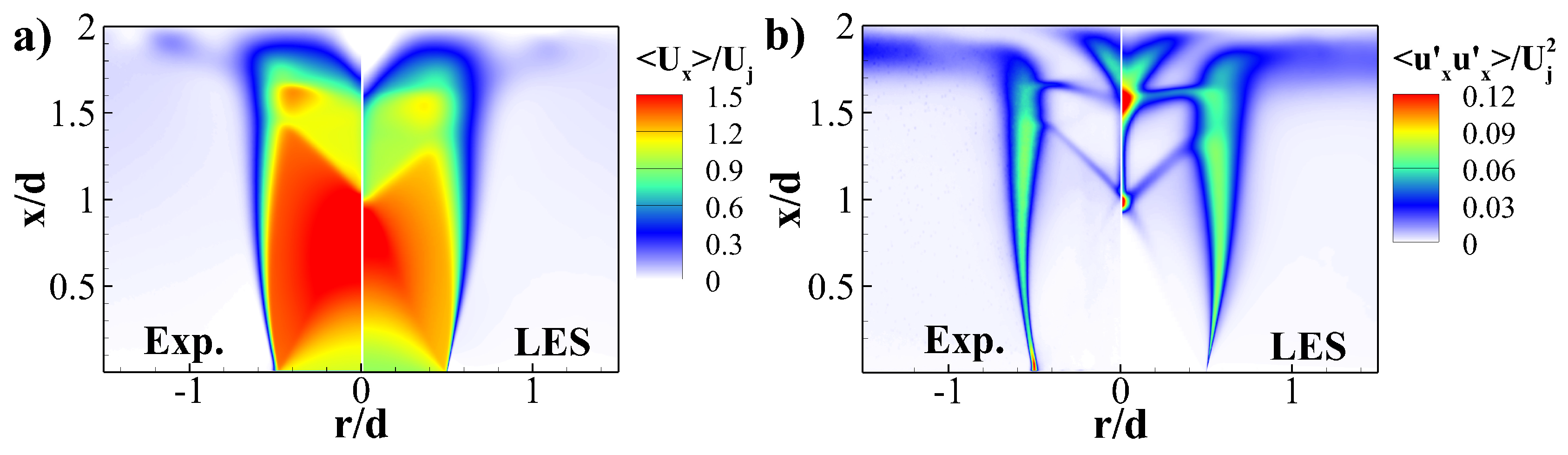
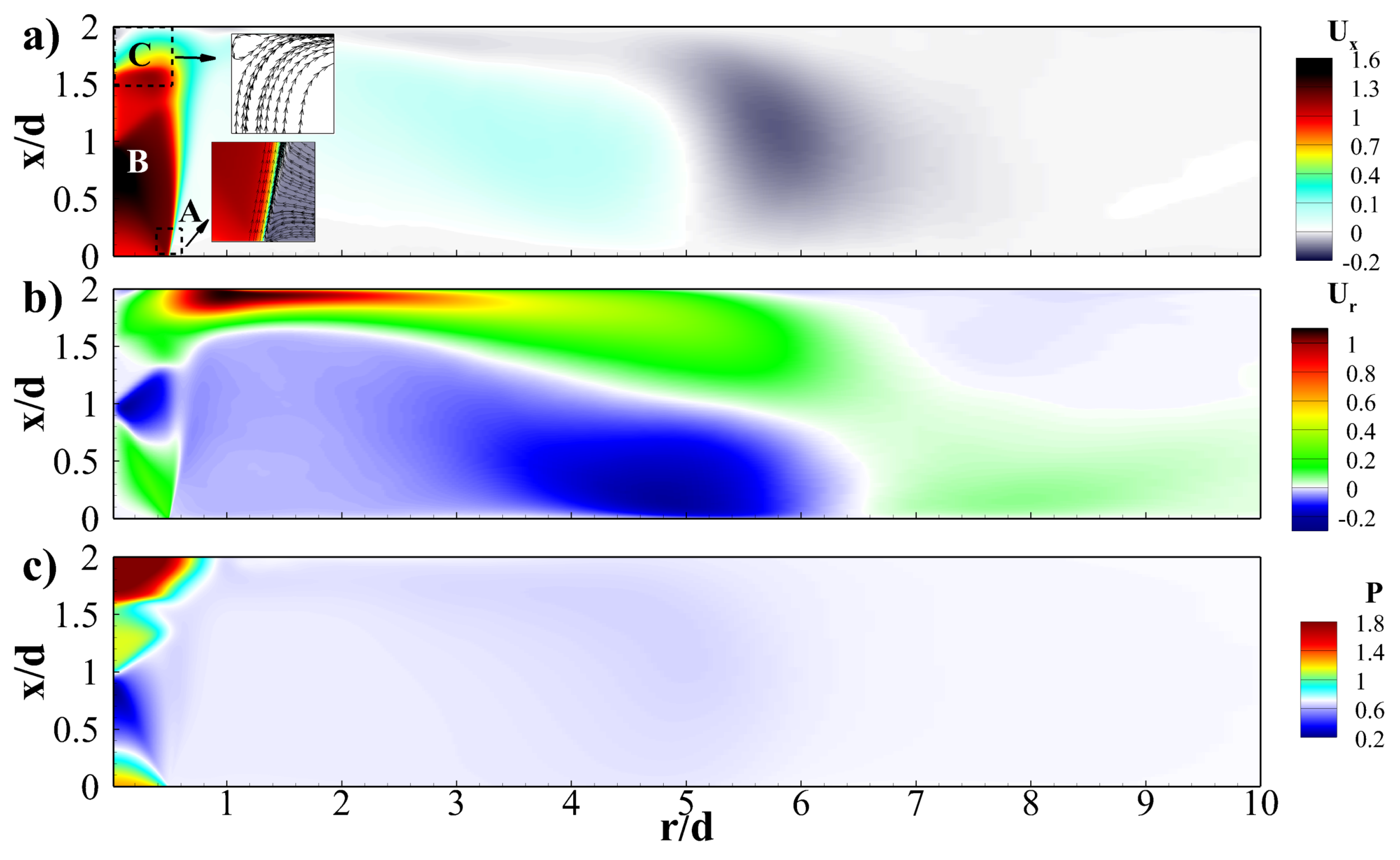
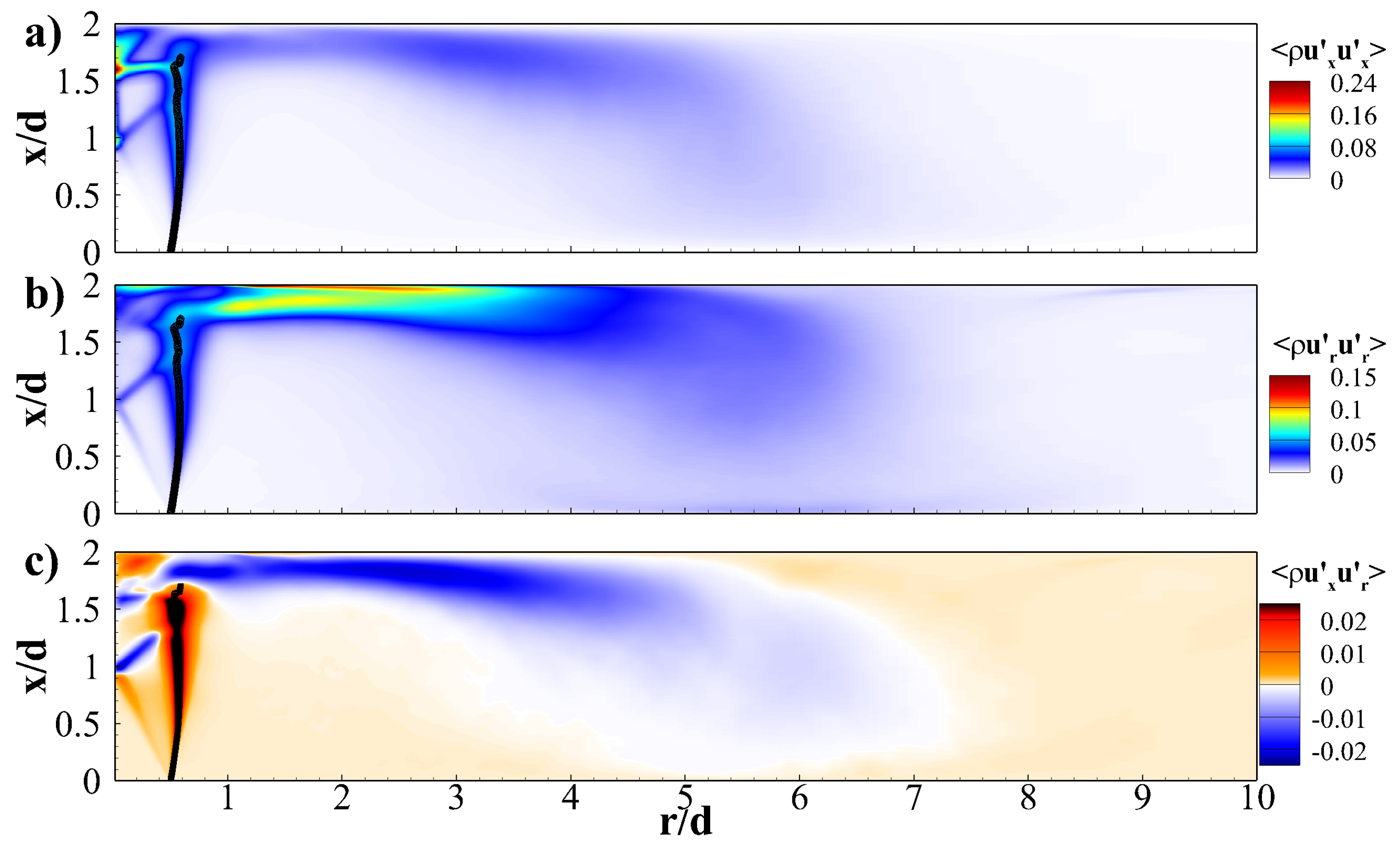
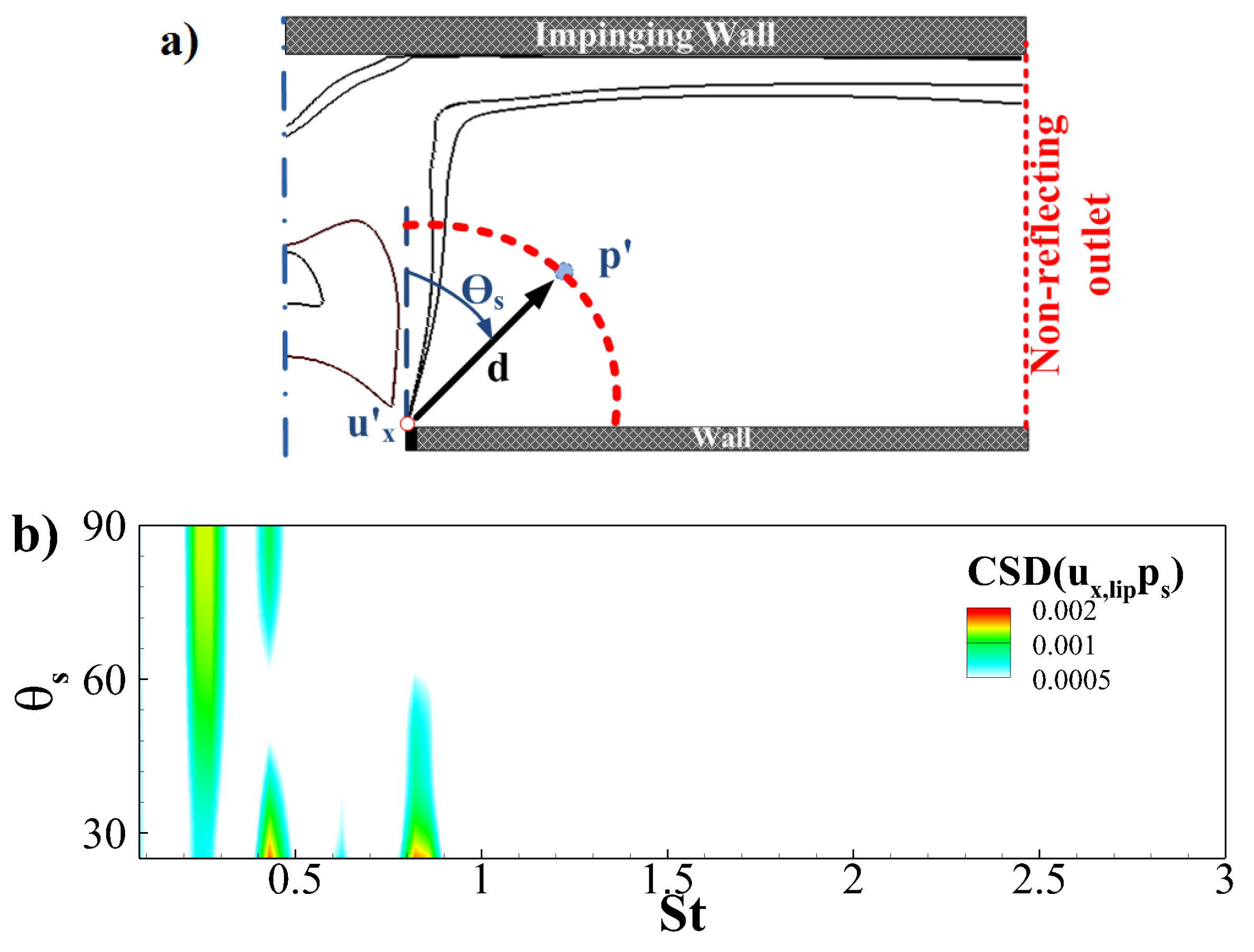
5.1. Characteristics of the Flow-Field
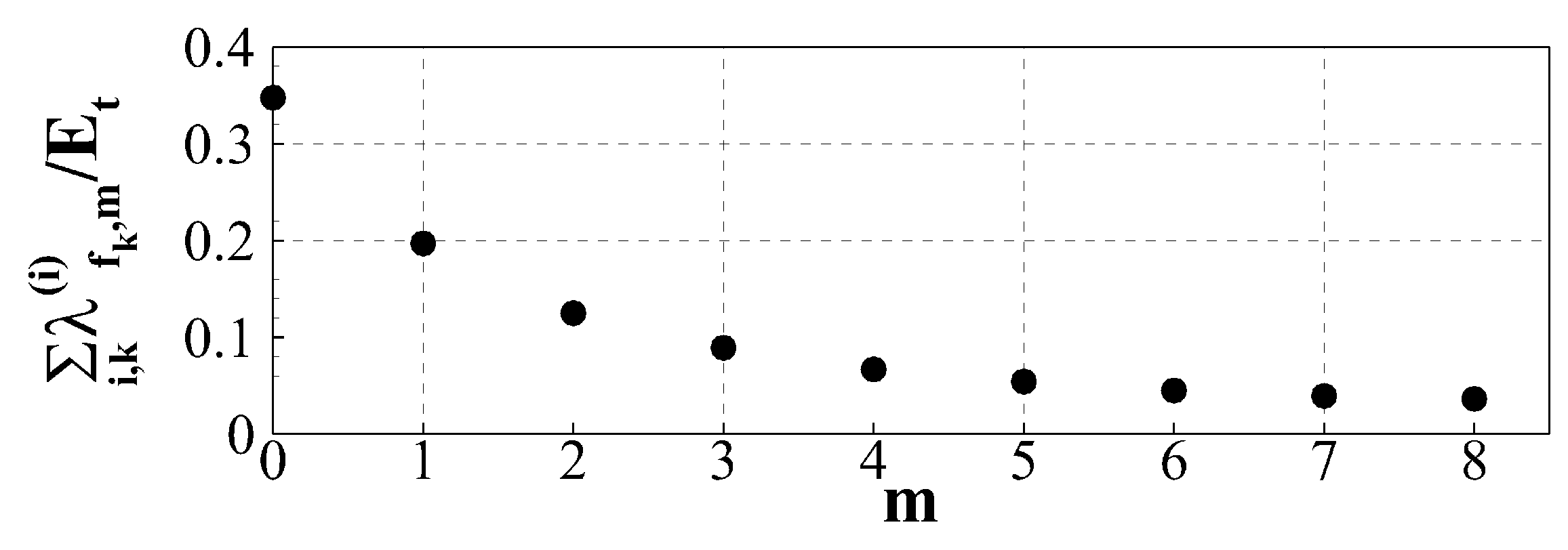
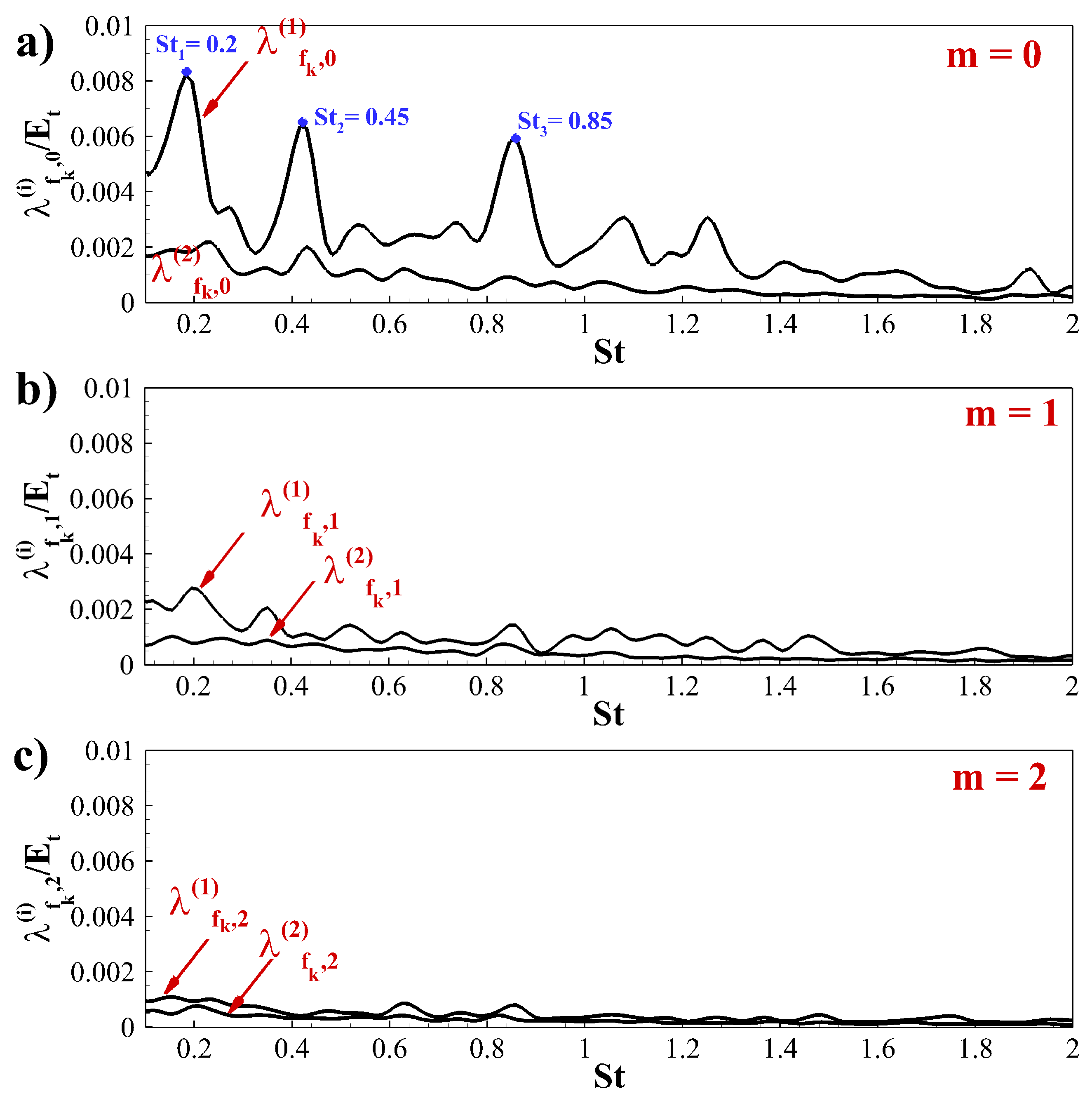
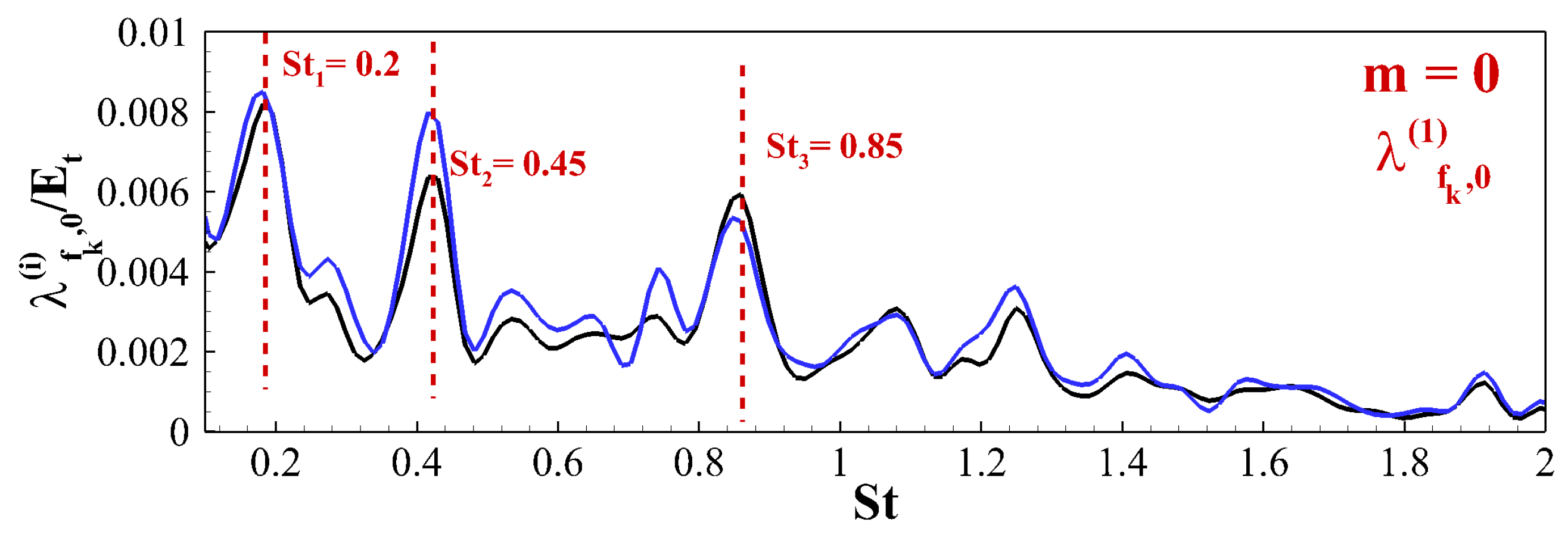
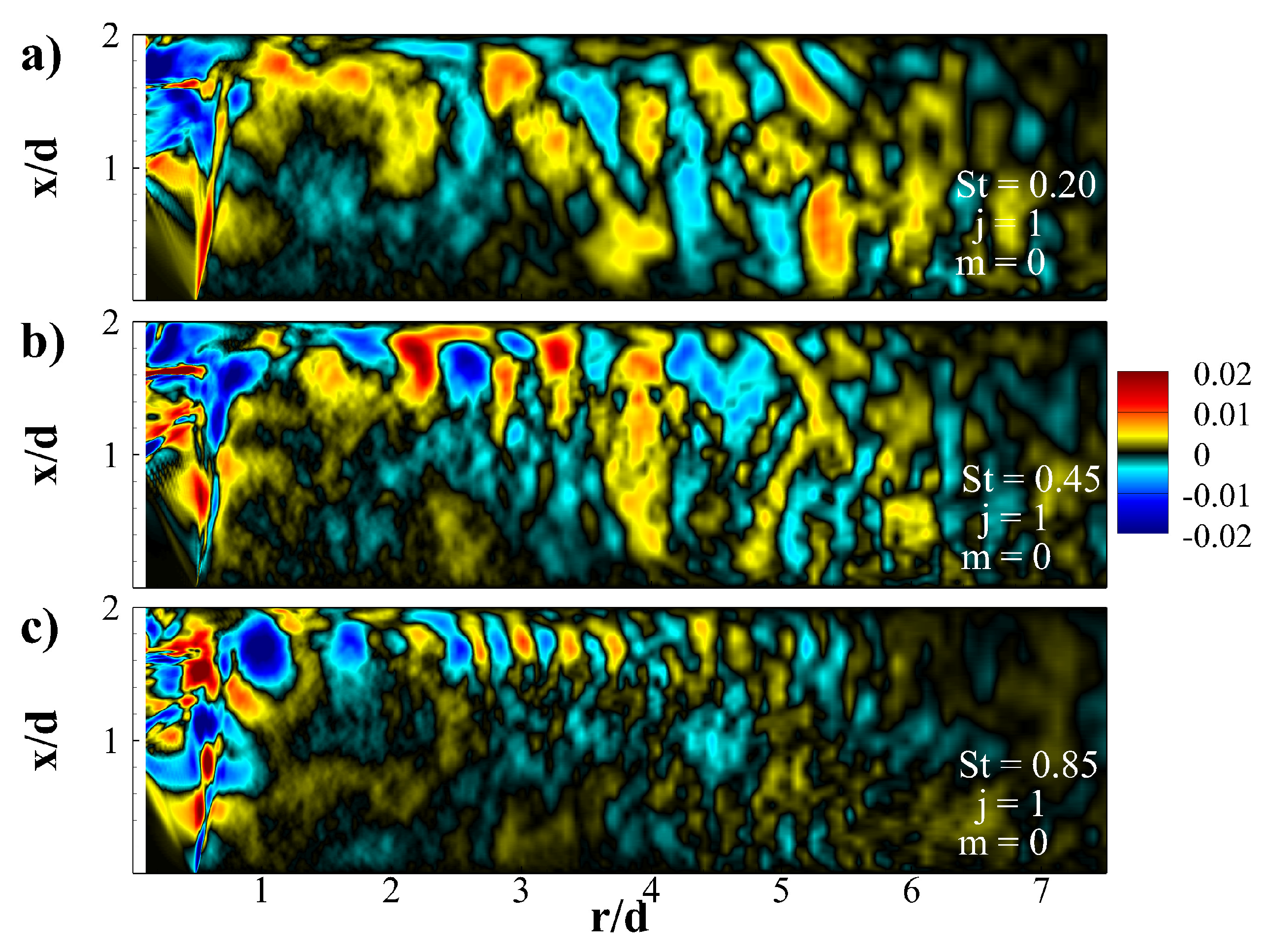
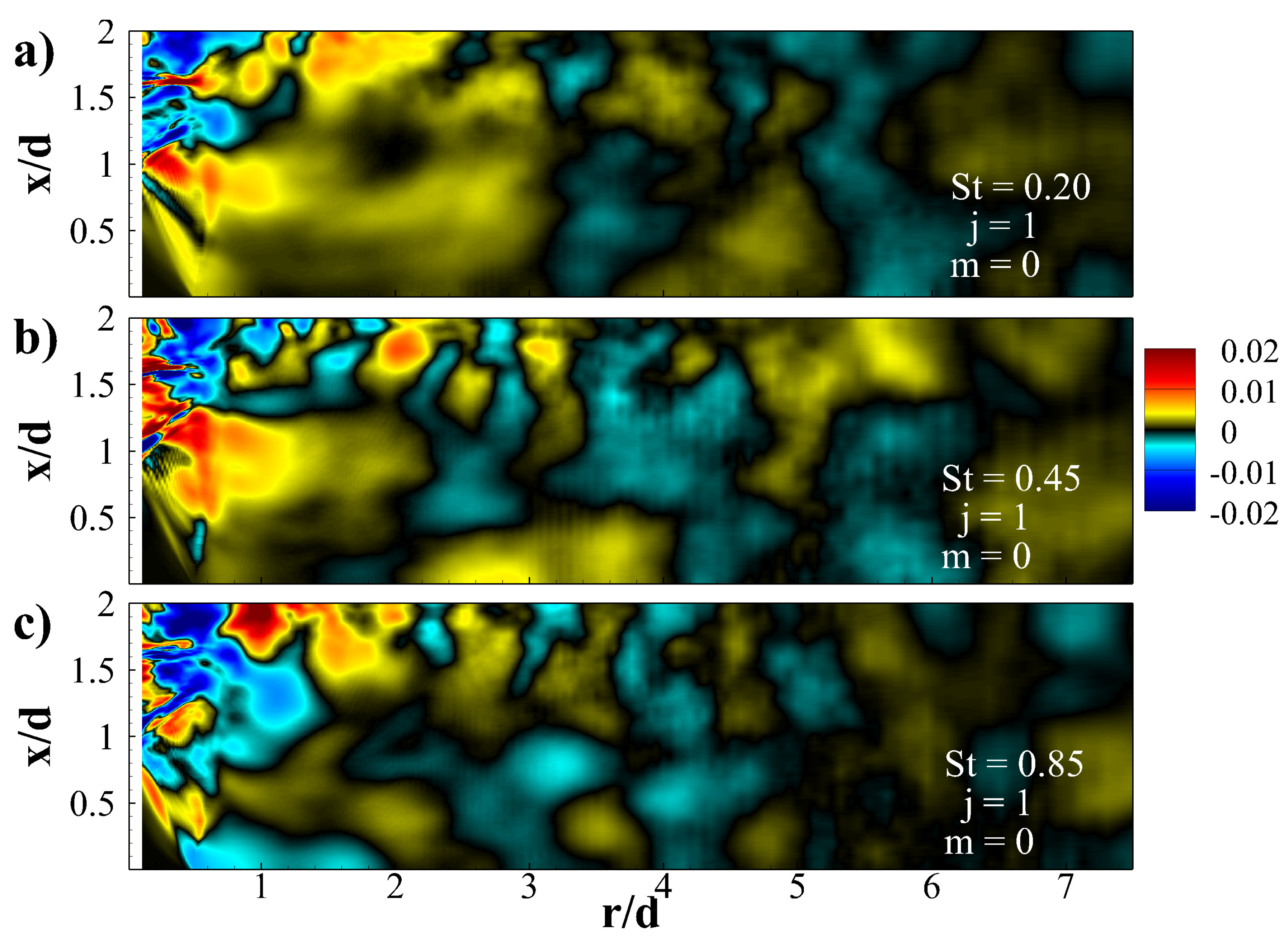
5.2. Spectral Proper Orthogonal Decomposition (SPOD) Modes
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Raman, G.; Srinivasan, K. The powered resonance tube: From Hartmann’s discovery to current active flow control applications. Prog. Aerosp. Sci. 2009, 45, 97–123. [Google Scholar] [CrossRef]
- Powell, A. The sound-producing oscillations of round underexpanded jets impinging on normal plates. J. Acoust. Soc. Am. 1988, 83, 515–533. [Google Scholar] [CrossRef]
- Henderson, B.; Powell, A. Experiments concerning tones produced by an axisymmetric choked jet impinging on flat plates. J. Sound Vib. 1993, 168, 307–326. [Google Scholar] [CrossRef]
- Mason-Smith, N.; Edgington-Mitchell, D.; Buchmann, N.A.; Honnery, D.R.; Soria, J. Shock structures and instabilities formed in an underexpanded jet impinging on to cylindrical sections. Shock Waves 2015, 25, 611–622. [Google Scholar] [CrossRef]
- Gojon, R.; Bogey, C. Flow Structure Oscillations and Tone Production in Underexpanded Impinging Round Jets. AIAA J. 2017, 55, 1792–1805. [Google Scholar] [CrossRef]
- Amili, O.; Edgington-Mitchell, D.; Honnery, D.; Soria, J. Interaction of a supersonic underexpanded jet with a flat plate. In Fluid-Structure-Sound Interactions and Control; Springer: Heidelberg/Berlin, Germany, 2016; pp. 247–251. [Google Scholar]
- Mitchell, D.M.; Honnery, D.R.; Soria, J. The visualization of the acoustic feedback loop in impinging underexpanded supersonic jet flows using ultra-high frame rate schlieren. J. Vis. 2012, 15, 333–341. [Google Scholar] [CrossRef]
- Gojon, R.; Bogey, C.; Marsden, O. Large-eddy simulation of underexpanded round jets impinging on a flat plate 4 to 9 radii downstream from the nozzle. In Proceedings of the 21st AIAA/CEAS Aeroacoustics Conference, AIAA Aviation Forum, Dallas, TX, USA, 22–26 June 2015; p. AIAA 2015-2210. [Google Scholar]
- Stegeman, P.; Ooi, A.; Soria, J. Proper Orthogonal Decomposition and Dynamic Mode Decomposition of Under-Expanded Free-Jets with Varying Nozzle Pressure Ratios. In Instability and Control of Massively Separated Flows; Springer: Heidelberg/Berlin, Germany, 2015; pp. 85–90. [Google Scholar]
- Edgington-Mitchell, D.; Oberleithner, K.; Honnery, D.R.; Soria, J. Coherent structure and sound production in the helical mode of a screeching axisymmetric jet. J. Fluid Mech. 2014, 748, 822–847. [Google Scholar] [CrossRef]
- Karami, S.; Stegeman, P.C.; Theofilis, V.; Schmid, P.J.; Soria, J. Linearised dynamics and non-modal instability analysis of an impinging under-expanded supersonic jet. J. Phys. Conf. Ser. 2018, 1001, 012019. [Google Scholar] [CrossRef]
- Henderson, B.; Bridges, J.; Wernet, M. An experimental study of the oscillatory flow structure of tone-producing supersonic impinging jets. J. Fluid Mech. 2005, 542, 115–137. [Google Scholar] [CrossRef]
- Towne, A.; Schmidt, O.T.; Colonius, T. Spectral proper orthogonal decomposition and its relationship to dynamic mode decomposition and resolvent analysis. J. Fluid Mech. 2017, 825, 1113–1152. [Google Scholar] [CrossRef]
- Schmid, P.J. Nonmodal stability theory. Annu. Rev. Fluid Mech. 2007, 39, 129–162. [Google Scholar] [CrossRef]
- Bagheri, S.; Schlatter, P.; Schmid, P.J.; Henningson, D.S. Global stability of a jet in crossflow. J. Fluid Mech. 2009, 624, 33–44. [Google Scholar] [CrossRef]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef]
- Schmidt, O.T.; Towne, A.; Colonius, T.; Cavalieri, A.V.; Jordan, P.; Brès, G.A. Wavepackets and trapped acoustic modes in a turbulent jet: coherent structure eduction and global stability. J. Fluid Mech. 2017, 825, 1153–1181. [Google Scholar] [CrossRef]
- Sieber, M.; Paschereit, C.O.; Oberleithner, K. Spectral proper orthogonal decomposition. J. Fluid Mech. 2016, 792, 798–828. [Google Scholar] [CrossRef]
- Bogey, C.; Gojon, R. Feedback loop and upwind-propagating waves in ideally expanded supersonic impinging round jets. J. Fluid Mech. 2017, 823, 562–591. [Google Scholar] [CrossRef]
- Krothapalli, A.; Rajkuperan, E.; Alvi, F.; Lourenco, L. Flow field and noise characteristics of a supersonic impinging jet. In Proceedings of the 4th AIAA/CEAS Aeroacoustics Conference, Toulouse, France, 2–4 June 1998; p. 2239. [Google Scholar]
- Weightman, J.L.; Amili, O.; Honnery, D.; Edgington-Mitchell, D.; Soria, J. On the Effects of Nozzle Lip Thickness on the Azimuthal Mode Selection of a Supersonic Impinging Flow. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. AIAA 2017-3031. [Google Scholar]
- Lumley, J.L. Stochastic Tools in Turbulence; Dover Publications: Mineola, NY, USA, 2007. [Google Scholar]
- Glauser, M.N.; Leib, S.J.; George, W.K. Coherent structures in the axisymmetric turbulent jet mixing layer. In Turbulent Shear Flows 5; Springer: Heidelberg/Berlin, Germany, 1987; pp. 134–145. [Google Scholar]
- Delville, J.; Ukeiley, L.; Cordier, L.; Bonnet, J.; Glauser, M. Examination of large-scale structures in a turbulent plane mixing layer. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 1999, 391, 91–122. [Google Scholar] [CrossRef]
- Bodony, D.J.; Lele, S.K. On using large-eddy simulation for the prediction of noise from cold and heated turbulent jets. Phys. Fluids 2005, 17, 085103. [Google Scholar] [CrossRef]
- Kawai, S.; Lele, S.K. Large-eddy simulation of jet mixing in supersonic crossflows. AIAA J. 2010, 48, 2063–2083. [Google Scholar] [CrossRef]
- Lilly, D.K. A proposed modification of the Germano subgrid-scale closure method. Phys. Fluids A Fluid Dyn. 1992, 4, 633–635. [Google Scholar] [CrossRef]
- Martin, M.P.; Piomelli, U.; Candler, G.V. Subgrid-scale models for compressible Large Eddy Simulations. Theor. Comput. Fluid Dyn. 2000, 13, 361–376. [Google Scholar]
- Mohseni, K.; Colonius, T. Numerical treatment of polar coordinate singularities. J. Comput. Phys. 2000, 157, 787–795. [Google Scholar] [CrossRef]
- Bogey, C.; Marsden, O.; Bailly, C. Large-eddy simulation of the flow and acoustic fields of a Reynolds number 105 subsonic jet with tripped exit boundary layers. Phys. Fluids 2011, 23, 035104. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S.K. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Karami, S.; Hawkes, E.R.; Talei, M.; Chen, J.H. Stabilisation mechanisms in a turbulent lifted slot-jet flame at a low lifted height. J. Fluid Mech. 2015, 777, 633–689. [Google Scholar] [CrossRef]
- Mani, A. Analysis and optimization of numerical sponge layers as a nonreflective boundary treatment. J. Comput. Phys. 2012, 231, 704–716. [Google Scholar] [CrossRef]
- Liu, J.; Kaplan, C.R.; Oran, E.S. A Brief Note on Implementing Boundary Conditions at a Solid Wall Using the FCT Algorithm; Technical Report; Naval Research Lab: Washington, DC, USA, 2006. [Google Scholar]
- Ducros, F.; Ferrand, V.; Nicoud, F.; Weber, C.; Darracq, D.; Gacherieu, C.; Poinsot, T. Large-eddy simulation of the shock/turbulence interaction. J. Comput. Phys. 1999, 152, 517–549. [Google Scholar] [CrossRef]
- Lo, S.C.; Aikens, K.; Blaisdell, G.; Lyrintzis, A. Numerical investigation of 3-D supersonic jet flows using large-eddy simulation. Int. J. Aeroacoust. 2012, 11, 783–812. [Google Scholar] [CrossRef]
- Larsson, J.; Lele, S.; Moin, P. Effect of Numerical Dissipation on the Predicted Spectra For Compressible Turbulence; Annual Research Briefs 2007; Center for Turbulence Research: Stanford, CA, USA, 2007; pp. 47–57. [Google Scholar]
- Kennedy, C.A.; Carpenter, M.H. Several new numerical methods for compressible shear-layer simulations. Appl. Numer. Math. 1994, 14, 397–433. [Google Scholar] [CrossRef]
- Kennedy, C.A.; Carpenter, M.H.; Lewis, R.M. Low-storage, explicit Runge–Kutta schemes for the compressible Navier–Stokes equations. Appl. Numer. Math. 2000, 35, 177–219. [Google Scholar] [CrossRef]
- Stegeman, P.C.; Pérez, J.M.; Soria, J.; Theofilis, V. Inception and evolution of coherent structures in under-expanded supersonic jets. J. Phys. Conf. Ser. 2016, 708, 012015. [Google Scholar] [CrossRef]
- Stegeman, P.C.; Soria, J.; Ooi, A. Interaction of Shear Layer Coherent Structures and the Stand-Off Shock of an Under-Expanded Circular Impinging Jet. In Fluid-Structure-Sound Interactions and Control; Springer: Heidelberg/Berlin, Germany, 2016; pp. 241–245. [Google Scholar]
- Stegeman, P.; Soria, J.; Ooi, A. Dynamic Mode Decomposition of Near Nozzle Instabilities in Large-Eddy Simulations of Under-Expanded Circular Jets. In Proceedings of the 19th Australasian Fluid Mechanics Conference, Melbourne, Australia, 8–11 December 2014. [Google Scholar]
- Sirovich, L. Turbulence and the dynamics of coherent structures. I. Coherent structures. Quart. Appl. Math. 1987, 45, 561–571. [Google Scholar] [CrossRef]
- Gordeyev, S.V.; Thomas, F.O. Coherent structure in the turbulent planar jet. Part 1. Extraction of proper orthogonal decomposition eigenmodes and their self-similarity. J. Fluid Mech. 2000, 414, 145–194. [Google Scholar] [CrossRef]
- Citriniti, J.; George, W.K. Reconstruction of the global velocity field in the axisymmetric mixing layer utilizing the proper orthogonal decomposition. J. Fluid Mech. 2000, 418, 137–166. [Google Scholar] [CrossRef]
- Markesteijn, A.P.; Semiletov, V.; Karabasov, S.A.; Tan, D.J.; Wong, M.; Honnery, D.; Edgington-Mitchell, D. Supersonic Jet Noise: An Investigation into Noise Generation Mechanisms using Large Eddy Simulation and High-Resolution PIV Data. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017; p. AIAA 2017-3029. [Google Scholar]
- Edgington-Mitchell, D.; Honnery, D.R.; Soria, J. The underexpanded jet Mach disk and its associated shear layer. Phys. Fluids 2014, 26, 1578. [Google Scholar] [CrossRef]
- Dauptain, A.; Cuenot, B.; Gicquel, L.Y.M. Large-eddy simulation of stable supersonic jet impinging on flat plate. AIAA J. 2010, 48, 2325–2338. [Google Scholar] [CrossRef]
- Ho, C.M.; Nosseir, N.S. Dynamics of an impinging jet. Part 1. The feedback phenomenon. J. Fluid Mech. 1981, 105, 119–142. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Ahuja, K.K. Theoretical model of discrete tone generation by impinging jets. J. Fluid Mech. 1990, 214, 67–87. [Google Scholar] [CrossRef]
- Weightman, J.; Amili, O.; Honnery, D.; Edgington-Mitchell, D.; Soria, J. Effects of nozzle lip thickness on the global modes of an impinging supersonic jet. In Proceedings of the Australian Conference on Laser Diagnostics in Fluid Mechanics and Combustion, Melbourne, Australia, 1 December 2015; pp. 167–172. [Google Scholar]
- Gudmundsson, K.; Colonius, T. Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 2011, 689, 97–128. [Google Scholar] [CrossRef]
- Husain, H.S.; Hussain, F. Experiments on subharmonic resonance in a shear layer. J. Fluid Mech. 1995, 304, 343–372. [Google Scholar] [CrossRef]
- Arbey, H.; Williams, J.F. Active cancellation of pure tones in an excited jet. J. Fluid Mech. 1984, 149, 445–454. [Google Scholar] [CrossRef]
- Vejrazka, J.; Tihon, J.; Marty, P.; Sobolik, V. Effect of an external excitation on the flow structure in a circular impinging jet. Phys. Fluids 2005, 17, 105102. [Google Scholar] [CrossRef]
- Schmidt, O.T.; Towne, A.; Rigas, G.; Colonius, T.; Brès, G.A. Spectral analysis of jet turbulence. arXiv 2017, arXiv:1711.06296. [Google Scholar]
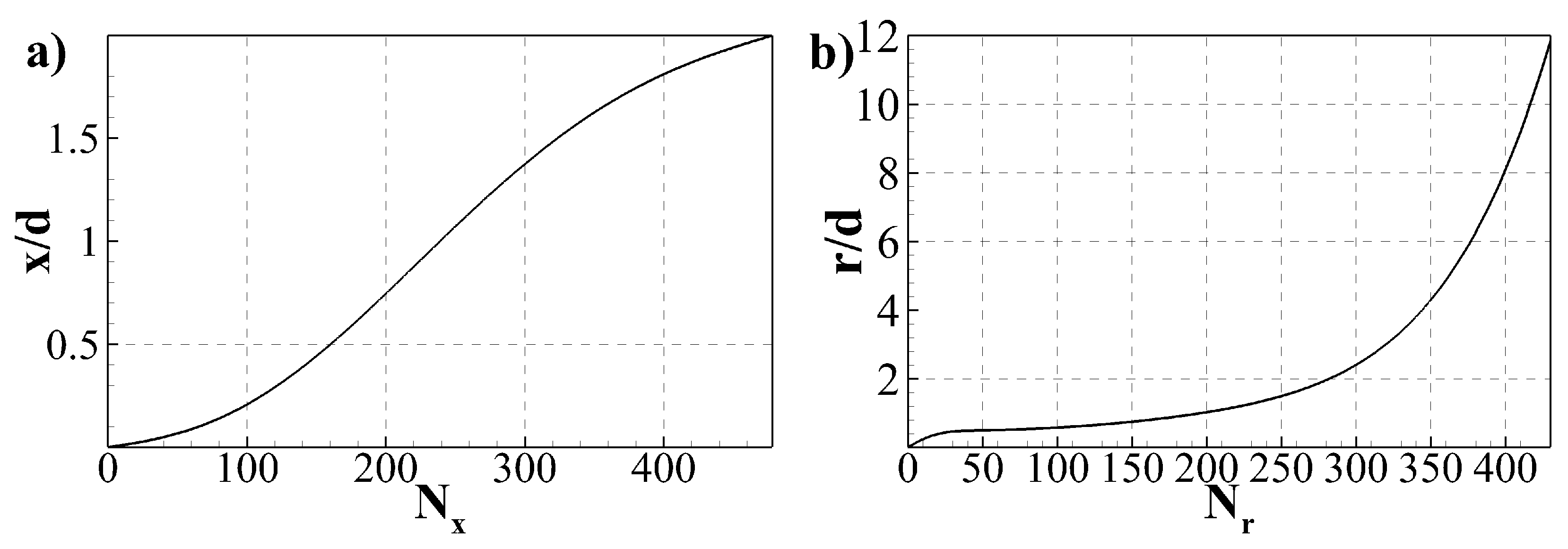
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karami, S.; Soria, J. Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD). Aerospace 2018, 5, 73. https://doi.org/10.3390/aerospace5030073
Karami S, Soria J. Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD). Aerospace. 2018; 5(3):73. https://doi.org/10.3390/aerospace5030073
Chicago/Turabian StyleKarami, Shahram, and Julio Soria. 2018. "Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD)" Aerospace 5, no. 3: 73. https://doi.org/10.3390/aerospace5030073
APA StyleKarami, S., & Soria, J. (2018). Analysis of Coherent Structures in an Under-Expanded Supersonic Impinging Jet Using Spectral Proper Orthogonal Decomposition (SPOD). Aerospace, 5(3), 73. https://doi.org/10.3390/aerospace5030073





