1. Introduction
In a highly publicized event on 6 February 2018, SpaceX successfully launched a Falcon Heavy carrying a Tesla Roadster, pushing the car and the upper stage out of Earth’s gravitational grip and into orbit around the Sun. The Tesla is now drifting on a Mars-crossing orbit and it is not expected to make any further course corrections. The Roadster was used as a mass simulator and had no scientific instruments on board other than three cameras which transmitted live video back to Earth for several hours after the launch.
In this paper, we investigate the fate of the Tesla over the next few tens of million years. The Roadster bears many similarities to Near-Earth Asteroids (NEAs), which diffuse through the inner Solar System chaotically through (i) repeated close encounters with the terrestrial planets, and (ii) the effects of mean-motion and secular resonances. Initially, NEAs reach their orbits from the more distant main belt via strong resonances (such as the secular
resonance or the strong 3:1 mean-motion resonance with Jupiter). When entering these escape routes, many NEAs are driven onto nearly-radial orbits that plunge into the Sun (e.g., [
1]), with only a small fraction of them managing to decouple from this fate through close encounters with terrestrial planets. These survivors then typically spend millions of years scattering between the terrestrial planets before eventually colliding with one of them or impacting the Sun (or possibly physically disintegrating at small heliocentric distances; e.g., [
2]). Because of the terrestrial planets’ minute size relative to the size of the inner Solar System, the frequency of impacts onto these bodies is small. Even the largest of them, the Earth, has only a slightly more than 2% chance to be hit by any of the objects entering the NEA population (e.g., [
3,
4]).
The situation of the Tesla is slightly different. On one hand, the Tesla is currently far from the strong resonances in the main belt that can drive bodies onto Sun-grazing paths, and is therefore analogous to the above-mentioned long-lived NEAs. On the other hand, the initial Tesla orbit grazes that of the Earth, so one might expect an initial period with enhanced collision probabilities with the Earth before it is randomized onto a more NEA-like trajectory. It is therefore unclear whether the Tesla is likely to diffuse to distant, strong resonances and meet the same fate as the wider NEA population, or whether it would first strike one of the terrestrial planets. Perhaps a more direct analogy is the fate of impact ejecta from the Earth and Moon, which was considered by Gladman et al. [
5] and Bottke et al. [
6]. Both studies found substantial collision probabilities with the terrestrial planets, but their ejecta have different ejection velocities from the Earth–Moon system than the Tesla. Both studies found that larger ejection velocities lead to fewer Earth impacts due to the decrease in gravitational focusing. Given the peculiar initial conditions and even stranger object, it therefore remains an interesting question to probe the dynamics and eventual fate of the Tesla.
Because the Tesla was launched from Earth, the two objects have crossing orbits and will repeatedly undergo close encounters. While the impact probability of such Earth-crossing objects can be estimated precisely on human timescales (e.g., [
7,
8]), the Roadster’s chaotic orbit can not be accurately predicted beyond the first several encounters (beyond the next few centuries). As is typical in chaotic systems, we can therefore only draw conclusions in a statistical sense from long-term orbital integrations of a suite of nearby initial conditions.
We describe our numerical setup in
Section 2. The results of short-term integrations over 1000 years are presented in
Section 3. Long-term integrations spanning many millions of years are discussed in
Section 4 and we determine collision probabilities over these timescales in
Section 5. We summarize our results in
Section 6.
2. Numerical Setup and Yarkovsky Effect
We use the
REBOUND integrator package [
9] to query JPL’s NASA Horizons database for the initial ephemerides of all Solar System planets and the Tesla. As initial conditions, we use the NASA JPL solution #7 for the Tesla, generated on February 15th. We start the integrations at a time at which the Tesla is not expected to make any more course corrections. The integrations were carried out in the centre-of-mass frame of the Solar System and we use the high order Gauß-Radau
IAS15 integrator [
10]. This integrator uses an adaptive timestep and can handle frequent close encounters with high accuracy. The error in the conservation of energy is close to the double floating point precision limit. Using an even higher precision integrator would not further improve the results because, as we show below, nearby trajectories diverge due to close encounters, i.e., not due to numerical precision.
In our numerical model, we do not integrate the orbit of the Moon and instead use a single particle with the combined mass of the Earth and the Moon. We incorporate the effects of general relativity by adding an additional component to the Sun’s gravitational potential that yields the approximate apsidal precession rates of the planets [
11]. Ignoring this precession can lead to qualitatively very different results in the long-term evolution of the Solar System [
12].
Given the object’s comparatively high surface-area to mass ratio, one might wonder whether non-gravitational forces could play an important role. In particular, the Yarkovsky effect caused by delayed thermal emission as the object rotates causes a secular drift in the semi-major axis. Assuming a cylindrical shape with diameter ∼4 m and length ∼15 m for the combined second stage and Tesla, a useful point of comparison is 2009 BD, the smallest asteroid (about 4 m across) with a measured Yarkovsky drift of
au Myr
(e.g., [
13]). The second stage is made of aluminum-lithium alloy. If we assume a nominal (
http://www.matweb.com/search/datasheet.aspx?matguid=a79a000ba9314c8d90fe75dc76efcc8a&ckck=1) density for this surface material of ∼3000 kg m
, a heat capacity of ∼1000 J kg
K
, and a thermal conductivity of ∼100 W m
K
, then the thermal inertia is of order
in SI units. This is roughly an order of magnitude larger than might be expected for 2009 BD (e.g., [
14]). Given that the Tesla rotates quickly compared to the thermal re-emission timescale with a rotation period of
min (as reported by J. J. Hermes, UNC,
https://twitter.com/jotajotahermes/status/962545252446932993), the body is in the limit of large thermal parameter
, so the Yarkovsky drift scales inversely with the thermal inertia (e.g., [
15]). However, the effect also scales inversely with the bulk density of the body. Assuming a total mass of ∼10,000 kg for the combined second stage and Tesla, this yields a density of ∼100 kg m
, an order of magnitude lower than typical asteroids. Thus, the effect of a larger thermal inertia is offset by the reduced density. Thus, a reasonable estimate for the strength of the Yarkovsky effect is ∼0.05 au Myr
, i.e., close to that of 2009 BD.
We incorporate the Yarkovsky effect in our simulations as an additional transverse acceleration
, with
r the heliocentric distance, which changes the semi-major axis over long timescales (e.g., [
16]). In particular, we studied in detail the nominal value of
au Myr
estimated above. However, we also tried out a wide variety of
values, including the reference solution with
, and found no effect on the evolution over the timescales we studied in this paper. This is because the Yarkovsky drift is overwhelmed by the random walk in semi-major axis from close encounters. As an example, over the 1000 yrs probed in
Figure 1, one would expect a Yarkovsky drift of at most ∼5
au, which is negligible compared to the ∼0.05–0.1 au diffusion in semi-major axis from close approaches over the same timescale. Even when effects from softer gravitational tugs due to Mars or Mercury are considered, the Yarkovsky effect should still be safely negligible. Our tests thus directly verify this often-quoted assumption in the NEA population models (e.g., [
2,
3,
17]).
Therefore, without loss of generality, we present the simulations with in the following sections. All results from our other runs are the same within statistical uncertainties.
3. Evolution over the Next Few Hundred Years
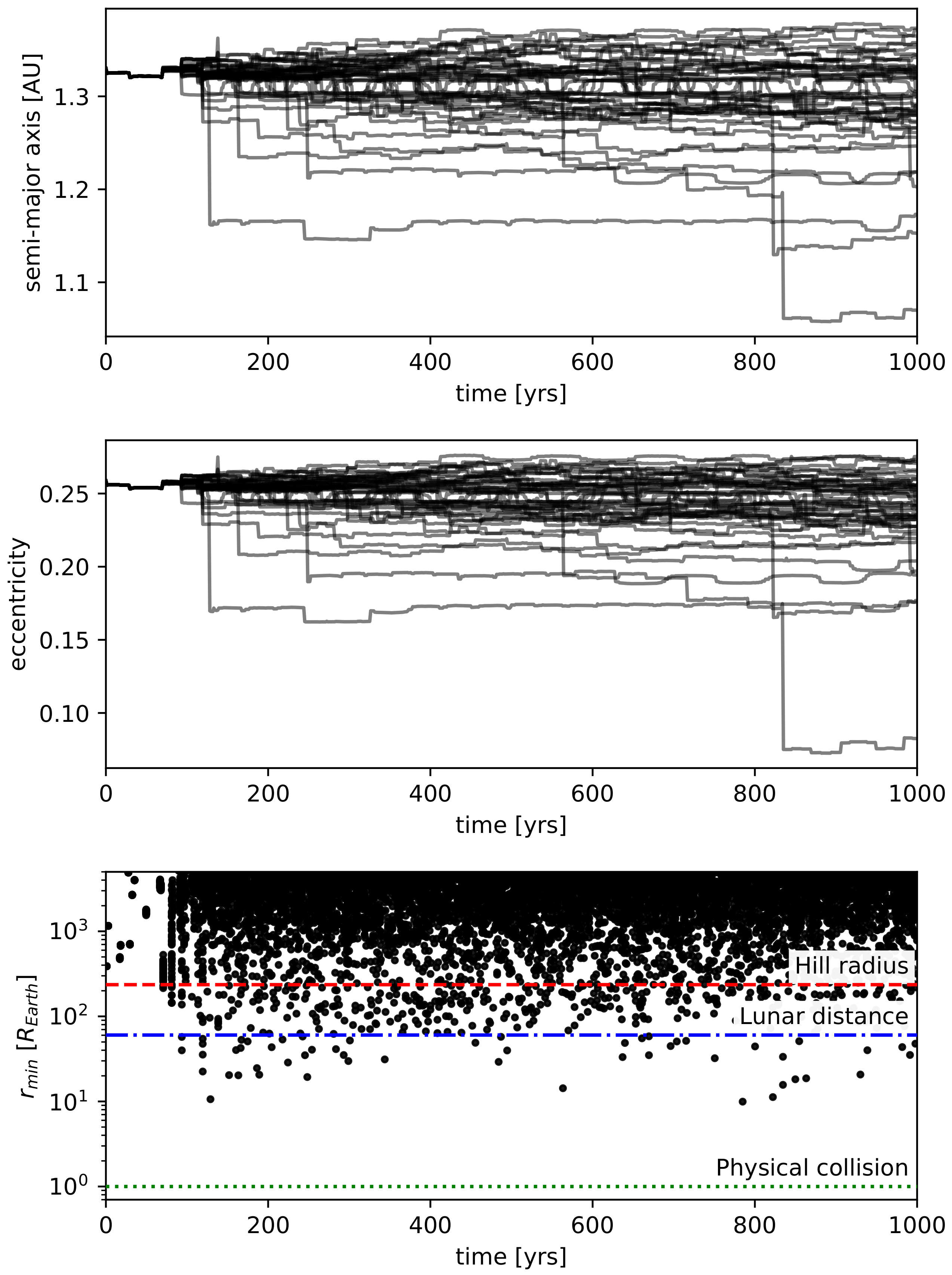
To obtain an initial insight into the Roadster dynamics, we first integrate the evolution of 48 realizations of its orbit over the next 1000 years. The initial velocity of the Tesla is perturbed by a random factor of the order of
to evaluate how chaotic the orbital evolution is. This factor is comparable to the uncertainty in the orbital parameters we used for the simulations. Although orbital parameters obtained at a later time will have smaller uncertainties, we do not expect a qualitative difference beyond the first few close encounters. We plot the semi-major axis, the eccentricity, and the close approach distance to Earth for all 48 orbits in
Figure 1.
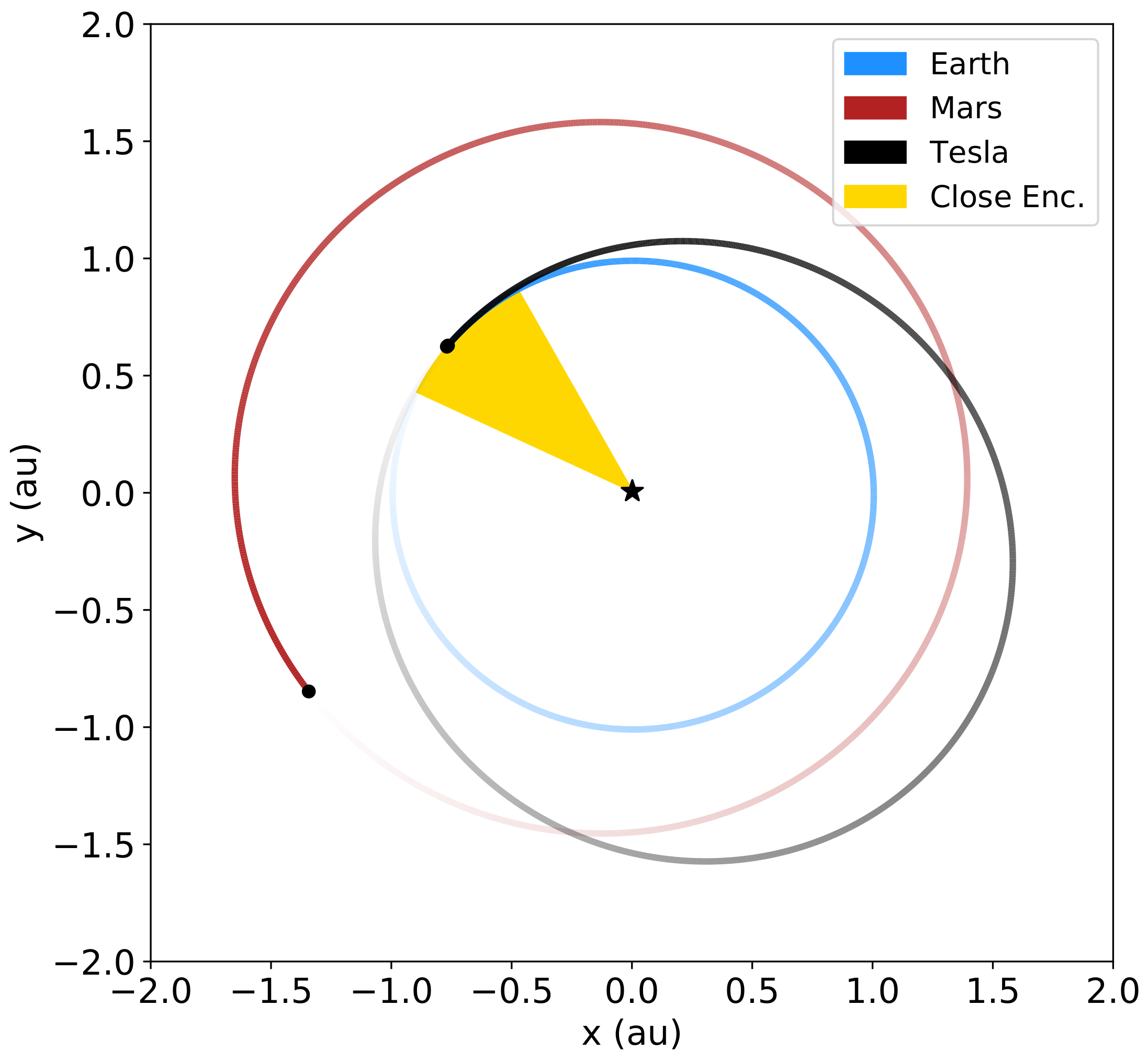
Given that the Tesla was launched from Earth, the two objects have intersecting orbits and repeatedly undergo close encounters. The bodies reach the same orbital longitude on their synodic timescale of ∼2.8 yrs. Of course, the majority of these conjunctions will happen along directions where the two orbits do not cross. We therefore look for conjunctions in an inertial direction where the two orbits come within about one Hill sphere of crossing. Because the Roadster’s initial orbit lies approximately tangent to that of the Earth at the former’s perihelion, encounters within one Hill sphere of the Earth are possible over an enhanced range of orbital phases (yellow wedge in
Figure 2).
In particular, expanding around the Roadster’s perihelion so that
,
where we have used that
, with
and
as the orbital radii of the Tesla and Earth from the Sun, respectively, and
a,
e and
f are the Roadster’s orbital semi-major axis, eccentricity, and true anomaly, respectively. Given
,
au and Earth’s Hill radius of ≈0.01 au, the Tesla can reach within a Hill sphere within ±0.3 rad of perihelion, or over ≈10% of its orbit (yellow wedge in
Figure 2). Roughly every tenth conjunction will therefore result in a close encounter, yielding
yrs, approximately matching the results in
Figure 1.
As a first approximation, one can view the orbit of the Tesla as a sequence of patched conic sections; between encounters, the Roadster follows a Keplerian orbit around the Sun, while, when it enters the Earth’s Hill sphere, it follows a hyperbolic trajectory around the planet that “ejects” it onto a modified heliocentric orbit. Because the close encounters happen initially at perihelion and the new Keplerian orbit must still pass through the location of the encounter, the changes in the semi-major axis and eccentricity are strongly correlated (compare the top and middle panel of
Figure 1). Typical individual encounters are strong enough to change the orbital elements by a few percent at a time. The cumulative effect of successive encounters can be qualitatively understood as a random walk.
After less than a hundred years, the trajectories, initially perturbed only by , diverge quickly after a particular close encounter with Earth. In our sample of 48 short-term simulations, we do not observe any physical collisions with the Earth over the next 1000 years. We note however that we do not attempt to give an accurate probability for this kind of event. With more accurate ephemerides, it will be possible to calculate this probability much more accurately. Here, we simply point out the sensitivity of the subsequent orbital evolution on the precise impact parameter of this encounter. The sensitivity for this and all subsequent encounters will make it impossible to accurately predict the orbital evolution for more than a few hundred years, even with highly accurate ephemerides.
We can, however, draw conclusions about the statistical properties of the ensemble of simulations. This kind of analysis is common in studies of chaotic systems such as our Solar System (e.g., [
12]).
4. Long-Term Evolution
We now turn to the long-term dynamical evolution for which we integrate 240 realizations of the Tesla for 15 Myr into the future. Each realization is initialized in the same way as the short-term integrations. We choose to look at 240 realizations so that we can estimate the probabilities for the most likely outcomes accurately. We might miss highly unlikely outcomes with probabilities of less than 1%.
Figure 3 shows the evolution of the objects in semi-major axis and eccentricity space. The star shows the initial orbit. The colour corresponds to time. The solid black curves indicate the set of orbits that has an aphelion or perihelion that intersects the orbit of Mercury, Venus, Earth, or Mars.
As we have seen in
Section 3, the short-term evolution is dominated by close encounters with the Earth. We can see in
Figure 3 that the phase space region enclosed by the aphelion and perihelion lines of Earth remains highly populated even on a million year timescale. Thus, the orbit remains in a region that is dominated by close encounters with the Earth. At later times, interactions with Venus become more frequent. Close encounters with Mars are also possible, although occur less frequently. While the region bounded by the lines corresponding to Mercury is almost completely empty, one would expect it to become populated on longer timescales.
Over long timescales, one can also note horizontal tracks in
Figure 3 that are outside the phase space regions where close encounters with any of the planets are possible. This evolution in eccentricity at constant semi-major axis is due to temporary sticking to the network of weak, mean-motion resonances with terrestrial planets (see [
18]). Additionally, numerous secular resonances crossing the planet-crossing orbital space (e.g., [
18,
19,
20,
21]) make the eccentricities and inclinations of the Roadster clones to slowly increase. Overall, Roadster clone orbits undergo vigorous chaotic mixing in the NEA space having no chance to hide from planetary or solar impacts on very long timescales.
5. Collision Probabilities
As a simplest estimate of the collision time with Earth, we can imagine encounters occurring every
(
Section 3), each of which has a collision probability given by the planet’s cross-sectional area relative to that of the Hill sphere. This yields a collision time of ∼1.6 Myr. However, the above grossly underestimates the collision time because the Tesla can, at least temporarily, diffuse into configurations that do not cross the Earth or even any of the terrestrial planets (see
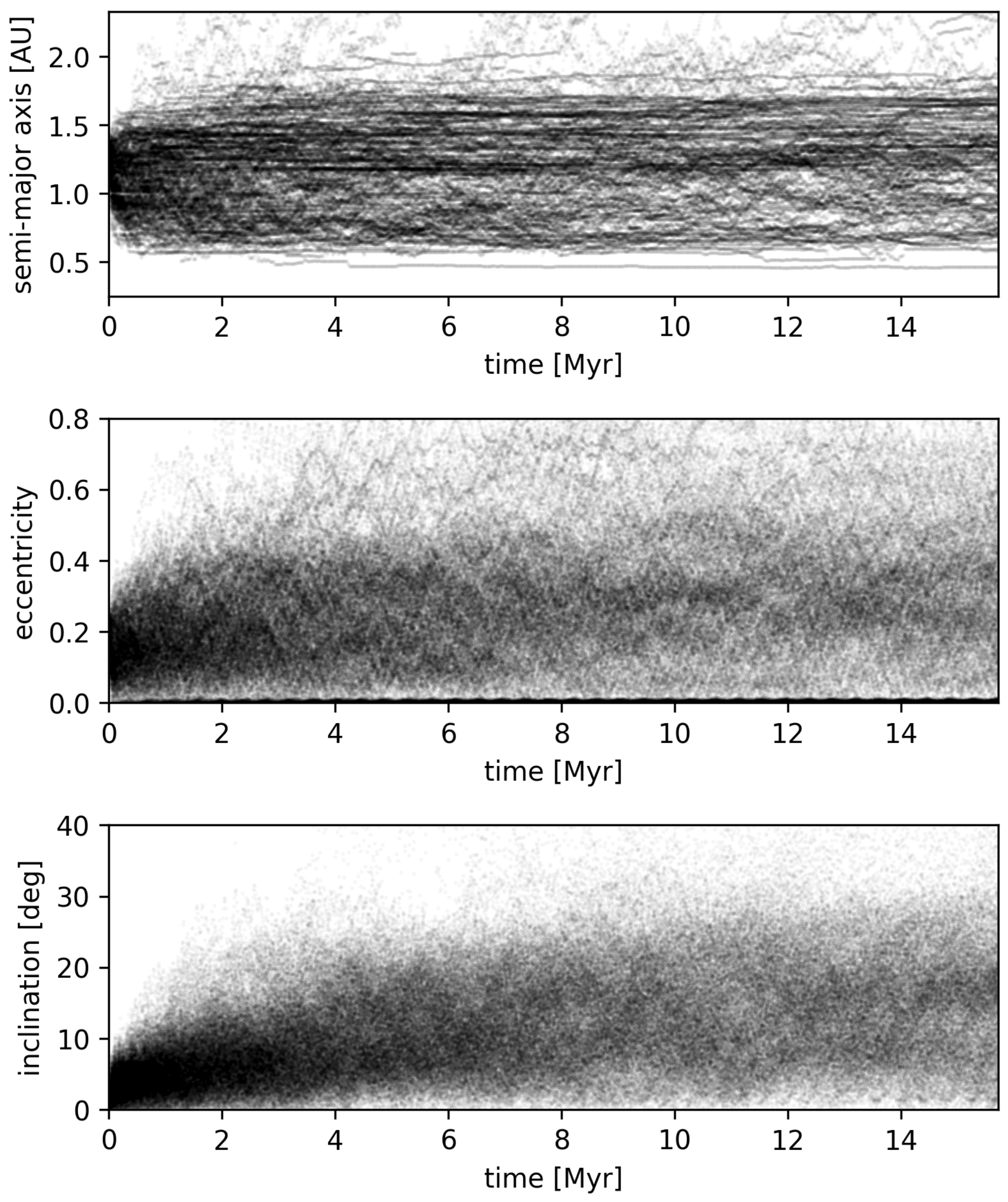
Figure 3). The Tesla orbits also spread to high eccentricities and inclinations that further increase the collision time (the growth in these parameters can be seen in the bottom panel of
Figure 4). Because of its chaotic orbital evolution, we determine collision timescales with the terrestrial planets using statisical results from the direct numerical integrations.
The top panel on
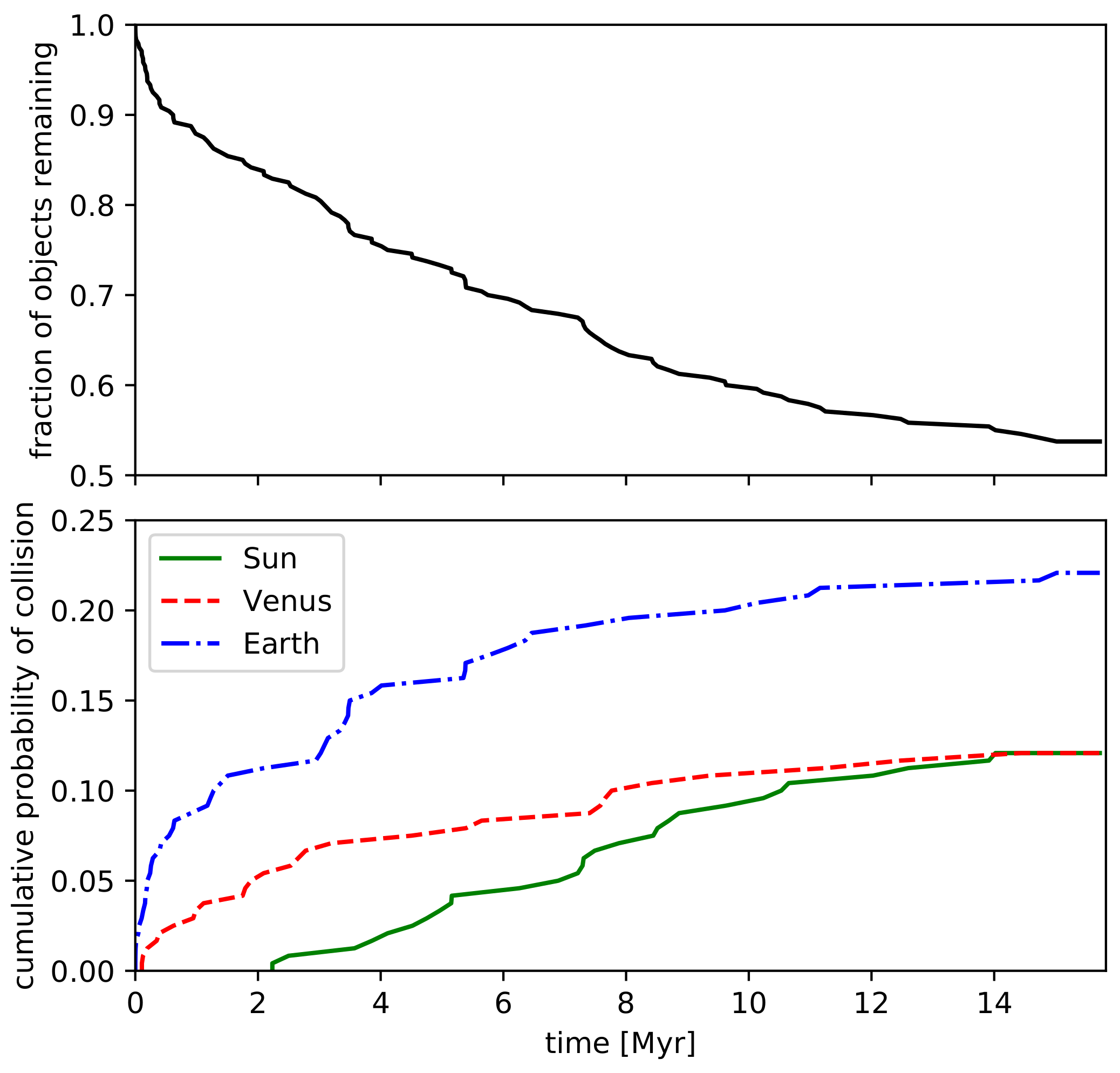
Figure 5 confirms that, after about one million years in our simulations, the decay curve of the Roadster realizations becomes shallower, reaching the 50% level at only ≈17 Myr (thus about ten times longer than estimated above). The bottom part of the same figure shows the observed collision frequency with all Solar System planets and the Sun for our long-term integrations. We find that, after 15 Myr, the probability of a collision with Earth and Venus has grown to ≈22% and ≈12%, respectively. Furthermore, we observed the first collision with the Sun after 2 Myr, reaching a collision probability of ≈12% after 15 Myr. Although there were several close encounters with Mars and Mercury in our simulations, none of them resulted in a physical collision. In some of our other runs, we sometimes do see rare impacts on Mars and Mercury. Given that we have a sample of 240 realizations, this is statistically consistent with the conclusion that at most a few percent of realization will impact Mars or Mercury.
These collision rates are smaller than the ≈50% impact probability over 1 Myr of lunar ejecta studied by [
5]. By contrast, our results are comparable to the estimated collision probabilities of ∼20% with the Earth within 1 Myr for the ejecta from giant impacts with the Earth in [
6]. We attribute this difference to the different ejection speeds, and therefore initial eccentricities, of the various objects. (Note that the characteristic ejection speeds considered by Gladman et al. [
5], i.e., 2.5–3.5 km s
, were smaller than the
km s
of the Tesla and the mean ejecta speeds considered by Bottke et al. [
6]. Additionally, the latter reference considered a more compact configuration of the giant planets, which complicates a direct comparison with our results.)
Only over very long timescales can the Tesla diffuse beyond 2 au and encounter strong resonances that send it into the Sun before the planets sweep it up.
Figure 4 shows the evolution of the various Tesla clones’ orbital semi-major axis, eccentricity and inclination. All Roadsters start at
au and the vast majority do not diffuse beyond 1.7 au over 15 Myr because most of the Earth-crossing phase space volume to diffuse into lies at lower semi-major axes, as can be seen in
Figure 3. As can be seen in
Figure 4, most orbits remain at inclinations of less than
in our integrations. We expect that the orbits that reach a high enough inclination will have longer lifetimes and are more likely to escape the terrestrial planet zone through resonant and secular interactions. This is confirmed in
Figure 5, where one can see that the rate of collisions with the Sun is roughly constant, whereas collisions with Earth and Venus taper off after a few million years.
6. Conclusions
In this paper, we have investigated the fate of the Tesla Roadster launched by SpaceX with their Falcon Heavy rocket on 6 February 2018. The Tesla is currently on an Earth and Mars crossing orbit. Its first close encounter that may come within a lunar distance of the Earth will occur within the next 100 years. On timescales significantly longer than a century, continued close encounters will render precise long-term predictions of the object’s chaotic orbit impossible.
However, using an ensemble of several hundred realizations, we were able to statistically determine the probability of the Tesla colliding with the Solar system planets on astronomical timescales. Although some of the orbits experience effects due to mean-motion and secular resonances criss-crossing the NEA space, the orbital evolution remains initially dominated by close encounters with the terrestrial planets, in particular Earth, Venus and Mars. About half of our 15 Myr integrations result in a collision with the Earth, Venus, and the Sun. Specifically, we numerically determined a collision probability of ≈22% and ≈12% with the Earth and Venus over this timescale, respectively. Overall, our results imply the dynamical half-life of the Tesla to be 15 Myr, similar to other NEAs decoupled from major escape routes from the main belt (e.g., [
3,
4]).
References