The Public Safety Zones around Small and Medium Airports
Abstract
:1. Introduction
2. Airport Risk Plans Adopted in Italy
- human presence restriction;
- identification of non-compatible land uses which could amplify accident consequences.
3. Methodology for Redefining Risk Plans
3.1. Theoretical Studies on Risk Assessment in the Surrounding Areas of the Italian Airports
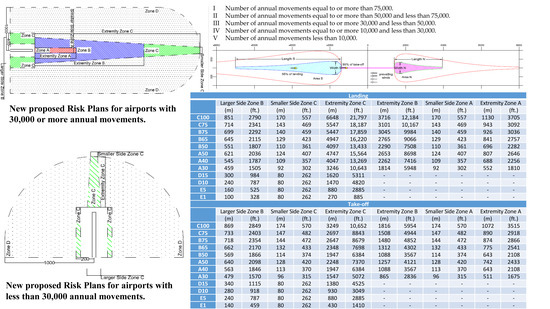
- I
- Number of annual movements equal to or more than 75,000.
- II
- Number of annual movements equal to or more than 50,000 and less than 75,000.
- III
- Number of annual movements equal to or more 30,000 and less than 50,000.
- IV
- Number of annual movements equal to or more 10,000 and less than 30,000.
- V
- Number of annual movements less than 10,000.
- N: total number of aircraft of class x;
- Movi: number of movements of the ith aircraft;
- MTOWW: weighted maximum take-off weight of the reference aircraft;
- MTOWi: maximum take-off weight of the ith aircraft;
- IRW: weighted accident rate of the reference aircraft;
- IRi: accident rate of the ith aircraft.
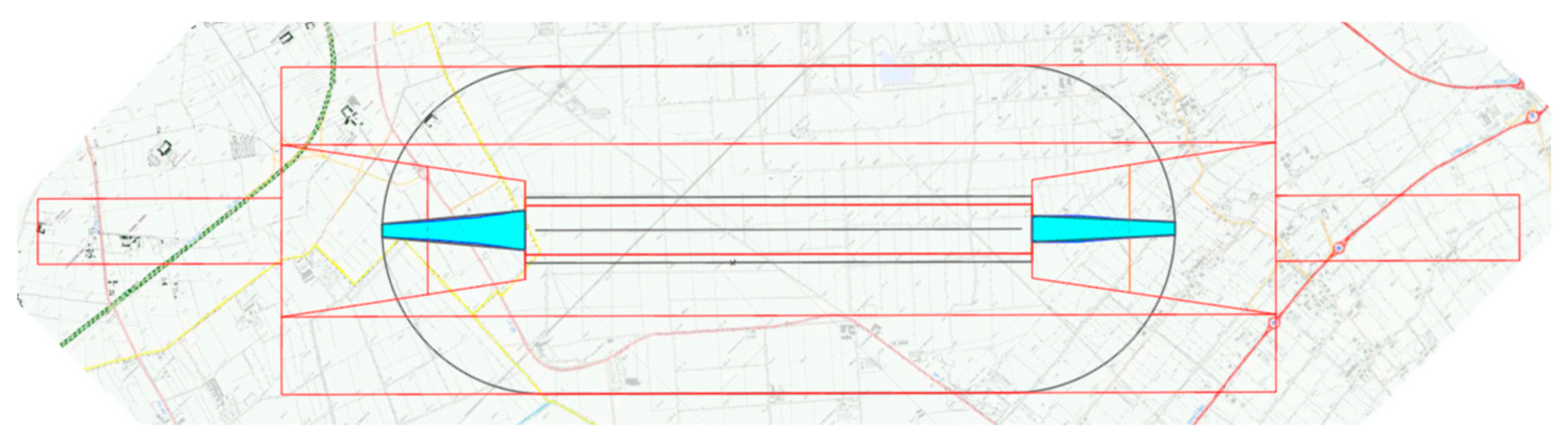
3.2. Definition of the Risk Plans according to the Risk Analysis
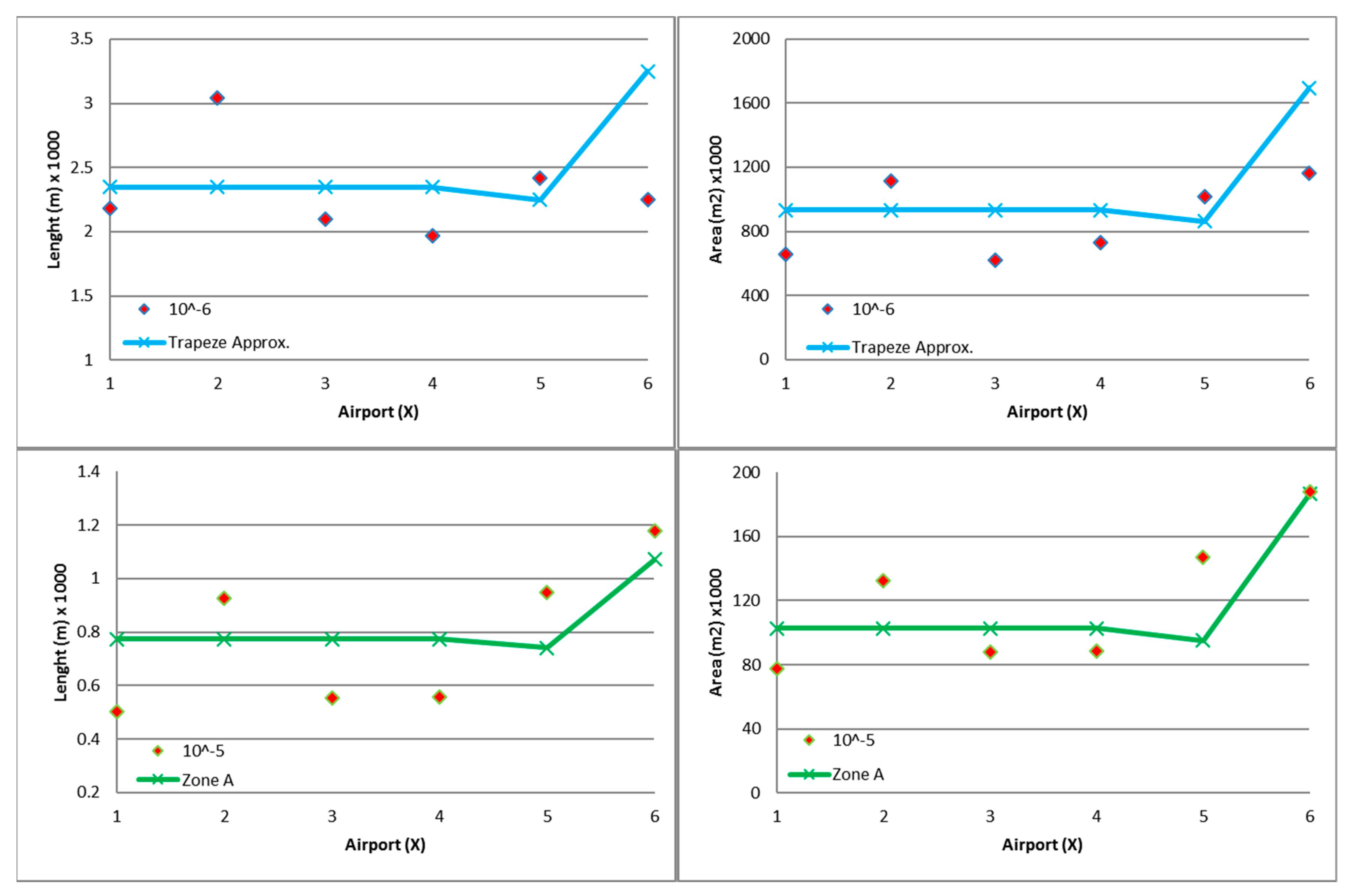
- variable sizes of PSZs as a function of annual movements;
- new shapes and dimensions for PSZs.
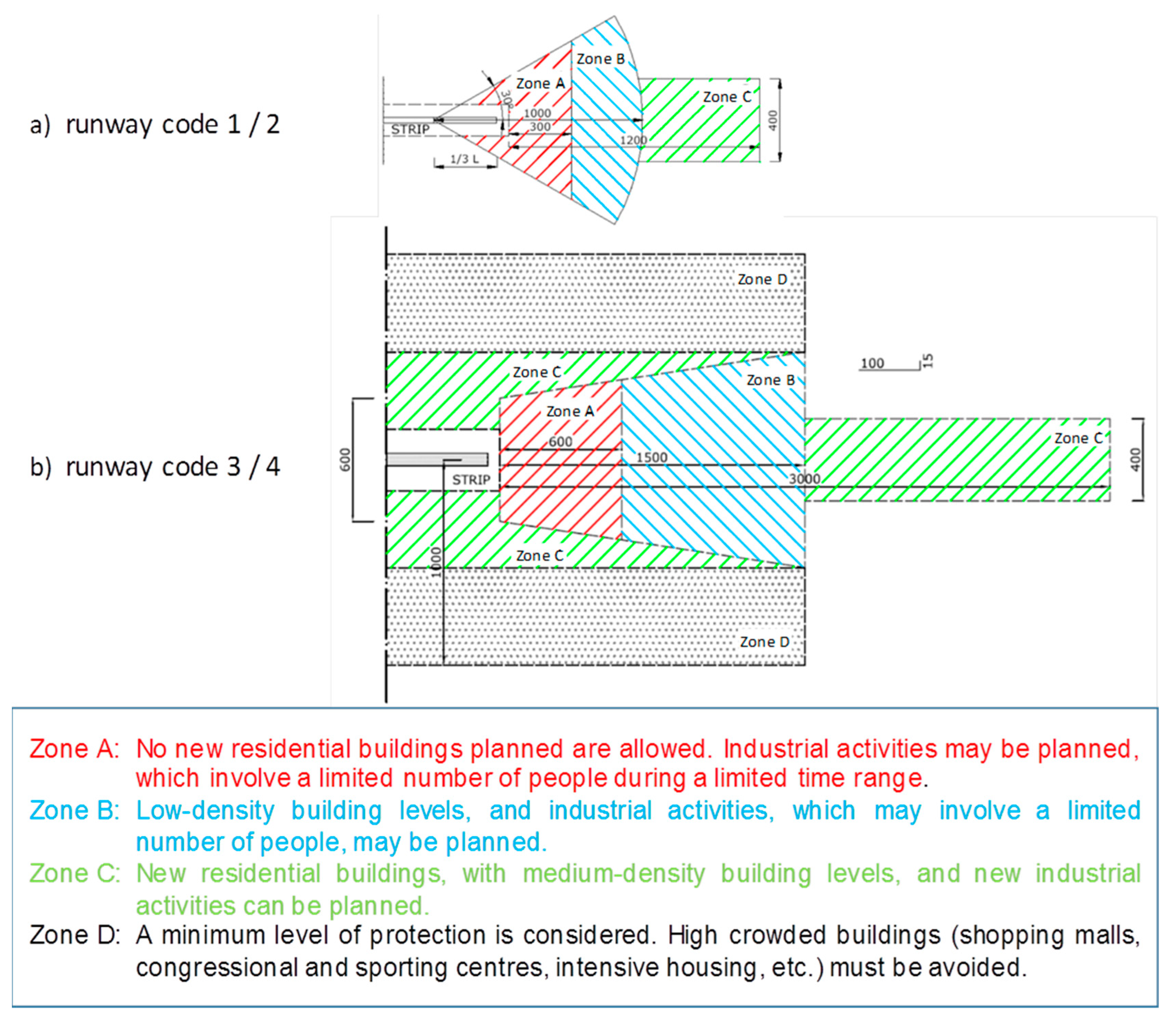
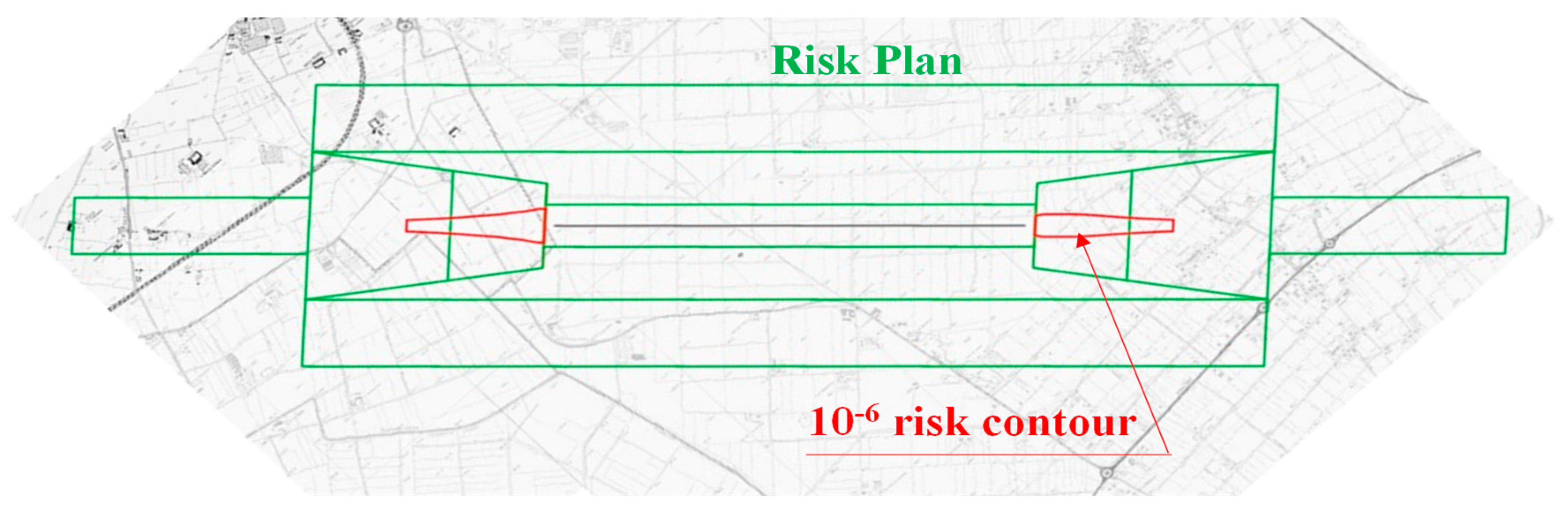
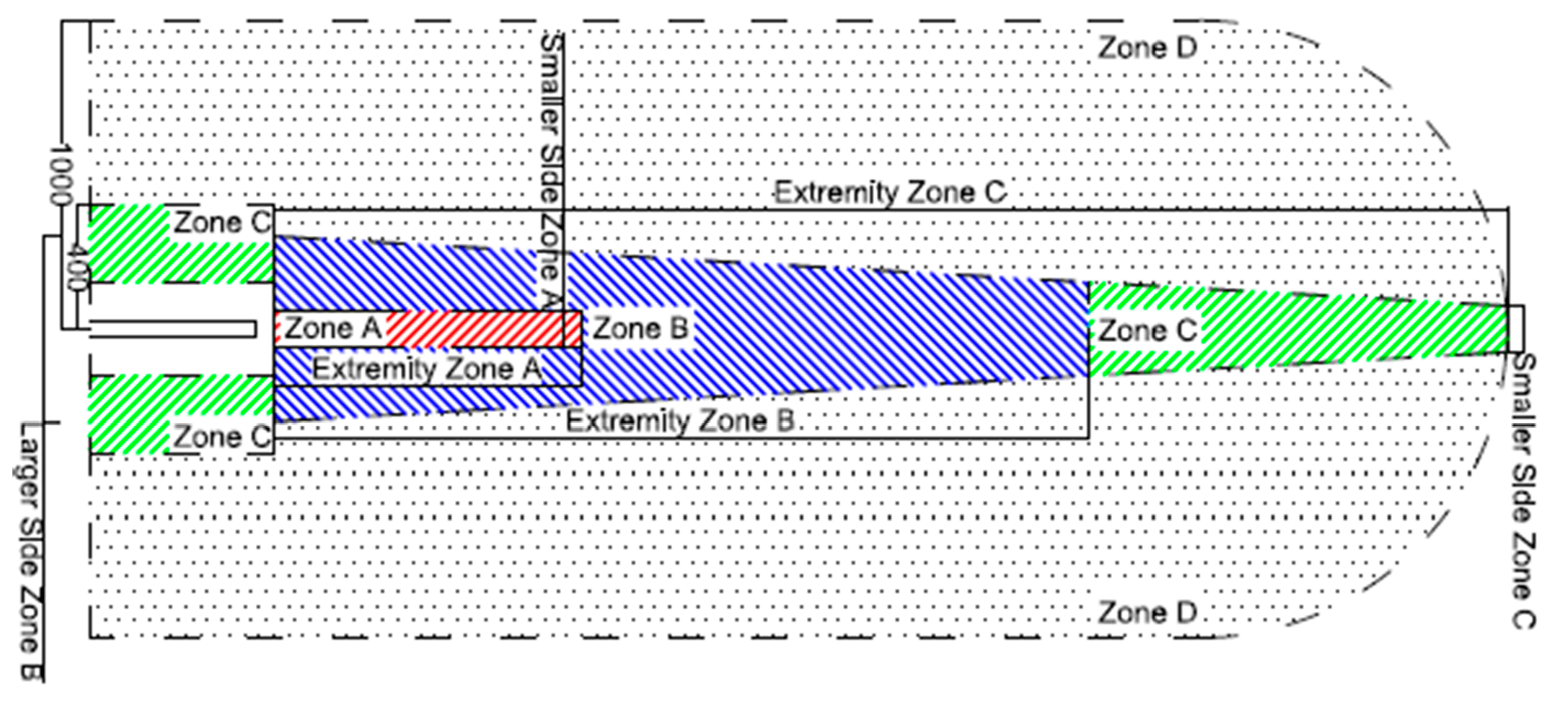
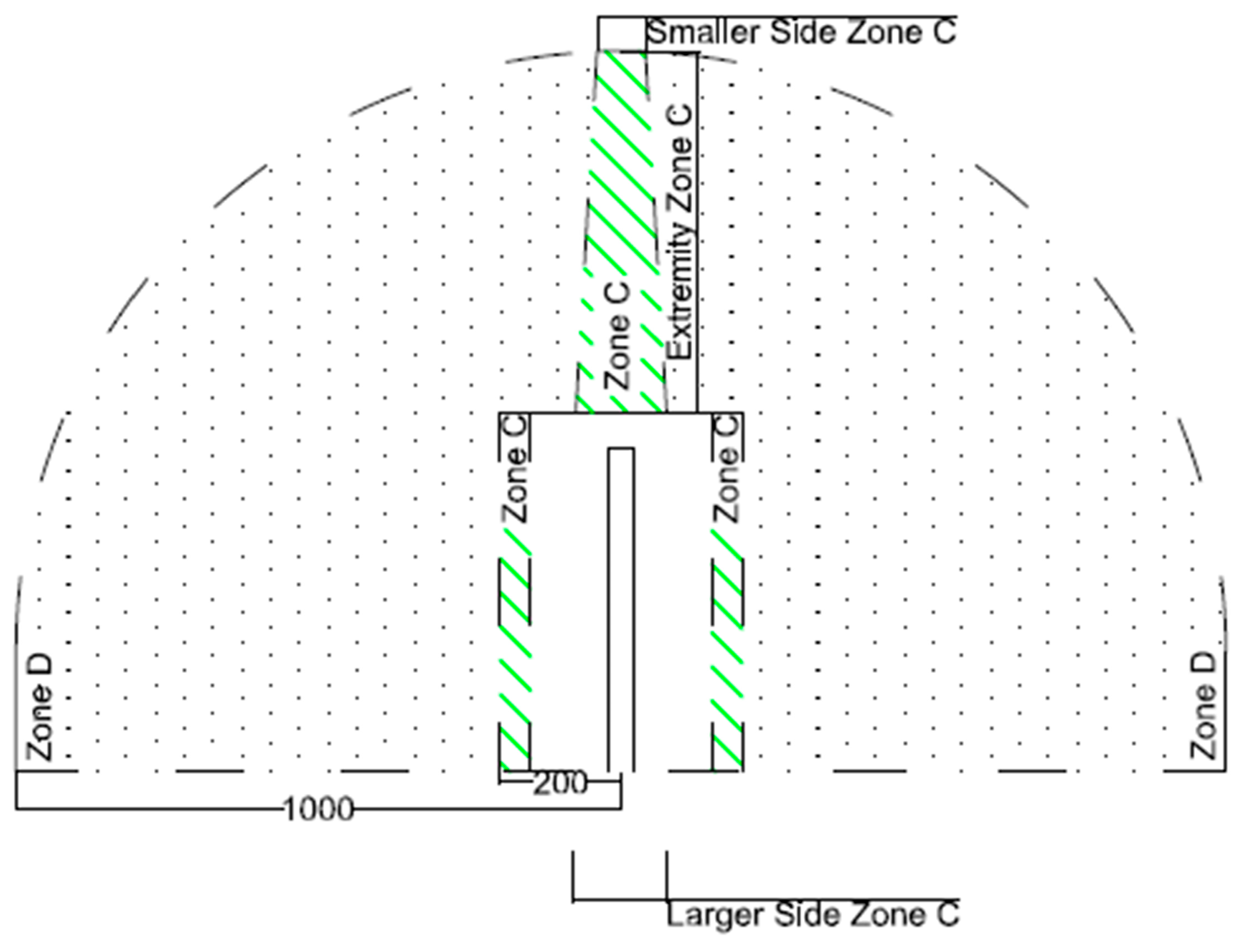
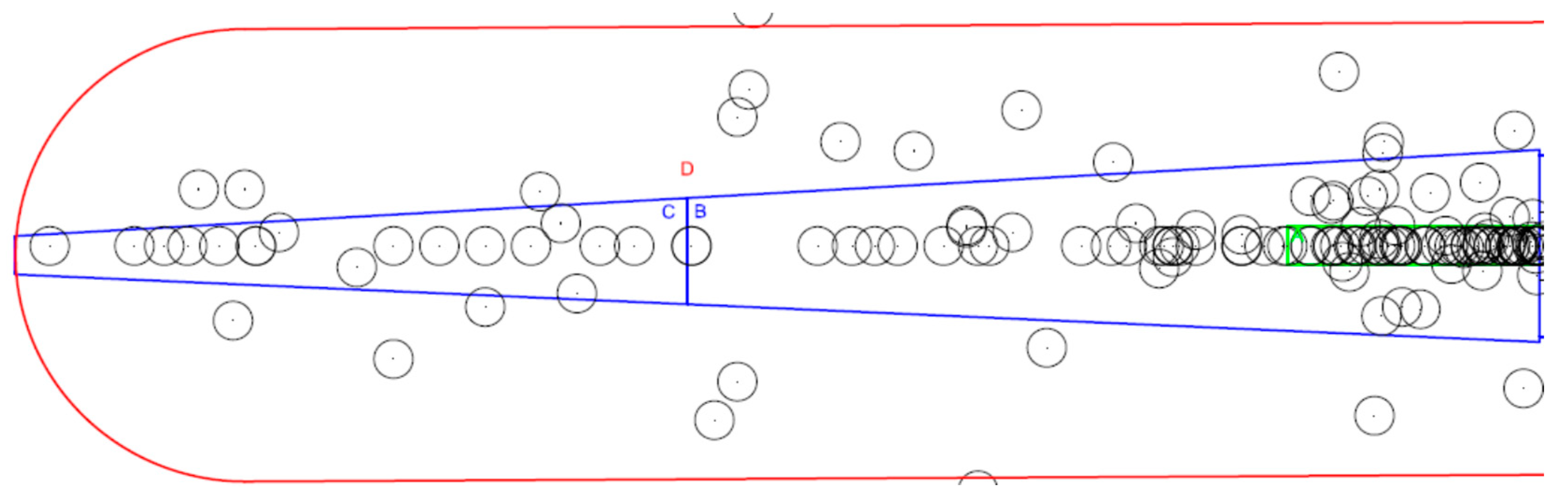
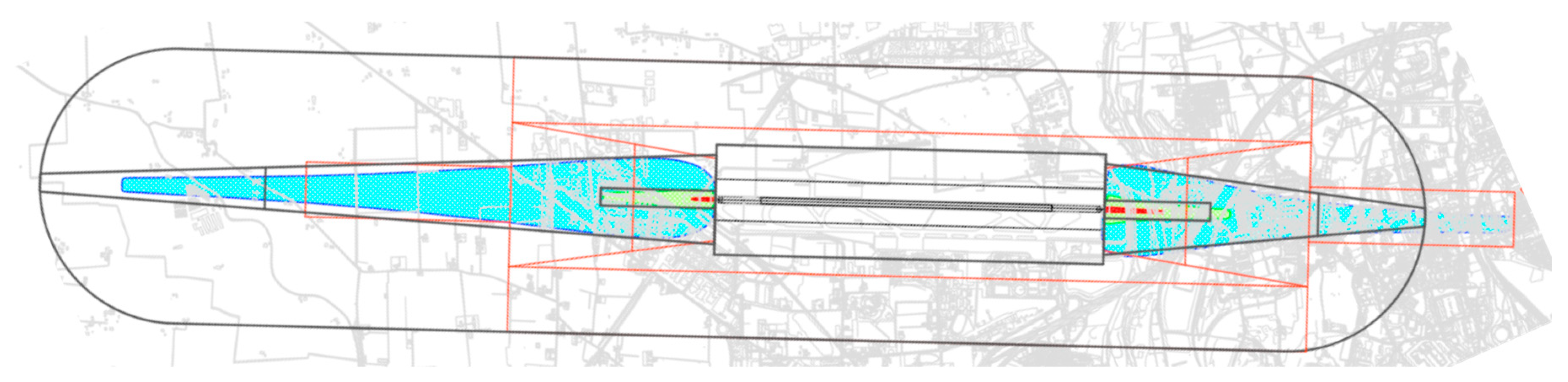
- the boundaries of Zone C approximate 10−6 risk contour totally if there are not Zone A and Zone B; while, if there is Zone B, they approximate 10−6 risk contour only containing the most extreme area;
- the boundaries of Zone A approximate 10−5 risk contour fully;
- the boundaries of Zone B approximate 10−6 risk contour only containing the area between Zone A and Zone C.
- larger Side Zone B, defined as the maximum width of the Zone, near the runway;
- smaller Side Zone C, defined as the minimum width of the Zone, near Extremity Zone C;
- extremity Zone C, defined as the maximum distance of the runway end from the 10−6 risk contour, along the runway centreline.
- smaller Side Zone A: it is defined approximately as the width of 10−5 risk contour.
- extremity Zone A: it is defined as the maximum distance of the runway end from the 10−5 risk contour, along the runway centreline. Its size changes for the runway ends, depending on the type of aviation operation (landing or take-off).
- Zone C, extended for the entire length of the strip, with a distance of 400 m (1311 ft.) from the runway axis for A, B, C and D categories, or with a distance of 200 m (656 ft.) from the runway axis for E category, tying an area often within the airport boundary;
- Zone D, extended for the whole length of the strip, with a distance of 1000 m (3279 ft.) from the runway axis. It continues over the runway ends for the extension of the Zone B, if present and Zone C; then it links up to end of the Zone C with a semi-circumference of 1000 m (3279 ft.) radius, for all airport categories.
4. Conclusions
Author Contributions
Conflicts of Interest
References
- Boeing Commercial Airplanes. Statistical Summary of Commercial Jet Airplane Accidents Worldwide Operations 1959–2015; Boeing Commercial Airplanes: Seattle, WA, USA, 2016. [Google Scholar]
- DfT Circular 01/2010. Control of Development in Airport Public Safety Zones; Department for Transport: London, UK, 2010.
- Smith, E. Third Party Risk. UK Sustainable Cities and Aviation Network; Report; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Environmental Resources Management Ireland Ltd. Calculation of Third Party Individual Risk: Determining PSZs for Airports; ERM: Dublin, Ireland, 2005. [Google Scholar]
- NLR, AA.VV. Third Party Risk Analysis for Aircraft Accidents around Airports; Report; National Aerospace Laboratory NLR: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Ale, B.J.M.; Piers, M. The assessment and management of third party risk around a major airport. J. Hazard. Mater. 2000, 71, 1–16. [Google Scholar] [CrossRef]
- Pikaar, C.J.M.; De, J.; Weijts, J. An Enhanced Method for the Calculation of Third Party Risk around Large Airports with Application to Schiphol; NLR-CR-2000-147; NLR Amsterdam: Amsterdam, The Netherlands, 2000. [Google Scholar]
- Cardi, A.; Di Mascio, P.; Di Vito, M.; Pandolfi, C. Distribution of air accidents around runways. Procedia Soc. Behav. Sci. 2012, 53, 861–870. [Google Scholar] [CrossRef]
- Moretti, L.; Di Mascio, P.; Nichele, S.; Cokorilo, O. Runway veer-off accidents: Quantitative risk assessment and risk reduction measures. Saf. Sci. 2018, 104, 157–163. [Google Scholar] [CrossRef]
- California Department of Transportation (CDP). California Airport Land Use Planning Handbook; State of California, Department of Transportation, Division of Aeronautics: Sacramento, CA, USA, October 2011.
- Airport Cooperative Research Program (ACRP) Report 27. Enhancing Airport Land Use Compatibility Volume 1: Land Use Fundamentals and Implementation Resources; The National Academies Press: Washington, DC, USA, 2010; ISBN 978-0-309-43094-4. [Google Scholar] [CrossRef]
- Ho-Huu, V.; Hartjes, S.; Visser, H.G.; Curran, R. An Efficient Application of the MOEA/D Algorithm for Designing Noise Abatement Departure Trajectories. Aerospace 2017, 4, 54. [Google Scholar] [CrossRef]
- Sarrat, C.; Aubry, S.; Chaboud, T.; Lac, C. Modelling Airport Pollutants Dispersion at High Resolution. Aerospace 2017, 4, 46. [Google Scholar] [CrossRef]
- Italian Legislative Decree ILD of 9-5-2005 n. 96. Revisione Della Parte Aeronautica del Codice Della Navigazione, a Norma Dell’articolo 2 Della L. 9 Novembre 2004, n. 265; Published by the Italian Official Gazette of 8-6-2005, n. 131, S.O.; Italian Official Gazette: Rome, Italy, 2005. (In Italian) [Google Scholar]
- ENAC Ente Nazionale per L’aviazione Civile (Italian Civil Aviation Authority). Regolamento per la Costruzione e L’esercizio Degli Aeroporti; Edition n. 21-10-2003; Italian Civil Aviation Authority: Rome, Italy, 2003.
- Čokorilo, O. Quantified risk assessment modelling of aircraft landing operations. Sci. Res. Essays 2011, 6, 4406–4413. [Google Scholar]
- Moretti, L.; Cantisani, G.; Caro, S. Airport veer-off risk assessment: An Italian case study. ARPN J. Eng. Appl. Sci. 2017, 12, 900–912. [Google Scholar]
- Guarascio, M.; Lombardi, M.; Rossi, G.; Sciarra, G. Risk analysis and acceptability criteria. WIT Trans. Built Environ. 2007, 94, 8. [Google Scholar] [CrossRef]
- Attaccalite, L.; Di Mascio, P.; Loprencipe, G.; Pandolfi, C. Risk assessment around airport. Procedia Soc. Behav. Sci. 2012, 53, 851–860. [Google Scholar] [CrossRef]
- Di Mascio, P.; Loprencipe, G. Risk analysis in the surrounding areas of one-runway airports: A methodology to preliminary calculus of PSZs dimensions. ARPN J. Eng. Appl. Sci. 2016, 11, 13641–13649. [Google Scholar]
- ENAC Ente Nazionale per L’aviazione Civile (Italian Civil Aviation Authority). Policy di Attuazione Dell’art. 715 Del Codice Della Navigazione. Definizione Della Metodologia e Della Policy di Attuazione del Risk Assessment; Edition. n. 12-01-2010; Italian Civil Aviation Authority: Rome, Italy, 2010. (In Italian)
- National Transportation Safety Board. Available online: http://www.ntsb.gov/_layouts/ntsb.aviation/index.aspx (accessed on 15 March 2017).
- Aviation Safety Network. Available online: https://aviation-safety.net/ (accessed on 15 March 2017).
- ICAO International Civil Aviation Organization Accident Investigation Section. Available online: http://www.icao.int/safety/airnavigation/AIG/Pages/default.aspx (accessed on 15 March 2017).

| Percentage | |||||||
| Airplane Class | A | B | C | D | E | F | |
| Airport Category | |||||||
| I | 0.01 | 0.44 | 98.96 | 0.54 | 0.04 | 0.01 | |
| II | 1.00 | 5.22 | 88.70 | 4.98 | 0.09 | 0.01 | |
| III | 0.50 | 1.92 | 93.90 | 2.43 | 1.24 | 0.01 | |
| IV | 18.00 | 3.32 | 78.68 | 0 | 0 | 0 | |
| V-5 | 25.00 | 5.88 | 69.12 | 0 | 0 | 0 | |
| V-1 | 70.00 | 2.35 | 27.65 | 0 | 0 | 0 | |
| MTOW (t) | |||||||
| Airplane Class | A | B | C | D | E | F | |
| Airport Category | |||||||
| I | 9 | 16 | 68 | 172 | 270 | 405 | |
| II | 9 | 17 | 57 | 111 | 212 | 405 | |
| III | 9 | 15 | 59 | 133 | 175 | 405 | |
| IV | 8 | 37 | 74 | 0 | 0 | 0 | |
| V | 8 | 62 | 76 | 0 | 0 | 0 | |
| IR | |||||||
| Airplane Class | A | B | C | D | E | F | |
| Airport Category | |||||||
| I | 0.01 | 0.47 | 0.27 | 0.54 | 0.01 | 0.79 | |
| II | 0.63 | 0.88 | 0.21 | 0.38 | 0.20 | 0.79 | |
| III | 0.24 | 0.69 | 0.23 | 0.46 | 0.34 | 0.80 | |
| IV | 0.06 | 0.02 | 0.26 | 0 | 0 | 0 | |
| V | 0.06 | 0.54 | 0.26 | 0 | 0 | 0 | |
| Area N | Width N | Length N | Area S | Width S | Length S | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (m2) × 1000 | (yd2) × 1000 | (m) | (ft.) | (m) | (ft.) | (m2) × 1000 | (yd2) × 1000 | (m) | (ft.) | (m) | (ft.) | |
| I-100 | 1459 | 1745 | 870 | 2852 | 3250 | 10,656 | 2817 | 3370 | 850 | 2787 | 6650 | 21,803 |
| I-75 | 1036 | 1239 | 730 | 2393 | 2700 | 8852 | 2063 | 2468 | 710 | 2328 | 5550 | 18,197 |
| II-75 | 996 | 1191 | 720 | 2361 | 2650 | 8689 | 1992 | 2383 | 700 | 2295 | 5450 | 17,869 |
| II-65 | 833 | 996 | 660 | 2164 | 2350 | 7705 | 1700 | 2033 | 650 | 2131 | 4950 | 16,230 |
| II-50 | 605 | 724 | 570 | 1869 | 1950 | 6393 | 1261 | 1508 | 550 | 1803 | 4100 | 13,443 |
| III-50 | 776 | 928 | 640 | 2098 | 2250 | 7377 | 1592 | 1904 | 620 | 2033 | 4750 | 15,574 |
| III-40 | 594 | 711 | 560 | 1836 | 1950 | 6393 | 1234 | 1476 | 550 | 1803 | 4050 | 13,279 |
| III-30 | 416 | 498 | 480 | 1574 | 1550 | 5082 | 880 | 1053 | 460 | 1508 | 3250 | 10,656 |
| IV15 | 259 | 310 | 340 | 1115 | 1380 | 4525 | 345 | 413 | 300 | 984 | 1620 | 5311 |
| IV10 | 153 | 183 | 280 | 918 | 930 | 3049 | 237 | 283 | 240 | 787 | 1470 | 4820 |
| V5 | 127 | 152 | 240 | 787 | 880 | 2885 | 114 | 136 | 160 | 525 | 880 | 2885 |
| V1 | 49 | 59 | 140 | 459 | 430 | 1410 | 24 | 29 | 100 | 328 | 270 | 885 |
| Landing | ||||||||||||
| Larger Side Zone B | Smaller Side Zone C | Extremity Zone C | Extremity Zone B | Smaller Side Zone A | Extremity Zone A | |||||||
| (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | |
| C100 | 851 | 2790 | 170 | 557 | 6648 | 21,797 | 3716 | 12,184 | 170 | 557 | 1130 | 3705 |
| C75 | 714 | 2341 | 143 | 469 | 5547 | 18,187 | 3101 | 10,167 | 143 | 469 | 943 | 3092 |
| B75 | 699 | 2292 | 140 | 459 | 5447 | 17,859 | 3045 | 9984 | 140 | 459 | 926 | 3036 |
| B65 | 645 | 2115 | 129 | 423 | 4947 | 16,220 | 2765 | 9066 | 129 | 423 | 841 | 2757 |
| B50 | 551 | 1807 | 110 | 361 | 4097 | 13,433 | 2290 | 7508 | 110 | 361 | 696 | 2282 |
| A50 | 621 | 2036 | 124 | 407 | 4747 | 15,564 | 2653 | 8698 | 124 | 407 | 807 | 2646 |
| A40 | 545 | 1787 | 109 | 357 | 4047 | 13,269 | 2262 | 7416 | 109 | 357 | 688 | 2256 |
| A30 | 459 | 1505 | 92 | 302 | 3246 | 10,643 | 1814 | 5948 | 92 | 302 | 552 | 1810 |
| D15 | 300 | 984 | 80 | 262 | 1620 | 5311 | - | - | - | - | - | - |
| D10 | 240 | 787 | 80 | 262 | 1470 | 4820 | - | - | - | - | - | - |
| E5 | 160 | 525 | 80 | 262 | 880 | 2885 | - | - | - | - | - | - |
| E1 | 100 | 328 | 80 | 262 | 270 | 885 | - | - | - | - | - | - |
| Take-Off | ||||||||||||
| Larger Side Zone B | Smaller Side Zone C | Extremity Zone C | Extremity Zone B | Smaller Side Zone A | Extremity Zone A | |||||||
| (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | (m) | (ft.) | |
| C100 | 869 | 2849 | 174 | 570 | 3249 | 10,652 | 1816 | 5954 | 174 | 570 | 1072 | 3515 |
| C75 | 733 | 2403 | 147 | 482 | 2697 | 8843 | 1508 | 4944 | 147 | 482 | 890 | 2918 |
| B75 | 718 | 2354 | 144 | 472 | 2647 | 8679 | 1480 | 4852 | 144 | 472 | 874 | 2866 |
| B65 | 662 | 2170 | 132 | 433 | 2348 | 7698 | 1312 | 4302 | 132 | 433 | 775 | 2541 |
| B50 | 569 | 1866 | 114 | 374 | 1947 | 6384 | 1088 | 3567 | 114 | 374 | 643 | 2108 |
| A50 | 640 | 2098 | 128 | 420 | 2248 | 7370 | 1257 | 4121 | 128 | 420 | 742 | 2433 |
| A40 | 563 | 1846 | 113 | 370 | 1947 | 6384 | 1088 | 3567 | 113 | 370 | 643 | 2108 |
| A30 | 479 | 1570 | 96 | 315 | 1547 | 5072 | 865 | 2836 | 96 | 315 | 511 | 1675 |
| D15 | 340 | 1115 | 80 | 262 | 1380 | 4525 | - | - | - | - | - | - |
| D10 | 280 | 918 | 80 | 262 | 930 | 3049 | - | - | - | - | - | - |
| E5 | 240 | 787 | 80 | 262 | 880 | 2885 | - | - | - | - | - | - |
| E1 | 140 | 459 | 80 | 262 | 430 | 1410 | - | - | - | - | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di Mascio, P.; Perta, G.; Cantisani, G.; Loprencipe, G. The Public Safety Zones around Small and Medium Airports. Aerospace 2018, 5, 46. https://doi.org/10.3390/aerospace5020046
Di Mascio P, Perta G, Cantisani G, Loprencipe G. The Public Safety Zones around Small and Medium Airports. Aerospace. 2018; 5(2):46. https://doi.org/10.3390/aerospace5020046
Chicago/Turabian StyleDi Mascio, Paola, Giuseppe Perta, Giuseppe Cantisani, and Giuseppe Loprencipe. 2018. "The Public Safety Zones around Small and Medium Airports" Aerospace 5, no. 2: 46. https://doi.org/10.3390/aerospace5020046
APA StyleDi Mascio, P., Perta, G., Cantisani, G., & Loprencipe, G. (2018). The Public Safety Zones around Small and Medium Airports. Aerospace, 5(2), 46. https://doi.org/10.3390/aerospace5020046