Modeling and Dynamics of HTS Motors for Aircraft Electric Propulsion
Abstract
1. Introduction
2. Architectures of HTS Machines for Hybrid and All-Electric Propulsion
3. Dynamics of HTS Motors
3.1. Dynamics of an HTS DC Motor
3.2. Dynamics of an HTS Brushless DC Motor
3.3. Dynamics of an HTS Synchronous Motor
4. Propeller Load Torque
- (i)
- Aerodynamic interference between any of the blade elements is absent;
- (ii)
- Only the two-dimensional section lift and drag forces are utilized to evaluate the forces on the blade elements.
5. Dynamic Model of Motor-Propeller System
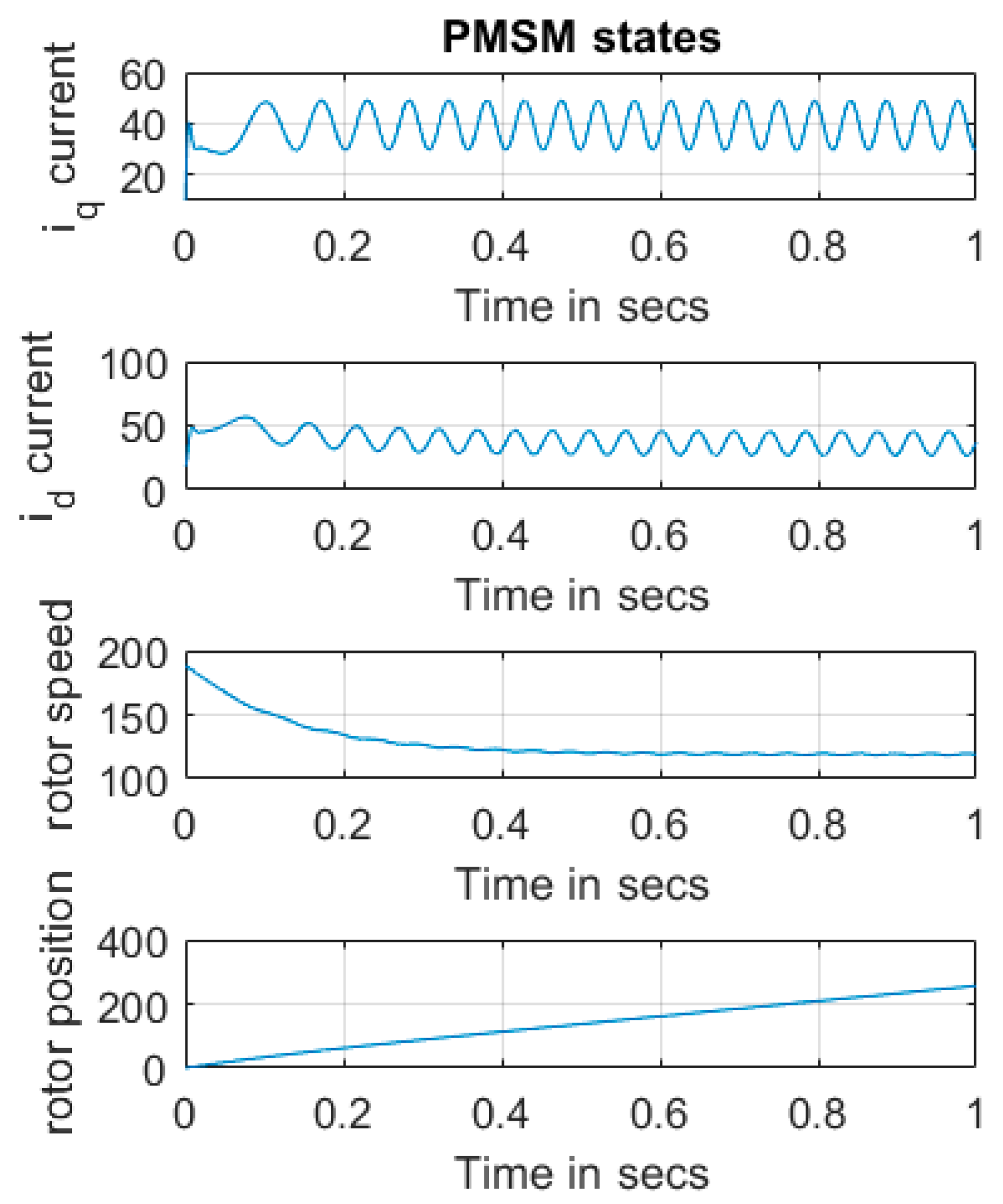
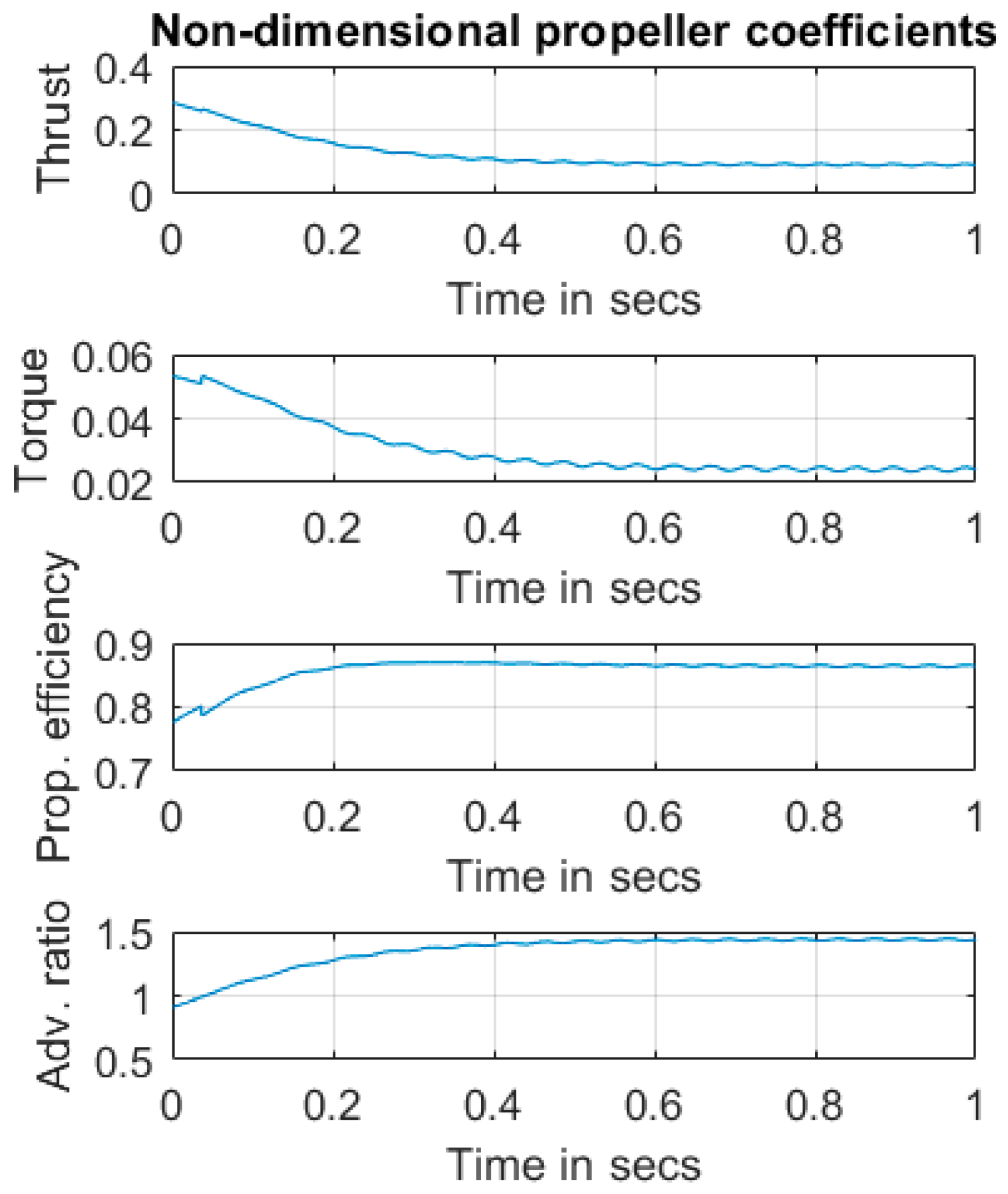
6. Typical Simulation Results
7. Discussion and Conclusions
Conflicts of Interest
References
- Bednorz, J.G.; Müller, K.A. Possible high Tc superconductivity in the Ba-La-Cu-O system. Z. Phys. B 1986, 64, 189–193. [Google Scholar] [CrossRef]
- Wu, M.K.; Ashburn, J.R.; Torng, C.J.; Hor, P.H.; Meng, R.L.; Gao, L.; Huang, Z.J.; Wang, Y.Q.; Chu, C.W. Superconductivity at 93K in a New Mixed-Phase Y-Ba-Cu-O Compound System at Ambient Pressure. Phys. Rev. Lett. 1987, 58, 908–910. [Google Scholar] [CrossRef] [PubMed]
- Ford, P.J.; Saunders, G.A. The Rise of the Superconductors; CRC Press: Boca Raton, FL, USA, 2005. [Google Scholar]
- Goyal, A. Second-Generation HTS Conductors; Kluwer Academic Publishers: Dordrecht, The Netherlands, 2005. [Google Scholar]
- Bardeen, J.; Cooper, L.N.; Schrieer, J.R. Microscopic theory of superconductivity. Phys. Rev. 1957, 106, 162–164. [Google Scholar] [CrossRef]
- Bardeen, J.; Cooper, L.N.; Schrieer, J.R. Theory of superconductivity. Phys. Rev. 1957, 108, 1175–1204. [Google Scholar] [CrossRef]
- Joshi, C.H.; Prum, C.B.; Schiferl, R.F.; Driscoll, D.I. Demonstration of two synchronous motors using high temperature superconducting field coils. IEEE Trans. Appl. Supercond. 1995, 5, 968–971. [Google Scholar] [CrossRef]
- Frank, M.; Frauenhofer, J.; Van Hasselt, P.; Nick, W.; Neumueller, H.W.; Nerowski, G. Long-term operational experience with first Siemens 400 kW HTS machine in diverse configurations. IEEE Trans. Appl. Supercond. 2003, 13, 2120–2123. [Google Scholar] [CrossRef]
- Eckels, P.W.; Snitchler, G. 5 MW high temperature superconductor ship propulsion motor design and test results. Nav. Eng. J. 2005, 117, 31–36. [Google Scholar] [CrossRef]
- Masson, P.J.; Soban, D.S.; Upton, E.; Pienkos, J.E.; Luongo, C.A. HTS motors in aircraft propulsion: Design considerations. IEEE Trans. Appl. Supercond. 2005, 15, 2218–2221. [Google Scholar] [CrossRef]
- Neumuller, H.W.; Nick, W.; Wacker, B.; Frank, M.; Nerowski, G.; Frauenhofer, J.; Rzadki, W.; Hartig, R. Advances in and prospects for development of high-temperature superconductor rotating machines at Siemens. Supercond. Sci. Technol. 2006, 19, S114–S117. [Google Scholar] [CrossRef]
- Oswald, B.; Best, K.-J.; Soell, M.; Duffner, E.; Gawalek, W.; Kovalev, L.K.; Krabbes, G.; Prusseit, W. HTS motor program at OSWALD, present status. IEEE Trans. Appl. Supercond. 2007, 17, 1583–1586. [Google Scholar] [CrossRef]
- Kalsi, S.S. Rotating AC machines. In Applications of High Temperature Superconductors to Electric Power Equipment; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011; Chapter 4. [Google Scholar]
- Kwon, Y.K.; Kima, H.M.; Baik, S.K.; Lee, E.Y.; Lee, J.D.; Kim, Y.C.; Lee, S.H.; Hong, J.P.; Jo, Y.S.; Ryu, K.S. Performance test of a 1 MW class HTS synchronous motor for industrial application. Phys. C Supercond. 2008, 468, 2081–2086. [Google Scholar] [CrossRef]
- Ishmael, S.; Goodzeit, C.; Masson, P.; Meinke, R.; Sullivan, R. Flux pump excited double-helix rotor for use in synchronous machines. IEEE Trans. Appl. Supercond. 2008, 18, 693–696. [Google Scholar] [CrossRef]
- Luongo, C.A.; Masson, P.J.; Nam, T.; Mavris, D.; Kim, H.D.; Brown, G.V.; Waters, M.; Hall, D. Next generation more-electric aircraft: A potential application for HTS superconductors. IEEE Trans. Appl. Supercond. 2009, 19, 1055–1068. [Google Scholar] [CrossRef]
- Kovalev, K.L.; Dezhin, D.S.; Kovalev, L.K.; Poltavets, V.N.; Ilyasov, R.I.; Golovanov, D.S.; Oswald, B.; Best, K.-J.; Gawalek, W. HTS high-dynamic electrical motors. Available online: http://snf.ieeecsc.org/sites/ieeecsc.org/files/EUCAS2009-ST152.pdf (accessed on 12 February 2018).
- Oswald, B.; de Waele, A.T.A.M.; Söll, M.; Reis, T.; Maier, T.; Oswald, J.; Teigelkötter, J.; Kowalski, T. Project Sutor: Superconducting speed-controlled torque motor for 25.000 Nm. Phys. Procedia 2012, 36, 765–770. [Google Scholar] [CrossRef][Green Version]
- Armstrong, M.; Ross, C.; Phillips, D.; Blackwelder, M. Stability, Transient Response, Control, and Safety of a High-Power Electric Grid for Turboelectric Propulsion of Aircraft; NASA/CR-2013-217865; NASA: Hanover, MD, USA, 2013.
- Tsukamoto, O. Present status and future trends of R&D for HTS rotational machines in Japan. Phys. C Supercond. 2014, 504, 106–110. [Google Scholar]
- Okazaki, T.; Sugimoto, H.; Takeda, T. Liquid nitrogen cooled HTS motor for ship propulsion. In Proceedings of the Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar]
- Rambabu, S. Modeling and Control of a Brushless DC Motor. Master’s Thesis, Department of Electrical Engineering, National Institute of Technology, Rourkela, India, 2007. [Google Scholar]
- Vepa, R. Dynamic modelling simulation and control of energy generation. In Wind Power Generation and Control; Lecture Notes in Energy Series No. 20; Springer Verlag: London, UK, 2013; Chapter 4. [Google Scholar]
- Han, W.; Liu, J.; Liu, C.; Chen, L.; Su, X.; Zhao, P. Flap motion of helicopter rotors with novel, dynamic stall model. Open Phys. 2016, 14, 239–246. [Google Scholar] [CrossRef]
- Perera, P.D.C.; Blaabjerg, F.; Pedersen, J.K.; Thgersen, P. A sensorless, stable V/f control method for permanent-magnet synchronous motor drives. IEEE Trans. Ind. Apps. 2003, 39, 783–791. [Google Scholar] [CrossRef]
- Agarlita, S.C.; Coman, C.E.; Boldea, I. Stable V/f control system with controlled power factor angle for permanent magnet synchronous motor drives. IET Electr. Power Appl. 2006, 2, 278–286. [Google Scholar] [CrossRef]
- Brock, S.; Pajchrowski, T. Energy-Optimal V/f Control of Permanent Magnet Synchronous Motors for Fan Applications. Zesz. Probl. Masz. Elektr. 2011, 92, 169–174. [Google Scholar]
- Stellas, D. Sensorless Scalar and Vector Control of a Subsea PMSM. Master’s Thesis, Department of Energy and Environment, Division of Electric Power Engineering, Chalmers University of Technology, Göteborg, Sweden, 2013. [Google Scholar]
- Paitandi, S.; Sengupta, M. Analysis, design, implementation of sensorless V/f control in a surface mounted PMSM without damper winding. Sādhanā 2017, 42, 1317–1333. [Google Scholar] [CrossRef]




| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Phase voltage (max) | 28 V | Supply frequency | 60 Hz |
| 0.0078 H | 0.0078 H | ||
| Pole pairs | 2 | (incl. source resistance) | 2.03 Ω |
| 0.616 Wb | (sc) (incl. source resistance) | 0.203 Ω | |
| (sc) | 2 × 0.616 Wb | Rotor inertia, J | 0.20095 |
| Rotor damping, B | 0.4675 | Synchronous speed, | |
| Desired electrical speed | 0.7 × | Number of blade elements | 10 |
| Propeller diameter | 1.1 m | Taper ratio | 0.8 |
| Root chord | 0.45 m | AR | 4.07 |
| Hub diameter | 0.125 × propeller diameter | Hub blade twist | |
| Tip blade twist | Blade profile | NACA0024 | |
| 0.008 | −0.03 | ||
| 0.01 | 1.11 + 0.018 AR | ||
| 0.1 | 30 m/s |
© 2018 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vepa, R. Modeling and Dynamics of HTS Motors for Aircraft Electric Propulsion. Aerospace 2018, 5, 21. https://doi.org/10.3390/aerospace5010021
Vepa R. Modeling and Dynamics of HTS Motors for Aircraft Electric Propulsion. Aerospace. 2018; 5(1):21. https://doi.org/10.3390/aerospace5010021
Chicago/Turabian StyleVepa, Ranjan. 2018. "Modeling and Dynamics of HTS Motors for Aircraft Electric Propulsion" Aerospace 5, no. 1: 21. https://doi.org/10.3390/aerospace5010021
APA StyleVepa, R. (2018). Modeling and Dynamics of HTS Motors for Aircraft Electric Propulsion. Aerospace, 5(1), 21. https://doi.org/10.3390/aerospace5010021




