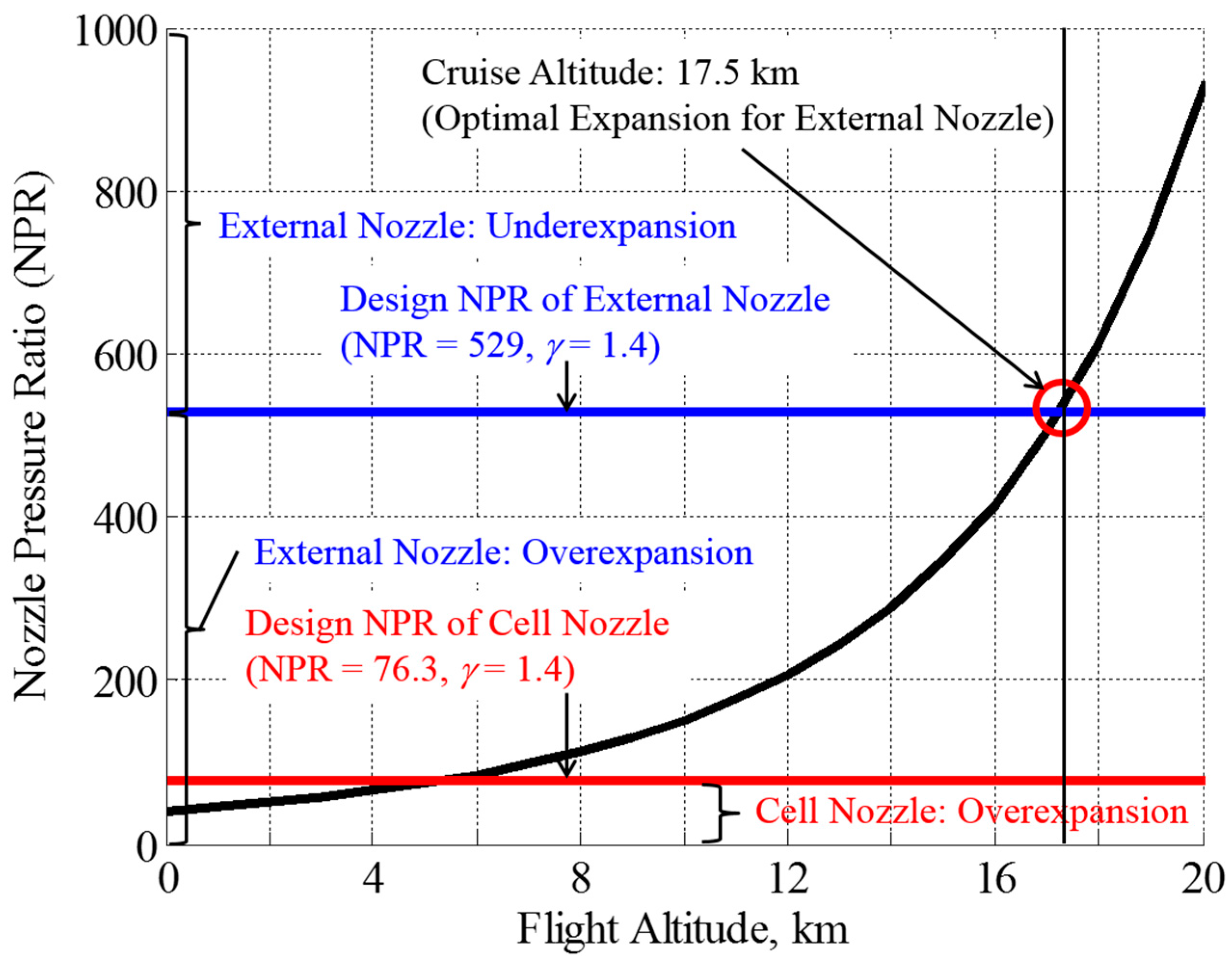
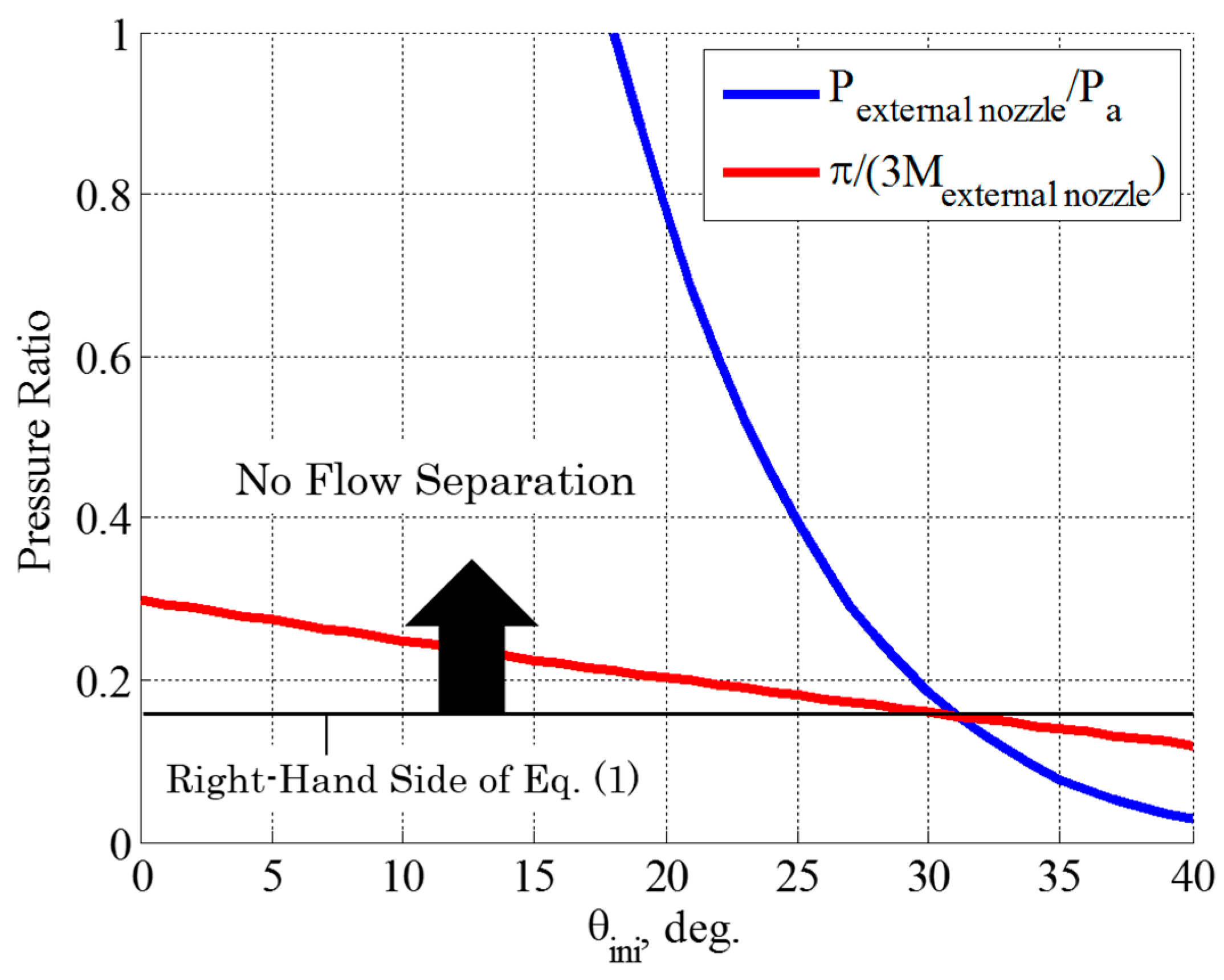
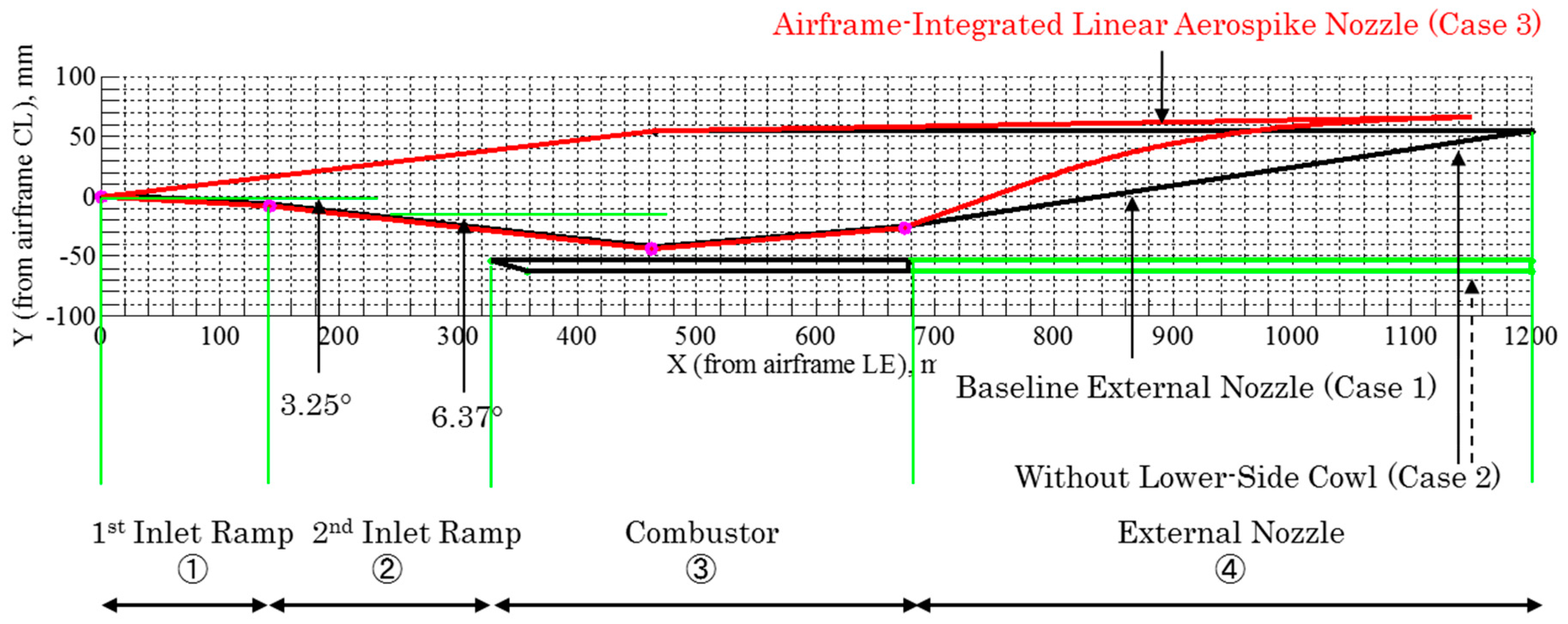
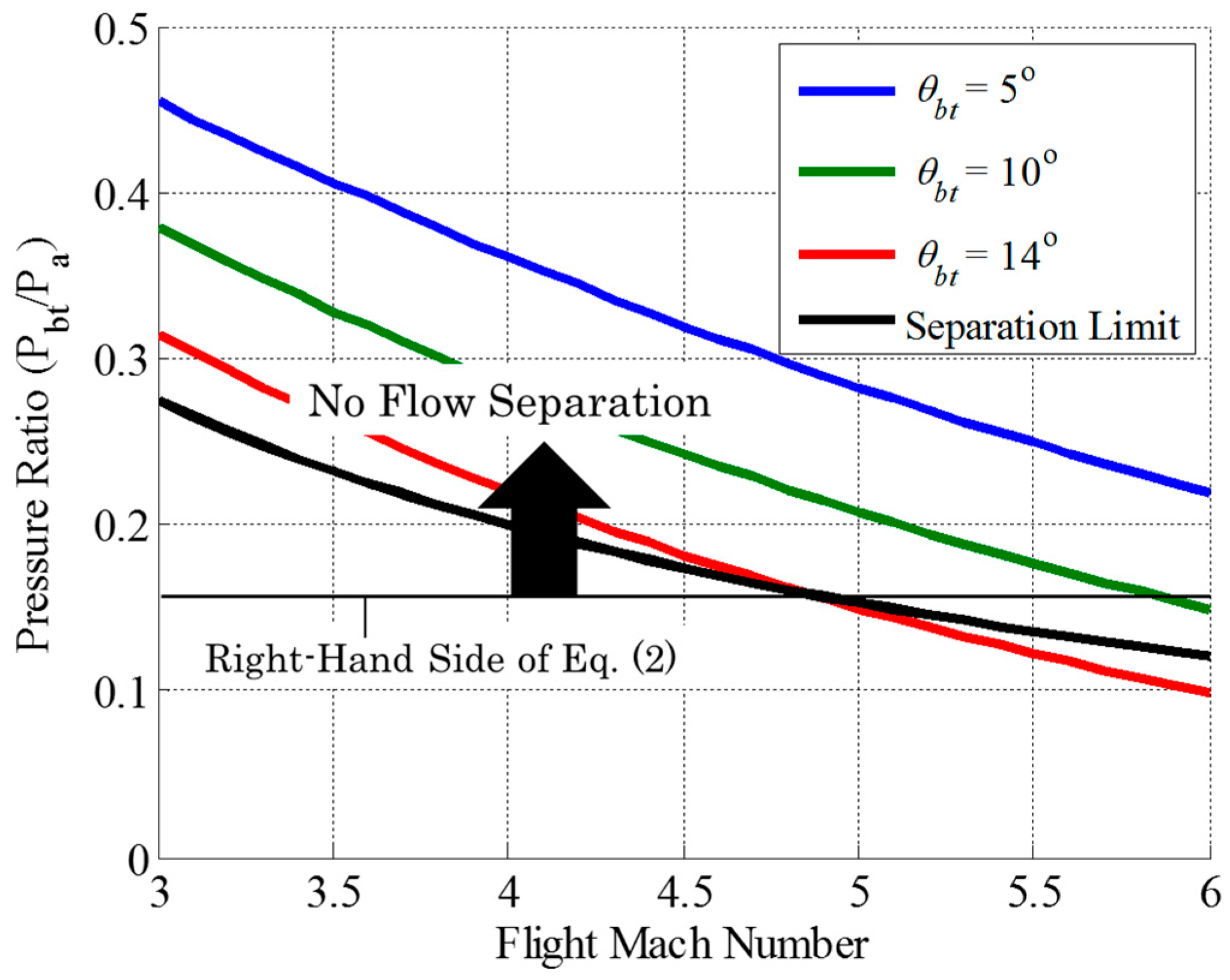
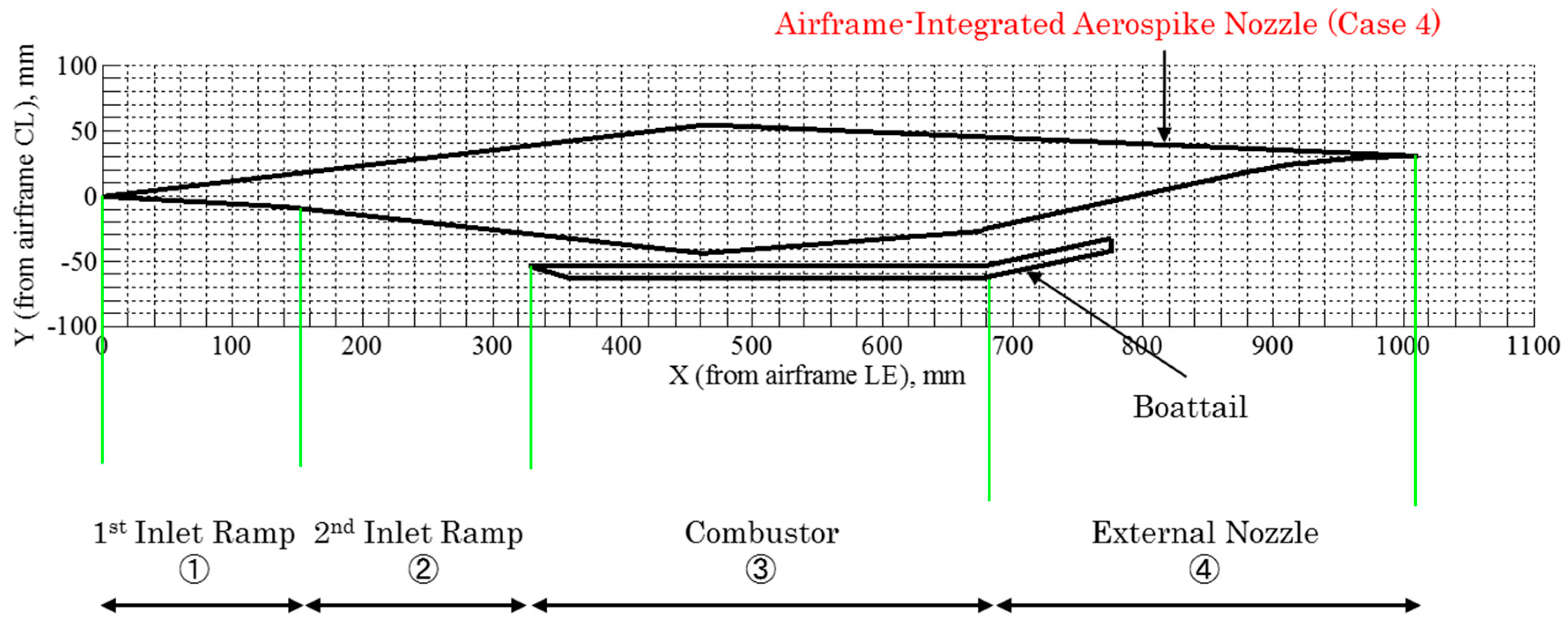
1. Introduction
The concept of a long-range hypersonic air transportation system is considered to be highly beneficial for coping with the increasing demands for faster intercontinental air travel and transportation. For example, with respect to an intercontinental travel duration such as between Tokyo and Washington, D.C., a commercial airliner takes approximately 12 h for the cruise phase at an approximate cruise flight speed of Mach 0.85. If the cruise flight speed can be increased, for example, to Mach 5, the flight duration could potentially be reduced to approximately 2 to 3 h. This reduction in flight duration is substantial and would have a significant impact on the industry as well as the air travel market. Over the flight envelope which involves a wide range of altitudes and distances in dense atmosphere after taking off horizontally from the ground, the cruise phase dominates the overall travel time. A scramjet is favorable as the primary engine for a hypersonic aircraft at the cruise phase accounting for the cycle efficiency, thus increasing propulsion efficiency. The airframe shape would be a waverider design, considering the hypersonic flight operations to minimize wave drag [
1,
2,
3,
4,
5,
6,
7]. The airframe and the propulsion system of a hypersonic aircraft that has a waverider shape equipped with a scramjet engine must be designed together, as parts of the airframe will be parts of the engine [
1].
Numerous concerns and technical challenges still remain for the realization of practical and sustainable hypersonic air transportation systems such as supersonic to hypersonic cruise and propulsion efficiencies [
1], economic impacts regarding fuel consumption efficiency, and environmental concerns such as emissions and noise levels. One of the key technologies to resolve these concerns is an advanced airframe-integrated propulsive nozzle system. The propulsive nozzle plays an important role in the entire propulsion system; the nozzle translates the combustion energy gained in the combustor to the thrust that moves vehicle forward at all flight conditions including on-design and off-design conditions. Development of the airframe-integrated propulsive nozzle system is highly recommended to improve the hypersonic cruise and propulsion efficiencies as well as reducing noise levels. Therefore, designing such a novel airframe-propulsion integration, namely, airframe-integrated advanced nozzle configuration as part of the airframe aftbody is considered critical [
8].
To date, many insights on the aftbody configuration for hypersonic aircraft have been provided through numerous studies on the scramjet nozzle [
4,
9,
10]. Those studies mainly focused on an open-style external nozzle configuration comprised of a straight ramp as opposed to a simple divergent duct nozzle [
3]. The open-style external nozzle appears as the airframe aftbody that causes the primary engine exhaust flow to flow along the airframe surface. With an asymmetric straight ramp external nozzle [
9], interactions between the simulated engine exhaust flow and the hypersonic external flow were investigated and showed that the role of intercepting shock formed between those two kinds of flows on determining the ramp surface pressure. Mitani et al. [
10] conducted a large-scale combustion test with the aid of computational simulation on the straight ramp external nozzle, and showed that the lift thrust was generated by the external nozzle as well as showing positive net thrust generation. Thus, many insights into employing the straight ramp external nozzle have been obtained. In addition to the straight ramp configuration, Takahashi [
8,
11] proposed a concept of an airframe-propulsion integration employing a linear aerospike nozzle, namely an airframe-integrated linear aerospike propulsion system [
8,
11], in order to gain more thrust force from the external nozzle portion. The linear aerospike nozzle configuration can also address the concerns of increasing the propulsion efficiency and the airframe integration and potentially noise reduction.
The linear aerospike nozzle concept has the altitude-compensating features [
12,
13,
14,
15] that enable maintaining near-optimal thrust performance at any flight altitude, unlike a conventional bell-shaped nozzle, which reaches maximum performance at only one specific altitude (i.e., the design altitude). This is why the variable geometry nozzle has been employed with the bell-shaped nozzle for existing practical high-speed aircraft. The linear aerospike nozzle can adjust the exhaust flow expansion automatically to the ambient pressure. Additionally, a clustered linear aerospike nozzle concept is beneficial when considering the operational needs of the aircraft such as the attitude control or thrust vectoring [
16,
17]. Furthermore, the use of an aerospike nozzle facilitates efficient utilization of the entire back area of a rectangular vehicle body (e.g., waverider) to minimize the aftbody base drag. Another advantage of the aerospike nozzle is its low noise generation as has been demonstrated in aircraft applications using a plug nozzle [
18,
19].
Many insights into the aerospike nozzle have been provided by numerous studies involving ground tests [
15,
20], numerical simulations [
21,
22,
23], conceptual studies [
11,
12], and flight tests as part of the Linear Aerospike SR-71 experiment, which was part of the X-33 program [
24,
25] with regard to freestream effects [
14,
26,
27,
28,
29,
30]. Additionally, the mechanism of open/closed wake conditions [
31], clustering effects [
32] and side wall effects [
33] on the flowfield characteristics, skin friction features on the spike surface [
34], and structural and heat loads [
35] have been investigated. Among these numerous studies, Takahashi et al. [
29,
30] demonstrated that thrust performance can be significantly improved even at off-design in-flight conditions under the presence of external flow with a boattail-equipped aftbody configuration integrated into the airframe. This insight is particularly important because the flight performance was anticipated to decrease under transonic flight conditions [
26] and off-design flight conditions [
36] because of the locally decreased flow and static pressure acting on the airframe and nozzle surfaces. Although a large boattail angle, which appears right upstream of the primary engine nozzle exit, may lead to pressure decrease on its surface and thus generate aerodynamic drag, utilizing the freestream effect may be still beneficial for increasing thrust by automatically adjusting flow expansion to the change of atmospheric air [
8,
11]. The key physics on the thrust enhancement by the employment of the aerospike nozzle as the external nozzle is that the nozzle wall acts as a compression wall for the exhaust flow and the slip surface forming between the exhaust flow and the external flow determines the wall surface pressure.
While those important insights for thrust improvement by the employment of the aerospike nozzle with the boattail were obtained, this configuration involves complex design features such as the boattail inclination angle, which results in inclining the primary thrust direction. A simpler installation of an external nozzle through a minor modification of the baseline design should be considered. In view of simpler installation of the external nozzle to the airframe, a linear-spike nozzle configuration which possesses a compression wall feature without having the boattail should also be evaluated. In this regard, it is important to evaluate the benefit of employing the linear-spike nozzle configuration as an alteration of the baseline configuration of a simple divergent duct nozzle of a waverider. To this end, it is vital to demonstrate the hypersonic cruise and propulsion efficiencies as well as the flight attitude characteristics by evaluating an airframe-integrated linear-spike propulsion system in its vehicle integration feasibility designed for hypersonic air transportation systems.
The major goal of this study was to evaluate the feasibility of the proposed airframe-integrated linear-spike propulsion concepts which are applied to the aftbody portion of the hypersonic baseline aircraft geometry in regards to thrust augmentation capability and trim balance. While previous studies [
8,
29,
30] emphasized the importance of the boattail portion which appeared right upstream of the primary thruster, this study evaluated no boattail configuration for a contoured linear-spike nozzle to cope with the dual-mode ramjet flowpath in addition to the baseline case. An aerospike-type configuration with the boattail was also compared. The performance evaluation was based on the pressure distribution on the external nozzle obtained by computational work. The computational code was validated by comparing the spike surface pressure to that obtained by corresponding experiments and the quasi-one-dimensional analytical model established in previous studies [
8,
29,
30], which predicted thrust values for each thrust component under in-flight conditions.
4. Results and Discussion
The insights gained from the performance evaluation for the airframe-integrated linear-spike propulsion system adopted for the aftbody portion of the hypersonic aircraft are discussed in this section and cover the following topics of interest: flowfield characteristics, thrust performance by the external nozzle section, and the trim balance.
4.1. Flowfield Characteristics
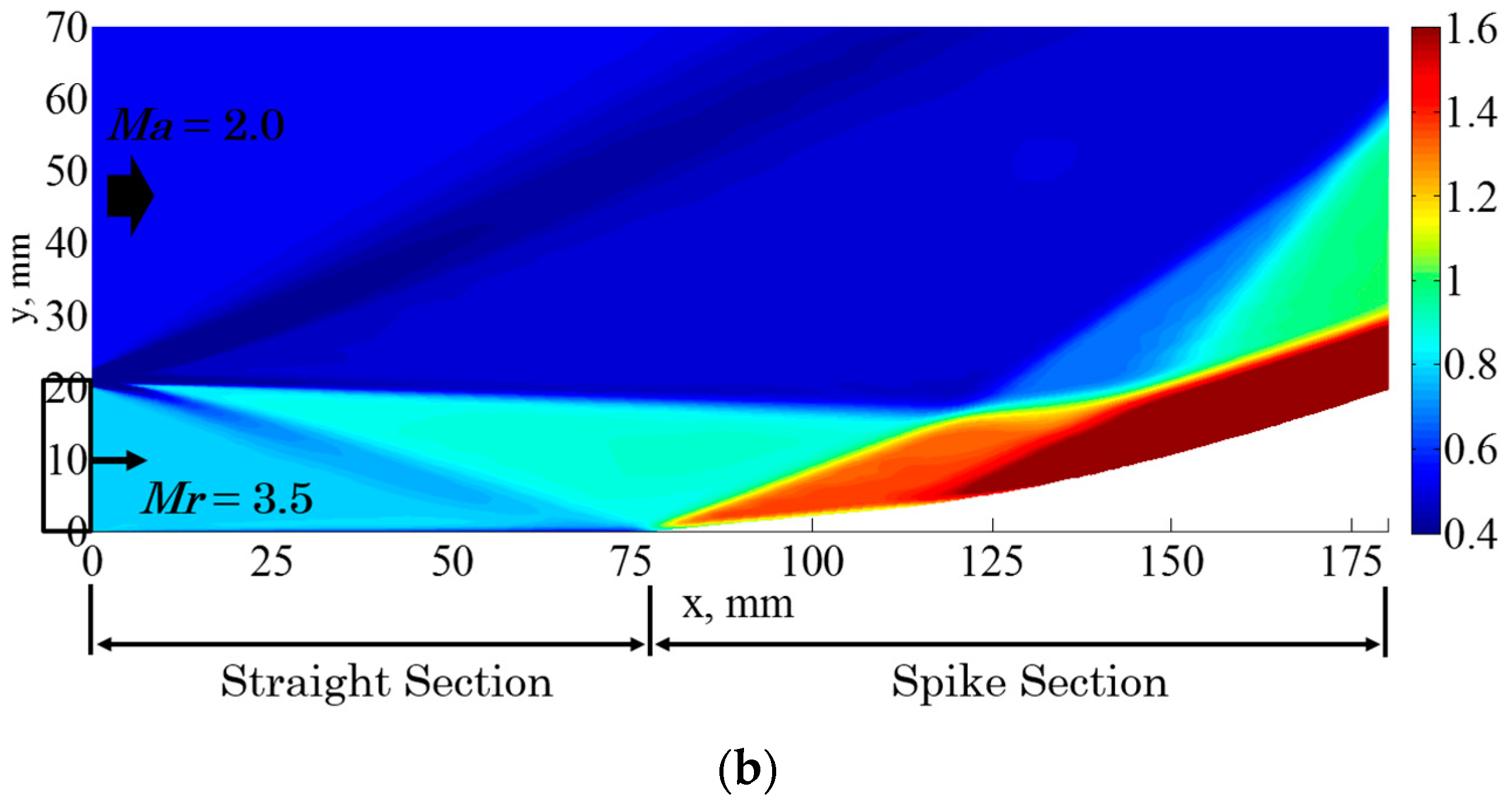
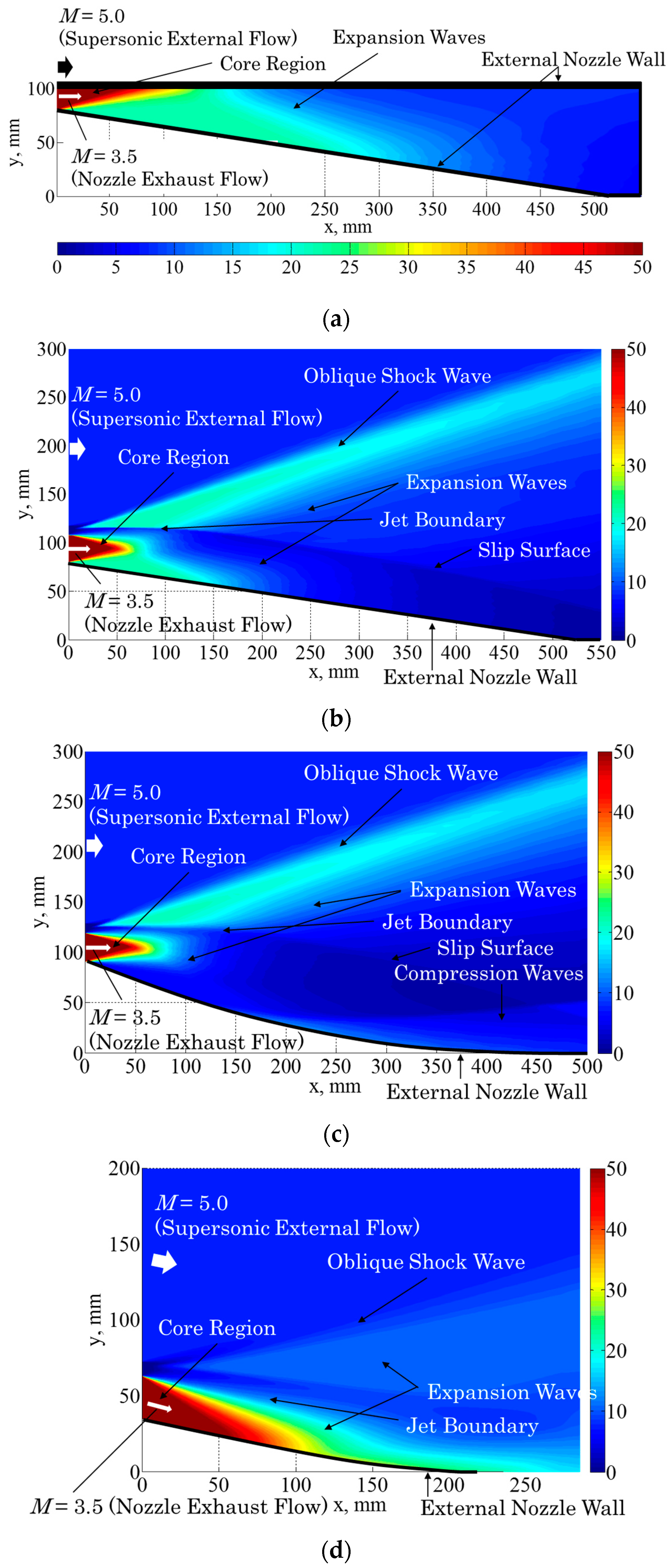
Flowfields around the aftbody portion for Cases 1 to 4 at the cruise flight condition calculated by CFD are shown in
Figure 11: (a) Case 1; (b) Case 2; (c) Case 3; and (d) Case 4. The color bar indicates the pressure distribution on the external nozzle. Case 1 (
Figure 11a) shows the flowfield which is similar to the well-known divergent nozzle flowfield because the configuration is a simple straight divergent nozzle. The nozzle flow shows a near optimal-expansion feature because the exit pressure at the external nozzle is approximately equivalent to the ambient pressure. The nozzle exhaust flow flows parallel to the airframe axis for this baseline configuration.
Some remarkable differences in flow feature compared to that seen in Case 1 are seen in Case 2 (
Figure 11b). The cell nozzle flow rapidly expands right after the cell nozzle exit as the nozzle wall is an expansion wall for the exhaust flow with an initial angle of 8.7°. This is attributable to the fact that the other side of the nozzle wall (lower body-side cowl) is open, and therefore the nozzle flow expands to the ambient pressure level and is inclined to the wall as it flows along the nozzle wall. Additionally, the flowfield in the aftbody portion involves some outstanding flow features generated by the presence of the supersonic external flow, such as the oblique shock wave emanating from the first interacting location between the external flow and the jet boundary, expansion fans forming behind the oblique shock wave, and slip surface appearing between those two kinds of flows. The expansion waves emanating from the bottom wall of the cell nozzle exit (at the expansion corner) reflect at the jet boundary and the resultant reflected expansion waves eventually form an envelope shock wave. For this kind of large expansion condition of the cell nozzle, this envelope shock wave plays an important role in translating ambient pressure to the spike nozzle surface [
22].
Case 3 (
Figure 11c) shows a similar flow structure to that seen in Case 2 (
Figure 11b) but with some distinct differences. The flow feature near the nozzle exit is similar to that of Case 2 such as in terms of the core length and the oblique shock wave angle, but its expansion is larger as the initial wall inclination angle is larger than that of Case 2. At the interaction between the cell nozzle exhaust flow and the external flow, the external flow generates an oblique shock wave at the first contact with the jet boundary. This feature is also similar to that of Case 2 but is larger in this case. Approximately 200 mm downstream from the cell nozzle exit, some local compression feature is seen toward the end of the wall. This is attributable to the fact that the contour geometry has a compression wall feature for the local exhaust flow.
Distinct differences in flow feature compared to those observed in Cases 1 to 3 are seen for Case 4 (
Figure 11d). The cell nozzle exhaust flow flows along the wall, and therefore the flow expansion is limited compared to that observed in Cases 2 and 3. Additionally, the core region of the cell nozzle remains much longer and is inclined toward the wall. The core length is much longer than that seen in Case 1. The nozzle wall contour for this case acts as a compression wall for the cell nozzle flow. This is because the nozzle contour was designed by use of the method of characteristics which provides less wavy flow feature because reflected expansion and compression waves cancel one another out. Therefore, simple flow expansion is seen and the flowfield is not complicated compared to other cases. The elevated wall pressure is a benefit of having the boattail section, which causes the cell nozzle flow inclined to the airframe axis. Note that this is the primary reason in the thrust enhancement by the positive freestream effect. It should be noted that this inclination of the cell nozzle may lose some thrust performance in addition to the boattail drag depending on the flight condition. In order to evaluate the benefit of employing this external nozzle configuration, the thrust performance will be evaluated in a later section.
4.2. Nozzle Surface Pressure Comparison
Since the nozzle surface pressure has a large contribution to generating thrust [
8], the spike surface pressure was examined to evaluate the thrust performance of employing the airframe-integrated external nozzle configuration.
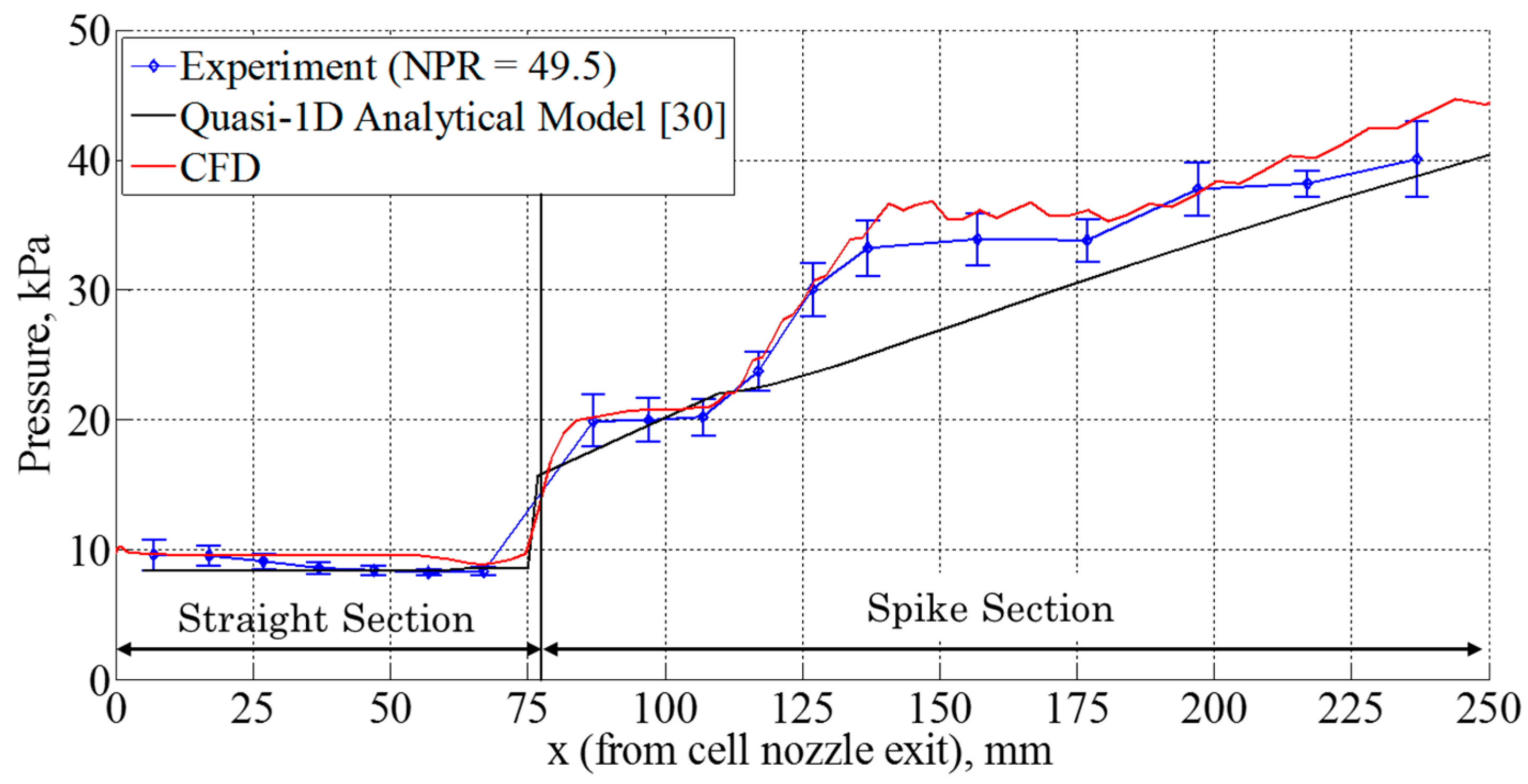
Figure 12 compares the pressure distribution on the external nozzle among Cases 1 to 4. Note that this pressure distribution was obtained for an assumed two-dimensional flowfield and on the centerline of the airframe.
In
Figure 12, the pressure distribution for the baseline case (Case 1) shows that the pressure near the cell nozzle exit until
x = 250 mm where the first Mach wave impinges on the nozzle wall is constant because no influence by the flow is seen in this area inside the first Mach wave. This is the core region of the cell nozzle flow. After the first Mach wave impingement point on the wall, the nozzle surface pressure gradually decreases as it goes downstream because expansion waves emanating from the cell nozzle exit impinge on the wall of the simple divergent duct. This feature can be predicted by the Prandtl–Meyer expansion theory. Case 2 shows shorter core length compared to that of Case 1. By the oblique shock wave generated at the first contact between the external flow and the jet boundary, the cell nozzle flow is pushed toward the wall surface and therefore the flow expansion was limited. Consequently, the core region length was reduced. Downstream from the core region, the pressure continues to decrease. The wall pressure becomes lower than the ambient pressure at approximately 220 mm. Considering that the ambient pressure level is 8 kPa for this calculation, the pressure distribution in the remaining 300 mm portion downstream of the
x = 220 mm becomes aerodynamic drag. This would indicate that the thrust performance is not beneficial compared to the configuration of Case 1.
Case 3 shows similar core length to that observed in Case 2. However, a significant difference in pressure distribution is seen. The pressure in the core region is much lower than that in Cases 1 and 2. This is attributed to larger expansion by the larger initial expansion angle of the wall as seen in
Figure 11c. Right downstream the core region, the pressure increases until
x = 200 mm; then the pressure gradually decreases as flow goes downstream. Since the wall contour was designed as a linear-spike configuration, the wall downstream of the core region acts as a compression wall for the cell nozzle flow as mentioned above. Therefore, the wall pressure initially increases. Then, the pressure should continue to increase [
8] or remain at the ambient pressure level by balancing with environmental pressure. However, since the nozzle contour was not optimized in this study, a slight pressure decrease downstream of
x = 200 mm is seen. The main cause of this decrease is considered to be incident expansion waves emanating from the cell nozzle lip. Pressure values on the wall surface generally stay above the ambient pressure level.
Case 4 shows a distinct difference in pressure distribution compared to the other cases. The core region where the pressure is leveled (i.e., approximately x = 0 mm–50 mm) is much shorter than the other cases; but the pressure value remains at approximately the ideal exit pressure of the cell nozzle. Downstream of the core region, the pressure gradually decreases as flow goes downstream. This observation is different from that given by experiment. In the experiment, the pressure continues to increase as flow moves downstream; however, this case shows the opposite trend. The primary reason for this inconsistency is attributable to the ambient pressure level and flow conditions. The experimental case had relatively large environmental pressure level compared to the cell nozzle exit pressure; the simulated flight condition was at 5 km above sea level. Since the slip surface between the external flow and cell nozzle flow plays a key role in determining the spike surface pressure by balancing these two pressures, the environmental pressure level is important. The environmental pressure in this case is much lower than the cell nozzle exit pressure. Therefore, by balancing the wall pressure with the environmental pressure across the slip surface, the wall pressure was determined and showed a gradually decreasing trend. The slower decrease compared to the baseline case is due to the freestream effect. It should be noted that the boattail flow was assumed to flow on the wall without separation and the boattail Mach number was 5.0 for this case. More systematically parametric study is needed to deepen the feature of the external nozzle flowfield.
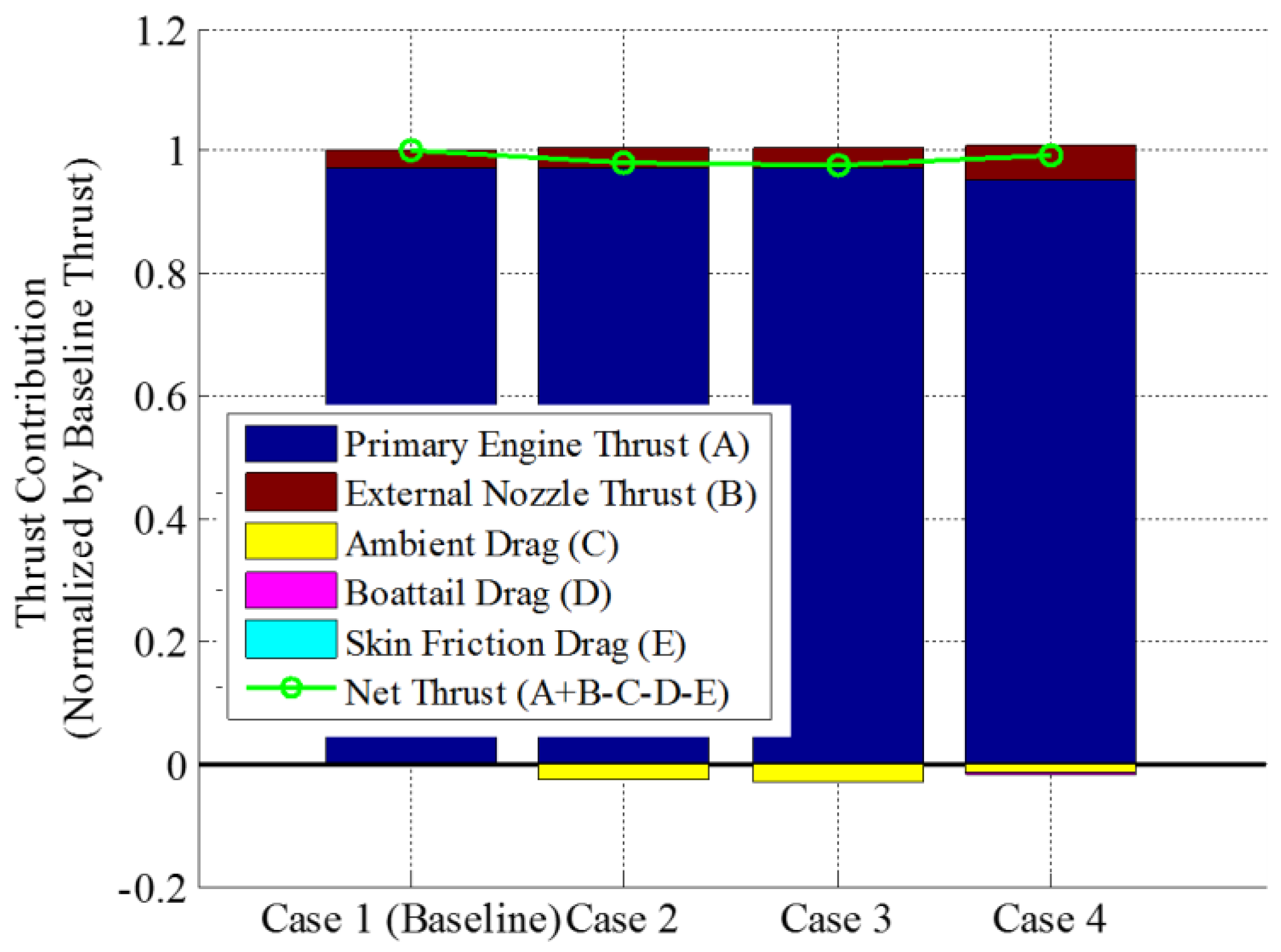
4.3. Thrust Breakdown
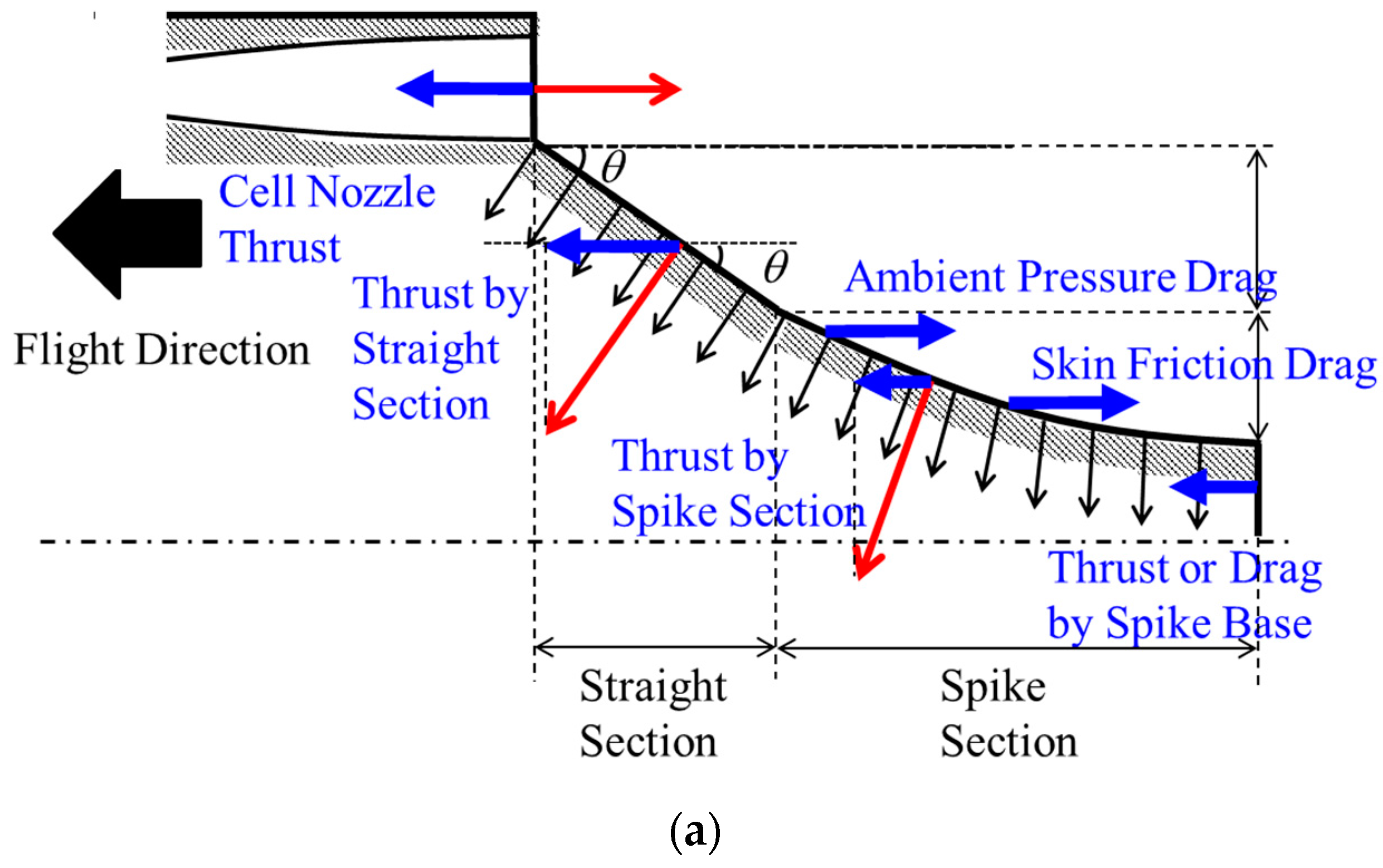
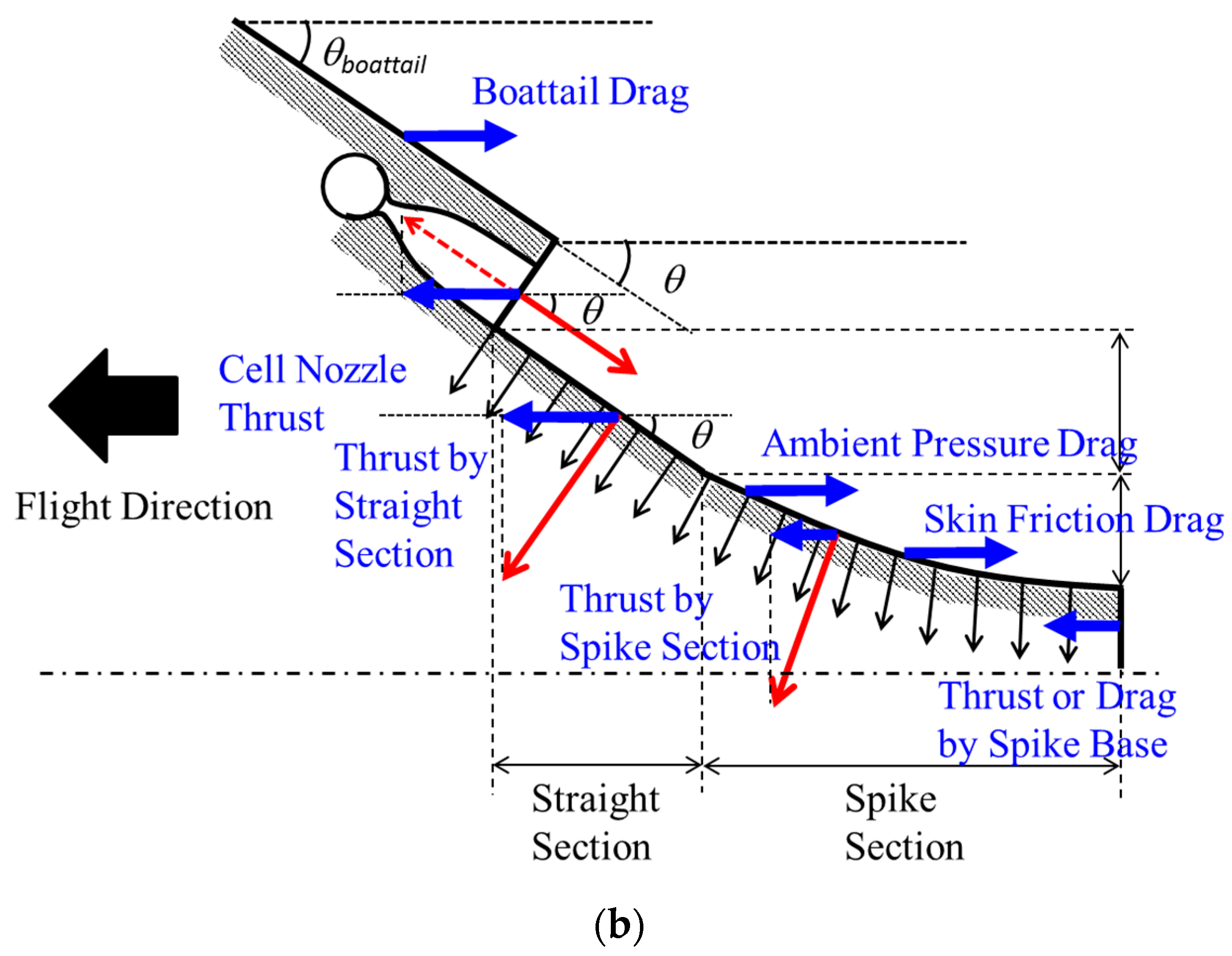
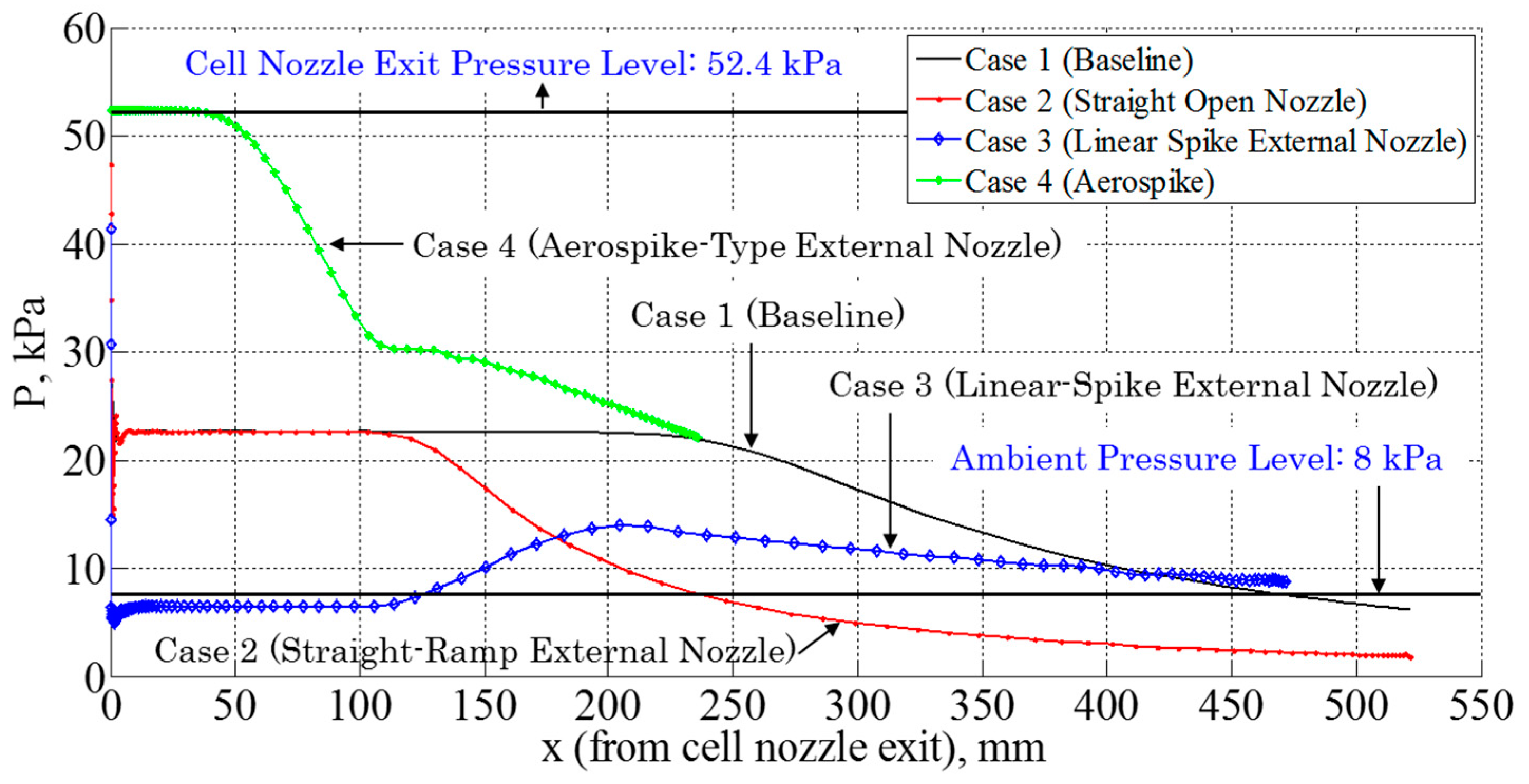
Figure 13 shows the contribution of each thrust or drag component normalized by the total net thrust in the case of the Mach 5.0 on-design flight condition of Case 1. The ambient pressure was fixed at 8 kPa corresponding to the supersonic cruise altitude of approximately 17.5 km above sea level. The cell nozzle total pressure was 4.0 MPa. In this evaluation, the thrust components of the primary engine thrust generated by the cell nozzle, the thrust generated by the external nozzle surface pressure, and drags associated with the ambient pressure and the skin friction were considered. The boattail drag was also considered for Case 4. Each thrust component was calculated by each corresponding term per Equations (3)–(6) for the baseline case, per Equations (3), (5) and (7) for Cases 2 and 3, and per Equations (3), (8) and (9) for Case 4. These thrust components are compared among Cases 1 to 4.
For the baseline case (Case 1), the thrust generated by the primary engine (denoted as the cell nozzle) obviously has the largest contribution to the total net thrust. The ambient pressure drag is included in Equation (5). The contribution of the external nozzle to the total thrust is small and the skin friction drag is also less significant. For Case 2, though the primary thrust has the largest contribution to the total thrust, the thrust generated by the external nozzle surface pressure shows a notable contribution. Ambient pressure drag has the largest negative impact on the total thrust. This is attributable to the area of the nozzle surface which is exposed to ambient pressure. Therefore, the smaller the airframe base height, the smaller the ambient pressure drag. The total thrust can be slightly smaller than that of the baseline case. Case 3 shows a similar trend to that observed in Case 2. The total thrust is nearly identical to that of Case 2. This is because of the large initial expansion angle of the external nozzle which results in much reduced surface pressure and because of having the compression wall feature toward the end of the spike section which results in recovering the surface pressure as seen in
Figure 12. Notably, Case 4 shows a large contribution by the thrust generated by the external nozzle surface pressure. The ambient pressure drag is smaller than in other cases because of the shorter spike length. The boattail drag is also less significant. This is because the ambient pressure level for this premised flight condition was low. The primary engine thrust is reduced because of the boattail inclination. The total net thrust is also nearly identical to those of other cases. Thus, the external nozzle shows no significant impact on the thrust compared to the baseline case for the current cruise condition. Note that the thrust generated by the spike surface pressure could become comparable to the thrust generated by the primary engine depending on the configuration and operation conditions due to the positive freestream effect [
8]. This fact indicates that the thrust could nearly be doubled by employing the aerospike nozzle without considering other associated drags at off-design conditions. However, associated drags due to the employment of the aerospike nozzle cannot be neglected. In this study, only a limited number of cases were evaluated in regards to the initial expansion angle of the external nozzle and the boattail angle. These angles would be optimized to obtain the maximum thrust by the employment of the external nozzle. Thus, the external nozzle gives some benefits in terms of increasing thrust and potentially reducing airframe weight.
4.4. Trim Balance Evaluation for the Baseline and Proposed Cases
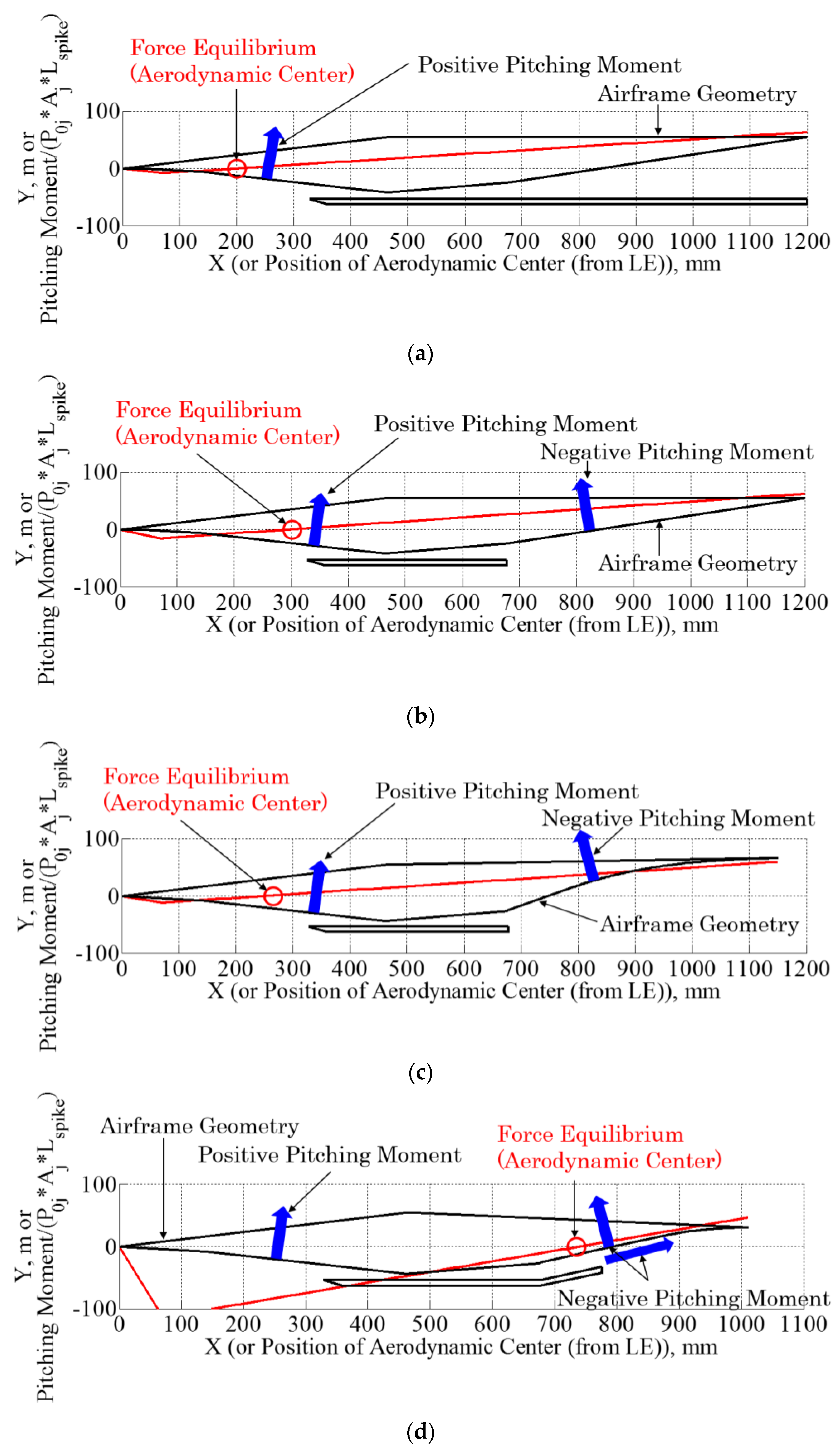
The flight characteristics with respect to the longitudinal static stability of the aircraft were evaluated by investigating the pitching moment coefficient and the aerodynamic center location, as the flight control characteristics, such as the trim of the aircraft, are crucial to the effectiveness of the propulsion system integration to the airframe. This aspect is especially important for the presently proposed configuration, as the external nozzle of the waverider vehicle generates lift force in addition to generating the thrust force. Note that the wing and other attitude control devices were not considered in this evaluation. The balance of the pitching moment was evaluated in the steady flight (cruise) condition. The x-coordinate of the aerodynamic center (xa.c.) was varied from the airframe leading edge to the trailing edge of the external nozzle in the horizontal direction. The y-coordinate of the aerodynamic center (ya.c.) was on the airframe axis that passes through the airframe leading edge. The pitching moment was then calculated around the aerodynamic center by considering the force balance. As a general definition, a positive pitching moment corresponded to the force acting on the airframe in the nose-up direction while a negative pitching moment was assumed for the force acting in the nose-down direction. The force for calculating the positive pitching moment was the pressure force acting on the surface of the leading edge. The force for the negative pitching moment was the sum of the pressure forces acting on the external nozzle surface; this is particularly applied to the proposed Cases 2 to 4. Note that the force generated by the external nozzle portion for the baseline case did not generate the negative pitching moment accounting for the force direction. The pressure forces for the forebody were calculated as the average value acting on the entire surface of the leading edge portion. The distance for calculating the moment was taken as the length between the aerodynamic center and the midpoint of the area where the force was applied. The cell nozzle thrust was taken into account for the negative pitching moment only for Case 4 since the cell nozzle thrust force direction for other cases is horizontal.
The calculated pitching moment is featured in
Figure 14 for each case with the airframe geometry superimposed. The magnitude of the pitching moment was normalized by some factor for the purpose of displaying it with the airframe geometry. For the baseline case, the aerodynamic center or the force equilibrium point where the force balance becomes zero appears near the leading edge. This is because the pitching moment mainly acting on the aircraft for this case is the force acting on the forebody (i.e., no lift force is generated by the external nozzle). Therefore, stabilizers would play an important role in the flight stability and enabling a steady cruise flight.
For Case 2, the aerodynamic center location was found at approximately 300 mm downstream from the leading edge. This location is slightly closer to the airframe midpoint compared to that of Case 1. The aerodynamic center location for Case 3 is nearly identical to that found in Case 2. The primary reason for this observation is attributable to thrusts generated by the external nozzle portion for those two cases are nearly identical as seen in
Figure 13. Those locations are relatively upstream side compared to the true airframe center location. Therefore, stabilizers would play a significant role in making a steady flight. Differently, the aerodynamic center location for Case 4 appears at approximately 20% of airframe length downstream from the true airframe center. This is attributable to (a) the thrust generated by the external nozzle pressure was larger than other thrust components and (b) the cell nozzle thrust direction was angled which resulted in increasing the negative pitching moment. For those evaluated cases, some stabilizers or methods such as the redistribution of the fuel tank [
41] would be favorable to be applied depending on the flight sequence to ensure a steady flight. Therefore, those proposed configurations are feasible in terms of the trim balance with a possibility for further improvement in the balance by stabilizing devices. As mentioned before, optimization study in terms of the initial expansion angle of the external nozzle portion should be conducted.
4.5. Advanced Configuration of Airframe-Integrated Aerospike Propulsion System
Based on the insights obtained through the conceptual study for the employment of the linear-spike external nozzle, some other configurations for the airframe-integrated external nozzle can be proposed. One of the methods is to install the spike nozzle portion (Case 4) in both sides of the aircraft. Namely, twin-nozzle configuration can be considered. This configuration would eliminate the thrust orientation while generating thrust forces.
Figure 15 presents the mesh grids used to compute the flowfield for this configuration. Two linear-spike external nozzles were installed on both sides of the rectangular-shaped airframe fuselage. The top-view of the airframe is displayed. The computed area covered downstream area of the spike nozzle as well as the spike surface. The total number of grids was 39,536. The minimum grid resolution was 0.1 mm as well as that used for other four cases as described in previous sections. The conditions for this calculation are summarized in
Table 1.
Figure 16a displays the pressure distribution showing the flowfield characteristics for the advanced airframe-integrated aerospike-type external nozzle configuration. The flowfield is similar to that seen in the full-length aerospike nozzle [
13,
14,
15,
16,
17,
19,
22,
23]. The expansion waves are emanating from the boattail lip. The slip line formed between the external flow and the jet exhaust flow is seen on both sides of the airframe. In the area downstream of the spike nozzle, obviously the jet exhaust flows flowing on both sides of the spike surface interact each other on the center axis of the airframe. There is no wake region behind the spike edge for this condition. Further downstream of the spike edge, the tail shock waves are seen. The pressure distribution and thereby thrust forces generated from both sides of the spike surface are symmetrical. Therefore, no asymmetric force in the lateral direction is generated by this configuration. Note that the thrust vectoring [
16,
17] is possible by controlling the thrust force generated from each cell nozzle. For example, the right-hand side of the cell nozzle generates the full thrust; and the left-hand side of the cell nozzle generates the 50% of the full thrust, the vehicle will have the momentum which makes the vehicle attitude turning toward the left direction. The pressure distribution on the airframe center axis is presented in
Figure 16b. Only the right-hand side is presented by assuming the symmetrical flow structure in terms of the center axis. The wall pressure distribution is basically the same as that observed in
Figure 12. The pressure keeps decreasing in the area downstream of the spike edge and then becomes lower than the ambient pressure level at approximately 100 mm downstream the spike edge. Those high-pressure regions contribute to the positive thrust, and therefore this configuration is beneficial for the thrust enhancement and is considered to be feasible as an airframe-integrated external nozzle.