The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine
Abstract
:1. Introduction
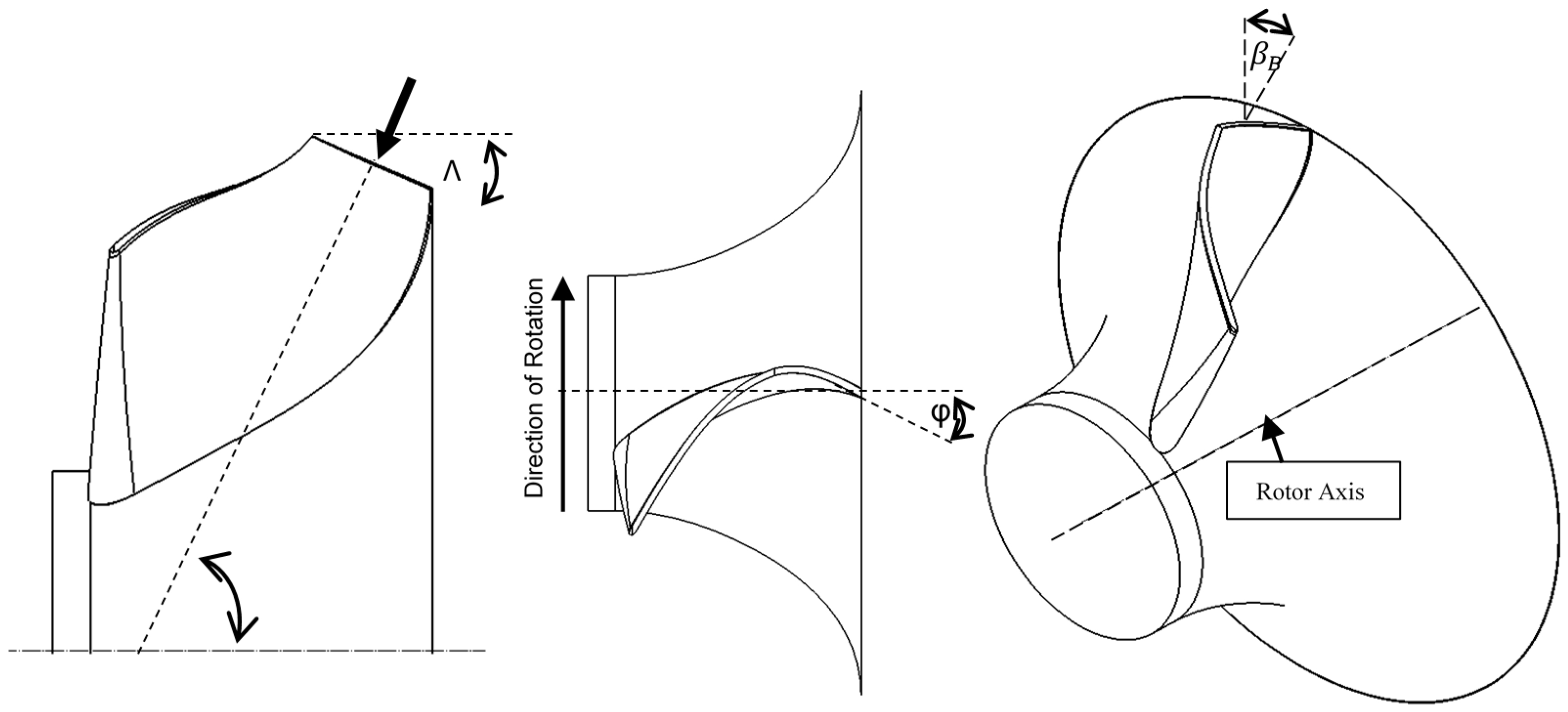
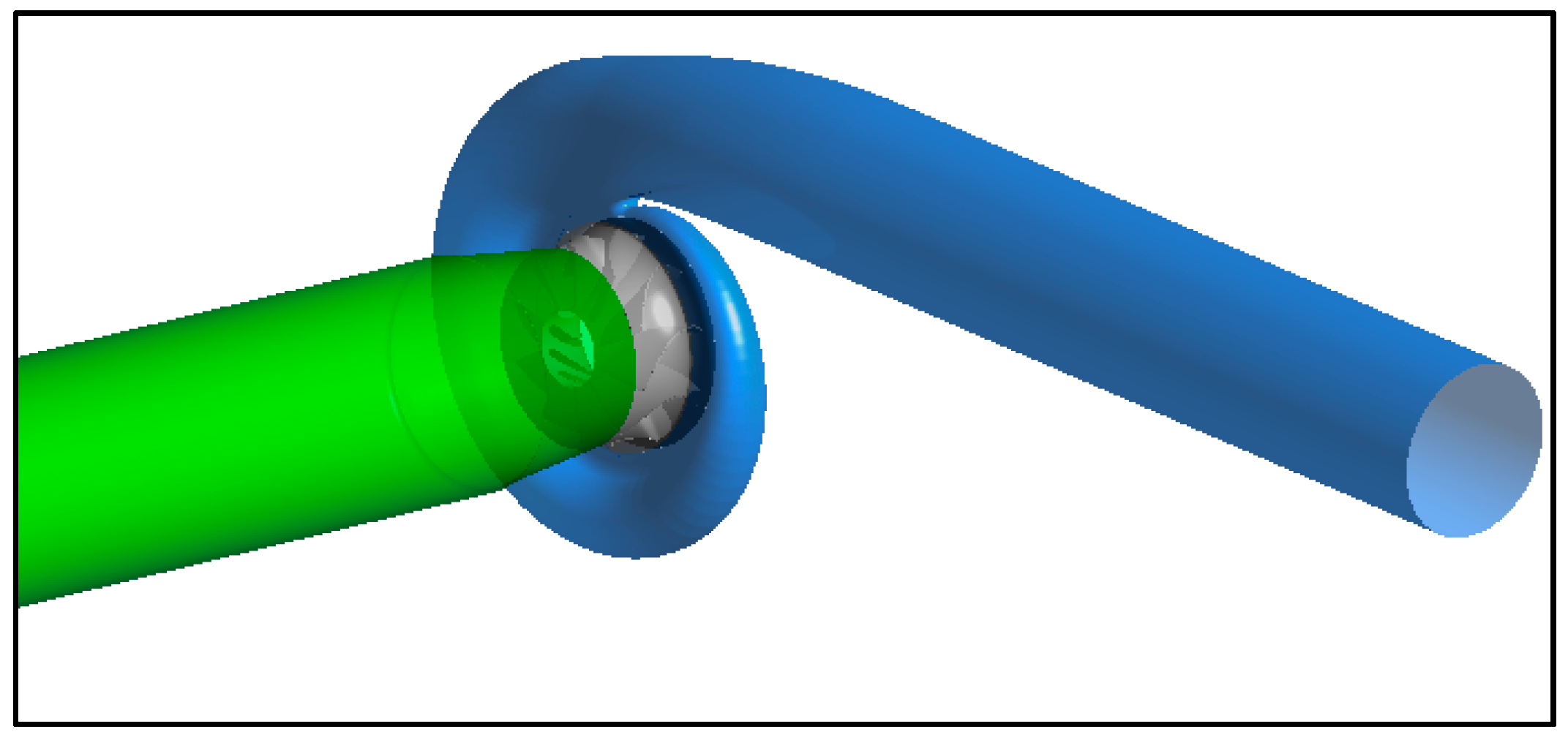
2. Turbine Design
3. Computational Approach
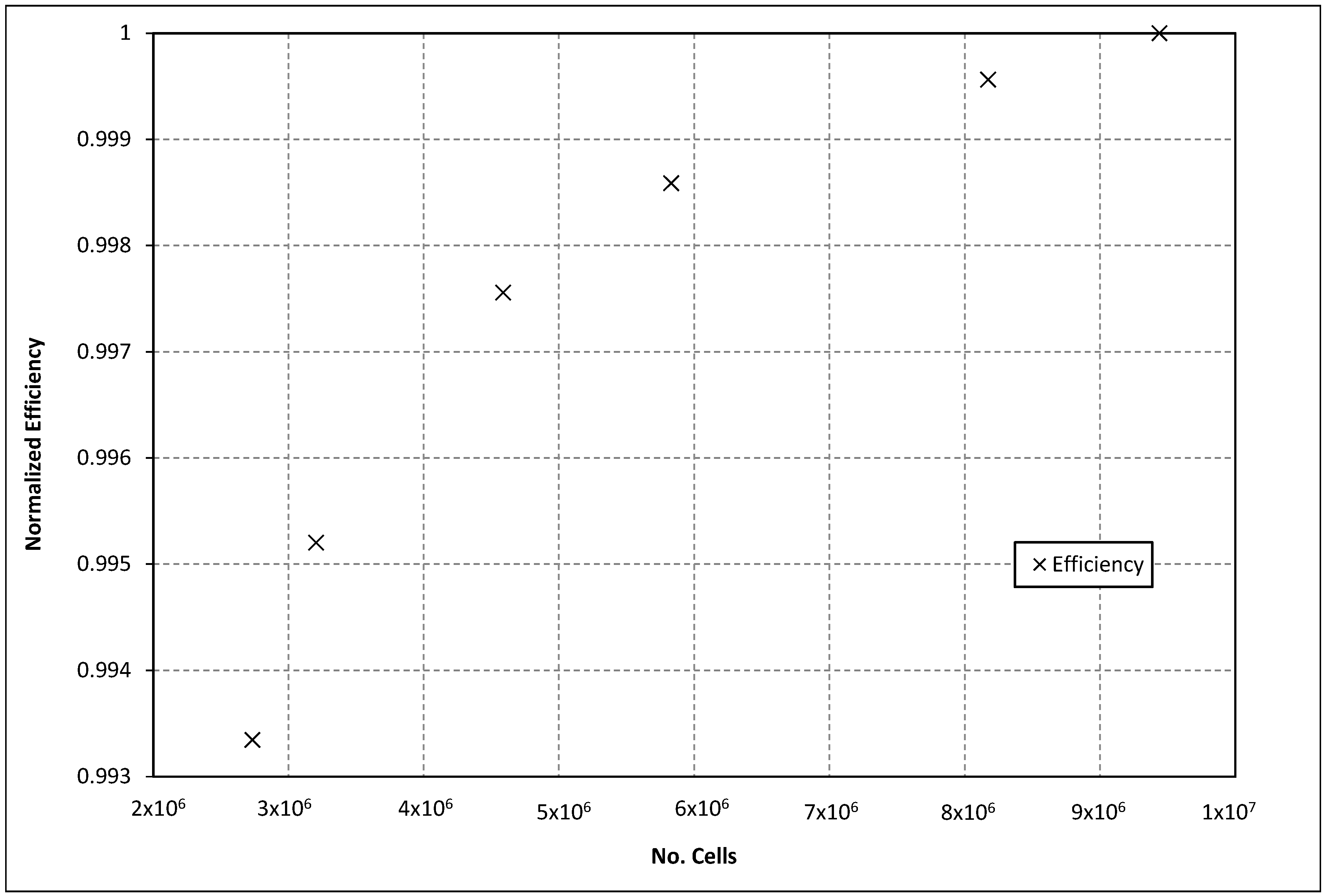
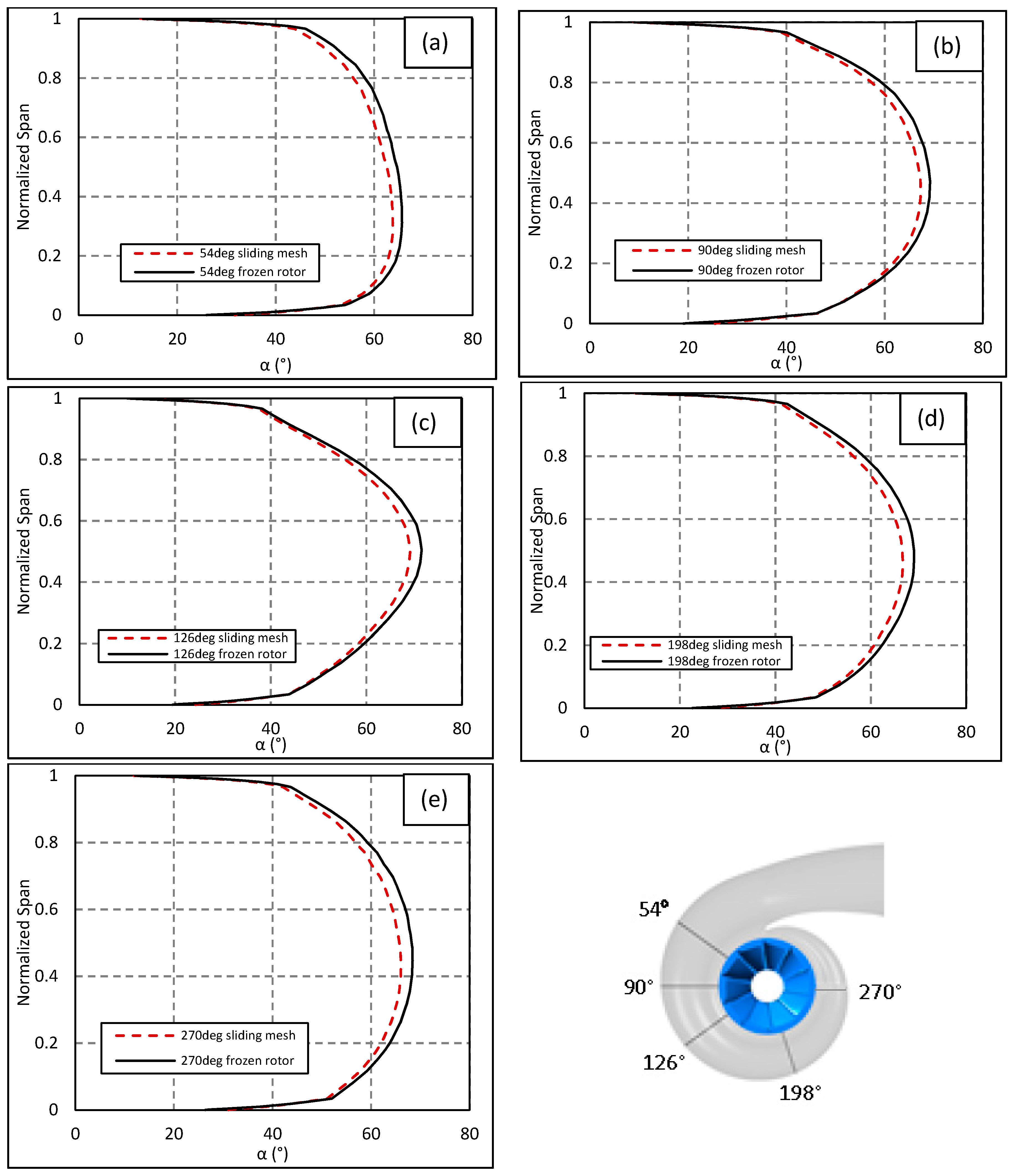
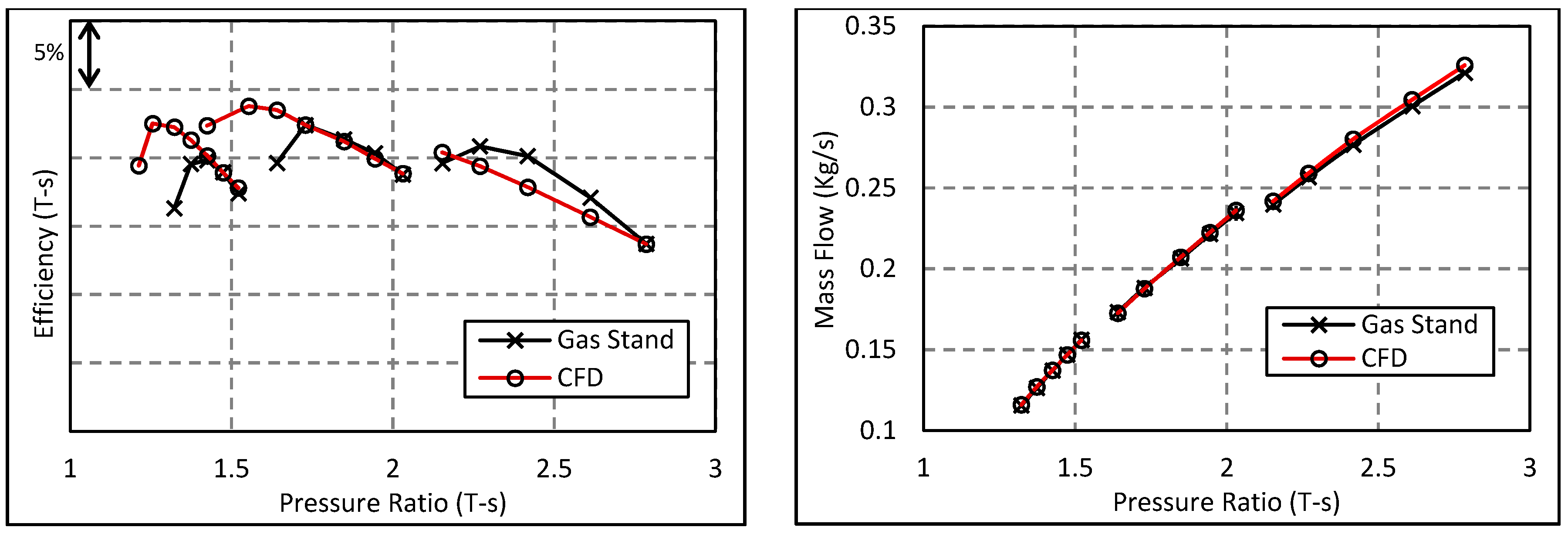
Computational Validation
4. Results and Discussion
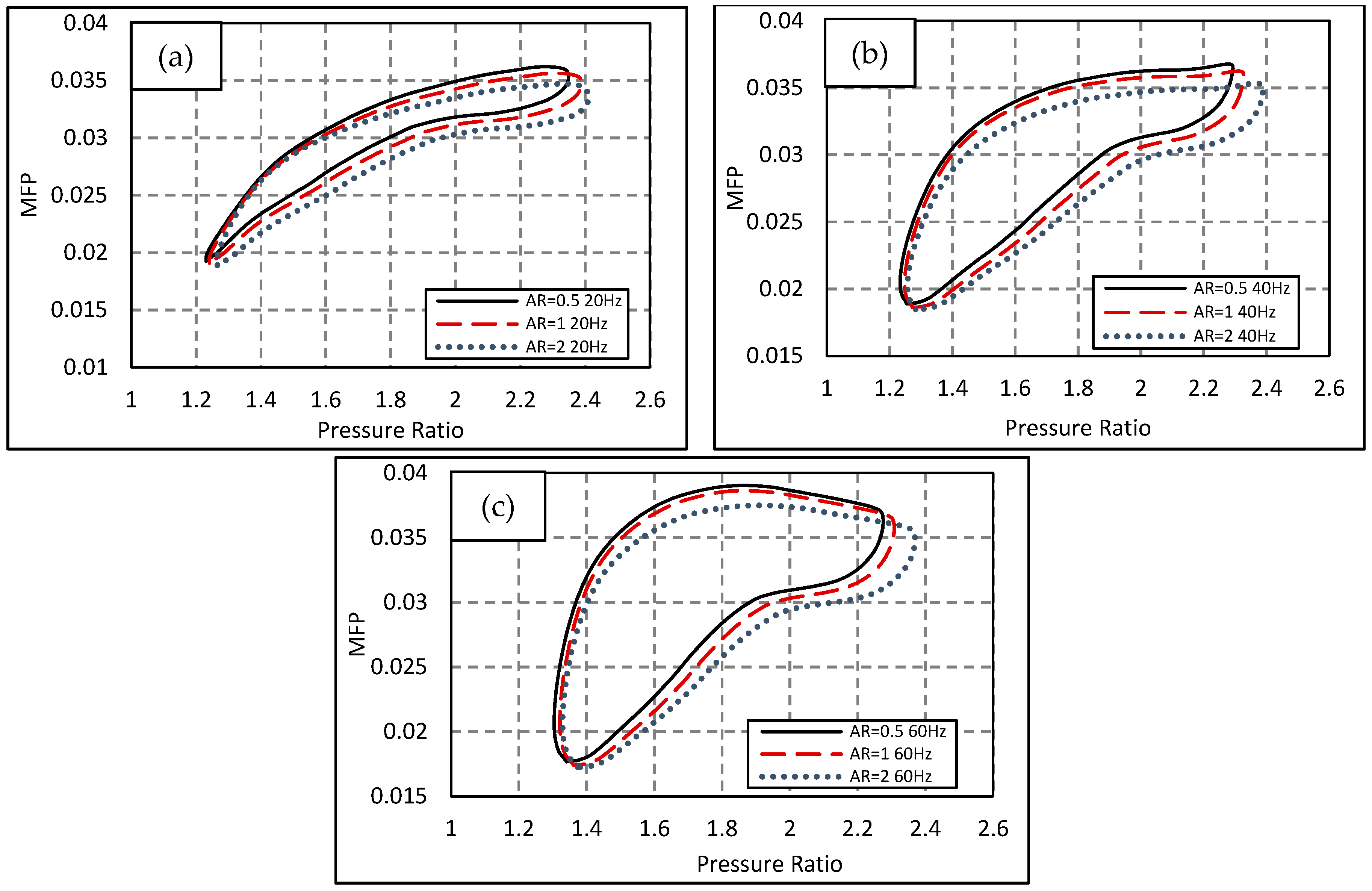
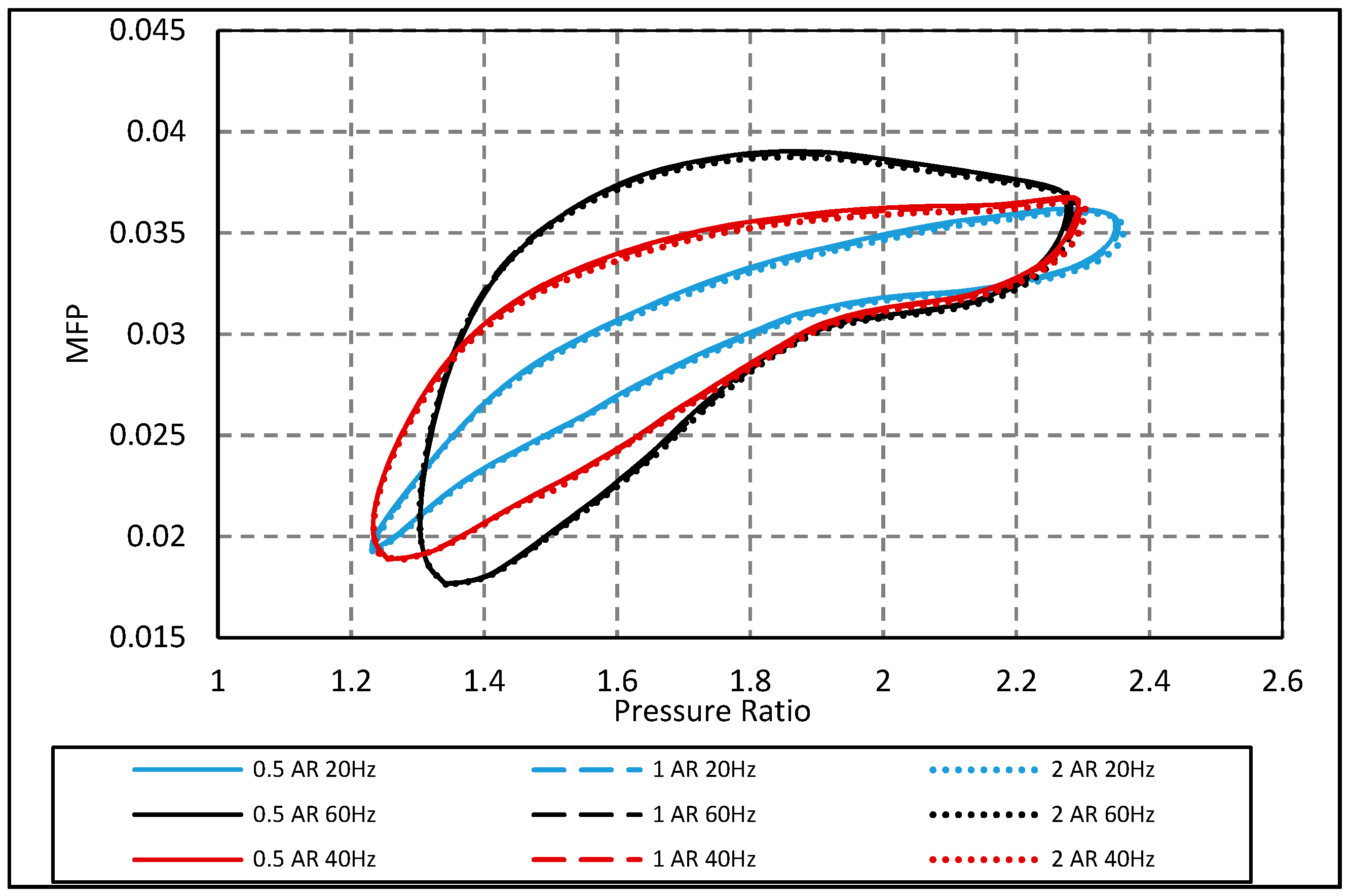
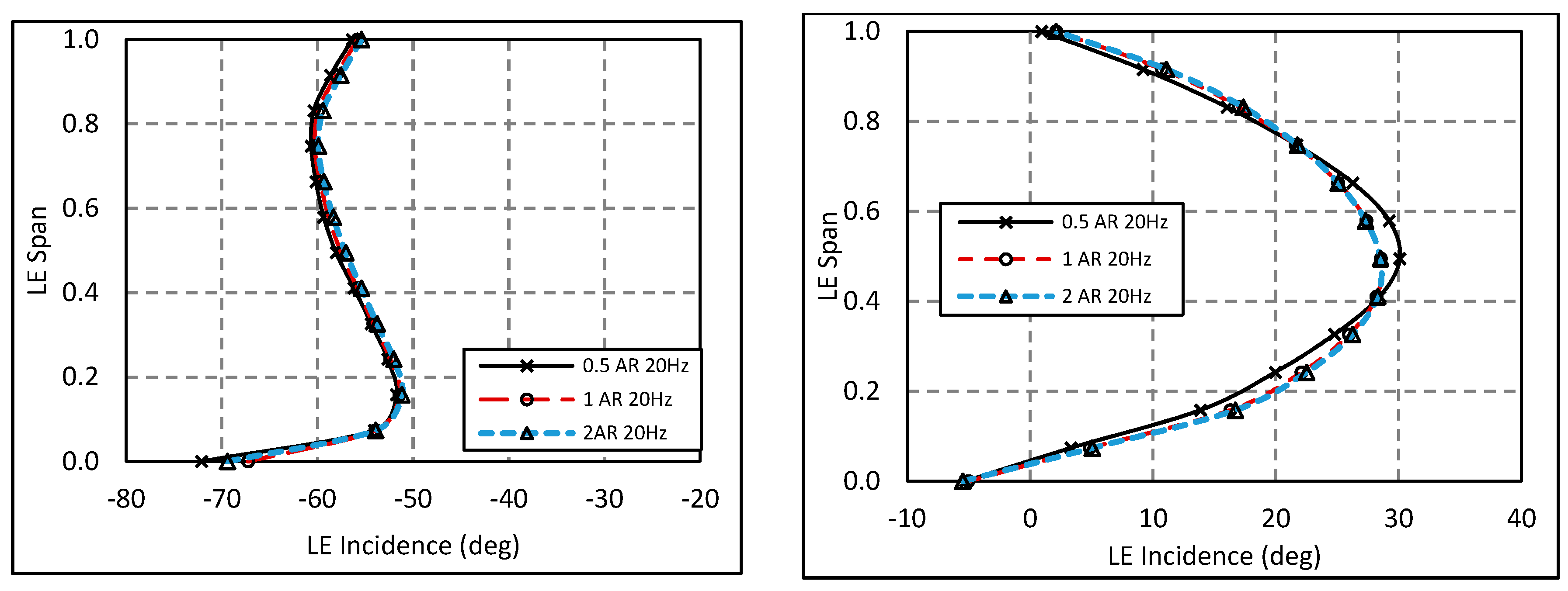
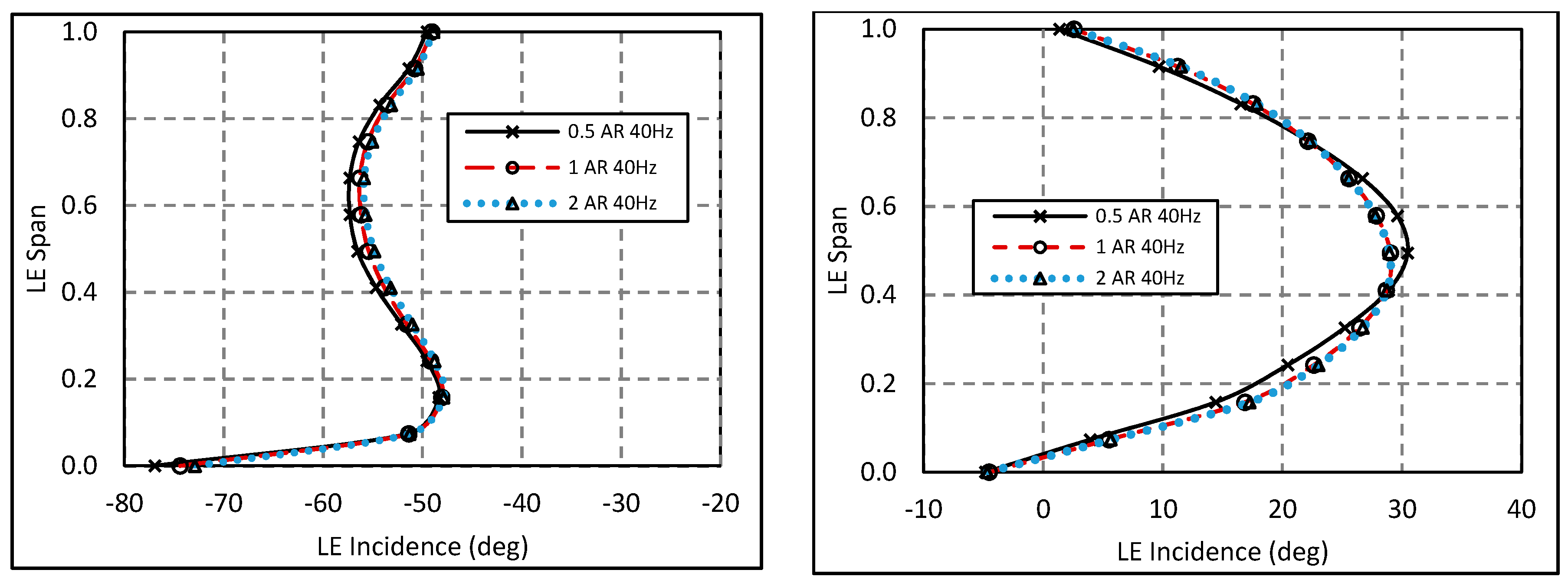
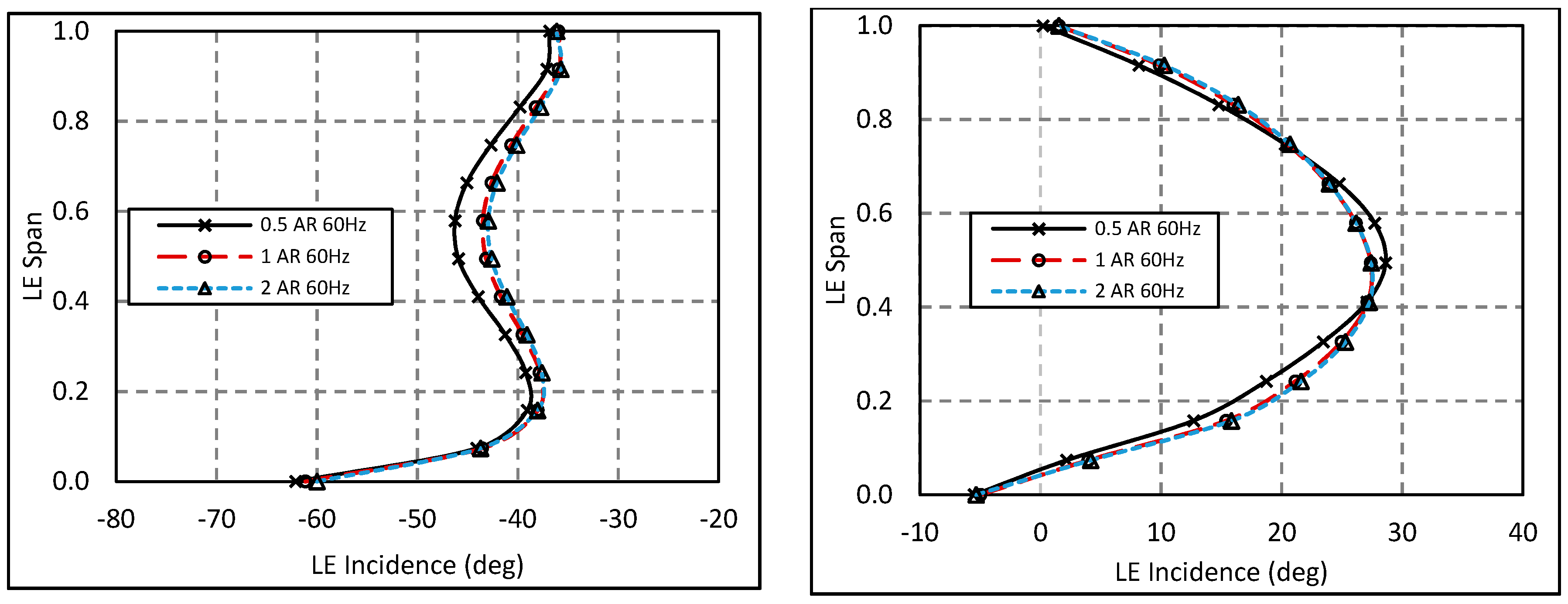
4.1. Impact of Volute Ascpect Ratio on MFP
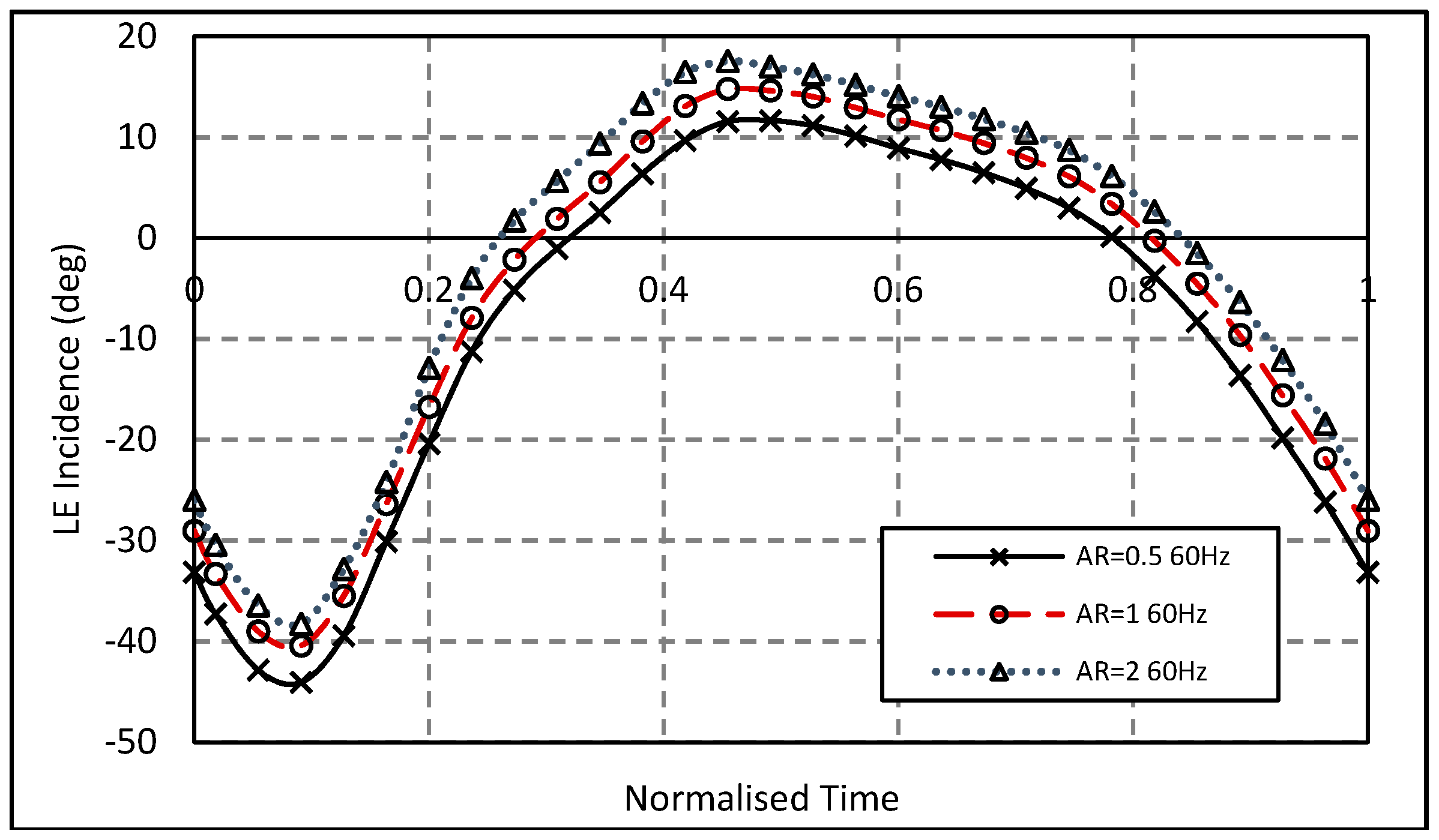
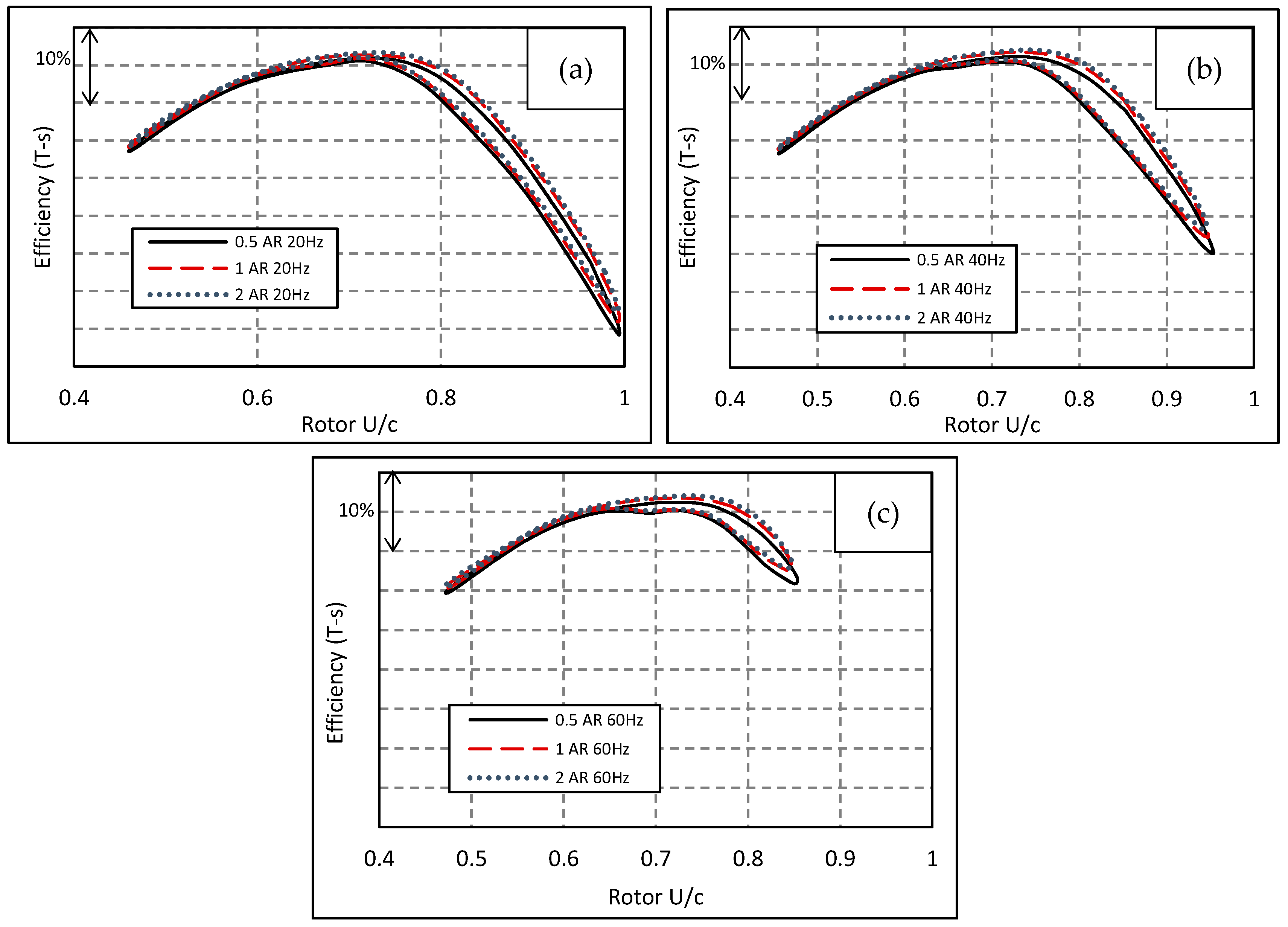
4.2. Aspect Ratio Effect with Constant MFP
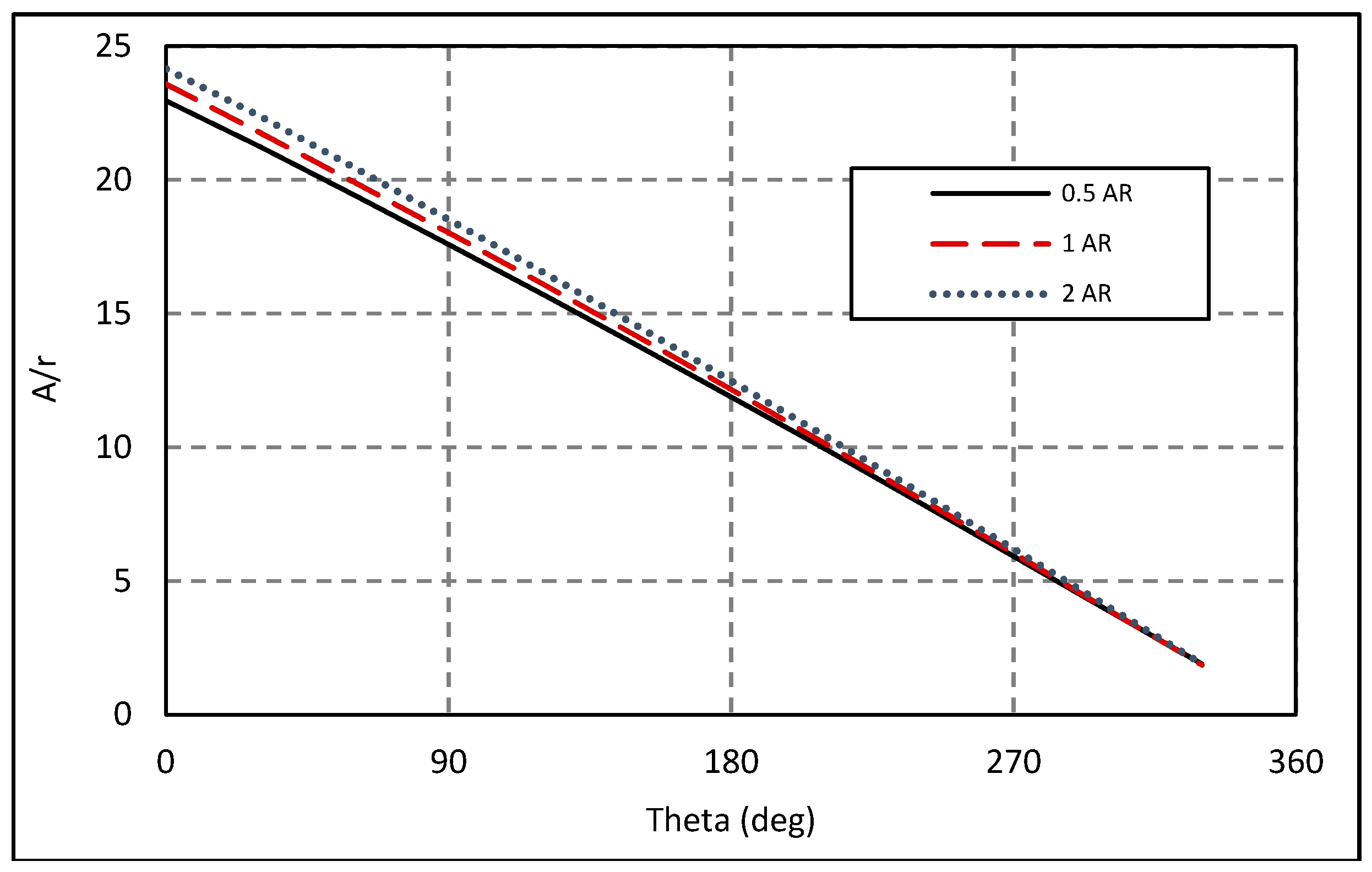
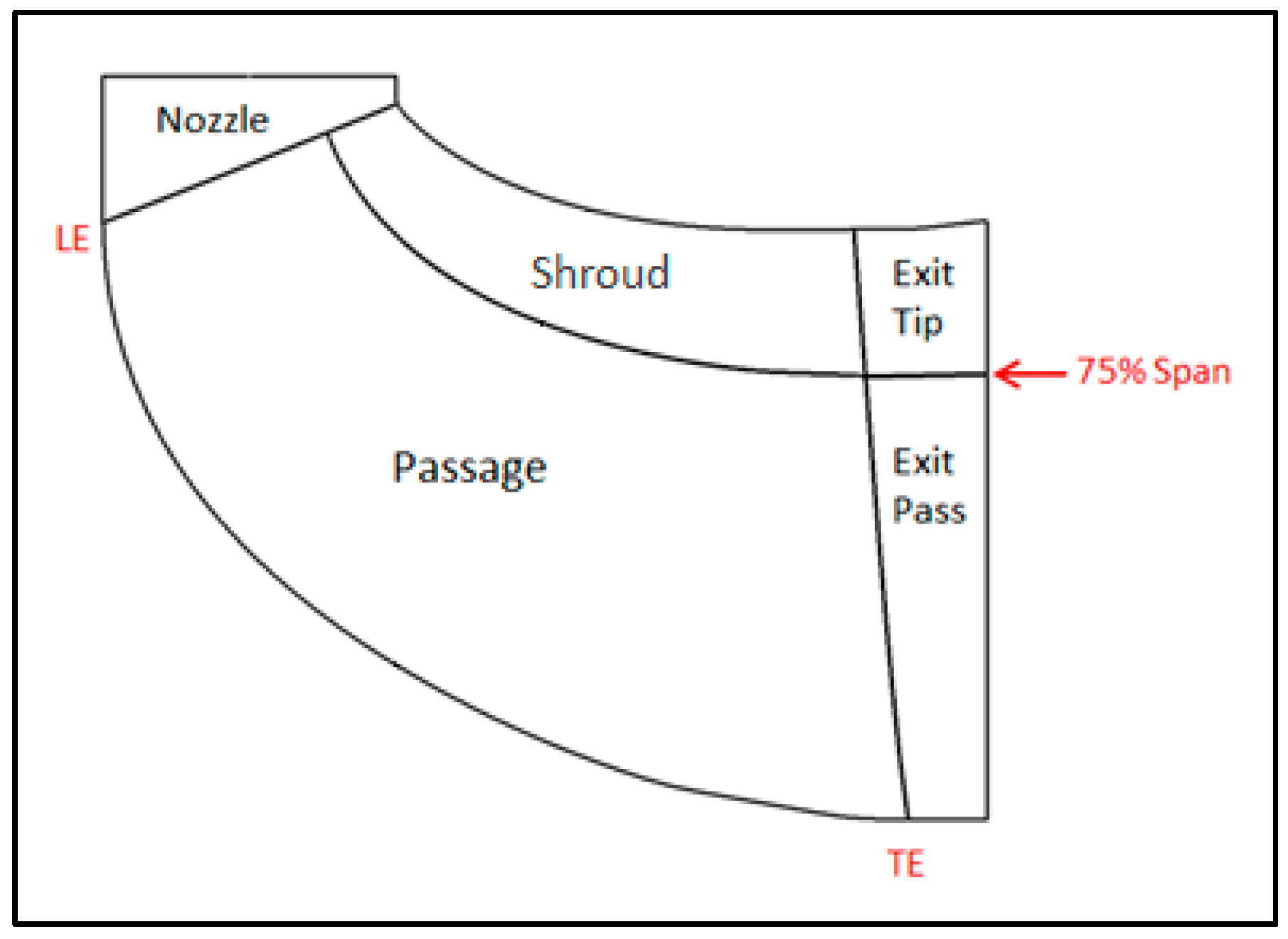
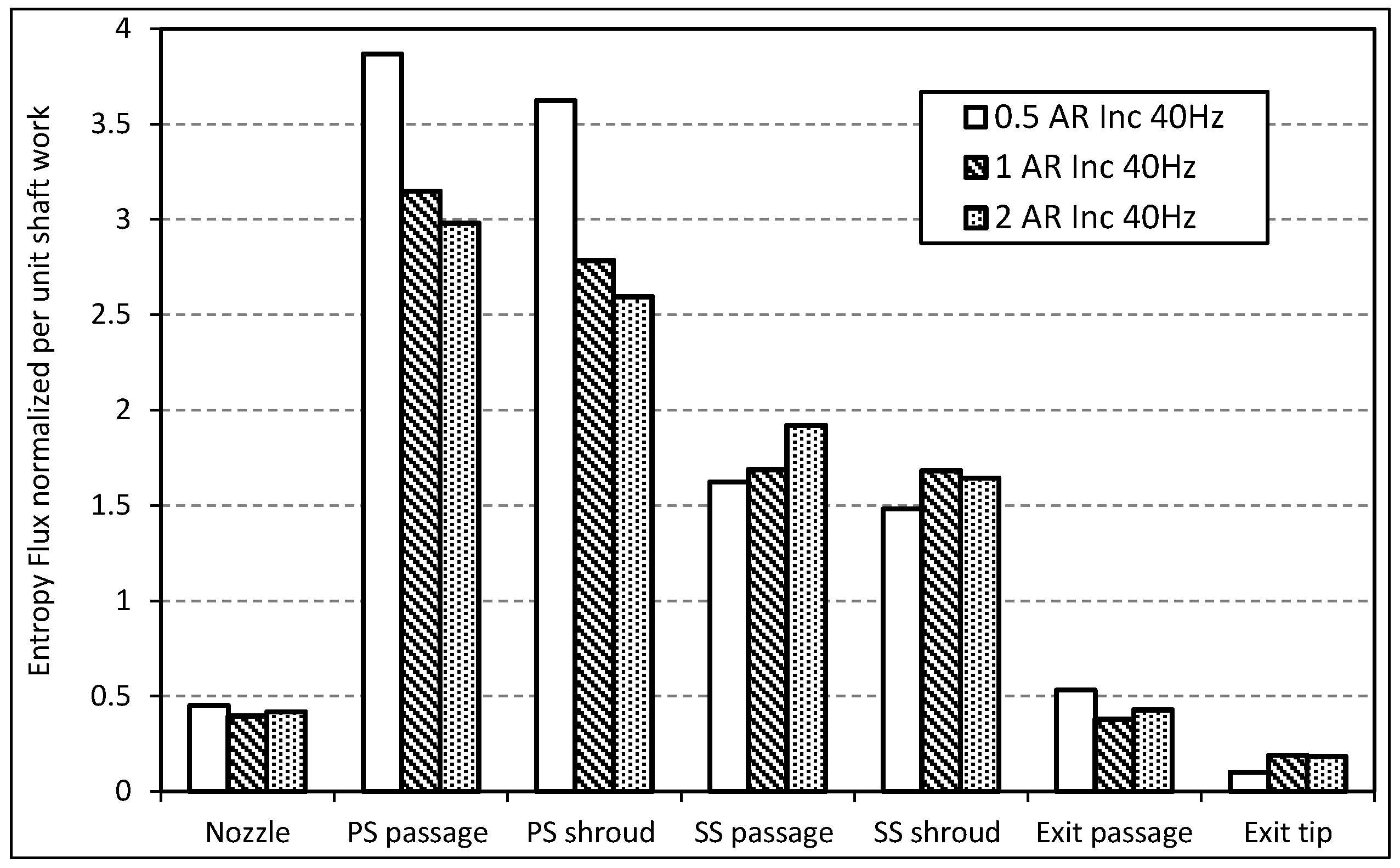
4.3. Secondary Flow Structures
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| AR | Aspect Ratio |
| A/r | Area Radius Ratio |
| Dean Number | |
| Absolute Velocity | |
| CFD | Computational Fluid Dynamics |
| d | Diameter |
| LE | Leading Edge |
| LES | Large Eddy Simulation |
| MFP | Mass Flow Parameter |
| Mass Flow | |
| Mass Flow Pulsation Number | |
| PR | Pressure Ratio |
| PS | Pressure Surface |
| Radius of Curvature | |
| Reynolds Number Based on Diameter | |
| SAS | Scaled Adaptive Simulation |
| SST | Shear Stress Transport |
| SS | Suction Surface |
| TE | Trailing Edge |
| Bulk Pipe Velocity | |
| Blade Speed | |
| Velocity Ratio | |
| URANS | Unsteady Reynolds Averaged Navier Stokes |
| Relative Velocity | |
| Greek Letters | |
| Relative Flow Angle | |
| Blade Angle | |
| Flow Cone Angle | |
| Blade Cone Angle | |
| Blade Camber Angle | |
| Density | |
| Dynamic Viscosity | |
| Subscripts | |
| T-T | Total to Total Pressure |
| T-s | Total to Static Pressure |
References
- Rajoo, S.; Martines-Botas, R. Mixed Flow Turbine Research: A Review. J. Turbomach. 2008, 130, 044001. [Google Scholar] [CrossRef]
- Abidat, M.; Hachemi, M.; Hamidou, M.K.; Baines, N.C. Predictions of the Steady and Non-Steady Performance of a Highly Loaded Mixed Flow Turbine; Institue of Mechanical Engineers: Westminster, UK, 1998. [Google Scholar]
- Karamanis, N.; Martinez-Botas, R.; Su, C. Mixed flow turbines: Inlet and exit flow under steady and pulsating conditions. J. Turbomach. 2001, 123, 359–371. [Google Scholar] [CrossRef]
- Palfreyman, D.; Martinez-Botas, R. The pulsating flow field in a mixed flow turbocharger turbine: An experimental and computational study. ASME J. Turbomach. 2004, 697–708. [Google Scholar] [CrossRef]
- Abidat, M.; Baines, N.; Firth, M. Design of a highly loaded mixed flow turbine. Proc. Inst. Mech. Eng. Part A J. Power Energy 1992, 206, 95–107. [Google Scholar] [CrossRef]
- Palfreyman, D.; Martinez-Botas, R. Numerical Study of the Internal Flow Field Characteristics in Mixed Flow Turbines; ASME: New York, NY, USA, 2002. [Google Scholar]
- Japikse, D.; Baines, N.C. Introduction to Turbomachinery; Oxford University Press: Oxford, UK, 1994. [Google Scholar]
- Morrison, R.; Spence, S.; Kim, S.; Filsinger, D.; Leonard, T. Investigation of the effects of flow conditions at rotor inlet on mixed flow turbine performance for automotive applications. In Proceedings of the International Turbocharging Seminar, Tianjin, China, 21–22 September 2016. [Google Scholar]
- Yang, M.; Martinez-Botas, R.; Rajoo, S.; Yokoyama, T.; Ibaraki, S. An investigation of volute cross-sectional shape on turbocharger turbine under pulsating conditions in internal combustion engine. Energy Convers. Manag. 2015, 105, 167–177. [Google Scholar] [CrossRef]
- Meghnine, M.A.; Hamidou, M.K.; Hamel, M. Influence of the volute cross-sectional shape on mixed inflow turbine performances. Adv. Mech. Eng. 2017, 9. [Google Scholar] [CrossRef]
- Yang, M.; Martinez-Botas, R.; Rajoo, S.; Yokoyama, T.; Ibaraki, S. Influence of Volute Cross-Sectional Shape of a Nozzleless Turbocharger under Pulsating Flow Condition. In Proceedings of the ASME Turbo Expo, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Cerdoun, M.; Ghenaiet, A. Analyese of flow structures through radial turbine twin-entry volute under pulsatile flows. In Proceedings of the International Conference on Turbocharges and Turbocharging, London, UK, 17–18 May 2016; Institution of Mechanical Engineers: Westminster, UK, 2016. [Google Scholar]
- Lee, S.; Jupp, M.; Nickson, A. The influence of secondary flow structures in a turbocharger turbine housing in steady state and pulsating flow conditions. In Proceedings of the 2016 7th International Conference on Mechanical and Aerospace Engineering (ICMAE), London, UK, 18–22 July 2016; IEEE: Piscataway, NJ, USA, 2016. [Google Scholar]
- Galindo, J.; Hoyas, S.; Fajardo, P.; Navarro, R. Set-Up Analysis and Optimisation of CFD Simulations for Radial Turbines. Eng. Appl. Comput. Fluid Mech. 2013, 7, 441–460. [Google Scholar]
- ANSYS Workbench; ANSYS17.0; ANSYS, Inc.: Canonburg, PA, USA, 2017.
- Roclawski, H.; Gugau, M.; Langecker, F.; Böhle, M. Influence of Degree of Reaction on Turbine Performance for Pulsating Flow Conditions. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Yang, M.; Martinez-Botas, R.; Srithar, R.; Ibaraki, S.; Yokoyama, T.; Deng, K. Unsteady Behaviours of a Volute in Turbocharger Turbine under Pulsating Conditions. In Proceedings of the Global Power and Propulsion Forum, Zurich, Switzerland, 16–18 January 2017. [Google Scholar]
- Cerdoun, M.; Ghenaiet, A. Analyses of steady and unsteady flows in a turbocharger’s radial turbine. Proc. Inst. Mech. Eng. Part E J. Process Mech. Eng. 2015, 229, 130–145. [Google Scholar] [CrossRef]
- Yang, B.; Newton, P.; Martinez-Botas, R. Unsteady Evolution of Secondary Flows in A Mixed Turbine. In Proceedings of the Global Power and Propulsion Forum, Zurich, Switzerland, 16–18 January 2017. [Google Scholar]
- Hellstrom, F.; Fuchs, L. Numerical Computation of the Pulsatile Flow in a Turbocharger with Realistic Inflow Conditions from an Exhaust Manifold; ASME: New York, NY, USA, 2009. [Google Scholar]
- Menter, F.; Egorov, Y. A Scale-Adaptive Simulation Model Using Two-Equation Models. In Proceedings of the 43rd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 2005. [Google Scholar]
- Simpson, A.T.; Spence, S.; Watterson, J.K. A comparison of the flow structures and losses within vaned and vaneless stators for radial turbines. J. Turbomach. 2009, 131, 031010. [Google Scholar] [CrossRef]
- Zimmermann, R.; Baar, R.; Enghardt, L.; Hakensson, S. Investigation on Pulsating Turbine Flow Radial Turbines. In Proceedings of the Aachen Colloquium Automobile and Engine Technology, Aachen, Germany, 5–7 October 2015. [Google Scholar]
- Newton, P.J. An Experimental and Computational Study of Pulsating Flow within a Double Entry Turbine with Different Nozzle Settings. Ph.D. Thesis, Imperial College London, London, UK, 2014. [Google Scholar]
- Lee, S.P.; Jupp, M.L.; Nickson, A.K.; Allport, J.M. Analysis of a tilted turbine housing volute design under pulsating inlet conditions. In Proceedings of the ASME Turbo Expo 2017: Turbomachinery Technical Conference and Exposition, Charlotte, NC, USA, 26–30 June 2017; American Society of Mechanical Engineers: New York, NY, USA, 2017. [Google Scholar]
- Dean, W.R. Note on the motion of fluid in a curved pipe. Lond. Edinb. Dubl. Phil. Mag. 1927, 4, 208–223. [Google Scholar] [CrossRef]
- Dean, W.R. The stream-line motion of fluid in a curved pipe (Second paper). Lond. Edinb. Dubl. Phil. Mag. 1928, 5, 673–695. [Google Scholar] [CrossRef]
- Kalpakli Vester, A. Vortices in Turbulent Curved Pipe Flow-Rocking, Rolling and Pulsating Motions; KTH Royal Institute of Technology: Stockholm, Sweden, 2014. [Google Scholar]



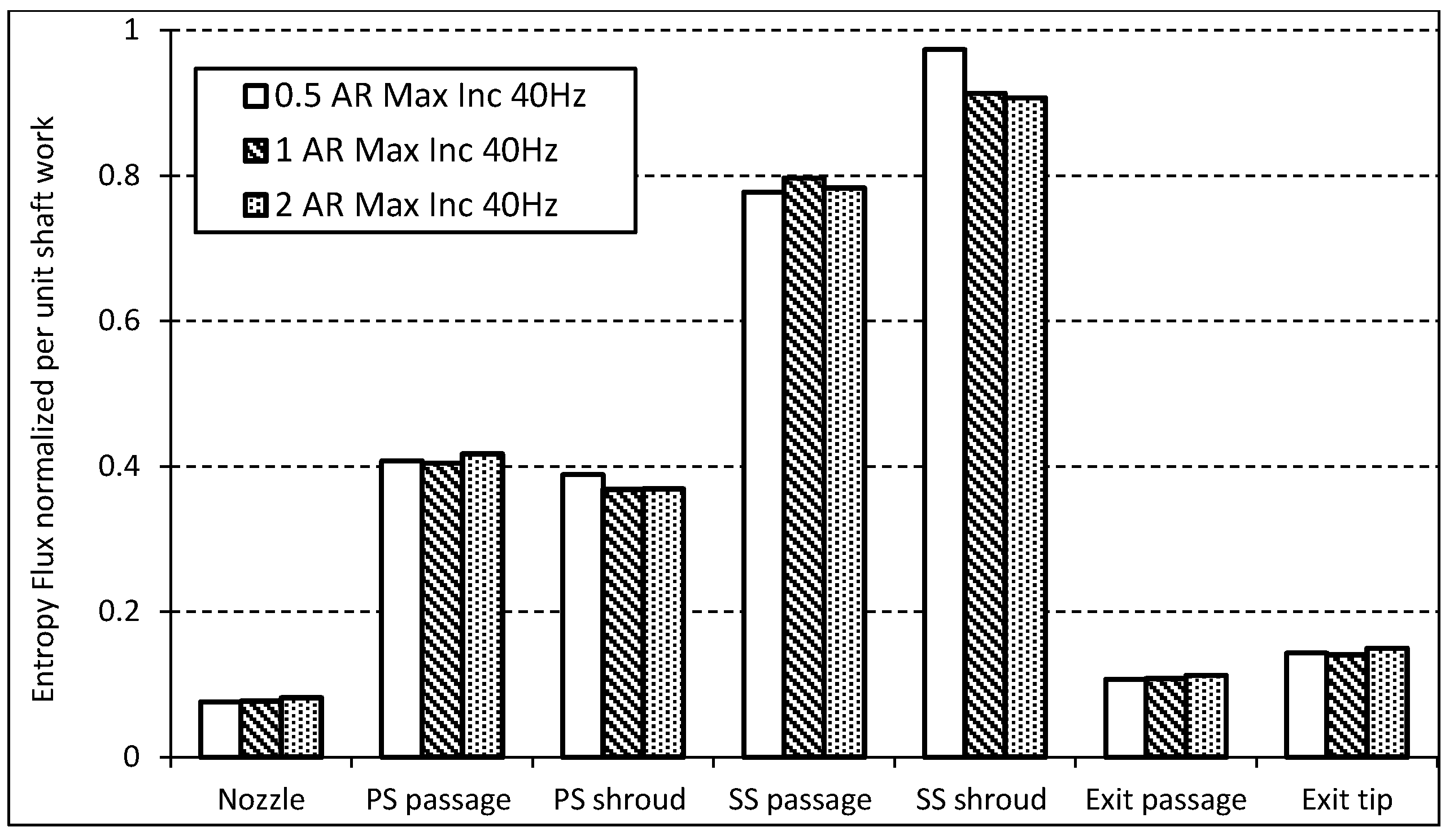
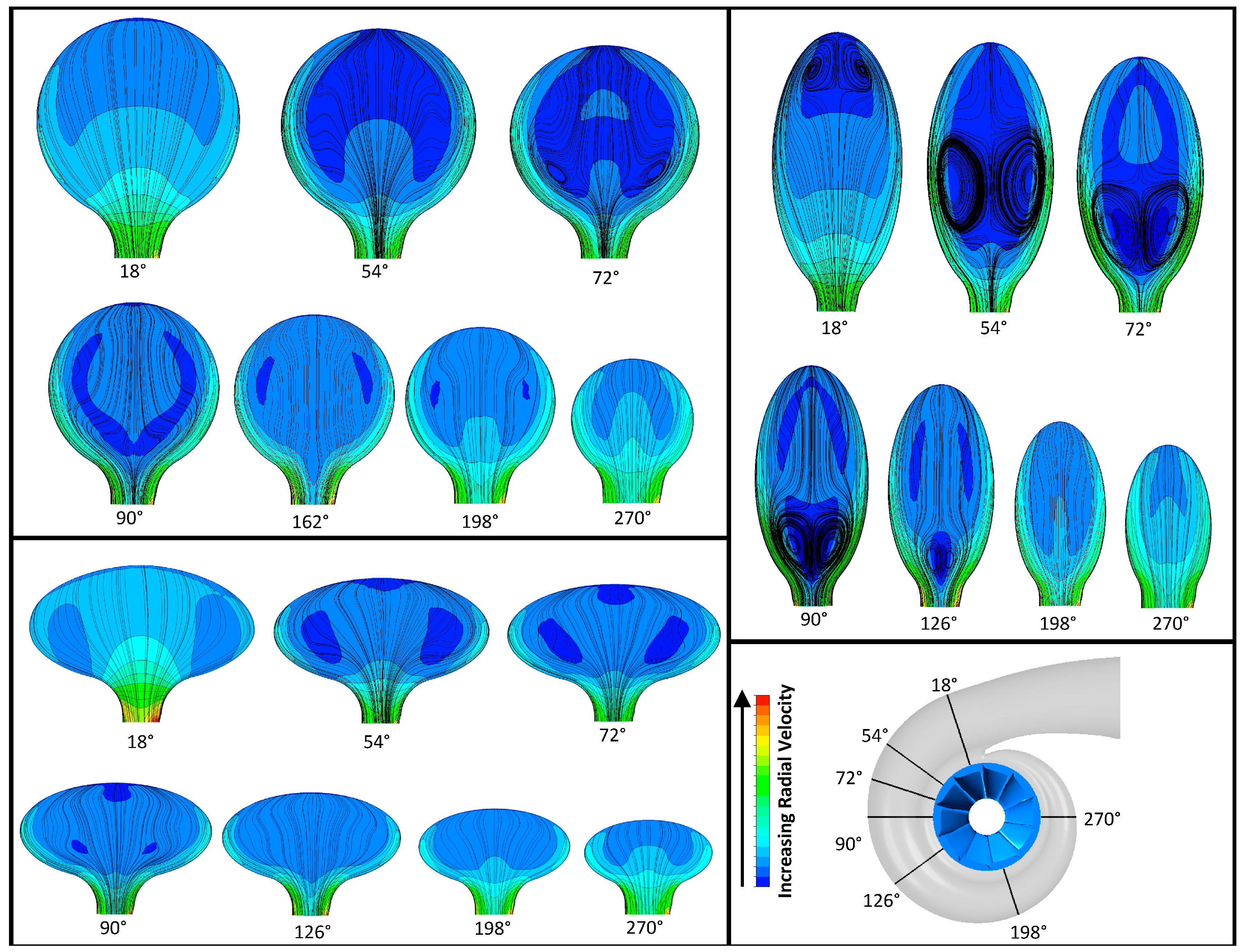

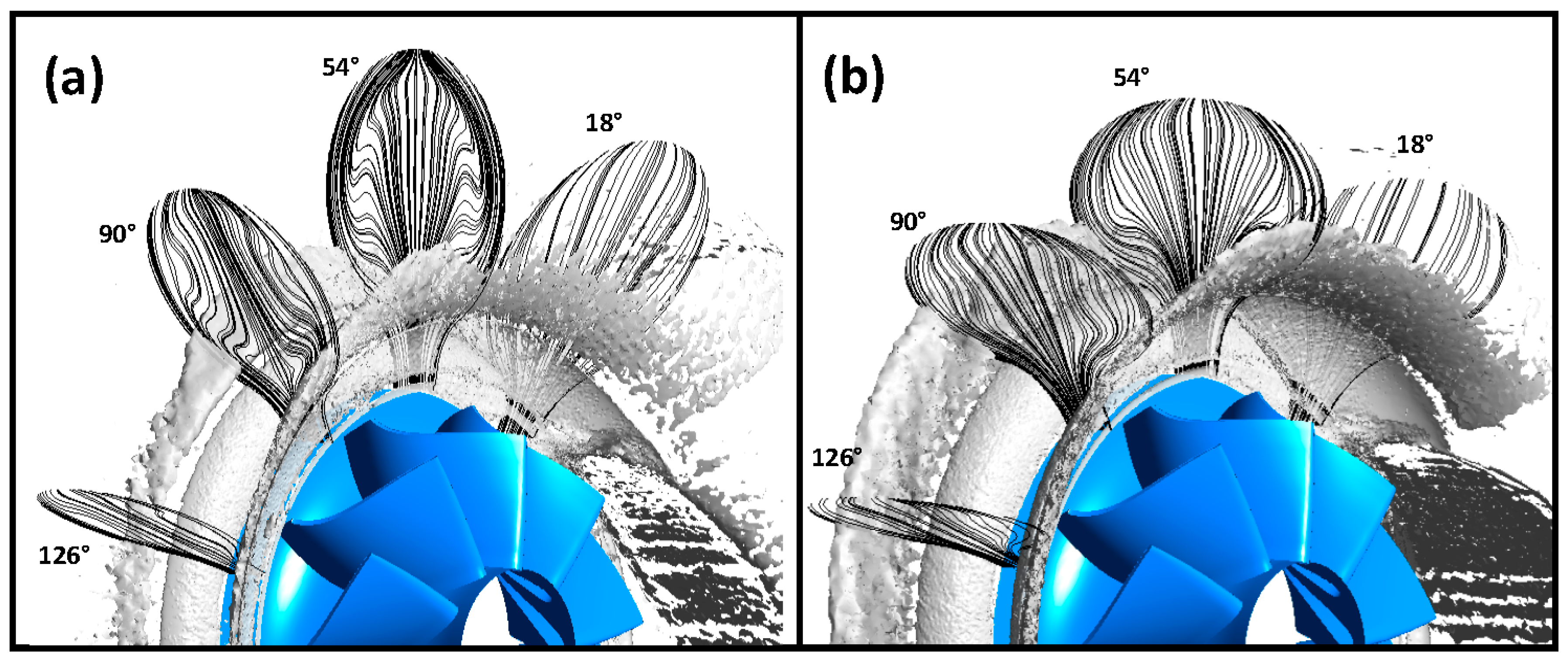
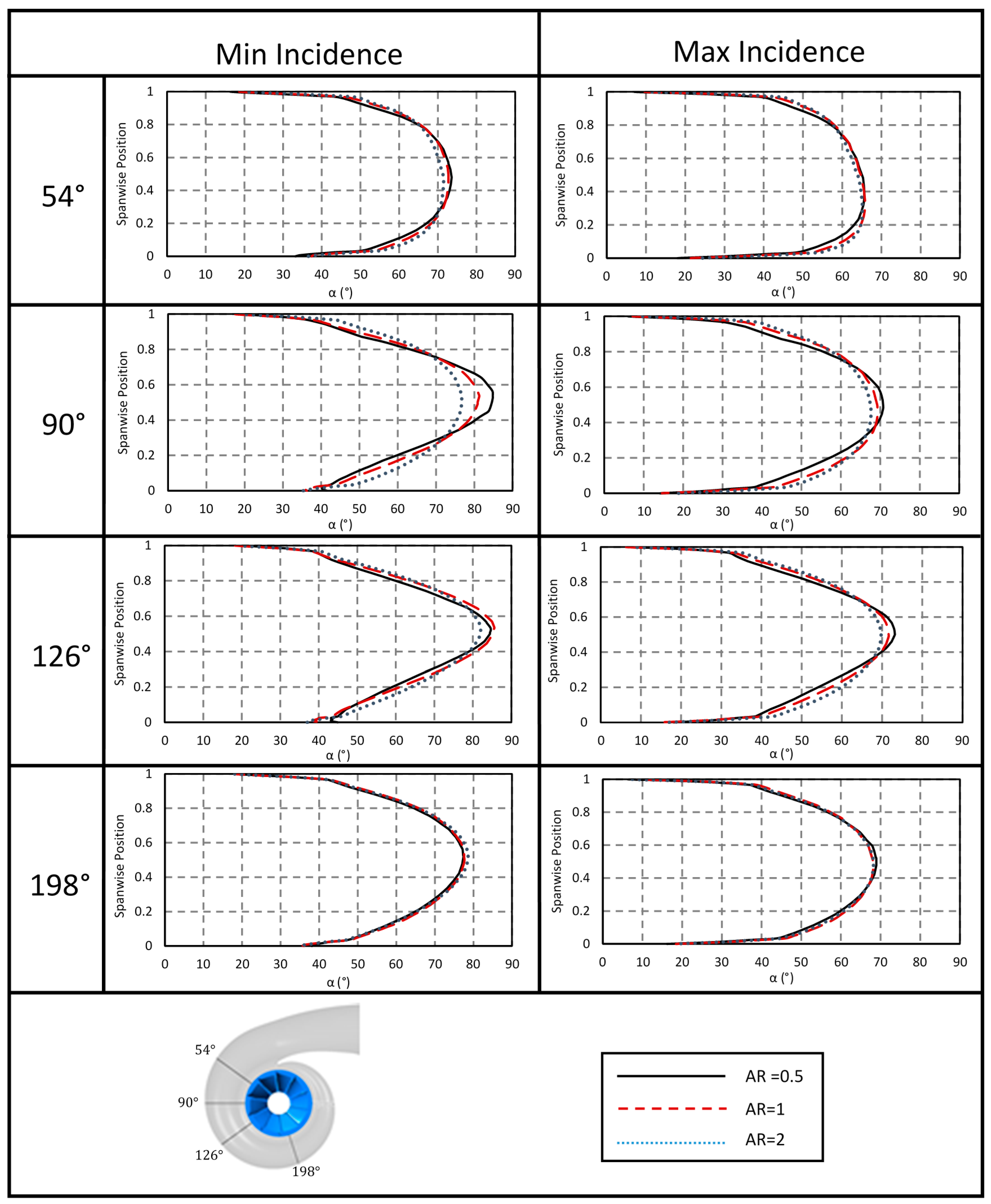
| Frequency | Aspect Ratio | 0.5 | 1 | 2 |
|---|---|---|---|---|
| 20 Hz | Eff Min U/cs | 99.02% | 99.94% | 100.00% |
| Eff Max U/cs | 92.41% | 96.48% | 100.00% | |
| Cycle AVG Rotor Eff | 98.96% | 99.75% | 100.00% | |
| Cycle AVG Stage Eff | 98.53% | 99.57% | 100.00% | |
| Volute Pt Loss Coefficient | 0.1231 | 0.1064 | 0.1061 | |
| 40 Hz | Eff Min U/cs | 99.12% | 100.00% | 99.99% |
| Eff Max U/cs | 93.85% | 97.96% | 100.00% | |
| Cycle AVG Rotor Eff | 99.00% | 99.77% | 100.00% | |
| Cycle AVG Stage Eff | 98.59% | 99.61% | 100.00% | |
| Volute Pt Loss Coefficient | 0.1221 | 0.1056 | 0.1057 | |
| 60 Hz | Eff Min U/cs | 98.83% | 99.71% | 100.00% |
| Eff Max U/cs | 97.04% | 99.38% | 100.00% | |
| Cycle AVG Rotor Eff | 99.01% | 99.73% | 100.00% | |
| Cycle AVG Stage Eff | 98.60% | 99.59% | 100.00% | |
| Volute Pt Loss Coefficient | 0.1195 | 0.1032 | 0.1035 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, S.P.; Barrans, S.M.; Jupp, M.L.; Nickson, A.K. The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine. Aerospace 2017, 4, 56. https://doi.org/10.3390/aerospace4040056
Lee SP, Barrans SM, Jupp ML, Nickson AK. The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine. Aerospace. 2017; 4(4):56. https://doi.org/10.3390/aerospace4040056
Chicago/Turabian StyleLee, Samuel P., Simon M. Barrans, Martyn L. Jupp, and Ambrose K. Nickson. 2017. "The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine" Aerospace 4, no. 4: 56. https://doi.org/10.3390/aerospace4040056
APA StyleLee, S. P., Barrans, S. M., Jupp, M. L., & Nickson, A. K. (2017). The Impact of Volute Aspect Ratio on the Performance of a Mixed Flow Turbine. Aerospace, 4(4), 56. https://doi.org/10.3390/aerospace4040056




