Modeling Plasma via Electron Impact Ionization

Abstract

Variable and potential plasma applications in aerospace engineering are exemplified by ion thrusters, flow control by plasma actuator, enhanced ignition and combustion stability. The operational environments span a range from the rarefied to continuum gasdynamic regimes; however, the ionization process in practical applications is mostly by electron impact. The fundamental ionization mechanisms by electron impact consist of electron secondary mission and the cascading process. In an alternating electric field, unsteady and random micro discharges or streamers are always presented; therefore the discharge physics imposes a formidable challenge for incisive understanding. Meanwhile, the ionized species constitute hundreds of metastable chemical species; under this circumstance the physics-based modeling for analyzing the inhomogeneous medium becomes necessary. A summary of the physics-based modeling for electron impact ionization from the Boltzmann distribution equation to the inelastic particle kinetics formulation is delineated.

1. Introduction

Plasma as a working medium in aerospace engineering applications has introduced an added physical dimension through electromagnetic effects [1]. Although the electrically conducting medium is globally neutral, it infuses additional mechanisms in the form of remote acting force by electrostatic and Lorentz accelerations, as well as by Joule heating. Joule heating provides a flow control mechanism by modifying the boundary-layer displacement distance over the electrodes that leads to virtue leading edge [2,3] and virtual variable inlet cross-section area inlet [4] applications. In the region of charge separation, the periodic electrostatic force is the mechanism for flow control using plasma actuators [5]. In an inhomogeneous medium, the charged particles also alter the transport properties with forced diffusion via the electromagnetic drift motion by the charged particles, as well as by ambipolar diffusion [6]. Through these intrinsic properties of plasma, this working medium can perform tasks that electrically neutral gas cannot.

Moving free charged particles will induce a magnetic field perpendicular to their paths and the applied electric field; therefore, plasma is always associated with an electromagnetic field. According to Coulomb’s law and Biot-Savart’s law, the motion of an electrically charged particle always consists of a rectilinear and rotational component [7,8]. The rectilinear acceleration is aligned with the externally applied electric field and the gyration intrinsically revolves around a combined induced and applied magnetic field. In the absence of an electric field, the angular acceleration is restricted in the plane perpendicular to the magnetic field. A moving charge q with a velocity u in a steady and uniform electromagnetic field with an applied magnetic flux density B will be pushed by a force normal to B, and also directly accelerated by the electric field intensity E. The force that is perpendicular to the directions of the charged particle velocity and the magnetic field is the Lorentz force or acceleration, $\mathit{u}\times \mathit{B}$.

The trajectory of the drift motion of a charged particle in an electromagnetic field is very complex. In the presence of both electric and magnetic fields, the charged particle in any inertial frame will execute a helical motion. The electric force usually is decomposed to components parallel and perpendicular to the magnetic field. The relationship between the electric intensity in a transformed (reference) frame moving with the mean velocity of plasma and the laboratory (fixed) frame is ${\mathit{E}}_{tr}=\mathit{E}+\mathit{u}\times \mathit{B}$. In the non-relativistic approximation, the transformed magnetic flux density is ${\mathit{B}}_{tr}=\mathit{B}-\mathit{u}\times \mathit{E}/c^2$, where c is designated as the speed of light. In the case when the coordinates system is moving with a velocity perpendicular to both the electric and magnetic field or on a laboratory frame, the helix trajectory will become a prolate cycloid with loops or the curtate cycloid [9].

The magnetic field produces Hall effects [10] by the gyrating acceleration of charged particles in plasma; the circulatory motion is evolving around and in a plane perpendicular to the axis of the magnetic field. Due to a disparity in unit mass of plasma composition, a transverse current is generated by the different curvature of electron trajectory from that of the heavier ion. The Hall current therefore will be shown to be dependent on the ratio of electron cyclotron frequency to the electron collision frequency. Since the perpendicular electric force normal to the magnetic field, $q{E}_{\perp }$ accelerates or decelerates the particle based on the polarity of charge carried, the radius of the curvature of the particle’s trajectory will change according to the normal electric field component. Accentuated by the vastly different mass of electron and ion, the Larmor radius of the ion will be greater than that of the electron, and the Larmor frequency of the ion which will be lower than the electron. Because the drift velocity must be identical to the paired ion and electron, the curvature of the ion trajectory is greater than that of electron. Thus, the collision frequency of the ion-neutral is greater than the electron-neutral collision, and the ion motion will be retarded by the more frequent collisions with neutral species.

The drift velocity of the ion and electron will differ and an electric current is produced normal to both electric and magnetic fields and flows in the opposite direction of the drift velocity, to be identified as Hall current [11]. In essence, the curvature of the electron trajectory in a magnetic field is responsible for a transverse current, or the Hall current. This electric current leads to a voltage difference across plasma due to interaction of charged particles’ motion with an external applied magnetic field that is transverse to both the electric and magnetic fields. The Hall effects become the principal mechanisms for the Magnetohydrodynamics (MHD) electric generator [12], ion thruster [13], and the scramjet MHD energy bypass concept [14].

The plasma sheath is another unique feature of plasma existing at the interface of different media, which is directly connected to the vastly different unit mass between the electron and ion; in an order of magnitude around two thousand to one. In free space and without the presence of an externally applied electric field, the electron and ion pair in plasma is restrained within a separation distance by the Debye shielding length to each other by the electrostatic force. However, near the interface boundary the charged particles separate, and the higher collision rate of the electron with a surface is much greater than that of the ion making the surface acquire a net negative potential [15]. The ions will recombine on the surface and return the plasma to a neutral medium; the electrons either recombine or enter the conduction band, making an electric conducting material. Most importantly, the plasma loses the globally electric neutral property in this region and the electric potential increases monotonically toward a negative value from the unperturbed neutral state. When the collision process reaches an equilibrium state, the net electric current at the interface surface vanishes. A plasma boundary layer is formed over the interface known as the plasma sheath, which often has the same order of magnitude of the Debye shielding length. The charged separation in the plasma sheath of a dielectric barrier discharge (DBD) leads to momentum transfer by collisions between ions with neutral particles. The interaction produces a wall of jet-like stream and is known as the electric wind for flow control [5,16].

2. Ionization Processes

The atomic structure of any element consists of a positively charged nucleus with heavily massed concentration, and surrounded by one electron or multiple electrons in orbital motion. The pulsating and gyrating motion of electrons must possess a sufficient amount of energy to hold their trajectories in different shells and can be traced to the binding force of electronic energy, which is frequently dominated by the ionization potential. For multi-electron atoms, the interactions between electrostatic repulsion and the interaction with their magnetic moments are quite complex and affect the ionization potential. Therefore, the principal quantum number of an atom cannot be exclusively determined by the relative energy levels. In the circumstance of a partially filled inner shell, it must follow the Pauli principle to complete the shell [17,18]. The fully filled or partially filled electron shells are important in determining the chemical behavior of the atom.

The energy of an atom or molecule in a gaseous medium has multiple internal components. The internal degrees of freedom of a molecule include the translational, rotational, vibrational, and electronic modes [19]. The electronic mode has also been referred to as nuclear excitation and can be further split into dissociation and ionization. All these internal excitations are quantized, and the bridge between the microstate of individual particle and macroscopic properties of gas mixture is linked by statistic mechanics through theories of probability and distribution functions. The internal energy distributions of a gas molecule or atom have been made easily understood by quantum mechanics in equilibrium state through the partition functions. From statistic thermodynamics, the total energy of a molecule is additive and the partition functions on the other hand are factorized. Such results correspond to the Born-Oppenheimer approximation [18].

Ionization processes for atoms and molecules are similar although there are some additional complexities for molecular processes because of the increased internal degrees of freedom. In general, the energy required by highly excited states of atoms and molecules may be provided separately by thermal, chemical, electrical and radiative resources or by a combination of all mechanisms. However, the predominant ionizing mechanism is through the collision process. The process involves inelastic collision, electron impact, radiative interactions and charge exchange; meanwhile the depletion process involves the dissociation, three-body, dielectric recombination and electron attachment. The production and depletion of charged components in an ionized gas is determined by a vastly different collision cross-section and polarity [17,20]. However, the ionization energies for most common gas species in air are from 12.2 to 15.58 eV (1 eV = 1.602 × 10⁻¹² erg), which becomes a significant amount of energy requirement for practical engineering applications, when the charge number density is often measured in the order of 10¹⁹/m³. At the same time, a typical life span of the excited state is about 10 ns or 10⁻⁸ s. Therefore, the ionization of gas is always exists in a transient state in time and space.

The electron impact ionization is the most commonly adopted procedure for laboratory-generated plasma and for aerospace applications. The energy transfer depends on inelastic and elastic collisions and the energy is supplied by an externally applied electric field. The temperature of the partially ionized gas is always substantially lower than the characteristic ionization temperature, and the ionized components frequently will not reach thermodynamic equilibrium. Atoms are ionized by high-energy electron collisions at the outer limits of the Maxwellian distribution; electron avalanches generated in an electric field evolve in time and space along the drift direction of free electrons. Therefore, the rate of electron impact ionization is not measured by the ionization frequency, but the ionization coefficient $\alpha =\nu /u_d$ cm⁻¹ which is directly linked to the particle collision frequency $\nu$ and the electron drift velocity u_d. A unique phenomenon in gas discharge is by the secondary emission that produces breakdown for discharge within the electrode gap and is sustained by a small amount of electric current. The fundamental mechanism is the electron tunneling discovered by Penning in 1928 [20]. The process usually takes place over a duration of 10⁻⁹ to 10⁻⁴ s.

Electrical extraction or the electron impact ionization process is produced by an externally applied electric field; an electron is forcefully extracted from an atom by the electric field intensity. The applied electric field can be a direct current (DC) or an alternating current (AC) with an electric field intensity greater than the breakdown voltage of a specific gas medium. The breakdown voltage can be as low as a few hundred volts in near vacuum and a thousand volts at atmospheric conditions, which are described by Pachan’s law determining the gap distance and the ambient pressure between electrodes. Meanwhile, frequencies of the alternating electric field can be slow, varying and up to the microwave range. Nevertheless, the charged particles are most effectively produced by subsequent collisions of electrons with atoms or molecules.

$$\begin{array}{l}E(A)\Rightarrow A^{+}+e^{-}\\ e^{-}+A\Rightarrow 2e^{-}+A^{+}\end{array}$$

(1)

Ionization is achieved when a valence electron collides with an incident electron and receives an amount of energy greater than the atomic ionization potential. The Townsend similarity law describing the ionization by electron impact gives the simplest and the widest range of applicability; an important feature of the law is that it depends upon only the classic parameter $(\mathit{E}/P)$, which is a measure of energy gain between collisions.

$$\alpha =A\exp (-Bp/\left|E\right|)$$

(2)

The ionization coefficient can be modeled by A = 15 and B = 365 for air plasma in the $\left|\mathit{E}\right|/p$ range from 100 to 800 (V/Torr·cm). The model holds reasonably well even at a higher values of $\left|\mathit{E}\right|/p$ [21].

Another electron impact process of atomic ionization for plasma generation is also possible. An atom can be initially excited by collision and elevated to a higher energy state and then ionized through a sequence of excited states. In this case, the process is termed stepwise ionization. On the other hand, the one-step ionization is considered to be direct ionization.

An enormous amount of energy is needed to generate localized volumetric plasma domain. According to Raizer [20], the lowest ionization potential is 34 eV for electron beams, and the value increases to 65.7 eV for direct current discharge (DCD), and finally reaches a value of 81 eV per ion-electron pair for discharge at the radio frequency. For electron impact ionization, electrons are elevated to a highly excited state but the positive and negative charged ions still retain their ambient conditions. For this reason, the partially ionized gas is often identified as “cold” plasma. The charge number density is generally limited to a value of 10¹³/cm³. Because the weakly partially ionized plasma is generated either by DCD or dielectric barrier discharge (DBD), the electromagnetic force usually exerts only a small perturbation to the mainstream flow. Therefore, the plasma actuator for flow control is the most effective at flow bifurcations such as the onset of dynamic stall and vortical separation [22]. However, the effect of electromagnetic-aerodynamic interactions can also be amplified easily by an externally applied transverse magnetic field. On the other hand, the inviscid-viscous interaction accentuated by Joule heating on the leading edge of a control surface is naturally occurring for hypersonic flows [2].

3. Direct Current and Dielectric Barrier Discharge

Electron impact is the most important ionization mechanism in gas discharge. The energy transfer depends on inelastic and elastic collisions in an externally applied electric field. The temperature of plasma is always substantially lower than the ionization potential, because ionization by electron collisions takes place at the outer limits of the Maxwellian distribution. A subsequent electron avalanche in an electric field evolves not only in time but also in space along the drift direction of free electrons.

The electron secondary emission on the cathode is a unique phenomenon in gas discharge that produces electric breakdown within the electrode gap and is sustained by a small current. The main mechanism of the secondary emission is by the accumulation of positive charged ions next to the cathode creating a narrow potential barrier with an electric intensity on the order of the surrounding nucleus. An electron from the cathode, either in a conductor or dielectrics, immediately tunnels into the ion layer to neutralize it. The tunneling action leads to electric breakdown, and the process transforms a dielectric medium between electrodes into a conductor. The process usually takes place at time scales from 10⁻⁴ to 10⁻⁹ s [20].

Ionization by electron collision may appear as a spark and the discharge current is limited by the resistance of its external circuit. The following primary elements of breakdown are the electron avalanche, and the threshold of a steep rate of atomic ionization is governed by electron collisions. The breakdown is controlled by the ignition potential

$$I_{bd}=B(pd)/[c+\ln (pd)]$$

(3)

which is essentially the Paschen curve. The product of pd (pressure and gap distance between electrodes) is a manifestation of the similar law for gas discharge by Townsend. The minimum value of E/P, which is a measure of energy gain between collisions, corresponds to the Stoletov point. For air, c = 1.18, (pd)_min = 0.83 torr·cm, and (E/P) = 365 V/(cm·torr), and the minimum voltage for breakdown is around 300 V at low pressure [20]. In general, the degree of ionization in number density for a normal discharge is around ${10}^8<n_e<{10}^{12}$/cm³.

The direct current discharge (DCD) has one obvious feature: it is macroscopically time independent. The normal glow discharge has an electric current between 10⁻⁵ to 10⁻³ Ampere. When the pressure is near atmospheric, the breakdown is likely to result in an arc. The electric potential in an arc across the electrodes usually drops to tens of volts. The glow-to-arc transition is not predictable. In the glow discharge, the essential supply of electrons is mainly from secondary emission by bombardment with positive ions onto the cathode. In an arc, another known source is the thermoionic emission from the cathode. The transient discharge or spark can occur over a wide range of electric current.

The DCD adopted for aerospace engineering is usually operated in the voltage-current range where the power source supply can provide more than the minimum current I_d [20]. In this current-voltage range, the discharge has a strong dependence on the shape of electrode and the gas pressure (or, correctly, the gas density). At a higher pressure and from a sharp-point electrode, a corona discharge will be emitted. However, in a low pressure gas, a normal glow discharge sets in. If the power source cannot supply the minimum current, the spark will repetitively ignite in the discharge gap. The electric current densities of these types of discharges have a range from 10⁻³ to 10 A/cm². The glow discharge is neither in thermal equilibrium nor able to maintain charge neutrality. However, the components of plasma have a Maxwellian energy distribution at a very low temperature, and the ions exist at a slightly higher temperature than their environment, but the electrons have very high temperatures of a few eV or 10⁴ to 10⁵ K. The structure of DCD is well known and consists of a cathode layer over the cathode and on top of that by a positive column connecting to the anode. The detailed structure of the positive column is extremely intriguing, and has been described admirably clearly by Raizer, but from experimental observation the dominant feature is overwhelmed by the cathode layer glow as exhibited in the photograph of Figure 1. The cathode layer is actually the plasma sheath in which the cathode fall takes place and Joule heating is concentrated.

The electron impact ionization produced by an alternative current (AC) cycle is not substantially different from a direct current (DC) field. However, if one electrode is coated by a dielectric film similar to that of a dielectric barrier discharge (DBD), then the charges accumulated on the electrode surface will reduce the electrical intensity between electrodes and prevent the transition from discharge to spark. This discharge is also known as the silent discharge [23]. The discharge cycle in DBD is dominated by the random streamers, filaments or microdischarges in time and space [23,24]. The streamer or the microdischarge is a channel weakly ionized by the primary avalanche in a strong electric field. The formation is random, within a time scale of a short duration of microseconds and within the electrode gap. The space charges also generate an additional electric field by themselves, which makes it different from corona discharge. When the microdischarge is initiated from anode to cathode it is known as the cathode-directed or positive streamer; otherwise it is said to be anode-directed or negative streamer. However, if the electron avalanche transforms into streamer before it reaches electrode, as it does in a microwave, the streamer grows toward both electrodes. A unique feature of DBD at atmospheric pressure is the self-limited behavior preventing itself from transition to arc. It is the consequence of accumulated charges over the dielectrics that effectively reduce the electric field intensity across the electrode gap.

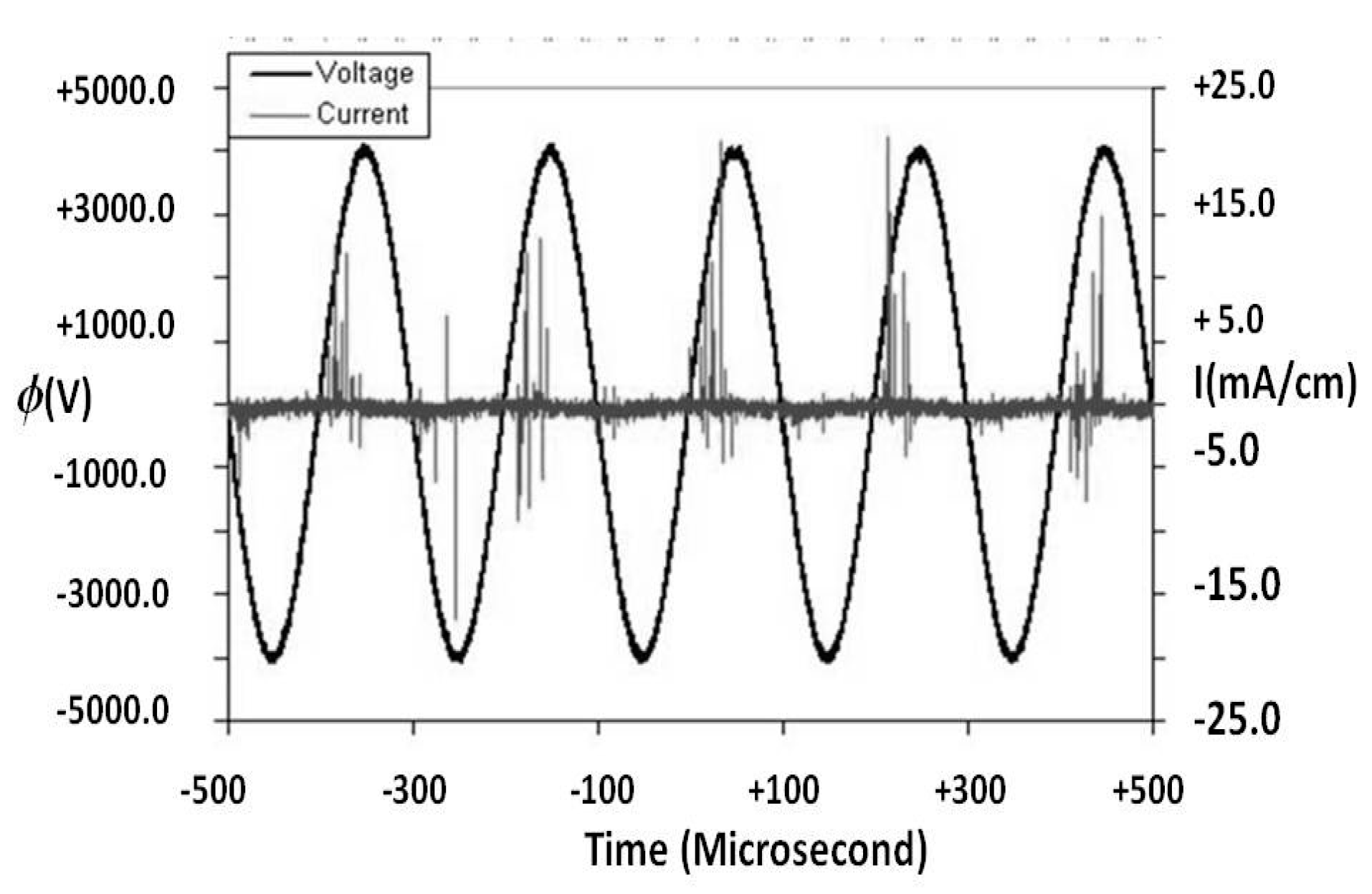
In an AC cycle, when the externally applied electric field intensity exceeds the electric breakdown voltage threshold, the plasma will ignite. The cyclic experimental recording of the current and voltage relationship is displayed in Figure 2. The oscillatory spikes of the electric current are incurred by the initiation of the microdischarges that immediately follow the plasma ignition. The onset of ionization depends on the gas medium, electrode gap distance, and the electric permittivity of the dielectric. In dry air the breakdown voltage of a typical DBD for flow control has a value slightly above 2.0 kV. After the breakdown, conductive current appears between electrodes by electron motion. The electric field intensity across the electrode and the dielectric drops from the electromotive force (EMF) of the external source, but retains nearly a constant value because of the self-limiting characteristics of a DBD, which prevent the discharge from transitioning to an arc. The discharge ceases when the applied voltage falls below the breakdown criterion, and the voltage-current relationship returns to the applied AC field. The phenomenon repeats itself as soon as the absolute magnitude of the externally applied voltage is greater than the breakdown value in both positive and negative polarities. This voltage-current relationship is routinely recorded by experimental observations.

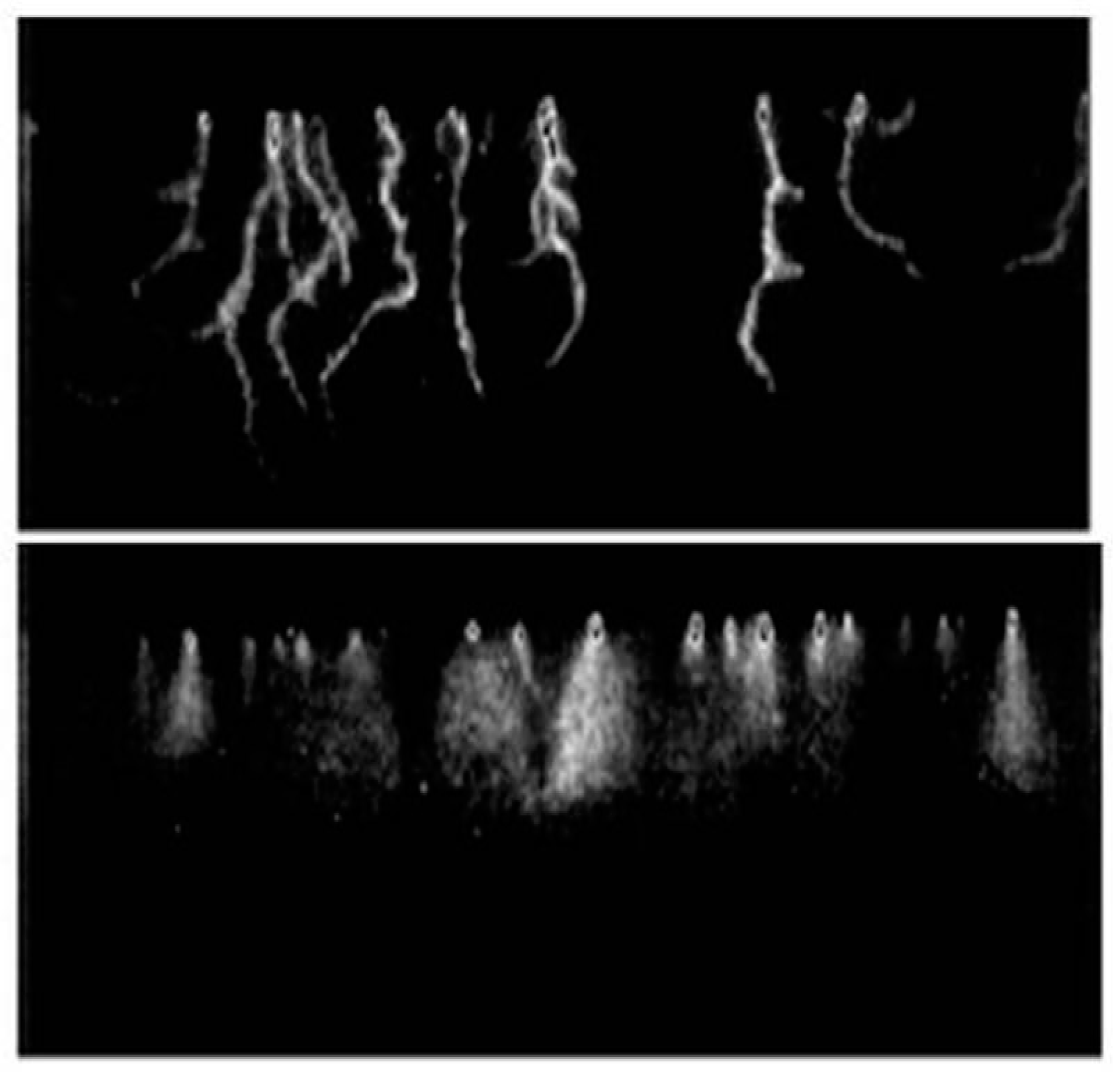
A distinguished DBD microdischarge structure has been brought out by the high-speed, image-intensified photographs in each AC cycle phase by Enloe et al. [16]. The microdischarges or streamers are initiated from either the anode or the cathode of the AC cycle. In DBD operation, the exposed metallic electrode and the dielectric act alternatively as the cathode and anode. Therefore, the random microdischarges are initiated from electrodes as either the positive or the negative corona discharges, but the avalanche process transforms the discharges into streamers before they reach the receiving electrode. In the negatively biased AC phase, the negative streamers must propagate against the electron drift motion or the electric field, thus the negative streamers are more diffusive than the positive streamers. This difference in microdischarges structure over a complete AC cycle is clearly displayed by Figure 3. At present, a direct computational simulation for the random and multiple microdischarges in time and space is beyond our reach.

4. Formulation of Plasma in Rarefied Gas Domain

Electron impact ionization has been widely used for ion engines or ion thrusters. There are two basic types of ion thrusters presently adopted for geosynchronous satellite station maintenance and deep space exploration known as the gridded electrostatic ion thruster and the Hall effects thruster. The operational environments for both are identical and in a rarified gas regime. The typical operating conditions of an ion thruster usually have the maximum electron number density around 10¹³/cm³ (10¹⁹/m³), and the electron temperature is in the order of 3 eV or greater. The plasma in the discharge chamber of the ion thruster exists in a similar state to the lowest pressure direct current plasma actuators for flow control. The rarefied gas condition is measured by the Knudsen number; $K_n=\lambda /L$ and $\lambda$ is the mean free path, L denotes a characteristic length of the system to be analyzed. At a typical xenon neutral particle number density of 10¹⁹/m³ and a collision cross-section of 5 × 10⁻²⁰ m² respectively, the mean free path yields a value of about 1.4 m for the ion thruster. This value is several times greater than most characteristic dimensions of a typical ionization chamber; therefore, an ion thruster is operated in the rarefied gasdynamic regime. Numerical simulations must be carried out by particle dynamics formulation, usually through a combination of Boltzmann distribution functions by Monte-Carlo techniques.

Ionization is achieved by electron impact on cesium, argon, krypton, and most commonly xenon, because of their relatively low atomic ionization potentials. A contemporary implementation of an ionization chamber employs a hollow cathode inserted into the ionizing chamber, which provides the secondary electron emission [9]. High energy electrons from the hollow cathode collision with neutrals in the ionization chamber and produce positively charged ions. The positively charged ions are extracted from the ionization chamber and are accelerated downstream of the engine by a system of electric grids.

The Hall effects thruster relies on the interaction of charged particle motion with a magnetic field to provide acceleration by the Lorentz force $J\times B$. The ionized gas is accelerated by electric potential and a radial magnetic field between a cylindrical anode and cathode. At the center of the thruster, a magnetic field is generated by an electric coil winding over a spike; at the end of the spike the electrons are trapped by the magnetic field and attracted to the anode [13]. Some electrons spiral toward the anode to become the Hall current and close the electric circuit. The streamwise force accelerates charges along the thruster, and transfers streamwise momentum to neutral particles by collisions in a microscopic polarized field. As a consequence, the thruster’s charged particle number densities are greater than that of the electrostatic ion thruster.

In the rarefied gas regime, the coupled electron and ion pairs always move in random motion with kinetic and potential energy of their own. Their behavior in microscopic scales can only be meaningfully described through statistic means. According to the Liouville’s theorem [19], the phase space occupied by a group of particles will not change due to the motion of these particles. The rate of changes of the distribution function for singly-charged particles is governed by the Boltzmann equation:

$$\partial f/\partial t+c\cdot \nabla f+(e/m)(\mathit{E}+\mathit{u}\times \mathit{B})\nabla f={(\partial f/\partial t)}_c$$

(4)

The Boltzmann equation represents the equation of change; the left-hand hand terms are the time rate of change per unit volume in phase space by the convective processes at the phase velocity c and electromagnetic force. The right-hand side term represents the effect of inter-particle collisions.

Vlasov treats the Boltzmann equation by omitting the right-hand-side collision integral term, but explicitly includes the electromagnetic force in the rate equation [25]. By this approximation, the distribution function is evolved in time only by the contributions from the macroscopic smoothed electromagnetic field. Vlasov considers the short-range effects by Coulomb force, which are intensive, but the long-range effect becomes the most dominant mechanism for plasma. In any event, the basic approach is based on the theory of kinetics with long-range Coulomb interaction. Similar to the Fokker-Plank formulation, the probability distribution function is now analyzed as a nonlinear partial different equation instead of the integro-differential system [11].

The governing equations now consist of the rate equation for the distribution functions and the full set of Maxwell equations in the time domain; the latter are included to ensure that the evolution of plasma is supported by a self-consistent electromagnetic field. The approximated formulation is simply given as

$$\partial f(u_i,x_i)/\partial t+u_i\nabla \cdot f(u_i,x_i)+(e/m)(e+u_i\times B)\nabla f(u_i,x_i)=0$$

(5)

By means of a multi-fluid model concept, the description of the distribution function has been further split into electrons and positively charged ions to show the effects of different polarities. Since the short-range effect by collisions is neglected in comparison to the long-range electromagnetic forces, the Maxwell equations must be included in Vlasov’s governing equations system:

$$\begin{array}{l}\partial f_i/\partial t+u\cdot \nabla f_i+(e/m_e)(\mp \mathit{E}+\mathit{u}\times \mathit{B})\cdot \nabla f_i=0\\ \partial \mathit{E}/\partial t+\nabla \times \mathit{B}=\mu \mathit{J}\\ \partial \mathit{B}/\partial t+\nabla \times \mathit{E}=0\\ \nabla \cdot \mathit{E}=\rho /\epsilon ,\nabla \cdot \mathit{B}=0\end{array}$$

(6)

where the subscript i denotes the negative or positive charged particles. The minus sign in front of the electric field intensity E is associated with the electrons and negative charges.

The associated boundary conditions for the electromagnetic field on a stationary frame of reference can be given as Equation (7). It is convenient to describe the boundary condition by the tangential and normal components on the media interface [26]. These interface boundary conditions of two different media 1 and 2 for electric and magnetic field intensity E and H, as well as electric and magnetic flux density D and B become:

$$\begin{array}{l}\widehat{\mathit{n}}\times ({\mathit{E}}_1-{\mathit{E}}_2)=0\\ \widehat{\mathit{n}}\cdot ({\mathit{B}}_1-{\mathit{B}}_2)=0\\ \widehat{\mathit{n}}\cdot ({\mathit{D}}_1-{\mathit{D}}_2)={\rho }_s\\ \widehat{\mathit{n}}\times ({\mathit{H}}_1-{\mathit{H}}_2)={\mathit{J}}_s\end{array}$$

(7)

The tangential electric field intensity E and the normal component of the magnetic flux density B are continuous across the interface boundary. However, the normal component of the electric displacement D is discontinuous across the interface; the difference must be balanced by the surface charge density ${\rho }_s$. Similarly, the discontinuity of the tangential components of the magnetic field strength H is equal to the surface current density J_s. These boundary conditions are paramount when analyzing the plasma generation via electron impact.

Most current methods of computational electromagnetic-aerodynamics in rarefied gas regimes adopt the particle-in-cell (PIC) approach in combination with a direct simulation Monte Carlo (DSMC) technique [27,28]. In a full PIC-DSMC simulation, all particles, including the neutral and charged species, are tracked by the macro particle assumption. In other words, the huge amounts of particles are separated into distinct groups of identical characteristics. In fact, the PIC-DSMC scheme stimulates dynamics of the electrical charge carried and neutral macro particles. The basic governing equations are the classic Newton-Lorentz equations for charged particle motion, and the electric field distribution is determined by Poisson equation of electromagnetics:

$$\begin{array}{l}{\mathit{u}}_{\mathit{i}}=\frac{d{\mathit{x}}_i}{dt}\\ m_i\frac{d{\mathit{u}}_i}{dt}=q(\mathit{E}+{\mathit{u}}_i\times \mathit{B})\\ {\nabla }^2\phi =\frac{e}{\epsilon }(n_{-}-n_{+})\end{array}$$

(8)

In a full PIC-DSMC computational simulation, all charged particles are tracked by the macro-particle assumption. In theory, each macro particle represents billions to trillions of real particles of rarefied plasma; the total number of the tracked particles can still easily exceed 10⁸. The required huge computational resources for macro-particle simulation must satisfy the peculiar and stringent computational stability criteria of PIC-DSMC algorithms in time and space. The numerical procedure also suffers from statistical noise of a large number of sampled macro particles. Meanwhile, the physical fidelity of modeling has imposed a severe resolution limitation by the Debye shielding length in space and time through the charge number density. In short, the computational simulations by the Lagrangian formulation are analyzing plasmadynamics in the rarefied gas regime, and the computational resource requirement is extremely demanding.

The electrostatic ion thrust NSTAR (Solar Technology Application Readiness) has been generated by Mahalingam [29]. Computational solutions are obtained on the static frame by solving the Maxwell equations and the macro particle are advanced on the dynamic frame governing by the Newton-Lorentz equations. Ionization by electron impact is modeled through ionization potential and the probability potential via the three-body collision process. The considered particles consist of xenon, single- and double-charged xenon ions (Xe⁺ and Xe⁺⁺), as well electrons. A total of 1.267 million individual macro particles were carried out on 8383 uneven spaced cells. The numerical simulation has taken advantage of the axisymmetric configuration; the numerical analyses were performed only in the top-half meridional plane of symmetry.

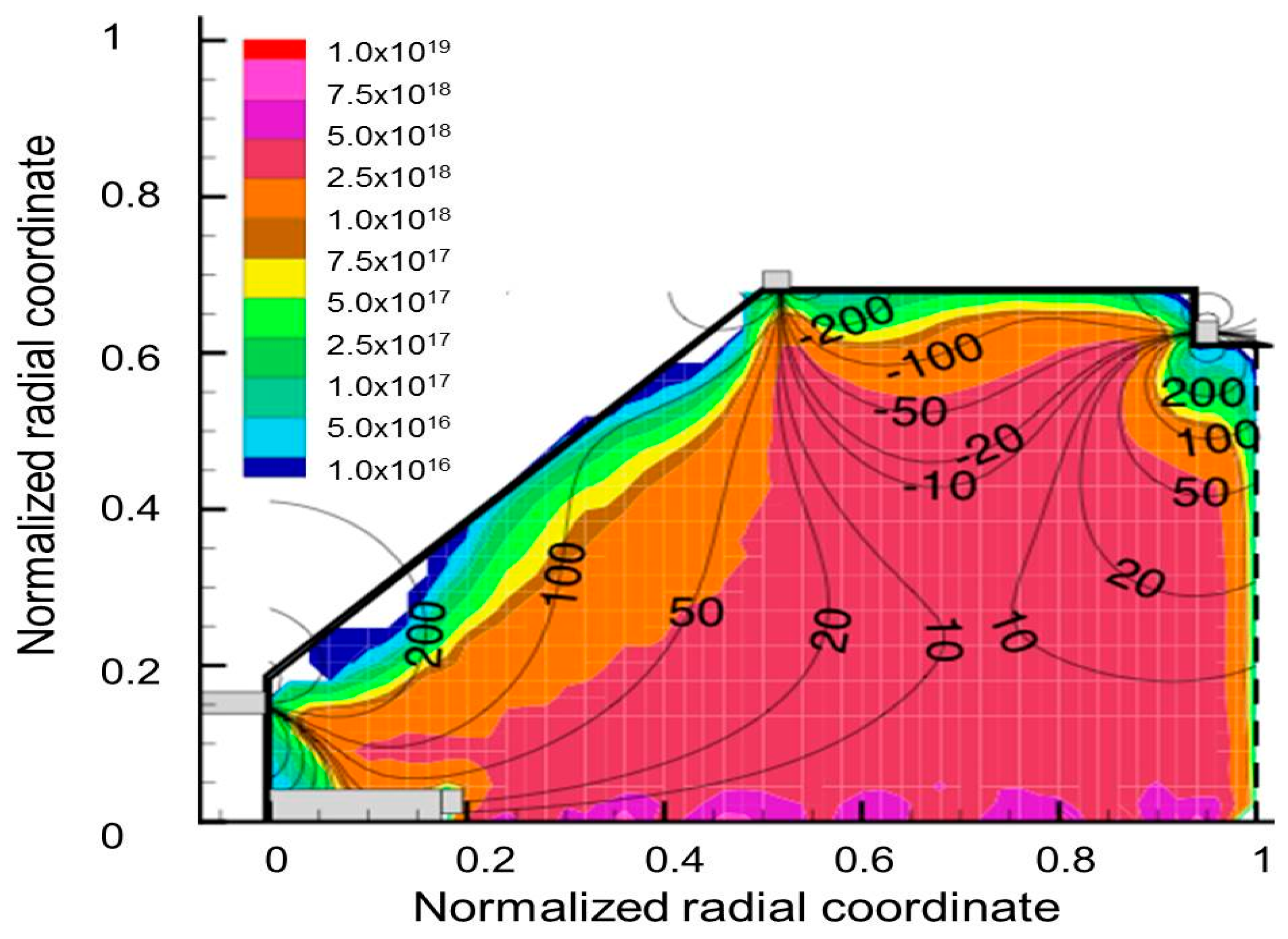
The selected contour of the singly charged xenon ions is presented in Figure 4 with respect to the normalized axial location and at steady state of the TH-15 operation condition. The charge number density spans a range from 10¹⁶ to 10¹⁹ per cubic meter (10¹⁰ to 10¹³/cm³. The three magnet rings function well to confine the charged particles away from the solid chamber surface; the lines of magnetic field intensity are also superimposed on the ion contour plot. The contours of the computational simulated primary electrons are displayed in Figure 4, and the specific comparison of the key ion engine performance data with experimental measurements is given in

Table 1. Specific comparison of performance parameters with data.

Parameters	Computational Results	Experimental Data
Beam Current	1.78 Amp	1.78 Amp
Discharge Current	17.8 Amp	14.9 Amp
Thrust	87.0 mN	92.4 mN

.

5. Plasma Modeling by Chemical Kinetics

The ionization process by electron impact is drastically different from thermal excitation, but the non-equilibrium ionized species concentrations must still satisfy the law of mass action. For this reason, ionization processes are frequently treated as chemical reactions. For the ionization of air by thermal excitation, the number of chemical species is usually around ten and involves only thirty elementary reactions [1]. For ionization by electron impact, the number of ionized species is greater, and the number of elementary reactions increases to hundreds. It is obvious the required effort for computational simulation is tremendous and tedious. For most investigations, finite chemical reaction rates are developed on a limited experimental database.

According to chemical kinetic theory, any complex chemical reaction can be broken down into multiple single-step, elementary reactions. The permissible chemical reactions are the sum of all the elementary reactions as described by the law of mass action. This fundamental law, Equation (9) may be viewed as a statement of conservation of total number of elementary atoms of reactants. At the microscopic scale, the chemical reaction must be modeled by chemical kinetics or quantum chemical-physical kinetics. All chemical reactions can be expressed as a collection of elementary reactions

$${\displaystyle \sum _i{\nu }_i^{\prime }}{N}_i\rightleftarrows {\displaystyle \sum _i{\nu }_i^{″}}{N}_i$$

(9)

where ${\nu }_i^{\prime }$ and ${\nu }_i^{″}$ are the stoichiometric coefficients for reactants and products respectively. These coefficients are integers denoting the number of molecules that are partaking in the reaction, and $N_i$ is the mole concentration of the reacting species.

The law of mass action is actually an empirical formulation confirmed by numerous experimental observations. The chemical reactions are described by the rate of generation and depletion of a chemical species in proportion to the products of the concentrations that rise to a power equal to the corresponding stoichiometric coefficient, ${\nu }_i$ [19]. For a finite-rate or non-equilibrium chemical reaction, the forward and backward rates are given as:

$$\begin{array}{l}{R}_{f,i}=k_{f,i}(T)\mathsf{\Pi }{(\frac{{\rho }_i}{M_i})}^{{\nu }_i^{\prime }}\\ R_{b,i}=k_{b,i}(T)\mathsf{\Pi }{(\frac{{\rho }_i}{M_i})}^{{\nu }_i^{″}}\end{array}$$

(10)

The symbols $k_{f,i}$ and $k_{b,i}$ are the so-called reaction rate constants, which are functions of the temperature and independent of the concentration of the reacting species. The net rate of reaction change to the concentration of any chemical species is the combined results of all the individual elementary, one-step reactions:

$$R_i=k_{f,i}(T)\mathsf{\Pi }{(\frac{{\rho }_i}{M_i})}^{{\nu }_i^{\prime }}-k_{b,i}\mathsf{\Pi }{(\frac{{\rho }_i}{M_i})}^{{\nu }_i^{"}}$$

(11)

The chemical reaction rate is governed by the empirical Arrhenius formula, which recognized that the reaction rate constant has a strong temperature dependence:

$$\frac{d\ln k_i}{dt}=\frac{{\epsilon }_i}{k{T}^2}$$

(12)

The overall rate of a non-equilibrium chemical reaction is a dynamic balance of the forward and backward chemical reactions.

$$\frac{d{w}_i}{dt}=M_i{\displaystyle \sum _{j=1}^J\left({{\nu }^{″}}_{i,j}-{{\nu }^{\prime }}_{i,j}\right)}\left\{k_{f,j}{\displaystyle \prod _{k=1}^{N_{kf}}{\left(\frac{{\rho }_k}{M_k}\right)}^{{{\nu }^{\prime }}_{k,j}}-k_{b,j}{\displaystyle \prod _{k=1}^{N_{kb}}{\left(\frac{{\rho }_k}{M_k}\right)}^{{{\nu }^{″}}_{k,j}}}}\right\}$$

(13)

For electron impact ionization, the main chemical reactions fall into four groups, electron-molecule, atom-molecule, decomposition, and synthesis processes. The dielectric barrier discharge (DBD) has been studied most thoroughly; the pioneering effort is due to Elisson and Kogelshatz [23]. The non-equilibrium chemical kinetics associated with DBD in the atmosphere is well known because it has been applied as an ozone generator for years. They have been identified by plasma chemistry in micro discharge by 30 species through 143 elementary reactions. In a more recent work by Bogdanov et al. 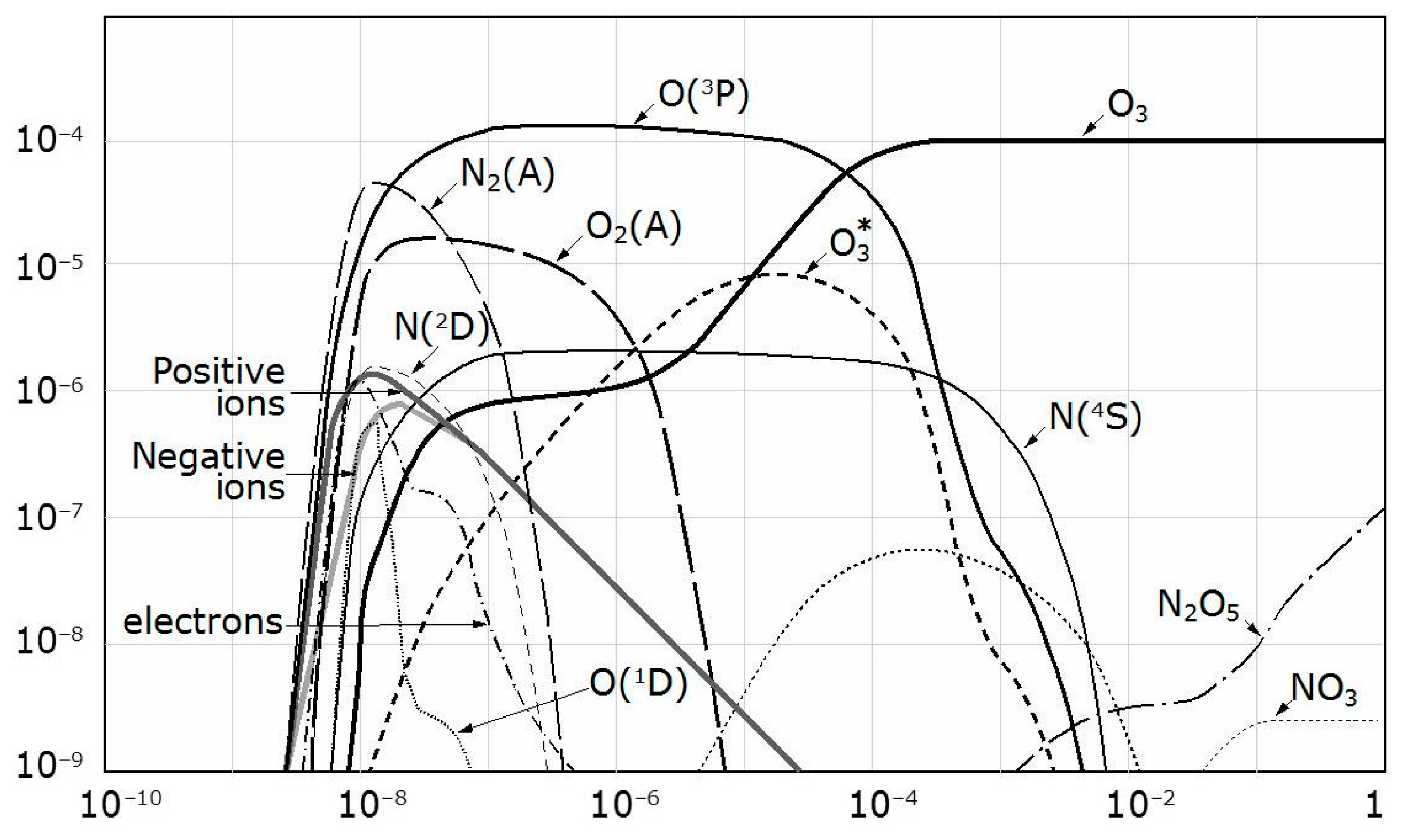[30], the chemical-physics kinetics of atmospheric plasma have been investigated by 576 chemical reactions involving vibrational excitations of nitrogen and oxygen, ozone, positive and negative ions, besides oxide-nitrides. For reason of clarity, these species $N(4S,2D,2P)$, $O{(}^{3}P{,}^{1}S{,}^{1}D)$ and $N_2^{+}(A^3{\mathsf{\Sigma }}_u^{+},B^3{\mathsf{\Pi }}_g,A^1{\mathsf{\Pi }}_g,C^3{\mathsf{\Pi }}_u)$ are abbreviated as $N_2(A)$ in Figure 5. Similarly, the ionized oxygen $O_2(X^3{\mathsf{\Sigma }}_u^{+},A^1\Delta ,B^1\mathsf{\Pi })$ also are abbreviated as $O_2(A)$. The ionized air also has the compositions of ozone molecules ${\mathrm{O}}_3$, as well as negatively charged ions $({\mathrm{N}}_2{\mathrm{O}}^{-},{\mathrm{NO}}^{-},{\mathrm{O}}^{-},{\mathrm{O}}_2^{-},{\mathrm{O}}_3^{-},\dots )$ and positively charged ions $({\mathrm{N}}^{+},{\mathrm{O}}^{+},{\mathrm{NO}}^{+},{\mathrm{NO}}_2^{+},\dots )$ respectively.

In Figure 5, the data are derived from the work by Elisson et al. [23] by including only the metastable chemical species for the time elapsing up to one second. The air ionization by electron collision for most species is seen to initiate and approach the equilibrium state in less than 40 ns. The much greater mobility of electrons compared to ions leads to a lower electron concentration in the discharge region characterized by charge separation. The highest species concentrations at the shortest time scale belong to $\mathrm{O}{(}^{3}P),{\mathrm{N}}_2(A^3{\mathsf{\Sigma }}_u^{+}),$ and ${\mathrm{O}}_2(A^1\Delta )$. Only the molecular compositions of O₃ and N₂O persist over a period more than one-tenth of one microsecond and after the ignition. One may notice that most constituents of the partially ionized air in DBD are transient radicals.

For DBD, most charge carriers vanish after about 50 ns, and the chemical reactions proceed without the interaction with the charge carriers. The ionization energy for these reactions varies widely from a few and up to thousands of electron volts. Regardless, the ionizations can still be analyzed as chemical reactions and the non-equilibrium reactions described in Arrhenius form:

$$k_i=k_{i,}{}_o{T}^n\exp (-E_a/kT)$$

(14)

The rate constants k_i,o for different reactions are given in terms of cm³/s (two-body collision) or cm⁶/s (three-body collision), and are usually given as a function of V cm² and the temperatures of electrons and ions [31].

Bogdanov et al. [30] also have found that the concentration of the negatively charged ions is relatively lower than the positively charged counterpart. Their research also shows that the $O_2^{-}$ plays a dominant role in a DBD plasma actuator. Since DBD is a non-equilibrium transient discharge, the mean energy state of the electrons and heavy particles is considerably different, but the energy transfer to the internal states of molecule or atom is very effective.

In DBD applications, the charged particles’ interaction with the dielectrics is important. The ionization by photoemission is negligibly small for nitrogen because the energy of photons in the visible range is too small to cause the emission of electrons Raizer [20] also has pointed out that photoemission cannot compete with electron impact ionization because the collision cross sections of oxygen and nitrogen molecules and atoms near the emission threshold are rather large (10⁻¹⁶ cm²). This process however can only supply the seeding electrons that are needed to start the avalanche in streamer propagation.

The other important processes in ionization are desorption of electrons and surface recombination at the medium interface. At the relatively short duration of microdischarge versus the microsecond time scale of an AC cycle; the instantaneous surface recombination is an acceptable approximation. However, the secondary emission of electrons from the surface during ionization is the dominant mechanism, and the ionization of DBD is still a basic Townsend process [6,20]. This observation is the foundation of ionization by electron collisions.

Chemical kinetics models for low-temperature plasma generation span a very wide range of complexity, from the detailed description by Elisson et al. [23], Bogdanov et al. [30] to simplified approximations by Solov’ev et al. [31], Singh et al. [32], Pancheshnyi et al. [33], and Rafatov et al. [34]. Solov’ev et al. simplify their selection of the elementary chemical reactions based on comparable reaction rates of species to the characteristic time scale in the order of 30 ns for DBD in atmospheric air. A total of sixteen key reactions are considered, including 4 charge-exchange reactions in a chain of conversion. Singh and Roy reduce the chemical kinetic model by omitting the metastable species along with ${\mathrm{N}}^{4+}$ and ${\mathrm{O}}^{4+}$ from these reactions, which have extremely high recombination rates. In general, numerical results show that the number density in DBD of negatively charged ions is small as compared to that of positively charged ions.

Recently, Rafatov et al. [34] adopt an extended fluid model for ionization from the elastic collision to the trapping radiation by a compromise between the strictly fluid and chemical kinetic model to analyze the direct current discharge with seven elementary reactions. The unique features of their chemical kinetic model are the further refined ionization processes into the direct, stepwise, and penning ionizations and some of the rate constants are calculated from the local Boltzmann equation. In particular, numerical examples even include the electron collision cross-sections for ionization in argon as the functions of electron energy.

All these approaches are rational and the fidelity to physics in computational simulation for non-equilibrium chemical reactions is solely dependent on the empirical rate constants. For this reason, a validation process is difficult and remains incomplete. In summary, the chemical rate constants are the weakest link of ionization models for both the high-temperature thermal excitation and electron collision ionization. In addition, the complete system of differential equations, especially species conservation equations, are extremely stiff, becoming a formidable computational challenge.

6. Inelastic Collision Ionization Model

Surzhikov and Shang [21] developed an alternative and effective ionization model different from chemical kinetic theory via the classic drift-diffusion theory [35]. In order to analyze ionization by the inelastic collision kinetics within a trackable scope, the charged particles are simplified into a group of particles according to their electric polarity. The underlying idea is really the multi-fluid plasma model. On this foundation, the plasma is treated as multiple fluids with different velocities and partial pressures as a heterogeneous medium. The common starting point for deriving the multi-fluid model of plasma dynamics is through gas kinetic theory by a combination of the Boltzmann and Maxwell equations in the time domain. By this approach, the detailed description of chemical composition of ionized gas is lost but will be gained by a vastly efficient analytic capability for ionization through electron impact.

From the gas kinetic theory, the momentum transfer equation via binary collision approximation has been developed for electrons and positively and negatively charged ions [20,21]. The plasma model is constructed by multi-fluid and multi-temperature model consisting of a total of four fluid components, natural particles, electrons, and positively and negatively charged ions. The equation of all charged particle motions is obtained after an integration transformation operation from the approximate Boltzmann distribution function [11,36]:

$$m_i{n}_i[\frac{\partial {\mathit{u}}_i}{\partial t}+({\mathit{u}}_i\cdot n_i){\mathit{u}}_i]=-\nabla p-{\stackrel{=}{\tau }}_i-\mathsf{\Sigma }{m}_i{n}_i{\nu }_{ij}({\mathit{u}}_i-{\mathit{u}}_j)-e{n}_i(\mathit{E}+\mathit{u}\times B)$$

(15)

where the symbol ${\stackrel{=}{\mathbf{\tau }}}_i$ denotes the shear stress tensor for different chemical species. The collision frequency ${\nu }_{ij}$ is designated for the binary collision frequency between different species. Equation (15) shows that the particles’ motion is driven by the combined effects of partial pressure gradient, shear stress of each species, momentum transfer by collisions between particles, and the remote-acting electrostatic force and Lorentz acceleration.

Under atmospheric pressure, the number density of neutral particles in a weakly ionized gas are usually over 10¹⁸/cm³. However, the number densities of electrons and positively charged ions are lower than 10¹³/cm³. The negatively charged ions number density has a value even sparser than that of its positively charged counterpart [30]. Therefore, the degree of ionization for the weakly ionized gas has a value around 10⁻⁵. In other words, the number density of neutral particles is overwhelmed by that of the electrons or ions: $n_n>>n_e,n_{+},n_{-}$. The convective velocity of the organized motion for the neutral particles is characterized by speed of sound versus the speed of light for charged particles motion. Thus, the inertia of the neutral particle’s organized motion and the viscous forces are negligible. The equation of charged species motion reduces to:

$$k{T}_i\nabla n_i+e{n}_i(\mathit{E}+{\mathit{u}}_i\times \mathit{B})+m_i{n}_i{\nu }_{in}({\mathit{u}}_i-{\mathit{u}}_n)+m_i{n}_i{\nu }_{i+}({\mathit{u}}_i-{\mathit{u}}_{+})+m_i{n}_i{\nu }_{i-}({\mathit{u}}_i-{\mathit{u}}_{-})=0$$

(16)

where the different species velocities, temperatures, and number densities are denoted by the subscript i, and the symbols ${\nu }_{in}$, ${\nu }_{i+}$, and ${\nu }_{i-}$ are characterized by the collision frequencies between neutral and charged species. Again, the differences in velocities among charged particles are negligible in comparison with the vast differences between neutral and charged species. The collision frequency between charged particles and neutral is orders of magnitude greater than the collision frequencies between charged particles: ${\nu }_{en}>>{\nu }_{e+},{\nu }_{e-}$; Equation (16) can now be written as the species velocities of electron, positively and negatively charged ions as:

$$n_e{\mathit{u}}_e=-d_e\nabla n_e-{\mu }_e{n}_e(\mathit{E}+{\mathit{u}}_e\times \mathit{B})$$

(17)

$$n_{+}{\mathit{u}}_{+}=-d_{+}\nabla n_{+}+{\mu }_{+}{n}_{+}(\mathit{E}-{\mathit{u}}_{+}\times \mathit{B})$$

(18)

$$n_{-}{\mathit{u}}_{-}=-d_{-}\nabla n_e-({\mu }_{-}{n}_e\mathit{E}+{\mathit{u}}_{-}\times \mathit{B})$$

(19)

From the definition and the Einstein relationship for drift velocity and diffusion [20,21], it is recognized that ${\mathit{\mu }}_e$ and $d_e$ are the electron mobility and the thermal diffusion of the electron, as well as the counterparts for the positive and negative ions:

$$\begin{array}{l}{\mu }_e=e/m_e{\nu }_{en},d_e=k{T}_e/m_e{\nu }_{en}\\ {\mu }_{\pm }=e/m_{\pm }{\nu }_{\pm n},d_{\pm }=k{T}_{\pm }/m_{\pm }{\nu }_{\pm n}\end{array}$$

(20)

From the known charged species velocities, the continuity equation for plasmadynamics can be expressed explicitly as the species conservation equation:

$$\frac{\partial {\rho }_i}{\partial t}+\nabla \cdot [{\rho }_i(\mathit{u}+{\mathit{u}}_i)]=\frac{d{w}_i}{dt}$$

(21)

The species conservation equation by diffusion-drift model is equally valid for all weakly ionized gas other than electron impact ionizations, including thermal excitation and chemical reaction. The inelastic collision ionization model becomes a standard bearer for electron impact ionizations [22]. The shortcoming of this model, as with MHD theory, is incurred from the multi-fluid and multi-temperature model, which makes no distinctions between different metastable species. The weakly ionized gas is analyzed as a medium consisting of one neutral and three charged species of different polarities:

$$\frac{\partial n_i}{\partial t}-\nabla \cdot [d_i\nabla n_i\mp n_i{\mu }_i(\mathit{E}+{\mathit{u}}_i\times \mathit{B})]=\frac{d{w}_i}{dt}$$

(22)

where the subscript i of the charge number density is designated for the electron, and the positive or negative ions. The minus sign in front of the drift motion term is associated with the electrons and the negative ions. The rate of chemical change on the right-hand side of the equation represents the production and depletion rates of ionized species. These rates can be either been determined by the inelastic collision models or any approximations based on known ionization processes.

The Einstein relationship describes the interrelationship between the mobility charged spices, d_i and the drift velocity, μ_i of charged species. The values of the drift velocity are determined by the ratios between the elementary electric charge and the product by mass and collision frequency of charge species. Ultimately the drift velocity is a function of |E|/p to reflect the energy gain between collisions [21].

$${\mu }_e=\frac{e}{m_e{\nu }_{en}}\approx {\mu }_e(\left|\mathit{E}\right|/p);d_e=\frac{k{T}_e}{e}{\mu }_e$$

(23)

$${\mu }_{\pm }=\frac{e}{m_{\pm }{\nu }_{\pm n}}\approx {\mu }_{\pm }(\left|\mathit{E}\right|/p);d_{\pm }=\frac{k{T}_{\pm }}{e}{\mu }_{\pm }$$

(24)

The electron drift velocity of ionized air usually has a typical value of around 10⁷ cm/s for the |E|/p ratios up to 50. By virtue of the heavier mass of ions, its drift velocities are much slower than that of electrons; the drift velocity of ions is about 10⁵ cm/s.

The degree of ionization is controlled by the production and depletion of charged species of the ionization model, which groups the ionized species according to their electric polarities. The basic approach using the inelastic collision ionization model recognizes that the ionized species appear in a trace amount in either the mass or the molar fraction. The non-equilibrium electron impact ionized processes are contributed by the electron/molecular, dissociative recombination, ion-ion recombination, and electron attachment interactions. The dominant ionized species such as the N₂$(A^3{\mathsf{\Sigma }}_u^{+})$ and O₂($b^1{\mathsf{\Sigma }}_d^{+}$) exist only in the metastable states. Meanwhile, the composition of ionized species is the net balance between ionization, detachment, attachment, and recombination processes. These energy transfers by collisions are controlled by quantum chemical kinetics.

The empirical similarity law of Townsend [20] is the cornerstone for electronic impact ionization process. The ionization process follows a complex chain of events. First the Penning penetration is initiated by charge accumulation on the cathode that leads to the secondary emission, and then followed by the electron cascading. The ionization coefficient $\alpha =A\exp (-Bp/\left|\mathit{E}\right|)$ in Townsend’s similarity law determines the ionization rate by electron impact over a unit distance. This coefficient is a slow varying function of the reduced electric field $\left|\mathit{E}\right|/p$, thus Townsend’s law has a very wide valid range:

$$(\frac{\alpha }{p})=15\exp [-\frac{365}{(\left|\mathit{E}\right|/p)}],1/\mathrm{cm}\times \mathrm{Torr}$$

(25)

The recombination and attachment processes represent the dominant mechanism for depletion of electron concentration. The dissociative recombination is the fastest mechanism of the bulk recombination of a weakly ionized gas, and is a simple binary chemical reaction. The decay rate with time of plasma is often given as:

$${(\frac{d{n}_e}{dt})}_{dis}=-\beta n_{+}{n}_e;{(\frac{d{n}_{+}}{dt})}_{dis}=-\beta n_{+}{n}_e$$

(26)

and the typical value of coefficient $\beta$ has been assigned a value based on the experimentally determined characteristic decay rate [20].

The ion-ion recombination process is another key mechanism of charge neutralization. The process depends on the ambient pressure condition; it is mostly by binary collision in a low-pressure environment, like the charge transfer. But the process switches to triple collisions under moderate pressure with a much slower reaction rate. Nevertheless, the ion-ion recombination rate can be determined by the collision kinetics:

$${(\frac{d{n}_{+}}{dt})}_r=-{\beta }_i{n}_{+}{n}_{-};{(\frac{d{n}_{-}}{dt})}_r=-{\beta }_i{n}_{+}{n}_{-}$$

(27)

For negatively charged electron generation, the electron attachment and detachment are the dominant processes. The electron temperature exerts a strong influence on most triple-collision reactions [1]. A sufficiently high energy must be exchanged for a strongly bound charged species to achieve the dissociative attachment.

$${(\frac{d{n}_e}{dt})}_a=-{\nu }_a{n}_e$$

(28)

The charge attachment process for DBD simulations has a wide range of inelastic collision approximation formulations [1]. However, it is known that under atmospheric pressure, the attachment frequency of electrons is around 10⁸/s dry air. This experimental observation supports the physics-based formulation for most DBD simulations [22]:

$${(\frac{d{n}_e}{dt})}_{de}=k_d{n}_n{n}_e;{(\frac{d{n}_{-}}{dt})}_{de}=-k_d{n}_n{n}_{-}$$

(29)

At the standard atmospheric condition, the electron detachment is the least known, especially for the metastable species N₂($A^3{\mathsf{\Sigma }}_u^{+}$) and O₂($b^1{\mathsf{\Sigma }}_d^{+}$). By an indirect estimate, the discharge rate is characterized by a value of 10⁻¹⁴ cm³/s. It is also interesting to note that weakly ionized plasma can persist in negatively charged gas at a lower value of $\left|\mathit{E}\right|/p$ than that by a short pulse discharge.

From the above brief discussion, the plasma generation and depletion processes by electron impact ionization through the complex chemical-physics involved quantum mechanics have been modeled by the inelastic collision for the multi-fluid, multi-temperature model [21,22]. The absence of an externally applied magnetic field, the model equations become:

$$\begin{array}{l}\frac{\partial n_e}{\partial t}-\nabla \cdot (n_e{\mu }_e\mathit{E}+d_e\nabla n_e)=\alpha (\left|E\right|)\left|{\Gamma }_e\right|-\beta n_{+}{n}_e-{\nu }_a{n}_e+{\kappa }_d{n}_n{n}_e\\ \frac{\partial n_{+}}{\partial t}+\nabla \cdot (n_{+}{\mu }_{+}\mathit{E}-d_{+}\nabla n_{+})=\alpha (\left|E\right|)\left|{\Gamma }_e\right|-\beta n_{+}{n}_e-{\beta }_i{n}_{+}{n}_{-}\\ \frac{\partial n_{-}}{\partial t}-\nabla \cdot (n_{-}{\mu }_{-}\mathit{E}+d_{-}\nabla n_{-})={\nu }_a{n}_e-{\kappa }_d{n}_n{n}_{-}-{\beta }_i{n}_{+}{n}_{-}\end{array}$$

(30)

The modeling equations also have an important physical attribute in that the sum of all the species conservation equations according to its signs of polarization satisfied fully the electric charge conservation law, $\partial {\rho }_e/\partial t+\nabla \cdot J=0$. The charge conservation law is an invaluable tool to verify the global behavior of the plasma, which is easier to verify than using the Maxwell equations in the time domain. The specific values of all proportional coefficients in the electron impact inelastic collision model, Equation (14) are well known. In short, the ion-ion recombination coefficient is given as ${\beta }_i$ = 1.6 × 10⁻⁷ cm³/s, the electron attach frequency is, ${\nu }_a$ = 10⁸/s, and the coefficient of detachment has the maximum value of ${\kappa }_d$ = 8.6 × 10⁻¹⁰ cm³/s. The all cited values can be verified by the discharged electrical current from experimental data [1].

7. Computational Simulations

Computational simulations for direct current discharge (DCD) and dielectric barrier discharge (DBD) that utilize the inelastic collision model for electron impact ionization are presented in the following. The objectives of the presentation are intended to be a partial validation for discharge physics fidelity in applications and to substantiate some experimental stipulations. In fact, the DCD plasma generation process is adopted for all types of ion thrusters. The two types of DCD and DBD electron impact ionization are nearly exclusively used for flow control via plasma actuators for easy implementation. Specially, the side-by-side electrode configuration minimizes the degradation of aerodynamic performance and will not be parasitic when deactivated. In order to fully illustrate the discharge characteristics, the simulated results are duplicated according to the practical electrode arrangements for aerospace engineering applications.

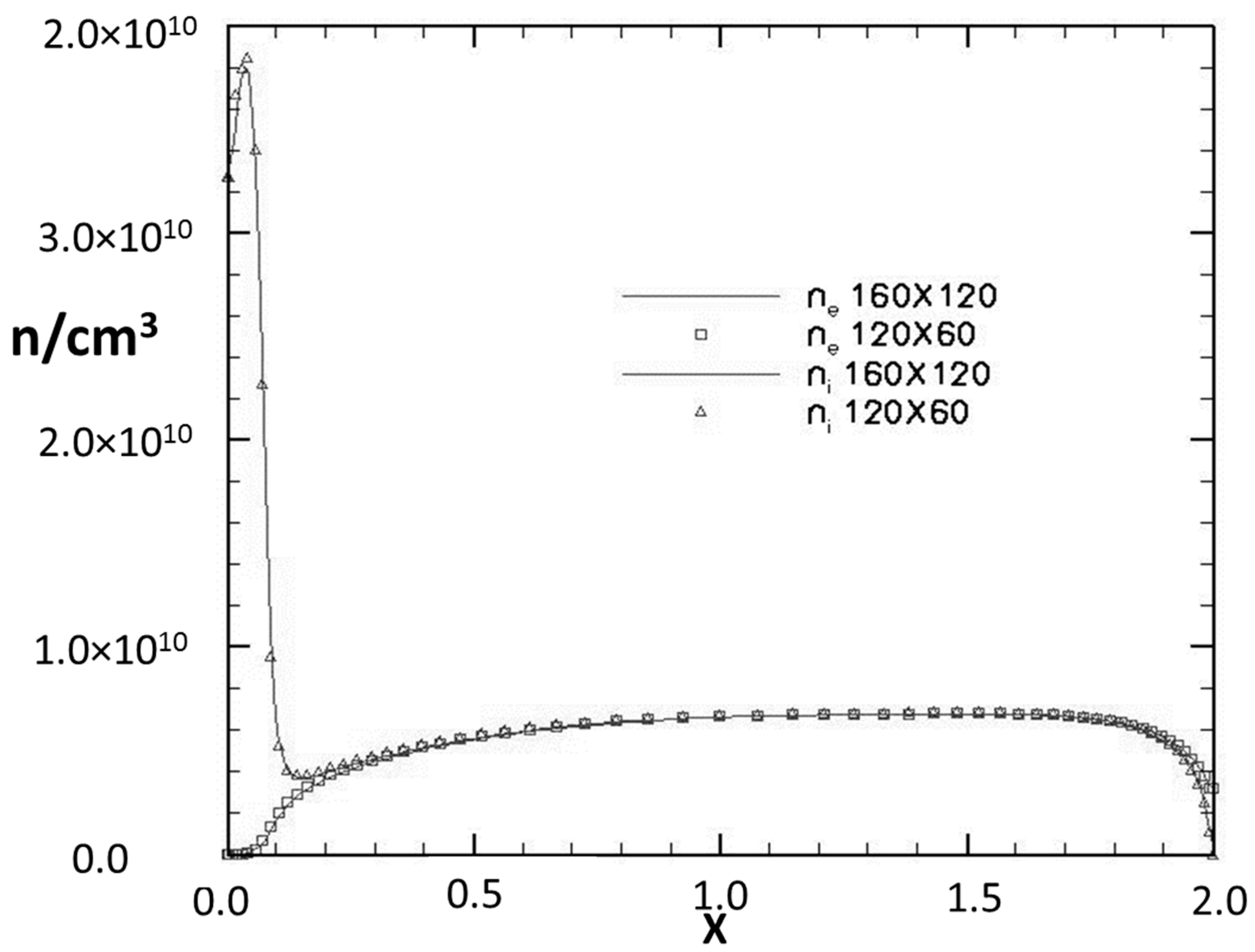
The numerical resolution for the electron impact ionization is rather stringent because of the criterion is imposed by the Debye shielding length. Figure 6 presents a numerical grid resolution study of the classic discharge arrangement between two parallel electrodes that extend to infinity. The discharge is maintained at an EMF (Electromotive Force) of 2.0 kV in an electrical circuit under the ambient pressure of 10 Torr. The discharge breakdown occurs within the gap of 2 cm. Two grid systems of (160 × 120) and (120 × 60) are used, and the finest mesh spacing in the coordinate normal to electrode is Δx = 1.67 × 10⁻³ cm. The electron and ion number densities are depicted by the square and triangle symbols. The cathode layer structure is accurately predicted by the fine- and the coarse-mesh calculations in terms of the layer thickness and the maximum ion number density. The maximum discrepancy between two numerical results is less than 0.05%. The agreement of the two numerical solutions in the positive column and the anode layer is nearly perfect. Therefore, it is ascertained that a grid-independent numerical simulation for the diffuse DCD is achieved.

The structure of the DCD is characterized by the positive column connecting the anode and cathode layers. The electric potential intensity drops by nearly two orders of magnitude from the electrode surface within the cathode fall. At the pressure level of 10 Torr, the maximum normal electric field intensity on the cathode exceeds a value of 8.0 × 10³ V/cm, decreases to a value of 3.5 × 10² V/cm, and rises again to a moderate level on the anode. The cathode fall becomes steeper when the ambient pressure is elevated. The computational simulations, in fact, have captured all essential physics of direct current discharges in different ambient environments. An interesting observation has also been made obvious by numerical simulations: the thickness of the cathode layer increases when the secondary emission coefficient is lowered accordingly. This behavior reflects a reduction of ionization efficiency.

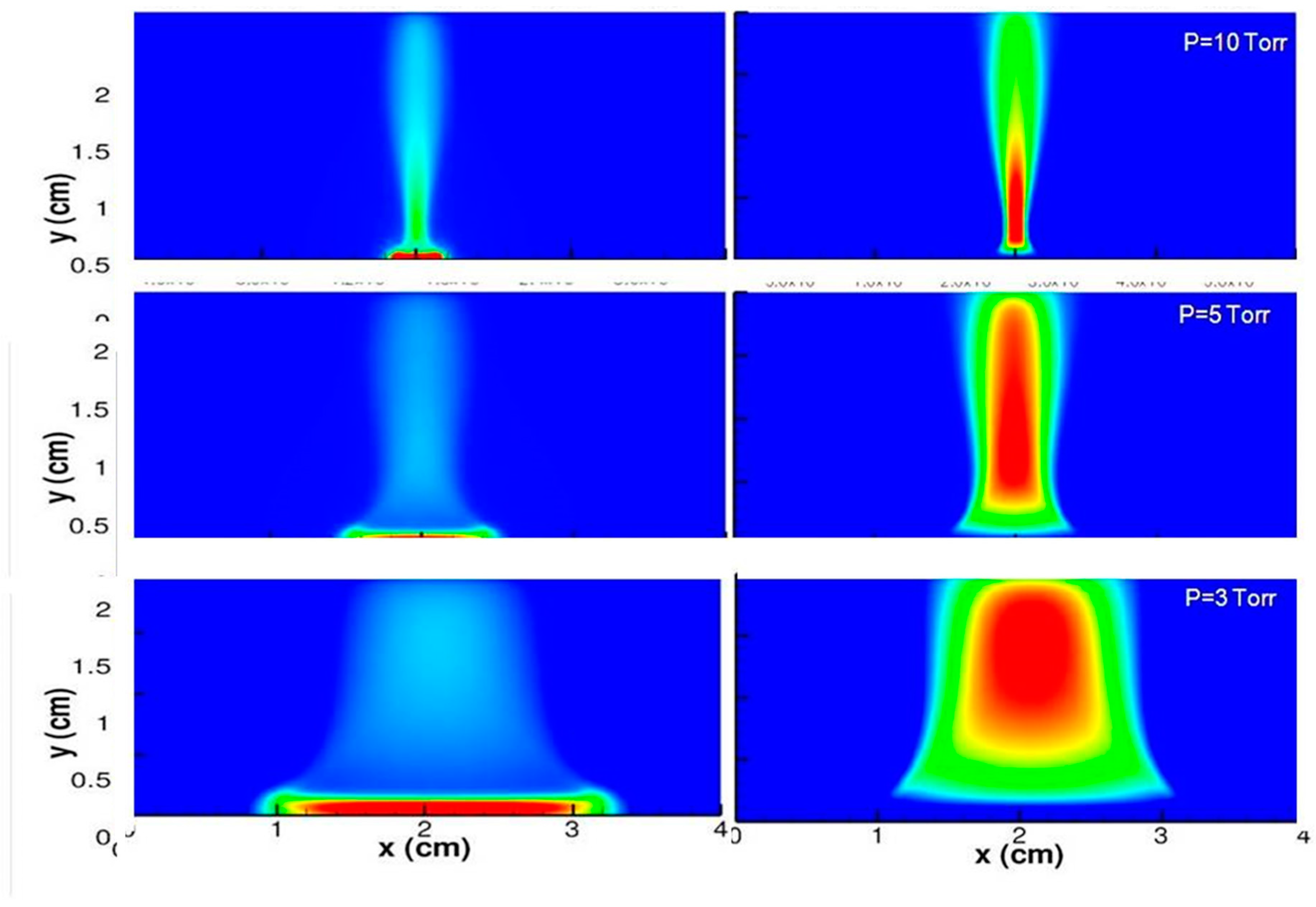
The inelastic collision model has been exclusively applied to plasma-based flow control actuators for hypersonic flow control [2,3]. The key mechanism of DCD is based on the thermal effect that derived from Joule heating in the cathode layer immediately above the cathode in addition to the electrode heating. In Figure 7, the positive ion contours are presented to the left of the electron counterpart. The overall structure of DCD in terms of the cathode layer and positive column is completely captured by the computational simulations. The constricted cathode layer thickness is clearly diminished by the increasing ambient pressure from 3, 5, to 10 Torr and at the temperature of 300 k. The numerical results are fully substantiated by the classic theory by Von Engel and Steenbeck [35]. In addition, the simulated results also show the intensified Joule heating over the cathode surface. The cathode layer thickness decreases as the ambient density is increased, and the width of the cathode layer also shrinks from 2.66 to 0.58 cm corresponding to the pressure rise from 3 to 10 Torr [22].

The side-by-side electrodes placement for DCD is the most efficient configuration for high-speed flow control. In practice, the cathode is always placed upstream of the anode, because the Joule heating is concentrated close to the cathode. The combined Joule and electrode heating increases the displacement thickness of a shear layer that creates an external flow deflection and leads to a stronger supersonic viscous-inviscid aerodynamic interaction. In fact, the magnitude of the pressure interaction is inversely proportional to the Reynolds number based on the distance measured from the leading edge. Therefore, a DCD for hypersonic flow control is the most effective when placed close to a sharp leading edge of a control surface.

The specific DC discharge configurations are generated under the most practical application conditions as displayed in Figure 8 by an electromotive force (EMF) of 0.5 kV. The two-dimensional computational domain has a dimension of 5.0 by 5.0 cm. In this configuration, the cathode and anode have identical widths of 0.5 cm and the separation distance between electrodes is 1.0 cm. The cathode is placed on the left of the anode with edges being located at 1.0 and 1.5 cm from the left boundary of the computational domain. For these computations, a non-uniform 120 × 60 grid mesh was used, with a minimum grid spacing of 5 × 10⁻³ cm clustering near the horizontal edges of the electrode and with a minimum perpendicular spacing of 1.67 × 10⁻³ cm over the electrode surfaces. The result of a finer 250 × 120 non-uniform mesh was also obtained for the purpose of comparison. The agreement was very good and indicates computational simulations with a minimum numerical error. At an ambient pressure of 5 Torr, the computed electrical potentials across the electrodes were 437.37 and 441.75 V for the fine and coarse grid systems; the corresponding total currents in the discharge field yields the value of 5.21 and 5.19 mA, respectively.

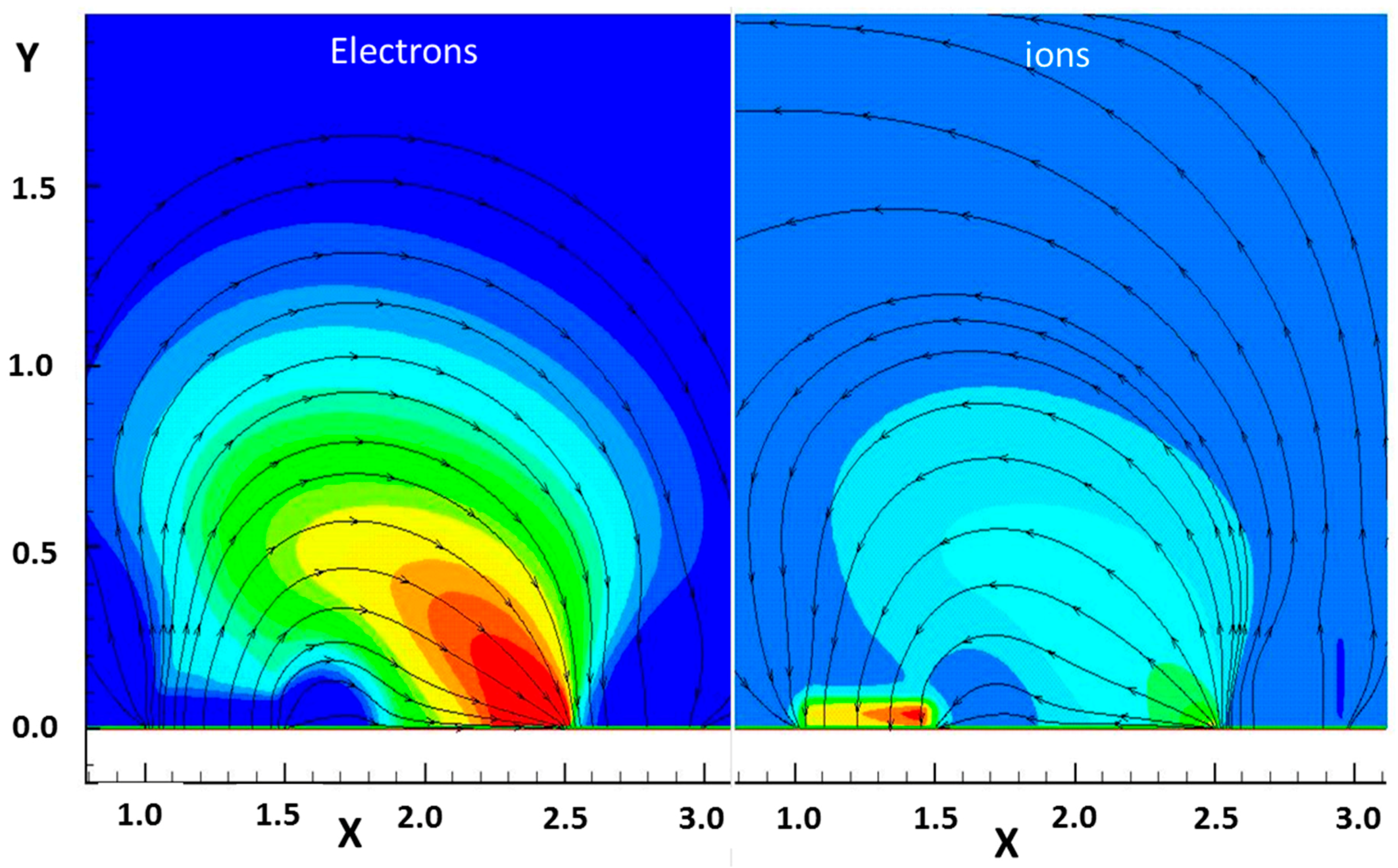
In Figure 8, the electric field intensity vector traces are superimposed over ion number density contours on the right-hand-side of the composite graph. Similarly, the discharge current vector traces are appended to electron number density distribution on the left-hand side of the graph. The maximum ion number density has a value of 5.76 × 10¹⁰/cm³ over the edge of the cathode and the maximum electron number density of the discharge field is 3.02 × 10¹⁰/cm³. The electrons are nearly absent in the cathode layer, except the secondary emission from the electrode which is easily observed. The average thickness of the cathode layer from the computational simulation is 0.125 cm, which is comparable to the classic one-dimensional result of 0.15 cm by Von Engel and Steenbeck [35].

The dielectric barrier discharge (DBD) arrangement in application is simply two electrodes placed along a line; one of the electrodes is exposed and the other is recessed and encapsulated beneath a thin dielectric film of a few microns’ thickness. For flow control, the exposed-embedded electrodes are aligned in the same direction to coincide with the induced so-called electric wind [16]. The best illustration for imposing the appropriate physics law is by imposing the discontinuous interface boundary across an exposed electrode and over a dielectric surface for the DBD. In the absence of an externally applied magnetic field, only the interface boundary condition for the electric field is necessary. From Equation (7), the required interface boundary conditions for DBD are:

$$\widehat{\mathit{n}}\times ({\mathit{E}}_d-{\mathit{E}}_p)=0$$

(31)

$$\widehat{\mathit{n}}\cdot ({\mathit{D}}_d-{\mathit{D}}_p)={\rho }_e$$

(32)

The subscripts p and d are associated with the electric field intensity E and displacement D is characterized the variables either within the plasma medium or on the dielectrics. According to the Maxwell equations, the tangential electrical field strength E, Equation (31) shall be continuous across the media interface, but the discontinuous electric displacement normal to the plasma and dielectric interface must be balanced by the local surface charge density. Although the electric current and charge number density may be infinite for a perfect electric conductor, the magnitude of the surface property is still definable as ${\rho }_{e,s}=e{\displaystyle \int (n_{+}}-n_e-n_{-})d\Delta$. It is the integrand of charged number densities over an infinitesimal distance $\Delta$ normal to the media interface and has a physical dimension of Coulombs/cm².

In fact, the discontinuous interface condition descripted by Equation (32) is required by the electromagnetic field. This requirement must be satisfied regardless of any possible chemical-physics processes on the media interface. For the global neutral and isotropic plasma, the electric field intensity E can be derived from the electric potential function, E = −$\nabla$ϕ. Substitute this relationship to the critical interface boundary condition and invoke the constitute relation between electric field intensity and electric displacement; $D=\epsilon E$ to get:

$${\epsilon }_p\frac{\partial {\phi }_p}{\partial n}-{\epsilon }_d\frac{\partial {\phi }_d}{\partial n}={\rho }_{e,s}.$$

(33)

The notations of ${\epsilon }_p$ and ${\epsilon }_d$ in Equation (33) denote the relative electric permittivity of plasma and dielectrics respectively. The relative value of ${\epsilon }_p$ for weakly ionized plasma has a value of unity, on the other hand, the relative electric permittivity of a dielectric, ${\epsilon }_d$ is substantially different to have the value up to 7.0 varying from polystyrene to rubber.

The boundary conditions for simulating DBD include the secondary emission phenomenon over the cathode by setting the normal component of electron flux density of electrons to be proportional to the counterpart of positively charged ions flux by an emission coefficient $\gamma$ [20,37]. The gradients of the approaching positively charged ions number density are unaltered.

$$\begin{array}{l}\overrightarrow{n}\cdot {\Gamma }_e=-\gamma \overrightarrow{n}\cdot {\Gamma }_{+}\\ \overrightarrow{n}\cdot \nabla n_{+}=0\end{array}$$

(34)

On the anode, the necessary boundary conditions are reflected by the repulsion of all positively charged ions, and by allowing the gradient of electron number density to be invariant.

$$\begin{array}{l}{n}_{+}=0\\ \overrightarrow{n}\cdot \nabla n_e=0\end{array}$$

(35)

For the above boundary conditions, it is tactically assumed that the electrode surfaces are perfectly catalytic. At the farfield boundary, all variables including the electric field potential vanish asymptotically. All these imposed boundary conditions are either the Neumann or Dirichet types and proven to be well-posed and accurately describe the physics phenomena.

For DBD, the most critical and discontinuous boundary conditions are imposed on plasma and electrode interfaces either on the exposed metallic or the dielectric surface. By substituting the surface current density into Equation (33), we have:

$$\frac{\partial {\phi }_p}{\partial n}=\frac{{\epsilon }_d}{{\epsilon }_p}\frac{\partial {\phi }_d}{\partial n}+\frac{e}{{\epsilon }_p}{\displaystyle \int (n_{+}}-n_e-n_{-})d\Delta$$

(36)

Equation (36) reveals explicitly the most outstanding characteristics of DBD that can prevent the discharge transition to arc. The electric field intensity across the electrode gap is substantially reduced by the surface charge accumulation and the large difference between relative electric permittivity of the surface material and the plasma. It is important to recognize that the self-limited characteristic for DBD transition to arc is the direct consequence of satisfying the discontinuous interface boundary condition of the Maxwell equation in the time domain.

During the DBD process, there are two electric current components; one of component is the displacement current that exemplifies the typical sine wave pattern by most AC electric fields. Another small component is the conductive current in the mille ampere range by the microdischarges after the electric breakdown. The disturbance to the AC voltage-current relationship becomes an important verification for the inelastic collision ionizing model [22]. The ionization model is built on Townsend’s discharge mechanism together with the bulk and ion-ion recombination, as well as, the electron attachment and detachment. If the ionization model by the chemical-physics kinetics is not able to describe a reasonable discharge composition, the calculated conductive current of a DBD will be clearly erroneous. 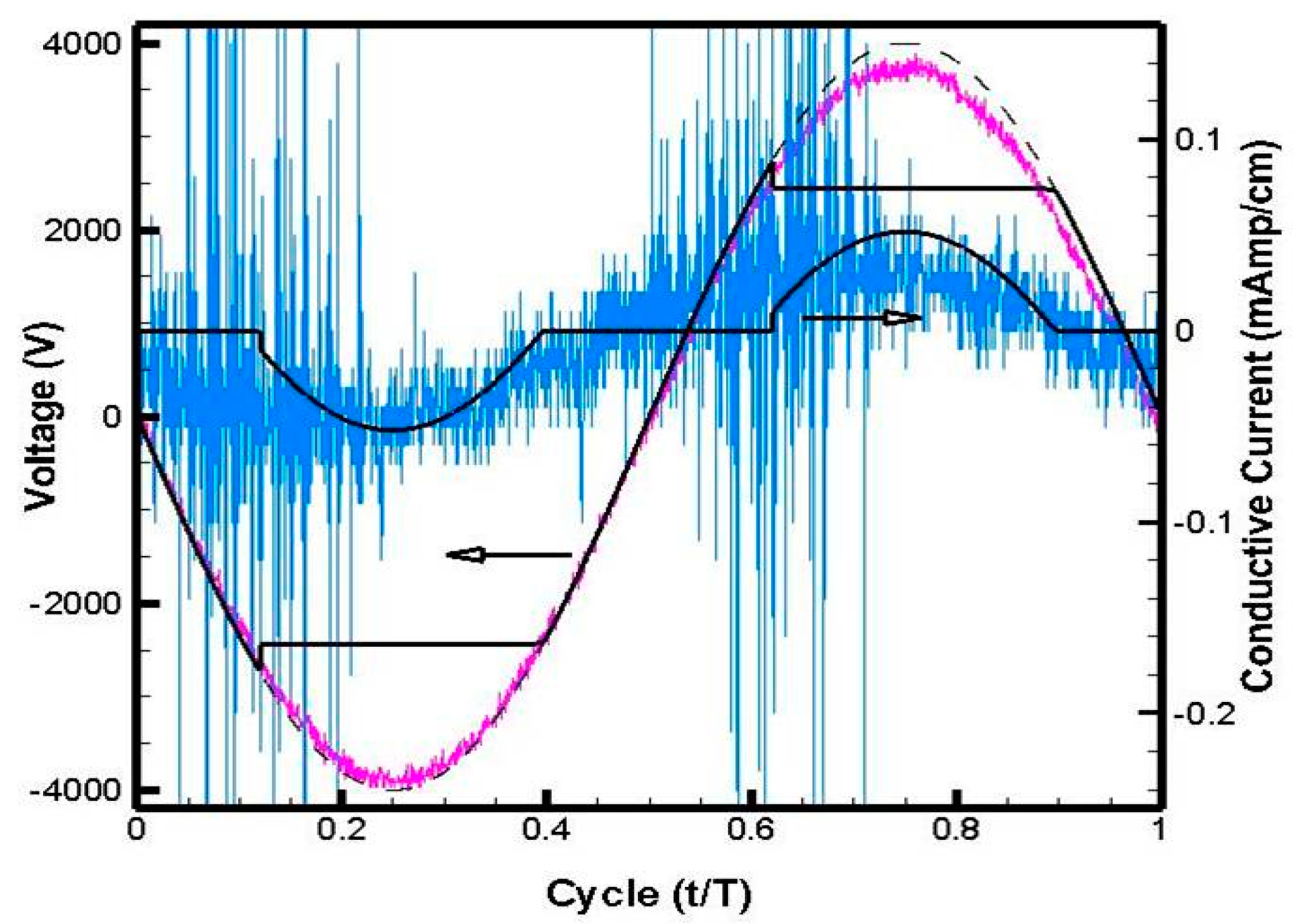Figure 9 describes the collected experimental data at an AC cycle of 5 kHz that is driven by an EMF of 4.0 kV. The simulated conductive current and electric intensity across the discharge are represented by the black lines for the calculated magnitude and duration of the discharge. The calculated conductive current by the ionization model displays correctly the global DBD behavior from the onset of the electric breakdown until the periodic discharged ceased. The computational simulation is embedded within the scattering data band of the microdischarges for the entire AC cycle.

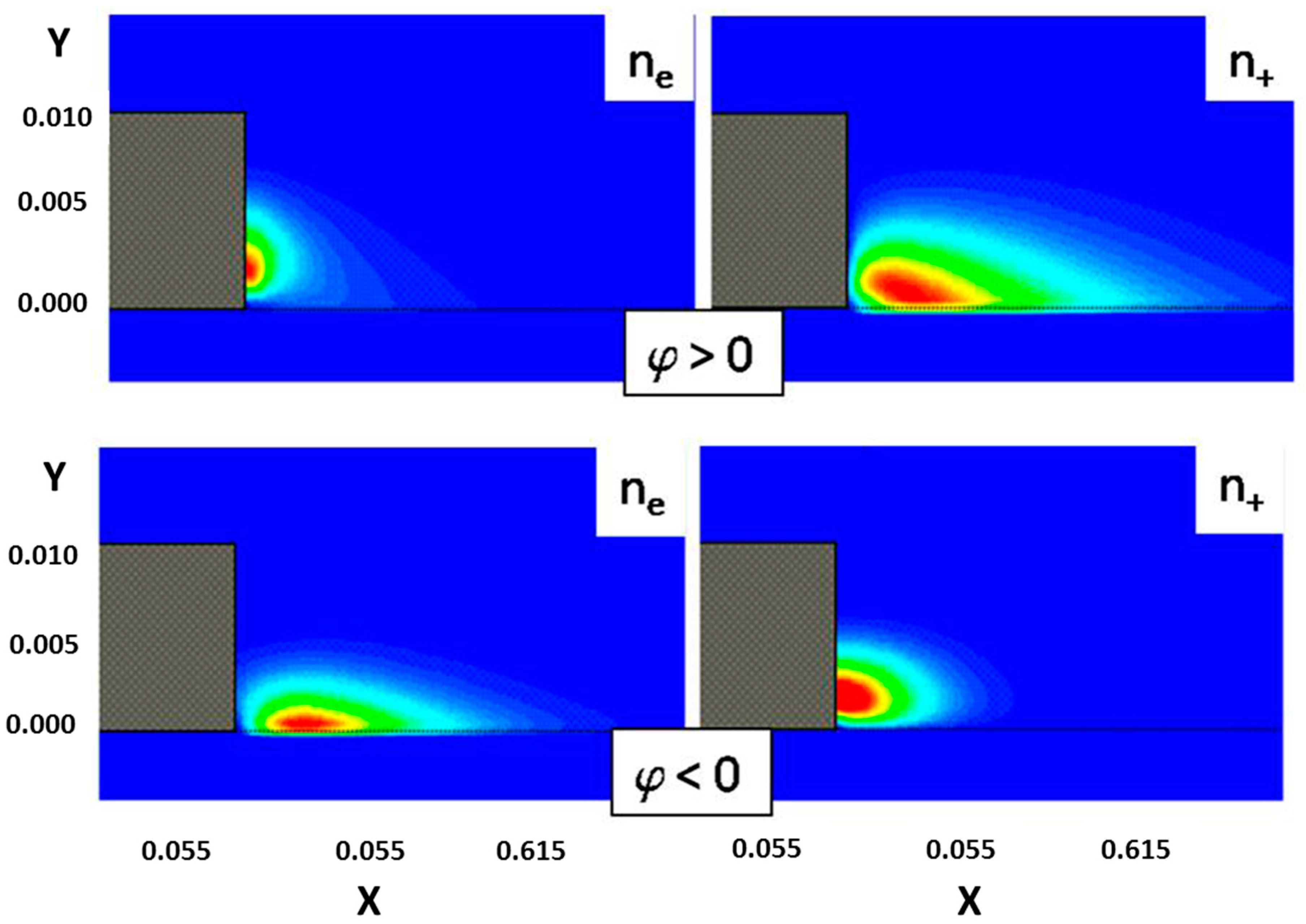
The DBD is a time-dependent phenomenon and varying rapidly according to the period of an AC cycle in microseconds. Therefore, the typical discharge structure is best presented at the peaks of its EMF value. In Figure 10, the time-dependent computational charge number densities for DBD are depicted at the instants when the peak values of the EMF of ±3.0 kV are applied. At the instant the exposed electrode carries a positive voltage of 3.0 kV, the secondary electrons emission from the dielectrics, which acts as the cathode, attracts an overwhelming positively charged particle accumulation over the barrier surface. The accumulated positive charges reduce the electrical potential of the DBD field across the electrodes. At this instant, all the electrons propagate toward the anode and are concentrated over the edge of the anode, as shown in the left-hand side of the upper panel.

When the electrical polarity in the AC cycle is reversed, the exposed electrode becomes the cathode and all positively charged ions are now expelled from the dielectrics and concentrate near the lower edge of the exposed electrode, as shown by the right-hand side of the lower panel. At the same time, the electrons are accelerated from the exposed electrode toward the dielectrics-embedded electrode. The accumulated electrons over the dielectrics diminish the electrical intensity within the DBD field. The propagations of the positively charged ions and electrons within an AC cycle are clearly illustrated by the computational simulations.

The electric wind is generated by momentum transfer via collisions between positively charged ions and neutral particles. The periodic electrostatic force derives from free space charge separation during the cyclic dynamic events caused by an applied AC voltage [22,37,38]. The dominant dynamic force at a given point in time can be given as a product of the number density of separated charges and the electrical field intensity vector.

$$\mathit{F}\approx e(n_{+}-n_{-}-n_e)\mathit{E}$$

(37)

According to Equation (17), the force vector must follow the combined sign of electric field vector E and a net difference of positive ions and negative ions and electrons.

For the globally neutral plasma and in the absence of induced magnetic field intensity, the electrical field intensity is described by the negative gradient of the electrical potential $\mathit{E}=-\nabla \phi$. In a three-dimensional formulation, the periodic electrostatic force has three components:

$$F_x=e(n_e+n_{-}-n_{+})\frac{\partial \phi }{\partial x}$$

(38)

$$F_y=e(n_e+n_{-}-n_{+})\frac{\partial \phi }{\partial y}$$

(39)

and

$$F_z=e(n_e+n_{-}-n_{+})\frac{\partial \phi }{\partial z}$$

(40)

From the above equations, the orientation of a periodic electrostatic force in a DBD is determined by the sign of product from the electric field potential derivatives and the net charged particle density. Charge separation occurs only in the plasma sheath or within the gap of the electrodes, and the faster mobility of electrons leads to a greater number density of ions in this region. From the ionization kinetics model, the number density of positively charged ions is much greater than that of the negatively charged counterparts. So the net charge particle density in Equation (38) though (40) in the sheath region is mostly negative. The orientation of the periodic electrodynamic force is thus dictated by the sign of the gradient of the externally applied electric field potential. In this instance, the electrical potential decreases from the exposed electrode toward the dielectric surface when the exposed electrode acts as an anode. The gradient of the electric potential or the electric field intensity is negative. The resultant force from Equation (38) has a positive sign, thus the x-component electrostatic force is directed away from the exposed electrode toward the dielectric covered electrode. In other words, the x-component of the force is directed toward the dielectric surface in the positively biased AC phase. In this AC phase, the separated ions propagate from the anode toward the dielectric encapsulated cathode. The moving ions collide and transfer momentum to stationary neutral particles to generate the so-called electric wind moving away from the exposed electrode toward the dielectrics.

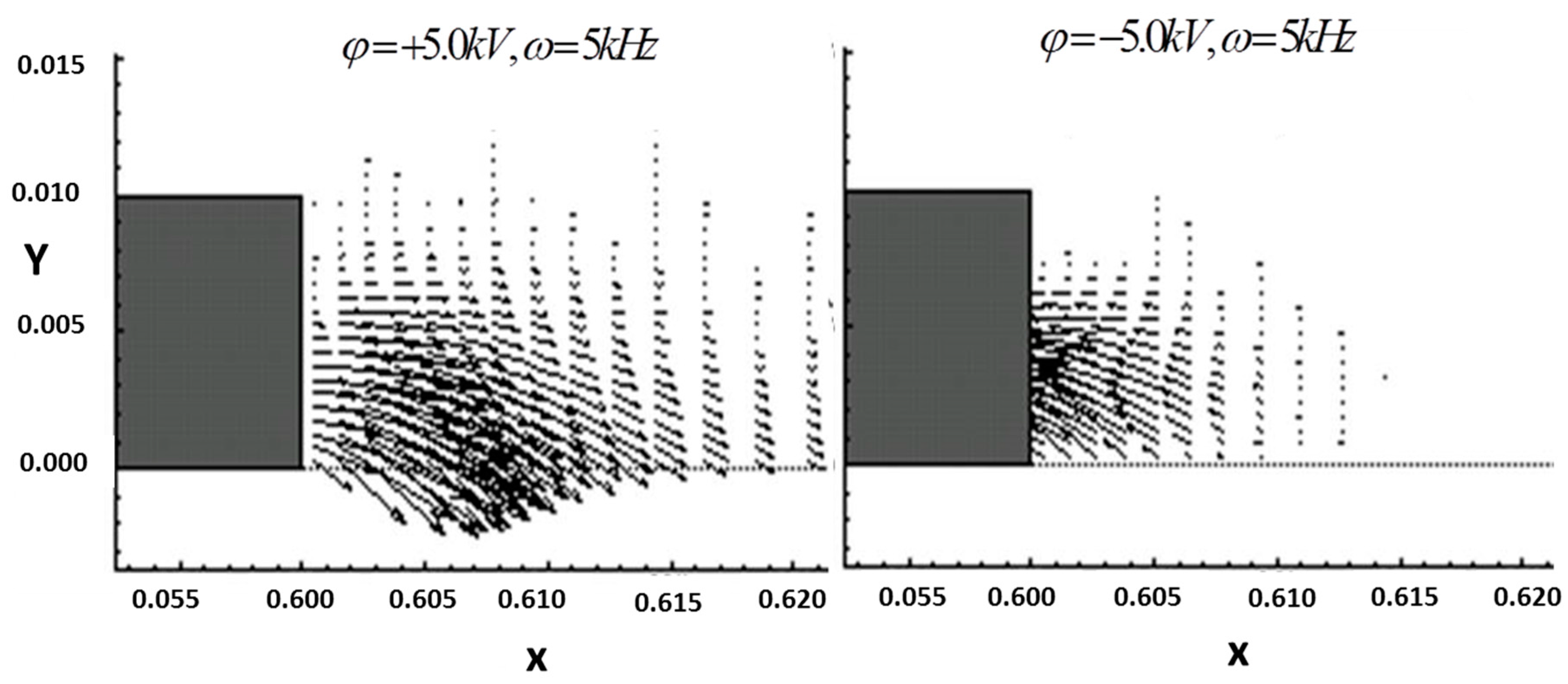
However, the resultant force of DBD will change its orientation when the polarity is switched in the AC cycle and the gradient of electric potential is now positive; the charged separation induced electrostatic force in the negative-biased AC cycle is now directed toward the exposed electrode, as depicted in Figure 11. Therefore, the DBD-induced periodic electrostatic force by charge separation reverses its direction within a negatively biased AC cycle. In other words, the unbalanced periodic electrostatic force that was generated by DBD in a complete AC cycle is the net resultant force between opposing orientations. The numerical results, in fact, substantiate the experimental stipulation that the periodic electrostatic force generated by DBD is push and pull [16]. In application, the resulting so-called electric wind is moving away from the exposed electrode toward the dielectrics.

In summary, the modeling of plasma by electron impact utilizing the combination of classic drift-diffusion theory and inelastic collision kinetics has demonstrated its ability to capture the essential physics. However like classic magnetohydrodynamics theory, which is built on the multi-fluid and multi-temperature formulation, the detailed composition of the partially ionized gas and its consequence is unaccounted for. For an incisive understanding and for the demarcating evaluation of innovations, the shortcomings of global modeling becomes glaring. The short fall is clearly revealed when applied to validating phenomena such as the MHD scramjet bypass and plasma-assisted ignition and enhanced combustion stability [1].

8. Concluding Remarks

A better understanding of plasma has its own right as the most common state of matter in the universe either by mass or volume. Plasma as a working medium brings many added physical dimensions for innovation. Unfortunately, plasma does not exist in an environment that is easily reproduced in ground-based facilities; instead, computational simulations must be relied upon.

All existing electron impact ionization models for aerospace engineering are woefully inadequate for weeding out unproductive innovations and for guiding the future research and technology development. Therefore, there is ample room for plasma modeling improvements. The foremost issue in the research arena may reside in acquiring an accurate physical description of the ionization process involving the transient and metastable chemical species at the outer limits of the Boltzmann-Maxwell distribution, thereby narrowing down exaggerated research findings. In this respect, it may be mandatory to bring the ab inito computational quantum physical chemistry capability to address these fundamental concerns.

At present, the first step of improvement is to apply direct computational simulation via concurrent computation technology to investigate micro discharge structures. It should be fertile ground for basic research.