1. Introduction
Due to the high demand of air transport, the aviation industry is expected to develop rapidly in the coming years [
1]. To adapt to this requirement, the increase of aircraft and airport operations is necessary and important. However, the increase in these operations often results in negative impacts on the quality of life of near-airport communities, such as noise and pollutant emissions [
2]. As a result, the protest of communities surrounding airports becomes a major restriction that policymakers have to deal with when accomodating additional operations. In order to develop air transport sustainably, it is important to investigate potential solutions for decreasing its adverse influences. In recent years, a series of projects aiming to develop the aviation sector sustainably have been launched by European and national authorities, including CleanSky [
3], the Atlantic Interoperability Initiative to Reduce Emission (AIRE) [
4], and the Asia and South Pacific Initiative to Reduce Emission (ASPIRE) [
5]. Various strategies have been proposed, such as making new policies and standards, developing advanced aircraft technologies and sustainable alternative fuels, and changing aircraft/airport operational procedures [
6]. Among them, the change of aircraft/airport operational procedures may be a potential option in the short-term as it can be adapted more quickly and often at less cost as compared to the other options [
6]. The optimal design of new routes for departures and arrivasls is one of the possible solutions that has been broadly studied in the past few years [
7,
8].
In order to design optimal environmentally friendly terminal routes, different approaches have been proposed in recent years. Visser and Wijnen [
9,
10] developed an optimization tool called NOISHHH that combines a noise model, an emissions inventory model, a geographic information system, and a dynamic trajectory optimization algorithm to generate environmentally optimal departure and arrival trajectories. Later, this tool was also adapted to optimize noise abatement terminal routes based on area navigation [
11,
12,
13]. Prats et al. [
14,
15] employed a lexicographic optimization technique to deal with aircraft departure trajectories for minimizing noise annoyance. Khardi and Abdallah [
16] studied a comparison of direct and indirect methods in solving a system of ordinary differential equations (ODEs) to optimize aircraft flight paths to reduce noise. Recently, Matthes et al. [
17] presented a concept for multi-criteria environmental assessment of aircraft trajectories where the mathematical framework for environmental assessment and optimization of aircraft trajectories was developed. Despite being quite efficient in searching optimal trajectories, these techniques belong to the group of gradient-based methods that have certain limitations in solving optimization problems. For example, due to the use of gradient information to search for an optimal solution, these methods are often only suitable for optimization problems whose objective and constraint functions are differentiable and whose decision variables are continuous. Moreover, their solutions are often trapped in local optima if the considered problems are nonlinear and contain more than one local optimal solution. Nevertheless, current optimization problems become more and more complex due to the integration of operational constraints in realistic scenarios. It is therefore quite difficult to construct differentiable optimization problems. Also, these techniques are single-optimization methods, which means that only a single optimal solution is obtained after each time the optimization problem is solved.
By considering the above research gaps, different gradient-free optimization techniques have also been applied. Torres et al. [
18] proposed a non-gradient optimizer called multi-objective mesh adaptive direct search (multi-MADS) to synthesize optimal departure trajectories for NO
x-emissions and noise at a single measurement point. Recently, Hartjes and Visser [
19] employed an elitist non-dominated sorting genetic algorithm (NSGA-II) combined with a novel trajectory parameterization technique for the optimal design of departure trajectories with environmental criteria. This approach was then also applied by Zhang et al. [
20] to optimize departure routes at Manchester Airport. From the obtained results in [
18,
19,
20], it is clear that the use of non-gradient multi-objective optimization methods is a potential approach for designing new routes. These methods readily overcome the limitations of gradient-based methods in dealing with discontinuous problems and integer or discrete design variables and can find out a set of non-dominated optimal solutions, which helps to present more options to policymakers and authorities. However, one of the major limitations of the methods in this group is their computational cost. Because they feature random searches with multiple design points at the same time, these methods require many evaluations of the objective and constraint functions which are quite time-consuming. These restrictions again have motivated researchers to develop computationally efficient approaches that can balance the expected results and computation cost effectively.
Until now, besides multi-MADS and NSGA-II, there are various multi-objective optimization algorithms available in the literature that may be considered potential candidates for solving these kinds of problems. However, they have not yet been properly investigated. Among them, the multi-objective evolutionary algorithm based on decomposition (MOEA/D) [
21] has recently emerged as a powerful method and has received much attention from researchers. According to recent studies [
21,
22], MOEA/D has been demonstrated to be more efficient than NSGA-II and some other methods regarding both the quality of solutions and the convergence rate, which are promising features for solving large-scale real-world problems. Nonetheless, the application of MOEA/D to real engineering problems is still somewhat limited, especially in the field of aerospace engineering. In this paper, MOEA/D is considered for the optimal design of aircraft noise abatement departure routes. As mentioned before, however, MOEA/D is a gradient-free optimization method, and hence its computation cost is still signficant. In order to make the applied algorithm more efficient, a new implementation in the definition of the optimization problem for MOEA/D is introduced that can help to reduce the computational cost significantly. Furthermore, the efficiency of the MOEA/D version in this paper is also considerably enhanced by the integration of some recently developed advantageous features. These include an adaptive replacement strategy [
23], a stopping condition criterion [
24], and a constraint-handling technique [
25]. Also, to reduce redundant evaluations of infeasible solutions derived from operational constraints during different flight phases, the new trajectory parameterization technique recently proposed in [
19] is also applied. The robustness and reliability of the proposed method are validated through two numerical examples at Schiphol Airport in The Netherlands.
3. Formulation of the Optimization Problem
The main objective of the study is to design optimal departure routes which can help reduce considerably the adverse impact of aircraft noise on people living in the vicinity of airports. However, purely focusing on noise impact may result in a significant increase in fuel consumption, which is against the interests of stakeholders like airline companies. To balance this conflict, therefore, fuel consumption is also taken into account as the second objective.
While fuel consumption can readily be evaluated by the change of the aircraft weight from Equations (6)–(9), noise impact is harder to quantify. In order to measure the influence of aircraft noise on communities surrounding airports, the percentage of people who are likely to be awakened due to aircraft noise exposure is utilized in this paper. This criterion was proposed by the American National Standards Institute (ANSI) in 2008 and is defined as follows [
27]:
where
is the percentage of awakened people owing to the noise of an aircraft.
is the indoor sound exposure level in decibel (dB) and is evaluated by using a replica of the integrated noise model (INM) that has been the Federal Aviation Authorities’ (FAA) standard regulatory noise model since the late 1970s [
19]. Because SEL obtained from INM represents an outdoor value, an amount of 15 dB is subtracted to obtain
, accounting for the sound absorption of an average house with an open window [
28]. It should be noted that only SEL values that are larger than or equal to 50 dB are taken into account, while those that are less than 50 dB are ignored, and their probabilities are set to zero [
29].
By considering two objectives (noise and fuel) at the same time, a bi-objective optimization problem is formulated as follows:
where
x is the vector of ground track variables.
and
are the vectors of the flight path angle setting and throttle setting variables for each segment. The variable μ is the bank angle, which is defined by
. The parameter
is the allowable value of μ, which is dependent on altitude as specified by ICAO [
26]. The parameters
and
are, respectively, the prescribed final altitude and equivalent airspeed of the flight procedures.
4. MOEA/D Algorithm and New Implementations
4.1. MOEA/D Algorithm
The multi-objective evolutionary algorithm based on decomposition (MOEA/D), first proposed by Zhang and Li [
21], has been recognized as one of the most popular multi-objective evolutionary algorithms to date [
30]. In MOEA/D, a multi-objective optimization problem (MOP) is transformed into a set of single optimization sub-problems by applying decomposition approaches, and then evolutionary algorithms are utilized to optimize these sub-problems simultaneously. With the use of different decomposition methods and different evolutionary algorithms, various versions of MOEA/D have been developed in recent years, e.g., MOEA/D-DE [
22], MOEA/D-DRA [
31], MOEA/D-XBS [
21], and MOEA/D-GR [
23]. Although different variants of MOEA/D are available in literature, a powerful single version of MOEA/D that integrates different advantages of the current versions is not yet in place. With the aim of developing an efficient version of MOEA/D for real-life problems, a powerful MOEA/D version is therefore developed in this study that is a combination of MOEA/D-DE [
22], an adaptive replacement strategy [
23], a stopping condition criterion [
24], and a constraint-handling technique [
25]. The general framework of MOEA/D is presented in Algorithm 1. For more details, readers are encouraged to refer to [
22,
23,
24,
25,
32].
| Algorithm 1. MOEA/D algorithm |
Input:A multi-objective optimization problem as Equation (15); A stopping criterion; N: number of sub-problems; : a set of N weight vectors; Tm: size of mating neighbourhood; Trmax: maximum size of replacement neighbourhood; δ: the probability that mating parents are selected from the neighborhoods; MaxIter: maximum iteration; FEs = 0: the number of function evaluations;
|
Step 1. Initialization- 1.1.
Find the Tm closest weight vectors to each weight vector based on the Euclidean distances of any two weight vectors. For each sub-problem set where are the closest weight vectors to ; - 1.2.
Create an initial population by uniformly randomly sampling from design space Ω. Evaluate the fitness value of each solution , i.e., and set ; - 1.3.
Initialize ideal point by setting and nadir point by setting ; - 1.4.
Set FEs = FEs + N, and generation: gen = 1;
|
| Step 2. Update |
| while (the stopping condition is not satisfied) |
| for ; do |
- 2.1.
Selection of mating/update range
|
| Set |
| where rand is a uniformly distributed random number in [0, 1]; |
- 2.2.
Reproduction: randomly select three parent individuals from Bm and generate a solution by applying “DE/rand/1” operator, and then perform a mutation operator on to create a new solution y; - 2.3.
Repair: if any element of y is out of Ω, its value will be randomly regenerated inside Ω; - 2.4.
Evaluate the fitness value of new solution y; - 2.5.
Update of z* and : for each j = 1,…, m if then set , and if then set ; - 2.6.
Update of solutions: use an adaptive replacement strategy in [ 23]:
|
| end for |
| Set FEs = FEs + N, and gen = gen + 1; |
| Step 3. Stopping condition |
| Use a stopping criterion in [24]. |
| if (stopping criterion is satisfied or MaxIter is reached) |
| Stop the algorithm; |
| end if |
| end while |
| Output: Pareto set ; Pareto front . |
4.2. New Implementations
Although MOEA/D has been demonstrated to be more efficient than NSGA-II and other methods, and in this study, its performance has also been strongly supported by the integration of the powerful features recently developed, like other population-based optimization methods, MOEA/D is still time-consuming, requiring a significant amount of model evaluations. Since the considered problem is a constrained optimization problem, there could be many trial solutions evaluated by MOEA/D during the optimization process that violate the constraints (or are infeasible). The evaluations of these solutions may lead to a significant increase in the computational cost of the algorithm, while they may not provide helpful information for searching an optimal solution.
In an effort to avoid the above problem, a new implementation on the setting of the optimization problem and MOEA/D is introduced. More specifically, for the considered problem, the computational cost is mainly spent on two main tasks: one for solving the ODEs to obtain the fuel objective and the necessary inputs for calculating noise and to evaluate the constraints of the optimization problem (for example, the final conditions of velocity and altitude, and the bank angle constraints), and the other for computing the noise objective. While the computational cost of the first task is not so significant, the computational expense of the second task is quite considerable. In MOEA/D, after a new solution is found, its objectives and constraints are measured and compared with those of previous solutions. The solutions with the better objectives and/or the better level of constraint violation will be selected for the next generation. It is readily clear that if there is a comparison between a feasible solution and an infeasible solution, the feasible one will be selected, and in the case of comparing two infeasible solutions, the solution with the lowest level of constraint violation will be chosen. By recognizing this feature, a new decision has been made for the algorithm to decide whether or not the noise calculation of a new solution is executed. Particularly, after the fuel objective and constraints of a new solution are assessed, a quick check and comparison of the level of constraint violation between them are executed first. If the new solution violates the constraints or has a higher level of constraint violation compared to, respectively, a feasible solution or an infeasible solution at the previous generation, its noise calculation will not be executed. In that case, the update procedures 2.5 and 2.6 of MOEA/D in Algorithm 1 are ignored as well.
With the above new implementation, the computational cost of noise calculation only is spent on either feasible solutions or on the infeasible solution with the lowest level of constraint violation, and hence the computational cost of the whole optimization process will be significantly reduced.
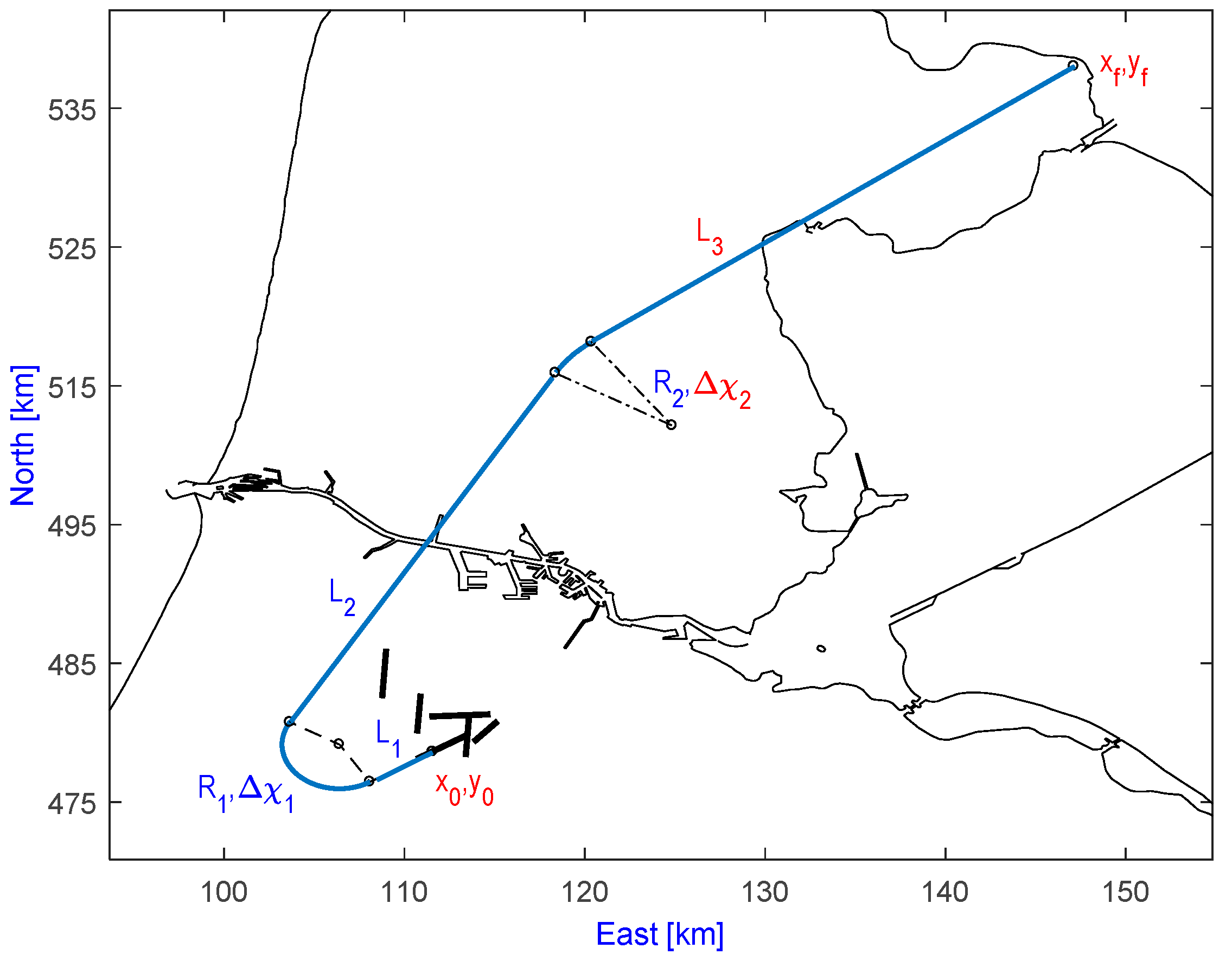
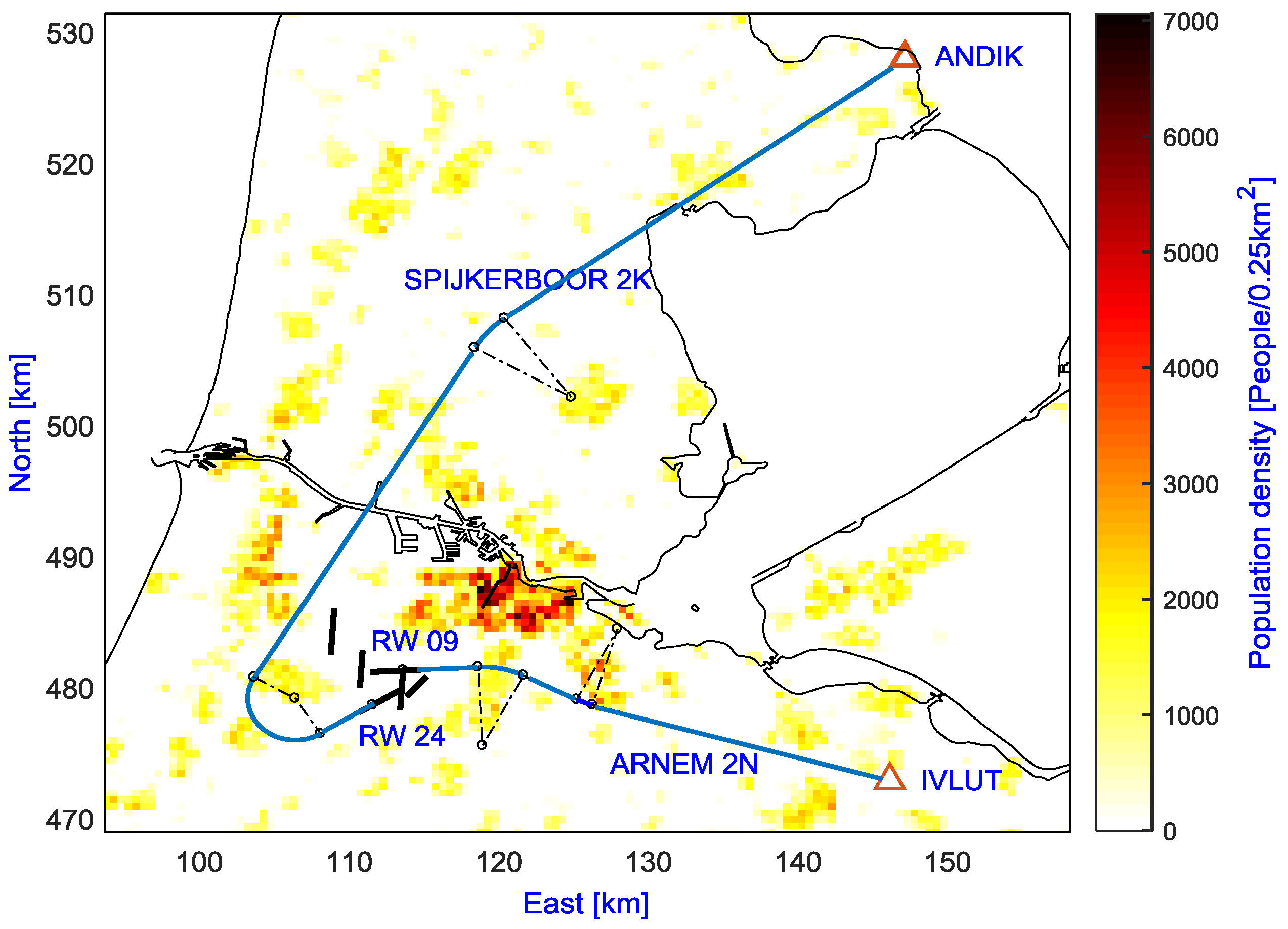
5. Numerical Example
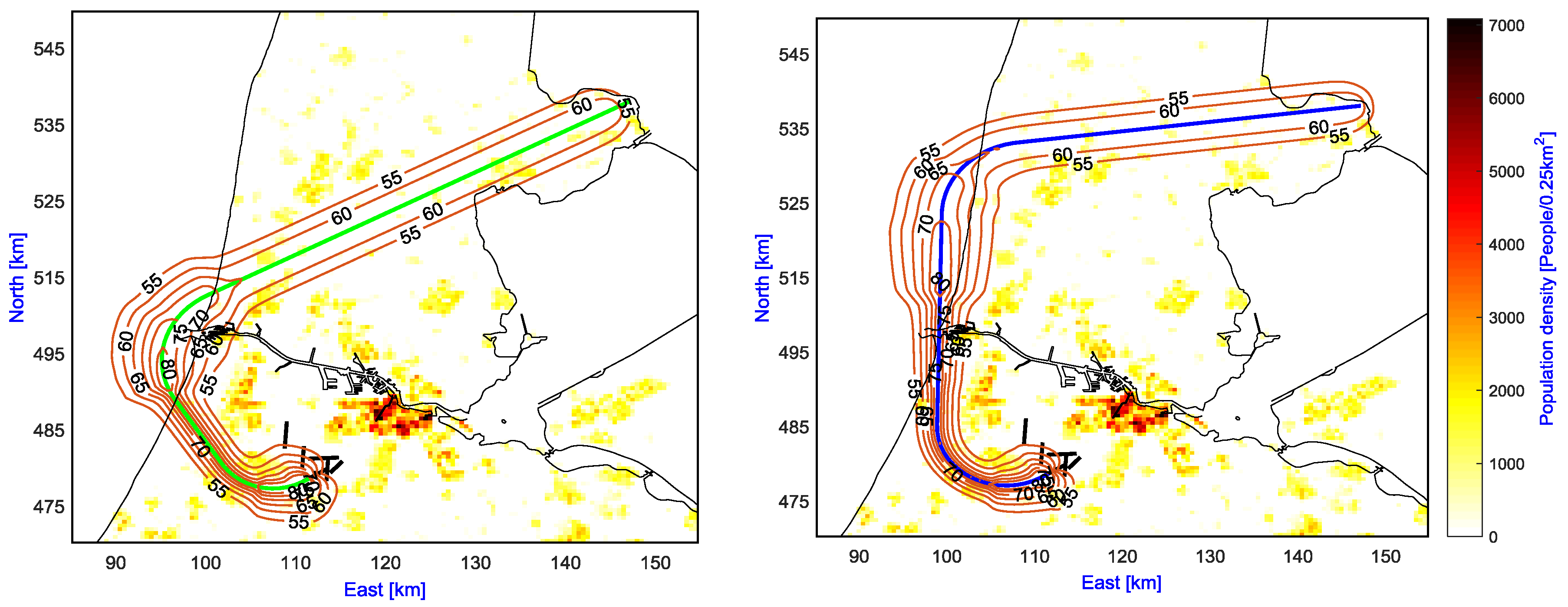
In order to demonstrate the capabilities and efficiencies of MOEA/D for conducting the optimal design of noise abatement departure routes, two standard instrument departures (SID) currently in use at Schiphol Airport are considered in this section. The first SID is called SPIJKERBOOR2K, which starts at runway 24 and finishes at the ANDIK intersection, and the other one is ARNEM2N, which starts at runway 09 and terminates at the IVLUT intersection, as shown in
Figure 2. These routes pass closely by the communities of Hoofddorp, Haarlem, and Amstelveen, where most of the noise nuisance occurs. For both departures, the optimized trajectory starts at 35 ft, a take-off safety speed of
V2 + 10 kts, with the landing gear retracted and departure flaps selected and is terminated at an altitude of 6000 ft and an equivalent airspeed (EAS) of 250 kts. The ground tracks are constructed by three straight legs and two turns, as shown in
Figure 2, which results in five design variables, while the vertical path is subdivided into 10 segments and parameterized as the study in [
19], which results in an additional 18 design variables. For the reference case, the ground track is fixed to conform to the current SID, while the vertical path is optimized for fuel burn after finishing the NADP-1. The details of the parameterization can be found in Hartjes and Visser [
19]. Two noise-exposed regions of 66 km × 59 km and 36.5 km × 20 km with a population grid cell size of 500 m × 500 m [
33] are used for the SPIJKERBOOR2K and ARNEM2N SIDs, respectively. A Boeing 737–800 with two engines is used as the aircraft model, based on the Base of Aircraft Data (BADA), with an initial mass of 68 tons (85% of the maximum take-off weight) as a representative take-off mass.
To compare the performance of MOEA/D, the well-known NSGA-II [
34] is also applied to solve these problems. A population size of 50 is used for both methods, and the algorithms will stop when either their convergence criteria are satisfied or the maximum number of iterations (
MaxIter) is reached, where
MaxIter is set at 1000. All algorithms are implemented in Matlab 2016b on a Core i5, 8 GB RAM desktop.
5.1. Departure Route SPIJKERBOOR2K
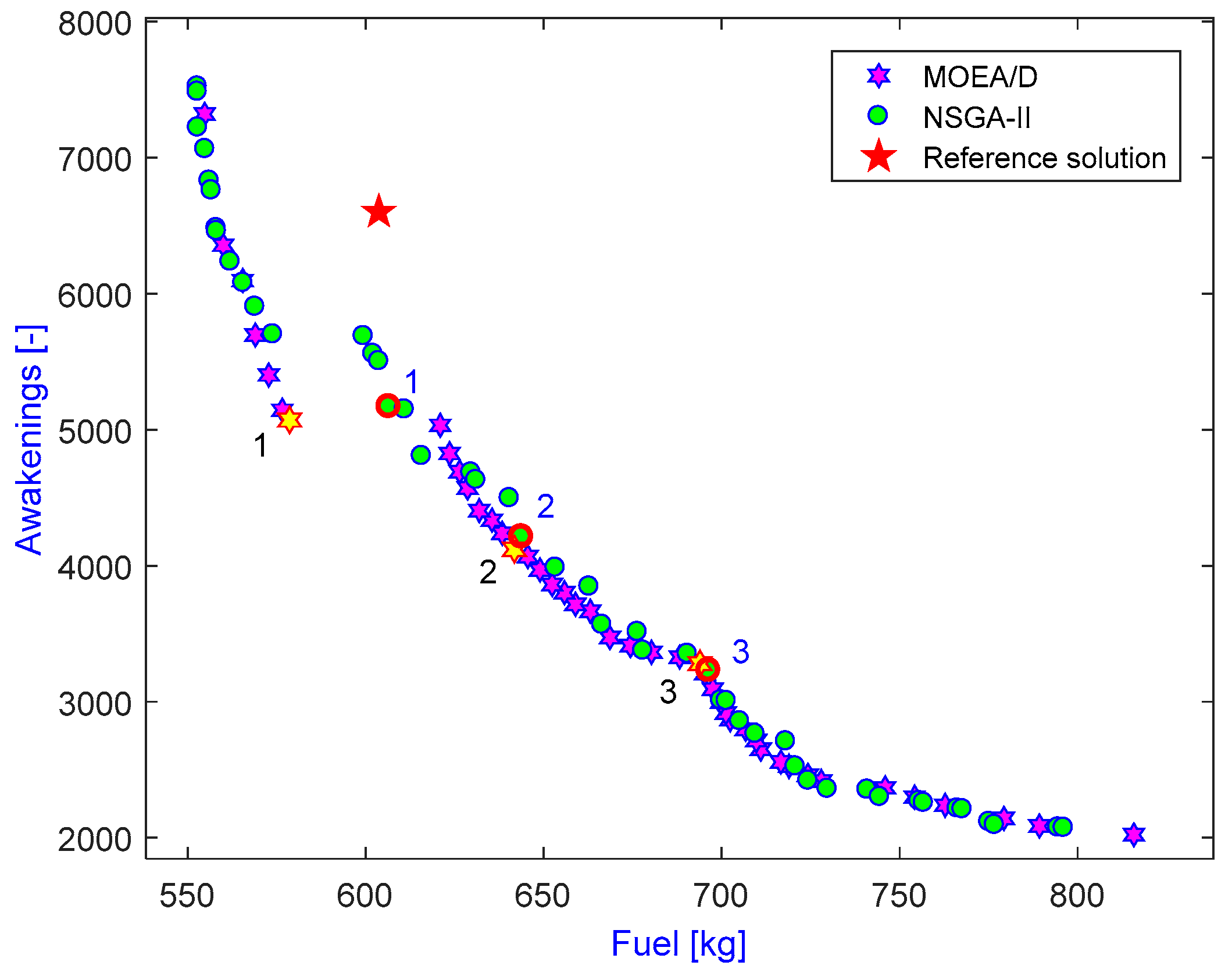
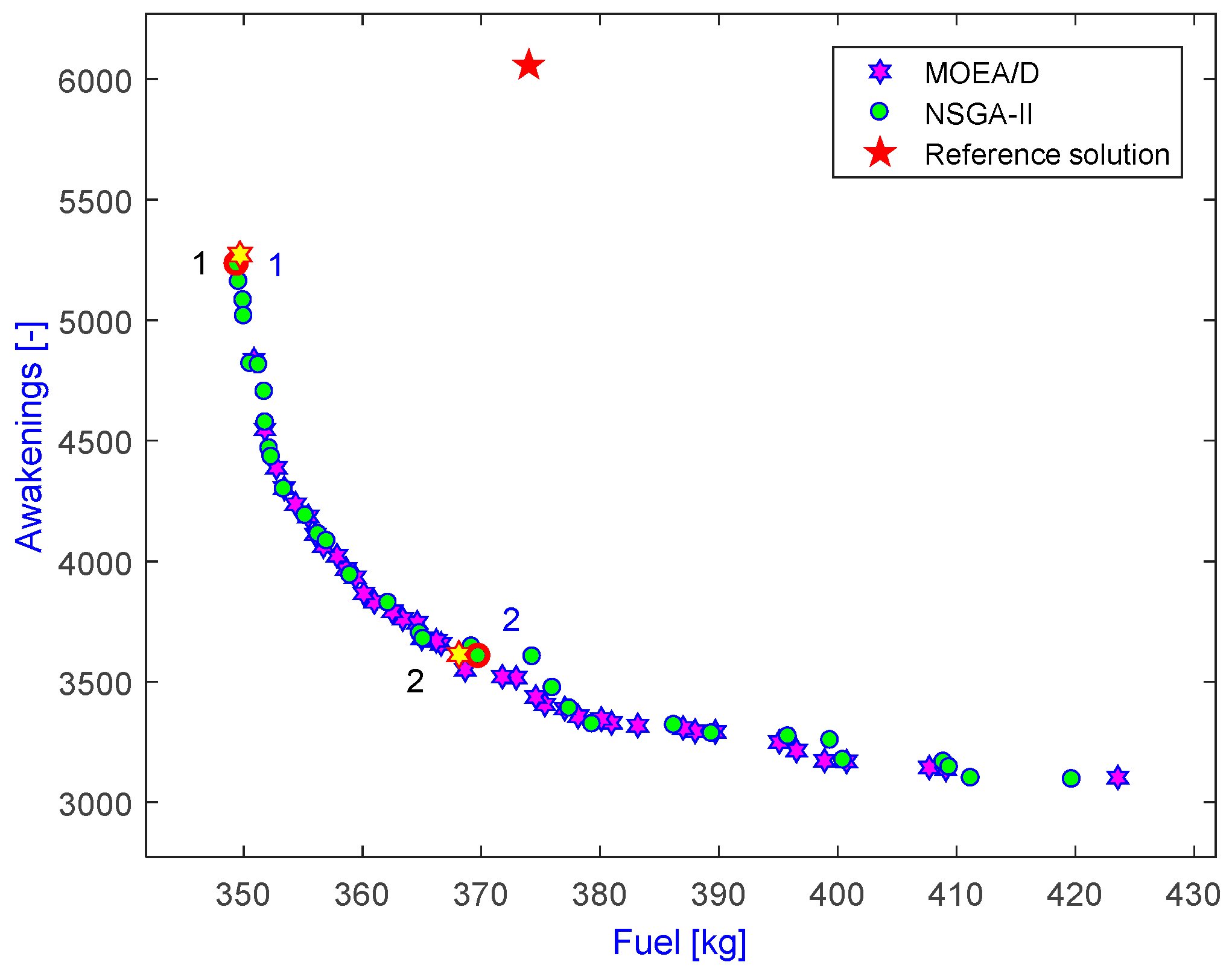
The Pareto-optimal solutions obtained by the methods are shown in
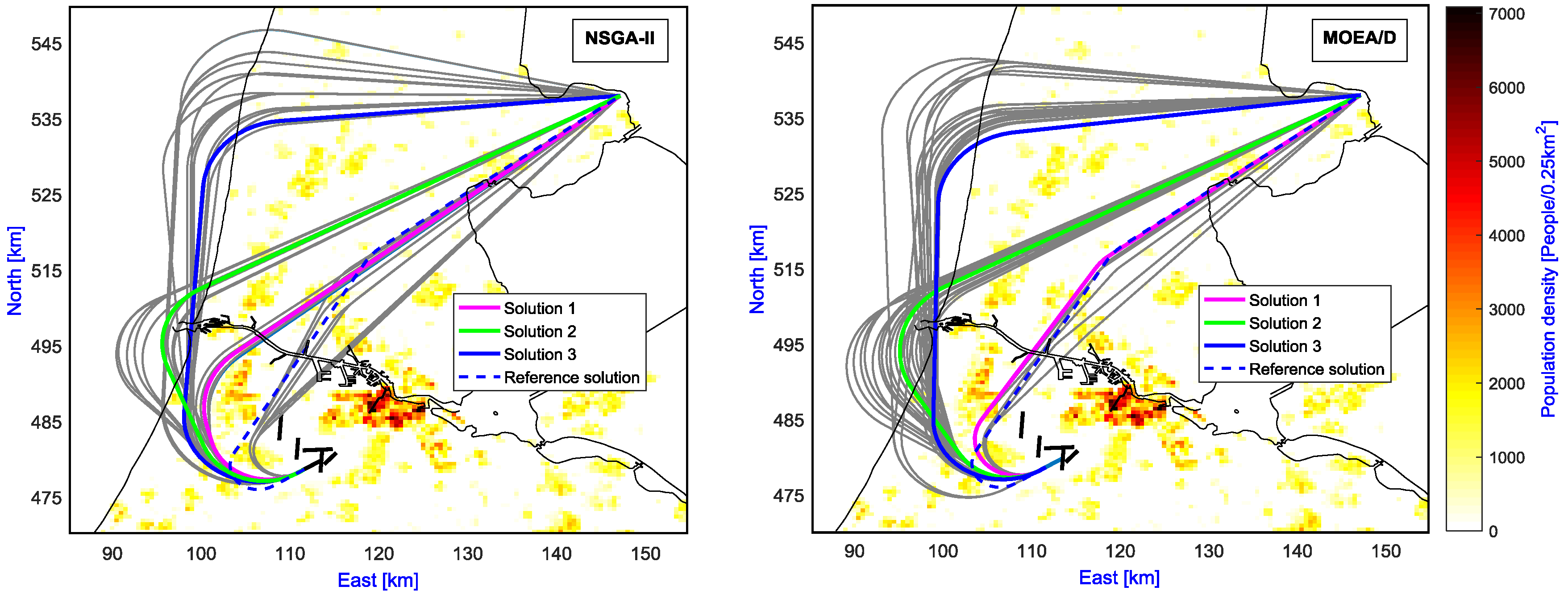
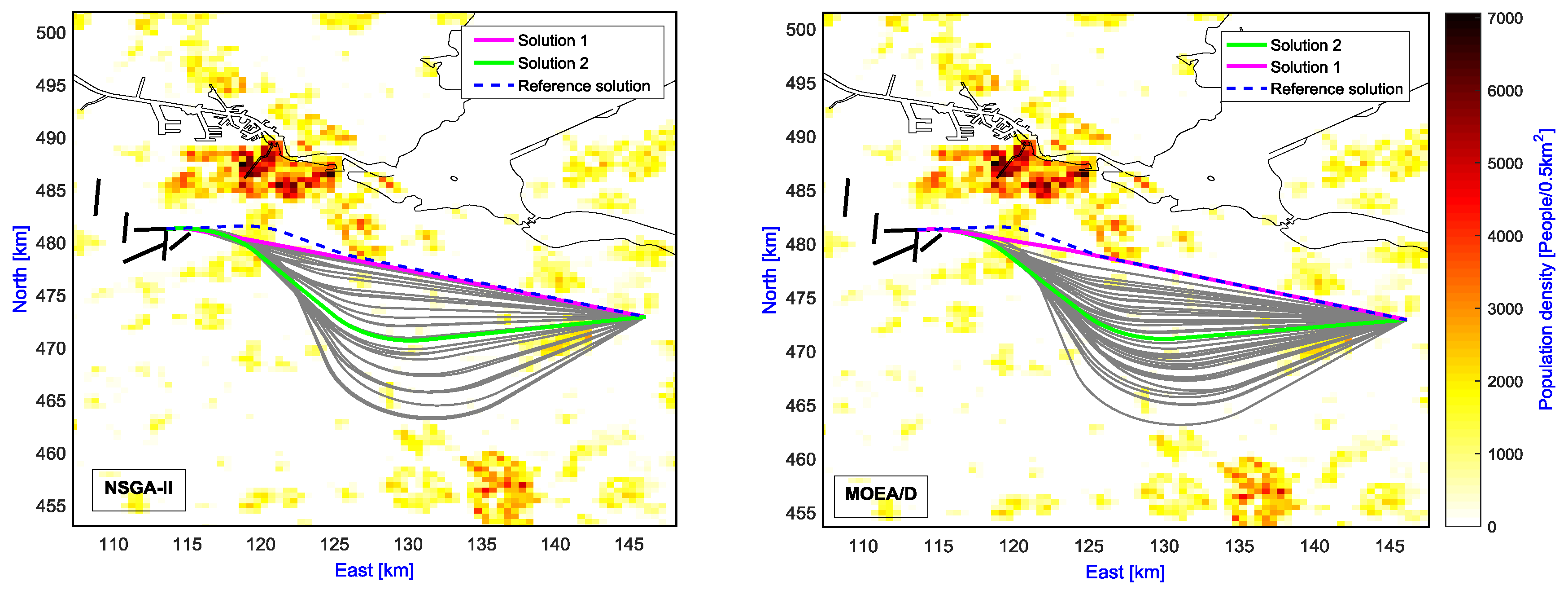
Figure 3, and their corresponding ground tracks are illustrated in
Figure 4. The cases highlighted in
Figure 3 by a yellow star and red circle are also highlighted in
Figure 4 and further discussed in the text. From a comparison of solution methods in
Figure 3, it can be seen that the quality of solutions obtained by MOEA/D is generally better than those achieved by NSGA-II. Specifically, MOEA/D provides many solutions that dominate those of NSGA-II with a significantly lower computational effort. In order to achieve these results, MOEA/D requires 23,357 model evaluations, in which only 8399 involve a noise calculation. Hence, the total computation time is only 2.2 h, while NSGA-II requires 50,500 evaluations resulting in 9.59 h computation time for a full evaluation.
From an engineering point of view, it can be seen that the obtained ground tracks in
Figure 4 are quite reasonable and appropriate. There are three different groups of ground tracks generated by MOEA/D and four groups by NSGA-II, all of them trying to avoid noise-sensitive communities. These results also help to explain why there are some gaps in the Pareto fronts. In comparison to the reference case, it can be observed that most of the optimal solutions offer a better environmental performance. In particular, as shown in the left of
Figure 3, there are some cases that perform better for both objectives, whereas the remaining solutions on the right are much better regarding awakenings, although there is a slight increase in fuel burn.
For a performance comparison, the number of people expected to be awakened and the fuel burn of the three representative cases are extracted from the Pareto fronts (numbered as shown in
Figure 3 and
Figure 4) and listed in
Table 1 along with the results of the reference case. The vertical profiles of the MOEA/D computed cases are given in
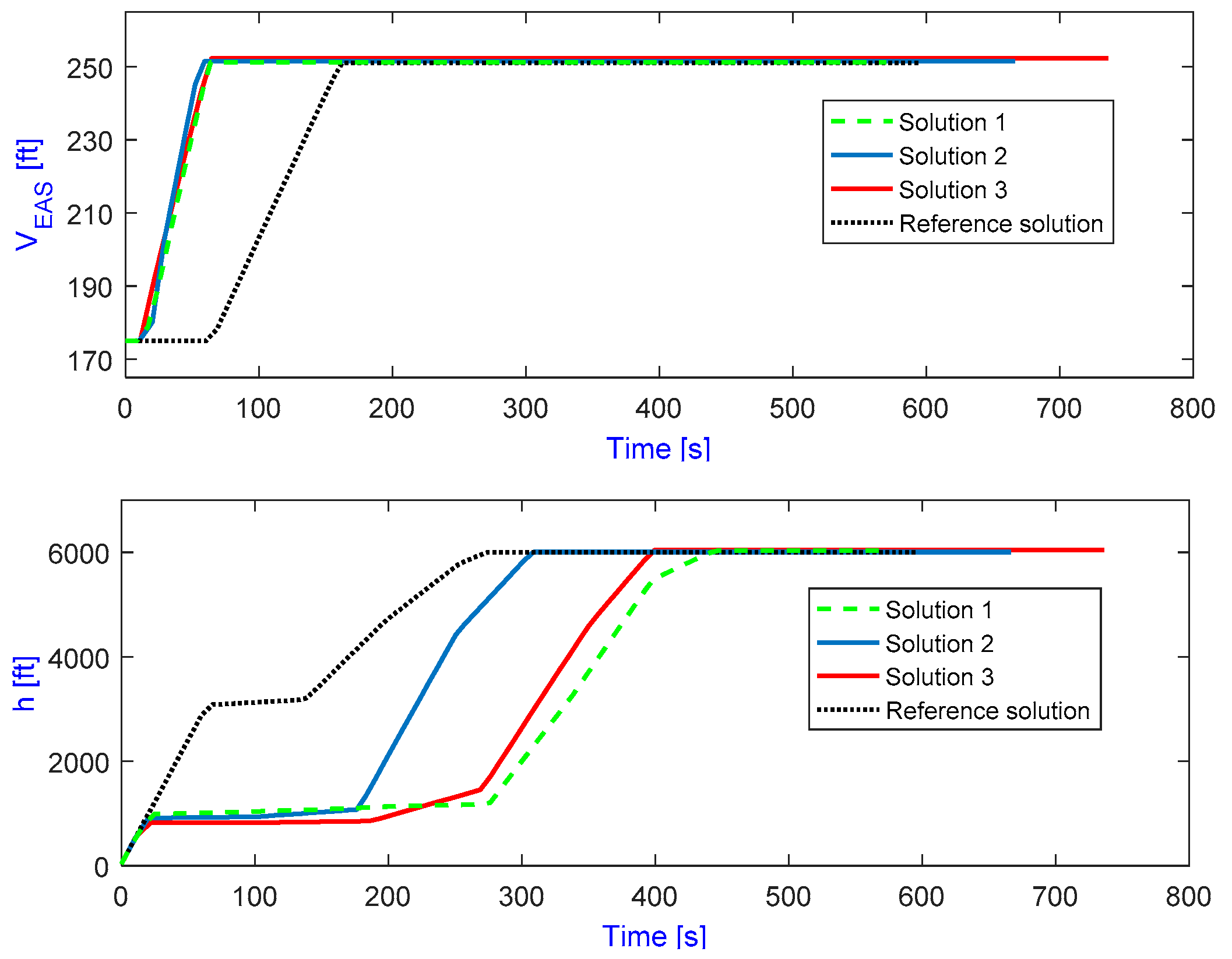
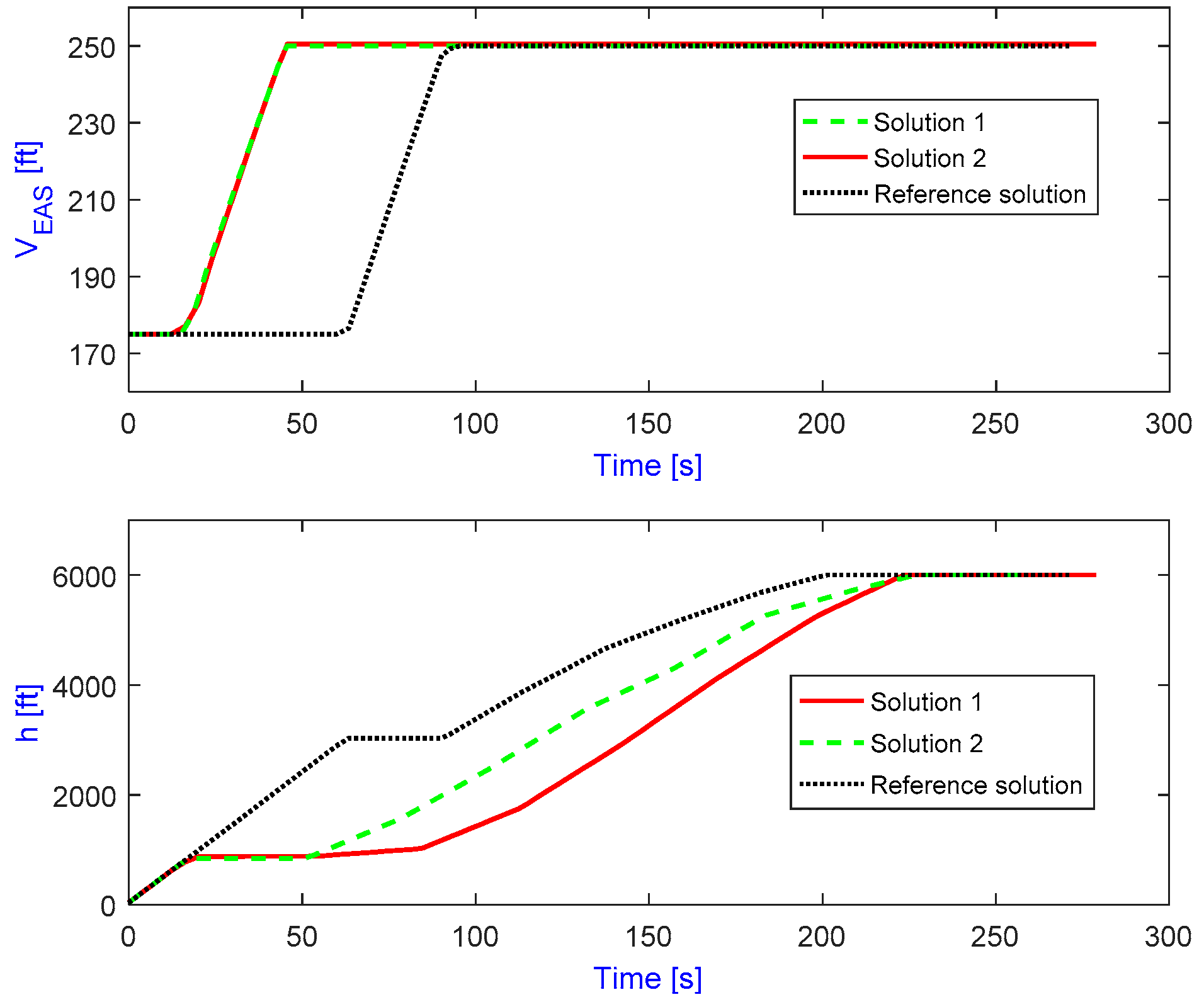
Figure 5. Compared to the reference case, it can be seen that all solutions are non-dominated, either better at awakenings and worse at fuel burn or vice versa, except for case 1. Despite having almost the same ground track length with an optimal combination of the ground track and vertical profile, case 1 offers much better performance in terms of all three criteria. From
Table 1, it can also be seen that the difference between the objective values of the three representative cases is significant, especially in terms of the number of awakenings. A relatively small detour allows a significant part of the communities surrounding the airport to be avoided, and, considering the exponential relationship between noise and awakenings, consequently leads to a significant reduction in the noise criterion. By taking a closer look at
Figure 5, it can be seen that in the first phase of flight, for all optimal cases, the aircraft prefers to fly at a low altitude with a high speed to pass over populated regions. This is because the spread of aircraft noise at a low altitude is smaller than that at a higher altitude due to increased lateral attenuation, and hence it leads to a significant reduction of awakenings. Also, maintaining a low altitude allows the aircraft to accelerate to a high airspeed sooner, which leads to lower exposure times and hence to lower SEL-values, while the source noise levels do not increase significantly. From
Figure 5, it also becomes clear that the time during which the aircraft stays at a low altitude is dependent on the population density distribution underneath the flight path. This is also clearly depicted in
Figure 6, where the noise level contours of cases 2 and 3 are illustrated.
5.2. Departure Route ARNEM2N
The Pareto-optimal solutions obtained by MOEA/D and NSGA-II for this example are illustrated in
Figure 7, while the ground tracks are provided in
Figure 8. Again, some representative cases are highlighted in the figures. To acquire these results, NSGA-II requires 45,000 model evaluations in 4.36 h, while MOEA/D converges after 24,122 model evaluations in 1.99 h, with only 17,010 requiring a noise calculation. Compared to the previous example, the obtained ground tracks, in this case, are more divergent. This is because there is no area with a high concentration of population within the investigated region except for a small area close to runway 09. However, this region has been avoided by most of the optimal solutions. It can also be seen from
Figure 7 that all optimal solutions dominate the reference case.
For a comparison of specific values, the number of awakenings and fuel burn of the representative cases extracted from the Pareto-optimal solutions (as highlighted in
Figure 7) are given in
Table 2. The vertical profiles of the MOEA/D cases are also provided in
Figure 9. From the table, it can be seen that all optimal cases have better results regarding fuel burn and awakenings compared to the reference case, while case 1 significantly outperforms the reference case on all considered criteria (i.e., fuel burn, awakenings, and time). As the airspeed and altitude histories are concerned, their behavior is almost the same as in the previous example. The aircraft often fly at a low attitude with a relatively high speed when passing over densely populated areas in the first phases, while the time during which an aircraft flies at a low attitude depends on the population distribution underneath a flight path.
Summarizing, based on the obtained results, it can be concluded that MOEA/D is an effective method for solving the optimal design problem of noise abatement departure routes. Compared to NSGA-II, MOEA/D generally outperforms NSGA-II in terms of both the quality of solutions and computation time.
6. Conclusions
In this study, a novel and efficient application of MOEA/D for the optimal design of noise abatement departure routes is presented. Besides the typical advantages, the performance of MOEA/D is also considerably enhanced by the integration of recently developed features, which include an adaptive replacement strategy, a stopping condition criterion, and a constraint-handling technique. Also, the performance of the entire optimization process is significantly improved by the implementation on the setting of the optimization problem and the MOEA/D algorithm. Owing to this implementation, the computational cost of solving the optimization problems is sharply reduced.
The applicability and effectiveness of MOEA/D and the new implementations are demonstrated through two example scenarios of departure routes at Schiphol Airport in the Netherlands: SPIJKERBOOR2K and ARNEM2N. For comparison purposes, NSGA-II is also applied to solve these problems. The comparative results show that MOEA/D is generally better than NSGA-II when considering the quality of solutions and much better regarding the convergence rate and overall computational cost.
With these promising results, in future work, MOEA/D will be extended to consider different routes at other airports, and its performance will also be investigated in different associated problems like route and runway allocations. Furthermore, the performance of the algorithm will also be further enhanced to deal with large and complex problems, especially in the distribution of solutions and the convergence rate.