Trajectory Tracking of a Tri-Rotor Aerial Vehicle Using an MRAC-Based Robust Hybrid Control Algorithm
Abstract
:1. Introduction
2. The Tri-Rotor System Model and Preliminaries
2.1. System Dynamics
2.2. Main Engine (Electric Motors)
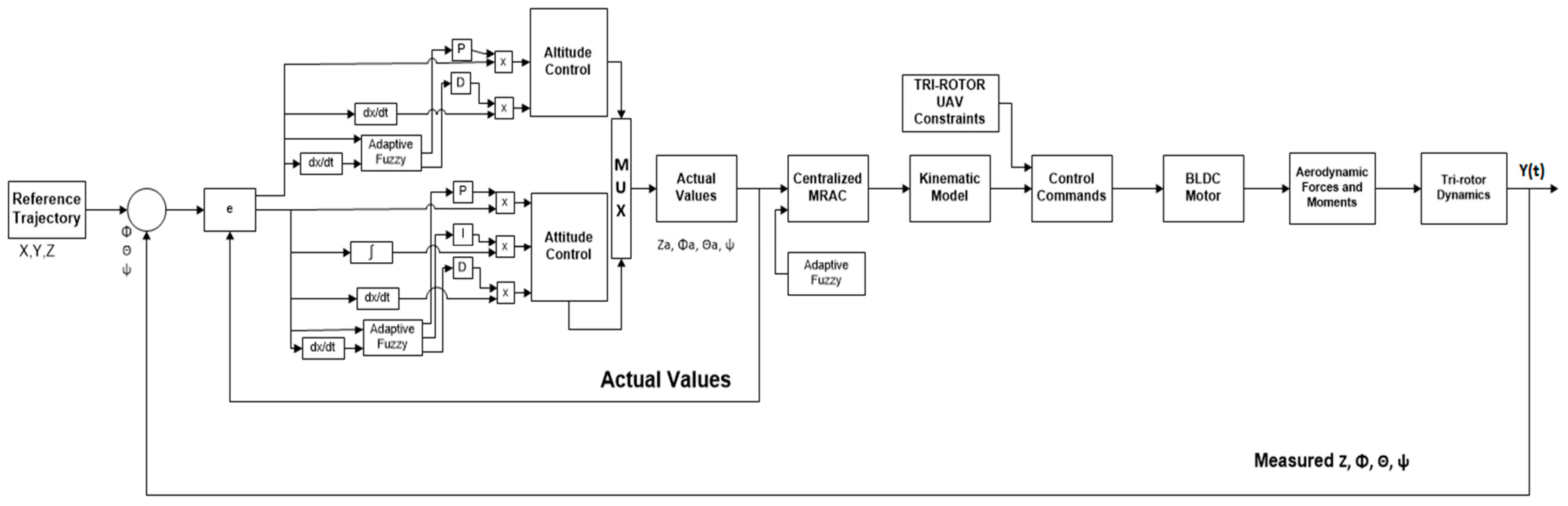
3. Design of the Control Algorithm
3.1. The Control Objective and Its Approach
- I.
- Clockwise
- II.
- Anticlockwise
- I.
- Nose-Up
- II.
- Nose-Down
- .
3.2. Model Reference Adaptive Control
3.3. Positional Control
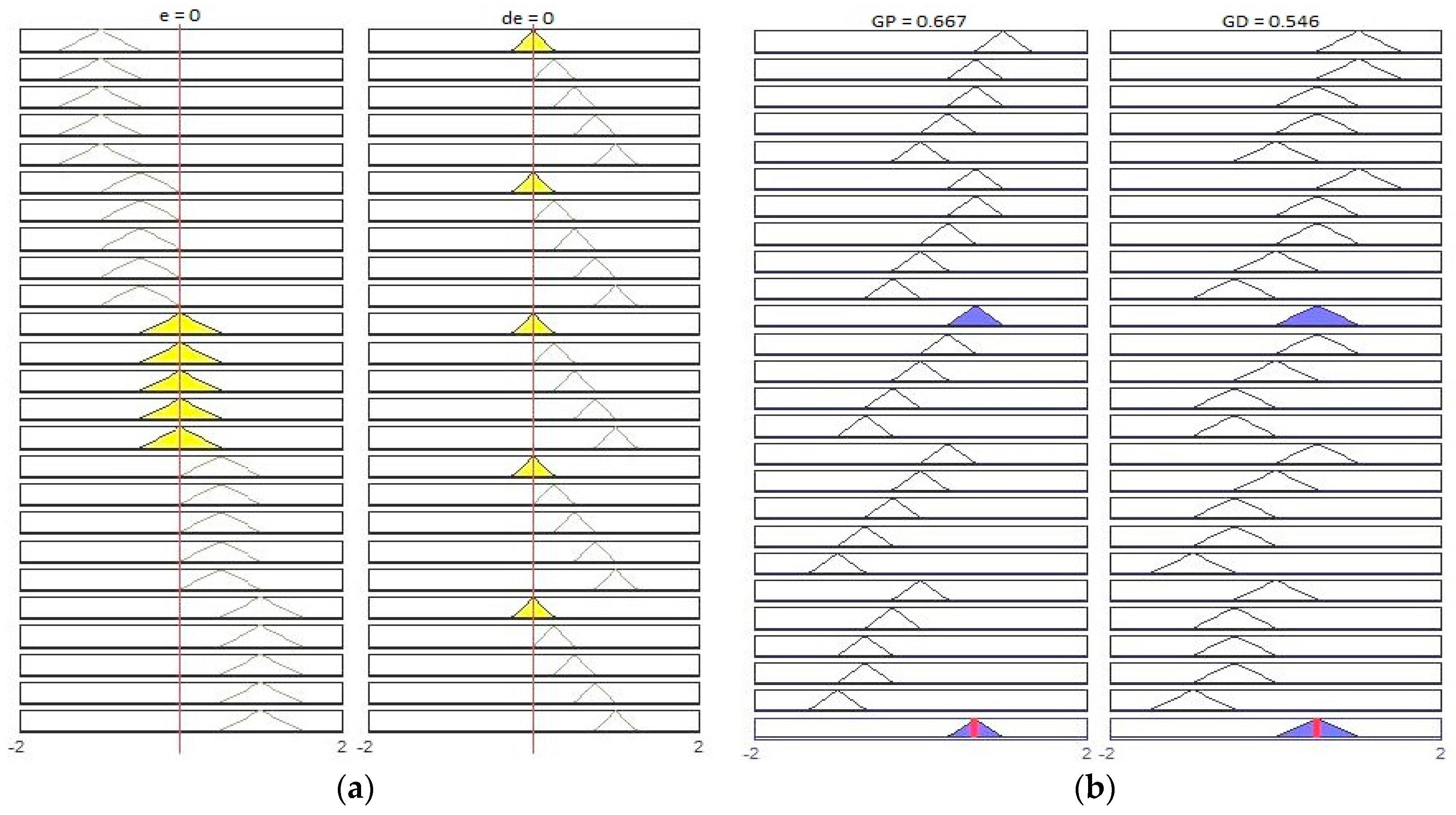
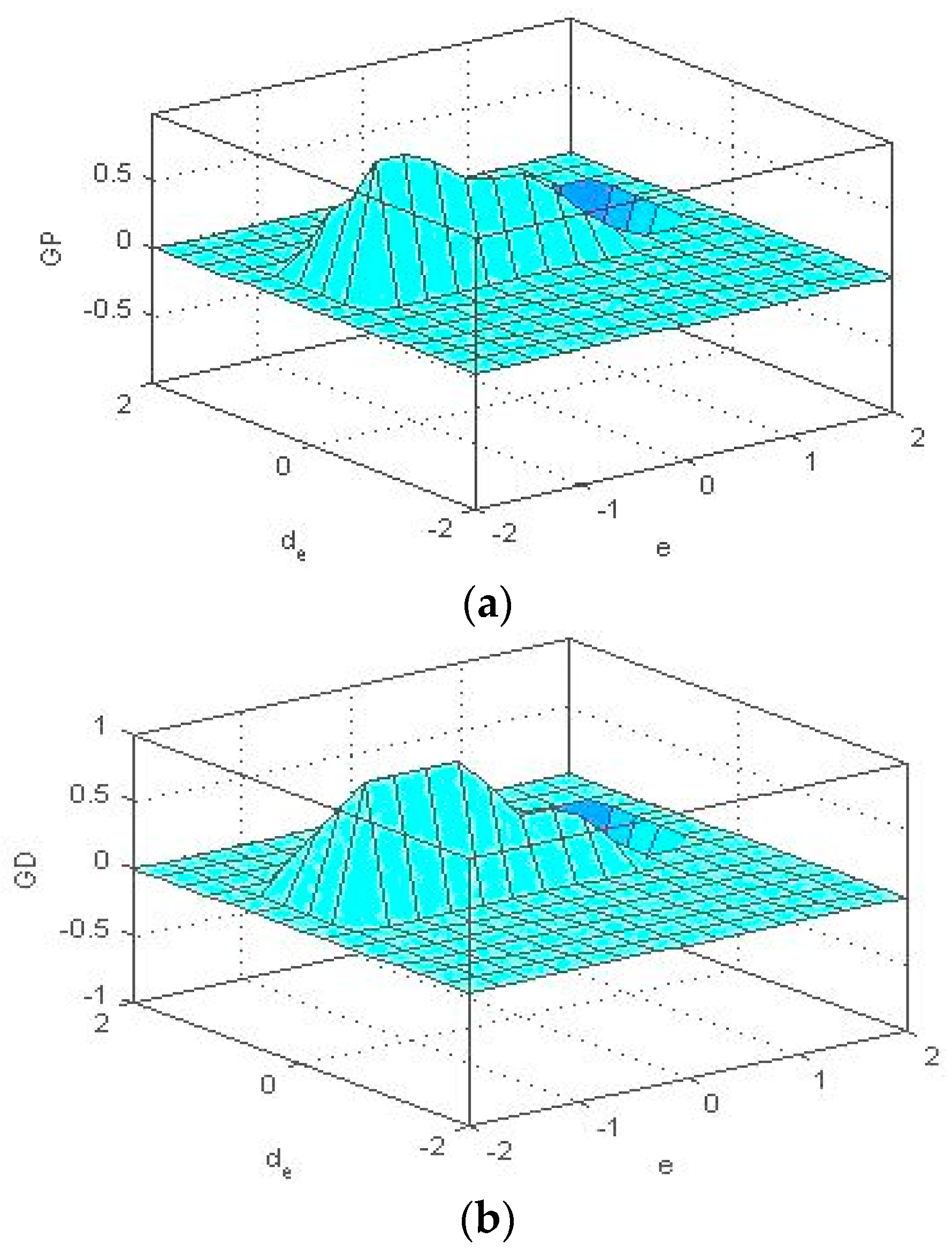
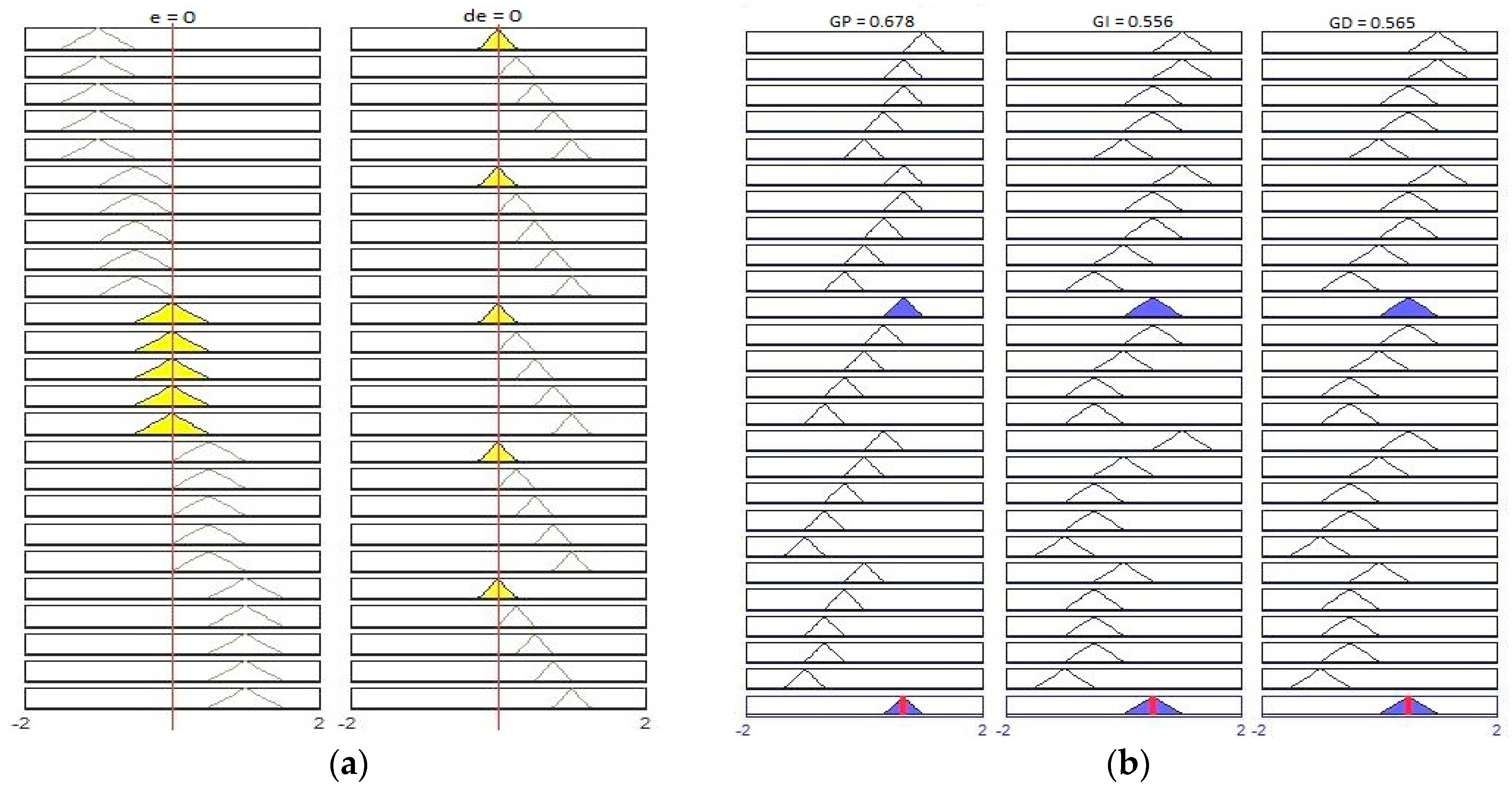
3.4. Altitude Control
3.5. Attitude Control
4. Simulation Results and Discussion
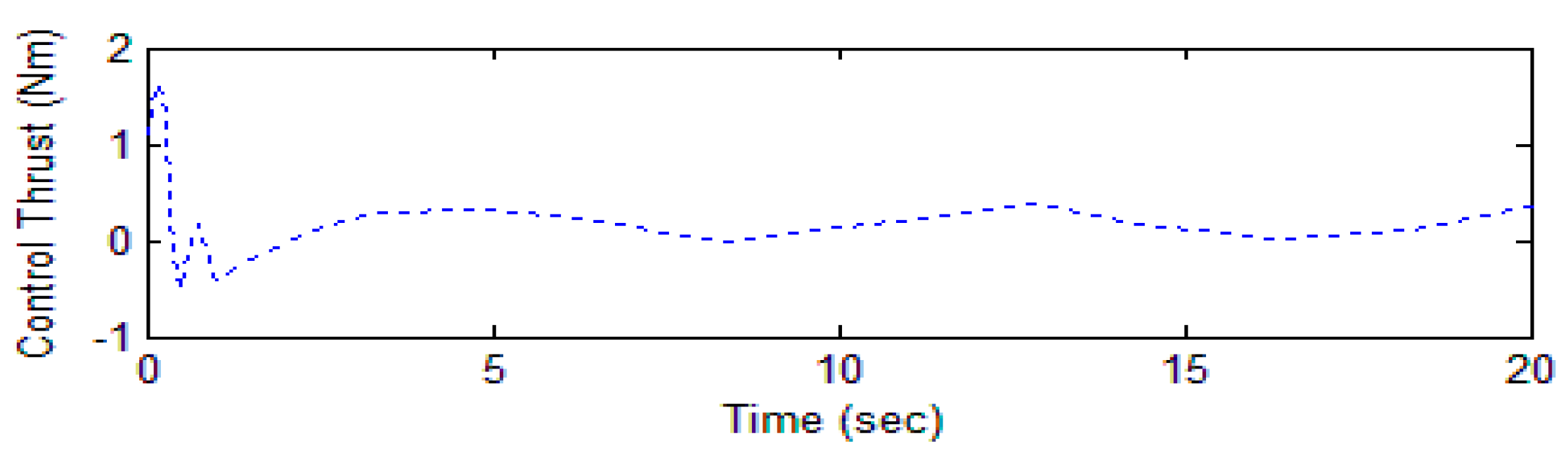
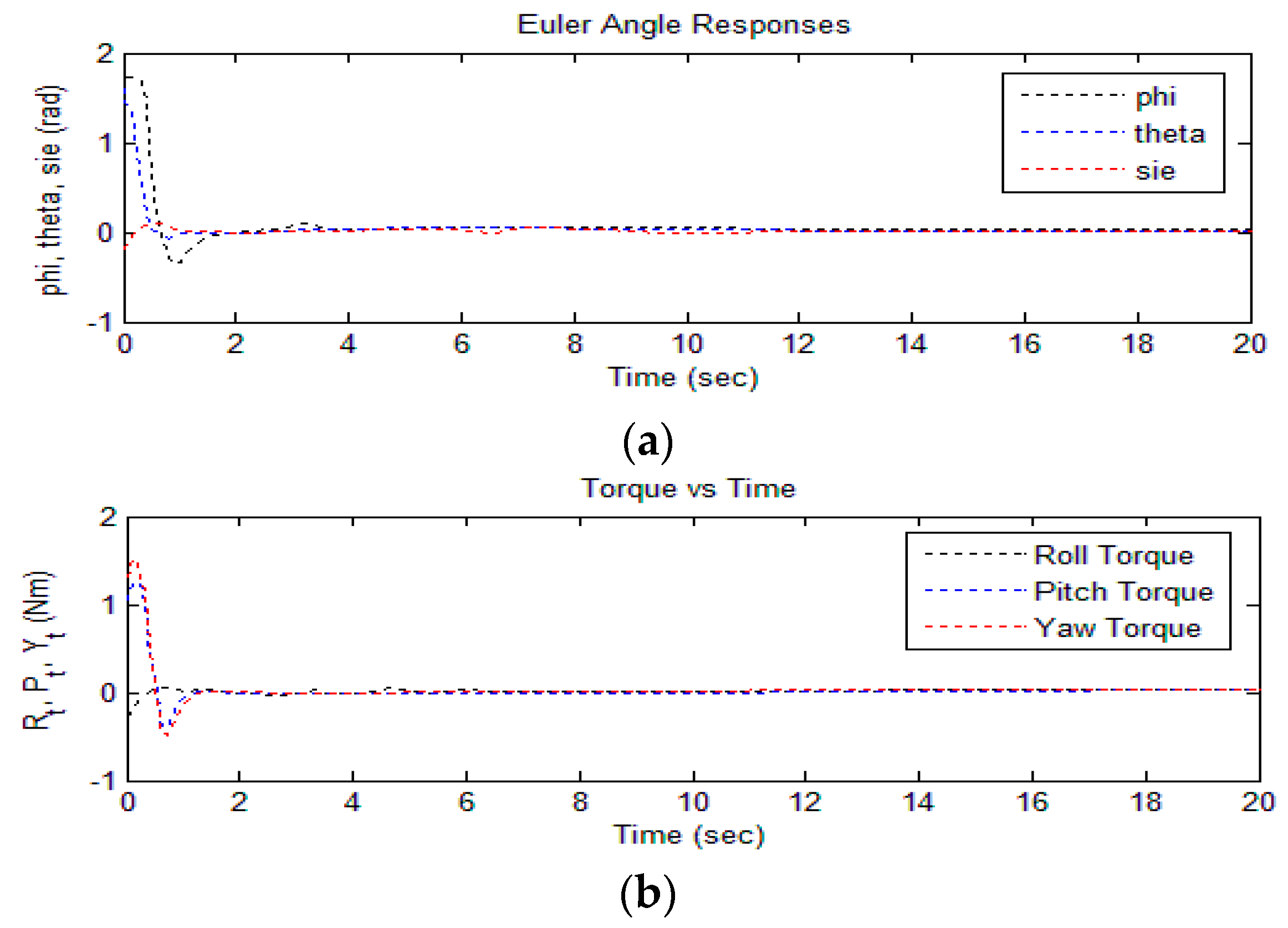
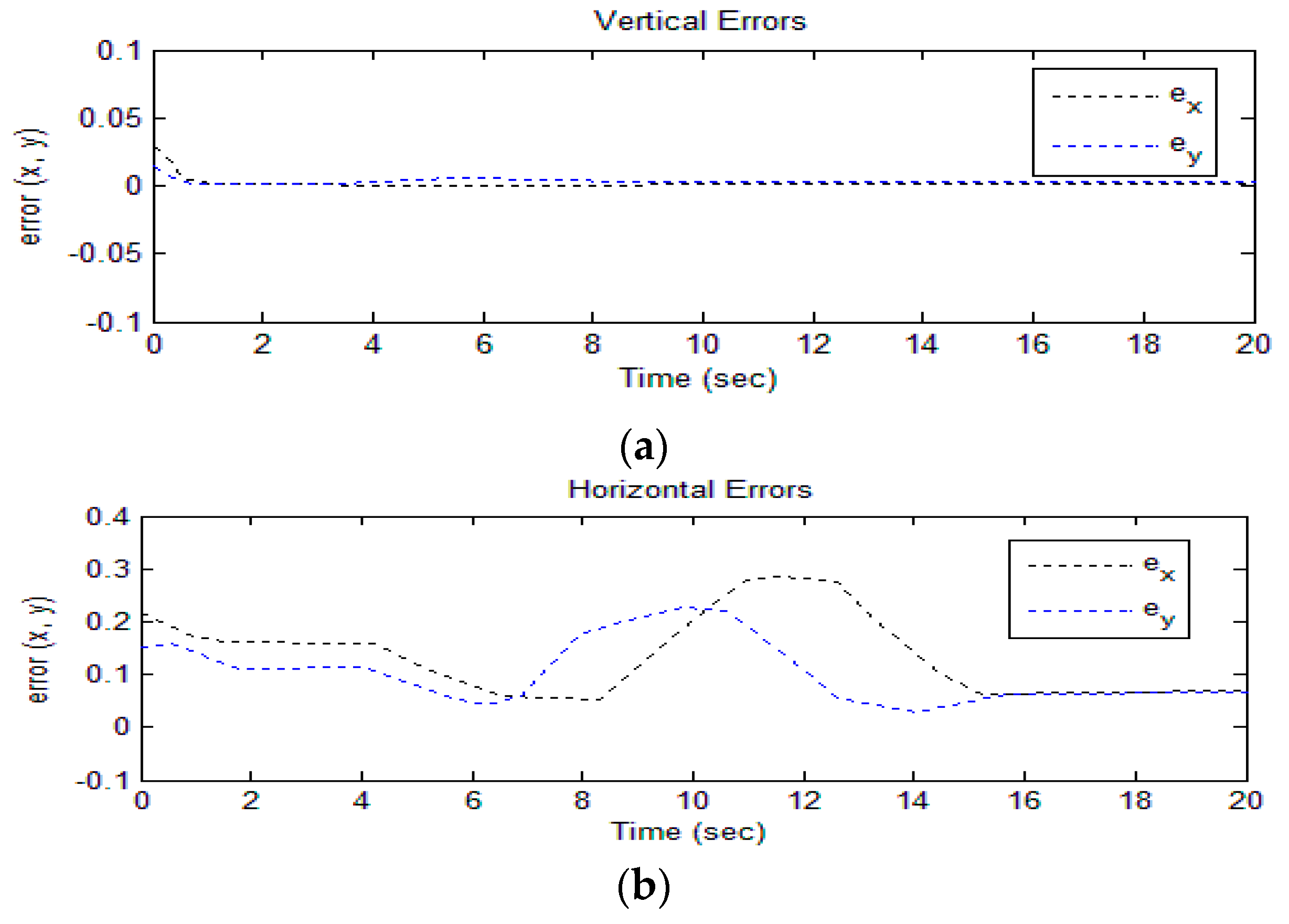
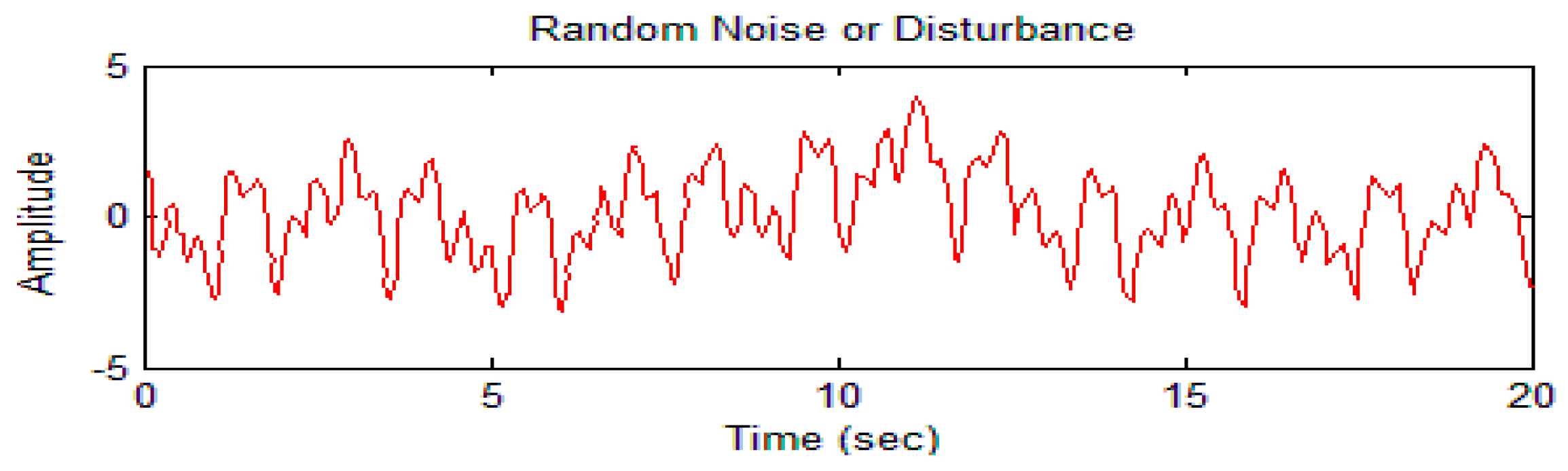
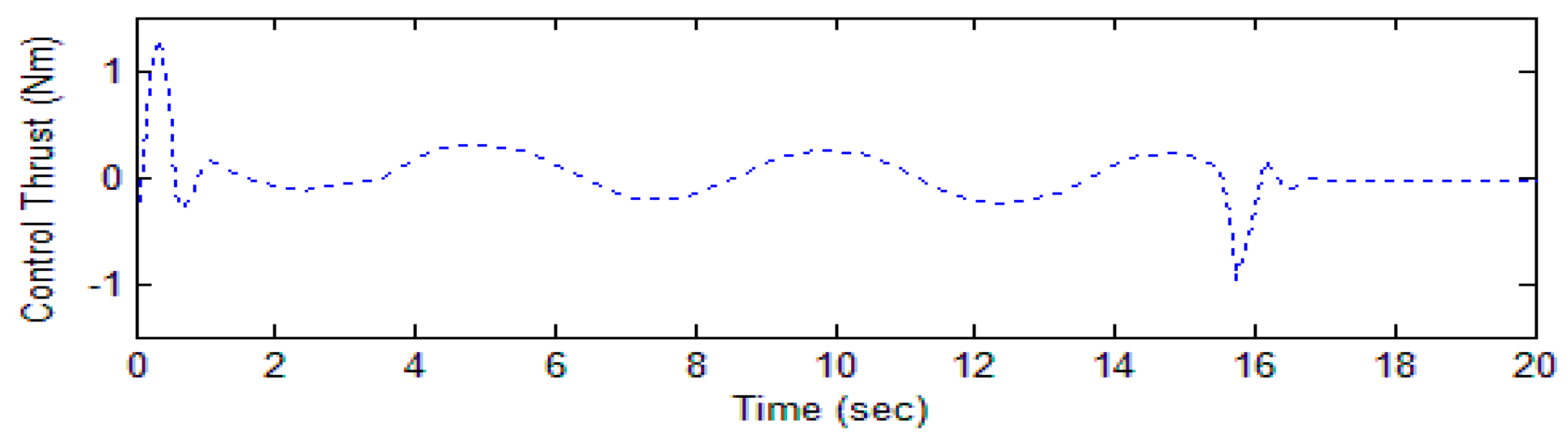
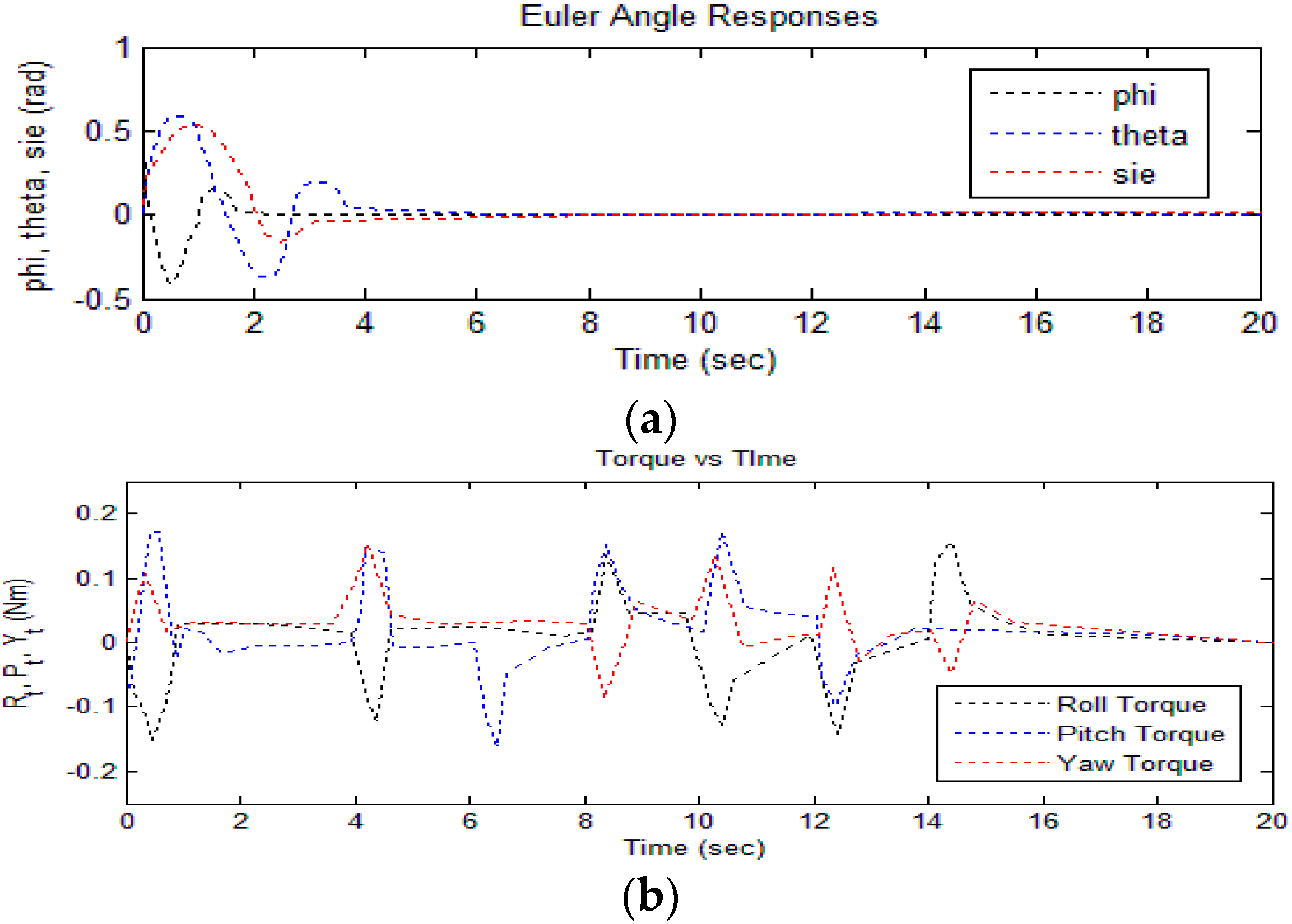
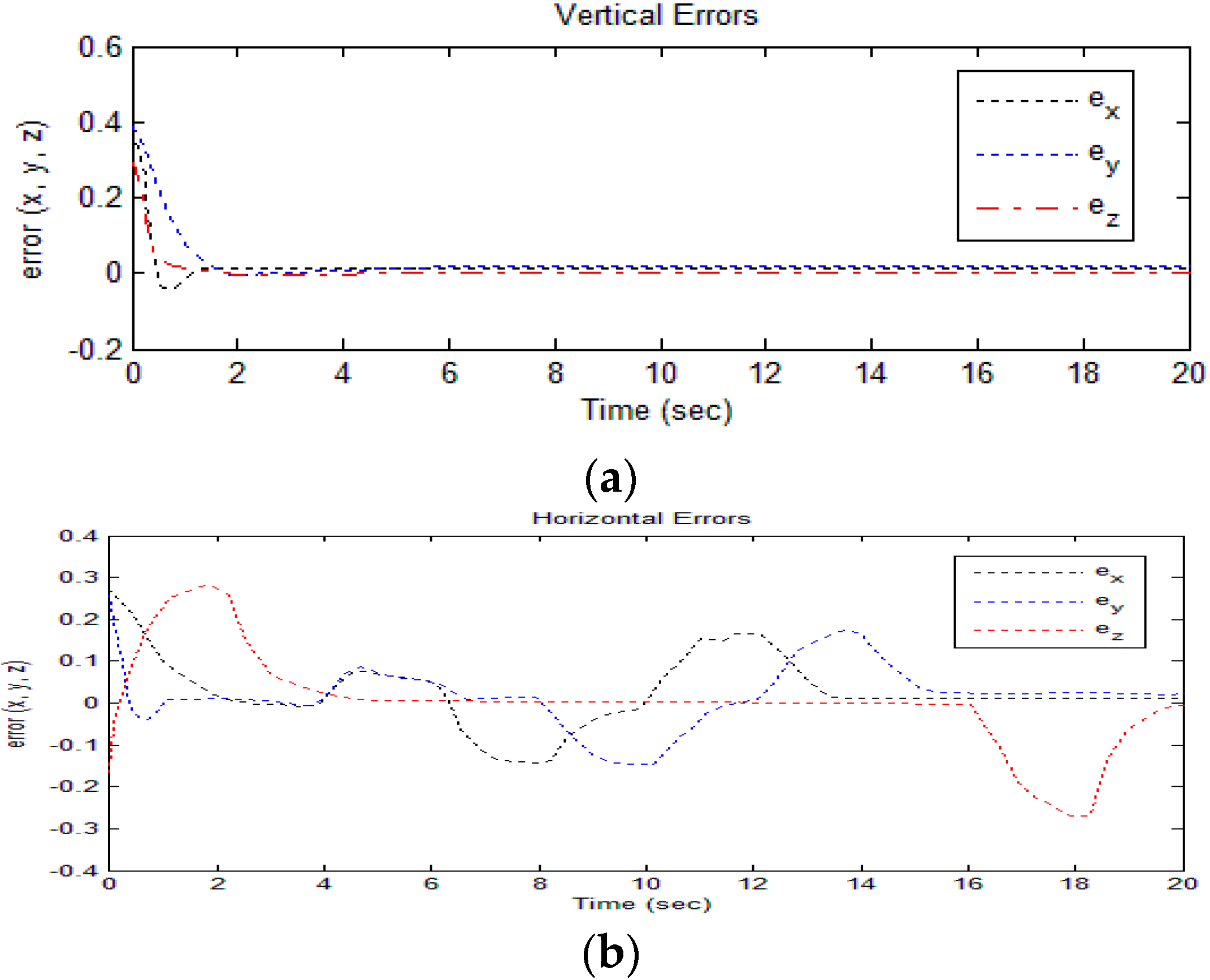
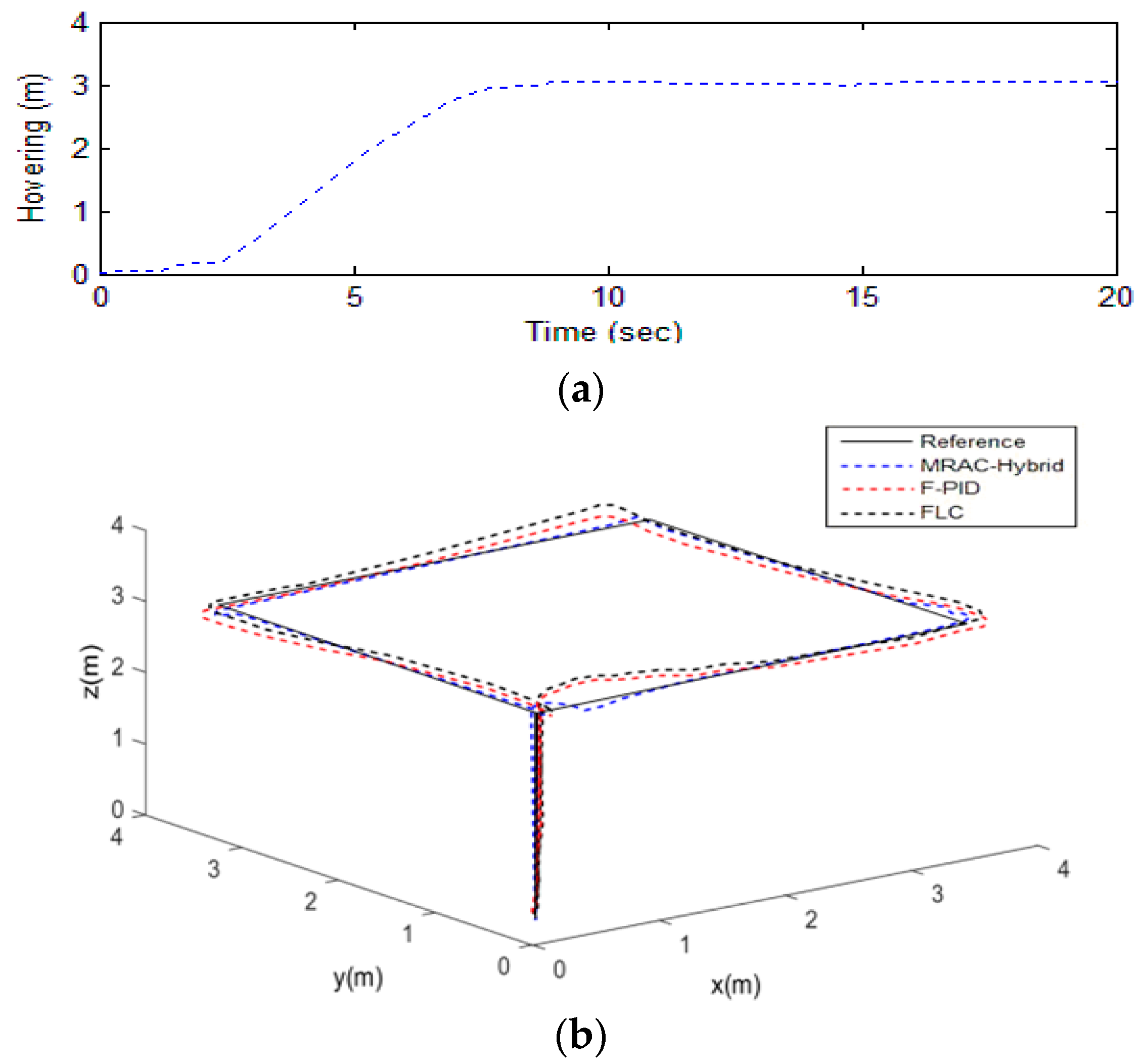
4.1. Simulation Case I
4.2. Simulation Case II
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Nonami, K. Prospect and recent research & development for civil use autonomous unmanned aircraft as UAV and MAV. J. Syst. Des. Dyn. 2007, 1, 120–128. [Google Scholar]
- Langelaan, J.W.; Alley, N.; Neidhoefer, J. Wind field estimation for small unmanned aerial vehicles. J. Guid. Control Dyn. 2011, 34, 1016–1030. [Google Scholar] [CrossRef]
- Kerns, A.J.; Shepard, D.P.; Bhatti, J.A.; Humphreys, T.E. Unmanned aircraft capture and control via GPS spoofing. J. Field Robot. 2014, 31, 617–636. [Google Scholar] [CrossRef]
- Johnson, E.N.; Turbe, M.A. Modeling, control, and flight testing of a small-ducted fan aircraft. J. Guid. Control Dyn. 2006, 29, 769–779. [Google Scholar] [CrossRef]
- Bracken, C.; Lyon, R.D.; Mansour, M.J.; Molnar, A.; Saulnier, A.; Thompson, S.; Sharpe, J. Surveillance Drones: Privacy Implications of the Spread of Unmanned Aerial Vehicles (UAVs) in Canada; Surveillance Studies Centre: Queen’s University, Kingston, UK, 30 April 2014. [Google Scholar]
- Corcoran, M. Drone Journalism: Newsgathering Applications of Unmanned Aerial Vehicles (UAVs) in Covering Conflict, Civil Unrest and Disaster; Australian Broadcasting Corporation: Sydney, Australia, January 2014. [Google Scholar]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and considerations of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Casbeer, D.W.; Kingston, D.B.; Beard, R.W.; McLain, T.W. Cooperative forest fire surveillance using a team of small unmanned air vehicles. Int. J. Syst. Sci. 2006, 37, 351–360. [Google Scholar] [CrossRef]
- Everaerts, J. The use of unmanned aerial vehicles (UAVs) for remote sensing and mapping. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2008, 37, 1187–1192. [Google Scholar]
- Rango, A.; Laliberte, A.; Herrick, J.E.; winters, C.; Havstad, K.; Steele, C.; Browning, D. Unmanned aerial vehicle-based remote sensing for rangeland assessment, monitoring, and management. J. Appl. Remote Sens. 2009, 3, 033542. [Google Scholar]
- Ali, Z.A.; Wang, D.B.; Loya, M.S. SURF and LA with RGB Vector Space Based Detection and Monitoring of Manholes with an Application to Tri-rotor UAS Images. Int. J. Eng. Technol. 2017, 9, 32–39. [Google Scholar]
- Sane, S.P.; Dickinson, M.H. The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Exp. Biol. 2002, 205, 1087–1096. [Google Scholar] [PubMed]
- Sababha, B.H.; Al Zu’bi, H.M.; Rawashdeh, O.A. A rotor-tilt-free tricopter UAV: Design, modelling, and stability control. Int. J. Mechatron. Autom. 2015, 5, 107–113. [Google Scholar] [CrossRef]
- Ali, Z.A.; Wang, D.B.; Aamir, M. Design a robust RST controller for stabilization of a tri-copter UAV. Pak. J. Eng. Technol. Sci. 2016, 5, 60–71. [Google Scholar]
- Kurnaz, S.; Cetin, O.; Kaynak, O. Fuzzy logic based approach to design of flight control and navigation tasks for autonomous unmanned aerial vehicles. J. Intell. Robot. Syst. 2009, 54, 229–244. [Google Scholar] [CrossRef]
- Nho, K.; Agarwal, R.K. Automatic landing system design using fuzzy logic. J. Guid. Control Dyn. 2000, 23, 298–304. [Google Scholar] [CrossRef]
- İrfanoğlu, B.; Alwafi, H. Attitude and Altitude Control of Two Wheeled Trirotor Hybrid Robot. Int. J. Sci. Knowl. 2013, 2, 42–56. [Google Scholar]
- Chen, Y.-C.; Teng, C.-C. A model reference control structure using a fuzzy neural network. Fuzzy Sets Syst. 1995, 73, 291–312. [Google Scholar] [CrossRef]
- Goodwin, G.C.; Mayne, D.Q. A parameter estimation perspective of continuous time model reference adaptive control. Automatica 1987, 23, 57–70. [Google Scholar] [CrossRef]
- Parks, P.C. Liapunov redesign of model reference adaptive control systems. IEEE Trans. Autom. Control 1966, 11, 362–367. [Google Scholar] [CrossRef]
- Kreisselmeier, G.; Anderson, B. Robust model reference adaptive control. IEEE Trans. Autom. Control 1986, 31, 127–133. [Google Scholar] [CrossRef]
- Janabi, A.; Talib, H.; Sultan, L. Fuzzy Logic Controller. U.S. Patent 5,499,319, 12 March 1996. [Google Scholar]
- Berenji, H.R. Fuzzy logic controllers. In An Introduction to Fuzzy Logic Applications in Intelligent Systems; Springer: New York, NY, USA, 1992; pp. 69–96. [Google Scholar]
- Mamdani, E.H. Advances in the linguistic synthesis of fuzzy controllers. Int. J. Man Mach. Stud. 1976, 8, 669–678. [Google Scholar] [CrossRef]
- Sugeno, M. An introductory survey of fuzzy control. Inf. Sci. 1985, 36, 59–83. [Google Scholar] [CrossRef]
- Kim, B.S.; Calise, A.J. Nonlinear flight control using neural networks. J. Guid. Control Dyn. 1997, 20, 26–33. [Google Scholar] [CrossRef]
- Sadeghzadeh, I.; Mehta, A.; Zhang, Y.; Rabbath, C.A. Fault-tolerant trajectory tracking control of a quadrotor helicopter using gain-scheduled PID and model reference adaptive control. In Proceedings of the Annual Conference of the Prognostics and Health Management Society, Montreal, QC, Canada, 25–29 September 2011; Volume 2.
- Chao, H.; Cao, Y.; Chen, Y. Autopilots for small unmanned aerial vehicles: A survey. Int. J. Control Autom. Syst. 2010, 8, 36–44. [Google Scholar] [CrossRef]
- Mohammadi, M.; Shahri, A.M. Adaptive nonlinear stabilization control for a quadrotor UAV: Theory, simulation and experimentation. J. Intell. Robot. Syst. 2013, 72, 105–122. [Google Scholar] [CrossRef]
- Ali, Z.A.; Wang, D.B.; Javed, R.; Akbar, A. Modeling & Controlling the Dynamics of Tri-rotor UAV Using Robust RST Controller with MRAC Adaptive Algorithm. Int. J. Control Autom. 2016, 9, 61–76. [Google Scholar]
- Ali, Z.A.; Wang, D.; Aamir, M. Fuzzy-Based Hybrid Control Algorithm for the Stabilization of a Tri-Rotor UAV. Sensors 2016, 16, 652. [Google Scholar] [CrossRef] [PubMed]
- Ali, Z.A.; Wang, D.; Masroor, S.; Shafiq, M. Attitude and Altitude Control of Trirotor UAV by Using Adaptive Hybrid Controller. J. Control Sci. Eng. 2016, 2016, 6459891. [Google Scholar] [CrossRef]
- Ali, Z.A.; Wang, D.; Safwan, M.; Jiang, W.; Shafiq, M. Trajectory Tracking of a Nonholonomic Wheeleed Mobile Robot Using Hybrid Controller. Int. J. Model. Optim. 2016, 6, 136. [Google Scholar]
- Sanchez, E.N.; Becerra, H.M.; Velez, C.M. Combining fuzzy, PID and regulation control for an autonomous mini-helicopter. Inf. Sci. 2007, 177, 1999–2022. [Google Scholar] [CrossRef]
- Papachristos, C.; Tzes, A. Modeling and control simulation of an unmanned tilt tri-rotor aerial vehicle. In Proceedings of the 2012 IEEE International Conference on Industrial Technology (ICIT), Athens, Greece, 19–21 March 2012; pp. 840–845.
- Yoo, D.W.; Oh, H.D.; Won, D.Y.; Tahk, M.J. Dynamic modeling and control system design for Tri-rotor UAV. In Proceedings of the 3rd International Symposium on Systems and Control in Aeronautics and Astronautics (ISSCAA), Harbin, China, 8–10 June 2010; pp. 762–767.
- Yoo, D.W.; Oh, H.D.; Won, D.Y.; Tahk, M.J. Dynamic modeling and stabilization techniques for tri-rotor unmanned aerial vehicles. Int. J. Aeronaut. Space Sci. 2010, 11, 167–174. [Google Scholar] [CrossRef]
- Peters, D.A.; Chen, S.Y. Momentum Theory, Dynamic Inflow, and the Vortex-Ring State. J. Am. Helicopter Soc. 1982, 27, 18–24. [Google Scholar] [CrossRef]
- Moseler, O.; Isermann, R. Application of model-based fault detection to a brushless DC motor. IEEE Trans. Ind. Electron. 2000, 47, 1015–1020. [Google Scholar] [CrossRef]
- Hosseini-Suny, K.; Momeni, H.; Janabi-Sharifi, F. Model reference adaptive control design for a teleoperation system with output prediction. J. Intell. Robot. Syst. 2010, 59, 319–339. [Google Scholar] [CrossRef]



| Parameters | Mass, m | g | L | Ix | Iy | Iz |
|---|---|---|---|---|---|---|
| Values | 0.785 | 9.81 | 0.3050 | 0.3105 | 0.3105 | 0.3212 |
| SI Units | kg | m/s2 | m | Kg·m2 | Kg·m2 | Kg·m2 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license ( http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ali, Z.A.; Wang, D.; Aamir, M.; Masroor, S. Trajectory Tracking of a Tri-Rotor Aerial Vehicle Using an MRAC-Based Robust Hybrid Control Algorithm. Aerospace 2017, 4, 3. https://doi.org/10.3390/aerospace4010003
Ali ZA, Wang D, Aamir M, Masroor S. Trajectory Tracking of a Tri-Rotor Aerial Vehicle Using an MRAC-Based Robust Hybrid Control Algorithm. Aerospace. 2017; 4(1):3. https://doi.org/10.3390/aerospace4010003
Chicago/Turabian StyleAli, Zain Anwar, Daobo Wang, Muhammad Aamir, and Suhaib Masroor. 2017. "Trajectory Tracking of a Tri-Rotor Aerial Vehicle Using an MRAC-Based Robust Hybrid Control Algorithm" Aerospace 4, no. 1: 3. https://doi.org/10.3390/aerospace4010003
APA StyleAli, Z. A., Wang, D., Aamir, M., & Masroor, S. (2017). Trajectory Tracking of a Tri-Rotor Aerial Vehicle Using an MRAC-Based Robust Hybrid Control Algorithm. Aerospace, 4(1), 3. https://doi.org/10.3390/aerospace4010003







