An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System
Abstract
:1. Introduction
2. Research Aims
2.1. Overlapping Rotor System d/D = 0
2.1.1. Thrust Sharing
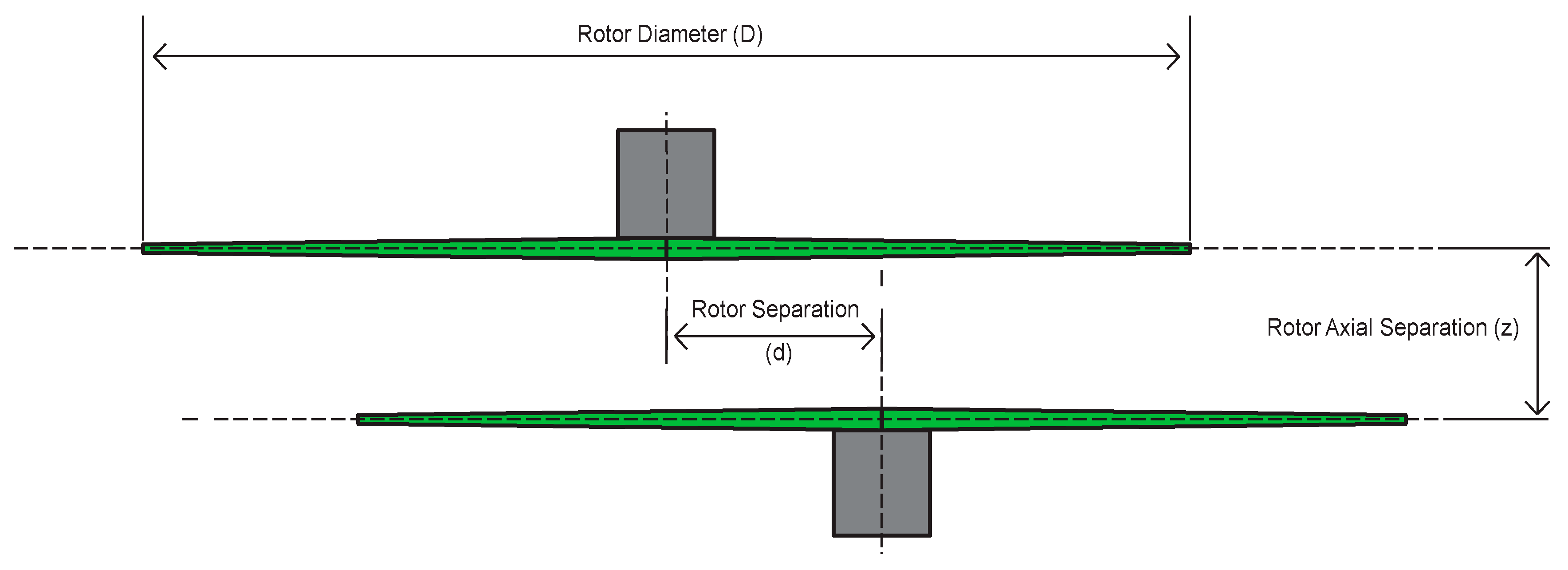
2.1.2. Vertical or Axial Rotor Separation (z/D)
2.1.3. Co-Rotating Rotor Performance
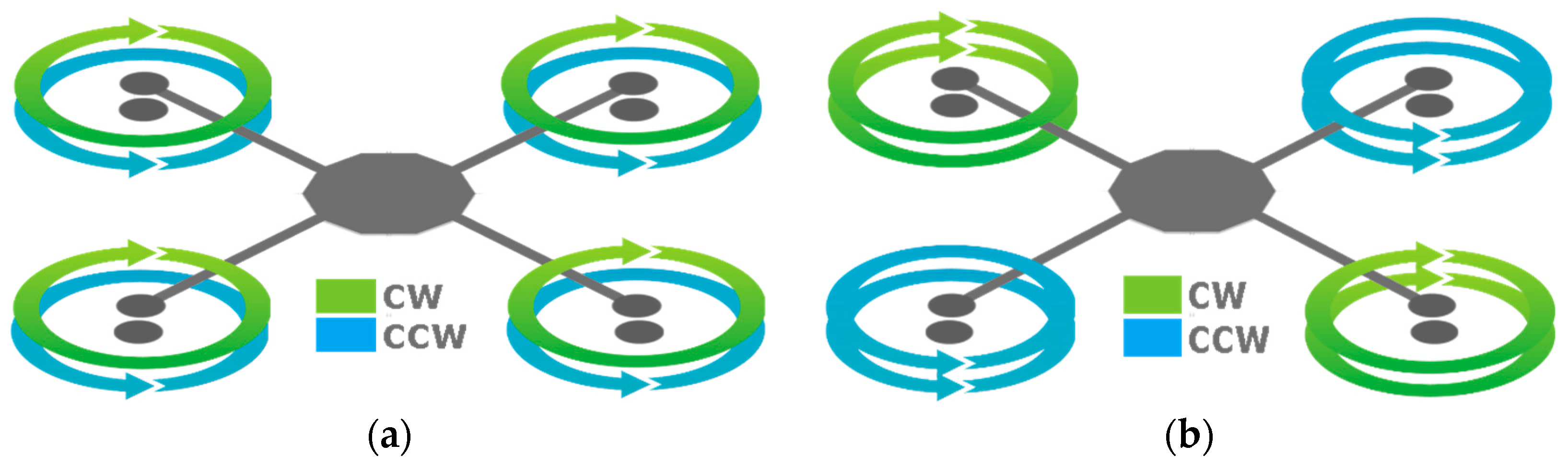
2.2. Overlapping Rotor System d/D > 0
Various Overlapping Rotor d/D Ratios
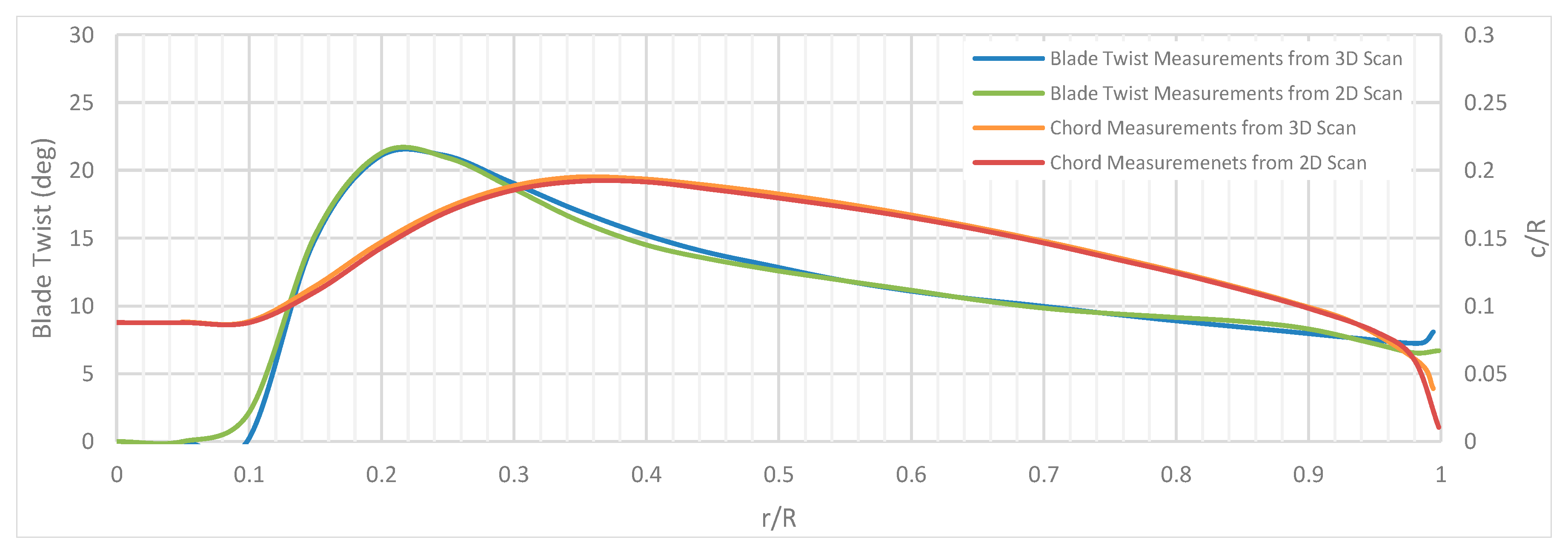
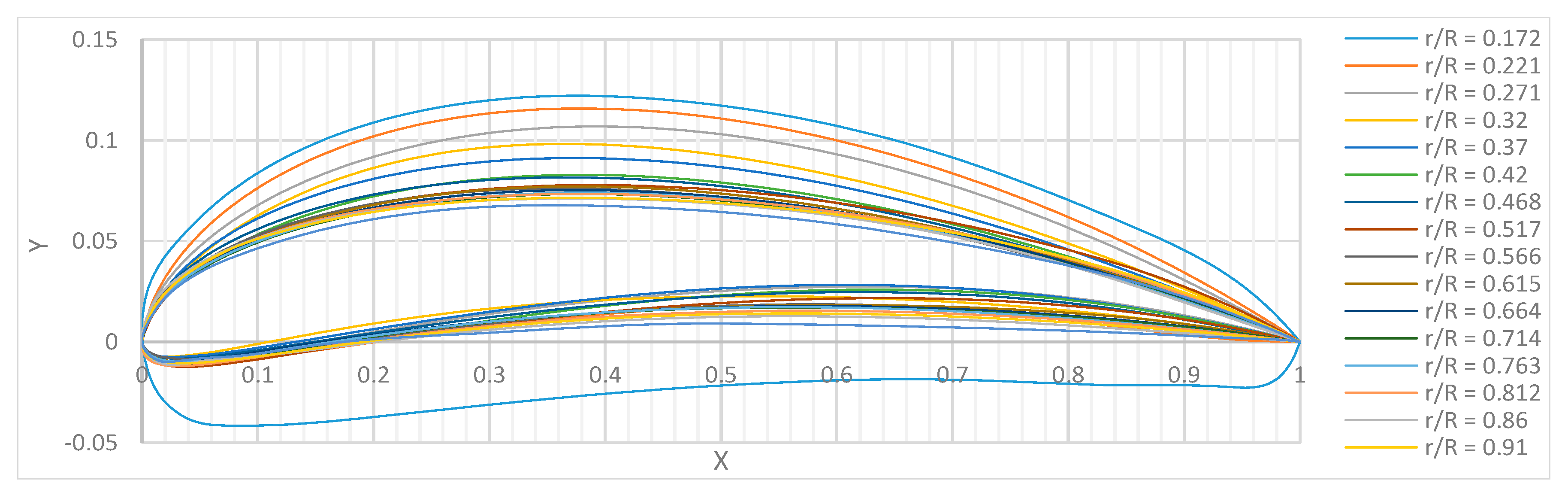
3. Rotor Geometry
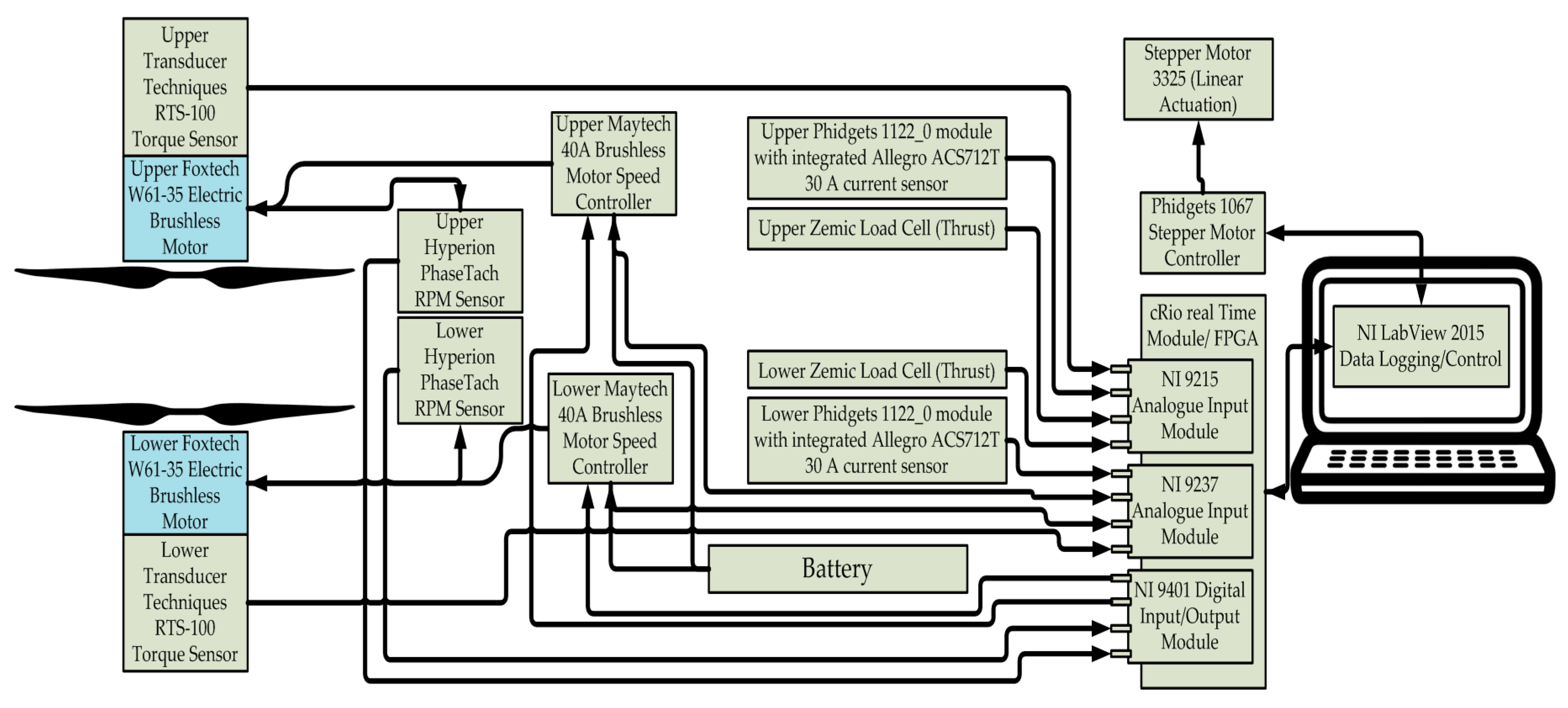
4. Experimental Setup
5. Results
- Isolated single rotor tests;
- Overlapping rotor tests d/D = 0 (co-axial); and
- Overlapping rotor tests d/D ≠ 0.
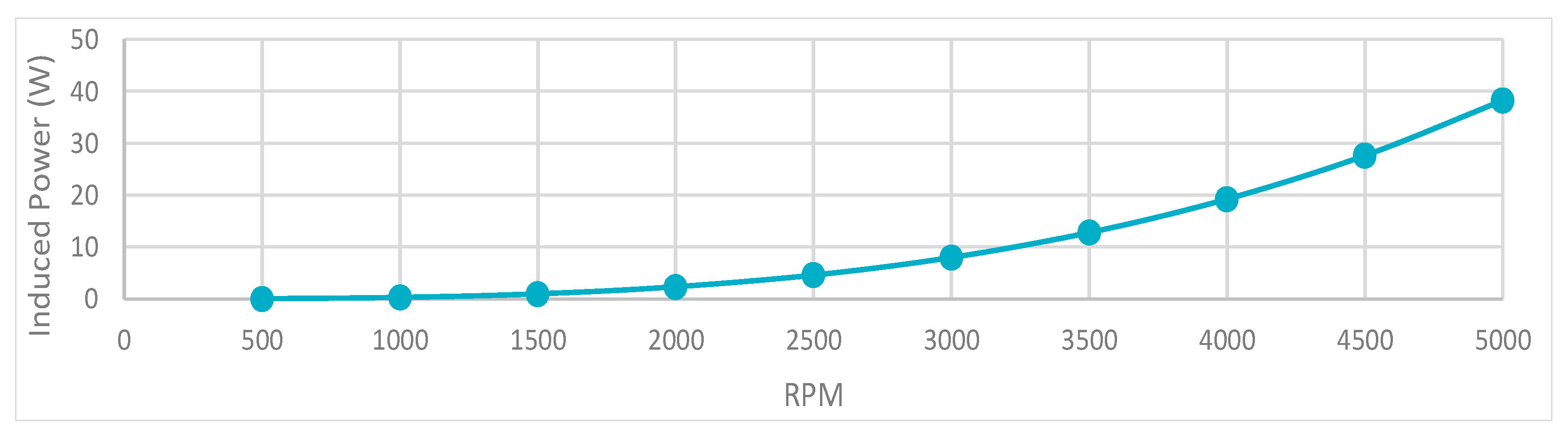
5.1. Isolated Single Rotor Tests
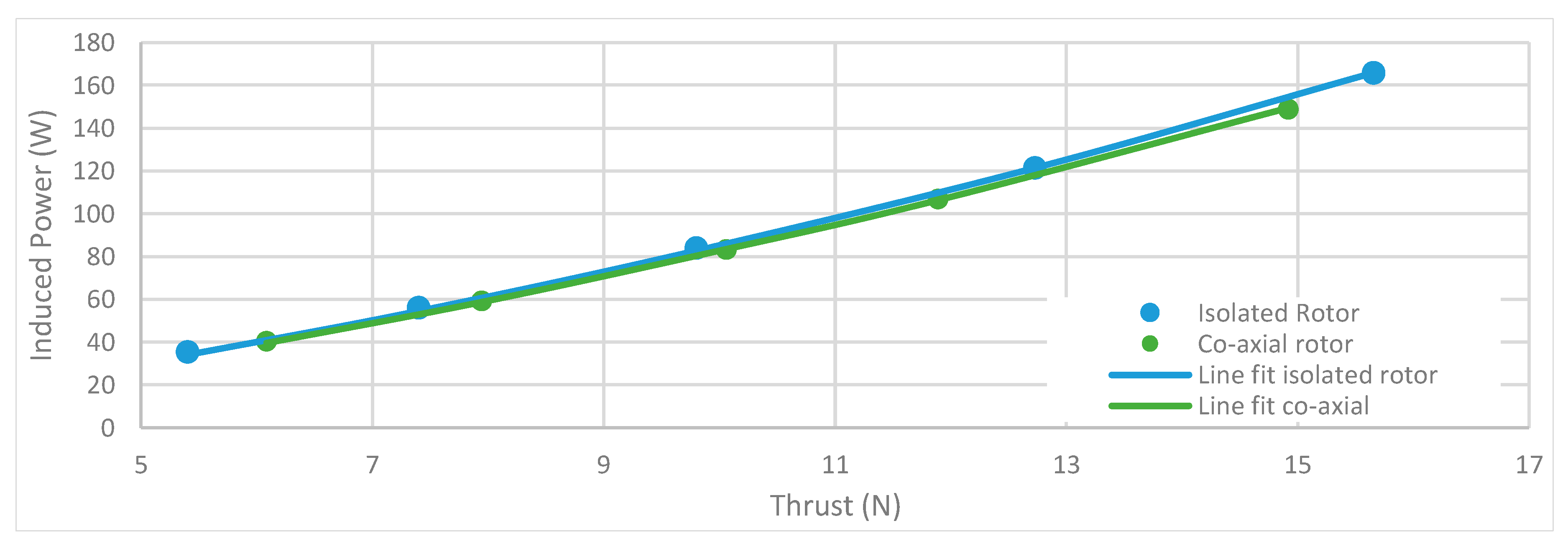
5.2. Overlapping Rotor Tests d/D = 0 (Co-Axial)
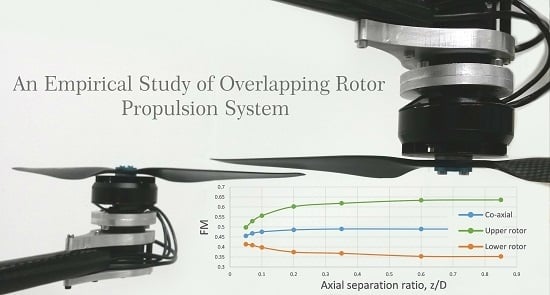
5.3. Overlapping Rotor Tests d/D ≠ 0
6. Conclusions
- A high quality small UAV off-the-shelf rotor has been measured to have a zero lift drag coefficient, = 0.019.
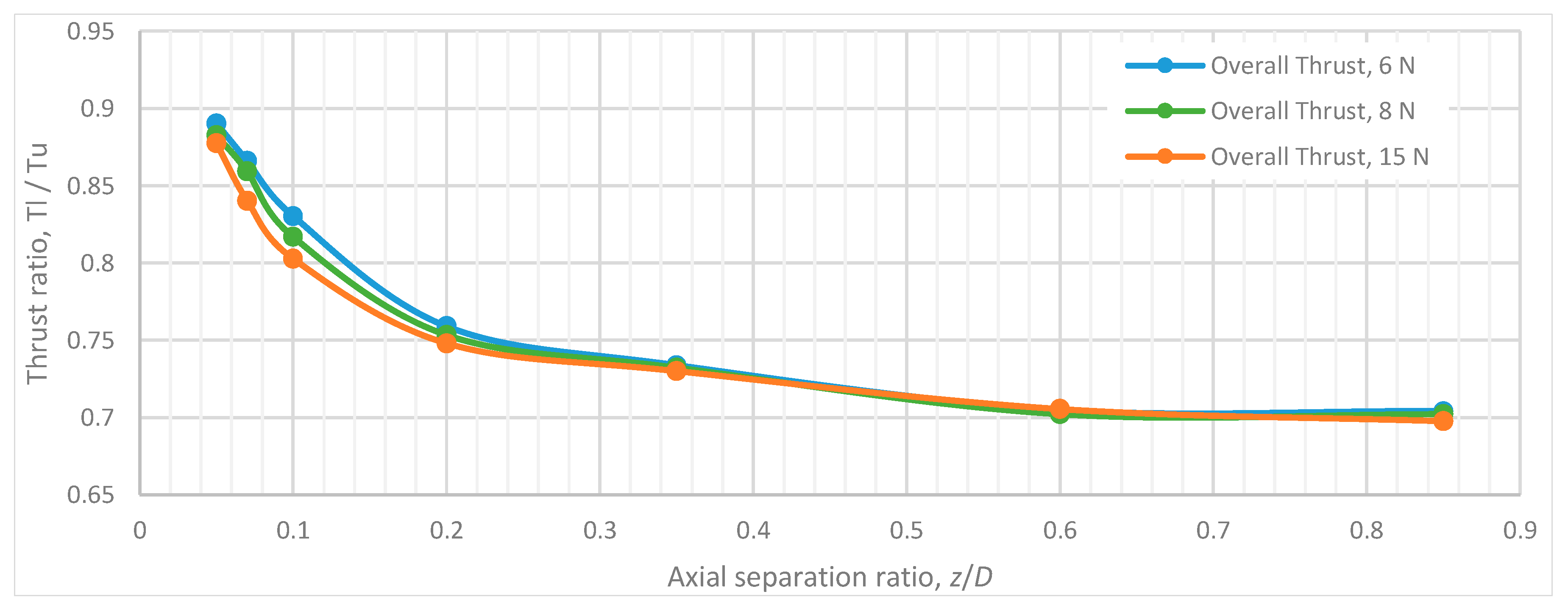
- A thrust sharing change of 21% was measured over the tested axial separation distances 0.05 < z/D < 0.85, when fixed pitch rotors were operated in the torque-balanced setup. The upper rotor produced more thrust than the lower at any tested z/D ratio.
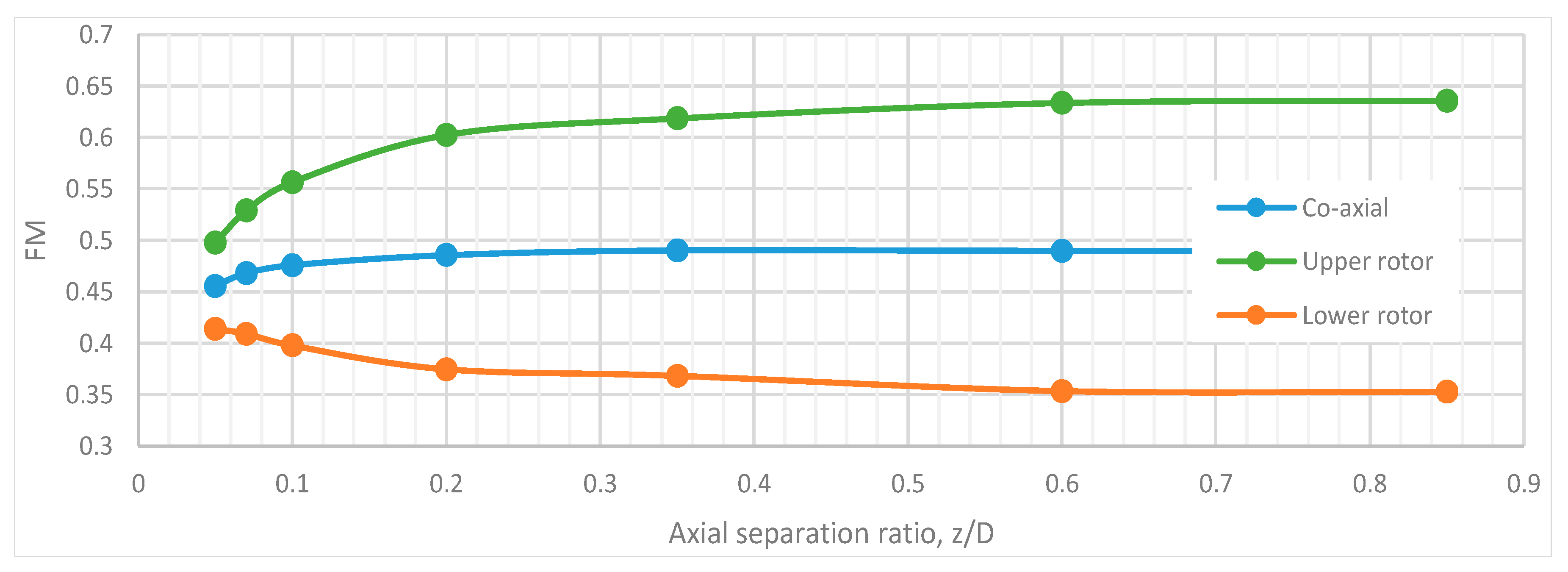
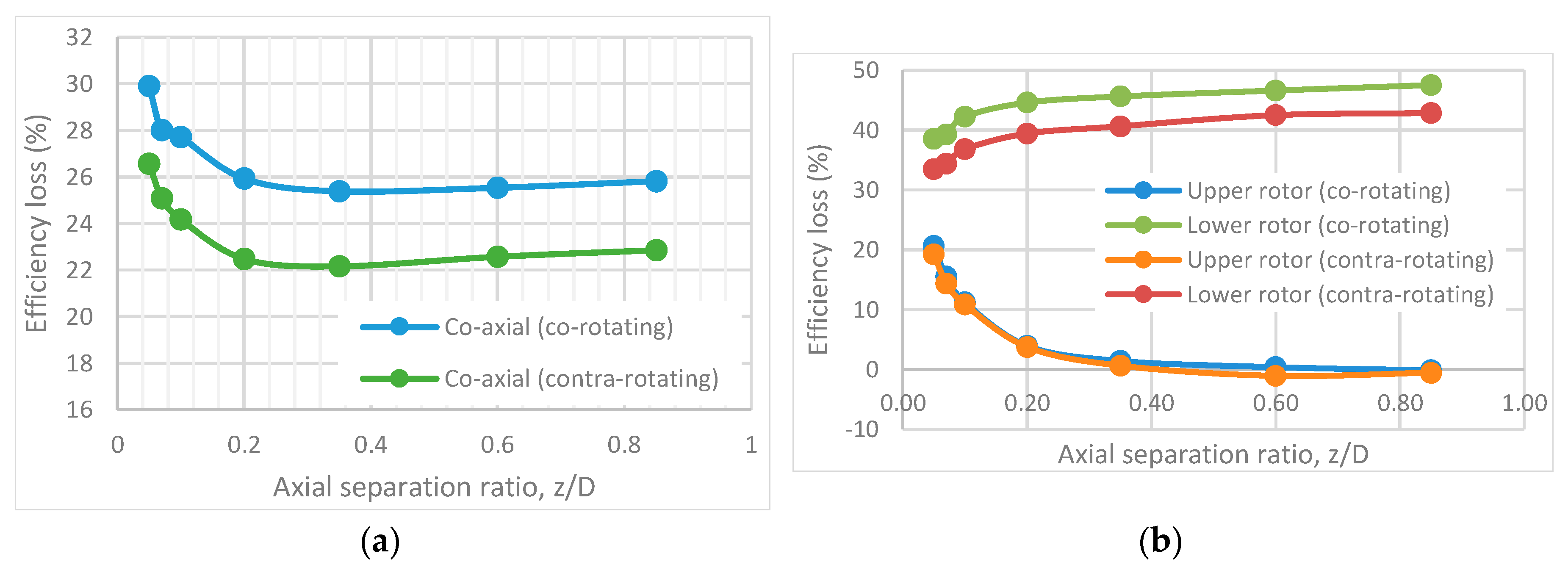
- Highly-twisted small UAV rotors in a conventional torque-balanced co-axial configuration are 22% less efficient when compared to two isolated rotors whose combined solidity is equal to that of a co-axial system. Momentum theory predicts a 26% increase in the induced power for torque-balanced co-axial rotor setups. The rotor axial separation from z/D > 0.25 had no effect on the overall system performance. The lowest performance figure of 26% loss over two isolated rotors was observed at z/D = 0.05.
- When comparing upper and lower rotors in a co-axial torque-balanced setup, it has been observed that the upper rotor operates at a higher efficiency than the lower rotor throughout the tested 0.05 < z/D < 0.85 range. Interference of the upper to the lower rotor was apparent throughout 0.05 < z/D < 0.85. Lower to upper rotor interference was observed only at 0.05 < z/D < 0.6 and the peak decrease the upper rotor efficiency was observed to be 21%. On the other hand, the lower rotor efficiency increased by 10% over the same axial separation range (0.05 < z/D < 0.6). These upper and lower rotor performance deviations affected the overall performance of the system at z/D < 0.25.
- The upper and lower rotors were compared to a single isolated rotor’s performance when operating in a co-axial torque balanced setup. At the range of axial separation of z/D > 0.6 the upper rotor operates at a similar performance to that observed on a single isolated rotor. In contrast, the lower rotor at the same axial separation range experiences an efficiency loss of 42%, which decreased to 33% at z/D = 0.05.
- Swirl recovery effects were observed in the overall co-axial rotor performance by running two co-rotating rotors in a co-axial setup, when the upper and lower rotor torque was equal. The results were compared to the conventional co-axial setup running rotors in the torque-balanced mode. Overall, the conventional co-axial rotor system was measured to be approximately 4% more efficient throughout all tested axial ratios 0.05 < z/D < 0.85, revealing the magnitude of the swirl recovery contribution to the overall system performance.
- Swirl recovery effects were observed on the individual upper and lower co-axial rotor performance by running two co-rotating rotors in a co-axial setup when the upper and lower rotor torque was equal. This was then compared to the results of a conventional co-axial setup running rotors in the torque-balanced mode. The lower rotor in a co-axial co-rotating system runs approximately 4% less efficiently throughout all tested axial separations 0.05 < z/D < 0.85. No differences in upper rotor performance were detected. These measurements have revealed that swirl recovery has little to no effect on the upper rotor and all of the efficiency gains are linked to the lower rotor.
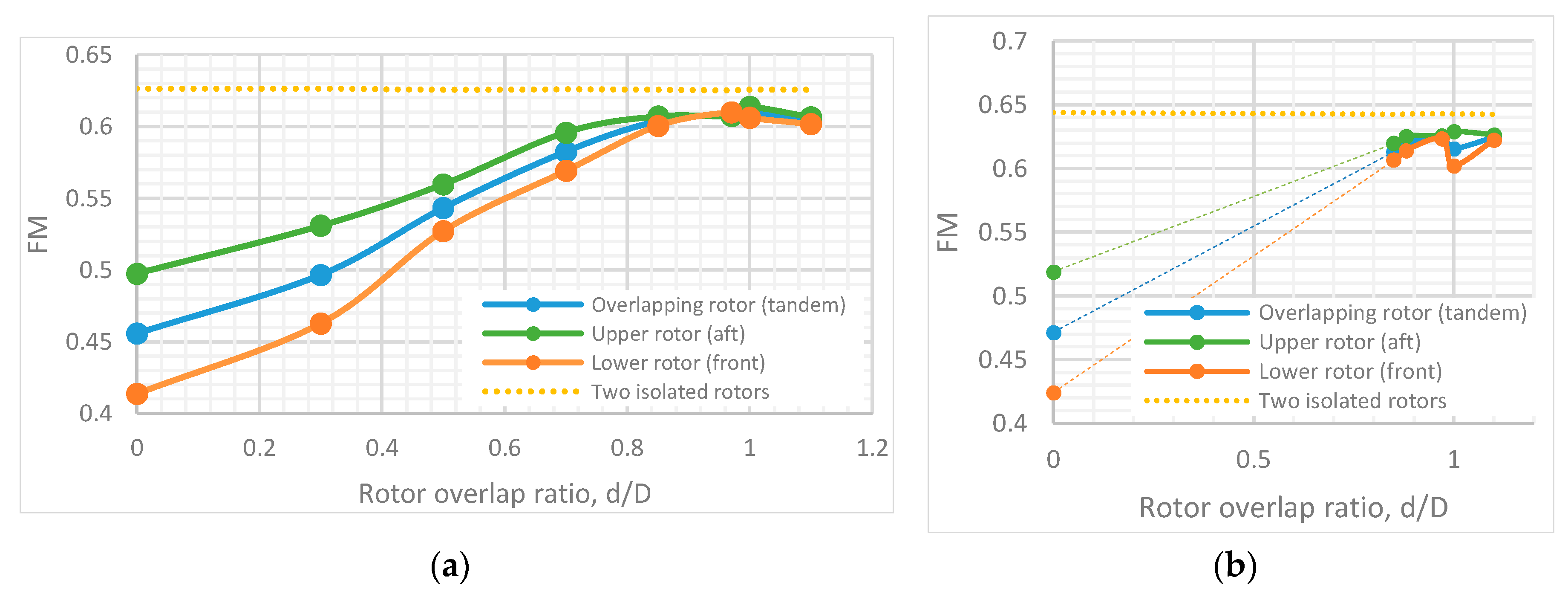
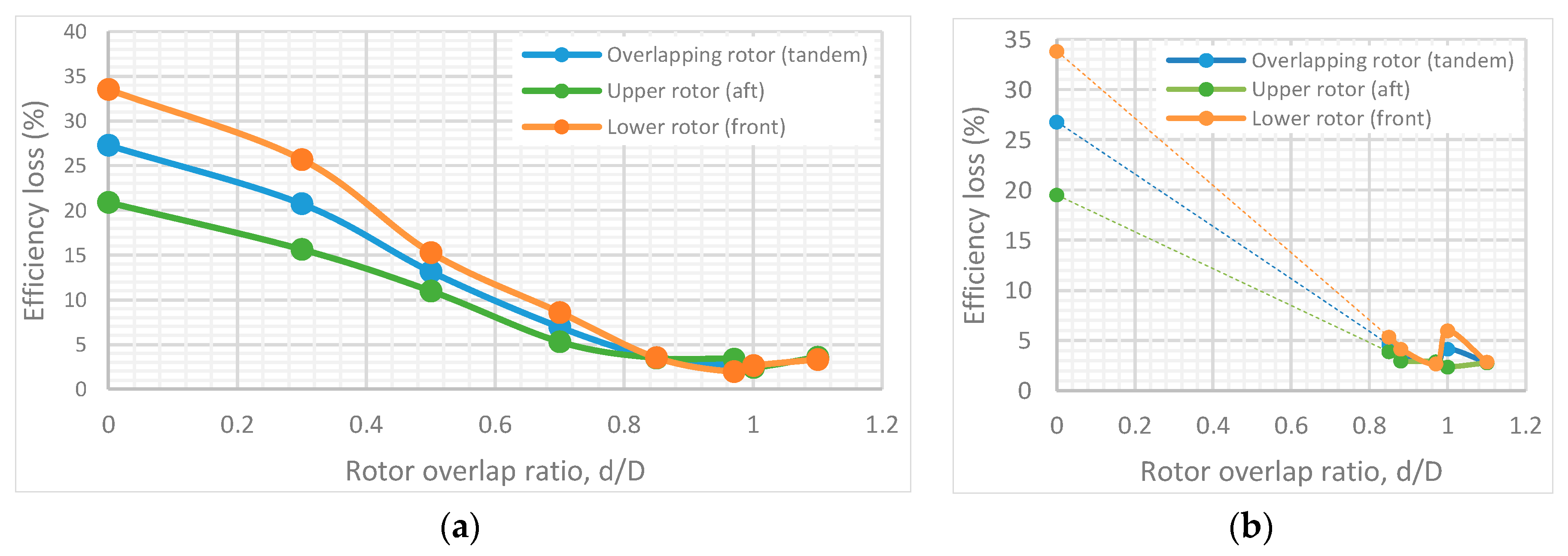
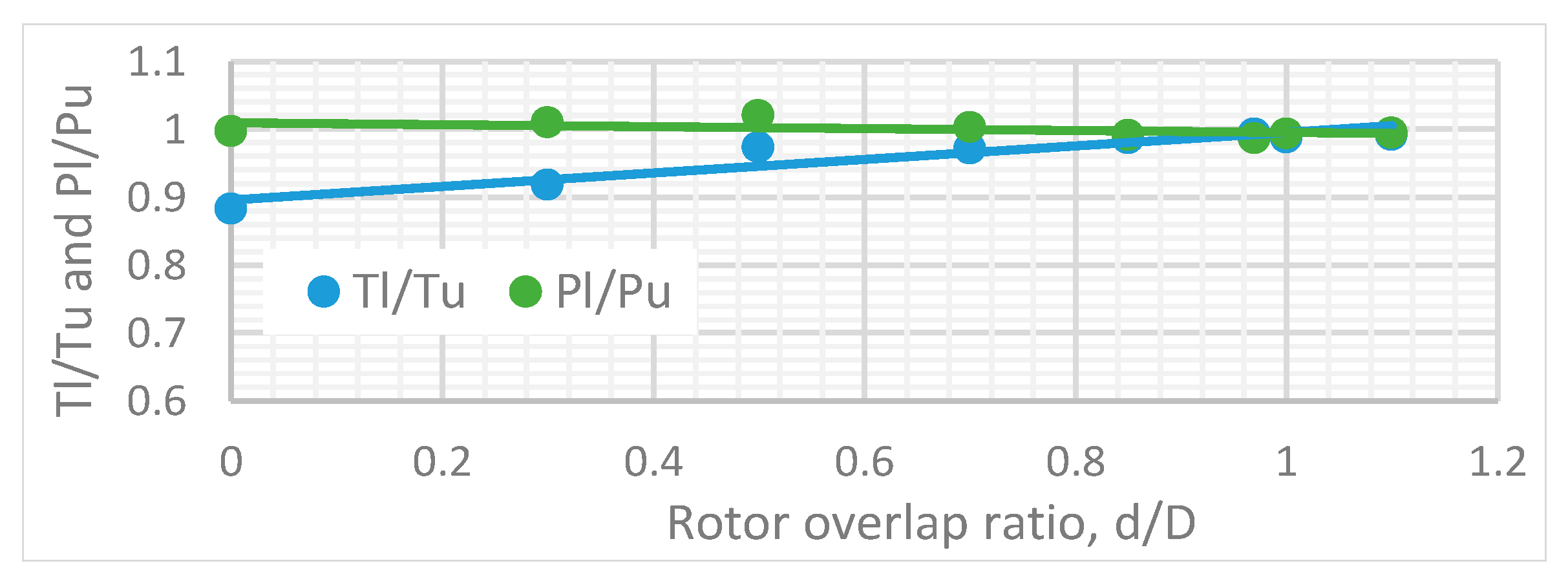
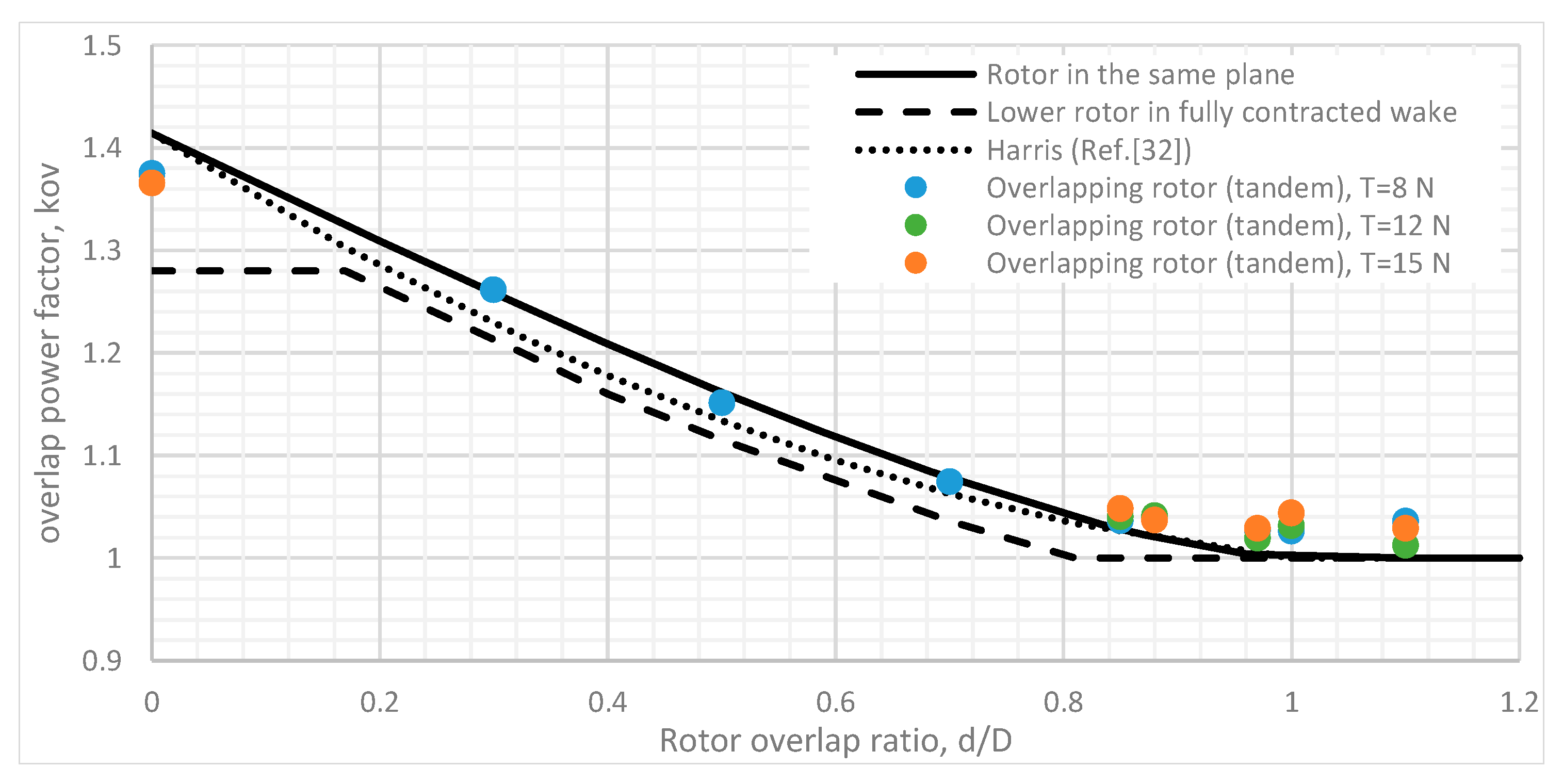
- The performance of a partially-overlapped (tandem) multi-rotor system, in a torque-balanced setup, was tested at an axial separation ratio z/D = 0.05 and the results were compared to two isolated rotors. The overall efficiency of the system increased through the overlap range of 0 < d/D < 1. The efficiency of the system started to decrease again at d/D > 1. The peak efficiency of the system was observed at d/D = 0.97, but was approximately 3% less efficient when compared to the performance of two isolated rotors.
- Performance of the upper (aft) rotor of a partially-overlapped torque-balanced system tested at z/D = 0.05 was better than the lower (front) rotor, up to d/D > 0.95. The lower rotor was observed to operate at a slightly higher efficiency in the region 0.95 < d/D < 1 at an overall thrust of 8 N. At a higher overall thrust of 15 N, such a performance change was not present. Dependencies on the overall thrust were recorded at d/D = 1 also, and with the increase of thrust the lower rotor performance decreased.
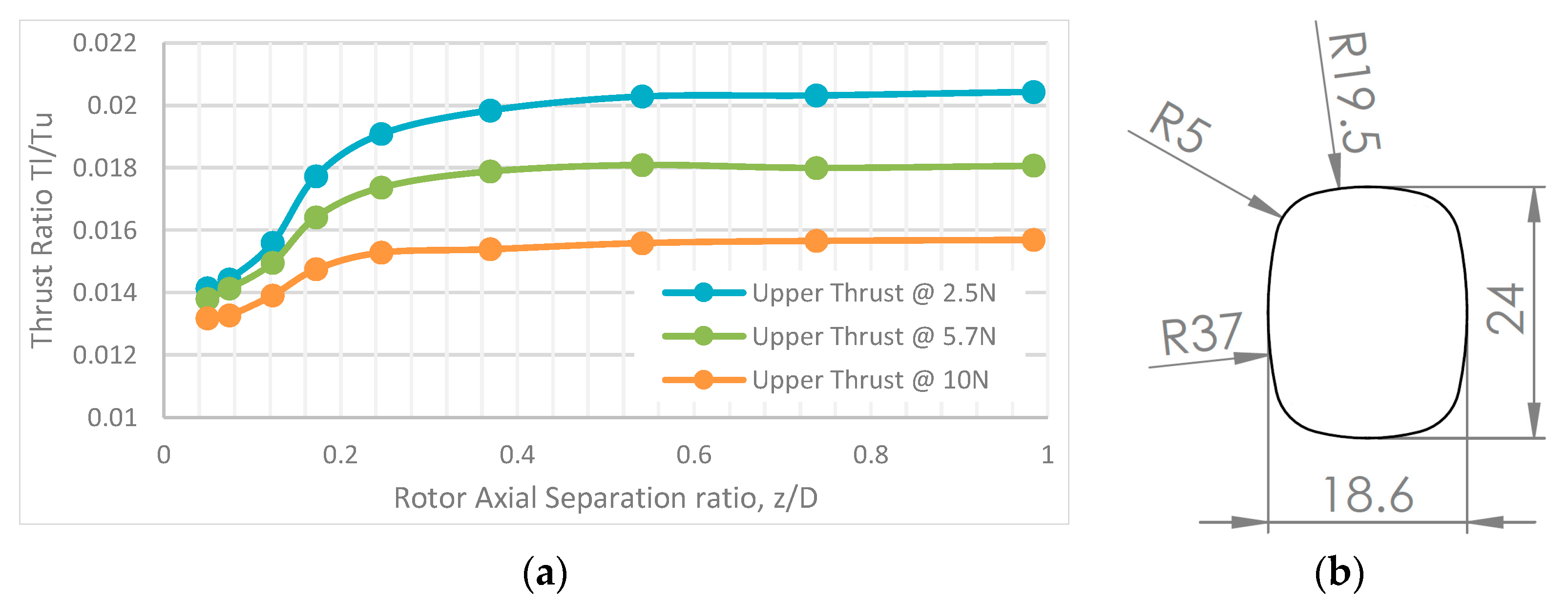
- Dependencies on the axial separation ratio z/D when rotors are operating in partial overlap of d/D = 0.85 at a torque-balanced state were recorded. Through the tested axial separation range of 0.05 < z/D < 0.85, approximately a 2% increase in overall performance was recorded. Most of the gains occurred at z/D < 0.35.
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Nomenclature
| Rotor disk area, , m2 | |
| Rotor blade chord, m | |
| Zero-lift drag coefficient | |
| Rotor diameter, m | |
| Rotor separation, m | |
| Rotor overlap ratio | |
| Non-dimensional chord length | |
| Induced power factor | |
| Induced power factor from interference | |
| Induced power factor from overlap rotor interference | |
| Induced rotor power, W | |
| Zero-lift induced rotor power, W | |
| Rotor torque, Nm | |
| Rotor radius, m | |
| Distance from the blade root to the blade section, m | |
| Non-dimensional radial position | |
| Rotor thrust, N | |
| Rotor axial separation distance, m | |
| Rotor axial separation ratio | |
| Blade section angle of attack, deg | |
| Blade section pitch angle, deg | |
| Density of air (sea-level), 1.225 kg/m3 | |
| Blade section inflow angle, deg |
References
- Aboulafia, R. World Military and Civil Aircraft Briefing; TEAL Group Corporation: Fairfax, VA, USA, 2016. [Google Scholar]
- Prior, S.; Shen, S.-T.; Erbil, M.A.; Brazinskas, M.; Mielniczek, W. HALO the winning entry to the DARPA UAVForge challenge 2012. In Design, User Experience, and Usability. User Experience in Novel Technological Environments; Marcus, A., Ed.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 8014, pp. 179–188. [Google Scholar]
- Deters, R.W.; Selig, M.S. Static testing of micro propellers. In Proceedings of the 26th AIAA Aplied Aerodynamics Conference, Honolulu, HI, USA, 18–21 August 2008.
- Zhou, Y.; Wang, Z.J. Effects of surface roughness on separated and transitional flows over a wing. AIAA J. 2012, 50, 593–609. [Google Scholar] [CrossRef]
- Coleman, C.P. A Survey of Theoretical and Experimental Coaxial Rotor Aerodynamic Research; NASA-TP-3675; National Aeronautics and Space Administration National Technical Information Service: Moffett Field, CA, USA, 1997; p. 26.
- Nagashima, T.; Ouchi, H.; Sasaki, F. Optimum performance and load sharing of coaxial rotor in hover. J. Jpn. Soc. Aeronaut. Space Sci. 1978, 26, 293. [Google Scholar]
- Shinohara, K. Optimum Aerodynamic Character of the Coaxial Counter Rotating Rotor System; The National Defense Academy: Yokosuka, Japan, 1977. [Google Scholar]
- Harrington, R.D. Full-Scale-Tunnel Investigation of the Static-Thrust Performance of a Coaxial Helicopter Rotor; NACA-TN-2318; National Advisory Committee: Langley Field, VA, USA, 1951; p. 23.
- Dingeldein, R.C. Wind-Tunnel Studies of the Performance of Multirotor Configurations; National Advisory Committee for Aeronautics: Langley Field, VA, USA, 1 August 1954.
- Cheney, M.C. The ABC helicopter. J. Am. Helicopter Soc. 1969, 14, 10–11. [Google Scholar] [CrossRef]
- Rorke, J.B. Hover Performance Tests of Full Scale Variable Geometry Rotors; NASA: Washington, DC, USA, 1975.
- Arents, D.N. An Assessment of the Hover Performance of the XH-59A Advancing Blade Concept Demonstration Helicopter; Eustis Directorate: Fort Eustis, VA, USA, 1977. [Google Scholar]
- Bohorquez, F. Rotor Hover Performance and System Design of an Efficient Coaxial Rotary Wing Micro Air Vehicle. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2007. [Google Scholar]
- Lee, T.E. Design and Performance of a Ducted Coaxial Rotor in Hover and Forward Flight. Ph.D. Thesis, University of Maryland, College Park, MD, USA, 2010. [Google Scholar]
- Ramasamy, M. Hover performance measurements toward understanding aerodynamic interference in coaxial, tandem, and tilt rotors. J. Am. Helicopter Soc. 2015, 60, 1–17. [Google Scholar] [CrossRef]
- McAlister, K.W.; Tung, C.; Rand, O.; Khromov, V.; Wilson, J.S. Experimental and numerical study of a model coaxial rotor. In Proceedings of the 62nd American Helicopter Society Annual Forum, Phoenix, AZ, USA, 2006.
- Theys, B.; Dimitriadis, G.; Hendrick, P.; De Schutter, J. Influence of propeller configuration on propulsion system efficiency of multi-rotor unmanned aerial vehicles. In Proceedings of the 2016 International Conference on Unmanned Aircraft Systems (ICUAS), Arlington, VA, USA, 7–10 June 2016.
- Stepniewski, W.Z. Basic Theories of Rotor Aerodynamics (With Application to Helicopters). In Rotary-Wing Aerodynamics; Dover Publications: New York, NY, USA, 1979; Volume 1. [Google Scholar]
- Bender, G.L.; Sullivan, P.J.; Yamakawa, G.M.; Robbins, R.D.; Herbst, M.K.; Williams, R.A. Airworthiness and Flight Characteristics Test of the CH-47D Helicopter; USAAEFA: St. Louis, MO, USA, 1984. [Google Scholar]
- Prior, S.D.; Bell, C.J. Empirical measurements of small unmanned aerial vehicle co-axial rotor systems. J. Sci. Innov. 2011, 1, 1–18. [Google Scholar]
- Andrew, M.J. Coaxial Contrarotating Twin Rotor Aerodynamics. Ph.D. Thesis, University of Southampton, Southampton, UK, 1983. [Google Scholar]
- Johnson, W. Influence of lift offset on rotor performance. In Proceedings of the AHS Technical Specialists Meeting on Aeromechanics, San Francisco, CA, USA, 23–25 January 2008.
- Stepniewski, W.Z.; Sloan, L.H. Experimental Investigation of PV-14 Overlap; 14-A-03; Piasecki Corp.: Essington, PA, USA, 1948. [Google Scholar]
- Griffiths, D.; Leishman, J.G. A study of dual-rotor interference and ground effect using a free-vortex wake model. In Proceedings of the 58th AHS International Annual Forum, Montreal, QC, Canada, 11 June 2002.
- Heyson, H.H. An Evaluation of Linearized Vortex Theory as Aplied to Single and Multiple Rotors Hovering in and out of Ground Effect; NASA TN D-43; National Aeronautics and Space Administration: Washington, DC, USA, 1959.
- Sweet, G.E. Hovering Measurements for Twin-Rotor Configurations with and without Overlap; NASA TN D-534; National Aeronautics and Space Administration: Washington, DC, USA, 1960.
- Drela, M. XFOIL: An analysis and design system for low reynolds number airfoils. In Low Reynolds Number Aerodynamics: Proceedings of the Conference Notre Dame, Indiana, USA, 5–7 June 1989; Mueller, T.J., Ed.; Springer: Berlin/Heidelberg, Germany, 1989; pp. 1–12. [Google Scholar]
- Leishman, J.G.; Ananthan, S. Aerodynamic optimization of a coaxial proprotor. In Proceedings of the 62nd AHS International Annual Forum, Montreal, QC, Canada, 9 May 2006.
- Glauert, H. The Elements of Aerofoil and Airscrew Theory; Cambridge University Press: New York, NY, USA, 1983. [Google Scholar]
- Leishman, J.G. Principles of Helicopter Aerodynamics, 2nd ed.; Cambridge University Press: New York, NY, USA, 2006; p. 826. [Google Scholar]
- Leishman, J.G.; Syal, M. Figure of merit definition for coaxial rotors. J. Am. Helicopter Soc. 2008, 53, 290–300. [Google Scholar] [CrossRef]
- Harris, F.D. Technical note: Twin rotor hover performance. J. Am. Helicopter Soc. 1999, 44, 34–37. [Google Scholar] [CrossRef]





© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brazinskas, M.; Prior, S.D.; Scanlan, J.P. An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System. Aerospace 2016, 3, 32. https://doi.org/10.3390/aerospace3040032
Brazinskas M, Prior SD, Scanlan JP. An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System. Aerospace. 2016; 3(4):32. https://doi.org/10.3390/aerospace3040032
Chicago/Turabian StyleBrazinskas, Mantas, Stephen D. Prior, and James P. Scanlan. 2016. "An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System" Aerospace 3, no. 4: 32. https://doi.org/10.3390/aerospace3040032
APA StyleBrazinskas, M., Prior, S. D., & Scanlan, J. P. (2016). An Empirical Study of Overlapping Rotor Interference for a Small Unmanned Aircraft Propulsion System. Aerospace, 3(4), 32. https://doi.org/10.3390/aerospace3040032