Comparison of Power Requirements: Flapping vs. Fixed Wing Vehicles
Abstract
:1. Introduction
2. Performance Relations
3. Flapping Wing Vehicles
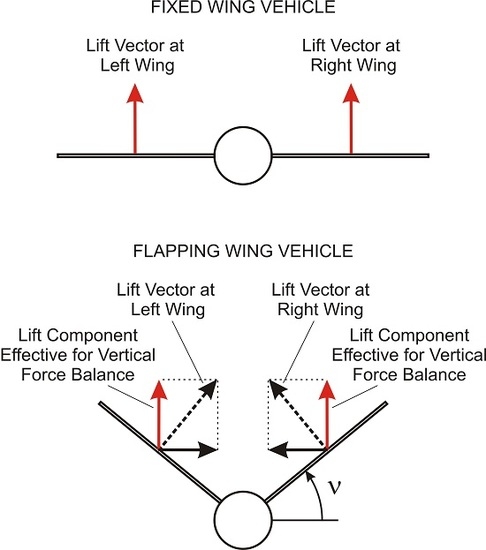
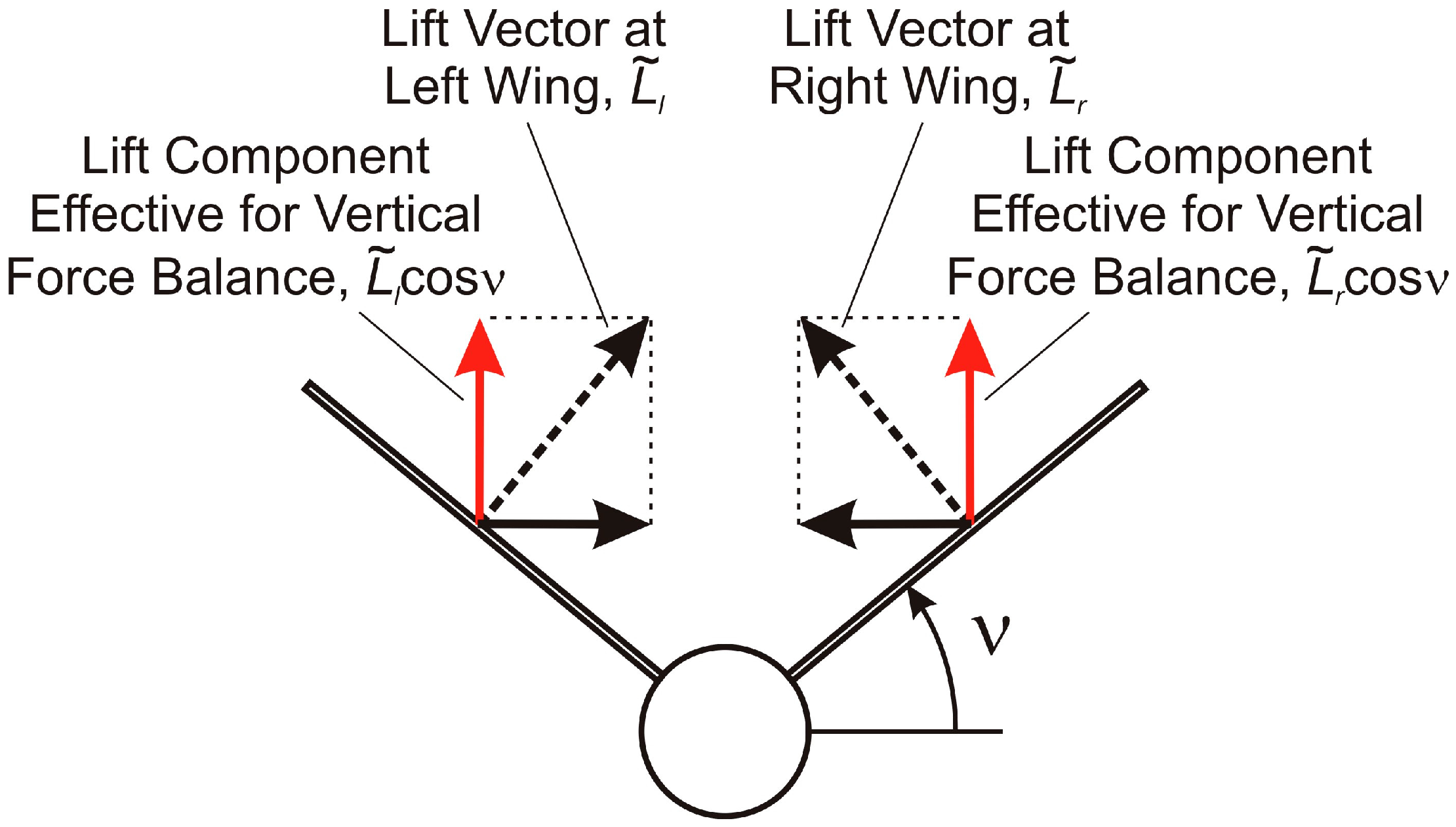
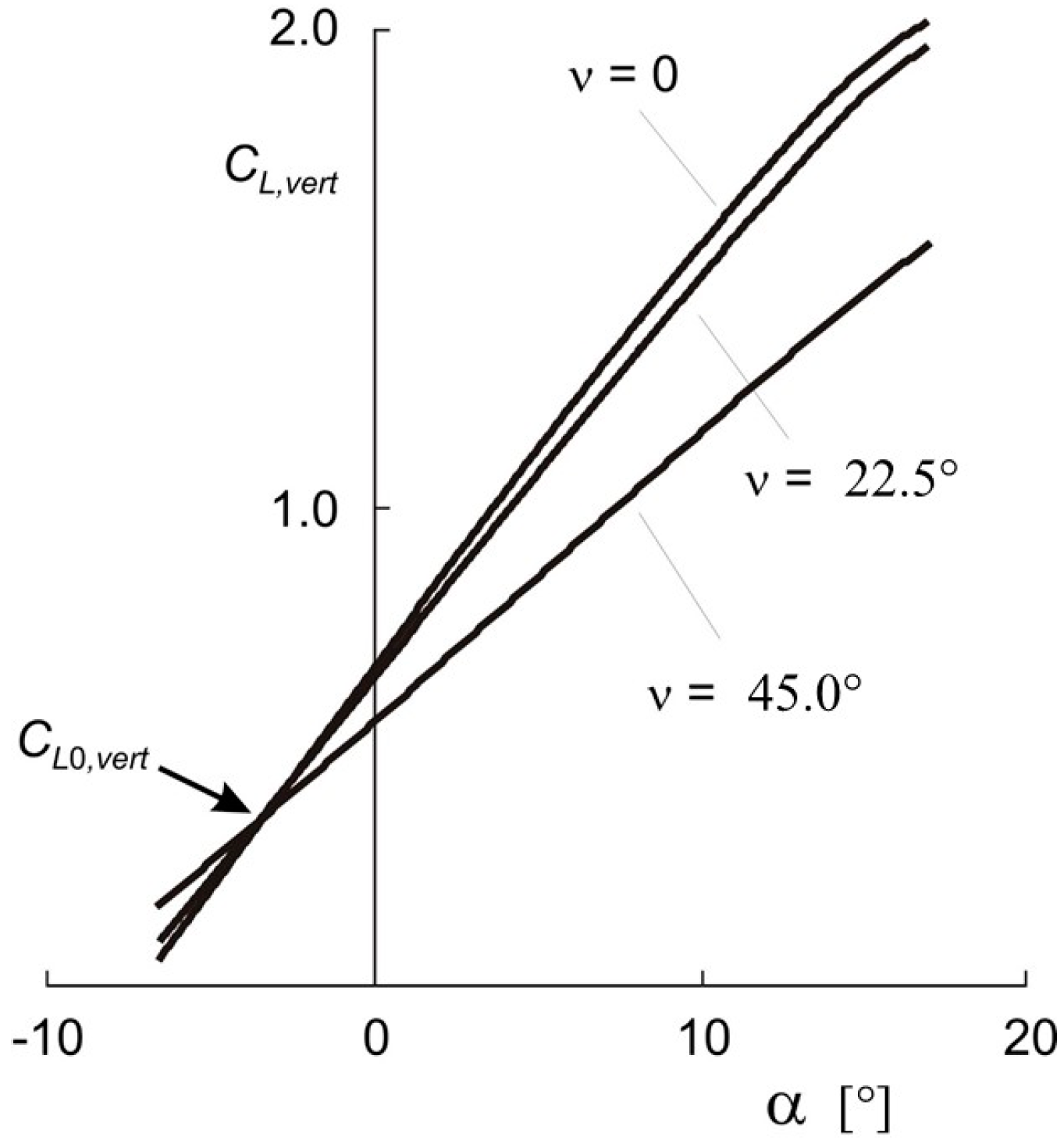
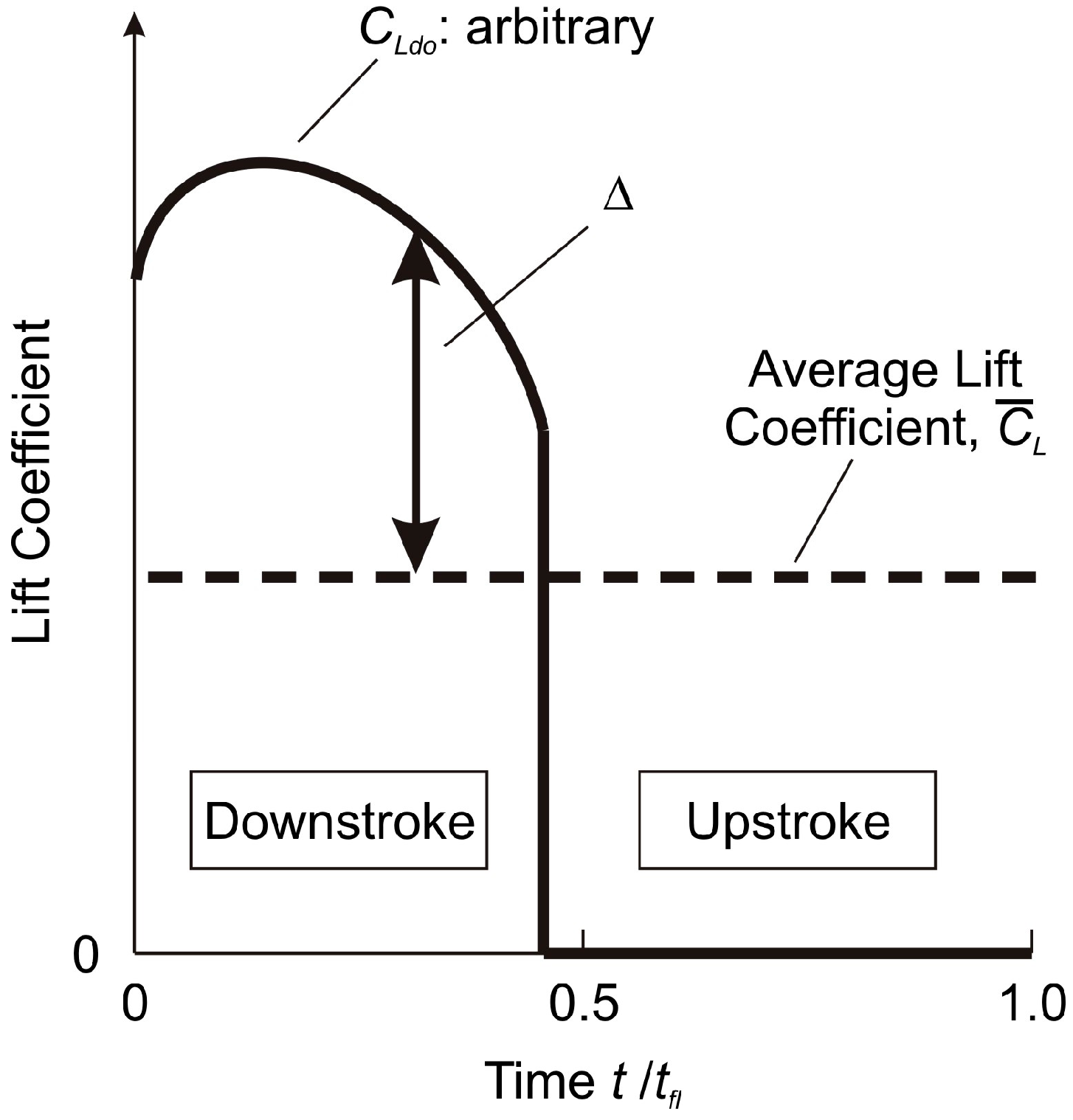
3.1. Modeling of Lift Characteristics of Flapping Wing Vehicles
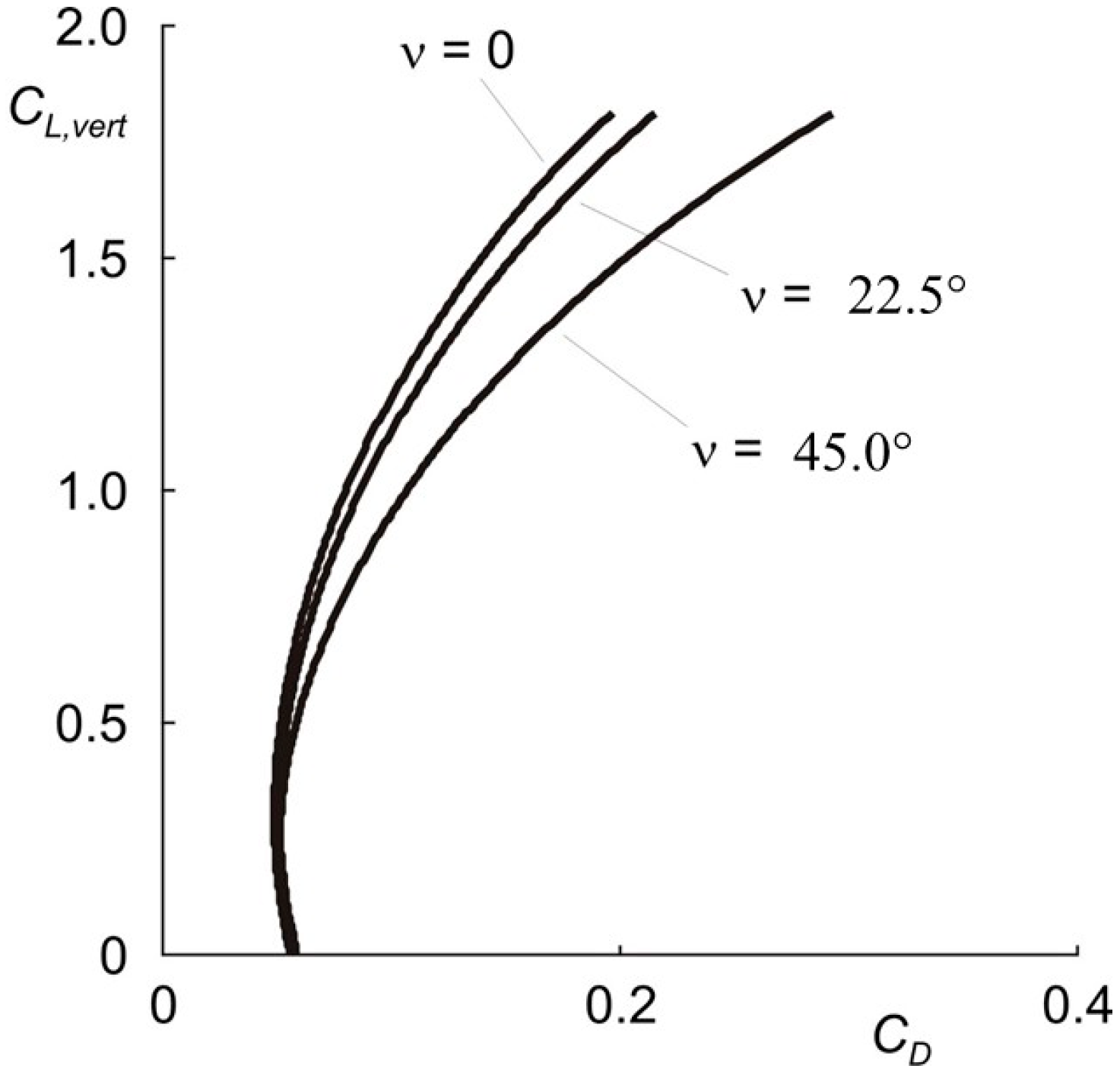
3.2. Modeling of Drag Characteristics of Flapping Wing Vehicles
- (1)
- Tilting of lift vector due to flapping the wings, resulting in the term .
- (2)
- Changes in the amount of the lift vector in the course of the flapping cycle, resulting in the term .
3.3. Power Requirements of Flapping Wing Vehicles
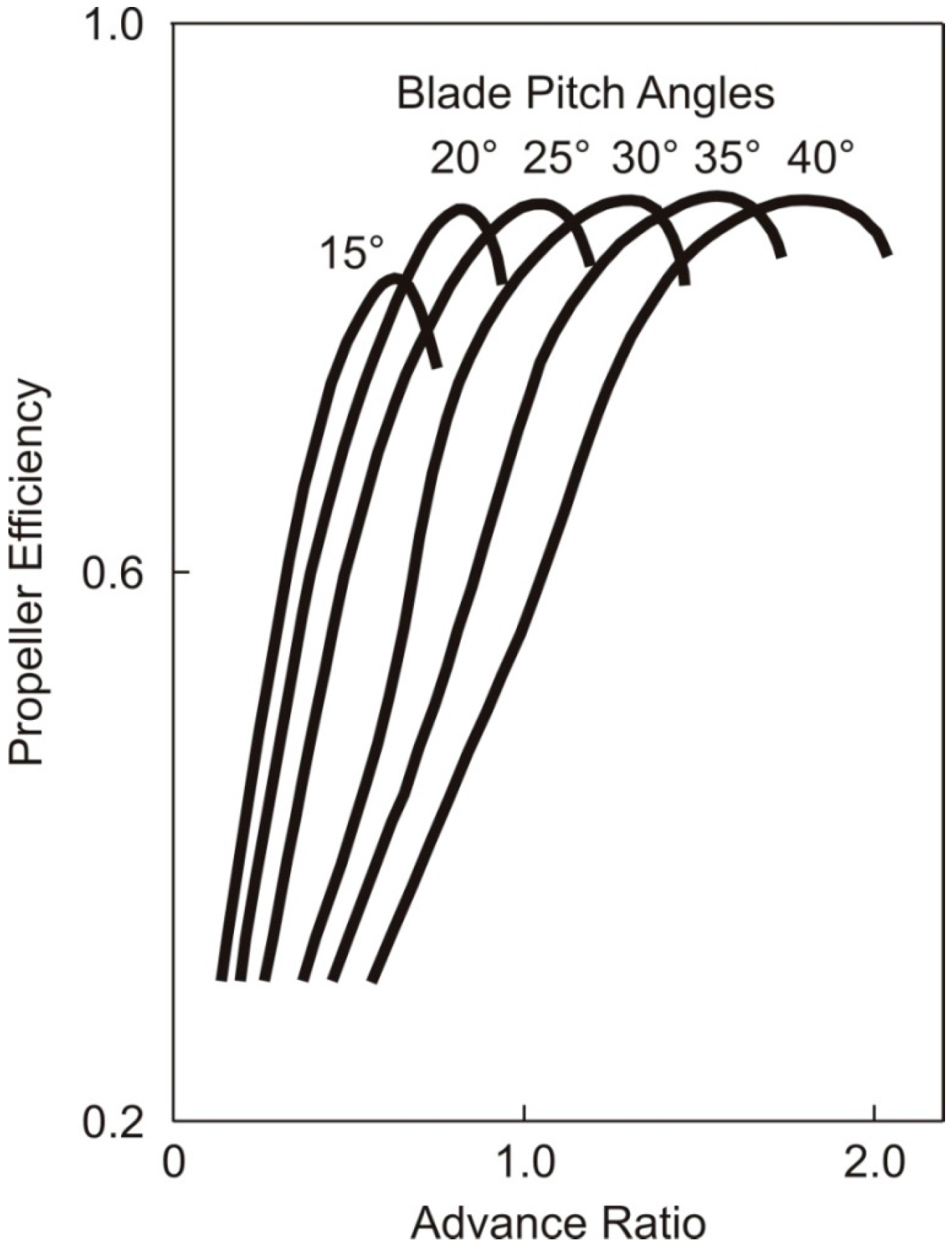
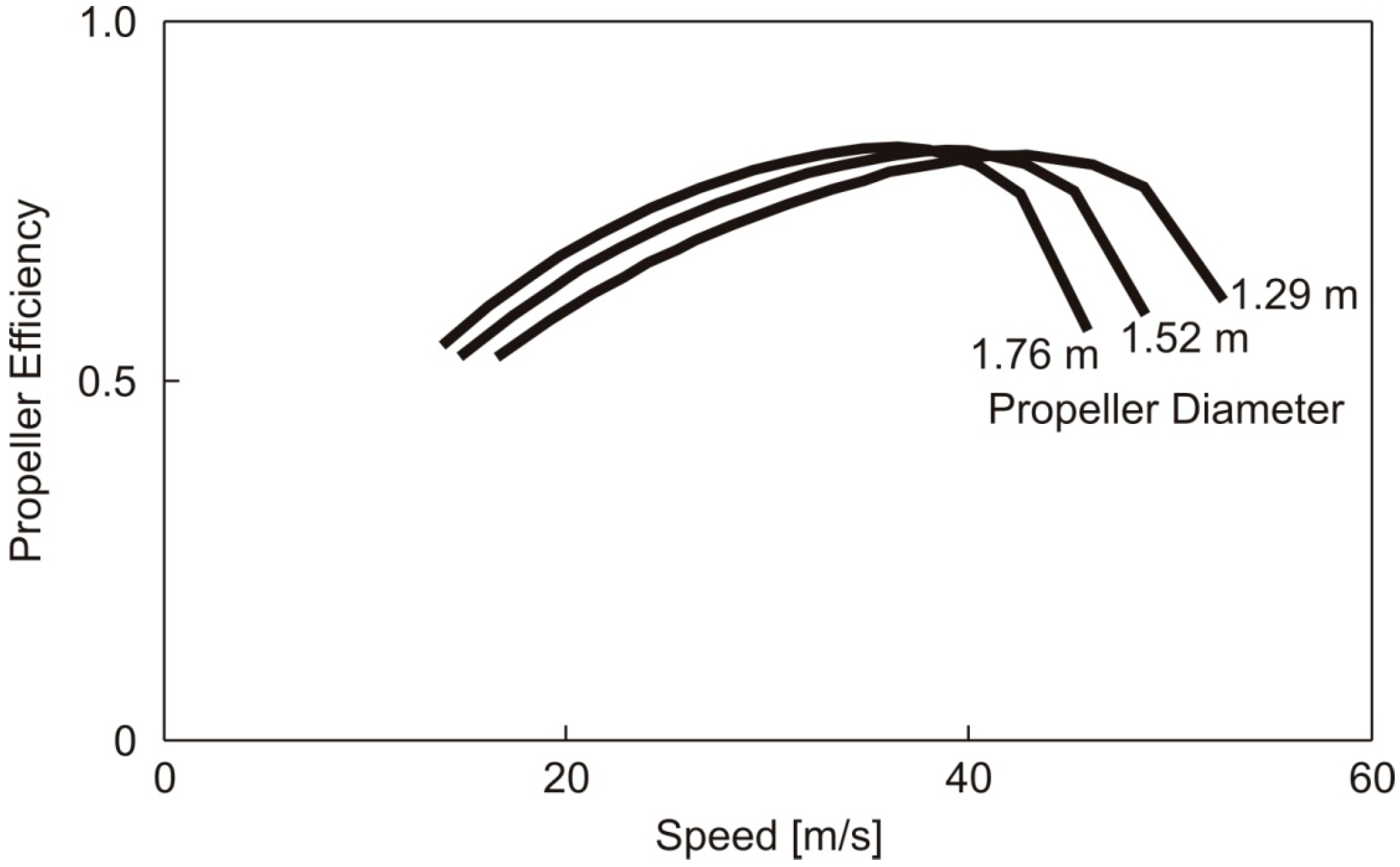
4. Fixed Wing Vehicles
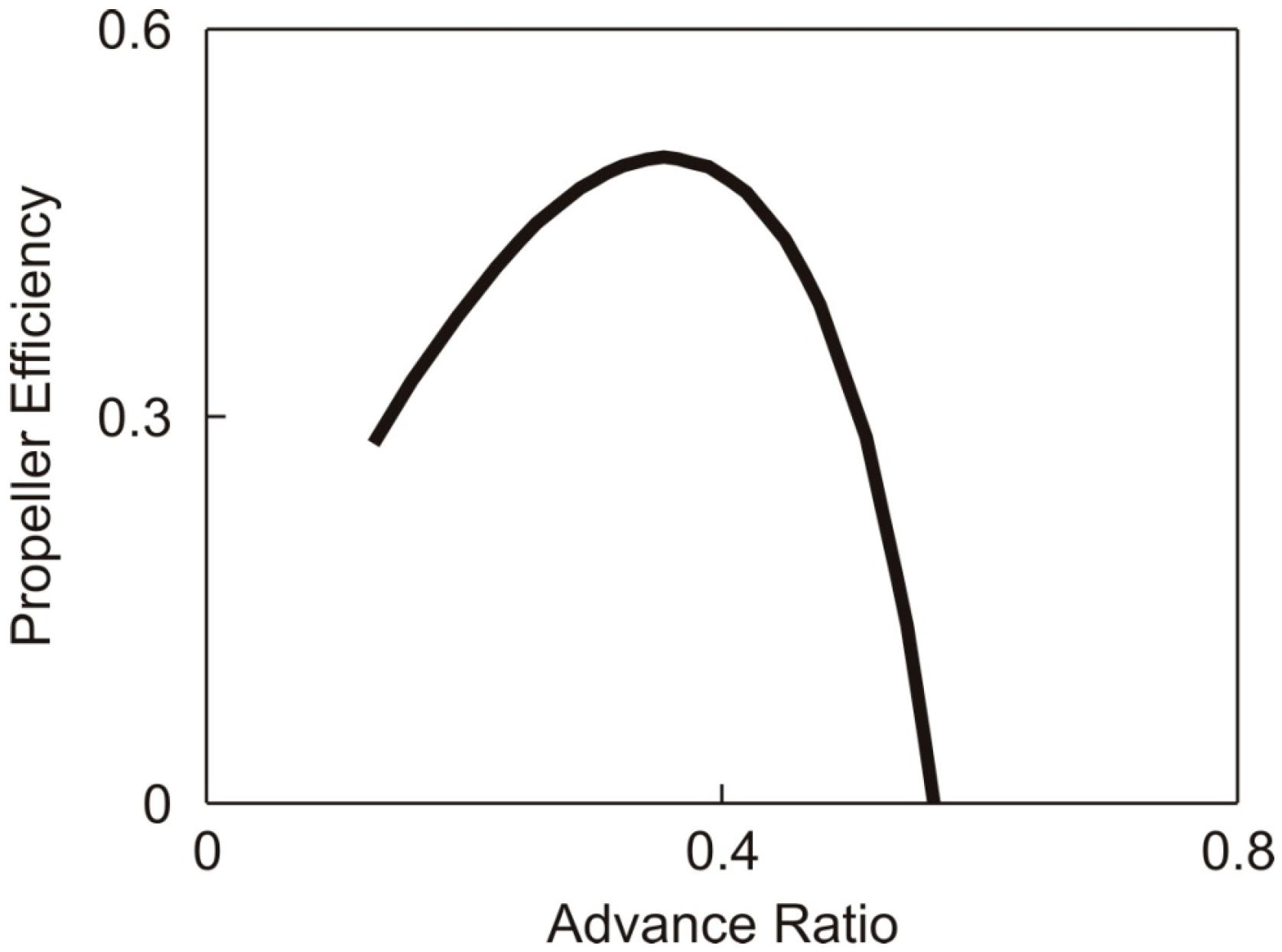
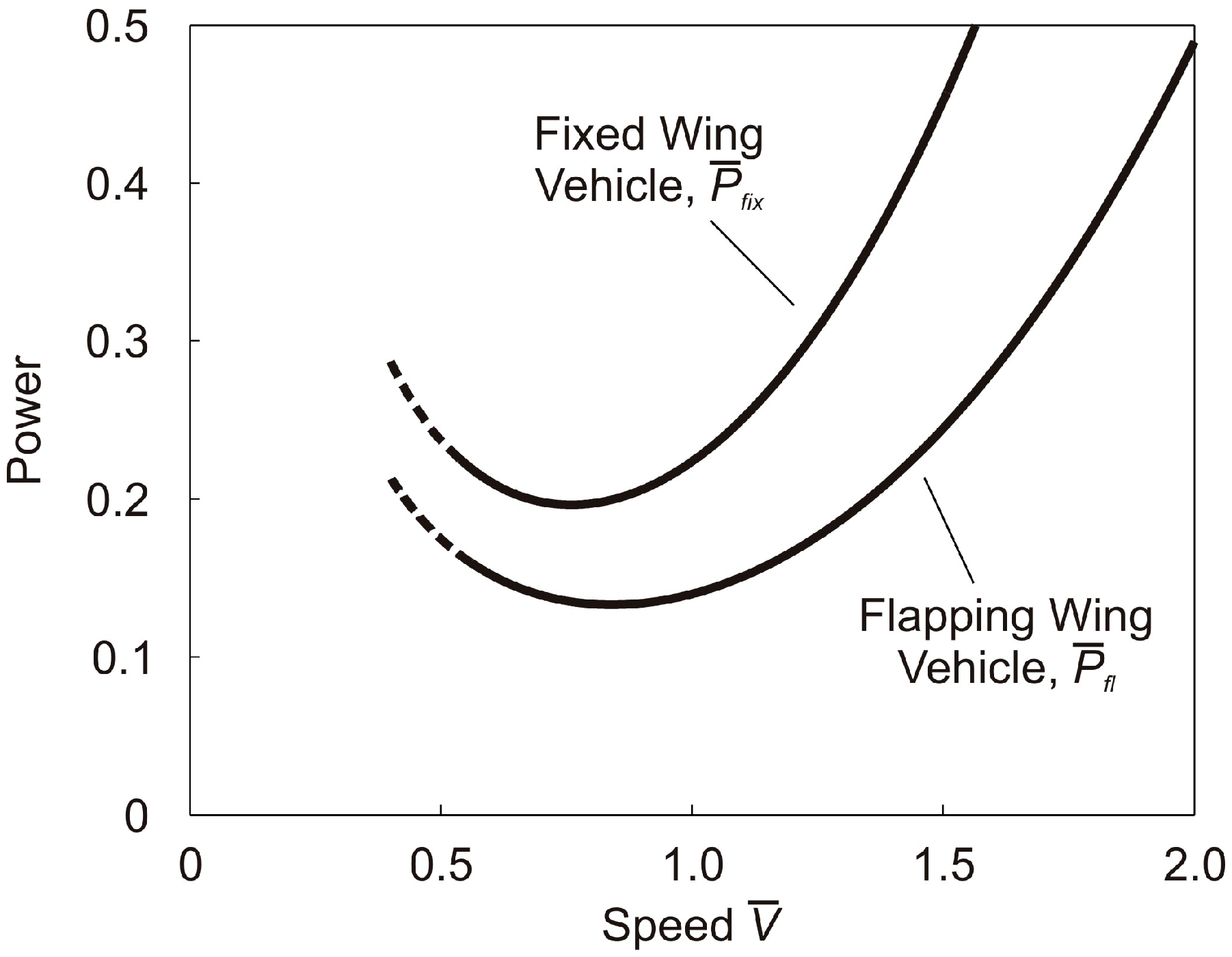
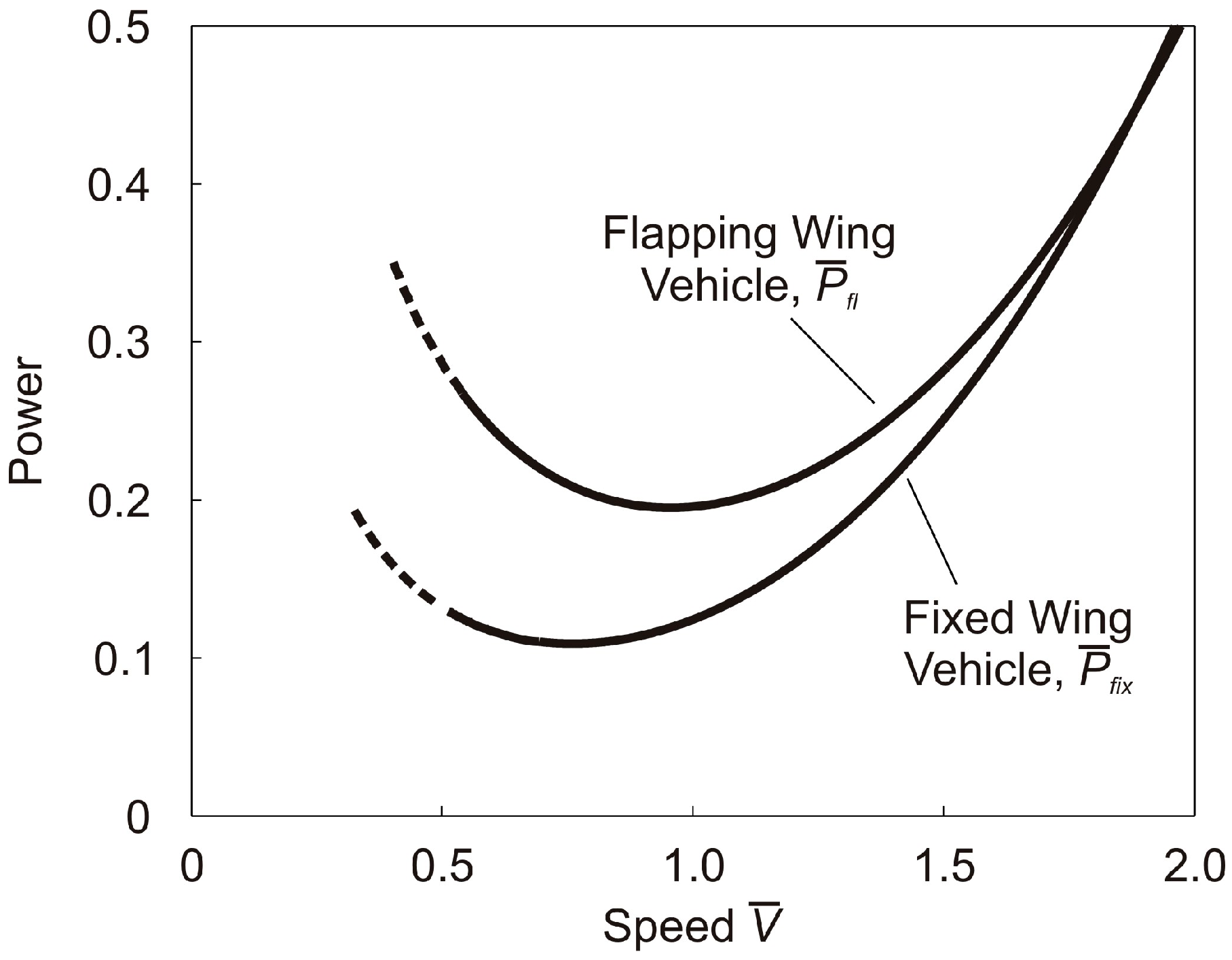
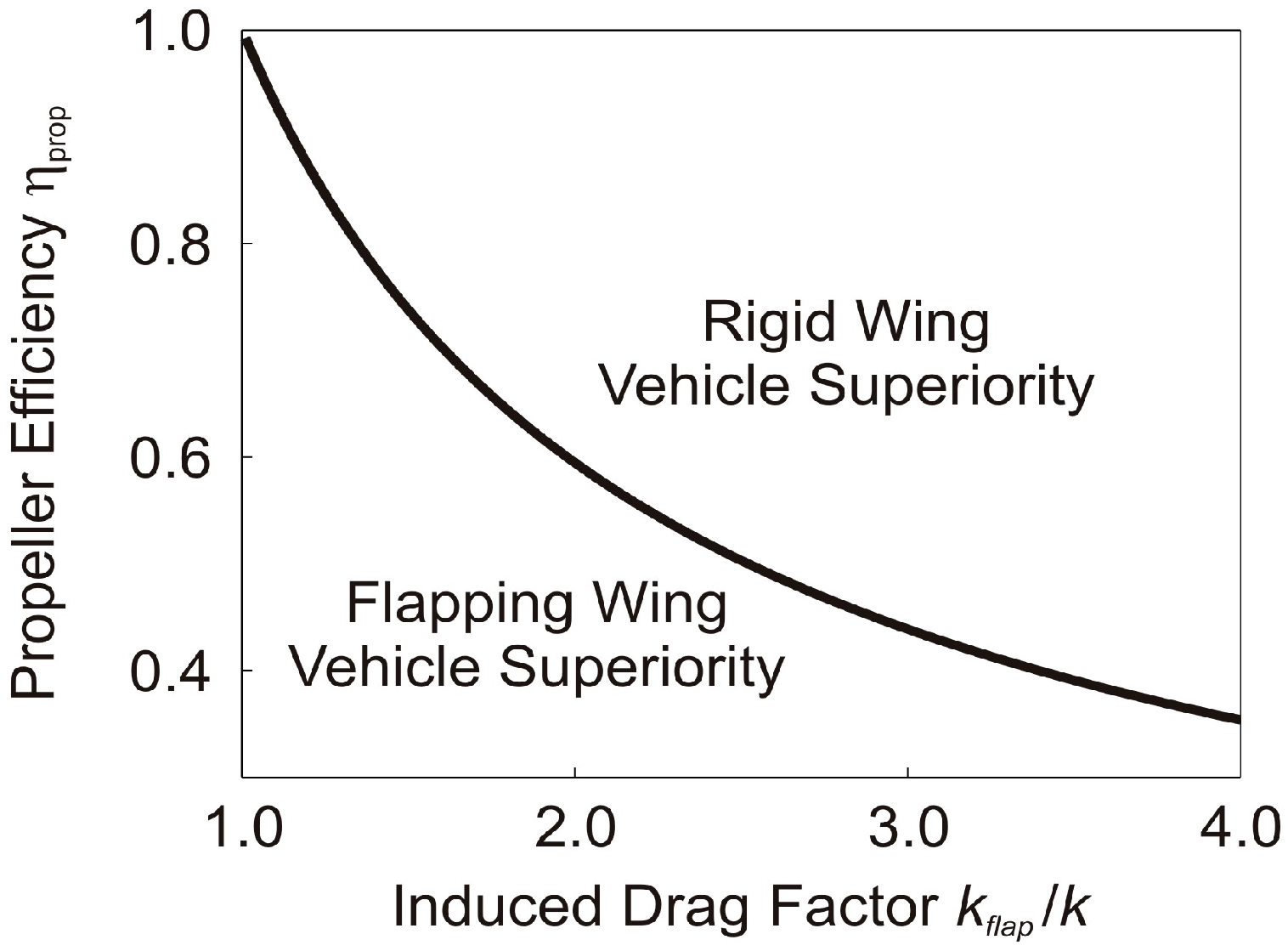
5. Comparison of Power Required by Flapping and Fixed Wing Vehicles
6. Conclusions
Conflicts of Interest
Nomenclature
| wing span | |
| drag coefficient | |
| lift coefficient | |
| drag | |
| acceleration due to gravity | |
| , | lift dependent drag factor |
| lift | |
| mass | |
| power | |
| reference area | |
| time | |
| speed | |
| minimum-drag speed | |
| non-dimensional speed, | |
| aspect ratio, | |
| tilt angle of lift vector | |
| propeller efficiency | |
| air density |
References
- Muller, T.J.; DeLaurier, J.D. An overview of micro air vehicle aerodynamics. In Fixed and Flapping Wing Aerodynamics for Micro Air Vehicle Applications; Mueller, T.J., Ed.; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2001; Volume 195. [Google Scholar]
- Shyy, W.; Aono, H.; Chimakurthi, S.K.; Trizila, P.; Kang, C.-K.; Cesnik, C.E.S.; Liu, H. Recent progress in flapping wing aerodynamics and aeroelasticity. Prog. Aerosp. Sci. 2010, 46, 284–327. [Google Scholar] [CrossRef]
- DeLaurier, J.D. The development and testing of a full-scale piloted ornithopter. Can. Aeronaut. Space J. 1999, 45, 72–82. [Google Scholar]
- Brüning, G.; Hafer, X.; Sachs, G. Flugleistungen, 4th ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Anderson, J.M.; Streitlien, K.; Barrett, D.S.; Triantafyllou, M.S. Oscillating foils of high propulsive efficiency. J. Fluid Mech. 1998, 360, 41–72. [Google Scholar] [CrossRef]
- Paranjape, A.A.; Chung, S.-J.; Hilton, H.H. Optimizing the forces and propulsive efficiency in bird-scale flapping flight. In Proceedings of the AIAA Atmospheric Flight Mechanics Conference, Boston, MA, USA, 19–22 August 2013; p. 4916.
- Pesavento, U.; Wang, Z.J. Flapping wing flight can save aerodynamic power compared to steady flight. Phys. Rev. Lett. 2009, 103, 118102. [Google Scholar] [CrossRef] [PubMed]
- Mazaheri, K.; Ebrahimi, A.; Karimian, S. Performance analysis of a flapping-wing vehicle based on experimental aerodynamic data. J. Aerosp. Eng. 2012, 25, 45–50. [Google Scholar] [CrossRef]
- Wang, Z.J. Aerodynamic efficiency of flapping flight: Analysis of a two-stroke model. J. Exp. Biol. 2008, 211, 234–238. [Google Scholar] [CrossRef] [PubMed]
- Hall, K.C.; Hall, S.R. Minimum induced power requirements for flapping flight. J. Fluid Mech. 1996, 323, 285–315. [Google Scholar] [CrossRef]
- Lentink, D.; Dickinson, M.H. Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Exp. Biol. 2009, 212, 2691–2704. [Google Scholar] [CrossRef] [PubMed]
- Lentink, D. Exploring the Biofluiddynamics of Swimming and Flight. Ph.D. Thesis, Wageningen University, Wageningen, The Netherlands, September 2008. [Google Scholar]
- Heerenbrink, M.K.; Johansson, L.C.; Hedenström, A. Power of the wingbeat: Modelling the effects of flapping wings in vertebrate flight. Proc. R. Soc. A 2015, 471, 20140952. [Google Scholar] [CrossRef] [PubMed]
- Sachs, G. Aerodynamic cost of flapping. J. Bionic Eng. 2015, 12, 61–69. [Google Scholar] [CrossRef]
- Sachs, G. New model of flap-gliding flight. J. Theor. Biol. 2015, 377, 110–116. [Google Scholar] [CrossRef] [PubMed]
- Sane, S.P.; Dickinson, M.H. The control of flight force by a flapping wing: Lift and drag production. J. Exp. Biol. 2001, 204, 2607–2626. [Google Scholar] [PubMed]
- Heuser, H. Lehrbuch der Analysis, Teil 1, 8th ed.; B.G. Teubner: Stuttgart, Germany, 1990. [Google Scholar]
- Pennycuick, C.J. Modelling the Flying Bird; Elsevier Ltd.: Oxford, UK, 2008. [Google Scholar]
- Tobalske, B.W. Biomechanics and physiology of gait selection in flying birds. Physiol. Biochem. Zool. 2000, 73, 736–750. [Google Scholar] [CrossRef] [PubMed]
- Cvrlje, T.; Breitsamter, C.; Weishäupl, C.; Laschka, B. Euler and Navier-Stokes simulations of two-stage hypersonic vehicle longitudinal motions. J. Spacecr. Rocket. 2002, 37, 242–251. [Google Scholar] [CrossRef]
- Jiang, L.; Moelyadi, M.A.; Breitsamter, C. Aerodynamic Investigations on the Unsteady Stage Separation of a TSTO Space Transport System; Forschungsbericht FLM-2003/34; Lehrstuhl für Fluidmechanik, Abteilung Aerodynamik, Technische Universität München: München, Germany, 2003. [Google Scholar]
- Cvrlje, T. Instationäre Aerodynamik des Separationsvorgangs zwischen Träger und Orbiter. Ph.D. Thesis, Technische Universität München, München, Germany, 2001. [Google Scholar]
- Herzog, K. Anatomie und Flugbiologie der Vögel; Gustav Fischer Verlag: Stuttgart, Germany, 1968. [Google Scholar]
- McCormick, B.W. Aerodynamics, Aeronautics, and Flight Mechanics; Wiley: Hoboken, NY, USA, 1979. [Google Scholar]
- Hepperle, M. Auslegung eines Propellers für Ultraleicht-Flugzeuge. Available online: http://www.mh-aerotools.de/company/paper_2/ulprop.htm (accessed on 7 June 2016).
- Deters, R.W.; Ananda, G.K.; Selig, M.S. Reynolds number effects on the performance of small-scale propellers. In Proceedings of the 32nd AIAA Applied Aerodynamics Conference, Atlanta, GA, USA, 16–20 June 2014; pp. 2014–2151.


© 2016 by the author; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sachs, G. Comparison of Power Requirements: Flapping vs. Fixed Wing Vehicles. Aerospace 2016, 3, 31. https://doi.org/10.3390/aerospace3040031
Sachs G. Comparison of Power Requirements: Flapping vs. Fixed Wing Vehicles. Aerospace. 2016; 3(4):31. https://doi.org/10.3390/aerospace3040031
Chicago/Turabian StyleSachs, Gottfried. 2016. "Comparison of Power Requirements: Flapping vs. Fixed Wing Vehicles" Aerospace 3, no. 4: 31. https://doi.org/10.3390/aerospace3040031
APA StyleSachs, G. (2016). Comparison of Power Requirements: Flapping vs. Fixed Wing Vehicles. Aerospace, 3(4), 31. https://doi.org/10.3390/aerospace3040031