Linearized Euler Equations for the Determination of Scattering Matrices for Orifice and Perforated Plate Configurations in the High Mach Number Regime
Abstract
:1. Introduction
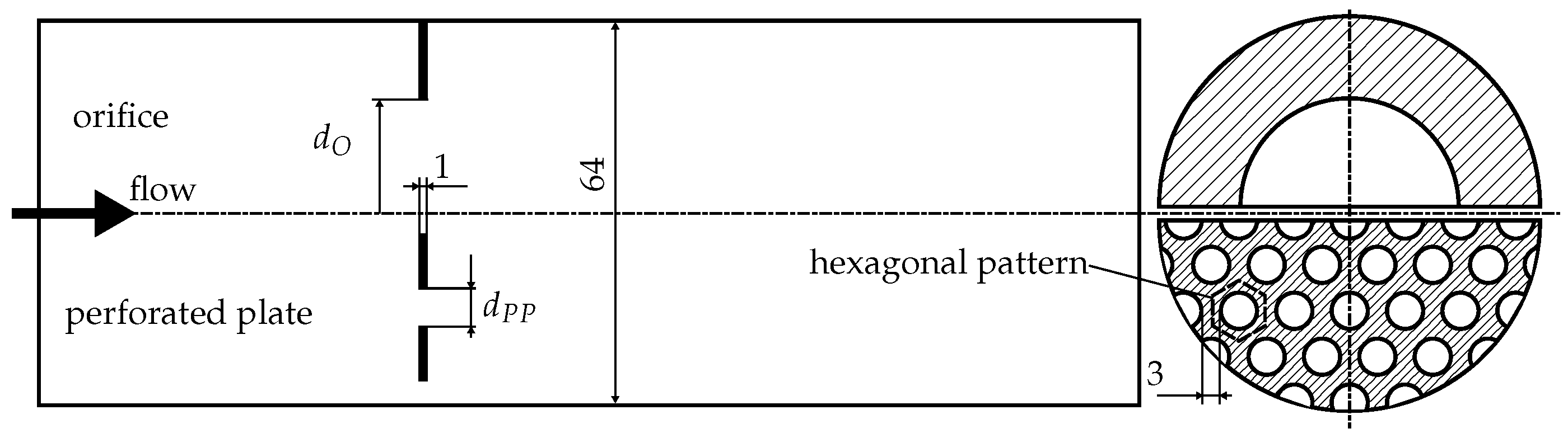
2. Test Case Description
3. Numerical Procedure
3.1. Mean Flow Computation
3.2. Stabilized Linearized Euler Equations in Frequency Space
3.3. Numerical Setup for Orifice and Perforated Plate Configurations
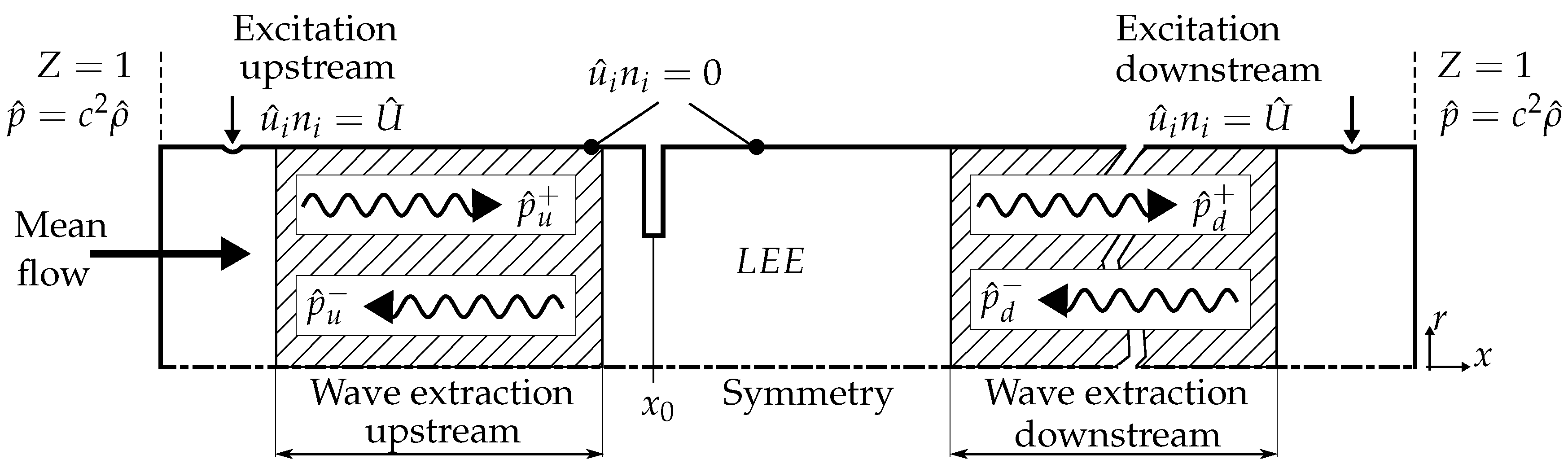
3.4. Wave Extraction and Evaluation of Scattering Matrix
4. Scattering Matrices for Orifice and Perforated Plates
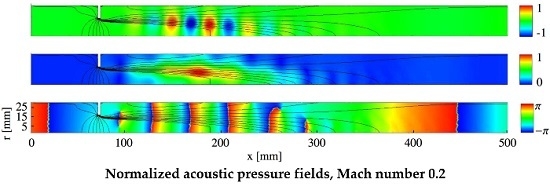
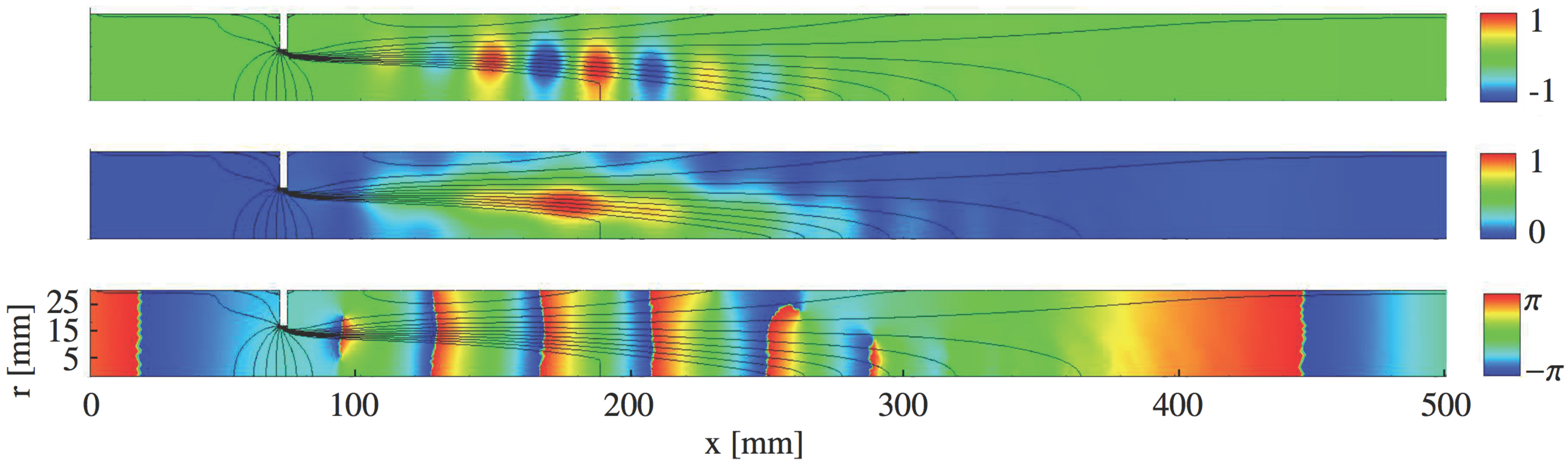
4.1. Acoustic Fields for Perforated Plate and Orifice
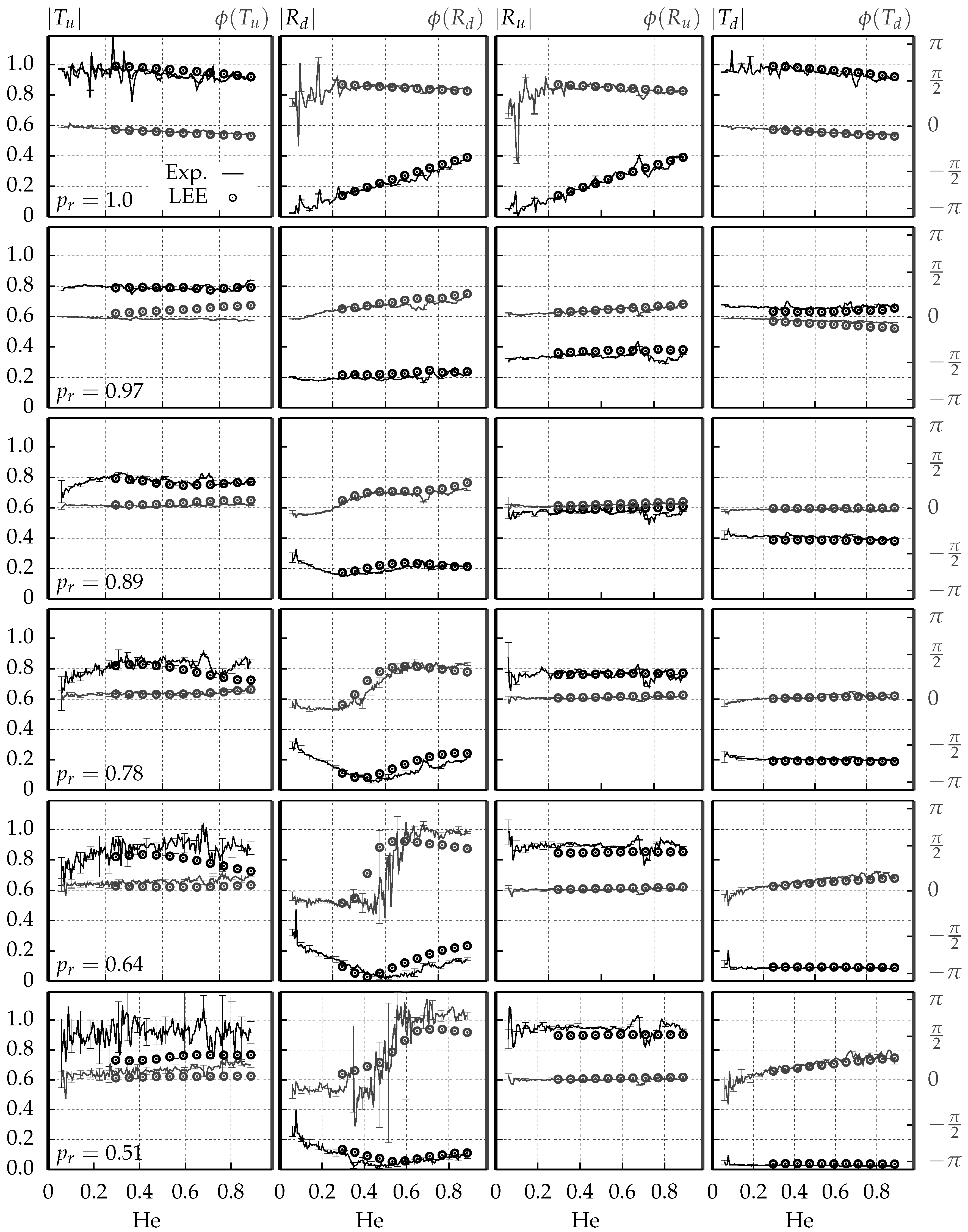
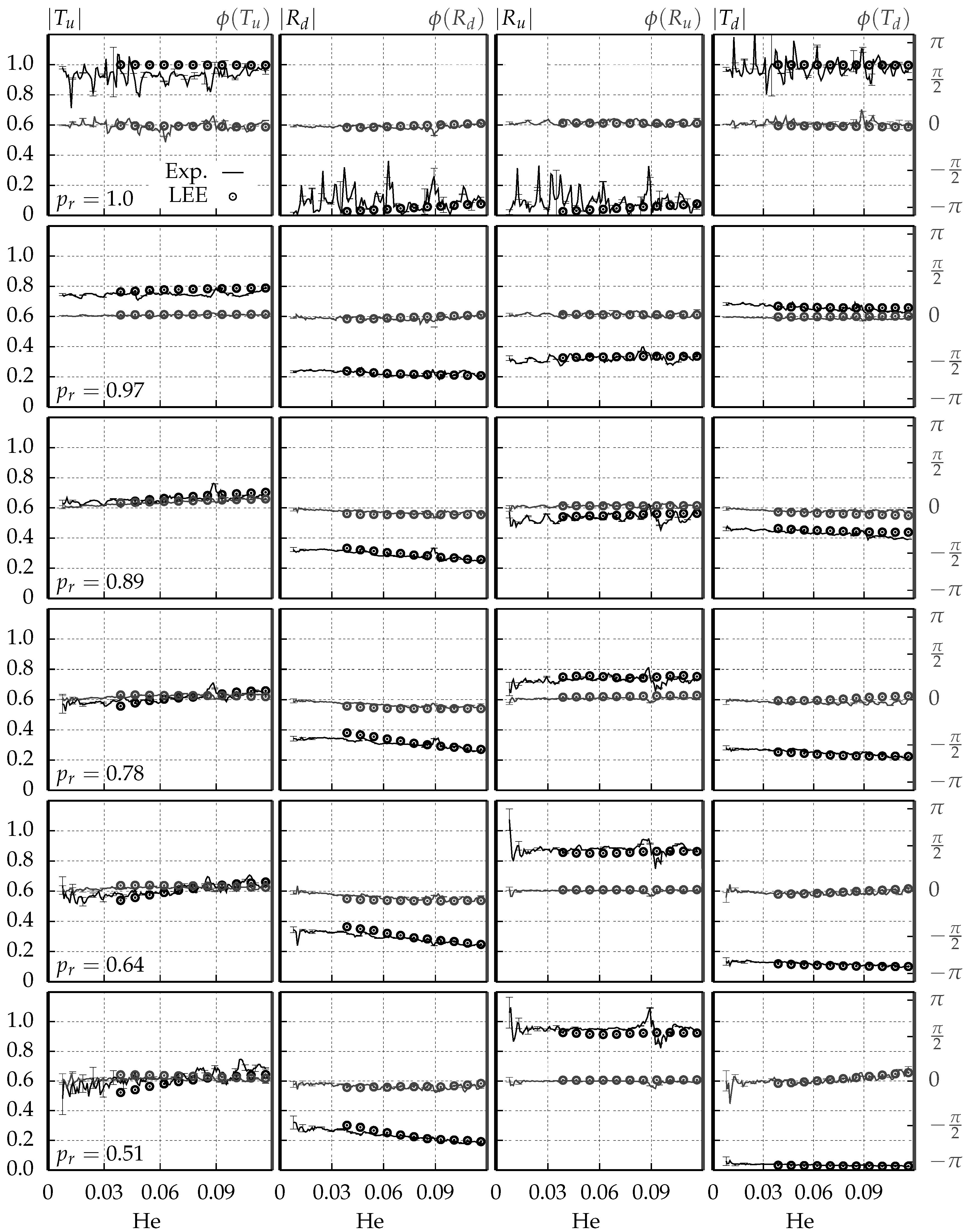
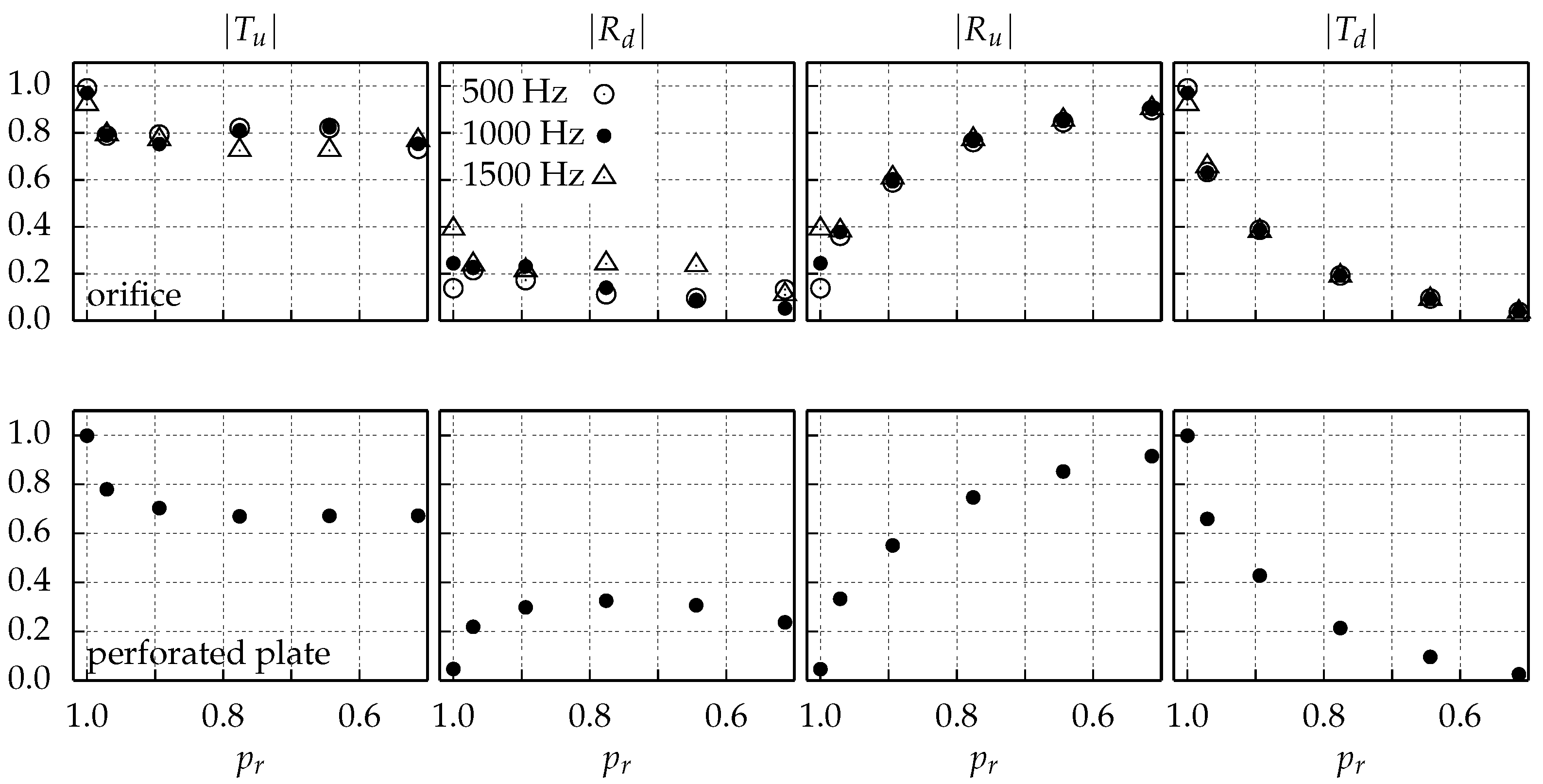
4.2. Scattering Matrices and Comparison to Experimental Data
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| LEE | Linearized Euler Equations |
| CFD | Computational Fluid Dynamic |
| CAA | Computational Aeroacoustic |
| CFL | Courant–Friedrichs–Lewy number |
References
- Kathan, R. Verlustmechanismen in Raketenbrennkammern. Ph.D. Thesis, Technische Universität München, München, Germany, 2013. [Google Scholar]
- Karal, F.C. The analogous acoustical impedance for discontinuities and constrictions of circular cross section. J. Acoust. Soc. Am. 1953, 25, 327–334. [Google Scholar] [CrossRef]
- Bechert, D. Sound absorption caused by vorticity shedding, demonstrated with a jet flow. J. Sound Vib. 1980, 70, 389–405. [Google Scholar] [CrossRef]
- Boij, S.; Nilsson, B. Reflection of sound at area expansions in a flow duct. J. Sound Vib. 2003, 260, 477–498. [Google Scholar] [CrossRef]
- Boij, S.; Nilsson, B. Scattering and absorption of sound at flow duct expansions. J. Sound Vib. 2006, 289, 577–594. [Google Scholar] [CrossRef]
- Boij, S. Flow effects on the acoustic end correction of a sudden in-duct area expansion. J. Acoust. Soc. Am. 2009, 126, 995–1004. [Google Scholar] [CrossRef] [PubMed]
- Salikuddin, M.; Syed, A.; Mungur, P. Acoustic characteristics of perforated sheets with throughflow in a high intensity noise environment. J. Sound Vib. 1994, 169, 145–177. [Google Scholar] [CrossRef]
- Dowling, A.; Hughes, I. Sound absorption by a screen with a regular array of slits. J. Sound Vib. 1992, 156, 387–405. [Google Scholar] [CrossRef]
- Dupère, I.; Dowling, A. The absorption of sound near abrupt axisymmetric area expansions. J. Sound Vib. 2001, 239, 709–730. [Google Scholar] [CrossRef]
- Howe, M. On the theory of unsteady high reynolds number flow through a circular aperture. Proc. R. Soc. A Math. Phys. Eng. Sci. 1979, 366, 1725. [Google Scholar] [CrossRef]
- Bellucci, V.; Flohr, P.; Pasc, C. Numerical and experimental study of acoustic damping generated by perforated screens. AIAA J. 2004, 42, 1543–1549. [Google Scholar] [CrossRef]
- Lee, S.; Ih, J.; Peat, K.S. A model of acoustic impedance of perforated plates with bias flow considering the interaction effect. J. Sound Vib. 2007, 303, 741–752. [Google Scholar] [CrossRef]
- Mendez, S.; Eldredge, J. Acoustic modeling of perforated plates with bias flow for Large-Eddy Simulations. J. Comput. Phys. 2009, 228, 4757–4772. [Google Scholar] [CrossRef]
- Ronneberger, D.; Physikalisches Institut der Universität Göttingen. Theoretische und Experimentelle Untersuchung der Schallausbreitung Durch Querschnittssprünge und Lochplatten in Strömungskanälen: Abschlußbericht; Contract Ro-369-11-12-14; Deutsche Forschungsgemeinschaft (DFG): Bonn, Germany, 1987. [Google Scholar]
- Föller, S.; Polifke, W. Identification of aero-acoustic scattering matrices from large eddy simulation. Application to a sudden area expansion of a duct. J. Sound Vib. 2012, 331, 3096–3113. [Google Scholar] [CrossRef]
- Alenius, E. Flow Duct Acoustics: An LES Approach. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2012. [Google Scholar]
- Lacombe, R.; Föller, S.; Jasor, G.; Polifke, W.; Auregan, Y.; Moussou, P. Identification of aero-acoustic scattering matrices from large eddy simulation: Application to whistling orifices in duct. J. Sound Vib. 2013, 332, 5059–5067. [Google Scholar] [CrossRef]
- Kierkegaard, A.; Boij, S.; Efraimsson, G. A frequency domain linearized Navier–Stokes equations approach to acoustic propagation in flow ducts with sharp edges. J. Acoust. Soc. Am. 2010, 127, 710–719. [Google Scholar] [CrossRef] [PubMed]
- Kierkegaard, A.; Efraimsson, G. Simulations of acoustic scattering in duct systems with flow. In Proceedings of the 20th International Congress on Acoustics (ICA 2010), Sydney, Australia, 23–27 August 2010.
- Kierkegaard, A. Frequency Domain Linearized Navier-Stokes Equations Methods for Low Mach Number Internal Aeroacoustics. Ph.D. Thesis, KTH Royal Institute of Technology, Stockholm, Sweden, 2011. [Google Scholar]
- Kierkegaard, A.; Allam, S.; Efraimsson, G.; Åbom, M. Simulations of whistling and the whistling potentiality of an in-duct orifice with linear aeroacoustics. J. Sound Vib. 2012, 331, 1084–1096. [Google Scholar] [CrossRef]
- Bechara, W.; Bailly, C.; Lafon, P.; Candel, S.M. Stochastic approach to noise modeling for free turbulent flows. AIAA J. 1994, 32, 455–463. [Google Scholar] [CrossRef]
- Mankbadi, R.R.; Hixon, R.; Shih, S.H.; Povinelli, L.A. Use of linearized Euler equations for supersonic jet noise prediction. AIAA J. 1998, 36, 140–147. [Google Scholar] [CrossRef]
- Tam, C.K.W.; Auriault, L. Jet mixing noise from fine-scale turbulence. AIAA J. 1999, 37, 145–153. [Google Scholar] [CrossRef]
- Ma, Z.K.; Smith, M.G.; Richards, S.K. Attenuation of slat trailing edge noise using acoustic liners. Int. J. Aeroacoust. 2006, 5, 311–333. [Google Scholar] [CrossRef]
- Özyörük, Y.; Tester, B.J. Application of frequency-domain linearized Euler solutions to the prediction of aft fan tones and comparison with experimental measurements on model scale turbofan exhaust nozzles. J. Sound Vib. 2011, 330, 3846–3858. [Google Scholar] [CrossRef]
- Zhang, X. Aircraft noise and its nearfield propagation computations. Acta Mech. Sin. 2012, 28, 960–977. [Google Scholar] [CrossRef]
- Nicoud, F.; Wieczorek, K. About the zero Mach number assumption in the calculation of thermoacoustic instabilities. Int. J. Spray Combust. Dyn. 2009, 1, 67–111. [Google Scholar] [CrossRef]
- Gikadi, J.; Schulze, M.; Schwing, J.; Föller, S.; Sattelmayer, T. Linearized Navier-Stokes and Euler equations for the determination of the acoustic scattering behaviour of an area expansion. In Proceedings of the 18th AIAA/CEAS Aeroacoustics Conference, Colorado Springs, CO, USA, 4–6 June 2012.
- Gikadi, J.; Föller, S.; Sattelmayer, T. Impact of turbulence on the prediction of linear aeroacoustic interactions: Acoustic response of a turbulent shear layer. J. Sound Vib. 2014, 333, 6548–6559. [Google Scholar] [CrossRef]
- Poinsot, T.; Lele, S. Boundary conditions for direct simulations of compressible viscous flows. J. Comput. Phys. 1992, 101, 104–129. [Google Scholar] [CrossRef]
- Jaensch, S.; Sovardi, C.; Polifke, W. On the robust, flexible and consistent implementation of time domain impedance boundary conditions for compressible flow simulations. J. Comput. Phys. 2016, 314, 145–159. [Google Scholar] [CrossRef]
- Wagner, M.; Schulze, M.; Sattelmayer, T. Experimental investigation of acoustic properties of orifices and perforated plates in the high mach number regime. In Proceedings of the International Congress on Sound and Vibration (ICSV), Bangkok, Thailand, 7–11 July 2013.
- Morgenweck, D.; Pieringer, J.; Sattelmayer, T. Numerical determination of nozzle admittances in rocket engines. In New Results in Numerical and Experimental Fluid Mechanics VII; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Köglmeier, S.; Kaess, R.; Morgenweck, D.; Tudisco, P.; Sattelmayer, T. Modelling of acoustic absorbers for liquid rocket combustion chambers. In Proceedings of the Space Propulsion Conference, Cologne, Germany, 19–22 May 2014.
- Denayer, H.; Tournadre, J.; Roeck, W.D.; Desmet, W.; Martinez-Lera, P. Combined numerical and experimental study of a slit resonator under grazing flow. In Proceedings of the 20th AIAA/CEAS Aeroacoustics Conference (AIAA Aviation), Atlanta, GA, USA, 16–20 June 2014.
- Ji, C.; Zhao, D. Numerical investigation of acoustically excited flow through an orifice using lattice boltzmann method. In Proceedings of the 9th AIAA/CEAS Aeroacoustics Conference, Hilton Head, SC, USA, 12–14 May 2003.
- Denayer, H.; Roeck, W.D.; Toulorge, T.; Desmet, W. Acoustic characterization of a helmholtz resonator under grazing flow conditions using a hybrid methodology. In Proceedings of the 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, 27–29 May 2013.
- Rao, P.; Morris, P. Use of finite element methods in frequency domain aeroacoustics. AIAA J. 2006, 44, 1643–1652. [Google Scholar] [CrossRef]
- Donea, J.; Huerta, A. Finite Element Methods for Flow Problems; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Kaess, R.; Huber, A.; Polifke, W. A time-domain impedance boundary condition for compressible turbulent flow. In Proceedings of the 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), Vancouver, BC, Canada, 5–7 May 2008.
- Åbom, M. A note on the experimental determination of acoustical two-port matrices. J. Sound Vib. 1992, 155, 185–188. [Google Scholar] [CrossRef]
- Åbom, M.; Bodén, H. Error analysis of two-microphone measurements in ducts with flow. J. Acoust. Soc. Am. 1988, 83, 2429–2438. [Google Scholar] [CrossRef]
- Bodén, H.; Åbom, M. Influence of errors on the two-microphone method for measuring acoustic properties in ducts. J. Acoust. Soc. Am. 1986, 79, 541–549. [Google Scholar] [CrossRef]
- Lung, T.; Doige, A. A time-averaging transient testing method for acoustic properties of piping systems and mufflers with flow. J. Acoust. Soc. Am. 1983, 73, 867. [Google Scholar] [CrossRef]
- Munjal, M.L.; Doige, A. Theory of a two source-location method for direct experimental evaluation of the four-pole parameters of an aeroacoustic element. J. Sound Vib. 1990, 141, 323–333. [Google Scholar] [CrossRef]
- Paschereit, C.O.; Schuermans, B.; Polifke, W.; Mattson, O. Measurement of Transfer Matrices and Source Terms of Premixed Flames. J. Eng. Gas Turbines Power 2002, 124, 239–247. [Google Scholar] [CrossRef]
- Seybert, A.; Ross, D. Experimental determination of acoustic properties using a two-microphone random-excitation technique. J. Acoust. Soc. Am. 1977, 61, 1362–1370. [Google Scholar] [CrossRef]
- Marble, F.E.; Candel, S.M. Acoustic disturbance from gas non-uniformities convected through a nozzle. J. Sound Vib. 1977, 55, 225–243. [Google Scholar] [CrossRef]
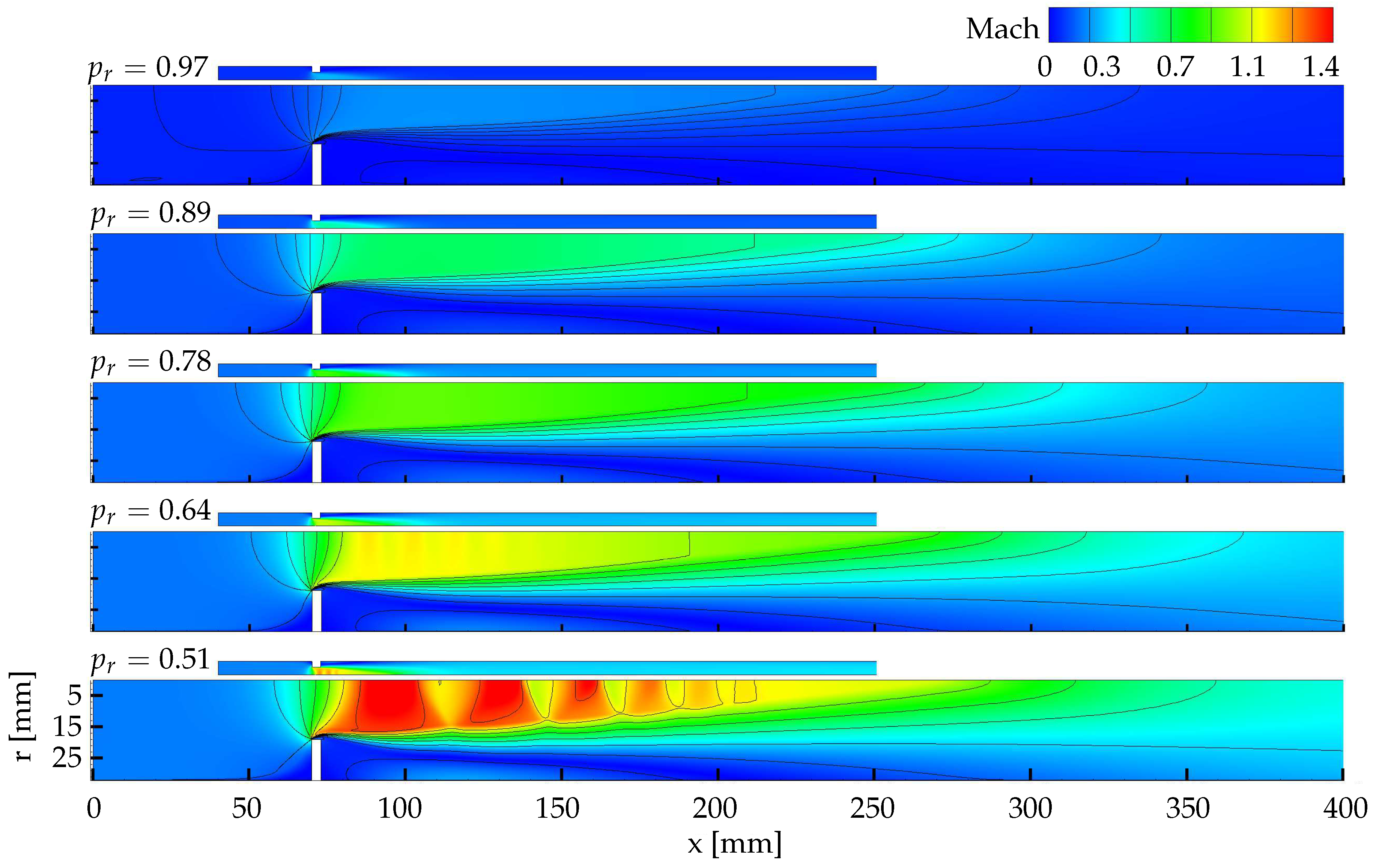
| Static Pressure Ratio | Static Pressure Downstream (Bar) | Mass Flow (g/s) | Ma |
|---|---|---|---|
| 1.0 | 0.937 | 0.0 | 0 |
| 0.97 | 0.937 | 83.8 | 0.2 |
| 0.89 | 0.937 | 160.8 | 0.4 |
| 0.78 | 0.937 | 234.7 | 0.6 |
| 0.64 | 0.938 | 330.5 | 0.8 |
| 0.51 | 0.944 | 455.4 | 1.0 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Schulze, M.; Wagner, M.; Sattelmayer, T. Linearized Euler Equations for the Determination of Scattering Matrices for Orifice and Perforated Plate Configurations in the High Mach Number Regime. Aerospace 2016, 3, 33. https://doi.org/10.3390/aerospace3040033
Schulze M, Wagner M, Sattelmayer T. Linearized Euler Equations for the Determination of Scattering Matrices for Orifice and Perforated Plate Configurations in the High Mach Number Regime. Aerospace. 2016; 3(4):33. https://doi.org/10.3390/aerospace3040033
Chicago/Turabian StyleSchulze, Moritz, Michael Wagner, and Thomas Sattelmayer. 2016. "Linearized Euler Equations for the Determination of Scattering Matrices for Orifice and Perforated Plate Configurations in the High Mach Number Regime" Aerospace 3, no. 4: 33. https://doi.org/10.3390/aerospace3040033
APA StyleSchulze, M., Wagner, M., & Sattelmayer, T. (2016). Linearized Euler Equations for the Determination of Scattering Matrices for Orifice and Perforated Plate Configurations in the High Mach Number Regime. Aerospace, 3(4), 33. https://doi.org/10.3390/aerospace3040033