Abstract
The present study aimed at studying the transition of annular lift fan aircraft through computational fluid dynamics (CFD) simulations. The oscillations of lift and drag, the optimization for the figure of merit, and the characteristics of drag, yawing, rolling and pitching moments in transition are studied. The results show that a two-stage upper and lower fan lift system can generate oscillations of lift and drag in transition, while a single-stage inner and outer fan lift system can eliminate the oscillations. The characteristics of momentum drag of the single-stage fans in transition are similar to that of the two-stage fans, but with the peak of drag lowered from 0.63 to 0.4 of the aircraft weight. The strategy to start transition from a negative angle of attack −21° further reduces the peak of drag to 0.29 of the weight. The strategy also reduces the peak of pitching torque, which needs upward extra thrusts of 0.39 of the weight to eliminate. The peak of rolling moment in transition needs differential upward thrusts of 0.04 of the weight to eliminate. The requirements for extra thrusts in transition lead to a total thrust–weight ratio of 0.7, which makes the aircraft more efficient for high speed cruise flight (higher than 0.7 Ma).
1. Introduction
A helicopter can fly, hover, and land almost anywhere, but its performance is limited with a theoretical top speed of 200 kn (370 km/h), above which it suffers from dissymmetry of lift. Rotors work well in a hover, but in forward flight, air hits the rotor blades at dramatically different speeds. Some designs have successfully created hovering and high speed aircraft, including the Bell Boeing V-22 Osprey tiltrotor that can fly at 275 kn (509 km/h) and the Sikorsky X2 compound helicopter that flew at 260 kn (480 km/h), but both made significant aerodynamic comprises to hovering efficiency or range [1]. The Osprey does not hover very efficiently because the propellers have high disk loading.
If the rotors only work in hover but are closed in ducts during high speed cruise flight, the limit to the top speed of rotorcraft will be eliminated. To achieve the high lift efficiency and high cruise speed for VTOL (vertical takeoff and landing) aircraft, we proposed an annular lift fan aircraft in a previous study [2] (Figure 1). CFD (Computational fluid dynamics) simulations indicated that the annular lift fan craft had the same or higher lift efficiency as a helicopter and could fly faster than a helicopter or tiltrotor based on aerodynamic drag predictions [2]. In fact, as the annular duct is closed in forward flight, there is no theoretical limit to the top speed.

Figure 1.
Annular lift fan aircraft.
The concept of the annular lift fan originated from lift fan, including the fan-in-wing and fan-in-fuselage configurations, which were first implemented in the jet powered experimental aircraft Ryan GE XV-5 in the 1960s [3,4]. The fan-in-fuselage was recently incorporated in the F-35B II Lightning Joint Strike Fighter [5]. The problem with the current lift fan system is that the size is so constrained by the sizes of fuselage or wing that the disk loading has to be high, thus leading to low lift efficiency (power loading). To increase the fan area and decrease the disk loading, the best way is to move the fuselage to the center and place the lift fan and wing around the central fuselage. In this way, the fan area and fuselage size are greatly increased and the lift efficiency improved. During cruise flight, the annular duct is closed and becomes part of wing to provide aerodynamic lift [2].
For VTOL aircraft, hovering like a helicopter or cruising like a fixed wing craft are relatively simple. The transitions, especially from vertical takeoff to forward aerodynamic flight, are most complex, involving phenomena of both hover and forward flight and complicated interactions between the induced flow and freestream flow. Successful transition is vital for VTOL designs. Failed transitions contributed a lot to the “V/STOL (vertical/short takeoff and landing) Wheel of Misfortune”, a diagram that depicts the dozens of mostly failed concepts and can be easily found on the Internet. Even for successful transitions, an automatic flight control system is also needed to reduce the pilot’s workload [6].
In our previous study of the annular lift fan aircraft, the lift and momentum drag in transition were investigated to find the best transition strategy [2]. It was observed that the lift and drag oscillated during the transition (Figure 2), which may cause harmful vibration of the aircraft. The oscillations only occurred in transition mode but never in hover mode, but the reasons of the oscillations and the real effects on the aircraft were unknown. In the present work, the transition was studied in detail and in depth to eliminate the oscillations. Once the oscillations were improved, the configuration of the annular lift fan aircraft was optimized for hovering efficiency [7], and then the pitching, rolling, and yawing moments as well as the momentum drag during transition were further investigated with the optimized model.

Figure 2.
Lift and drag coefficients (CL and CD) in transition, at angle of attack −21°, freestream speed 30 m/s, and rotational speeds of fans 135 and 143 rpm.
2. Geometry Definition
The typical configuration of annular lift fan aircraft is shown in Figure 1. The lift fan set contains two-stage fans, including an upper fan and a lower fan mounted in the annular duct located between the central fuselage and the outer wing [2] (Figure 1). The two fans counter rotate at the same or different speeds to eliminate torque and are tip-driven during VTOL by the two turbofan engines incorporated in the outer wing.
For this two-stage fan system, however, it is impossible to eliminate the oscillations in transition, because the oscillations are caused by the complex interactions of the upper and lower fans (see below). Therefore, the configuration was improved to replace the two-stage fans with single-stage fans, which include an inner fan and an outer fan, mechanically coupled by gears inside the ring baffle located between the two fans (Figure 3). The gears make the two fans counter rotate at the same speed to eliminate torque. Two jet engines incorporated in the outer wing (Figure 1, not shown in Figure 3) tip-drive the outer fan. One engine can also drive the fan for engine out safety. The radii of the two fans were determined for the fans to eliminate torque in hover mode. The length of inner fan blades is 1.35 m (r = 6.35–5 m); the length of outer fan blades is 0.65 m (r = 7.1–6.45 m).

Figure 3.
Annular lift fan aircraft with single-stage fans (engines not shown).
The geometry was optimized for hovering efficiency [7] and transition. The optimized aircraft has the figure of merit 0.733 with power loading 4.50 kg/kw. The optimization also reduced the diameter of aircraft from 20 to 18 m to reduce the peak of pitching moment in transition because the width of outer wing contributed a lot to the nose up pitching moment.
The central fuselage area was 78.5 m2, much larger than that of a conventional helicopter. The fan area of 75.3 m2 was also much larger than a conventional ducted fan. The optimized fans had 36 blades respectively with pitch angle 27° and chord length 0.5 m. A generic airfoil with a flat surface and a cambered surface was used for the fan blades (Figure 4b). The maximum thickness was 4% of the chord length at about 20% from the leading edge. There were no clearance gaps between the fan tip and the duct wall because the fans were tip-driven by the jet engines in the outer wing. The weight of the aircraft was 10.433 tons, the same as the maximum takeoff weight of the Apache helicopter.

Figure 4.
(a) Surface mesh on single-stage fan craft; and (b) cross section mesh inside the annular duct to show the blade geometry. Different colors mean different blocks.
3. Computational Mesh
The unstructured mesh technique was used in the study. CFD methods based on unstructured grids have an advantage of easily handling complex geometries and can improve the solution accuracy by refining cells locally as required [8]. The unstructured meshes in this study were created using ANSYS Meshing 17.0 (ANSYS, Inc., Canonsburg, PA, USA).
The mesh for the single-stage fans craft was created in a 20 R × 15 R × 15 R flow field (Figure 4) where R is the radius of the aircraft, R = 9 m unit. A dimension sensitivity study was carried out to make sure that the dimension was big enough so that the simulation results would not change with the computational fluid domain (data not shown). The flow field was divided into three volumes in which the two small blocks were dedicated to the fans.
Mesh sensitivity study was carried out with three cases considered (Table 1). The result showed that the difference between medium and fine grid was small; thus, all simulations were performed with medium grid of 4.2 M elements.

Table 1.
Grid sensitivity analysis in transition.
4. Boundary Condition and Simulation Setup
CFD simulations were performed using ANSYS Fluent 17.0 (ANSYS, Inc., Canonsburg, PA, USA), which has been extensively used in various studies [9,10,11,12,13]. Steady and unsteady Reynolds-averaged Navier–Stokes (RANS) equations for the mean flow quantities were solved.
A pressure-based solver type with absolute velocity formulation, the Green-Gauss node based gradient option were used in the analyses. The shear stress transport (SST) k–ω turbulence model developed by Menter [14,15] was selected. The semi implicit method for pressure linked equations (SIMPLE) scheme was used to resolve the pressure-velocity coupling with the second order discretization for the pressure equation, the third order monotonic upstream-centered scheme for conservation laws (MUSCL) for the momentum, turbulent kinetic energy and turbulent dissipation rate [10]. Unsteady calculations (URANS) were performed. The areas surrounding the fans were designated as sliding mesh. Sliding interfaces separated the rotating domain from the stationary domain. The initial data for the unsteady run were obtained from steady calculations. Velocity-inlet and pressure-outlet conditions were imposed over the front and rear surfaces of the computational domain to simulate a freestream flow. Pressure-inlet and pressure-outlet boundary conditions were applied over the top and bottom surfaces of the computational domain.
5. Numerical Model Validation
The validation of transition mode was performed using a three-dimensional fan-in-wing configuration with a fan rotating in the plane of a wing [3]. One single circular fan was submerged at the rear part of the wing as in the case of the annular lift fan (Figure 5a). The clearance gap between the rotor blade tip and the shroud housing was 0.8% of the fan’s diameter. Ten chords were used in each direction from the wing to create the computational domain. The mesh contained 5.8 M tetrahedral cells without boundary layers. The settings for the transition study were used. With 30 m/s freestream velocity, corresponding to a Reynolds number Re = 1.5 × 106, and fan rotational speed of 21,000 rpm, the CFD predictions of CL and Cm showed a good agreement with the experimental data (Figure 5b,c), which came from Thouault [3], while CD was a little under-predicted.

Figure 5.
(a) Streamlines in the central plane of the fan-in-wing configuration; (b) lift coefficient; (c) drag coefficients; and (d) pitching moment, as a function of the angle of attack. The experimental data come from Thouault [3].
6. Results
6.1. Oscillations and Elimination
The lift and drag of the two-stage fan aircraft were observed to oscillate in transition as shown in Figure 2. The oscillation occurred at any rotational speeds and angles of attack for a variety of free stream speeds, and the amplitude of oscillations increases with the free stream speed. The amplitude is usually about 10%–20% of the average value. The possible reasons of the oscillations were investigated. The grids were first carefully examined to exclude the artifacts caused by imperfect meshes. Then the rotational speeds, the size of the aircraft, the number of blades, and the pitch angle were changed and stator was used to try to eliminate the oscillations. It was found that the frequencies of oscillations only related with the rotational speeds of fans and the number of blades. For both fans with 36 blades, the frequency could be calculated: f = (n1 + n2) × 36/60, where n is the rotational speeds of the fans, rpm. Obviously the oscillations came from the strong interactions between the two-stage fans. When one stage of the fan was removed and only the upper fan remained, the oscillations disappeared. The oscillations did not occur in hover mode but only in transition mode probably because of the dissymmetric airflow acting on the upper and lower fans. In hover mode, the airflow is symmetric. In transition mode, there is an incoming backward free stream flow. Air hits the upper fan blades at different speeds as the blades advance and retreat at right and left side of the vehicle. This causes a distorted upstream flow for the lower fan, resulting in the lower fan to generate unbalanced forces. As the upper fan blades rotate and cut the incoming free stream flow, the upstream flow of the lower fan becomes periodically interrupted, leading to the oscillations of total lift and drag. Because the two fans are positioned closely in an enclosed duct, the interactions between the fans are strong, resulting in the big amplitude of oscillation.
The two-stage fans can reduce the swirl of wake in hover mode, thus may have higher figure of merit, however it seems impossible to eliminate the oscillations and associated harmful vibration in transition with this configuration. This is different from coaxial helicopters in forward flight because the airflow between the fans in the annular duct is enclosed.
Single-stage ducted fans were observed not to cause serious oscillations during transition. Although single-stage fans might have lower hovering efficiency due to the swirl loss, they save the space in the duct to realize larger radius of inlet lip and longer diffuser exit, which increase the figure of merit [7]. In fact, the optimized single-stage fans had the same figure of merit 0.733 as the two-stage fans [7]. Single-stage fans also save duct space for stator and struts that connect the central fuselage and the outer wing. Single-stage fans also halve the weight of the two-stage fans.
One fan may produce torque, so two coaxial single-stage fans coupled by gears to counter rotate at the same speed were used in the study. The lengths of inner and outer fans were selected to eliminate the torque (Figure 3).
As shown in Figure 6, the oscillations were eliminated. There were still irregular fluctuations, but the amplitudes were much smaller. The reason for the fluctuations is not known, but they are probably due to the strong unsteadiness on the fan blade loading generated by a large inflow distortion.

Figure 6.
Lift and drag coefficients of single-stage fans aircraft in transition, at freestream speed 30 m/s, angle of attack −21°, and rotational speed of fans 136 rpm.
It can be seen in Figure 6 that, although the total lifts was the same (as the aircraft weight), the lift coefficients of single-stage and two-stage fan aircraft were different at the same freestream speed. This is because the aircraft areas were different. The diameter of the two-stage fan aircraft was reduced from 20 to 18 m in the single-stage aircraft. In other words, the width of outer wing was reduced from 3 to 2 m, in order to reduce the drag and pitching moment in transition. Thus, the two-stage fan aircraft’s area of 314 m2 was larger than 254 m2 of the single-stage one, which made the lift coefficients different. The effect of smaller outer wing was significant, with the drag coefficient reduced 48%.
6.2. Transition Characteristics from Takeoff to Forward Flight
6.2.1. Momentum Drag
The momentum drag of the single-stage fans in transition mode showed similar characteristics to the two-stage fans in the previous study [2], but the peak of drag lowered from 0.63 to 0.4 of aircraft weight (Figure 7, Spot A). The strategy to start transition flight from a negative angle of attack (AOA) −21° with a forward force produced by the lift fan system (negative net drag) to increase the drag along the arrows B to C to D further lowered the peak of drag to about 0.29, as shown in Figure 7 (Spot C). When the forward speed reaches a certain level (30 m/s, Spot C), the aircraft changes its attitude to a positive angle of attack 15° and slows down the rotational speeds of fans to reduce the lift. When the speed of aircraft reaches 40 m/s, the minimum takeoff speed for aerodynamic flight (Spot D), it then closes the duct to start cruise flight. The rotational speeds of fans were adjusted to maintain the lift equal to the weight during transition (Table 2). The rotational speed decreased with the increase of forward speed because the aerodynamic lift increased with the speed, even for the negative angle of attack −21°. For the larger outer wing of the two-stage fan aircraft, the rotational speed increased with the forward speed at −21° because the aerodynamic lift became more negative with the speed.

Figure 7.
Computed time-averaged drag coefficient to lift coefficient ratio at different angles of attack in transition mode. The lift and drag coefficients were calculated on the total lift or drag, including the aerodynamic lift or drag and those generated by the lift fans. The arrows indicate the recommended strategy to increase forward speed and drag in transition.

Table 2.
The rotational speeds of the annular fans in transition.
6.2.2. Pitching Moment
Because of the interactions of induced flow and incoming freestream flow, the yawing, rolling, and pitching moments also changed in transition. The attitude controls should be performed through changing the directions of the jet thrusts from the two turbofan engines, respectively, to eliminate the yawing, rolling and pitching torques.
The yawing torque was weak in transition. Once the torque was eliminated by the counter rotating lift fans in hover mode, it remained small in transition, because the two fans were separated and the effects of the inflow on the fans could be offset each other. This is an advantage of single-stage fans over two-stage fans, for which the interactions of upper and lower fans may generate net yawing torque in transition.
The pitching moments at the geometrical center of the aircraft during transition are shown in Figure 8. The highest peak of pitching moment in transition is about 0.25 at Spot A. It can be seen that the strategy to start forward flight from a negative angle of attack −21° also reduced the peak of pitching moment to about 0.155 (Spot C). The pitching moment was primarily caused by the low pressure on the top surface and high pressure on the bottom surface of the leading part of the outer wing (Figure 9a), so narrower outer wing could reduce the pitching moment. The induced flow by the annular fans intensified the suction effect on the leading edge (Figure 9b). Furthermore, the incoming flow generated an apparent asymmetric pressure attribution about the lateral axis on the top and bottom surfaces of the aircraft (Figure 9c,d).

Figure 8.
Computed time-averaged pitching moment coefficient (Cmp) to lift coefficient ratio at different angles of attack in transition mode. The arrows show how the pitching moment increases by the recommended strategy.

Figure 9.
(a) Static pressure in the central plane of the aircraft; (b) surface streamlines in the central plane; (c) pressure on the top surfaces; and (d) pressure on the bottom surfaces; the flight direction is toward left. The freestream speed is 30 m/s, angle of attack 0°. The pressure distributions are symmetrical about the longitudinal axis, but asymmetrical about the lateral axis.
To start forward flight from angle of attack −21° (Figure 8, Spot B), the peak of pitching moment was 0.155 at Spot C (Figure 8). The radius of the aircraft is 9 m. If the distance from the jet nozzles to the central plane is 7 m, the pitching torque will need upward thrusts of 0.39 of the aircraft weight to eliminate (Figure 10). The upward thrusts also provide part of lift, thus the rotational speeds of the fans can be slowed down to reduce the fan lift and pitching moment. With 0.29 forward thrust to overcome momentum drag and 0.39 downward thrust to eliminate the pitching torque, total extra thrust of 0.5 of the aircraft weight will be needed (Figure 10).

Figure 10.
Thrust vectoring for attitude control and to eliminate the pitching torque.
With extra thrusts of 0.5 to overcome the drag and eliminate the pitching torque, and thrust of 0.2 to drive the lift fan, total thrusts of 0.7 of the aircraft weight are required for the aircraft to complete the transition, which is thrust–weight ratio of 0.7. According to the aerodynamic drag and cruise speed prediction, with the thrust–weight ratio of 0.7, the aircraft can reach maximum speed of 0.7 Ma [2]. The performances are close to the BAE Systems Hawk 128 trainer jet aircraft (thrust–weight ratio 0.65, maximum speed 0.84 Ma), but the Hawk 128 is much smaller, with wingspan of only 9.94 m. With the same thrust–weight ratio, increasing the weight or decreasing the size of aircraft increases the maximum cruise speed, at the expense of higher disc loading thus lower power loading. This feature may be useful in practice, after all, hovering and VTOL only takes a short time in a flight envelope.
Therefore, due to the requirement of thrust–weight ratio 0.7 in transition, the annular lift fan aircraft is more efficient for high speed cruise flight rather than low speed flight like a helicopter. In another word, this kind of aircraft cannot completely replace helicopters, especially in the low speed domain of 20~40 m/s, due to the high momentum drag and pitching moment.
6.2.3. Rolling Moment
The rolling moment in transition was primarily caused by the break of symmetry of pressure distribution about the longitudinal axis on the outer wing, ring baffle, and fuselage. The dissymmetry of pressure on the counter rotating inner and outer fans could roughly offset each other.
The reasons why the symmetry was broken are not clear, but the rolling moment is not as serious as the pitching moment in transition. According to Figure 11, the peak of rolling moment at Spot C is 0.017. If the distance between the jet engines is 15 m, the rolling torque will need differential upward thrusts of 0.04 of the aircraft weight to eliminate. For the aircraft with extra thrusts of 0.5 of the weight, this is not a problem.
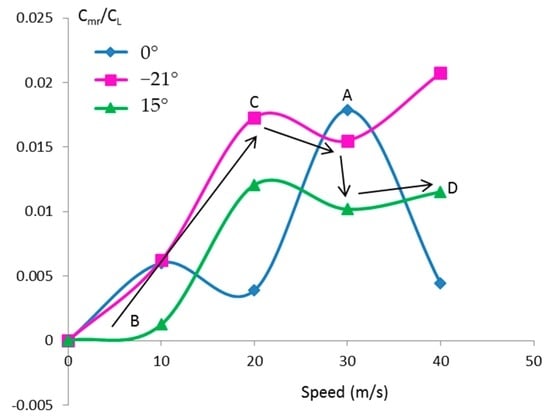
Figure 11.
Computed time-averaged rolling moment coefficient (Cmr) to lift coefficient ratio at different angles of attack in transition mode. The rolling moment increases along the arrows by the recommended strategy.
6.2.4. Transition from Cruise Flight to Landing
The transition from forward flight to landing is much simpler than from takeoff to forward flight because the lift does not have to be maintained equal or higher than the weight when the aircraft is descending, thus the lift fans will not be opened and work until the forward speed has slowed down to as low as 10 m/s. At this speed and angle of attack 0° or 15°, the pitching and rolling moments have become low enough not to cause any problems (see Figure 8 and Figure 11). The momentum drag helps deceleration in landing thus is not a problem.
7. Conclusions
The aerodynamic characteristics of the annular lift fan aircraft in transition were studied in detail using the ANSYS FLUENT 17.0 software. The configuration of the two-stage annular lift fans with upper and lower fan found it difficult to eliminate the oscillations of lift and drag in transition, due to the strong interactions of fans. Thus, single-stage fans with inner fan and outer fan coupled to counter rotate at the same speeds and optimized for the figure of merit were used to study transition characteristics.
The CFD simulation results showed the severe oscillations of lift and drag were eliminated by single-stage fans in transition, but small fluctuations still existed. The momentum drag characteristic in transition mode was similar to that of the two-stage fans, but with the peak of drag reduced from 0.63 to 0.4 of the aircraft weight. Starting transition from an angle of attack −21° further reduced the peak to 0.29.
The nose up pitching moment caused by the suction effect on the leading edge of the outer wing was a big problem in transition. Even starting transition from −21°, the peak of pitching torque still required extra upward thrusts of 0.39 of the aircraft weight to eliminate. These requirements for the extra thrusts in transition led to the thrust–weight ratio 0.7, which enabled the aircraft more efficient for high speed cruise flight (higher than 0.7 Ma). To further increase the cruise speed, the aircraft can also be made smaller or heavier, at the cost of lower lift efficiency in hover mode.
The rolling moment in transition was caused by the dissymmetric airflow over the left and right side surfaces on the outer wing, ring baffle and fuselage. The peak of rolling torque needed differential upward thrusts of 0.04 of the aircraft weight to eliminate, thus was not a serious problem for the aircraft with total extra thrusts of 0.5 of the weight.
The yawing torque was very weak and remained small in transition, thus could be neglected.
The transition from forward flight to landing was much simpler than from takeoff to forward flight because the lift did not need to be maintained in descending and the transition speed to start the annular lift fan system to land could be very low when the pitching and rolling moments had already become very small.
For VTOL aircraft, transition is the most complicated process as speeds, attitude, and torques need to be controlled. An automatic transition flight control system to assist the pilot is necessary.
Author Contributions
Yun Jiang proposed the ideas, performed the CFD simulation and wrote the manuscript. Bo Zhang analyzed the data and provided software support.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| T | thrust | N |
| ρ | density of air | kg·m−3 |
| A | area of lift fan | m2 |
| σ | duct diffusion ratio | |
| η | efficiency | |
| P | power | kw |
| F | drag | N |
| v | forward speed | m·s−1 |
| n | rotational speed | rpm |
References
- VTOL X-Plane. Available online: https://en.wikipedia.org/wiki/VTOL_X-Plane (accessed on 20 December 2015).
- Jiang, Y.; Zhang, B.; Huang, T. CFD study of an annular-ducted fan lift system for VTOL aircraft. Aerospace 2015, 2, 555–580. [Google Scholar] [CrossRef]
- Thouault, N.; Breitsamter, C.; Adams, N.A. Numerical and experimental analysis of a generic Fan-in-wing configuration. J. Aircr. 2009, 46, 656–666. [Google Scholar] [CrossRef]
- Asmus, F.J. Design and development of the tip turbine lift fan. Ann. N. Y. Acad. Sci. 1963, 107, 147–176. [Google Scholar] [CrossRef]
- Bevilaqua, P.M. Genesis of the F-35 joint strike fighter. J. Aircr. 2009, 46, 1825–1836. [Google Scholar] [CrossRef]
- Muraoka, K.; Odaka, N.; Kubo, D.; Sato, M. Transition flight of quad tilt wing VTOL UAV. In Proceedings of the 28th International Congress of the Aeronautical Sciences, Brisbane, Australia, 23–28 September 2012.
- Jiang, Y.; Zhang, B. Numerical optimization of hovering efficiency of an annular lift fan aircraft. Aerospace 2016. under review. [Google Scholar]
- Xu, H.Y.; Ye, Z.Y.; Shi, A.M. Numerical study of propeller slipstream based on unstructured overset grids. J. Aircr. 2012, 49, 384–389. [Google Scholar] [CrossRef]
- Blocken, B.; Defraeye, T.; Koninckx, E.; Carmekiet, J.; Hespel, P. CFD simulations of the aerodynamic drag of two drafting cyclists. Comput. Fluids 2013, 71, 435–445. [Google Scholar] [CrossRef]
- Simioni, N.; Ponza, R.; Benini, E. Numerical assessment of pneumatic devices on the wing/fuselage junction of a tiltrotor. J. Aircr. 2013, 50, 752–763. [Google Scholar] [CrossRef]
- Malipeddi, A.K.; Mahmoudnejad, N.; Hoffmann, K.A. Numerical analysis of effects of leading-edge protuberances on aircraft wing performance. J. Aircr. 2012, 49, 1336–1344. [Google Scholar] [CrossRef]
- Qu, Q.; Lu, Z.; Liu, P.; Agarwal, R.K. Numerical study of aerodynamics of a Wing-in-Ground-Effect craft. J. Aircr. 2014, 51, 913–924. [Google Scholar] [CrossRef]
- Al-Garni, A.Z.; Saeed, F.; Al-Garni, A.M. Experimental and numerical investigation of 65 degree Delta and 65/40 degree double-delta wings. J. Aircr. 2008, 45, 71–75. [Google Scholar] [CrossRef]
- Menter, F.R. Zonal two equation k–ω turbulence models for aerodynamic flows. In Proceedings of the 24th AIAA Fluid Dynamics Conference, Orlando, FL, USA, 6–9 July 1993.
- Menter, F.R. Two-equation eddy viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).