Aerodynamic Modeling of NREL 5-MW Wind Turbine for Nonlinear Control System Design: A Case Study Based on Real-Time Nonlinear Receding Horizon Control
Abstract
:1. Introduction
2. Modeling
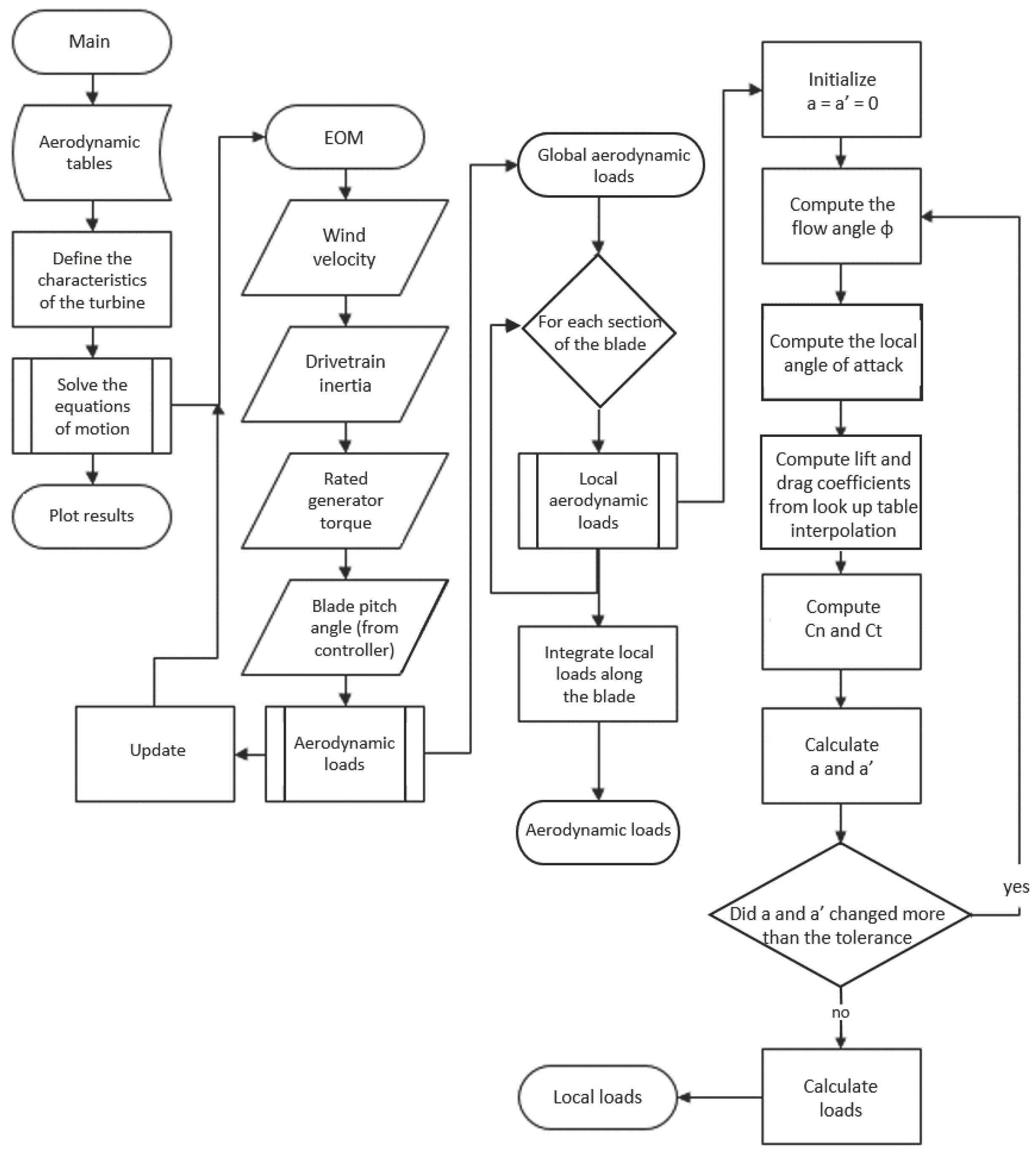
2.1. Aerodynamic Modeling
2.1.1. Local Loads Definition
2.1.2. Global Loads Definition
2.2. Equations of Motion
2.2.1. Onshore Wind Turbines
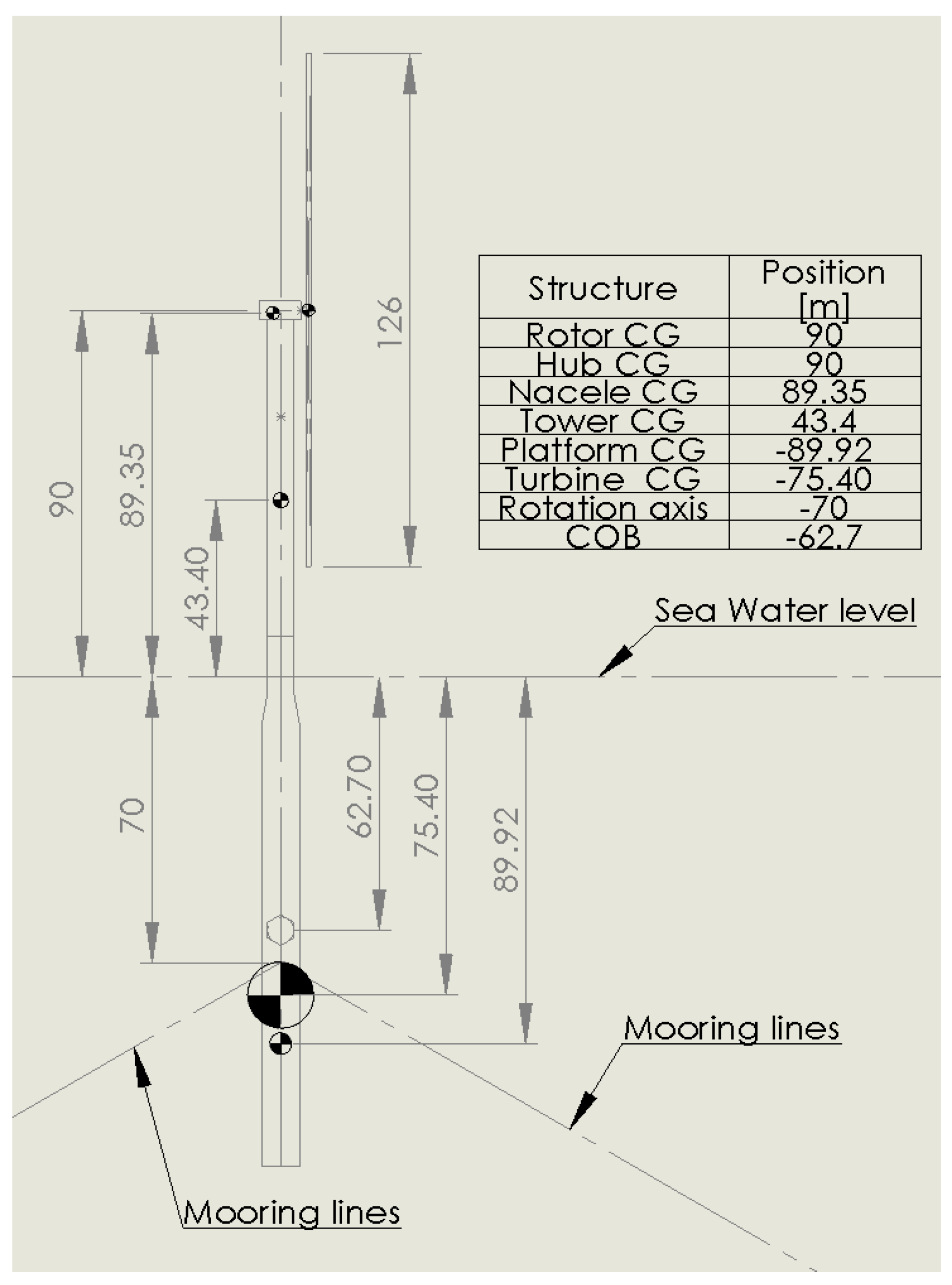
2.2.2. Offshore Wind Turbines
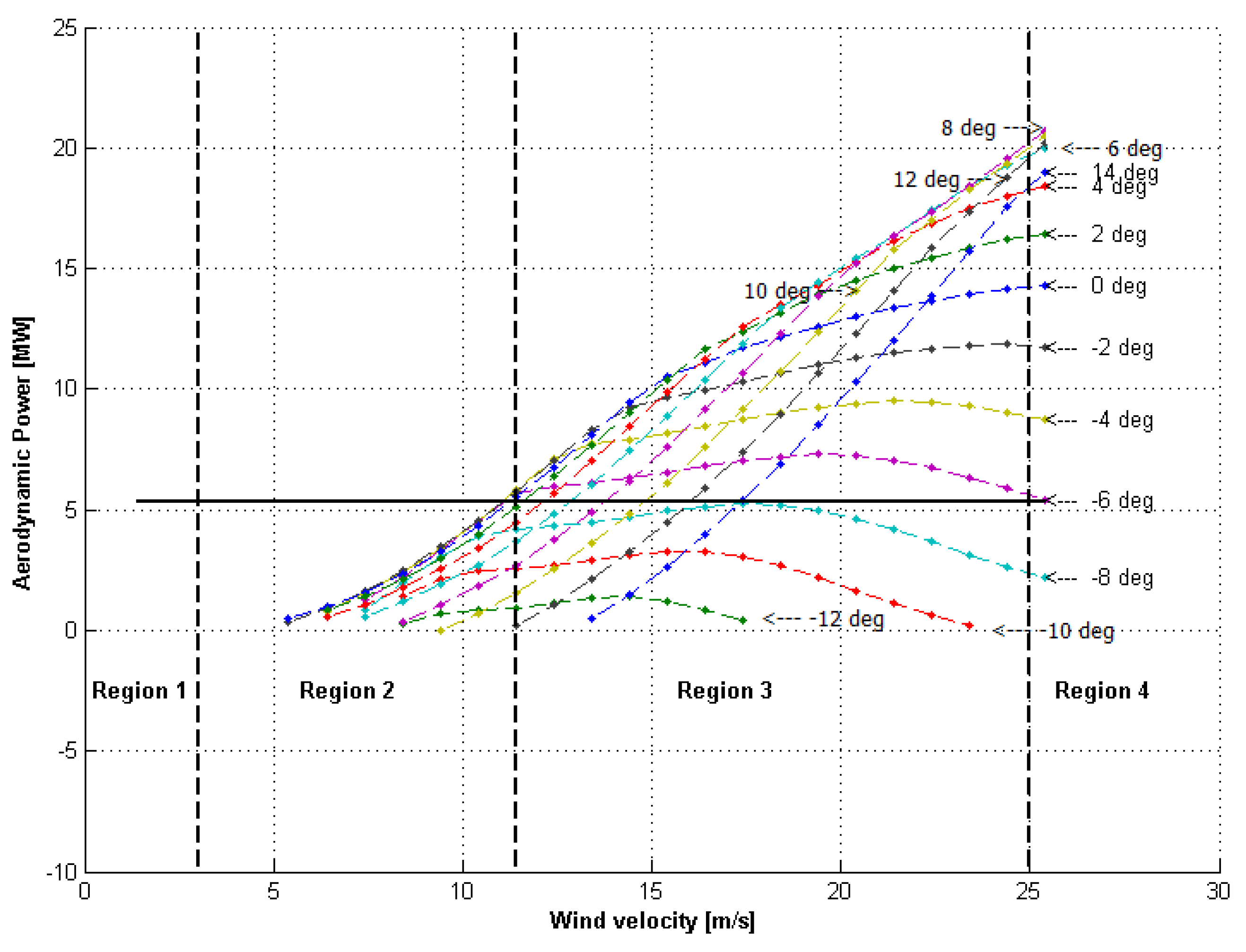
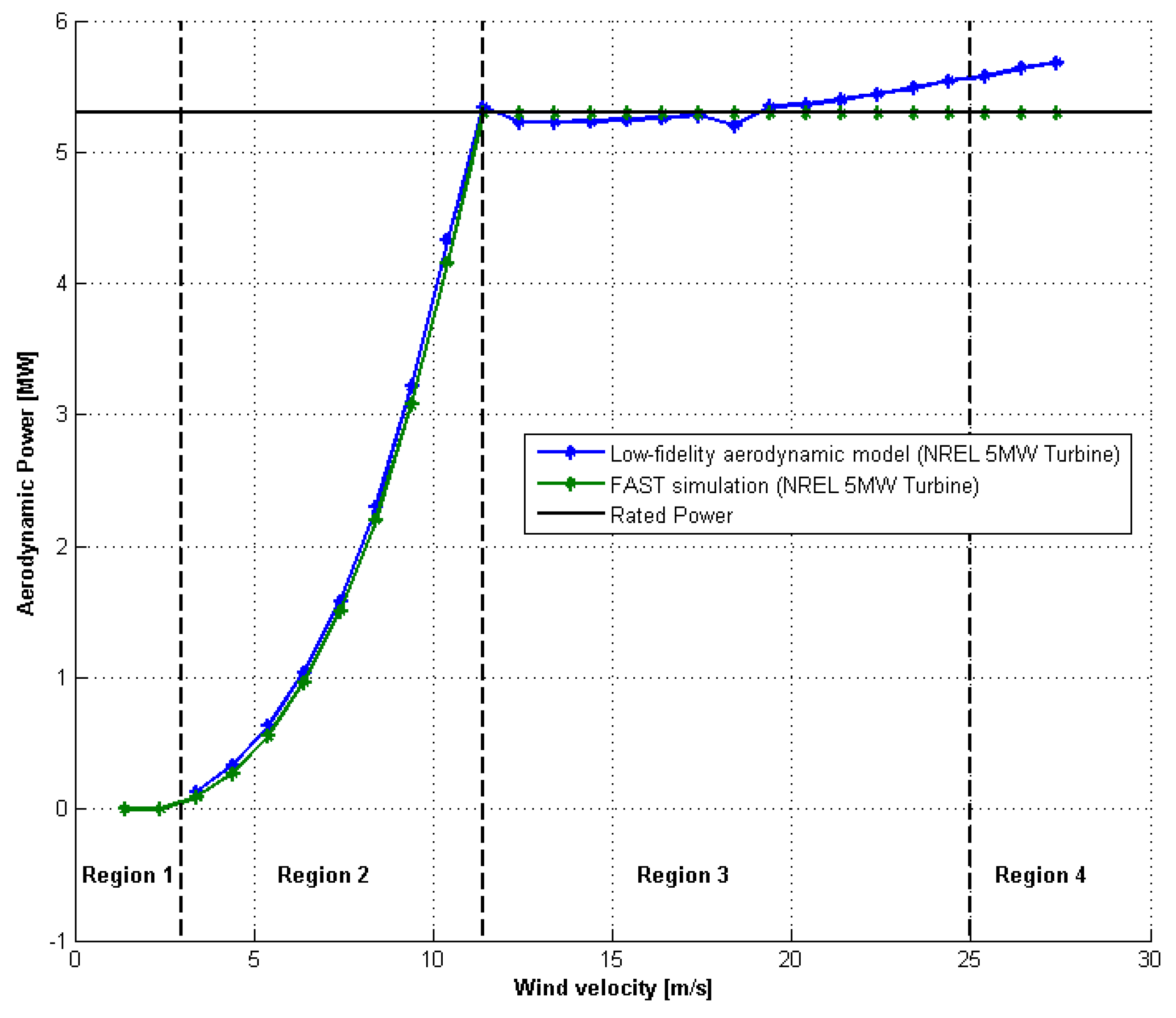
2.2.3. Power Curve
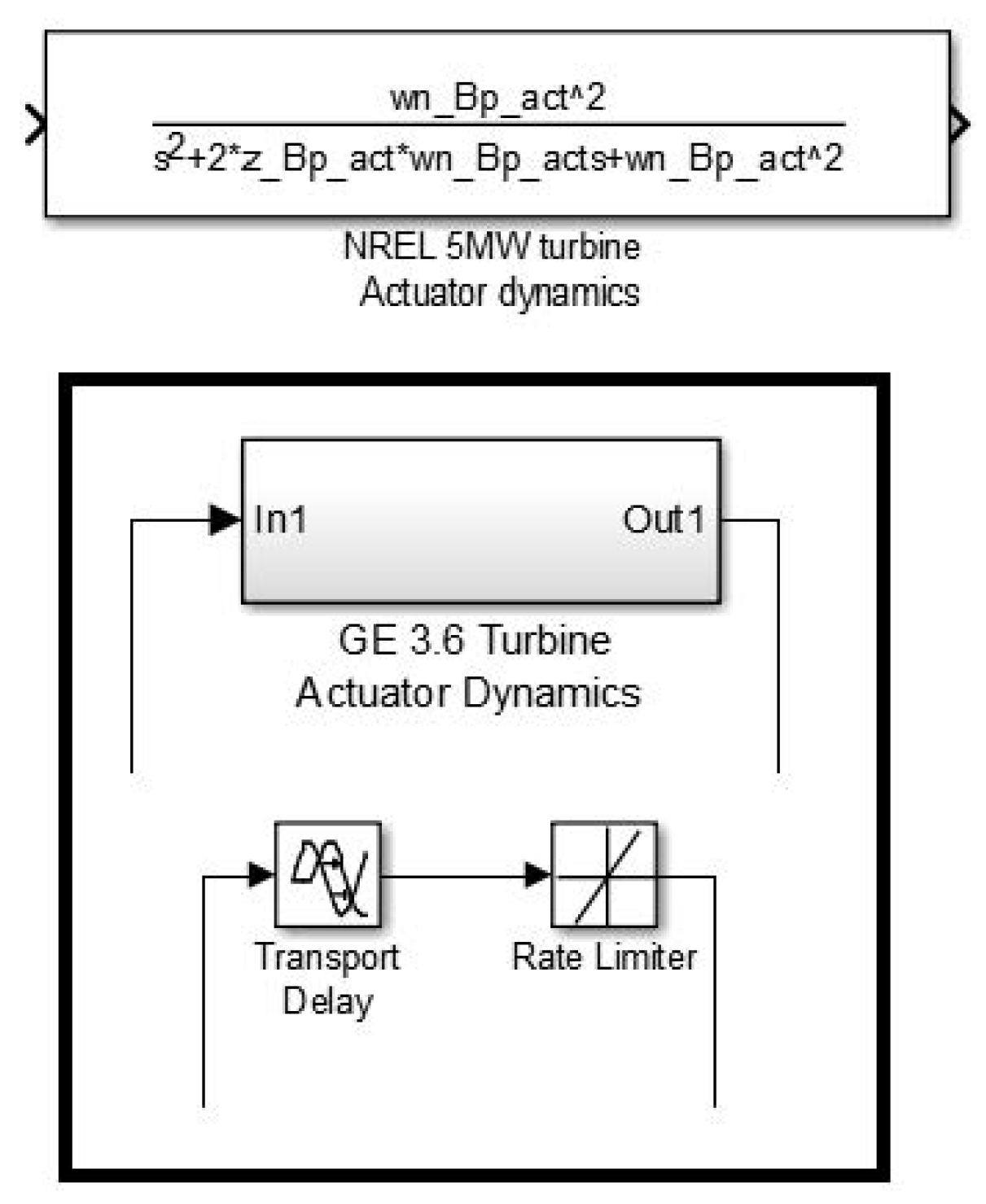
2.2.4. Actuator Dynamics
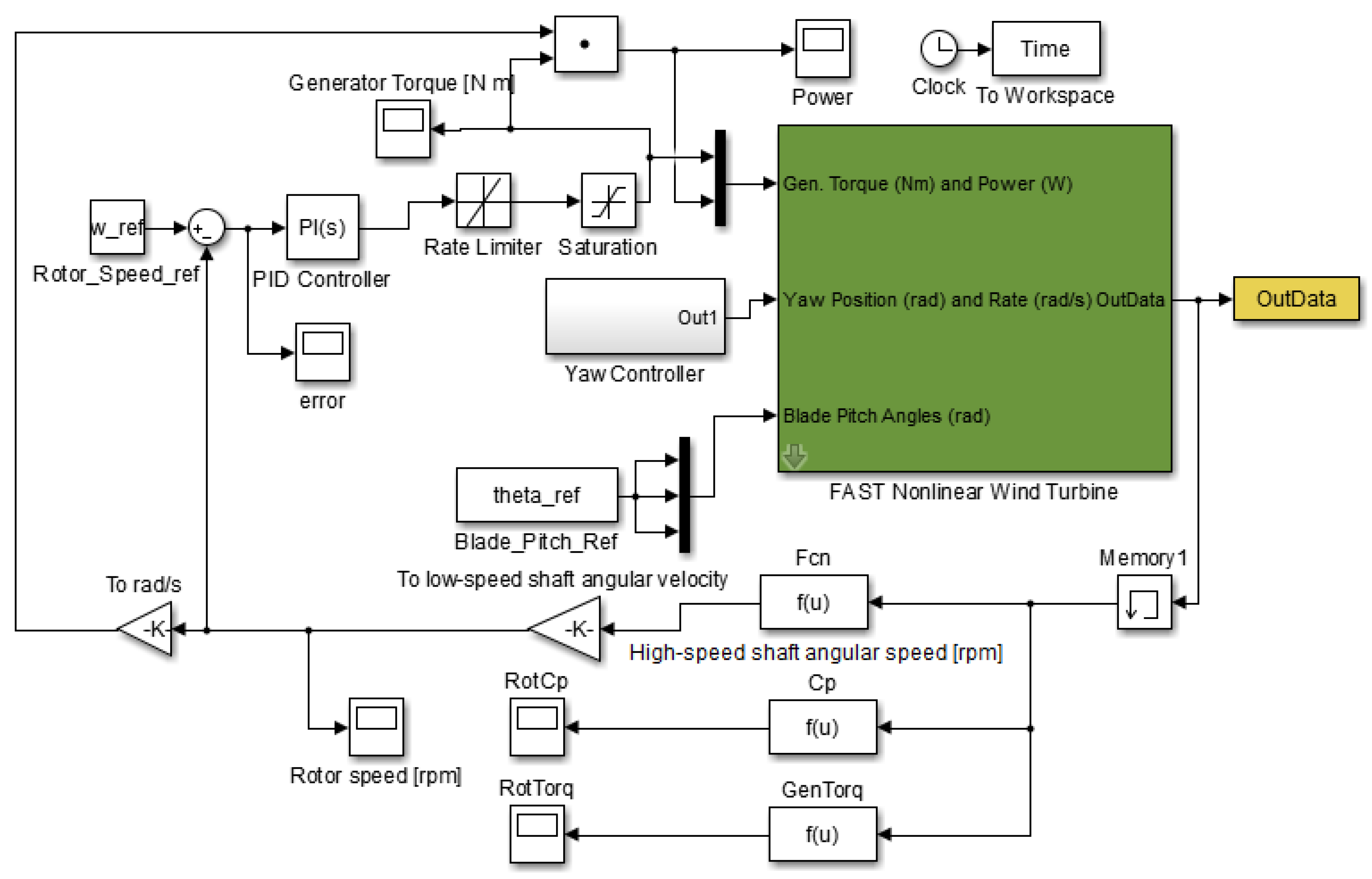
3. Control Analysis and Design Overview
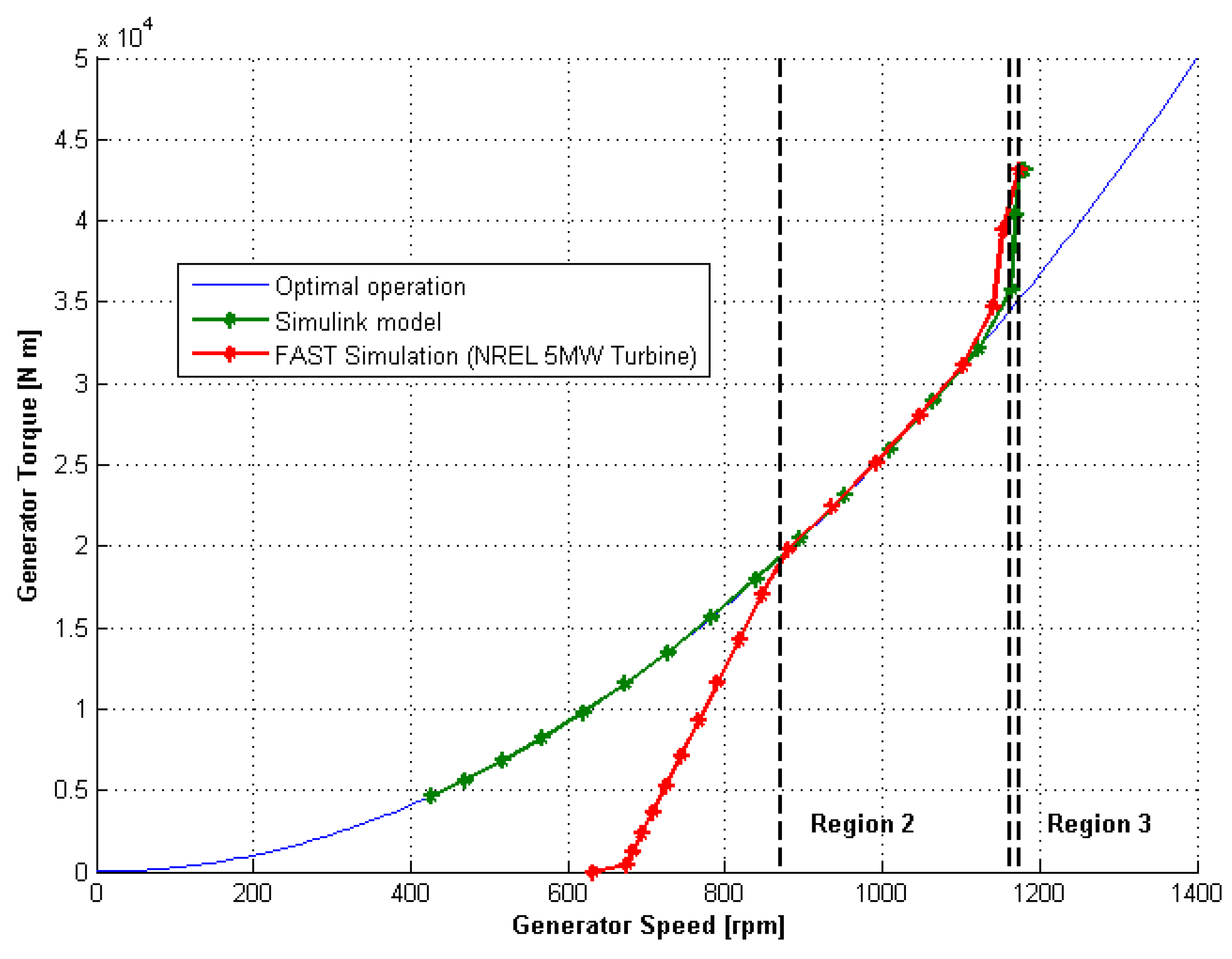
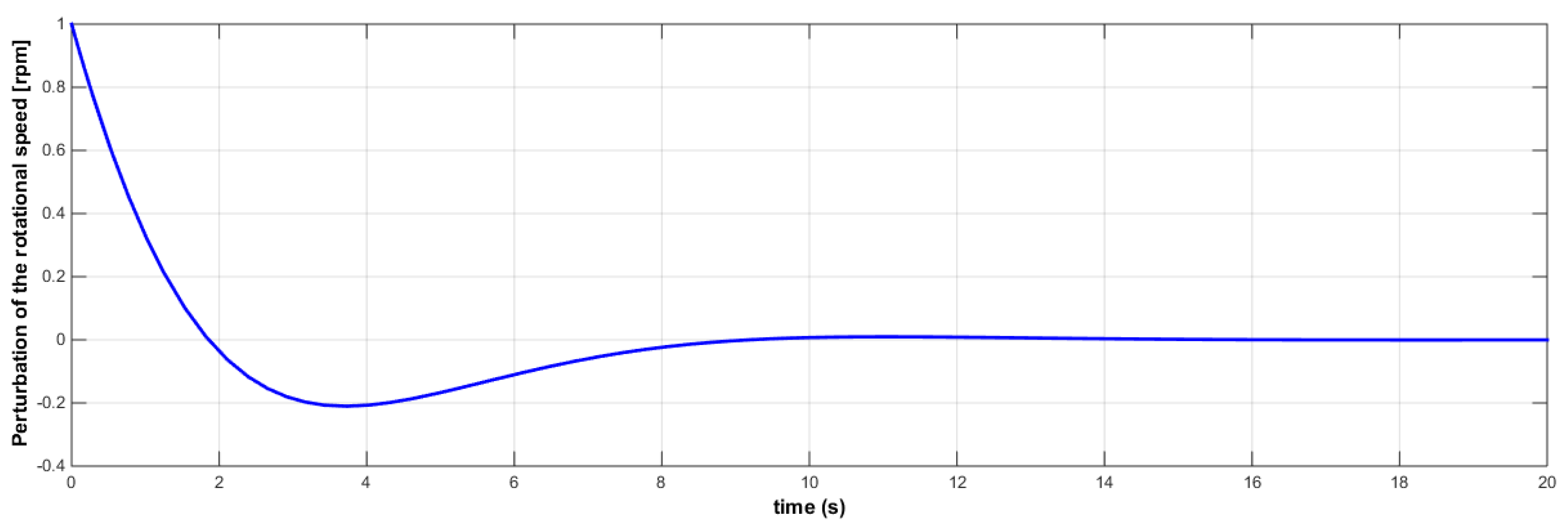
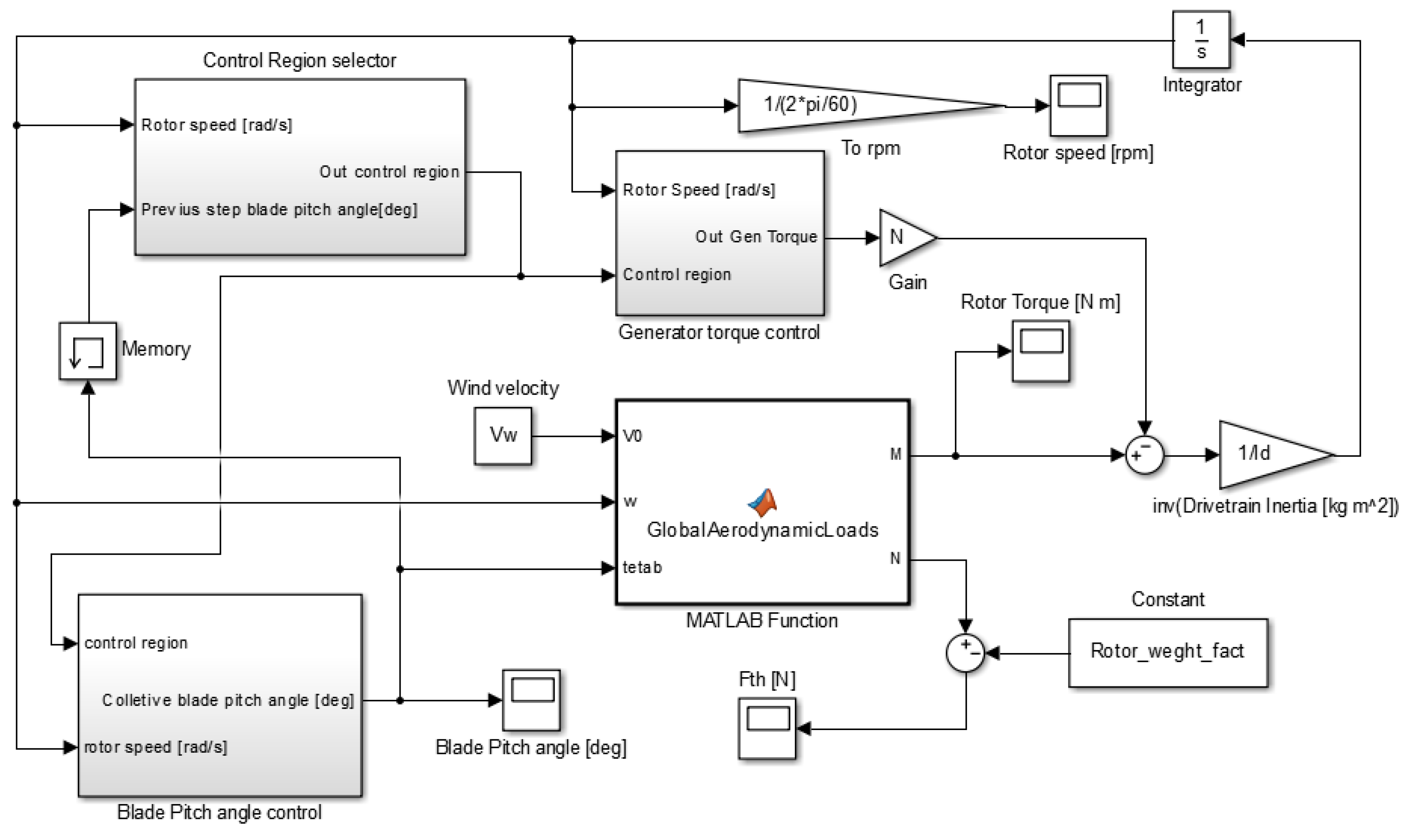
3.1. Generator-Toque Control
3.1.1. Formulation
3.1.2. Low-Fidelity Model Analysis
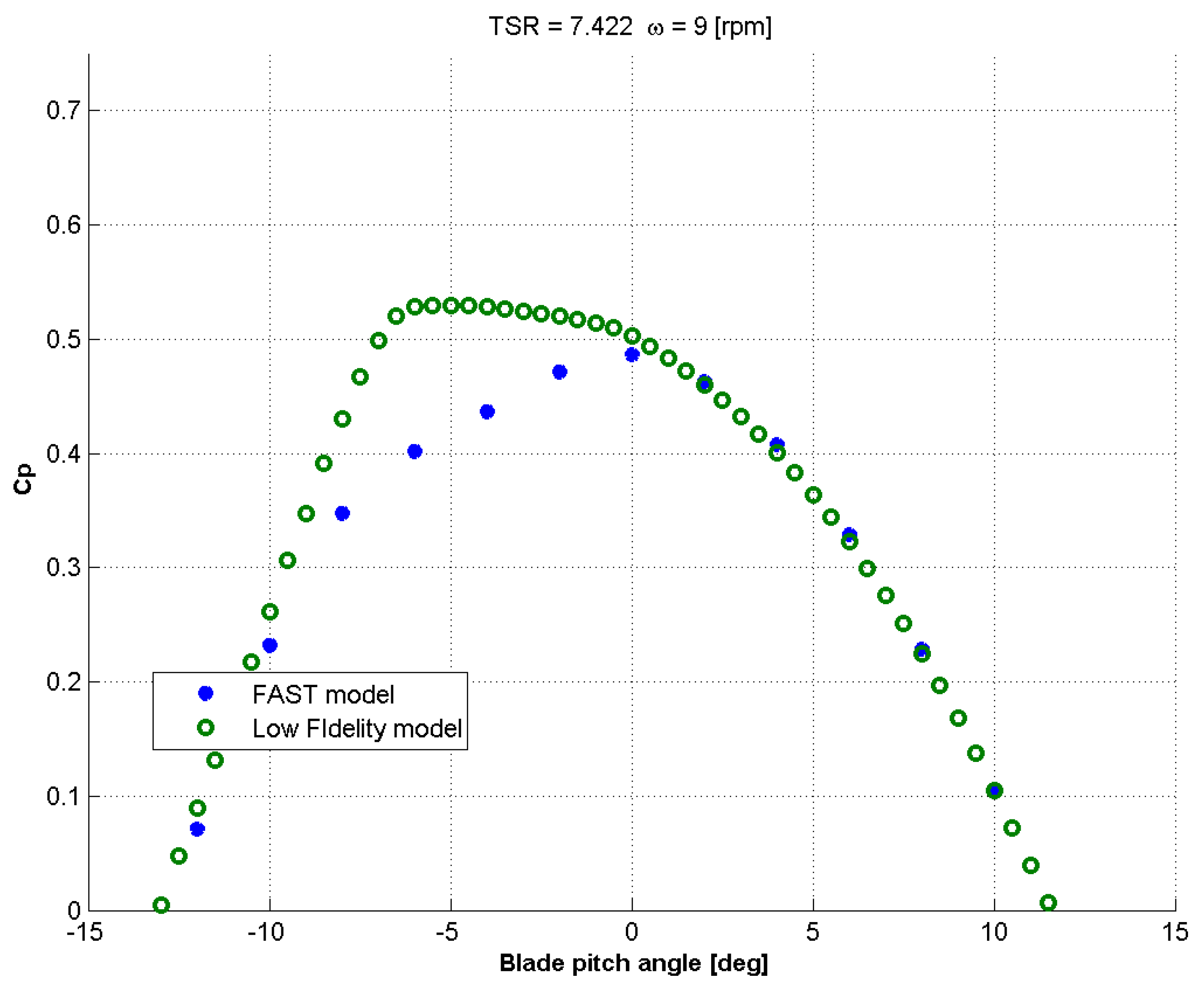
3.1.3. FAST Analysis
3.2. High Bandwidth Blade-Pitch Control for the Onshore NREL 5-MW Wind Turbine
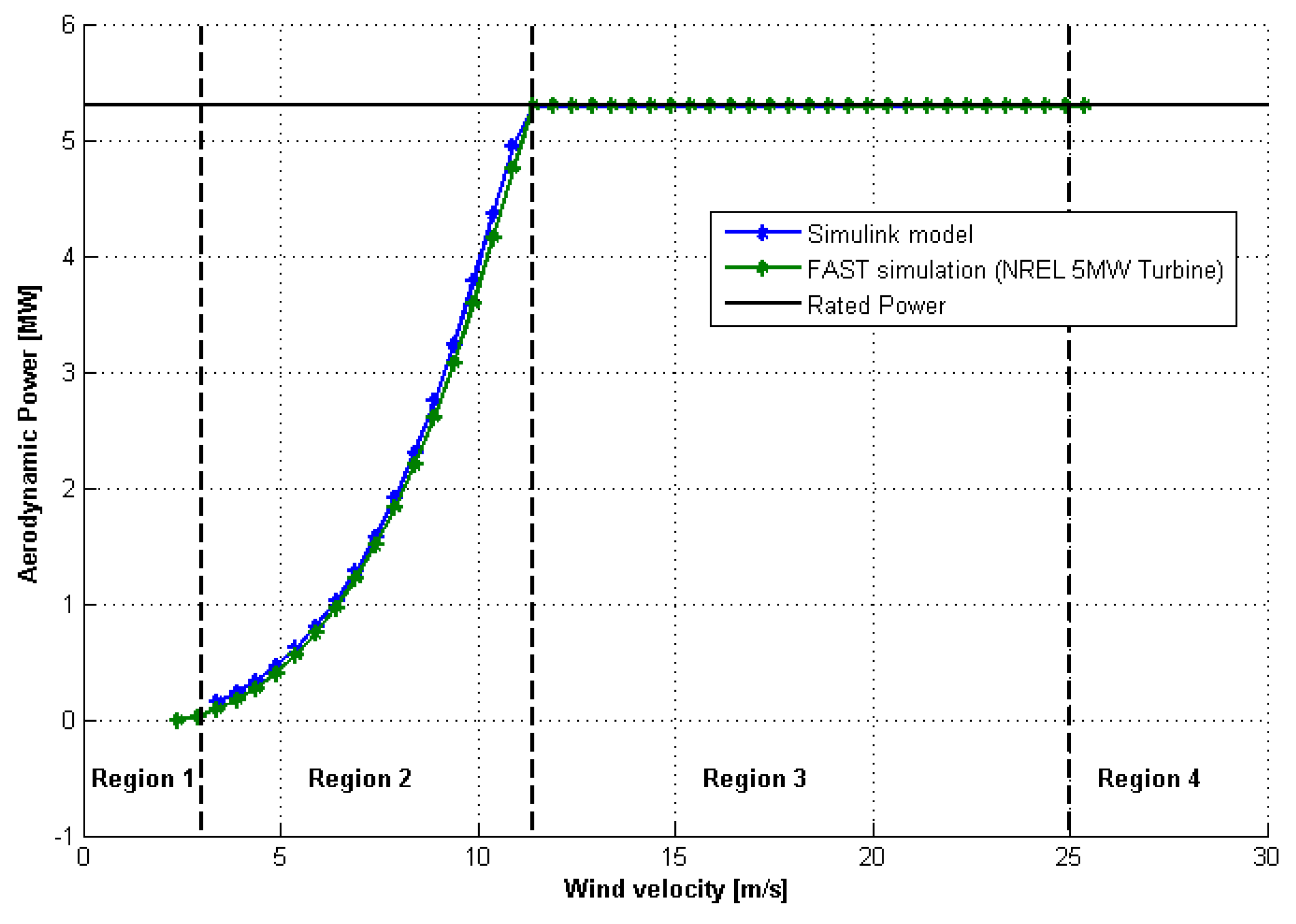
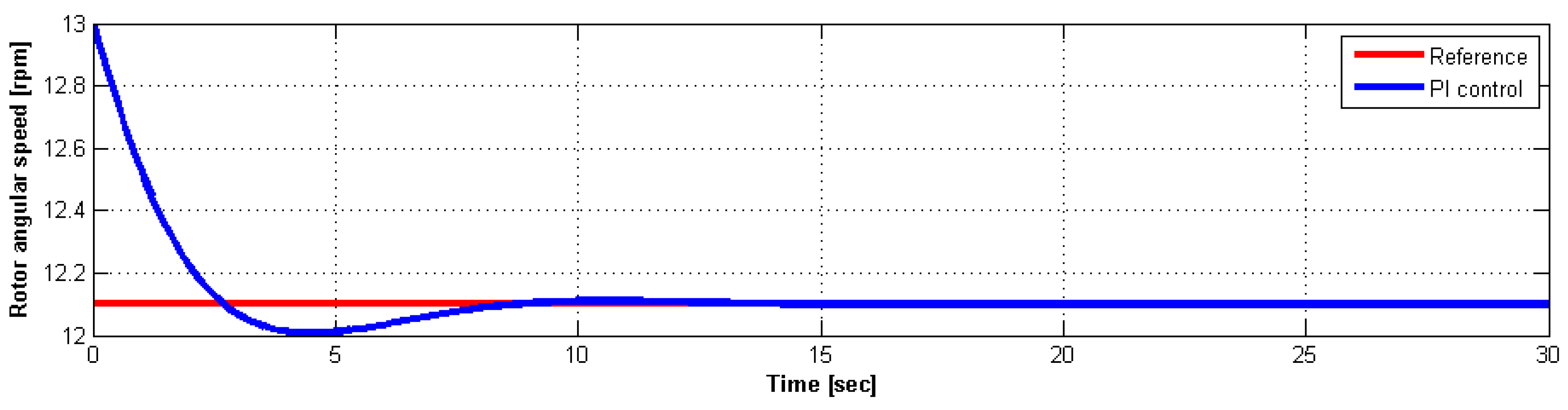
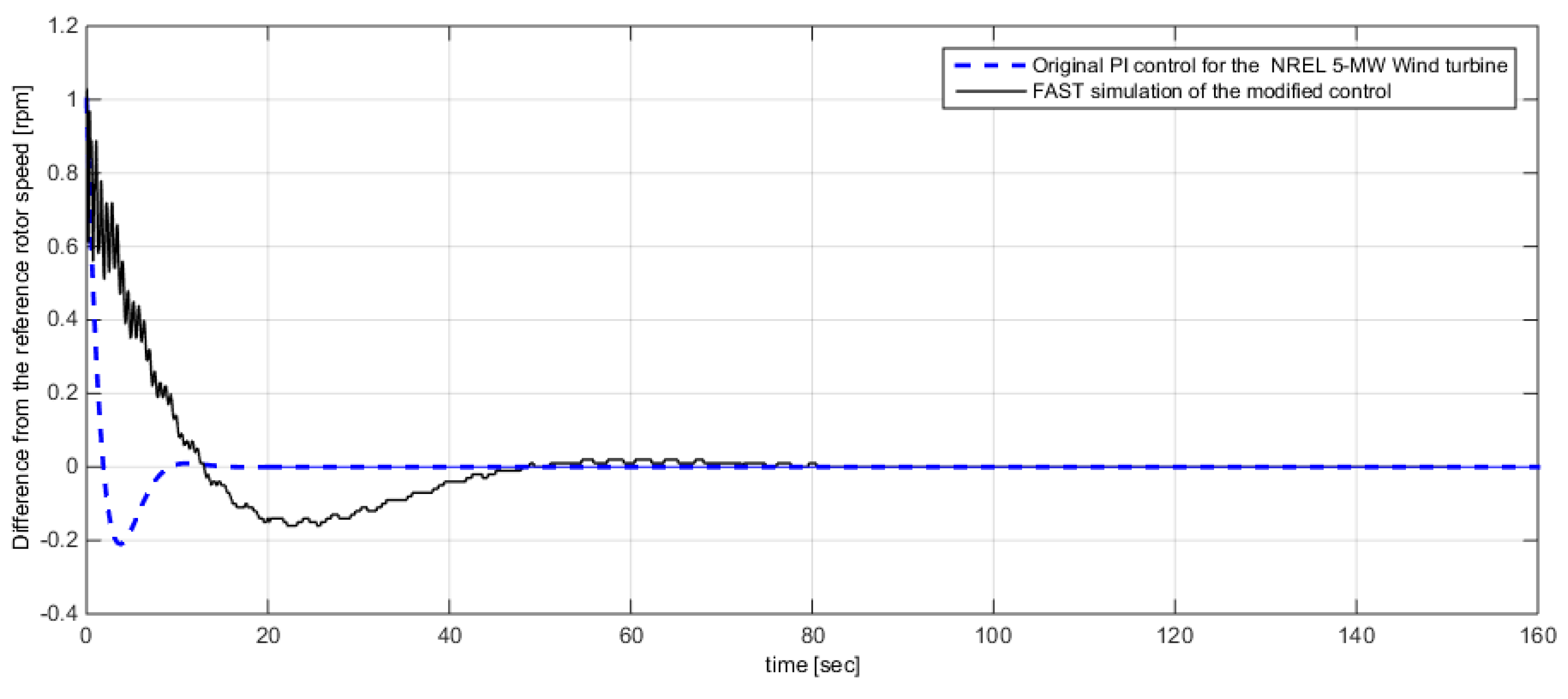
3.3. Simulink Tuned PI Blade-Pitch Control for the Onshore NREL 5-MW Wind Turbine
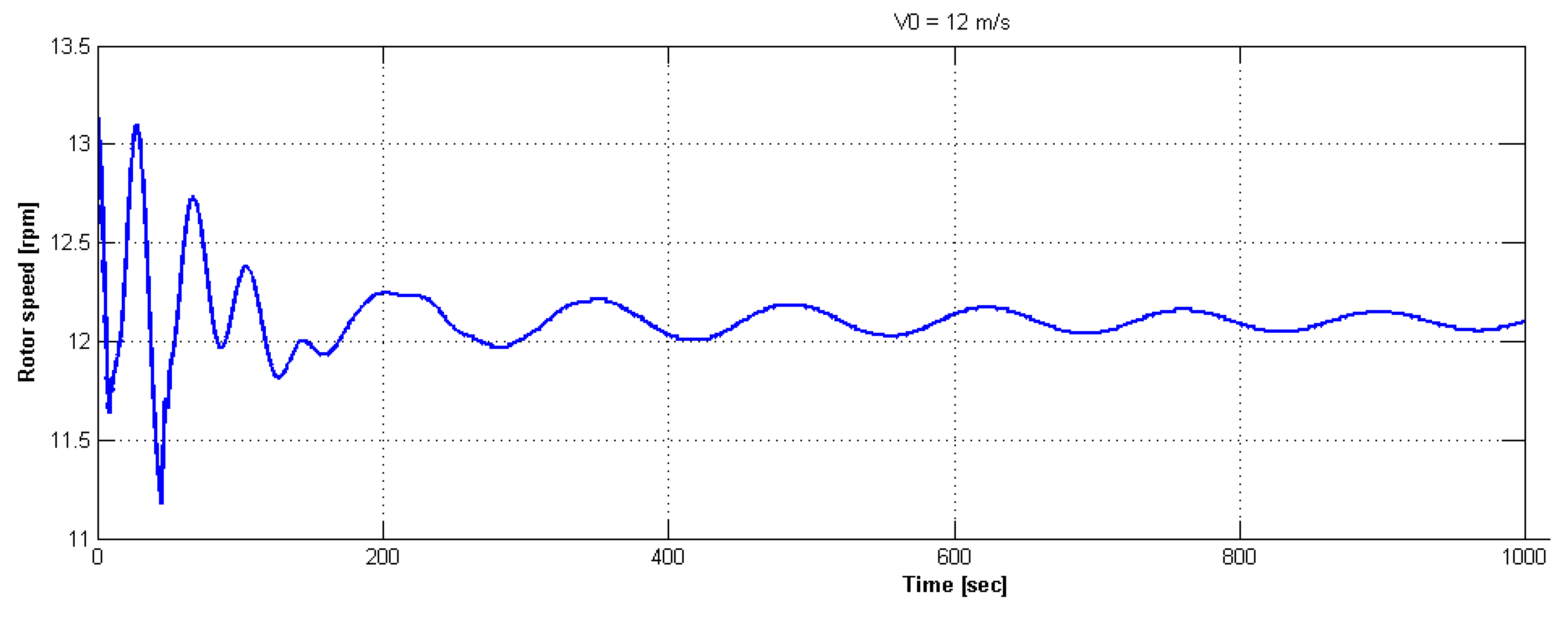
3.4. Low Bandwidth Blade-Pitch Control for the Offshore NREL 5-MW Wind Turbine
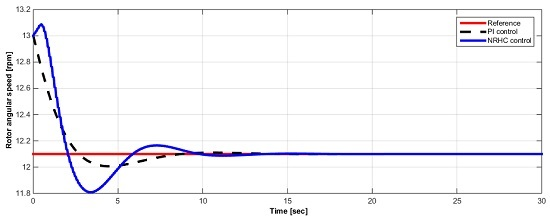
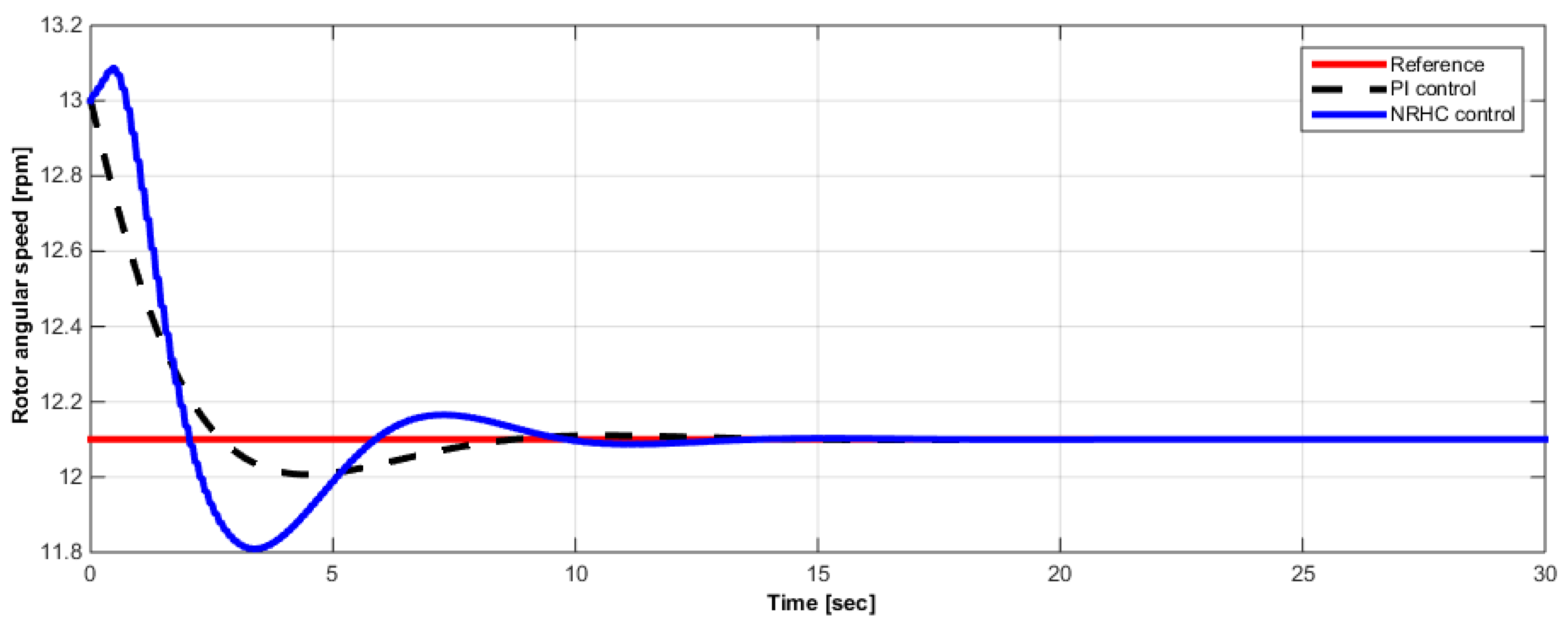
4. Real-Time NRHC Control
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ozdemir, A. Preview Control for Wind Turbines. Ph.D. Thesis, University of Minnesota, Minneapolis, MN, USA, 2013. [Google Scholar]
- Jonkman, J.M.; Buhl, M.L., Jr. FAST User’s Guide; Technical Report No. NREL/EL-500-38230; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Song, Y.D.; Dhinakaran, B.; Bao, X.Y. Variable speed control of wind turbines using nonlinear and adaptive algorithms. J. Wind Eng. Ind. Aerodyn. 2000, 85, 293–308. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Houria, S. Nonlinear control with wind estimation of a DFIG variable speed wind turbine for power capture optimization. Energy Convers. Manag. 2009, 50, 885–892. [Google Scholar] [CrossRef]
- Boukhezzar, B.; Houria, S. Nonlinear control of a variable-speed wind turbine using a two-mass model. IEEE Trans. Energy Convers. 2011, 26, 149–162. [Google Scholar] [CrossRef]
- Beltran, B.; Tarek, A.; Mohamed, E.H.B. Sliding mode power control of variable-speed wind energy conversion systems. IEEE Trans. Energy Convers. 2008, 23, 551–558. [Google Scholar] [CrossRef]
- Wu, F.; Zhang, X.P.; Ju, P.; Sterling, M. Decentralized nonlinear control of wind turbine with doubly fed induction generator. IEEE Trans. Power Syst. 2008, 23, 613–621. [Google Scholar]
- Schlipf, D.; Schlipf, D.J.; Kühn, M. Nonlinear model predictive control of wind turbines using LIDAR. Wind Energy 2013, 16, 1107–1129. [Google Scholar] [CrossRef]
- Galvani, P.A.; Sun, F.; Turkoglu, K. Aerodynamic Modelling of the 5-MW Wind Turbine for Development and Application of Real-Time Nonlinear Receding Horizon Control. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, San Diego, CA, USA, 4–8 January 2016; p. 173.
- Bryson, A.; Ho, Y. Applied Optimal Control; Hemisphere: New York, NY, USA, 1975. [Google Scholar]
- Chen, C.; Shaw, L. On receding horizon feedback control. Automatica 1982, 18, 349–352. [Google Scholar] [CrossRef]
- Ohtsuka, T.; Fujii, H. Real-Time Optimization Algorithm for Nonlinear Receding-Horizon Control. Automatica 1999, 33, 1147–1154. [Google Scholar] [CrossRef]
- Thomas, Y. Linear quadratic optimal estimation and control with receding horizon. Electron. Lett. 1975, 11, 19–21. [Google Scholar] [CrossRef]
- Kwon, W.; Bruckstein, A.; Kailath, T. Stabilizing state-feedback design via the moving horizon method. Int. J. Control 1983, 37, 631–643. [Google Scholar] [CrossRef]
- Mayne, D.; Michalska, H. Receding horizon control of nonlinear systems. IEEE Trans. Autom. Control 1990, 35, 814–824. [Google Scholar] [CrossRef]
- Mayne, D.; Michalska, H. An implementable receding horizon controller for stabilization of nonlinear systems. In Proceedings of the 29th IEEE Conference Decision and Control, Honolulu, HI, USA, 5–7 December 1990; pp. 3396–3397.
- Moriarty, P.J.; Hansen, A.C. AeroDyn Theory Manual; National Renewable Energy Laboratory: Golden, CO, USA, 2005.
- Hansen, M.O. Aerodynamics of Wind Turbines; Routledge: London, UK, 2008. [Google Scholar]
- Butterfield, S.; Musial, W.; Scott, G. Definition of a 5-MW Reference Wind Turbine for Offshore System Development; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- Fischer, B. Reducing rotor speed variations of floating wind turbines by compensation of non-minimum phase zeros. IET Renew. Power Gener. 2013, 7, 413–419. [Google Scholar] [CrossRef]
- Jonkman, J.M. Dynamics Modeling and Loads Analysis of an Offshore Floating Wind Turbine. Ph.D. Thesis, University of Colorado, Boulder, CO, USA, 2007. [Google Scholar]
- Miller, N.W.; Price, W.W.; Sanchez-Gasca, J.J. Dynamic Modeling of GE 1.5 and 3.6 Wind Turbine-Generators. In GE-Power Systems Energy Consulting; General Electric Company: Schenectady, NY, USA, 2003. [Google Scholar]
- Johnson, K.E. Adaptive Torque Control of Variable Speed Wind Turbines; National Renewable Energy Laboratory: Golden, CO, USA, 2004; pp. 54–57.
- Larsen, T.J.; Hanson, T.D. A method to avoid negative damped low frequent tower vibrations for a floating, pitch controlled wind turbine. J. Phys. Conf. Ser. 2007, 75, 12073. [Google Scholar] [CrossRef]
- Jonkman, J.M. Definition of the Floating System for Phase IV of OC3; National Renewable Energy Laboratory: Golden, CO, USA, 2010.
- Ohtsuka, T. Time-variant receding-horizon control of nonlinear systems. J. Guid. Control Dyn. 1998, 21, 174–176. [Google Scholar] [CrossRef]
- Kabamba, P.; Longman, R.; Sun, J.-G. A homotopy approach to the feedback stablilization of linear systems. J. Guid. Control Dyn. 1987, 10, 422–432. [Google Scholar] [CrossRef]
- Ohtsuka, T.; Fujii, H. Stabilized continuation method for solving optimal control problems. J. Guid. Control Dyn. 1994, 17, 950–957. [Google Scholar] [CrossRef]
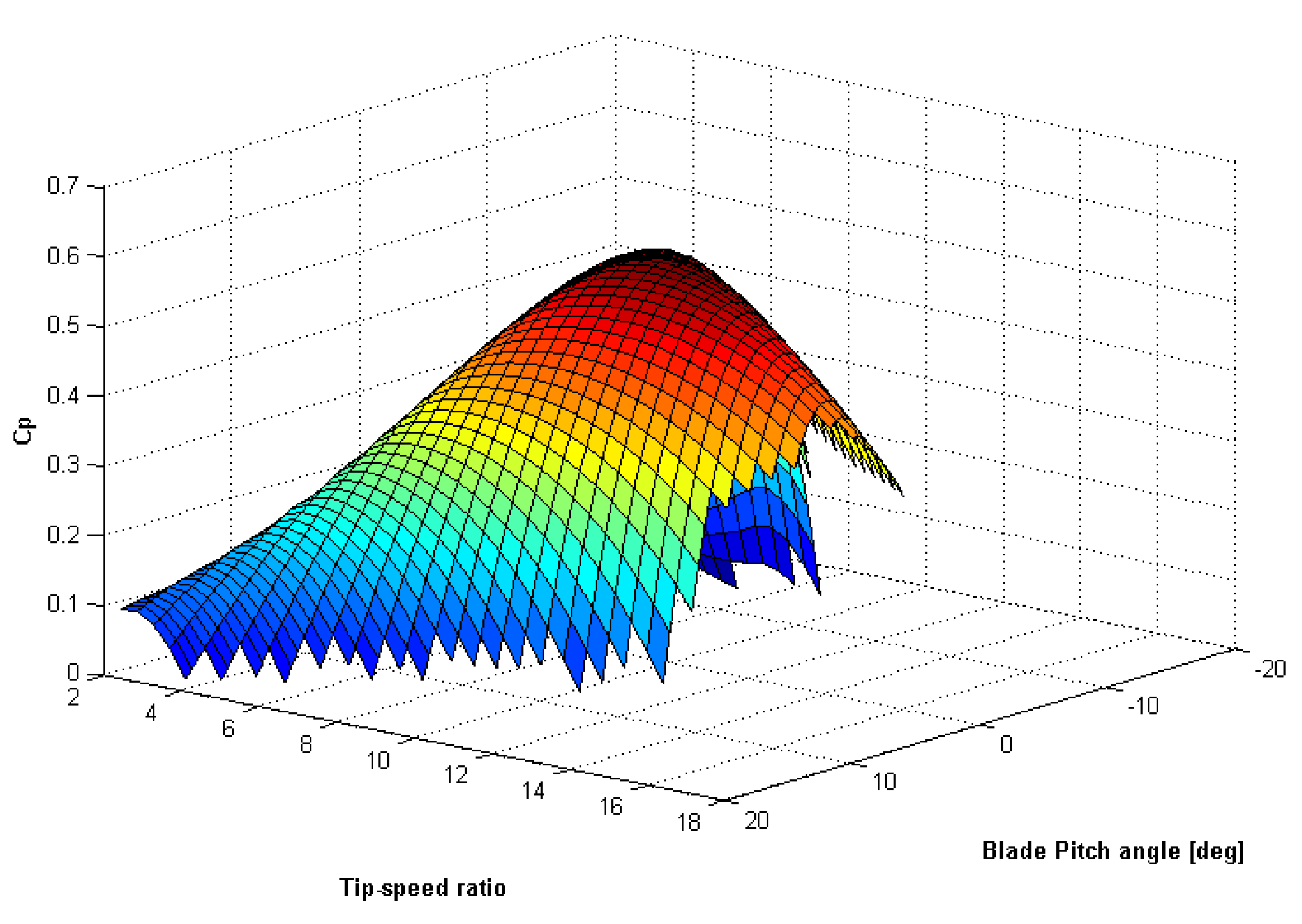
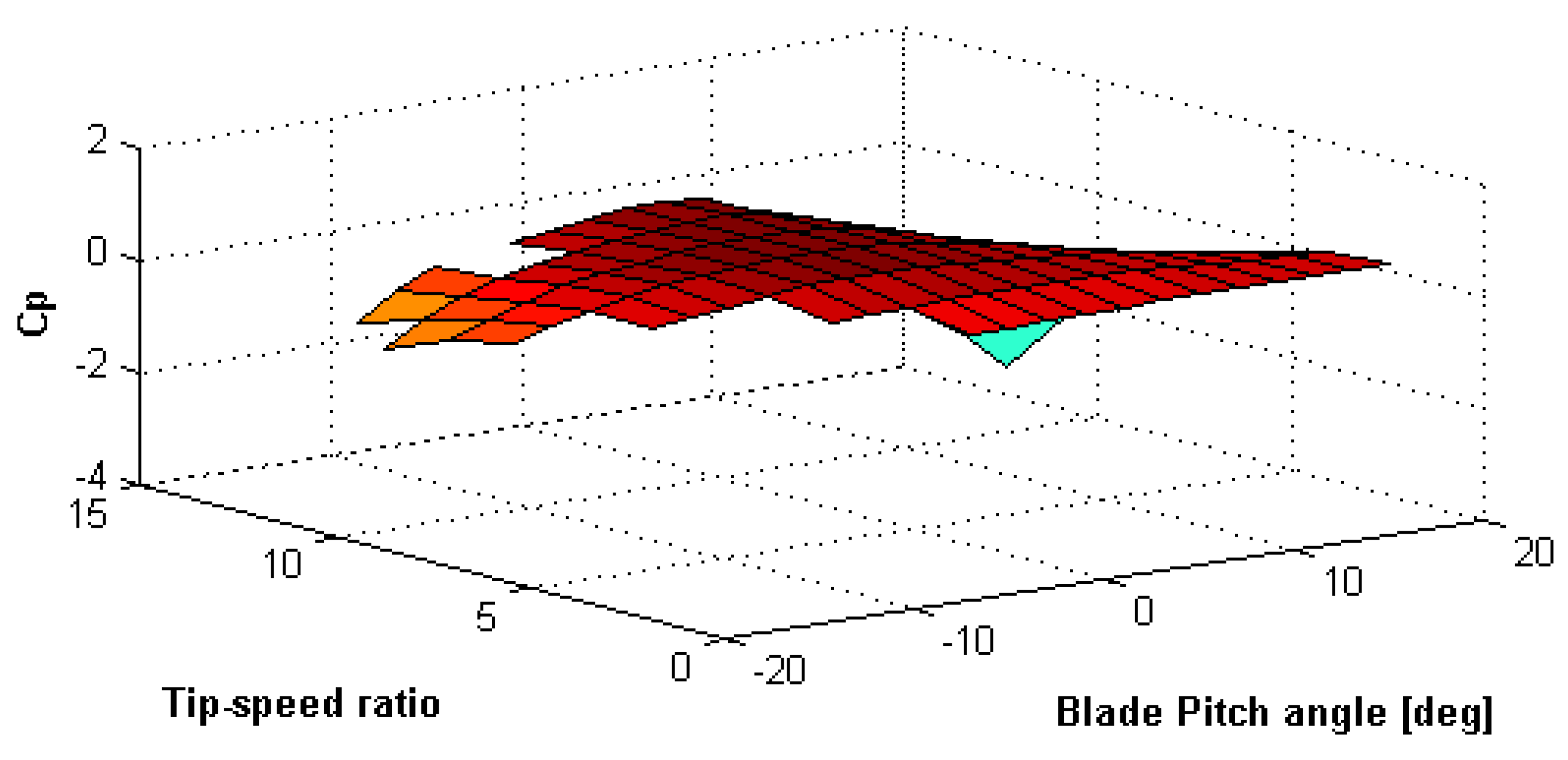
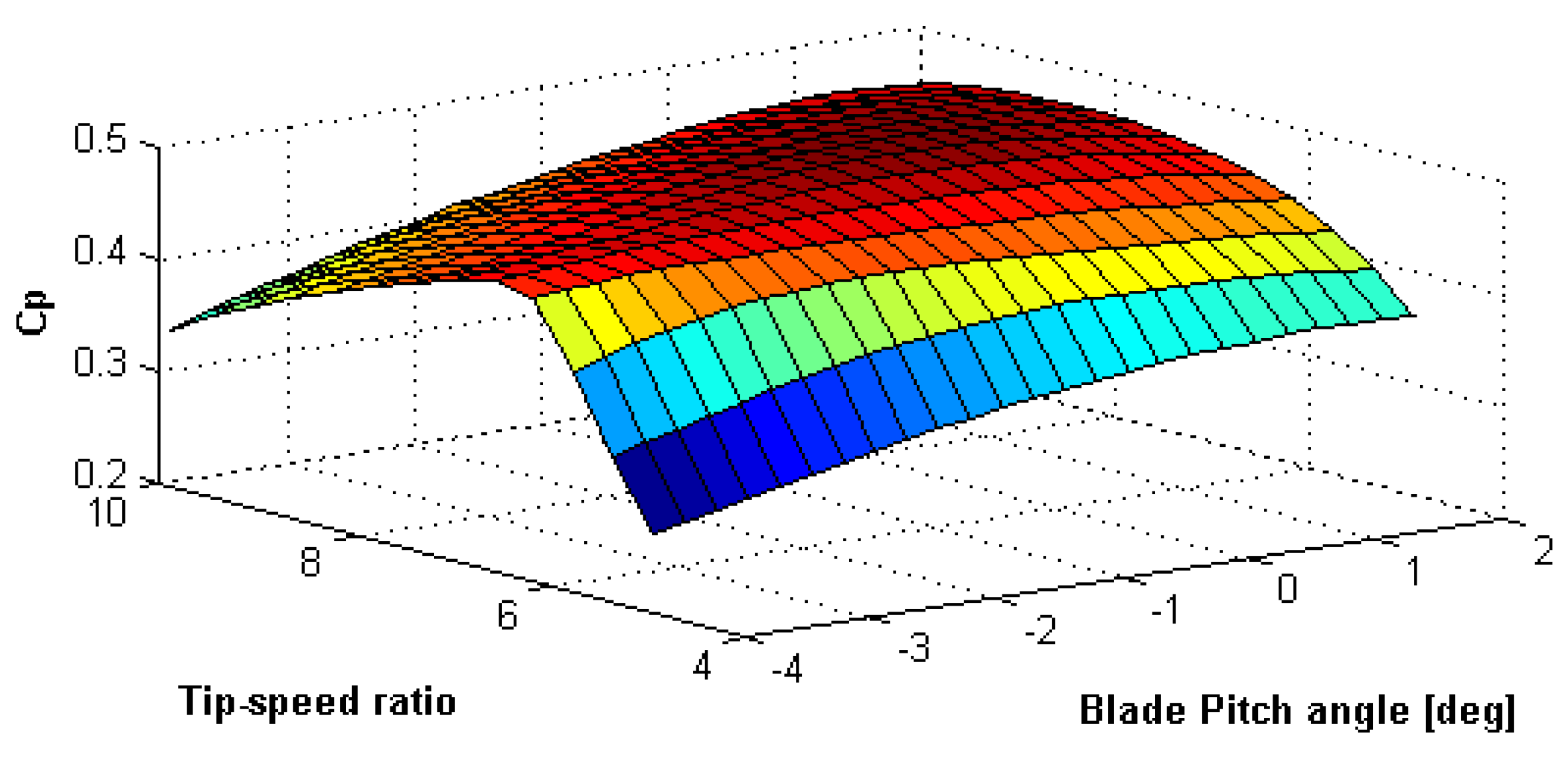
| Wind Velocity (m/s) | TSR | Blade Pitch (deg) | ω (rpm) | K (N m/(rad/s)) | |
|---|---|---|---|---|---|
| 3 | 0.55048 | 8.7965 | −2.5 | 4 | 1.54 × 10 |
| 4 | 0.5515 | 9.0713 | −2.5 | 5.5 | 1.41 × 10 |
| 5 | 0.55095 | 9.2363 | −2.5 | 7 | 1.34 × 10 |
| 6 | 0.55055 | 9.3462 | −2.5 | 8.5 | 1.29 × 10 |
| 7 | 0.55145 | 8.9535 | −2.5 | 9.5 | 1.47 × 10 |
| 8 | 0.5515 | 9.0713 | −2.5 | 11 | 1.41 × 10 |
| 9 | 0.55126 | 9.163 | −2.5 | 12.5 | 1.37 × 10 |
| 10 | 0.5513 | 8.9064 | −2.5 | 13.5 | 1.49 × 10 |
| 11 | 0.55153 | 8.9964 | −2.5 | 15 | 1.45 × 10 |
| 12 | 0.5515 | 9.0713 | −2.5 | 16.5 | 1.41 × 10 |
| Model | TSR | Blade Pitch | ω | K | |
|---|---|---|---|---|---|
| (deg) | (rpm) | (N m/(rad/s)) | |||
| FAST | 0.48698 | 7.422 | −0.25 | 9 | 2.2746 × 10 |
| Low-fidelity model | 0.5515 | 9.0713 | −2.5 | 11 | 1.41 × 10 |
| Wind Velocity | TSR | Blade Pitch | ω | K | |
|---|---|---|---|---|---|
| (m/s) | (deg) | (rpm) | (N m/(rad/s)) | ||
| 4 | 0.4879 | 7.4220 | −0.25 | 4.50 | 2.279 × 10 |
| 6 | 0.4878 | 7.4220 | −0.25 | 6.75 | 2.278 × 10 |
| 8 | 0.4870 | 7.4220 | −0.25 | 9.00 | 2.275 × 10 |
| 10 | 0.4852 | 7.5869 | −0.25 | 11.50 | 2.122 × 10 |
| 12 | 0.4806 | 7.2846 | −0.25 | 13.25 | 2.374 × 10 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galvani, P.A.; Sun, F.; Turkoglu, K. Aerodynamic Modeling of NREL 5-MW Wind Turbine for Nonlinear Control System Design: A Case Study Based on Real-Time Nonlinear Receding Horizon Control. Aerospace 2016, 3, 27. https://doi.org/10.3390/aerospace3030027
Galvani PA, Sun F, Turkoglu K. Aerodynamic Modeling of NREL 5-MW Wind Turbine for Nonlinear Control System Design: A Case Study Based on Real-Time Nonlinear Receding Horizon Control. Aerospace. 2016; 3(3):27. https://doi.org/10.3390/aerospace3030027
Chicago/Turabian StyleGalvani, Pedro A., Fei Sun, and Kamran Turkoglu. 2016. "Aerodynamic Modeling of NREL 5-MW Wind Turbine for Nonlinear Control System Design: A Case Study Based on Real-Time Nonlinear Receding Horizon Control" Aerospace 3, no. 3: 27. https://doi.org/10.3390/aerospace3030027
APA StyleGalvani, P. A., Sun, F., & Turkoglu, K. (2016). Aerodynamic Modeling of NREL 5-MW Wind Turbine for Nonlinear Control System Design: A Case Study Based on Real-Time Nonlinear Receding Horizon Control. Aerospace, 3(3), 27. https://doi.org/10.3390/aerospace3030027