Research on Shockwave/Boundary Layer Interactions Induced by Double Compression Corners Under Hypersonic Quiet and Noise Inflow Conditions

Abstract

The problem of shock wave/boundary layer interaction induced by compression corners widely exists in the external and internal flows of various supersonic/hypersonic aircraft. In practical engineering applications, multistage continuous compression is often used in the fin/rudder structure, while in internal flow, multistage compression schemes are usually employed at the inlet to enhance total pressure recovery; therefore, it is necessary to investigate the characteristics of multistage compression corner shockwave/boundary layer interactions. In basic research, it is usually simplified as the double compression corner shockwave/boundary layer interaction issue. In this paper, an experimental study of hypersonic shock/boundary layer interaction characteristics is conducted under quiet and noise inflow conditions, respectively, for the double compression corner model. Using high-speed Schlieren, the typical structure of shockwave/shockwave interaction and shockwave/boundary layer interaction above the corner is explored under both quiet and noisy incoming flow conditions. Then, based on gray average, root-mean-square analysis, Fast Fourier transform, proper orthogonal decomposition, and dynamic mode decomposition methods, the time-average and unsteady characteristics of the double compression corner configuration-induced separation were studied, and a comparative analysis was conducted. The difference law between wind tunnel noise level and interaction characteristics was summarized. Finally, the characteristic length and spectral characteristics of unstable waves that dominated the stability of the plate boundary layer were studied. The formation mechanism of separation is discussed, which provides technical support for the internal and external aerodynamic design and targeted optimization of hypersonic vehicles.

1. Introduction

Shockwave/boundary layer interaction is a widely prevalent phenomenon in the external and internal flows of all types of hypersonic or supersonic aircraft. It is a typical flow phenomenon common in the high-speed flight of aircraft. It is also one of the key problems in the design and development of hypersonic aircraft and engines [1].

The shockwave and boundary layer interaction flow phenomena in the flow field of hypersonic/hypersonic aircraft primarily include compression corner [2], plate-incident shockwave interaction [3], internal channel three-dimensional interaction [4], swept-back compression corner [5], column–skirt interaction [6], and others. Among them, flat-incident shockwave interaction and internal channel three-dimensional interaction primarily occur within the internal flow of an aircraft. In contrast, back-swept compression corner and pillar–skirt interaction primarily occurs in the external flow of an aircraft [6]. Shockwave/boundary layer interaction induced by a compression corner is common in both the internal and external flow of aircraft. The compression corner SWBLI phenomenon occurs when the compression surface profile in the inlet is deflected [7]. In the outflow, the compression corner SWBLI phenomenon often occurs at the body joint of the aerodynamic profile [8]. In practical engineering applications, continuous compression is usually applied at the joints of the external body or in the external fin/rudder structure. In internal flow, multistage compression schemes are often employed at the inlet to enhance total pressure recovery. Therefore, the compression corner SWBLI in the actual scene is usually a multistage compression corner shockwave/boundary layer interaction problem. The multi-channel shock structure in the multistage compression corner shockwave/boundary layer interaction flow field makes the flow field structure more complex [9]. It is usually simplified to Double Compression Ramp Shockwave/Boundary Layer Interaction (DCR-SWBLI) in research [10].

However, at present, in the research field of corner-induced shockwave/boundary layer interaction characteristics under supersonic/hypersonic compression, most of the research focuses on the interaction characteristics under supersonic conventional noise, and relatively few studies have been conducted on the interaction characteristics under multistage/double compression corner shockwave/boundary layer interaction and hypersonic conditions. There are fewer studies on low-noise conditions or quiet downflows [11,12]. It should be emphasized that, in the actual working environment of hypersonic vehicles, the difference between the current surface wind tunnel inflow disturbance/noise level and the upper atmosphere inflow disturbance/noise level is a key factor affecting vehicle design.

Compared with the experimental results of the conventional wind tunnel and the quiet wind tunnel in ref. [13,14,15,16,17], the conventional hypersonic wind tunnel has significant free flow noise. It cannot replicate the turbulent structure of the real, quiet high-altitude flight environment, which directly affects research on hypersonic boundary layer transition and the shockwave/boundary layer interaction mechanism. In contrast, the free flow turbulence of the quiet wind tunnel is comparable to that of the real flight environment. The experimental results for predicting boundary layer transition or disturbance regions are in closer agreement with the theoretical analysis results. Therefore, aiming at the difference in orders of magnitude in turbulence between the experimental flow field of a hypersonic vehicle in the ground wind tunnel and the real flight environment [18], based on the quiet wind tunnel, if the multistage compression corner disturbance characteristics can be studied in both quiet mode (incoming turbulence less than 0.1%), low noise mode (incoming turbulence 0.1~0.5%), and conventional noise mode (incoming turbulence greater than 2.0%) [19], it will provide more powerful support for the design of the external profile of the aircraft or the advanced air intake system [20,21].

Based on the hypersonic quiet wind tunnel, this paper presents an experimental study on the characteristics of hypersonic shockwave/boundary layer interaction under quiet and noisy incoming flow conditions for the double compression corner-plate model. It explored the typical shockwave/boundary layer interaction and the typical structure of shockwave/shockwave interaction above the corner under conditions of quiet and noisy incoming flow using the high-speed Schlieren method. Based on the gray average, RMS analysis, spatial FFT, the POD method, and the DMD method, the time-average and unsteady characteristics of double compression corner configuration-induced separation were studied, and the relationship between wind tunnel noise level and interaction characteristics was summarized. Finally, the characteristic length and spectral characteristics of unstable waves that dominated the stability of the flat boundary layer were discussed. The formation mechanism of separation is discussed, which provides technical support for the internal and external aerodynamic design and targeted optimization of hypersonic vehicles.

2. Experimental Arrangement and Method

The Φ300 mm hypersonic low noise wind tunnel of China Aerodynamics Research and Development Center is the first hypersonic low noise wind tunnel with Ludwig tube operation mode in China [22]. The whole experiment system mainly included a low noise wind tunnel, flat-plate compression corner model, high-speed Schlieren system, synchronous control system, etc.

2.1. Hypersonic Low Noise Wind Tunnel and the High-Speed Schlieren System

The experiments were carried out in the Φ300mm hypersonic quiet wind tunnel of the Ultra-High Speed Aerodynamics Institute of the China Aerodynamics Research and Development Center. The actual picture of the wind tunnel is shown in Figure 1.

The experimental condition is set at Mach 6 and the total temperature is 457 K. According to the operation characteristics of the wind tunnel, after the establishment of the flow field, the flow field in the test section first experiences a noise flow state (unit Reynolds number is 9.4 × 10⁶) for a period of time, and then enters a quiet flow field state (unit Reynolds number is 5.7 × 10⁶). The characteristics of shockwave/boundary layer interaction induced by double compression corner are studied under different noise levels under fixed incoming flow conditions. The test conditions are shown in

Table 1. Main parameters of incoming stream.

Ma∞ (U∞/c)	Re/m (ρU∞/μ)	U∞ (m/s)	T0 (K)	TS (K)	P0 (MPa)	PS (Pa)	ρ (kg/m3)	Field
6.10	5.7 × 106	899.7	457	54.1	0.33	178.7	0.012	quiet
5.90	9.4 × 106	896.1		57.4	0.41	287.0	0.017	noise

.

It is tough to conduct contact measurements in the highly advanced environment of Mach 6. In addition, the research must also consider the influence of plasma and pay closer attention to the changes in the structure of the wave system. Therefore, we have chosen the most stable and mature non-contact measurement method for flow field measurement. High-speed Schlieren imaging is performed using a masterconjugate mirror system. Unlike the conventional Schlieren system, the slit and knife-edge use the same horizontal structure of off-axis polished objects, as shown in Figure 2. In this structure, spherical mirrors used in the traditional Z-Schlieren system can eliminate spherical aberrations and non-point aberrations [23]. In the experiment, a Phantom V2512 model camera was used, along with a Nikon lens with a focal length of 200 mm and an f-value of 1/4. The knife-edge cut ratio was set to 0.5. The maximum resolution of the camera used in the experiment was 2048 pixels × 2048 pixels. The target size was 20.48 mm × 20.48 mm, the pixel size was 10 μm, the frame frequency of the Schlieren was set to 50 kHz, and the exposure time was 2.7 μs.

2.2. Double Compression Corner-Flat Model and Synchronous Control System Settings

The experimental model adopts the combination model of the double compression corner and plate. The plate length is 427.7 mm, the width is 160 mm, and the leading edge wedge angle is 10°. The leading edge of the double compression corner is located at a flow direction of the plate, x = 257 mm, and the angles of the two folds are 30° and 45°, respectively. The total flow direction length is 55 mm. The flow direction length of the first bend angle is about 40 mm, and the height of the model is about 38 mm. Figure 3 illustrates the design of the combined model, featuring a double compression corner and a flat plate. Considering the possible existence of three-dimensional effects in hypersonic flow fields, this study focuses on two-dimensional shockwave/boundary layer interaction problems. Therefore, the corner width was not set to be the same as the plate width, but was made smaller than the plate width (40 mm) to minimize the interaction of three-dimensional effects on this experiment to the greatest extent. The blockage ratio of this model in the wind tunnel is 5.4%, which meets the normal start-up conditions of the wind tunnel.

The synchronization control settings are shown in Figure 4. In the characteristic research experiment, it is essential to determine the accurate delay time according to the flow state of the quiet wind tunnel. According to different delay trigger times, the interaction flow field data under quiet flow and noise flow conditions are recorded by a high-speed CCD camera. Among them, the delay time of the delay signal is 50 μs.

2.3. Overview of Research Method

After the test condition is determined, the time sequence snapshot of quiet flow and conventional noise flow is recorded by the high-speed Schlieren system. Through gray average analysis, root-mean-square analysis, fast Fourier transform spectrum analysis, proper orthogonal decomposition (POD), dynamic mode decomposition analysis (DMD) and spatial Fourier transform, the results of average flow field, flow field pulsation, flow field characteristic spectral characteristics, flow field unsteady characteristic structure, unsteady dynamic mode of flow field and boundary layer unstable wave development are, respectively, analyzed analysis of interaction characteristics.

3. Research on Hypersonic Shockwave/Boundary Layer Interaction Characteristics

3.1. Time-Average Characteristic Analysis

First, the basic structure results of the interaction flow field are focused on. Figure 5 and Figure 6 show the instantaneous Schlieren comparison results and the average Schlieren gray comparison results under the conditions of noisy incoming flow and quiet incoming flow, respectively.

The schlieren results reveal the formation of a classic double compression corner shockwave/boundary layer interaction flow field structure in the hypersonic flow, along with a shock–shock interaction structure directly above the compression corner. A background shockwave is observed obliquely upstream of the flat plate, generated by the tip effect at the model’s leading edge, whose influence on the study and flow field can be neglected. From the flat-plate leading edge to the compression corner leading edge, the laminar boundary layer exhibits a linear growth trend, progressively thickening along the freestream direction. During the development of the boundary layer, a distinct “lift-up” trend is observed at a specific location, accompanied by the emergence of a faint separation shock. This point is identified as the onset of flow separation, and the region between this point and the intersection of the boundary layer with the model leading edge is defined as the separation zone. Due to the “obstruction” caused by the compression corner model, the gas is compressed, leading to the formation of a strong reattachment shock nearby, which reflects intensely after the shockwave. At the leading edge of the second compression corner, the gas is compressed again, generating a second intense shockwave. The interaction between this shock and the first reattachment shock results in the formation of an even stronger shockwave and a relatively weaker reflected shock, with a slip line emerging between the two. Based on the interpretation of the noisy flow field results, the separation zone length is measured to be 62.5 mm.

In contrast, although the quiet flow field exhibits a generally consistent structure with the noisy flow field, the distribution and spatial positioning of the flow structures show notable differences. This is primarily reflected in the earlier onset of flow separation and a significantly larger separation zone compared to the noise flow field. The separation zone length in this case is 90 mm, representing a 44% increase relative to the noisy flow field.

We further analyze the reasons for the differences in the separation zone of the two. Under identical model configurations and Mach numbers, the larger separation zone observed in a quiet tunnel is fundamentally governed by the decisive influence of freestream disturbance levels on boundary layer stability. The exceptionally low freestream turbulence in a quiet field enables the boundary layer to maintain a laminar state over a greater streamwise extent. This laminar boundary layer, characterized by a “skinny” velocity profile and insufficient near-wall momentum, exhibits high sensitivity to the adverse pressure gradient induced by the shockwave, leading to premature and facile separation. In contrast, the high-disturbance environment of a conventional noise field promotes an early transition to a turbulent boundary layer. The robust momentum mixing inherent to turbulence continuously transports high-momentum fluid toward the near-wall region, thereby enhancing its resistance to the adverse pressure gradient and suppressing separation. Even when separation occurs, the subsequent reattachment process is facilitated by more intense mixing, resulting in a smaller overall separation bubble compared to the quiet field scenario.

Figure 7 shows the RMS comparison results of the disturbed flow field. It can be seen that the pulsation level of the boundary layer is higher when the noise is flowing down, and the pulsation levels of the secondary shockwave, intense shockwave, and slip line are also higher, indicating that the unsteady characteristics of the disturbed flow field are more pronounced under noise incoming.

3.2. Analysis of Unsteady Characteristics

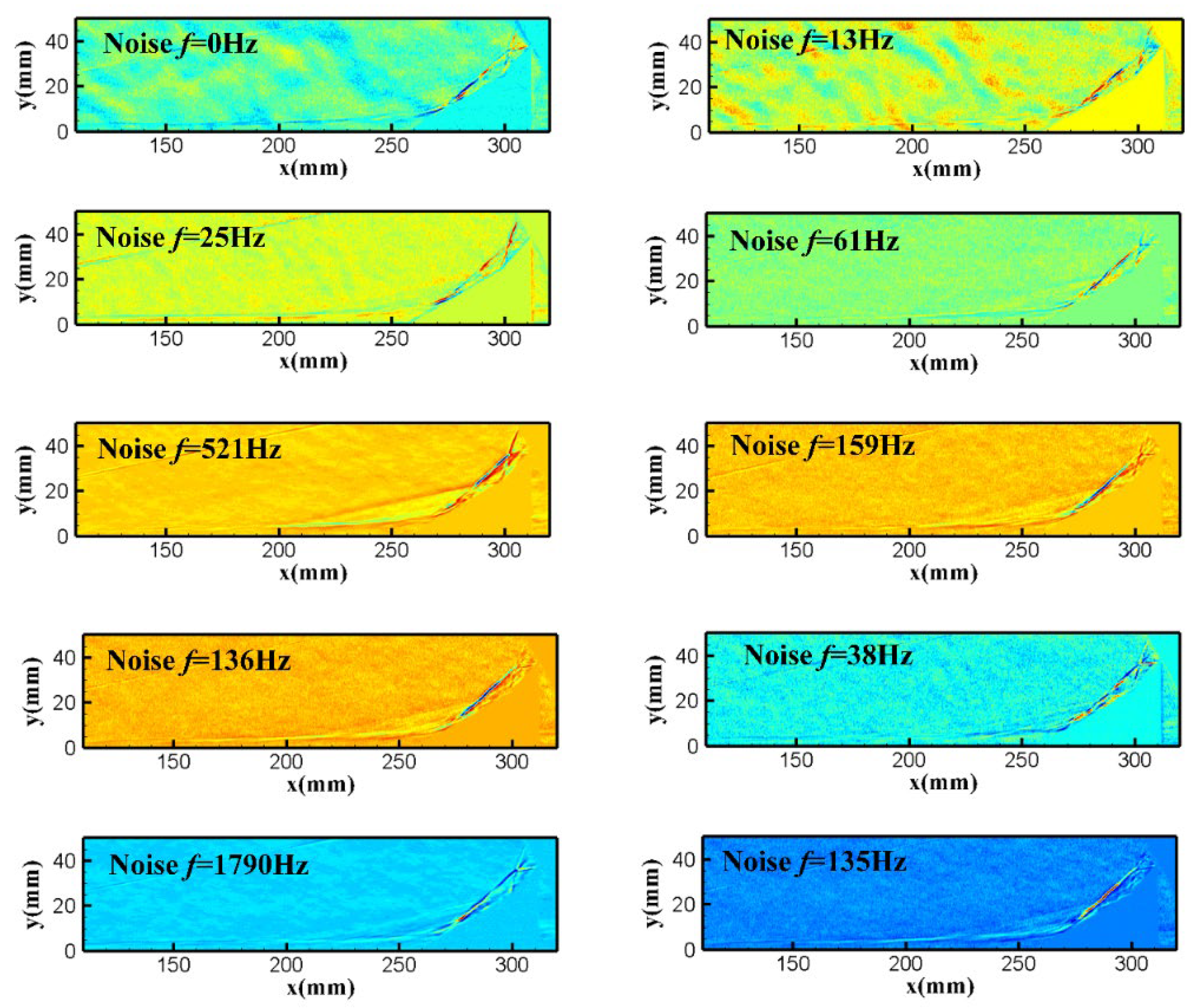
To study the unsteady characteristics of the interaction flow field, a gray matrix is selected for the Fourier transform based on the time-series Schlieren image, allowing for the monitoring of the unsteady characteristics of different interaction structures. The selected gray monitoring area is a straight line, approximately 62 pixels in length, and the selected time period is 500 ms. Fourier transform is performed on the gray time-series changes in the time period, and the characteristic frequency of the unsteady oscillation of the corresponding interaction structure is obtained.

The selection area of the grayscale matrix is shown in Figure 8. Grayscale matrix ① corresponds to the root of the attached shockwave, grayscale matrix ② corresponds to the middle of the attached shockwave, grayscale matrix ③ corresponds to the slip line region, and grayscale matrix ④ corresponds to the strong shock region.

During the PSD analysis process, Hanning and Blackman windows with 50% overlap were used, detrending was applied via a third-order Butterworth low-pass filter at 20 kHz, and Welch’s method with multiple block averaging was employed. Figure 9 reflects the PSD curve obtained from the unsteady analysis of the Fourier transform. It can be observed that under the condition of noise flow, the main frequency components of the root of the secondary shockwave, the middle of the secondary shockwave, and the strong shockwave region are apparent, and the frequency peaks of the slip line region are more prominent. For quiet downflow, no obvious main frequency information can be extracted from the middle and strong shock region of the secondary shockwave. However, clear frequency information can be extracted from the root and slip line region of the secondary shockwave.

From the comparative analysis of each region, the unsteady motion in the slip line region is the most intense. The unsteady motion characteristics of the secondary shockwave and the intense shockwave are not apparent in the middle of the secondary shockwave and the strong shockwave region, which is consistent with the results of RMS.

4. Analysis of the Separation Formation Mechanism

4.1. Boundary Layer Spatial FFT Results

Shockwave/boundary layer interaction characteristics are closely related to the development of the boundary layer, which is determined by the development of various unstable waves in the boundary layer. First, the grayscale matrix of the separation region is taken for spatial FFT analysis, and the flow direction of the separation region is x = 203.6 mm–257.6 mm. The flow direction of the separation region under quiet downflow is from x = 178.2 mm to 257.6 mm. Figure 10 shows the spatial FFT results of the boundary layer in the separation region. It can be seen that the two types of unstable waves dominating the development of the boundary layer under incoming noise have strong nonlinear interactions, while the PSD envelope boundary corresponding to the two types of unstable waves under incoming quiet is evident. It shows that the two kinds of unstable wave structures that dominate the quiet flow are still in the independent development stage. It can be seen that the development of the boundary layer of noise flowing down is more adequate.

Then, the full flow Schlieren gray matrix was selected for spatial FFT analysis, and the selected flow direction range was x = 102.5 mm to 257.6 mm, as shown in Figure 11. Through comparative analysis, it is found that only one type of instability wave dominates the development of the boundary layer, as reflected in the quiet flow current. At the same time, two types of instability waves jointly determine the development of the all-flow boundary layer state. To sum up, the factors affecting the development of the boundary layer state are relatively simple; the disturbance factors in the boundary layer are few, and the development of relatively single unstable waves is insufficient, resulting in a low-energy amplitude, which weakens the ability to resist the inverse pressure gradient.

4.2. POD Analysis Results

FFT analysis can obtain the spectrum information of the flow structure in the flow field. The flow structure with high spectral intensity makes a greater contribution to the flow field. In contrast, the flow structure with low spectral intensity and no obvious structural characteristics corresponds to the random turbulent components in the flow field. Proper orthogonal decomposition (POD), a principal component analysis method, decomposes the flow field into different modes based on the contribution rate of each mode, thereby filtering out secondary structures and noise to obtain the main flow structure [24]. The mechanism of hypersonic shockwave/boundary layer interaction-induced separation is further analyzed. Figure 12 and Figure 13 show the POD analysis results for spatial interaction structures with noise flow and quiet flow, respectively.

It should be noted that no matter the noise flow or the quiet flow, MOD1 reflects the steady information of the flow field, which is similar to the gray average result of the whole interaction flow field by comparison. The other modes have the highest energy proportion among the unsteady modes, which reflects the main flow field structure of hypersonic shockwave/boundary layer interaction-induced separation. The main structure reflected by MOD2, MOD3, and MOD4 is the reattached shockwave. In addition, MOD4 also highlights the wake structure of the shockwave–shock interaction region and the linear development of the boundary layer. The outstanding feature of the residual mode analysis interaction structure is the special interaction structure in which the reattached shockwave interacts with the separation region, exhibiting obvious unsteady motion characteristics. It is a characteristic structure of the wall separation region associated with the motion of the space shockwave/shockwave interaction structure. The special interaction structure of quiet flow and shockwave contact with the separation region is more evident in the modal analysis results, and MOD2 is the representative mode.

4.3. DMD Analysis Results

For some complex flows, some low-energy features may have a significant impact on the dynamic characteristics of the flow field. Therefore, a method to evaluate the flow evolution based on the characteristic values of the dynamic system emerges, namely the DMD method (Dynamic Mode Decomposition method). DMD sorted the system according to frequency and extracted the characteristic frequency of the system, allowing for the observation of the contribution of flow structures with different frequencies to the flow field [25]. In the study, the standard DMD algorithm was adopted, with a maximum rank value of 200. Figure 14 shows the DMD analysis results of spatial interaction structures with noise incoming and quiet incoming, respectively. Based on the processing with the DMD method, if the eigenvalues are all distributed within the unit circle, it indicates that the computational system is statistically stable and convergent. As shown in Figure 14a,b, the eigenvalue spectrum obtained via the DMD method reveals that all eigenvalues are distributed near |ξ(μi)| = 1, suggesting that the investigated Schlieren sequence holds significant relevance for DMD analysis. The moduli corresponding to the frequencies of all DMD modes are presented in Figure 14c,d, where the magnitude of each modulus represents the energy proportion of its associated coherent structure. Figure 15 and Figure 16 show the DMD analysis results for spatial interaction structures with noise and quiet incoming, respectively.

Similarly, when the characteristic frequency of the flow field is 0, it means that the DMD mode reflects the steady flow field structure. Through comparative analysis, the DMD steady mode results are similar to the Schlieren gray average results, reflecting the scientific nature of using the DMD method to analyze hypersonic shockwave/boundary layer interaction flow fields. Compared with the DMD characteristic frequency of noise flow and quiet flow, the characteristic frequency of quiet flow is obviously lower. However, the special interaction structure of the contact between the secondary shockwave and the separation region is also captured in the two interaction flow fields, where the corresponding frequency of the structure is f = 25 Hz when the noise is flowing down, and the corresponding frequency of the structure is f = 30 Hz when the silence is flowing down. It is worth noting that the overall separation structure of the hypersonic shockwave/boundary layer interaction flow field is resolved in the DMD analysis. The characteristic frequency of the overall separation structure corresponding to the noise flow downstream is f = 521 Hz. In contrast, the characteristic frequency of the quiet flow downstream is f = 73 Hz, which is consistent with the RMS analysis results of the interaction flow field. Except for the apparent three-dimensional effect and the influence of boundary laminar flow state, the dimensionless parameter Strouhal number (St) of the low-frequency unsteady peak of SWBLI under investigation is basically between 0.02 and 0.04 [26]. After calculation, the St of the noise flow field is 0.036, and the St of the quiet flow field is 0.007. The noise flow field conforms to the conventional St interval. However, for the quiet flow field, its boundary laminar flow state is entirely different from that of the noise flow field; therefore, it is also a normal phenomenon for it to fall outside the conventional range.

5. Conclusions

In this paper, an experimental study of hypersonic shock/boundary layer interaction characteristics is conducted under quiet and noisy incoming flow, conditions, respectively, for the double compression corner-plate model. Using high-speed Schlieren imaging, the typical structures of shock/boundary layer interaction and shock/shock interaction above the corner are explored under both quiet and noisy incoming flow conditions. Then, based on the gray average, RMS analysis, spatial FFT, POD, and DMD methods, the time-average and unsteady characteristics of the double compression corner configuration-induced separation were studied, and the difference law of the wind tunnel noise level on interaction characteristics was summarized. Finally, from the perspective of the development of unstable waves leading to the stability of the flat-plate boundary layer, the formation mechanism of separation is discussed. This provides technical support for the aerodynamic design inside and outside the hypersonic vehicle and the research and optimization of targeted effects (drag, total pressure loss, heating load downstream, etc.).