Unsteady Aerodynamics of Continuously Morphing Airfoils from Transonic to Hypersonic Regimes
Abstract
1. Introduction
2. Methodology
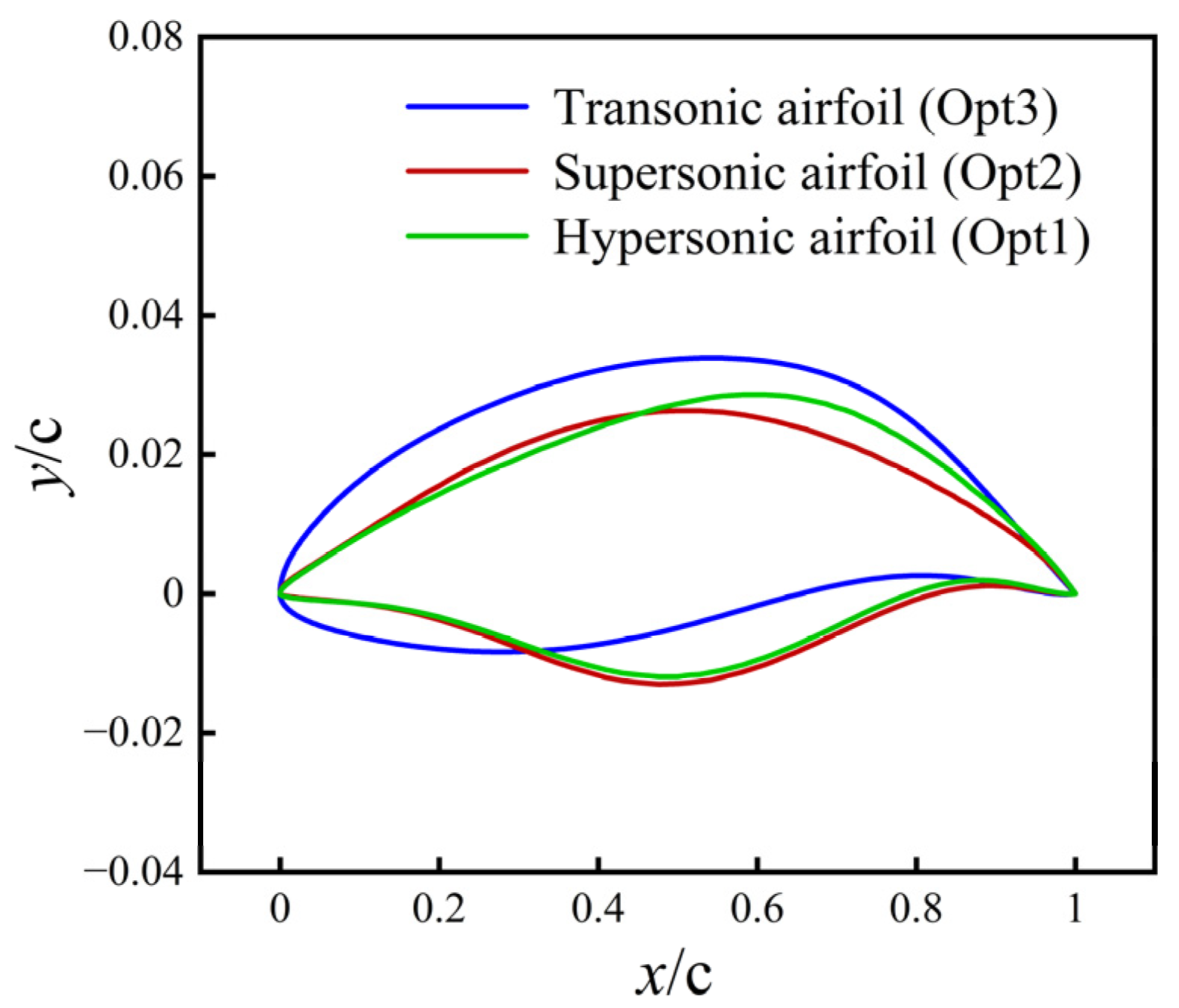
2.1. Baseline Airfoils and Performance Tendencies
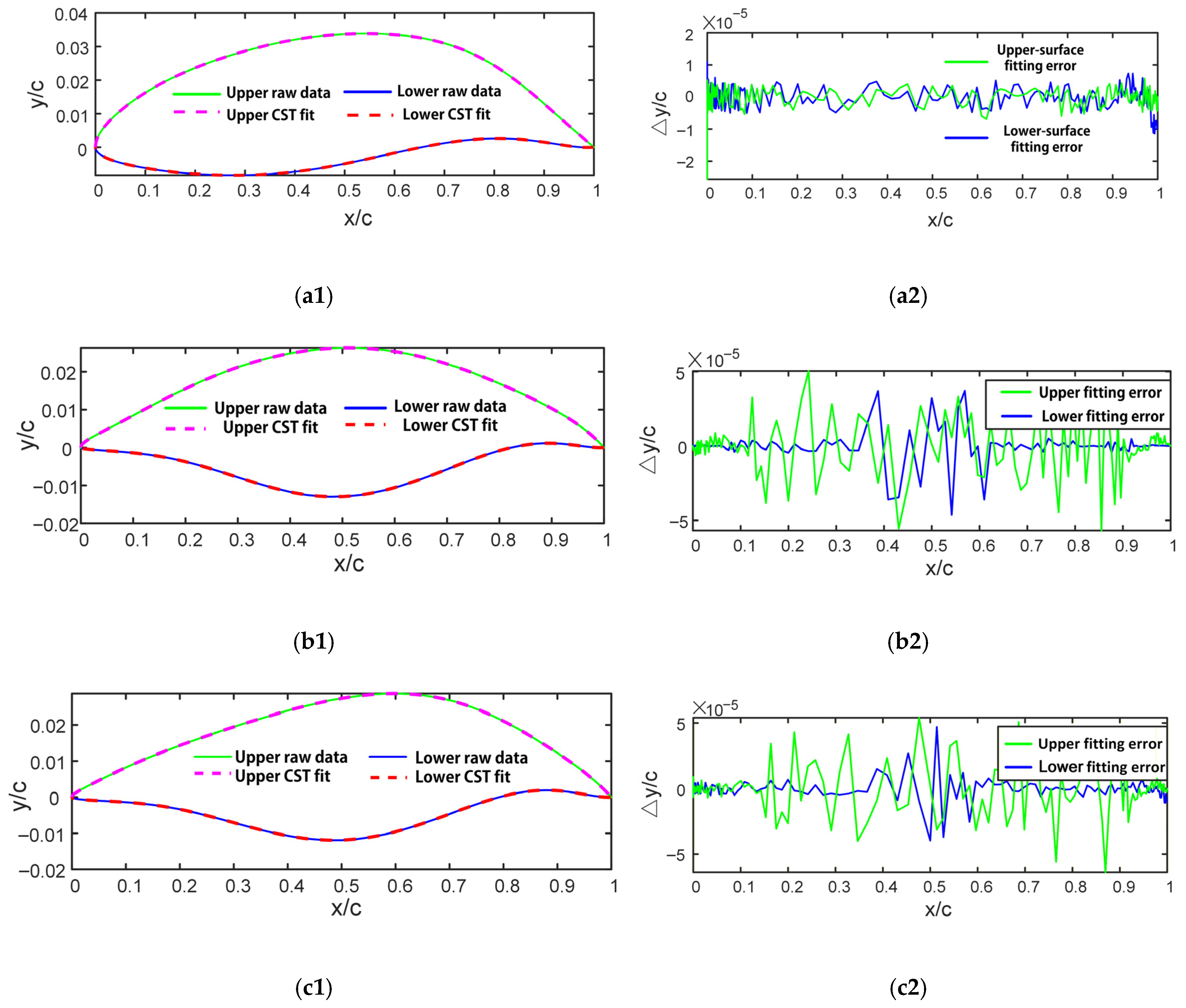
2.2. CST Parameterization and Geometric Reconstruction
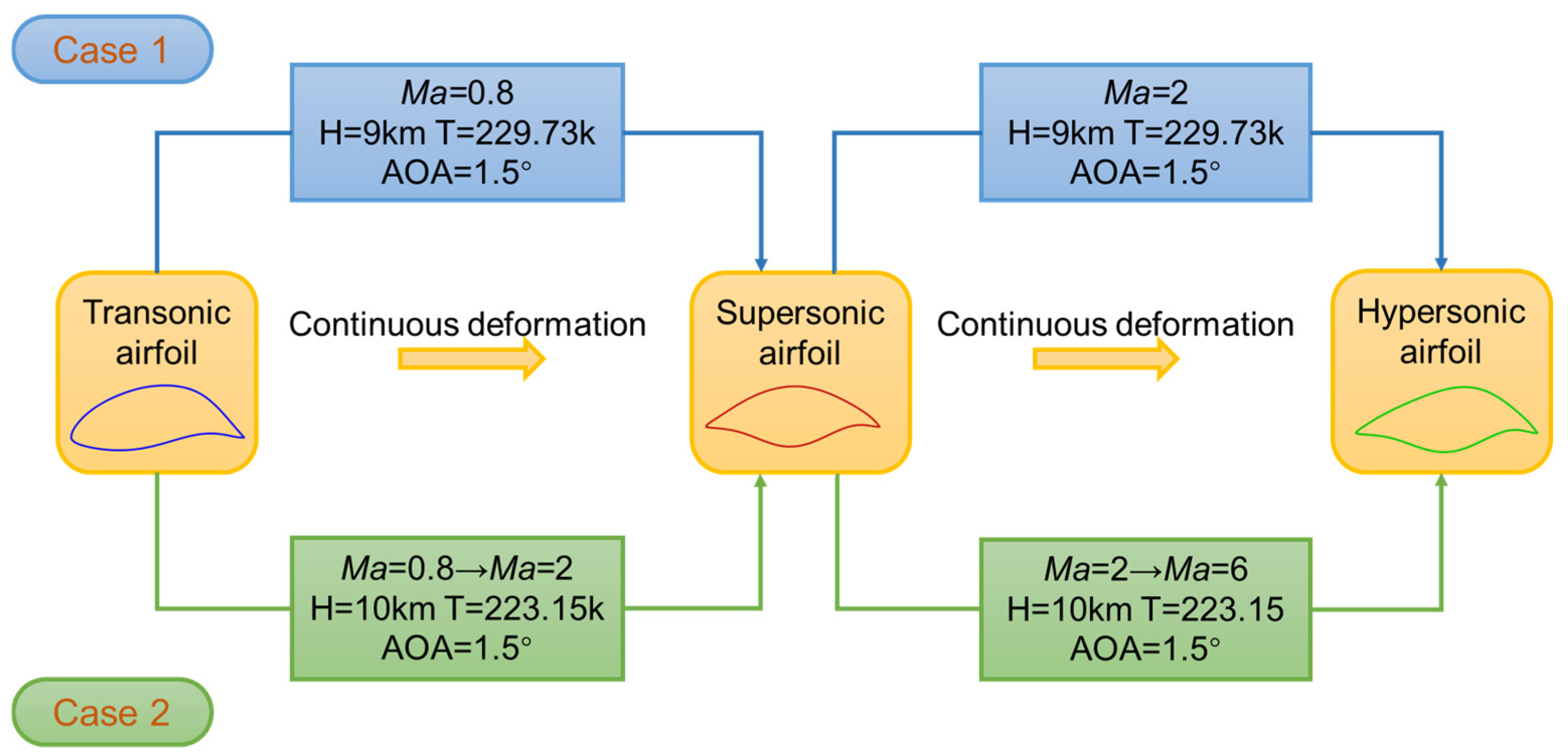
2.3. Morphing Trajectory and Mach Number Scheduling
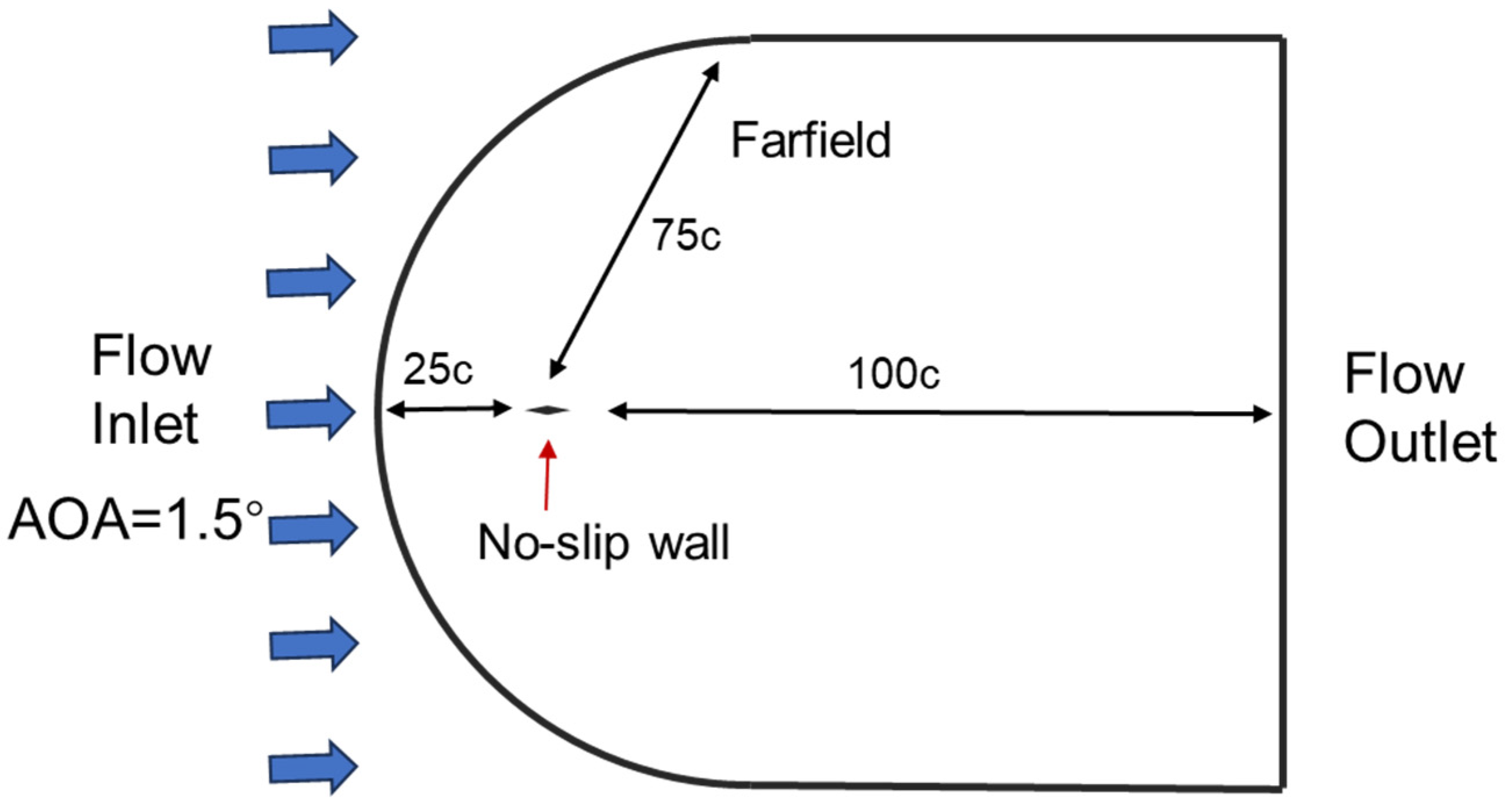
2.4. Computational Domain and Grid Generation
2.5. Dynamic Mesh and Unsteady Solver Settings
2.6. Numerical Model Credibility and Methodological Consistency
3. Results and Discussion
3.1. Case 1: Constant Mach Morphing as a Physical Reference
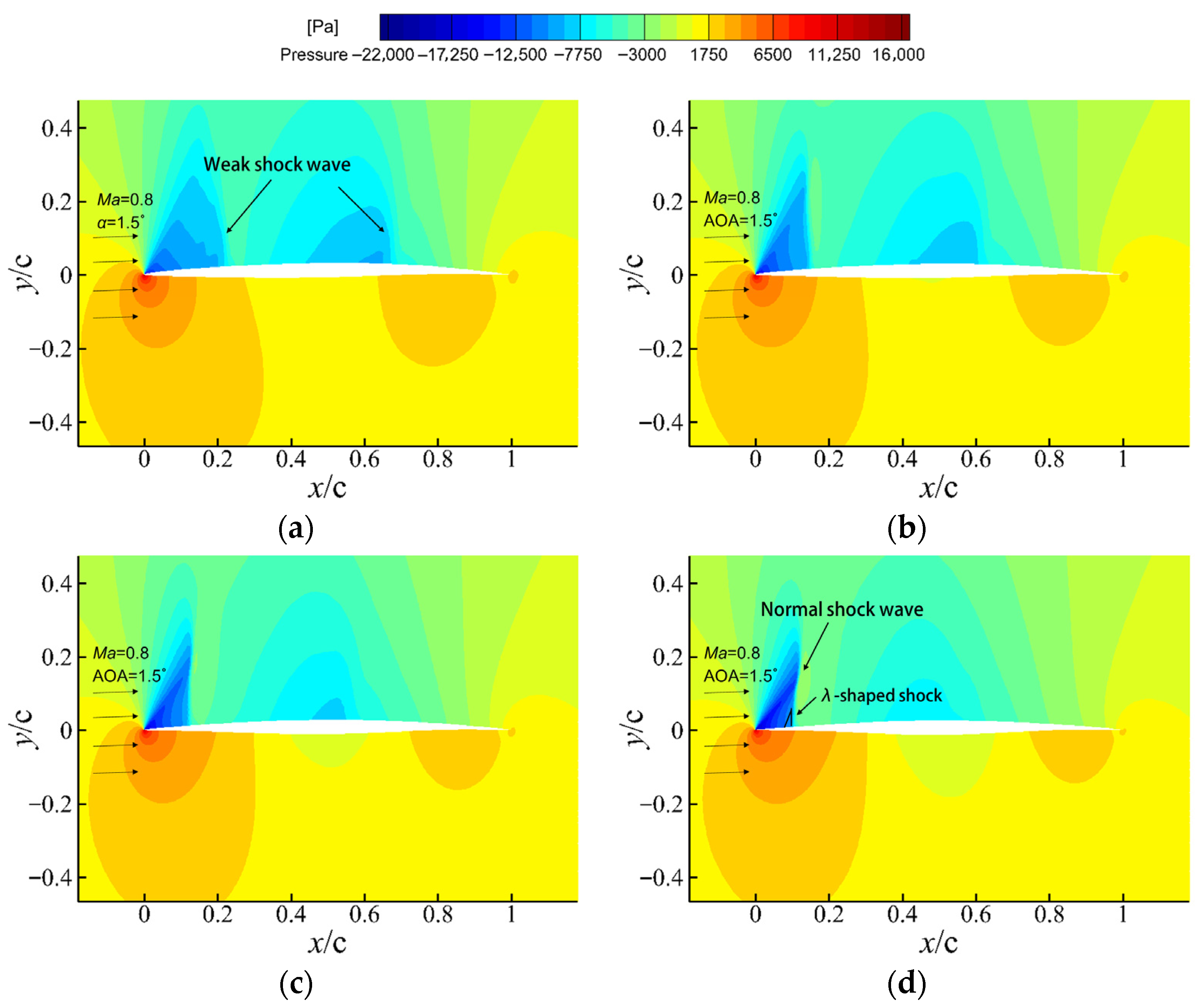
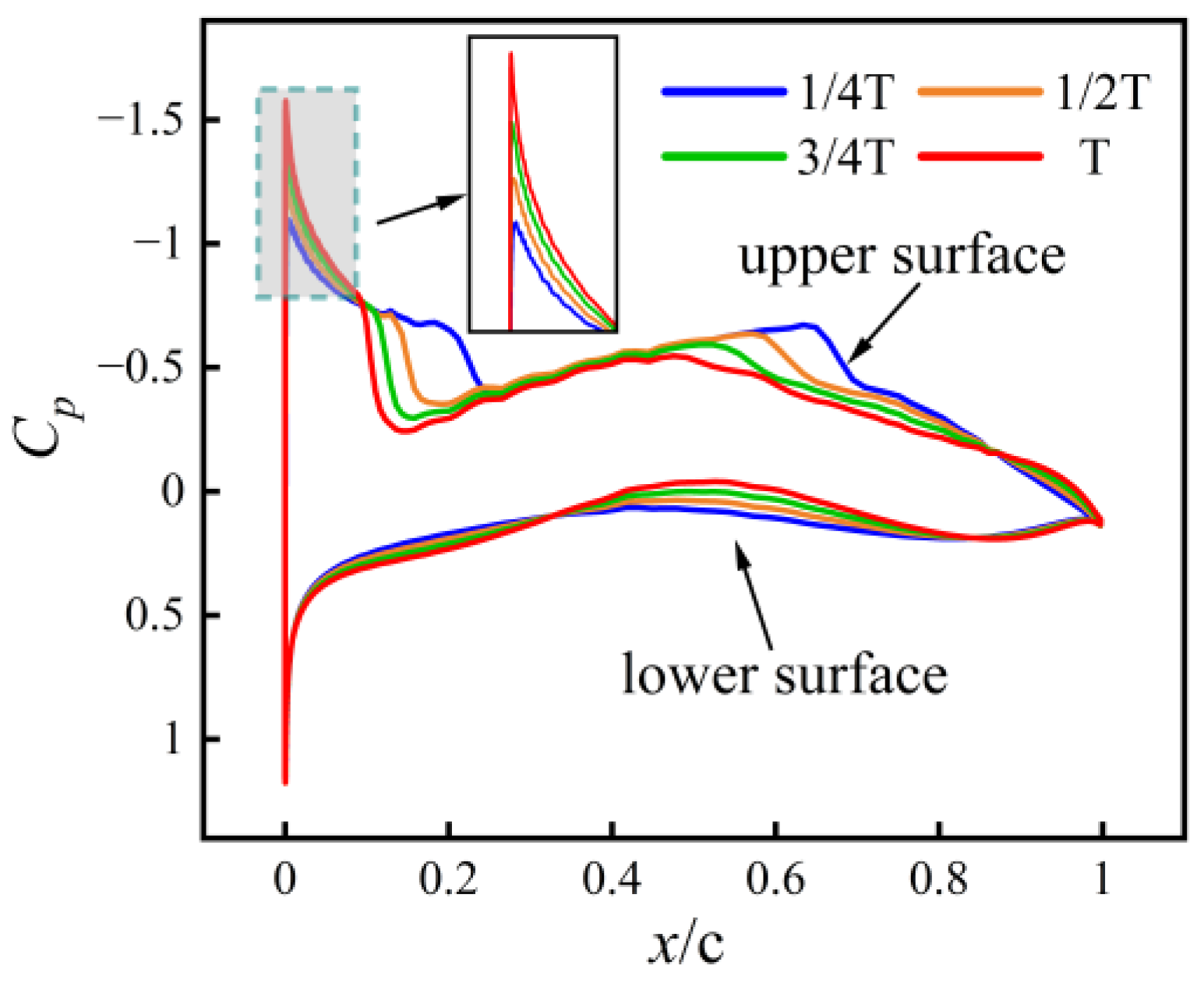
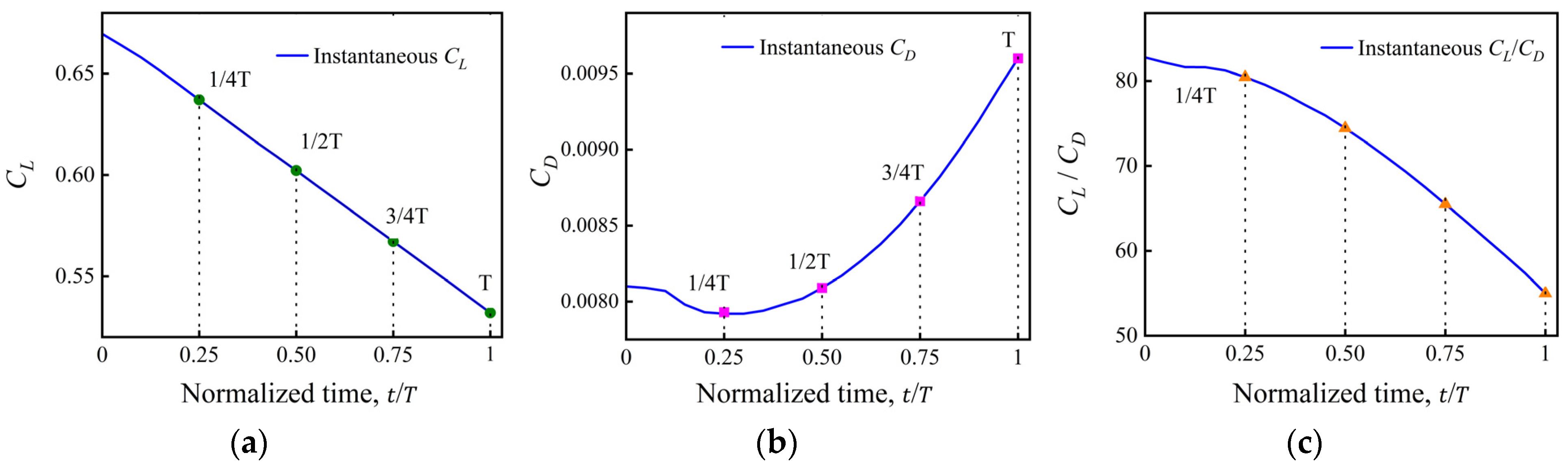
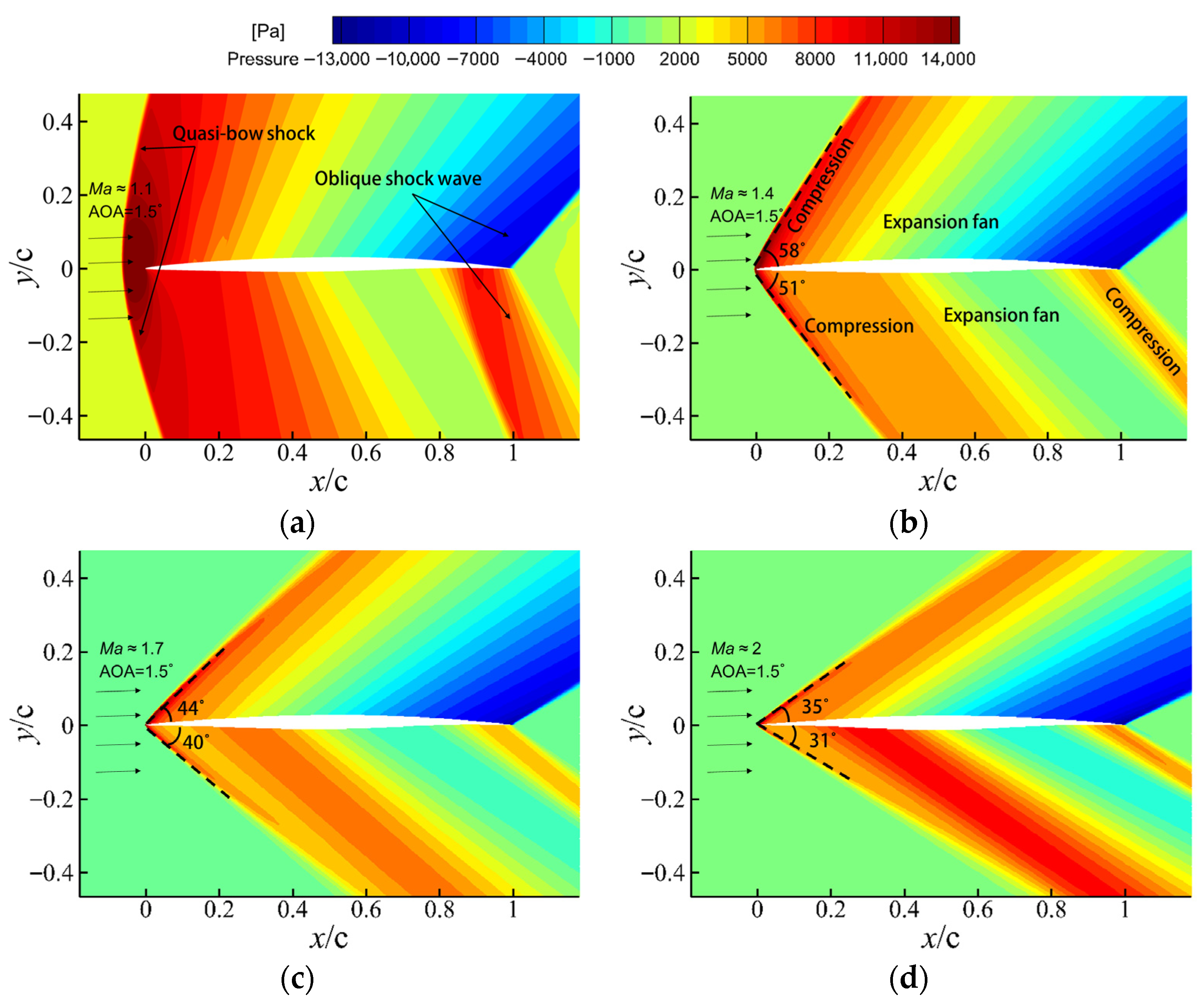
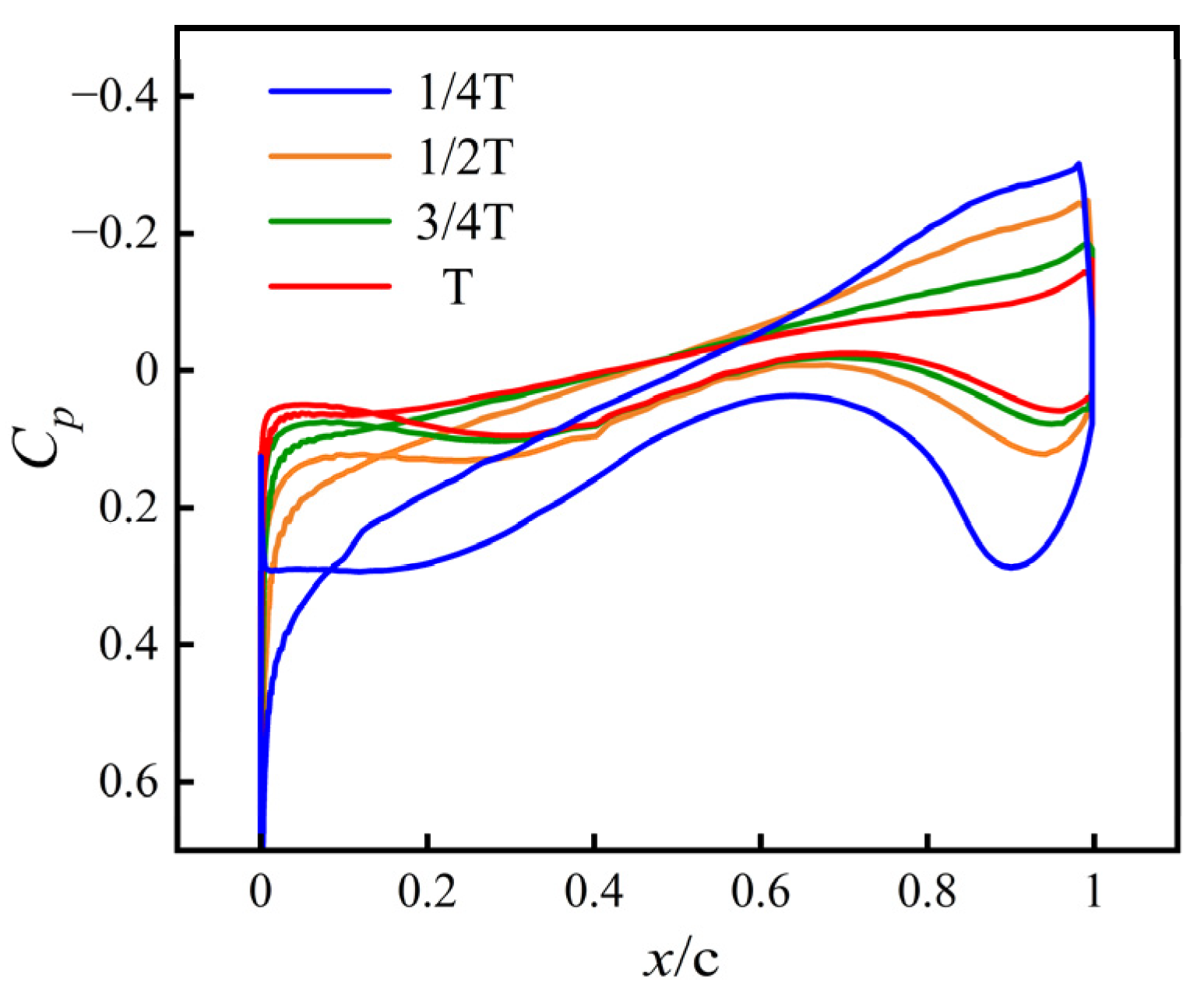
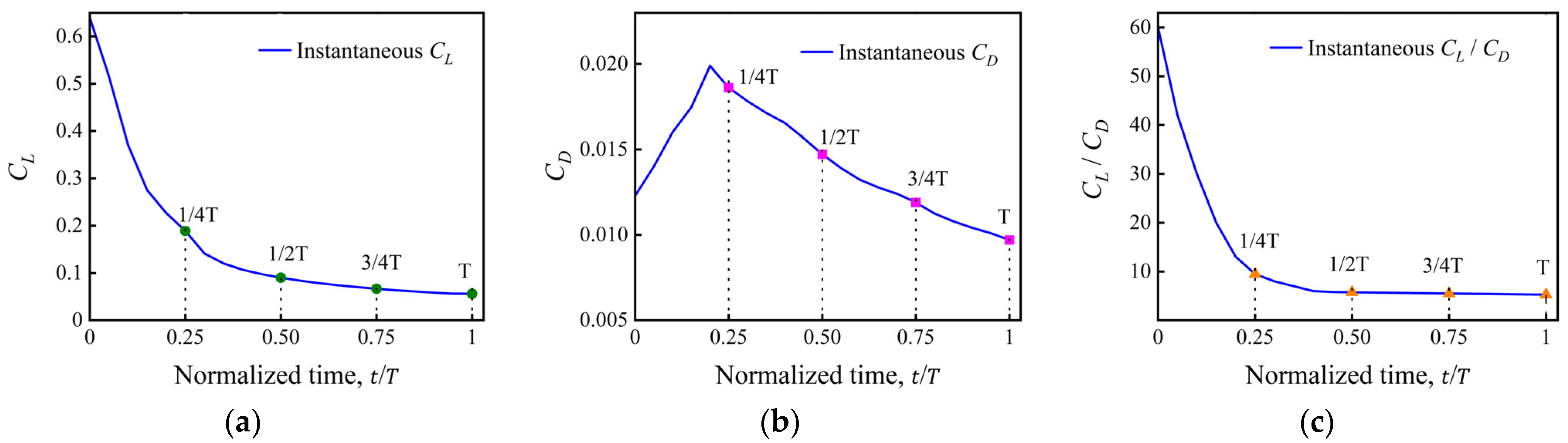
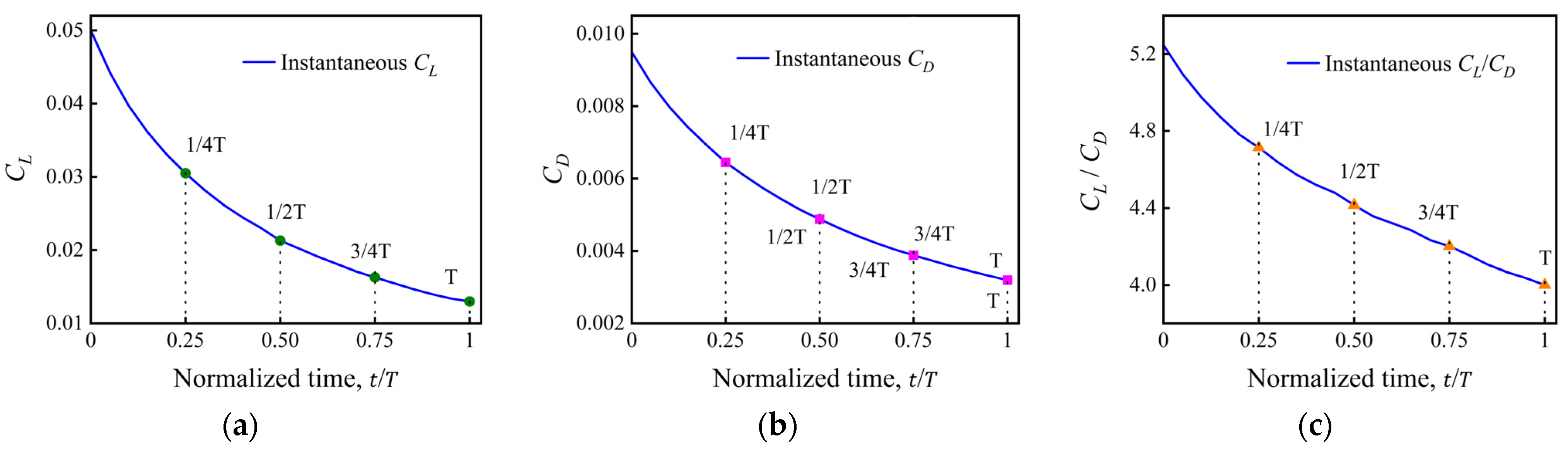
3.1.1. Transonic Morphing at Ma = 0.8
- •
- Pressure Contours
- •
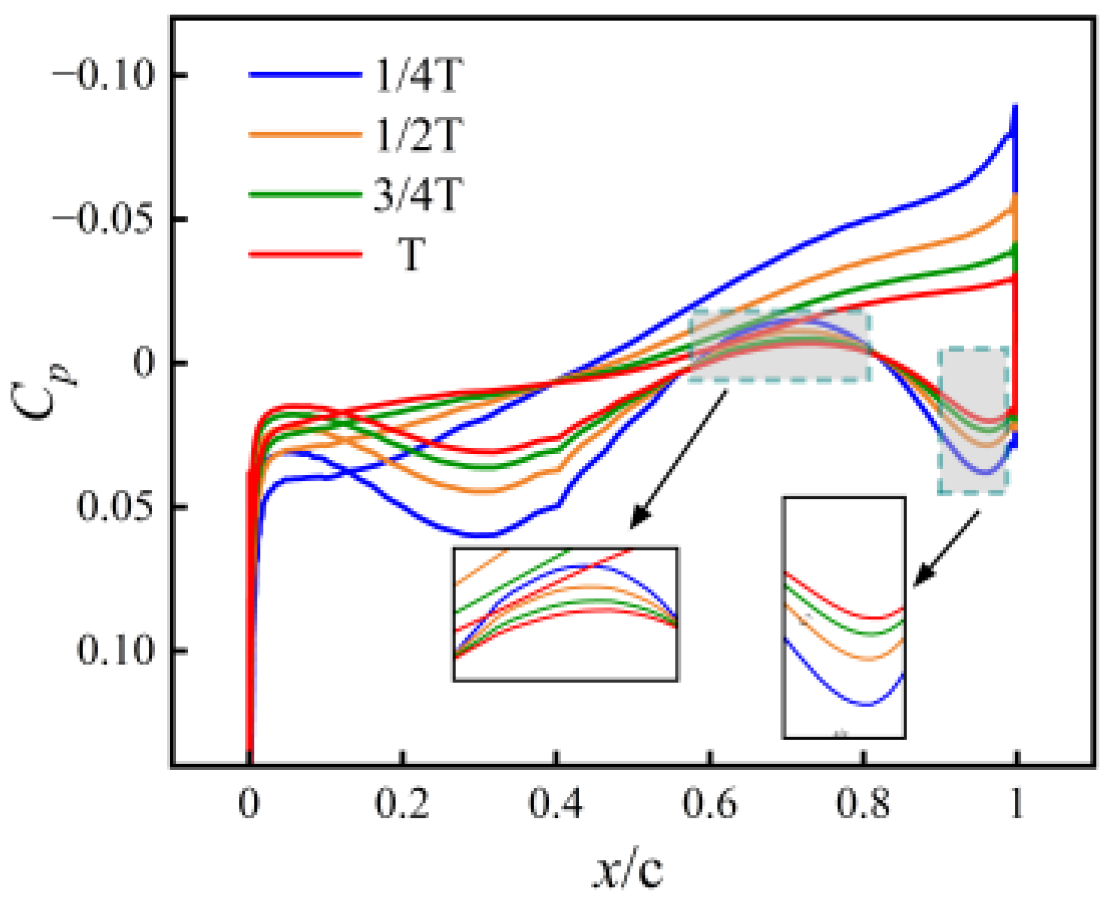
- Pressure coefficients
- •
- Aerodynamic coefficients
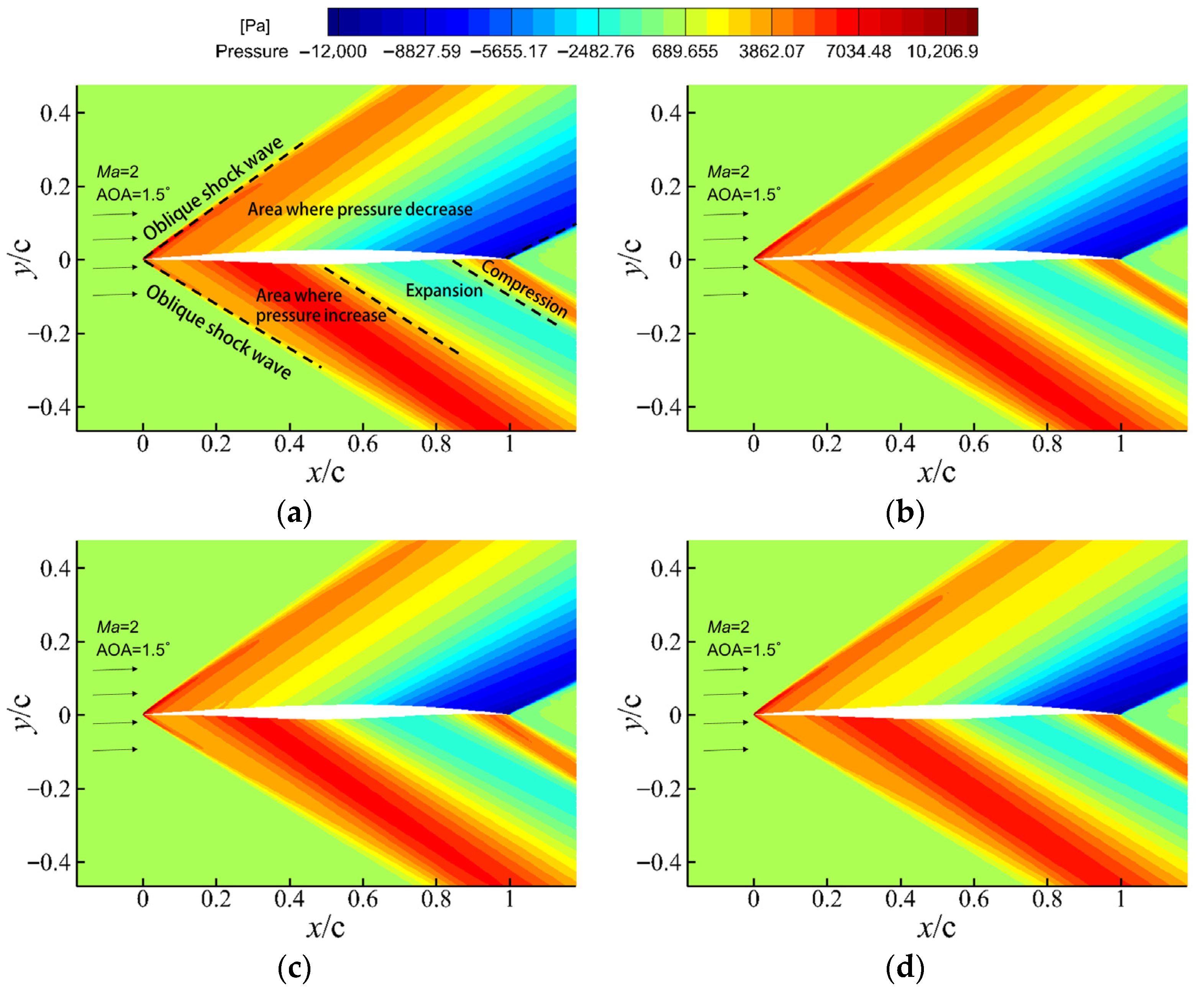
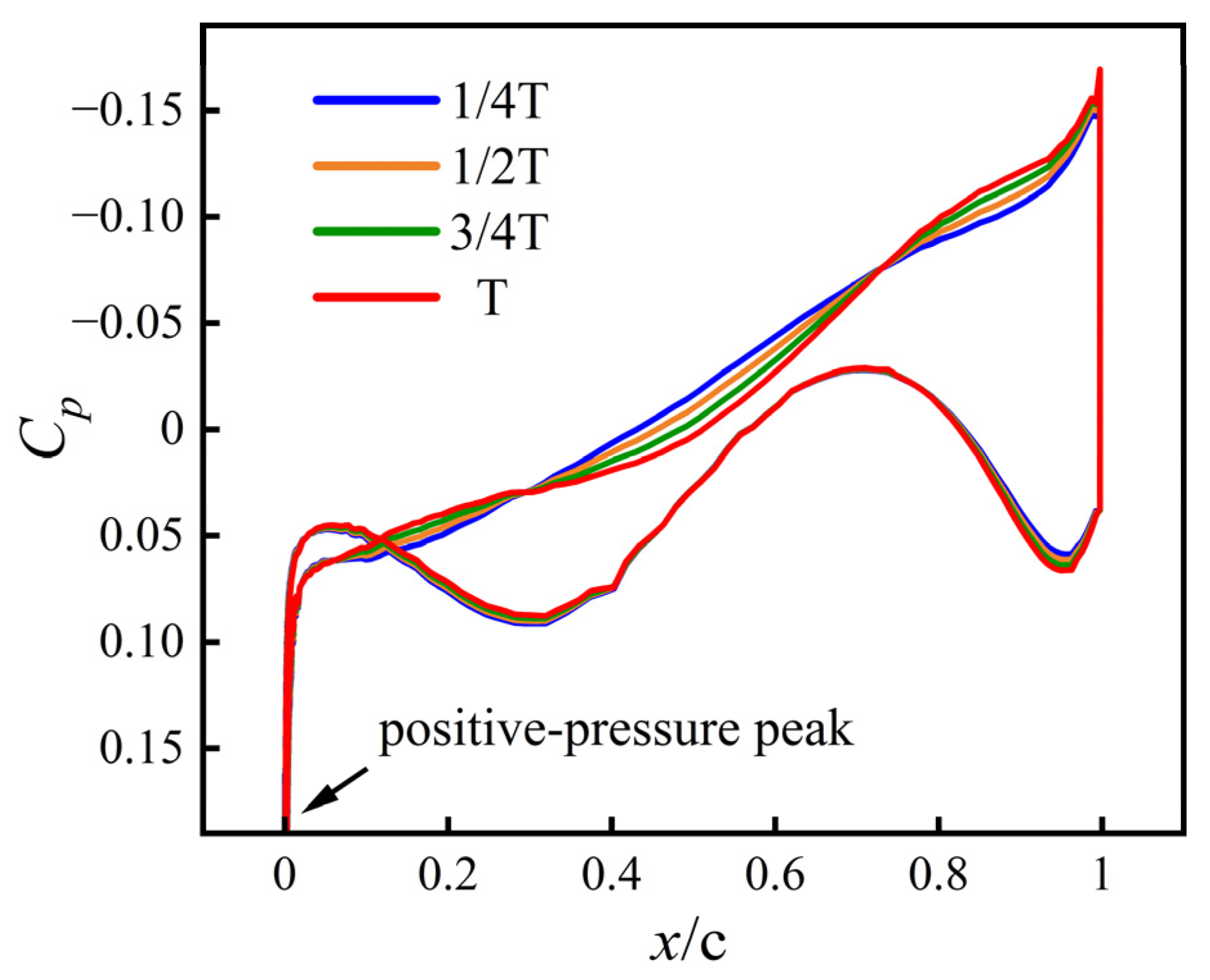
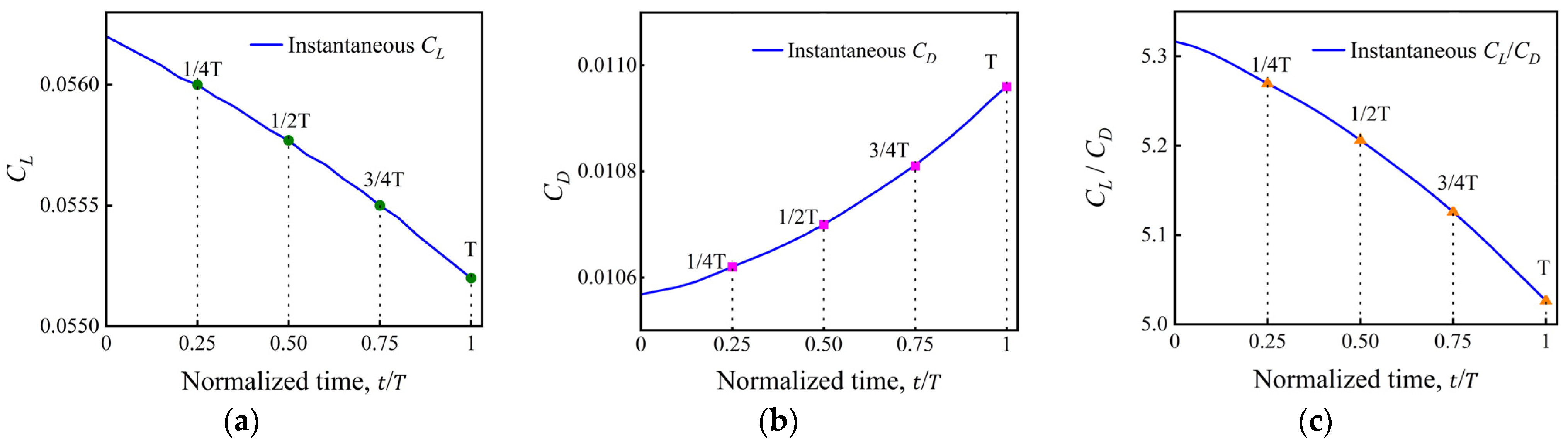
3.1.2. Supersonic Morphing at Ma = 2
- •
- Pressure Contours
- •
- Pressure coefficients
- •
- Aerodynamic coefficients
3.2. Case 2: Coupled Morphing–Acceleration as a Unified Transonic–Hypersonic Adaptation Process
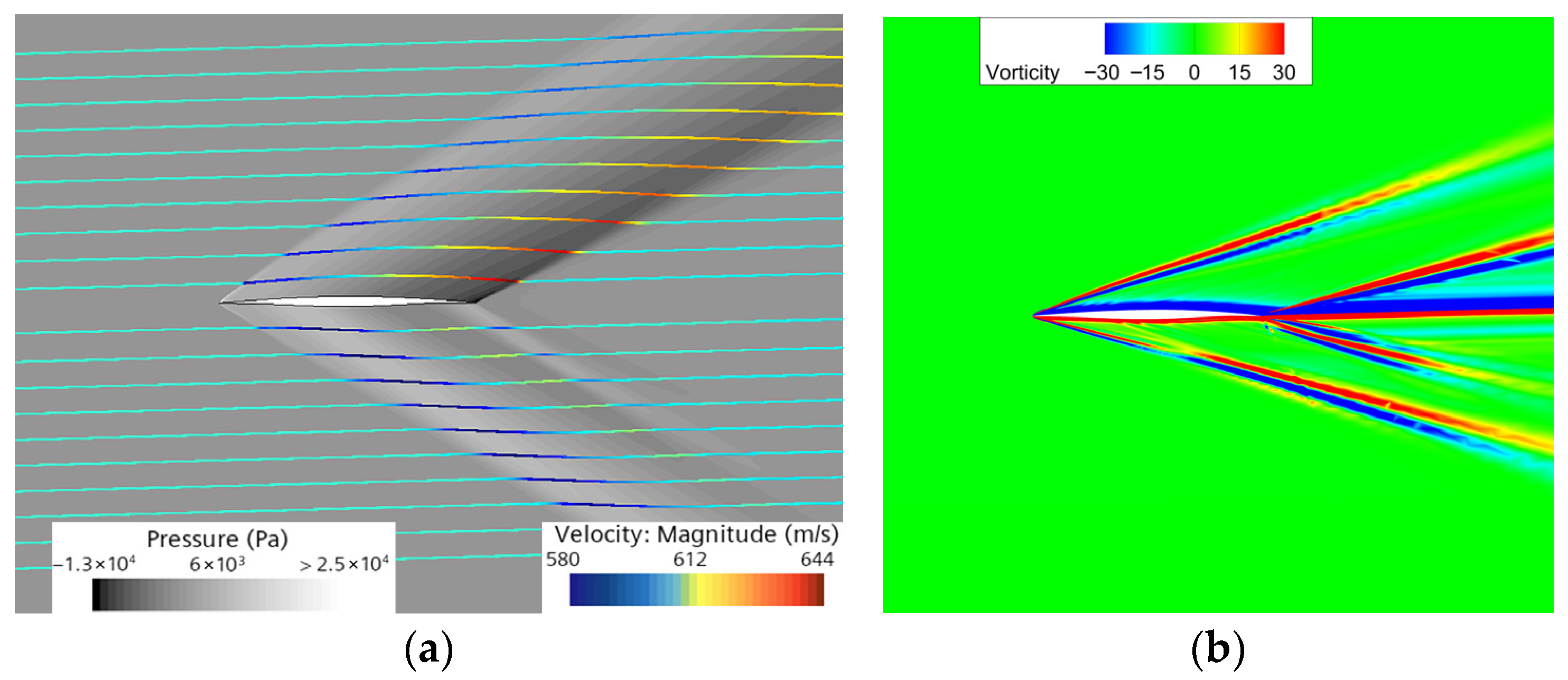
3.2.1. Stage 1: Transonic ⟶ Supersonic (Ma = 0.8 ⟶ 2)
- •
- Pressure Contours
- •
- Pressure coefficients
- •
- Aerodynamic coefficients
- •
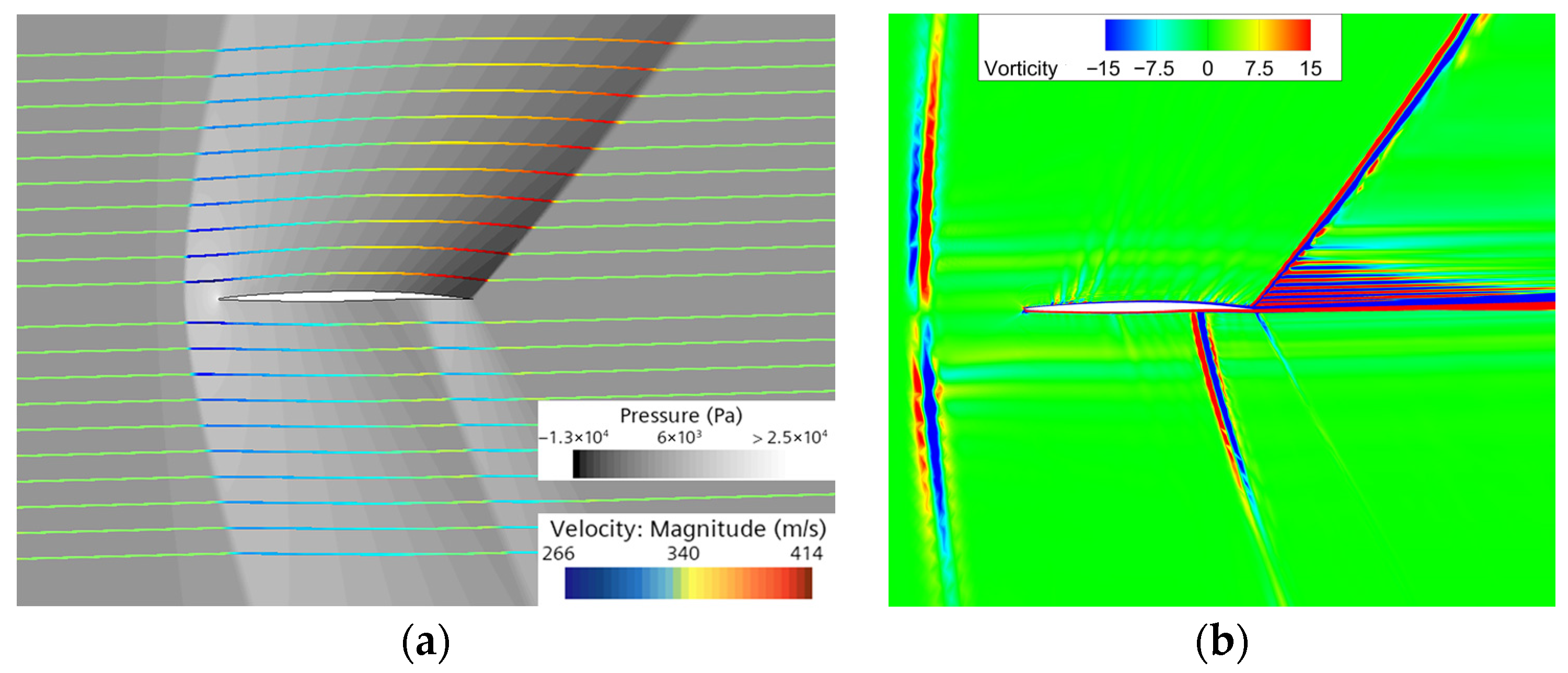
- Streamlines and vorticity at Ma = 1.1
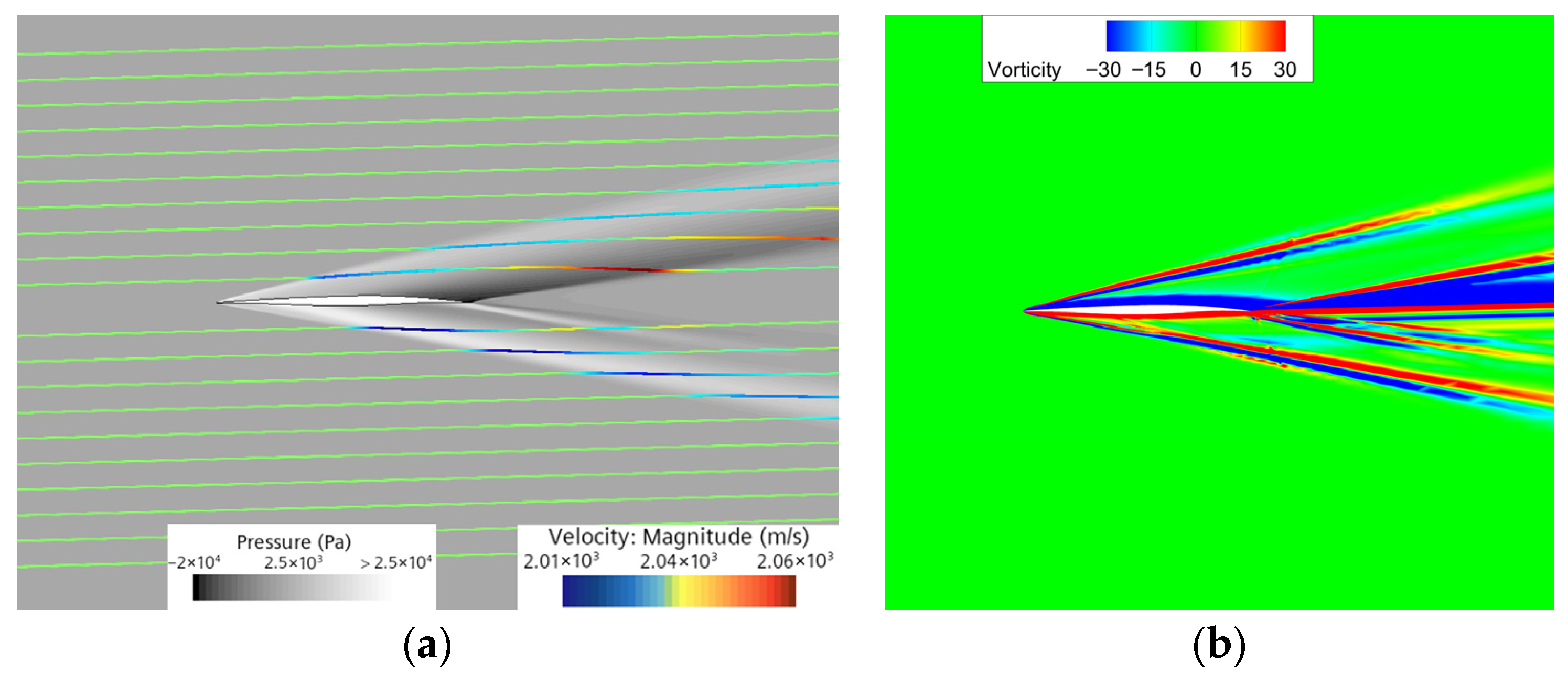
3.2.2. Stage 2: Supersonic → Hypersonic (Ma = 2 → 6)
- •
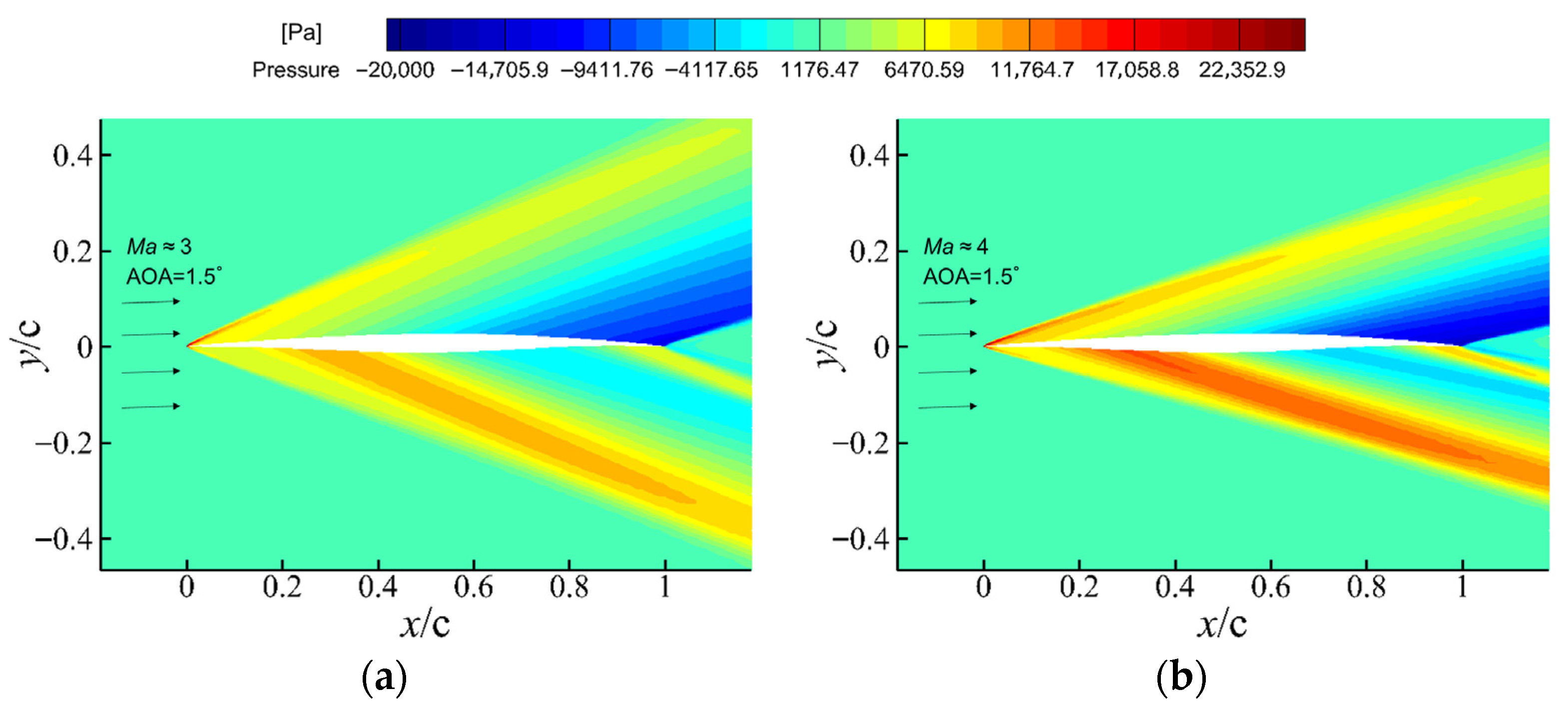
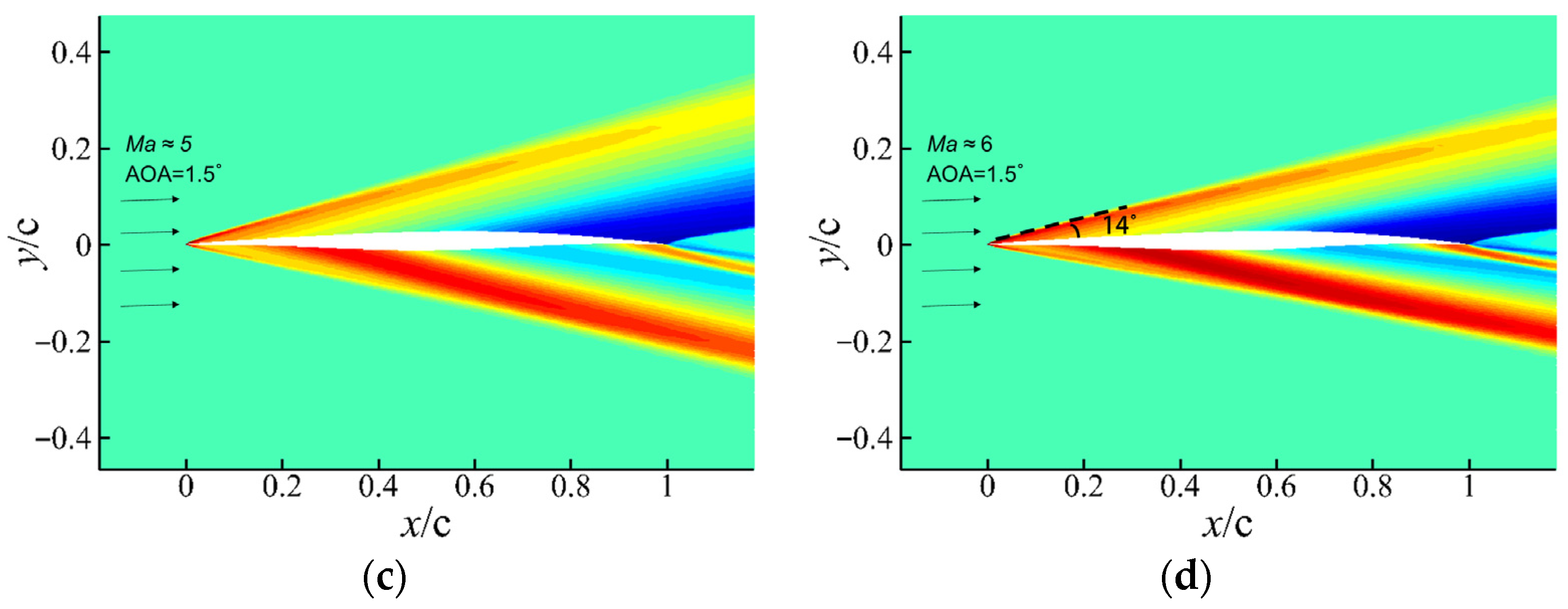
- Pressure Contours
- •
- Pressure coefficients
- •
- Aerodynamic Coefficients
- •
- Streamline and Vorticity Structures at Ma = 2 and Ma = 6
4. Conclusions
- Continuous curvature variation ensures a smooth and stable deformation process. The CST interpolation eliminates slope discontinuities, enabling shock structures to migrate steadily along the surface with no oscillation, separation, or abrupt load changes throughout all simulations.
- The transonic regime exhibits the strongest sensitivity to shape evolution. At Ma = 0.8, the upper-surface suction peak shifts noticeably during the morphing process, resulting in a 19.4% decrease in lift and a 19% increase in drag, which together cause a 28.8% reduction in lift-to-drag ratio. This behavior highlights the pronounced coupling between shock position and pressure distribution in transonic flows.
- The supersonic deformation stage remains highly robust. At Ma = 2, the characteristic “compression–expansion–recompression’’ structure is preserved, and the aerodynamic response is mild, with lift changing by only 1.4% and drag by 2.6% across the morphing interval, demonstrating the inherent robustness of supersonic flow fields to smooth geometric deformation.
- Across the entire wide-speed-range envelope (Ma = 0.8–6), the morphing airfoil maintains L/D > 4, indicating a consistently acceptable aerodynamic efficiency for conceptual high-speed lifting surface design compared with fixed-geometry configurations operating far from their design points.
- The results indicate a common tendency in flow adaptation across transonic, supersonic, and hypersonic regimes. Continuous geometric deformation influences the organization of compression and expansion wave systems and is accompanied by systematic shock migration. Meanwhile, the wake vorticity field exhibits a gradual transition from organized shear layers to more complex vortical structures as the Mach number increases, reflecting differing sensitivities of the flow field to geometric perturbations.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| CST | Class–Shape Transformation |
| URANS | Unsteady Reynolds-Averaged Navier–Stokes |
| RBF | Radial Basis Function |
| CFD | Computational Fluid Dynamics |
| SST | Shear Stress Transport |
| SBLI | Shock–Boundary-Layer Interaction |
| NSGA-II | Nondominated Sorting Genetic Algorithm II |
| AOA | Angle of Attack |
References
- Barbarino, S.; Bilgen, O.; Ajaj, R.M.; Friswell, M.I.; Inman, D.J. A review of morphing aircraft. J. Intell. Mater. Syst. Struct. 2011, 22, 823–877. [Google Scholar] [CrossRef]
- Chu, L.; Li, Q.; Gu, F.; Du, X.; He, Y.; Deng, Y. Design, modeling, and control of morphing aircraft: A review. Chin. J. Aeronaut. 2022, 35, 220–246. [Google Scholar] [CrossRef]
- Chen, S.; Jia, M.; Liu, Y.; Gao, Z. Deformation modes and key technologies of aerodynamic layout design for morphing aircraft. Acta Aeronaut. Astronaut. Sin. 2024, 45, 6. [Google Scholar]
- Kabir, A.; Al-Obaidi, A.S.M. A survey of trailing-edge morphing airfoil studies: Configurations, performance, and applications. In Proceedings of the 9th International Conference on Recent Advances and Innovations in Engineering (ICRAIE), Kuala Lumpur, Malaysia, 23–24 August 2025; IEEE: New York, NY, USA, 2025; pp. 183–188. [Google Scholar]
- Weisshaar, T.A. Morphing aircraft technology—New shapes for aircraft design. In Multifunctional Structures/Integration of Sensors and Antennas; RTO: Paris, France, 2006. [Google Scholar]
- Manor, D.; Johnson, D. Landing the wave-rider: Challenges and solutions. In Proceedings of the AIAA/CIRA 13th International Space Planes and Hypersonic Systems and Technologies Conference, Capua, Italy, 16–20 May 2005; Paper No. 3201; AIAA: Reston, VI, USA, 2005. [Google Scholar]
- National Research Council. Decadal Survey of Civil Aeronautics: Foundation for the Future; National Academies Press: Washington, DC, USA, 2006. [Google Scholar]
- Leite, B.; Afonso, F.; Suleman, A. Aerodynamic shape optimization of a symmetric airfoil from subsonic to hypersonic flight regimes. Fluids 2022, 7, 353. [Google Scholar] [CrossRef]
- Xie, Z.; Zhao, Z.T.; Huang, W.; Liu, C.Y.; Choubey, G. Aerodynamic analysis of hypersonic gliding vehicles with wide-speed range based on the cuspidal waverider. Fluid Dyn. 2024, 59, 622–637. [Google Scholar] [CrossRef]
- Tauber, M.E.; Menees, G.P.; Adelman, H.G. Aerothermodynamics of transatmospheric vehicles. J. Aircr. 1987, 24, 594–602. [Google Scholar] [CrossRef]
- Viviani, A.; Pezzella, G. Next generation launchers aerodynamics. TC 2012, 37, 661. [Google Scholar]
- Burdette, D.A.; Martins, J.R.R.A. Design of a transonic wing with an adaptive morphing trailing edge via aerostructural optimization. Aerosp. Sci. Technol. 2018, 81, 192–203. [Google Scholar] [CrossRef]
- Schuet, S.; Lombaerts, T.; Acosta, D.; Wheeler, K.; Kaneshige, J. An adaptive nonlinear aircraft maneuvering envelope estimation approach for online applications. In Proceedings of the AIAA Guidance, Navigation, and Control Conference, National Harbor, MD, USA, 9–13 January 2014; Paper No. 0268; AIAA: Reston, VI, USA, 2014. [Google Scholar]
- Mowla, M.N.; Asadi, D.; Durhasan, T.; Jafari, J.R.; Amoozgar, M. Recent advancements in morphing applications: Architecture, artificial intelligence integration, challenges, and future trends—A comprehensive survey. Aerosp. Sci. Technol. 2025, 161, 110102. [Google Scholar] [CrossRef]
- Mangano, M.; Martins, J.R.R.A. Multipoint aerodynamic shape optimization for subsonic and supersonic regimes. J. Aircr. 2021, 58, 650–662. [Google Scholar] [CrossRef]
- Johnson, D.; Thomas, R.; Manor, D. Stability and control analysis of a wave-rider TSTO second stage. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001; Paper No. 2001-1834; AIAA: Reston, VI, USA, 2001. [Google Scholar]
- Zhang, Y.; Luo, J.; Zheng, Y.; Liu, Y. Aerodynamic Optimization of Airfoil in Wide Range of Operating Conditions Based on Reinforcement Learning. Aerospace 2025, 12, 443. [Google Scholar] [CrossRef]
- Yu, J.; Zhou, G.; Han, Q.; Jia, H.; Zhang, P.; Liu, S.; Li, W. Data mining of Pareto-optimal wide-Mach-number-range airfoil shapes. In Proceedings of the 2nd Aerospace Frontiers Conference (AFC 2025), Beijing, China, 11–14 April 2025; Springer Nature: Singapore, 2025; pp. 118–128. [Google Scholar]
- Wei, C.; Li, R.; Xu, P.; Duan, Y.; Wang, S.; Chang, Y. Aerodynamic shape optimization for a hypersonic vehicle flying over a range of speeds. J. Phys. Conf. Ser. 2025, 3006, 012043. [Google Scholar] [CrossRef]
- Longtin Martel, S.; Bashir, M.; Botez, R.M.; Wong, T. A Pareto multi-objective optimization of a camber morphing airfoil using non-dominated sorting genetic algorithm. In Proceedings of the AIAA SciTech 2023 Forum, San Diego, CA, USA, 23–27 January 2023; Paper No. 1583; AIAA: Reston, VI, USA, 2023. [Google Scholar]
- Liu, B.; Liang, H.; Han, Z.H.; Yang, G. Surrogate-based aerodynamic shape optimization of a morphing wing considering a wide Mach-number range. Aerosp. Sci. Technol. 2022, 124, 107557. [Google Scholar] [CrossRef]
- Mangano, M. Multi-Point Aerodynamic Shape Optimization for Airfoils and Wings at Supersonic and Subsonic Regimes. Master’s Thesis, Delft University of Technology, Delft, The Netherlands, 20 May 2019. [Google Scholar]
- Zhang, Y.; Han, Z.; Zhou, Z.; Tang, J.; Zhang, K.; Song, W. Aerodynamic design optimization of wide-Mach-number-range airfoils for hypersonic vehicles. Acta Aerodyn. Sin. 2021, 39, 111–127. [Google Scholar]
- Szulc, O.; Doerffer, P.; Flaszyński, P.; Suresh, T. Numerical modelling of shock wave–boundary layer interaction control by passive wall ventilation. Comput. Fluids 2020, 200, 104435. [Google Scholar] [CrossRef]
- Anderson, J.D. Modern Compressible Flow: With Historical Perspective; McGraw-Hill: New York, NY, USA, 2003. [Google Scholar]
- Gaitonde, D.V. Progress in shock wave/boundary layer interactions. Prog. Aerosp. Sci. 2015, 72, 80–99. [Google Scholar] [CrossRef]
- John, B.; Kulkarni, V.N.; Natarajan, G. Shock wave–boundary layer interactions in hypersonic flows. Int. J. Heat Mass Transf. 2014, 70, 81–90. [Google Scholar] [CrossRef]
- Chen, Y. Shock wave–boundary layer interaction: A survey of recent development. Highlights Sci. Eng. Technol. 2024, 1, A43. [Google Scholar] [CrossRef]
- Zheng, C.; Feng, Y.; Zheng, X. Effect of bulk viscosity on the hypersonic compressible turbulent boundary layer. J. Fluid Mech. 2024, 982, A24. [Google Scholar] [CrossRef]
- Viola, N.; Roncioni, P.; Gori, O.; Fusaro, R. Aerodynamic Characterization of Hypersonic Transportation Systems and Its Impact on Mission Analysis. Energies 2021, 14, 3580. [Google Scholar] [CrossRef]
- Pezzella, G.; Viviani, A. Aerodynamic analysis of a high-speed aircraft from hypersonic down to subsonic speeds. Mater. Res. Proc. 2023, 3, 230–233. [Google Scholar]
- Kulfan, B.M. Universal parametric geometry representation method. J. Aircr. 2008, 45, 142–158. [Google Scholar] [CrossRef]
- Kulfan, B.; Bussoletti, J. Fundamental parametric geometry representations for aircraft component shapes. In Proceedings of the 11th AIAA/ISSMO Multidisciplinary Analysis and Optimization Conference, Portsmouth, VA, USA, 6–8 September 2006; AIAA: Reston, VI, USA, 2006. [Google Scholar]
- Xiang, J.; Liu, K.; Li, D.; Cheng, C.; Sha, E. Unsteady aerodynamic characteristics of a morphing wing. Aircr. Eng. Aerosp. Technol. 2019, 91, 1–9. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, T.; Liu, Z.; Yu, M.; Shao, J.; Price, W.G.; Hudson, D. RBF-based interpolation and its application in flow–structure interaction. In Proceedings of the ISOPE International Ocean and Polar Engineering Conference, Shanghai, China, 11–16 October 2020; ISOPE: Cupertino, CA, USA, 2020. [Google Scholar]
- Blazek, J. Computational Fluid Dynamics: Principles and Applications; Butterworth-Heinemann: Oxford, UK, 2015. [Google Scholar]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. AIAA J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef]
- Deshpande, A. Unsteady Dynamics of Shock-Wave Boundary-Layer Interactions. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 2021. [Google Scholar]
- Mehta, R.C. Exact solutions to the oblique shock wave equation. In Proceedings of the World Congress on Aeronautics, Nano, Bio, Robotics, and Energy, Incheon, Republic of Korea, 25–28 August 2015. [Google Scholar]
- Silnikov, M.V.; Chernyshov, M.V.; Uskov, V.N. Analytical solutions for Prandtl–Meyer wave—Oblique shock overtaking interaction. Acta Astronaut. 2014, 99, 175–183. [Google Scholar] [CrossRef]
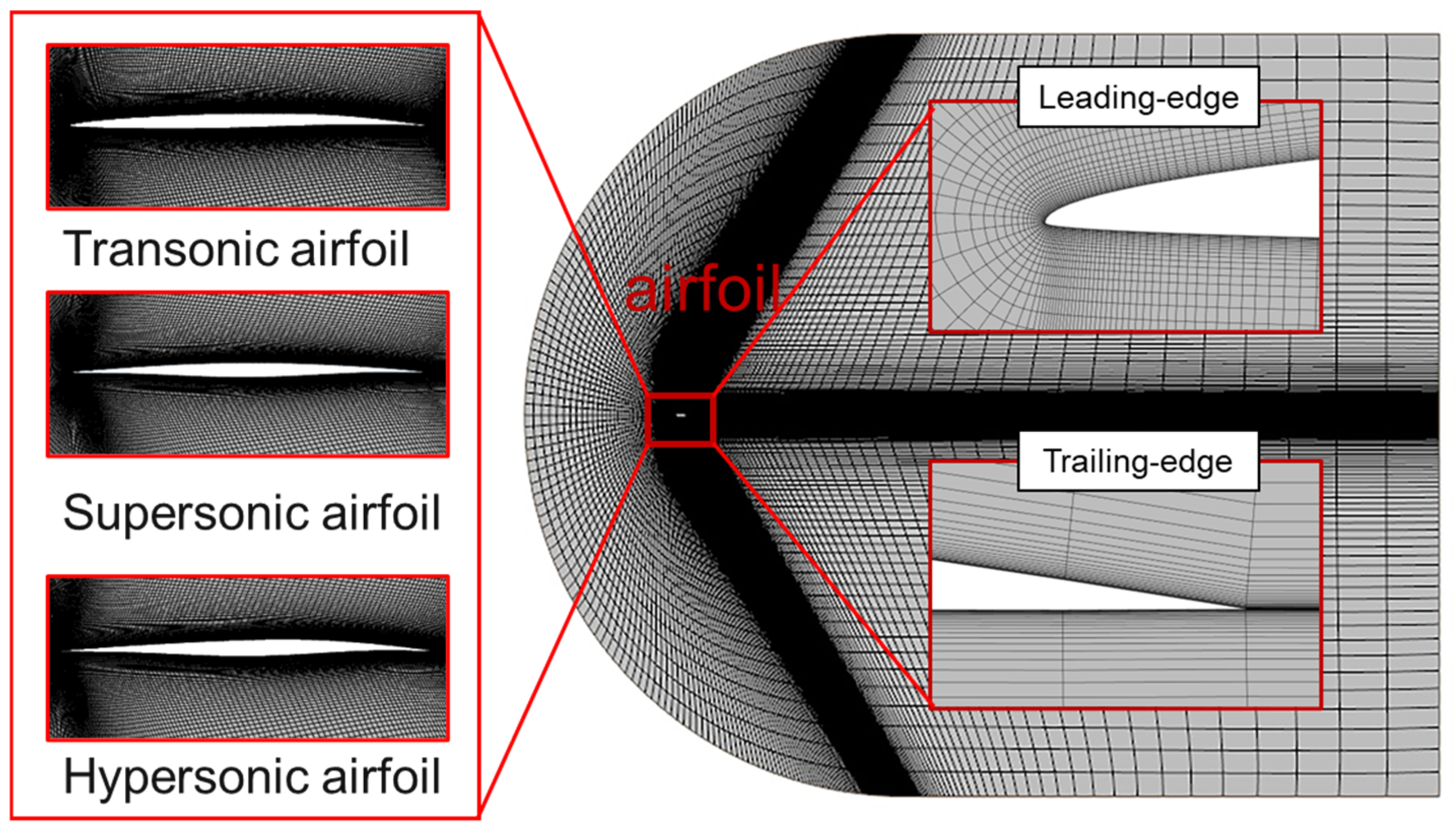
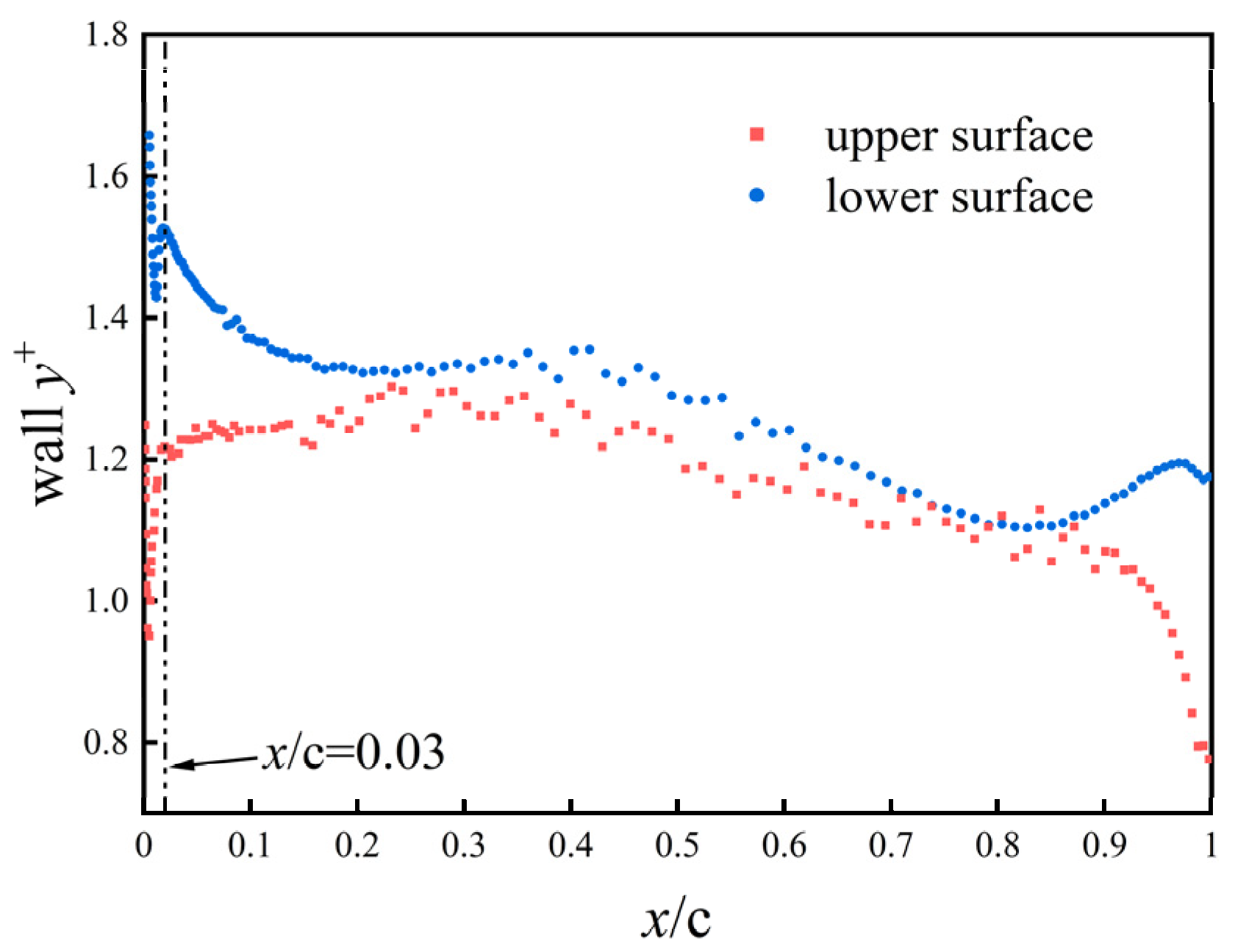
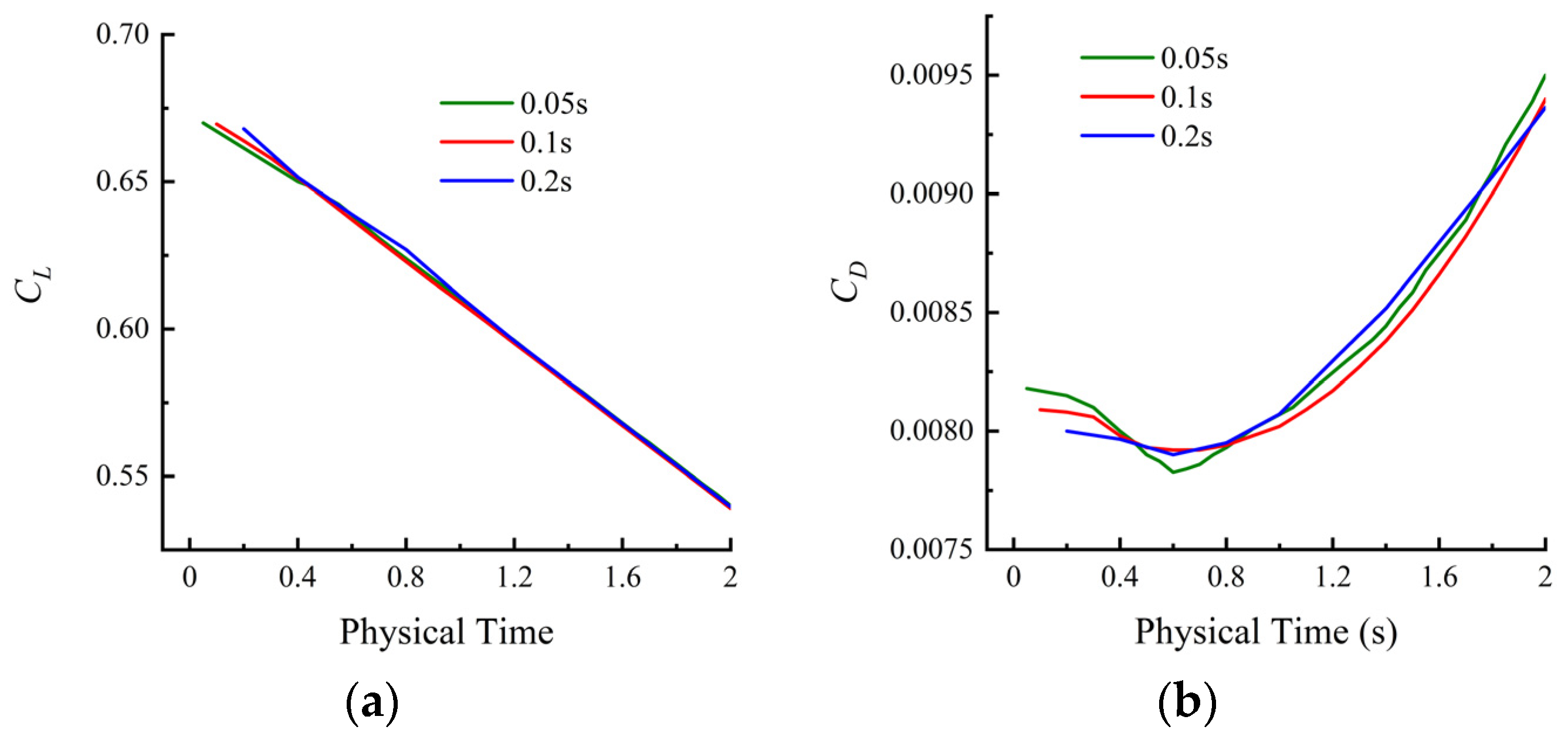
| Mesh Numbers | |||||
|---|---|---|---|---|---|
| Mesh 1 | 0.0581 | 3.3% | 0.01023 | 3.2% | |
| Mesh 2 | 0.0577 | 2.7% | 0.01088 | 2.9% | |
| Mesh 3 | 0.0562 | 0.01057 |
| Surface | |||
|---|---|---|---|
| Upper | 1.30276 | 1.14660 | 0.77667 |
| Lower | 1.47897 | 1.28019 | 1.10365 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2026 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license.
Share and Cite
Zhi, L.; Zhai, R.; Yang, Y.; Shi, X.; Wang, Z. Unsteady Aerodynamics of Continuously Morphing Airfoils from Transonic to Hypersonic Regimes. Aerospace 2026, 13, 103. https://doi.org/10.3390/aerospace13010103
Zhi L, Zhai R, Yang Y, Shi X, Wang Z. Unsteady Aerodynamics of Continuously Morphing Airfoils from Transonic to Hypersonic Regimes. Aerospace. 2026; 13(1):103. https://doi.org/10.3390/aerospace13010103
Chicago/Turabian StyleZhi, Linyi, Renqing Zhai, Yu Yang, Xintong Shi, and Zhigang Wang. 2026. "Unsteady Aerodynamics of Continuously Morphing Airfoils from Transonic to Hypersonic Regimes" Aerospace 13, no. 1: 103. https://doi.org/10.3390/aerospace13010103
APA StyleZhi, L., Zhai, R., Yang, Y., Shi, X., & Wang, Z. (2026). Unsteady Aerodynamics of Continuously Morphing Airfoils from Transonic to Hypersonic Regimes. Aerospace, 13(1), 103. https://doi.org/10.3390/aerospace13010103








