1. Introduction
Many spacecraft are equipped with a multitude of actuators for which desired control actions can be realized in a non-unique way. For such over-actuated systems, a decision process is required to distribute the control commands over a set of available actuators while considering secondary objectives such as minimizing fuel consumption and avoiding reaction wheel (RWL) zero crossings or saturation, among others. This decision process is commonly referred to as the actuator management or control allocation problem [
1].
Often, such tasks can be formulated as convex optimization problems, which can be efficiently solved via numerical optimization. However, due to risk aversion and the lack of computational resources, it has been common practice to develop tailored mission-specific solutions that avoid numerical optimization altogether. Instead, the considered approaches typically rely on (sub-optimal) solutions that may be tedious to develop and fail to take advantage of a wide range of alternative possibilities. Indeed, the use of the available degrees of freedom in spacecraft is often not fully exploited, leaving actuators in cold redundancy, constraining operations by modes or (pre-computed) lookup tables (LUTs) [
2], or by considering pseudoinverse-based solutions [
1]. See also [
3,
4] for explicit examples of the Proba-3 and Solar Orbiter missions, respectively. The first two approaches typically increase the design and verification effort, and the third one neither accounts for actuator constraints nor allows for mixing the use of different types of actuators. Fortunately, recent years have witnessed an extraordinary increase in the availability of computational resources on board spacecraft. This comes with many advantages, such as the ability to reliably solve numerical optimization tasks in real-time for control allocation as well as optimized guidance [
5], model predictive [
6,
7,
8] and data-driven [
9] control schemes, and on-board model identification [
10], among others.
To further elaborate, [
11] provides an overview of common control allocation approaches covering several cases in which numerical optimization is required, with special focus on linear programs (LPs) that can be effectively solved by means of the well-known simplex algorithm; see also [
12]. When considering the more general class of quadratic programs (QPs), however, dual-primal interior point methods (IPMs) offer more flexibility and improved scalability. Even for LPs, the authors of [
13] demonstrate that primal-dual algorithms can be more efficient in terms of FLOPS for solving thrust dispatching problems if compared with simplex methods. We refer to [
14] for a survey on maximum computation times of deterministic solutions for IPMs. Another application of optimization-based control allocation is found in [
15]. Here, the authors consider IPMs for solving a similar problem as is addressed in the present paper while focusing on a different field of engineering, namely, aircraft.
Other (hybrid) control allocation schemes based on mixed optimization problems are addressed in, e.g., [
16,
17]. In [
16], a variable cost function adapts objectives to different re-entry phases, while [
17] formulates a multi-objective optimization problem that is solved considering the Pareto Front barycenter. Fault-tolerant actuator management has also been explored in, e.g., [
18,
19], often requiring dedicated modes or even software updates. Using fault detection and isolation (FDI) monitoring, the authors of [
19] enable reconfiguration through redundant units, although without hybridizing actuators or considering constraints. Another line of work addresses adaptive allocation under actuator uncertainty using Lyapunov-based methods [
20], improving stability, but again without enabling hybridization or constraint handling. Finally, optimization-based allocation can be embedded in model predictive control (MPC) schemes, unifying guidance, control, and allocation in a single algorithm [
21,
22]. Given some useful advantages such as real-time adaptability, there are also relevant drawbacks in terms of, e.g., verification.
Recent works, such as [
23], investigate fault-tolerant dynamic thruster allocation in systems equipped with Thrust Vector Control (TVC). Several methodologies are examined and compared, including pseudoinverse, convex optimization, and nonlinear optimization-based allocation strategies. The study concludes that optimization-based approaches yield superior performance, with convex optimization offering a favorable trade-off between performance and computational complexity. Nonetheless, concerns remain regarding their real-time applicability and implementation feasibility, which the authors suggest as directions for future research. In a complementary study, ref. [
24] formulates an optimization-based approach for fault-tolerant thrust dispatching that incorporates Minimum Impulse Bit (MIB) constraints. This problem is solved offline to generate LUTs. The reported computational performance ranges from microseconds to milliseconds on an i7 processor, depending on the MIB settings. However, the authors note that this method is best suited for maneuvers with stringent performance requirements, given the associated increase in propellant consumption. Additionally, they highlight the inherent conservativeness of LUT-based solutions, particularly in handling faults and non-attainable commands, when compared with online optimization techniques.
To address the limitations mentioned above, we introduce a novel optimization-based actuator management framework designed to efficiently allocate control commands across an available set of actuators subject to a wide range of possible constraints and objectives, such as minimizing fuel/propellant/power consumption, RWL null-space management, continuous or periodic RWL desaturation via magnetic torquers or thrusters, automatic reconfiguration after actuator failures, and actuator operational domains, among others. The core of our approach is a convex optimization formulation [
25], solved using a custom-built, real-time optimization engine called SOTB (Sener Optimization Toolbox)—specifically developed for space applications such as optimal line-of-sight steering [
26] and re-entry control [
27]. This toolbox leverages an interior-point method (IPM) for efficiently solving quadratic programs (QPs), and its real-time performance is validated through processor-in-the-loop (PIL) experiments.
A major contribution of our work is the integration of a variety of control allocation problems into a single, standalone piece of software that can be straightforwardly adopted in real missions. A second contribution lies in the comprehensive demonstration of the method on a realistic benchmark derived from the ALTIUS mission [
28], as well as on a generic thrust allocation scenario. Here, we emphasize that our work extends well beyond what is presented in [
15], as we also focus on the tailoring of a dedicated solver for space applications and the verification thereof on space-graded hardware. While the present paper does not address the topic of actuator uncertainty—note that this can be easily done by considering the more general class of semi-definite programs at the cost of a higher computational load; see e.g., [
29,
30]—the mentioned reference (i.e., [
20]) presents relevant and complementary research that can (in part) be covered in our setting with minor modifications.
The remainder of the paper is structured as follows:
Section 2 describes how a variety of realistic actuator management problems can be formulated as a QP. Subsequently, it is shown in
Section 3 how all these problems can be subsumed into a general algorithm, which can be adapted for specific mission needs, as shown in
Section 4 for the ALTIUS mission. This is followed by a solver customization in
Section 5. Then, in
Section 6, we provide an overview of simulation results, which include real-time tests that were performed on space-graded hardware. The paper is concluded with some final remarks in
Section 7.
2. Actuator Management for Space Applications: A Concise Overview
Before we present our results, let us first provide some further context by giving a concise overview of typical actuator management problems that appear in space applications. Limiting the focus on satellites, one typically considers momentum-exchanging devices for attitude and orbit control [
31]. Here, reaction wheels (RWLs) are the most widely adopted actuators for attitude control. In support of this, magnetic torquers (MTs) or thrusters (THRs) can be used to desaturate the wheels (i.e., RWLs wind up due to the absorption of external torque perturbations). In the case of small- to medium-sized satellites in low-Earth orbit, MTs can be considered in a continuous desaturation scheme. Alternatively, thrusters must be adopted to periodically offload the wheels. It is also not uncommon that spacecraft attitudes are controlled with thrusters, as is done in missions such as Euclid [
32], Proba-3 [
33], and LISA [
34].
From a mathematical point of view, given a control command
on a spacecraft, the control allocation problem is defined by finding physical actuator actions
by means of solving the equation
Here, represents the control or dispatching matrix, which maps the actuator actions into forces and torques acting on the spacecraft. For a six DOF control problem, the matrix B must have rank 6 to ensure full controllability. One can show that at least seven thrusters are needed for realizing controllability in six DOF, or at least three RWLs for a three-axis stabilized attitude control, all depending on the particular configuration. On the other hand, it is common practice to consider redundant schemes in which more actuators are available than strictly required. In such cases, the matrix B has a null space which can be exploited to generate identical actions with different combinations of actuators (i.e., the solution of (1) is non-unique). This opens up the possibility to impose additional constraints on the control allocation problem, such as minimizing fuel consumption when using thrusters, avoiding zero-crossings in RWL clusters, and desaturating RWLs with MTs, among others.
Many of these problems can be formulated as convex optimization problems, or, more specifically, quadratic programs (QPs), which admit the form:
Here, is the optimization variable (typically but not limited to ), while , (i.e., Q is positive semi-definite), , , and gather the control allocation problem structure.
Several toolkits capable of efficiently solving this optimization problem are readily available. Well-known (open-source) examples include
ACADOS [
35] and
CVX [
36], which, through user-selectable solvers, not only solve the problem but can also generate autocoded
C implementations. Alternatively,
quadprog from
MATLAB (2024b version was used) can be employed to reproduce the experiments presented in this work (see
Section 6.4). Nonetheless, due to software memory constraints and hardware limitations, tailored solvers with fully accessible code are generally preferred for maximizing performance, especially in space applications. This motivated the development of a dedicated yet generic solver for control allocation, which we introduce in
Section 5.
The simplest and most common solution to this problem is for the special case in which
,
,
,
, and
. This corresponds to the (unconstrained) least-squares problem where we minimize the
-norm (i.e.,
) subject to
. This problem has the following analytical solution:
Here, denotes the Moore–Penrose or pseudoinverse of B. Although convenient, this solution has severe limitations since actuator constraints are not accounted for, which could result in commands that exceed the actuator limits. In addition, the minimization of the -norm would be inappropriate for thruster dispatching, where one typically prefers to minimize the -norm (i.e., ), which corresponds to minimizing the fuel consumption.
In the following subsections, we provide a selected overview of representative space-related control allocation problems that can be formulated as special cases of (2) and solved using the aforementioned toolkits.
2.1. Thrust Dispatching
Thrust dispatching is one of the most common control allocation problems in space applications in which the least-squares solution is inadequate. As already highlighted, this requires including constraints as well as minimizing the
-norm rather than the
-norm. The problem can then be formulated as
Here
B denotes the dispatching matrix,
f the commanded force/torque vector,
q the all-ones vector, and
the thrust command with range
. To avoid the unfeasibility of (4c) and mixed integer programming as in (4b), this formulation can be relaxed as follows (and leaving minimum impulse bit (MIB) management to a pulse width modulator (PWM)) [
37]:
Here the quadratic term is essentially a soft constraint with Q being a positive semi-definite weighting matrix. Engineers often try to avoid solving this optimization problem in real time by exploiting symmetry in the thruster layout and/or by considering pre-computed lookup tables. This can potentially lead to sub-optimal solutions and extra development costs in terms of engineering and verification effort, which can be avoided with the general solution presented in this paper.
Remark 1. In case control commands are larger than the authority envelope, Formulation (5a,b) minimizes the mismatch between the commanded and executed forces and torques, which may result in a (slight) misalignment between the two. If this is not desirable, the additional constraint with can be included. This forces the commanded and generated forces and torques to be aligned and essentially scales the control action such that it is confined to the authority envelope.
Remark 2. In connection to the latter, the null space of B (if it exists) can be exploited to reduce the number of optimization variables by performing the substitution . Here and and are new optimization variables. The latter is an auxiliary variable that scales f such that U can always be confined to (5b).
By also slightly modifying the cost function, problem (5a,b) can be written as: Note that, compared with (5a,b), the reduction is limited to a maximum of variables (i.e., 5 in the case of a six DOF thrust dispatching problem). Furthermore, this procedure makes it cumbersome to deal with degraded scenarios, as it requires computing and for all possible subsets of actuators. Also, it is incompatible for , while (5a,b) would still be capable of generating feasible solutions.
2.2. Reaction Wheel Null-Space Management
Motivated by redundancy or improved agility, many spacecraft are equipped with more than three RWLs. When all RWLs are operational, the system becomes over-actuated, and the extra DOF(s) can be exploited for different purposes, such as enforcing an operational range to minimize zero-crossings, avoid saturation, or reduce excitations by avoiding certain eigenfrequencies of the RWL cluster. This is called null-space management. Conventional pseudoinverse-based solutions usually do not exploit this DOF, which prevents reaching the full operational range, as illustrated in
Figure 1. Here, the red zonotope depicts the torque actuation envelope of a typical RWL cluster, while the blue ball highlights the significantly smaller reachable subset that can be attained with conventional pseudoinverse-based approaches.
Exploiting the extra DOF as suggested above can be effectively done by means of solving the following QP:
Here,
B denotes the dispatching matrix,
f the commanded torque vector,
with
the torque and torque range of the RWLs, and
the momentum envelope. In addition,
and
are diagonal weighting matrices while
,
, denotes the stored angular momentum in each wheel,
the current state, and
the time of action of
, i.e., the control allocation step. Other objectives exploiting null-space management and more realistic envelopes coupling maximum torque with momentum are covered in
Section 4.
2.3. Control Moment Gyroscopes (CMGs)
Control momentum gyro (CMG) allocation is an active field of research focusing on challenges such as avoiding or escaping singularities; see [
38,
39] and references therein. CMGs are useful alternatives to RWLs, especially in agile environments, as they can generate high torques per unit of mass. This comes at the price of several complexities, such as nonlinear behavior and, especially, singularities. Indeed, CMGs are wheels that are spinning at high (constant) rates and can rotate perpendicular to their spinning axis. Although this generates high torques induced by the gyroscopic effects, singularities may occur in CMG clusters, preventing torques from being generated in certain directions. Mathematically, this means that the dispatching matrix
, which depends on the gimbal angle
, is not full of rank for all
with
defining the gimbal range. In turn, this implies that
cannot be computed for all
. To avoid these singularities, practical implementations often rely on over-confining the actuation envelope at the cost of reduced momentum capabilities.
Alternatively, the full envelope can be exploited while avoiding singularity issues by solving the following optimization problem:
This algorithm is similar to the previous one with the difference that the problem now depends on the gimbal angles in each CMG before and after torque allocation, i.e., and respectively. In addition, the cost function includes the (non-convex) regularization term which prevents the matrix from becoming singular for some . Here, is a tunable scalar penalty that balances the objective of staying away from singularity against the rest of the cost function.
This term can potentially be replaced by the semi-definite constraint
which enforces the minimum eigenvalue of
to be larger than
, where
is a user-defined tunable parameter. Since
contains trigonometric functions, relaxation schemes known from robust control theory can be applied to obtain a genuine semi-definite program (SDP). On the other hand, solving SDPs in real time is still computationally challenging. To this end, alternative formulations have been studied in, e.g., [
26]. Here, it was shown that the non-convex term can be removed. The presented scheme enables optimal crossing through singular zones, exploiting null space while minimizing torque errors over slews. CMGs are not further studied in this paper. However, the solution presented in the sequel is compatible with the approach taken in [
26].
3. A Generic Optimization-Based Algorithm for Actuator Management
Now that we have given ample motivation for optimization-based control allocation, let us present our main contribution of the paper—a unifying approach that covers the problems described in the previous section and many others. In this algorithm, the full range of each actuator and the null space of the entire hybrid cluster can be managed while minimizing a cost function that gathers the objectives stated in
Section 1 by means of a convex formulation. Convex optimization is a key ingredient due to benefits such as guarantees for convergence and convergence rates, the absence of local optima, and the availability of efficient solvers. The reader is referred to
Section 5 for further details in this direction. The algorithm is designed to cover generic satellite cases with typical actuator suites, yet with the flexibility to cover special cases such as the ones described in
Section 2. The default set of actuators considered in the sequel is reaction wheels, magnetic torquers, and thrusters. The algorithm also allows changing the configuration (i.e., which subset of actuators is used) without requiring any modification at the algorithm level. This facilitates the adaptation to different attitudes and orbit control system (AOCS) modes, to hardware failure scenarios, and even to different missions with similar architectures.
The key to translating control allocation problems into convex optimization algorithms is the formulation of high-level objectives by means of mathematical constraints or cost penalties compatible with (2a,b). This has resulted in the following QP:
As before, B denotes the dispatching matrix, f the commanded force/torque vector, and with the to-be-computed vector containing the reaction wheel, magnetic torquer, and thruster actions, respectively, i.e., . Then with denotes the stored angular momentum in each wheel, the reference objective values, the current state, and the time of action of U, i.e., the control allocation step. Finally, , , and are (symmetric) positive semi-definite (diagonal) weighting matrices of compatible dimensions, while r weights the linear part of the cost function.
To reduce the computational load, the variable
h can be removed from the problem through the equality constraint (10c). Then only the most limiting constraint in the RWL’s action, i.e., saturation in torque or momentum, is maintained in each optimization call in (11b). After that, the remaining optimization variables, i.e., the actuator commands, are normalized with
. Without loss of generality, except for the thrusters, the actuator bounds are assumed to be symmetric. Grouping terms and ignoring constant offsets of the cost function we obtain:
with
Note that
and
are scalar functions of
that determine the most restrictive lower and upper bounds on the RWL torque, respectively, depending on the scenario at the specific control allocation call, i.e., whether bounded by momentum saturation or torque limits. Here
H admits the following structure
with
being the diagonal elements of
W (from Equation (10a–d)),
, while
such that
, and where
is the dispatching matrix for the normalized variables, i.e.,
. Finally, the linear cost term
c is given by
Note here the slight abuse of notation by keeping the same weighting variables as in the non-normalized case.
The optimal control problem can be complemented with an upper software layer that updates its internal state according to the current system status. This state is composed of the parameters that define the current capabilities of the control allocation algorithm and includes the current shape of the MTs’ dispatching matrix according to Earth’s magnetic field, the actuators’ availability, and the stored angular momentum
in each of the RWLs. To adapt to potential fail scenarios, the columns in
B corresponding to a potentially failed actuator are set to zero. This is more elegant compared with changing the problem formulation and considering a different mode for each possible scenario. In addition, this has significant advantages in terms of software coding since the problem size and the maximum number of FLOPS are kept the same regardless of the situation. Further note that the optimization problem always has a feasible solution. By construction of (11b) we deactivate the constraint on
if
but maintain the constraint on the torque to prevent further increasing
(i.e.,
). The functionalities of this preconditioning can be extended to cover the specifications of different missions, as shown in
Section 4.
Remark 3. Some authors prefer to set the command as hard constraints, i.e., direct allocation methods, as in (4c).
On the other hand, in (10a–d), the constraint is relaxed into a quadratic cost penalty with other objectives, such that we obtain a mixed optimization problem [11]. This enables the computation of unrealizable command inputs without rendering the problem infeasible. This can be interpreted as an abstraction layer between the control and the actuators and eases the implementation of recovery functionalities, i.e., working in degraded scenarios. Although the tuning of the cost function is mission-specific, in general, torque and force errors result in high penalties so that minimization of the term becomes a priority over actuation efficiency, i.e., . Here, we emphasize that the momentum is constrained. Hence, the relative value of with respect to the other penalties drives the priority given to RWLs’ desaturation over other objectives but does not risk exceeding the capabilities of the actuators. In the presence of thrusters, it is expected that such that propellant consumption is minimized and thruster usage is reserved for situations in which force is required or the rest of the actuators does not have enough power to generate the requested torque. The relative cost between and shall also be adjusted such that desaturation with thrusters is minimized. In Section 4, an algorithm modification is presented to avoid the use of thrusters when required. Remark 4. The penalty W and (10c)
drive the RWL’s angular momentum to a desired total reference angular momentum over time by computing the state , , for the next time step, , as in (10c).
Note that minimizing the RWL’s angular momentum to or any other value for which (with being the RWL’s configuration sub-matrix) differs from removing the system’s residual angular momentum. The presented formulation offloads the RWLs even if the spacecraft has a certain angular rate, e.g., in science nadir pointing, which would create a residual net momentum. In the proposed scheme, the controller can compensate for the small gyroscopic effects that may arise from this situation in feedforward. This decision is derived from the considered use cases in which a certain speed operation range is desired for each wheel to minimize vibrations during science. Alternatively, the cost function can be modified to minimize residual momentum aswhere J is the spacecraft inertia matrix and ω is the spacecraft angular rate in the body frame with respect to the inertial frame. Remark 5. In the absence of magnetic torquers, periodically scheduled RWL desaturation by means of thrusters is common practice and can also be covered by the presented algorithm. This avoids the continuous use of thrusters and thereby unnecessary torque perturbations. During the desaturation task, the cost W should be chosen larger such that the use of thrusters is autonomously triggered for RWL offloading, while for the rest of operations W should be chosen such that the penalty is sufficiently smaller than .
Remark 6. The constraints (10b,d) are flexible and adaptable to other convex envelopes, suitable for torque-momentum relations in RWLs. Without solver modifications, affine sets such as can be considered as well. Then (10b)
can be replaced with , to obtain (11b).
In the generic formulation above, for simplicity, is defined by the block matrix formed by the identity I and , with . See Section 4 for a different example. Remark 7. Complexity in the simultaneous consideration of the MIB and zero-force thruster constraints is discussed in Section 2.1. To convexify the problem, the thruster’s action lower-bound constraint is set to a constant. The value used for generality in (11d)
is zero. However, it can be set to any arbitrary constant below 1 without losing convexity. This is useful for missions with high-accuracy demands that work in differential thrusting schemes, i.e., all thrusters active above the MIB. 4. A General Benchmark Problem Derived from the ALTIUS Mission
Let us now provide a more general example derived from a real mission. The Atmospheric Limb Tracker for Investigation of the Upcoming Stratosphere (ALTIUS) mission is realized by a spacecraft that accommodates four RWLs for attitude control, three MTs for (continuous) RWL desaturation, and four (hot-gas) thrusters for orbit control [
28]. This is a relevant case study consisting of a rich set of actuators that can be used in a realistic fashion to demonstrate the potential of hybrid optimized control allocation for a wide range of missions with similar configurations.
4.1. Conventional Control Allocation Approach
In the original GNC design, the actuators are deployed in a conventional way:
Nominally, torque commands are allocated deterministically to three RWLs, leaving a fourth one in cold redundancy. In addition, when more agility is required, the complete RWL cluster is considered, where the available null-space is exploited to regulate the RWL angular rates by means of a PID controller [
3]. Consequently, the RWL’s operational range is not taken into account. The RWLs are operated at 4 Hz.
The RWLs are offloaded by means of the MTs. This proceeds by selecting one MT during each sampling interval of 1 Hz and generating the maximum torque it can provide. The selection of the MT is based on the maximum torque of the Earth’s magnetic field and the direction of residual momentum. Offloading is then achieved by commanding the generated torque with an opposite sign to the RWLs.
The thrusters are only used during propulsive maneuvers for orbital maintenance. All four thrusters are mounted parallel to the z-axis of the body reference frame. This means that they can only generate torque about the corresponding x and y axes, but not without also generating a net force. The induced torques are minimized by working in pairs, and perturbations are absorbed by the RWLs. The thrusters work at 1 Hz.
4.2. Potential Advantages for an Optimization-Based Solution
Conventional approaches have some obvious advantages in terms of the low complexity of the design solution and the implementation thereof. On the other hand, the use of real-time embedded optimization could potentially improve the system’s performance in various ways. For example:
The (nonlinear) operational domain of the RWLs in terms of available torque and stored angular momentum is known (see
Figure 2). As mentioned above, this range constraint is not taken into account when considering (pseudo)inverse-based solutions. On the other hand, these types of constraints can be straightforwardly included in the proposed algorithm (as long as they are convex), potentially allowing the agility of the system to be improved.
Operating the MTs as described above could lead to difficulties during the desaturation process. For example, this may lead to chattering behavior for angular rates around zero or to incomplete desaturation cycles (if thresholds are considered). Instead, when considering all MTs simultaneously in combination with the proposed optimization algorithm, they can be operated in an optimal way by directly computing the required currents (as opposed to just saturating them).
The null space of the RWL cluster can be exploited to minimize, for example, zero crossings or the excitation of modal frequencies, thereby extending the lifetime of the RWLs and reducing jitter effects at the payload level. Note that the computation of to-be-allocated torques to the individual RWLs and the null-space objective is done simultaneously by minimizing a single cost function subject to the range constraints shown in
Figure 2. This minimizes potential mismatches between commanded and executed torques and avoids the need for heuristic implementations, as one would require when considering pseudoinverse-based solutions such as in, e.g., [
3].
The flexibility to reconfigure the actuator manager in case of failures can be significantly improved. The approach presented in this paper offers the capability to instantly adapt after actuator failures and continue operating the spacecraft in degraded scenarios without the need to include additional sub-modes for specific anticipated scenarios.
Apart from these, there is further upside potential in hybridizing the control allocation. For example, the MTs can be used to contribute to control torque demands, or the thrusters could be considered for periodic desaturation. Altogether, the proposed approach has relevant potential to enhance the spacecraft’s agility, autonomy, safety, and performance. In the following subsections, it is shown how these improvements can be realized.
4.3. Algorithm Hybridization
To formulate the ALTIUS control allocation task as an optimization problem of the form (11a–d), two generic adaptations are required, namely, (1) the use of thrusters is only allowed during propulsive (i.e., ) maneuvers, and (2) the actuators work at different sampling frequencies.
4.3.1. Only Using Thrusters During Propulsive Maneuvers
As already highlighted, the thrusters are not supposed to be operated when the force request is zero. Generally, if the cost function is properly tuned and as long as the torque commands are realizable by the remaining subset of actuators (i.e., the RWLs and MTs), this behavior can be straightforwardly enforced. On the other hand, thrusters could also be utilized to contribute to the torque generation if the torque command exceeds RWLs and MTs’ capabilities, even when zero force is requested. Here, we emphasize that with sufficient degrees of freedom in the thruster layout, one would be able to realize torque commands without generating net forces.
To prevent the use of thrusters when not performing propulsive maneuvers and considering that torque cannot be generated by thrusters without also generating force, due to the thruster layout, the condition
if then can be added, with
being the thruster dispatching matrix. This automatic action resembles a decision-making step in a multi-objective optimization [
17].
4.3.2. Operating Under Different Actuator Frequencies
To resolve the dual frequency problem, we proceed as follows. In the first GNC cycle, which runs at 4 Hz, the optimization problem (11a–d) is solved for all variables . Subsequently, in the next three GNC cycles, the optimization problem is solved for the subset of variables, , while the remaining variables, , are kept frozen with the values obtained in the first GNC cycle. This ensures that torques and forces that are being executed at 1 Hz are not ignored in the control allocation in subsequent three GNC cycles.
In addition to this, the cost function must be modified to link the control allocation cycles and maximize the performance. Indeed, even though we command the MTs/THRs at 1 Hz, the total angular momentum will continue to evolve at a rate of 4 Hz. Hence, after completion of the first GNC cycle, we should continue minimizing the angular momentum in the next three GNC cycles; otherwise, one would observe a chattering behavior of the angular momentum around . More precisely, we proceed as follows:
The minimization of the angular momentum is carried out over a one-second window for the initial full control allocation step (hereafter denoted with the subscript f), i.e., we set in (14) and (15).
In the subsequent three optimization steps, where we solve the partially frozen control allocation problem (hereafter denoted with the subscript p), we set . In addition, we modify the weight W to avoid the chattering of the angular momentum around .
The constraint (11b) is maintained with for both cases.
The modification of the weight
W proceeds in a systematic and generic fashion by considering an ideal desaturation scenario, i.e., for the case where no torques are requested. Taking the first optimality condition
the objective is that
is frozen in the consecutive three allocation steps without enforcing it by constraints. If we denote by
the
consecutive GNC cycle after the initial one, then this objective translates into
. After some elementary operations and defining
, we can infer from (17) that
Note here that we assumed
(i.e., no saturation constraints are active), which is a suitable hypothesis for the purpose of the cost adaptation. By now defining
and
, we obtain the following modified diagonal elements of
W:
One concern with this state-dependent cost adaptation is that it introduces a potential singularity issue in case and or when . The former is related to a scenario in which the RWL is desaturated and no torque is being commanded, i.e., when and . The latter is a consequence of after optimization. For the first case, cost adaptation is not required because the RWLs have not acted. For the second, the penalty in the cost function disappears if is maintained, making the cost w tend to infinity. However, in practice, this is not required as long as w is sufficiently larger than , where denotes the weighting matrix of RWL’s actions. These issues can be easily avoided by setting thresholds in the limits where the cost adaptation leads to singularities.
In the ALTIUS case, we mostly have
, except when
. To simplify the implementation, when
, the limit of
is taken such that
In practice, this simplification is sufficient for achieving the desired behavior. Note again that the rationale and formulas obtained above are generic and apply to any scenario with multiple frequencies.
4.4. Optimal Control Allocation Approach
Given the procedure from the previous section, let us now show how the ALTIUS control allocation problem is a special case of (11a–d), when accounting for the following constraints, functionalities, and objectives:
All four RWLs are exploited while (i) accounting for the range constraint shown in
Figure 2, (ii) exploiting the cluster’s kernel to minimize zero-crossings, and (iii) setting the reference angular momentum
to a specific value where model frequencies are not excited.
All three MTs are used to command torque and desaturate the RWLs.
When thrusters are required for propulsive maneuvers, they are also used for desaturating the RWLs and for generating torque if suitable.
To incorporate avoiding zero-crossings by exploiting the RWL cluster’s kernel, a soft constraint
was added; it becomes active whenever the wheel speed crosses the threshold
(see
Figure 3). Here
,
, and
,
, penalize the zero crossings and
,
, is a vector of auxiliary optimization variables.
Given all the aforementioned details, the ALTIUS control allocation problem can now be formulated as
with
and
:
Here,
m is the normalized slope of the line depicted in
Figure 2, while
is the point where the slope of the constraint changes. As suggested in
Section 4.3.1, we set
if
in the upper software layer. Finally, the algorithm follows the modification proposed in
Section 4.3.2: For each 2nd–4th sampling interval (at 4 Hz), we freeze the variables
with the values obtained in the first sampling interval, and adjusting
and
only in the cost terms, and set
.
5. A Customized Solver for Control Allocation Problems
Given the Equation (11a–d) from
Section 3 (or equivalently (2a,b) from
Section 2), let us now focus our attention on the control allocation problem, which can be efficiently solved in real-time. For this purpose, we derive a customized primal-dual interior-point method (IPM) solver based on our previous work reported in [
26], which covers the development of a more generic solver called SOTB (SENER optimization toolbox) for quadratically constrained quadratic programs (QCQP). This is a MATLAB-based toolbox for real-time embedded optimization that facilitates the rapid prototyping and testing of QCQPs in space-graded hardware. For further reference, we refer the reader to [
27], where the solver is adopted in an MPC scheme as part of the Space Rider mission.
In the derivation that is presented next, the aim is to exploit the specific structure and sparsity of the control allocation problem, thereby minimizing the required memory resources and the number of FLOPS. To do so, we start by considering the primal-dual formulation of (2a,b), which can be solved via the Karush–Kuhn–Tucker (KKT) optimality conditions [
40]. These are necessary and sufficient for optimality and can be expressed as
Here, the vectors , , , and consist of the optimization parameters, the slack variables, and the Lagrange multipliers, respectively. The remaining matrices and vectors are defined in (2a,b). Here we highlight that , , is also referred to as the Hessian matrix of the optimization problem (2a,b); is the Jacobian matrix of the inequality constraint (2b); and is the diagonal concatenation of the slack variable s.
Obtaining a direct solution from (24) is typically challenging due to the nonlinear condition
. To overcome this challenge, the problem can be relaxed by employing a smoothing logarithmic barrier augmentation method to obtain
with
being the barrier parameter and
the all-ones vector [
40]. The original KKT conditions of (24) can then be linearized around
and solved in an iterative procedure by finding the Newton search direction
for the system of equations.
where
.
The structure of (11a–d) allows us to apply a series of Schur factorizations yielding the so-called normal equations
where
. In this form, only the term
needs to be inverted in every iteration. To do this efficiently, we can exploit the underlying structure of (26a) with the aim of minimizing the number of FLOPS in each iteration. For the generic formulation in (11a–d), the structure of
A is given by
Here, denotes the sum of the total number of actuators n and the auxiliary variables . The latter are used for defining the soft constraints on actuation ranges, which are all collected in the matrix .
In the sequel, we assume
to be diagonal, which is a mild assumption with respect to (11a–d) and essentially means that we do not allow for cross-correlations between actuation ranges of different actuators in the customized solver. Given this assumption, we can reduce the number of operations by computing the elements of
as follows:
Here we denoted the diagonal entries of and by and , respectively. This significantly reduces the cost of computing and makes the required number of FLOPS scale linearly with N and .
Similarly, the right-hand side of (26a) can also be further simplified. First, since
, the terms
are obtained for
. If we denote by
this yields
For computing the inverse of (and hence obtaining the search direction ), we assume that such that also . Then the inverse can be efficiently computed using a Cholesky factorization. Note that this is a mild assumption, as Q can be forced to be positive definite. Alternatively, the inverse must be computed in a potentially less efficient way, which is not further pursued in this paper. Finally, the search direction for the dual variables and can be obtained in a similar fashion by simplifying (26b) and (26c), respectively (although without the need to compute any additional inverse).
The IPM was coded considering a dedicated central-path algorithm with good numerical performance and robustness [
40]. To conclude,
Figure 4 depicts a flowchart diagram summarizing the key steps of the overall algorithm. In the following section, it is demonstrated that the overall code works efficiently in real-time on space-graded hardware and requires a limited number of iterations independent of the application.
6. A Selected Overview of Test Results
Let us now present a selection of test results to demonstrate the capabilities of the developed algorithm and the customized solver. These results were obtained by performing simulations within a realistic environment that encompasses, among other features, a detailed dynamic kinematic environment and a complete AOCS/GNC. (The simulation models utilized in this study were developed by SENER Aeroespacial and have undergone extensive verification and validation (V&V) through multiple space projects. They are integral components of an in-house simulation facility dedicated to the V&V of GNC algorithms). For comparison,
Section 6.1 presents simulation results for a nominal scenario of the ALTIUS benchmark problem, obtained using a conventional control allocation approach similar to the one described in
Section 4.1. Subsequently,
Section 6.2 provides the results for the same scenario using the algorithm introduced in
Section 4. Then, in
Section 6.3, we show how the control allocation algorithm can also cope with degraded scenarios in the same simulation environment. Finally, in
Section 6.4, we demonstrate the numerical performance of the algorithm and customized solver in a dedicated breadboard environment comprising a space-graded GR740 (LEON 4) processor. The main parameters used for the simulations are found in
Appendix A.
Remark 8. Note that the aim of the presentation is to demonstrate that the proposed algorithm performs well in realistic benchmark scenarios rather than providing an exhaustive overview of the ALTIUS AOCS functional performances. We also emphasize that the presented results are inspired by the ALTIUS mission. However, they were obtained considering an alternative AOCS (and actuator manager) that was developed in the scope of a different activity. For a comprehensive overview of the ALTIUS mission, including the original AOCS design and associated test results, the reader is referred to [28]. 6.1. ALTIUS Benchmark: Conventional Approach
As highlighted above, this section provides a selection of test results obtained for the ALTIUS benchmark problem. Specifically, we focus on the performance of the control allocation algorithm for a scenario in which the spacecraft performs a series of 7 slew maneuvers which all share the same Absolute Performance Error (APE) requirement of 1 degree. After each maneuver, a specific limb-looking target must be acquired with an APE accuracy of 25 arcsec. The test is completed by performing a maneuver for which the thrusters are utilized. Note that these maneuvers are relatively agile and require all four RLWs to complete the transitions within the specified time.
We first evaluate the system’s performance for the conventional control allocation approach as sketched in
Section 4.1, with the sole difference that we consider a pseudoinverse-based solution to allocate the commanded torques among the four available RWLs. Hence, the control allocation is performed as follows:
Force requests are distributed by allocating thrust to thruster pairs. This minimizes the residual torque.
One of the magnetic torquers is saturated in the most favorable direction to reduce the stored angular momentum in the RWLs.
The torque command is combined with the residual torque induced by the thrusters and the contribution of the magnetic torquers. The final RWL actuation is then computed using the pseudoinverse-based solution.
Figure 5 shows the computed attitude APE for 100 simulation runs in which we varied all relevant uncertain parameters. The dashed lines represent the APE requirement bounds, which are 1 deg during the slew and
maneuvers and 25 arcsec during science observations. Although the requirement is met during the slew maneuvers, it is clearly violated during the science and
operations. In the case of science operations, the pseudoinverse-based solution can cause some RWLs to saturate, preventing the GNC from adequately attaining all limb-looking targets. During
-maneuvers, the RWLs must absorb the induced torques (see
Figure 6), which can lead to momentum saturation or reduced torque capabilities (see
Figure 2), ultimately resulting in large APEs.
In addition to the APE performance, the RWL’s stored momentum in each wheel is shown in
Figure 6. It is evident that the reference angular momentum,
, cannot be tracked with the pseudoinverse-based solution without further degrading the performance during the slew and
maneuvers. Moreover, a steady-state angular momentum closer to the wheel speed limits increases the likelihood of saturation during these maneuvers, thus yielding larger tracking errors. In addition, using the magnetic torquers as suggested is not suitable for this objective, as they act on the total angular momentum of the cluster. Consequently, without further modifications, this control allocation strategy leads to frequent zero-crossings in the RWLs, which is undesirable.
In the following subsections, we demonstrate how the proposed optimization-based actuator manager can effectively address these limitations while integrating additional capabilities, such as the following:
Minimizing errors induced by RWL saturation through explicit constraints in the optimization, ensuring compliance with the APE requirements;
Operating the RWLs in desirable regions without compromising on agility or performance;
Continuously desaturating the RWLs within the optimization with magnetic torquers operating efficiently and in harmony with the other objectives;
Executing maneuvers within error requirements thanks to actuator hybridization: thrusters no longer need to operate in pairs, and their usage is optimized in coordination with the rest of the actuators, thereby alleviating RWL loading;
Ensuring robustness to degraded scenarios, as the same algorithm remains applicable even in the presence of actuator failures.
6.2. ALTIUS Benchmark: A Nominal Scenario
Next, we repeat the previous test with the proposed optimization-based approach while keeping all other conditions unchanged.
Figure 7 depicts the computed attitude APE for 100 simulation runs. As can be seen, apart from some small transients when entering science, the AOCS (including the actuator manager) is now well capable of achieving the requirements, even considering the relatively demanding guidance profiles.
To confirm that the actuators are used as intended,
Figure 8 depicts the corresponding actuator commands. We recall that the thrusters are only used when a
is requested. As can be seen, the MTs (top row) are mostly saturated for continuous desaturation, while the RWLs (middle row) only reach their operational limits when required during the slew maneuvers. In addition, the RWLs absorb part of the thruster-induced torques during the
maneuver at the end of the test. Also, observe that the actual pulses after passing through the PWM are visible in the plot (bottom row).
Focusing on the RWL cluster’s null-space and the continuous desaturation,
Figure 9 shows the evolution of the angular momentum in each RWL. As can be seen, the stored angular momentum is nicely maintained around the reference point
Nms, while zero crossings are avoided whenever possible. In addition, the RWL operational constraints (cf.
Figure 2) are also correctly enforced as shown in
Figure 10. Here, we emphasize that the full envelope can be utilized, while, on the other hand, the autonomous allocation prioritizes a working region for each RWL. Also note that the dynamic response of the RWLs may result in small temporary violations of the torque-momentum envelope. Thanks to the constraint (11b), the control allocation algorithm accounts for the expected torque induced by this behavior to minimize the command errors.
6.3. ALTIUS Benchmark: Degraded Scenario
To continue, let us demonstrate the versatility of the control allocation algorithm by considering a highly degraded scenario that starts with the full actuator set being available, after which several fail: At s, RWL#1 is lost, and at RWL#2 becomes unavailable. At that moment, a safe configuration (Sun pointing) is acquired. This is realized by means of the two remaining RWLs and the thrusters to ensure the full controllability of the spacecraft’s attitude. It is emphasized that this comes at the price of generation due to ALTIUS’ thruster layout. At and s, respectively, the first and second RWLs that failed become available again so that the thrusters are no longer needed for attitude control. Then, at s, a slew is commanded as a preparation for a maneuver at s, which is performed while only two of the four thrusters are available. The latter will generate a significant torque disturbance that must be absorbed by the RWLs.
The effectiveness of the optimal hybrid control allocation and robustness against actuator failures is reflected in
Figure 11, which depicts the computed APE. As can be seen, the APE remains relatively small, even considering the severe stress cases.
Next,
Figure 12 and
Figure 13 depict the computed torque and force allocation errors, respectively (i.e., the difference between requested and realized torques and forces). These are zero whenever the full set of actuators is available. On the other hand, when the two RWLs are unavailable, torque and force errors are generated due to the complementary use of thrusters. These errors can be interpreted as disturbances (uncertainties) that must be absorbed by the attitude controller. To minimize the impact on the pointing performance, the control allocation algorithm prioritizes torque over force error minimization. This is also visible during the
maneuver where the applied forces are limited by the actuator manager to ensure that the RWL can cope with the large torque disturbances induced by the unavailability of two thrusters.
To continue,
Figure 14 depicts the stored angular momentum in the RWLs. As can be seen, the failed RWLs (i.e., #1 and #2) stop rotation by internal friction, and the
is set to zero to avoid any residual momentum. Once operational again,
is set to its original value. Finally, during the
maneuver, the RWLs successfully absorb the induced torque, even though only two of the four thrusters are available. For completeness,
Table 1 summarizes the results obtained for Tests A and B. Note that there are no command errors above the solver tolerance in Test A.
6.4. Processor-in-the-Loop Verification
Let us finally focus on the numerical performance of the developed algorithm. To do so, the software was auto-coded and emulated, first on an Intel i9-12900HK @ 2.5 GHz processor and, subsequently, on a dedicated breadboard environment that houses a space-graded GR740 (LEON 4) processor.
6.4.1. A Generic Thrust Dispatching Problem
We first focus on a 6 DOF thrust dispatching problem with 12 thrusters. This problem was initially implemented in combination with a more generic, non-customized QCQP solver [
26] and, subsequently, with the customized one from
Section 5. The relevant parameters used for this example are found in
Appendix B.
To test the algorithm’s nominal performance, we generated random inputs to the control allocation function and recorded the time and number of iterations needed to obtain a feasible solution and a numerical signature as output. In addition, to test degraded scenarios, we varied the number of available thrusters between 1 and 11. The results are depicted in
Figure 15 in the form of box plots. Here, the interquartile range (IQR) box denotes the 25–75 percentile, the whiskers mark the min–max quartiles, which are defined by the
deviations with respect to the IQR box range, the blue line highlights the median, and the blue circles indicate variability outside the min–max range. Let us first highlight that we always obtained a feasible solution, even for the severely degraded scenarios. It is also satisfactory to observe that the computational efficiency was improved by almost two orders of magnitude when compared with the generic QCQP solver. The worst-case time needed to compute a solution with the GR740 processor was less than 1 ms, and even less than 11 μs on the Intel i9. In terms of number of iterations and numerical signature, we obtained the same results (for the same seeds) with both processors, never more than 10 iterations for the customized solver. All this clearly demonstrates the numerical efficiency and robustness of the developed algorithm and the customized solver.
To evaluate the algorithm’s scalability, we conducted an additional test by introducing randomly configured thrusters to the existing setup.
Figure 16 shows the average computation times and the
variability for 1000 random thrust dispatching tests per configuration, totaling
simulations. (The thrust dispatching scenario was selected for this experiment due to its simplicity in generating random problems of varying size. However, the underlying problem structure and solver remain consistent with those used in more complex formulations, such as the ALTIUS benchmark, where only the preconditioning is modified). These tests were executed on a 12th Gen Intel(R) Core(TM) i7-12800H processor running at 2.40 GHz, employing three different solvers: (i) the generic SOTB QP solver, (ii) the customized one presented in
Section 5, and (iii)
quadprog from the
MATLAB Optimization Toolbox.
We emphasize that these tests were carried out in MATLAB without the use of autocoding, leading to (slight) variations in average computation times across different tests. All solvers were configured with a uniform tolerance of . It is also important to note that this performance comparison is limited to nominal scenarios (i.e., those without actuator failures) since only the customized solver is designed to operate under such conditions. Further observe that the customized solver is an order of magnitude faster compared with the generic SOTB QP solver. Similarly, it outperforms (on average) the commercial quadprog solver for problem sizes up to about 56 optimization variables (note here that the quantitative comparison with quadprog is limited without the use of autocoding). The customized solver is also significantly more stable, as indicated by the substantially lower values. Moreover, the computational time scales linearly with ∼, with N being the number of optimization variables. Hence, these results clearly demonstrate the computational efficiency of the customized solver.
6.4.2. The ALTIUS Benchmark Problem
Finally, let us address the numerical performance of the customized solver for the ALTIUS benchmark problem. Again, the test was performed by generating random inputs to the control allocation function and recording the numerical signature, time, and number of iterations needed to obtain a feasible solution. Once more, the numerical equivalence in both processors was verified by obtaining the same signature and number of iterations for the same seeds. In addition, to test degraded scenarios, we assumed that at least 1 RWL was available while the rest of the actuators could randomly fail. The results are shown in
Figure 17 for the 1 and 4 Hz cycles, both for the nominal as well as the degraded scenario. As can be seen, the worst-case time needed to obtain a feasible solution with the GR740 processor is less than 2.5 and 1 ms for the 1 and 4 Hz cycles, respectively, for the nominal and the degraded scenarios. Moreover, the worst-case results obtained with the Intel i9 are even less than 18 μs. As can also be seen in the right plot, the solver requires a minimum of 4 and a maximum of 16 iterations to generate a feasible solution. All this demonstrates that even (relatively) complex control allocation problems can be effectively addressed by means of real-time embedded optimization techniques with all the potential advantages that were highlighted throughout the paper. Finally, the results depicted in
Figure 15 and
Figure 17 are summarized in
Table 2.
7. Final Remarks and Conclusions
In this paper, we have formulated a generic and versatile optimization-based algorithm for the systematic distribution of control commands to a set of available actuators while minimizing objectives such as fuel consumption and considering complex operational constraints. The proposed approach aids the realization of increasingly complex missions, reduces the operational complexity, and embeds failure management in a smart way. To further optimize performance, a custom solver was developed, tailored to maximize computational efficiency and enable the integration of these techniques into space missions. The algorithm’s effectiveness was demonstrated on a representative benchmark problem derived from the ALTIUS mission. The results indicate that the algorithm consistently produces feasible solutions and maintains functionality even under severely degraded conditions. In addition, the algorithm’s numerical efficiency was validated on a dedicated breadboard equipped with the space-grade GR740 (LEON 4) processor. The observed computation times for obtaining feasible solutions suggest that real-time embedded optimization is viable for satellite applications. These techniques are anticipated to be applicable to other space missions, including guidance and control systems.
A relevant limitation of the proposed algorithm is its reliance on convex constraints and sets. Nevertheless, the formulation is sufficiently generic to accommodate a wide range of actuators commonly used in space missions. For exceptions, such as control moment gyroscopes (CMGs), the necessary modifications have been addressed within the paper to ensure compatibility. Another potential limitation arises from hardware constraints, particularly for processors with lower performance than the GR740 and for larger problems consisting of more optimization variables. However, this can be mitigated by the fact that not all actuators may be required for a specific operation, allowing for the use of different autonomous actuator managers tailored to various subsets and modes.
The presented algorithm is currently being implemented for several missions, including an orbit transfer vehicle and a rendezvous and docking mission. Ongoing tests are being conducted, including different degraded scenarios, such as actuator performance degradation. Future developments will focus on the incorporation of online methods for calibrating the system matrices dynamically with the aim of enhancing the algorithm’s adaptability and resilience.
Author Contributions
Conceptualization, J.R. and J.V.; methodology, J.R., J.V., I.C. and V.P.; software, J.R.; validation, J.R. and V.P.; formal analysis, J.R.; investigation, J.R. and J.V.; writing—original draft preparation, J.R. and J.V.; visualization, J.R. and J.V.; supervision, J.V.; project administration, J.V.; funding acquisition, J.V. and I.C. All authors have read and agreed to the published version of the manuscript.
Funding
The authors are thankful for the funding provided by the European Space Agency (ESA) in the scope of the project “Virtual AOCS sensors and actuators for an all-in-one-mode AOCS”, contract no. 4000140236/22/NL/MGu, which was carried out by Sener Aeroespacial S.A. (Spain) in collaboration with Redwire Space (Belgium).
Data Availability Statement
Data sharing is not applicable in this article.
Acknowledgments
The authors would also like to thank ESA for making available their breadboard environment for the processor-in-the-loop verification of the developed algorithms.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AOCS | Attitude and Orbit Control System |
| APE | Absolute Performance error |
| CMG | Control Momentum Gyro |
| DOF | Degree of Freedom |
| FLOPS | FLoating-point Operations Per Second |
| GNC | Guidance, Navigation, and Control |
| IPM | Interior Point Method |
| IQR | inter quartile range |
| KKT | Karush–Kuhn–Tucker |
| LP | Linear Program |
| MIB | Minimum Impulse Bit |
| MPC | Model Predictive Control |
| MT | Magnetic torquer |
| PWM | Pulse Width Modulator |
| QCQP | Quadratically Constraint Quadratic Program |
| SDP | Semi-Definite Program |
| QP | Quadratic Program |
| RWL | Reaction Wheel |
| THR | Thruster |
Appendix A. Main Parameters Used for the ALTIUS Benchmark Problem
The main parameters used for simulating the ALTIUS scenario in
Section 6 are provided in
Table A1. In addition, the parameters associated with the tuning of the control allocation algorithm for this scenario are summarized in
Table A2.
Table A1.
Main (nominal) parameters of the ALTIUS scenario simulation.
Table A1.
Main (nominal) parameters of the ALTIUS scenario simulation.
| Variable | Value |
|---|
| Inertia diagonal terms () | kg· m2 |
| Inertia off-diagonal terms () | kg· m2 |
| Max. slew | 180 deg |
| Max. slew rate | deg/s |
| Max./min. RWL momentum () | Nms |
| Ref. momentum () | Nms |
| Envelope ref. () | Nms |
| (Normalized) envelope slope (m) | |
| Zero-crossing threshold () | Nm |
| Allocation steps () | s |
| Max./min. RWL torque () | Nm |
| Max./min. MT dipole () | Am2 |
| Max. thrust () | 1 N |
Table A2.
Solver parameters for the ALTIUS control allocation.
Table A2.
Solver parameters for the ALTIUS control allocation.
| Parameter | Value |
|---|
| |
| |
| |
| W | |
| |
| |
| D | 10 |
| d | 1 |
| Convergence threshold | |
The dispatching matrices for the RWLs, MTs, and THRs with which one can generate the matrix
(force and torque in body frame) are given by:
with
being the Earth’s magnetic field in the body frame, in Tesla.
Appendix B. Main Parameters Used for the Thruster Dispatching Test
The parameters considered for the control allocation algorithm in the thrust dispatching tests in
Section 6.4.1 are summarized in
Table A3. The employed dispatching matrix is omitted to avoid confusion as the performance results in terms of allocation errors are not discussed in this test.
Table A3.
Main parameters for testing thrust dispatching computational performance.
Table A3.
Main parameters for testing thrust dispatching computational performance.
| Variable | Value |
|---|
| Max. thrust () | 200 N |
| Parameter
| Value |
| 1 |
| |
| |
| Convergence threshold | |
References
- Johansen, T.A.; Fossen, T.I. Control allocation—A survey. Automatica 2013, 49, 1087–1103. [Google Scholar] [CrossRef]
- Martel, F. Optimal 6 axis command of a space vehicle with a precomputed thruster selection catalogue table. In Proceedings of the 18th International Symposium on Space Flight Dynamics, Munich, Germany, 11–15 October 2004. [Google Scholar]
- Kron, A.; St-Amour, A.; de Lafontaine, J. Four Reaction Wheels Management: Algorithms Trade-Off and Tuning Drivers for the PROBA-3 Mission. IFAC Proc. Vol. 2014, 47, 9685–9690. [Google Scholar] [CrossRef]
- Cantiello, I.; Chapman, P.; Monroig, G.; Passarin, F.; Daoud-Moraru, A. Solar Orbiter fine pointing Mode improvement in flight: Challenges and achievements. Acta Astronaut. 2023, 213, 264–276. [Google Scholar] [CrossRef]
- Malyuta, D.; Reynolds, T.P.; Szmuk, M.; Lew, T.; Bonalli, R.; Pavone, M.; Açıkmeşe, B. Convex Optimization for Trajectory Generation: A Tutorial on Generating Dynamically Feasible Trajectories Reliably and Efficiently. IEEE Control Syst. Mag. 2022, 42, 40–113. [Google Scholar] [CrossRef]
- Eren, U.; Prach, A.; Koçer, B.B.; Raković, S.V.; Kayacan, E.; Açıkmeşe, B. Model Predictive Control in Aerospace Systems: Current State and Opportunities. J. Guid. Control. Dyn. 2017, 40, 1541–1566. [Google Scholar] [CrossRef]
- Hewing, L.; Gramlich, D.; Verhoek, C.; Polonio, R.; Veenman, J.; Ardura, C.; Tóth, R.; Ebenbauer, C.; Scherer, C.; Preda, V. Enhancing the Guidance, Navigation and Control of Autonomous Parafoils using Machine Learning Methods. In Proceedings of the 12th International Conference on Guidance, Navigation and Control Systems, Chengdu, China, 12–16 June 2023; pp. 1–15. [Google Scholar] [CrossRef]
- Gramlich, D.; Scherer, C.W.; Häring, H.; Ebenbauer, C. Synthesis of constrained robust feedback policies and model predictive control. In Proceedings of the 2024 European Control Conference, Stockholm, Sweden, 25–28 June 2024; pp. 3476–3483. [Google Scholar] [CrossRef]
- Berberich, J.; Koch, A.; Scherer, C.W.; Allgöwer, F. Robust data-driven state-feedback design. In Proceedings of the American Control Conference, Denver, CO, USA, 1–3 July 2020; pp. 1532–1538. [Google Scholar] [CrossRef]
- Christidi-Loumpasefski, O.O.; Nguyen, D.; Nanos, K.; Rekleitis, G.; Paraskevas, I.; Regamey, Y.J.; Verhaeghe, A.; Casu, D.; Papadopoulos, E.; Ankersen, F. Towards On-Board Identification of Space Systems. In Proceedings of the International Symposium on Artificial Intelligence, Robotics and Automation in Space, Virtual, 19–21 October 2020; pp. 1–8. [Google Scholar]
- Bodson, M. Evaluation of Optimization Methods for Control Allocation. J. Guid. Control. Dyn. 2002, 25, 703–711. [Google Scholar] [CrossRef]
- Durham, W. Computationally Efficient Control Allocation. J. Guid. Control Dyn. 2001, 24, 519–524. [Google Scholar] [CrossRef]
- Servidia, P.; Sánchez-Peña, R. Spacecraft thruster control allocation problems. IEEE Trans. Autom. Control 2005, 50, 245–249. [Google Scholar] [CrossRef]
- Yang, Y.; Gao, Z. A New Method for Control Allocation of Aircraft Flight Control System. IEEE Trans. Autom. Control 2020, 65, 1413–1428. [Google Scholar] [CrossRef]
- Wang, Q.; Li, Q.; Cheng, N.; Song, J. Robust control allocation method in the presence of control effector failure. In Proceedings of the IEEE International Conference on Information and Automation, Hailar, China, 28–30 July; pp. 660–664. [CrossRef]
- Zhang, X.; Mu, R.; Chen, J.; Wu, P. Hybrid multi-objective control allocation strategy for reusable launch vehicle in re-entry phase. Aerosp. Sci. Technol. 2021, 116, 106825. [Google Scholar] [CrossRef]
- Gomes dos Santos, W.; Marconi Rocco, E.; Boge, T.; Frei, H.; Rems, F. A novel solution for the spacecraft mixed actuators problem based on a multiobjective optimization method. In Proceedings of the 25th International Symposium on Space Flight Dynamics, Munich, Germany, 19–23 October 2015. [Google Scholar]
- Dennehy, C.J.; Kunz, N. NASA Workshop on Hybrid (Mixed-Actuator) Spacecraft Attitude Control. NASA/TM-2014-218539, 1 October 2014. Available online: https://ntrs.nasa.gov/citations/20140013265 (accessed on 17 September 2025).
- Shen, Q.; Wang, D.; Zhu, S.; Poh, E. Robust Control Allocation for Spacecraft Attitude Tracking Under Actuator Faults. IEEE Trans. Control Syst. Technol. 2016, 25, 1068–1075. [Google Scholar] [CrossRef]
- Tohidi, S.S.; Yildiz, Y.; Kolmanovsky, I. Adaptive control allocation for constrained systems. Automatica 2020, 121, 109161. [Google Scholar] [CrossRef]
- Preda, V.; Hyslop, A.; Bennani, S. Optimal Science-time Reorientation Policy for the Comet Interceptor Flyby via Sequential Convex Programming. CEAS Space J. 2022, 14, 173–186. [Google Scholar] [CrossRef]
- Taborda, P.; Matias, H.; Silvestre, D.; Lourenço, P. Convex MPC and Thrust Allocation With Deadband for Spacecraft Rendezvous. IEEE Control Syst. Lett. 2024, 8, 1132–1137. [Google Scholar] [CrossRef]
- Navarro-Tapia, D.; Simplicio, P.; Marcos, A. Fault-Tolerant Dynamic Allocation Strategies for Launcher Systems. Aerospace 2025, 12, 393. [Google Scholar] [CrossRef]
- Botelho, A.; Rosa, P.; Lemos, J. Explicit Spacecraft Thruster Control Allocation with Minimum Impulse Bit. IEEE Trans. Control Syst. Technol. 2024, 33, 833–844. [Google Scholar] [CrossRef]
- Boyd, S.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Ramírez, J.; Hewing, L. Sequential Convex Programming for Optimal Line of Sight Steering in Agile Missions. arXiv 2022, arXiv:2206.06061. [Google Scholar] [CrossRef]
- Ramírez, J.; Cardín, J.; Gutierrez, H.; Cacciatore, F.; Preda, V. Embedded Optimization for Space Rider Reentry Module Parafoil GNC. Int. Astronaut. Congr. 2023. IAC-23,D2,3,10,x78434. Available online: https://www.google.com/url?sa=t&source=web&rct=j&opi=89978449&url=https://airdrive.eventsair.com/eventsairwesteuprod/production-atpi-public/031c84d0ca2a408b80bbf61a4679e56c&ved=2ahUKEwi2rdqUoOaPAxXaSWwGHXiUDjUQFnoECBgQAQ&usg=AOvVaw3lnZcQu1eoSB-7JyNsd3AA (accessed on 17 September 2025).
- St-Amour, A.; Woo, P.; Sobiesiak, L.; Lobo-Fernandes, B.; Travis, W.; Langelier, M.K.; de Lafontaine, J.; Debois, S.; Wenderski, P. ALTIUS Attitude and Orbit Control System Software and System-Level Test Results. In Proceedings of the ESA GNC Conference, Sopot, Poland, 12–16 June 2023; Available online: https://www.esa-gnc.eu/paper/?paper_id=23084 (accessed on 17 September 2025).
- Gramlich, D.; Holicki, T.; Scherer, C.W.; Ebenbauer, C. A Structure Exploiting SDP Solver for Robust Controller Synthesis. IEEE Control Syst. Lett. 2023, 7, 1831–1836. [Google Scholar] [CrossRef]
- Häring, H.; Gramlich, D.; Ebenbauer, C.; Scherer, C.W. Trajectory generation for the unicycle model using semidefinite relaxations. Eur. J. Control 2024, 80, 101063. [Google Scholar] [CrossRef]
- Markley, L.; Crassidis, J. Fundamentals of Spacecraft Attitude Determination and Control; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Llorente-Martinez, S.; Agenjo, A.; Sanchez-Maestro, R.; Meijer, L.; Saponara, M.; Rosso, C.; Cacciatore, F. Performance achievement and verification of unprecedented stability AOCS for EUCLID. In Proceedings of the ESA GNC Conference, Sopot, Poland, 12–16 June 2023; pp. 1–16. [Google Scholar] [CrossRef]
- Veenman, J.; Serrano-Lombillo, D.; Sánchez-Maestro, R. Robust Control Design Methodology of the 6DoF Flight-Formation of PROBA-3. In Proceedings of the ESA GNC Conference, Salzburg, Austria, 29 May–2 June 2017; pp. 1–11. [Google Scholar]
- Sánchez-Maestro, R.; Veenman, J.; Cardin, J.; Grzymisch, J.; Preda, V. GNC functional architecture design and implementation of the LISA drag-free control system. In Proceedings of the ESA GNC Conference, Sopot, Poland, 12–16 June 2023; pp. 1–15. [Google Scholar] [CrossRef]
- Verschueren, R.; Frison, G.; Kouzoupis, D.; Frey, J.; van Duijkeren, N.; Zanelli, A.; Novoselnik, B.; Albin, T.; Quirynen, R.; Diehl, M. Acados—A modular open-source framework for fast embedded optimal control. Math. Program. Comput. 2021, 14, 147–183. [Google Scholar] [CrossRef]
- CVX Research, Inc. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0. 2012. Available online: https://cvxr.com/cvx (accessed on 17 September 2025).
- Sagliano, M.; Seelbinder, D.; Theil, S.; Lu, P. Six-Degree-of-Freedom Rocket Landing Optimization via Augmented Convex–Concave Decomposition. J. Guid. Control. Dyn. 2023, 47, 1–16. [Google Scholar] [CrossRef]
- Papakonstantinou, C.; Lappas, V.; Schaub, H.; Kostopoulos, V. Global Steering for Control Moment Gyroscope Clusters Using Heuristic Variable Search Techniques. J. Spacecr. Rocket. 2021, 58, 1–12. [Google Scholar] [CrossRef]
- Geshnizjani, R.; Kornienko, A.; Ziegler, T.; Lohr, J.; Fichter, W. Torque Optimal Steering of Control Moment Gyroscopes for Agile Spacecraft. J. Guid. Control. Dyn. 2021, 44, 629–640. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006. [Google Scholar]
Figure 1.
Torque envelope for a typical tetrahedral RWL configuration with 45-degree cant angle.
Figure 1.
Torque envelope for a typical tetrahedral RWL configuration with 45-degree cant angle.
Figure 2.
ALTIUS RWL torque-momentum envelope.
Figure 2.
ALTIUS RWL torque-momentum envelope.
Figure 3.
Zero crossing relaxed constraint sketch.
Figure 3.
Zero crossing relaxed constraint sketch.
Figure 4.
Flowchart diagram of the autonomous actuator management algorithm [
40].
Figure 4.
Flowchart diagram of the autonomous actuator management algorithm [
40].
Figure 5.
Attitude absolute performance error (APE) with classic control allocation approach.
Figure 5.
Attitude absolute performance error (APE) with classic control allocation approach.
Figure 6.
Stored angular momentum in RWLs with classic control allocation approach.
Figure 6.
Stored angular momentum in RWLs with classic control allocation approach.
Figure 7.
Attitude absolute performance error (APE).
Figure 7.
Attitude absolute performance error (APE).
Figure 8.
Actuator commands after allocation.
Figure 8.
Actuator commands after allocation.
Figure 9.
Stored angular momentum in RWLs.
Figure 9.
Stored angular momentum in RWLs.
Figure 10.
Stored momentum versus torque evolution.
Figure 10.
Stored momentum versus torque evolution.
Figure 11.
Attitude absolute performance error (APE) in degraded scenario (note: different axes scale).
Figure 11.
Attitude absolute performance error (APE) in degraded scenario (note: different axes scale).
Figure 12.
Torque errors in degraded scenario (note: different axes scale).
Figure 12.
Torque errors in degraded scenario (note: different axes scale).
Figure 13.
Force errors in degraded scenario.
Figure 13.
Force errors in degraded scenario.
Figure 14.
Stored angular momentum in RWLs in degraded scenario.
Figure 14.
Stored angular momentum in RWLs in degraded scenario.
Figure 15.
Computational performance for a generic thrust dispatching problem: (A) nominal with customized solver, (B) degraded with customized solver, and (C) nominal with non-customized solver.
Figure 15.
Computational performance for a generic thrust dispatching problem: (A) nominal with customized solver, (B) degraded with customized solver, and (C) nominal with non-customized solver.
Figure 16.
Computation times as funtion of problem size in nominal scenarios and for different solvers, obtained on a computer with 12th-generation i7 processor.
Figure 16.
Computation times as funtion of problem size in nominal scenarios and for different solvers, obtained on a computer with 12th-generation i7 processor.
Figure 17.
Computational performance for the ALTIUS benchmark problem obtained with the customized solver: (A) nominal 1 Hz cycle, (B) nominal 4 Hz cycle, (C) degraded 1 Hz cycle, and (D) degraded 4 Hz cycle.
Figure 17.
Computational performance for the ALTIUS benchmark problem obtained with the customized solver: (A) nominal 1 Hz cycle, (B) nominal 4 Hz cycle, (C) degraded 1 Hz cycle, and (D) degraded 4 Hz cycle.
Table 1.
Test results summary Test A and B.
Table 1.
Test results summary Test A and B.
| Test | ALTIUS Nominal (A) | ALTIUS Degraded (B) |
|---|
| Max. APE (deg) | | |
| Max. Torque error (Nm) | < | |
| Max. Force error (N) | < | |
Table 2.
Summary test results Altius benchmark problem.
Table 2.
Summary test results Altius benchmark problem.
| Figure | Figure 15 | Figure 17 |
|---|
| Test | A | B | C | A | B | C | D |
| Solver | Custom | Generic | Custom |
| Scenario | Nominal | Degraded | Nominal | Nominal | Degraded |
| Max. Compt. Time GR740 (ms) | 0.88 | 0.95 | 76.50 | 2.20 | 0.70 | 2.40 | 0.80 |
| Med. Compt. Time GR740 (ms) | 0.48 | 0.64 | 44.00 | 1.20 | 0.40 | 1.10 | 0.40 |
| Max. Number of iterations | 8 | 10 | 12 | 14 | 11 | 16 | 13 |
| Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
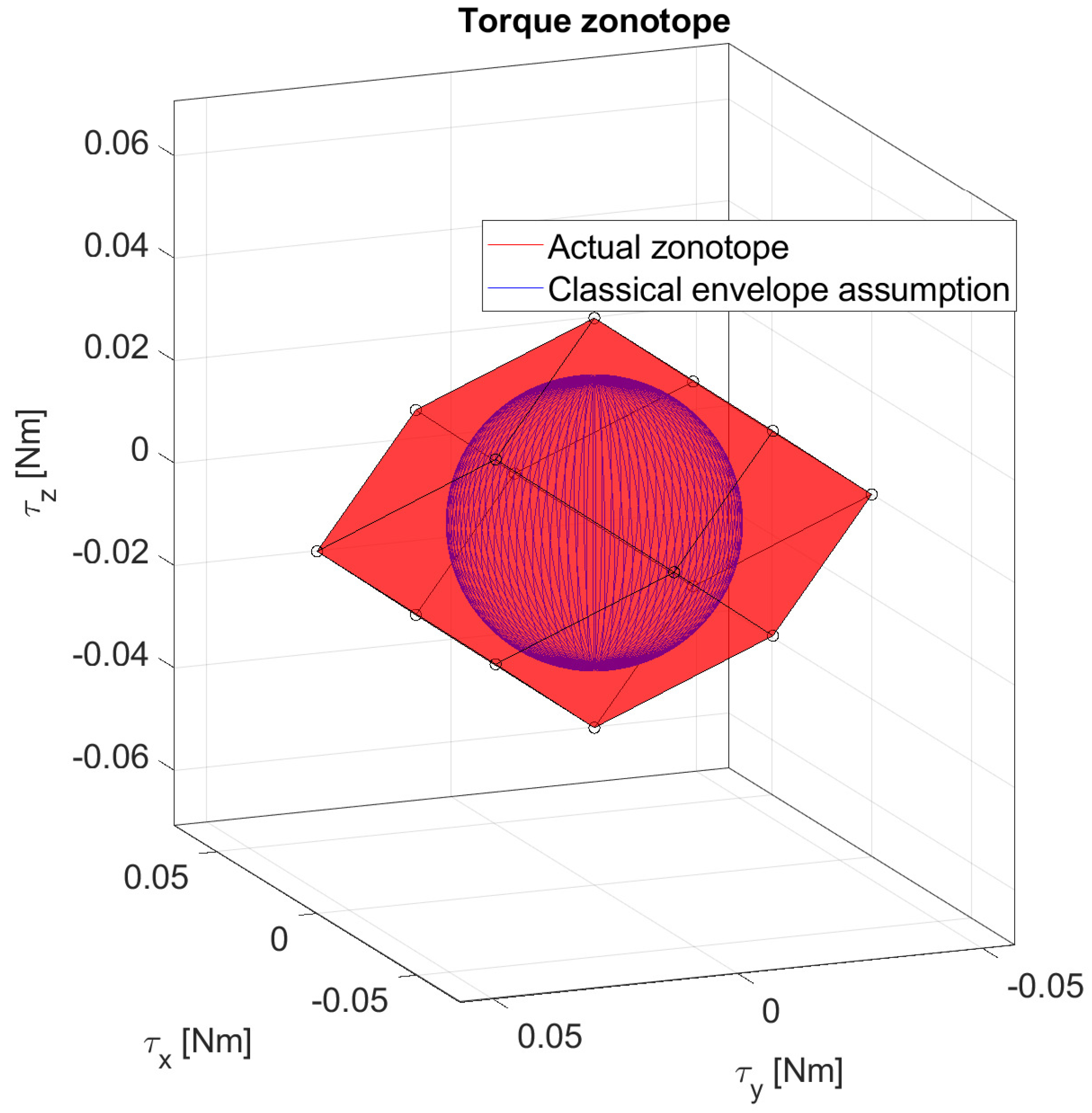
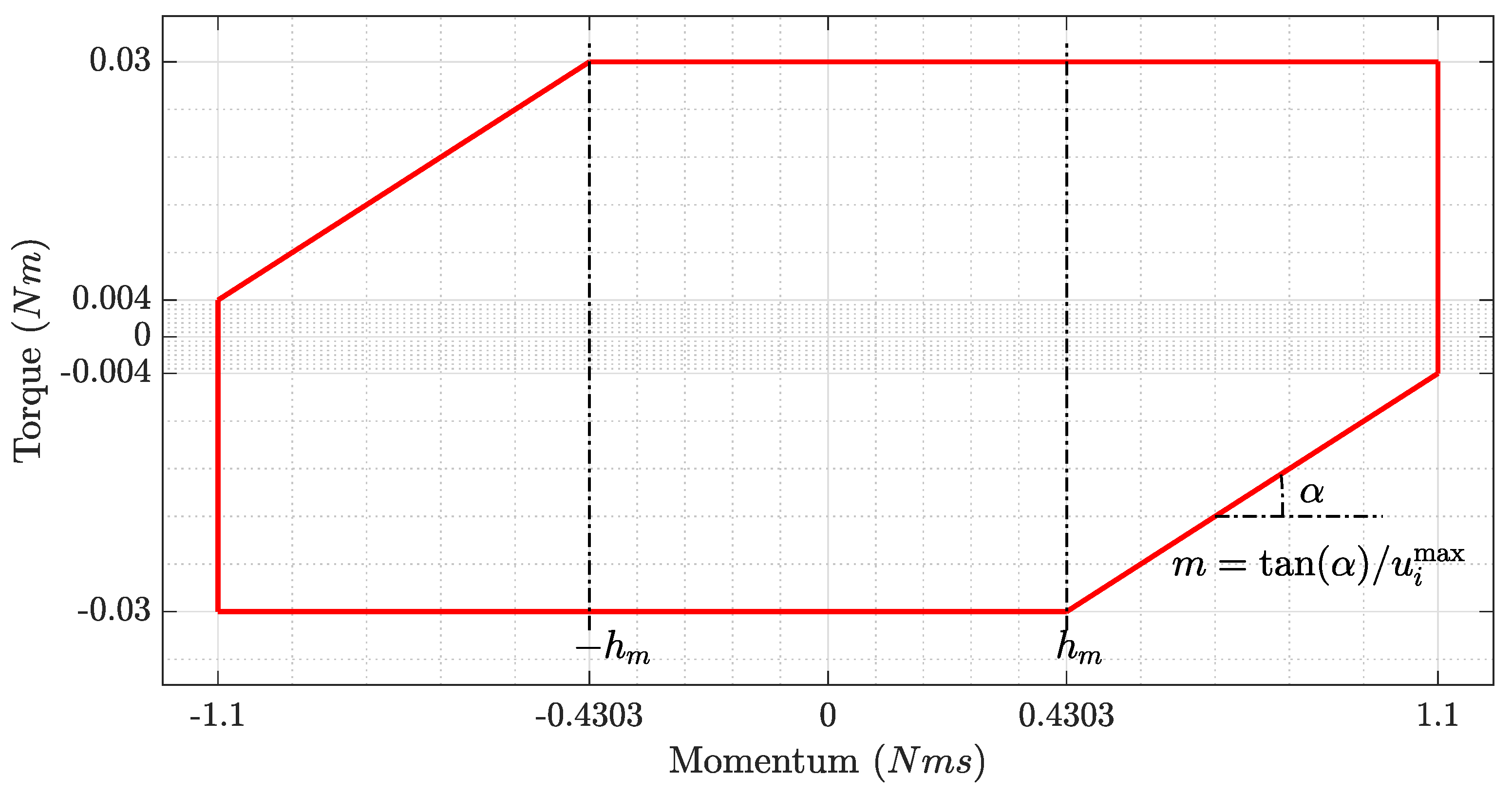
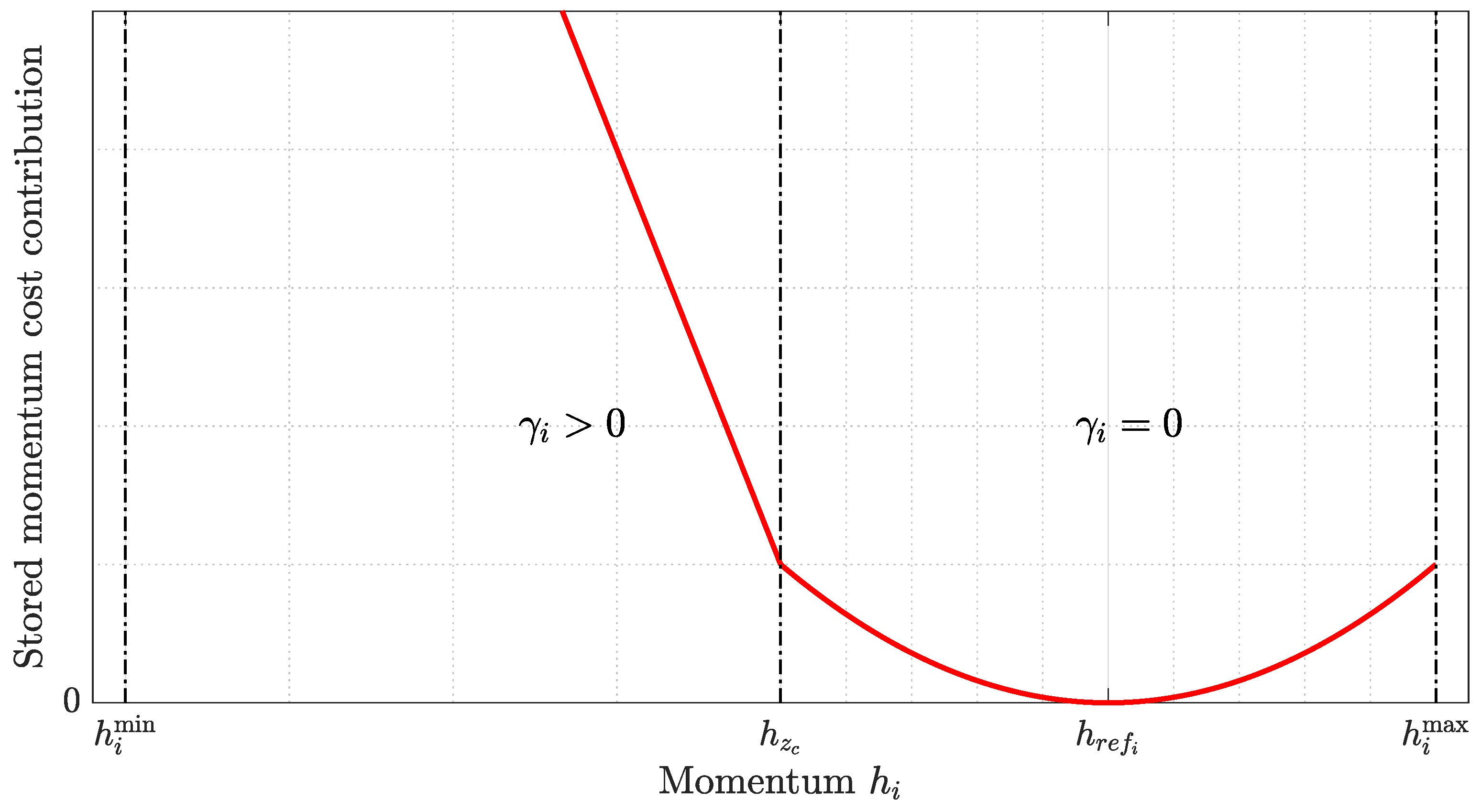
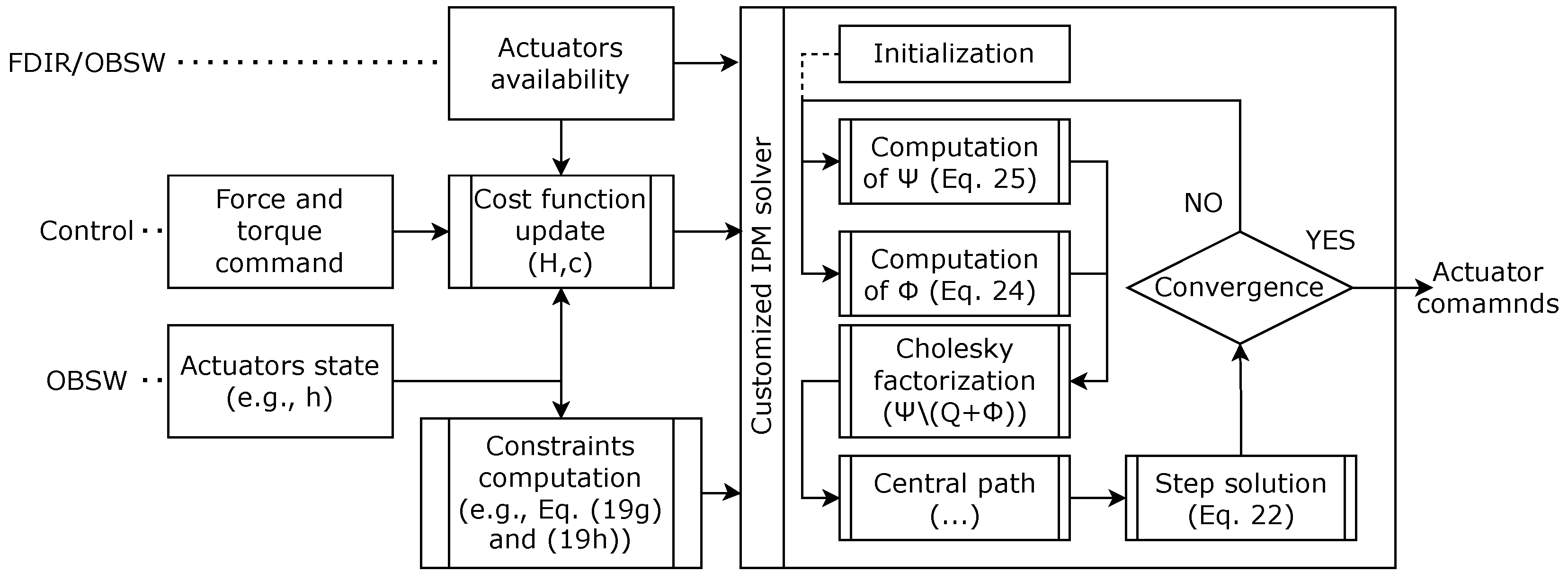


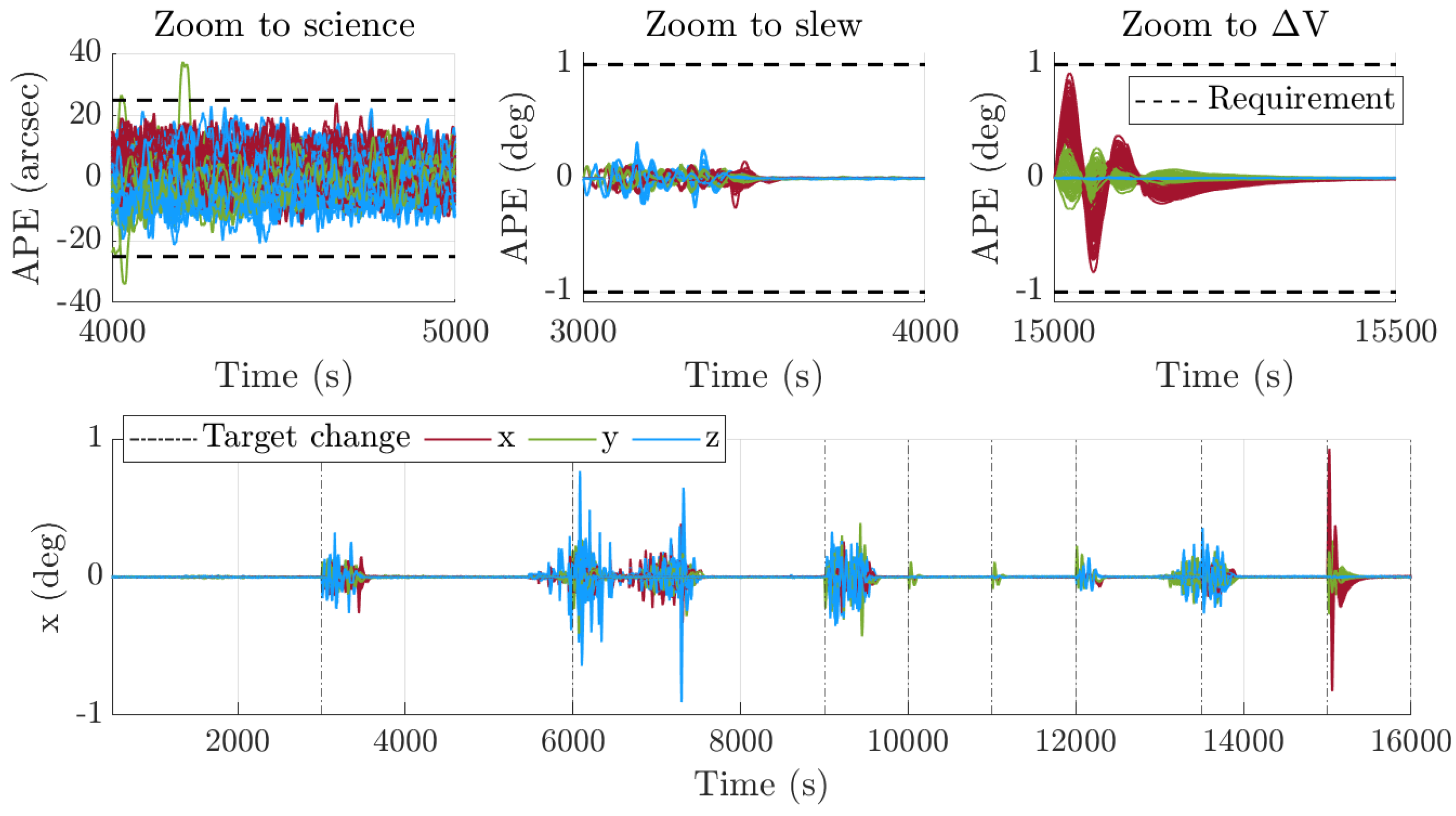


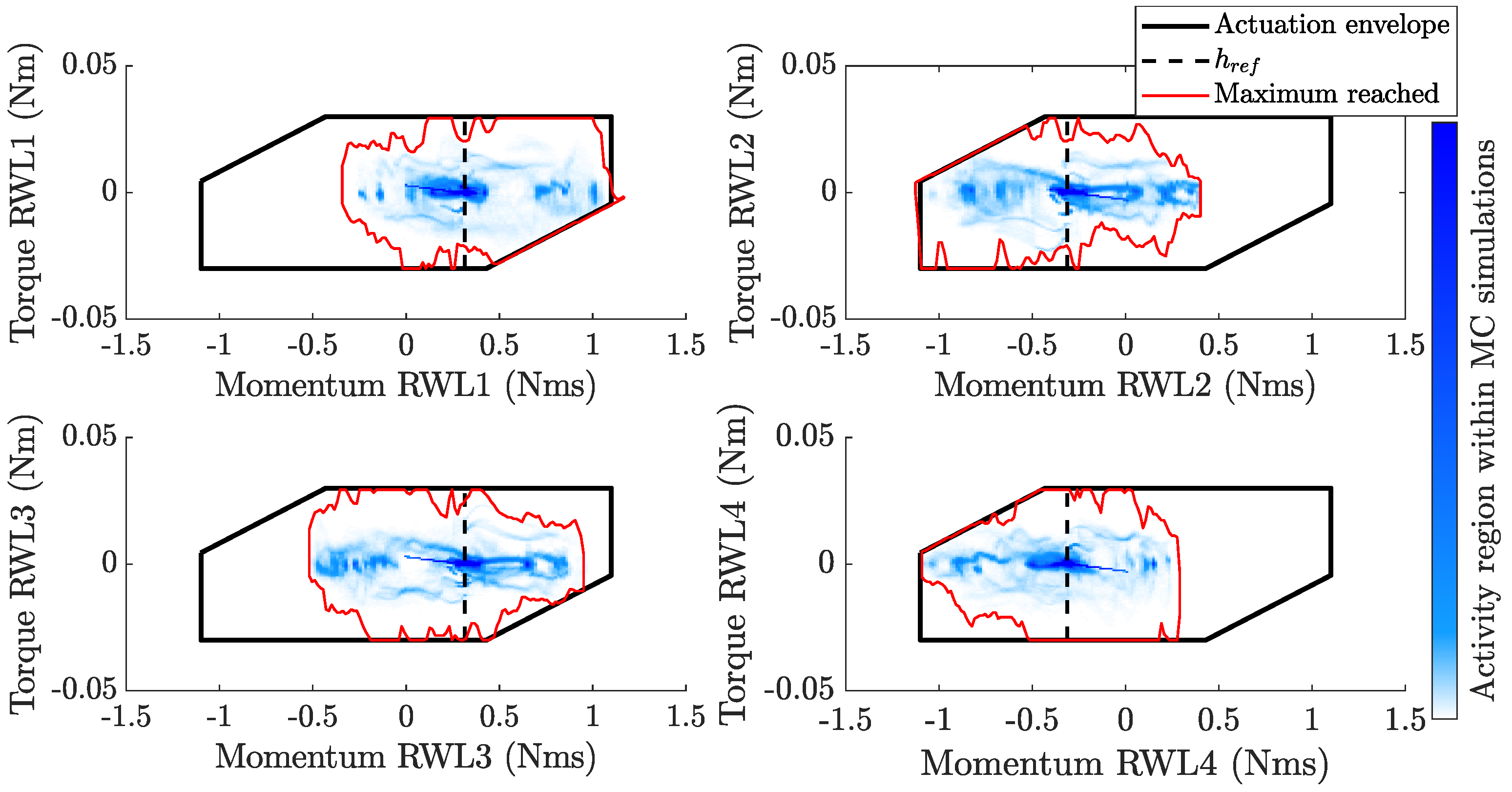




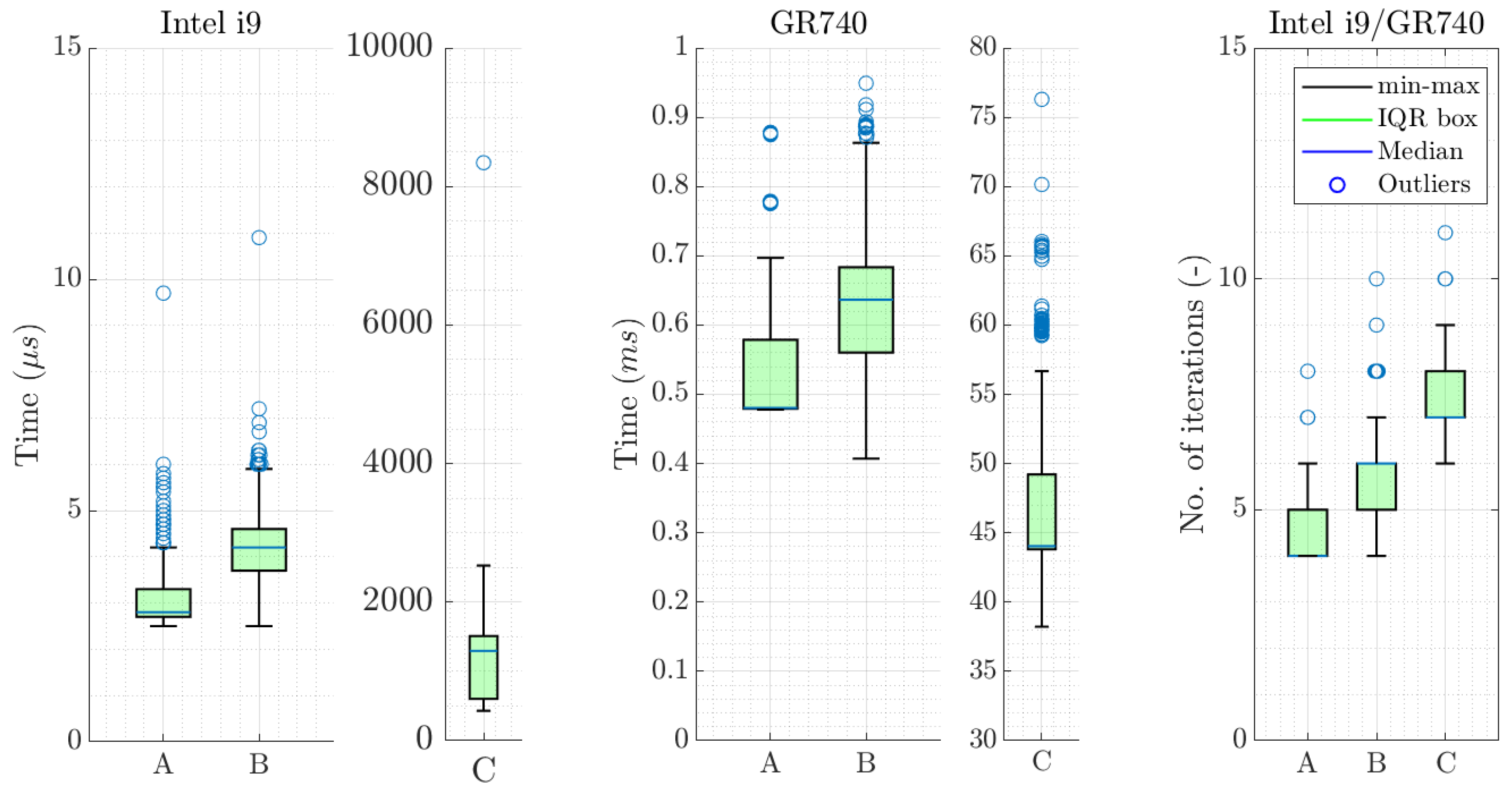
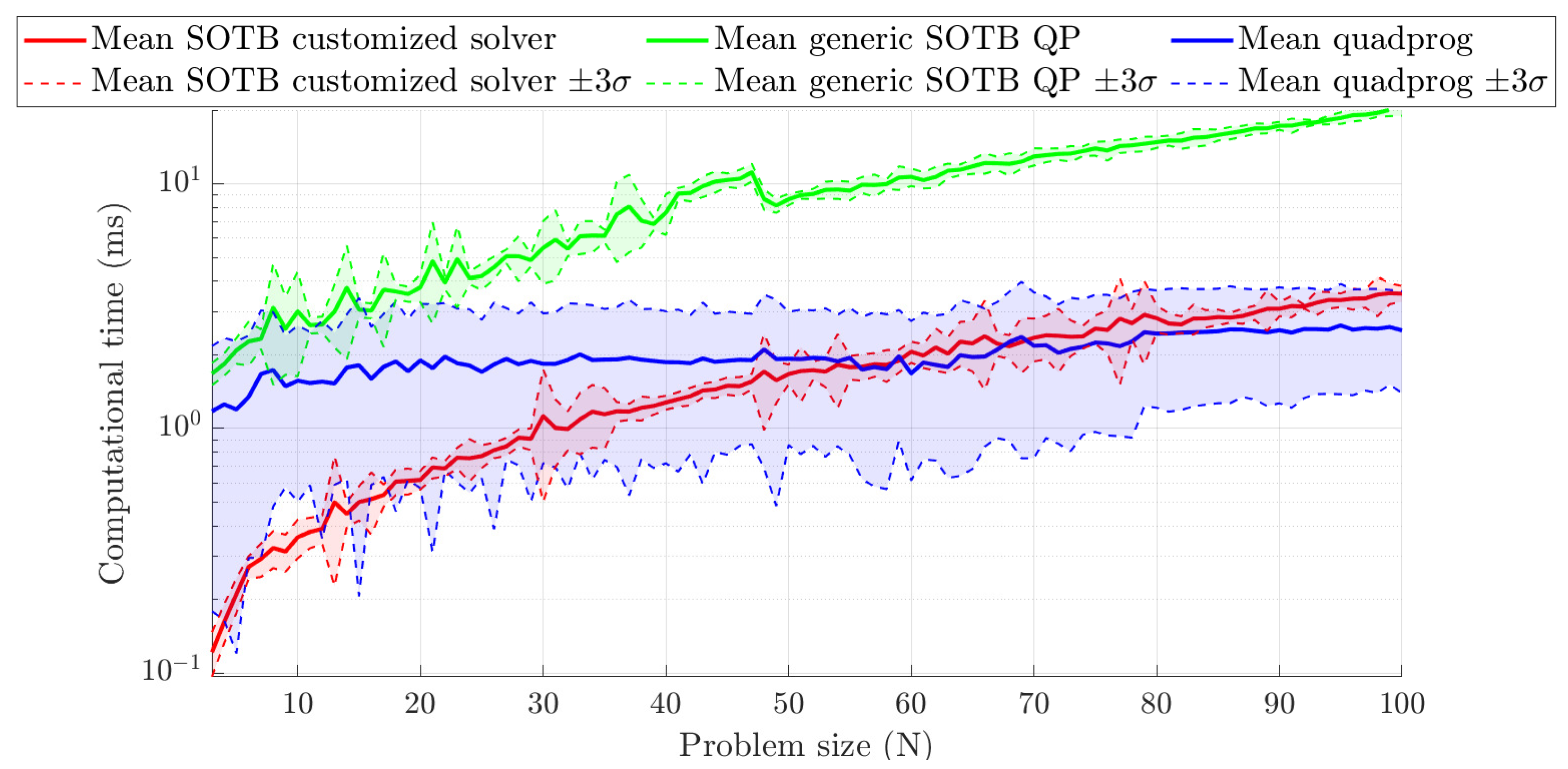



_Zhu.png)



