1. Introduction
Multi-airport terminal areas refer to designated controlled airspace regions that encompass multiple airports within a certain geographic area. These regions are characterized by interconnected surrounding airspace and overlapping traffic flows, where flight operations such as departures, arrivals, and related flight activities are organized and managed. The complexity of terminal airspace structures involving multiple airports is marked by high intricacy, large flight volume, and complex conflict situations among aircraft. Analyzing the air traffic complexity in such areas helps to improve airspace resource utilization and reduce flight delays, and it provides a scientific basis for airspace resource allocation, controller strategy formulation, and safety risk management, thereby ensuring the stable operation of high-density flight flows. Consequently, the analysis of air traffic complexity in multi-airport terminal zones has become a key research focus in academia and industry.
Currently, research on air traffic complexity mainly concentrates on three aspects: (1) complexity analysis based on Air Traffic Control (ATC) cognition, (2) analysis from the traffic situation perspective, and (3) complexity analysis using complex network theory. In the field of ATC cognitive complexity, Histon et al. [
1] pioneered the concept of cognitive complexity, laying a solid foundation for in-depth structural analysis of control cognition. Subsequently, Cong et al. [
2], from the dimensions of structural and operational features, established a multi-dimensional indicator system for sector complexity and employed K-means clustering to analyze the complexity across multiple sectors. However, cognitive complexity assessments are primarily based on controller workload, making them susceptible to human factors. To reduce subjective influence, recent studies have shifted towards analyzing air traffic complexity from the perspective of traffic situation. Zhang et al. [
3] focused on disorder and disturbances within two-dimensional airspace traffic flows, evaluating inherent traffic flow complexity to accurately depict air traffic operational conditions. Cao et al. [
4] incorporated machine learning models to explore the intrinsic relationship between operational complexity factors and sector complexity, training on multi-indicator datasets to evaluate sector complexity levels. Wen et al. [
5] proposed a spatio-temporal hybrid deep learning model that leverages spatial and temporal features related to complexity data for sector complexity prediction.
With advances in machine learning, there are more options for analyzing air traffic complexity. However, the selection of complexity indicators remains largely unchanged, primarily extracting factors from a macroscopic traffic flow perspective. Complex systems, particularly complex network theories, have been increasingly used to describe air traffic complexity in recent years, offering an effective research approach. Complex network modeling abstracts nodes and their relationships within complex systems. Wang et al. [
6,
7,
8] proposed constructing weighted conflict networks with aircraft as nodes and flight connections as edges, using network metrics like node degree and connectivity rate to assess local and overall airspace complexity. Wu et al. [
9,
10,
11] built flight state networks with aircraft as nodes and communication relations via airborne collision avoidance systems (ACASs) as edges, utilizing metrics such as node strength, average clustering coefficient, and betweenness centrality to describe dynamic traffic conditions, as well as employing principal component analysis (PCA), factor analysis, and entropy weighting to monitor airspace trends and identify key nodes—effectively reducing subjective bias and enhancing precision in complexity recognition. Bi et al. [
12], building on these studies, optimized flight state networks using velocity obstacle methods to preempt potential conflicts, aiding controllers in early detection of conflicts and area complexity.
However, existing complex network models are primarily limited to single-layer topological analyses and focus on relationships between a single factor. Air traffic complexity is inherently a multi-factor, cross-system issue. Multi-layer networks can better characterize this complexity, and the emergence of interdependent network theory provides new avenues for research. Buldyrev et al. [
13] first introduced interdependent network theory, establishing a simple interdependent network model to analyze coupled system relationships. Shao et al. [
14] proposed a one-to-many interdependent network model based on inter-layer coupling. Wang et al. [
15,
16,
17] constructed static interdependent air traffic networks with airports, air routes, and control sectors as sub-networks, studying structural vulnerabilities, failure propagation mechanisms, and relationships between network resilience, topology, and traffic flow. Li et al. [
18,
19] developed coupled interdependent models of control networks and flight state networks, reflecting interactions between controllers and aircraft, and systematically analyzed the characteristics and evolution processes of such networks.
This paper aims to solve the problem of identifying and evaluating the complexity of air traffic in multi-airport terminal areas. To improve the utilization efficiency of airspace resources and reduce flight delays, this paper constructs a route segment–flight state interdependent network model and uses the complexity indicators of nodes in this model to reflect the air traffic situation.
Different from most existing methods based on single-layer network analysis, the interdependent network model constructed in this paper can simultaneously consider the mutual influence between aircraft operating states and route structures, effectively making up for the deficiencies of traditional methods in this regard. Currently, most existing complex network models conduct complexity analysis based on free flight. However, under China’s current air traffic control system, aircraft need to fly along established air routes.
In view of this, this paper takes the aircraft and route segments above the multi-airport terminal area as nodes to construct an interdependent network model that is more suitable for China’s operating environment, thus enabling a more accurate reflection of the air traffic situation.
3. Construction of an Interdependent Network of Multi-Airport Terminal Areas in Guangdong–Hong Kong–Macao
This paper selects the practical scenarios of multiple airport terminal areas in the Guangdong–Hong Kong–Macao Greater Bay Area to validate and analyze the interdependent network model. The Guangdong–Hong Kong–Macao Greater Bay Area is composed of three core airports—Hong Kong, Guangzhou, and Shenzhen—as well as other important airports such as Macau and Zhuhai. Within the multiple airport terminal areas, flight route density is high, and complex relationships exist.
On normal operation days (without interference from the pandemic or special control measures), the total number of inbound and outbound flights at the core airports in the Guangdong–Hong Kong–Macao Greater Bay Area (Guangzhou Baiyun, Shenzhen Bao’an, Hong Kong International, Zhuhai Jinwan, and Macao International) is approximately 2500–3000 flights per day. Most of these flights experience route intersections and overlapping arrival and departure paths in the terminal area.
The peak hours for route operations are from 08:00 to 11:00 (morning peak) and from 17:00 to 21:00 (evening peak). During these two periods, the density of aircraft on the terminal area routes increases significantly, and the risk of conflicts rises. The average length of the route segments is about 20–40 km, with the shortest being less than 15 km and the longest about 60 km.
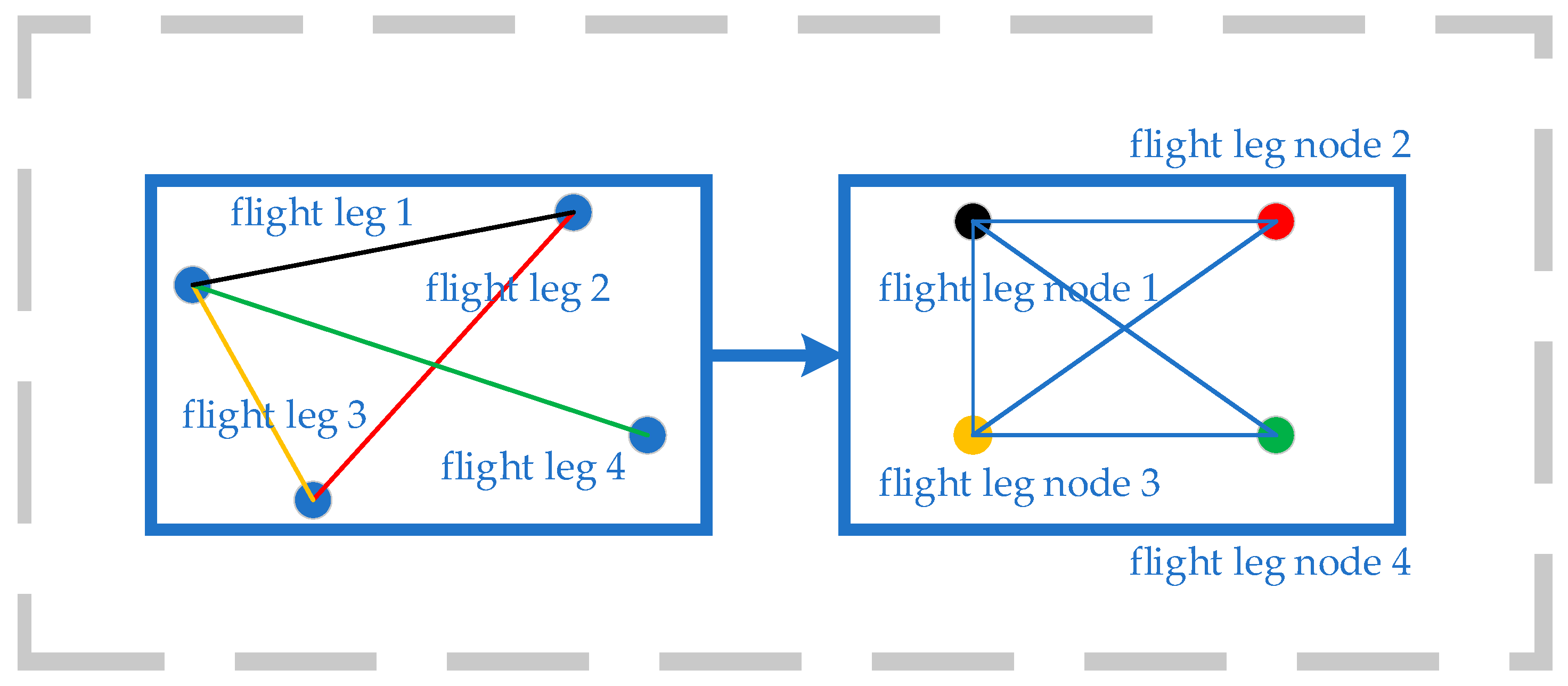
In this paper, a “route segment” refers to the section of the route connecting two waypoints, similar to the “jet airways” internationally. All the route segments in this paper are derived from the route charts issued by the Civil Aviation Administration of China and are part of the fixed route system. All civil aviation flights in this airspace operate in accordance with Instrument Flight Rules (IFR).
Taking the actual air traffic data of the case in this paper as an example, during peak hours, the horizontal relative positions of aircraft within the route segments are often less than 20 km, and the vertical separation of some aircraft is less than 300 m. There are numerous potential conflict threats, which are exactly the operating states that the indicators proposed in this paper aim to capture and quantify.
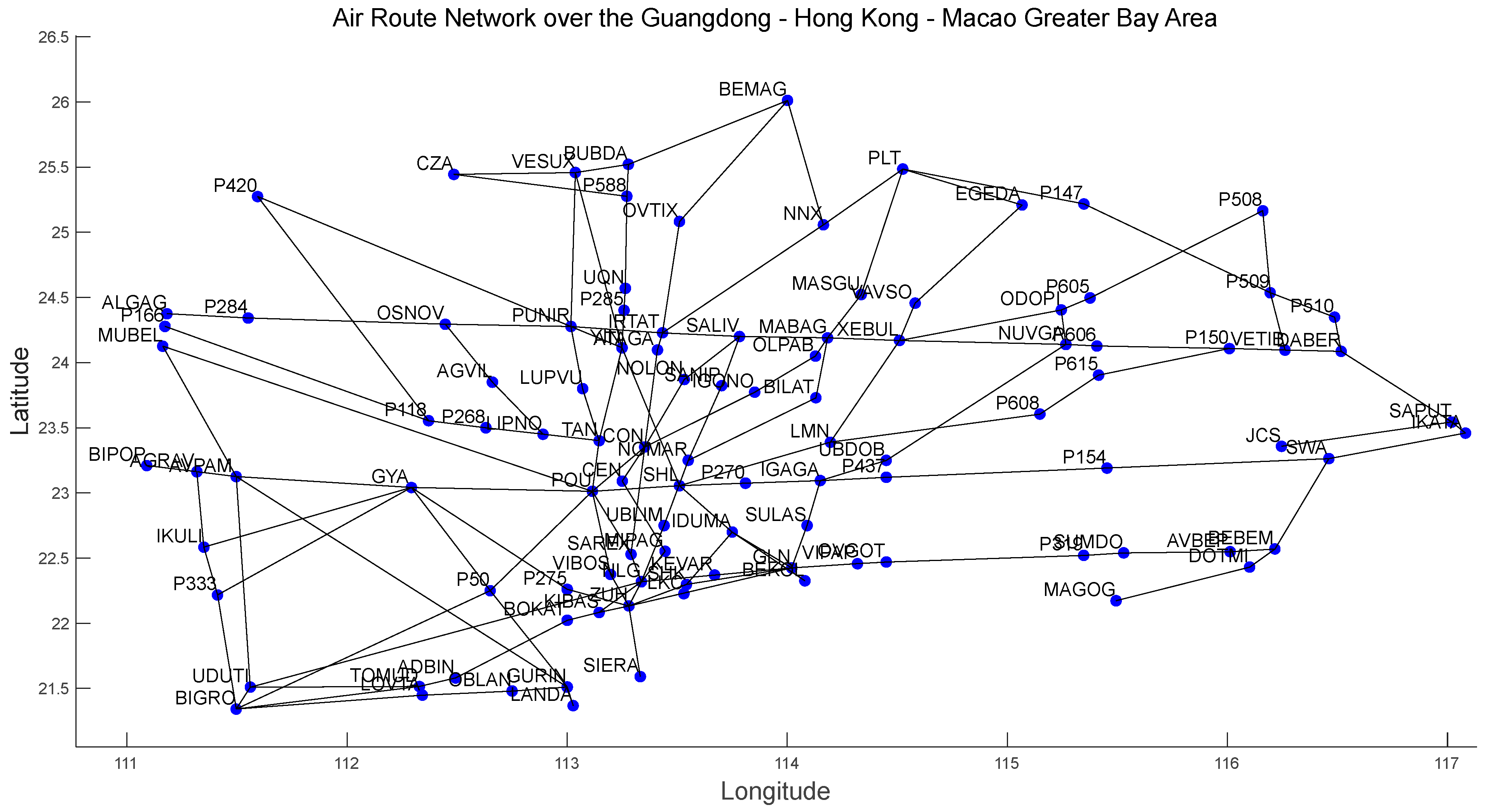
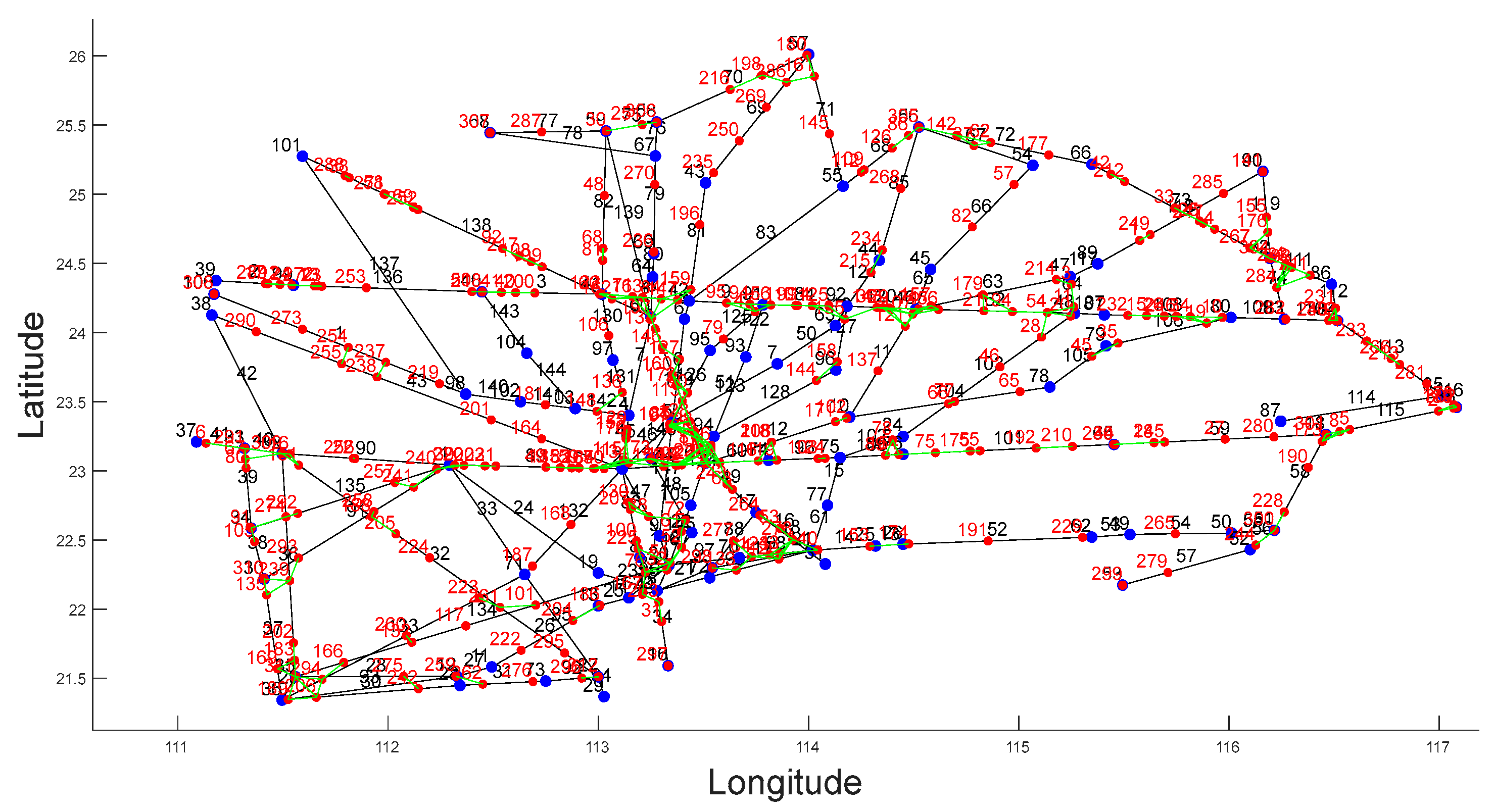
According to the aeronautical charts published by the Civil Aviation Administration of China on 1 August 2023, we identified the navigation points and their longitude and latitude over the airspace of the multiple airport terminal areas in the Greater Bay Area, along with their connectivity relationships. The resulting airway map over the Greater Bay Area is shown in
Figure 4, which contains a total of 148 segments. The blue dots represent the navigation points in the airspace of the Greater Bay Area, the black lines denote the flight segments, and the labels are the names of the navigation points.
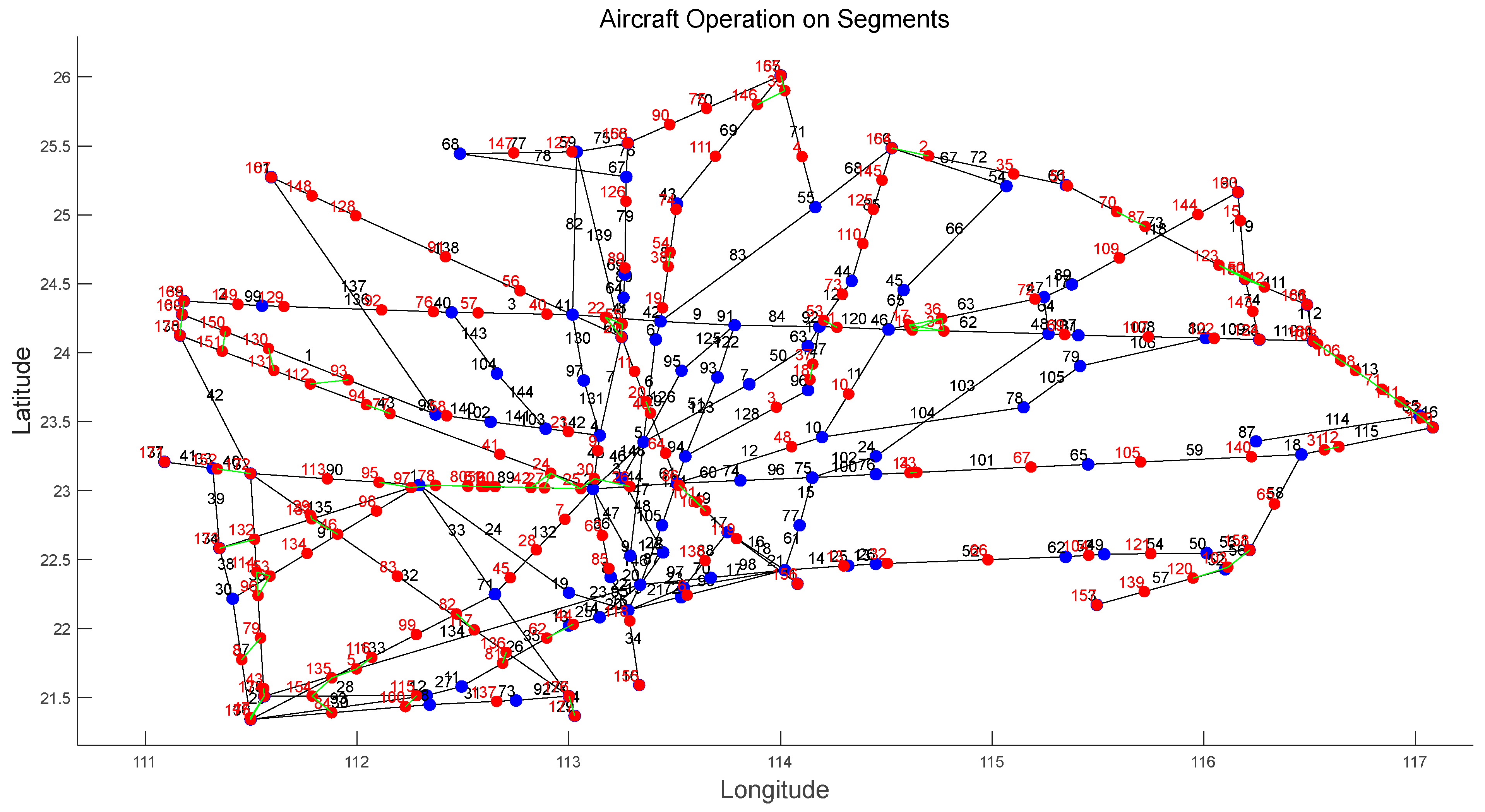
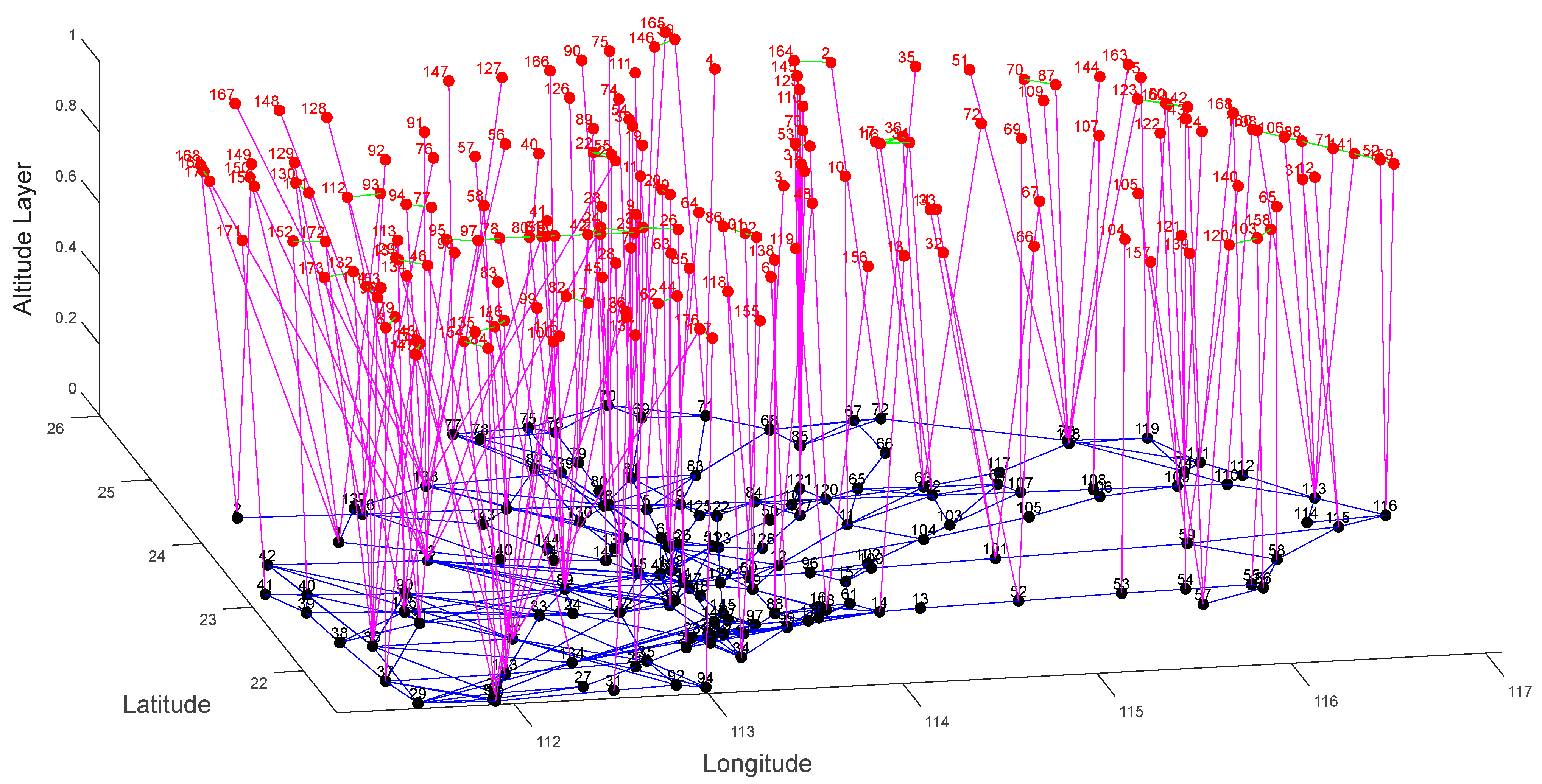
We numbered the flight segments and collected air traffic flow data over the Guangdong–Hong Kong–Macao Greater Bay Area at 14:20 on 18 June 2024. At this timestamp, there is a total of 173 aircraft in the airspace. The traffic situation diagram is shown in
Figure 5, where the red points and numbers represent the aircraft in operation and their corresponding IDs. Based on the criteria outlined in
Section 2.1 for determining aircraft conflict situations, if two aircraft are found to be in conflict, a green edge is established between their respective aircraft nodes.
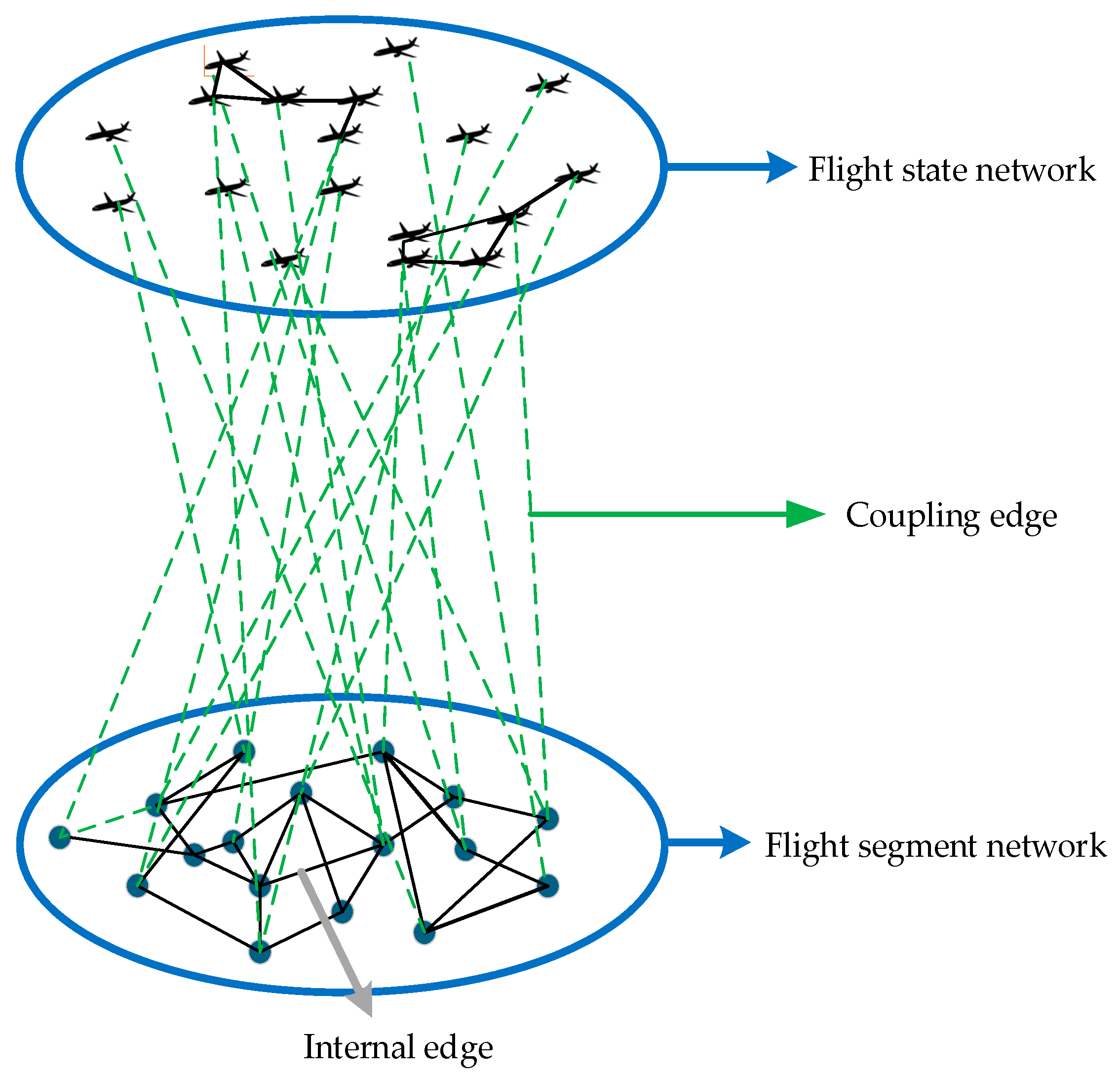
In the interdependent network model, the weighted adjacency matrix of the interdependent network can be used to represent the air traffic conditions over the Guangdong–Hong Kong–Macao Greater Bay Area. At this moment, there are 173 aircraft in flight, so the weighted adjacency matrix is a square matrix of size (148 + 173) × (148 + 173). The number 173 represents the total aircraft flying over the airspace of the multiple airport terminal areas at this time.
The matrix can be divided into four parts: The top-left 173 × 173 submatrix records the conflict levels between individual aircraft. The bottom-right 148 × 148 submatrix is an adjacency matrix indicating the connectivity between 148 flight segments; a value of 1 signifies that two segments share a common point, while 0 indicates no shared point. The bottom-left 148 × 173 matrix and the top-right 173 × 148 matrix are transposes of each other; they record the weights of inter-layer coupling edges.
Based on the air situation diagram at the current moment, the weighted adjacency matrix A of the interdependent network model at this moment is calculated, and its expression is as follows:
Based on the adjacency matrix, the interdependent network model for the Guangdong–Hong Kong–Macao Greater Bay Area at 14:20 on 18 June 2024, is depicted in
Figure 6. In the figure, red nodes represent aircraft nodes, black nodes represent flight segment nodes, green edges denote conflict edges within the flight status network, purple edges indicate inter-layer coupling edges, and blue edges represent connections between flight segments.
Next, based on the route segment–flight state interdependent network model established above, we will establish the complexity indicators for this interdependent network model, and analyze the complexity of each route segment and the overall air traffic situation. The end-users of the complexity indicators established in this paper to reflect the air traffic situation include air traffic controllers, airspace planners, airline operation dispatchers, and the airspace management department of the Civil Aviation Administration, etc.
These indicators are mainly used for real-time operation monitoring and short-term early warning, which are specifically reflected in the following aspects: Firstly, conduct real-time complexity assessment to help controllers identify the current complexity of the airspace and potential risk areas. Secondly, assist in traffic management decision-making, providing a scientific basis for traffic allocation and further optimizing flight schedule arrangements. Thirdly, serve as an early-warning system. When the complexity index exceeds the threshold, it can promptly issue warnings for possible congestion or conflicts. Fourthly, carry out historical trend analysis. By analyzing the complexity change patterns during specific periods, it can provide references for future planning.
5. Overall Complexity Analysis of Air Traffic Based on Dependency Networks
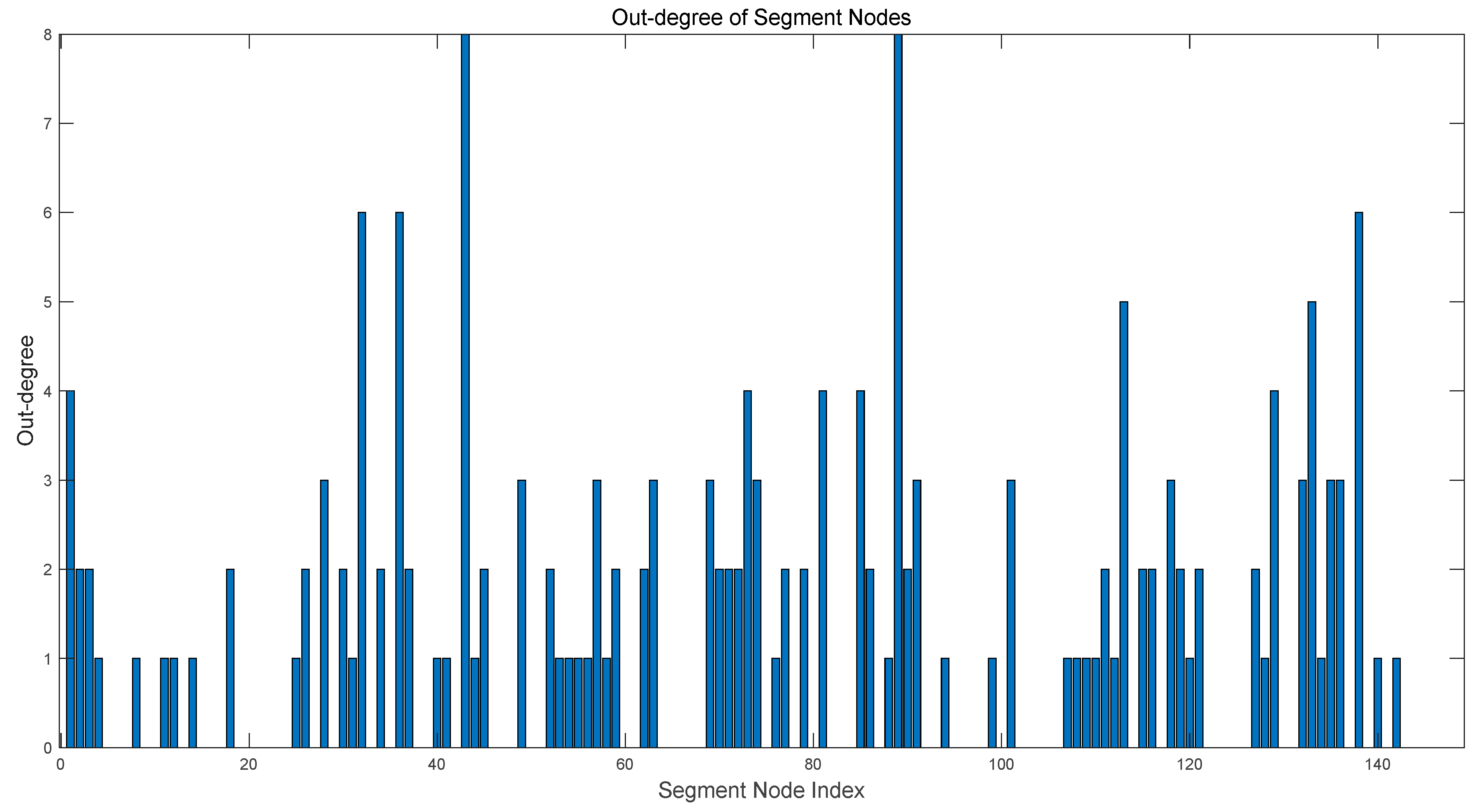
Analysis of Segment Node Complexity can reveal the complexity and significance of each flight segment. Additionally, the analysis of the overall dependency network’s complexity provides insights into the air traffic complexity within the entire multi-airport terminal area.
To accurately evaluate the overall characteristics of the air traffic network, we select three indicators that reflect the network’s overall performance: the average node information entropy, the average node weighted clustering coefficient, and the average node strength. These metrics are used to analyze the complexity of air traffic in multi-airport terminal areas. The integration is performed using the Analytic Hierarchy Process (AHP), ultimately deriving a Flight State Network Complexity Index (P) to represent the overall complexity of the air traffic system.
Information entropy measures the diversity and uncertainty of a node’s connection pattern. In the dependency network model, a higher node information entropy indicates greater uncertainty in the node’s state—such as aircraft flight status and segment utilization—making the system more complex and variable. For a node
i, its information entropy
H(
i) can be calculated using the following formula:
where
N(
i) is the set of neighboring nodes of node
i.
pij is the connection probability between node
i and its neighbor node
j, which can be obtained by normalizing the edge weights:
where
represents the edge weight between node
i and node
j.
The average node information entropy is the mean value of the information entropy across all nodes in the network. It provides an overall measure of the node information entropy for the entire network. The average node information entropy reflects the overall uncertainty and complexity of the entire air traffic network. A higher average node information entropy indicates that the feature distribution of nodes is relatively dispersed, resulting in a more complex network structure and interaction relationships. Consequently, the overall operation of air traffic becomes more intricate.
The weighted clustering coefficient is a metric used to assess the local connectivity density around a node within a complex network. It reflects the tightness of connections among neighboring nodes and the distribution of edge weights. When multiple aircraft are flying within a specific area and are relatively close to each other—implying potential flight conflicts—the connection weights between these nodes and their neighbors tend to be higher. As a result, the clustering coefficient increases, indicating that the air traffic in that region is more complex and may carry a higher risk of flight conflicts. For a node
i, its weighted clustering coefficient
C(
i) can be calculated using the following formula:
The degree of a node is denoted as , and the strength of a node is denoted as .
The average node weighted clustering coefficient is the mean value of the weighted clustering coefficients over all nodes in the network. The average node-weighted clustering coefficient reflects the local clustering characteristics of the entire network. A higher average weighted clustering coefficient indicates more frequent and tighter interactions among aircrafts and between flight segments.
Node strength is an index used to measure the connection strength between a node and its neighbors, which reflects the importance and activity level of the node in the network. The expression of node strength has been mentioned above.
The average node strength is the mean value of the strengths of all nodes in the network, reflecting the overall activity level and connection intensity of the entire network. A higher average node strength indicates that flights between aircraft within the entire air traffic network tend to have more frequent conflicts and higher conflict intensities, reflecting a higher level of airspace congestion; conversely, a lower average node strength suggests relatively smoother air traffic with fewer conflicts and lower conflict intensity.
Because, during our calculation of the average node strength weight using the Analytic Hierarchy Process (AHP), the difference between the average node strength and the average node information entropy, as well as the average node weighted clustering coefficient, was excessively large, we employed the tanh function to limit the average node strength within the range (0, 2).
The expressions for the average node information entropy, the average node weighted clustering coefficient, and the average node strength are as follows:
The network complexity index (P) is obtained by weighted combination of the three aforementioned network complexity indicators using the AHP. AHP is a multi-criteria decision-making method used for decision analysis; it constructs judgment matrices to compare the importance of different factors and computes their weights. The specific steps are as follows:
First, construct the judgment matrix W. In this case, it is a 3 × 3 matrix representing the relative importance among three factors: average node information entropy, average node weighted clustering coefficient, and average node strength. The element Wij indicates the importance of factor i relative to factor j.
Second, calculate the factor weights. To do this, we use the geometric mean method: take the logarithm of each element in each row of the judgment matrix, compute the average, then exponentiate to obtain the geometric mean for each factor. These geometric means are normalized so that their sum equals 1, yielding the weights for each factor.
Third, perform a consistency check. This step is crucial in AHP to ensure the logical consistency of the judgment matrix. The consistency index (
I) is calculated using the formula:
represents the maximum eigenvalue of the judgment matrix. In the Analytic Hierarchy Process (AHP), the judgment matrix is constructed by pairwise comparison of the relative importance of various factors.
n is the order of the judgment matrix, that is, the number of rows or columns of the matrix, which represents the number of factors involved in the comparison.
The calculation formula for the Consistency Ratio (
R) is as follows:
is the Random Index, and its value depends on the order
n of the judgment matrix.
If
R < 0.1, the judgment matrix is considered to have satisfactory consistency; otherwise, adjustments to the judgment matrix are necessary. Based on the experimental result,
R = 0.0332, which meets the criteria. Finally, the formula for calculating the complexity index is as follows:
The variables are the indicator weights obtained through the Analytic Hierarchy Process. These weights reflect the relative importance of each indicator in the calculation of the complexity index. According to the experimental results, , , .
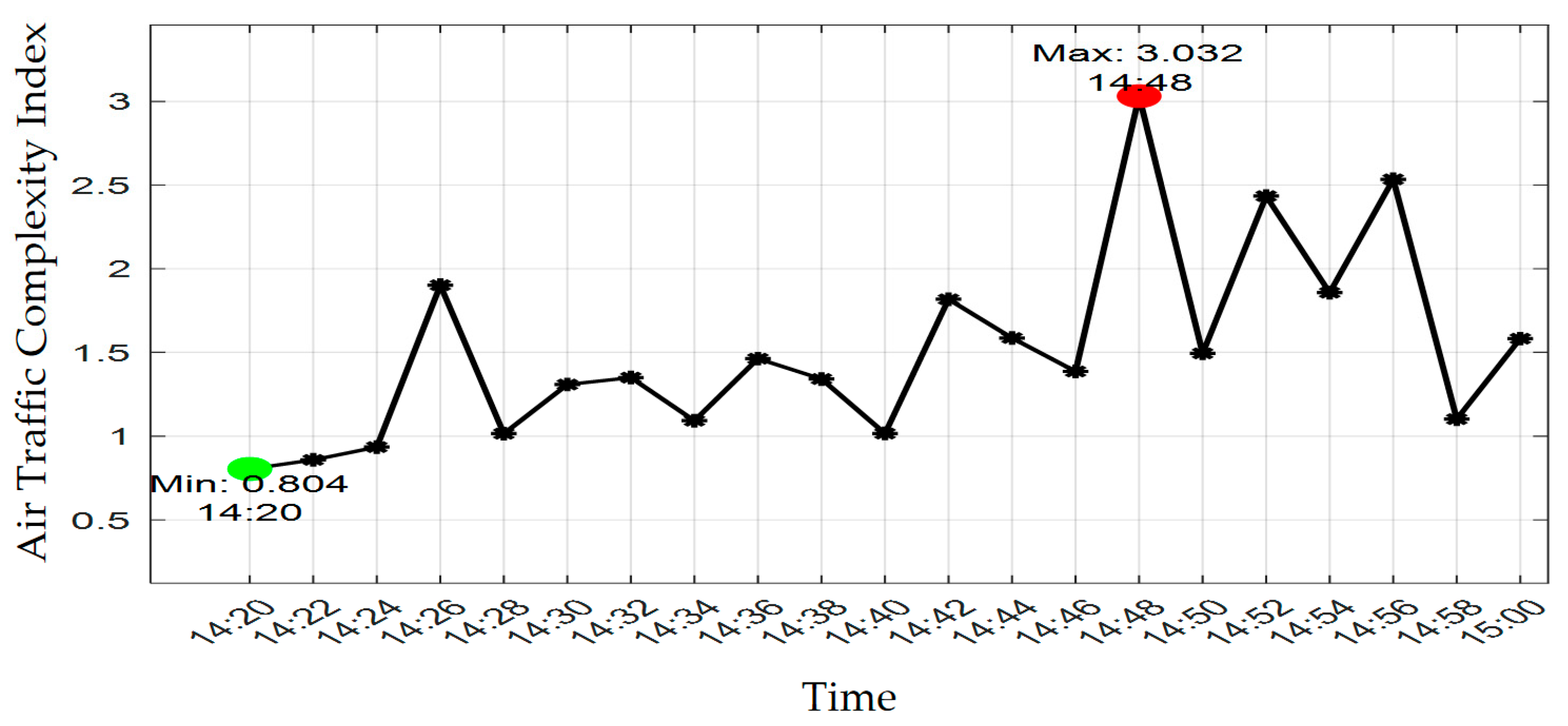
Based on the air situation maps from 14:20 to 15:00 on 18 June 2024, we derived the dependency network models for this time period. Using these dependency network models, the variation of the Guangzhou–Hong Kong–Macau multi-airport terminal area complexity index is shown in
Figure 10, with a time step of 2 min.
Based on
Figure 10, we can observe that at 14:20 on June 18, 2024, the dependency network complexity index is at its lowest value of 0.8. The air situation map corresponding to this time is shown in
Figure 5 above. Conversely, at 14:48 on 18 June 2024, the dependency network complexity index reaches its highest value of 3.0, and the air situation map at this time is depicted in
Figure 11.
Based on
Figure 5, at 14:20, the number of aircraft flying over the Guangdong–Hong Kong–Macau terminal area is relatively low, with fewer flight conflicts among the three major airports: Hong Kong, Guangzhou, and Shenzhen. According to
Figure 11, at 14:48, the number of aircraft operating in the Guangdong–Hong Kong–Macau terminal area increases, and the frequency of flight conflicts among Hong Kong, Guangzhou, and Shenzhen airports also rises. This indicates that the variation of the dependence network complexity index is consistent with the actual air traffic situation in the multi-airport terminal area of Guangdong–Hong Kong–Macau. Therefore, it validates that the segment–flight state dependence network model can effectively reflect the overall complexity of air traffic. This research provides a theoretical basis and practical significance for the analysis of air traffic complexity in multi-airport terminal areas.