Advanced Implementation of the Asymmetric Distribution Expectation-Maximum Algorithm in Fault-Tolerant Control for Turbofan Acceleration
Abstract
1. Introduction
- (1)
- This paper proposes a theoretical viewpoint of substantial probability, which constitutes the foundation of fault-tolerant control methods for turbofan engine acceleration schedules. This discovery presents significant theoretical progress in probability theory.
- (2)
- This paper derives the iterative formulas of ADEMA applicable for fault-tolerant control in acceleration schedules, relying solely on the real-time fuel output from the four schedules and their cumulative variances.
2. Probability Bases of Methods
2.1. Viewpoint of Frequency School
2.2. Viewpoint of Bayesian School
2.3. Viewpoint of Non-Frequency and Non-Bayesian Schools
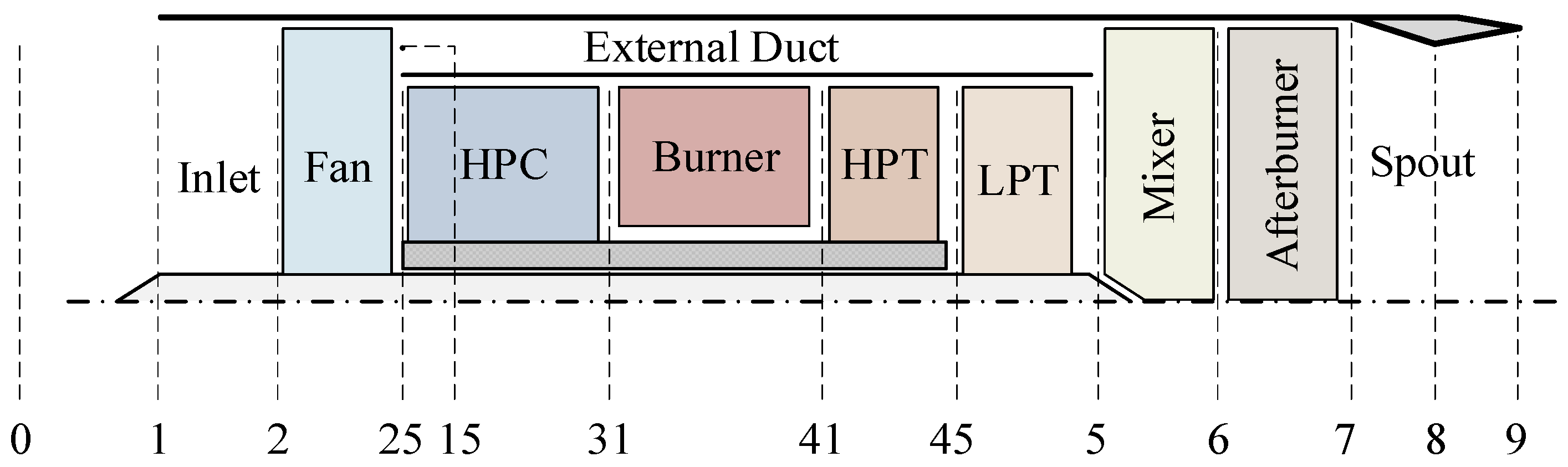
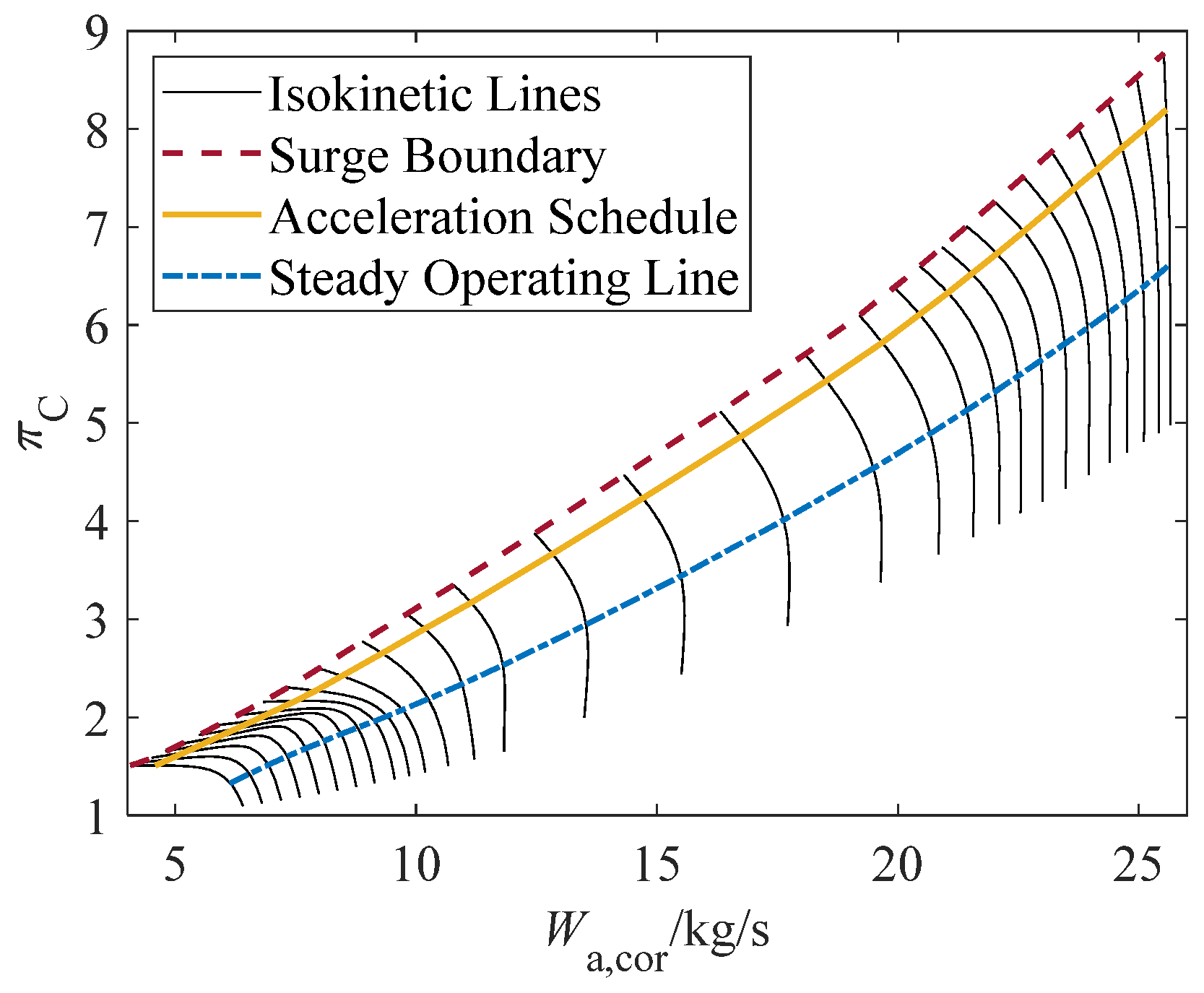
3. Background of Fault-Tolerant Control for Turbofan Acceleration
| Disturbance Factor * | Normal Deviation | Significant Fault |
|---|---|---|
| Lex | [0, 100 kW]∙(nH,Cor2)2 | Extra [0, 200 kW] |
| pt2 sensor | [−1.5%, 1.5%] | ±[1.5%, 15%] |
| pt25 sensor | [−1.5%, 1.5%] | ±[1.5%, 15%] |
| pt31 sensor | [−1.5%, 1.5%] | ±[1.5%, 15%] |
| Wf metering | [−3%, 3%] | ±[3%, 21%] |
| Tt2 sensor | [−0.6%, 0.6%] | ±[0.6%, 6%] |
| Tt25 sensor | [−0.6%, 0.6%] | ±[0.6%, 6%] |
| ΔSEC | [−0.2%, 0.2%] | Extra [−2%, 0] |
| ΔSWC | [−0.2%, 0.2%] | Extra [−4%, 0] |
| ΔSEHT | [−0.2%, 0.2%] | Extra [−2%, 0] |
| ΔSWHT | [−0.2%, 0.2%] | Extra [−2%, 2%] |
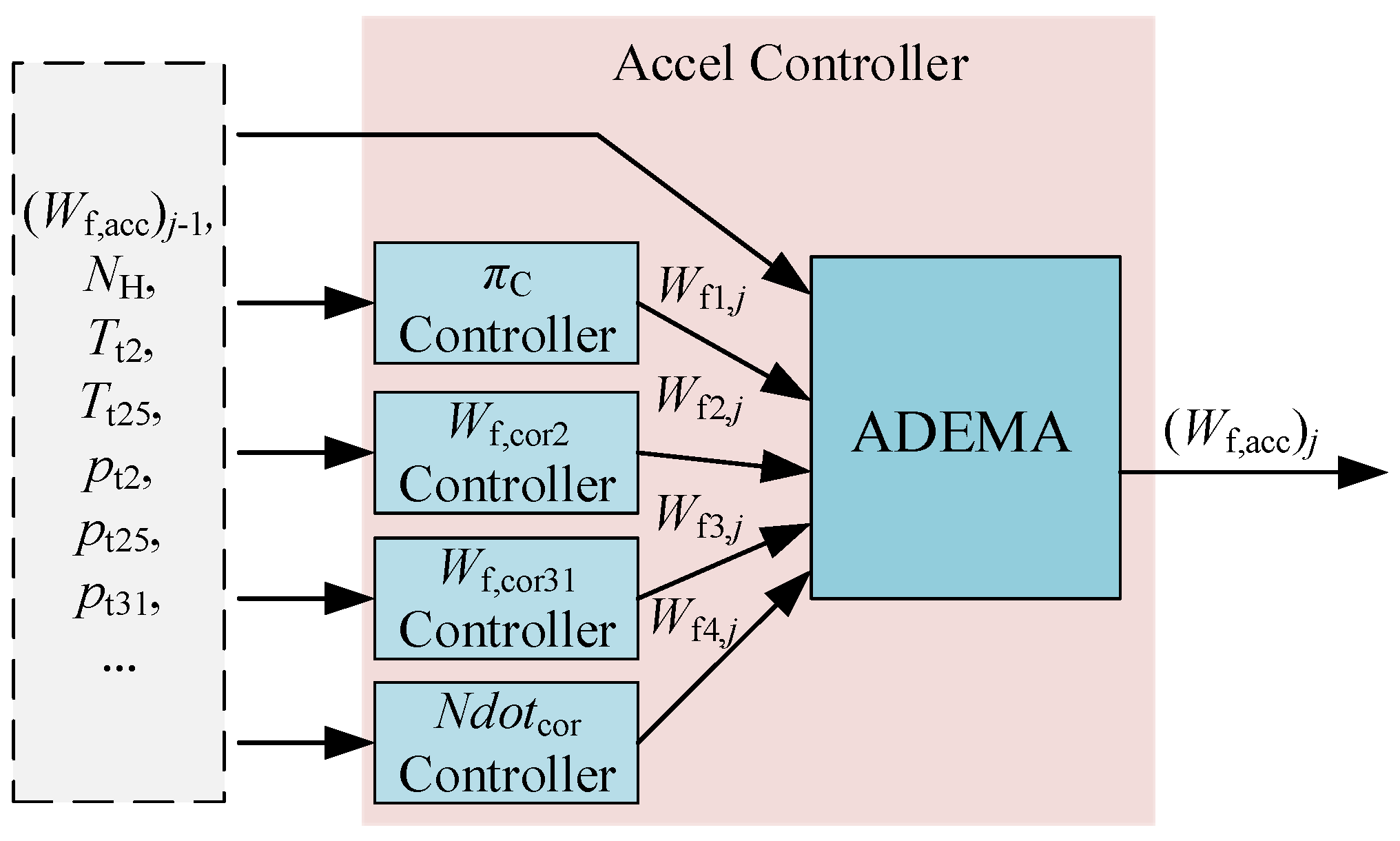
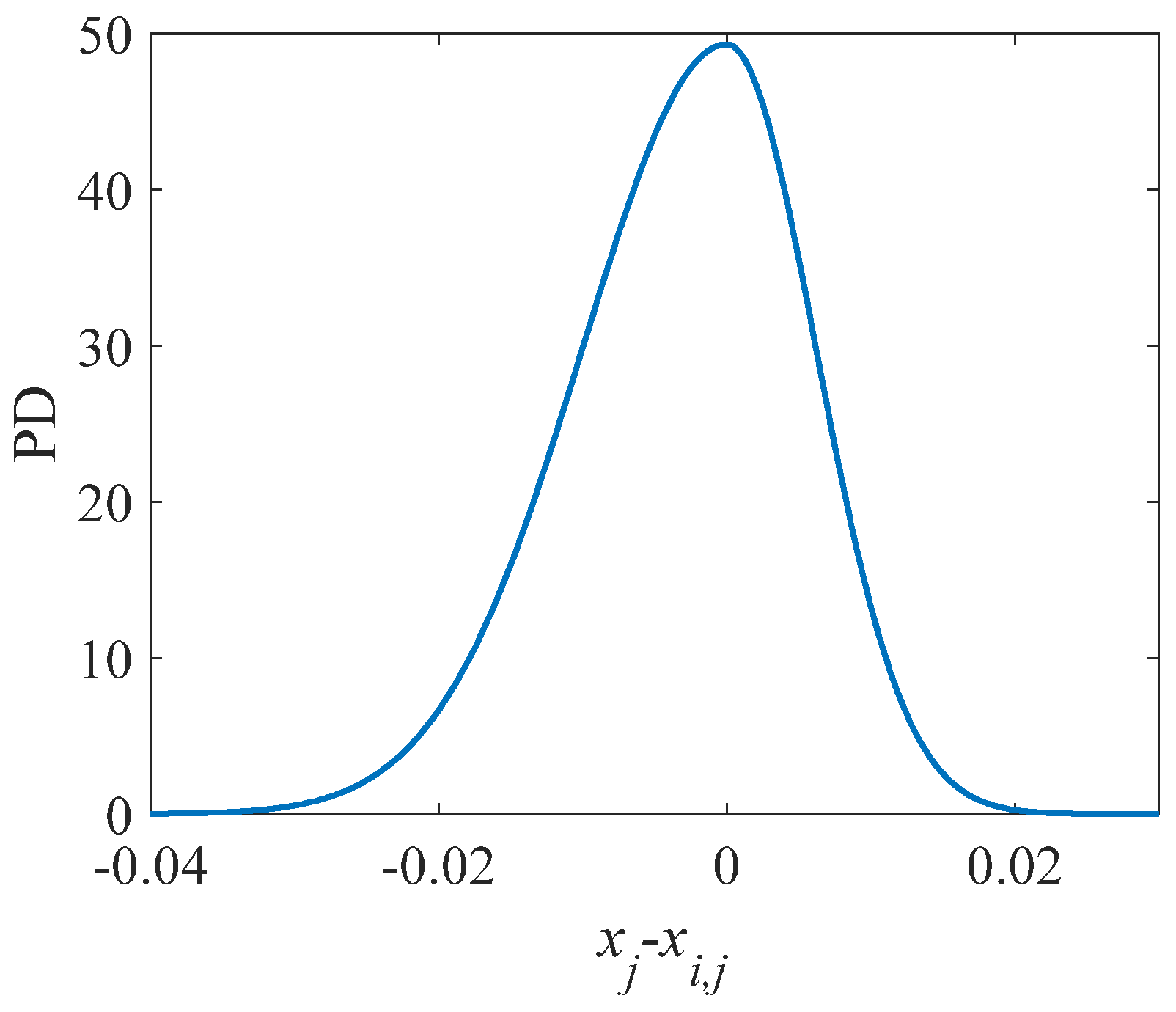
4. ADEMA Derivation
- E-step;
- 2.
- M-step.
| Algorithm 1 ADEMA method. |
| Input: Relative values of four acceleration schedule fuels: xi,j; Initial value of relative acceleration fuel output at time j: (xj)0; Probabilities of not being updated yet or their initial presuppositions: ωi = P(z = i); Set the coefficient cA; The iteration step initialization: k = 0. Process: 1. Calculate hi,j according to Equation (42), and refer to Equation (49) for σj; 2. Calculate γi,j according to Equation (39), and refer to Equation (43) for distribution; 3. k = k + 1, and calculate the new (xj)k according to Equation (44); 4. Repeat the above steps until the error |(xj)k−(xj)k-1| is less than the set value ε (like 0.001); 5. Calculate (Wf,acc)j based on the final (xj)end; 6. Refer to Equation (52) to check whether ωi needs to be updated. Output: |
| Output the final acceleration fuel flow at time j: (Wf,acc)j. |
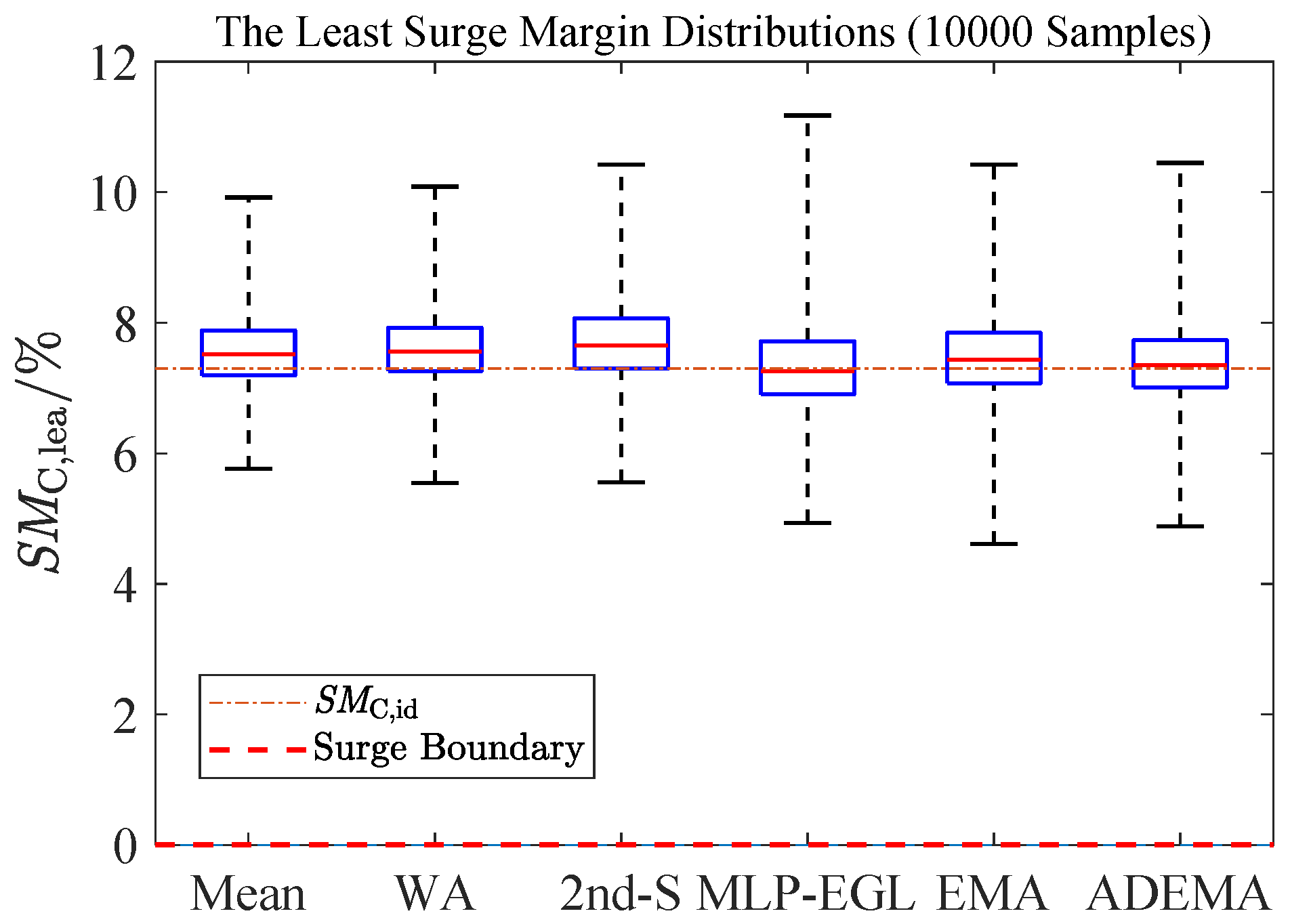
5. Verification Results
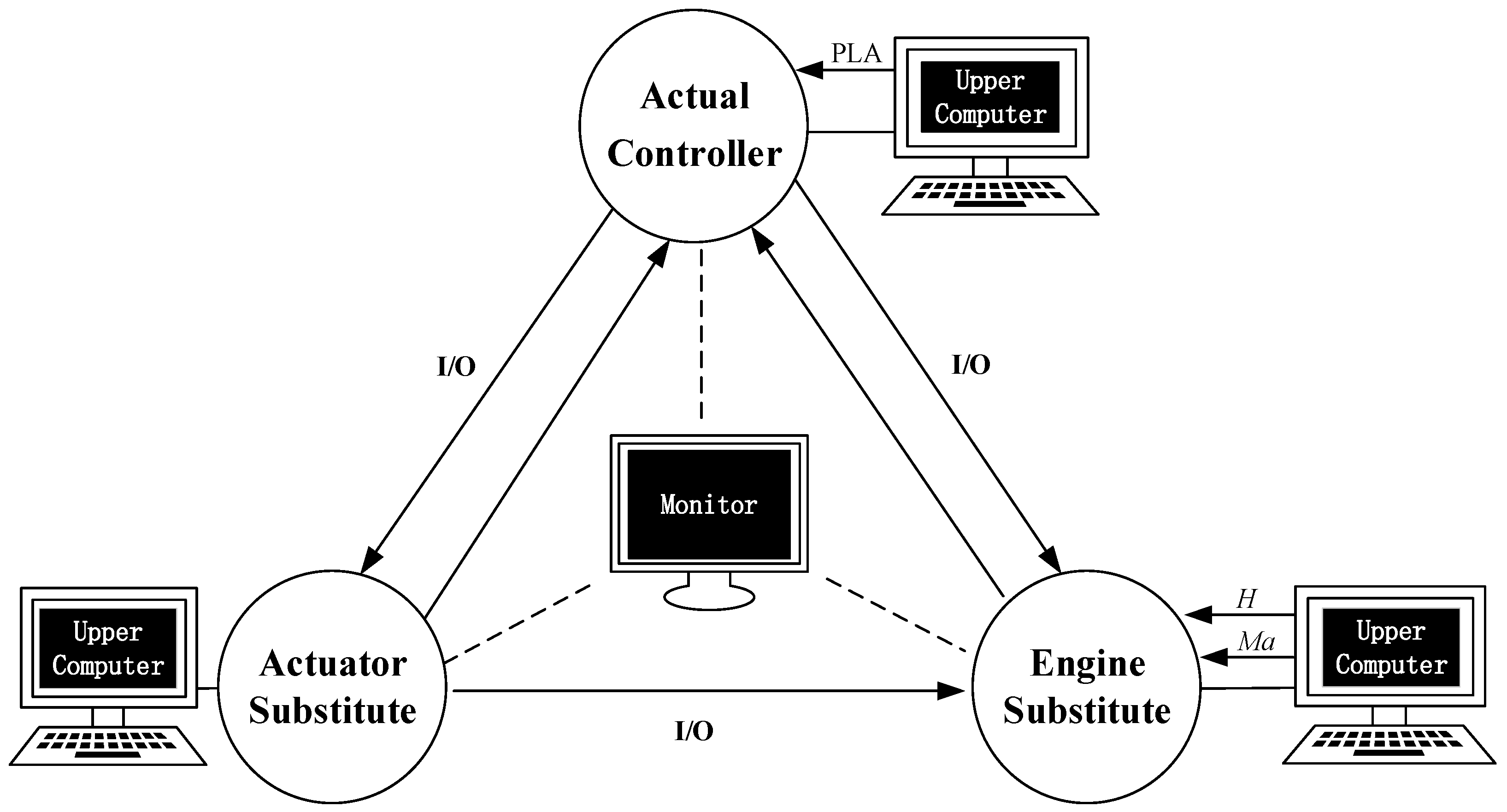
5.1. Operation Test Under Simple Fault Conditions
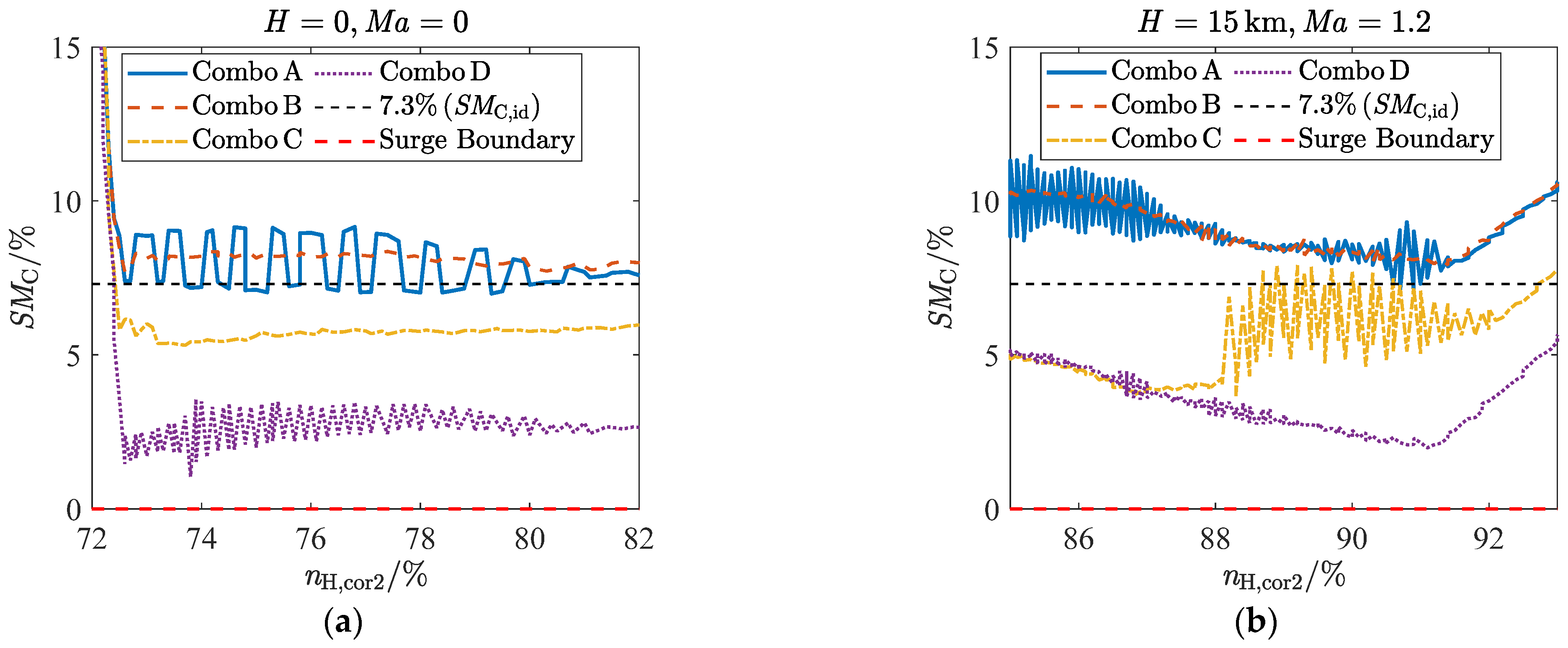
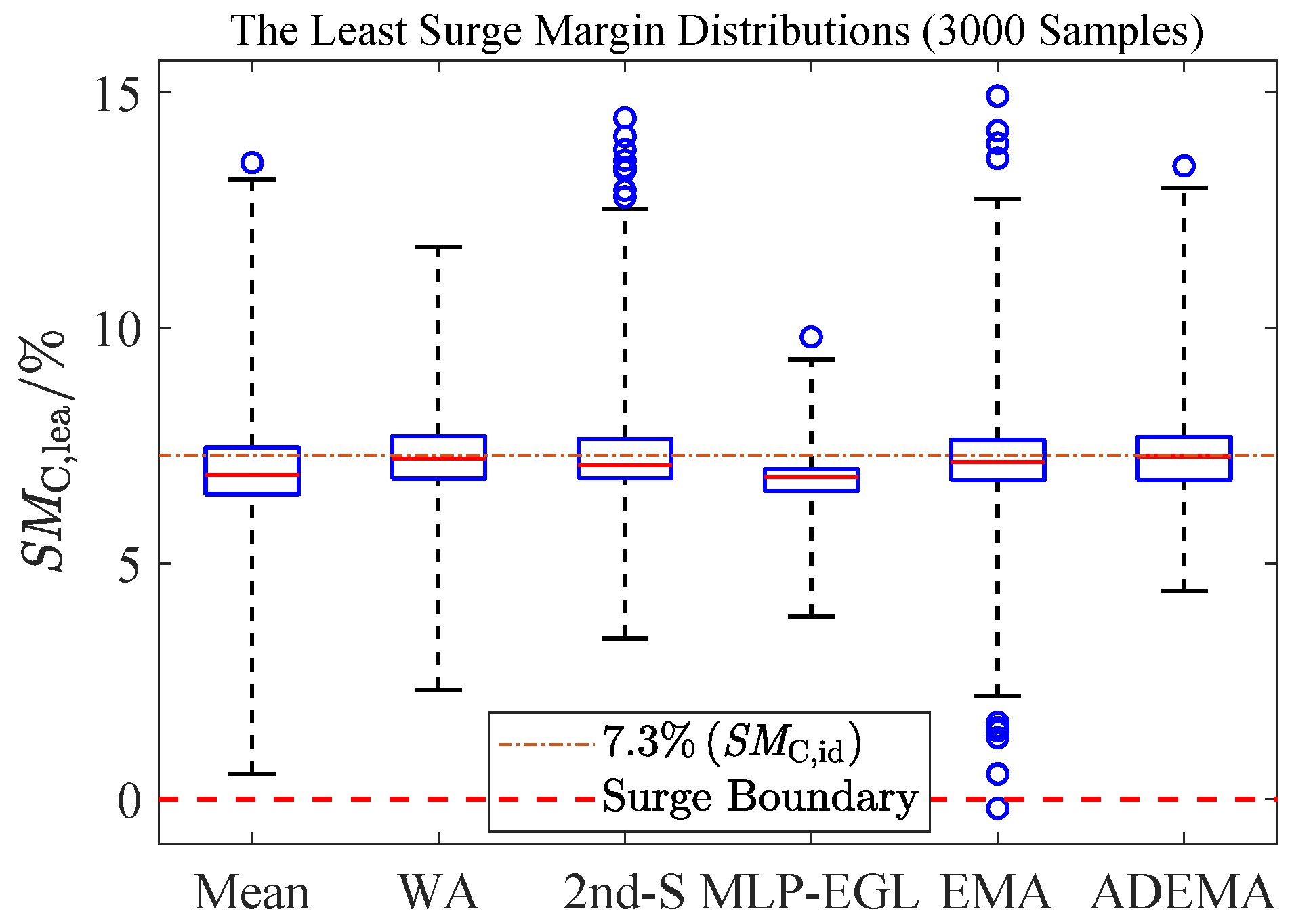
5.2. Sea Level Statistics
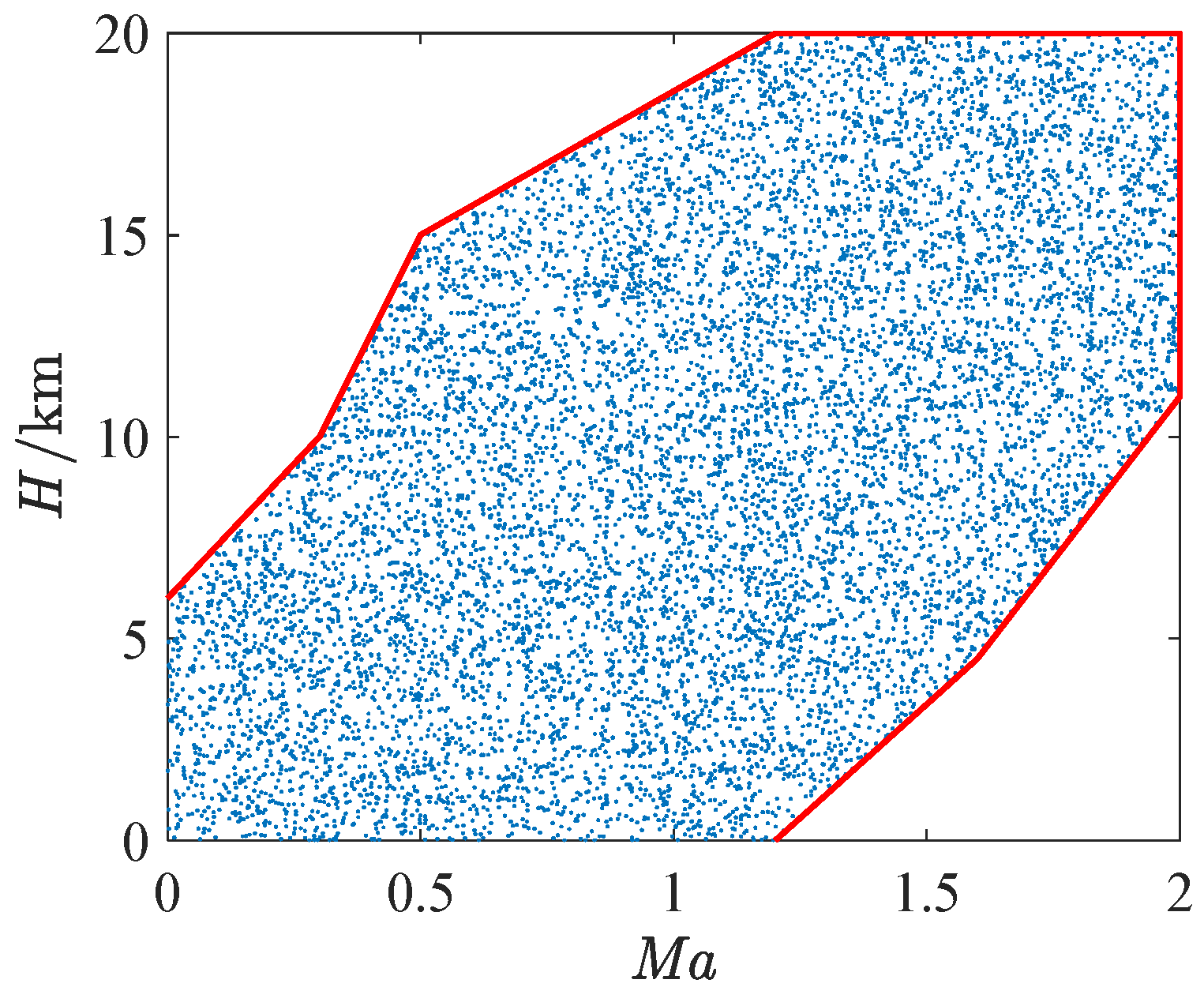
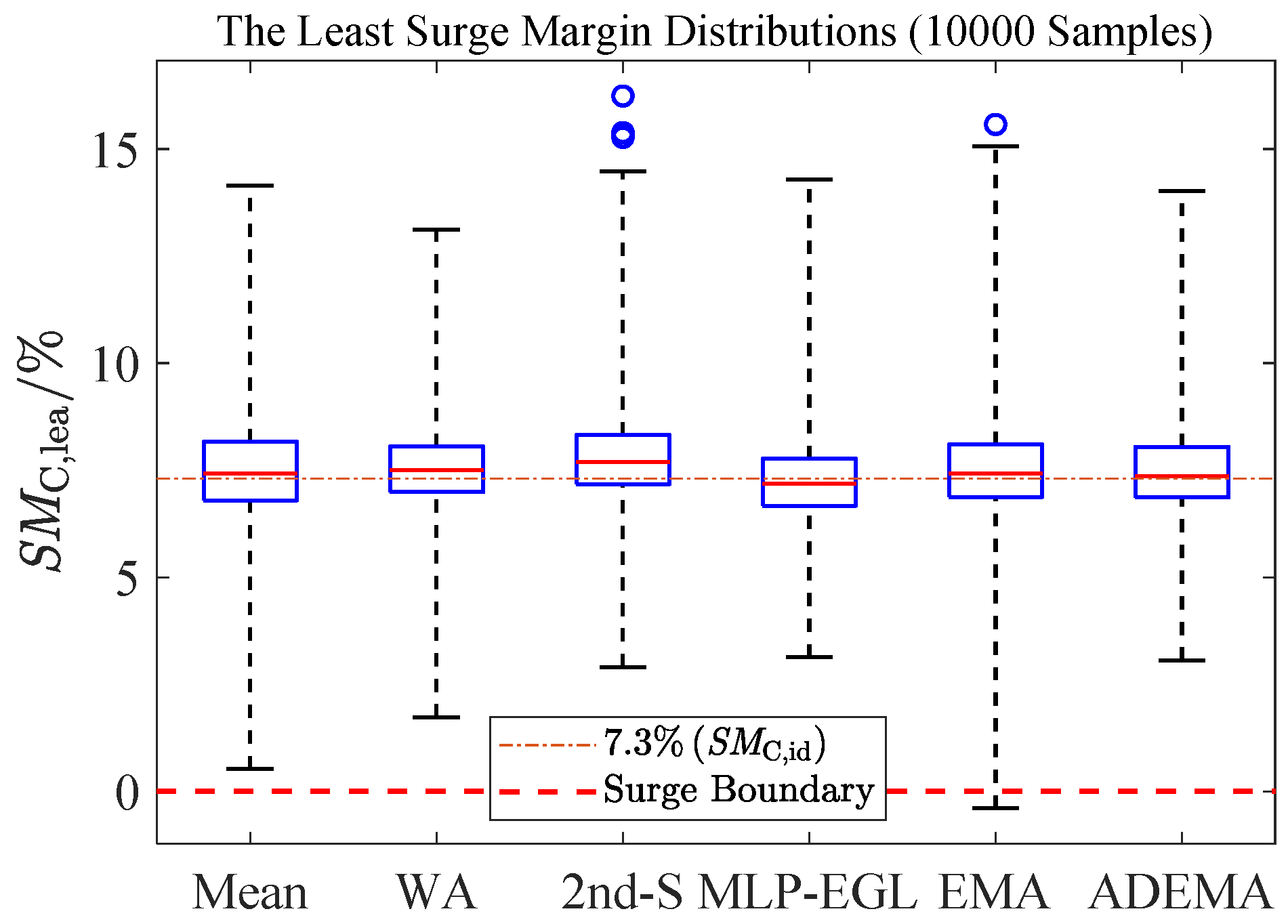
5.3. Flight Envelope Statistics
| Mean | WA | 2nd-S | MLP-EGL | EMA | ADEMA | |
|---|---|---|---|---|---|---|
| Mode [%] | 7.31 | 7.36 | 7.45 | 7.13 | 7.28 | 7.21 |
| Median [%] | 7.42 | 7.50 | 7.70 | 7.19 | 7.42 | 7.37 |
| Mean [%] | 7.49 | 7.52 | 7.80 | 7.25 | 7.47 | 7.47 |
| Absolute error of median [%] | 0.12 | 0.20 | 0.40 | −0.11 | 0.12 | 0.07 |
| Relative error of median [%] | 1.64 | 2.74 | 5.48 | 1.51 | 1.64 | 0.96 |
| Standard deviation [%] | 1.33 | 1.03 | 1.03 | 0.96 | 1.17 | 1.01 |
| Minimum [%] | 0.53 | 1.73 | 2.90 | 3.14 | −0.39 | 3.06 |
| Maximum [%] | 14.14 | 13.12 | 16.24 | 14.28 | 15.57 | 14.01 |
6. Conclusions
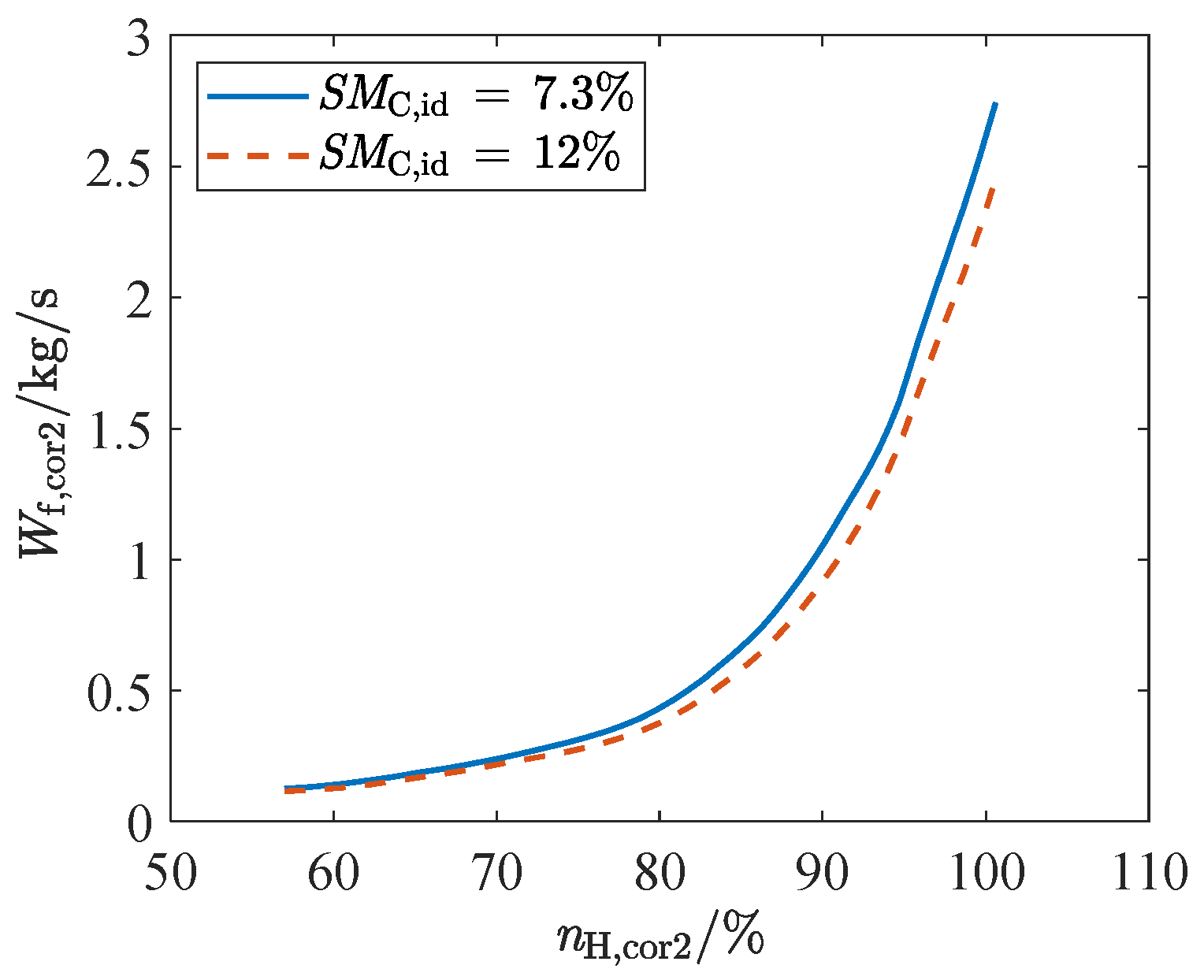
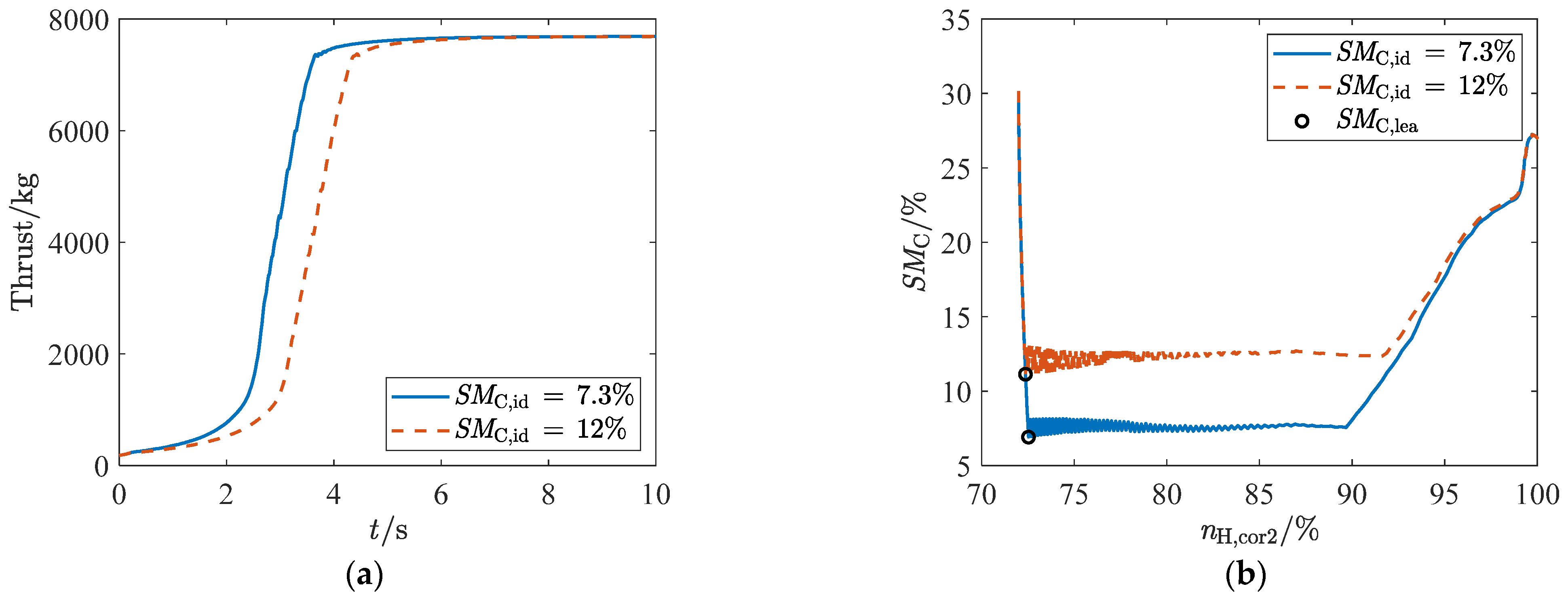
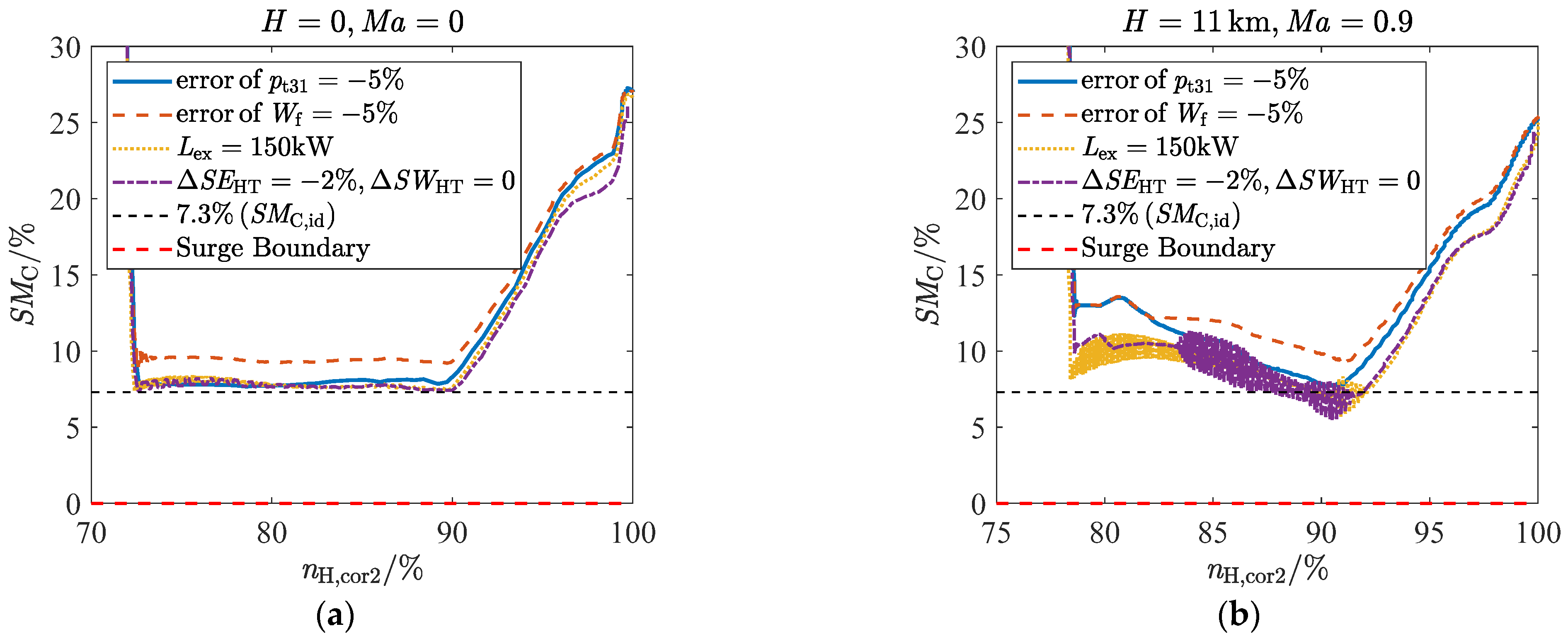
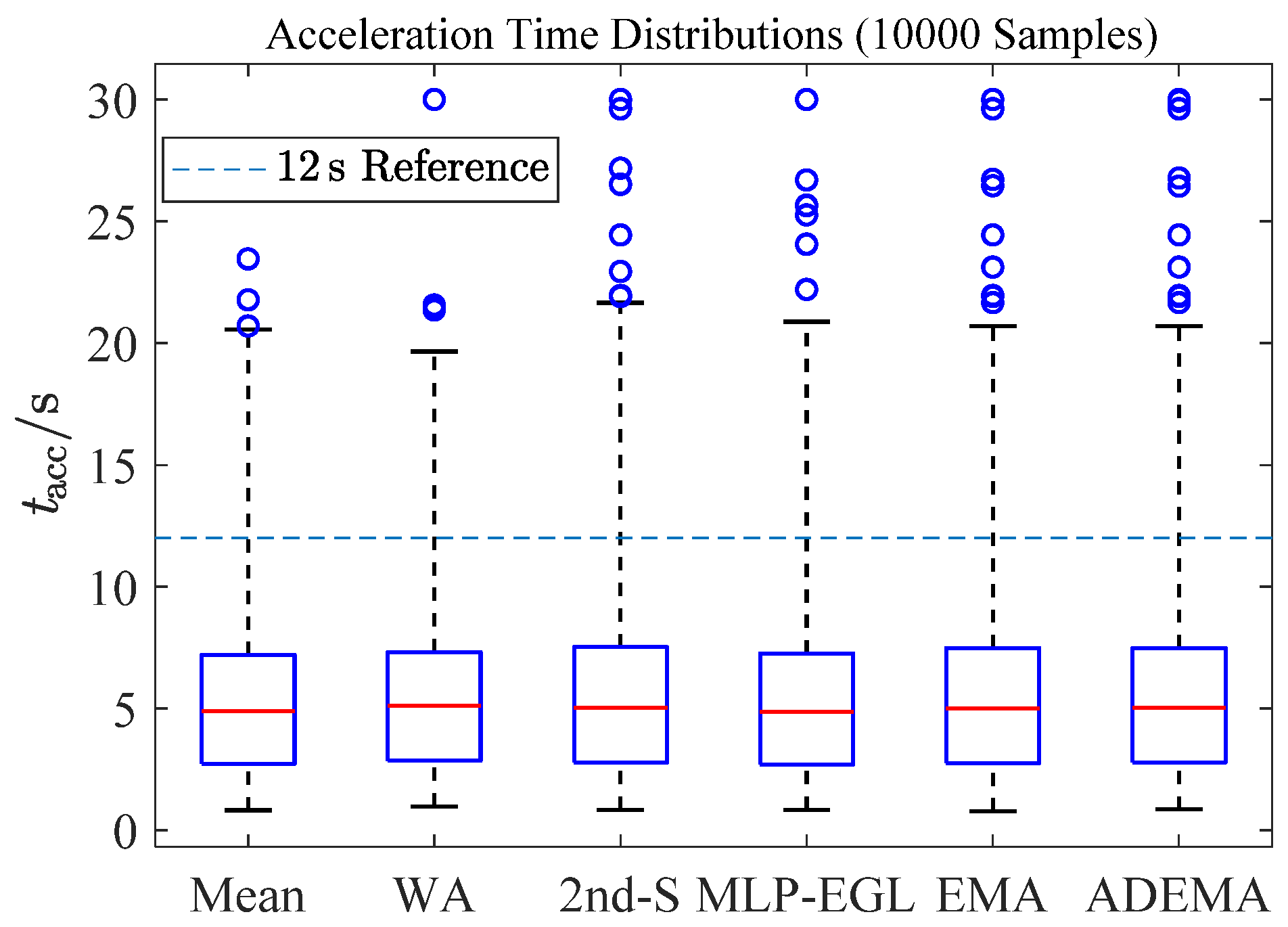
- During operation test under simple fault conditions, it was shown that the ADEMA based on a four-redundancy configuration can better withstand the effects of a single significant fault and other normal deviations (including minor faults), but cannot completely block the effects of two significant faults. Furthermore, the fault-tolerant capability of the acceleration schedules makes low margin design possible, that is, a 7.3% SMC,id can decrease acceleration time by 16.5% compared to a 12% SMC,id;
- In the context of sea level statistics, ADEMA exhibits the highest minimum SMC,lea and accuracy, with its standard deviation only slightly exceeding that of MLP-EGL. ADEMA reduces the median estimation error of MLP-EGL by 96%;
- In the context of flight envelope statistics, ADEMA showcases the highest accuracy, the second highest minimum SMC,lea and the second smallest standard deviation. ADEMA decreases the median estimation error of MLP-EGL by 36%.
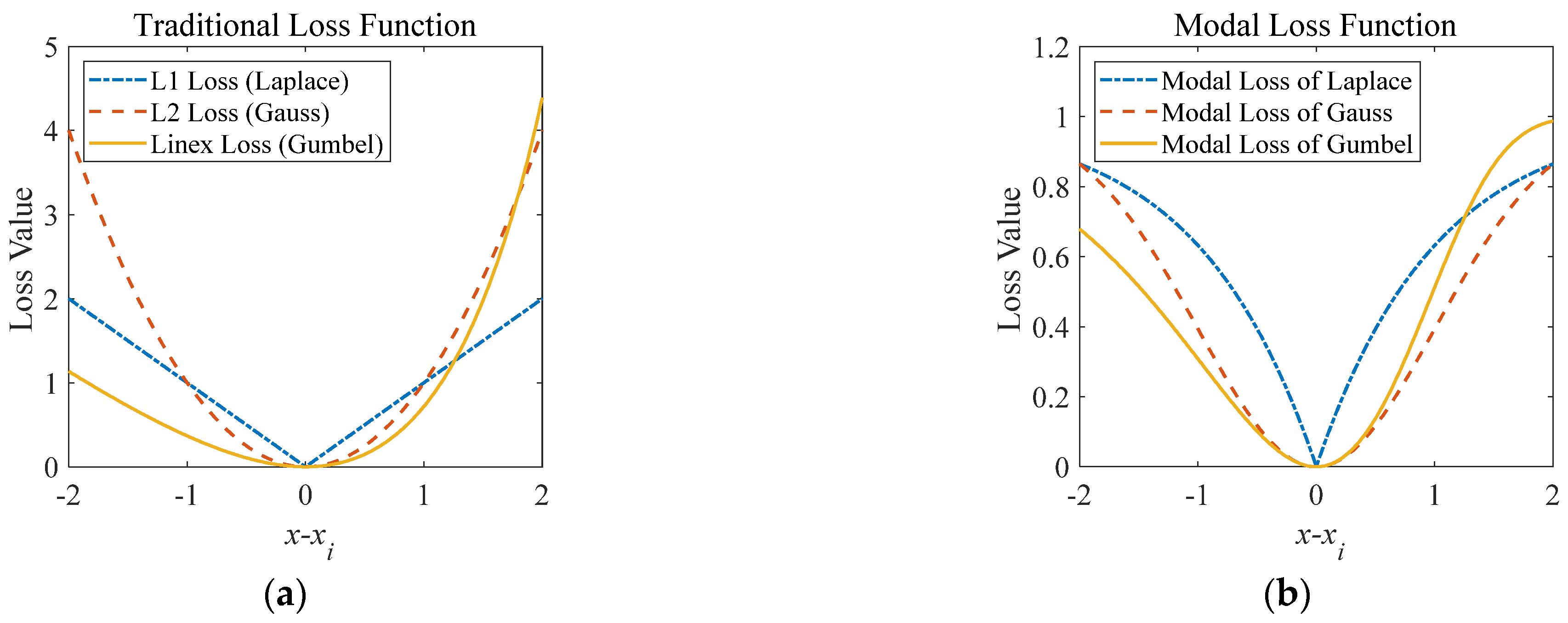
- While both frequentist and Bayesian frameworks center their optimization on variance reduction, substantial probability shifts the emphasis to the accuracy in a narrow sense.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ADEMA | Asymmetric Distribution Expectation-Maximum Algorithm |
| CLM | Component Level Model |
| EMA | Expectation-Maximum Algorithm |
| HIL | Hardware-In-the-Loop |
| HPC | High-Pressure Compressor |
| HPT | High-Pressure Turbine |
| LPT | Low-Pressure Turbine |
| MLP-EGL | Multi-Layer Perceptron with Exponential Gumbel Loss |
| N-dot | Speed Derivative |
| WA | Weighted Average |
| 2nd-S | the 2nd Smallest value |
References
- Jaw, L.C.; Mattingly, J.D. Aircraft Engine Controls: Design, System Analysis, and Health Monitoring; American Institute of Aeronautics and Astronautics: Reston, VA, USA, 2009; pp. 119–124. [Google Scholar]
- Walsh, P.P.; Fletcher, P. Gas Turbine Performance; Blackwell Science: Hoboken, NJ, USA, 2004; pp. 459–464. [Google Scholar]
- Wang, J.; Zhang, W.; Hu, Z. Model-Based Nonlinear Control of Aeroengines; Springer Singapore Pte. Limited: Singapore, 2021; pp. 185–194. [Google Scholar]
- Connolly, J.W.; Csank, J.; Chicatelli, A. Advanced Control Considerations for Turbofan Engine Design. In Proceedings of the 52nd AIAA/SAE/ASEE Joint Propulsion Conference, Salt Lake City, UT, USA, 25–27 July 2016. [Google Scholar]
- Wei, Z.; Zhang, S. Auto-updating model-based control for thrust variation mitigation and acceleration performance enhancement of gas turbine aero-engines. Propuls. Power Res. 2023, 13, 394–415. [Google Scholar] [CrossRef]
- MYERS, L.; Burcham, F.W., Jr. Preliminary flight test results of the F100 EMD engine in an F-15 airplane. In Proceedings of the 20th Joint Propulsion Conference, Cincinnati, OH, USA, 11–13 June 1984. [Google Scholar]
- Dubrova, E. Fault-Tolerant Design; Springer: New York, NY, USA, 2013; pp. 12–17. [Google Scholar]
- Gu, Z.; Pang, S.; Li, Y.; Li, Q.; Zhang, Y. Turbo-fan engine acceleration control schedule optimization based on DNN-LPV model. Aerosp. Sci. Technol. 2022, 128, 107797. [Google Scholar] [CrossRef]
- Wang, Y.; Fang, J.; Song, W.; Ji, C.; Zhang, H.; Zhao, Q. Surge-Elimination Strategy for Aero-Engine Transient Control. J. Dyn. Syst. Meas. Control. 2024, 146, 041007. [Google Scholar] [CrossRef]
- Wang, K.; Xu, M.; Li, M.; Geng, J.; Liu, J.; Song, Z. A multi-input based full envelope acceleration schedule design method for gas turbine engine based on multilayer perceptron network. Aerosp. Sci. Technol. 2022, 130, 107928. [Google Scholar] [CrossRef]
- Song, K.; Jia, L.; Chen, Y.; Tan, T. Design of acceleration control schedule for adaptive cycle engine based on direct simulation model. Chin. J. Aeronaut. 2024, 37, 307–318. [Google Scholar] [CrossRef]
- Khalid, S.J.; Diegelman, J. Improving Turbofan Transient Characteristics with Multiple Variable Geometry Closed Loop Control. In Proceedings of the AIAA Propulsion and Energy 2020 Forum, Virtual Event, 24–28 August 2020. [Google Scholar]
- Zhang, X.; Liu, J.; Li, M.; Geng, J.; Song, Z. Fusion Control of Two Kinds of Control Schedules in Aeroengine Acceleration Process. J. Propuls. Technol. 2022, 43, 344–357. [Google Scholar]
- Cai, C.; Zheng, Q.; Wang, Y.; Zhang, H.; Sun, F. Research on Optimal Control Method for Turbofan Engine Acceleration Process with Variable Air Bleed Considering High Pressure Turbine Guide Vane Life. Int. J. Aeronaut. Space 2023, 24, 475–487. [Google Scholar] [CrossRef]
- Wang, K.; Liao, Z.; Xu, M.; Li, M.; Duan, B.; Liu, J.; Song, Z. Robust acceleration schedule design for gas turbine engine using multilayer perceptron network with adaptive sample class weighting. Aerosp. Sci. Technol. 2024, 154, 109500. [Google Scholar] [CrossRef]
- Zhang, X.; Wang, K.; Geng, J.; Li, M.; Song, Z. A fault-tolerant acceleration control strategy for turbofan engine based on multi-layer perceptron with exponential Gumbel loss. Energy 2024, 294, 130873. [Google Scholar] [CrossRef]
- Mohammadi, E.; Montazeri-Gh, M. Active Fault Tolerant Control with self-enrichment capability for gas turbine engines. Aerosp. Sci. Technol. 2016, 56, 70–89. [Google Scholar] [CrossRef]
- Liu, L.; Liu, T.; Chen, C.L.P.; Wang, Y. Modal-Regression-Based Broad Learning System for Robust Regression and Classification. IEEE Trans. Neur. Net. Lear. 2024, 35, 12344–12357. [Google Scholar] [CrossRef] [PubMed]
- Yao, W.; Lindsay, B.G.; Li, R. Local modal regression. J. Nonparametric Stat. 2012, 24, 647–663. [Google Scholar] [CrossRef]
- Yao, W.; Li, L. A New Regression Model: Modal Linear Regression. Scand. J. Stat. 2014, 41, 656–671. [Google Scholar] [CrossRef]
- Feng, Y.; Fan, J.; Suykens, J.A.K. A Statistical Learning Approach to Modal Regression. J. Mach. Learn. Res. 2020, 21, 1–35. [Google Scholar]
- Wang, K.; Li, S. Robust distributed modal regression for massive data. Comput. Stat. Data Anal. 2021, 160, 107225. [Google Scholar] [CrossRef]
- Liu, Q.; Huang, X.; Bai, R. Bayesian modal regression based on mixture distributions. Comput. Stat. Data Anal. 2024, 199, 108012. [Google Scholar] [CrossRef]
- Li, L.; Yuan, Y.; Zhang, X.; Wu, S.; Zhang, T. Fault-Tolerant Control Scheme for the Sensor Fault in the Acceleration Process of Variable Cycle Engine. Appl. Sci. 2022, 12, 2085. [Google Scholar] [CrossRef]
- Qiu, X.; Chang, X.; Chen, J.; Fan, B. Research on the Analytical Redundancy Method for the Control System of Variable Cycle Engine. Sustainability 2022, 14, 5905. [Google Scholar] [CrossRef]
- Zhou, J.; Liu, Y.; Zhang, T. Analytical Redundancy Design for Aeroengine Sensor Fault Diagnostics Based on SROS-ELM. Math. Probl. Eng. 2016, 2016, 8153282. [Google Scholar] [CrossRef]
- Zhang, Z.; Huang, X.; Zhang, T. Analytical Redundancy of Variable Cycle Engine Based on Proper Net considering Multiple Input Variables and the Whole Engine’s Degradation. Int. J. Aerosp. Eng. 2021, 2021, 9959264. [Google Scholar] [CrossRef]
- Ma, Y.; Du, X.; Sun, X.; Zhao, F. Active fault tolerant tracking control of turbofan engine based on virtual actuator. ISA Trans. 2022, 122, 247–259. [Google Scholar] [CrossRef] [PubMed]
- Cheng, D.; Liu, L.; Yu, Z. CNN-Based Intelligent Fault-Tolerant Control Design for Turbofan Engines with Actuator Faults. IEEE Access 2021, 9, 28122–28139. [Google Scholar] [CrossRef]
- Ring, D.; Christiansson, A.; Härefors, M. Fault Tolerant Multivariable Control of a Military Turbofan Engine. In Proceedings of the 16th Triennial World Congress, Lisbon, Portugal, 21–24 May 2005. [Google Scholar]
- Peng, K.; Zhang, Z.; Yang, F.; Jiao, C. Active Fault-tolerant Control of Auxiliary Power Unit Based on Analytical Redundancy and Heterogeneous Redundancy Design. In Proceedings of the 2019 IEEE 10th International Conference on Mechanical and Aerospace Engineering, Brussels, Belgium, 22–25 July 2019. [Google Scholar]
- GJB10890-2023; General Specification for Digital Control System of Aircraft Engines. Army GADO: Beijing, China, 2023.
- Ren, C.; Sun, D.; Dey, D.K. Bayesian and frequentist estimation and prediction for exponential distributions. J. Stat. Plan. Infer. 2006, 136, 2873–2897. [Google Scholar] [CrossRef]
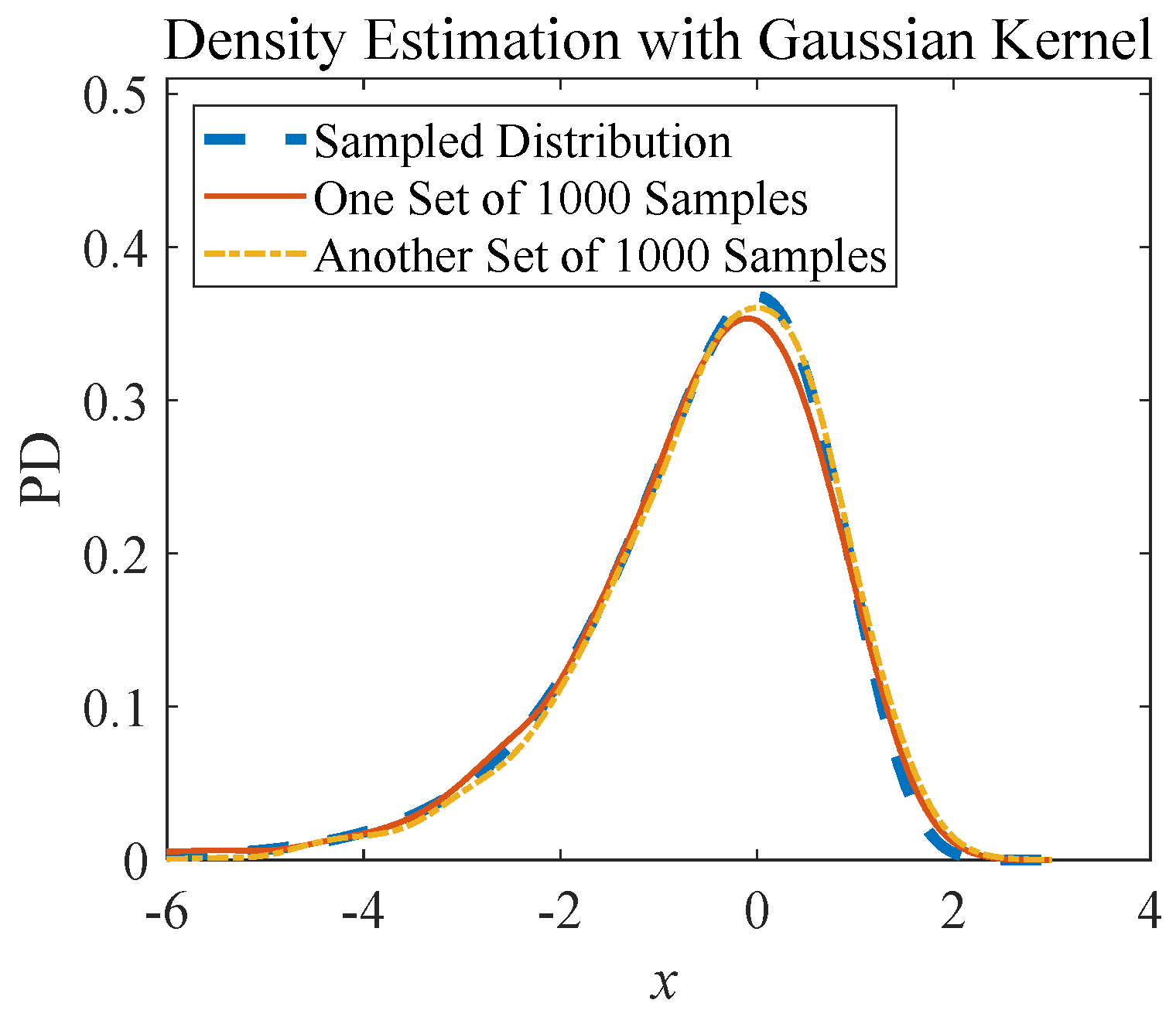
- Silverman, B.W. Density Estimation for Statistics and Data Analysis; Taylor & Francis Group: Oxfordshire, UK, 1998. [Google Scholar]
- Qiu, X. Neural Networks and Deep Learning; China Machine Press: Beijing, China, 2019. [Google Scholar]
- Liu, Z.; Liu, Y.; Yu, Y.; Yang, R. Advanced fuel limit design to improve dynamic performance of marine three-shaft gas turbine. Appl. Therm. Eng. 2024, 236, 121649. [Google Scholar] [CrossRef]
- ISO 2314:2009(E); Gas Turbines-Acceptance Tests. ISO: Geneva, Switzerland, 2009.
- Zhao, H.; Liao, Z.; Liu, J.; Li, M.; Liu, W.; Wang, L.; Song, Z. A highly robust thrust estimation method with dissimilar redundancy framework for gas turbine engine. Energy 2022, 245, 123255. [Google Scholar] [CrossRef]
- Liao, Z.; Wang, J.; Liu, J.; Geng, J.; Li, M.; Chen, X.; Song, Z. Uncertainties in gas-path diagnosis of gas turbines: Representation and impact analysis. Aerosp. Sci. Technol. 2021, 113, 106724. [Google Scholar] [CrossRef]
- Xu, M.; Liu, J.; Li, M.; Geng, J.; Wu, Y.; Song, Z. Improved hybrid modeling method with input and output self-tuning for gas turbine engine. Energy 2022, 238, 121672. [Google Scholar] [CrossRef]
- Xu, M.; Wang, J.; Liu, J.; Li, M.; Geng, J.; Wu, Y.; Song, Z. An improved hybrid modeling method based on extreme learning machine for gas turbine engine. Aerosp. Sci. Technol. 2020, 107, 106333. [Google Scholar] [CrossRef]
- Song, K.; Jia, L.; Chen, Y.; Tan, T.; Fan, P. Optimization of ACE mode transition control schedule considering geometric adjustment speed. Int. J. Turbo Jet Eng. 2024, 40 (Suppl. 1), s389–s398. [Google Scholar] [CrossRef]


| Measurement Type | Normal Accuracy | Degraded Accuracy |
|---|---|---|
| Pressure | ±0.3% | ±0.5% |
| Temperature | ±0.15% | ±0.2% |
| Fuel flow | ±0.65% | ±1.0% |
| Disturbance Factor | Combo A | Combo B | Combo C | Combo D |
|---|---|---|---|---|
| Lex | 100 kW∙(nH,Cor2)2 | 100 kW∙(nH,Cor2)2 | 100 kW∙(nH,Cor2)2 | 100 kW∙(nH,Cor2)2 + 200 kW |
| pt2 sensor | −0.1% | −0.1% | −10% | −0.1% |
| pt25 sensor | 0.5% | 0.5% | 0.5% | 0.5% |
| pt31 sensor | −1% | −10% | −1% | −1% |
| Wf metering | −1.5% | −1.5% | 15% | 15% |
| Tt2 sensor | −0.2% | −0.2% | −0.2% | −0.2% |
| Tt25 sensor | 0.2% | 0.2% | 0.2% | 0.2% |
| ΔSEC | 0 | 0 | 0 | 0 |
| ΔSWC | 0 | 0 | 0 | 0 |
| ΔSEHT | 0 | 0 | 0 | 0 |
| ΔSWHT | 0 | 0 | 0 | 0 |
| Mean | WA | 2nd-S | MLP-EGL | EMA | ADEMA | |
|---|---|---|---|---|---|---|
| Mode [%] | 6.86 | 6.91 | 6.86 | 6.87 | 7.27 | 7.46 |
| Median [%] | 6.88 | 7.23 | 7.09 | 6.84 | 7.16 | 7.28 |
| Mean [%] | 6.96 | 7.25 | 7.31 | 6.78 | 7.14 | 7.27 |
| Absolute error of median [%] | −0.42 | −0.07 | −0.21 | −0.46 | −0.14 | −0.02 |
| Relative error of median [%] | −5.75 | −0.96 | −2.88 | −6.30 | −1.92 | −0.27 |
| Standard deviation [%] | 1.23 | 0.97 | 0.92 | 0.66 | 1.00 | 0.82 |
| Minimum [%] | 0.53 | 2.31 | 3.41 | 3.87 | −0.20 | 4.41 |
| Maximum [%] | 13.51 | 11.74 | 14.46 | 9.81 | 14.93 | 13.44 |
| Mean | WA | 2nd-S | MLP-EGL | EMA | ADEMA | |
|---|---|---|---|---|---|---|
| Median [s] | 3.74 | 3.72 | 3.76 | 3.72 | 3.74 | 3.74 |
| Standard deviation [s] | 0.20 | 0.17 | 0.19 | 0.13 | 0.19 | 0.18 |
| Proportion of tacc > 5 s [%] | 0 | 0 | 0.20 | 0 | 0.17 | 0.13 |
| Minimum [s] | 3.08 | 3.14 | 3.20 | 3.24 | 3.00 | 3.32 |
| Maximum [s] | 4.96 | 4.72 | 5.48 | 4.38 | 5.60 | 5.56 |
| Mean | WA | 2nd-S | MLP-EGL | EMA | ADEMA | |
|---|---|---|---|---|---|---|
| Median [s] | 4.90 | 5.10 | 5.04 | 4.85 | 5.00 | 5.02 |
| Standard deviation [s] | 3.22 | 3.10 | 3.41 | 3.33 | 3.41 | 3.39 |
| Proportion of tacc > 12 s [%] | 3.94 | 3.48 | 5.00 | 4.35 | 4.97 | 4.91 |
| Mean | WA | 2nd-S | MLP-EGL | EMA | ADEMA | |
|---|---|---|---|---|---|---|
| Mode [%] | 7.46 | 7.42 | 7.52 | 7.10 | 7.36 | 7.30 |
| Median [%] | 7.52 | 7.56 | 7.65 | 7.26 | 7.43 | 7.35 |
| Mean [%] | 7.57 | 7.61 | 7.70 | 7.36 | 7.47 | 7.39 |
| Absolute error of median [%] | 0.22 | 0.26 | 0.35 | −0.04 | 0.13 | 0.05 |
| Relative error of median [%] | 3.01 | 3.60 | 4.79 | 0.55 | 1.78 | 0.68 |
| Standard deviation [%] | 0.54 | 0.53 | 0.59 | 0.71 | 0.66 | 0.62 |
| Minimum [%] | 5.76 | 5.54 | 5.55 | 4.94 | 4.61 | 4.88 |
| Maximum [%] | 9.92 | 10.08 | 10.42 | 11.17 | 10.42 | 10.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Geng, J.; Wang, K.; Li, M.; Song, Z. Advanced Implementation of the Asymmetric Distribution Expectation-Maximum Algorithm in Fault-Tolerant Control for Turbofan Acceleration. Aerospace 2025, 12, 829. https://doi.org/10.3390/aerospace12090829
Zhang X, Geng J, Wang K, Li M, Song Z. Advanced Implementation of the Asymmetric Distribution Expectation-Maximum Algorithm in Fault-Tolerant Control for Turbofan Acceleration. Aerospace. 2025; 12(9):829. https://doi.org/10.3390/aerospace12090829
Chicago/Turabian StyleZhang, Xinhai, Jia Geng, Kang Wang, Ming Li, and Zhiping Song. 2025. "Advanced Implementation of the Asymmetric Distribution Expectation-Maximum Algorithm in Fault-Tolerant Control for Turbofan Acceleration" Aerospace 12, no. 9: 829. https://doi.org/10.3390/aerospace12090829
APA StyleZhang, X., Geng, J., Wang, K., Li, M., & Song, Z. (2025). Advanced Implementation of the Asymmetric Distribution Expectation-Maximum Algorithm in Fault-Tolerant Control for Turbofan Acceleration. Aerospace, 12(9), 829. https://doi.org/10.3390/aerospace12090829




