Multi-Stage Coordinated Azimuth Control for High-Precision Balloon-Borne Astronomical Platforms
Abstract
1. Introduction
- Establish a unified dynamic model for the azimuth channel applicable to multi-level composite control systems of balloon-borne platforms, revealing the gondola–turret coupling mechanism.
- Propose a dual-layer control architecture that integrates fiber-optic gyro velocity loop feedback and adaptive fuzzy PID, simultaneously enhancing disturbance rejection and robustness.
- Design a gain adaptation mechanism to avoid multi-level control interference, combined with an anti-windup strategy to ensure actuator safety margins, guaranteeing robust azimuth pointing control under extreme operating conditions.
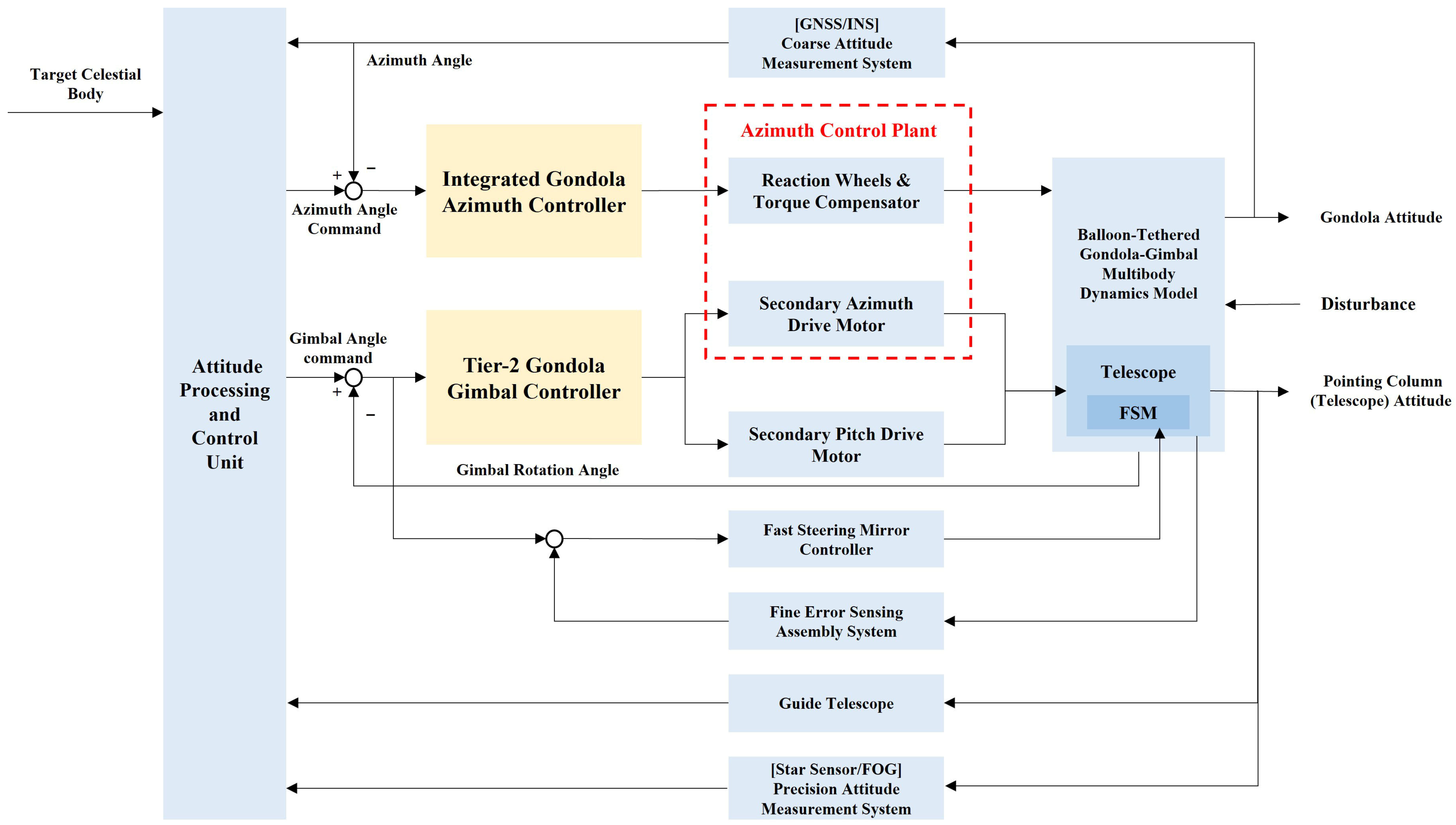
2. System Composition and Principles
- The “outer azimuth + inner elevation” structure is employed in Japan’s FUJIN planetary telescope [12], and the coronagraph project of the Yunnan Observatories, Chinese Academy of Sciences [13]. This configuration enables independent development and testing of the turntable. However, to ensure sufficient structural stiffness, the mass inertia moment of the azimuth frame is intentionally increased, leading to potential dynamic coupling between the turntable’s azimuth–axis control and the integrated azimuth control system, which may induce control coordination conflicts.
- The “outer pitch and inner azimuth” structure is utilized in the Solar Telescope BST of Beijing Astronomical Observatory, Chinese Academy of Sciences [14] and NASA’s WASP high-precision pointing gondola [15,16]. This design features reduced mass and inertia in both elevation and azimuth channels of the secondary turntable, minimizing interference with the integrated gondola azimuth control system and facilitating higher pointing accuracy. Nevertheless, a significant drawback is that standalone debugging of the secondary turntable is infeasible, necessitating dedicated interface adapters for calibration and testing.
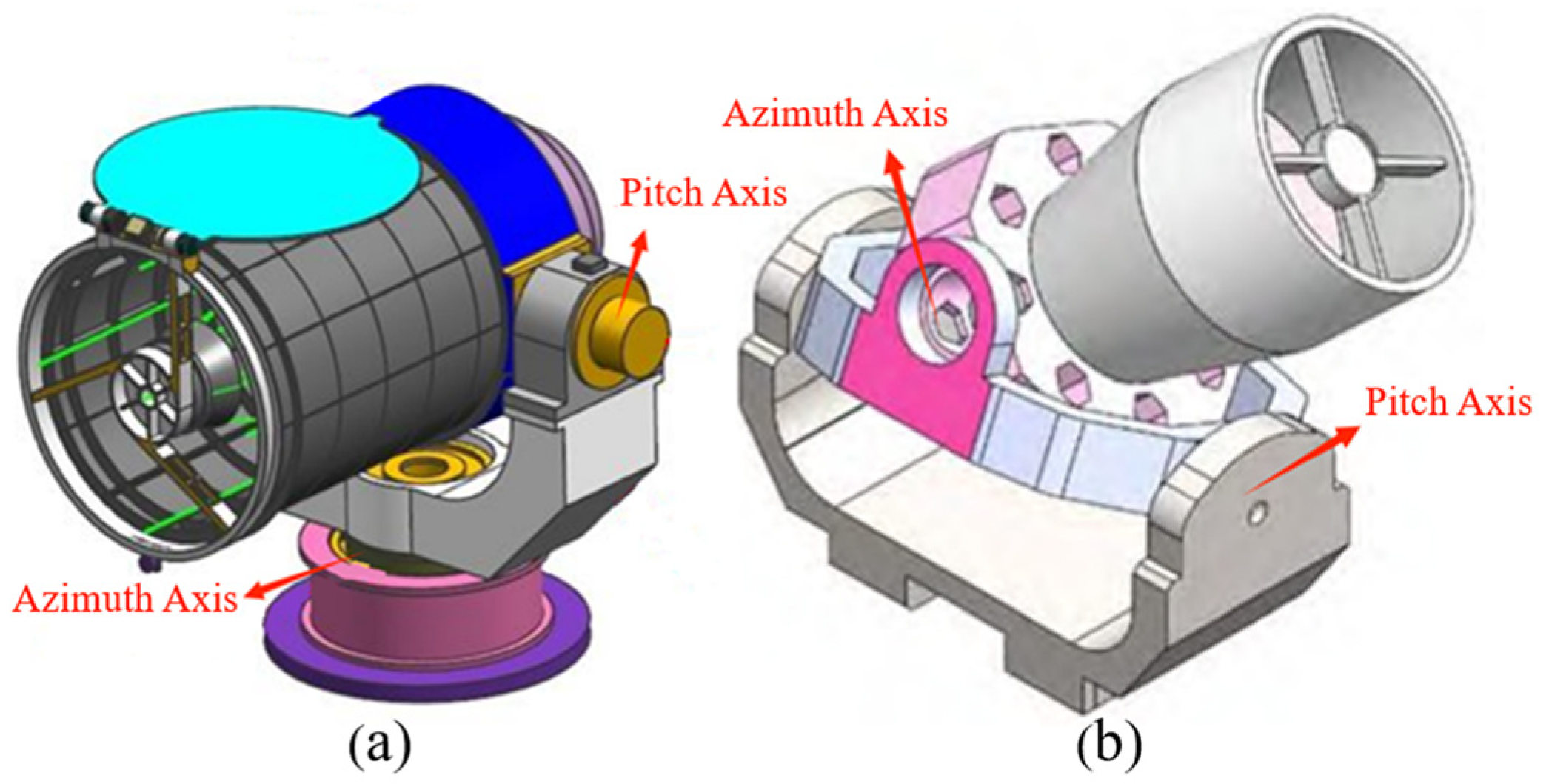
3. Dynamics Modeling
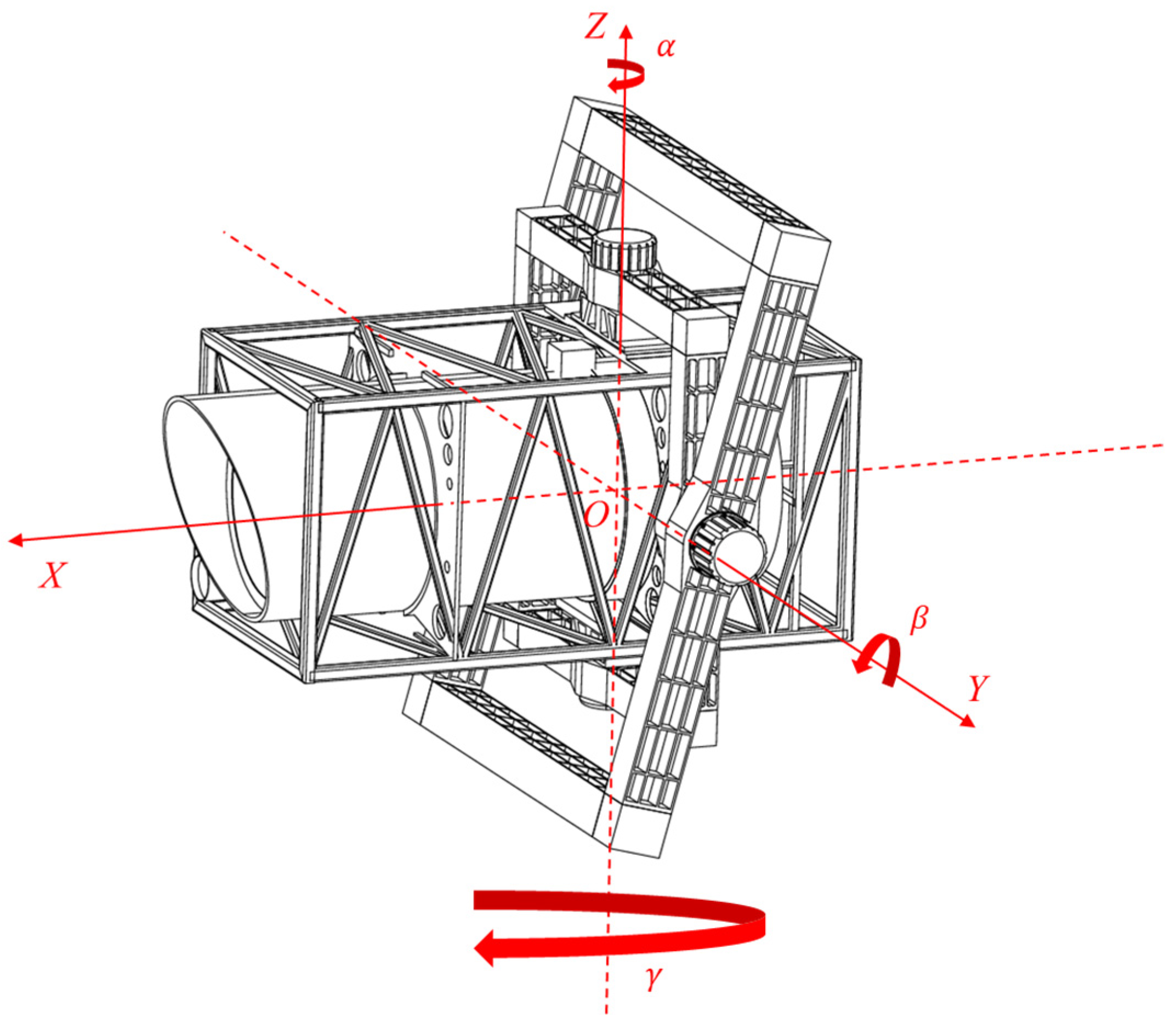
3.1. Parameters and Coordinate System Definitions
- The outer gimbal, inner gimbal, and pointing column are considered ideal rigid bodies, with elastic deformation and structural resonance effects neglected during motion;
- The mass and rotational inertia of auxiliary components (e.g., sensors, cables) beyond the primary structure are negligible, ensuring that the system’s center of mass and inertia tensor are solely determined by the primary structure;
- The pointing axis, inner gimbal axis, and outer gimbal axis are assumed to intersect at a common spatial point O, defined as the theoretical center of rotation for the gimbal system, with the total center of mass of the secondary gimbal system coinciding with this point;
- The outer gimbal is rigidly connected to the gondola, whereby translational/oscillatory disturbances of the gondola are transmitted through the base of the outer gimbal.
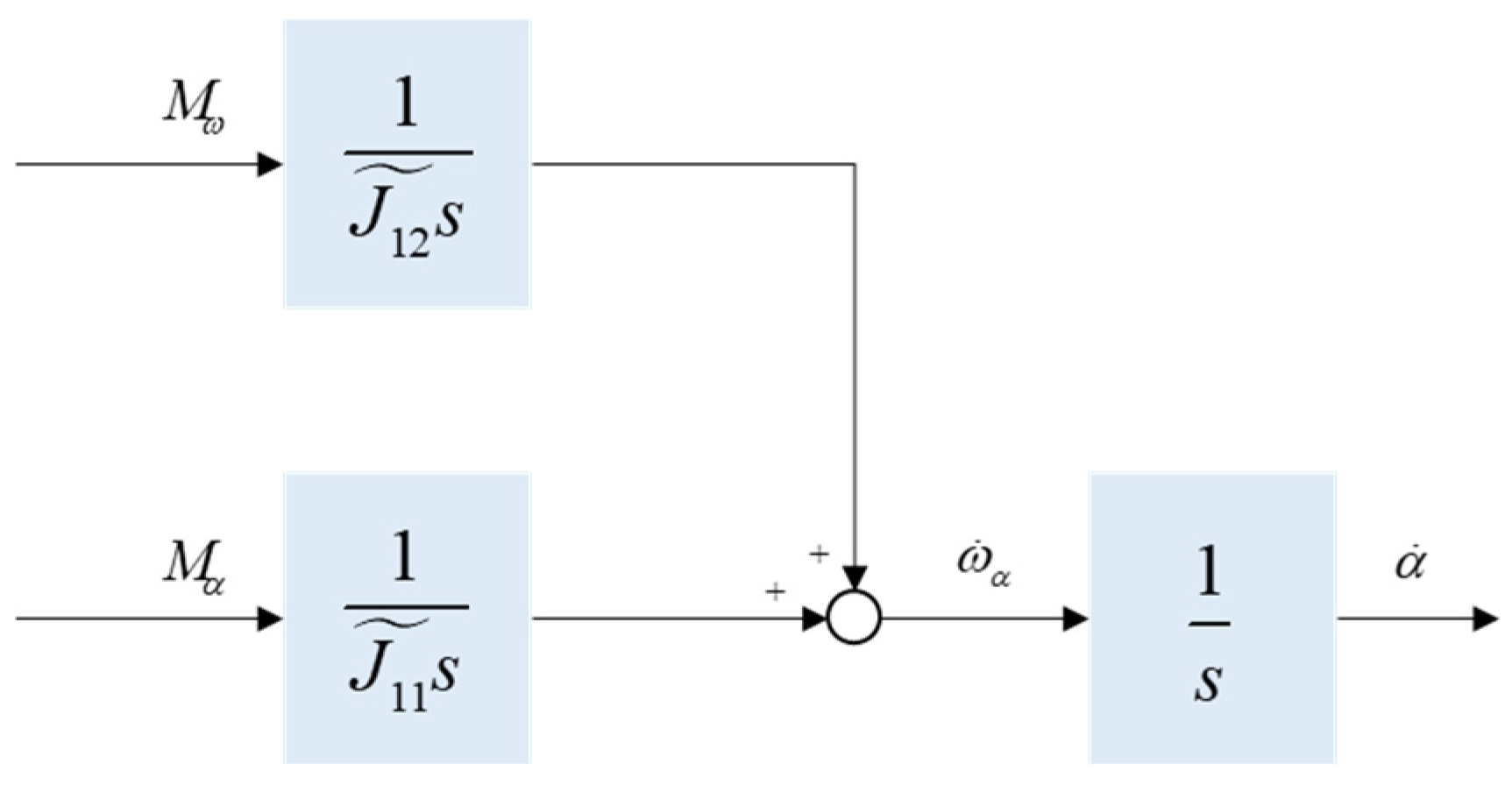
3.2. Lagrangian Modeling
4. Control Algorithm Design and Analysis
- By optimizing the velocity-loop feedback design and developing an intelligent position-loop control algorithm, the gimbal pointing accuracy and system robustness are enhanced;
- Developing the gain adaptive regulation mechanism to achieve dynamic matching of hierarchical responses, fundamentally eliminating the mutual interference phenomena between primary and secondary controls. Concurrently, an anti-windup protection strategy is integrated to effectively mitigate the risk of actuator saturation failure.
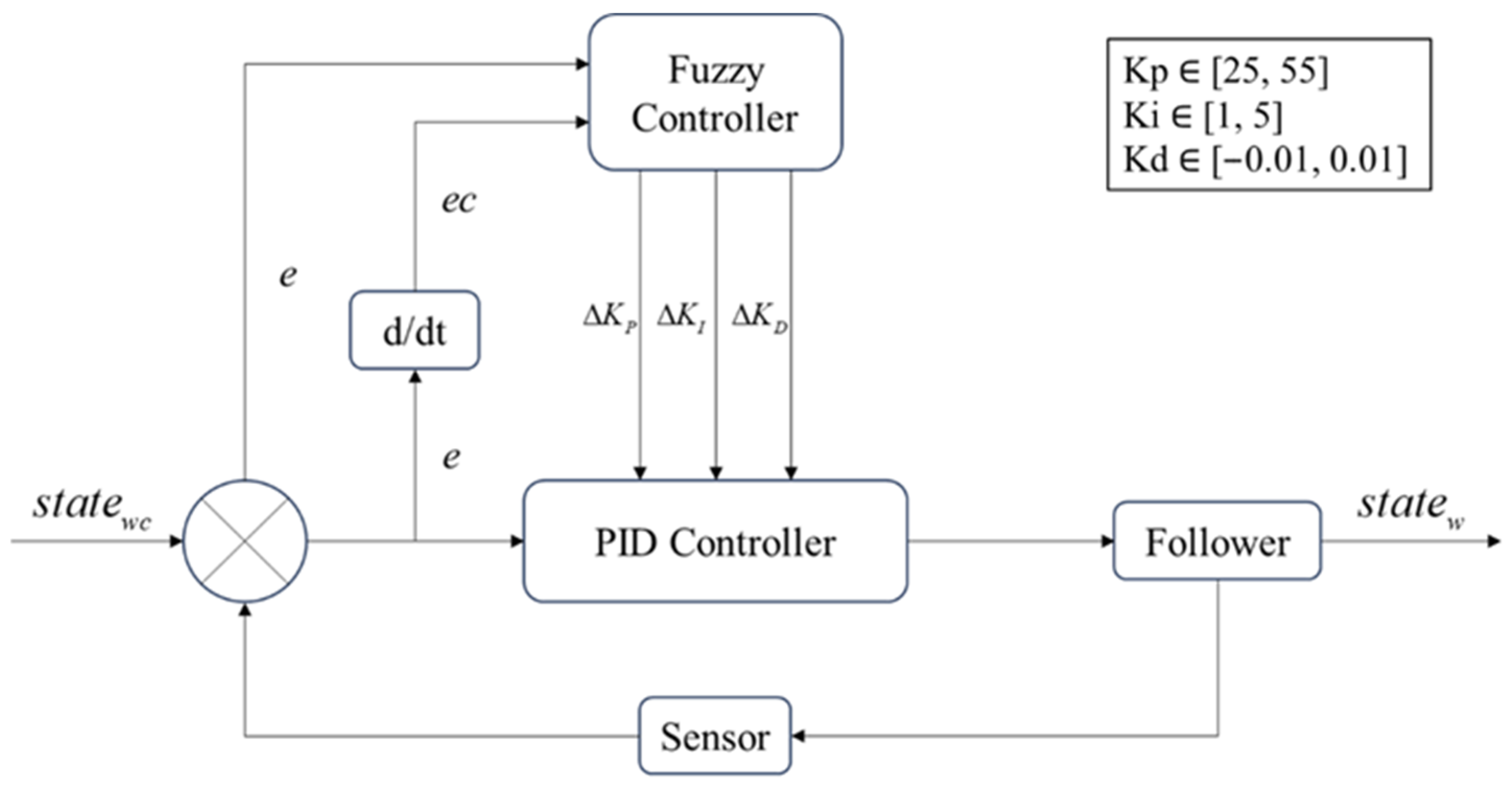
4.1. Controller Design
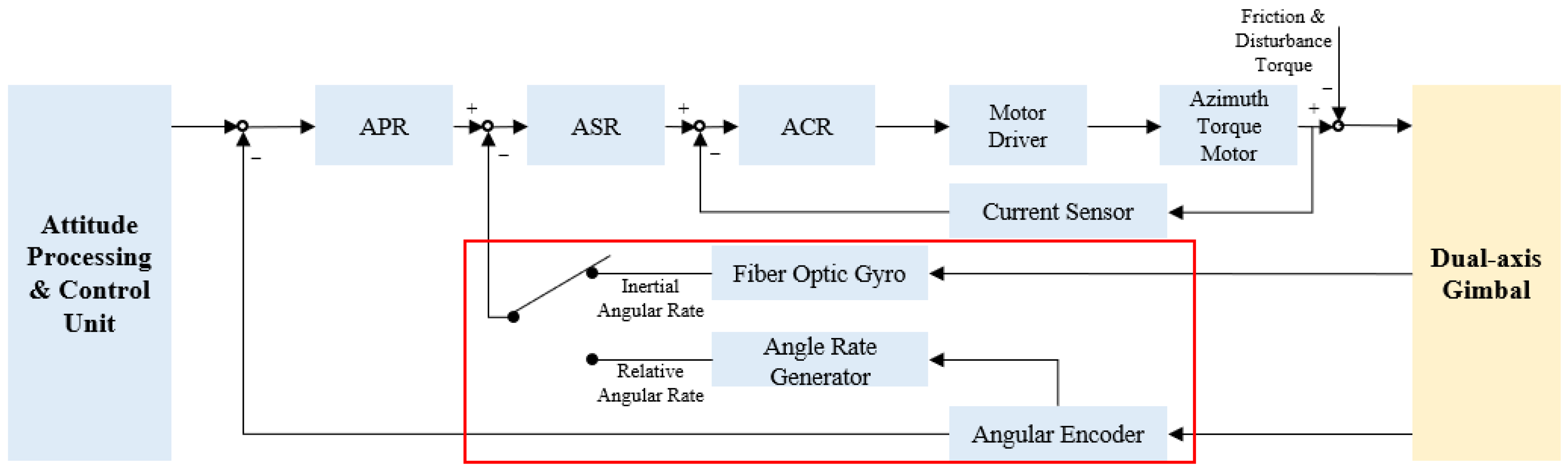
4.1.1. Current-Loop Control Design
4.1.2. Velocity-Loop Control Design
4.1.3. Position-Loop Control Design
4.2. Control Protection Strategies
- Gain adaptation resolves inter-level torque interference phenomena;
- Anti-windup design suppresses the risk of actuator saturation failure.
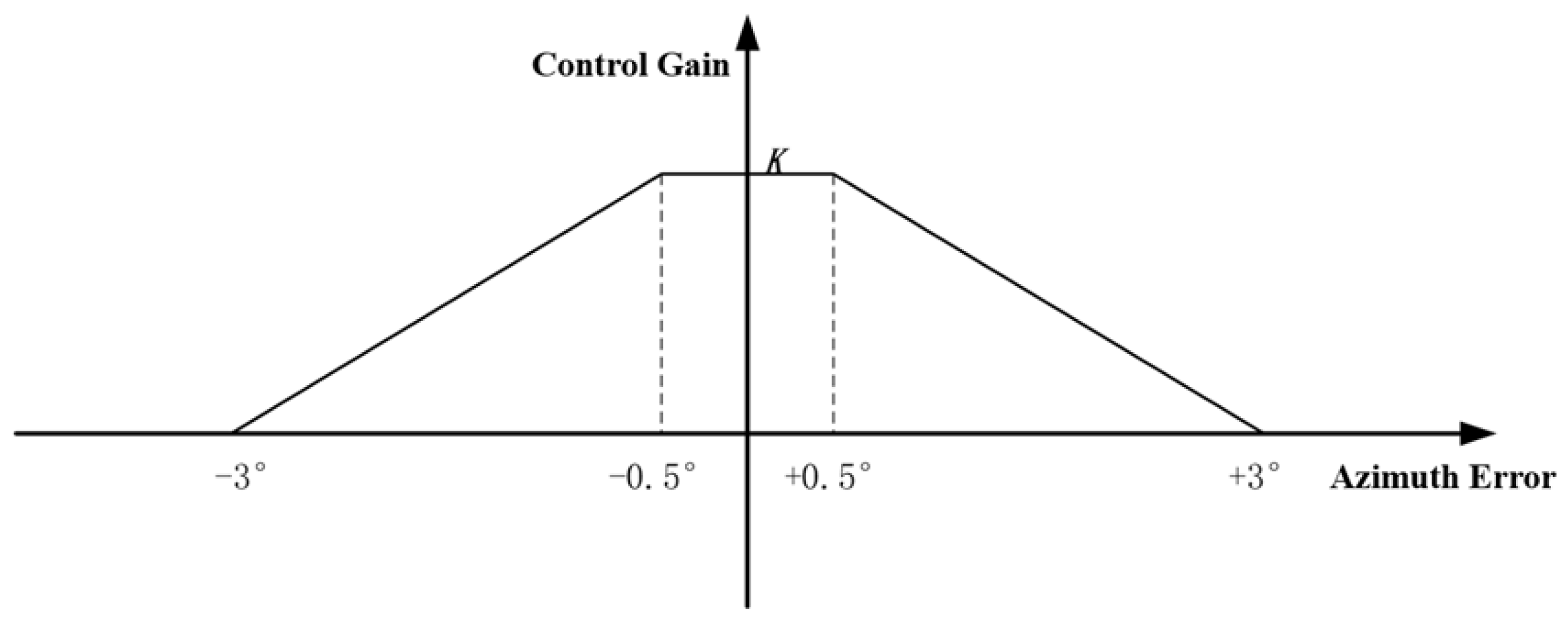
4.2.1. Gain Adaptation Processing
- When the azimuth deviation exceeds 3°, only the integrated gondola azimuth control system is activated, while the tier-2 system remains disabled.
- When the azimuth deviation enters the 3° range, the tier-2 system engages with low-gain progressive engagement under the integrated system’s operation, avoiding abrupt torque disturbances to the primary control.
- Once the tier-2 azimuth deviation falls within 0.5°, the tier-2 system operates at its full nominal gain K for precision control.
4.2.2. Anti-Windup Processing

5. Simulation Study
5.1. Simulation Preparation
- Gondola–Gimbal Dynamics Model: Implements the dynamics equations derived in Section 3, utilizing predefined disturbance profiles and inertia parameters from appended tables to characterize rigid-body interactions between the payload and gimbal platform;
- Gondola Anti-Twist Decoupling Controller: Accepts gondola azimuth motion feedback and balloon tether twist angle as inputs, generating anti-twist motor torque commands to neutralize azimuthal torsion through real-time cable-induced disturbance compensation;
- Integrated Azimuth Control Architecture:
- Flywheel Controller: Regulates overall gondola orientation via synergistic actuation with the anti-twist controller;
- Gimbal Azimuth Controller: Stabilizes high-precision pointing of the inner frame;
- Master Azimuth Controller: Fuses coarse azimuth references from the flywheel subsystem with fine-pointing feedback from the gimbal.
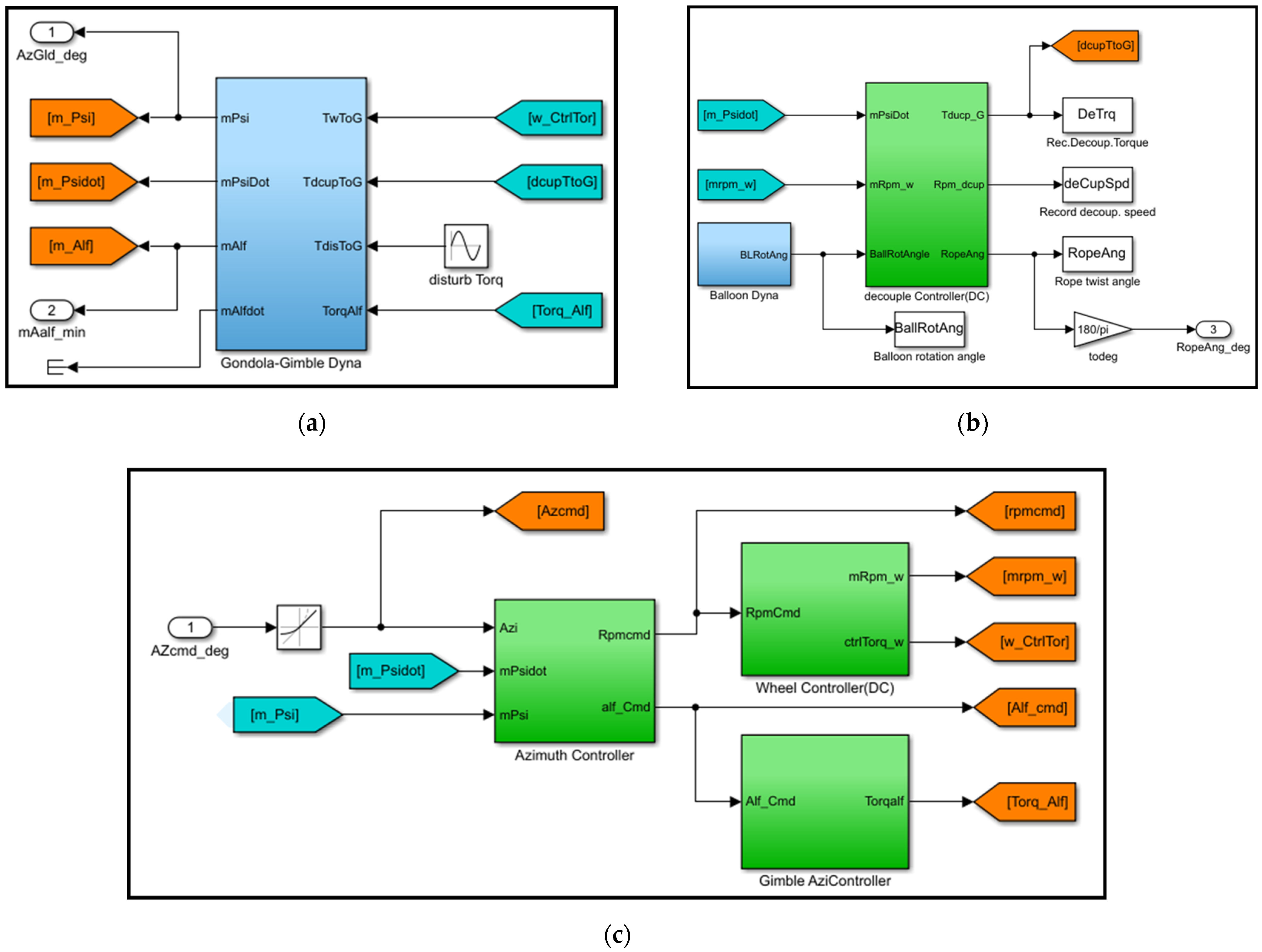
5.2. Simulation Verification
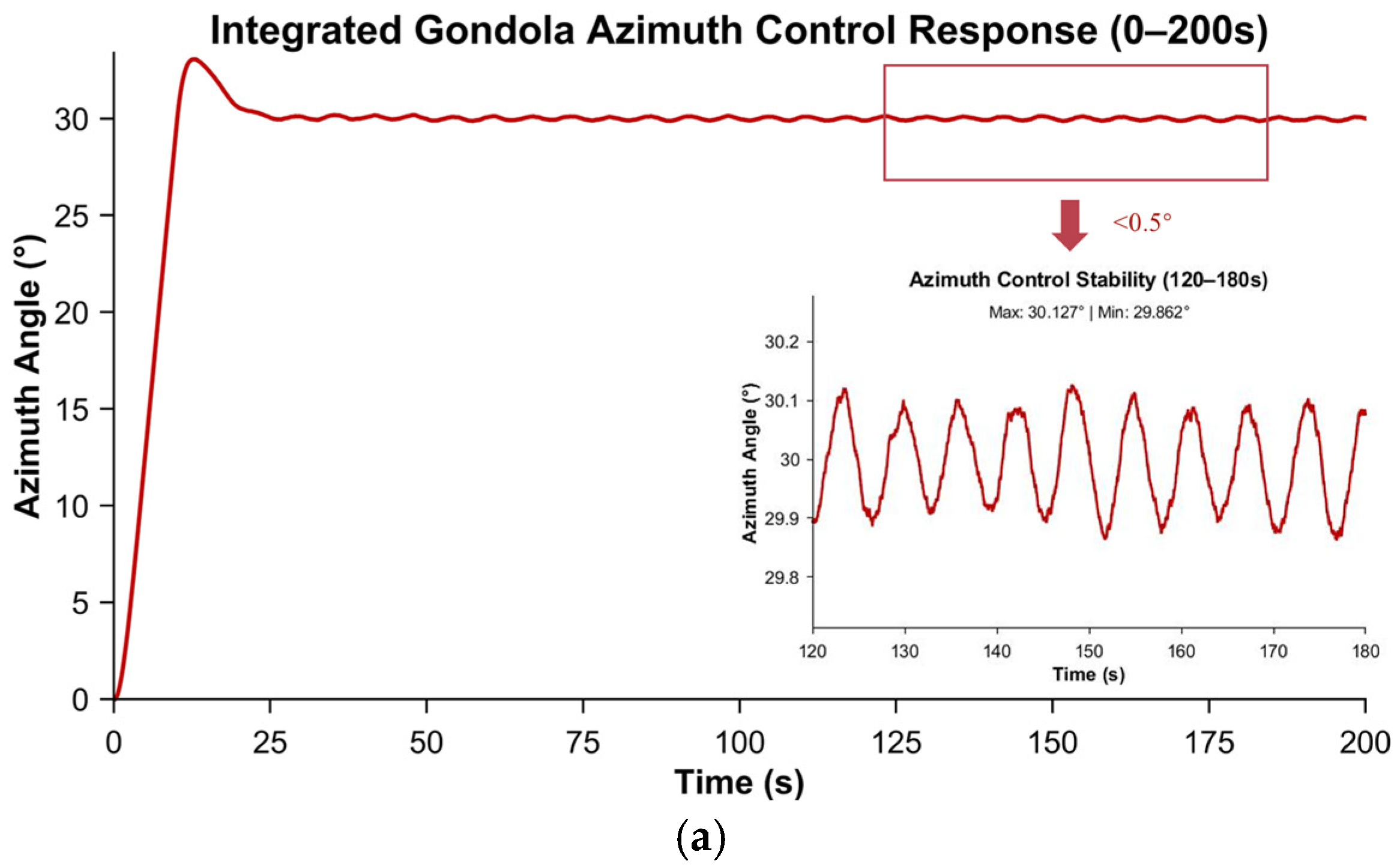
5.2.1. Velocity Loop Feedback Control Verification
5.2.2. Position Loop Algorithm Optimization Verification
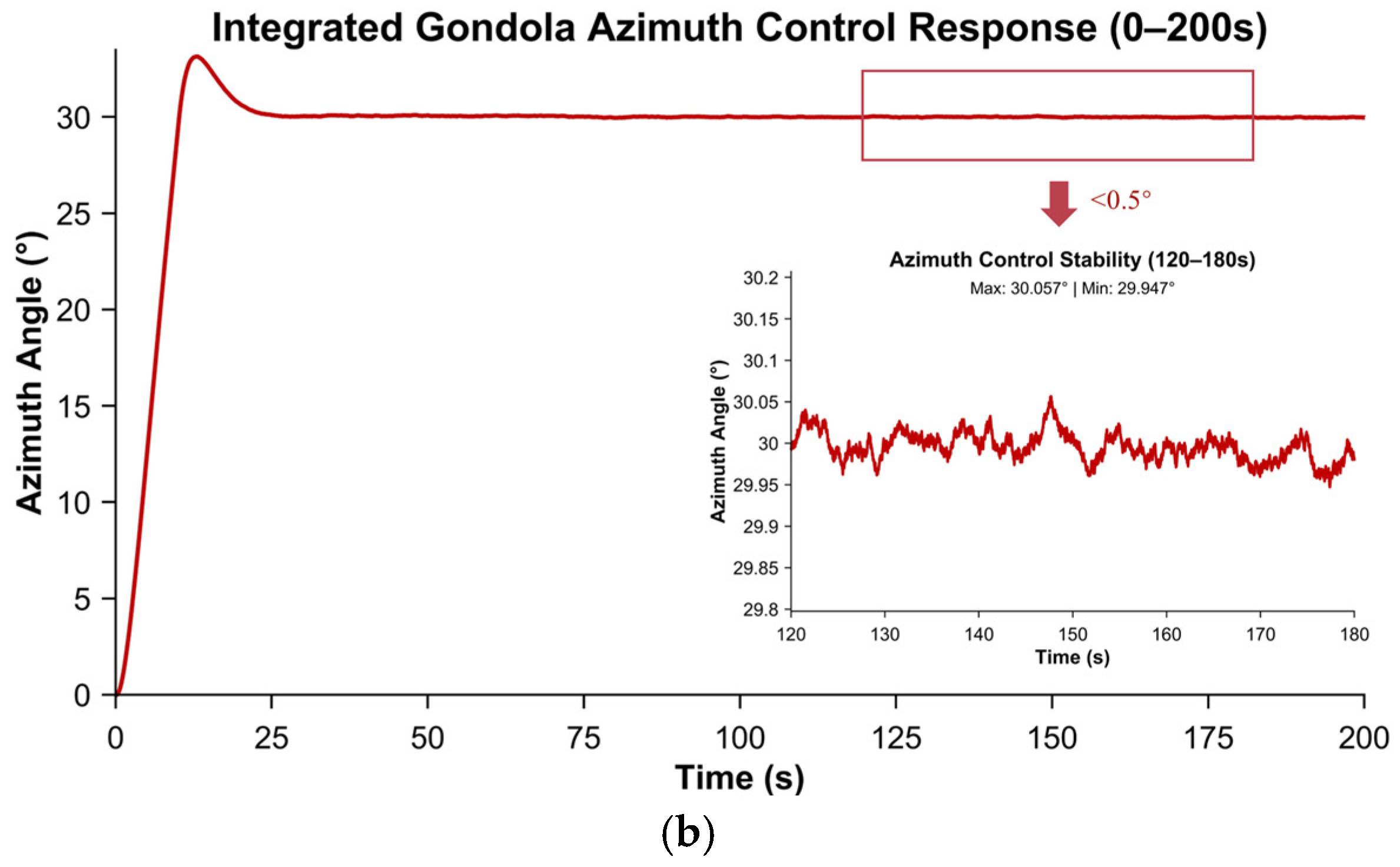
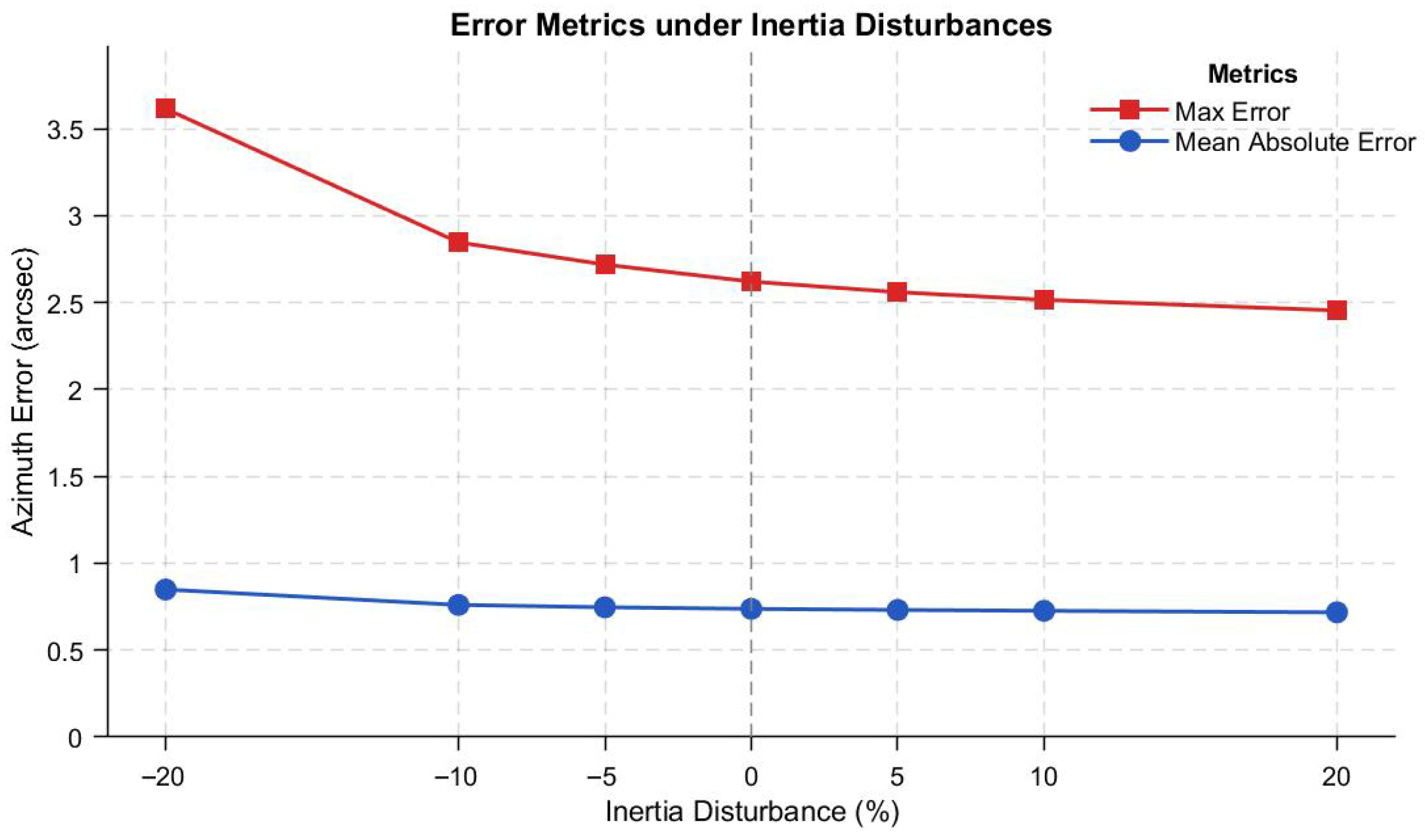
5.2.3. Robustness Verification of Pointing Accuracy Under Payload Inertia Uncertainty
6. Conclusions
- A unified nonlinear dynamic model for the azimuth channel was established for the first time, accurately characterizing the inertial coupling effects between the integrated gondola azimuth control system and the tier-2 gondola gimbal pointing system, thereby laying a theoretical foundation for control strategy design.
- A precision control algorithm was constructed through fiber-optic gyroscope velocity-loop feedback and an adaptive fuzzy PID position loop, achieving high disturbance rejection and strong robustness. This was supplemented by a dual-protection strategy integrating gain adaptation and anti-windup constraints, ensuring stable operation of the multi-level control system under extreme conditions.
- High-fidelity multi-condition simulations verified that the proposed control system attains < 20″ steady pointing accuracy under typical wind disturbances (0.7 Hz) and sensor noise, while maintaining control errors below 5″ under ±20% payload inertia perturbations, providing a rigorously validated theoretical design paradigm for near-space astronomical observation platforms.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameters | Numerical Values | Parameter Application Notes |
|---|---|---|
| Nominal level-flight altitude | 35 km | Balloon Dyna model parameter |
| Balloon sphere volume | 10,000 m3 | |
| Balloon sphere height | 18.3 m | |
| Balloon sphere maximum diameter | 30.5 m | |
| Balloon sphere volume | 0.45 | |
| Horizontal added mass coefficient of sphere | 0.7 | |
| Telescope gondola suspension point position L1 | 2.5 m | |
| Distance from gondola CG to suspension point L2 | 3 m | |
| Suspension cable length L3 | 50 m | |
| Equivalent stiffness of suspension cable | 1.372 N·m/rad | |
| Reference structural gross weight | 672 kg | Total mass of gondola and gimbal system |
| Reference suspended weight (gondola weight) | 600 kg | |
| Gondola moment of inertia about X-axis (through CG) Jox | 200 kg·m2 | Inertia tensor of mounting-base frame |
| Gondola moment of inertia about Y-axis (through CG) Joy | 200 kg·m2 | |
| Gondola moment of inertia about azimuth axis (Z-axis) Joz | 150 kg·m2 | |
| Telescope body moment of inertia (X-axis) Jix | 8 kg·m2 | Inertia tensor of pointing-axis frame |
| Telescope body moment of inertia (Y-axis) Jiy | 12 kg·m2 | |
| Telescope body moment of inertia (Z-axis) Jiz | 12 kg·m2 | |
| Inner gimbal moment of inertia (X-axis) Jmx | 12 kg·m2 | Inertia tensor of inner-gimbal frame |
| Inner gimbal moment of inertia (Y-axis) Jmy | 8 kg·m2 | |
| Inner gimbal moment of inertia (Z-axis) Jmz | 8 kg·m2 | |
| Telescope gravity G | 600 N | Derived from payload mass: G = mg (g = 9.8 m/s2) |
| Parameter Categories | Parameters | Numerical Values |
|---|---|---|
| Rated Performance | Rated Torque | 5 N·m |
| Rated Speed | 30 rpm | |
| Rated Voltage | 24 V | |
| Rated Current | 4 A | |
| Electrical Parameters | Armature Resistance | 4.74 Ω |
| Armature Inductance | 0.019 H | |
| Back-EMF Constant | 1.72 V·s/rad | |
| Torque Constant | 1.32 N·m/A | |
| Mechanical Parameters | Static Friction Torque | 0.04 N·m |
| Dynamic Friction Coefficient | 0.01 N·m |
| Parameters | Numerical Values |
|---|---|
| Triaxial FOG Accuracy | 0.01°/h |
| GNSS/INS Accuracy | Azimuth: ≤0.05° |
| Pitch/Roll: ≤0.03° Gyro: 0.01°/h Velocity: ≤0.1 m/s Position: 5 m (CEP) | |
| Reaction Wheel/Torque Motor | Torque: 0.05 N·m |
| Dynamic Friction: 0.02 N·m·s/rad | |
| Gimbal Servo Motor | Torque: 0.04 N·m |
| Dynamic Friction: 0.02 N·m·s/rad |
| Parameters | Numerical Values |
|---|---|
| Atmospheric density | 0.00675~0.00848 kg/m3 |
| Maximum relative wind speed vm | 9 m/s |
| Gondola aerodynamic frontal area Ap | 4 m2 |
| Aerodynamic drag coefficient Cd | 0.7 |
| Aerodynamic disturbance force on gondola Fa | 0.765~0.962 N |
| Eccentricity distance between aerodynamic load application point and center of mass dp | 0.5 m |
| Effective frontal area of telescope assembly At | 0.5 m2 |
| Aerodynamic disturbance force on telescope assembly Ft | 0.095~0.120 N |
| Eccentricity distance of telescope payload application point dt | 1 m |
References
- Huang, W.; Zhang, X.; Li, Z.; Wang, S.; Huang, M.; Cai, R. Development status and application prospect of near space science and technology. Sci. Technol. Rev. 2019, 37, 46–62. [Google Scholar]
- Li, Y.; Huang, W.; Zhou, J.; Zhang, X.; Zhang, H. Development status and prospects of near space observatories. Chin. J. Space Sci. 2024, 44, 1068–1085. [Google Scholar] [CrossRef]
- Pascale, E.; Ade, P.A.; Bock, J.J.; Chapin, E.L.; Chung, J.; Devlin, M.J.; Dicker, S.; Griffin, M.; Gundersen, J.O.; Halpern, M.; et al. The balloon-borne large aperture submillimeter telescope: BLAST. Astrophys. J. 2008, 681, 400–414. [Google Scholar] [CrossRef]
- Rhodes, J.; Dobke, B.; Booth, J.; Massey, R.; Liewer, K.; Smith, R.; Amara, A.; Aldrich, J.; Berge, J.; Bezawada, N.; et al. Space-quality data from balloon-borne telescopes: The High Altitude Lensing Observatory (HALO). Astropart. Phys. 2012, 38, 31–40. [Google Scholar] [CrossRef]
- Kassarian, E.; Sanfedino, F.; Alazard, D.; Evain, H.; Montel, J. Modeling and stability of balloon-borne gondolas with coupled pendulum-torsion dynamics. Aerosp. Sci. Technol. 2021, 112, 106607. [Google Scholar] [CrossRef]
- Shoji, Y.; Tanabe, T.; Sato, N. Highly precise pointing control system on a balloon-borne telescope for optical observations of planets. In Proceedings of the 8th International Symposium on Space Technology and Science, Tokyo, Japan, 5–12 June 2010; pp. Pm_15–Pm_20. [Google Scholar]
- Fairbrother, D.A. The NASA Balloon Program—Positioning for the future. In Proceedings of the AIAA Balloon Systems Conference, Dallas, TX, USA, 15–19 June 2015. [Google Scholar]
- Lecinski, A.; Card, G.; Knölker, M.; Hardy, B. The design and performance of the gondola pointing system for the Sunrise II balloon-borne stratospheric solar observatory. J. Astron. Instrum. 2017, 6, 1740007. [Google Scholar] [CrossRef]
- Kassarian, E.; Sanfedino, F.; Alazard, D.; Montel, J.; Chevrier, C.A. Robust line-of-sight pointing control on-board a stratospheric balloon-borne platform. arXiv 2021, arXiv:2112.10458. [Google Scholar]
- Romualdez, L.J. Design, Implementation, and Operational Methodologies for Sub-Arcsecond Attitude Determination, Control, and Stabilization of the Super-Pressure Balloon-Borne Imaging Telescope (SuperBIT). Ph.D. Thesis, University of Toronto, Toronto, ON, Canada, 2018. [Google Scholar]
- Yajima, N.; Kogaji, S.; Hashino, K. Research on the direction control system of a balloon-borne telescope. In Technical Report; Mechanical Engineering Laboratory, AIST: Tsukuba, Japan, 1986; Report No. 86-015. [Google Scholar]
- Shoji, Y.; Tanabe, T.; Sato, N. FUJIN-2: Balloon borne telescope for optical observation of planets. In Proceedings of the 14th International Symposium on Space Technology and Science, Tokyo, Japan, 3–9 July 2016; pp. Pk_95–Pk_102. [Google Scholar]
- Lin, J.; Song, T.; Sun, M.; Zhang, T.; Xu, F.; Wang, J.; Fu, Y.; Li, Y.; Kang, K.; Huang, M.; et al. A 50 mm balloon-borne white-light coronagraph: I. Basic structure and experiments on the ground. Sci. Sin.-Phys. Mech. Astron. 2023, 53, 259611. (In Chinese) [Google Scholar] [CrossRef]
- Ye, X.M. Study on High-Accuracy Attitude Control and Pointing Technology of a Large Balloon-Borne Solar Telescope. Ph.D. Thesis, National Astronomical Observatories, Chinese Academy of Sciences, Beijing, China, 1999. [Google Scholar]
- Stuchlik, D. The wallops arc second pointer-a balloon borne fine pointing system. In Proceedings of the AIAA Balloon Systems Conference, Dallas, TX, USA, 15–19 June 2015. [Google Scholar]
- Stuchlik, D. The NASA Wallops Arc-Second Pointer (WASP) system for precision pointing of scientific balloon instruments and telescopes. In Proceedings of the AIAA Balloon Systems Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Li, Y.; Zhou, J.; Zhang, X.; Zhao, C.; Xu, G. Dynamic modeling and control analysis of pitch/roll channels in the ball cabin system. J. Beijing Univ. Aeronaut. Astronaut. 2024. (In Chinese) [Google Scholar] [CrossRef]
- Li, Y.J.; Zhou, J.H.; Zhang, X.J. Dynamic modeling and parameter identification of azimuth channel for balloon gondola system. J. Beijing Univ. Aeronaut. Astronaut. 2024, 50, 2001–2008. [Google Scholar]
- Zhang, D.W.; Zhou, J.H.; Huang, W.N. Design of simplified anti-twist control system for high-altitude balloon gondola attitude control. Aerosp. Control 2016, 34, 76–82. [Google Scholar]
- Li, Y.J. Research on Attitude Control Technology of Balloon-Borne Gondola Based on Multi-Sensor Fusion. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2023. [Google Scholar]
- Yin, T.Z. Research on Lightweight Attitude Control System for Small and Medium-Sized Gondolas. Master’s Thesis, University of Chinese Academy of Sciences, Beijing, China, 2024. [Google Scholar]
- Tang, K.; Man, K.F.; Chen, G.; Kwong, S. An optimal fuzzy PID controller. IEEE Trans. Ind. Electron. 2001, 48, 757–765. [Google Scholar] [CrossRef]
- Phu, N.D.; Hung, N.N.; Ahmadian, A.; Senu, N. A new fuzzy PID control system based on fuzzy PID controller and fuzzy control process. Int. J. Fuzzy Syst. 2020, 22, 2163–2187. [Google Scholar] [CrossRef]
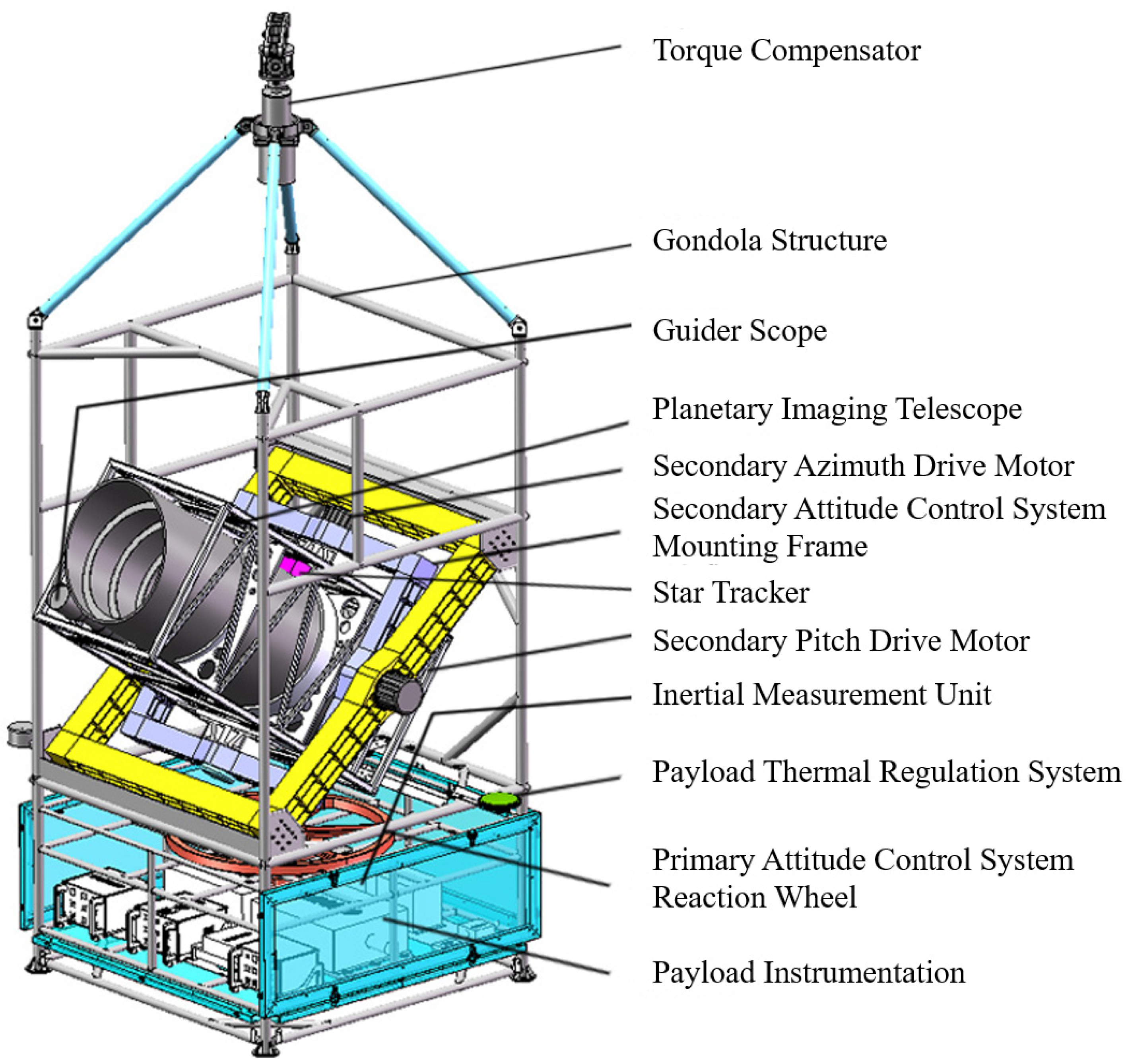
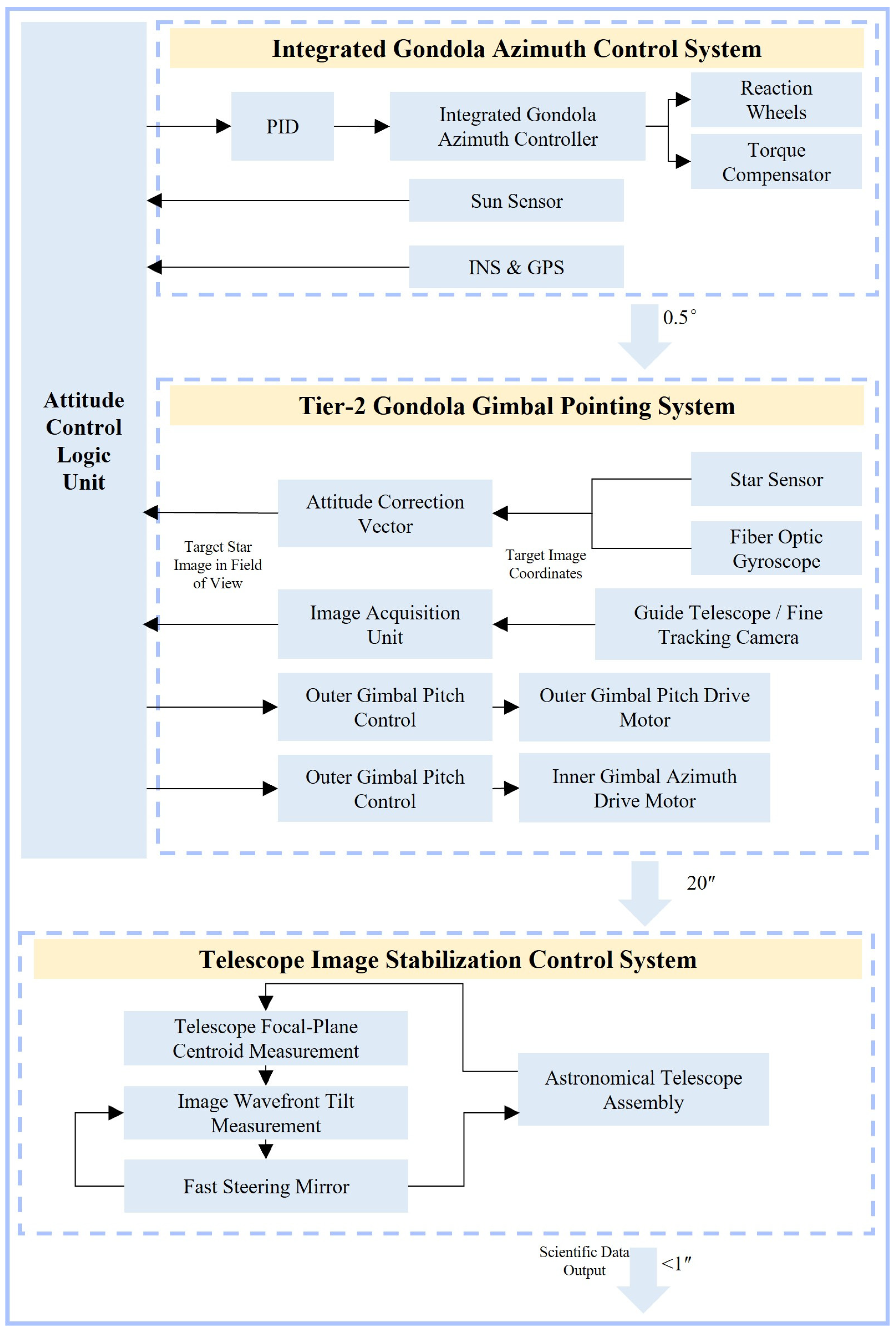



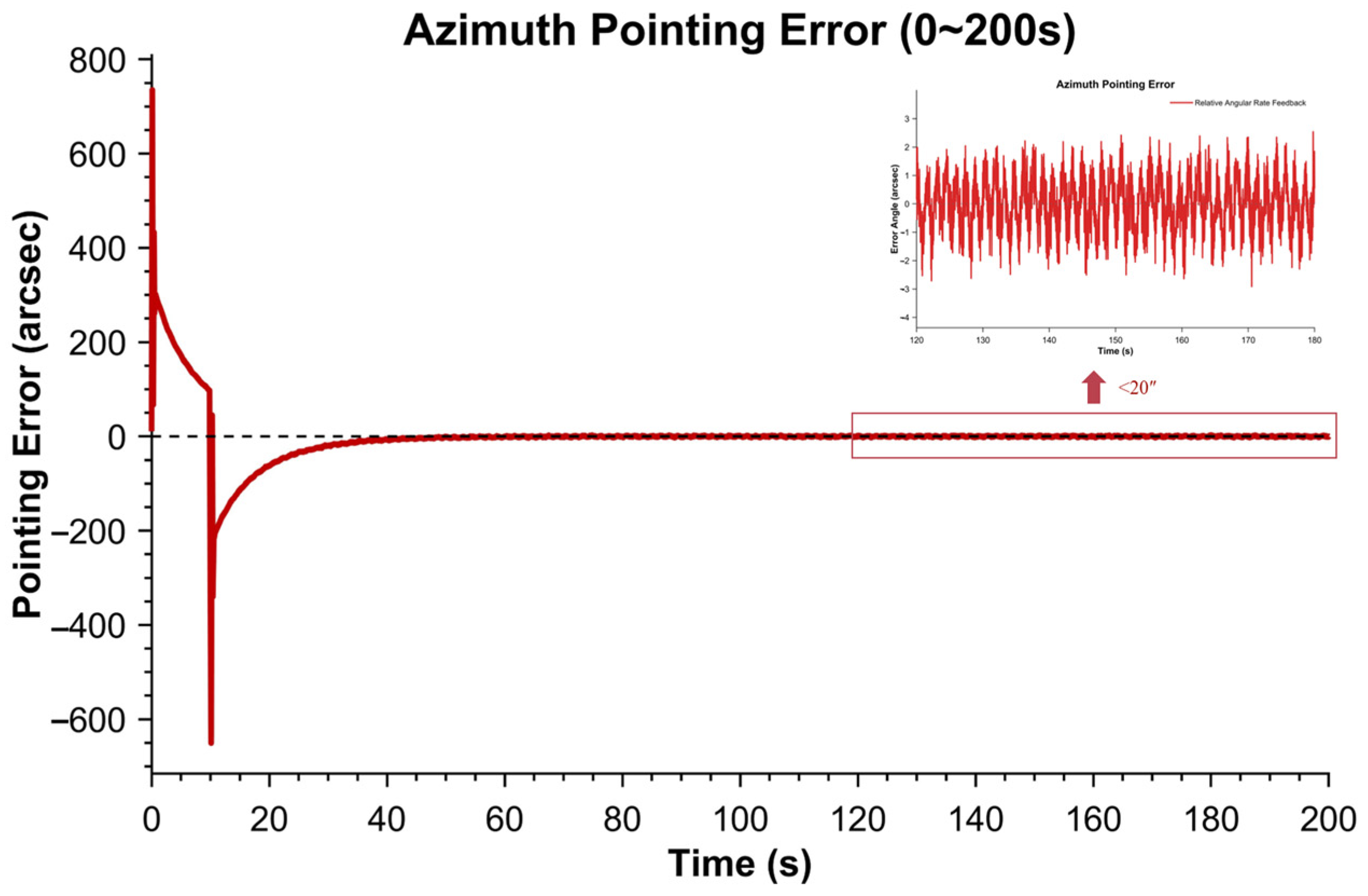

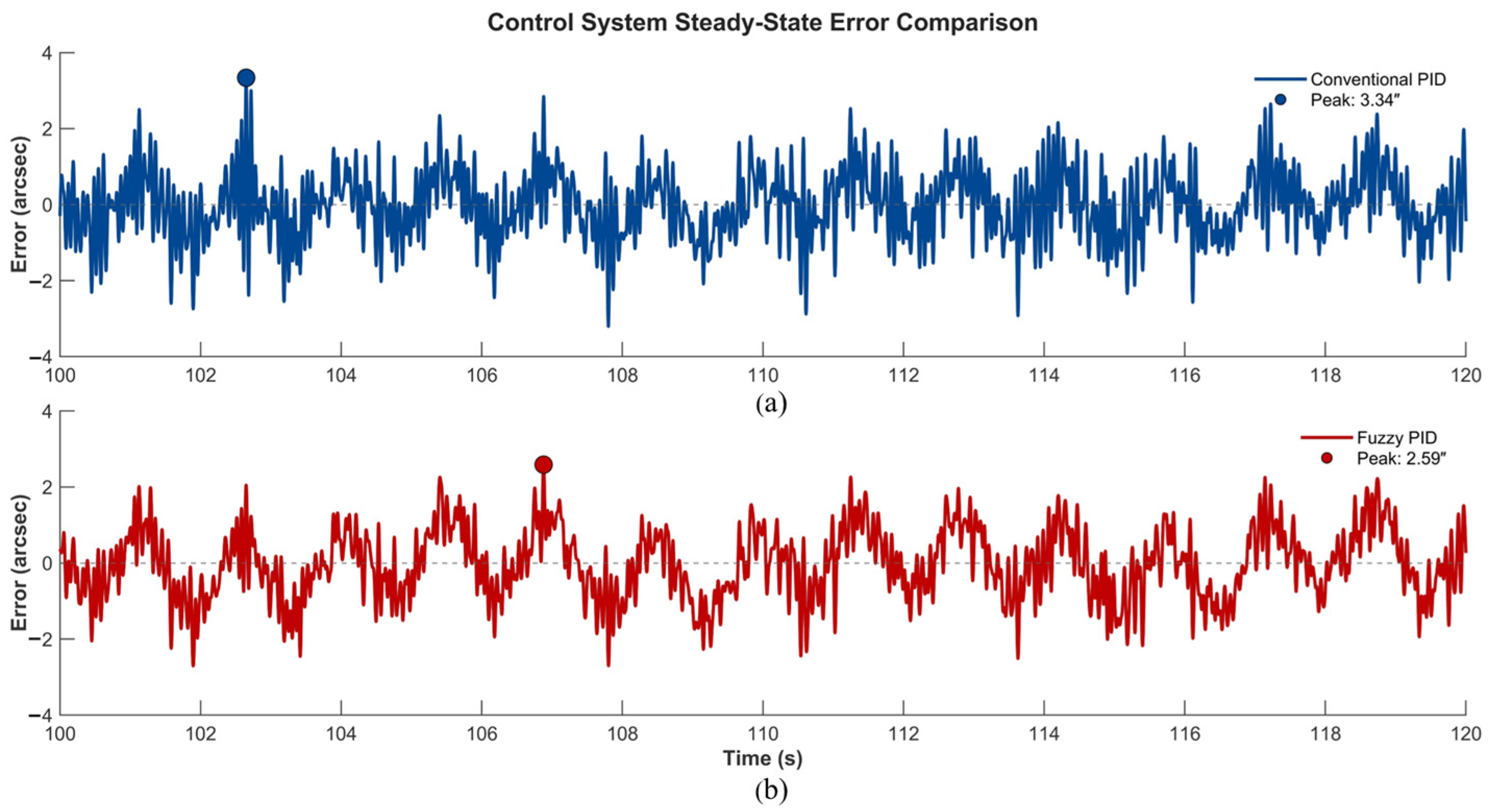
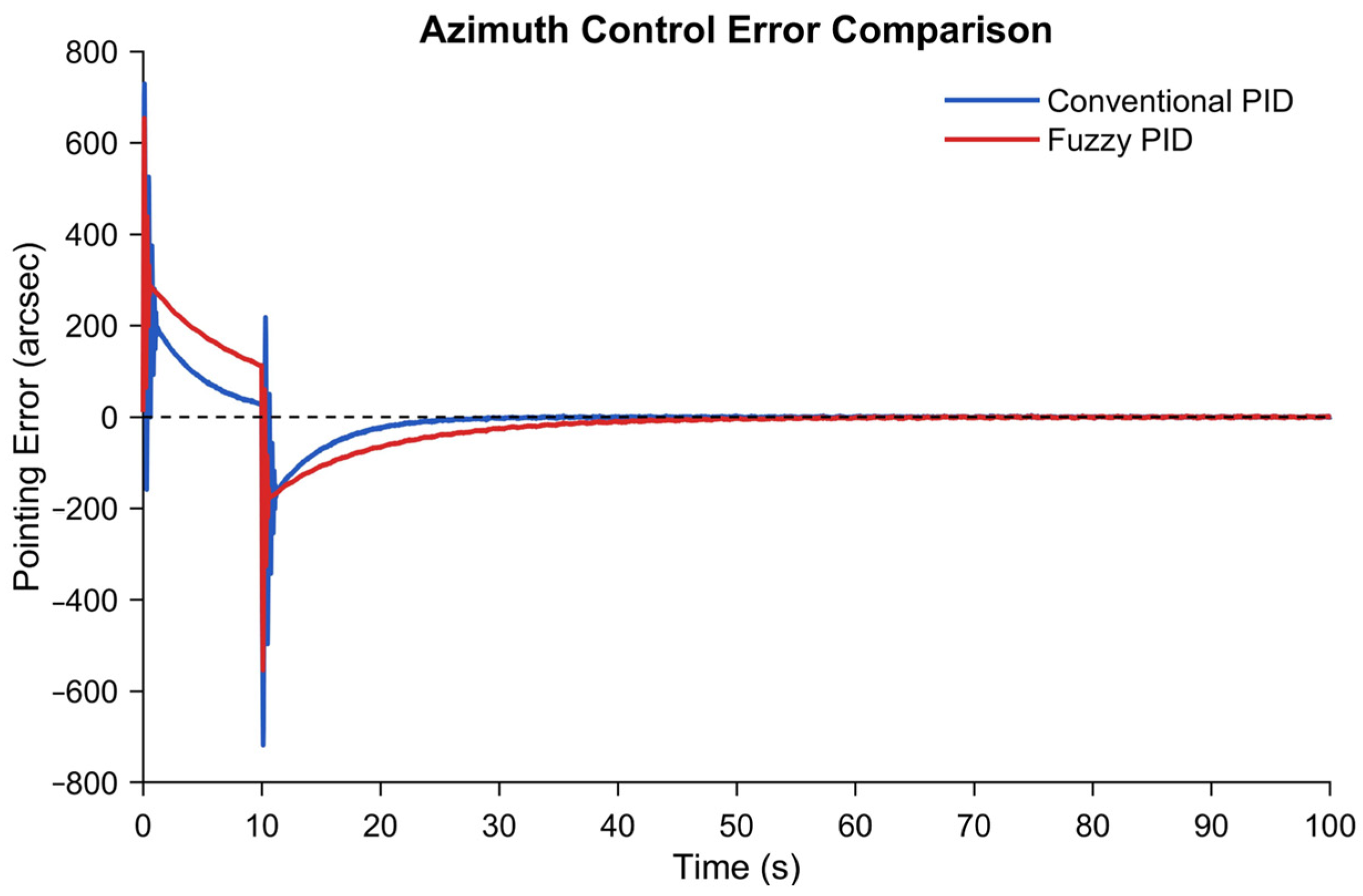
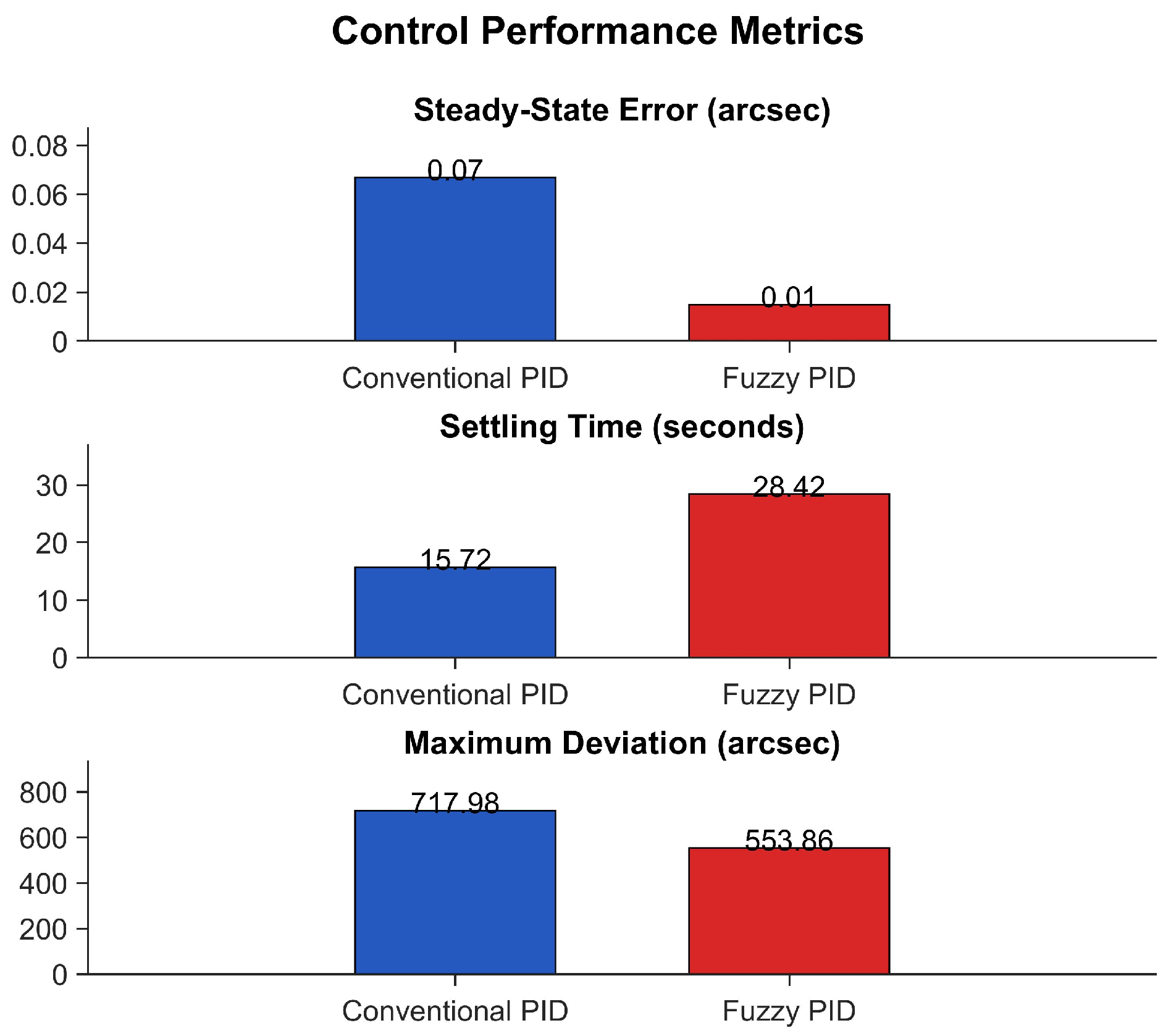


| Observation Type | Tracking Accuracy | Technical Challenges |
|---|---|---|
| High-resolution Optical | <0.1″ | Adaptive optics; high-speed feedback |
| Spectroscopic | 0.5″–1″ | Slit stabilization; real-time calibration |
| Time-domain Astronomy | 1″–2″ | Rapid-response control systems |
| Planetary Surface Imaging | <0.05″ | Dual star/target alignment |
| Galaxy/Nebula Studies | <0.1″–0.3″ | High-precision polar alignment |
| Mission/System | Primary Control Accuracy | Secondary Pointing Accuracy | Tertiary Image Stabilization Accuracy |
|---|---|---|---|
| Japan FUJIN * | 0.5° | 1′ | 0.1″ |
| China Balloon-borne Coronagraph | 0.5° | 20″ | 1″ |
| China BST | 0.1° | 20″ | / |
| NASA WASP * | 1~3° | 1″ | 0.1″ |
| Germany SUNRISE | 1° | 26″ | 0.04″ |
| ec | NB | NM | NS | ZO | PS | PM | PB | |
|---|---|---|---|---|---|---|---|---|
| e | ||||||||
| NB | ZE/NB/PS | PB/NB/NS | PM/NM/NB | PM/NM/NB | PS/NS/NB | ZO/ZO/NM | ZO/ZO/PS | |
| NM | PB/NB/PS | PB/NB/NS | PM/NM/NB | PS/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/ZO/ZO | |
| NS | PM/NB/ZO | PM/NM/NS | PM/NS/NM | PS/NS/NM | ZO/ZO/NS | NS/PS/NS | NS/PS/ZO | |
| ZO | PM/NM/ZO | PM/NM/NS | PS/NS/NS | ZO/ZO/NS | NS/PS/NO | NM/PM/NS | NM/PM/ZO | |
| PS | PS/NM/ZO | PS/NS/ZO | ZO/ZO/ZO | NS/PS/ZO | NS/PS/ZO | NM/PM/ZO | NM/PB/ZO | |
| PM | PS/ZO/PB | ZO/ZO/NS | NS/PS/PS | NM/PS/PS | NM/PM/PS | NM/PB/PS | NB/PB/PB | |
| PB | ZO/ZO/PB | ZO/ZO/PM | NM/PS/PM | NM/PM/PM | NM/PM/PS | NB/PB/PS | ZE/PB/PB | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cui, Y.; Zhou, J.; Li, Y.; Huang, W.; Liu, Y. Multi-Stage Coordinated Azimuth Control for High-Precision Balloon-Borne Astronomical Platforms. Aerospace 2025, 12, 821. https://doi.org/10.3390/aerospace12090821
Cui Y, Zhou J, Li Y, Huang W, Liu Y. Multi-Stage Coordinated Azimuth Control for High-Precision Balloon-Borne Astronomical Platforms. Aerospace. 2025; 12(9):821. https://doi.org/10.3390/aerospace12090821
Chicago/Turabian StyleCui, Yulang, Jianghua Zhou, Yijian Li, Wanning Huang, and Yongqi Liu. 2025. "Multi-Stage Coordinated Azimuth Control for High-Precision Balloon-Borne Astronomical Platforms" Aerospace 12, no. 9: 821. https://doi.org/10.3390/aerospace12090821
APA StyleCui, Y., Zhou, J., Li, Y., Huang, W., & Liu, Y. (2025). Multi-Stage Coordinated Azimuth Control for High-Precision Balloon-Borne Astronomical Platforms. Aerospace, 12(9), 821. https://doi.org/10.3390/aerospace12090821





