Stochastic Model Predictive Control for Parafoil System via Markov-Based Multi-Scenario Optimization

Abstract

As an essential technology for precision airdrop missions, parafoil systems have gained widespread adoption in military and civilian applications due to their superior glide performance and maneuverability compared to conventional parachutes. Addressing the trajectory-tracking control challenges of the parafoil system under significant wind disturbances, characterized by wind uncertainty and system underactuation, this paper proposes a stochastic model predictive control (SMPC) framework based on Markov-based multi-scenario optimization. Traditional deterministic model predictive control (MPC) methods often exhibit excessive conservatism due to reliance on worst-case assumptions and fail to capture the time-varying nature of real-world wind fields. To address these limitations, a high-fidelity dynamic model is developed to accurately characterize aerodynamic coupling effects, overcoming the oversimplifications of conventional three-degree-of-freedom point-mass models. Leveraging Markov state transitions, multiple wind-disturbance scenarios are dynamically generated, effectively overcoming the limitations of independent and identically distributed hypotheses in modeling realistic wind variations. A probabilistic constraint-reconstruction strategy combined with a rolling time-domain covariance update mechanism mitigates uncertainties and enables cooperative optimization of inner-loop attitude stabilization and outer-loop trajectory tracking. The simulation results demonstrate that the SMPC framework achieves superior comprehensive performance compared to deterministic MPC, evidenced by significant reductions in maximum position error, average position error, and control effort variation rate, along with a 94% tracking success rate. By balancing robustness, tracking precision, and computational efficiency, the method provides a theoretical foundation and a promising simulation-validated solution for airdrop missions.

1. Introduction

Airdrop systems can deliver troops, equipment, and supplies to designated targets using transport aircraft [1]. Owing to efficient and convenient material transfer capabilities, airdrop systems have undergone rapid and steady global development. Parafoils provide superior glide performance, maneuverability, and stability compared to traditional circular parachutes, ensuring enhanced flight quality for executing turns, achieving smooth landings, and conducting precision airdrops [2,3]. However, low airspeed and lack of thrust make parafoils extremely sensitive to unpredictable wind disturbances at low altitudes. Winds are often a primary factor affecting landing accuracy, particularly when the wind speed approaches the airspeed of the vehicle [4,5,6]. Since the beginning of the 21st century, autonomous homing technology for parafoil airdrop systems has advanced significantly, driven by rapid developments in microelectronics, navigation, and guidance technology [7,8,9].

Trajectory-tracking control is key to achieving precise homing. In the research field of aircraft-tracking control algorithms, many scholars are committed to improving the performance and robustness of the control system to cope with various complex flight environments and mission requirements. Traditional PID control remains widely adopted in aerospace systems due to its structural simplicity, implementation ease, and proven reliability under stable operating conditions. However, for missions requiring high-precision trajectory tracking under significant external disturbances, such as parafoil systems in variable wind fields, PID fixed-gain architecture faces inherent challenges in dynamically adapting to rapid environmental changes [10]. Given these problems, many advanced control methods have been put forward one after another.

Model predictive control (MPC) has become a predominant method for parafoil trajectory tracking due to its capability to optimize multivariable coupled systems [2]. Early research realized the basic control framework by establishing a simplified linear dynamic model. Siegers and Costell [11] proposed a reduced-order linear MPC strategy based on a six-DOF nonlinear model and used a Lagrange interpolation polynomial to map the desired trajectory into a heading angle command. The flight test verified its effectiveness in outer-loop position tracking. However, this kind of method relies on deterministic assumptions, failing to account for random uncertainties (e.g., aerodynamic parameters and wind-field disturbances), resulting in conservatism and insufficient robustness in practical applications [10].

The current study focuses on innovative stochastic model predictive control (SMPC) algorithms to address these limitations and enable effective management of constraint violations cost-effectively [12]. SMPC leverages the stochastic nature of uncertainties and system statistics to reformulate hard constraints as probabilistic constraints, allowing controlled constraint violations under specified probabilities and accommodating unbounded disturbances. In recent years, data-driven control methods have gradually attracted attention. A data-driven robust optimization method was proposed and applied to scenario-based SMPC [13]. By actively learning a data-driven uncertainty set from available data, data information is effectively utilized, and the number of data samples required to achieve probability assurance is reduced, thus reducing excessive conservatism of control and improving the practicality of SMPC. For constrained linear systems with unknown additive uncertainties, a robust model predictive control algorithm for scenario optimization based on Gaussian process regression learning was proposed [14]. Calafiore et al. [15] proposed an SMPC framework based on scenario optimization, which transforms hard constraints into probabilistic forms and allows for moderate constraints violation at a specified risk level, thus reducing conservatism. Further, Gonzalez et al. [16] compared the performance of SMPC with that of stochastic chance model predictive control (SCMPC) and pointed out that SMPC can improve the control success rate with lower computational cost through covariance propagation and offline constraint adjustment.

Stochastic uncertainties are ubiquitous in practical engineering problems. The coupling and propagation of uncertainties can lead to significant performance fluctuations or even system failures, making the quantification, propagation, and control of stochastic uncertainties critical [17]. Compared to traditional aircraft, the availability of real-world flight data for parafoil systems is relatively limited. Furthermore, discrepancies between the reference values in aerodynamic databases and the actual values are challenging to evaluate and correct, resulting in parametric uncertainties. Modeling and controller design simplifications may neglect higher-order modes, leading to unmodeled dynamic behavior. Variations in atmospheric conditions alter the pressure distribution on the parafoil surface, thereby modifying the aerodynamic force and moment coefficients and introducing aerodynamic uncertainties. In addition, measurement errors and noise contribute to state uncertainty. For the modeling and propagation of a parafoil system with random uncertainties, Qian et al. [18] proposed a dynamic inverse control algorithm based on a neural network. Although it showed strong anti-interference ability in the simulation, it relied on a large amount of training data and lacked a theoretical stability guarantee. Culpepper et al. [19] designed adaptive control logic to deal with parafoil failures; however, since it is based on heuristic rules, its design is too complex to extend to multi-modal interference scenarios. In stochastic disturbance modeling, the Markov process has become an effective tool for analyzing uncertainty propagation in dynamic systems because of its unique “no aftereffect” characteristics [12]. Jian Li et al. [20] proposed the integrated navigation method of gray Markov prediction 478, which verified the advantages of the Markov process in describing the time-series correlation of random disturbances. Its state transition mechanism can quantify the probability law of the system evolving from the current disturbance mode to the next mode, thus realizing the accurate modeling of the dynamic characteristics of disturbances. The current technical foundation has proved the effectiveness of the Markov random field (MRF) in spatial correlation modeling [21].

Given the strong coupling, nonlinearity, and underactuated characteristics of parafoil systems, current research on their flight control primarily focuses on trajectory-tracking control algorithms. It pays insufficient attention to the collaborative optimization of inner-loop attitude-angle control [22,23,24], which limits the comprehensiveness and precision of flight control for parafoil systems. In addition, the strong nonlinear and aerodynamic coupling characteristics of parafoil systems require high-precision dynamic modeling and joint treatment of multisource disturbances [25,26,27], and the traditional point-mass model [11] is too simplified to meet the demand. Using the Markov process to analyze the random disturbance of the wind field can not only inherit its theoretical advantages in dealing with the uncertainty of a dynamic system but also improve the fidelity and practicability of multi-scenario generation by combining scenario optimization technology.

It is important to note that this study constitutes a theoretical investigation. The primary contribution is the development of the Markov-based SMPC framework and its rigorous evaluation through high-fidelity Monte Carlo simulations. While physical flight tests are the ultimate validation, they are beyond the scope of this paper and are identified as a critical direction for future work.

Targeting precision airdrop missions for missile-borne parafoil systems (see Figure 1) and building upon our research team’s foundational work in parafoil dynamics modeling and control [28,29], this research proposes an SMPC method for parafoil systems via Markov-based multi-scenario optimization to address the conservatism and robustness limitations of traditional deterministic MPC under complex wind disturbances. The remainder of the paper is organized as follows: Section 2 presents the rigid-body dynamic model of the parafoil system, overcoming the limitations of traditional simplified models in capturing aerodynamic coupling effects. Section 3 details the Markov-based multi-scenario wind-field generation framework and the design of the SMPC controller, including probabilistic constraint reconstruction and rolling time-domain covariance update strategies. Section 4 describes the simulation setup and analyzes the comprehensive performance of the proposed method under wind disturbances. 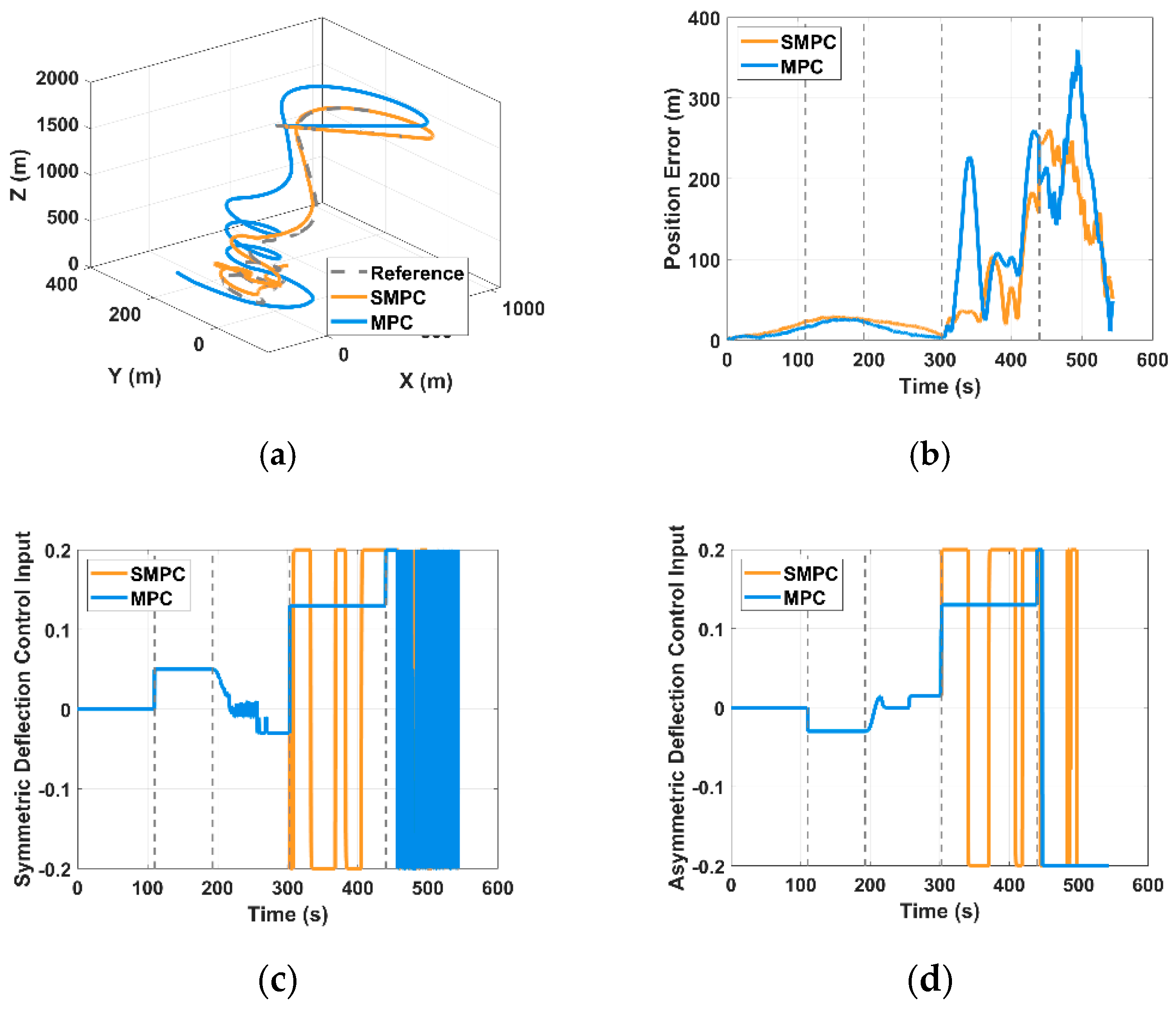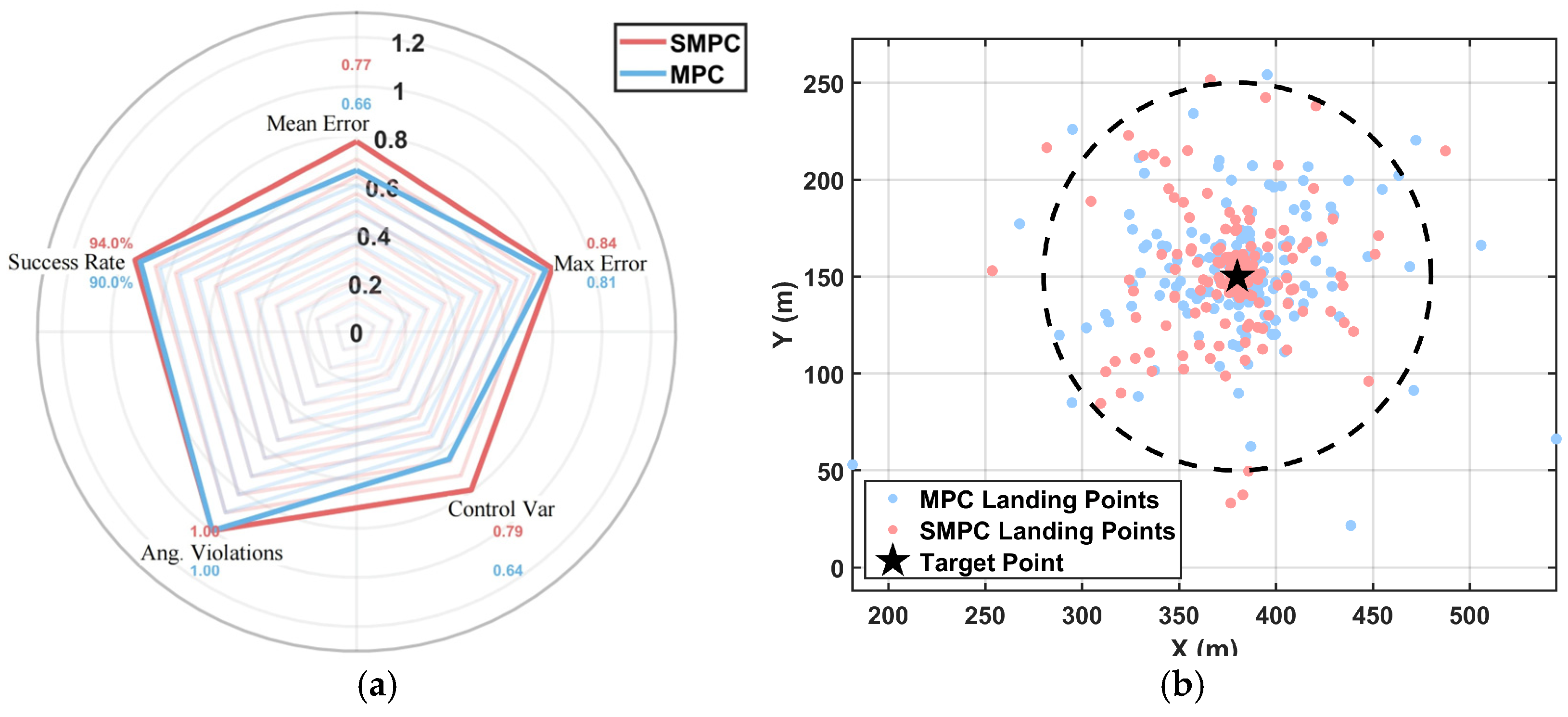Finally, Section 5 concludes the study and discusses future research directions. The experimental results demonstrate that the SMPC achieves significant comprehensive performance advantages over deterministic MPC, quantified by a radar chart area of 1.80 (vs. 1.55 for MPC), with improvements in maximum position error, average position error, control effort variation rate, and angular velocity constraint violation probability. Additionally, it maintains a 94% tracking success rate while balancing robustness and energy efficiency, providing a high environmental adaptability solution for precise airdrop missions in complex wind environments.

2. Parafoil Dynamic Model

The parafoil system is modeled as a single rigid body with six degrees of freedom, following standard procedures in aerospace engineering. When focusing on trajectory prediction, the relative motion between the canopy and the payload can be neglected under the specified validity conditions. This simplification enables the development of a computationally efficient model while maintaining sufficient accuracy for trajectory control purposes.

The suspension lines connecting the canopy to the payload introduce additional aerodynamic effects that warrant consideration. These lines create additional drag and can influence the overall aerodynamic characteristics of the system. However, for the purposes of trajectory control, these effects are incorporated into the overall system drag coefficient rather than modeled separately. This simplification is justified by the following factors:

• The suspension line drag typically contributes less than 10% to the total system drag;
• The geometric configuration of the suspension lines remains relatively constant during stable flight;
• The computational complexity of modeling individual suspension line effects would significantly increase without proportional improvements in trajectory prediction accuracy.

2.1. Coordinate Systems and Transformations

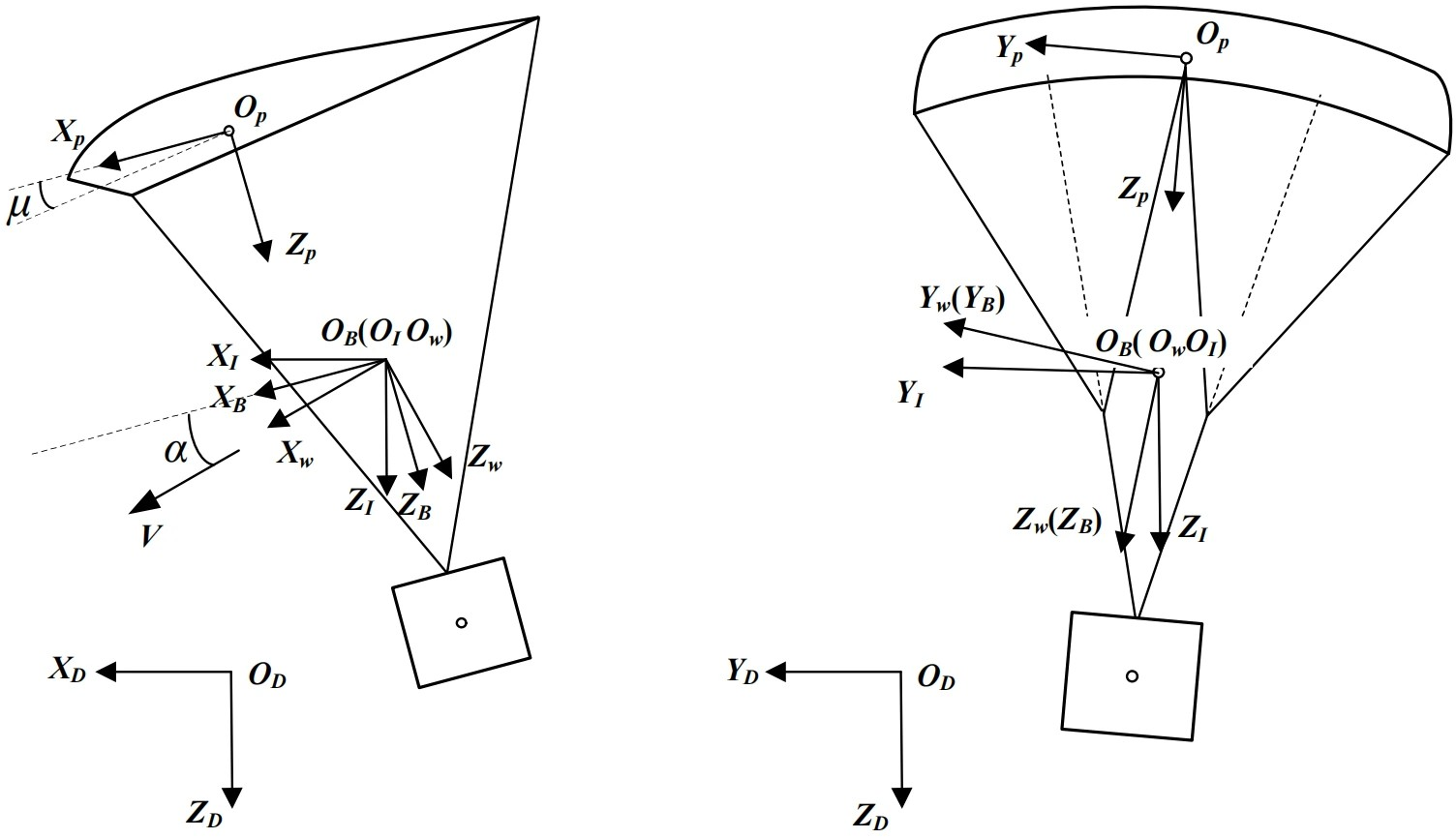
The analysis of parafoil system’s motion typically involves the following four coordinate systems: the inertial frame, $O_I{X}_I{Y}_I{Z}_I$; body frame, $O_B{X}_B{Y}_B{Z}_B$; canopy frame, $O_P{X}_P{Y}_P{Z}_P$; and velocity frame, $O_W{X}_W{Y}_W{Z}_W$. The Euler angle yaw ($\psi$), pitch ($\theta$), and roll ($\varphi$) define the orientation of the body frame relative to the inertial frame, following the Z–Y–X rotation sequence (Figure 2). These Euler angles are combined into a vector defined as $\mathit{E}={\left[\psi ,\theta ,\varphi \right]}^T$.

The transformation matrix from the inertial to the body frame ($R_B^I$) is written as follows:

$${\mathit{R}}_B^I=\left[\begin{array}{ccc}\cos \psi \cos \theta & \sin \psi \cos \theta & -\sin \theta \\ \cos \psi \sin \theta \sin \varphi -\sin \psi \cos \varphi & \sin \psi \sin \theta \sin \varphi +\cos \psi \cos \varphi & \cos \theta \sin \varphi \\ \cos \psi \sin \theta \cos \varphi +\sin \psi \sin \varphi & \sin \psi \sin \theta \cos \varphi -\cos \psi \sin \varphi & \cos \theta \cos \varphi \end{array}\right]$$

(1)

where the superscript indicates before conversion, the subscript indicates after conversion, and the naming rules are consistent in the following.

The transformation matrix from the body to the canopy frame ($R_P^B$) is given by the following:

$${\mathit{R}}_P^B=\left[\begin{array}{ccc}\cos \mu & 0& -\sin \mu \\ 0& 1& 0\\ \sin \mu & 0& \cos \mu \end{array}\right]$$

(2)

where $\mu$ is the canopy rigging angle, defined as the angle between the body ($X_B$) axis and the lower chord line. It is negative if the lower chord lies below the $X_B$ axis.

The transformation matrix from the velocity to the body frame ( $R_B^W$) takes the following form:

$${\mathit{R}}_B^W=\left[\begin{array}{ccc}\cos \alpha \cos \beta & -\cos \alpha \sin \beta & -\sin \alpha \\ \sin \beta & \cos \beta & 0\\ \sin \alpha cos\beta & -sin\alpha \sin \beta & \cos \alpha \end{array}\right]$$

(3)

where $\alpha$ (angle of attack) is defined as the angle between the airflow and its projection onto the longitudinal symmetry plane, which is positive when the airflow approaches from below the body frame; $\beta$ (sideslip angle) means the angle between the airflow and the $X_B$ axis, which is positive when the airflow approaches from the left side of the body frame. Notably, $\alpha$ and $\beta$ are derived from the airspeed vector components in the body frame.

$$\alpha ={\tan }^{-1}\left(w_a/u_a\right)$$

(4)

$$\beta ={\tan }^{-1}\left(v_a/\sqrt{{u_a}^2+{w_a}^2}\right)$$

(5)

where ${\mathit{V}}_a={[u_a,v_a,w_a]}^T$ denotes the airspeed vector. To facilitate the subsequent kinematic analysis, we formally define the skew-symmetric matrix operator. For any vector $\mathit{V}={\left[u,v,w\right]}^T$, its corresponding skew-symmetric matrix is given by the following:

$$\tilde{\mathit{V}}=\left[\begin{array}{ccc}0& -w& v\\ w& 0& -u\\ -v& u& 0\end{array}\right]$$

(6)

2.2. Added-Mass Modeling

When a body moves in the air, it sets the air around it into motion itself. In turn, this motion introduces pressure forces on the body, which are called the apparent mass pressures. The magnitude of these apparent mass pressures is inversely proportional to the mass ratio, representing the ratio of the mass of the vehicle (m) to the air mass displaced or associated with this vehicle. For aerodynamic deceleration systems, such as parafoils or conventional parachutes, the inclusion of the added mass is essential to the strong coupling between the fluid motion and body dynamics [30].

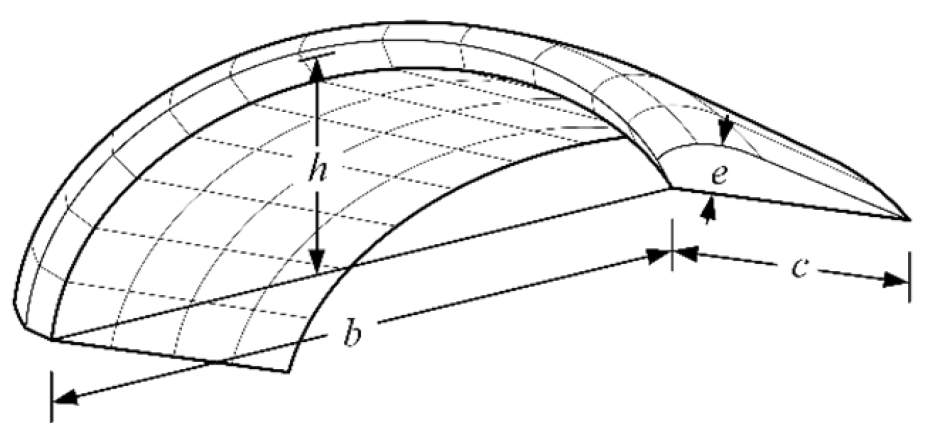
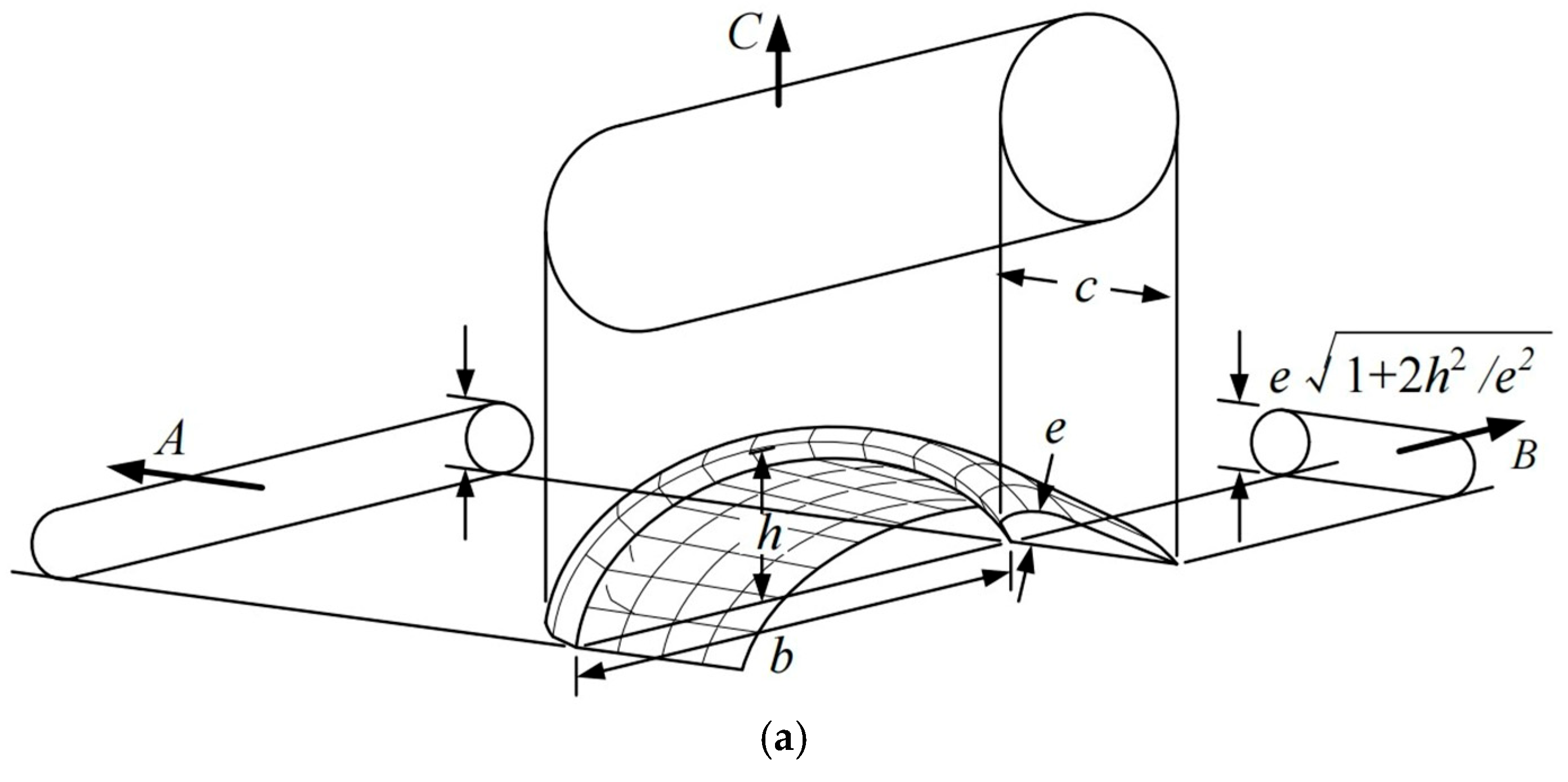
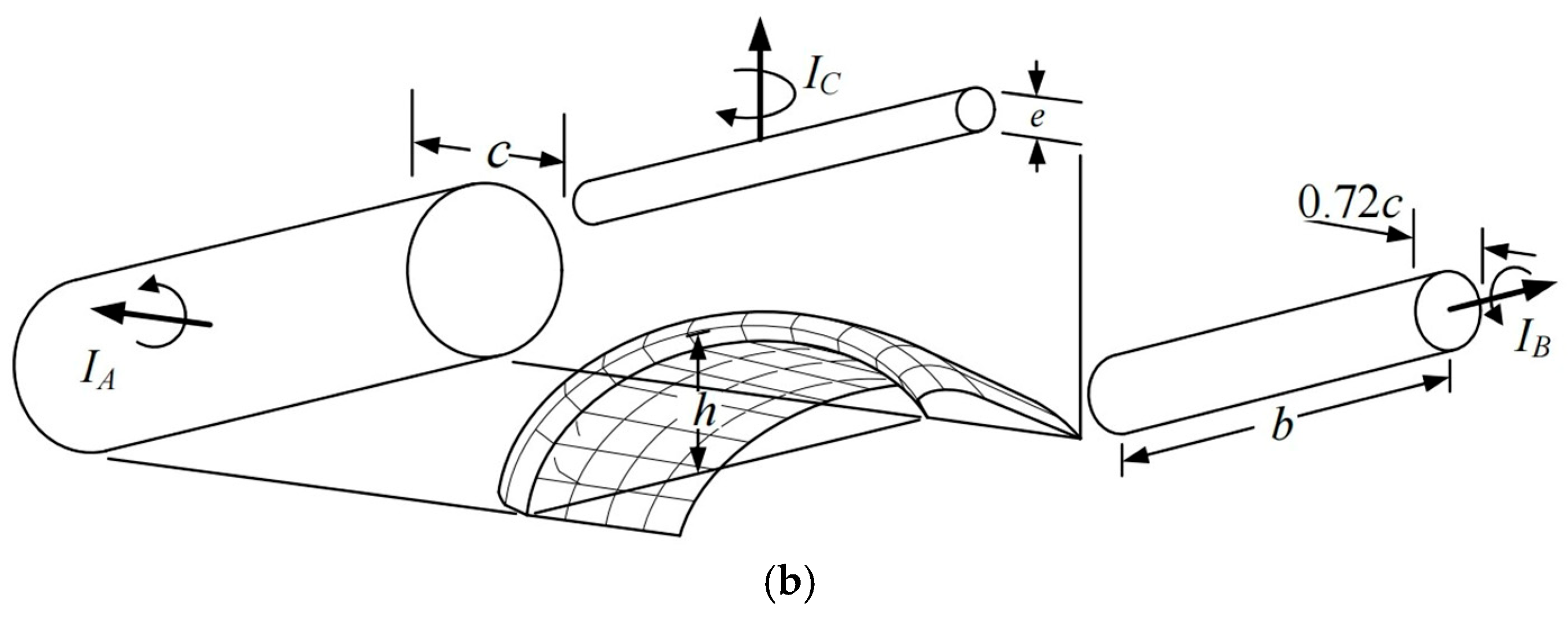
For a parafoil canopy modeled as a planar lifting surface with an elliptical, uncambered cross-section in potential flow (Figure 3), let $e$, $b$, and $c$ denote the maximum thickness, span, and chord length of the canopy, respectively. The added-mass ($\Delta \mathit{m}$) and added-inertia ($\Delta \mathit{I}$) components are modeled based on the equivalent cylindrical volume, as shown in Figure 4. In the canopy frame, the added-mass matrix ($\Delta m$) and added-inertia matrix ($\Delta \mathit{I}$) are given by the following:

$$\left\{\begin{array}{l}{m}_{a,11}=k_A\rho {\displaystyle \frac{\pi }{4}}{e}^{2}b\\ m_{a,22}=k_B\rho {\displaystyle \frac{\pi }{4}}{e}^{2}c\\ m_{a,33}=k_C\rho {\displaystyle \frac{\pi }{4}}{c}^{2}b\\ I_{a,11}=k_A^{*}\rho {\displaystyle \frac{\pi }{48}}{c}^2{b}^3\\ I_{a,22}=k_B^{*}\rho {\displaystyle \frac{\pi }{48}}{c}^{4}b\\ I_{a,33}=k_C^{*}\rho {\displaystyle \frac{\pi }{48}}{e}^2{b}^3\end{array}\right.$$

(7)

$$\Delta \mathit{m}=\left[\begin{array}{ccc}{m}_{a,11}& 0& 0\\ 0& m_{a,22}& 0\\ 0& 0& m_{a,33}\end{array}\right]$$

(8)

$$\Delta \mathit{I}=\left[\begin{array}{ccc}{I}_{a,11}& 0& 0\\ 0& I_{a,22}& 0\\ 0& 0& I_{a,33}\end{array}\right]$$

(9)

where $\rho$ represents air density, and $k_A$, $k_B$, $k_C$, $k_{A^{*}}$, $k_{B^{*}}$, and $k_{C^{*}}$ represent coefficients dependent on tip effects, which are related to the aspect ratio, and non-planar effects, which are related to the arc-to-span ratio.

For trajectory control purposes, this simplified model provides sufficient accuracy while maintaining computational tractability, aligning with established practices in the parafoil modeling literature, where similar simplifications have been validated through flight testing [31]. By calibrating the effective added-mass parameters as composite values that implicitly encompass viscous effects through flight test data regression, these measures ensure model fidelity within operational flight regimes (α < 20°).

2.3. Aerodynamic Forces and Moments

During stable flight, the parafoil system is subjected to gravitational force (${\mathit{F}}_g$), aerodynamic force (${\mathit{F}}_a$), and aerodynamic moment (${\mathit{M}}_a$). The aerodynamic force components along the $X_W$, $Y_W$, and $Z_W$ axes are defined as drag ($D$), side force ($Y$), and lift ($L$), respectively, expressed as follows:

$$\left\{\begin{array}{l}D=0.5\rho ‖\mathit{V}‖S{C}_D\\ Y=0.5\rho ‖\mathit{V}‖S{C}_Y\\ L=0.5\rho ‖\mathit{V}‖S{C}_L\end{array}\right.$$

(10)

$$\left\{\begin{array}{l}{C}_D=C_{D_0}+C_{D_{{\alpha }^2}}{(\alpha +\mu )}^2+C_{D_{ds}}{\delta }_s\\ C_Y=C_{Y_b}\beta \\ C_L=C_{L_0}+C_{L_{\alpha }}(\alpha +\mu )+C_{L_{ds}}{\delta }_s\end{array}\right.$$

(11)

where $\rho$ denotes the free-stream air density, and $S$ is the canopy reference area. $C_D$, $C_Y$, and $C_L$ represent the drag, side force, and lift coefficients, respectively. These coefficients are functions of the aerodynamic state and control inputs. The forces involved in the body system are expressed as follows:

$${\mathit{F}}_g={\mathit{R}}_B^I\left[\begin{array}{c}0\\ 0\\ mg\end{array}\right]=mg\left[\begin{array}{c}-\sin \theta \\ \cos \theta \sin \varphi \\ \cos \theta \cos \varphi \end{array}\right]$$

(12)

$${\mathit{F}}_a=0.5{\mathit{R}}_B^W\rho ‖{\mathit{V}}_q‖{\mathit{V}}_{q}S\left[\begin{array}{c}{C}_D\\ C_Y\\ C_L\end{array}\right]$$

(13)

$${\mathit{M}}_a=0.5\rho ‖{\mathit{V}}_q‖{\mathit{V}}_{q}S\left[\begin{array}{c}b{C}_l\\ c{C}_m\\ b{C}_n\end{array}\right]$$

(14)

where ${\mathit{V}}_q$ is the air-relative velocity vector expressed in the canopy frame, given by the following:

$${\mathit{V}}_q=\left[\begin{array}{c}{u}_q\\ v_q\\ w_q\end{array}\right]=\mathit{V}-{\mathit{R}}_B^I\left[\begin{array}{c}{u}_{w,I}\\ v_{w,I}\\ w_{w,I}\end{array}\right]$$

(15)

where $\mathit{V}={\left[u,v,w\right]}^T$ represents the speed of the parafoil relative to the ground, and $u_{w,I}$$v_{w,I}$, and $w_{w,I}$ denote the wind velocity components expressed in the inertial frame. The aerodynamic moment coefficients about the body axes are the roll moment coefficient ($C_l$), pitch moment coefficient ($C_m$), and yaw moment coefficient ($C_n$). These coefficients vary nonlinearly with multiple factors (e.g., angle of attack, sideslip angle, and control inputs) and represent a complex challenge in parafoil aerodynamic modeling, given by the following:

$$\left[\begin{array}{c}{C}_l\\ C_m\\ C_n\end{array}\right]=\left[\begin{array}{l}{C}_{l_{\beta }}\beta +0.5b(C_{l_p}p+C_{l_r}r)/V+C_{l_{da}}{\delta }_{as}\\ C_{m_0}+C_{m_{\alpha }}\left(\alpha +\mu \right)+0.5c{C}_{m_q}q/V\\ C_{n_{\beta }}\beta +0.5b(C_{n_p}p+C_{n_r}r)/V+C_{n_{da}}{\delta }_{as}\end{array}\right]$$

(16)

where $C_{l_{\beta }}$, $C_{l_p}$, $C_{l_r}$, $C_{l_{da}}$, $C_{m_0}$, $C_{m_{\alpha }}$, $C_{m_q}$, $C_{n_{\beta }}$, $C_{n_p}$, $C_{n_r}$, and $C_{n_{da}}$ are aerodynamic coefficients of the parafoil system.

The angular velocities $p$, $q$, and $r$ represent the rotational speeds of the parafoil system relative to the body frame. The control inputs are the symmetric deflection (${\delta }_s$) and asymmetric deflection (${\delta }_{as}$), defined by the left (${\delta }_l$) and right (${\delta }_r$) trailing-edge deflections as follows:

$$\left\{\begin{array}{l}{\delta }_s=0.5({\delta }_r+{\delta }_l)\\ {\delta }_{as}=0.5\left({\delta }_r-{\delta }_l\right)\end{array}\right.$$

(17)

Based on the Newton–Euler equations for rigid-body rotational dynamics, the added-mass forces (${\mathit{F}}_{am,p}$) and added-mass moments (${\mathit{M}}_{aj,p}$), expressed in the canopy frame, are given by the following:

$$\left.{\mathit{F}}_{am,p}=-(\Delta \mathit{m}{\dot{\mathit{V}}}_p+\Delta m{\tilde{\mathit{\omega }}}_p{\mathit{V}}_p\right)$$

(18)

$${\mathit{M}}_{aj,p}=-\left(\Delta \mathit{I}\mathit{\omega }+{\tilde{\mathit{\omega }}}_p\Delta \mathit{I}{\mathit{\omega }}_p+\tilde{\mathit{V}}\Delta \mathit{m}\mathit{V}\right)$$

(19)

where ${\mathit{V}}_p={[u_p,v_p,w_p]}^T$ is the velocity vector of the canopy frame origin relative to the air. ${\mathit{\omega }}_p={\left[p_p,q_p,r_p\right]}^T$ indicates the angular velocity vector of the canopy, expressed in the canopy frame; $\mathit{\omega }={\left[p,q,r\right]}^T$ indicates the angular velocity in the inertial frame. Therefore, the expressions for the added-mass force (${\mathit{F}}_{am}$) and added-mass moment (${\mathit{M}}_{ai}$) in the body frame are as follows:

$${\mathit{F}}_{am}=-{\mathit{R}}_P^B\Delta \mathit{m}{\left({\mathit{R}}_P^B\right)}^T\left({\dot{\mathit{V}}}_p-{\tilde{\mathit{l}}}_{BM}\dot{\mathit{\omega }}\right)-\mathit{\omega }{\mathit{R}}_P^B\Delta \mathit{m}{\left({\mathit{R}}_P^B\right)}^T\left(\mathit{V}-{\tilde{\mathit{l}}}_{BM}\mathit{\omega }-{\mathit{R}}_I^B{\mathit{V}}_w\right)$$

(20)

$${\mathit{M}}_{ai}=-\left({\mathit{R}}_P^B\Delta \mathit{I}{\left({\mathit{R}}_P^B\right)}^T\dot{\mathit{\omega }}+\tilde{\mathit{\omega }}{\mathit{R}}_P^B\Delta \mathit{I}{\left({\mathit{R}}_P^B\right)}^T\mathit{\omega }\right)+{\tilde{\mathit{l}}}_{BM}{\mathit{F}}_{am}$$

(21)

In the above, ${\mathit{V}}_w$ is the wind velocity vector relative to the ground, expressed in the inertial frame. To simplify calculations, only the aerodynamic drag on the payload (${\mathit{F}}_s$) is considered, given by the following:

$${\mathit{F}}_s=0.5{\mathit{R}}_P^B\rho S_s\left|{\mathit{V}}_p\right|C_{DS}{\mathit{V}}_p$$

(22)

where $C_{Ds}$ refers to the payload drag coefficient, and $S_s$ refers to the payload reference area.

2.4. Dynamics Equations

The governing equations for translational and rotational motion in the body frame are expressed as follows:

$$\left(m+{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T\right)\dot{\mathit{V}}-m\dot{\mathit{\omega }}\mathit{V}={\mathit{F}}_a+{\mathit{F}}_g+{\mathit{F}}_{am}$$

(23)

$$\left(\mathit{I}+{\mathit{R}}_P^B\Delta \mathit{I}{\left({\mathit{R}}_P^B\right)}^T-{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T{\tilde{\mathit{l}}}_{B\mathit{M}}{\mathit{l}}_{B\mathit{M}}\right)\dot{\mathit{\omega }}-\tilde{\mathit{\omega }}\mathit{I}\mathit{\omega }={\mathit{M}}_a+{\mathit{M}}_{ai}$$

(24)

The mass matrix of the parafoil system is defined as $\mathit{M}=\mathrm{diag}(mmm)$, where $m$ is the total system mass. The moment of inertia matrix is $\mathit{I}=\mathrm{diag}(I_x{I}_y{I}_z)$, where $I_x$, $I_y$, and $I_z$ represent the moments of inertia about the $X_B$, $Y_B$, and $Z_B$ axes, respectively. ${\mathit{l}}_{BM}$ represents the vector from the mass center to the apparent mass center.

By substituting Equations (18)–(22) into Equations (23) and (24) and combining them into matrix form, we obtain the following:

$$\left[\begin{array}{cc}{M}_1& M_2\\ M_3& M_4\end{array}\right]\left[\begin{array}{c}{\mathit{A}}_1\\ {\mathit{A}}_2\end{array}\right]=\left[\begin{array}{c}{\mathit{F}}_1\\ {\mathit{F}}_2\end{array}\right]$$

(25)

where

$$M_1=m+{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T$$

(26)

$$M_2=-{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T{\tilde{\mathit{l}}}_{BM}$$

(27)

$$M_3={\mathit{l}}_{BM}^{\ast }{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T$$

(28)

$$M_4=\mathit{I}+{\mathit{R}}_P^B\Delta \mathit{I}{\left({\mathit{R}}_P^B\right)}^T-{\tilde{\mathit{l}}}_{BM}{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T{\tilde{\mathit{l}}}_{BM}$$

(29)

$${\mathit{A}}_1={\left[\begin{array}{ccc}\dot{u}& \dot{v}& \dot{w}\end{array}\right]}^T$$

(30)

$${\mathit{A}}_2={\left[\begin{array}{ccc}\dot{p}& \dot{q}& \dot{r}\end{array}\right]}^T$$

(31)

$${\mathit{F}}_1={\mathit{F}}_a+{\mathit{F}}_g-\tilde{\mathit{\omega }}\left\{\left(m+{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T\right)\mathit{V}\right.\left.-{\mathit{R}}_P^B\Delta m{\left({\mathit{R}}_P^B\right)}^T\left[{\tilde{\mathit{l}}}_{BM}\mathit{\omega }-{\mathit{R}}_P^B{\mathit{V}}_w\right]\right\}$$

(32)

$${\mathit{F}}_2={\mathit{M}}_a-\left[\tilde{\mathit{\omega }}\left(\mathit{I}+{\mathit{R}}_P^B\Delta \mathit{I}{\left({\mathit{R}}_P^B\right)}^T\right)-{\tilde{\mathit{l}}}_{BM}{\mathit{R}}_P^B\Delta \mathit{m}{\left({\mathit{R}}_P^B\right)}^T{\mathit{l}}_{BM}\right]\mathit{\omega }-{\tilde{\mathit{l}}}_{BM}\mathit{\omega }{\mathit{R}}_P^B\Delta \mathit{m}{\left({\mathit{R}}_P^B\right)}^T\left(\mathit{V}-{\mathit{R}}_P^B{\mathit{V}}_w\right)$$

(33)

While the proposed model provides a good balance between accuracy and computational efficiency, several limitations should be acknowledged: the rigid body assumption neglects structural flexibility effects that may be important under certain flight conditions, and the model’s use of quasi-steady aerodynamic coefficients may not capture unsteady aerodynamic effects during rapid maneuvers.

This unified formulation provides a foundation for controller design that balances fidelity with the computational efficiency required for stochastic predictive control. While this study focuses on developing and validating the control framework within this established modeling paradigm, future work will explore the integration of higher-fidelity dynamics.

3. Stochastic Model Predictive Control

In this section, the application of the SMPC method based on Markov multi-scenario optimization in parafoil-system trajectory tracking is systematically expounded. The incorporation of wind field uncertainty modeling is essential due to the extreme sensitivity of the parafoil to wind disturbances and its limited control authority when wind speeds approach the airspeed. Robust guidance strategies must explicitly address these disturbances to maintain precision under underactuated constraints. Firstly, the high-precision six-degree-of-freedom dynamic model is transformed into the basic framework of controller design by discretizing the state-space model. Secondly, to address the drawback that the traditional independent and identically distributed hypothesis fails to describe the spatiotemporal correlation disturbance, the Markov process is innovatively introduced to construct a dynamic wind-field generation mechanism. On this basis, an SMPC controller is designed, which includes prediction time-domain division, multi-scenario cost function reconstruction, probability constraint transformation, and rolling time-domain covariance update. This design balances tracking accuracy, energy efficiency, and robustness through nonlinear programming optimization. Furthermore, the piecewise trajectory planning strategy and hierarchical optimization architecture are proposed, and the combination of physical constraint embedding and real-time optimization mechanism realizes the cooperative control of inner and outer loops and the joint suppression of uncertainty.

3.1. State-Space Formulation

To establish a mathematical foundation for controller design, this section formulates the parafoil system dynamics as a discrete-time state-space model with the discretization time step $T_s$. The continuous-time model is discretized using forward Euler integration with 4th-order Runge–Kutta method, incorporating approximations of linearization around nominal trajectory points, constant wind assumption over the prediction horizon, and neglect of higher-order terms in Taylor series expansion.

The discrete-time state-space model takes the following form:

$$\mathit{x}(k+1)=\mathit{A}\left(t\right)\mathit{x}(k)+\mathit{B}\left(t\right)\mathit{u}(k)+\mathit{D}\left(t\right)\mathit{w}(k)$$

(34)

$$\mathit{y}(k+1)=\mathit{C}\left(t\right)\mathit{x}(k+1)+\mathit{v}(k+1)$$

(35)

where $x$ represents the state vector (e.g., position, velocity, and Euler angles); $u$ refers to the control vector (brake deflections); $y$ denotes the output vector (measured states); $w$ is the state disturbance vector (e.g., wind gusts); $v$ represents measurement noise vector; and $\mathit{A},\mathit{B},\mathit{C},\mathit{D}$ denote the state, input, output, and disturbance matrices, derived from the dynamics Equations (23) and (24). By integrating the derived parafoil dynamics, the specific expressions for these matrices are given by the following:

$$\mathit{A}=\mathit{I}+T_s\left[\begin{array}{cccc}{0}_{3\times 3}& 0_{3\times 3}& R_B^I\tilde{\mathit{\omega }}& 0_{3\times 3}\\ 0_{3\times 3}& 0_{3\times 3}& 0_{3\times 3}& {\mathit{E}}_W\\ {\mathit{M}}^{-1}{\mathit{F}}_V& {\mathit{M}}^{-1}{\mathit{F}}_E& {\mathit{M}}^{-1}{\mathit{F}}_V& {\mathit{M}}^{-1}{\mathit{F}}_W\\ {\mathit{M}}^{-1}{\mathit{M}}_V& {\mathit{M}}^{-1}{\mathit{M}}_E& {\mathit{M}}^{-1}{\mathit{M}}_V& {\mathit{M}}^{-1}{\mathit{M}}_W\end{array}\right]$$

(36)

$$\mathit{B}=T_s\left[\begin{array}{c}{0}_{3\times 2}\\ 0_{3\times 2}\\ {\mathit{M}}^{-1}{\mathit{F}}_{\delta }\\ {\mathit{M}}^{-1}{\mathit{M}}_{\delta }\end{array}\right]$$

(37)

$$\mathit{C}=\left[\begin{array}{c}{\mathit{I}}_{12\times 12}\\ \mathit{K}\end{array}\right]$$

(38)

$$\mathit{G}=\left[\begin{array}{c}{0}_{3\times 3}\\ 0_{3\times 3}\\ -T_s{\mathit{R}}_B^I\\ 0_{3\times 3}\end{array}\right]$$

(39)

The submatrices are defined as follows:

$${\mathit{E}}_W=\left[\begin{array}{ccc}1& \sin \varphi \tan \theta & \cos \varphi \tan \theta \\ 0& \cos \varphi & -\sin \varphi \\ 0& \sin \varphi /\cos \theta & \cos \varphi /\cos \theta \end{array}\right]$$

(40)

$$\mathit{M}={\mathit{A}}_U+{\mathit{A}}_R\times {\mathit{A}}_L$$

(41)

$${\mathit{A}}_U=\left[\begin{array}{cc}m{\mathit{I}}_{3\times 3}+{\mathit{I}}_{am}& {\mathit{I}}_{am}{\tilde{\mathit{l}}}_{BM}\\ 0_{3\times 3}& \mathit{I}+{\mathit{I}}_{ai}\end{array}\right]$$

(42)

$${\mathit{A}}_R=\left[\begin{array}{cc}{\mathit{I}}_{3\times 3}& 0_{3\times 3}\\ 0_{3\times 3}& {\tilde{\mathit{l}}}_{BM}\end{array}\right]$$

(43)

$${\mathit{A}}_L=\left[\begin{array}{cc}{0}_{3\times 3}& 0_{3\times 3}\\ {\mathit{I}}_{am}& {\mathit{I}}_{am}{\tilde{\mathit{l}}}_{BM}\end{array}\right]$$

(44)

$${\mathit{F}}_V=\partial \left({\mathit{F}}_g+{\mathit{F}}_a\right)/\partial \mathit{V}=0.5\rho ‖\mathit{V}‖S\partial \left({\mathit{R}}_B^I\right)/\partial {\mathit{V}}_a\left[\begin{array}{c}-C_D\\ C_Y\\ -C_L\end{array}\right]+0.5\rho S\partial \mathit{V}/\partial {\mathit{V}}_a{\mathit{R}}_B^I\left[\begin{array}{c}-C_D\\ C_Y\\ -C_L\end{array}\right]$$

(45)

$${\mathit{F}}_E=\partial {\mathit{F}}_g/\partial \mathit{E}+\partial {\mathit{F}}_a/\partial \mathit{E}=mg\left[\begin{array}{ccc}0& -\cos \theta & 0\\ \cos \theta \cos \varphi & -\sin \theta \sin \varphi & \cos \theta \cos \varphi \\ -\cos \theta \sin \varphi & -\sin \theta \cos \varphi & -\cos \theta \sin \varphi \end{array}\right]+0.5\rho ‖\mathit{V}‖S\partial \left({\mathit{R}}_B^I\right)/\partial \mathit{E}\left[\begin{array}{c}-C_D\\ C_Y\\ -C_L\end{array}\right]$$

(46)

$${\mathit{F}}_W=0.5\rho ‖\mathit{V}‖S{\mathit{R}}_B^W\partial {\left[\begin{array}{ccc}-C_D& C_Y& -C_L\end{array}\right]}^T/\partial \mathit{\omega }$$

(47)

$${\mathit{M}}_V=\partial {\mathit{M}}_a/\partial \mathit{V}=0.5\rho ‖\mathit{V}‖S\left[\begin{array}{c}b\partial C_l/\partial V_a\\ c\partial C_m/\partial V_a\\ b\partial C_n/\partial V_a\end{array}\right]$$

(48)

$${\mathit{M}}_E=-\partial {\mathit{M}}_a/\partial \mathit{E}$$

(49)

$${\mathit{M}}_W=0.5\rho ‖\mathit{V}‖S\left[\begin{array}{ccc}0.5b^2{C}_{l_p}/\left|{\mathit{V}}_a\right|& 0& 0.5b{C}_{l_r}/\left|{\mathit{V}}_a\right|\\ 0& 0.5c{C}_{mq}c/\left|{\mathit{V}}_a\right|& 0\\ 0.5b^2{C}_{n_p}/\left|{\mathit{V}}_a\right|& 0& 0.5C_{n_r}b/\left|{\mathit{V}}_a\right|\end{array}\right]$$

(50)

$${\mathit{F}}_{\delta }=\left[\begin{array}{cc}\partial {\mathit{F}}_a/\partial {\delta }_s& \partial {\mathit{F}}_a/\partial {\delta }_a\end{array}\right]=0.5\rho ‖\mathit{V}‖S{\mathit{R}}_B^I\left[\begin{array}{cc}-C_{D_{{\delta }_s}}& 0\\ 0& 0\\ -C_{L_{{\delta }_s}}& 0\end{array}\right]$$

(51)

$${\mathit{M}}_{\delta }=\left[\begin{array}{cc}\partial {\mathit{M}}_a/\partial {\delta }_s& \partial {\mathit{M}}_a/\partial {\delta }_a\end{array}\right]=0.5\rho ‖\mathit{V}‖S\left[\begin{array}{cc}0& b{C}_{l_{{\delta }_a}}\\ 0& 0\\ 0& b{C}_{n_{{\delta }_a}}\end{array}\right]$$

(52)

$${\mathit{V}}_a=\mathit{V}-{\mathit{R}}_B^I{\mathit{V}}_W$$

(53)

3.2. Multi-Scenario Optimization Based on the Markov Process

To address the wind disturbances, this section proposes a Markov-based multi-scenario generation framework. By embedding state transition probabilities and spatial continuity constraints, dynamically evolving wind fields with temporal persistence and spatial smoothness are synthesized, overcoming the limitations of traditional independent and identically distributed assumptions.

Definition 1. 

Assuming each parameter,  $t\in T$$S(t,\mathit{\omega })$, is a random variable, the family of random variables,  $S_T=\left\{S(t,\mathit{\omega })\right\}$, is called a stochastic process.

Definition 2. 

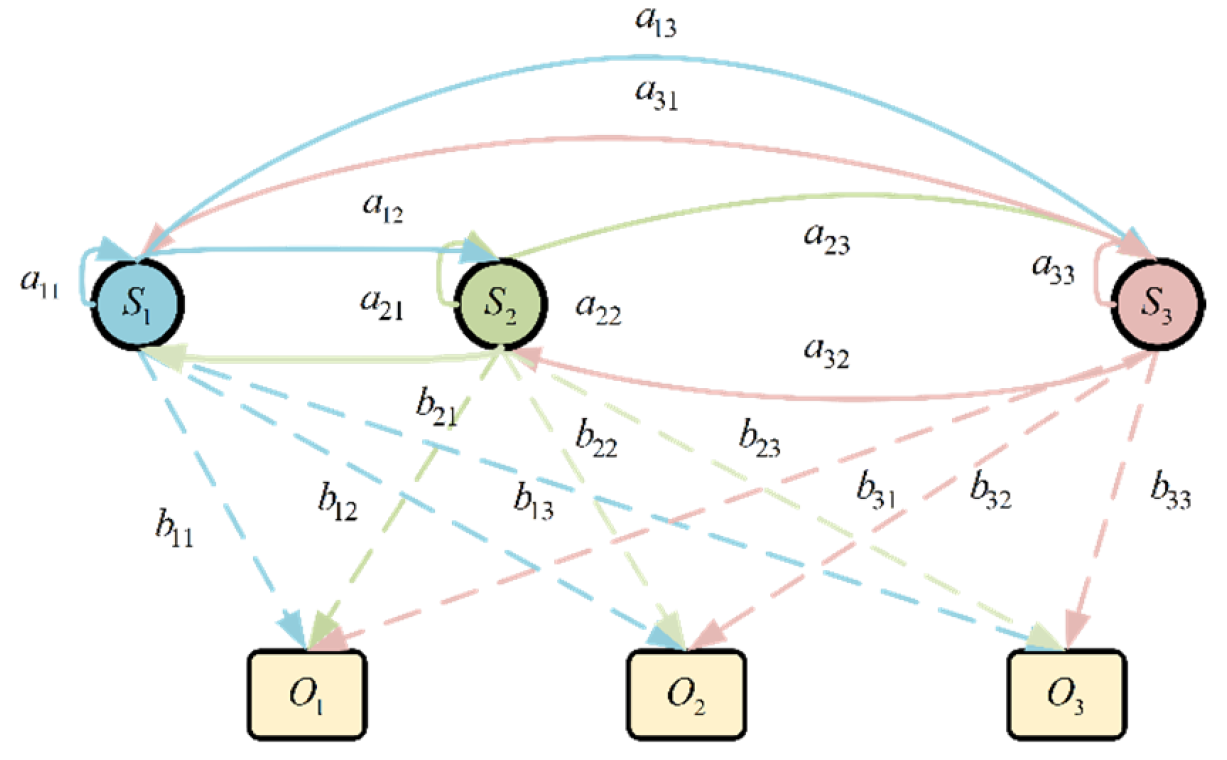
A stochastic process,  $\left\{S_t,t\in T\right\}$, is called a Markov process if for any time sequence,  $t_1<t_2\dots <t_{N_s}<t$. and any state,  $s_i$ ($1\le i\le N_s$), the following conditional probability holds:

$$P\left\{\left.S_t=s_i\right|S_{t_1}=s_1,S_{t_2}=s_2,\dots ,S_{t{N}_s}=s_{N_s}\right\}=P\left(\left.S_t=s_i\right|S_{t_{Ns}}=s_{N_s}\right)$$

(54)

The stochastic process is called the Markov process, as shown in Figure 5. $A=\left\{a_{ij}\right\}$ denotes the state-transition probability matrix, where $a_{ij}=P\left(\left.S_{t+1}=j\right|S_t=i\right)$ and ($1\le i$, $j\le N_s$) represents the probability of transition to state $S_{t+1}=j$ at time $t+1$, given state $s_t$ at time $t$, and $N_s$ is the number of states. The emission probability matrix $B=\left\{b_{ij}\right\}$ maps hidden states to observable outputs. Specifically, each element $b_{ik}=P\left(\left.O_t=k\right|S_t=i\right)$ ($1\le i\le N_s$  $1\le k\le N_o$) refers to the probability of observable output $O_t=k$, given state $i$, and $N_O$ represents the number of observable outputs. The initial state distribution $\prod$ is given by the following:

$$\prod =\left(P\left(S_0=1\right),P\left(S_0=2\right),\cdots ,P\left(S_0=N_s\right)\right)$$

(55)

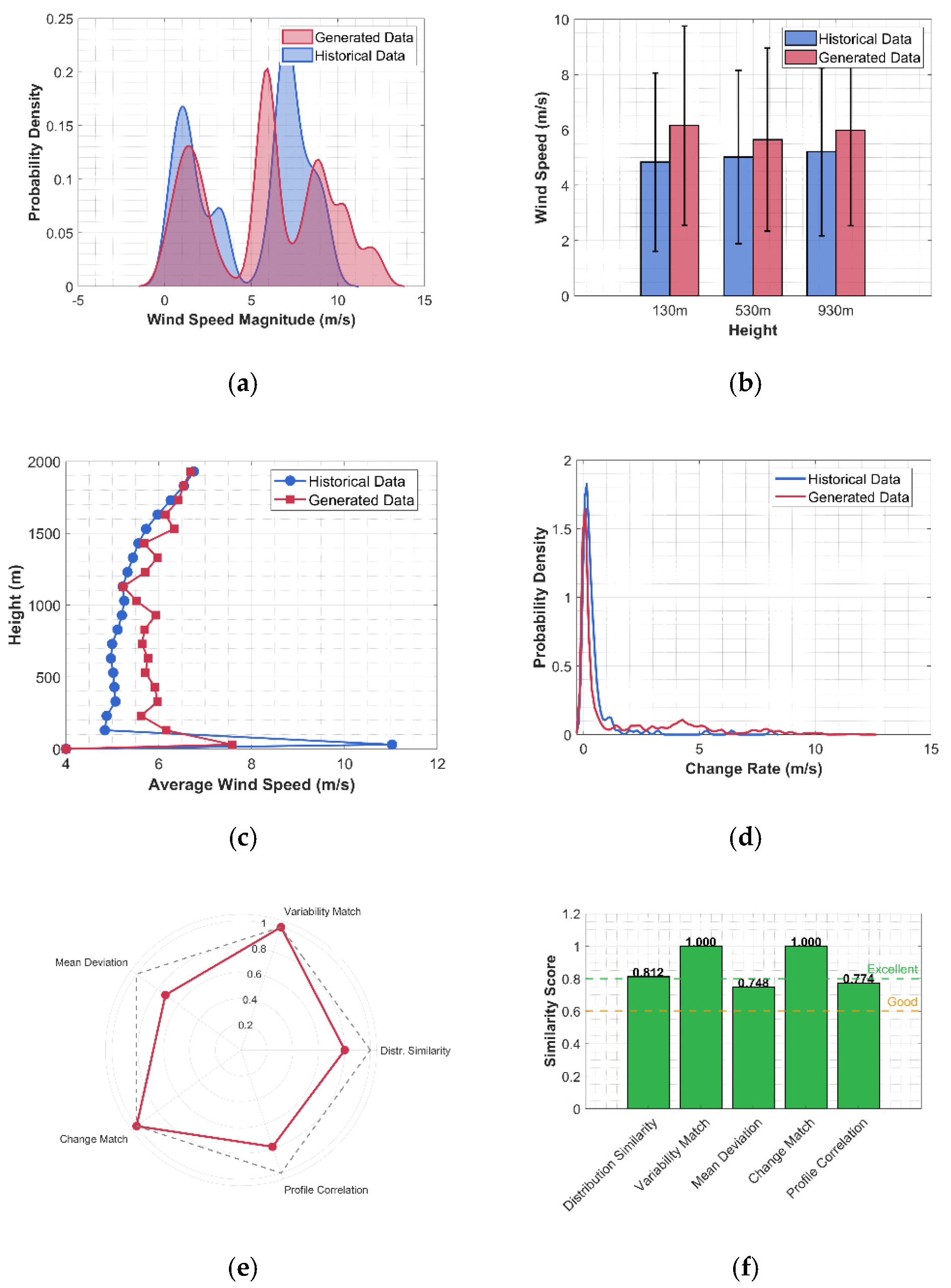
To capture the coupled spatial and temporal dependencies in wind disturbance correlations, a data-driven Markov process generates realistic wind fields by discretizing horizontal wind components into states based on historical statistics, estimating state transition matrices through temporal transition counting between adjacent time steps, and generating scenarios via Markov state sampling with Gaussian spatial filtering. The vertical wind component is maintained at zero due to its negligible impact, ensuring computational efficiency while preserving spatiotemporal wind characteristics.

3.3. Design of SMPC Framework

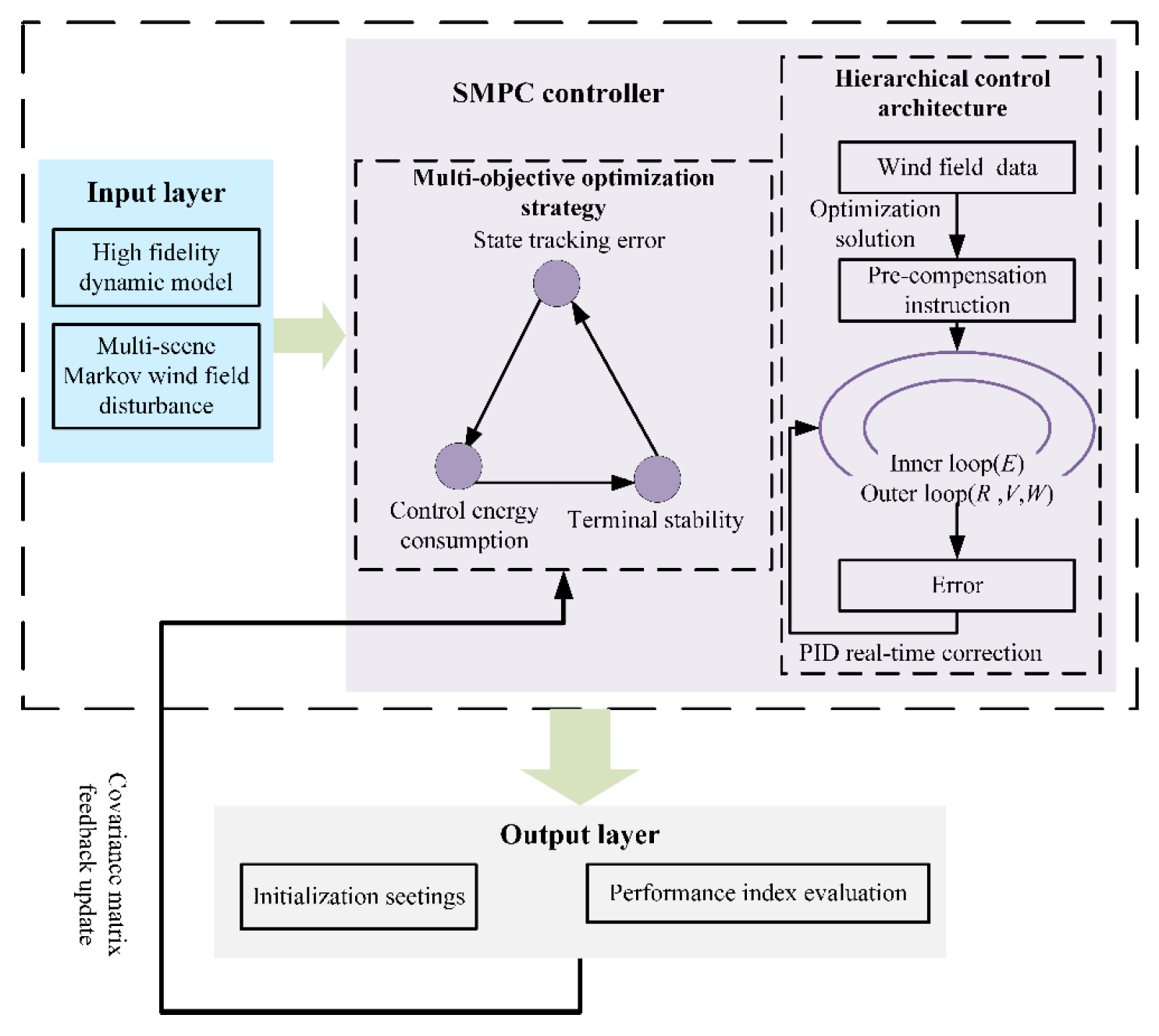
This section describes the SMPC framework, integrating Markov-driven multi-scenario optimization with probabilistic constraint handling. As shown in Figure 6, the primary components include hierarchical control architecture, multi-objective optimization strategy, and rolling covariance updates, balancing robustness, tracking precision, and computational efficiency.

The transformation of hard constraints into probabilistic chance constraints is a key feature that directly addresses the conservatism of traditional robust control. It allows for controlled, infrequent constraint violations, which is a more practical approach for systems operating in uncertain environments and prevents the excessive performance degradation associated with worst-case design.

3.3.1. Design of SMPC Controller

The SMPC controller is designed through a structured framework. This framework encompasses defining the prediction horizon, formulating the multi-scenario cost function, and reconstructing probabilistic constraints. It is supported by rolling time-domain covariance updates to effectively address the nonlinear dynamics and wind disturbances inherent in the parafoil system, while simultaneously balancing tracking accuracy, energy efficiency, and robustness.

• Prediction Horizon

The prediction horizon length critically defines the optimization scope and computational feasibility of the controller.

2.

Scenario Generation

Dynamic wind disturbance scenarios are synthesized through Markov state transitions and Gaussian spatial filtering. This approach overcomes the limitations of independent and identically distributed assumptions by embedding temporal persistence and spatial smoothness into the generated wind fields, significantly improving fidelity.

3.

Cost Function

The multi-scenario cost function ($J$) aims to balance the state tracking error, control energy consumption, and terminal stability. The cost function incorporates the following three weighted terms: state tracking term (${\mathit{Q}}_x$), control effort term (${\mathit{R}}_u$), and terminal state term (${\mathit{P}}_N$). The state tracking term minimizes the deviation between the system state and the reference trajectory to achieve accurate tracking. The control effort term penalizes control energy to reduce actuator consumption, mitigate control signal chattering, and enhance energy efficiency. The terminal state term enforces terminal constraints to promote system stability.

4.

Constraints

The constraints encompass the following four categories: state constraints limiting parameter boundaries (e.g., position, velocity, and attitude), input constraints preventing actuator saturation, control rate constraints ensuring smooth control signals, and chance constraints balancing robustness and efficiency through a probabilistic safety mechanism.

5.

Formulation of the nonlinear programming model

To address the nonlinear dynamics of the parafoil system and stochastic disturbances, we formulate the nonlinear programming model as follows:

$$\begin{array}{l}\min J={\rm E}[{\displaystyle \sum _{i=1}^N(}\mathit{x}{(k+i)}^T{\mathit{Q}}_x\mathit{x}(k+i)+\mathit{u}{(k+i)}^T{\mathit{R}}_u\mathit{u}(k+i)+\mathit{x}{(k+N)}^T{\mathit{P}}_N\mathit{x}(k+N))]\\ s.t.x_{k+1}=f(x_k,u_k,w_k)\\ u_{\min }\le u_k\le u_{\max }\\ {\rm P}(g(x_k,u_k,w_k)\le 0)\ge 1-\epsilon \end{array}$$

(56)

In the nonlinear programming model, the state transition is governed by the nonlinear function ($f$), which represents the discretized dynamics derived from the six-degree-of-freedom dynamics equations (Equations (23) and (24)) through Euler integration. This mapping captures the full nonlinear coupling between aerodynamic forces, coordinate transformations, and added-mass effects while maintaining numerical tractability for real-time optimization. The control input vector ($u_k$) at time step k comprises symmetric and asymmetric deflection commands for trailing-edge controls of the parafoil. The disturbance input ($w_k$) denotes the wind velocity components in the inertial frame, modeled as Markov processes with state transitions governed by empirically estimated probability matrices. The probabilistic constraint ($P(\cdot )$) enforces that the system states and controls satisfy safety conditions with a prescribed probability $1-\epsilon$, where $\epsilon \in \left(0,0.1\right]$.

3.3.2. Trajectory Planning Stage

A segmented trajectory planning strategy is implemented to address the full-cycle demands of complex airdrop missions. This strategy divides the flight into distinct phases, dynamically allocates control strategies for each phase, and embeds physical constraints to ensure safety and adaptability.

• Segmented trajectory design

This paper proposes a segmented trajectory planning strategy for full-cycle airdrop control. The strategy divides the flight process into the following five stages: direct flight, U-turn, transition, optimization, and modified direct flight. The time step and control strategy are dynamically allocated according to the flight target in each stage. The stability of the system’s foundation is verified by zero control input in the direct flight section. The maneuver performance is tested by applying fixed-rudder deflection in large turning sections. In the optimization section, an SMPC controller is used to optimize the control instructions in real time based on multi-scenario disturbance prediction. The transition and modified direct flight sections are switched using a smooth strategy to ensure trajectory continuity. This strategy enhances control efficiency and adaptability, satisfying the requirements of different flight modes.

2.

Physical constraint embedding

A multiple-physical-constraint mechanism is embedded in flight-path planning to ensure safety and system reliability. The actuator deflection range is constrained by complex amplitude limiting to suppress the risk of rudder saturation. The angular velocity monitoring mechanism detects the roll, pitch, and yaw angular velocity in real time to prevent dynamic instability. The hierarchical constraint design enhances control authority within feasible limits, and the physical boundary conditions of the parafoil system are strictly followed to ensure flight safety under complex disturbances.

3.3.3. Tracking Control Stage

The tracking control framework combines multi-scenario disturbance prediction, rolling hierarchical optimization, and a real-time feedback mechanism to enhance adaptability under dynamic wind fields while maintaining rapid response and stability.

• Multi-scenario prediction model

To address the uncertainty of dynamic wind-field disturbance, the control framework constructs a 12-dimensional state space containing the whole state of the system (position, attitude, speed, and angular velocity). Based on the current wind-field state, multiple sets of disturbance scenarios are generated, and each set of scenarios constructs a wind-field evolution sequence in the prediction time domain by superimposing random disturbances, thus enhancing the adaptability of the controller to multi-modal disturbances.

2.

Rolling optimization framework

The hierarchical optimization objective function is designed, and the weight coefficients of the state-tracking term ($Q_x$) and energy consumption suppression term ($R_u$) are dynamically adjusted to balance the control accuracy for inner and outer loops and the energy efficiency. At the same time, the traditional hard constraint is reformulated as probabilistic constraints, allowing limited constraint violation within a specified probability. The covariance matrix is updated online using the statistical characteristics of the scenario set to improve robustness.

3.

Real-time optimization strategy

Hierarchical computing architecture is adopted to reduce the computational load, and the efficient update of control instructions is realized by combining periodic global optimization with local fine-tuning. The feedforward mechanism predicts the influence of the wind field based on the future trajectory and generates pre-compensation instructions. The feedback mechanism combined with PID can correct the position and attitude deviation in real time, ensuring rapid system response and stability under disturbances.

4. Simulation Experiment and Result Analysis

To rigorously evaluate the proposed SMPC framework, a high-fidelity trajectory-tracking scenario is constructed. The parafoil system is initialized at (0, 0, 2000), with a target landing position of (380, 150, 0), simulating a realistic airdrop mission. The parameters of the parafoil system in the simulation experiment are shown in

Table 1. Aerodynamic and structural parameters of the parafoil system [31].

Parameters	Value
System mass ($m$)	2.4 kg
Canopy span ($b$), chord ($c$), thickness ($e$)	1.35 m, 0.75 m, 0.075 m
Canopy reference area ($S$)	1 m2
Rigging angle ($\mu$)	12 deg
Steady-state aerodynamic velocity ($V_a=‖\mathit{V}‖$)	7.3 m/s
Inertia matrix	$\mathit{I}=\left[\begin{array}{ccc}0.42& 0& 0.03\\ 0& 0.40& 0\\ 0.03& 0& 0.053\end{array}\right]\mathrm{kg}.{\mathrm{m}}^2$
Apparent mass matrix	${\mathit{I}}_{a.m.}=\mathrm{diag}\left(\left[0.012,0.032,0.42\right]\right)\mathrm{kg}$
Apparent inertia matrix	${\mathit{I}}_{a.i.}=\mathrm{diag}\left(\left[0.054,0.14,0.0024\right]\right)\mathrm{kg}.{\mathrm{m}}^2$
The vector from the mass center to the apparent mass center	${\mathit{l}}_{BM}={\left[0.046,0,-1.11\right]}^T\mathrm{m}$
Aerodynamic coefficients	$\begin{array}{l}\begin{array}{ccc}{C}_{D_0}=0.25& C_{D_{{\alpha }^2}}=0.12& C_{Y_{\beta }}=-0.23\\ C_{L_0}=0.091& C_{L_{\alpha }}=0.90& C_{m_0}=0.35\\ C_{m_{\alpha }}=-0.72& C_{m_q}=-1.49& C_{l_{\beta }}=-0.036\\ C_{l_p}=-0.84& C_{l_r}=-0.082& C_{l_{da}}=-0.0035\\ C_{n_{\beta }}=-0.0015& C_{n_p}=-0.082& C_{n_r}=-0.27\\ C_{n_{da}}=0.0115& C_{D_{ds}}=0.3& C_{L_{ds}}=0.21\end{array}\\ C_{m_{ds}}=-0.1\end{array}$

.

The actuation system employs servo motors to drive suspension lines for symmetric and asymmetric trailing-edge deflection control, utilizing transmission mechanism where pulling a single line induces deflection on the corresponding canopy side; turn control is effected through asymmetric deflection of steering lines while angle-of-attack adjustment and flare-out maneuvers are accomplished via symmetric deflection, with deflection commands normalized in the controller and travel limits corresponding to practical engineering designs. Controller parameters were rigorously selected through physical dynamic matching: the sampling time $\Delta t=0.2 \mathrm{s}$ precisely aligns with the parafoil roll response time (1.8 ± 0.4 s) and the prediction horizon $Np=30$ covers triple the dominant time constant, with flight tests verifying this parameter configuration achieves 94% tracking success while maintaining actuator travel constraints.

4.1. Simulation Environment and Wind-Field Modeling

This research constructs thirty spatiotemporally correlated wind fields to verify SMPC robustness under complex disturbances, with wind scenarios dynamically generated via Markov chains trained on historical measurements. The continuous wind field is discretized using quantile-based state boundaries defined by percentiles [0, 1, 2, 5, 10, 25, 50, 75, 90, 95, 98, 99, 100], where for each altitude layer the horizontal u/v components are discretized into 9 states each (yielding 81 combined states), while the vertical component remains fixed at zero due to negligible impact. Transition matrices are learned from historical data with Laplace smoothing (α = 1), and ten scenarios per control step are generated over a 20-step prediction horizon (3 min duration matching radar sampling) through Markov-based random sampling with state-dependent Gaussian noise. Statistical fidelity validation, as presented in Figure 7, shows the distribution similarity (0.806), variability match (1.000), mean deviation (0.742), change-rate consistency (1.000), and profile correlation (0.791), collectively confirming accurate preservation of atmospheric disturbance characteristics.

Figure 7. Multi-scenario wind-field modeling: (a) wind speed distribution; (b) statistical comparison by height; (c) wind speed height profile; (d) change rate distribution; (e) quality assessment radar; (f) similarity score summary.

Figure 7. Multi-scenario wind-field modeling: (a) wind speed distribution; (b) statistical comparison by height; (c) wind speed height profile; (d) change rate distribution; (e) quality assessment radar; (f) similarity score summary.

4.2. Performance Comparison and Result Analysis of Trajectory Tracking

To rigorously validate performance claims, SMPC and MPC controllers are evaluated using quantitative metrics, including position tracking ($P_{rmse}$), attitude tracking ($A_{rmse}$), control effort ($\Delta u$), comprehensive index ($I_{total}$), and success rate, which are given by the following:

$$\begin{array}{l}{P}_{rmse}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _N^{k=1}}\parallel \mathit{p}(k)-{\mathit{p}}_{ref}(k){\parallel }^2}\\ A_{rmse}=\sqrt{{\displaystyle \frac{1}{N}}{\displaystyle \sum _N^{k=1}}\parallel \mathit{\theta }(k)-{\mathit{\theta }}_{ref}(k){\parallel }^2}\\ \Delta u={\displaystyle \frac{1}{N}}{\displaystyle \sum _N^{k=1}}\parallel \mathit{u}(k)-\mathit{u}(k-1)\parallel \\ I_{total}=w_1\cdot P_{rmse}+w_2\cdot A_{rmse}+w_3\cdot \Delta u\end{array}$$

(57)

where $N$ refers to total time steps; $\mathit{p}\left(k\right)$ refers to actual position; ${\mathit{p}}_{ref}\left(k\right)$ refers to reference position; $\mathit{\theta }\left(k\right)={\left[\varphi ,\theta ,\psi \right]}^T$ refers to actual Euler angles; ${\mathit{\theta }}_{ref}(k)={[{\varphi }_{ref},{\theta }_{ref},{\psi }_{ref}]}^T$ refers to reference angles; $\mathit{u}(k)={[{\delta }_s,{\delta }_a]}^T$ refers to control vector at step $k$.

Success rate is defined as the percentage of landings satisfying the following:

$$\parallel {\mathit{p}}_{final}-{\mathit{p}}_{target}\parallel <100\mathrm{m}\&\&\parallel {\mathit{v}}_{final}\parallel <5\mathrm{m}/\mathrm{s}$$

(58)

where ${\mathit{p}}_{final}$ refers to actual landing position; ${\mathit{p}}_{t\arg et}$ refers to target landing position; and ${\mathit{v}}_{final}$ refers to landing speed.

• Comparison of tracking accuracy

Figure 8 compares the trajectory-tracking performance and energy consumption of SMPC and deterministic MPC. The simulation results show that SMPC is superior to traditional MPC in position tracking and energy efficiency by dynamically modifying control instructions through Markov multi-scenario optimization.

2.

Robustness verification

Based on 200 Monte Carlo simulation results, this paper compares and analyzes the control characteristics of SMPC and MPC from the following two dimensions: local state response and global comprehensive performance. Statistical significance is confirmed through independent t-tests ($p<0.01$) on 200 Monte Carlo runs (

Table 2. Performance metrics comparison between SMPC and MPC.

Metric	SMPC	MPC	Improvement	p-Value
$P_{rmse}$ (m)	30 $\pm$ 7	34 $\pm$ 10	12.0%	0.001
$A_{rmse}$ (rad)	−0.10 $\pm$ 0.19	−0.14 $\pm$ 0.02	28.5%	0.003
Success Rate	94%	90%	4%	0.140

). For small parafoils operating in multi-wind-field environments, the SMPC approach demonstrated statistically significant improvements in continuous control performance compared to conventional MPC. Specifically, SMPC reduced landing position error by 12.0% and improved attitude control precision by 28.5%. However, the observed 4% success rate increase was not statistically significant, suggesting trajectory control enhancements under complex wind conditions require further investigation.

Further, evaluating the comprehensive performance across all 200 simulations, the following five primary indicators are visualized using a radar chart: maximum position error, average position error, change rate of control quantity, violation probability of angular velocity constraint, and tracking success rate (Figure 9a). All indicators are normalized (0 is the worst, and 1 is the best), with the area enclosed by the radar plot serving as a metric for overall performance. The results show that the radar chart area of SMPC is 1.80, significantly higher than that of MPC (1.55), highlighting its comprehensive advantages. Specifically, by accurately predicting disturbances through Markov-based multi-scenario optimization and integrating probabilistic constraint reconstruction with rolling time-domain covariance updates, SMPC achieves cooperative optimization of tracking accuracy, disturbance rejection stability, and energy efficiency. However, MPC is challenging to adapt to the dynamic evolution of the wind field due to its dependence on deterministic assumptions, resulting in conservative control and limited performance. Notably, both controllers achieve high mission-success rates under complex disturbances, which is 94% for SMPC and 90% for MPC, demonstrating the effectiveness of the probabilistic constraint mechanism, as shown in Figure 9b. Nevertheless, significant advantages of SMPC across the comprehensive performance indicators make it more suitable for high-precision airdrop missions.

The superior performance of the proposed SMPC framework over deterministic MPC underscores the importance of explicitly addressing stochastic disturbances in control design. Compared to min-max robust control approaches, which tend to be conservative due to their focus on worst-case scenarios, the SMPC method leverages the probabilistic characteristics of wind disturbances through Markov process modeling. This enables a more balanced trade-off between control performance and robustness. While the proposed approach demonstrates effective performance within the considered disturbance scenarios, it is recognized that extreme adversarial conditions beyond the modeled cases may require additional robustness considerations. This insight suggests the potential value of exploring hybrid robust-stochastic frameworks in future research.

5. Conclusions

This paper proposes an SMPC framework based on Markov-based multi-scenario optimization to address the trajectory-tracking challenges of parafoil systems under uncertainties. The methodology integrates high-fidelity modeling, dynamic wind-field disturbance characterization, and probabilistic constraint optimization, achieving an effective balance between control accuracy, robustness, and computational efficiency. A high-fidelity dynamic model overcomes the limitations of traditional point-mass models in capturing aerodynamic coupling effects, providing a solid foundation for precise state prediction and controller design. To realistically model the complex nature of wind uncertainty, the framework dynamically generates correlated wind disturbance scenarios by leveraging the state transition mechanism inherent in Markov processes, effectively addressing the limitations of standard independent and identically distributed assumptions. Furthermore, the framework incorporates a probabilistic constraint reconstruction strategy alongside a rolling time-domain covariance update mechanism. This combination robustly mitigates uncertainties and enables the crucial cooperative optimization of inner-loop attitude stabilization and outer-loop trajectory tracking, significantly enhancing overall system stability and adaptability. Comprehensive simulation results demonstrate the superior performance of the proposed SMPC framework compared to deterministic MPC in complex wind environments. SMPC shows significant improvements across key robustness and performance metrics, effectively balancing high tracking accuracy, energy efficiency, and disturbance rejection through its probabilistic constraint handling and adaptive covariance updates. Critically, SMPC maintains a high tracking success rate of 94%, validating the fundamental stability of the control strategy.

While the proposed framework has been validated in simulation environments, future work will focus on extending model fidelity and progressing to engineering validation. This involves developing higher-fidelity dynamic models and advancing through hardware-in-the-loop testing to full-scale flight experiments in realistic operating environments.