Nose Landing Gear Shimmy Analysis with Variable System Stiffness Under Time-Varying Load
Abstract
1. Introduction
2. NLG Shimmy Model
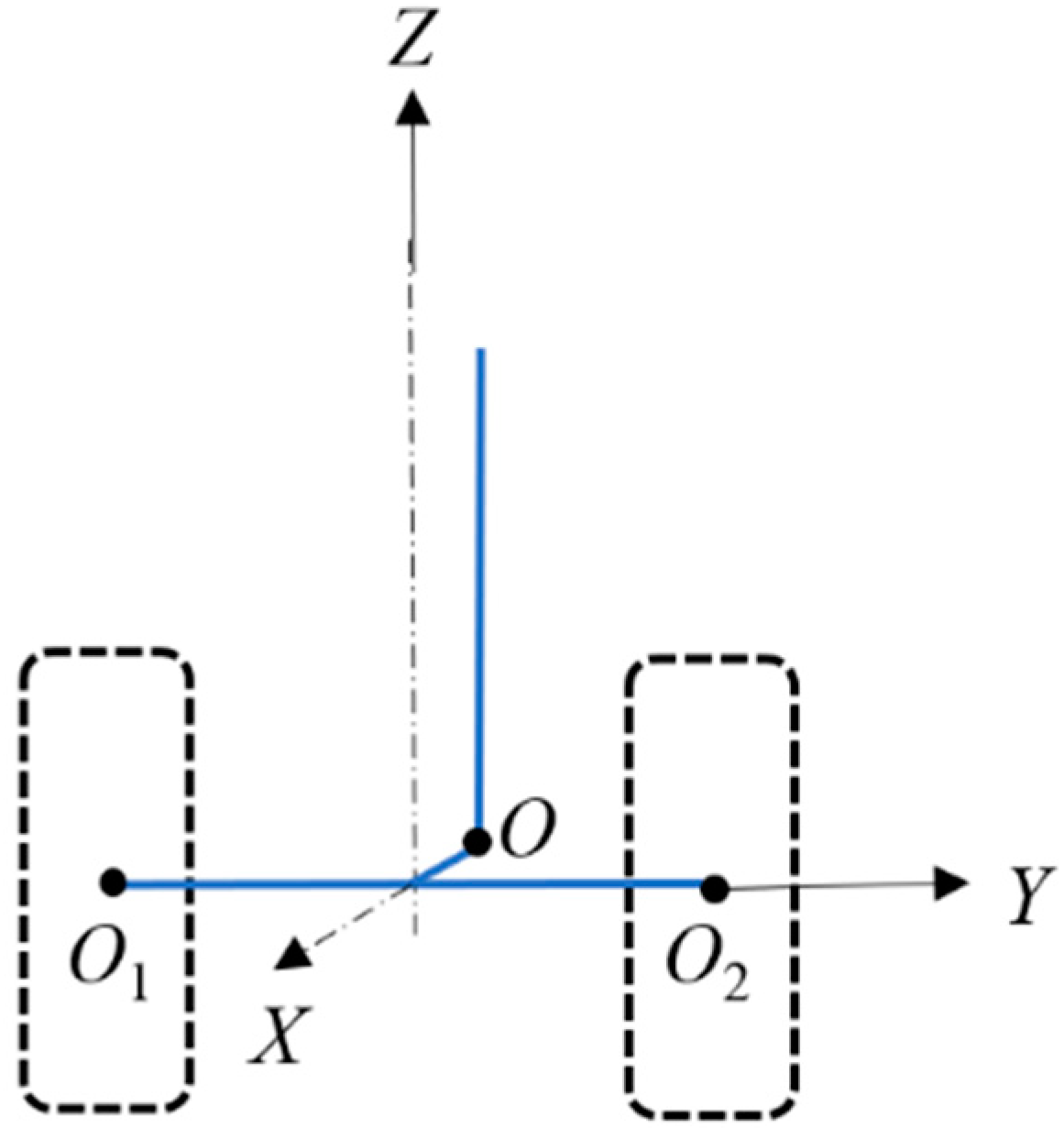
2.1. Physical Model
2.2. Mathematical Model
2.2.1. Dynamic Equations of Rotational and Lateral DoF
2.2.2. Mechanical Equilibrium of Vertical DoF
2.2.3. Tire Kinematics
2.2.4. Expression of Each Force Term
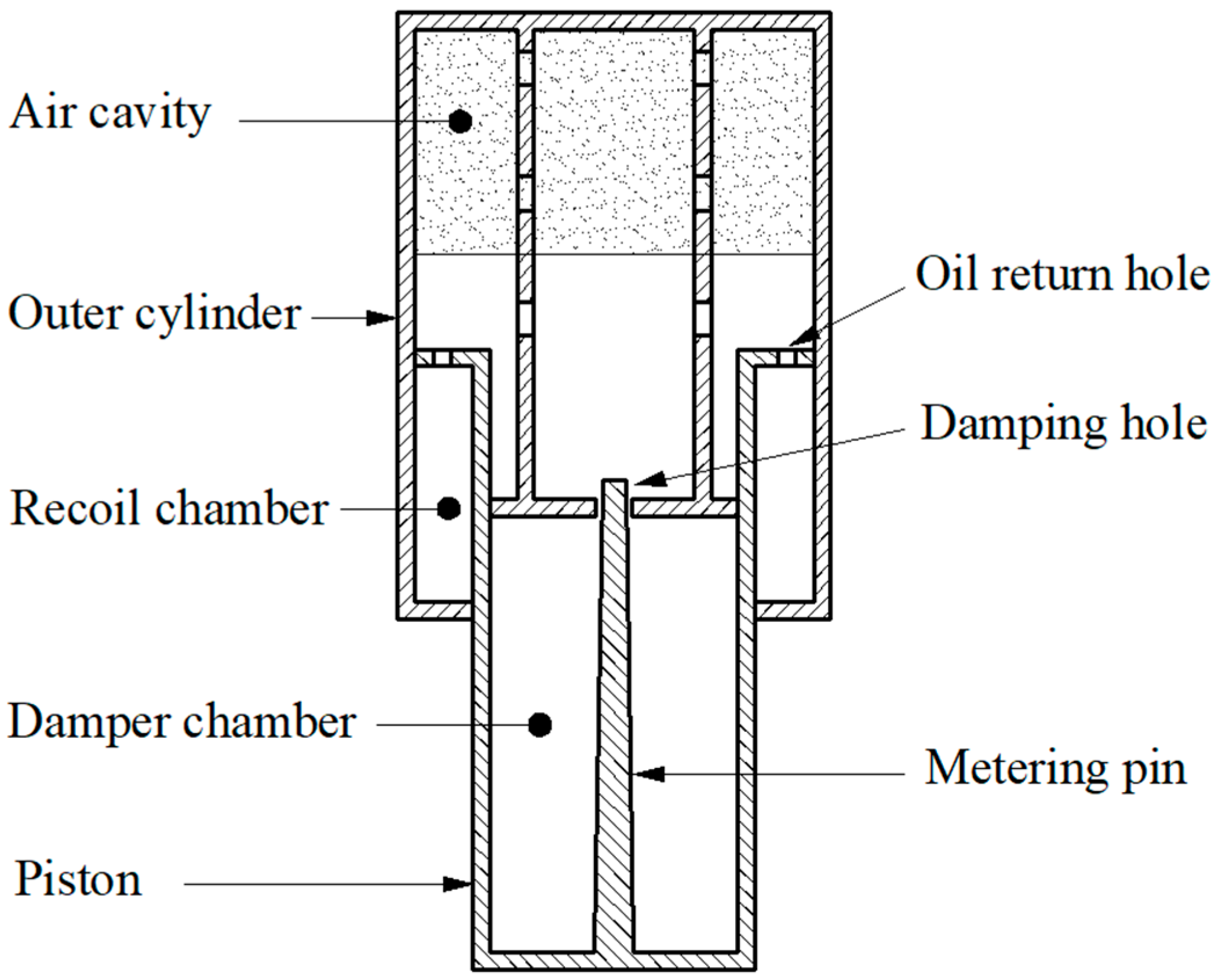
2.2.5. Oleo-Pneumatic Shock Absorber
2.2.6. MATLAB/Simulink Model Verification
3. Time-Varying System Stiffness Modeling
3.1. Full-Scale Static Stiffness Test of NLG
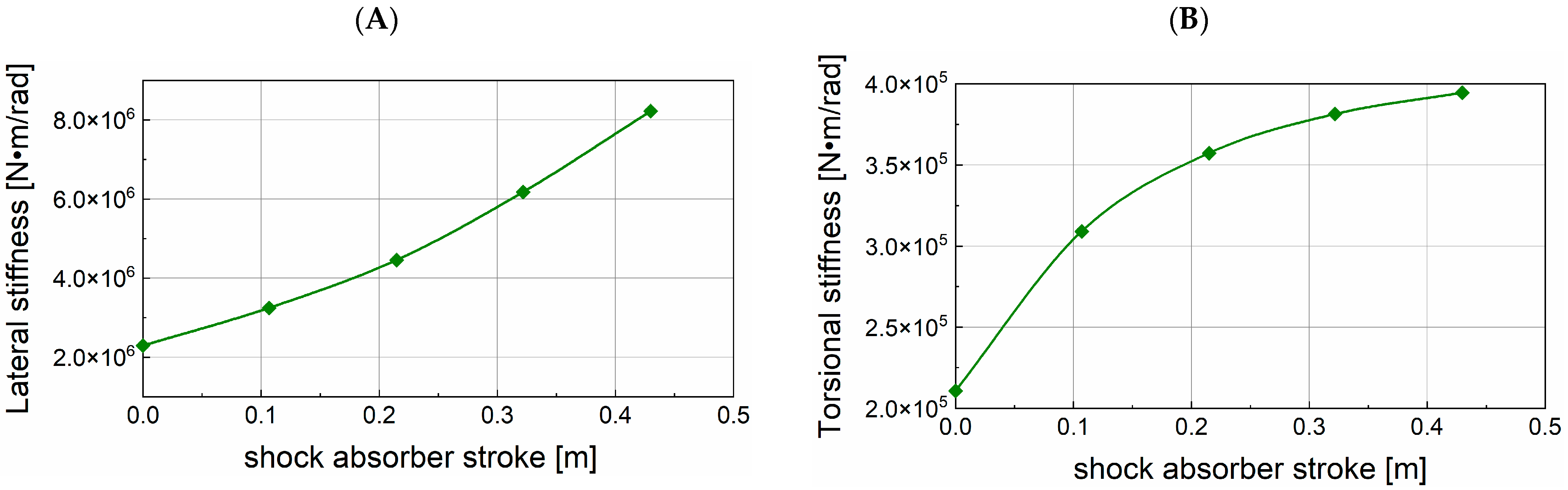
3.2. Relationship Between Shock Absorber Stroke and NLG Stiffness
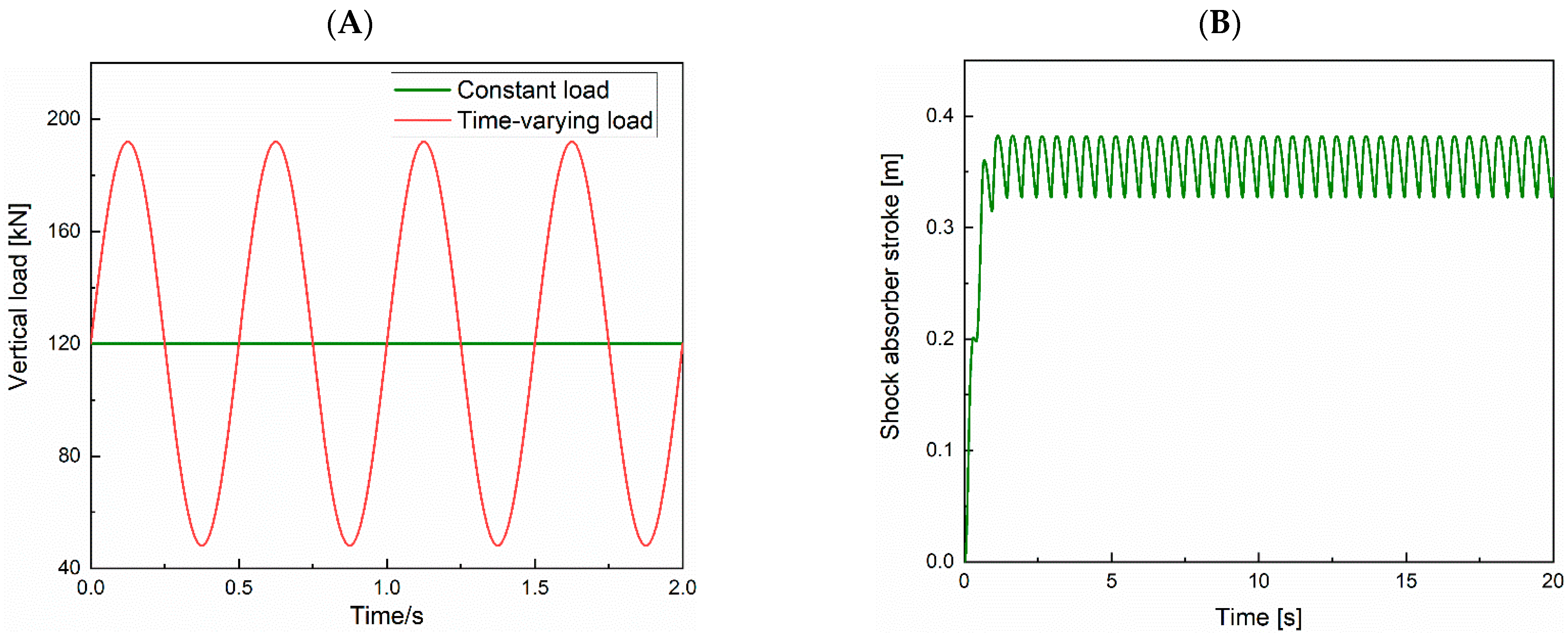
3.3. Stroke Variation in Shock Absorber with Time-Varying Load
4. Analysis and Discussion
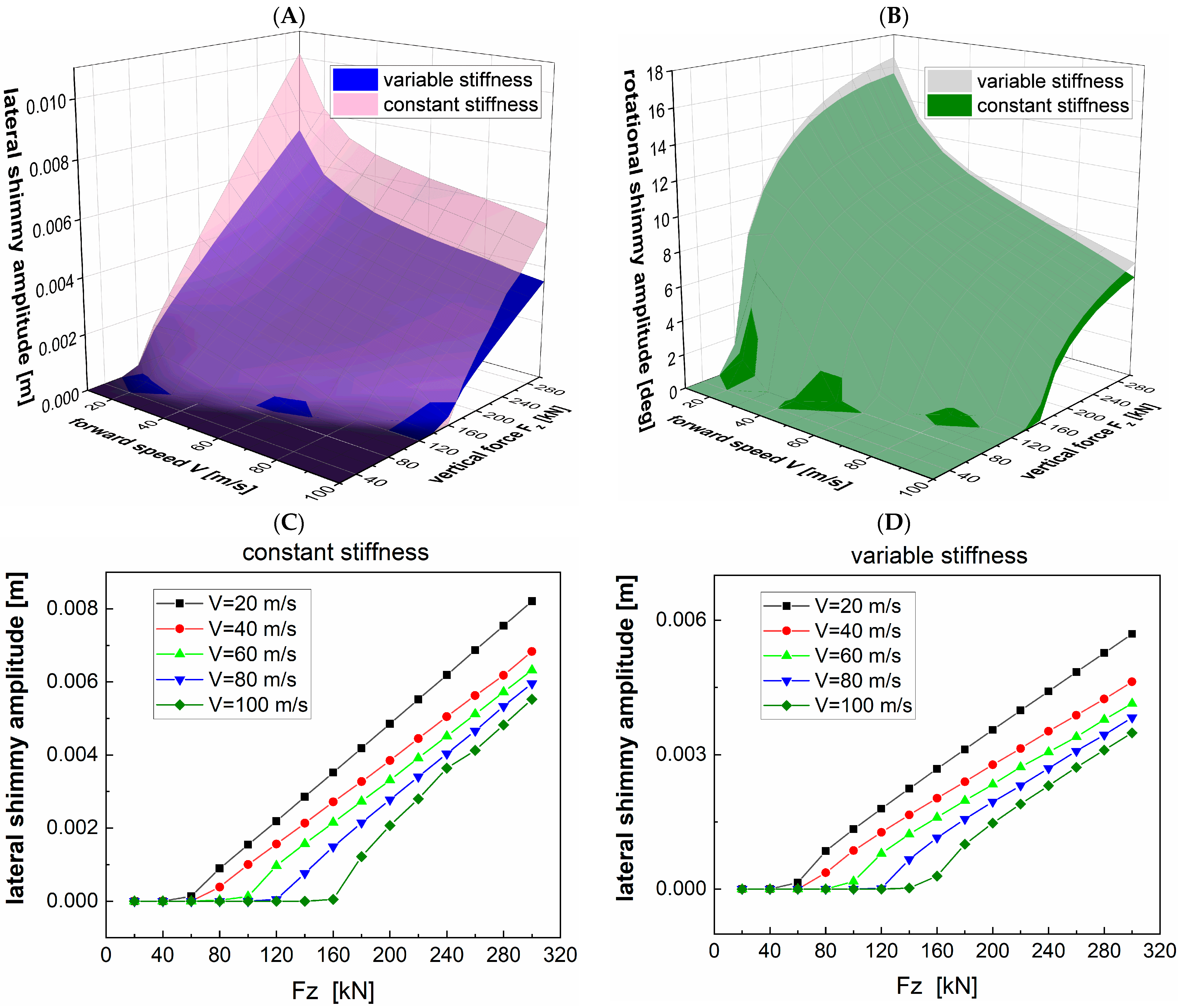
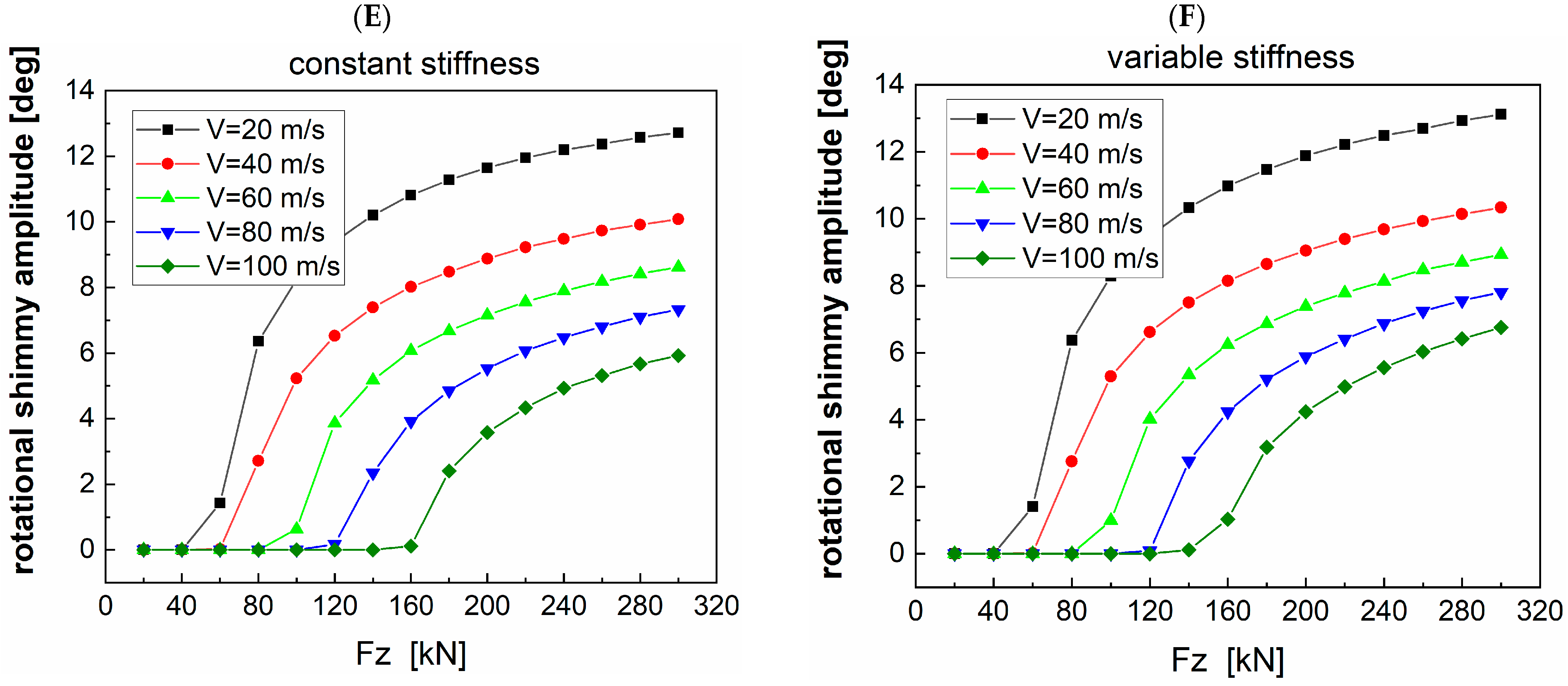
4.1. Shimmy Analysis Considering the Change in System Stiffness
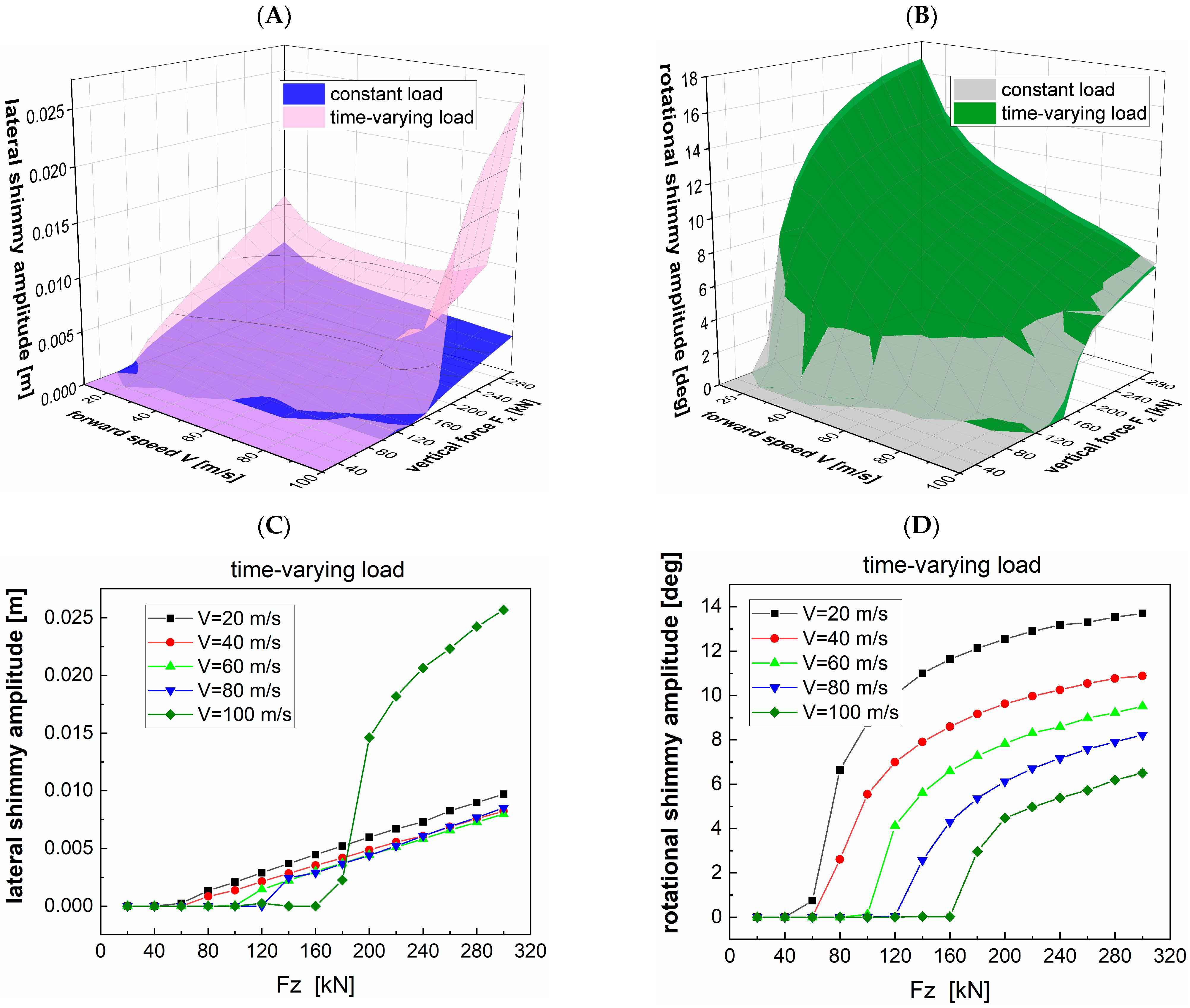
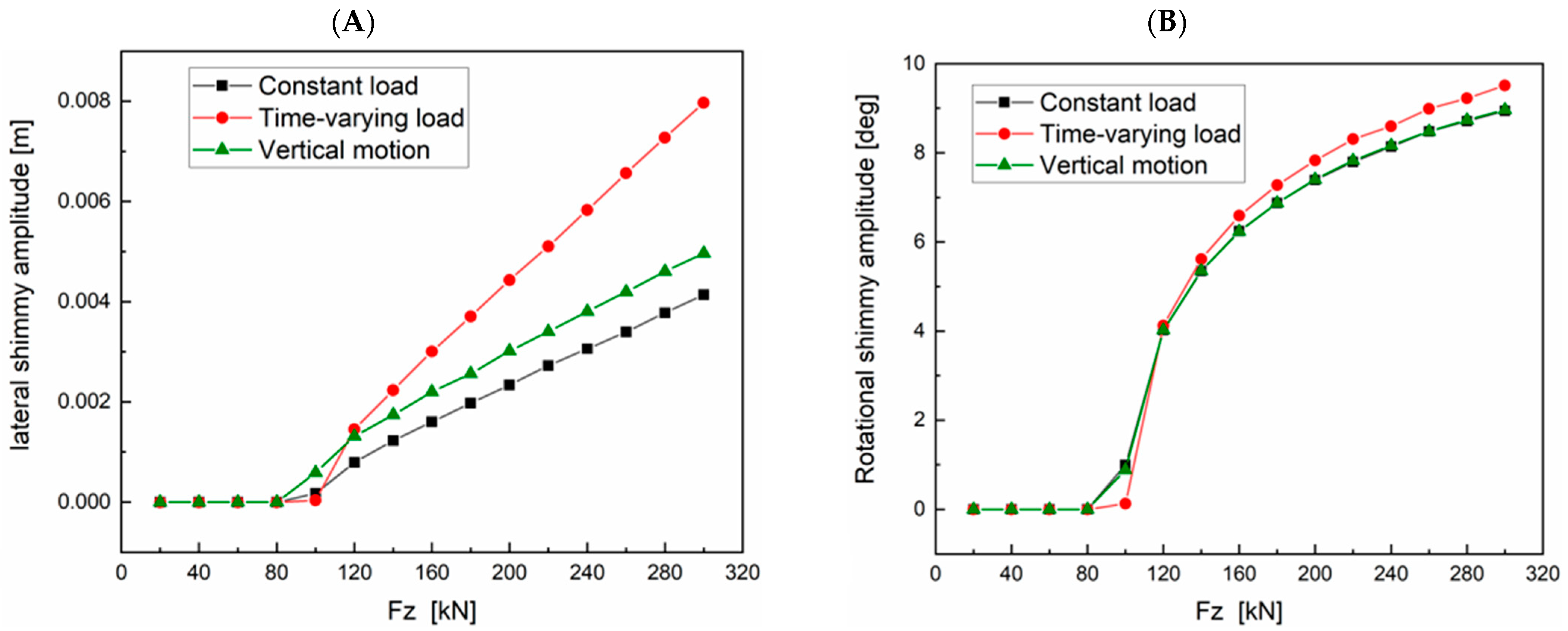
4.2. Influence of System Stiffness Change on Shimmy with Time-Varying Load
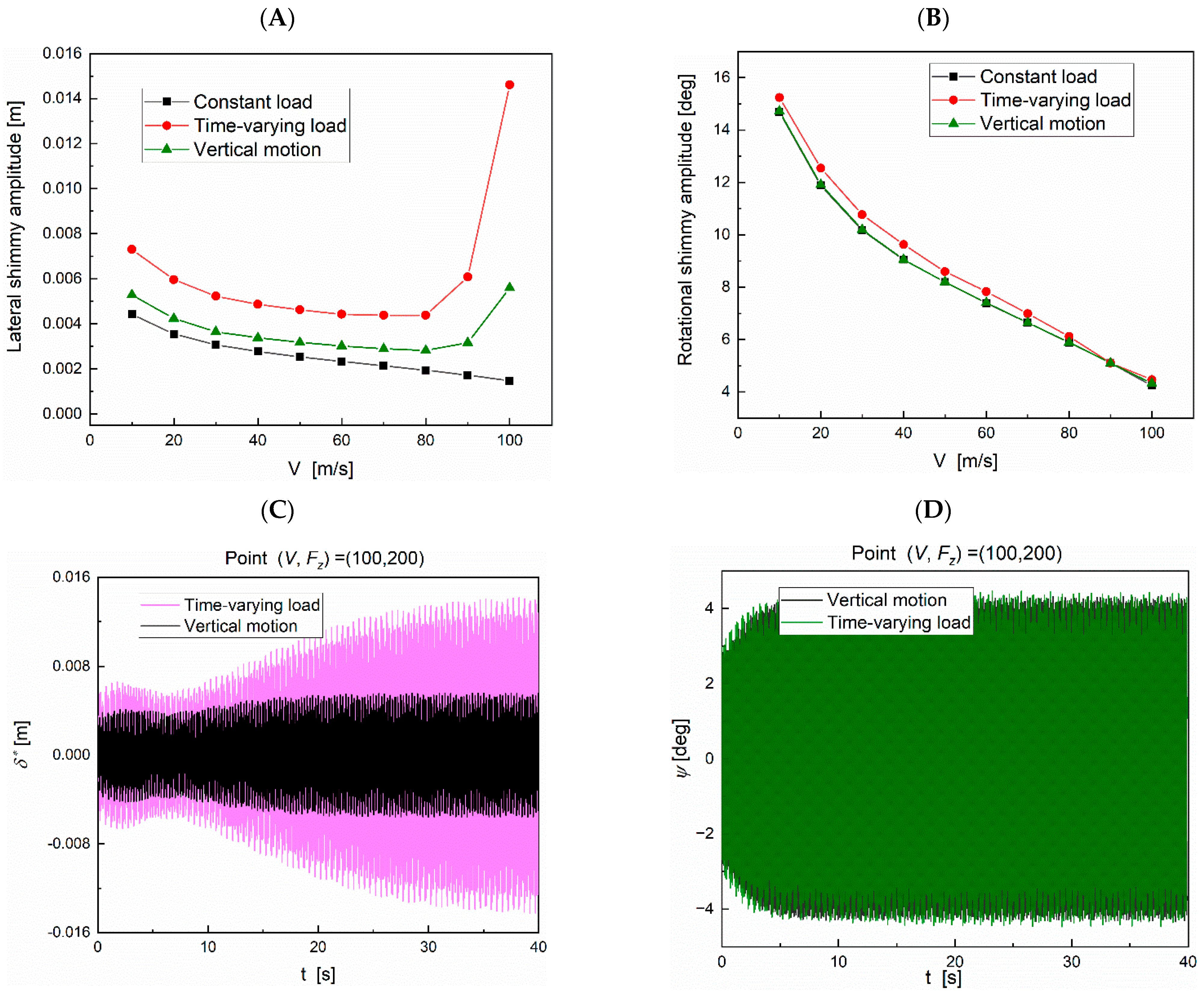
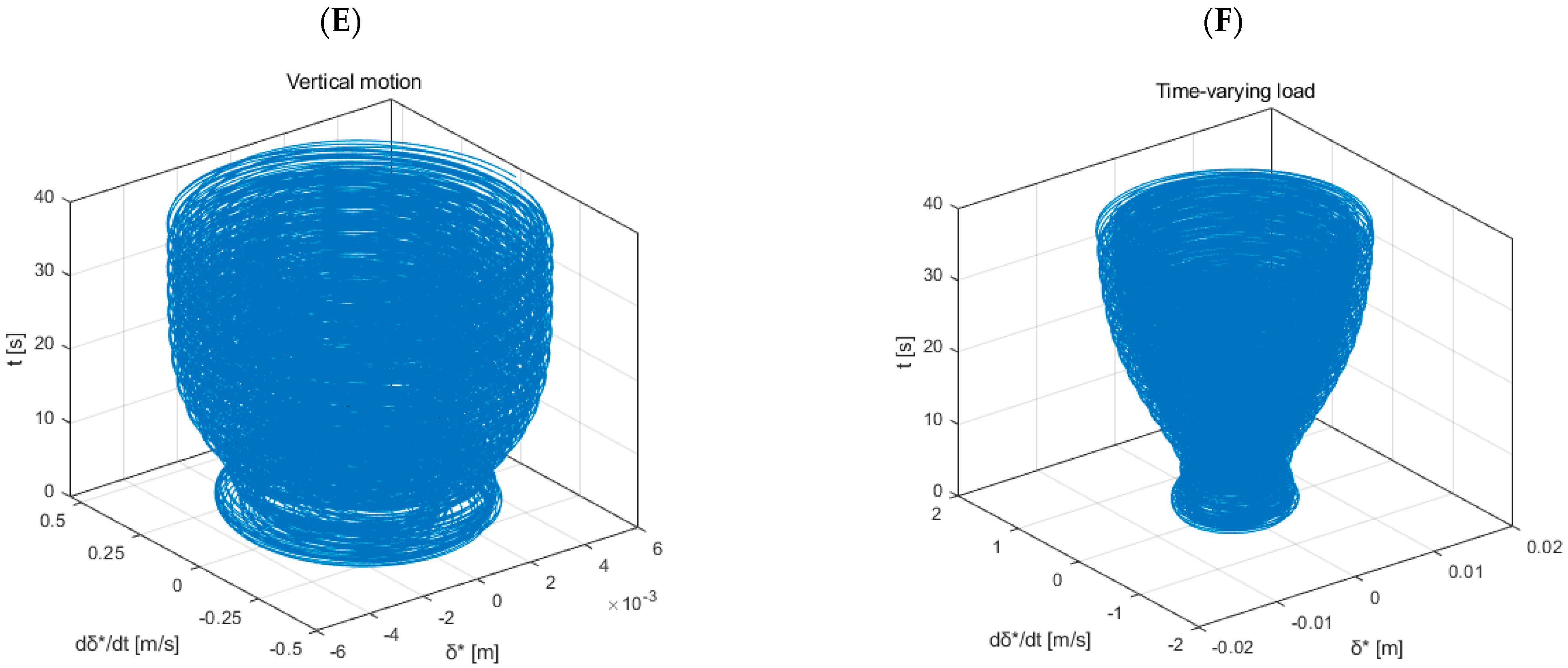
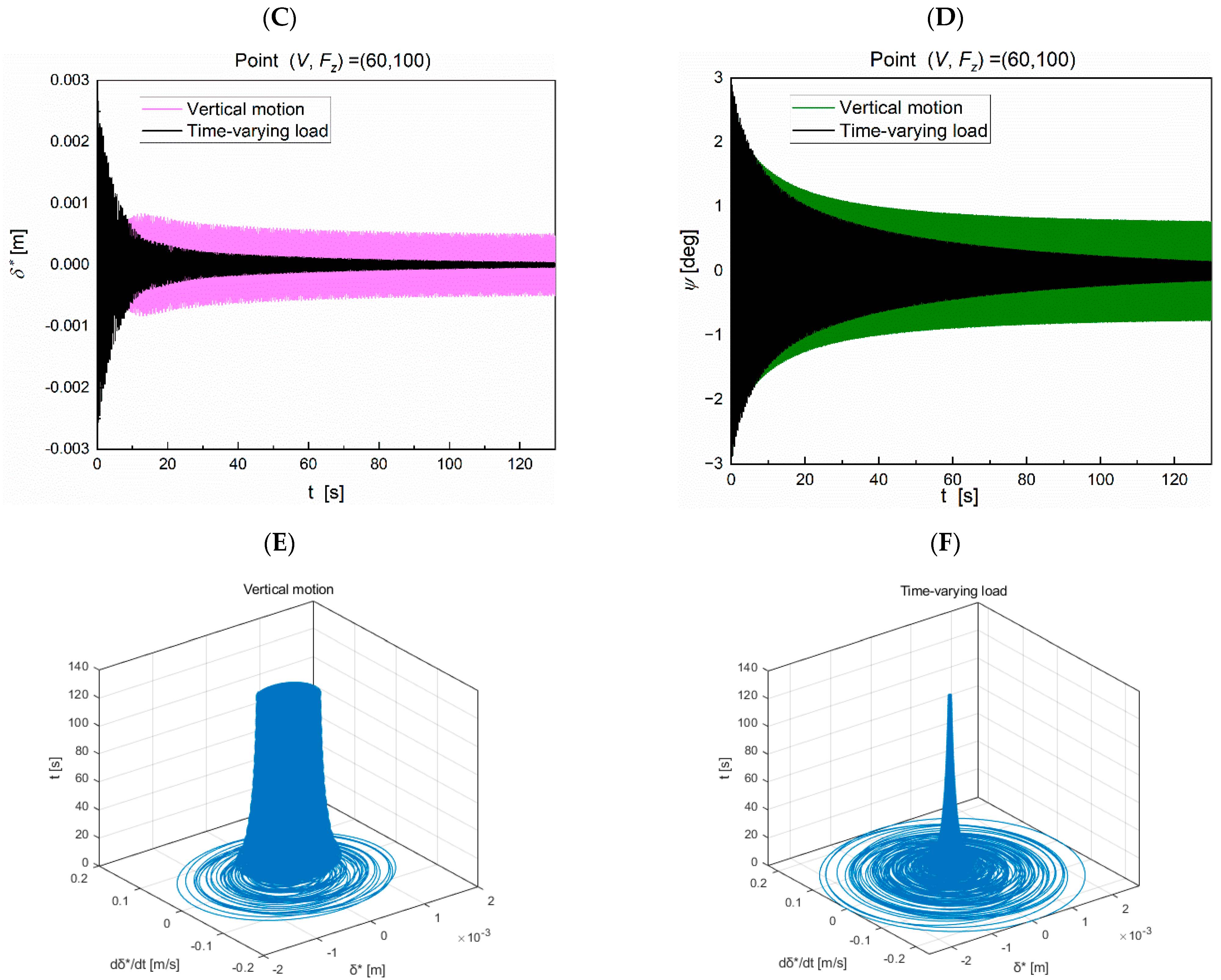
4.3. Effect of Vertical Motion on Shimmy of NLG with Variable System Stiffness
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- William, J. Moreland The Story of Shimy. J. Aeronaut. Sci. 1954, 21, 793–808. [Google Scholar]
- Coetzee, E. Shimmy in Aircraft Landing Gear. Airbus Rep. 2006, 1–11. [Google Scholar]
- Gordon, J.T. Perturbation Analysis of Nonlinear Wheel Shimmy. J. Aircr. 2002, 39, 305–317. [Google Scholar] [CrossRef]
- Grossman, D.T. F-15 Nose Landing Gear Shimmy, Taxi Test and Correlative Analyses; SAE International: Warrendale, PA, USA, 1980. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. On the Effectiveness of Shimmy Dampers in Stabilizing Nose Landing Gears. Aerosp. Sci. Technol. 2019, 91, 272–286. [Google Scholar] [CrossRef]
- Thota, P.; Krauskopf, B.; Lowenberg, M. Nonlinear Analysis of the Influence of Tyre Inflation Pressure on Nose Landing Gear Shimmy. In Proceedings of the AIAA Modeling and Simulation Technologies Conference, Chicago, IL, USA, 10–13 August 2009. [Google Scholar] [CrossRef]
- Howcroft, C.; Lowenberg, M.; Neild, S.; Krauskopf, B.; Coetzee, E. Shimmy of an Aircraft Main Landing Gear with Geometric Coupling and Mechanical Freeplay. J. Comput. Nonlinear Dyn. 2015, 10, 051011. [Google Scholar] [CrossRef]
- Kewley, S.; Lowenberg, M.; Neild, S.; Krauskopf, B. Investigation into the Interaction of Nose Landing Gear and Fuselage Dynamics. J. Aircr. 2016, 53, 881–891. [Google Scholar] [CrossRef]
- Terkovics, N.; Neild, S.; Lowenberg, M.; Krauskopf, B. Bifurcation Analysis of a Coupled Nose-Landing-Gear-Fuselage System. J. Aircr. 2014, 51, 259–272. [Google Scholar] [CrossRef]
- Thota, P.; Krauskopf, B.; Lowenberg, M. Interaction of Torsion and Lateral Bending in Aircraft Nose Landing Gear Shimmy. Nonlinear Dyn. 2009, 57, 455–467. [Google Scholar] [CrossRef]
- Thota, P.; Krauskopf, B.; Lowenberg, M. Multi-Parameter Bifurcation Study of Shimmy Oscillations in a Dual-Wheel Aircraft Nose Landing Gear. Nonlinear Dyn. 2012, 70, 1675–1688. [Google Scholar] [CrossRef]
- Thota, P.; Krauskopf, B.; Lowenberg, M. Bifurcation Analysis of Nose-Landing-Gear Shimmy with Lateral and Longitudinal Bending. J. Aircr. 2010, 47, 87–95. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Bian, H.; Yin, Y.; Wei, X. Shimmy Performance Analysis and Parameter Optimization of a Dual-Wheel Nose Landing Gear Coupled with Torsional Nonlinear Energy Sink and Considering Structural Nonlinear Factor. Chaos Solitons Fractals 2024, 187, 115330. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, T.; Yin, Y.; Wei, X. Reducing Shimmy Oscillation of a Dual-Wheel Nose Landing Gear Based on Torsional Nonlinear Energy Sink; Springer: Dordrecht, The Netherlands, 2024; Volume 112, ISBN 0123456789. [Google Scholar]
- Feng, G.; Jiang, B.; Ruan, S.; Zhang, M. Analysis of Shimming Performance and Clearance Influence under Manipulation State. J. Vibroeng. 2025, 27, 134–149. [Google Scholar] [CrossRef]
- Ruan, S.; Zhang, M.; Hong, Y.; Nie, H. Influence of Clearance and Structural Coupling Parameters on Shimmy Stability of Landing Gear. Aeronaut. J. 2023, 127, 1591–1622. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Investigation on the Effect of Coulomb Friction on Nose Landing Gear Shimmy. JVC/J. Vib. Control 2019, 25, 255–272. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Parametric Study of a Novel Nose Landing Gear Shimmy Damper Concept. J. Sound Vib. 2019, 457, 299–313. [Google Scholar] [CrossRef]
- Cheng, L.; Cao, H.; Zhang, L. Two-Parameter Bifurcation Analysis of an Aircraft Nose Landing Gear Model. Nonlinear Dyn. 2021, 103, 367–381. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Structural Design and Optimization of a Novel Shimmy Damper for Nose Landing Gears. Struct. Multidiscip. Optim. 2020, 62, 2783–2803. [Google Scholar] [CrossRef]
- Du, X.; Xu, Y.; Liu, Q.; Liu, C.; Yue, X.; Liu, X.; Kurths, J. Shimmy Dynamics in a Dual-Wheel Nose Landing Gear with Freeplay under Stochastic Wind Disturbances. Nonlinear Dyn. 2024, 112, 2477–2499. [Google Scholar] [CrossRef]
- Wong, J.; Ryan, L.; Kim, I.Y. Design Optimization of Aircraft Landing Gear Assembly under Dynamic Loading. Struct. Multidiscip. Optim. 2018, 57, 1357–1375. [Google Scholar] [CrossRef]
- Skinn, D.; Tipps, D.O.; Rustenburg, J. Statistical Loads Data for MD-82/83 Aircraft in Commuter Operations; U.S. Department of Transportation Federal Aviation Administration: Washington, DC, USA, 1999. [Google Scholar]
- Sura, N.K.; Suryanarayan, S. Lateral Response of Nonlinear Nose-Wheel Landing Gear Models with Torsional Free Play. J. Aircr. 2007, 44, 1991–1997. [Google Scholar] [CrossRef]
- Liu, J.; Ou, H.; He, J.; Wen, G. Topological Design of a Lightweight Sandwich Aircraft Spoiler. Materials 2019, 12, 3225. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Li, Y.; Hu, G.; Yang, M. Lightweight Research in Engineering: A Review. Appl. Sci. 2019, 9, 5322. [Google Scholar] [CrossRef]
- Huang, R.; Riddle, M.; Graziano, D.; Warren, J.; Das, S.; Nimbalkar, S.; Cresko, J.; Masanet, E. Energy and Emissions Saving Potential of Additive Manufacturing: The Case of Lightweight Aircraft Components. J. Clean. Prod. 2016, 135, 1559–1570. [Google Scholar] [CrossRef]
- Ahmad, M.A.; Rafiq, H.; Shah, S.I.A.; Khan, S.A.; Rizvi, S.T.U.I.; Shams, T.A. Selection Methodology of Composite Material for Retractable Main Landing Gear Strut of a Lightweight Aircraft. Appl. Sci. 2022, 12, 5689. [Google Scholar] [CrossRef]
- Rahmani, M.; Behdinan, K. Studying the Effect of Freeplay on Nose Landing Gear Shimmy Using a Fully Nonlinear Model. In Proceedings of the ASME 2018 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Quebec City, QC, Canada, 26–29 August 2018; Volume 6, pp. 1–11. [Google Scholar] [CrossRef]
- Hu, Y.; Hu, Y.; Lin, S.; Ma, J.; Li, S.; Li, J.; Wen, J. Theoretical Modeling and Dynamic Characteristics Analysis of Piezoelectric Inertial Actuator. Int. J. Mech. Sci. 2022, 225, 107363. [Google Scholar] [CrossRef]
- Wang, Y.; Wu, J.; Zhang, N.; Mo, W. Dynamics Modeling and Shift Control of a Novel Spring-Based Synchronizer for Electric Vehicles. Mech. Mach. Theory 2022, 168, 104586. [Google Scholar] [CrossRef]
- Li, Y.L.; Liu, B.F.; Wu, G.; Liu, Z.Q.; Ding, J.F.; Abubakar, S. Intelligent Prediction on Air Intake Flow of Spark Ignition Engine by a Chaos Radial Basis Function Neural Network. J. Cent. South Univ. 2020, 27, 2687–2695. [Google Scholar] [CrossRef]
- Yager, T.J. SAE TECHNICAL Aircraft Nose Gear Shimmy Studies. 2018. Available online: https://ntrs.nasa.gov/citations/19950062072 (accessed on 9 September 2025).
- Yin, Y.; Xu, K.; Nie, H.; Wei, X.; Wang, H. Dynamics Analysis of Spatial Landing-Gear Mechanism with Hinge Clearance and Axis Deviation. J. Aircr. 2021, 58, 30–42. [Google Scholar] [CrossRef]
- Mustashin, M.S.; Rahmani, M.; Behdinan, K. Experimental Characterization of a Novel Nose Landing Gear Shimmy Damper Using a Small-Scale Test Rig. Aerosp. Sci. Technol. 2021, 112, 106625. [Google Scholar] [CrossRef]
- Smiley, R.F. Correlation, Evaluation, and Extension of Linearized Theories for Tire Motion and Wheel Shimmy; NASA Technical Note 3632; NASA Technical Reports Server: Washington, DC, USA, 1956; pp. 1–145. [Google Scholar]
- Takács, D.; Orosz, G.; Stépán, G. Delay Effects in Shimmy Dynamics of Wheels with Stretched String-like Tyres. Eur. J. Mech. A/Solids 2009, 28, 516–525. [Google Scholar] [CrossRef]
- Ran, S.; Besselink, I.J.M.; Nijmeijer, H. Application of Nonlinear Tyre Models to Analyse Shimmy. Veh. Syst. Dyn. 2014, 52, 387–404. [Google Scholar] [CrossRef]
- Khapane, P.D. Soimulation of Asymmetric Landing and Typical Ground Maneuvers for Large Transport Aircraft. Aerosp. Sci. Technol. 2003, 7, 611–619. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, G.; Liu, P.; Yuan, L.; Ding, J.; Jiang, B. Evaluation of Joint Clearance Effects on the Shimmy of Nose Landing Gear. Aerospace 2023, 10, 772. [Google Scholar] [CrossRef]
- Orlando, C. Nose Landing Gear Simple Adaptive Shimmy Suppression System. J. Guid. Control Dyn. 2020, 43, 1298–1312. [Google Scholar] [CrossRef]
- Sanches, L.; Guimarães, T.A.M.; Marques, F.D. Nonlinear Energy Sink to Enhance the Landing Gear Shimmy Performance. Acta Mech. 2021, 232, 2605–2622. [Google Scholar] [CrossRef]
- Jiang, Y.; Feng, G.; Tang, H.; Zhang, J.; Jiang, B. Effect of Coulomb Friction on Shimmy of Nose Landing Gear under Time-Varying Load. Tribol. Int. 2023, 188, 108828. [Google Scholar] [CrossRef]





| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Structure parameters | |||
| lg0 | Fully extended height of NLG | 2.82 | m |
| φ | Rake angle | 0.1571 | rad |
| e | Mechanical trail | 0.12 | m |
| Moment of inertia of strut w.r.t. Z-axis | 100 | kg·m2 | |
| Moment of inertia of strut w.r.t. X-axis | 600 | kg·m2 | |
| Torsional stiffness of strut | 3.8 × 105 | N·m/rad | |
| Lateral stiffness of strut | 6.1 × 106 | N·m/rad | |
| Torsional damping of strut | 300 | N·m·s/rad | |
| Lateral damping of strut | 300 | N·m·s/rad | |
| Tire parameters | |||
| R | Radius of tire | 0.362 | m |
| L | Tire relaxation length | 0.3 | m |
| h | Contact patch length | 0.1 | m |
| Self-aligning coefficient of elastic tire | 1.0 | m/rad | |
| Restoration coefficient of elastic tire | 0.002 | rad−1 | |
| Vertical stiffness of tire | 4 × 106 | N/m | |
| Slip angle limit | 0.1745 | rad | |
| Damping coefficient of elastic tire | 270 | N·m2/rad | |
| I | Wheel moment of inertia | 0.1 | kg·m2 |
| D | Distance between the wheel centers | 0.1 | m |
| Shock absorber parameters | |||
| Pa0 | Initial gas pressure | 2,425,000 | Pa |
| V0 | Initial gas volume | 3.059 × 103 | m3 |
| Aa | Pressure area | 7.11 × 10−3 | m2 |
| ρ | Oil density | 860 | kg/m3 |
| Patm | Atmospheric pressure | 1,010,000 | Pa |
| n | Air variability index | 1.1 | - |
| kstrut | Structural limited stiffness | 1.96 × 108 | N/m |
| Smax | Maximum stroke | 0.43 | m |
| S | Stroke | - | m |
| Input parameters | |||
| Fz | Nose wheel vertical load | 20–400 | kN |
| V | Taxiing speed | 10–120 | m/s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, Y.; Sun, J.; Zhong, S.; Jiang, B. Nose Landing Gear Shimmy Analysis with Variable System Stiffness Under Time-Varying Load. Aerospace 2025, 12, 926. https://doi.org/10.3390/aerospace12100926
Jiang Y, Sun J, Zhong S, Jiang B. Nose Landing Gear Shimmy Analysis with Variable System Stiffness Under Time-Varying Load. Aerospace. 2025; 12(10):926. https://doi.org/10.3390/aerospace12100926
Chicago/Turabian StyleJiang, Yiyao, Jiyong Sun, Sheng Zhong, and Bingyan Jiang. 2025. "Nose Landing Gear Shimmy Analysis with Variable System Stiffness Under Time-Varying Load" Aerospace 12, no. 10: 926. https://doi.org/10.3390/aerospace12100926
APA StyleJiang, Y., Sun, J., Zhong, S., & Jiang, B. (2025). Nose Landing Gear Shimmy Analysis with Variable System Stiffness Under Time-Varying Load. Aerospace, 12(10), 926. https://doi.org/10.3390/aerospace12100926






