An Attack–Defense Non-Cooperative Game Model from the Perspective of Safety and Security Synergistically for Aircraft Avionics Systems

Abstract

The interconnectivity of avionics systems supports the need to incorporate functional safety and information security into airworthiness validation and maintenance protocols, which is critical. This necessity arises from the demanding operational environments and the limitations on defense resource allocation. This study proposes an optimization model for the strategic deployment of defense mechanisms, leveraging the dynamic interplay between attack and defense modeled by non-cooperative game theory and aligning with the maintenance schedules of civil aircraft. By developing an Attack–Defense Tree and conducting a non-cooperative game analysis, this paper outlines strategies from both the attacker’s and defender’s perspectives, assessing the impact of focused defense improvements on the system’s security integrity. The results reveal that the broad expansion of defense measures reduces their effectiveness, whereas targeted deployment significantly enhances protection. Monte Carlo simulations are employed to approximate equilibrium solutions across the strategy space, reducing computational complexity while retaining robustness in capturing equilibrium trends. This approach supports efficient allocation of defense resources, strengthens overall system security, and provides a practical foundation for integrating security analysis into avionics maintenance and certification processes.

1. Introduction

Traditional safety science focuses more on research in the science and technology of human and industrial safety [1]. Aircraft avionics systems, recognized as “safety-critical” operational entities essential for securing high-integrity flight operations [2], necessitate an unparalleled degree of reliability, robustness, and safety, which falls into this field. With stringent safety requirements, contemporary aircraft avionics systems exhibit a high degree of integration between software and hardware components, engaging with the physical world via synchronized sensing, computing, and control networks [3]. The standards ISA 84/IEC61511 [4] delineate that the safety of a system is designed to safeguard and monitor equipment against unintentional malfunctions or failures, aiming to maintain a secure operational process state.

As the synthesis, modularization, and integration of avionics systems increase, the interconnections between systems and equipment within subsystems become increasingly complex [5], and have led to the emergence of quintessential cyber–physical systems (CPS), as illustrated by advanced aircraft, including the A380 and B787 [6]. For example, sophisticated in-flight entertainment systems allow aircraft to create a Local Area Network (LAN) for onboard devices at certain altitudes, enabling the connectivity of passengers’ devices to the in-flight network [7]. However, this increasing openness and connection lead to the emergence of novel complex security risks of aircraft avionics systems [8]. Thus, these systems may be vulnerable to attacks due to insufficient security [9], such as ADS-B system cyberattacks [10], ILS spoofing [11], EFB DoS attacks [12], and so on. It can be seen that this heightened openness renders avionics systems susceptible to potential threats from malicious actors. Moreover, the emerging physical and cyber vulnerabilities of modern airliners demand comprehensive periodic maintenance of both hardware and software components on the ground to maintain airworthiness standards. However, this maintenance regimen often necessitates connections to terrestrial internet networks, markedly amplifying the risk of unauthorized access to the onboard network infrastructure.

While traditional system analyses have treated these aspects distinctly, the advancement of avionics systems has led to a more intricate interplay between safety and security [13], traversing multiple pathways and highlighting the burgeoning issues of converged security within these systems. Some research has already studied the particularity of safety and security synergistic analysis. Gou et al. [14] summarized system dynamics (SD) approaches for an in-depth analysis of safety and security. The author has proposed a dynamic fault tree model combined with an optimized extended fuzzy algorithm for aircraft avionics network transmission failure analysis [15]. However, there has still been a lack of research focused on exploring defense strategy management methods aimed at enhancing system security amidst the increased risks associated with the openness of avionics systems. From a macroscopic systems perspective, various security and safety threats exert a direct impact on the system’s continuous operational performance [16]. So, an entirely new perspective to protect aircraft avionics systems and avoid failure from the perspective of safety and security synergistically urgently needs to be proposed [17].

Another challenge in current attack–defense modeling is the issue of missing security strategies. This occurs when feasible defensive actions are not explicitly represented in the strategy space, leaving certain attack vectors insufficiently addressed. For example, an attack such as tampering with collected data may have multiple countermeasures (e.g., encryption, access control, and integrity checks), yet some models only include one or two. Prior studies [18,19] have shown that such omissions can bias equilibrium outcomes and reduce the effectiveness of defense allocation. In avionics systems, with their tightly coupled safety–security requirements and limited maintenance time, the risk of overlooking strategies is especially high.

To address existing issues, this study proposes an attack–defense non-cooperative game model as a systematic approach to modeling avionics systems through the lens of safety–security integration, i.e., the convergence of functional safety and information security. Based on this framework, this study quantitatively assesses the direct effects of specific attacks and defensive actions on system security. Therefore, the central focus of this study is the application of a non-cooperative attack–defense game model (NCADG-AS) to optimize defense strategy management in avionics systems. To ensure the model is tractable and realistic, we address supporting challenges, such as redundant nodes and missing security strategies, through pruning optimization and strategy space refinement. The main contributions can be outlined as follows:

• We develop a non-cooperative attack–defense game model (NCADG-AS) as the core framework to optimize defense strategy management for avionics systems under safety–security integration.
• To support the tractability and completeness of this model, we introduce an Attack–Defense Tree (ADT) pruning methodology that eliminates redundant nodes and incorporates missing security strategies, ensuring a consistent and manageable strategy space.
• To solve the NCADG-AS efficiently, we design a Monte Carlo–based approximation method for Nash equilibrium in the constrained strategy space, enabling robust and computationally feasible defense resource allocation.

The subsequent sections of this manuscript are structured as follows. Section 2 delineates the existing research advancements pertinent to the scope of this study. Section 3 elaborates on the safety–security integration analysis model introduced herein. Section 4 presents a case study of the proposed methodology, utilizing the data source from the display function within the Electronic Flight Instrument System (EFIS) as an illustrative example. Section 5 summarizes the findings of this research and proposes potential avenues for future investigation.

2. Related Works

2.1. Safety and Security for Avionics Systems

The network-level security configuration is completed in the design phase, resulting in a lack of information and network security update mechanisms during the aircraft’s service period. In the latest research on avionics system security [20], researchers have made efforts to enhance the functional safety and information security of avionics systems, but have not analyzed these two aspects in combination. Zimmer et al. [21] proposed an Embedded Modular Avionics (IMA) platform for specific hardware resource capacity requirements and functional safety and security requirements using the Design Problem Specification Language. Athavale et al. [22] investigated the use of commercial off-the-shelf (COTS) electronics in avionics architectures, highlighting the functional safety and information security implications of multi-core processor (MCP) applications. Smith et al. [23] pointed out that almost all aviation wireless technologies lack basic security mechanisms and demonstrated new wireless attacks against three security-relevant avionics systems. They found that all three attack scenarios had significant control impacts and disruption costs.

Existing security research for avionics systems focuses on optimizing the threat sensing process in the network bus, e.g., by considering AI techniques to resist DDoS attacks [24] or using machine learning for anomaly detection [25]. The FAA established the Aircraft Systems Information Security/Protection (ASISP) working group to build a risk assessment framework for avionics systems and to use attack tree modeling as a fundamental methodology for threat analysis [26]. U.S. Senator Edward Markey proposed the “2016 Enhanced Aircraft Cybersecurity and Resilience Standard” [27], which includes a provision to identify aircraft “electronic entry points”, which can help to segregate avionics-critical systems from non-critical systems. Considering the characteristics of avionics systems, including high reliability, high security, and extreme operating environments, existing converged security research results for ground network systems cannot be directly migrated for use.

To summarize, avionics systems are transitioning from proprietary, closed designs to open, interconnected architectures. Although safety–security integration risks are acknowledged, existing research and standards primarily focus on functional safety threats, emphasizing hardware and functional solutions. To meet the stringent airworthiness requirements of avionics systems, it is imperative to urgently develop an optimized model for defense strategy management that integrates a safety–security integration perspective.

2.2. Safety and Security Co-Analysis

For typical cyber–physical systems, including the aircraft avionics systems studied in this paper, safety and security are always interwoven instead of being two separate issues. Security risks can lead to functional failure through cascading effects [28], and in turn, safety risks also lead to the degradation of perception, computing, and transmission functions [29], which is especially true for avionics systems. For the above reasons, safety and security co-analysis has gained broad consensus.

On the one hand, co-analysis is the interaction mechanism. Luo et al. [30] explored the causal mechanisms underlying the mutual influence between safety and security, and found it to conform precisely to the problem of maximizing benefits in non-cooperative games. Sun et al. [31] presented a systematic methodology to address the challenge of integrating safety and security and resolve their contradictions. On the other hand, some specific analysis methods have been constructed for individual application scenarios. Castiglione and Lupu [18] proposed a methodology and developed a tool chain to systematically analyze and enumerate the security attacks leading to safety violations by lazily combining threat modeling, formal verification, and an attack graph. Their model was successfully used to discover threat scenarios in the Communication-Based Train Control System. Focusing on abnormal behaviors that affect system performance due to possible sensor faults and attacks, Kaloudi and Li [32] proposed an adaptive stress testing framework for safety and security co-analysis. Evaluation in an autonomous vehicle scenario showed that this methodology can analyze the interaction of malicious attacks with random faults and identify the incident caused by the interactions, along with the most likely path that leads to the incident.

Existing research about safety and security co-analysis provides robust methodologies but often conflates attacker and defender perspectives, leading to imprecise models. Furthermore, analyzing all safety and security elements often results in complex, redundant models that hinder efficient quantitative computation, particularly under the time constraints typical in avionics system maintenance. The attributes of a better model should be distinctly separated to reflect the specific objectives and strategies of each involved party, namely, the attacker and the defender.

2.3. Game Theory-Based Modeling

With the growing demand for responding to cyber threats and information attacks, the attack–defense game theory has emerged [33] and has been widely applied in safety and security modeling and analysis. An attack on or disruption of one target may impact other targets, which impacts the defender’s resource allocation across targets and the attacker’s strategy.

Wu et al. [34] used fuzzy variables, considering that the game process in the real world often contains a large amount of fuzzy information, assuming that the wireless sensor network (WSN) attack–defense Stackelberg game model operates in a fuzzy environment. Zhang et al. [35] used the zero-sum multilevel Markov Stackelberg game model for modeling the sequential behaviors of the attacker and defender and proposed cyber and physical risk mitigation frameworks, respectively. Peng et al. [36] used the cumulative prospective value as a maximization objective to describe the risk preferences of the two parties of the game and analyzed the impact of optimal strategy combinations. Wu et al. [19] propose a novel Stackelberg attack–defense game model (ADGM) framework to protect critical infrastructure systems. In this framework, the functional vulnerability of CISs that accounts for cascading effects is innovatively considered in the construction of the ADGM. Critical target selection and resource allocation problems are integrated into the strategy model, while cumulative prospect theory (CPT) is applied to evaluate payoffs considering the risk attitudes of agents. Zhang et al. [37] proposed a value-optimal IRSA (V-IRSA) mechanism for the S-IoT via a distributed noncooperative game theoretic approach, in which a utility function of the Cost of Information Value (CoIV) is developed to capture the loss of information value during packet transmission. Wu et al. [38] developed a noncooperative game-based fault-tolerant fuzzy containment controller for networked ASVs to achieve Nash equilibrium seeking. Using the Lyapunov functions, theoretical results show that the actions of ASVs can converge to the neighborhood region of the Nash equilibrium. Zhang et al. [39] investigated the game-theoretic strategy design problem between a multistatic multiple-input–multiple-output (MIMO) radar network and a jammer. The conflict between the jammer and the radar network is described as a two-player zero-sum game, and then mutual information (MI) is used as the utility function, where the radar network and the jammer can change their power allocation strategy so that the MI is optimized for the two players prospectively.

In non-cooperative attack–defense game models, finding optimal equilibrium solutions is critical, often represented by the probabilities of various strategies. However, in avionics systems, dismissing a defense method based on its low probability could be detrimental. Additionally, avionics systems typically rely on limited data types, which poses challenges for training data-driven models. Considering the combined effect of all attack methods is crucial. Safety–security integration analysis must encompass the entire strategy space to achieve robust security.

More recent research has further advanced attack–defense modeling and avionics cybersecurity. Hausken [40] and Hunt [41] provide comprehensive surveys of attacker–defender games, emphasizing optimization-based and stochastic formulations for improved defensive analysis. Habler et al. [42] investigate avionics-specific vulnerabilities through threat taxonomies such as STRIDE and MITRE ATT&CK, highlighting persistent gaps in system defenses. Lu [43] proposes a game-theoretic architecture for Air Traffic Management that integrates Bayesian Nash formulations with blockchain-based trust mechanisms. Robins [44] discusses the growing convergence of cybersecurity and safety requirements under evolving aviation regulations, while Florido-Benítez [45] categorizes recent cyber incidents in airports and airlines, identifying common attack vectors and hacker profiles. The CSC 2.0 report [46] further underscores these concerns by outlining a national roadmap for strengthening aviation cyber defenses amid escalating threats. These recent works demonstrate the timeliness and relevance of the NCADG-AS model, situating it within the latest advances in safety–security integration.

While the above works have enriched the field, most existing models remain either too descriptive or domain-specific, with limited adaptability to avionics contexts. For example, survey-based approaches [40,41] provide breadth but lack actionable frameworks for strategy optimization, while taxonomy-driven analyses [42] emphasize vulnerability classification without offering equilibrium-based defense guidance. Architectures such as those in [43] and regulatory discussions [44,45] highlight important directions but often assume idealized or generalized conditions. Compared to these methods, NCADG-AS addresses a critical gap by explicitly integrating safety–security co-analysis with a constrained game-theoretic framework, enabling tractable evaluation of adversarial strategies under avionics-specific constraints. This structured integration allows decision makers not only to identify vulnerabilities but also to prioritize defensive resource allocation more effectively.

3. Proposed NCADG-AS

3.1. Framework of NCADG-AS

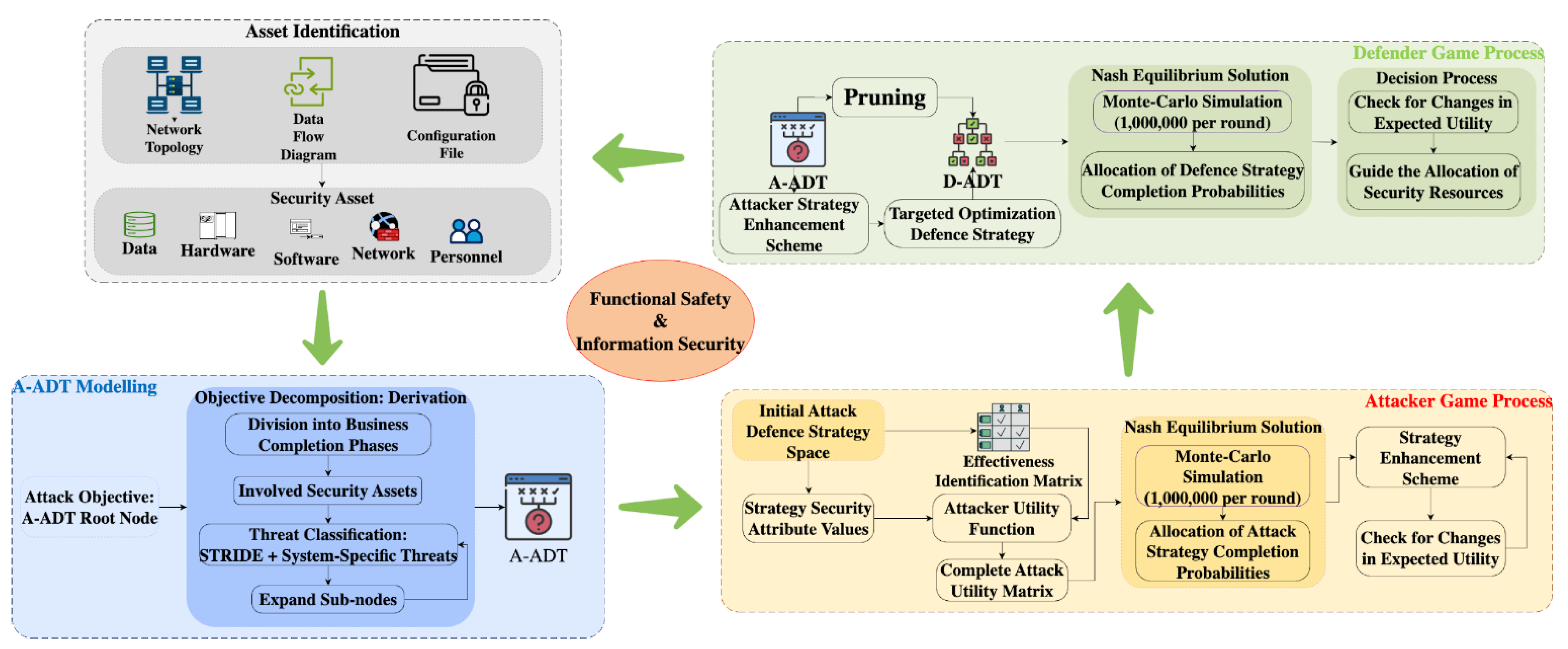
The procedural dynamics of the NCADG-AS are delineated in Figure 1, reflecting an alignment with the iterative decision perspective switch game. Utilizing this finite element model, the defender strategizes the optimization of security resource allocation, initiating with asset identification. This involves analyzing the system’s network topology and data flow diagram, and from the attacker’s viewpoint, pinpointing the attack targets based on the extent of functional impact and accessibility, which is the outcome sought through the attack means. In the modeling workflow, attack strategies are first enumerated through the A-ADT (an Attack–Defense Tree constructed from the attacker’s perspective), followed by defense strategies mapped via the D-ADT (an Attack–Defense Tree constructed from the defender’s perspective). This order reflects the construction workflow and the use of the attacker’s perspective to better inform defense optimization, rather than a sequential attacker–defender play. The NCADG-AS remains a non-cooperative framework, with attacker and defender utilities evaluated simultaneously under Nash equilibrium assumptions. Ultimately, in synergy with the real-world context and mindful of defense requisites and resource constraints, the deployment of security resources is optimally adjusted.

To conduct both qualitative and quantitative analyses of system security from a safety–security integration standpoint, the ADT is initially employed to delineate the mechanisms through which safety–security integration elements influence functional safety. We systematically differentiate between the strategies of the attacker and defender. Specifically, the ADT’s root node is independently identified as the reachability target for both parties. If the root node represents the attacker’s goal, such as “disrupt flight power system command transmission,” this ADT assumes the attribute “Attack,” labeled A-ADT. Conversely, if the root node epitomizes the defender’s aim, for instance, “Protect flight power system command transmission,” the ADT is attributed to “defense,” denoted as D-ADT.

The fundamental actions of the attacker and defender encapsulated by the ADT may initiate a cascading effect, where threats are transmitted from leaf nodes to root nodes via the ADT pathway. This process encompasses threats to both functional safety and information security. The attributes of attack–defense security scenarios, including role duality and behavioral interdependence, align with the principles of non-cooperative game theory. This alignment renders game theory-based security strategy formulation a prevalent methodology. We quantify the computation of system security using the utility values assigned to the attacker and the defender, wherein the attacker’s utility is enhanced, and the defender’s utility is diminished upon system compromise.

Moreover, this study integrates the implementation probability of strategies as a pivotal variable for determining game equilibrium, addressing the discord between anticipated occurrence probability and actual attack impact, alongside the inadequacy of defense strategy coverage. It employs Monte Carlo simulations to ascertain the equilibrium state of the NCADG-AS model.

3.2. ADT Modeling and Pruning Optimization

The international standard DO-326A [47] elucidates that defining the security scope entails identifying the subject, its external interfaces, the entities interacting with the subject through these interfaces, and the functionalities executed by the subject. To integrate functional safety and information security analyses for constructing a comprehensive A-ADT, we extend the simplistic threat scenarios of the target system into detailed data flow diagrams and network topologies. Concurrently, by scrutinizing system-related documents and existing configuration data, we discern the security assets prone to attacks, categorizing known attack vectors according to the Microsoft STRIDE threat taxonomy.

We designate the root node as the ultimate objective, progressively deconstructing it into sub-goals until the decomposition culminates at leaf nodes representing specific attack behaviors by the assailant. Subsequently, we embed pertinent defense strategies into the A-ADT based on the classified attack types. Upon completion of the tree construction, the necessity to prune the A-ADT arises for several reasons:

First, the A-ADT provides a detailed pathway of an attack, facilitating the analysis of attack traceability and the propagation path of threats. This detailed mapping, however, conflicts with the efficiency imperative of avionics systems due to the extensive time required to trace complex attack paths in avionics systems, without assurance of acceptable traceability outcomes. To enhance computational efficiency and conserve resources, we eliminate the intermediate attack pathways in the A-ADT, concentrating solely on specific attack behaviors.

Moreover, during the decomposition phase, attackers often utilize predicate strategies to augment the success likelihood of attacks. For example, information theft, serving as a predicate strategy for executing remote intrusion and denial-of-service attacks, does not directly compromise the system. To refine computational efficiency and economize on strategy space, we remove attack nodes that do not directly impact the system, focusing exclusively on attacks that inflict direct damage. This pruning step not only eliminates redundant and indirect nodes but also reduces the dimensionality of the strategy space, thereby improving computational tractability.

In addition, the NCADG-AS framework explicitly considers simultaneous and cascading attacks. Cascading attacks are represented as sequential dependencies in the A-ADT, where the success of one attack (e.g., information theft) increases the feasibility of subsequent ones (e.g., remote intrusion). Simultaneous attacks are modeled as parallel branches that may occur together, and their joint impact is incorporated into completion probability calculations during Monte Carlo simulation. This ensures that both multi-step and concurrent attack scenarios are captured realistically, while pruning prevents unnecessary expansion of the tree.

After excising the intermediate attack pathways and indirect attack nodes, it becomes imperative for the defender to develop a new D-ADT and refine the defense strategy based on insights gleaned from the attacker’s perspective. The target antithetical to the A-ADT’s root node is established as the root of the D-ADT, preserving only those attack leaf nodes that remain post-pruning.

Before the inception of the attacker’s game, the defender, oblivious to the attacker’s prioritized attacks, is compelled to deploy undifferentiated defense resources. Amidst the uncertainty of resource allocation requirements for each defense mechanism, the defender is inclined toward a maximalist defense addition, a method fraught with time consumption and inefficiency. Hence, leveraging game theory, we advocate the adoption of non-cooperative game theory to navigate the challenges delineated above.

3.3. Attack–Defense Game Model

Based on classical game theory, the basic structure of an NCADG-AS model is expressed by Equation (1).

$$G=\left[\left(A,D\right),(S_A,S_D),(U_A,U_D)\right]$$

(1)

where (A, D) denote the attacker and the defender, the two parties involved in the game. $(S_A,S_D)$ denote the strategy space of the attacker and the strategy space of the defender, respectively, and the initial strategy space is obtained by establishing A-ADT. The strategy space of the attacker consists of m strategies, as shown in Equation (2).

$$S_A=\left(S_A^1,S_A^2, \dots ,S_A^m\right)$$

(2)

The defender’s strategy space consists of n strategies, as shown in Equation (3).

$$S_D=\left(S_D^1,S_D^2, \dots ,S_D^n\right)$$

(3)

$(U_A,U_D)$ is a utility computation function for the attacker and the defender, and the inputs are the values of the security attributes of both strategies. In the non-cooperative game model, NCADG-AS, we use the completion probability (CP) of a strategy to calculate the probability of achieving the goal after the actual strategy is implemented, and the set of ${CP}_A=\left({cp}_A^1,{cp}_A^2, \dots ,{cp}_A^m\right)$ and the set of ${CP}_D=\left({cp}_D^1,{cp}_D^2, \dots ,{cp}_D^m\right)$ denote the probability that the attacker and the defender will successfully implement their strategies, respectively. To calculate the utility of both sides, we provide a calculation method that integrates the payoff, asset importance, and cost, which can be flexibly adapted to different scenarios by adjusting each parameter and weight.

The utility of an attack strategy is defined as the payoff minus the cost, as shown in Equation (4).

$$U_A\left(s_A^i,s_D^j\right)={payoff}_A^i-{cost}_A^i$$

(4)

where ${payoff}_A^i$ is the attacker’s gain after implementing the attack strategy $s_A^i$, calculated as shown in Equation (5).

$${payoff}_A^i={payoff}_{A_i}^{full}\cdot {importance}_{A_i}^{relative}\cdot {cp}_{A_i}$$

(5)

where ${importance}_{A_i}^{relative}$ denotes the relative importance of the asset associated with the strategy; the asset is the component or data information in the system. ${payoff}_{A_i}^{full}$ denotes the payoff and cost under each complete attack strategy, respectively; ${cp}_{A_i}$ denotes the completion probability of the strategy, and ${cost}_A^i$ denotes the cost of the attack, which varies with the value at risk and the completion probability. ${cost}_A^i$ is calculated as shown in Equation (6).

$${cost}_A^i={cost}_A^{single}\cdot {risk}_{A_i}^{full}\cdot {cp}_{A_i}$$

(6)

Equation (7) defines the risk value of a strategy as the expected loss, combining completion probability with asset importance.

$${risk}_{A_i}^{full}=\left|{payoff}_{A_i}^{single}-{cost}_{A_i}^{single}\right|$$

(7)

Equations (5)–(7) into Equation (4) yields the attacker’s utility calculation function, as shown in Equation (8).

$$\begin{array}{cc}{U}_A\left(s_A^i,s_D^j\right)& ={payoff}_{\mathrm{A}}^i-{cost}_{\mathrm{A}}^i\\ & ={payoff}_{A_i}^{full}\cdot {importance}_{A_i}^{relative}\cdot {cp}_{A_i}-{cost}_{A_i}^{single}\cdot {risk}_{A_i}^{full}\cdot {cp}_{A_i}\end{array}$$

(8)

The idea of calculating the defender’s utility is similar to the attackers, as well as payoff minus cost, as shown in Equation (9). The difference is that the attacker is more concerned with the combined utility under the influence of payoff, risk, and loss, while the defender is mainly concerned with the balance between payoff and cost.

$$U_D\left(s_A^i,s_D^j\right)={payoff}_D^i-{cost}_D^i$$

(9)

where ${payoff}_D^i$ is the gain of the defender after implementing the defense strategy $s_D^j$, calculated as shown in Equation (10).

$${payoff}_D^i={payoff}_D^{full}\cdot {importance}_{D_i}^{relative}\cdot {cp}_{D_i}$$

(10)

where ${cost}_D^i$ is the defense cost, defined as the cost of resources deployed by the defense strategy, calculated as shown in Equation (11).

$${cost}_D^j={cost}_{D_j}^{single}\cdot {cp}_{D_j}$$

(11)

where ${cp}_{D_j}\in {CP}_{D_i}$, ${CP}_{D_i}$ is the set of completion probabilities of a defense strategy, defined as the likelihood of implementing a particular defense strategy and successfully achieving the desired goal.

Substituting Equations (10) and (11) into Equation (9), the defender’s utility function is shown in Equation (12).

$$\begin{array}{cc}{U}_D\left(s_A^i,s_D^j\right)& ={payoff}_{\mathrm{D}}^i-{cost}_{\mathrm{D}}^i\\ & ={payoff}_{D_i}^{full}\cdot {importance}_{D_i}^{relative}\cdot {cp}_{D_i}-{cost}_{D_i}^{single}\cdot {cp}_{D_i}\end{array}$$

(12)

To ensure consistency, payoff, cost, and asset importance are normalized to the [0, 1] range, and completion probability is likewise constrained between 0 and 1. This normalization eliminates scale mismatches and clarifies the payoff–risk–cost relationship across Equations (5)–(7).

To strengthen the NCADG-AS beyond a conceptual framework, we formalize it as an optimization model. The decision variables are the attacker’s completion probabilities across strategies and the defender’s resource allocations, which determine defense completion probabilities. The formulation is subject to a defense budget and probability simplex constraints. The objectives are opposing: both parties maximize their own expected utilities, thereby constituting a non-cooperative optimization game.

Pure strategies serve as the atomic elements of the space, while mixed strategies are probability distributions over these elements. The constraints ensure feasibility without excluding pure strategies, so mixed strategies generalize rather than contradict the formulation.

Equilibrium solutions are derived through Monte Carlo simulation on the pruned Attack–Defense Tree. This method avoids exhaustive enumeration and is computationally feasible under irregular, constrained spaces where analytical or linear programming approaches are not applicable. With 10,000 iterations, convergence was observed as additional runs changed utilities by less than 1%, ensuring both robustness and tractability of equilibrium estimates.

Unlike analytical or linear programming approaches, which require a convex and fully enumerated strategy space, the pruned NCADG-AS model yields an irregular and constrained space. Monte Carlo simulation is therefore employed as an efficient approximation method, enabling tractable exploration and convergence to equilibrium outcomes under uncertainty.

After completing the utility calculation for a single strategy pair, the overall expected utility functions of the attacker and the defender are shown in Equations (13) and (14), respectively. When the attacker’s expected utility increases, the system security decreases. Conversely, when the defender’s expected utility increases, the system security increases. Therefore, the attacker can increase the expected utility by enhancing the attacks or optimizing the resource allocation to increase the expected utility, which in turn leads to a decrease in the system security.

$$E_A\left({CP}_A,{CP}_D\right)={\sum }_{i=1}^m{cp}_A^i{\sum }_{j=1}^n{U}_A\left(s_A^i,s_D^j\right)={\sum }_{i=1}^m{\sum }_{j=1}^n\left[{cp}_A^i\cdot U_A\left(s_A^i,s_D^j\right)\right]$$

(13)

$$E_D\left({CP}_A,{CP}_D\right)={\sum }_{j=1}^n{cp}_D^i{\sum }_{i=1}^m{U}_D\left(s_A^i,s_D^j\right)={\sum }_{j=1}^n{\sum }_{i=1}^m\left[{cp}_D^j\cdot U_D\left(s_A^i,s_D^j\right)\right]$$

(14)

The set of completion probabilities $\left({CP}_A, {CP}_D\right)$ is a characterization of the equilibrium solution in the NCADG-AS model with non-negative values.

The zero-sum assumption is applied to capture the fundamental adversarial nature of cyber–physical security in avionics, where an attacker’s gain generally translates to a defender’s loss. We acknowledge that certain safeguards, such as redundancy, could introduce partial non-zero-sum dynamics, but a zero-sum abstraction offers analytical tractability and is consistent with established attack–defense game literature. The halving of utilities for corresponding strategy pairs is introduced as a normalization step to prevent double-counting when interdependent strategies affect the same asset, thereby preserving balanced representation in the utility matrix.

3.4. Decision Perspective Switch and Equilibrium Optimal Solution

Following the NCADG-AS model specifications, the defender should strategically optimize its resource allocation to enhance expected utility by initially undertaking an adversarial analysis from the attacker’s viewpoint. To derive the attacker’s completion probability allocation strategy, the defender must first construct the attacker’s utility matrix. Subsequently, a Nash equilibrium solution is applied to maximize the attacker’s expected utility. The defender can then refine its completion probability allocation based on this equilibrium solution, ultimately improving its resource allocation in a targeted manner.

Within the NCADG-AS model, for attacker and defender, if $S_A^{*}, {UtilityMatrix}_A^{*}, {CP}_A^{*}$ and $S_D^{*}, {UtilityMatrix}_D^{*}, {CP}_D^{*}$ satisfy Equations (15) and (16), respectively, then $({CP}_A^{*},{CP}_B^{*})$ represents a Nash equilibrium solution in the current attack–defense strategy space. Here, $S_A^{*}$, $S_D^{*}$, ${UtilityMatrix}_A^{*}$, ${UtilityMatrix}_D^{*}$, ${CP}_A^{*}$ and ${CP}_B^{*}$, respectively, denote the current strategy spaces, utility matrices, and completion probability allocation outcomes for the attacker and defender.

$$E_A\left(S_A^{*},{UtilityMatrix}_A^{*},{CP}_A^{*}\right)\ge E_A\left({UtilityMatrix}_A^{*},{CP}_A^{any}\right),\forall {CP}_A^{*}{,CP}_A^{any}\in {CP}_A$$

(15)

$$E_D\left(S_D^{*},{UtilityMatrix}_D^{*},{CP}_D^{*}\right)\ge E_D\left({UtilityMatrix}_D^{*},{CP}_D^{any}\right),\forall {CP}_D^{*}{,CP}_D^{any}\in {CP}_D$$

(16)

Within the constraints of a pure strategy framework, attackers and defenders are restricted to allocating resources solely toward one of two types: high value (HCE) or equal value (ECE), significantly constraining the efficient utilization of resources.

The NCADG-AS facilitates participants in amalgamating their interests based on real-world contexts. This methodology delineates the dynamics between attack and defense strategies through the framework of the ADT. To elucidate the intricate interplay between adversarial strategies, a comprehensive identification matrix is devised, categorizing pairs of strategies where a direct relationship is discernible. To ensure a balanced advantage, encountering corresponding strategy pairs necessitates halving the singular strategy gain for one party.

In the context of a non-cooperative attack and defense game, the focal point for each party revolves around optimizing the utility of its strategy, irrespective of the opposing party’s strategic choices. This premise is grounded on the assumption of rationality, implying that each participant is logical and harbors realistic anticipations regarding the counteractions of fellow participants [48]. This suggests confidence among all game participants that adversarial strategies have been adequately implemented by the opposing party.

Within the framework of the predetermined non-cooperative game model, traditional mixed equilibrium solutions primarily focus on assigning probabilities that maximize utility, often culminating in the optimal assignment of a probability of 1 to a specific strategy and 0 to the remainder. However, considering the paramount security demands of avionics systems, it is crucial for the defender not to disregard any strategy within the strategy space during the formulation process. As such, a thorough evaluation of each potential strategy is essential to ensure the system’s robust and comprehensive defense against potential threats.

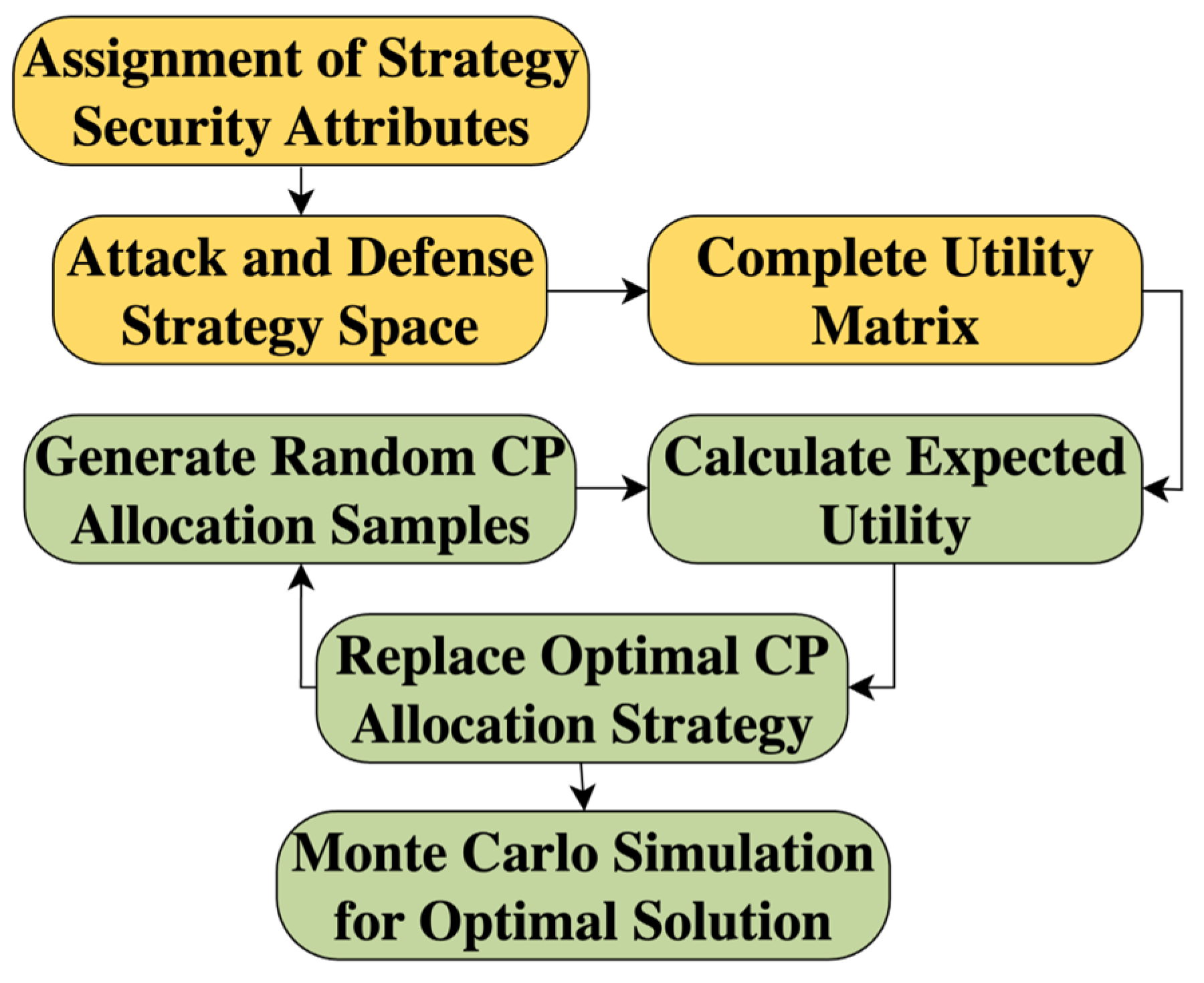
Under these circumstances, the traditional approach to mixed-strategy games for equilibrium determination appears limited. The Monte Carlo simulation, in contrast, presents a more comprehensive methodology, enabling an exhaustive assessment of the combined impacts of disparate strategies. This is accomplished by generating an extensive array of random samples across the entire strategic spectrum. Figure 2 depicts the workflow of the Monte Carlo simulation, indirectly deducing the optimal solution across numerous simulation iterations by maximizing the expected utility.

It should be noted that Monte Carlo provides an approximation rather than an exact Nash equilibrium. However, compared to exact algorithms such as Lemke–Howson, which are computationally expensive in large-scale games, Monte Carlo offers a tractable alternative that yields stable equilibrium tendencies with sufficient sampling.

This method offers a more detailed and holistic perspective on the equilibrium challenge within the game. Moreover, by relying on randomized sampling rather than exhaustive enumeration of all possible attack–defense combinations, the Monte Carlo method significantly reduces computational complexity while retaining robustness in equilibrium estimation.

Compared with traditional methods such as linear programming or reinforcement learning approaches like Q-learning, Monte Carlo simulation is more suitable for NCADG-AS because it avoids the need for closed-form payoff functions or large volumes of training data, while still providing tractable equilibrium estimates for complex avionics strategy spaces.

This approach also supports scalability to avionics systems with hundreds of components. Although the attack–defense tree can expand rapidly with system complexity, pruning eliminates redundant branches, and Monte Carlo simulation provides tractable equilibrium estimates without exhaustive search. These features enable the practical application of NCADG-AS to large-scale avionics architectures.

4. Experiment Design and Case Study

Diagrams were created using Microsoft Visio (Microsoft Corporation, Redmond, WA, USA; Version 2021). Code development was performed in PyCharm (JetBrains s.r.o., Prague, Czech Republic; Version 2023.2). Data analysis and plotting were conducted using Origin (OriginLab Corporation, Northampton, MA, USA; Version 2023).

4.1. Experiment Subject

Given that the EFIS (Electronic Flight Instrument System) for flight planning and information display serves as a critical human–computer interaction interface aboard civil airliners, its functionality is pivotal to ensuring that civil airliners can safely execute their intended flight missions. EFIS aggregates flight information necessary for pilots from a multitude of data sources, presenting a vulnerability whereby an attacker could gain access to one or more of these sources, potentially compromising the accurate display of flight information or even generating deceptive information capable of misleading pilots. The complexity introduced by these multiple data sources amplifies the potential for system threats. In light of EFIS’s essential role in flight operations and the prevalent risk extension from multiple data sources, this study elects the multi-data source scenario of EFIS for flight planning and information display as a focal point to exemplify and share insights on applying the NCADG-AS within avionic systems. The EFIS data flow model is derived from publicly available avionics architecture descriptions and standards such as ARINC 702A (Flight Management System), ARINC 753 (EFIS characteristics), and ARINC 664 (AFDX network) [49,50,51]. It does not rely on proprietary aircraft documentation, but serves as a representative abstraction to demonstrate NCADG-AS applicability.

Drawing from the avionics system topology of the A380 as described in [52], Figure 3 delineates the network configuration relevant to the EFIS for flight planning and information display functionalities. Within this network architecture, five AFDX switches are instrumental in facilitating data transmission pertinent to these functions. The pairwise representation of switches (e.g., sw1–sw2, sw3–sw5, and sw5–sw6) reflects the redundancy mechanism of the AFDX architecture defined in ARINC 664. Each data flow is transmitted over two independent but synchronized networks to ensure fault tolerance so that a single switch or link failure does not compromise EFIS data integrity or availability. Significantly, the Management and Control Display Unit (MCDU) plays a vital role within the FMS. Pilots interact with the MCDU to input commands, manage flight and navigation data, and interface with the FMS through the execution of flight plans and other operational directives. EFIS is tasked with presenting flight data and navigational information, typically encompassing an array of Liquid Crystal Display (LCD) screens and integrated circuits, strategically positioned within the cockpit’s instrument panel.

The network topology of the EFIS for flight planning and information display is employed to delineate the static configuration of system components associated with this function. Viewing the network topology as a static representation of spatial information within the system allows for a contrasting dynamic perspective offered by data flow diagrams, which illustrate the flow of data information. Data flow diagrams are extensively utilized in system analysis and design to visually represent processes and include the various stages through which data transits during transmission.

The data flow diagram depicted in Figure 4 showcases the entire process associated with the EFIS flight planning and information display function, encompassing data collection, transfer, processing, and visualization. The input data comprise pre-stored information from databases, real-time flight data sourced from internal sensors, and pilot input commands via the Management and Control Display Unit (MCDU). This comprehensive representation facilitates a deeper understanding of both the static interconnections and dynamic data movements within the EFIS, highlighting the intricate processes that underpin the functionality of flight planning and information display.

The EFIS serves as a critical data source for pilots during flight operations. Through the MCDU, pilots can input modifications to the flight plan, as well as set speed and altitude limits, adapting these inputs to actual flight conditions. Once the FMS processes the flight plan-related information, it is instantaneously displayed on the Primary Flight Display (PFD) and Navigation Display (ND) within the EFIS, allowing pilots to review or further adjust the information. This integrated operation is designed to mitigate the task load on pilots and significantly enhance the efficiency of flight mission execution.

If the EFIS data source is compromised due to an attack, pilots could be deprived of substantial flight information, posing a grave threat to the safety and integrity of the flight mission. The safeguarding of EFIS data sources is, therefore, paramount to maintaining operational safety and ensuring the seamless execution of flight missions.

4.2. Design and Model Parameters

This study exemplifies the methodology proposed herein through an illustrative analysis encompassing the construction of a two-attribute ADT, the aggregation of strategy space, the computation of the utility matrix, and the simulation of completion probability assignments. Within a specified mission, the attacker allocates probabilities across diverse attack strategies, with the aggregate probabilities equating to one. This denotes the attacker’s commitment to initiating an attack during the mission, with the assigned probabilities representing the completion likelihood of each strategy.

Given that the avionics system operates within an airborne execution environment, the management and deployment of attack and defense strategies necessitate ground-based preparation. The attacker’s selection of targets is influenced by several factors, including the attack cost, the expected payoff, the relative significance of the targeted assets, and the accessibility of the target. To maximize attack target accessibility, the attacker exploits all identified vulnerabilities, necessitating multiple rounds of game analysis to derive varying equilibrium solutions. During the ground system’s maintenance phase, data sources are particularly vulnerable compared to stages involving data transmission, processing, and display. Thus, data sources are considered the highest-level attack targets.

In terms of security attribute assignment, strategies are categorized to identify those achieving the highest value within the security attribute class. Following this, the remaining strategy types are assigned security attribute values based on this categorization. The assignment of multi-class security attribute values is pivotal for sensitivity analyses during the utility calculations of the non-cooperative game model, facilitating the depiction of system security fluctuations. These assignments are subject to continual refinement with updates to the attack information database.

The effectiveness identification matrix is constructed by mapping each defensive strategy to its targeted attack nodes and then assigning relative weights according to payoff, cost, and asset importance values. These weights are normalized to the [0, 1] range to ensure comparability across attributes. The resulting matrix provides a structured way to capture the contribution of each defensive measure to the overall system security posture and serves as the foundation for subsequent utility calculations.

The comprehensive payoff of strategies and the relative importance of assets are delineated by category, as illustrated in

Table 1. Strategy complete payoffs and corresponding asset relative importance.

Participant’s Strategy Category	Strategy Full Payoff	Strategy Targeted Asset	Asset Relative Importance
Information strategy	5	Physical strategy	5
Physical strategy	3	Information strategy	4
Information–physical strategy	3	Information–physical strategy	3
Indirect strategy	2	Indirect strategy	1

. Considering the enduring nature of cyber-attacks compared to physical functions and their broad impact on networked systems, physical strategies typically focus on safeguarding physical devices and premises, affecting a more constrained area.

Table 1 also portrays the relative importance of assets associated with respective strategies. Cyclic maintenance prioritizes physical inspections due to the avionics system’s imperative to guarantee functional fulfillment. The direct influence of physical hardware on the flight’s capacity to safely execute its mission underscores this prioritization.

In the non-cooperative game framework, participants solely focus on maximizing their payoffs. Each participant is tasked with calculating their respective strategy attribute values and utility matrix independently. The associated costs for implementing attack strategies and for the deployment of defense strategies are elaborately itemized in

Table 2. Initial attack and defense strategy single execution costs.

Attacker Strategy Category	Strategy Cost	Defender Strategy Category	Strategy Cost
Information strategy	4	Physical strategy	5
Physical strategy	2	Information strategy	3
Information–physical strategy	1	Information–physical strategy	1

. Notably, the avionics system employs physical countermeasures such as isolation, robust hardware, and architectures that remain opaque to an attacker. Yet, due to its complex and specialized nature, the avionics system predicates higher costs for both the attacker and defender, particularly in the analysis and implementation of information-centric strategies. Moreover, within the context of indirect attack strategies, sub-nodes may incorporate a diversity of sub-strategy types, further complicating the strategic landscape.

The information strategy concentrates on aspects, including data transmission, communication, and storage, typically addressed and mitigated through the implementation of advanced cybersecurity protocols. Conversely, the physical strategy pertains to tangible physical equipment, infrastructure, and system components, necessitating the adoption of disaster prevention initiatives, backup solutions, and consistent maintenance practices. Information–physical strategies pose the greatest risk within avionics systems, attributed to the confluence of cyber and physical strategies. This amalgamation intensifies due to the mutual influence of functional safety and information security, culminating in intricate and potentially severe consequences. The susceptibility to indirect attacks varies based on the specific nature of the attack, with the risk values associated with various attack strategies delineated in

Table 3. Attacker strategy risk values.

Participant’s Strategy Category	Strategy Full Risk Value
Information–physical strategy	2
Information strategy	1
Physical strategy	1

. This nuanced stratification underscores the multifaceted nature of threats in avionics systems, highlighting the critical need for a comprehensive security approach that addresses both information and physical domains, alongside their intersection.

The parameter assignments are guided by qualitative reasoning consistent with recent attack–defense game studies (e.g., [19]), which similarly rely on expert-informed payoff structures. To address concerns of subjectivity, a sensitivity analysis was conducted by varying payoff and cost parameters within reasonable bounds. Although absolute utility values shifted, the equilibrium dynamics and defender optimization results remained stable, demonstrating that the NCADG-AS model is robust to parameter variations.

A direct baseline or benchmark was not employed, as existing attack–defense models for avionics systems differ considerably in scope, assumptions, and attribute definitions, making one-to-one comparison infeasible. Instead, model robustness was evaluated through sensitivity analysis of parameter variations, which serves as a practical proxy for baseline validation by demonstrating the stability and reliability of NCADG-AS outcomes under diverse conditions.

In the absence of an attacker perspective analysis, the defender is inclined to enhance protection across all identified security risk points, albeit with the distribution of limited defense resources being indiscriminate. To demonstrate the detrimental effects of such untargeted optimization behavior, we propose an undifferentiated enhancement of the defense strategy, examining its repercussions on system security. Additionally, we assess the necessity of targeted defense strategy management and undertake strategy sensitivity analysis to gauge the influence of distinct defense strategies on system security.

5. Results and Discussion

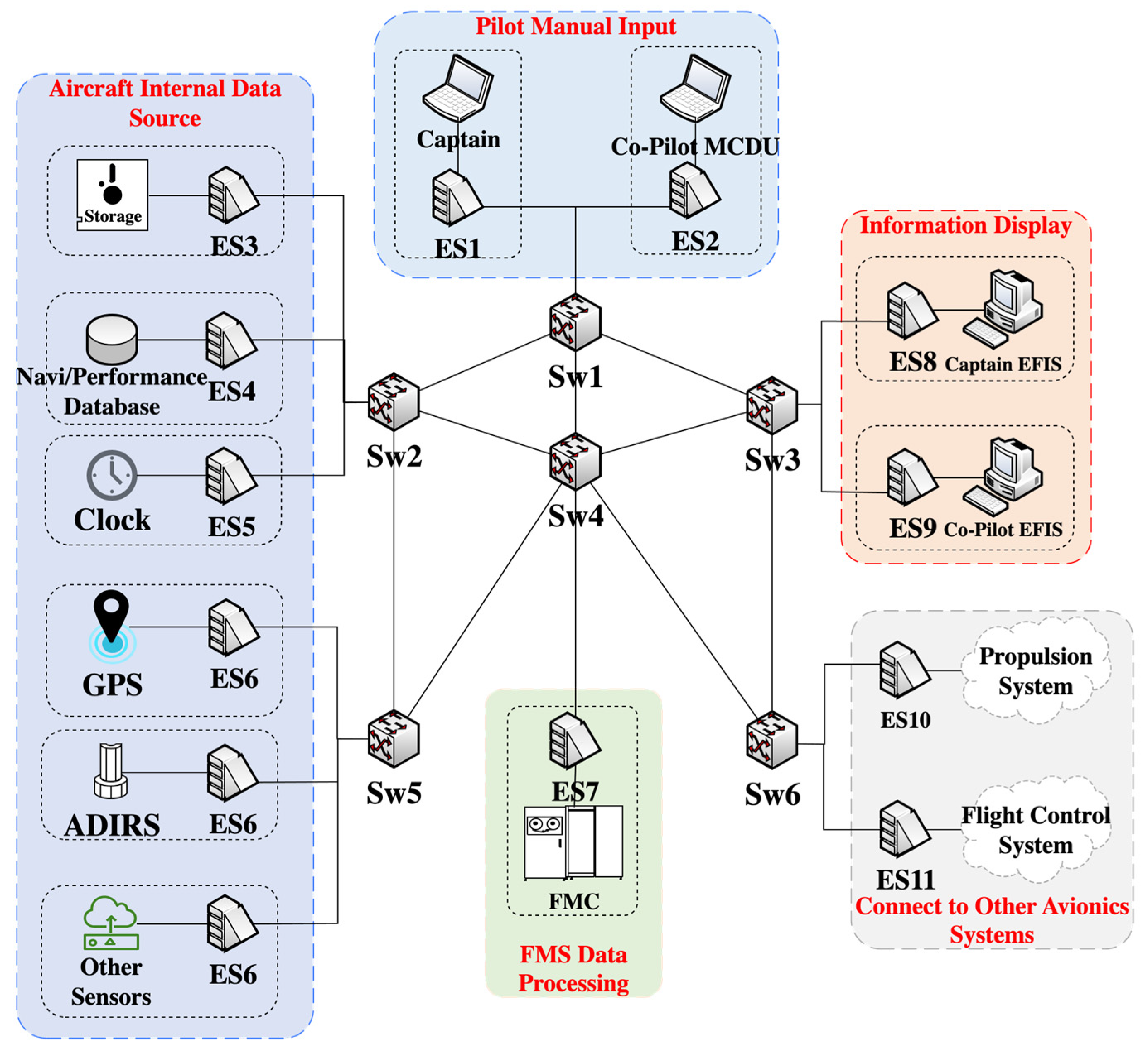
In practical avionics, the Electronic Flight Instrument System (EFIS) functions within a closed environment, relying on standardized protocols such as ARINC 429 [53] and ARINC 664/AFDX, and is safeguarded by multiple layers of protection, including authentication, encryption, and physical isolation. The threat scenarios analyzed in this section do not imply direct protocol bypasses. Instead, they represent simplified entry points (e.g., tampering with pilot inputs, exploiting vulnerabilities in preloaded ground data, or targeting onboard databases) that serve to demonstrate how the NCADG-AS framework evaluates attack–defense dynamics. This enables tractable modeling of adversarial interactions while remaining consistent with the operational constraints of avionics systems.

While the evaluation focuses on the EFIS as a representative avionics subsystem, this case study serves as an illustrative validation of the NCADG-AS framework rather than a comprehensive assessment of all avionics systems. EFIS was selected due to its central role in flight operations and the availability of well-defined interfaces and defense mechanisms. The framework is generalizable to other avionics subsystems, but applying it to different contexts requires tailoring of strategy sets and parameter assignments.

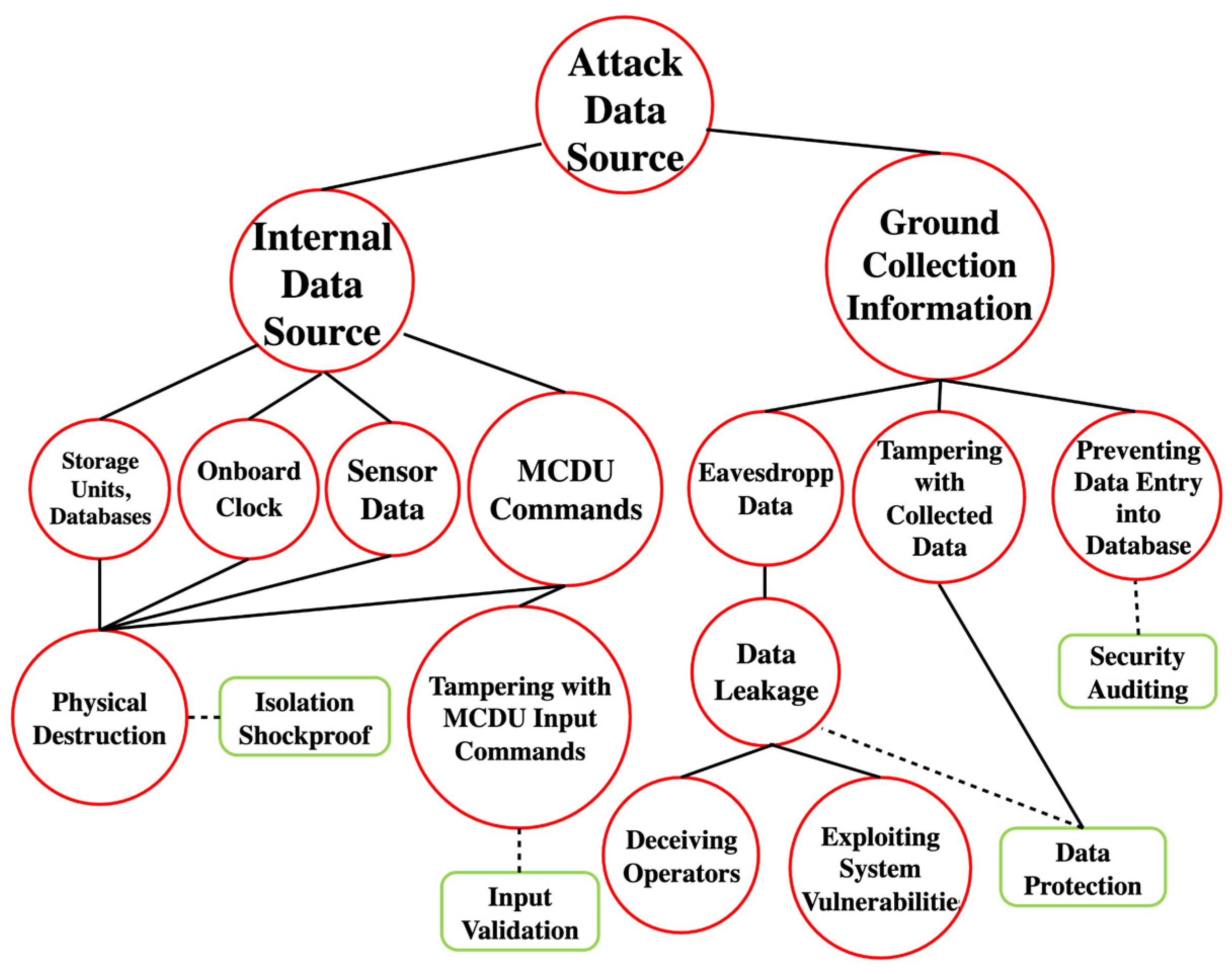
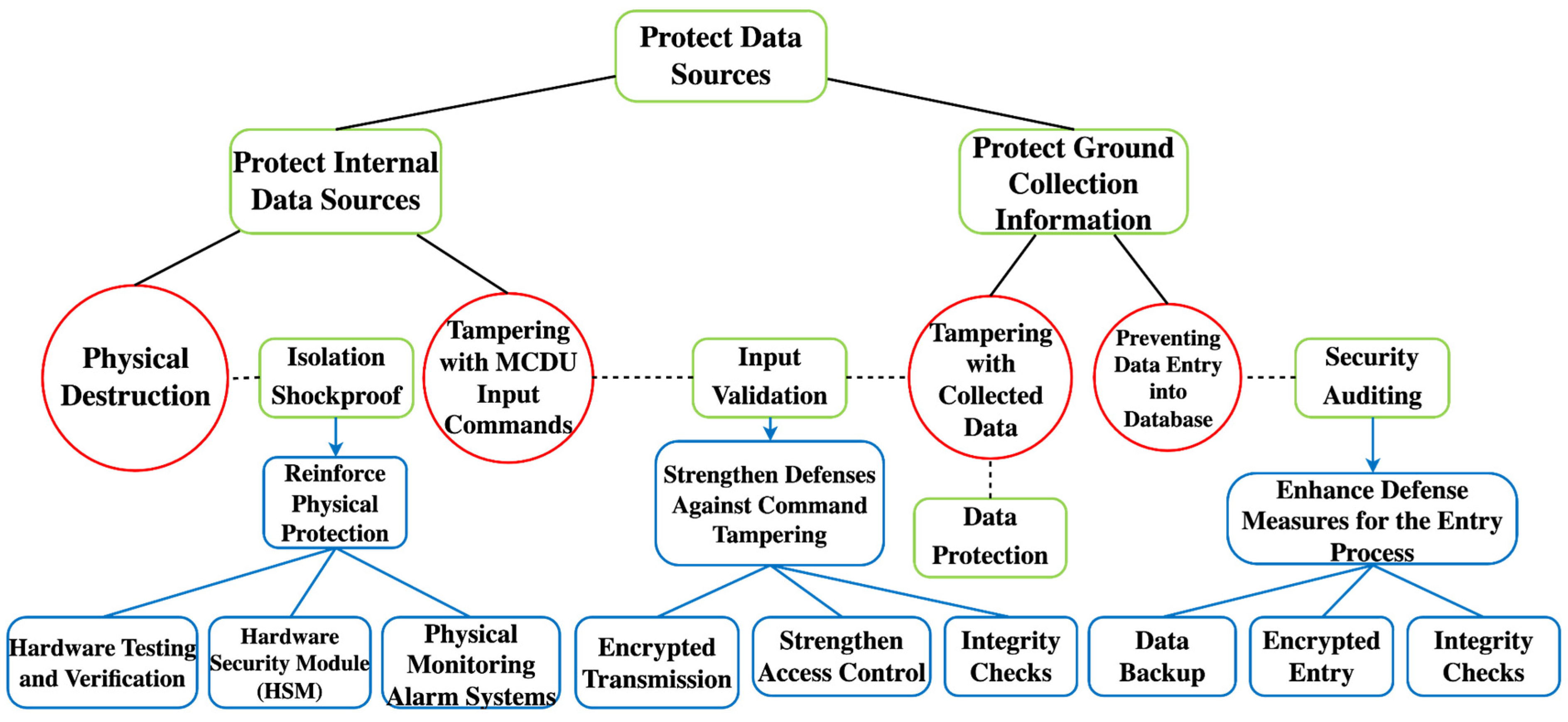
From the attacker’s perspective, an A-ADT for the “Attack on EFIS Flight Plan and Information Display Data Sources” security scenario is established, as shown in Figure 5. In this tree, red circular nodes represent attack attributes, while green square nodes signify defense attributes. In this threat scenario, data sources include both internal and external sources (information collected from the ground). Internal data sources primarily consist of onboard storage units, navigation databases, performance databases, onboard clocks, onboard sensors, and flight instructions input by pilots through the MCDU. Each internal data source element corresponds to specific components that the attacker can target for physical destruction. To counter physical damage, isolation shockproofing is a physical measure taken against vibrations and impacts during flight designed to ensure that the avionics systems remain operational in the face of external shocks, thereby maintaining the accuracy of flight data and system stability. For flight instructions manually input by pilots, attackers might attempt to tamper with these instructions, replacing real commands with false ones. Consequently, for data input, the defender adds input validation measures to combat this attack, which are aimed at ensuring the authenticity of the commands.

External data sources primarily refer to information collected in advance. When an aircraft is on the ground preparing for its next flight mission, the collected information, encoded in a standard format, can be entered into the flight database. Concerning ground-collected information, attackers can eavesdrop on data to further identify vulnerabilities and then selectively manipulate the data. Furthermore, the leakage of data can facilitate conditions for eavesdropping, with attackers potentially exploiting operator deception and scanning for system vulnerabilities to exfiltrate data. Defenders employ data protection mechanisms such as data encryption, secure transmission protocols, and integrity checks to mitigate the risks of data leakage and manipulation to some extent. Additionally, attackers may attempt to prevent the correct entry of data into the database. To minimize the risks associated with erroneous data entries, defenders can conduct security audits to verify the data in the database, ensuring its confidentiality, integrity, and availability.

After completing the initial A-ADT modeling, we can eliminate the intermediate nodes in the attack path and focus only on specific attack actions, i.e., the leaf nodes, to derive the initial strategy space for both attack and defense. In the data source A-ADT model, the attacker’s initial strategy space includes [“Physical Destruction”, “Tampering with MCDU Input Commands”, “Deceiving Operators”, “Exploiting System Vulnerabilities”, “Tampering with Collected Data”, “Preventing Data Entry into Database”]. The defender’s initial strategy space includes [“Isolation Shockproof”, “Input Validation”, “Data Protection”, “Security Auditing”].

To calculate the utility matrix for the attacker, it is imperative to ascertain the inter-strategy correlations derived from the A-ADT, signifying that those particular strategies are only effective against specific counterstrategies. This necessitates the construction of an effectiveness identification matrix, with the number of rows corresponding to the total count of present attacker strategies, and the number of columns corresponding to the total count of defender strategies. Strategy pairs that exhibit this specific interrelation are assigned a value of True, whereas all others receive a value of False. Within the matrix, these assignments are symbolized by check marks (for True) and crosses (for False), as illustrated in

Table 4. Attack data source valid identification matrix. √: applicable, ×: not applicable.

	Isolation Shockproof	Input Validation	Data Protection	Security Auditing
Physical Destruction	√	×	×	×
Tampering with MCDU Input Commands	×	√	×	×
Deceiving Operators	×	×	√	×
Exploiting System Vulnerabilities	×	×	√	×
Tampering with Collected Data	×	×	√	×
Preventing Data Entry into Database	×	×	×	√

. For the utility matrix computation, one strategy is fixed at a time, and the effectiveness identification matrix is traversed to identify any effective strategy pairs. If such pairs are found, the single execution reward for a strategy is reduced by half.

Attribute values are assigned according to the type of attack strategy, and a complete utility matrix with a strategy completion probability of 1 is calculated, as shown in

Table 5. Initial attack strategy complete attack utility matrix.

	Isolation Shockproof	Input Validation	Data Protection	Security Auditing
Physical Destruction	5.5	13	13	13
Tampering with MCDU Input Commands	16	6	16	16
Deceiving Operators	1	1	0	1
Exploiting System Vulnerabilities	1	1	0	1
Tampering with Collected Data	16	16	6	16
Preventing Data Entry into Database	7	7	7	2.5

. “Deceiving Operators” and “Exploiting System Vulnerabilities”, acting as sub-nodes of data leakage, aim to avoid causing direct damage to the system. This attack strategy employs an indirect method of attack, producing an effect opposite to that of immediate destructive attacks; hence, its direct payoffs are relatively limited. To covertly linger within the system, secretly gather information, or conduct malicious activities while evading detection by system administrators or security tools, this tactic is characterized by high concealment and minimal exposure. Although the importance of the corresponding assets is relatively low initially, it remains significant in terms of long-term overall security and risk management. If such risks are not assessed over time, the potential threat will continue to accumulate, possibly leading to intolerable risks.

Here, an example is provided to illustrate the method of calculating the complete utility of strategies. Based on Table 4, the strategy pair {“Physical Destruction”, “Isolation Shockproof”} is identified as True, indicating that a corresponding relationship exists, and thus, the payoff for the attacker executing the “Physical Destruction” strategy is halved. In Table 1, it is shown that when the utility of the “Physical Destruction” strategy is halved, its utility becomes 1.5. To calculate the utility of the “Physical Destruction” attack strategy, we can assign values to the security attributes of the “Physical Destruction” attack strategy based on other security attribute tables. When calculating the initial utility matrix, the strategy completion probability ${cp}_{A_i}=1$. Therefore, for the attacker, the utility of this strategy pair is calculated as $(3\times 0.5\times 5-2\times \left|3-2\right|\times 1)=5.5$. This result is entered into Table 5, and the utility of other strategy pairs for the attacker is calculated in a similar cycle. The method of calculating the utility of the strategy pair {“Physical Destruction”, “Isolation Shockproof”} for the defender follows the same principle.

Further, the overall expected utility for the attacker is calculated according to Equation (8). With the completion probabilities of each strategy being unknown, to solve for the distribution of completion probabilities that maximizes expected utility, it is necessary to identify strategies of higher priority. This study employs multiple iterations of Monte Carlo simulations to find the optimal distribution of completion probabilities.

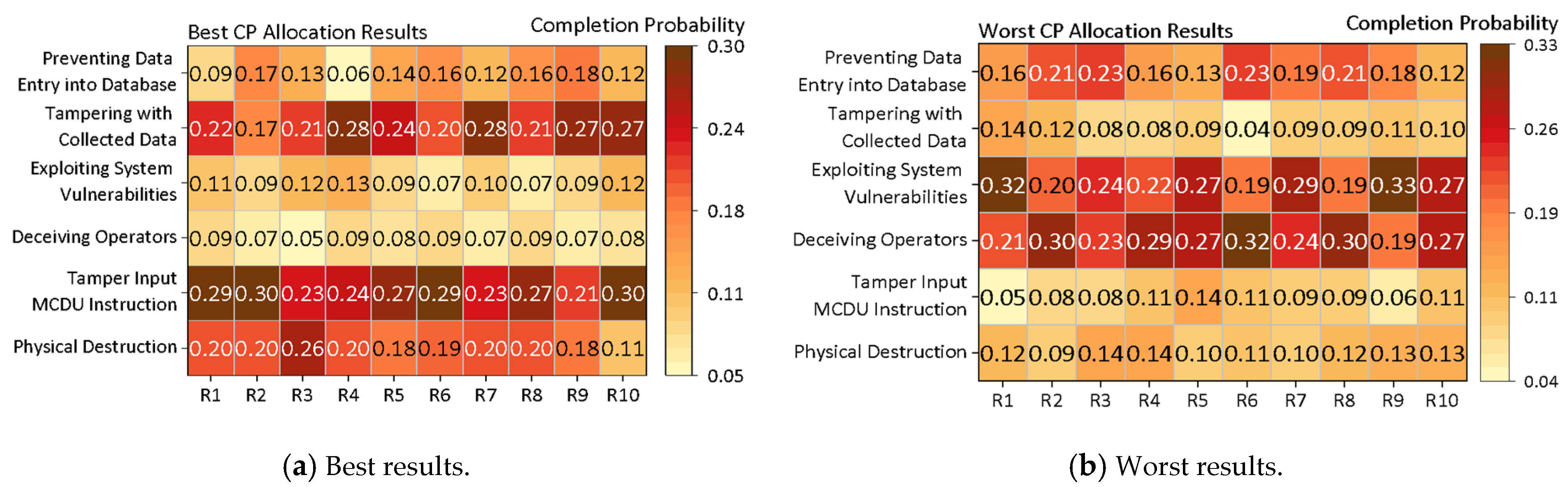
The initial game simulation results record the maximum and minimum expected utilities and corresponding distributions of attack completion probabilities for every 100,000 rounds of Monte Carlo simulations, as well as the overall average utility, ensuring that the sum of the completion probabilities for all strategies does not exceed 1. The optimal and worst distributions of attack completion probabilities from the game simulations, along with the distribution of outcomes, are illustrated in Figure 6.

In Figure 6a, it is shown that to achieve a higher expected utility, the attacker needs to increase the completion probabilities of “Physical Destruction”, “Tampering with MCDU Input Commands”, and “Tampering with Collected Data”. Attackers need to allocate more related resources to achieve higher completion probabilities, with particular emphasis on the strategies of “Tampering with MCDU Input Commands” and “Tampering with Collected Data”. Conversely, Figure 6b illustrates the distribution of completion probabilities corresponding to the minimum expected utility.

Building upon the existing strategic space, we can consider how to enhance the complete payoff of specific strategies. There are various methods of enhancement, such as attacker adopting sub-strategies to acquire more flight information, setting timed attack strategies to precisely execute “Tampering with MCDU Input Commands” at critical moments, increasing the success rate of attacks to boost the payoff of completed attacks, or remaining covert for extended periods using methods such as zero-day exploits to continuously collect information in preparation for the next attack before detection and defense is possible. However, it is important to note that while deploying security resources increases the payoff of strategy execution, it also raises the cost of the strategy. Therefore, costly and high-risk attack strategies should be avoided. To solve the expected utility in the next round, the utility matrix needs to be recalculated.

In the initial game simulation by the attacker, the two strategies contributing most to the maximum expected utility were “Tampering with MCDU Input Commands” and “Tampering with Collected Data”. Optimization of completion probabilities through Monte Carlo simulation calculations is conducted by improving the security attributes of both.

When an attacker attempts to enhance the strategy with the highest completion probability, this is referred to as “Enhanced the Top1 Strategy”. In a mixed strategy setting, increasing the payoff of the “Tampering with MCDU Input Commands” strategy to 7 increases the cost to 5 and the risk to 2. In this scenario, the utility matrix for the attacker is recalculated, updating the row for “Tampering with MCDU Input Commands” in the complete utility matrix to [18, 4, 18, 18], and the expected utility game outcomes are recorded.

Enhancing the security attributes of the top two-ranked strategies is referred to as “Enhanced the Top2 Strategies”. That is, the complete payoffs of “Tampering with MCDU Input Commands” and “Tampering with Collected Data” increase to 9 and 7, respectively, with both costs increasing to 5, updating the row for “Tampering with MCDU Input Commands” in the attacker’s complete utility matrix to [16, −2, 16, 16], updating the row for “Tampering with Collected Data” to [28, 28, 14, 28], and recording the expected utility simulation results. The risk value for “Tampering with Transmission Commands” increases to 4, rendering the utility negative for the attacker when the defender employs the corresponding strategy to “Tamper with Transmission Commands”.

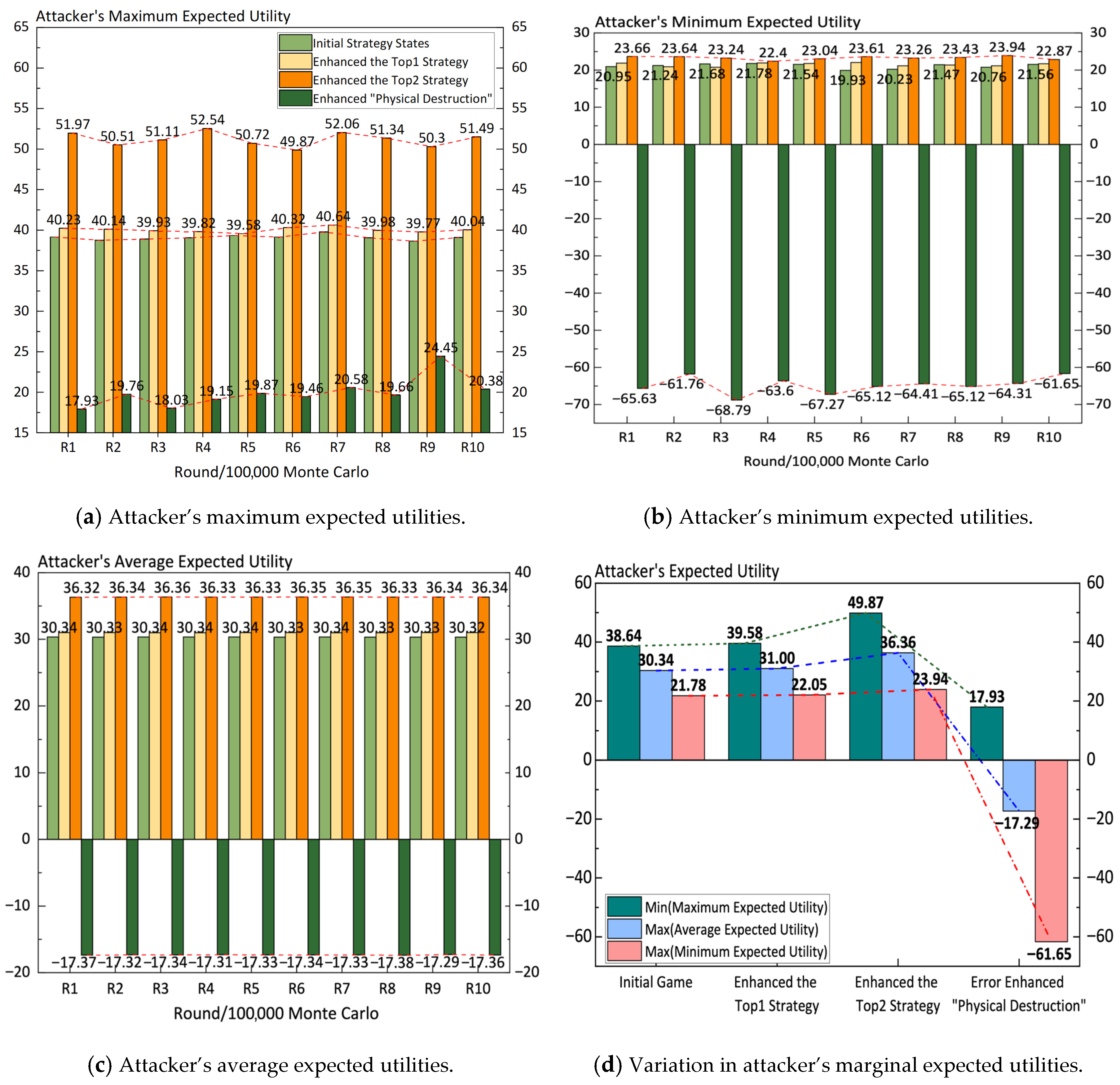
In the context of avionics networks, attackers face a dilemma when executing physical destruction, balancing between achieving the attack’s objectives and avoiding causing significant civil aviation accidents. To analyze whether enhancing the less controllable physical destruction can improve the attacker’s expected utility, the complete attack payoff of “Physical Destruction” is reduced to −1, with the cost increased to 7, and the risk increased to 8. The “Physical Destruction” row in the utility matrix is updated to [−58.5, −61, −61, 61], and the game simulation outcomes are recorded. The maximum expected utilities, minimum expected utilities, and average expected utilities over multiple rounds are categorized and displayed in four subfigures in Figure 7.

It can be observed that, regardless of the evaluation metric, increasing the use of the less controllable strategy of “Physical Destruction” significantly reduces the expected utility. Therefore, the attacker should avoid relying on less controllable physical destruction strategies. The simulation results of three optimal completion probability distributions, optimized based on initial game outcomes, are visually displayed in Figure 8.

Although the three enhanced strategies impact the expected utility to varying degrees, to achieve the highest possible expected utility value, the attacker is still required to focus on the information strategies of “Tampering with Collected Data” and “Tampering with MCDU Input Commands.” This entails maximizing the completion probabilities of these strategies as much as possible and allocating more resources toward them.

For the initial A-ADT, an initial game analysis is undertaken from the perspective of the defender. Security attributes for the defensive strategy space are assigned based on the category of strategy. Data leakage and eavesdropping, which do not cause immediate damage to the system, are classified as indirect attack strategies. “Data Protection,” as it addresses both indirect attack strategies and information strategies, involves the aggregation of the complete execution payoffs of both strategy types, with their relative importance summed similarly. The defender’s initial strategy complete utility matrix is depicted in

Table 6. Initial complete utility matrix for defensive strategies.

	Physical Destruction	Tampering with MCDU Input Commands	Deceiving Operators	Exploiting System Vulnerabilities	Tampering with Collected Data	Preventing Data Entry into Database
Isolation Shockproof	2.5	10	10	10	10	10
Input Validation	17	7	17	17	17	17
Data Protection	39	39	18	18	18	39
Security Auditing	8	8	8	8	8	3.5

.

Based on the initial game outcomes, the distribution of completion probabilities for the defender’s initial game is shown in Figure 9. To maximize the expected utility for the defender within an unoptimized defensive strategy space, more resources should be allocated to “Data Protection”.

Before solving for equilibrium from the attacker’s perspective, the defender does not know which attack strategies will be prioritized by the attacker. At this point, the defender makes non-specific modifications to the existing defense strategies to save computational time and resources. This involves removing intermediary attack paths, retaining only the modes of attack, and excluding non-direct attack methods. “Deceiving Operators” and “System Vulnerabilities” do not immediately harm the target. Furthermore, despite these two types of attack actions having minor direct impacts, their occurrence probabilities are overestimated in actual scenarios. To address this contradiction, the corresponding two leaf nodes are pruned. Non-targeted defense strategies are added to the pruned ADT, and the results of the D-ADT modeling are shown in Figure 10. The blue square nodes indicate the newly added non-targeted defense measures.

Although these indirect attack strategies (e.g., deceptive operators and exploiting vulnerabilities) do not cause immediate system damage, we recognize their potential significance in long-term persistent threats such as APTs or social engineering attacks. In this study, they are excluded from the core equilibrium analysis to maintain tractability, but their long-term cumulative risks are acknowledged and will be addressed in future extensions of the NCADG-AS framework.

We can update the strategy space and effectiveness identification matrix, assigning security attributes based on the category of the strategy. The defender’s utility matrix after non-specific strategy enhancement is shown in

Table 7. Utility matrix for non-specifically enhanced defensive strategies.

	Physical Destruction	Tampering with MCDU Input Commands	Tampering with Collected Data	Preventing Data Entry into Database
Isolation Shockproof	2.5	10	10	10
Hardware Testing and Verification	−0.5	4	4	4
Hardware Security Module (HSM)	2.5	10	10	10
Physical Monitoring Alarm Systems	2.5	10	10	10
Input Validation	17	7	7	17
Encrypted Transmission	17	7	7	17
Strengthen Access Control	17	7	7	17
Integrity Checks	17	7	7	7
Data Protection	39	39	18	39
Security Auditing	8	8	8	3.5
Data Backup	8	8	8	3.5
Encrypted Entry	17	17	17	7

.

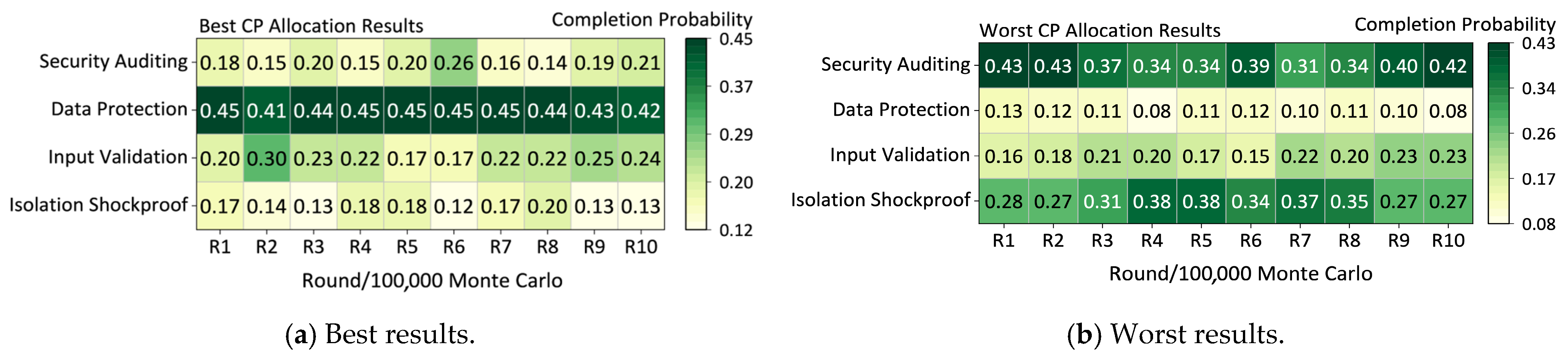
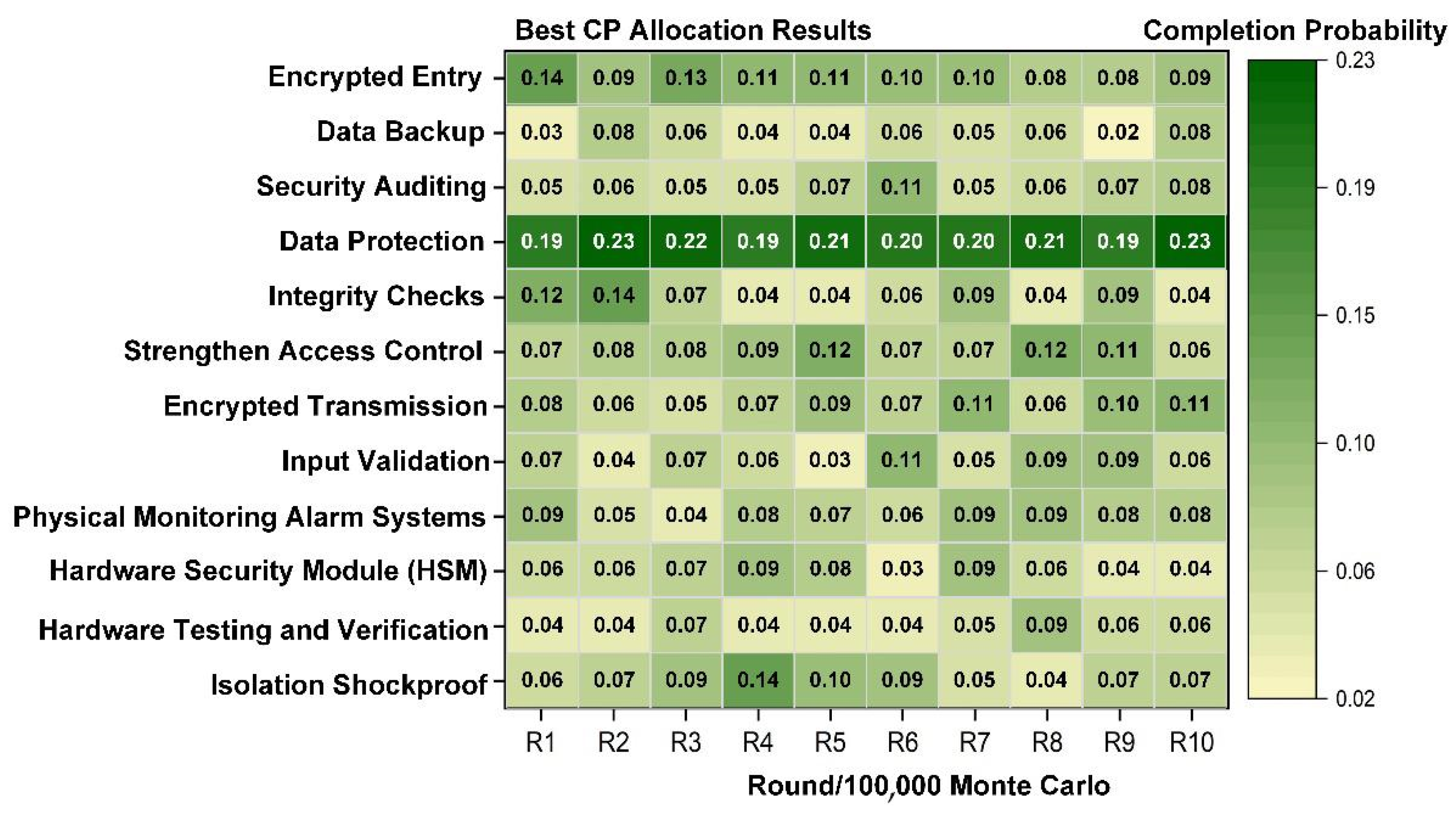
After the Monte Carlo game simulation, the optimal distribution results for the completion probability of non-specifically added defensive strategies are shown in Figure 11. Intuitively, as the strategy space expands with the addition of non-specific strategies, the completion probability allocated to each strategy decreases. It would be impractical for the defender not to allocate resources with focus, as this could significantly reduce the expected utility compared to the initial defensive game outcomes.

Non-specific enhancement of defensive strategies fails to increase the defender’s expected utility. Although the NCADG-AS results indicate that such enhancements yield limited gains under the modeled resource and probability constraints, this reflects the efficiency perspective of the model rather than a dismissal of practical relevance. In real avionics, even incremental and non-targeted measures can strengthen baseline resilience and reduce long-term risks. The purpose of NCADG-AS is to guide decision makers in prioritizing limited resources toward strategies with the greatest marginal benefit, thereby complementing—not replacing—broad, layered defenses.

Therefore, adjustments are made to the D-ADT to create a new defensive strategy space. Game analysis from the attacker’s perspective indicates that to maximize expected utility, a higher probability of attack must be allocated to “Tampering with MCDU Input Commands” and “Tampering with Collected Data,” thereby consuming more of the attacker’s computational resources.

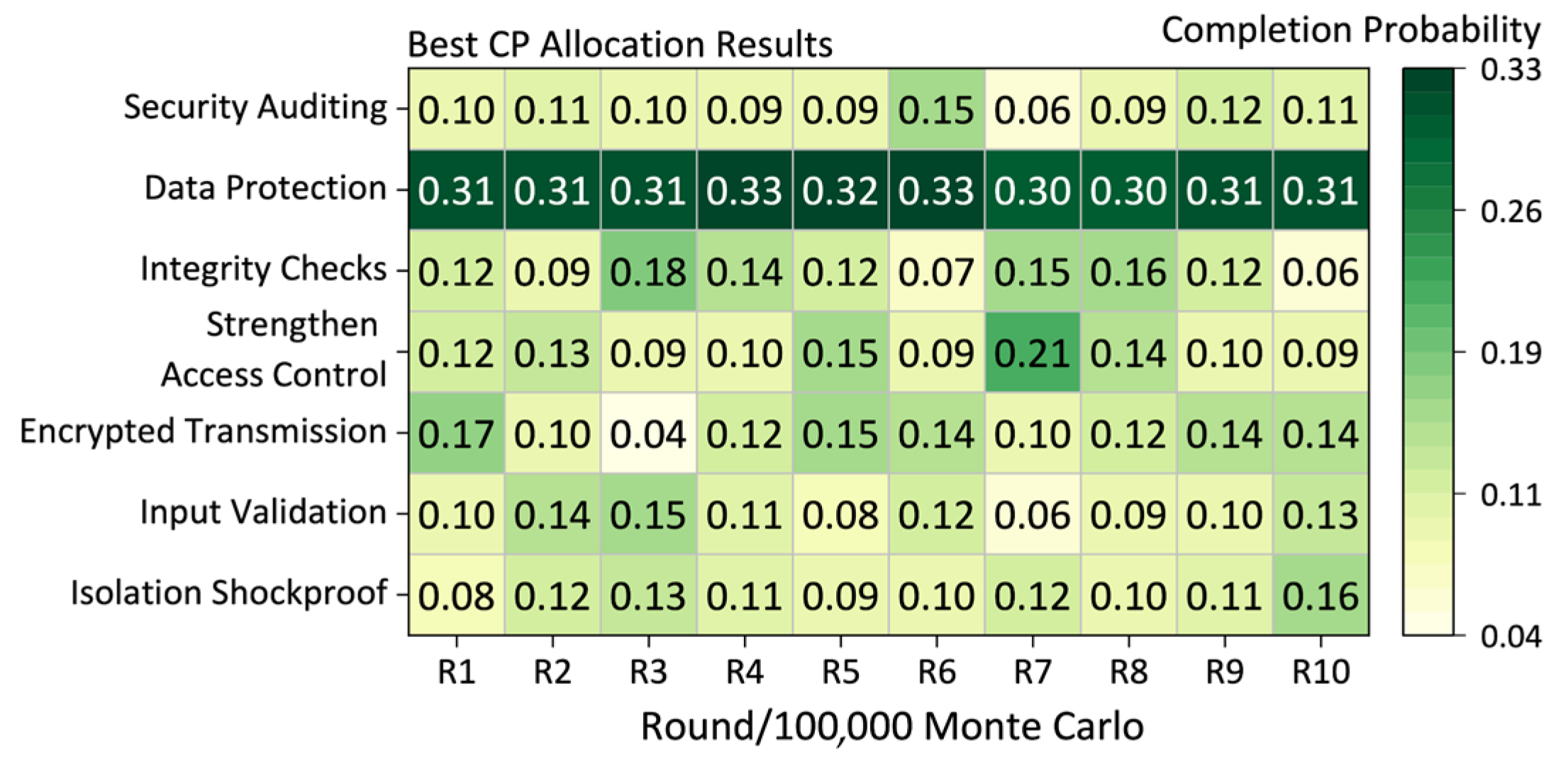
Consequently, defensive strategy enhancements are focused solely on these two attack methods while retaining other defensive strategies. After recalculating the defender’s utility matrix, multiple rounds of Monte Carlo simulations are conducted for the game analysis. The optimal distribution of completion probabilities after optimizing the defensive strategy space is depicted in Figure 12.

Upon the targeted addition of defense strategies, the security attributes of the defense strategies are optimized. If the defender considers prioritizing the deployment against attacks such as “Tampering with MCDU incoming commands” and “Tampering with collected data”, it is necessary to specifically enhance defense strategies such as “Input Validation”, “Encryption Transmission”, “Strengthen Access Control”, and “Integrity Checks”. The utility of the aforementioned defense strategies is, respectively, increased to 14, 12, 12, and 13, with the costs correspondingly rising to 4, 4, 5, and 5, denoted as “Targeted Enhanced Response Strategy Security Attributes”. Subsequently, the utility matrix is updated, and the expected utility values and the allocation of defense completion probabilities under these game conditions are recorded after solving for equilibrium.

Considering a targeted expansion of the initial defensive strategy space, if the top two strategies from the game outcomes, “Strengthen Access Control” and “Data Protection,” have their defensive utilities increased to 12 and 16, with costs rising to 5 and 6, respectively, this is marked as “Targeted Enhance Top2 Strategies Security Attributes”. The game outcomes under this condition are presented in

Table 8. Defender’s outcomes after targeted enhancement of Top 2 defensive strategy attributes.

100,000 per Round	Maximum Expected Utility	Completion Probability	Minimum Expected Utility	Completion Probability	Average Expected Utility
1	135.53	[0.08, 0.08, 0.14, 0.17, 0.13, 0.30, 0.10]	51.68	[0.18, 0.15, 0.21, 0.06, 0.15, 0.03, 0.22]	90.00
2	133.65	[0.11, 0.20, 0.08, 0.11, 0.10, 0.31, 0.09]	57.71	[0.27, 0.15, 0.16, 0.10, 0.14, 0.04, 0.14]	89.99
3	138.41	[0.09, 0.12, 0.07, 0.15, 0.10, 0.32, 0.15]	55.14	[0.15, 0.17, 0.11, 0.11, 0.19, 0.03, 0.24]	90.00
4	133.24	[0.10, 0.11, 0.09, 0.18, 0.12, 0.29, 0.11]	55.06	[0.12, 0.20, 0.17, 0.06, 0.21, 0.04, 0.20]	90.00
5	134.54	[0.11, 0.09, 0.10, 0.17, 0.08, 0.30, 0.15]	56.21	[0.21, 0.15, 0.17, 0.08, 0.19, 0.04, 0.16]	90.01
6	131.36	[0.06, 0.17, 0.10, 0.15, 0.10, 0.29, 0.13]	54.22	[0.14, 0.22, 0.20, 0.08, 0.11, 0.03, 0.22]	89.98
7	146.14	[0.10, 0.12, 0.07, 0.14, 0.11, 0.35, 0.11]	55.50	[0.22, 0.14, 0.18, 0.07, 0.21, 0.04, 0.14]	89.98
8	131.72	[0.10, 0.09, 0.12, 0.16, 0.14, 0.29, 0.10]	52.40	[0.14, 0.24, 0.10, 0.10, 0.18, 0.02, 0.22]	90.00
9	134.57	[0.12, 0.09, 0.12, 0.10, 0.14, 0.32, 0.11]	57.94	[0.16, 0.17, 0.08, 0.11, 0.24, 0.04, 0.20]	90.03
10	133.4	[0.05, 0.14, 0.14, 0.20, 0.09, 0.28, 0.10]	56.20	[0.21, 0.15, 0.18, 0.08, 0.17, 0.04, 0.17]	90.01

.

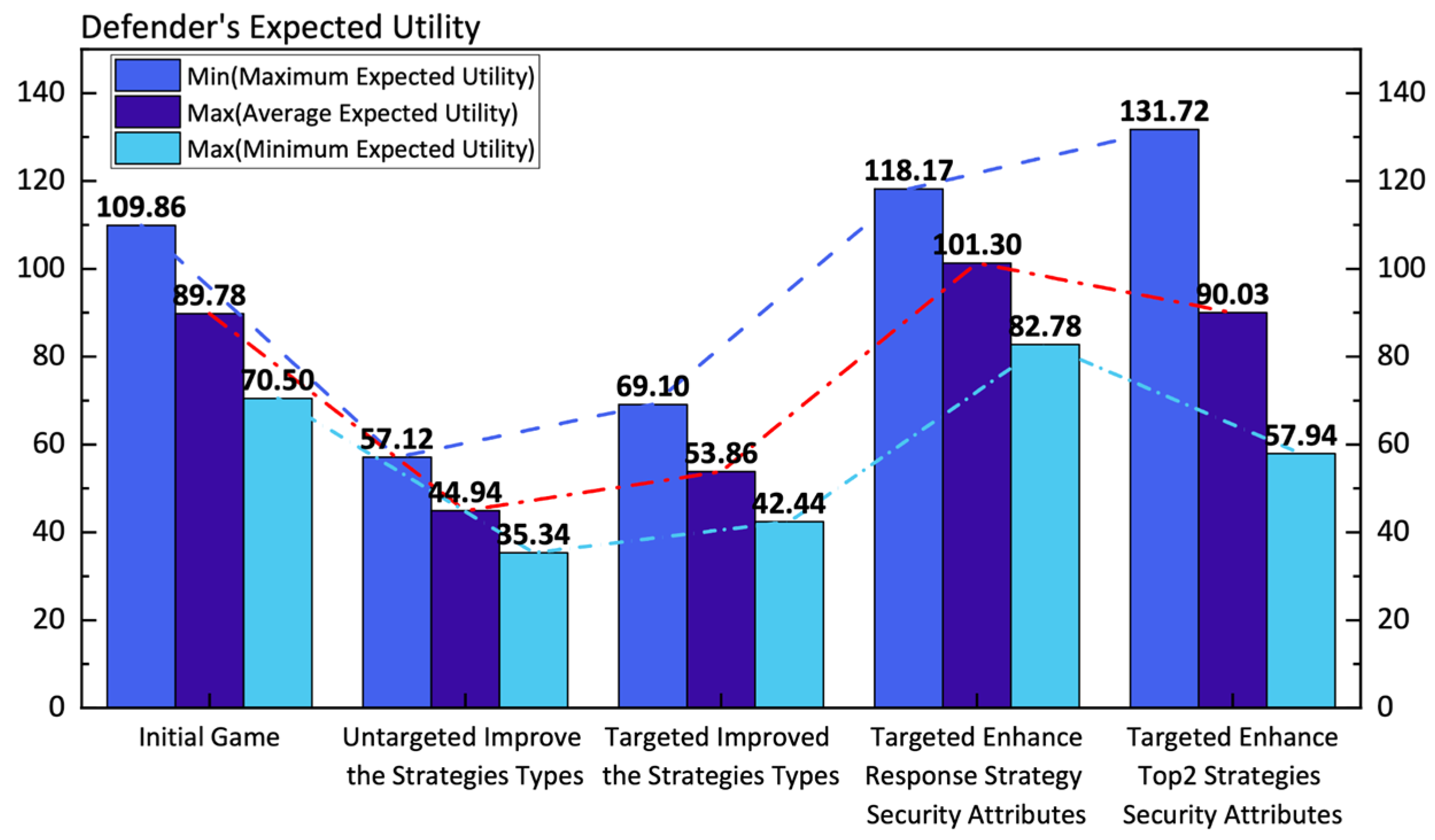
Visualization of the expected utility outcomes of the defender’s game under five different conditions is shown in Figure 13: initial game conditions, non-specifically enhanced defensive strategies, targeted enhancements of defensive strategies, targeted enhancements of defensive strategy attributes, and targeted enhancements of the attributes for the Top 2 defensive strategies. Non-specific enhancement of defensive strategies can lower the expected utility of the initial defensive strategy. To comprehensively increase one’s expected utility, the defender needs to adjust based on the game equilibrium results from the attacker’s perspective. Targeting specific defensive strategies for enhancement may lead to the dispersion of existing defensive probabilities. In this context, the defender should not only consider adding new defensive strategies for assets vulnerable to attack strategies but also increase the complete payoffs of existing defensive strategies. It is important to note that incorrectly allocating completion probabilities when enhancing the defense utility of the Top 2 strategies could prevent the defender from achieving the maximum expected utility, resulting in a significant reduction in overall expected utility.

To improve the completion probability distribution outcomes of the game model, defenders need to allocate security resources with greater precision. In this process, the allocation of physical strategy resources presents a binary problem. For example, for the “Isolation Shockproof” strategy, the decision maker simply needs to decide whether to add it or not. However, for some information strategies, such as “Strengthen Access Control” and “Data Protection,” the allocation of security resources involves a continuous quantity. To achieve higher strategy completion probabilities, defenders need to allocate more resources to higher-ranked defensive strategies after the game concludes. For physical strategies, this may involve adding certain equipment or facilities. For information strategies, it might require allocating more security computing resources or information defense resources.

Overall, the defender needs to consider the nature of different strategies in their resource allocation to enhance the completion probability of specific strategies more effectively. This differentiated resource allocation strategy helps ensure the system can appropriately respond to various threats and security challenges, thereby maximizing security enhancement. We acknowledge that modeling physical strategies as binary choices is a simplification; in reality, physical defenses differ in scale, strength, and duration. This abstraction was adopted for tractability within NCADG-AS, and future work will extend the framework to incorporate graded physical defenses for improved realism.

6. Conclusions

This study presented NCADG-AS, a non-cooperative Attack–Defense Game model tailored to avionics systems. By integrating pruned Attack–Defense Trees with Monte Carlo equilibrium estimation, the model enables tractable evaluation of attacker–defender interactions under aviation-specific constraints.

The EFIS case study showed that targeted defensive enhancements improved defender utility compared with non-specific measures, and sensitivity tests confirmed the robustness of equilibrium outcomes under parameter variations. These results demonstrate both the computational efficiency and practical value of the NCADG-AS framework. In addition, the framework improves computational efficiency through four customizations: (i) pruning of redundant and indirect nodes in ADTs, (ii) separation into A-ADT and D-ADT perspectives, (iii) targeted enhancement of defense strategies, and (iv) Monte Carlo sampling for tractable equilibrium estimation.

For real-time implementation, NCADG-AS is well-suited to avionics environments due to its pruning-based strategy reduction and Monte Carlo equilibrium estimation, which enhance computational efficiency while preserving feasibility. Practical deployment, however, must address integration with avionics data buses, compliance with safety–security standards, and low-latency requirements. Future work will focus on developing a simulation platform, analyzing cascading effects of intermediary nodes, validating threats under a converged security framework, and improving scalability through hierarchical decomposition and parallelized sampling.