Numerical Study on Self-Pulsation Phenomenon in Liquid-Centered Swirl Coaxial Injector with Recess
Abstract
1. Introduction
2. Numerical Methods
2.1. Injector Modeling
2.2. Simulation Model Setup
2.3. Simulation Conditions and Mesh Setup
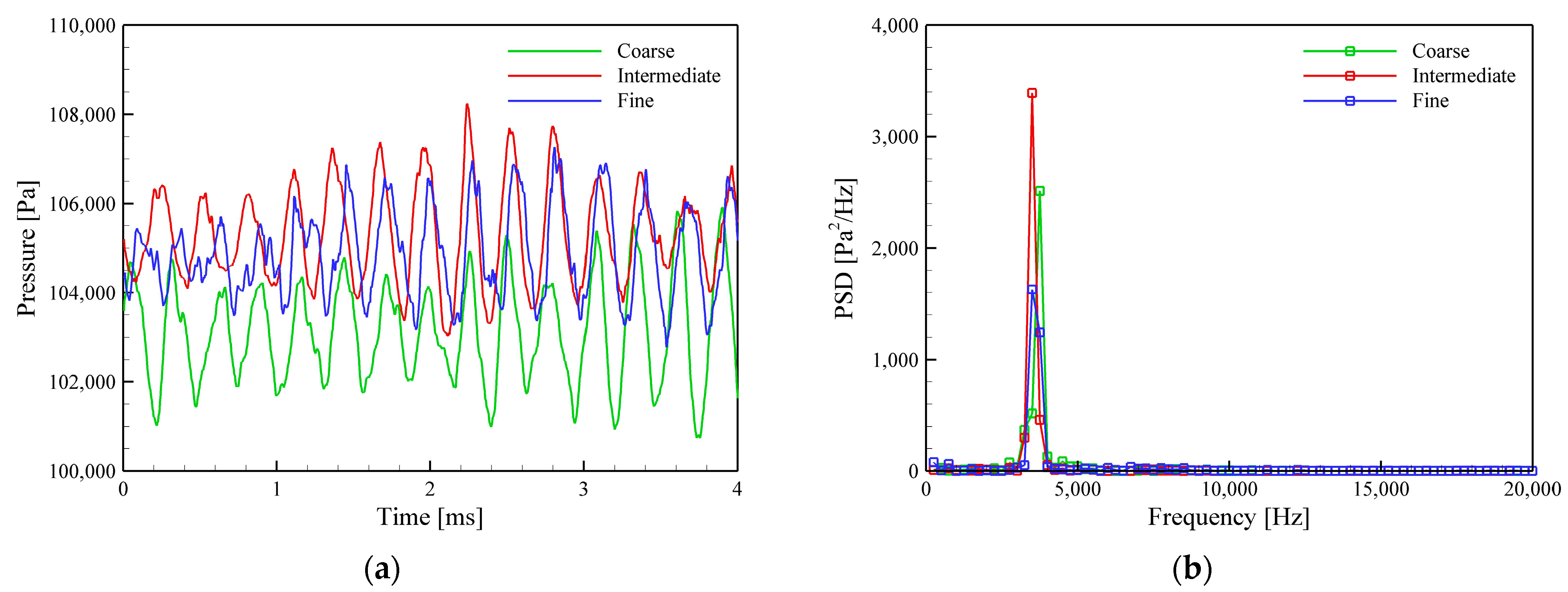
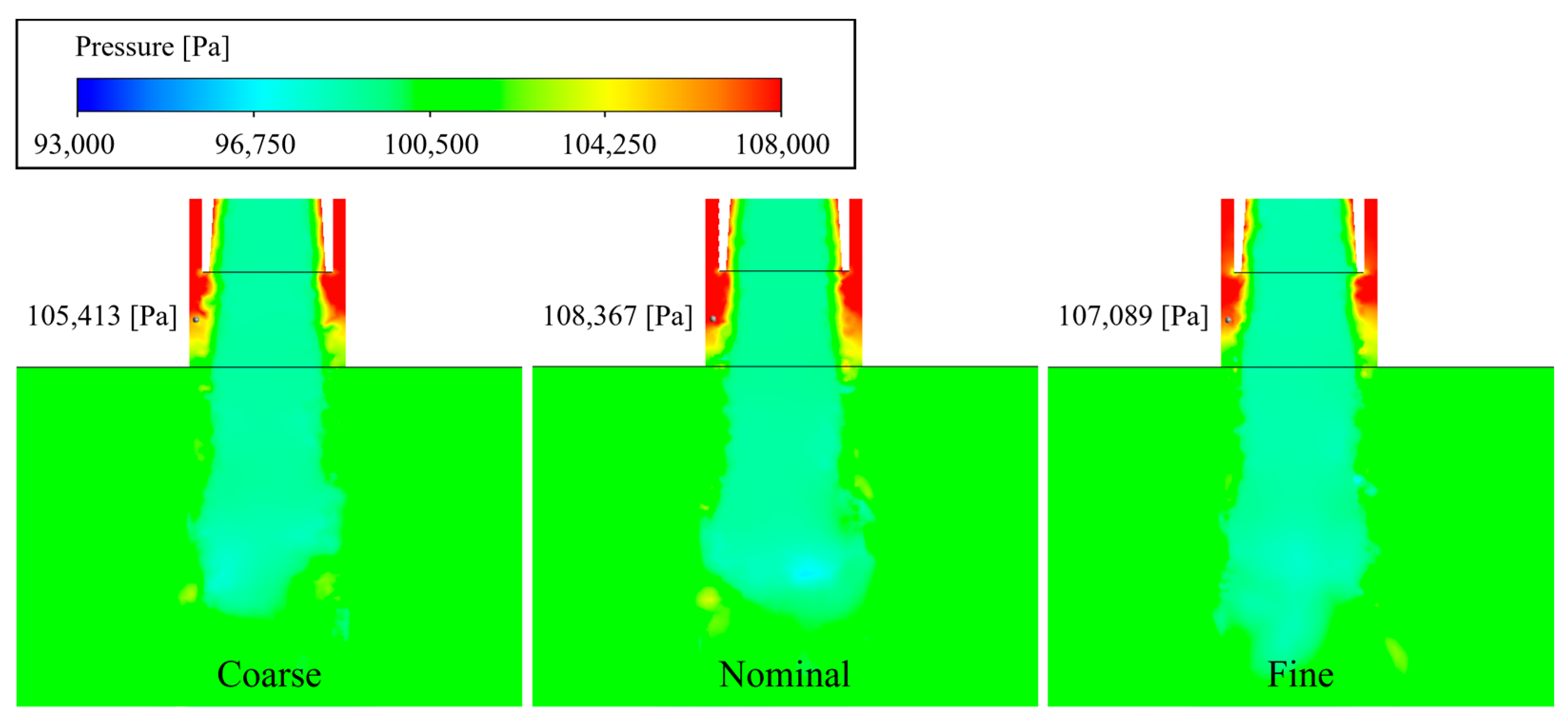
2.4. Mesh Independence Test
3. Results and Discussion
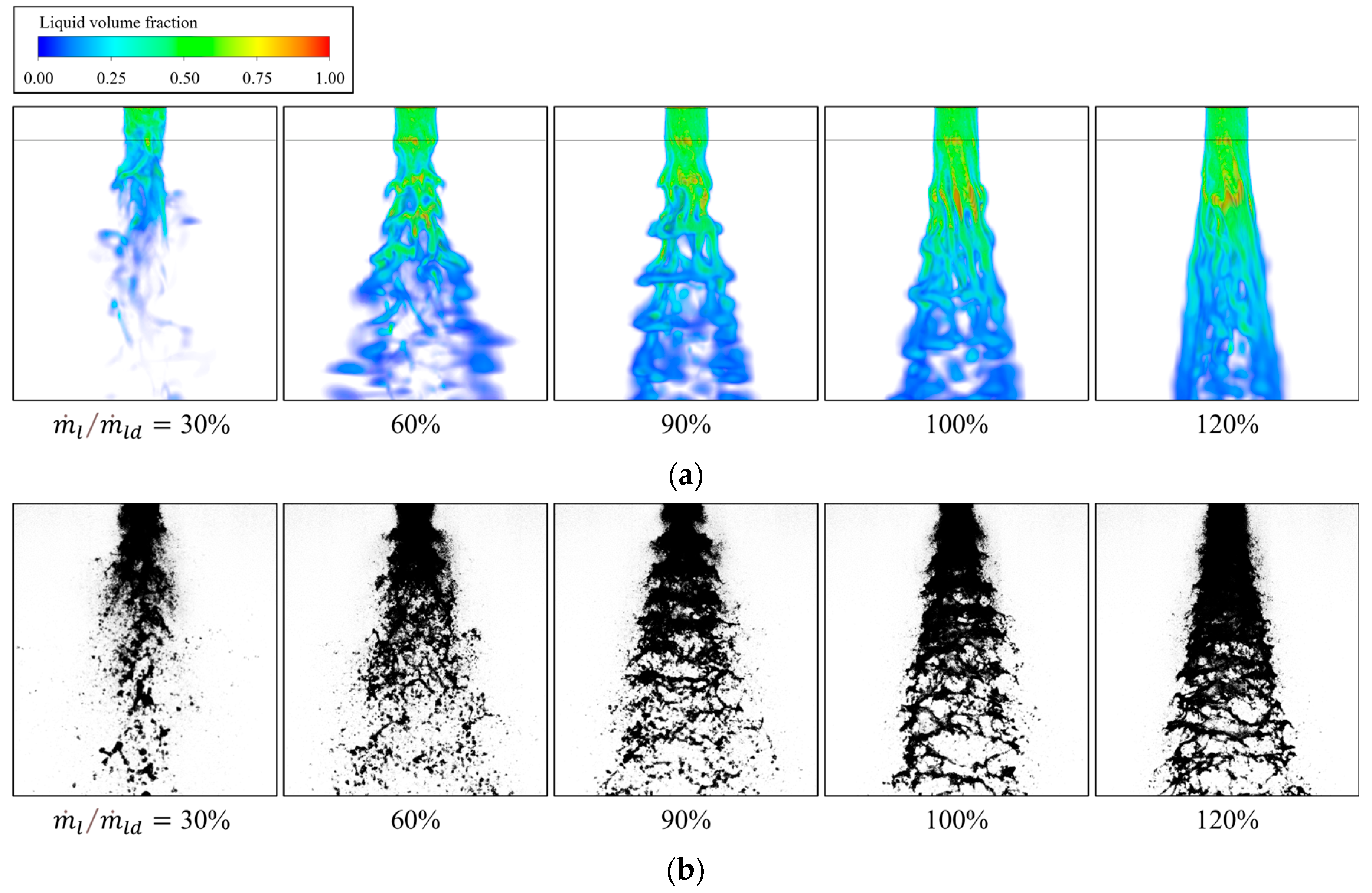
3.1. Spray Pattern
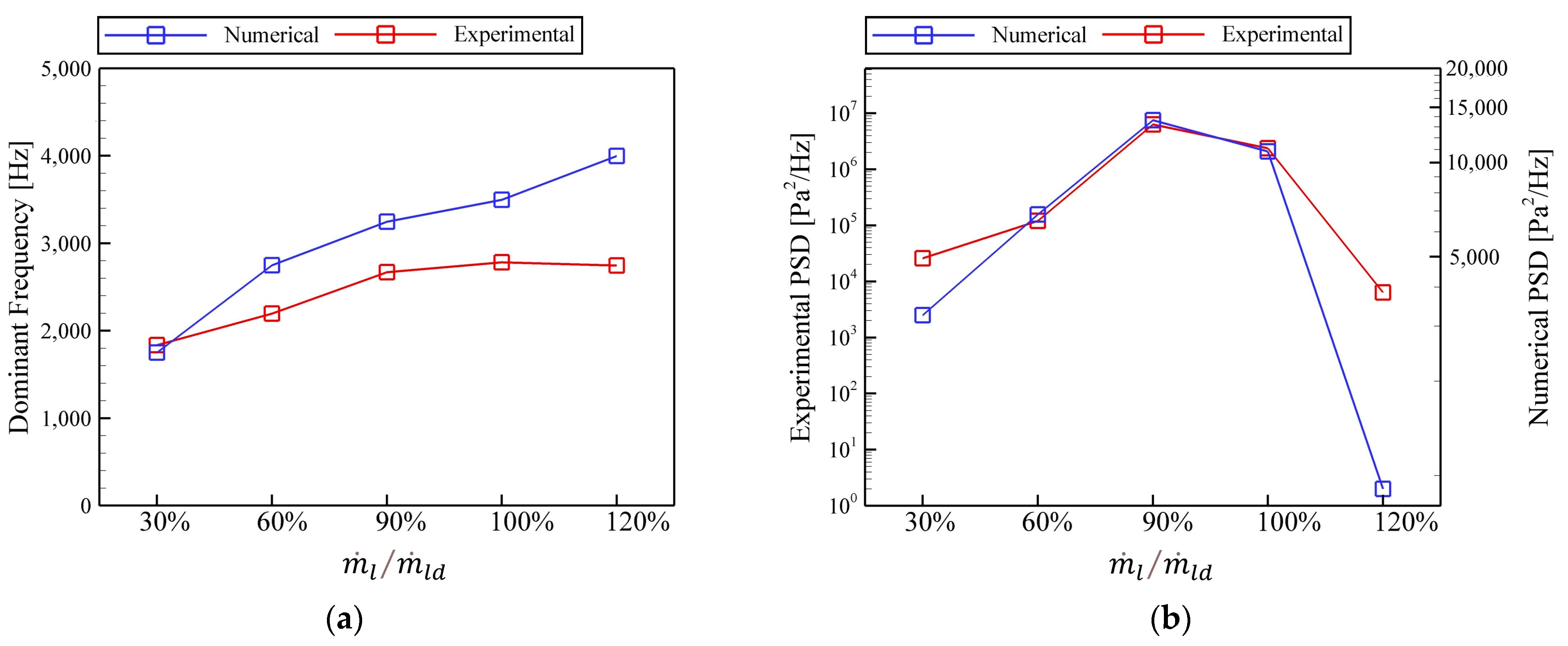
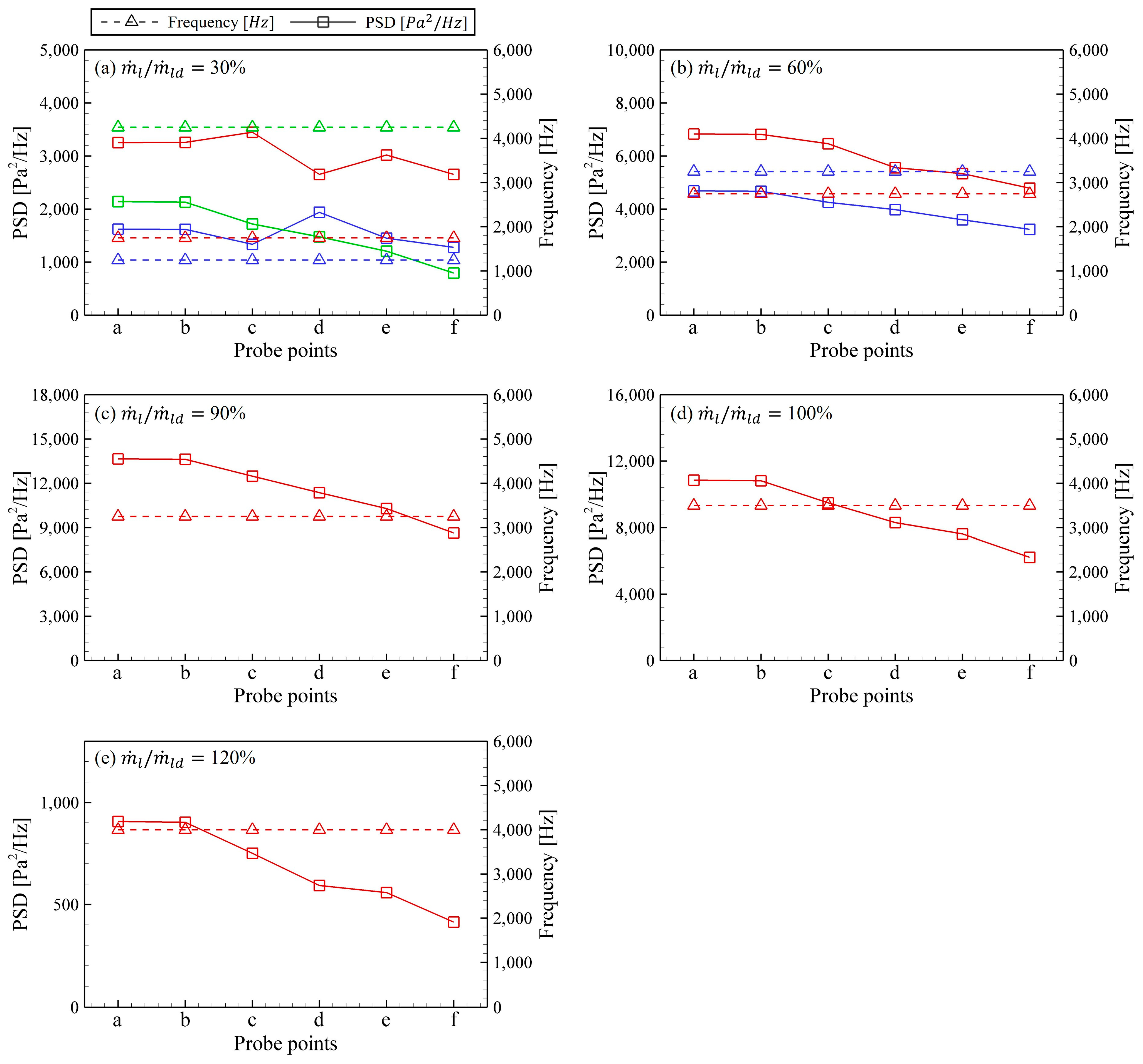
3.2. Analysis of Dominant Frequency in Self-Pulsation
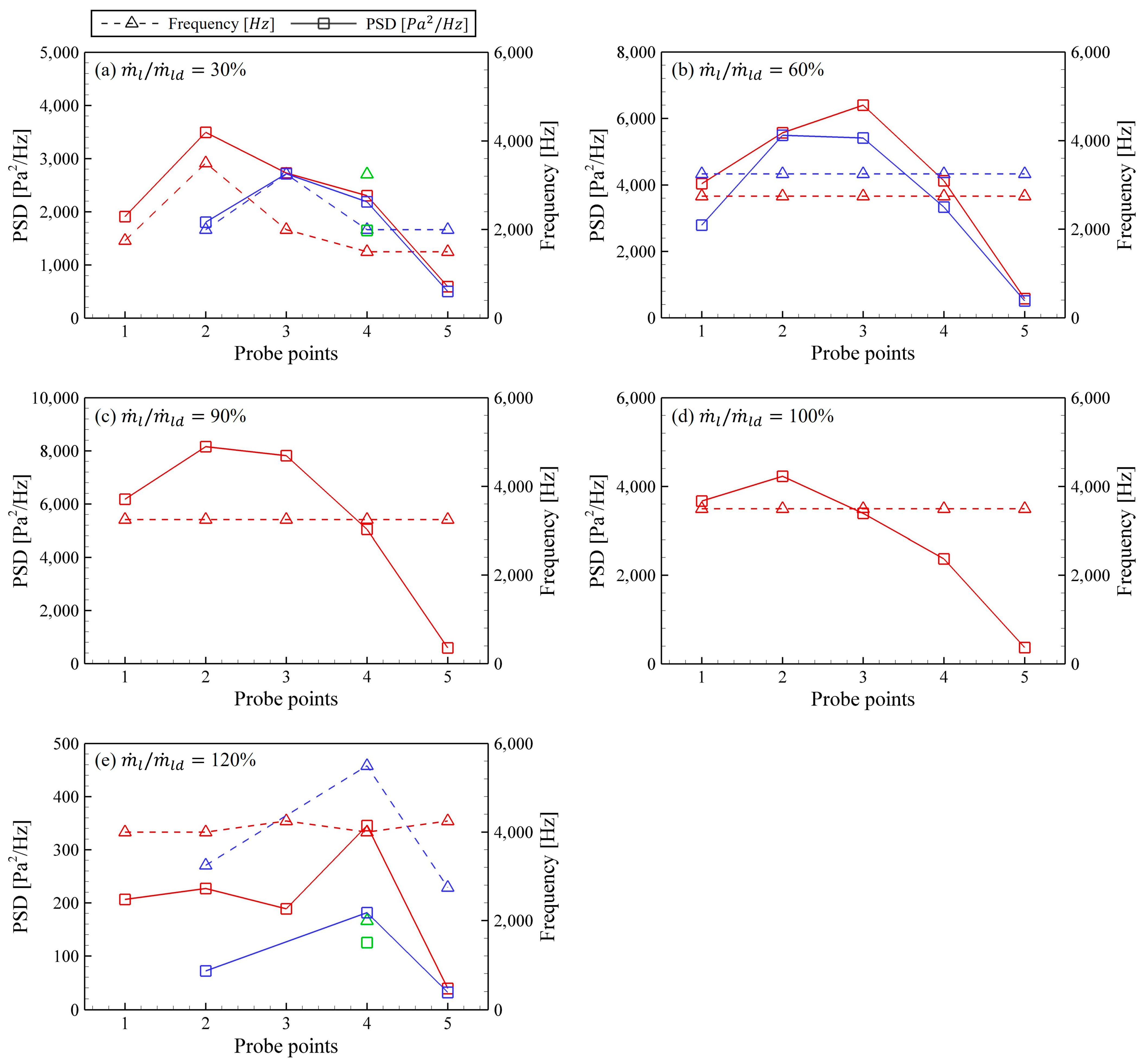
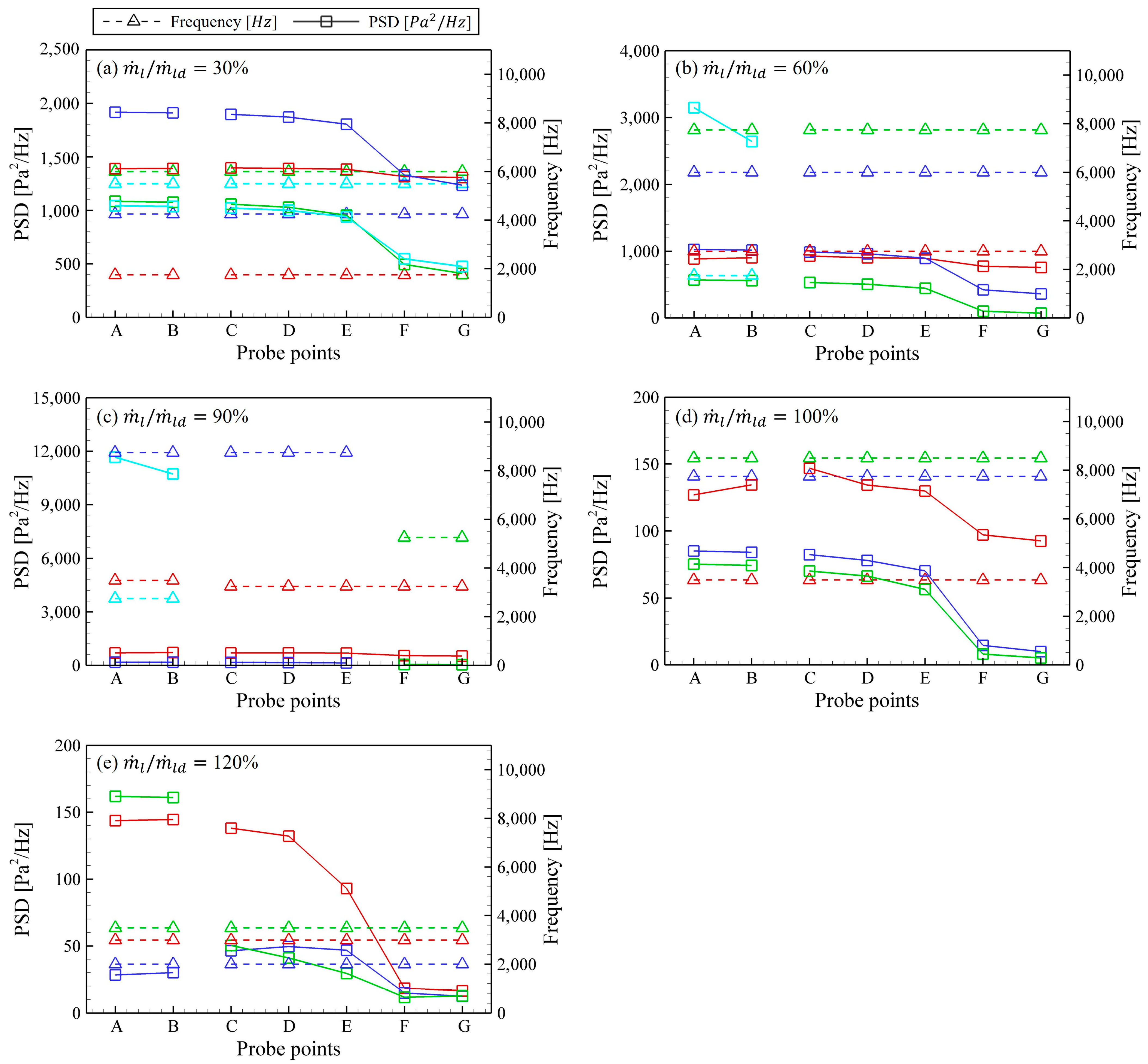
3.3. Self-Pulsation Analysis by Region
3.4. Self-Pulsation Mechanism
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kang, Z.; Wang, Z.; Li, Q.; Cheng, P. Review on pressure swirl injector in liquid rocket engine. Acta Astronaut. 2018, 145, 174–198. [Google Scholar] [CrossRef]
- Kim, S.; Yoon, J.; Yoon, Y. Internal flow characteristics of liquid–liquid swirl coaxial injectors with different recess lengths and oxidizer–fuel ratios. At. Sprays 2011, 21, 971–987. [Google Scholar] [CrossRef]
- Kim, D.; Jeong, W.; Im, J.; Yoon, Y. The characteristics of swirl coaxial injector under varying geometric and environmental conditions. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2024; AIAA: Reston, VA, USA, 2004. Paper 2004-3521. [Google Scholar] [CrossRef]
- Im, J.; Cho, S.; Yoon, Y.; Moon, I. Comparative study of spray characteristics of gas-centered and liquid-centered swirl coaxial injectors. J. Propul. Power 2010, 26, 1196–1204. [Google Scholar] [CrossRef]
- Lefebvre, A.; McDonell, V. Atomization and Sprays; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Fu, Q.; Yang, L. Dynamic characteristics of the recessed chamber within a gas-liquid coaxial injector. Adv. Mech. Eng. 2016, 8, 1–7. [Google Scholar] [CrossRef]
- Fu, Q. Numerical simulation of the internal flow of swirl atomizer under ambient pressure. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2016, 230, 2650–2659. [Google Scholar] [CrossRef]
- Liu, L.; Fu, Q.; Yang, L. Theoretical atomization model of liquid sheet generated by coaxial swirl injectors. Int. J. Multiph. Flow 2021, 142, 103725. [Google Scholar] [CrossRef]
- Huang, Y.; Zhou, J.; Hu, X.; Wang, Z. Acoustic model for the self-oscillation of coaxial swirl injector. In Proceedings of the 33rd Joint Propulsion Conference and Exhibit, Seattle, WA, USA, 6–9 July 1997. AIAA Paper 1997-3328. [Google Scholar] [CrossRef]
- Kang, Z.; Li, Q.; Cheng, P.; Zhang, X.; Wang, Z. Effects of recess on the self-pulsation characteristics of liquid-centered swirl coaxial injectors. J. Propul. Power 2016, 32, 1124–1132. [Google Scholar] [CrossRef]
- Eberhart, C.; Frederick, R. Fluid oscillations of a swirl coaxial injector under high-frequency self-pulsation. J. Propul. Power 2017, 33, 804–814. [Google Scholar] [CrossRef]
- Bazarov, V.; Yang, V. Liquid-propellant rocket engine injector dynamics. J. Propul. Power 1998, 14, 797–806. [Google Scholar] [CrossRef]
- Bazarov, V.; Lul’ka, L. Self-pulsation of liquid flow in coaxial air stream. Sov. Aeronaut. 1978, 3, 14–18. [Google Scholar]
- Zhou, J.; Hu, X.; Huang, Y.; Wang, Z. Flowrate and acoustics characteristics of coaxial swirling injector of hydrogen/oxygen rocket engine. In Proceedings of the 32nd Joint Propulsion Conference and Exhibit, Lake Buena Vista, FL, USA, 1–3 July 1996. AIAA Paper 1996-3135. [Google Scholar] [CrossRef]
- Bai, X.; Cheng, P.; Li, Q.; Sheng, L.; Kang, Z. Effects of self-pulsation on combustion instability in a liquid rocket engine. Exp. Therm. Fluid Sci. 2020, 114, 110038. [Google Scholar] [CrossRef]
- Tsohas, J.; Heister, S. Numerical simulations of liquid rocket coaxial injector hydrodynamics. J. Propul. Power 2011, 27, 793–810. [Google Scholar] [CrossRef]
- Yang, V.; Anderson, W. Liquid Rocket Engine Combustion Instability; Progress in Astronautics and Aeronautics; AIAA: Reston, VA, USA, 2012; Volume 169. [Google Scholar]
- Eberhart, C.; Lineberry, D.; Moser, M. Experimental cold-flow characterization of a swirl coaxial injector element. In Proceedings of the 45th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Denver, CO, USA, 2–5 August 2009. AIAA Paper 2009-5140. [Google Scholar] [CrossRef]
- Bazarov, V. Self-pulsations in coaxial injectors with central swirl liquid stage. In Proceedings of the 31st Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 10–12 July 1995. AIAA Paper 1995-2358. [Google Scholar] [CrossRef]
- Yang, L.; Ge, M.; Zhang, M.; Fu, Q.; Cai, G. Spray characteristics of recessed gas-liquid coaxial swirl injector. J. Propul. Power 2008, 24, 1332–1339. [Google Scholar] [CrossRef]
- Kim, J.; Han, Y.; Choi, H.S.; Yoon, Y. Study on spray patterns of gas-centered swirl coaxial (GCSC) injectors in high-pressure conditions. Aerosp. Sci. Technol. 2013, 27, 171–178. [Google Scholar] [CrossRef]
- Son, J.; Sohn, C.; Park, G.; Yoon, Y. Spray patterns and injection characteristics of gas-centered swirl coaxial injectors. J. Aerosp. Eng. 2017, 30, 04017035. [Google Scholar] [CrossRef]
- Chu, W.; Li, X.; Tong, Y.; Ren, Y. Numerical investigation of the effects of gas–liquid ratio on the spray characteristics of liquid-centered swirl coaxial injectors. Acta Astronaut. 2020, 175, 204–215. [Google Scholar] [CrossRef]
- Bai, X.; Li, Q.; Cheng, P.; Sheng, L.; Kang, Z. Investigation of self-pulsation characteristics for a liquid-centered swirl coaxial injector with recess. Acta Astronaut. 2018, 151, 511–521. [Google Scholar] [CrossRef]
- Im, J.; Yoon, Y. The effects of the ambient pressure on self-pulsation characteristics of a gas/liquid swirl coaxial injector. In Proceedings of the 44th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit AIAA, Hartford, CT, USA, 21–23 July 2008. Paper 2008-4850. [Google Scholar] [CrossRef]
- Im, J.; Kim, D.; Yoon, Y.; Roh, T.; Koo, J. Self-pulsation characteristics of a swirl coaxial injector with various injection and geometric conditions. In Proceedings of the 41st AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Tucson, AZ, USA, 10–13 July 2005. AIAA Paper 2005-3749. [Google Scholar] [CrossRef]
- Bai, X.; Cao, P.; Li, Q.; Cheng, P. The break phenomenon of self-pulsation for liquid-centered swirl coaxial injectors. Int. J. Multiph. Flow 2021, 142, 103708. [Google Scholar] [CrossRef]
- Ren, Y.; Guo, K.; Zhao, J.; Nie, W.; Tong, Y.; Chu, W. Numerical investigation of spray self-pulsation characteristics of liquid-centered swirl coaxial injector with different recess lengths. Int. J. Multiph. Flow 2021, 138, 103592. [Google Scholar] [CrossRef]
- Qiao, W.; Liang, C.; Liu, L.; Wang, S.; Zhang, B.; Yang, X.; Yang, L.; Fu, Q. Numerical study on the self-pulsation characteristics of LOX/GH2 swirl coaxial injector. Int. J. Aerosp. Eng. 2024, 1, 2249954. [Google Scholar] [CrossRef]
- Ahn, J.; Lim, H.; Jeong, G.; Ahn, K. Effect of the recess length on the dynamic characteristics of liquid-centered swirl coaxial injectors. Acta Astronaut. 2022, 199, 1–13. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent Theory Guide, Release 2023 R2; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- ANSYS Inc. ANSYS Fluent User’s Guide, Release 2023 R2; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Kang, Z.; Li, Q.; Cheng, P.; Zhang, X.; Wang, Z. Effects of self-pulsation on the spray characteristics of gas-liquid swirl coaxial injector. Acta Astronaut. 2016, 127, 249–259. [Google Scholar] [CrossRef]
- Li, J.; Lei, F.; Zhou, L.; Yang, A. Effects of misaligned impingement on atomization characteristics of impinging jet injector. J. Aerosp. Power 2019, 34, 2280–2293. [Google Scholar]
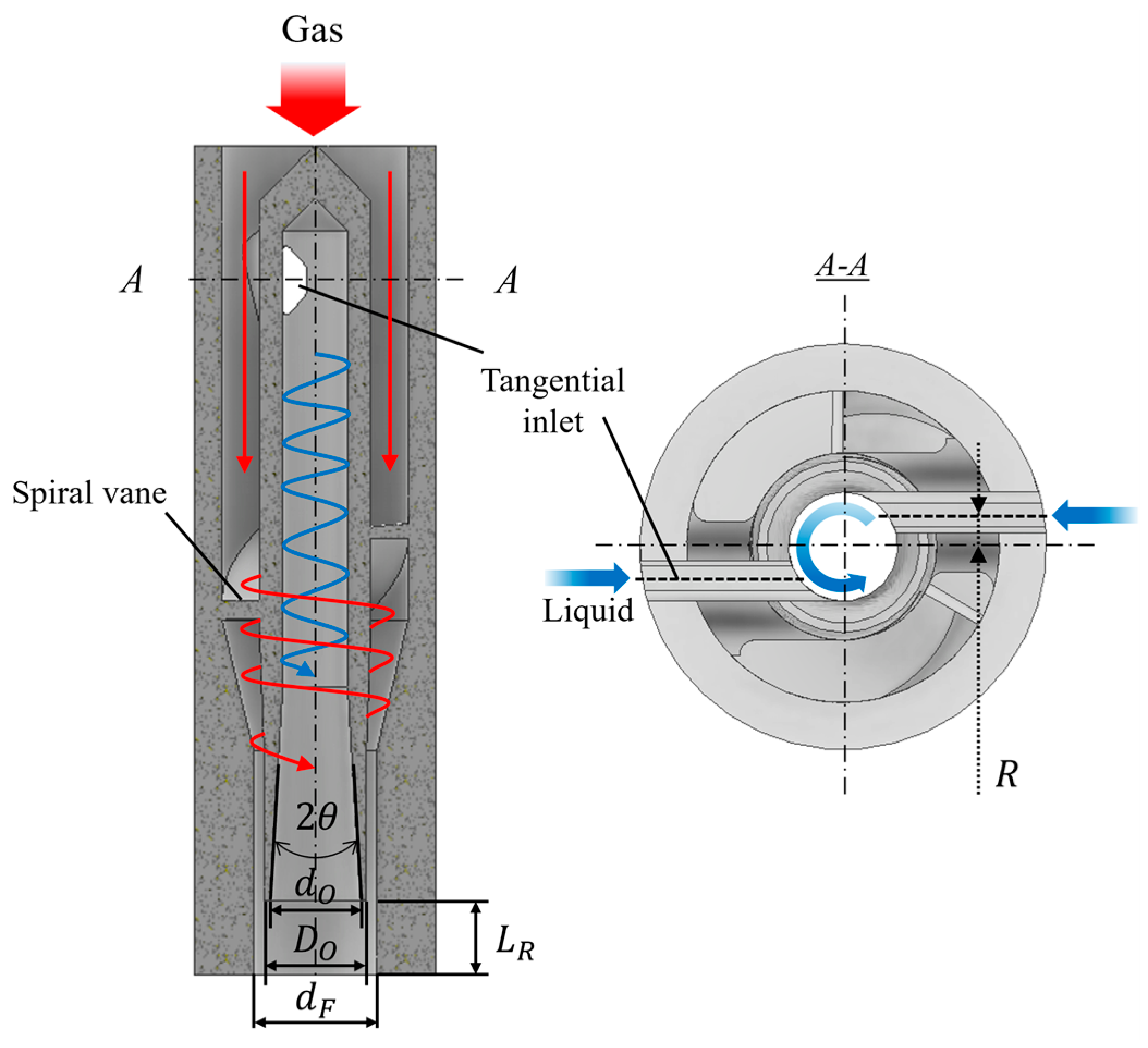
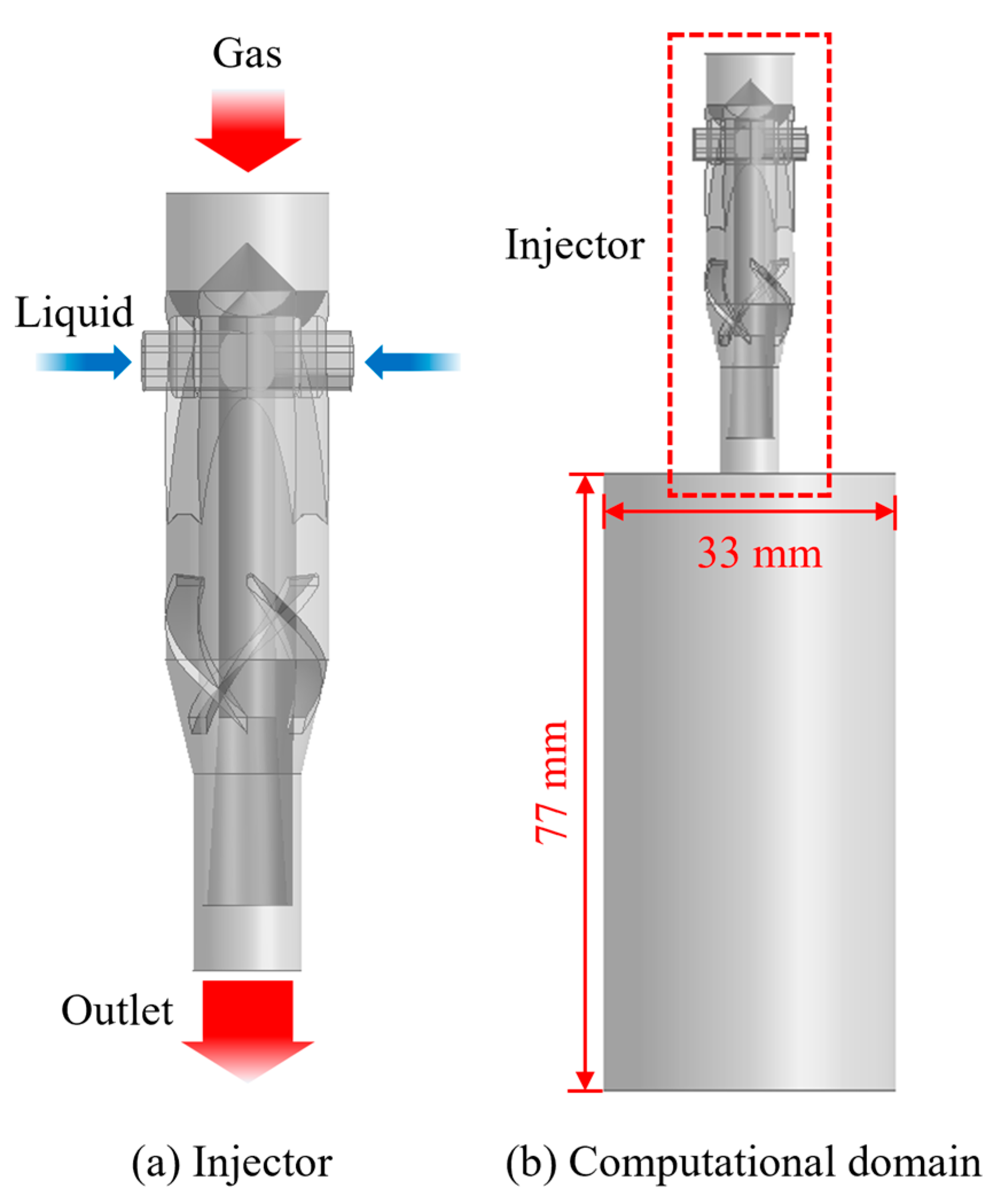
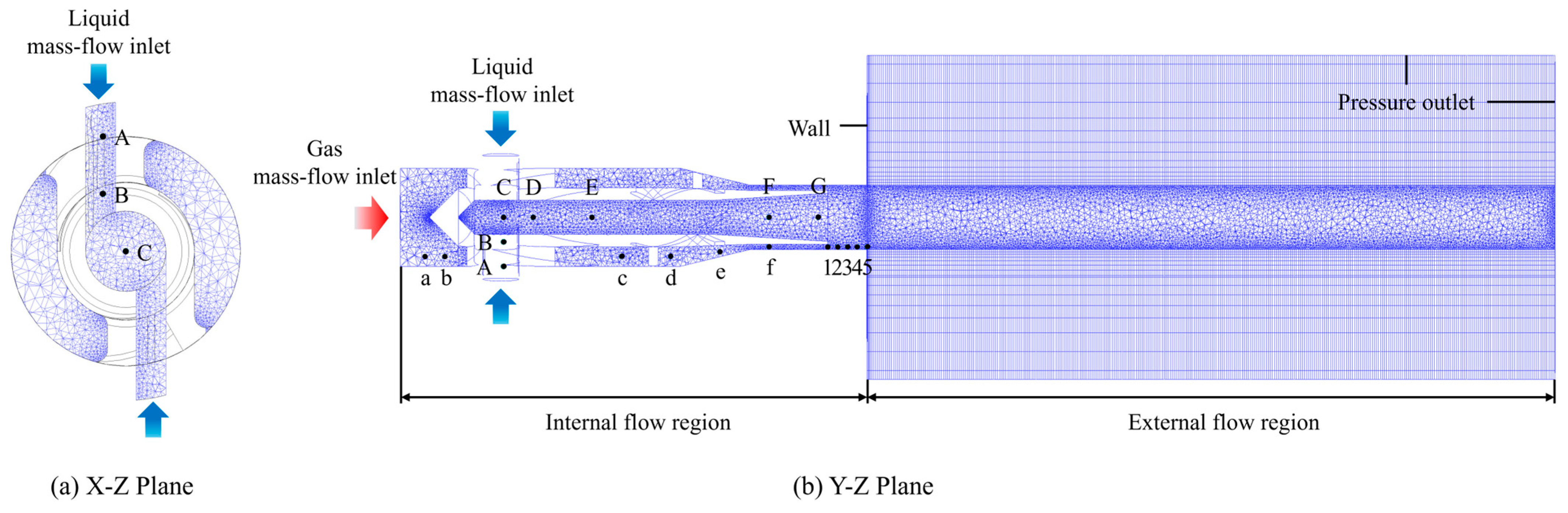


| Parameter | Value | Unit |
|---|---|---|
| 5.5 | mm | |
| 4.9 | mm | |
| 6.6 | mm | |
| 4.0 | mm | |
| 1.1 | mm | |
| 2θ | 7.0 | ° |
| [g/s] | 2.083 |
| [g/s] | 105.17 |
| [%] | 100 |
| [%] | 30, 60, 90, 100, 120 |
| Region | Probe Points |
|---|---|
| Recess | 1–5 |
| Gas line | a–f |
| Tangential hole | A, B |
| Gas core | C–G |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.; Jung, H.; Ahn, K. Numerical Study on Self-Pulsation Phenomenon in Liquid-Centered Swirl Coaxial Injector with Recess. Aerospace 2025, 12, 796. https://doi.org/10.3390/aerospace12090796
Lee J, Jung H, Ahn K. Numerical Study on Self-Pulsation Phenomenon in Liquid-Centered Swirl Coaxial Injector with Recess. Aerospace. 2025; 12(9):796. https://doi.org/10.3390/aerospace12090796
Chicago/Turabian StyleLee, Jiwon, Hadong Jung, and Kyubok Ahn. 2025. "Numerical Study on Self-Pulsation Phenomenon in Liquid-Centered Swirl Coaxial Injector with Recess" Aerospace 12, no. 9: 796. https://doi.org/10.3390/aerospace12090796
APA StyleLee, J., Jung, H., & Ahn, K. (2025). Numerical Study on Self-Pulsation Phenomenon in Liquid-Centered Swirl Coaxial Injector with Recess. Aerospace, 12(9), 796. https://doi.org/10.3390/aerospace12090796







