Analysis of the Compressive Buckling and Post-Buckling Behaviour of Wood-Based Sandwich Panels Used in Light Aviation
Abstract
1. Introduction
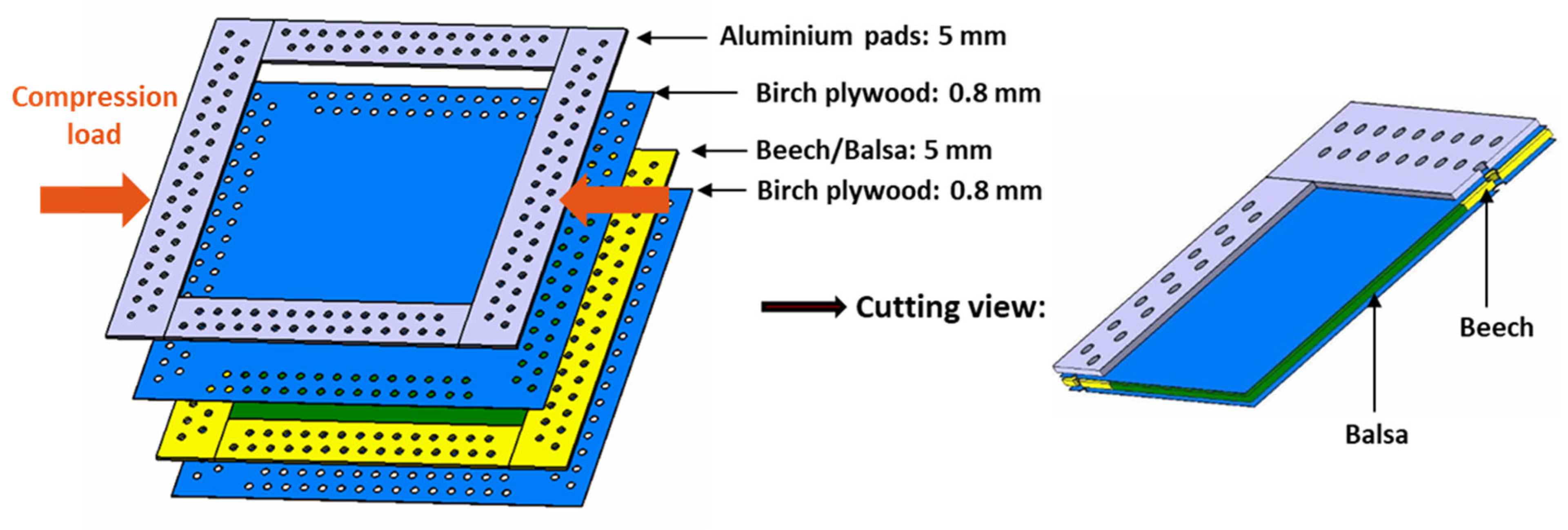
2. Materials and Manufacturing
3. Experimental Procedure
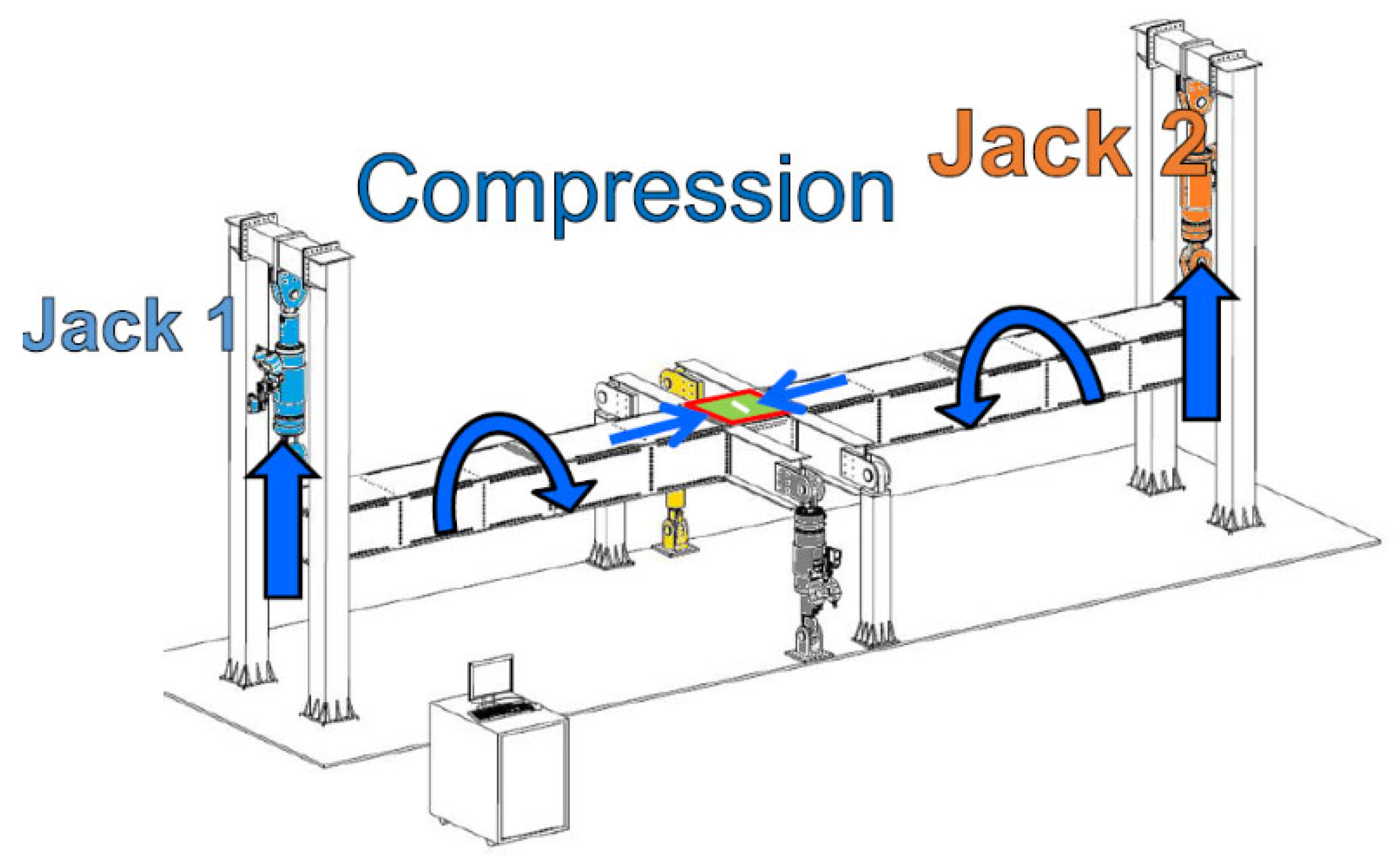
3.1. Vertex Test Rig
3.2. Test Monitoring
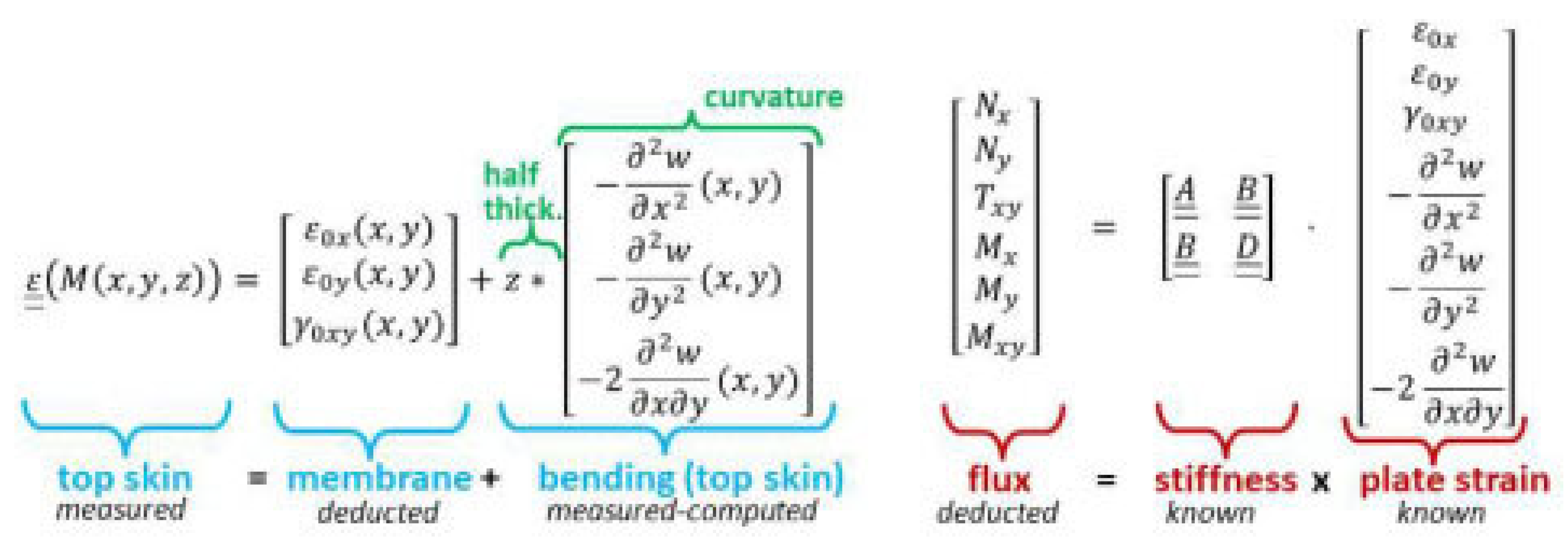
3.3. DIC and Data Reduction Methods
3.4. Virtual Test
4. Results and Discussion
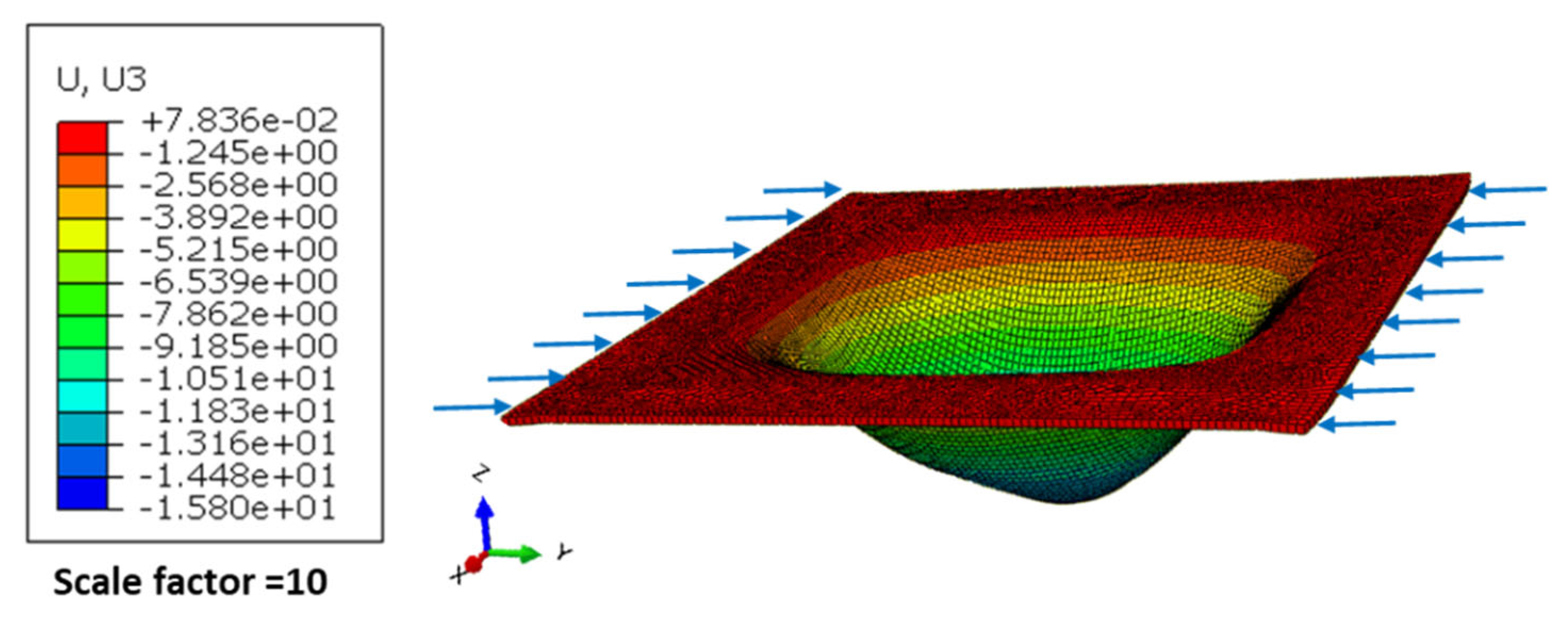
4.1. Overall Behaviour
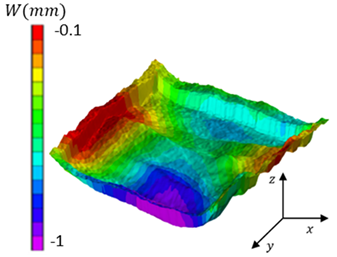
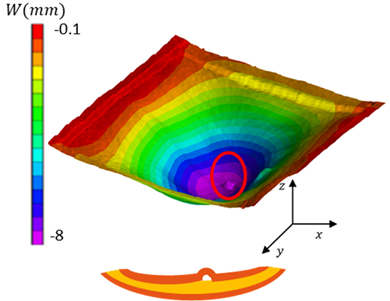
4.2. Influence of a Debonding Manufacturing Defect on the Buckling of Wood Sandwich Panels
4.3. Failure Scenarios
4.3.1. Failure Scenarios Observed for the Pristine Plates
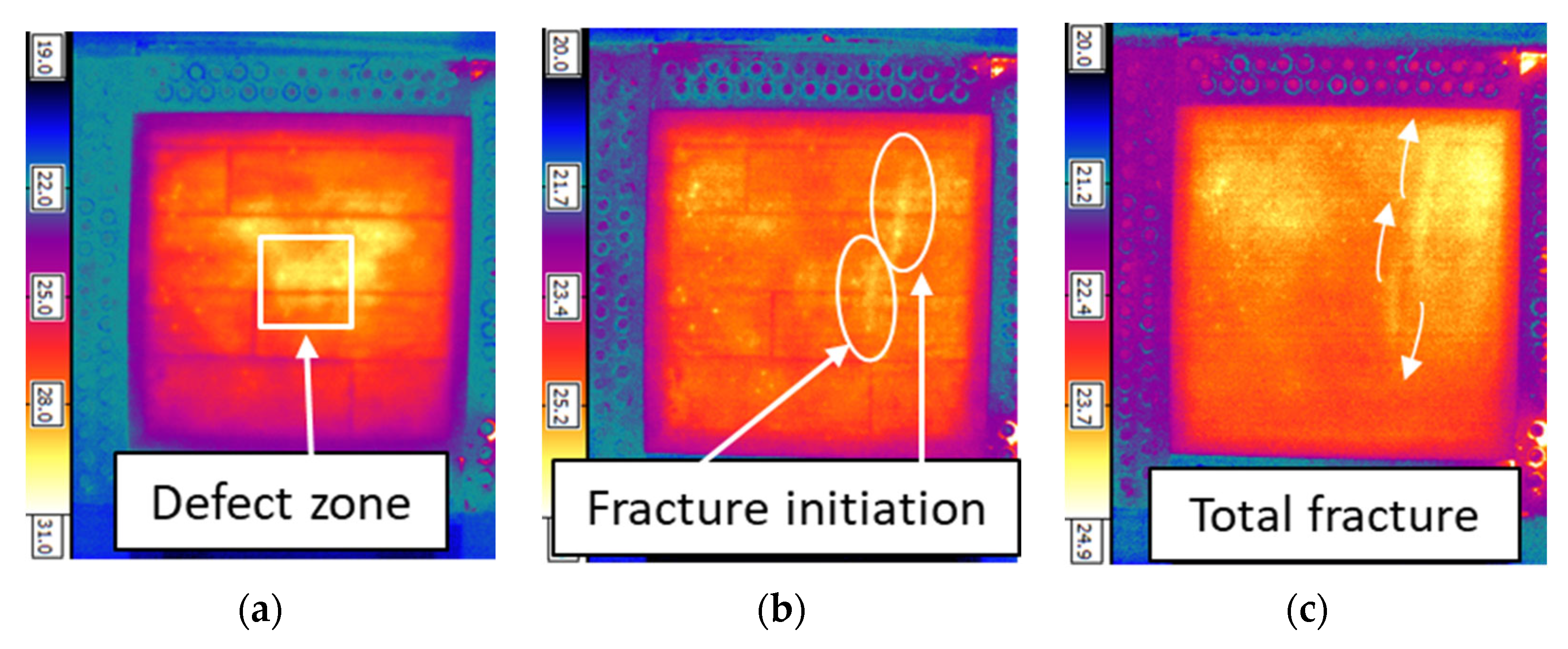
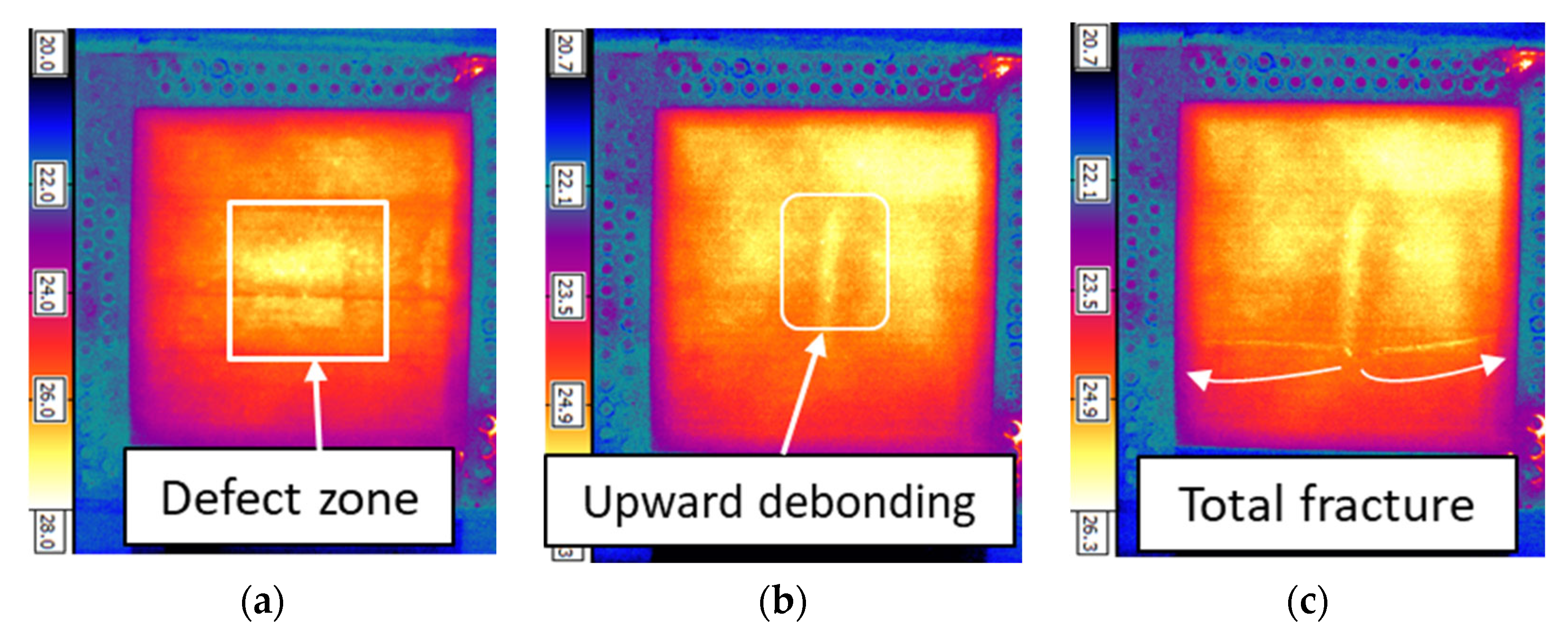
4.3.2. Failure Scenarios for the Plates with Bonding Defects
4.4. Fracture Surfaces
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Castanie, B.; Azoti, W.; Crouzeix, L.; Bello, A.; Taborda, R.P.; Mahmood, A.; Viste, A. Review of Monolithic Composite Laminate and Stiffened Structures in Aeronautic Applications. Compos. Part C Open Access 2025, 17, 100585. [Google Scholar] [CrossRef]
- Castanié, B.; Peignon, A.; Marc, C.; Eyma, F.; Cantarel, A.; Serra, J.; Curti, R.; Hadiji, H.; Denaud, L.; Girardon, S.; et al. Wood and plywood as eco-materials for sustainable mobility: A review. Compos. Struct. 2023, 329, 117790. [Google Scholar] [CrossRef]
- Sutherland, J. Revival of structural timber in Britain after 1945. Constr. Hist. Soc. 2010, 25, 101–113. Available online: https://www.jstor.org/stable/41613962 (accessed on 5 August 2025).
- Klemin, A. Aviation Surveyed. Sci. Am. 1944, 170, 214–216. Available online: https://www.jstor.org/stable/10.2307/24997774 (accessed on 5 August 2025). [CrossRef]
- Available online: https://avionsmauboussin.fr/en/elementor-9080/ (accessed on 5 August 2025).
- Guenther, R.; Tajmar, M.; Bach, C. Wood and Wood-Based Materials in Space Applications—A Literature Review of Use Cases, Challenges and Potential. Aerospace 2024, 11, 910. [Google Scholar] [CrossRef]
- Wurm, S.; Wagner, M.; Baumann, G.; Vitzthum, K.; Sehrschön, H.; Krenke, T.; Feist, F. Wood-steel hybrid beams for electric vehicle battery housings: A comparative study with aluminum profiles in bending load case. Eur. J. Wood Wood Prod. 2025, 83, 114. [Google Scholar] [CrossRef]
- Jennings, M.; Subhani, M.; Reiner, J.; Piazza, G.; Heyner, D. Towards manufacturing of full scale wood veneer automotive panel. In Proceedings of the 14th World Conference on Timber Engineering 2025 (WCTE 2025), Brisbane, Australia, 22–26 June 2025; pp. 2734–2742. [Google Scholar]
- Vladimirova, E.; Gong, M. Advancements and Applications of Wood-Based Sandwich Panels in Modern Construction. Buildings 2024, 14, 2359. [Google Scholar] [CrossRef]
- Wei, P.; Chen, J.; Zhang, Y.; Pu, L. Wood-based sandwich panels: A review. Wood Res. 2021, 66, 875–890. [Google Scholar] [CrossRef]
- Oliveira, P.R.; May, M.; Panzera, T.H.; Hiermaier, S. Bio-based/green sandwich structures: A review. Thin-Walled Struct. 2022, 177, 109426. [Google Scholar] [CrossRef]
- Smardzewski, J. Experimental and numerical analysis of wooden sandwich panels with an auxetic core and oval cells. Mater. Des. 2019, 183, 108159. [Google Scholar] [CrossRef]
- Smardzewski, J.; Wojciechowski, K.W. Study on the bending and failure behaviour of wooden sandwich panels with corrugated core, randomized gaps, and wood defects. Constr. Build. Mater. 2023, 409, 133924. [Google Scholar] [CrossRef]
- Zuccarello, B.; Bongiorno, F.; Militello, C. Structural Optimization of a High-Performance Green Sandwich Made of Sisal Reinforced Epoxy Facings and Balsa Core. Polymers 2024, 16, 3341. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; De Luycker, E.; Cantarel, A.; Castanie, B. Manufacturing and quasi-static bending behavior of wood-based sandwich structures. Compos. Struct. 2017, 182, 487–504. [Google Scholar] [CrossRef]
- Demircioğlu, T.; Balıkoğlu, F.; İnal, O.; Arslan, N.; Ay, I.; Ataş, A. Experimental investigation on low-velocity impact response of wood skinned sandwich composites with different core configurations. Mater. Today Commun. 2018, 17, 31–39. [Google Scholar] [CrossRef]
- Jendli, Z.; Haggui, M.; Monti, A.; El Mahi, A.; Guillaumat, L. Experimental analysis of low-velocity impact behaviour on flax-balsa biobased sandwich. Compos. Part C Open Access 2024, 14, 100489. [Google Scholar] [CrossRef]
- Smardzewski, J.; Majnusz, M.; Murlak, K. Bending and energy absorption performance of novel openwork wooden panels. Eur. J. Wood Wood Prod. 2022, 80, 515–528. [Google Scholar] [CrossRef]
- Basha, M.; Wagih, A.; Melaibari, A.; Lubineau, G.; Abdraboh, A.; Eltaher, M. Impact and post-impact response of lightweight CFRP/wood sandwich composites. Compos. Struct. 2022, 279, 114766. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; De Luycker, E.; Cantarel, A.; Bouvet, C.; Castanie, B. Experimental investigation of compression and compression after impact of wood-based sandwich structures. Compos. Struct. 2019, 220, 236–249. [Google Scholar] [CrossRef]
- Walley, S.M.; Perry, J.I. The High-Rate Mechanical Properties of Wood Mostly Obtained Using the Kolsky Bar: A Review. J. Dyn. Behav. Mater. 2025, 11, 284–337. [Google Scholar] [CrossRef]
- Wouts, J.; Haugou, G.; Oudjene, M.; Coutellier, D.; Morvan, H. Strain rate effects on the compressive response of wood and energy absorption capabilities—Part A: Experimental investigations. Compos. Struct. 2016, 149, 315–328. [Google Scholar] [CrossRef]
- Guélou, R.; Eyma, F.; Cantarel, A.; Rivallant, S.; Castanié, B. Crashworthiness of poplar wood veneer tubes. Int. J. Impact Eng. 2021, 147, 103738. [Google Scholar] [CrossRef]
- Baumann, G.; Müller, U.; Brandner, R.; Feist, F. Compression characteristics of birch wood over wide ranges of strain, strain-rate and temperature. Results Eng. 2025, 26, 104942. [Google Scholar] [CrossRef]
- Reiner, J.; Subhani, M.; Jennings, M. A comparison of energy absorption in axial crush tests between wood veneers, basalt fibre reinforced polymers and hybrid combinations. Structures 2025, 79, 109599. [Google Scholar] [CrossRef]
- Li, S.; Zhang, Y. Experiment on the impact response of aluminum alloy wood core sandwich composites. Adv. Mech. Eng. 2023, 15, 11. [Google Scholar] [CrossRef]
- Wouts, J.; Haugou, G.; Oudjene, M.; Morvan, H.; Coutellier, D. Strain rate effects on the compressive response of wood and energy absorption capabilities—Part B: Experimental investigation under rigid lateral confinement. Compos. Struct. 2018, 204, 95–104. [Google Scholar] [CrossRef]
- Guélou, R.; Eyma, F.; Cantarel, A.; Rivallant, S.; Castanié, B. Static and dynamic crushing of sandwich tubes with composite skins and three plywood cores (poplar, birch, and oak). Int. J. Crashworthiness 2023, 29, 626–647. [Google Scholar] [CrossRef]
- Baumann, G.; Brandner, R.; Müller, U.; Stadlmann, A.; Feist, F. A comparative study on the temperature effect of solid birch wood and solid beech wood under impact loading. Materials 2021, 14, 7616. [Google Scholar] [CrossRef]
- Susainathan, J.; Eyma, F.; De Luycker, E.; Cantarel, A.; Castanie, B. Numerical modelling of impact on wood-based sandwich structures. Mech. Adv. Mater. Struct. 2019, 27, 1583–1598. [Google Scholar] [CrossRef]
- Susainathan, J.; Barbero, E.; Sanchez, S.; Cantarel, A.; Eyma, F. Modelling of dynamic flexural response of composite eco-structure beams using a 3D elastic–plastic damage model. Compos. Struct. 2025, 364, 119119. [Google Scholar] [CrossRef]
- Müller, U.; Jost, T.; Kurzböck, C.; Stadlmann, A.; Wagner, W.; Kirschbichler, S.; Baumann, G.; Pramreiter, M.; Feist, F. Crash simulation of wood and composite wood for future automotive engineering. Wood Mater. Sci. Eng. 2019, 15, 312–324. [Google Scholar] [CrossRef]
- Pramreiter, M.; Bodner, S.C.; Keckes, J.; Stadlmann, A.; Feist, F.; Baumann, G.; Maawad, E.; Müller, U. Predicting strength of Finnish birch veneers based on three different failure criteria. Holzforschung 2021, 75, 847–856. [Google Scholar] [CrossRef]
- Fagerberg, L.; Zenkert, D. Effects of anisotropy and multiaxial loading on the wrinkling of sandwich panels. J. Sandw. Struct. Mater. 2005, 7, 177–194. [Google Scholar] [CrossRef]
- Kassapoglou, C. Design and Analysis of Composites Structures; Wiley: Hoboken, NJ, USA, 2010. [Google Scholar]
- Douville, M.-A.; Le Grognec, P. Exact analytical solutions for the local and global buckling of sandwich beam-columns under various loadings. Int. J. Solids Struct. 2013, 50, 2597–2609. [Google Scholar] [CrossRef]
- D’oTtavio, M.; Polit, O.; Ji, W.; Waas, A.M. Benchmark solutions and assessment of variable kinematics models for global and local buckling of sandwich struts. Compos. Struct. 2016, 156, 125–134. [Google Scholar] [CrossRef]
- Di Cara, G.; D’ottavio, M.; Polit, O. Variable kinematics finite plate elements for the buckling analysis of sandwich composite panels. Compos. Struct. 2023, 330, 117856. [Google Scholar] [CrossRef]
- Ginot, M.; D’OTtavio, M.; Polit, O.; Bouvet, C.; Castanié, B. Benchmark of wrinkling formulae and methods for pre-sizing of aircraft lightweight sandwich structures. Compos. Struct. 2021, 273, 114387. [Google Scholar] [CrossRef]
- Castanié, B.; Passieux, J.-C.; Périé, J.-N.; Bouvet, C.; Dufour, J.-E.; Serra, J. Multiaxial loading of aeronautic composite structures at intermediate scale: A review of VERTEX developments. Compos. Part C Open Access 2024, 13, 100439. [Google Scholar] [CrossRef]
- Grotto, F.; Peta, O.; Bouvet, C.; Castanié, B.; Serra, J. Testing structural elements under multiaxial loading: A numerical model of the bench to understand and predict complex boundary conditions. Aerospace 2024, 11, 68. [Google Scholar] [CrossRef]
- Grotto, F.; Bouvet, C.; Castanié, B.; Serra, J. Design and Testing of Impacted Stiffened CFRP Panels under Compression with the VERTEX Test Rig. Aerospace 2023, 10, 327. [Google Scholar] [CrossRef]
- Ginot, M.; Bouvet, C.; Castanié, B.; D’OTtavio, M.; Serra, J.; Mahuet, N. Local buckling on large sandwich panels applied to light aviation: Experimental and computation dialogue. Int. J. Solids Struct. 2023, 264, 112170. [Google Scholar] [CrossRef]
- Ginot, M.; Bouvet, C.; Castanié, B.; Serra, J.; Mahuet, N. Local buckling on large sandwich panels used in light aviation: Experimental setup and failure scenarios. Compos. Struct. 2022, 304, 116439. [Google Scholar] [CrossRef]
- Galos, J.; Das, R.; Sutcliffe, M.P.; Mouritz, A.P. Review of balsa core sandwich composite structures. Mater. Des. 2022, 221, 111013. [Google Scholar] [CrossRef]





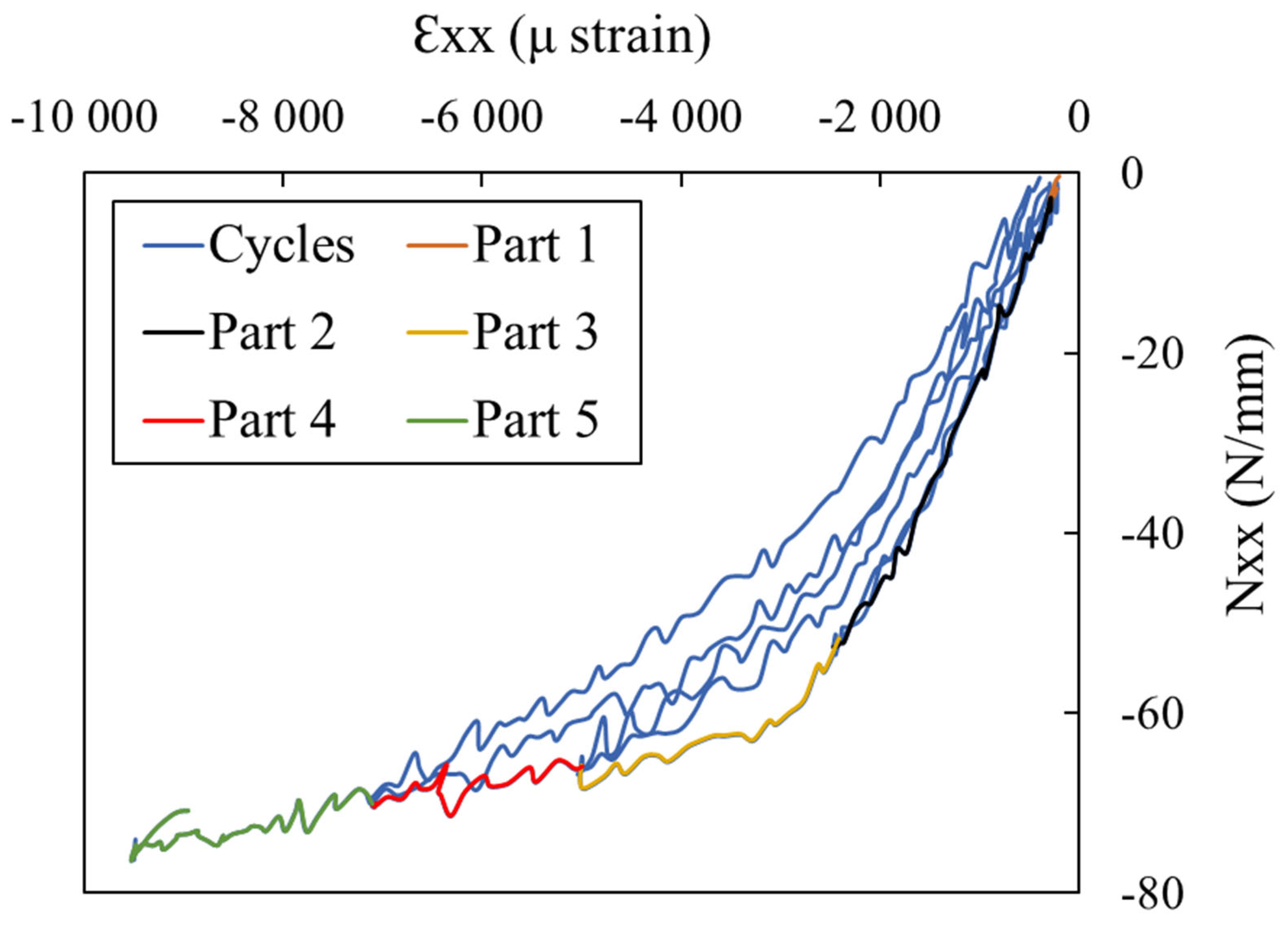









| I: Initial point | B: Buckling |
 |  |
| D: First debonding | F: Final point |
 | 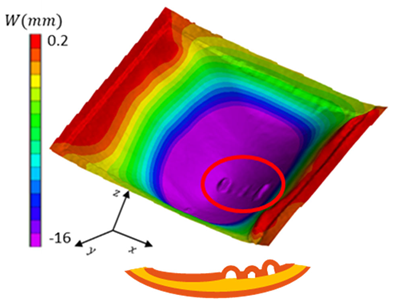 |
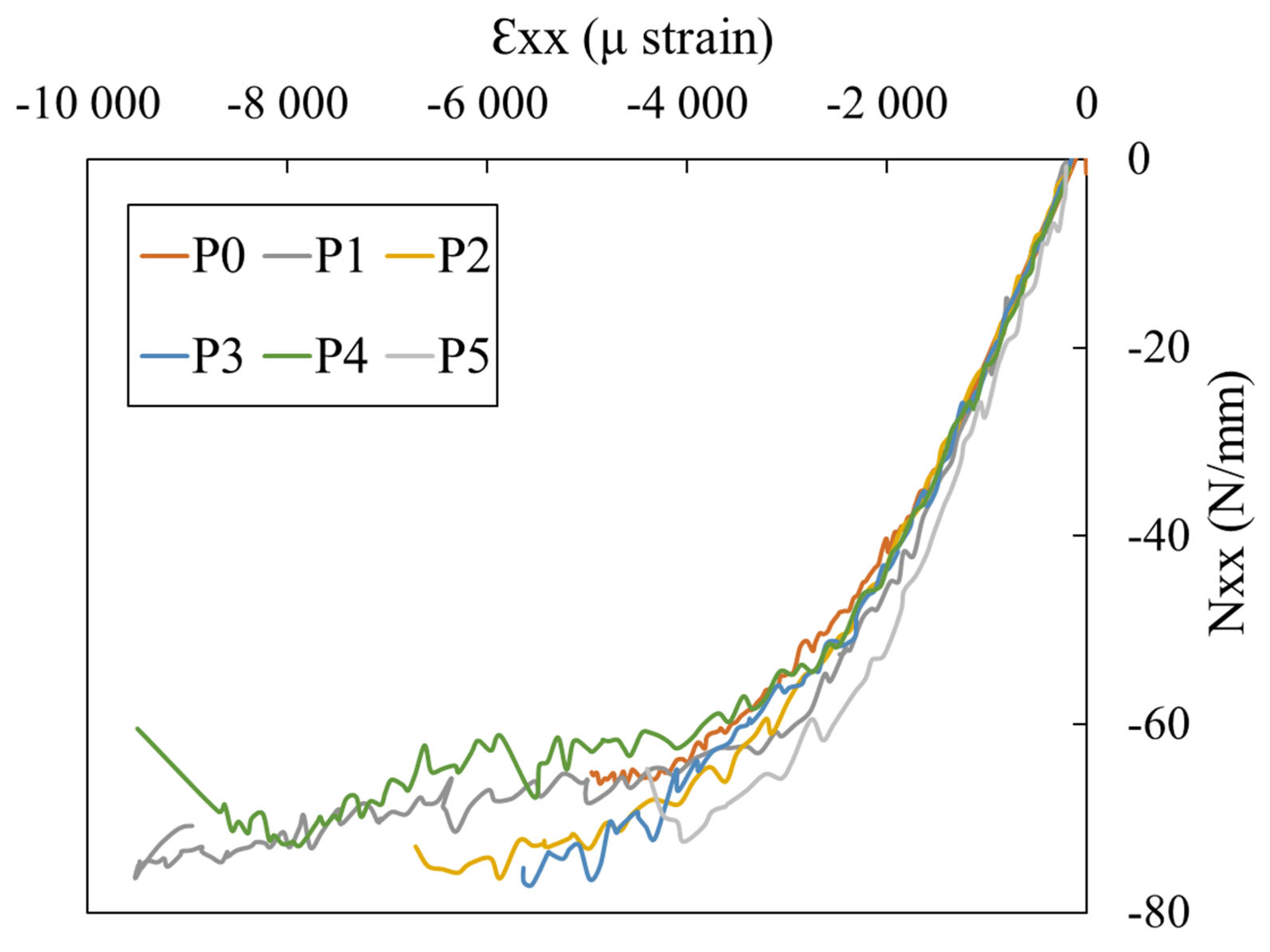
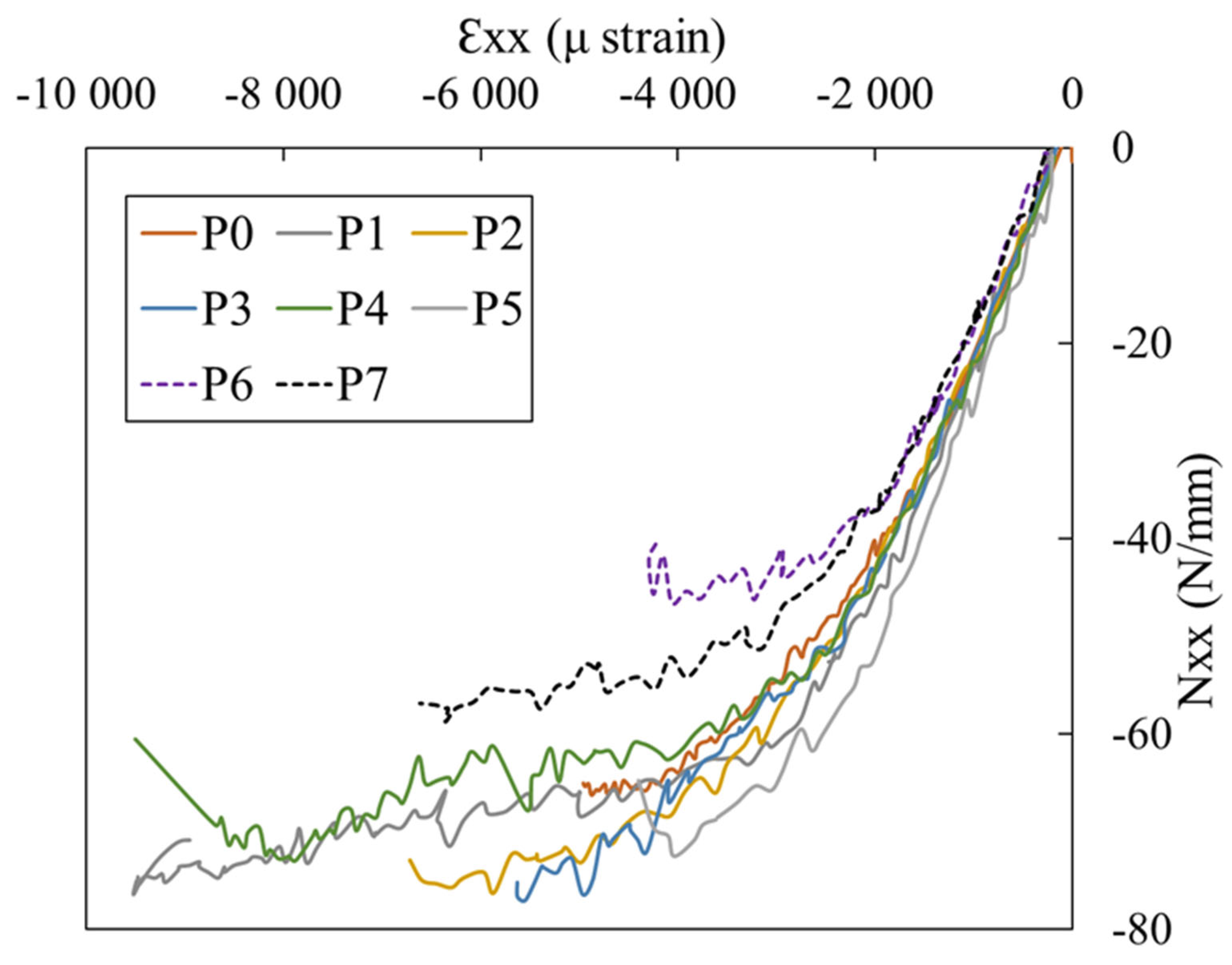
| Point B | Point D | |||
|---|---|---|---|---|
| (µstrain) | (N/mm) | (µstrain) | (N/mm) | |
| P0 | −1870 | −38 | −3510 | −55 |
| P1 | −1880 | −44 | −4650 | −66 |
| P2 | −1980 | −43 | −5417 | −72 |
| P3 | −1893 | −41 | −2350 | −49 |
| P4 | −2056 | −45 | No local debonding | |
| P5 | −1711 | −43 | −1831 | −43 |
| Mean load (Standard deviation) | −1898.33 (79.77) | −42.33 (1.88) | −3551.60 (1185.60) | −57 (9.60) |
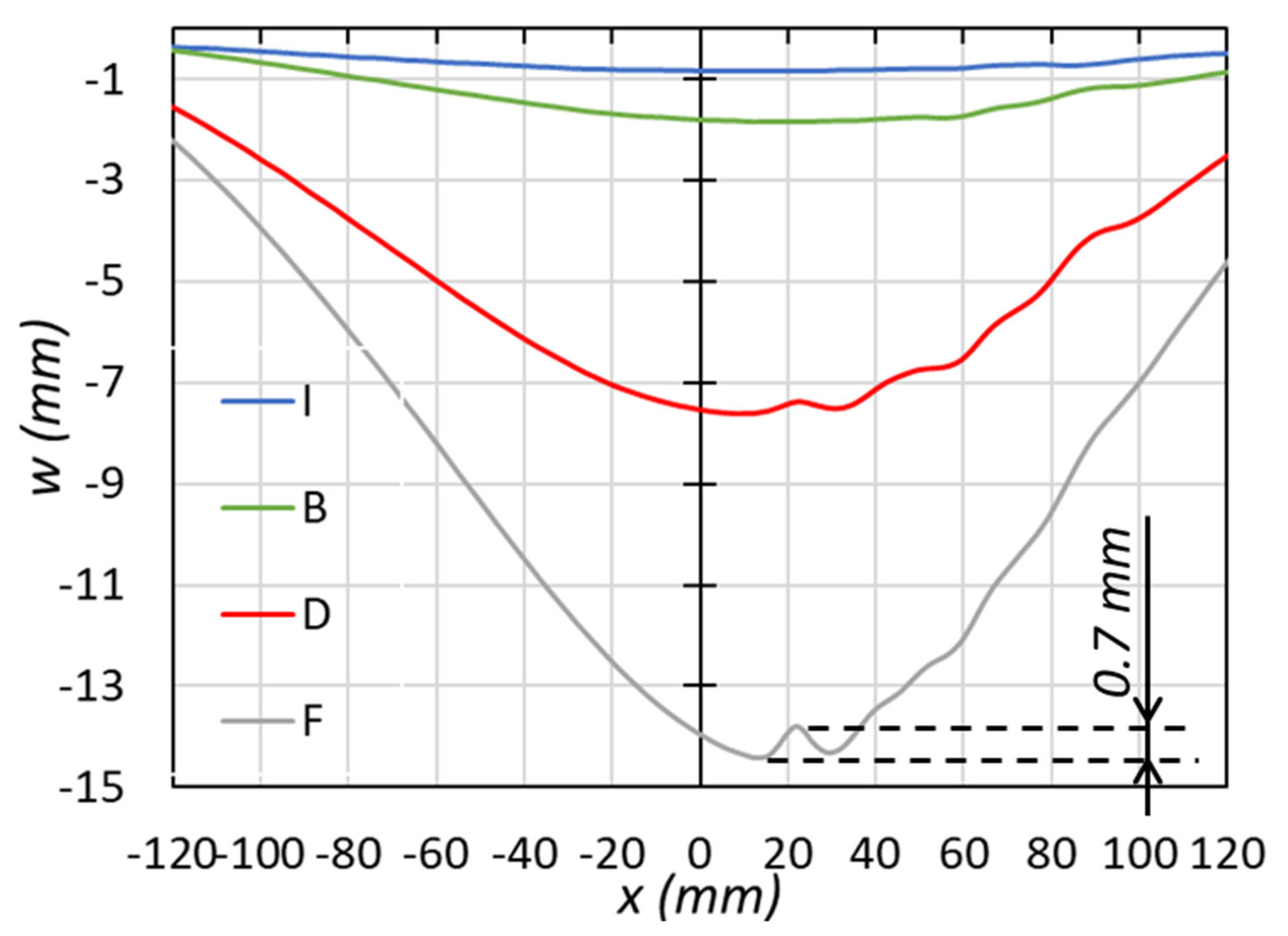
| I: initial point | : Upward buckling |
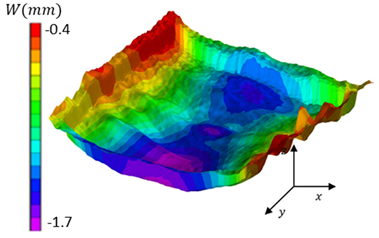 | 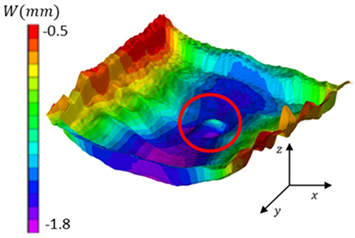 |
| B: Buckling | F: Final point |
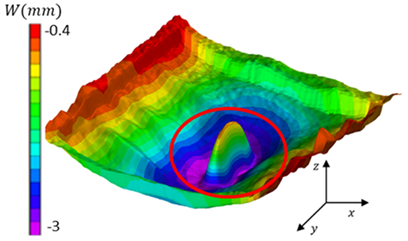 | 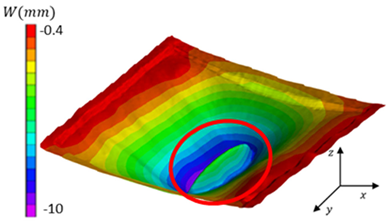 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hadiji, H.; Serra, J.; Curti, R.; Castanié, B. Analysis of the Compressive Buckling and Post-Buckling Behaviour of Wood-Based Sandwich Panels Used in Light Aviation. Aerospace 2025, 12, 782. https://doi.org/10.3390/aerospace12090782
Hadiji H, Serra J, Curti R, Castanié B. Analysis of the Compressive Buckling and Post-Buckling Behaviour of Wood-Based Sandwich Panels Used in Light Aviation. Aerospace. 2025; 12(9):782. https://doi.org/10.3390/aerospace12090782
Chicago/Turabian StyleHadiji, Hajer, Joel Serra, Remi Curti, and Bruno Castanié. 2025. "Analysis of the Compressive Buckling and Post-Buckling Behaviour of Wood-Based Sandwich Panels Used in Light Aviation" Aerospace 12, no. 9: 782. https://doi.org/10.3390/aerospace12090782
APA StyleHadiji, H., Serra, J., Curti, R., & Castanié, B. (2025). Analysis of the Compressive Buckling and Post-Buckling Behaviour of Wood-Based Sandwich Panels Used in Light Aviation. Aerospace, 12(9), 782. https://doi.org/10.3390/aerospace12090782






