Strong Tracking Unscented Kalman Filter for Identification of Inflight Icing
Abstract
1. Introduction
2. Model
2.1. Motion Equations
2.2. Icing Effect on Model
3. Parameter Identification Algorithm
3.1. UKF Algorithm
- Step 1:
- Initializing the state variable:
- Step 2:
- Making a matrix of by calculating the sigma points
- Step 3:
- Time updating produces a collection of modified samples by propagating each of the sigma points through the process model.
- Step 4:
- Measurement updating: An analysis of the cross-covariance between the anticipated states and measurements, as well as the weighted covariance of the predicted measurements, is performed.
- Step 5:
- To proceed to the following time step, repeat Steps 1 through 4.
3.2. Algorithm of the STUKF
- Step 1:
- Step 2:
- Step 3:
- Achieving modified using Equation (31).
- Step 4:
- Finishing the rest of UKF algorithm with the new , completing the update of and .
- Step 5:
- Repeating the above steps.
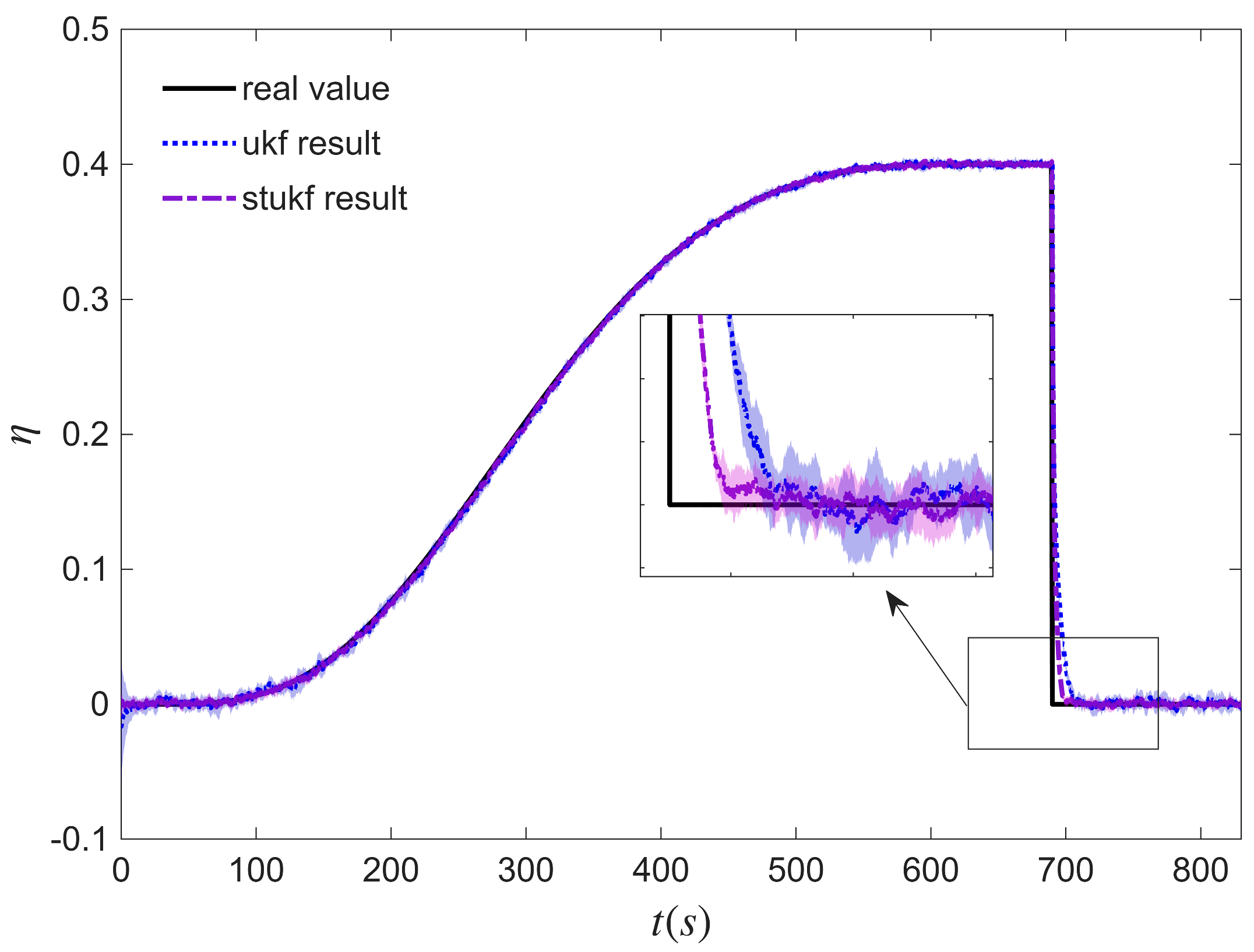
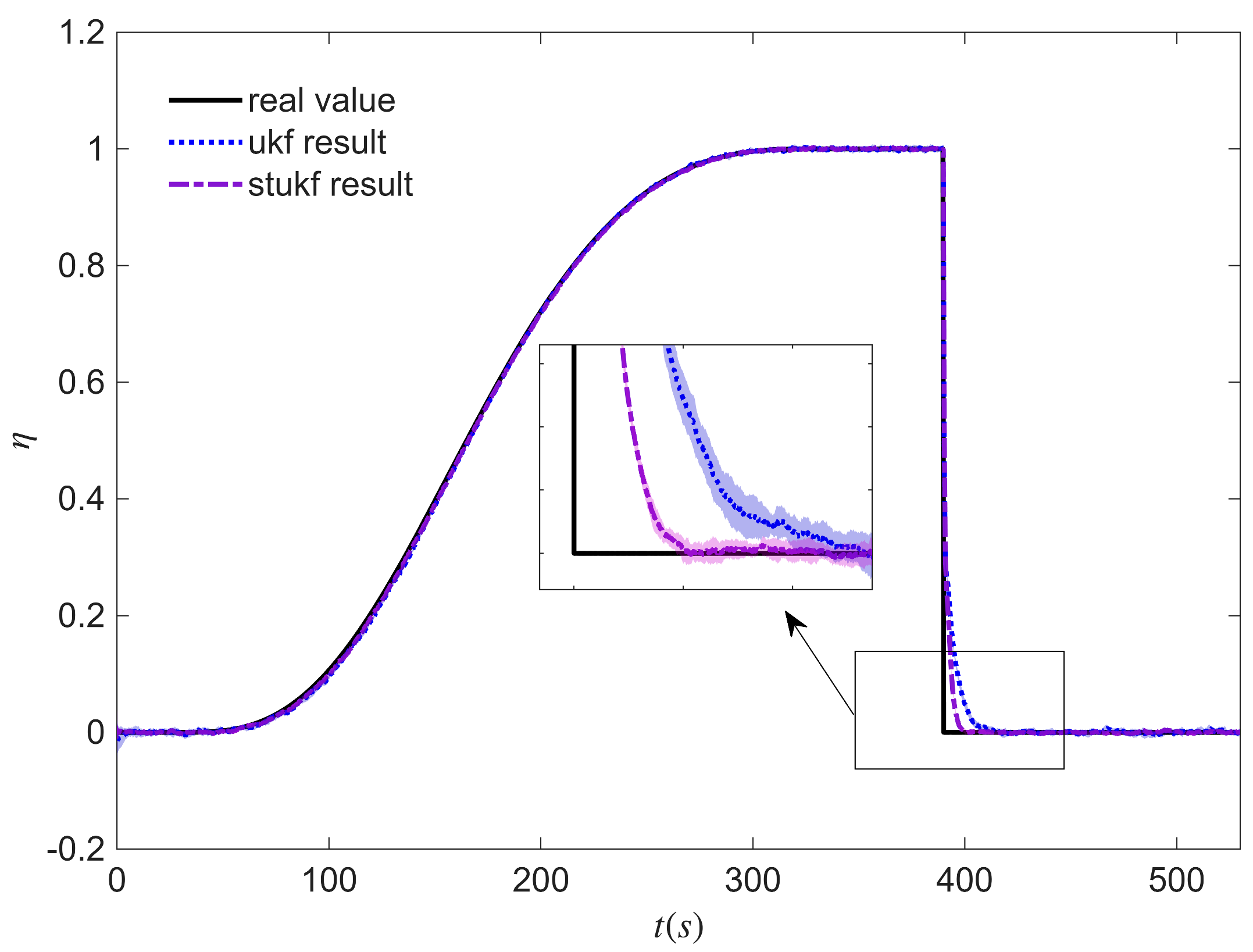
3.3. Identification of Icing Severity Parameter
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bragg, M.B. Aircraft Aerodynamic Effects Due To Large Droplet Ice Accretions. In Proceedings of the 34th Aerospace Sciences Meeting and Exhibit, AIAA Paper 96-0932, Reno, NV, USA, 15–18 January 1996. [Google Scholar] [CrossRef][Green Version]
- Caliskan, F.; Hajiyev, C. A Review of In-flight Detection and Identification of Aircraft Icing and Reconfigurable Control. Prog. Aerosp. Sci. 2013, 60, 12–34. [Google Scholar] [CrossRef]
- Cole, J.; Sands, W. Statistical Study of Aircraft icing accidents. In Proceedings of the 29th Aerospace Sciences Meeting and Exhibit, AIAA Paper 91-0558, Reno, NV, USA, 7–10 January 1991. [Google Scholar] [CrossRef]
- Merret, J.; Hossain, K.N.; Bragg, M.B. Envelope Protection and Atmospheric Disturbances in Icing Encounters. In Proceedings of the 40th Aerospace Sciences Meeting and Exhibit, AIAA Paper 2002-0814, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Bragg, M.B.; Perkins, W.R.; Sarter, N.B.; Basar, T.; Voulgaris, P.G.; Gurbacki, H.M.; Melody, J.W.; McCray, S.S. An Interdisciplinary Approach to Inflight Aircraft Icing Safety. In Proceedings of the 36th Aerospace Sciences Meeting and Exhibit, AIAA Paper 98-0095, Reno, NV, USA, 12–15 January 1998. [Google Scholar] [CrossRef]
- Bragg, M.; Basar, T.; Perkins, W.; Selig, M.; Voulgaris, P.; Melody, J.; Sarter, N. Smart Icing Systems for Aircraft Icing Safety. In Proceedings of the 40th Aerospace Sciences Meeting and Exhibit, AIAA Paper 2002-0813, Reno, NV, USA, 14–17 January 2002. [Google Scholar] [CrossRef]
- Melody, J.W.; Basar, T.; Perkins, W.R.; Voulgaris, P.G. Parameter Identification for Inflight Detection and Characterization of Aircraft Icing. Control Eng. Pract. 2000, 8, 985–1001. [Google Scholar] [CrossRef]
- Melody, J.W.; Hillbr, T.; Basar, T.; Perkins, W.R. H∞ Parameter Identification for Inflight Detection of Aircraft Icing: The Time-varying Case. Control Eng. Pract. 2001, 8, 1327–1335. [Google Scholar] [CrossRef]
- Aykan, R.; Hajiyev, C.; Caliskan, F. Kalman Filter and Neural Network-based Icing Identification Applied to A340 Aircraft Dynamics. Aircr. Eng. Aerosp. Technol. 2005, 77, 23–33. [Google Scholar] [CrossRef]
- Caliskan, F.; Aykan, R.; Hajiyev, C. Aircraft Icing Detection, Identification, and Reconfigurable Control Based on Kalman Filtering and Neural Networks. J. Aerosp. Eng. 2008, 21, 51–60. [Google Scholar] [CrossRef]
- Dong, Y.; Ai, J. Research on Inflight Parameter Identification and Icing Location Detection of the Aircraft. Aerosp. Sci. Technol. 2013, 29, 305–312. [Google Scholar] [CrossRef]
- Farghaly, M.B.; Aldabesh, A. Studying the Effect of Geometric Parameters of Anti-Icing System on the Performance Characteristics of an Airplane Wing: Computational Analysis. Case Stud. Therm. Eng. 2025, 73, 106733. [Google Scholar] [CrossRef]
- Menegaz, H.M.; Ishihara, J.Y.; Borges, G.A.; Vargas, A.N. A Systematization of the Unscented Kalman Filter Theory. IEEE Trans. Autom. Control 2015, 60, 2583–2598. [Google Scholar] [CrossRef]
- Zhou, D.; Wang, Q. Strong Tracking Filtering of Nonlinear Systems With Colored Noise. Trans. Beijing Inst. Technol. 1997, 17, 321–326. [Google Scholar]
- Li, M.; Zhu, B.L.; Wang, S.Y.; Zhang, Y.C.; Li, H.Y. Strong Tracking Unscented Kalman Filtering Algorithm Based on Satellite Attitude Determination System. Int. J. Future Gener. Commun. Netw. 2014, 7, 155–166. [Google Scholar] [CrossRef]
- Stevens, B.L.; Lewis, F.L.; Johnson, E.N. Aircraft Control and Simulation: Dynamics, Controls Design, and Autonomous Systems; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Bragg, M.B.; Hutchison, T.; Merret, J. Effect of Ice Accretion on Aircraft Flight Dynamics. In Proceedings of the 38th Aerospace Sciences Meeting and Exhibit, AIAA Paper 2000-0360, Reno, NV, USA, 10–13 January 2000. [Google Scholar] [CrossRef]
- Løw-Hansen, B.; Hann, R.; Stovner, B.N.; Johansen, T.A. UAV Icing: A Survey of Recent Developments in Ice Detection Methods. IFAC-PapersOnLine 2023, 56, 10727–10739. [Google Scholar] [CrossRef]
- Enache, A.; Wallisch, J.; van Beeck, J.; Hendrick, P.; Hann, R. Ice Accretion: Image Post-Processing Measurement Techniques for 2D Ice Shapes. Aerospace 2023, 10, 451. [Google Scholar] [CrossRef]
- Hann, R. Numerical Simulation of In-Flight Icing of Unmanned Aerial Vehicles. In Handbook of Numerical Simulation of In-Flight Icing; Springer: Berlin/Heidelberg, Germany, 2023. [Google Scholar] [CrossRef]
- Huang, P.; Li, H.; Wen, G.; Wang, Z. Application of Adaptive Weighted Strong Tracking Unscented Kalman Filter in Non-Cooperative Maneuvering Target Tracking. Aerospace 2022, 9, 468. [Google Scholar] [CrossRef]
- Tian, F.; Wang, S.; Fu, W.; Wei, T. Vehicle Target Tracking Algorithm Based on Improved Strong Tracking Unscented Kalman Filter. Appl. Sci. 2025, 15, 3276. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Wang, J. Strong Tracking UKF-Based Hybrid Algorithm and Its Application to Initial Alignment of Rotating SINS With Large Misalignment Angles. IEEE Trans. Ind. Electron. 2022, 70, 833–8343. [Google Scholar] [CrossRef]
- Liu, X.; Guan, J.; Jiang, R.; Gao, X.; Chen, B.; Ge, S. Robust Strong Tracking Unscented Kalman Filter for Non-linear Systems with Unknown Inputs. IET Signal Process. 2022, 16, 351–365. [Google Scholar] [CrossRef]
- Zhang, L.; Hou, Y. A Modified Strong Tracking Adaptive Kalman Filter for Precision Clock Synchronization. IEEJ Trans. Electr. Electron. Eng. 2023, 18, 1702–1711. [Google Scholar] [CrossRef]
- Zhou, Z.; Zhan, M.; Wu, B.; Xu, G.; Zhang, X.; Cheng, J.; Gao, M. A Novel Adaptive Unscented Kalman Filter Algorithm for SOC Estimation to Reduce the Sensitivity of Attenuation Coefficient. Energy 2024, 307, 132598. [Google Scholar] [CrossRef]
- Feng, S.; Li, X.; Zhang, S.; Jian, Z.; Duan, H.; Wang, Z. A Review: State Estimation Based on Hybrid Models of Kalman Filter and Neural Network. Syst. Sci. Control Eng. 2023, 11, 2173682. [Google Scholar] [CrossRef]
- Løw-Hansen, B.; Müller, N.C.; Coates, E.M.; Johansen, T.A.; Hann, R. Identification of an Electric UAV Propulsion System in Icing Conditions; SAE Technical Paper, No. 2023-01-1378; SAE: Warrendale, PA, USA, 2023. [Google Scholar] [CrossRef]
- Løw-Hansen, B.; Hann, R.; Johansen, T.A. UAV Icing: Ice Shedding Detection Method for an Electrothermal De-Icing System. In Proceedings of the AIAA Aviation Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3904. [Google Scholar] [CrossRef]
- Wallisch, J.; Hann, R. UAV Icing: Experimental Investigation of Ice Shedding Times with an Electrothermal De-icing System. In Proceedings of the AIAA AVIATION Forum, Chicago, IL, USA, 27 June–1 July 2022; p. 3905. [Google Scholar] [CrossRef]
- Singh, H.; Mishra, K.V.; Chattopadhyay, A. Inverse Unscented Kalman Filter. IEEE Trans. Signal Process. 2024, 72, 2692–2709. [Google Scholar] [CrossRef]
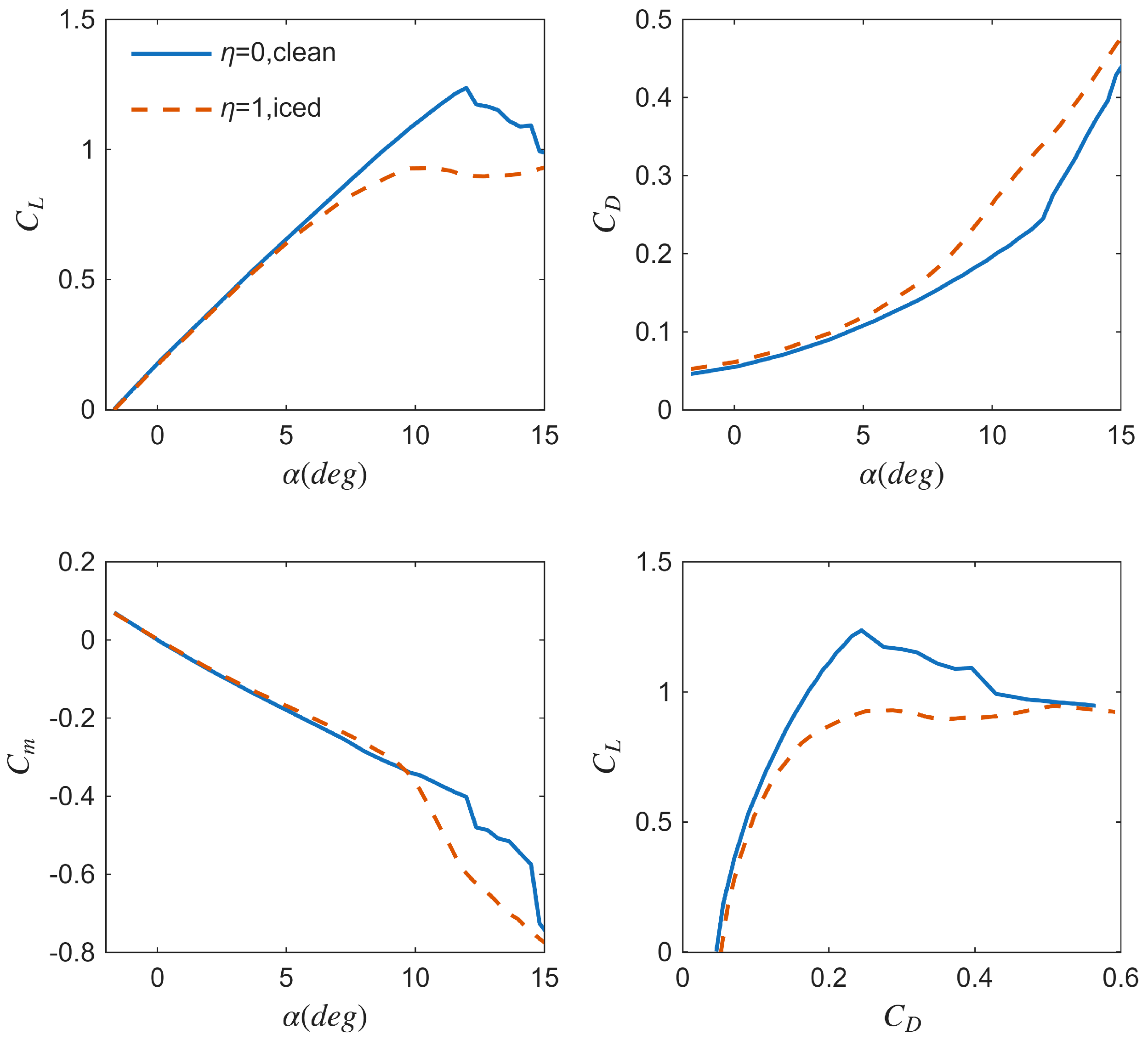




| clean | ||||||||||
| iced | ||||||||||
| clean | ||||||||||
| iced |
| 0.8464 m/s | 0.003 | 0.003 | 0.0069/s | 0.0069/s | 0.0069/s | 0.0293 | 0.0293 | 0.0293 |
| Process Noise Intensity | Moderate Icing | Severe Icing | ||
|---|---|---|---|---|
| UKF | STUKF | UKF | STUKF | |
| light | 0.0045 | 0.0035 | 0.0072 | 0.0057 |
| moderate | 0.0117 | 0.0037 | 0.0152 | 0.0058 |
| heavy | 0.0326 | 0.0040 | 0.0368 | 0.0063 |
| Process Noise Intensity | Moderate Icing | Severe Icing | ||||||
|---|---|---|---|---|---|---|---|---|
| light | 4.26 | / | / | 38.6 | 5.41 | 3.29 | 2.52 | 32.7 |
| moderate | 5.37 | / | / | 44.36 | 7.02 | 4.42 | 3.24 | 39.2 |
| heavy | 7.10 | / | / | 55.42 | 8.22 | 5.50 | 4.18 | 47.8 |
| Process Noise Intensity | Moderate Icing | Severe Icing | ||||||
|---|---|---|---|---|---|---|---|---|
| light | 4.12 | / | / | 8.32 | 3.57 | 2.01 | 1.77 | 5.64 |
| moderate | 4.56 | / | / | 9.13 | 3.98 | 2.05 | 1.83 | 6.17 |
| heavy | 4.88 | / | / | 11.16 | 4.17 | 2.07 | 1.91 | 6.89 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Ai, J. Strong Tracking Unscented Kalman Filter for Identification of Inflight Icing. Aerospace 2025, 12, 779. https://doi.org/10.3390/aerospace12090779
Luo H, Ai J. Strong Tracking Unscented Kalman Filter for Identification of Inflight Icing. Aerospace. 2025; 12(9):779. https://doi.org/10.3390/aerospace12090779
Chicago/Turabian StyleLuo, Huangdi, and Jianliang Ai. 2025. "Strong Tracking Unscented Kalman Filter for Identification of Inflight Icing" Aerospace 12, no. 9: 779. https://doi.org/10.3390/aerospace12090779
APA StyleLuo, H., & Ai, J. (2025). Strong Tracking Unscented Kalman Filter for Identification of Inflight Icing. Aerospace, 12(9), 779. https://doi.org/10.3390/aerospace12090779





