A Long Sequence Time-Series Forecasting Method for Early Warning of Long Landing Risks with QAR Flight Data
Abstract
1. Introduction
1.1. Long Landing Incident and QAR
1.2. Long Landing Research Progress
1.3. Aim and Structure of This Study
2. Extraction of Landing Phase Based on QAR Data
2.1. Classification and Characterization of QAR Data
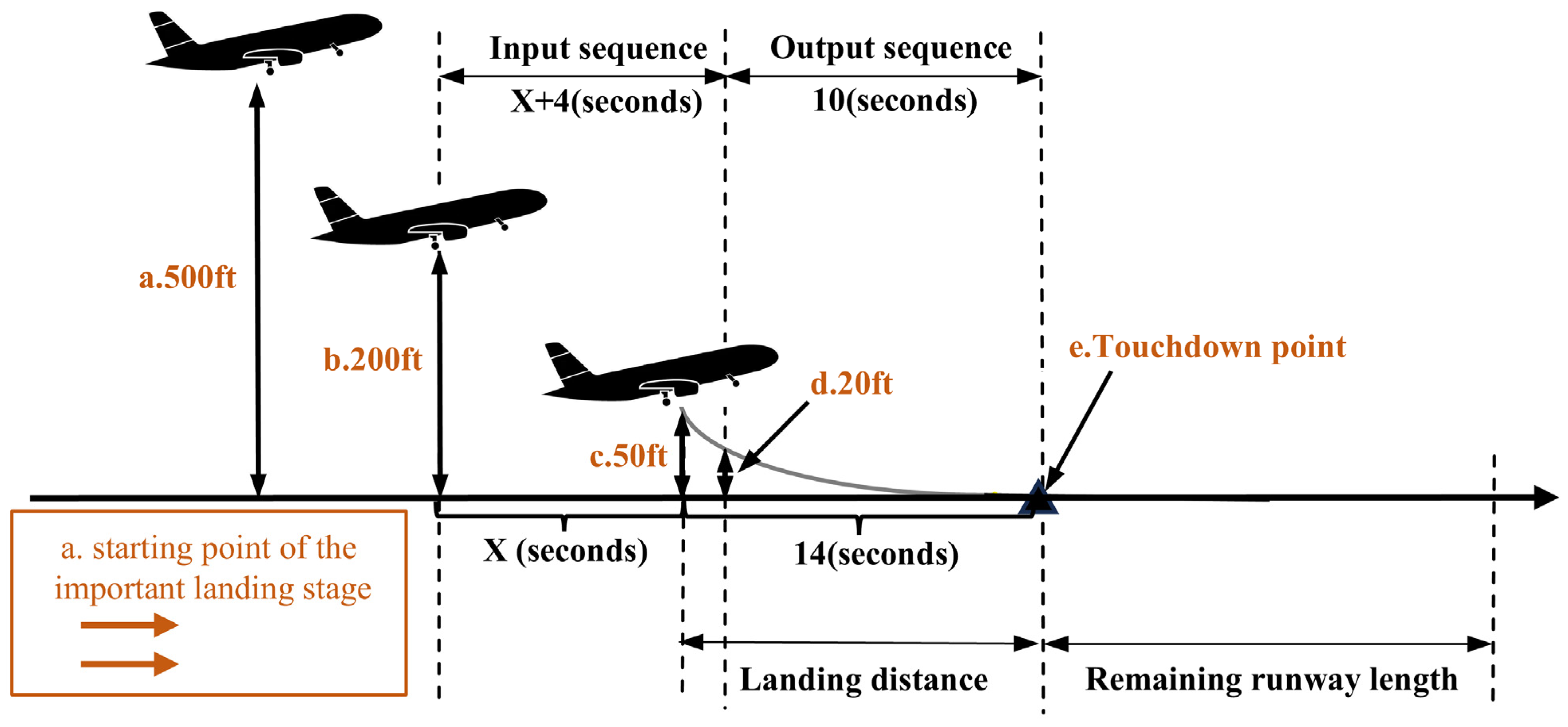
2.2. Definition of the Landing Phase
2.3. Application of Landing Phase Parameters
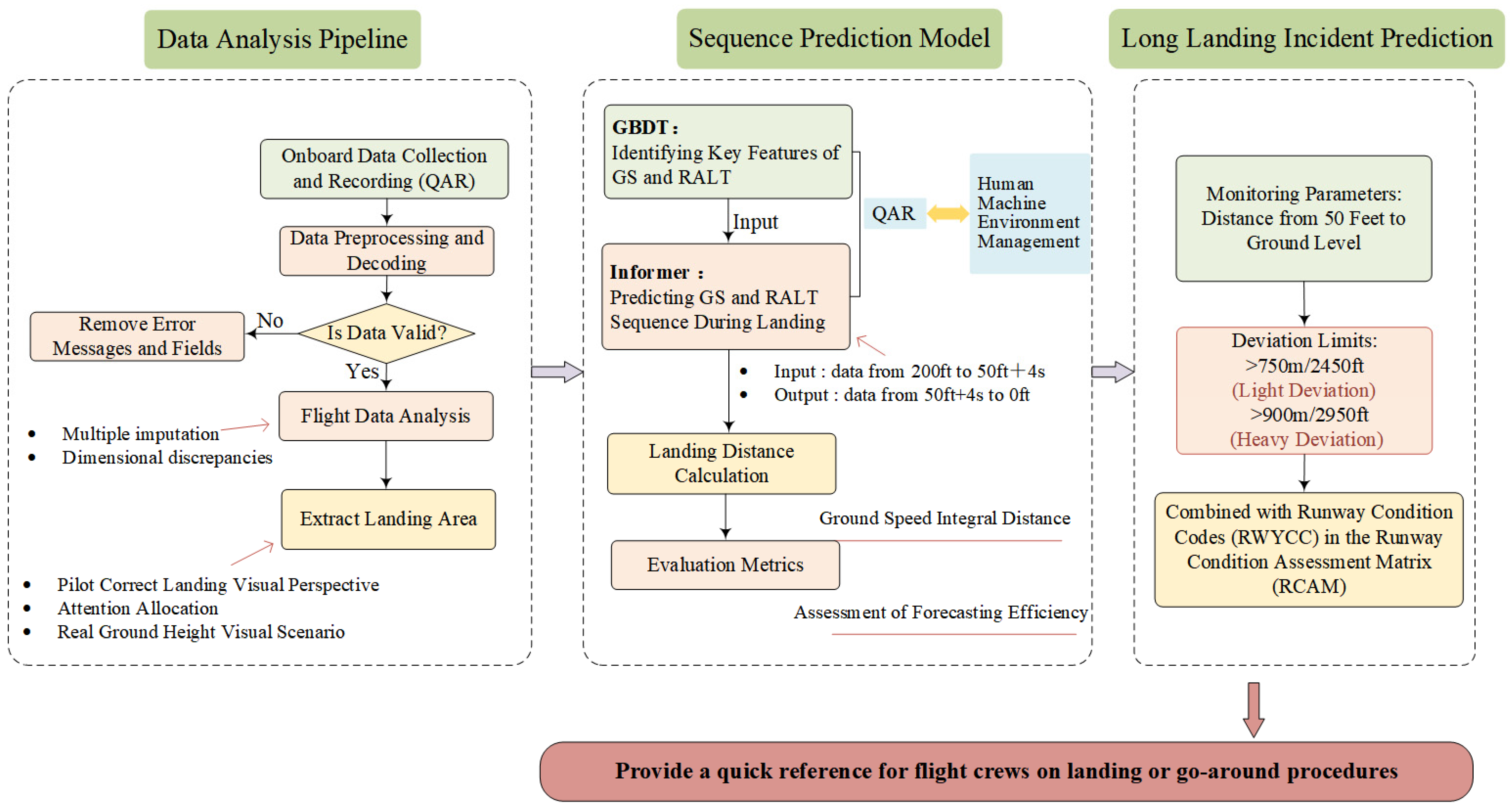
3. Methodology
3.1. Problem Formulation
3.2. Extraction of Key Features for Landing Distance Based on GBDT
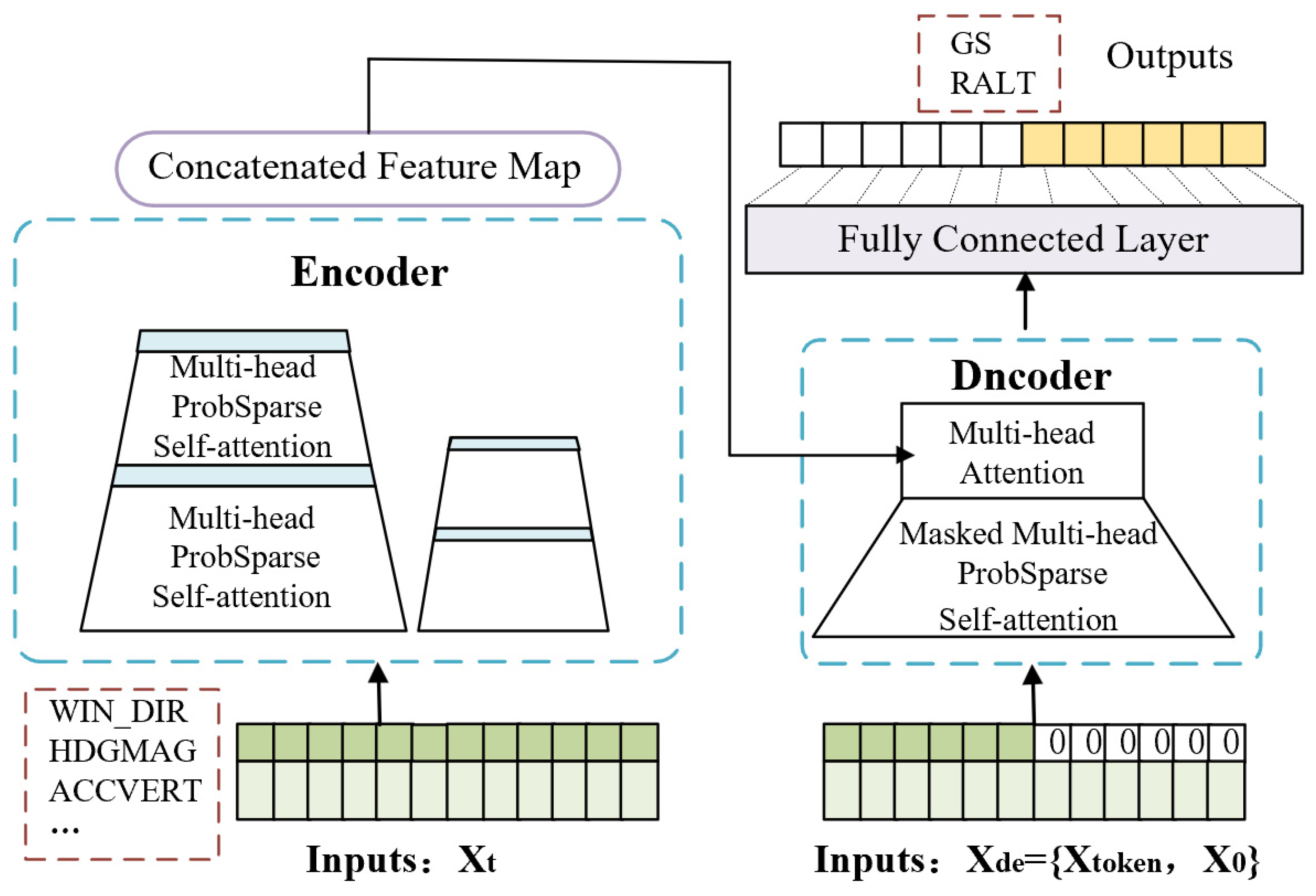
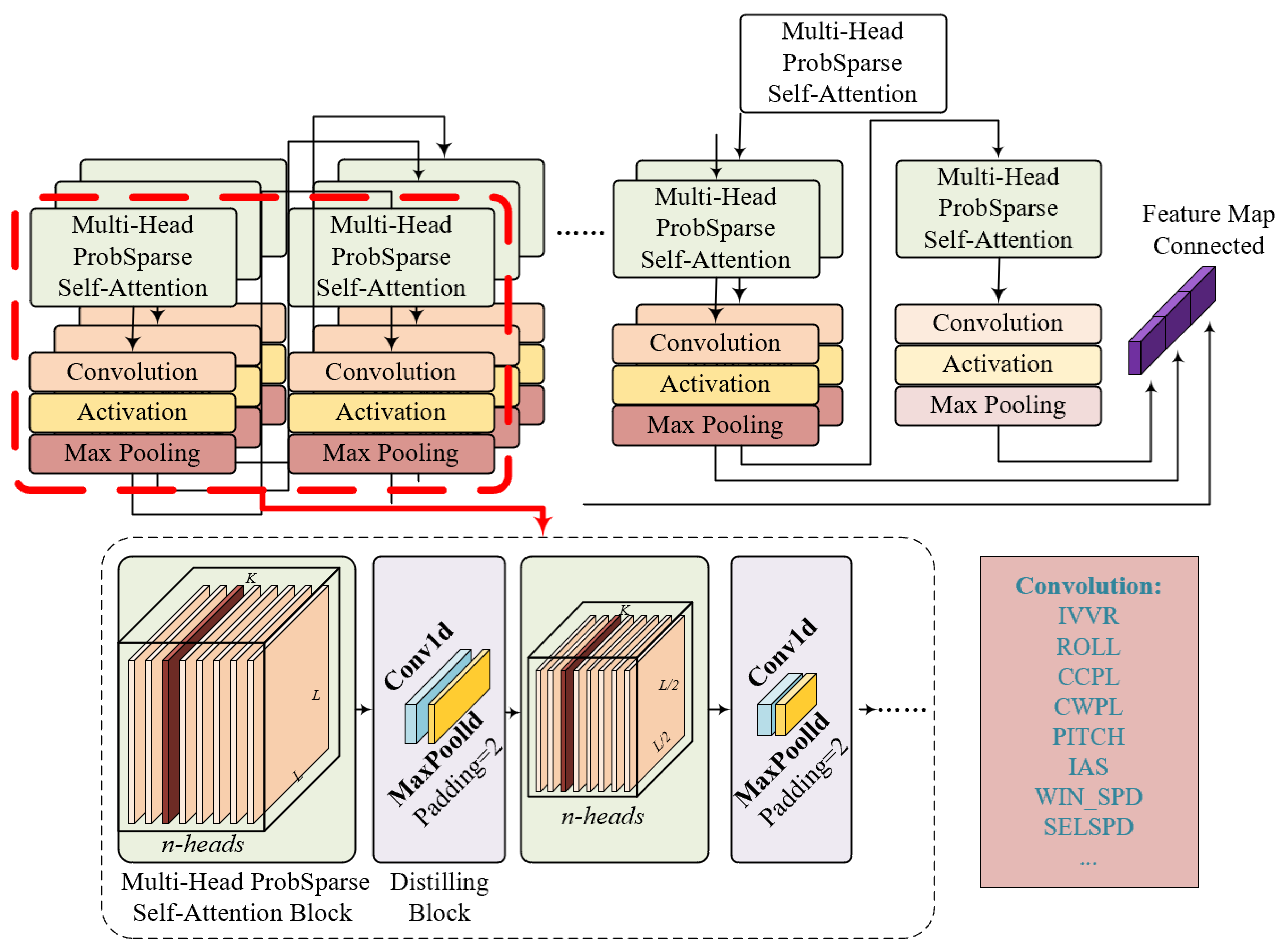
3.3. Long-Term Time Series Forecasting Based on Informer
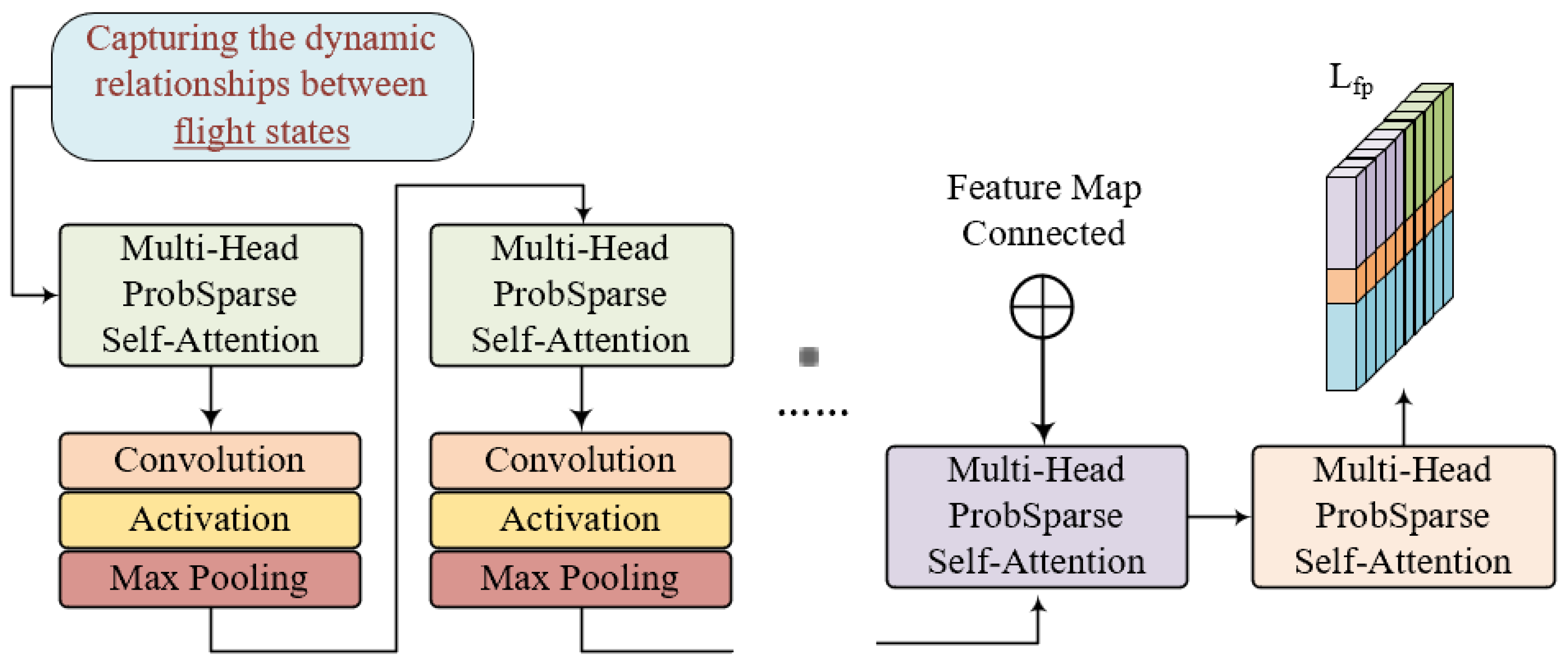
3.3.1. The ProbSparse Self-Attention Mechanism of Informer
3.3.2. The Structure of the Informer Encoder and Decoder
3.4. Baselines
- LSTM: Long Short-Term Memory networks are currently applied to time prediction (TP) tasks, with optimizations based on LSTM to improve prediction accuracy [25]. In this study, the basic LSTM model was used as a reference for the prediction of GS, RALT, and landing distance.
- Informer: This model focuses on time series (TP) tasks with long sequence inputs. It uses a multi-head attention framework combined with a distillation mechanism, overcoming the limitations of recurrent neural networks in handling long-term dependencies and enabling parallel computation. Informer reduces computational complexity during training and prediction through attention distillation and generative decoding strategies, enhancing speed.
4. Data Description and Experimental Results
4.1. Evaluation Metrics
4.2. Selection of Important Features for GS and RALT
4.3. Landing Distance Prediction
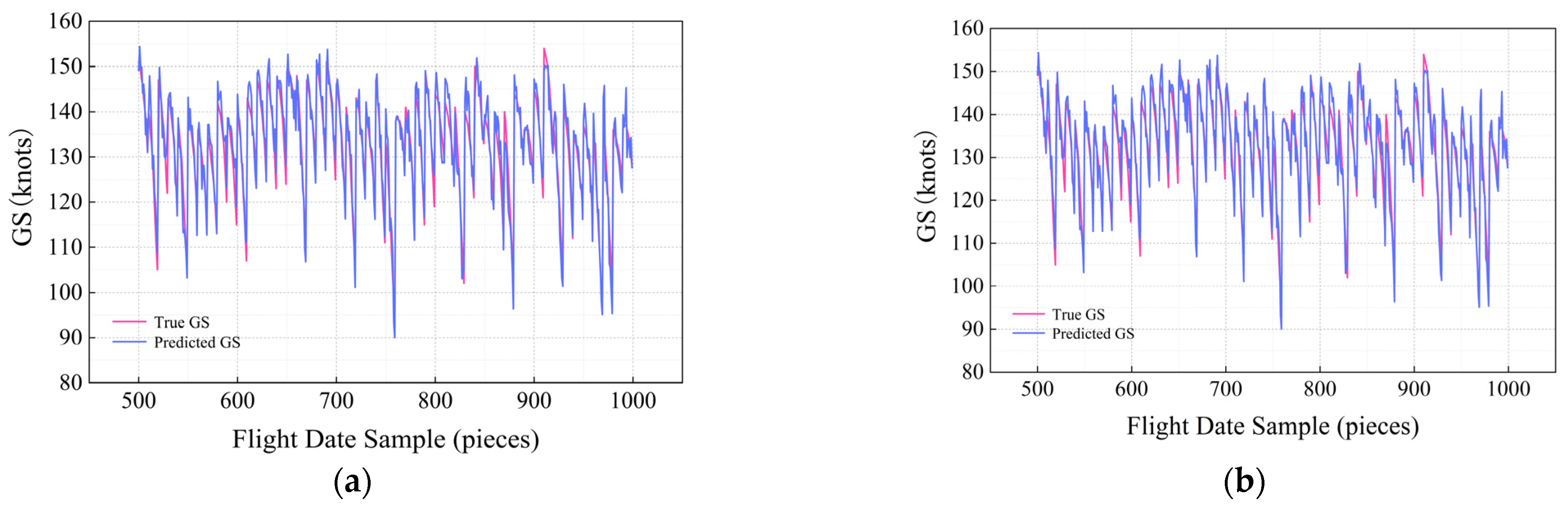
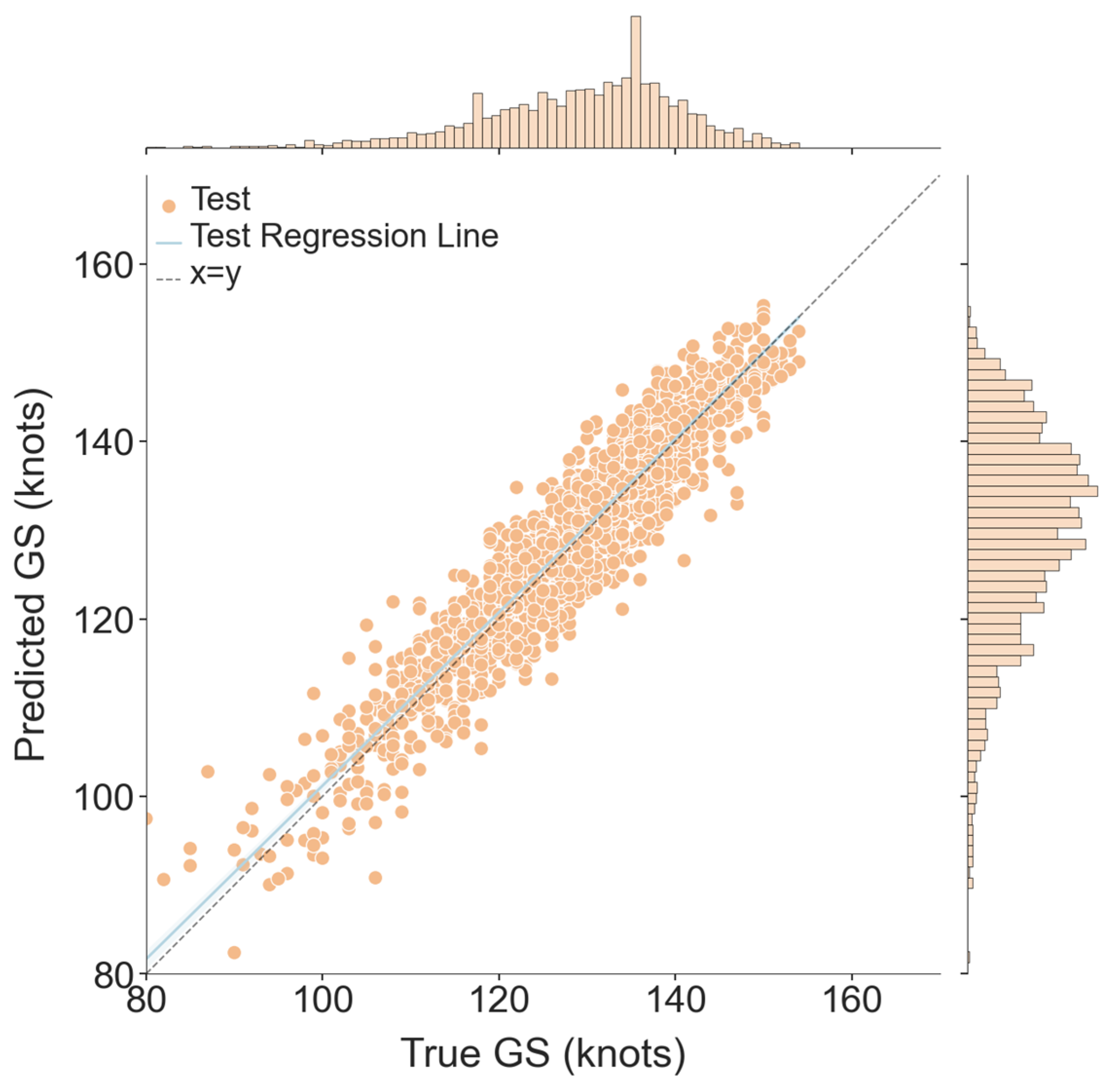
4.3.1. Prediction Results for GS
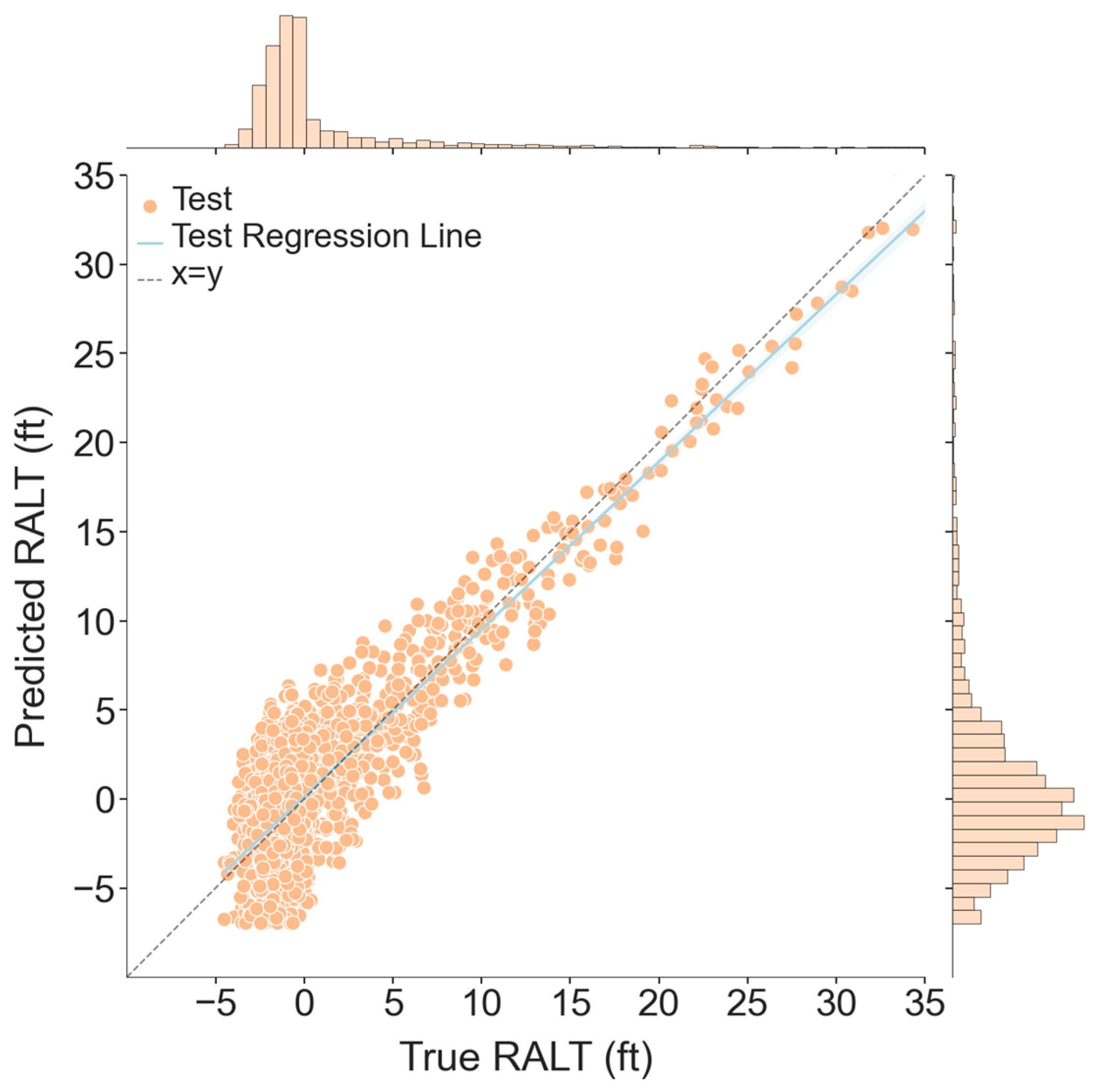
4.3.2. Prediction Results for RALT
4.3.3. Prediction Results for Landing Distance
5. Discussion
6. Conclusions
- (1)
- A comprehensive pipeline was constructed for the preprocessing of QAR data. This involves defining critical heights during the landing phase based on the pilot’s correct landing perspective, attention allocation, and the visual scene of actual altitude above ground level. The landing interval was effectively extracted from the QAR data to avoid redundancy. Additionally, using GBDT, multiple decision trees were constructed to capture the nonlinear relationships and interactions among features within the QAR data, identifying key characteristics of ground speed and radio altitude as indirect indicators of landing distance. The regression results of this algorithm have been validated to be superior.
- (2)
- A GBDT-Informer long sequence time-series forecasting model was established, which learns from QAR data and fits the implicit influences of human, machine, environment, and management factors on landing. The model separately predicts the sequences of ground speed and radio altitude within the landing interval and calculates the predicted landing distance. Effective metrics were constructed to evaluate the performance of long landing predictions. Validation using extensive QAR datasets demonstrates that the model achieves high fitting accuracy in predicting aircraft long landings. This predictive framework provides insights into the coupling relationships among multiple parameters in flight data and their interrelations with abnormal exceedance patterns, facilitating an extension of the pilot’s operational response time before an incident occurs. This allows for timely adjustments to the aircraft’s status and provides quick references for flight crews when making landing or go-around decisions, enhancing safety margins during the landing phase and improving runway management efficiency.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Hyperparameter Tuning Data for the GBDT-Informer Model
| Feathers | Hyperparameters | Performance Scores | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Number | Attation Mechanism | Model Network Structure | Training Configuration | |||||||||||
| ProbSparse | Encoder Layers | Decoder Layers | No. of Heads | Batch Size | Epoch Number | Learning Rate | Activation | Dropout | Optimization Function | RMSE | MAE | MAPE/% | ||
| GS | 1(BEST) | 5 | 2 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 2.95 | 3.06 | 3.43 |
| 2 | 5 | 1 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.21 | 2.41 | 3.99 | |
| 3 | 3 | 1 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.49 | 2.59 | 4.16 | |
| 4 | 5 | 3 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 4.00 | 2.96 | 4.46 | |
| 5 | 8 | 2 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 4.86 | 3.70 | 5.09 | |
| RALT | 1(BEST) | 5 | 2 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.01 | 2.30 | 4.08 |
| 2 | 8 | 2 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.63 | 2.36 | 5.29 | |
| 3 | 5 | 1 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.94 | 2,57 | 5.82 | |
| 4 | 3 | 1 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 3.97 | 2.42 | 5.15 | |
| 5 | 3 | 2 | 1 | 5 | 512 | 50 | 0.001 | GELU | 0.05 | Adam | 4.39 | 2.68 | 5.55 | |
References
- BOEING, 1959–2001, Statistical Summary of Commercial Jet Airplane Accidents. 2018. Available online: http://www.boeing.com/resources/boeingdotcom/company/about_bca/pdf/statsum.pdf (accessed on 5 June 2019).
- Flight Safety Foundation. Flight Safety Foundation ALAR Briefing Note 4.2—Energy Management; Flight Safety Foundation: Alexandria, VA, USA, 2000. [Google Scholar]
- Wang, L.; Wu, C.; Sun, R. Pilot Operating Characteristics Analysis of Long Landing Based on Flight QAR Data; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- 121/135-FS-2012-45; Implementation and Management of Flight Operation Quality Assurance. Civil Aviation Administration of China: Beijing, China, 2012.
- Aviation Office of Civil Aviation Administration of China. Annual Statistical Report on Incidents of CAAC; Aviation Office of Civil Aviation Administration of China: Beijing, China, 2011.
- Jasra, S.K.; Valentino, G.; Muscat, A.; Zammit-Mangion, D.; Camilleri, R. Evaluation of Flight Parameters During Approach and Landing Phases by Applying Principal Component Analysis. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020. [Google Scholar]
- Wang, L.; Wu, C.; Sun, R. An analysis of flight Quick Access Recorder (QAR) data and its applications in preventing landing incidents. Reliab. Eng. Syst. Saf. 2014, 127, 86–96. [Google Scholar] [CrossRef]
- Li, X.; Zhang, L.; Shang, J.; Li, X.; Qian, Y.; Zheng, L. A Runway Overrun Risk Assessment Model for Civil Aircraft Based on Quick Access Recorder Data. Appl. Sci. 2023, 13, 9828. [Google Scholar] [CrossRef]
- Li, R.; Pan, S.; Fang, H.; Xiong, Y.; Wang, F. Fault Prediction Technology of Civil Aircraft Based on Qar Data. In Proceedings of the 2017 International Conference on Sensing, Diagnostics, Prognostics, and Control (SDPC), Shanghai, China, 16–18 August 2017. [Google Scholar]
- Luo, W.; Wu, Z.; Chen, C. An Aircraft Fuel Flow Model of Cruise Phase Based on LSTM and QAR Data. In Proceedings of the 2020 13th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 12–13 December 2020. [Google Scholar]
- Kang, C.; Zhang, P. The Solution of FlySmart with Airbu. China Civ. Aviat. 2014. [Google Scholar]
- Run, S.; Ze, Y.; Lei, W. Study of flight safety evaluation based on QAR data. China Saf. Sci. J. 2015, 25, 87–92. [Google Scholar]
- Jian, W.; Wei, D.; Zheng, X.; Jian, W. Flight risk assessment method of transport aviation. China Saf. Sci. J. 2019, 29, 110–116. [Google Scholar]
- Flight Safety Foundation. Reducing the Risk of Runway Excursions—Report of the Runway Safety Initiative; Flight Safety Foundation: Alexandria, VA, USA, 2009. [Google Scholar]
- Payne, K.H.; Harris, D.A. Psychometric Approach to the Development of a Multidimensional Scale to Assess Aircraft Handling Qualities. Int. J. Aviat. Psychol. 2000, 10, 343–362. [Google Scholar] [CrossRef]
- AIRBUS. Getting to Grips with Aircraft Performance; Airbus Company: Blagnac, France, 2002. [Google Scholar]
- Federal Aviation Administration. Runway Overrun Prevention; AC No.: 91-79; Federal Aviation Administration: Washington, DC, USA, 2007. [Google Scholar]
- Australian Transport Safety Bureau. Runway Excursions; Aviation Research and Analysis Report-AR-2008-018; Central Office: Canberra, Australia, 2008.
- Wang, L. Effects of flare operation on landing safety: A study based on ANOVA of real flight data. Saf. Sci. 2018, 102, 14–25. [Google Scholar] [CrossRef]
- Boer, R.D. The automatic identification of unstable approaches from flight. In Proceedings of the 6th International Conference on Research in Air Transportation (ICRAT), Istanbul, Turkey, 26–30 May 2014. [Google Scholar]
- Jenkins, M.; Aaron, R.F. Reducing runway landing overruns. Aero Mag. 2012, 3, 14–19. [Google Scholar]
- Bukov, V.N.; Bykov, V.N.A. Predictive algorithm for runway overrun protection. J. Comput. Syst. Sci. Int. 2017, 56, 862–873. [Google Scholar] [CrossRef]
- Wen, R.; Wu, B.; Chu, S.; Wang, H. Prediction of landing distance for civil aircraft. China Saf. Sci. J. 2017, 27, 77–81. [Google Scholar]
- Yu, C. Flight Characteristics Analysis Based on QAR Data of a Jet Transport During Landing at a High-altitude Airport. Chin. J. Aeronaut. 2012, 25, 13–24. [Google Scholar] [CrossRef]
- Wang, L.; Wu, C.; Sun, R.; Cui, Z. An Analysis of Hard Landing Incidents Based on Flight QAR Data. In Proceedings of the International Conference on Engineering Psychology and Cognitive Ergonomics, Vancouver, BC, Canada, 9–14 July 2014. [Google Scholar]
- Tong, C.; Yin, X.; Wang, S.; Zheng, Z. A novel deep learning method for aircraft landing speed prediction based on cloud-based sensor data. Future Gener. Comput. Syst. 2018, 88, 552–558. [Google Scholar] [CrossRef]
- Kang, Z.; Shang, J.; Feng, Y.; Zheng, L.; Liu, D.; Qiang, B.; Wei, R. A Deep Sequence-to-Sequence Method for Aircraft Landing Speed Prediction Based on QAR Data. In Proceedings of the International Conference on Web Information Systems Engineering, Amsterdam, The Netherlands, 20–24 October 2020. [Google Scholar]
- Tong, C.; Yin, X.; Jun, L.; Zhu, T.; Lv, R.; Sun, L.; Rodrigues, J.J. An innovative deep architecture for aircraft hard landing prediction based on time-series sensor data. Appl. Soft Comput. 2018, 73, 344–349. [Google Scholar] [CrossRef]
- Peng, Z.; Tao, Y.; Ya, L. Servo System State Prediction Algorithn Based on Deep Learning. Comput. Appl. Softw. 2019. [Google Scholar]
- Chen, Z.; Ma, M.; Li, T.; Wang, H.; Li, C. Long sequence time-series forecasting with deep learning: A survey. Inf. Fusion 2023, 97, 101819. [Google Scholar] [CrossRef]
- Zhou, H.; Wang, D.; Li, H. Informer: Beyond efficient transformer for long sequence time-series forecasting. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; Volume 35, pp. 11106–11115. [Google Scholar]
- Li, Y.; Lin, Y.; Xiao, T.; Zhu, J. An efficient transformer decoder with compressed sub-layers. In Proceedings of the AAAI Conference on Artificial Intelligence, Vancouver, BC, Canada, 2–9 February 2021; pp. 13315–13323. [Google Scholar]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. In Proceedings of the Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; pp. 5998–6008. [Google Scholar]
- Liang, W.; Luo, S.; Zhao, G.; Wu, H. Predicting Hard Rock Pillar Stability Using GBDT, XGBoost, and LightGBM Algorithms. Mathematics 2020, 8, 765. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Xu, H. GBDT-LR: A Willingness Data Analysis and Prediction Model Based on Machine Learning. In Proceedings of the 2022 IEEE International Conference on Advances in Electrical Engineering and Computer Applications (AEECA), Dalian, China, 20–21 August 2022; pp. 396–401. [Google Scholar]
- Barros, R.C.; Basgalupp, M.P.; de Carvalho, A.C.P.L.F.; Freitas, A.A. A Survey of Evolutionary Algorithms for Decision-Tree Induction. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2012, 42, 291–312. [Google Scholar] [CrossRef]
- Porter, D.R. Introduction to Linear Regression Analysis. J. Appl. Stat. 2015, 25, 388. [Google Scholar] [CrossRef]
- Krishna, A.; Subash, V.; Krishnan, S. Comparative study of stock price prediction using SVR, KNN regressor, random forest regressor, LSTM and GRU (gated recurrent unit). AIP Conf. Proc. 2025, 3237, 030048. [Google Scholar]
- Saini, L.M.; Soni, M.K. Artificial Neural Network-Based Peak Load Forecasting Using Conjugate Gradient Methods. IEEE Power Eng. Rev. 2007, 22, 59. [Google Scholar] [CrossRef]
- Wu, Y.C.; Feng, J.W. Development and Application of Artificial Neural Network. Wirel. Pers. Commun. 2017, 102, 1645–1656. [Google Scholar] [CrossRef]





| Parameter Types | Type Description | Typical Example |
|---|---|---|
| Operational Parameters | Parameters that directly reflect the operating action of the unit | landing gear retraction, pedal action, spoiler switch, etc. |
| Positional Parameters | Parameters reflecting the position of the aircraft | altitude, latitude, longitude, etc. |
| System Parameters | Parameters that describe whether an on-board alarm is triggered or not | indicates airspeed, etc. |
| Environmental Parameters | Parameters that reflect the external environment of the aircraft | wind speed, wind direction, etc. |
| Number | Parameter | Meaning | Unit | Number | Parameter | Meaning | Unit |
|---|---|---|---|---|---|---|---|
| 1 | ALT | Altitude | ft | 15 | SELHDG | Selected Heading | ° |
| 2 | PITCH | Pitch Angle | ° | 16 | IVVR | Acceleration Rate | knot/h |
| 3 | ROLL | Roll Angle | ° | 17 | ENG2N1 | Engine 2 N1 Speed | RPM |
| 4 | IAS | Indicated Airspeed | knot | 18 | ENGTLA | Engine Thrust Level 1 | ° |
| 5 | VAPP | Vapp Reference Speed | knot | 19 | ENG1N1 | Engine 1 N1 Speed | RPM |
| 6 | HDGMAG | Magnetic Heading | ° | 20 | CCPR | Right Aileron Position | ° |
| 7 | GW_C | Corrected Aircraft Weight | kg | 21 | CWPL | Control Wheel Position 1A | ° |
| 8 | LONPC | Longitude | ° | 22 | ILSFR | ILS Frequency | MHz |
| 9 | LATPC | Latitude | ° | 23 | CCPL | Left Aileron Position | ° |
| 10 | VRTG | Vertical Load | kg | 24 | SELSPEED | Selected Speed | knot |
| 11 | WIN_DIR | Wind Direction | ° | 25 | V1_VREF | V1 and Vref Speed | knot |
| 12 | WIN_SPD | Wind Speed | knot | 26 | VR_VAPPR | Approach Speed | knot |
| 13 | ACCVERT | Vertical Acceleration | g | 27 | CWPR | Control Wheel Position 1B | ° |
| Feature | Machine Learning Algorithms | R2 |
|---|---|---|
| GS | GBDT | 97.60% |
| Random Forest | 92.38% | |
| Linear Regression | 71.09% | |
| SVM | 15.83% | |
| Decision Tree | 95.43% | |
| RALT | GBDT | 87.49% |
| Random Forest | 80.26% | |
| Linear Regression | 49.28% | |
| SVM | 3.21% | |
| Decision Tree | 67.99% |
| Zones | Selected Features |
|---|---|
| GS | ‘WIN_DIR’, ‘IAS’, ‘HDGMAG’, ‘WIN_SPD’, ‘ALTRAD’, ‘GW_C’ ‘PITCH’, ‘ACCVERT’ ‘CWPR’, ‘ROLL’, ‘SELHDG’, ‘IVVR’ ‘ENG2N1’, ‘ENGTLA’, ‘ENG1N1’, ‘CCPR’ ‘CWPL’, ‘P_ENERGY’, ‘ILSFRQ1’, ‘ILSFRQ2’ ‘CCPL’, ‘SELSPEED’, ‘V1_VREF’, ‘VR_VAPPR’ |
| RALT | ‘WIN_DIR’, ‘ACCVERT’, ‘HDGMAG’, ‘WIN_SPD’ ‘GNDSPD’, ‘GW_C’, ‘PITCH’, ‘K_ENERGY’ ‘CWPR’, ‘ROLL’, ‘SELHDG’, ‘IVVR’ ‘ENG2N1’, ‘ENGTLA’, ‘ENG1N1’, ‘CCPR’ ‘CWPL’, ‘IAS’, ‘ILSFRQ1’, ‘ILSFRQ2’ ‘CCPL’, ‘SELSPEED’, ‘V1_VREF’, ‘VR_VAPPR’ |
| Predictive Features | Machine Learning Algorithms (Based on the GBDT) | RMSE | MAE | MAPE/% |
|---|---|---|---|---|
| GS | GBDT-Informer | 2.95 | 3.06 | 3.43 |
| LSTM | 5.69 | 5.73 | 4.01 | |
| Transformer | 8.23 | 7.22 | 6.97 | |
| Linear Regression | 11.28 | 10.85 | 8.32 | |
| Decision Tree | 11.43 | 11.11 | 9.89 | |
| Random Forest | 10.52 | 10.18 | 9.46 | |
| RALT | GBDT-Informer | 3.01 | 2.30 | 4.08 |
| LSTM | 4.89 | 3.67 | 5.89 | |
| Transformer | 7.64 | 6.42 | 7.22 | |
| Linear Regression | 9.22 | 7.83 | 14.88 | |
| Decision Tree | 9.53 | 8.34 | 15.90 | |
| Random Forest | 10.27 | 7.47 | 16.45 | |
| Landing Distance | GBDT-Informer | 24.75 | 16.22 | 5.24 |
| LSTM | 42.62 | 28.13 | 7.53 | |
| Transformer | 52.33 | 35.48 | 8.37 | |
| Linear Regression | 171.84 | 148.18 | 17.15 | |
| Decision Tree | 159.34 | 139.72 | 16.19 | |
| Random Forest | 156.92 | 133.84 | 15.41 |
| Features | Models | RMSE | MAE | MAPE/% | Inference Times/ms |
|---|---|---|---|---|---|
| GS | GBDT-Informer | 2.95 | 3.06 | 3.43 | 601.70 |
| Informer | 4.95 | 3.80 | 3.92 | 701.38 | |
| RALT | GBDT-Informer | 3.01 | 2.30 | 4.08 | 582.40 |
| Informer | 4.11 | 2.70 | 5.74 | 693.26 | |
| Landing Distance | GBDT-Informer | 24.75 | 16.22 | 5.24 | / |
| Informer | 37.79 | 19.62 | 6.68 | / |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Z.; Chong, X.; Chen, Z.; Zhou, J.; Zhang, J.; Guo, P. A Long Sequence Time-Series Forecasting Method for Early Warning of Long Landing Risks with QAR Flight Data. Aerospace 2025, 12, 744. https://doi.org/10.3390/aerospace12080744
Zhou Z, Chong X, Chen Z, Zhou J, Zhang J, Guo P. A Long Sequence Time-Series Forecasting Method for Early Warning of Long Landing Risks with QAR Flight Data. Aerospace. 2025; 12(8):744. https://doi.org/10.3390/aerospace12080744
Chicago/Turabian StyleZhou, Zeyuan, Xiaolei Chong, Zhenglei Chen, Jicheng Zhou, Jichao Zhang, and Pengshuo Guo. 2025. "A Long Sequence Time-Series Forecasting Method for Early Warning of Long Landing Risks with QAR Flight Data" Aerospace 12, no. 8: 744. https://doi.org/10.3390/aerospace12080744
APA StyleZhou, Z., Chong, X., Chen, Z., Zhou, J., Zhang, J., & Guo, P. (2025). A Long Sequence Time-Series Forecasting Method for Early Warning of Long Landing Risks with QAR Flight Data. Aerospace, 12(8), 744. https://doi.org/10.3390/aerospace12080744






