Fast Buckling Analysis of Stiffened Composite Structures for Preliminary Aerospace Design
Abstract
1. Introduction
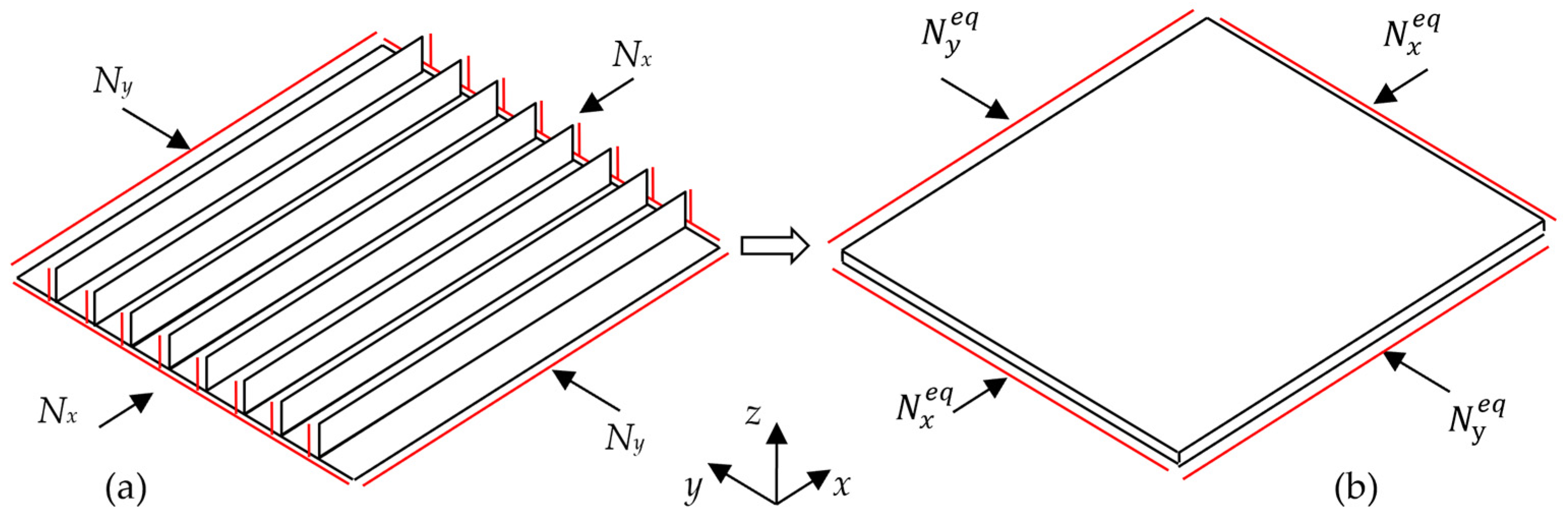
2. Calculation of Equivalent Stiffness Matrix and Load Vector of Composite Stiffened Panels
3. FEA Validation of Buckling Solutions for Orthotropically Stiffened Panels
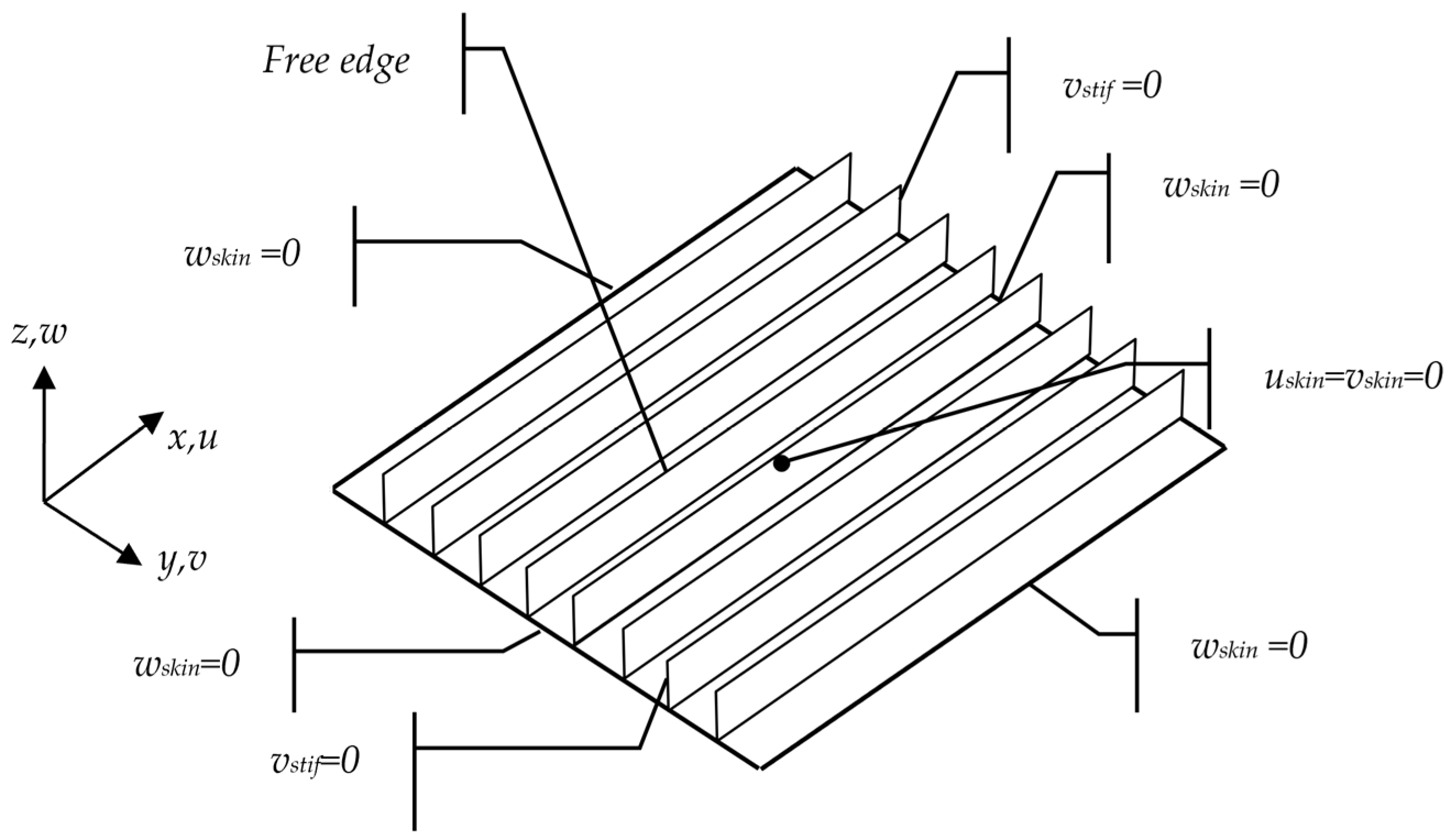
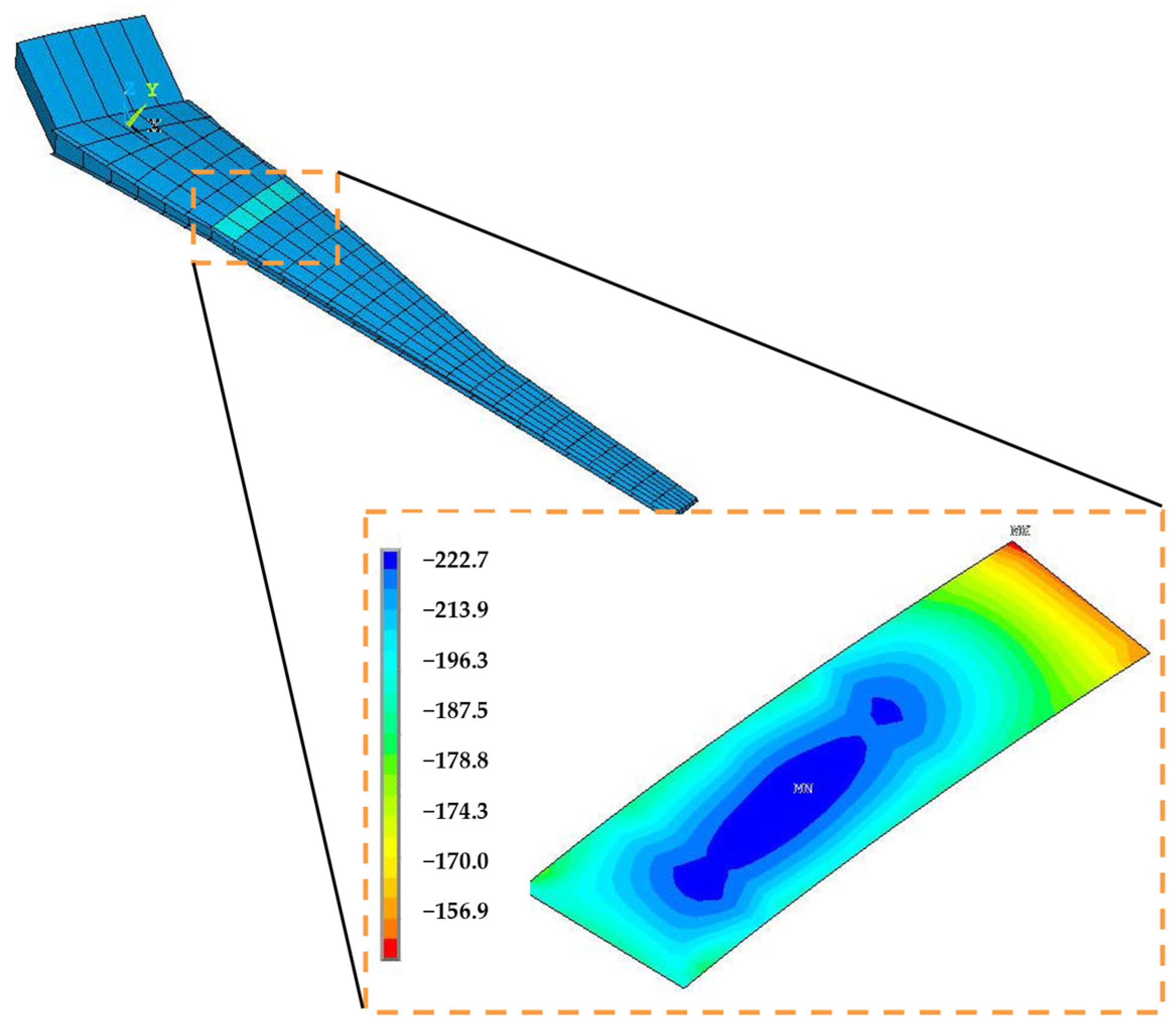
3.1. Detailed Description of the FE Model
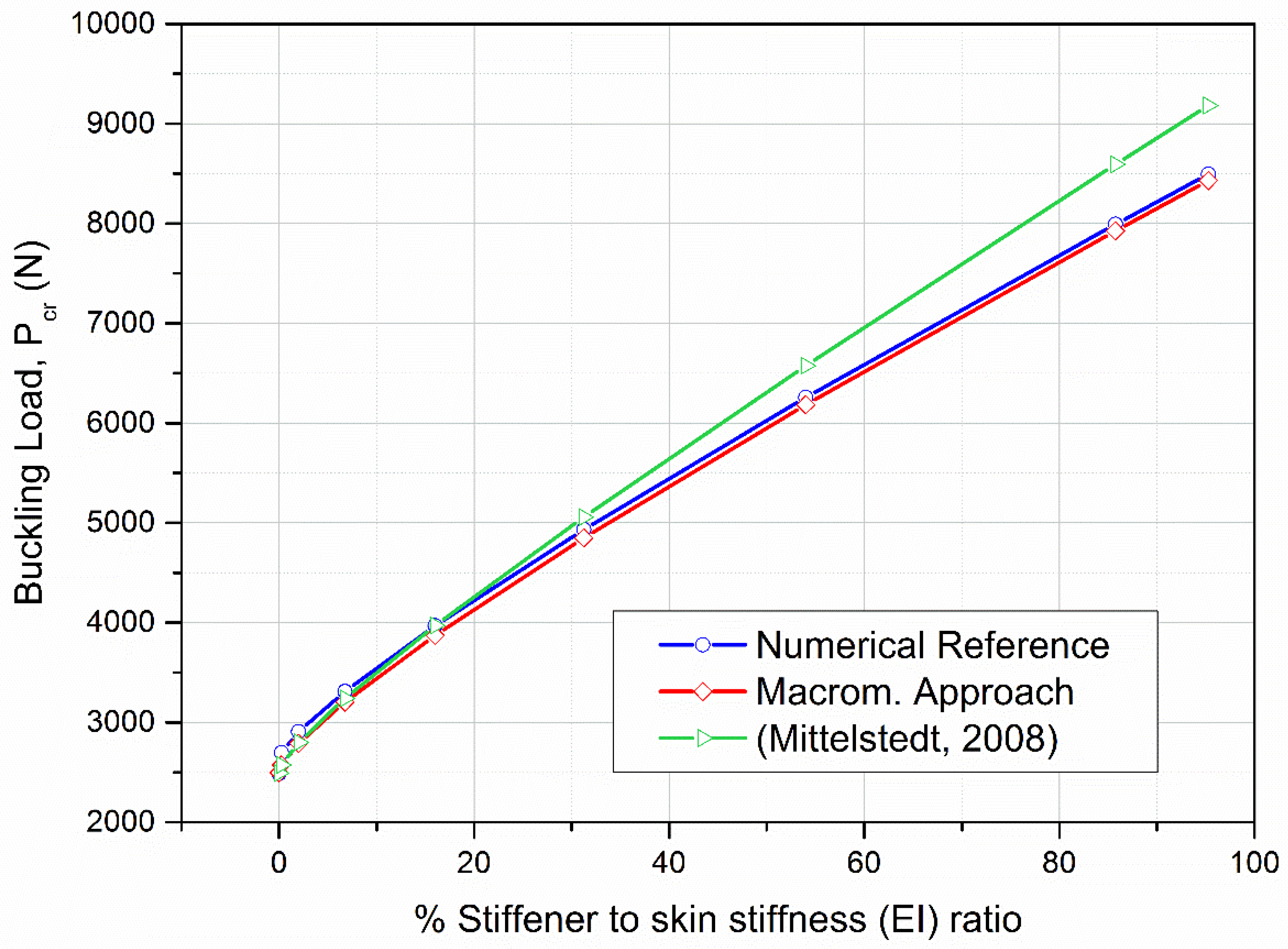
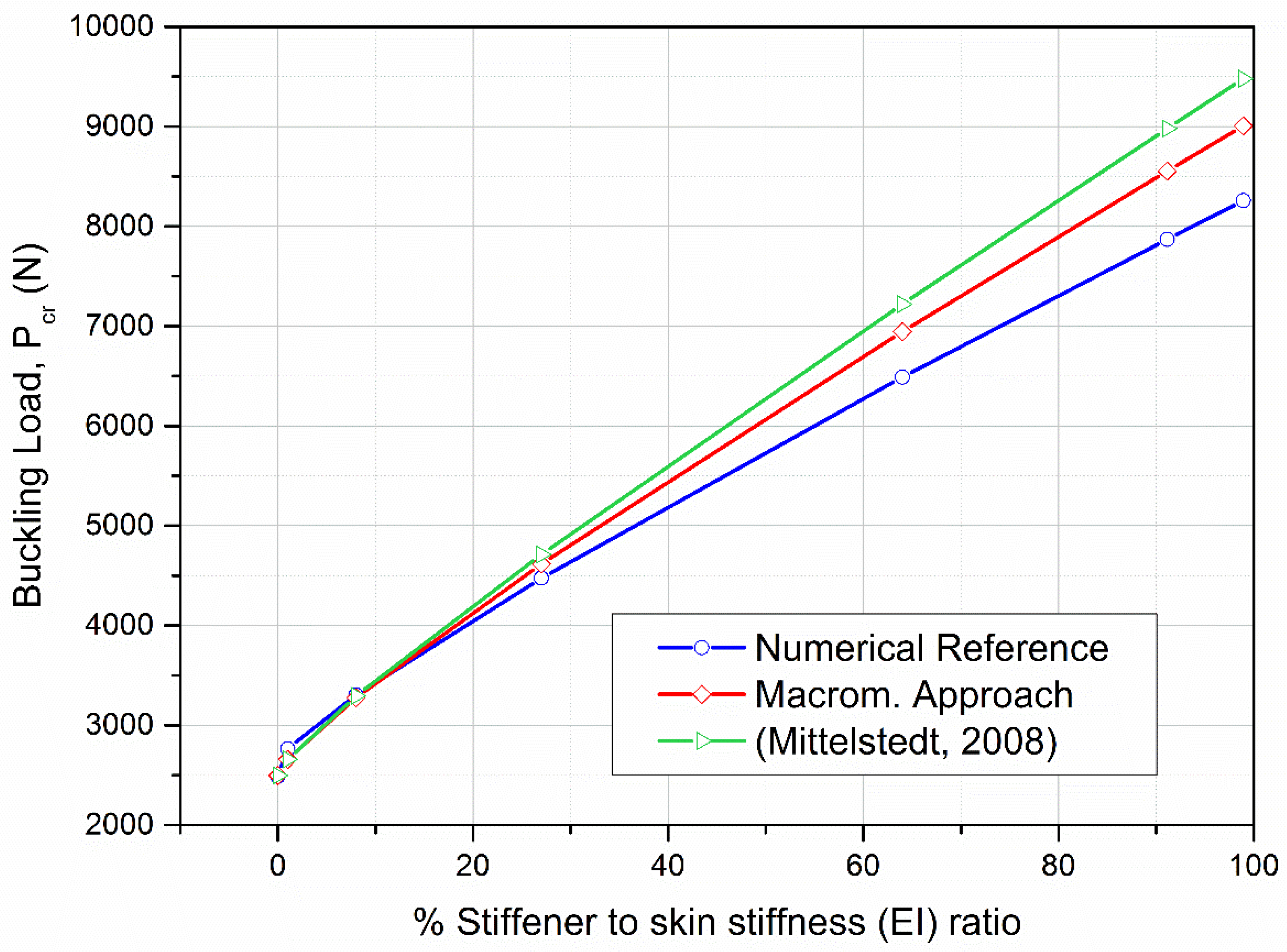
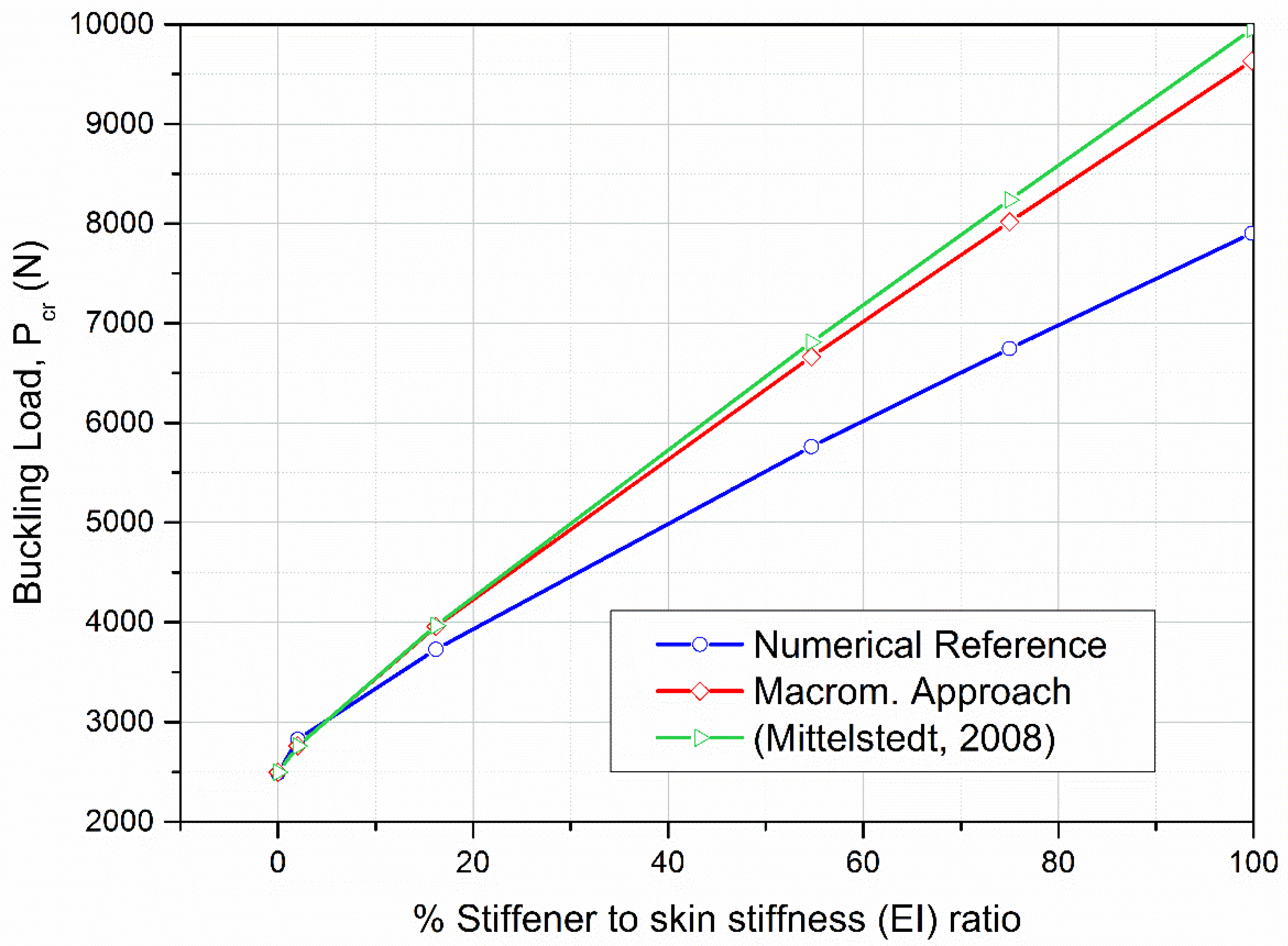
3.2. Comparison Results for the Case of Uniaxial Compression
Orthotropic Material
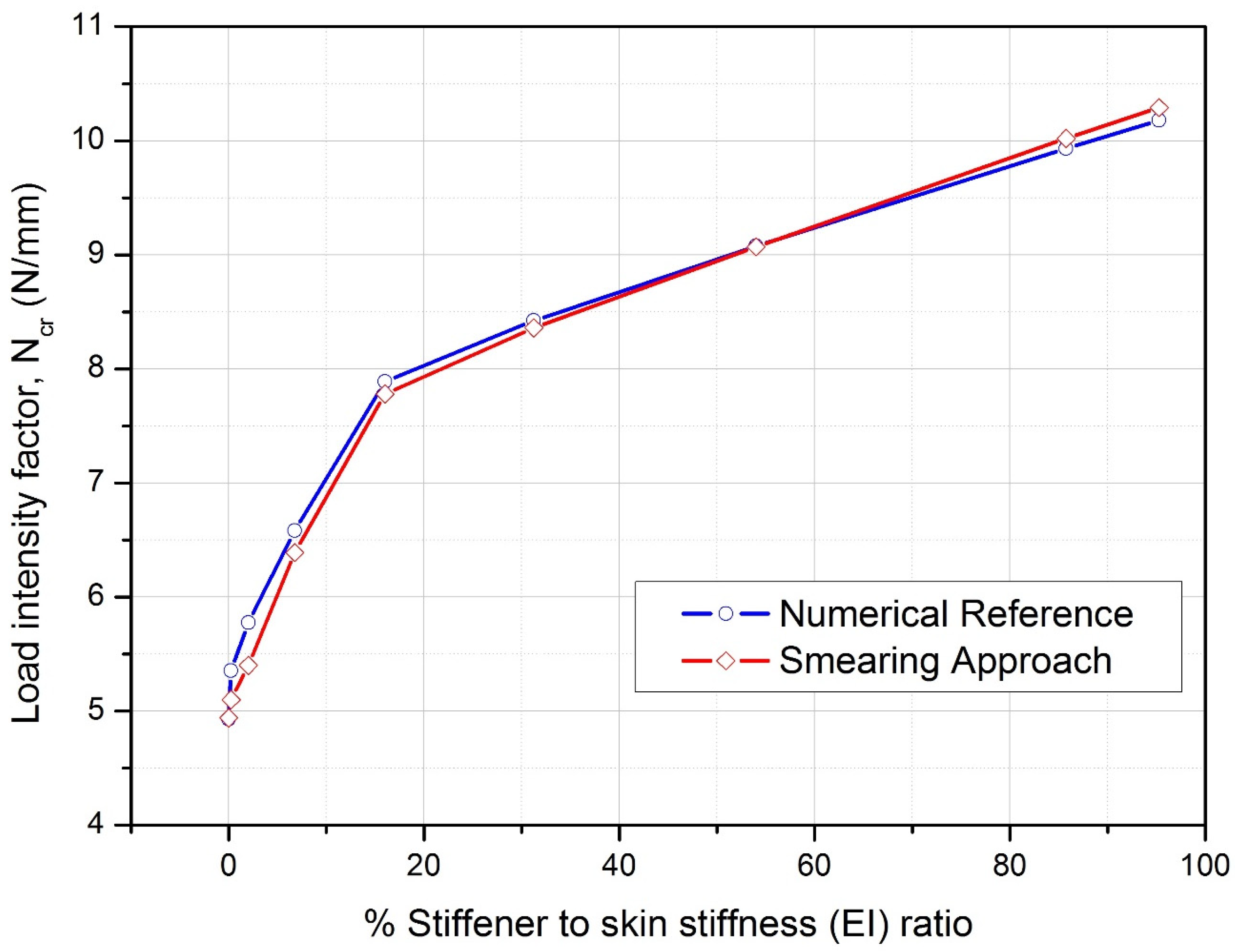
3.3. Compression in the Transverse Direction
4. Sizing Optimization of a Composite Aircraft Wing
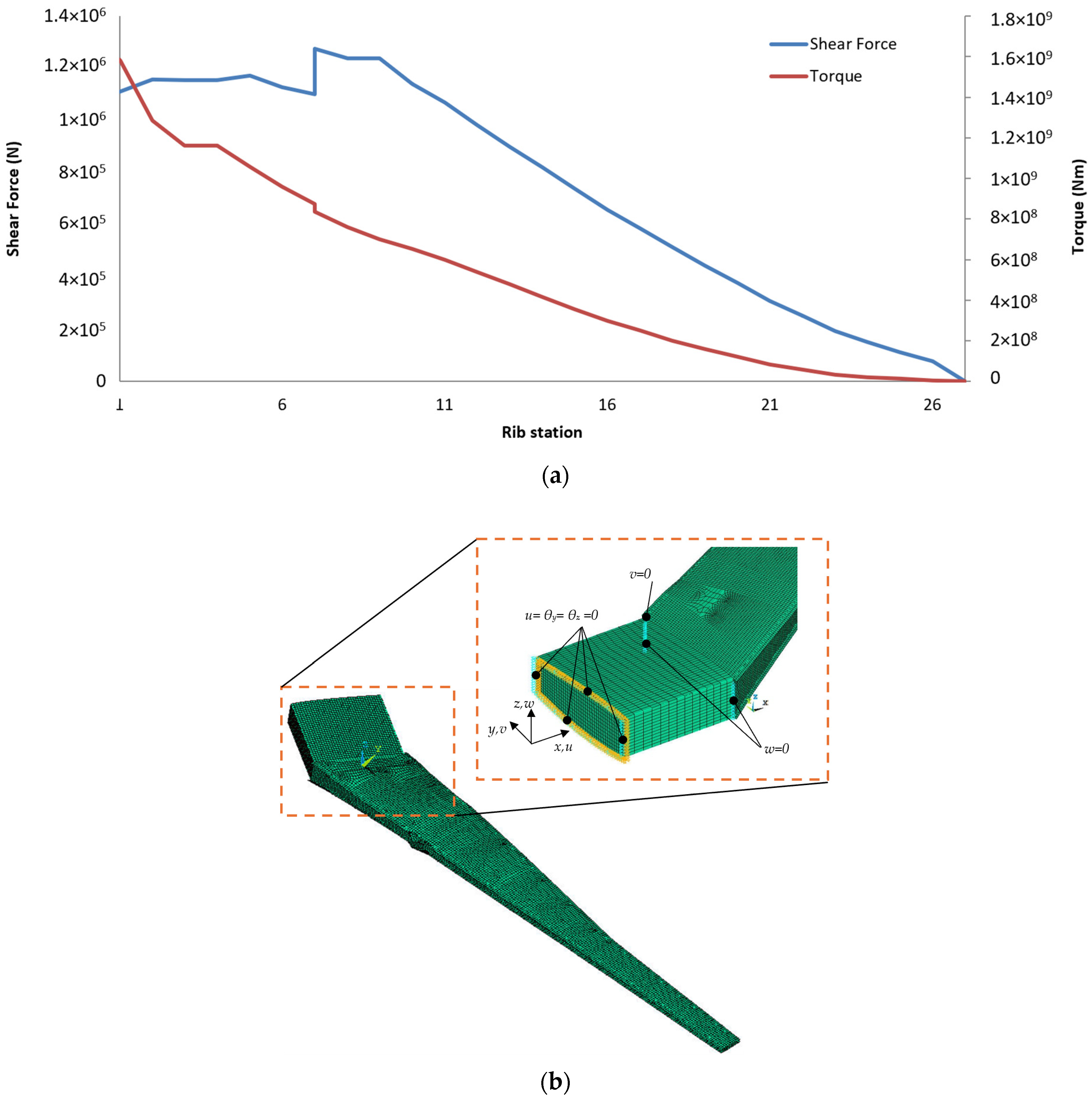
4.1. Modelling Approach for the Large-Scale Wing Structure
4.2. Description of the Simplified FE Wing Model
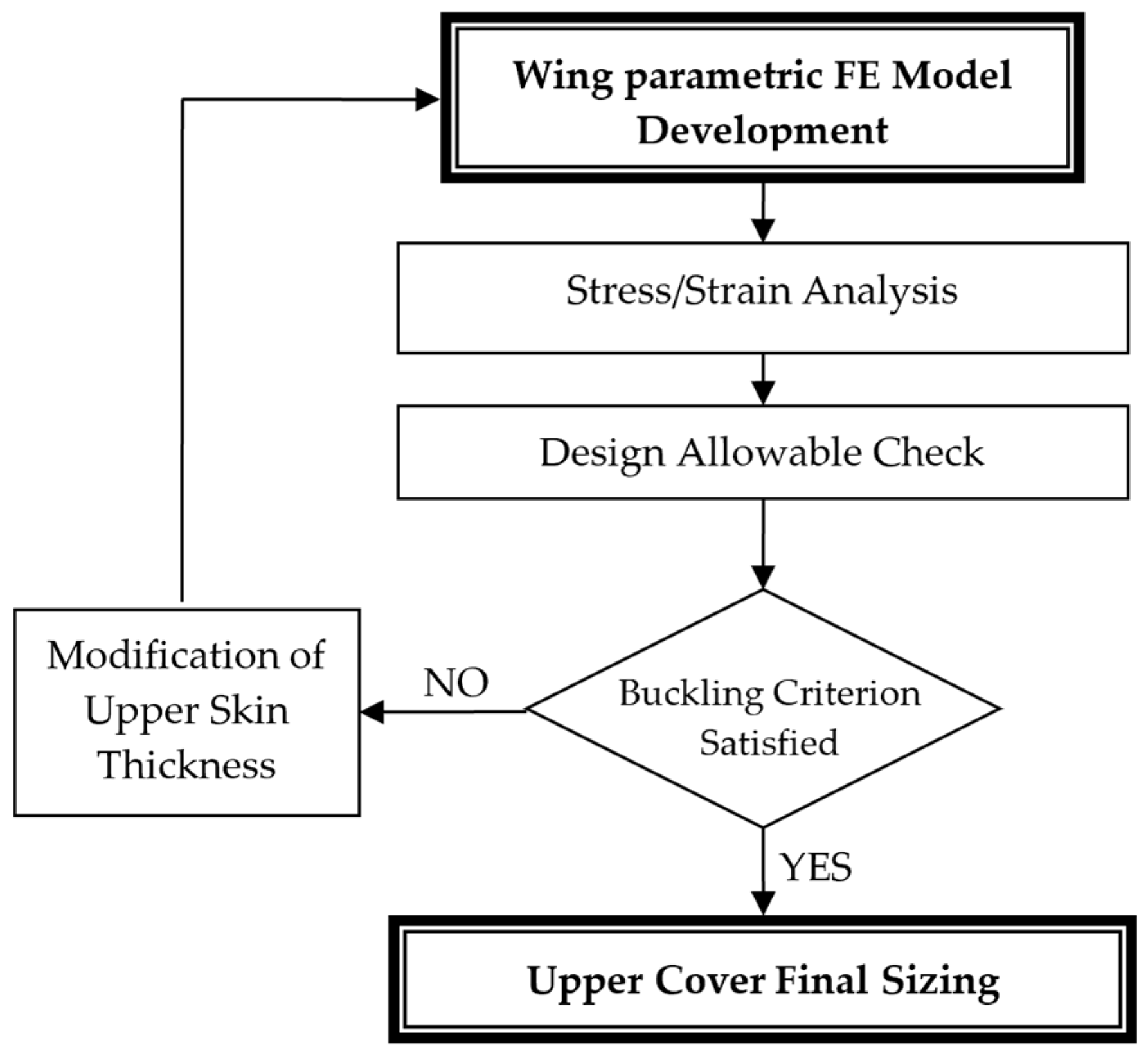
4.3. Buckling Constraint and Optimization Loop
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
| (%) | Numerical Reference (N) | (Mittelstedt, [17]) (N) | Macrom. Approach (N) | %Error w.r.t. Numerical Reference |
|---|---|---|---|---|
| 0.00% | 2489 | 2493 | 2497.5 | −0.34% |
| 0.25% | 2697.2 | 2574.5 | 2573.8 | 4.57% |
| 2.00% | 2907.5 | 2800.4 | 2791.1 | 4.00% |
| 6.75% | 3311.5 | 3242.4 | 3205.1 | 3.21% |
| 16.00% | 3968.6 | 3971.2 | 3873.0 | 2.41% |
| 31.25% | 4933.4 | 5058.4 | 4848.8 | 1.71% |
| 54.00% | 6258.2 | 6575.2 | 6183.6 | 1.19% |
| 85.75% | 7991.8 | 8591.6 | 7925.6 | 0.83% |
| 95.27% | 8494.2 | 9182.2 | 8430.1 | 0.76% |
| (%) | Numerical Reference (N) | (Mittelstedt, [17]) (N) | Macrom. Approach (N) | %Error w.r.t. Numerical Reference |
|---|---|---|---|---|
| 0.0% | 2497.5 | 2497.5 | 2497.5 | −0.34% |
| 1.0% | 2658.8 | 2658.3 | 2658.8 | 3.84% |
| 8.0% | 3274.9 | 3294.6 | 3274.9 | 0.89% |
| 27.0% | 4616.6 | 4712.3 | 4616.6 | −3.17% |
| 64.0% | 6943.5 | 7220.4 | 6943.5 | −7.02% |
| 91.1% | 8553.3 | 8979.2 | 8553.3 | −8.70% |
| 98.9% | 9007.3 | 9478.0 | 9007.3 | −9.09% |
| (%) | Numerical Reference (N) | (Mittelstedt, [17]) (N) | Macrom. Approach (N) | %Error w.r.t. Numerical Reference |
|---|---|---|---|---|
| 0.0% | 2489.0 | 2497.5 | 2497.5 | −0.34% |
| 2.0% | 2826.7 | 2760.624 | 2762.9 | 2.26% |
| 16.2% | 3730.5 | 3967.655 | 3959.3 | −6.13% |
| 54.7% | 5759.9 | 6809.01 | 6662.2 | −15.66% |
| 75.0% | 6746.0 | 8238.455 | 8017.5 | −18.85% |
| 99.8% | 7903.0 | 9951.406 | 9633.1 | −21.89% |
| (%) | Numerical Reference (N) | Macrom. Approach (N) | %Error w.r.t. Numerical Reference |
|---|---|---|---|
| 0.0% | 2464.2 | 2470 | −0.2% |
| 0.3% | 2704.3 | 2550 | 5.7% |
| 2.0% | 2945.2 | 2700 | 8.3% |
| 6.8% | 3389.1 | 3195 | 5.7% |
| 16.0% | 4102.4 | 3890 | 5.2% |
| 31.3% | 4422.8 | 4180 | 5.5% |
| 54.0% | 4810.9 | 4535 | 5.7% |
| 85.8% | 5313.5 | 5010 | 5.7% |
| 95.3% | 5458.8 | 5145 | 5.7% |
References
- Peng, L.X.; Liew, M.; Kitipornchai, S. Buckling and free vibration analyses of stiffened plates using FSDT mesh-free method. J. Sound Vib. 2006, 289, 421–449. [Google Scholar] [CrossRef]
- Stroud, W.J.; Greene, W.H. Buckling Loads for Stiffened Panels Subjected to Combined Longitudinal Compression and Shear Loadings: Results Obtained with PASCO, EAL and STAGS Computer Programs (NASA TM-83194); NASA Langley Research Center: Hampton, VA, USA, 1981.
- Wang, J.T.S.; Hsu, T.M. Discrete analysis of stiffened composite cylindrical shells. AIAA J. 1985, 23, 1753–1761. [Google Scholar] [CrossRef]
- Graciano, C.; LagFerqvist, O. Critical buckling of longitudinal stiffened webs subjected to compressive edge loads. J. Constr. Steel Res. 2003, 59, 1119–1146. [Google Scholar] [CrossRef]
- Grondin, G.Y.; Chen, Q.; Elwi, A.E.; Cheng, J.J. Stiffened steel plates under compression and bending. J. Constr. Steel Res. 1998, 45, 125–148. [Google Scholar] [CrossRef]
- Hosseini-Toudeshky, H.; Ovesy, H.R.; Kharazi, M. The development of an approximate method for the design of bead-stiffened composite panels. Thin-Walled Struct. 2005, 43, 1663–1676. [Google Scholar] [CrossRef]
- Moradi, B.; Parsons, I.D. A comparison of techniques for computing the buckling loads of stiffened shells. Comput. Struct. 1993, 46, 505–514. [Google Scholar] [CrossRef]
- Mukhopadhyay, M. Finite element buckling analysis of stiffened plates. Comput. Struct. 1990, 34, 795–803. [Google Scholar] [CrossRef]
- Rikards, R.; Chate, A.; Ozolinsh, O. Analysis for buckling and vibrations of composite stiffened shells and plates. Compos. Struct. 2001, 51, 361–370. [Google Scholar] [CrossRef]
- Toulios, M.; Caridis, P.A. The effect of aspect ratio on the elastoplastic response of stiffened plates loaded in uniaxial edge compression. Comput. Struct. 2002, 80, 1317–1328. [Google Scholar] [CrossRef]
- Heder, M. A simple method to estimate the buckling stress of stiffened panels. Compos. Struct. 1993, 26, 95–107. [Google Scholar] [CrossRef]
- Kumar, Y.V.S.; Mukhopadhyay, M. A new finite element for buckling analysis of laminated stiffened plates. Compos. Struct. 1999, 46, 321–331. [Google Scholar] [CrossRef]
- Grondin, G.Y.; Elwi, A.E.; Cheng, J.J.R. Buckling of stiffened steel plates—A parametric study. J. Constr. Steel Res. 1999, 50, 151–175. [Google Scholar] [CrossRef]
- Byklum, E.; Steen, E.; Amdahl, J. A semi-analytical model for global buckling and postbuckling analysis of stiffened panels. Thin-Walled Struct. 2004, 42, 701–717. [Google Scholar] [CrossRef]
- Loughlan, J. The buckling performance of composite stiffened panel structures subjected to combined in-plane compression and shear loading. Compos. Struct. 1994, 29, 197–212. [Google Scholar] [CrossRef]
- Loughlan, J.; Delaunoy, J.M. The buckling of composite stiffened plates with some emphasis on the effects of fiber orientation and loading configuration. Compos. Struct. 1993, 25, 485–494. [Google Scholar] [CrossRef]
- Mittelstedt, C. Closed-form buckling analysis of stiffened composite plates and identification of minimum stiffener requirements. Int. J. Eng. Sci. 2008, 46, 1011–1034. [Google Scholar] [CrossRef]
- Timoshenko, S.P.; Gere, J.M. Theory of Elastic Stability; McGraw-Hill Book Company: New York, NY, USA, 1961. [Google Scholar]
- Bedair, O.K. A contribution to the stability of stiffened plates under uniform compression. Comput. Struct. 1998, 66, 535–570. [Google Scholar] [CrossRef]
- Li, L.; Bettess, P. Buckling of stiffened plates and design of stiffeners. Int. J. Press. Vessel. Pip. 1997, 74, 177–187. [Google Scholar] [CrossRef]
- Mittelstedt, C. Closed-form analysis of the buckling loads of uniaxially loaded blade-stringer-stiffened composite plates considering periodic boundary conditions. Thin-Walled Struct. 2007, 45, 371–382. [Google Scholar] [CrossRef]
- Mittelstedt, C. Explicit analysis and design equations for buckling loads and minimum stiffener requirements of orthotropic and isotropic plates under compressive load braced by longitudinal stiffeners. Thin-Walled Struct. 2008, 46, 1409–1429. [Google Scholar] [CrossRef]
- Bruns-Treml, M. Program AESOP, Stability-Module; Airbus: Toulouse, France, 2001. [Google Scholar]
- Herbeck, L.; Wilmes, H. Design rules for a CFRP outer wing. In Proceedings of the 23rd Congress of International Council of the Aeronautical Sciences (Paper ICAS 2002-341), Toronto, ON, Canada, 8–13 September 2002. [Google Scholar]
- Schilling, J.C.; Mittelstedt, C. Local buckling analysis of omega-stringer-stiffened composite panels using a new closed-form analytical approximate solution. Thin-Walled Struct. 2020, 147, 106534. [Google Scholar] [CrossRef]
- Schilling, J.C.; El Atamann, D.; Voges, J.; Mittelstedt, C. Local buckling of omega-stringer stiffened composite panels under compression–shear interaction. Thin-Walled Struct. 2022, 180, 109838. [Google Scholar] [CrossRef]
- Schilling, J.C.; Mittelstedt, C. Shear buckling of omega-stringer-stiffened panels. Int. J. Mech. Sci. 2021, 207, 106646. [Google Scholar] [CrossRef]
- Schilling, J.C.; Mittelstedt, C. Approximate computational model for shear-loaded stiffened composite panels. Proc. Appl. Math. Mech. 2021, 21, e202100093. [Google Scholar] [CrossRef]
- Bisagni, C.; Vescovini, R. Fast Tool for Buckling Analysis and Optimization of Stiffened Panels. J. Aircr. 2009, 46, 2041–2053. [Google Scholar] [CrossRef]
- Bacarreza, O.; Aliabadi, M.H.; Apicella, A. Robust design and optimization of composite stiffened panels in post-buckling. Struct. Multidiscip. Optim. 2014, 50, 829–841. [Google Scholar] [CrossRef]
- Jaunky, N.; Knight, N.F.; Ambur, D.R. Formulation of an improved smeared stiffener theory for buckling analysis of grid-stiffened composite panels. Compos. Part B Eng. 1996, 27, 519–526. [Google Scholar] [CrossRef]
- Philips, J.L.; Guerdal, Z. Structural Analysis and Optimum Design of Geodesically Stiffened Composite Panels; Virginia Polytechnic Institute and State University, Center for Composite Materials and Structures: Blacksburg, VA, USA, 1990. [Google Scholar]
- Reddy, A.D.; Valisetty, R.R.; Rehfield, W. Continuous filament concepts for aircraft fuselage structures. J. Aircr. 1985, 22, 249–255. [Google Scholar] [CrossRef]
- Kidane, S.; Li, G.; Helms, J.; Pang, S.S.; Woldesenbet, E. Buckling load analysis of grid stiffened composite cylinders. Compos. Part B Eng. 2003, 34, 1–9. [Google Scholar] [CrossRef]
- Xu, Y.; Tong, Y.; Liu, M.; Suman, B. A new effective smeared stiffener method for global buckling of grid-stiffened composite panels. Compos. Struct. 2016, 158, 83–91. [Google Scholar] [CrossRef]
- Wang, B.; Tian, K.; Hao, P.; Zheng, Y.; Ma, Y.; Wang, J. Numerical-based smeared stiffener method for global buckling analysis of grid-stiffened composite cylindrical shells. Compos. Struct. 2016, 152, 807–815. [Google Scholar] [CrossRef]
- Luan, Y.; Ohlrich, M.; Jacobsen, F. Improvements of the smearing technique for cross-stiffened thin rectangular plates. J. Sound Vib. 2011, 330, 4274–4286. [Google Scholar] [CrossRef]
- Hao, P.; Wang, B.; Li, G.; Meng, Z.; Tian, K.; Tang, X. Hybrid optimization of hierarchical stiffened shells based on smeared stiffener method and finite element method. Thin-Walled Struct. 2014, 82, 46–54. [Google Scholar] [CrossRef]
- Wang, B.; Tian, K.; Hao, P.; Cai, Y.; Li, Y.; Sun, Y. Hybrid analysis and optimization of hierarchical stiffened plates based on asymptotic homogenization method. Compos. Struct. 2015, 132, 136–147. [Google Scholar] [CrossRef]
- Ye, L.; Zhu, S.; Jiang, W.; Xu, Y.; Ke, L. Design and optimization of composite sub-stiffened panels. Compos. Struct. 2020, 240, 112084. [Google Scholar] [CrossRef]
- Meng, Z.; Luo, X.; Zhou, H. Lightweight design of arcuately stiffened cylindrical shells based on smeared stiffener method and active learning strategy. Thin-Walled Struct. 2022, 174, 109167. [Google Scholar] [CrossRef]
- Zhang, G.; Hu, Y.; Yan, B.; Tong, M.; Wang, F. Buckling and post-buckling analysis of composite stiffened panels: A ten-year review (2014–2023). Thin-Walled Struct. 2024, 205, 112525. [Google Scholar] [CrossRef]
- Tsai, S.T.; Hahn, H.T. Introduction to Composite Materials; Technomic Publishing Company, Inc.: Basel, Switzerland, 1980. [Google Scholar]
- Ewing, M.S.; Hinger, R.J.; Leissa, A.W. On the validity of the reduced bending stiffness method for laminated composite plate analysis. Compos. Struct. 1988, 9, 301–317. [Google Scholar] [CrossRef]
- Narita, Y.; Leissa, A.W. Buckling studies for simply supported symmetrically laminated rectangular plates. Int. J. Mech. Sci. 1990, 32, 909–924. [Google Scholar] [CrossRef]
- ANSYS®; Mechanical Release 14.0; ANSYS Inc.: Canonsburg, PA, USA, 2007.
- Madier, D. Practical Finite Element Analysis for Mechanical Engineers; FEA Academy: Montreal, QC, Canada, 2020. [Google Scholar]
- Stamatelos, D. Analysis and Preliminary Design of Unconventional Aerostructures. Ph.D. Thesis, University of Patras, Patra, Greece, 2010. [Google Scholar]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stamatelos, D.G.; Labeas, G.N. Fast Buckling Analysis of Stiffened Composite Structures for Preliminary Aerospace Design. Aerospace 2025, 12, 726. https://doi.org/10.3390/aerospace12080726
Stamatelos DG, Labeas GN. Fast Buckling Analysis of Stiffened Composite Structures for Preliminary Aerospace Design. Aerospace. 2025; 12(8):726. https://doi.org/10.3390/aerospace12080726
Chicago/Turabian StyleStamatelos, Dimitrios G., and George N. Labeas. 2025. "Fast Buckling Analysis of Stiffened Composite Structures for Preliminary Aerospace Design" Aerospace 12, no. 8: 726. https://doi.org/10.3390/aerospace12080726
APA StyleStamatelos, D. G., & Labeas, G. N. (2025). Fast Buckling Analysis of Stiffened Composite Structures for Preliminary Aerospace Design. Aerospace, 12(8), 726. https://doi.org/10.3390/aerospace12080726






