2.3.2. Perturbation Magnitude Analysis
In precise orbit determination, the positions of major celestial bodies—such as the Moon and the Sun—are computed using the JPL DE ephemeris to assess N-body gravitational perturbations for dynamic orbit determination. In practical orbit determination computations, it is crucial to analyze the influence of N-body perturbations on the accuracy of the orbit determination. Based on the accuracy requirements, certain planetary bodies may be selectively included or excluded from the calculations. This strategy optimizes computational efficiency while ensuring the desired level of precision is maintained.
First, a perturbation magnitude analysis is performed. This analysis generally expresses the magnitude of perturbation as the ratio of the perturbative acceleration to the gravitational acceleration of the central body. This ratio quantifies the degree to which the actual orbit deviates from the ideal two-body orbit due to the influence of perturbative forces.
Based on the relevant perturbation equations, the minimum expression for the perturbation magnitude can be derived as follows [
28]:
Here, represents the required accuracy over the prediction arc, n denotes the mean motion (angular velocity), and is the integration time span. The first term is considered only when there is a periodic variation in the semi-major axis, which is caused by non-conservative forces, while the second term applies in cases involving only conservative forces.
Using the above expression to calculate the minimum perturbation magnitude, if , then the perturbative force must be taken into account; otherwise, it can be neglected. In this study, if the perturbation magnitude exerted by a major celestial body on the spacecraft exceeds the minimum threshold, the influence of that body must be included. Conversely, if the perturbation is below this threshold, the influence of that body may be disregarded, facilitating a preliminary simplification of the DE ephemeris.
To theoretically calculate the perturbation magnitudes of the Moon and various major planetary bodies, this study examines the operational conditions of navigation satellites in L3, L4, L5, L1, and DRO orbits. The perturbation magnitudes exerted by the Sun, the Moon, and other major planetary bodies are estimated based on N-body perturbations. Since N-body perturbations are conservative forces, the minimum perturbation magnitude is computed using the second term, with
set to 30 days and
set to 10 m. The results are presented in the following
Table 2.
It can be observed that for spacecraft in orbits such as L3, L4, and L5, which are not in close proximity to the Moon, the perturbation magnitudes from the Sun, Moon, Venus, Jupiter, and Saturn all exceed the minimum perturbation magnitude. Meanwhile, the perturbation from Mercury at L3 is comparable to the minimum value and can therefore be neglected. As shown in the table above, to maintain an orbit determination accuracy of 10 m over a 30-day period, deep-space spacecraft need only account for the perturbations from the Sun, Moon, Venus, Jupiter, and Saturn.
For spacecraft near the Moon in L1 and DRO orbits, the perturbation magnitudes from the Sun, Moon, Venus, and Jupiter also exceed the minimum threshold. Consequently, to achieve a 10 m orbit determination accuracy over a 30-day period, near-Moon spacecraft similarly need to consider only the perturbations from the Sun, Moon, Venus, and Jupiter.
In the study of the perturbative effects of various celestial bodies in an autonomous orbit determination environment, this section first employs the CLOD v1.0 software to perform a 30-day orbital extrapolation of the cislunar space navigation constellation spacecraft, commencing on 1 January 2028. The gravitational influences of each celestial body on the orbital prediction accuracy of the cislunar translational point probes are analyzed, forming the foundation for subsequent discussions on the selection of celestial bodies in the DE ephemeris and the exclusion of major planetary components with negligible effects.
First, the N-body gravitational effects of the celestial bodies included in the JPL DE436 ephemeris (excluding the nutation and planetary motion terms) are computed, and a 30-day orbital extrapolation is carried out. This extrapolation serves as the reference orbit. Subsequently, the gravitational influences of the Sun, Moon, and major planets such as Jupiter, Venus, and Saturn are considered incrementally. Orbital extrapolations are performed for durations of 5, 10, 15, 20, 25, and 30 days, and the resulting three-dimensional positions are compared to those of the reference orbit. The reference orbit incorporates all major celestial bodies from the JPL DE ephemeris, while other non-N-body perturbation parameters remain consistent with those used in the experiment. The resulting orbit determination accuracy is then represented using different colors corresponding to the various extrapolation intervals, thereby illustrating the impact of different celestial bodies and extrapolation durations on the forecast accuracy.
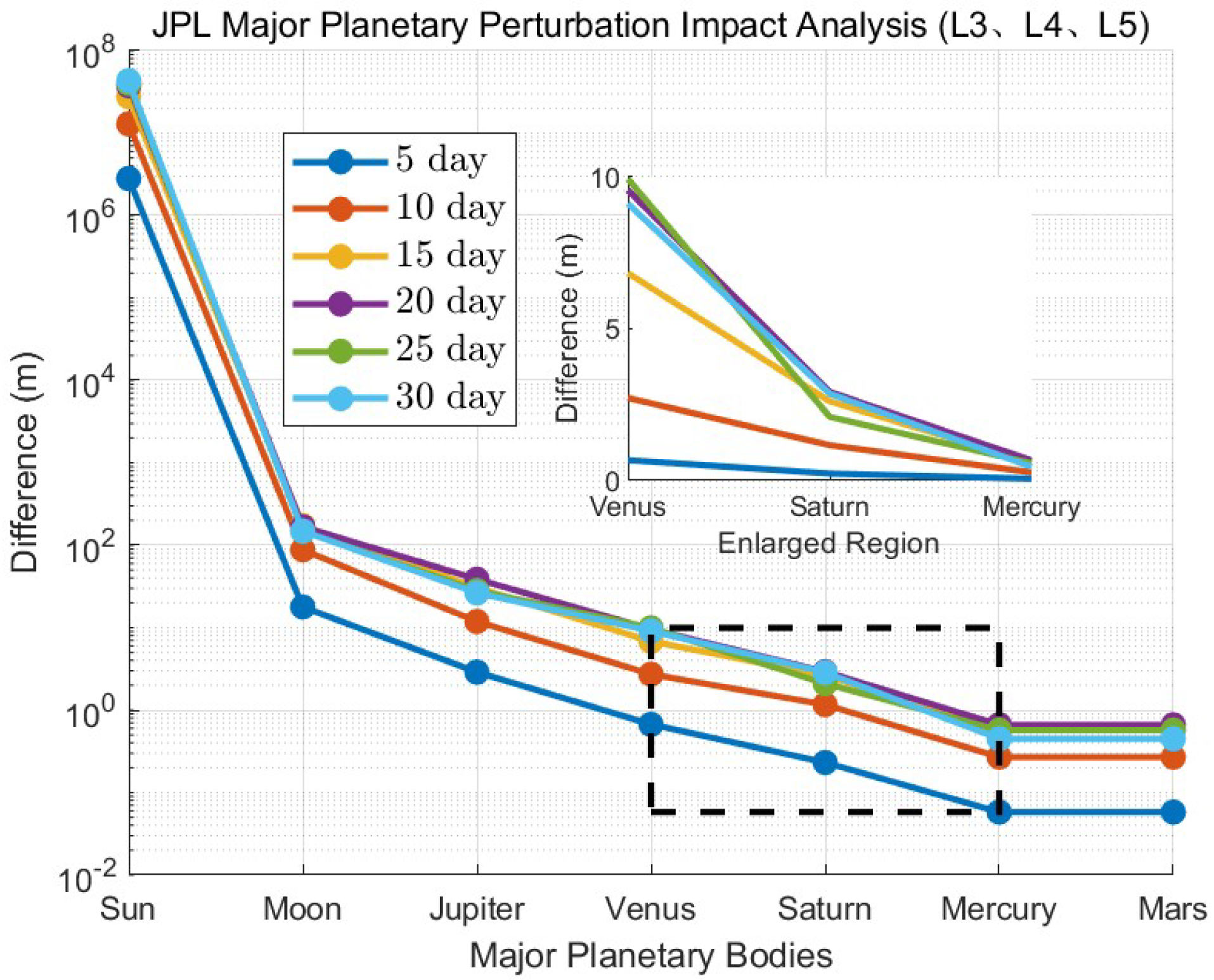
Since the theoretical perturbation magnitude calculations yield similar results for L3, L4, and L5 while the L1 and lunar DRO orbits are closer to the Moon and subject to significant lunar perturbations, and because the perturbative effects of various celestial bodies on navigation satellites at these positions exhibit distinct characteristics compared to those at the other three Lagrange points, the simulation process combines these three results and averages their impacts, as shown in
Figure 2.
It can be observed that, after accounting for the perturbations from the Sun, Moon, Jupiter, and Venus, the 30-day orbital extrapolation error for the navigation satellites at these three Lagrange points is approximately 10 m. When the perturbative effect of Saturn is additionally considered, the error is reduced to within 10 m, which aligns with the previously calculated perturbation magnitude results.
A statistical error analysis between the spacecraft at the L1 Lagrange point and the reference orbit is presented in
Figure 3. For a 15-day orbital extrapolation, including Venus results in an extrapolation error within 10 m, which is consistent with the theoretical perturbation magnitude analysis. However, for extrapolations exceeding 15 days, the error increases to within 700 m when Venus is considered, and the L1 orbit extrapolation begins to diverge beyond 15 days. These discrepancies may be attributed to the unique position of the L1 point or to the integration method employed. The CLOD v1.0 software used in this study utilizes an RKF7 (8) integrator with fixed step-size integration; it is possible that a variable step-size integrator may be required for accurate modeling at the L1 point.
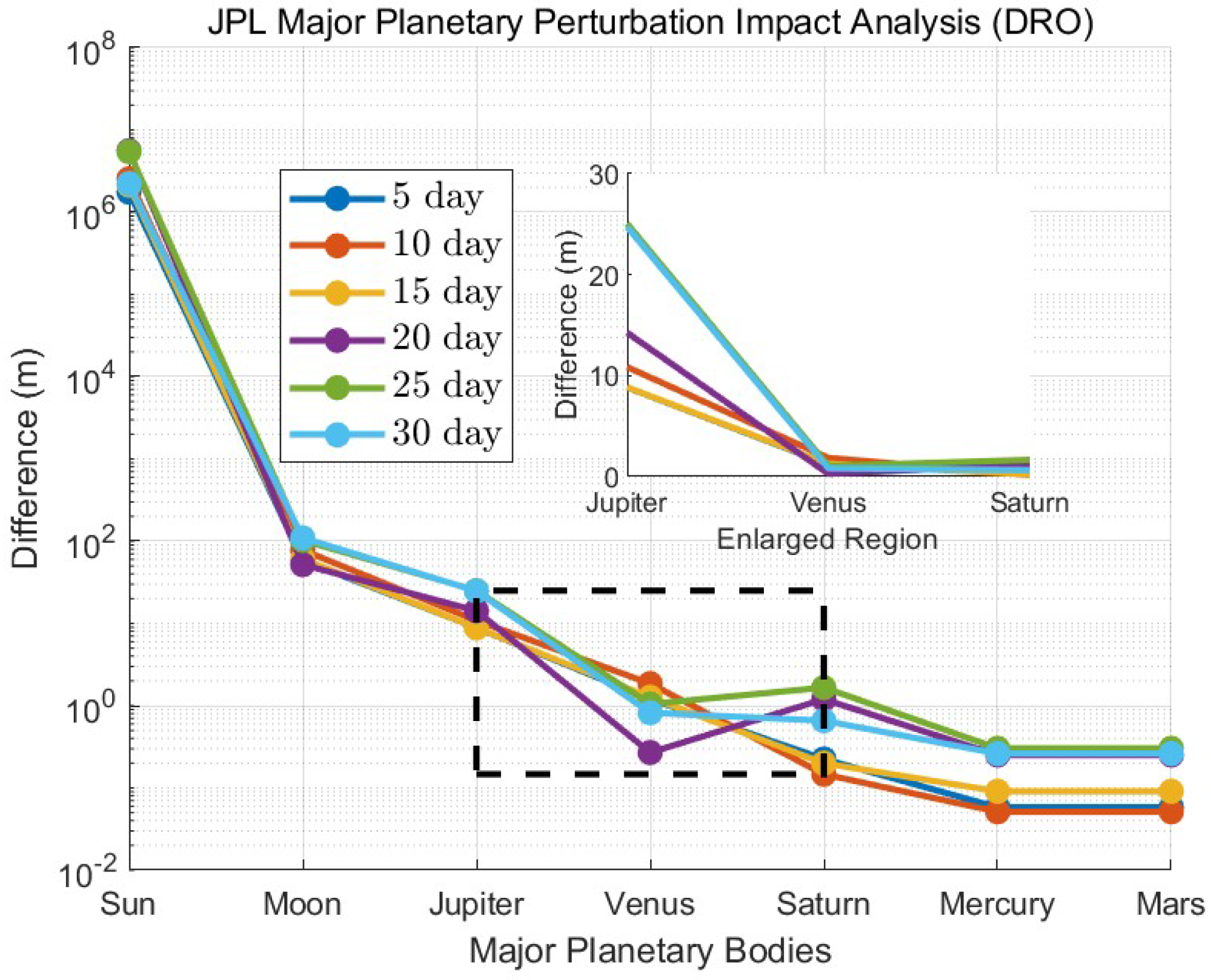
A statistical error analysis was performed for the spacecraft on the lunar DRO orbit relative to the reference orbit, with the results shown in
Figure 4. After incorporating Venus, the 30-day orbital extrapolation accuracy is within 2 m, which is consistent with the theoretical calculations.
The following can generally be observed:
Neglecting either the Sun or the Moon would significantly impact orbit determination accuracy, particularly the neglect of the Moon. The N-body gravitational forces of both the Sun and the Moon must be accounted for with sufficient precision.
It is observed that, except for the L1 orbit, for other spacecraft, the overall extrapolation accuracy can be maintained within 2 m after considering Saturn. Therefore, to ensure that the orbit extrapolation accuracy of cislunar spacecraft remains at the meter level over 30 days, the N-body perturbations in cislunar space need only consider the following five bodies: the Moon, the Sun, Venus, Saturn, and Jupiter. For spacecraft in the L1 orbit, within a 15-day extrapolation, only the perturbations from these five bodies need to be considered. The perturbations from other major planetary bodies can be excluded from the ephemeris. After removing these, the number of parameters for these five bodies in the JPL ephemeris is 483; including the starting and ending Julian days results in a total of 485 parameters. This represents a reduction of approximately 52% compared to the original 1018 parameters in the JPL ephemeris, resulting in a significant decrease in storage requirements.