Development and Evaluation of a Two-Dimensional Extension/Contraction-Driven Rover for Sideslip Suppression During Slope Traversal
Abstract
1. Introduction
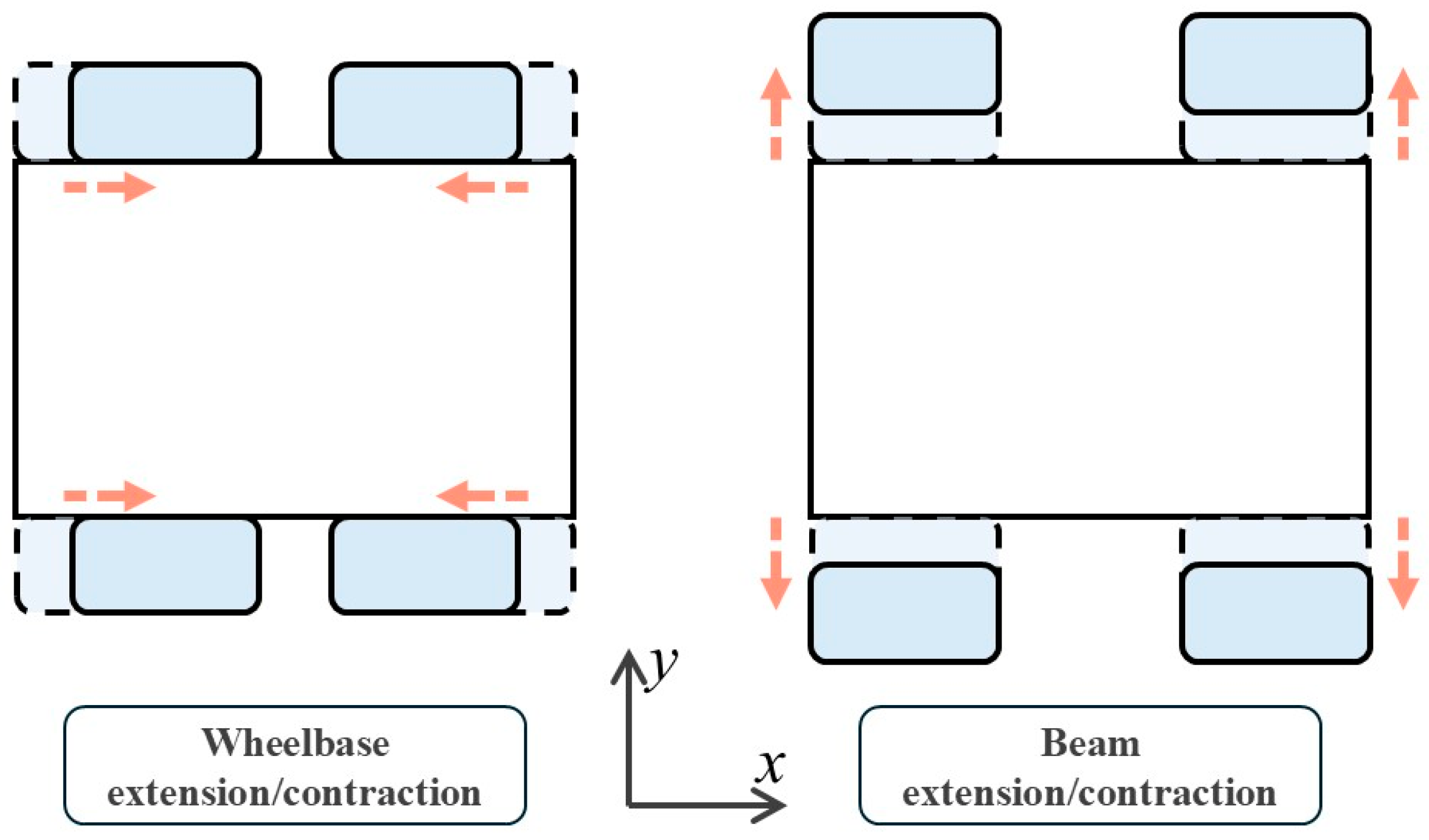
2. 2DPPL Mechanism and Theoretical Analysis
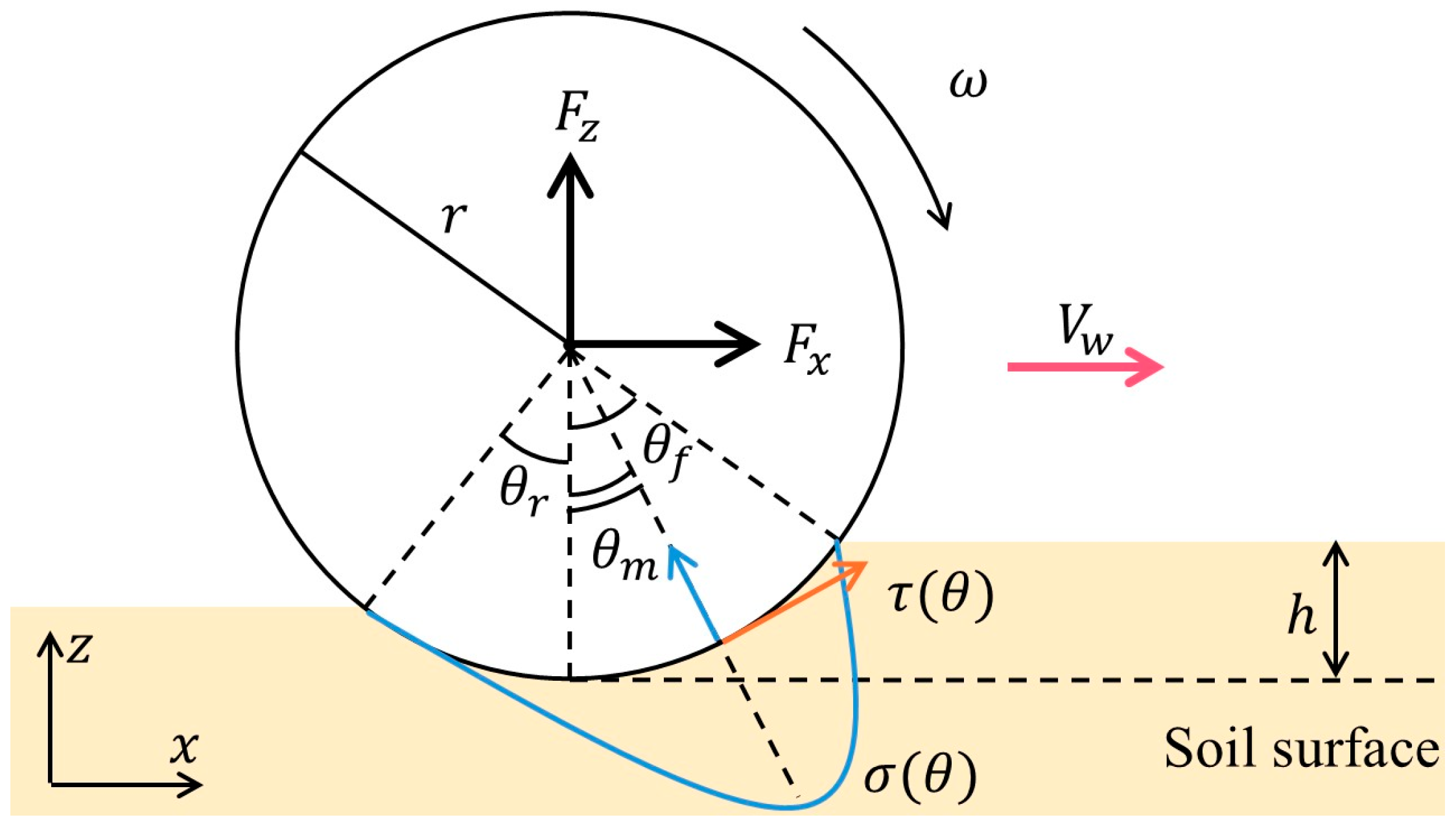
2.1. About Driving Wheel-Soil Interaction
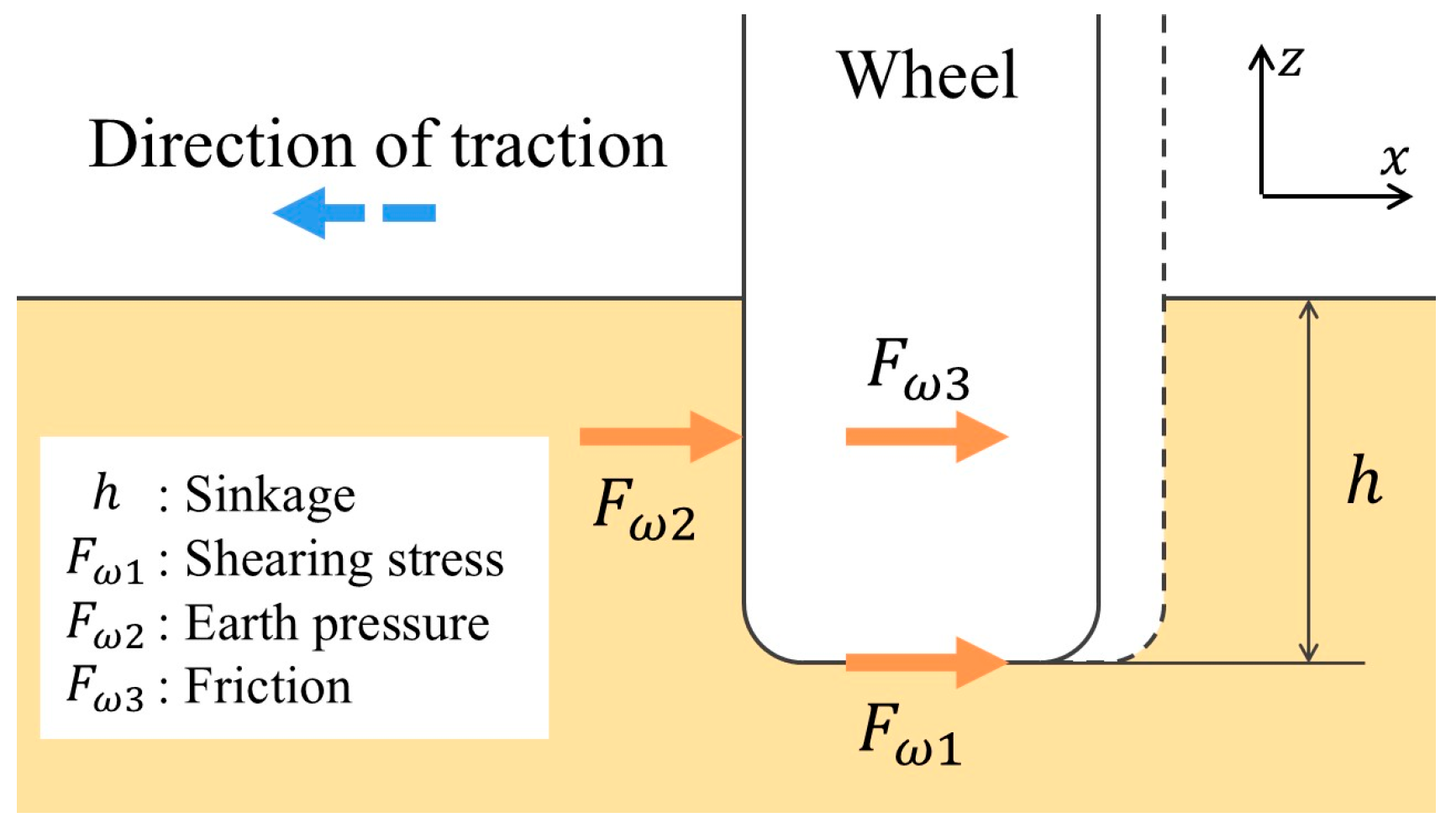
2.2. Resistance Force Between Wheel and Ground
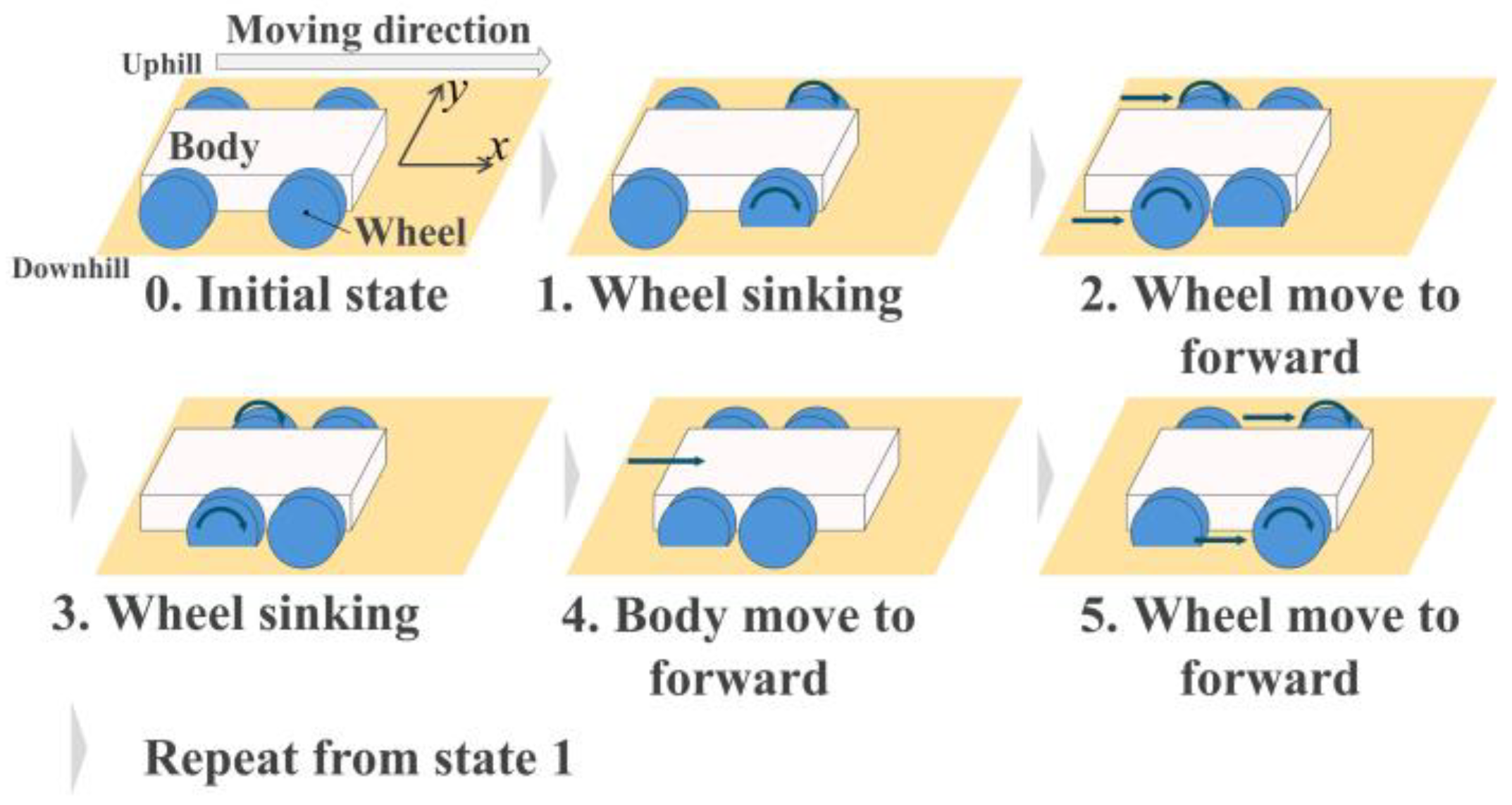
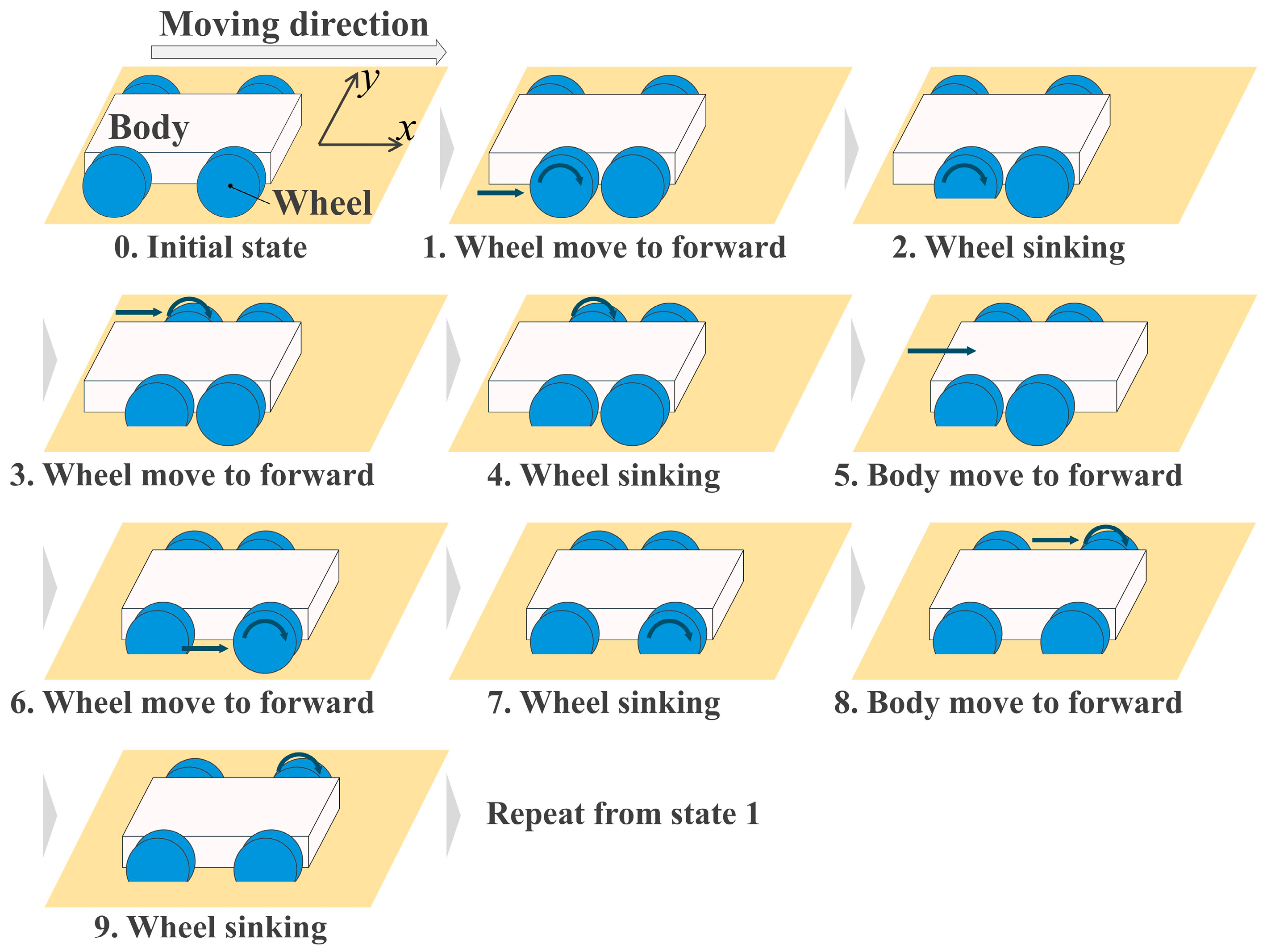
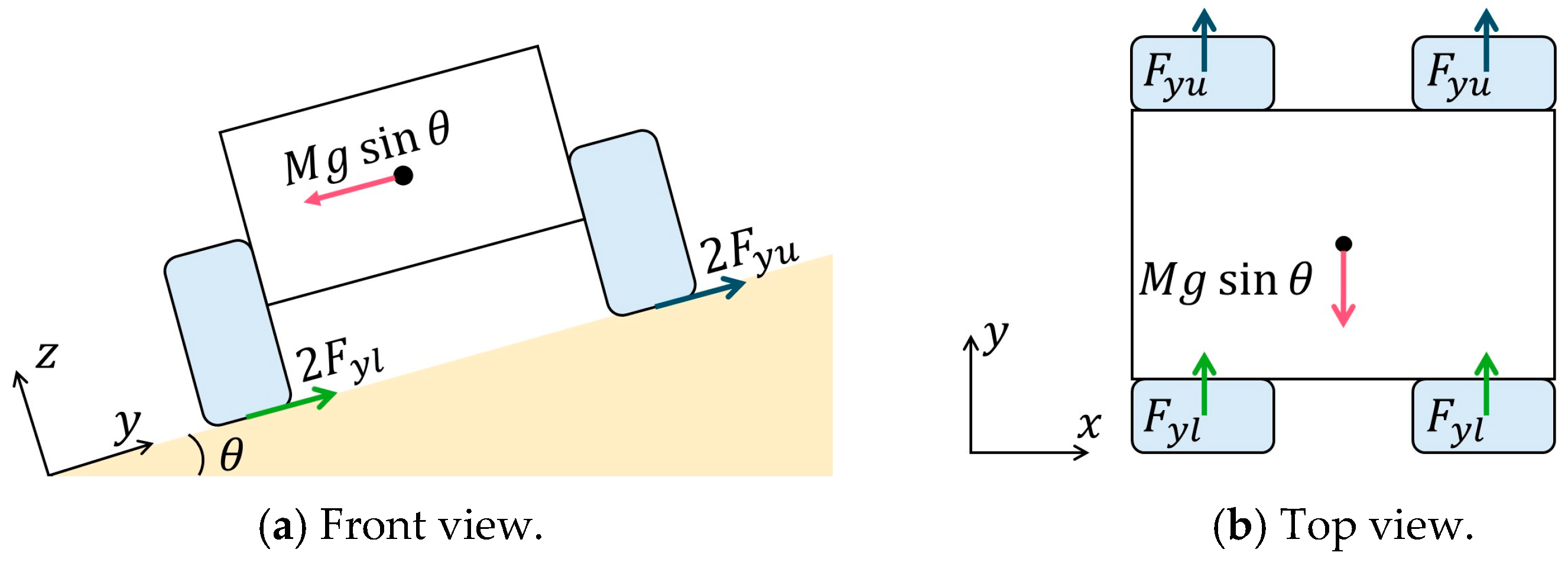
2.3. Effectiveness of Wheelbase Modulation in Slope Traversal
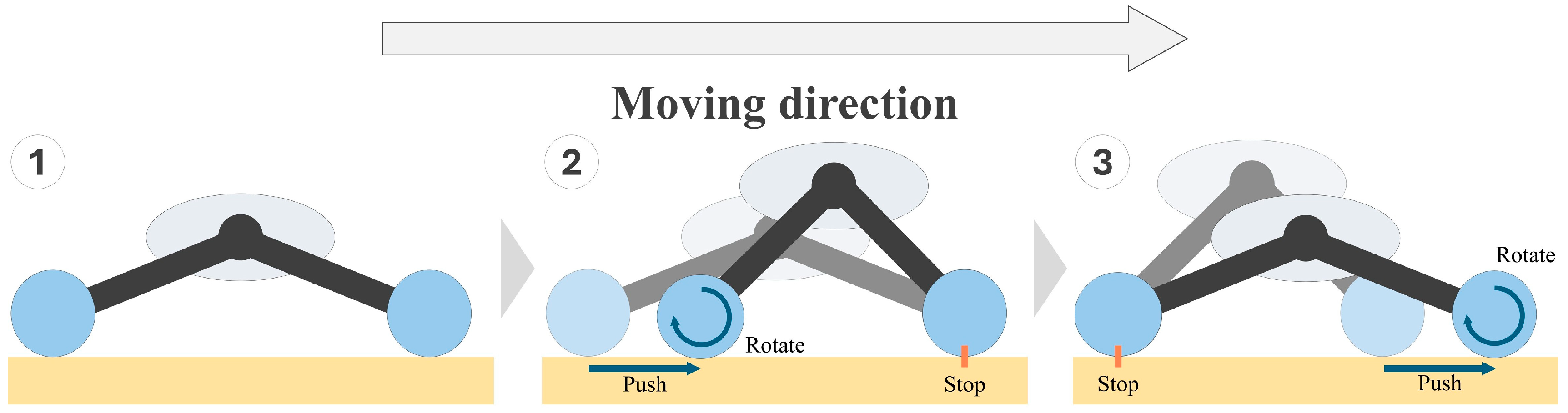
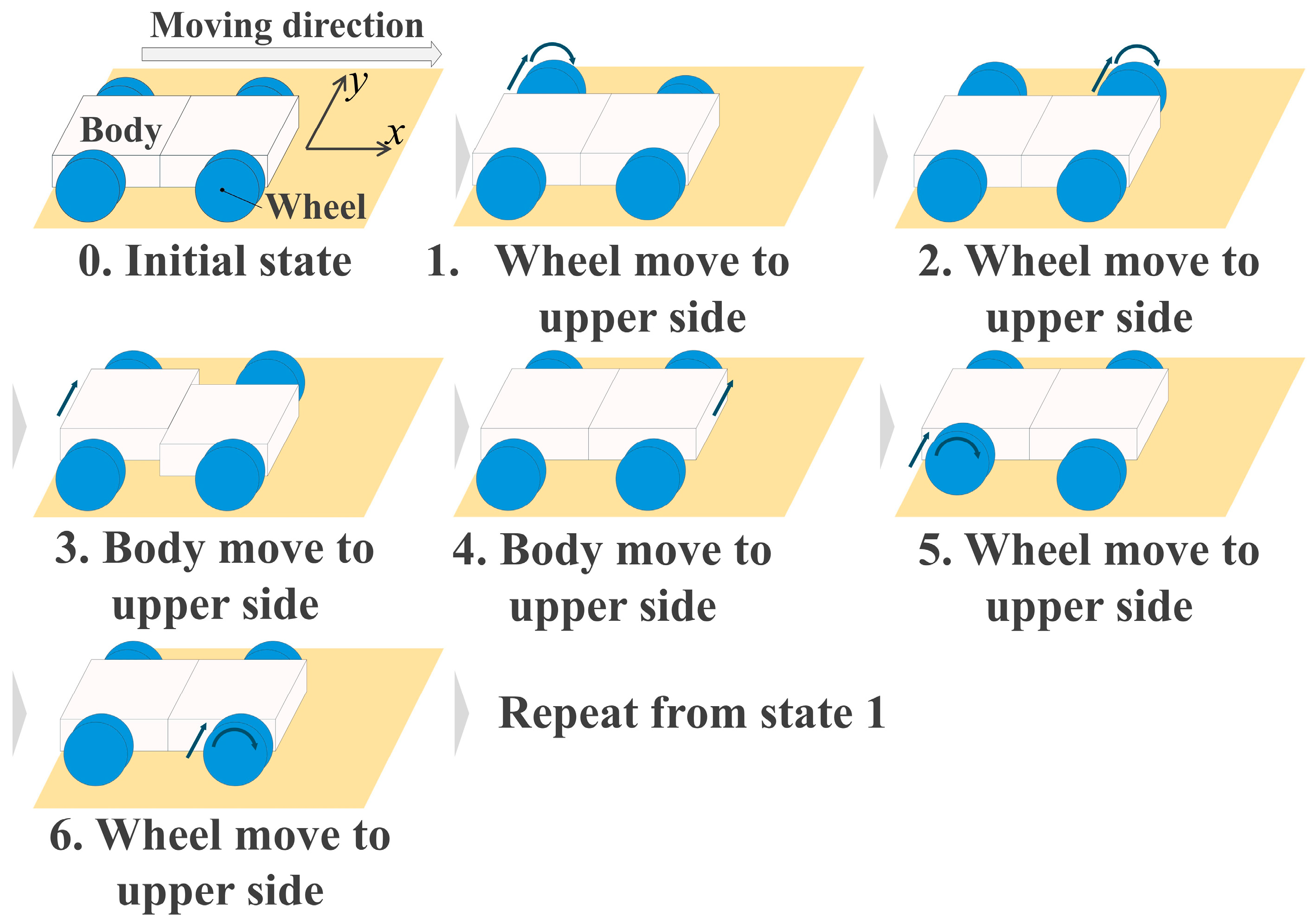
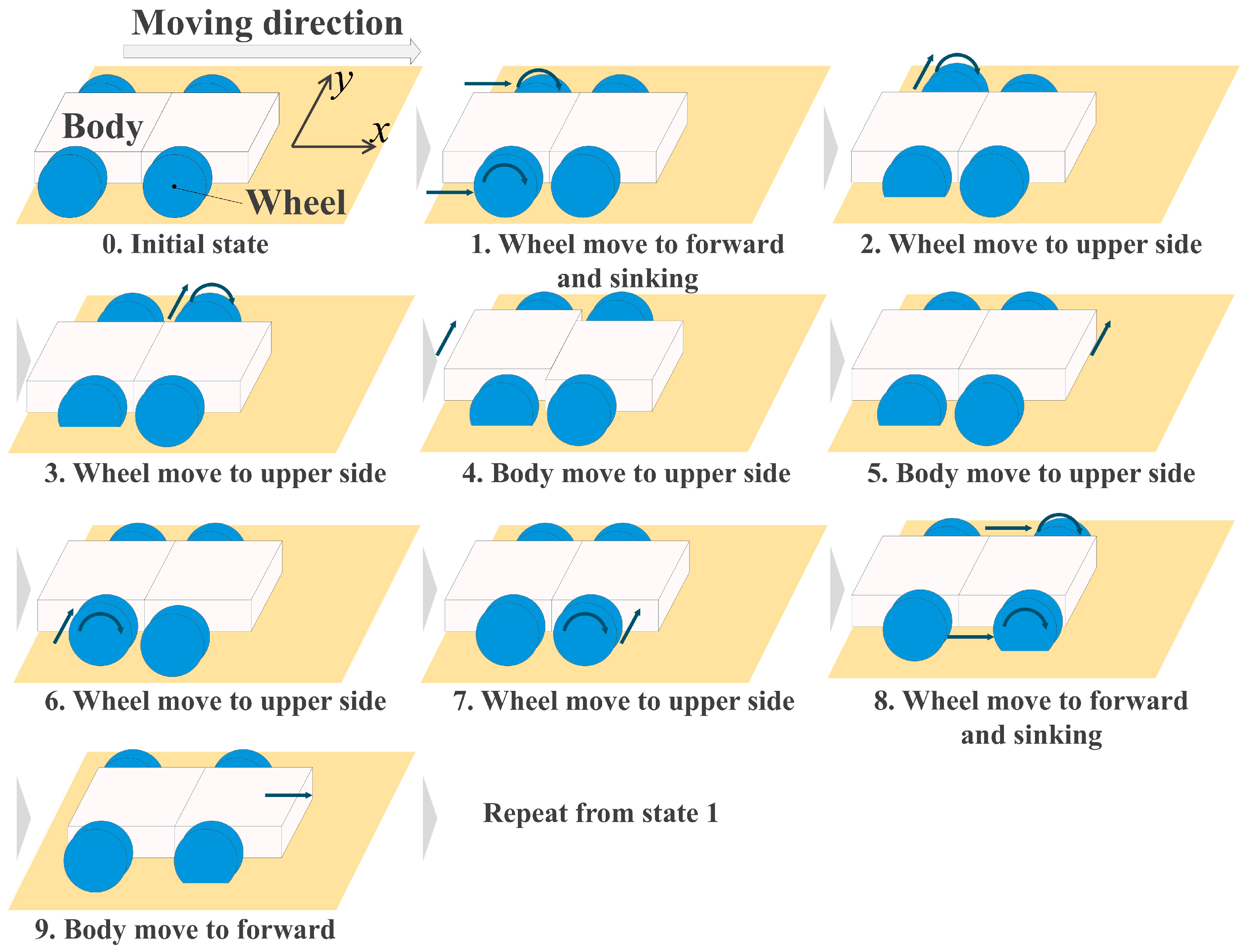
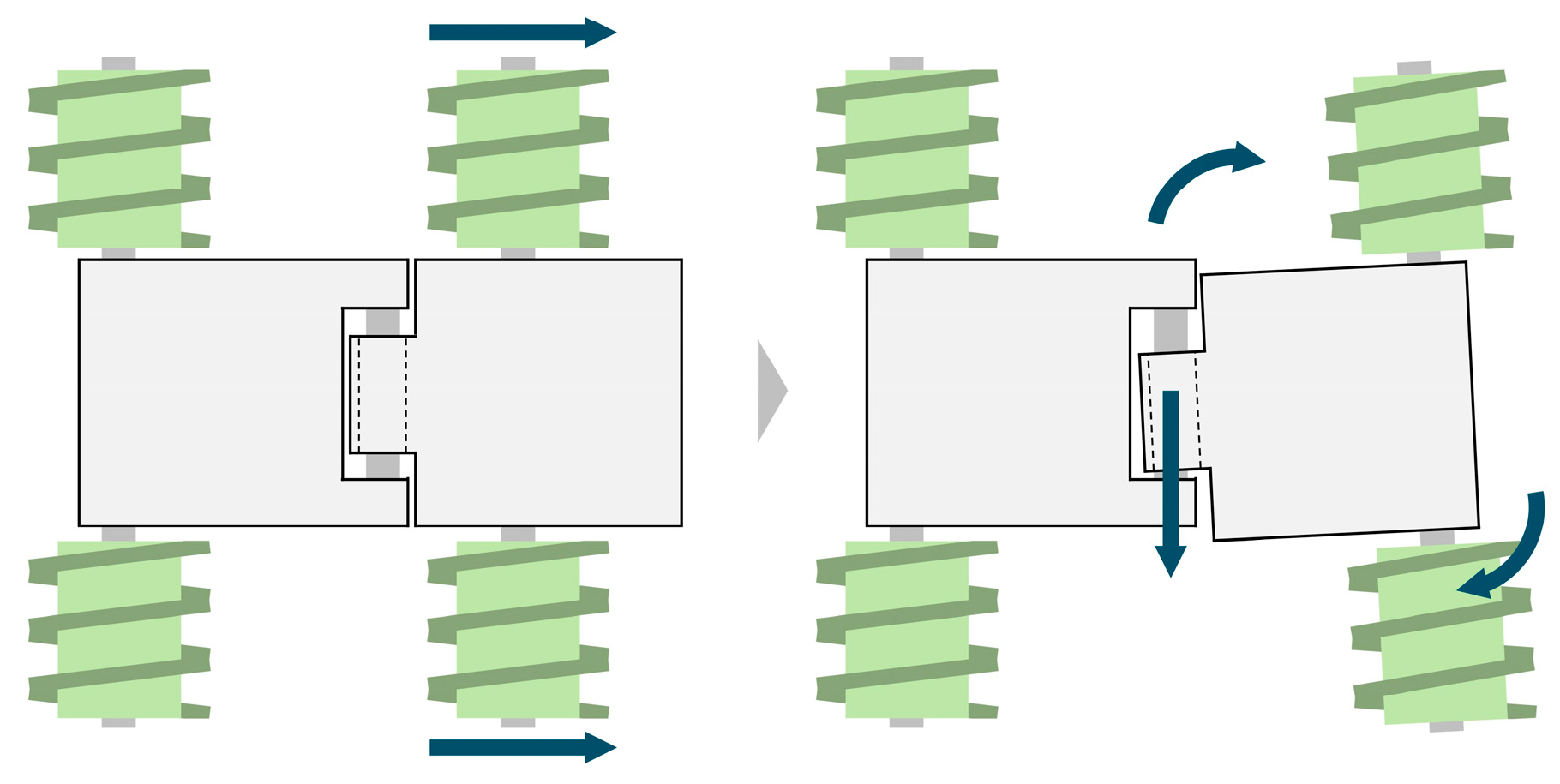
2.4. Beam Extension and Contraction Method
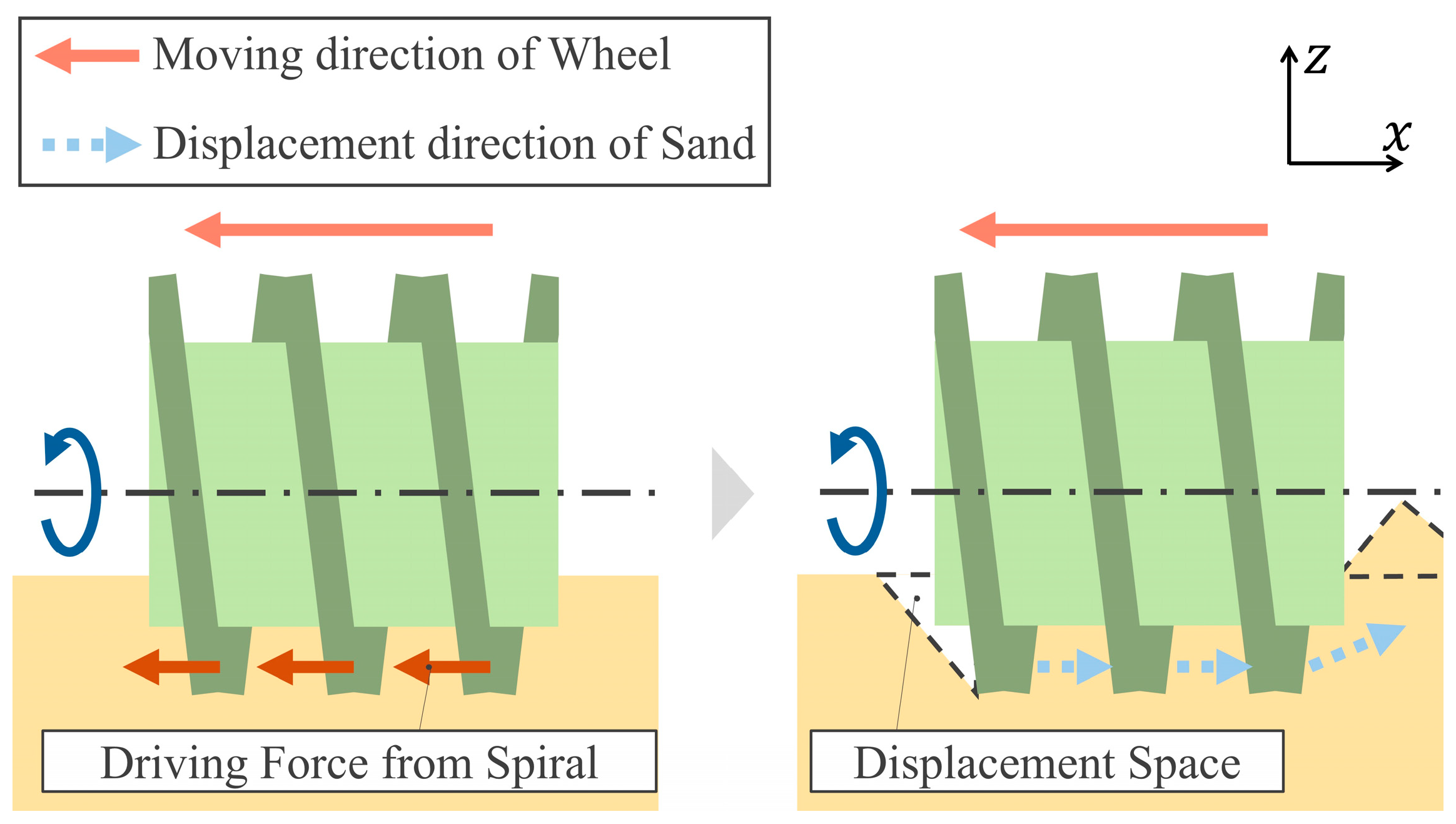
2.5. Use of Screw Wheels
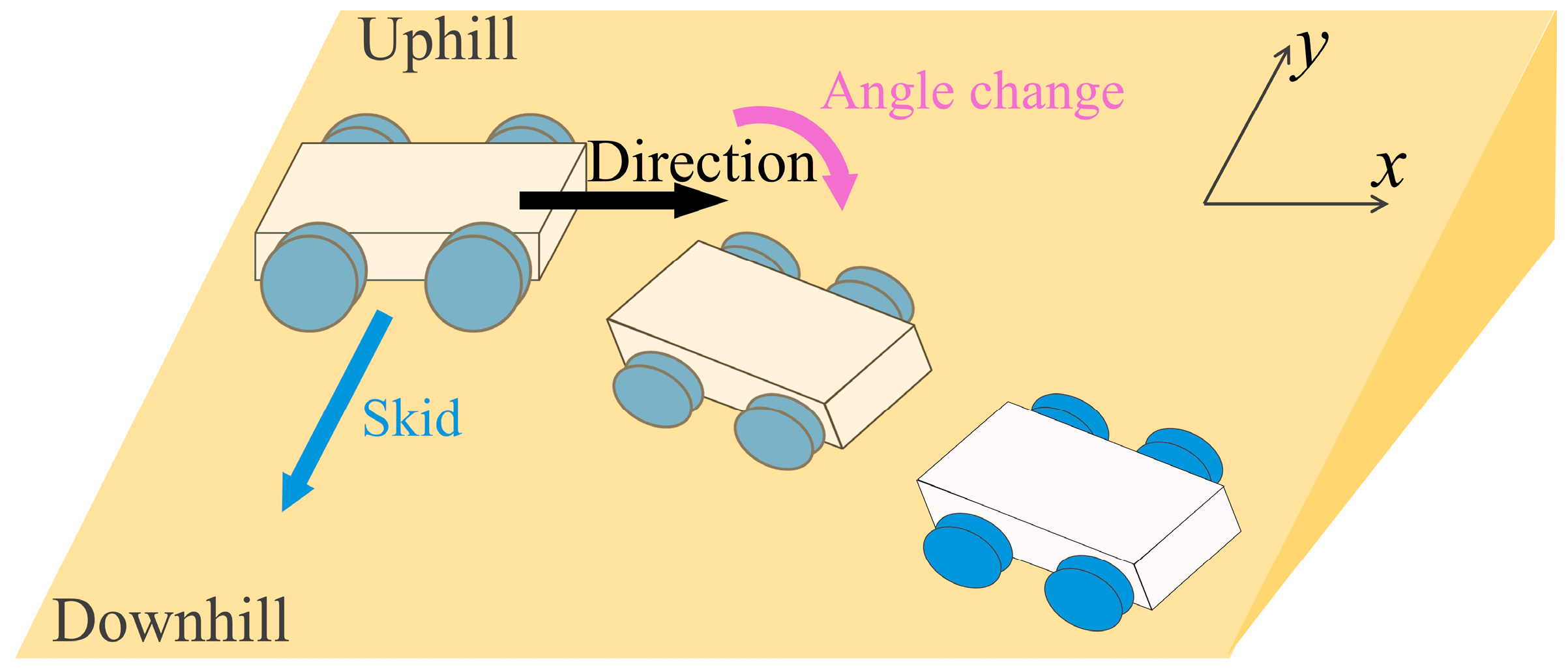
3. Measurement of Sideslip During Slope Traversal Experiments
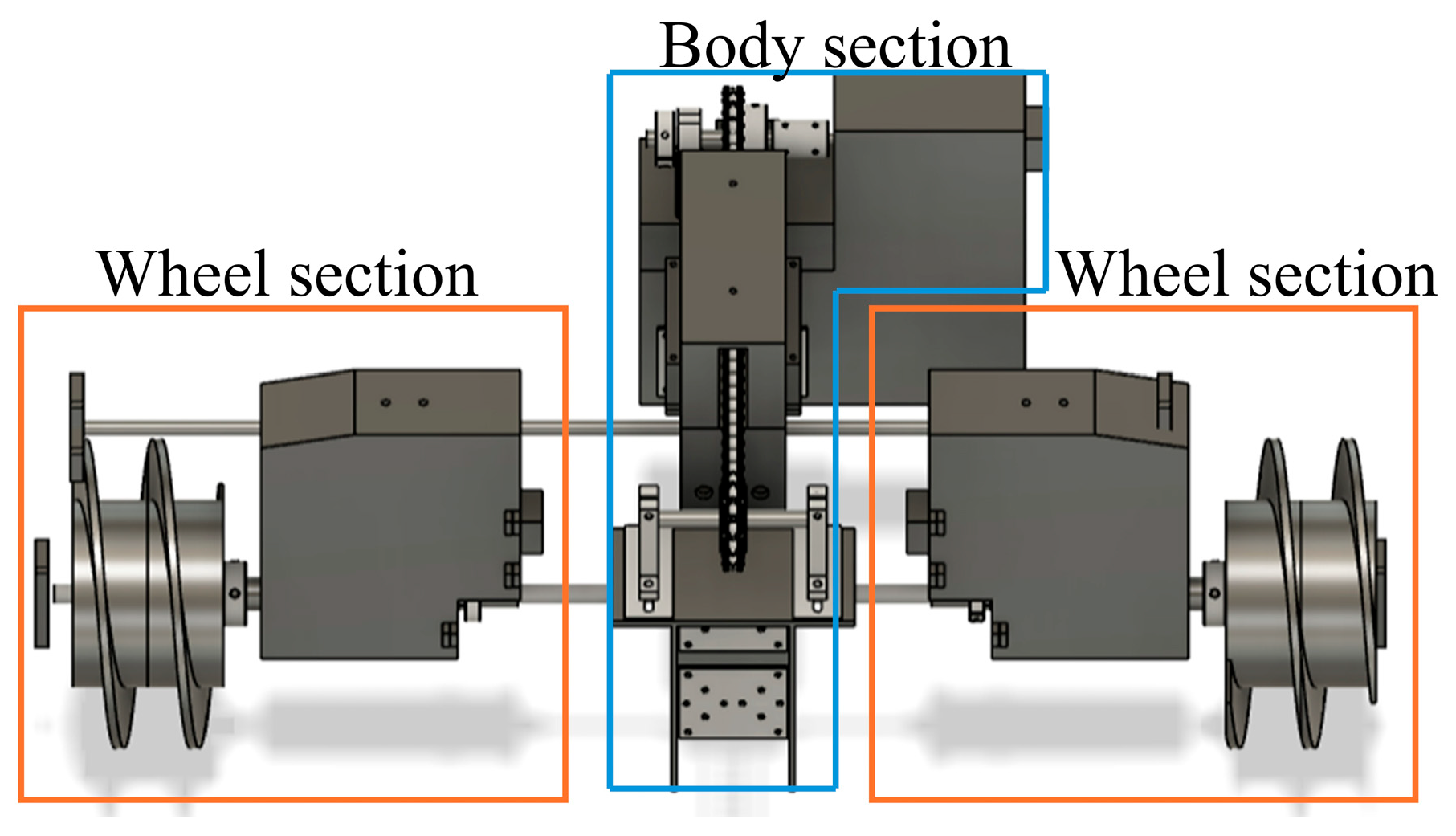
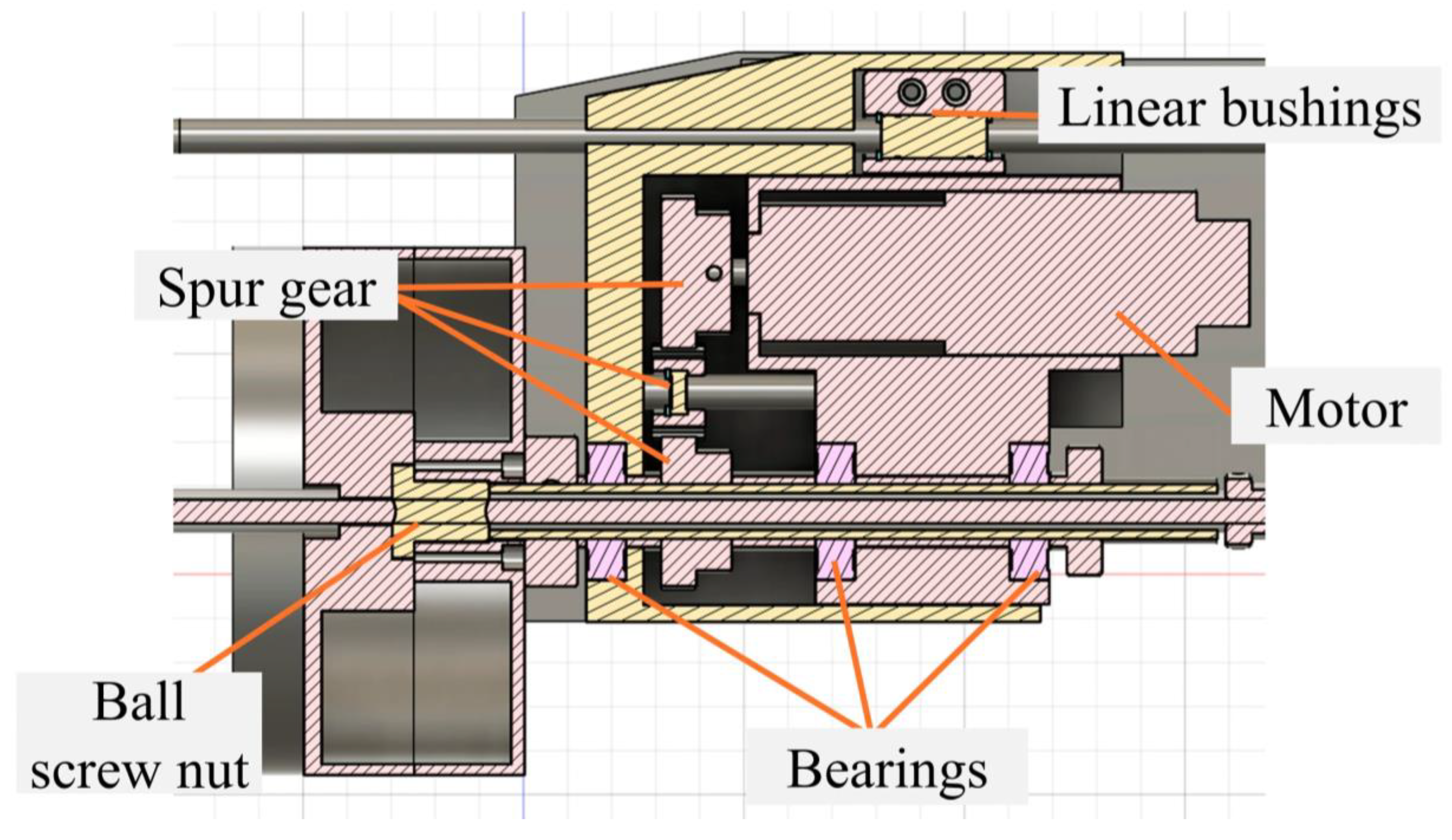
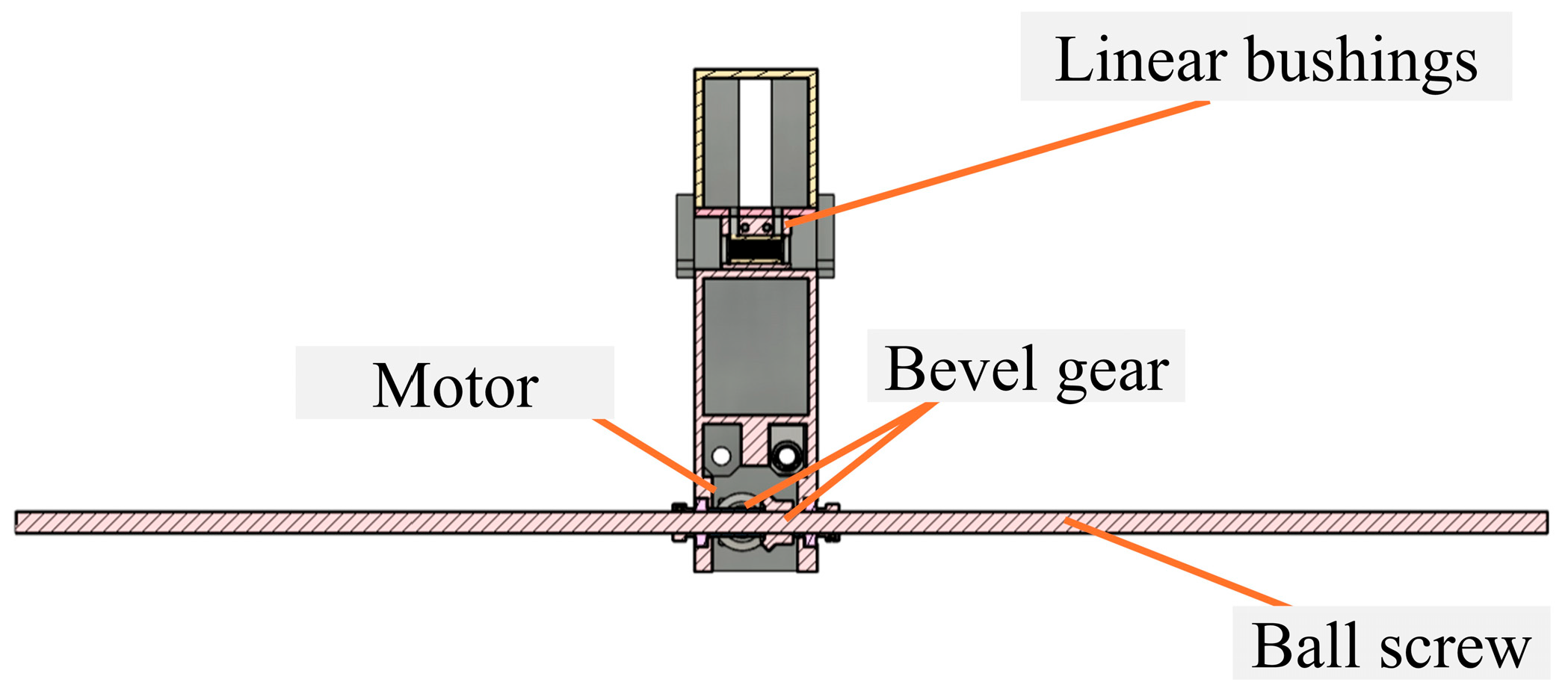
3.1. Testbed
3.2. Experimental Environment and Condition
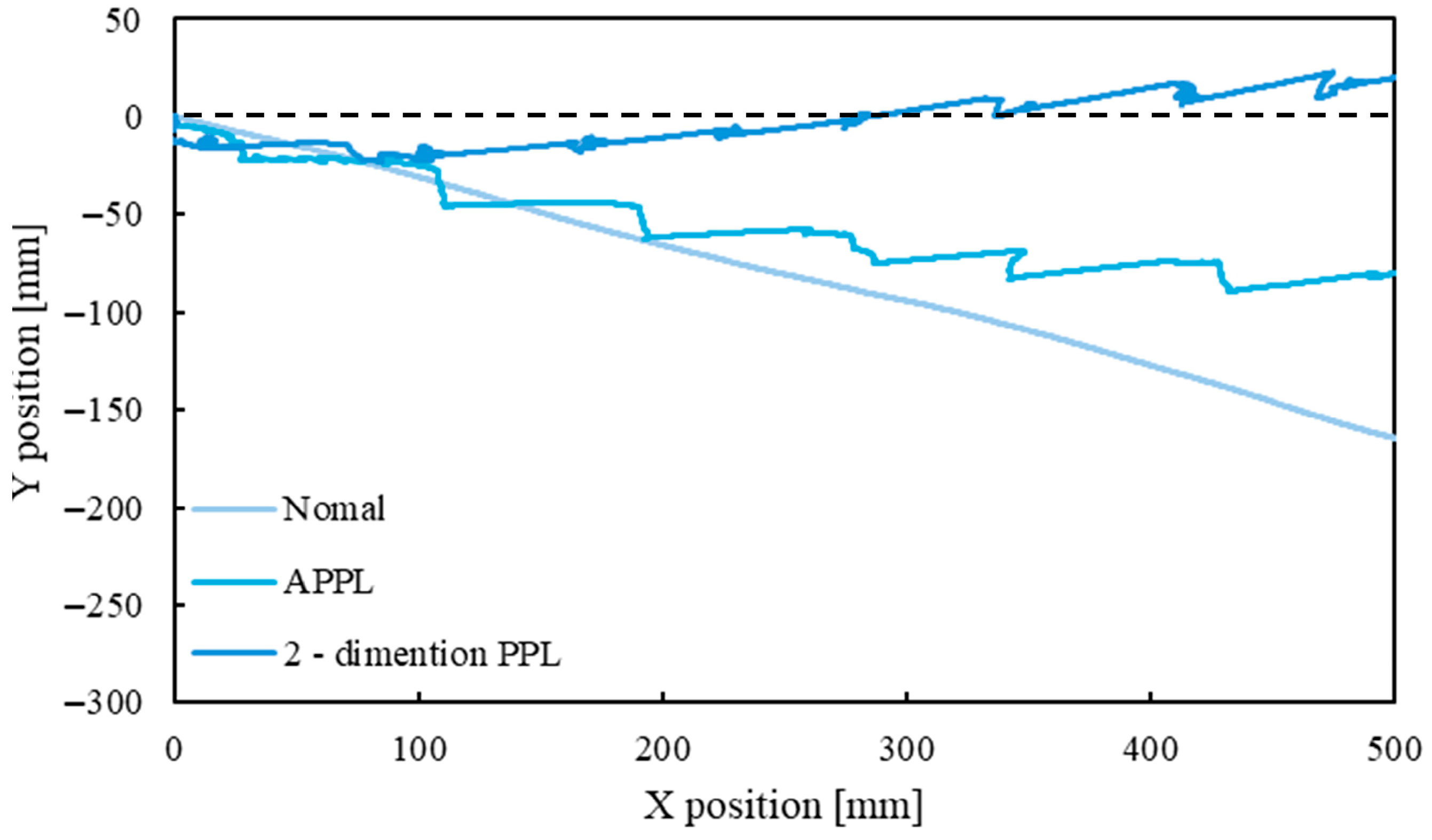
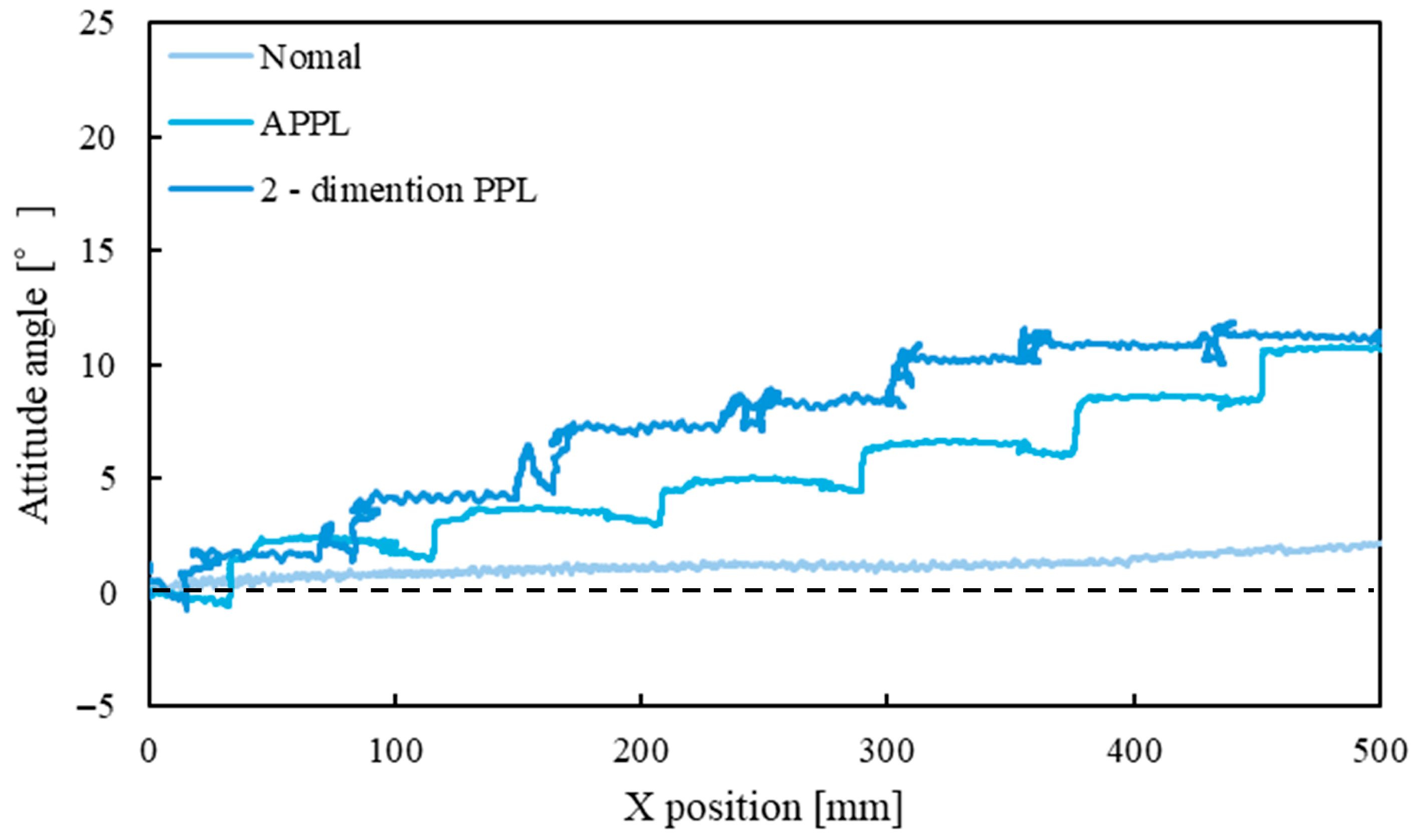
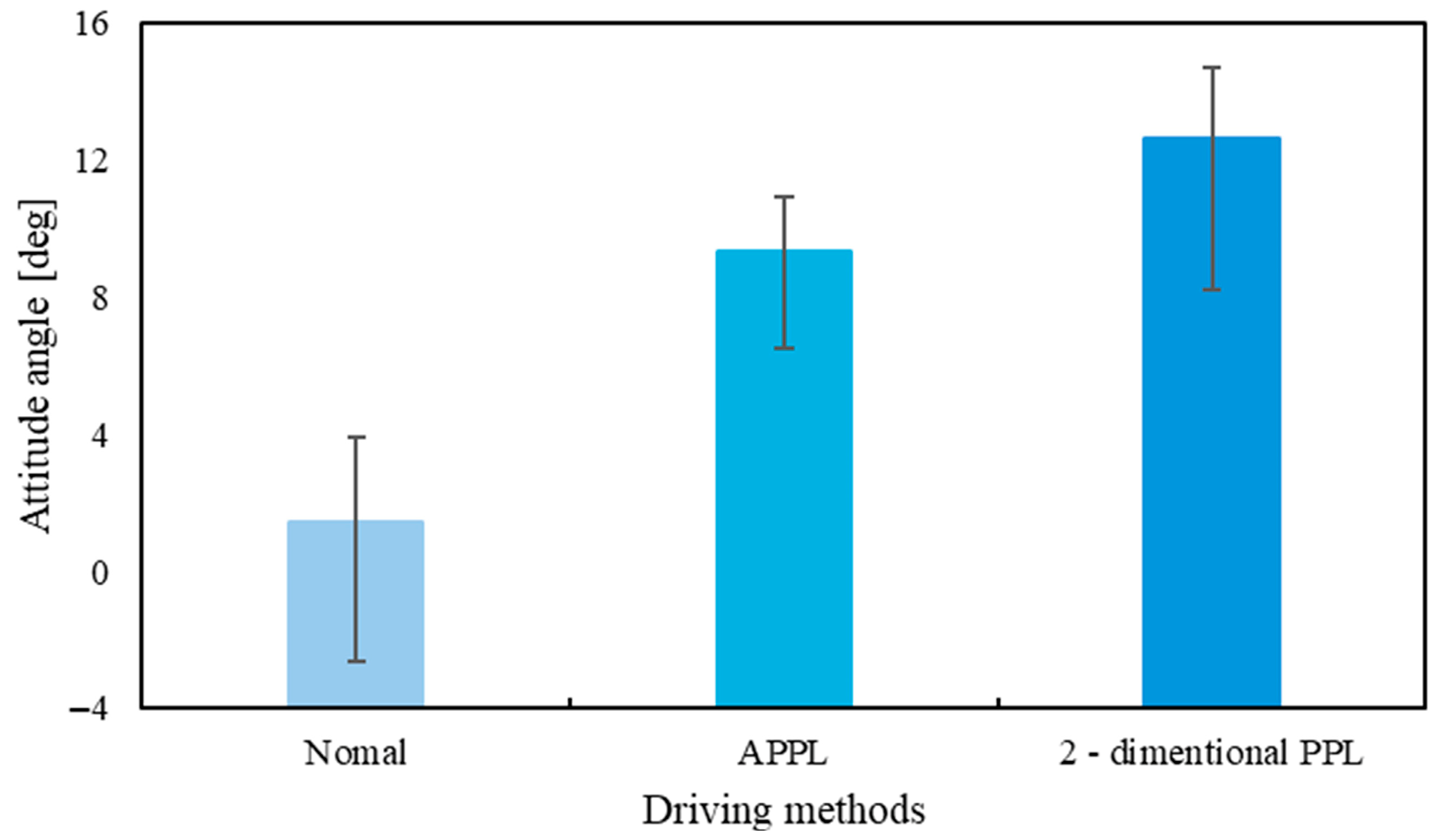
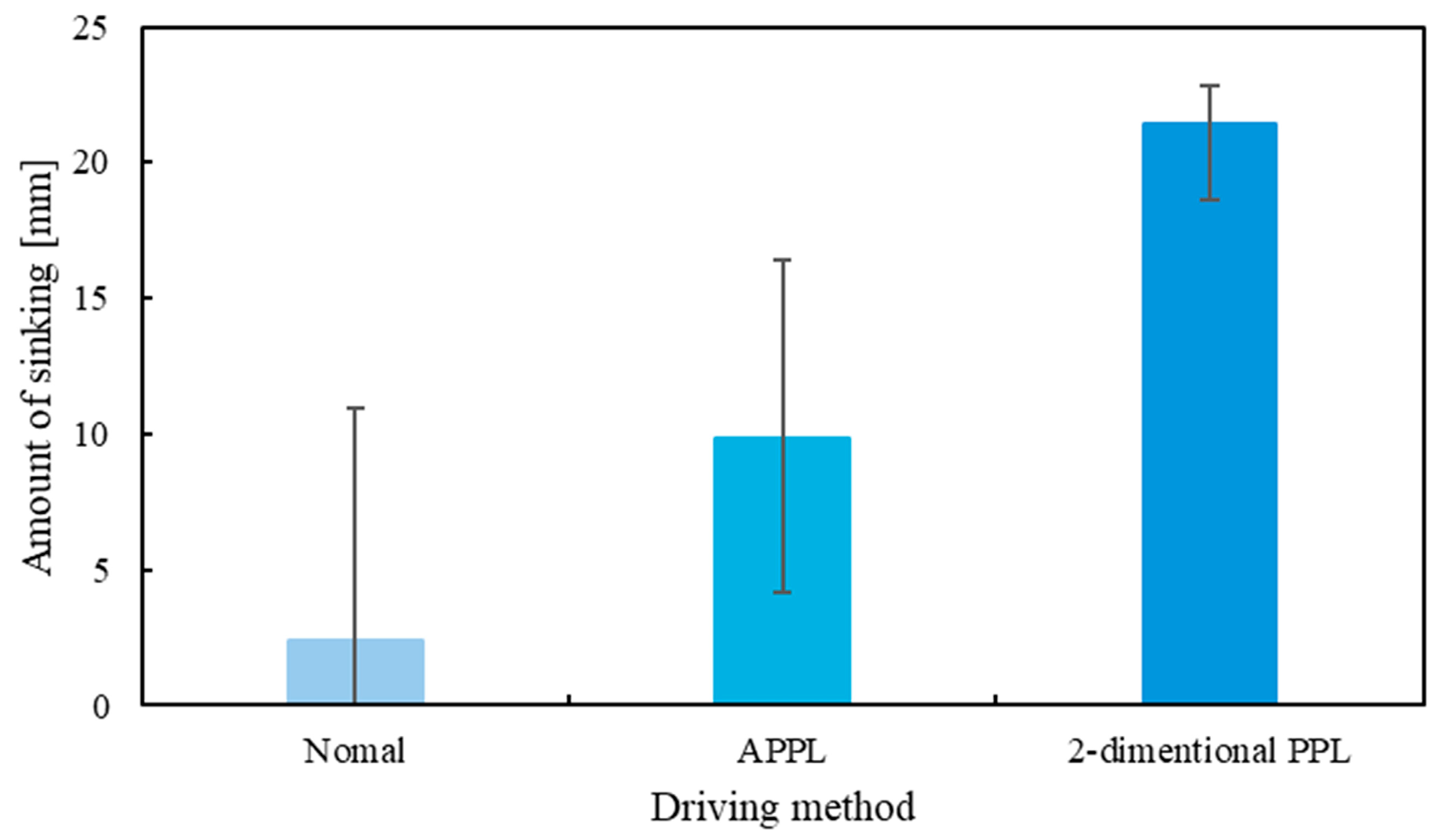
4. Results
5. Discussion
5.1. Discussion of Slope Traversal Experiment
5.2. Implications for Planetary Exploration
6. Conclusions and Future Work
- •
- A two-dimensional Push-Pull Locomotion (2DPPL) method, which combines beam extension/contraction and Archimedean screw wheels with wheelbase extension/contraction, was proposed and experimentally shown to significantly suppress sideslip during slope traversal compared to both normal (wheel-only) and APPL driving.
- •
- The experiments also showed that the 2DPPL method effectively prevented a decrease in attitude angle. However, both the APPL and 2DPPL method resulted in unintended increases in the attitude angle.
- •
- It was confirmed that beam extension/contraction induced wheel sinkage during the recovery motion, which contributed to increased ground support.
- •
- Optimization of recovery displacement and operation sequence.
- •
- Redesign of the beam extension and contraction mechanism.
- •
- Investigation of alternative screw wheel geometries.
- •
- Evaluation under reduced gravity conditions and with extraterrestrial regolith simulants.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Modulus | Unit | Name of parameters |
| - | Bottom area of soil wedge A | |
| mm | Width of wheel | |
| Lead angle | ||
| kN/m2 | Soil cohesion | |
| mm | Diameter of wheel | |
| N | Net driving force | |
| N | Driving force | |
| N | Driving force of upper wheel | |
| N | Driving force of | |
| N | Total ground reaction force | |
| N | Total ground reaction force (normal driving) | |
| N | Total ground reaction force (APPL) | |
| N | Total ground reaction force (4WAPPL) | |
| N | Ground reaction force (uphill) | |
| N | Ground reaction force (uphill, dynamic) | |
| N | Force acting parallel to slope | |
| N | Ground reaction force (downhill) | |
| N | Ground reaction force (downhill, dynamic) | |
| N | Total resistance force | |
| N | Shear force acting on the underside of the wheel | |
| N | Resistive force from soil deformation by the wheel | |
| N | Lateral friction between wheel sidewall and soil | |
| mm | Sinkage | |
| m | Shear displacement | |
| N/mn+1 | Pressure-sinkage modulus | |
| m | Shear deformation modulus | |
| N/mn+2 | Pressure-sinkage modulus | |
| mm | Beam length | |
| mm | Height of lug | |
| mm | Width of lug | |
| mm | Wheelbase length | |
| N | Weight | |
| - | Slip ratio | |
| mm | Pitch | |
| mm | Wheel radius | |
| - | Slip ratio | |
| mm/s | Wheel driving velocity | |
| Wheel angle | ||
| Wheel contact angle | ||
| Angle of the maximum normal stress | ||
| Wheel exit angle | ||
| N/m2 | Normal stress | |
| N/m2 | Shear stress | |
| rad/s | Angular velocity |
References
- Marshall, S.; Douglas, C.; Nicole, H.; Erin, M.; Jonathan, K.; Nate, M.; Kandyce, G. The Artemis Program: An Overview of NASA’s Activities to Return Humans to the Moon. In Proceedings of the 2020 IEEE Aerospace Conference, Big Sky, MT, USA, 7–14 March 2020; pp. 1–7. [Google Scholar] [CrossRef]
- Takayuki, I.; Seisuke, F.; Kazuki, K.; Hiroyuki, K.; Keiki, T.; Hirohisa, K.; Shujiro, S.; Shinichiro, S. Vision-based navigation and obstacle detection flight results in SLIM lunar landing. Acta Astronaut. 2025, 226, 772–781. [Google Scholar] [CrossRef]
- Stefano, C.; Chit, H.Y.; Yuichi, T.; Naoko, O.; Yasuhiro, K. Mission analysis for the Martian Moons Explorer (MMX) mission. Acta Astronaut. 2018, 146, 409–417. [Google Scholar] [CrossRef]
- Christopher, D.K.H.; Tanja, B.; Elisabeth, M.H.; Keyron, H.L.; Lisa, E.M.; Dabid, L.S.; Sandra, S.; Justin, I.S.; Benjamin, P.W.; Meenakshi, W.; et al. Sampling Mars: Geologic context and preliminary characterization of samples collected by the NASA Mars 2020 Perseverance Rover Mission. PNAS 2025, 122, e2404255121. [Google Scholar] [CrossRef]
- Arvidson, R.E.; Ashley, J.W.; Bell, J.F., III; Chojnacki, M.; Cohen, J.; Economou, T.E.; Farrand, W.H.; Fergason, R.; Fleischer, I.; Geissler, P.; et al. Wolff. Opportunity Mars Rover mission: Overview and selected results from Purgatory ripple to traverses to Endeavour crater. J. Geophys. Res. Planets 2011, 116, E00F15. [Google Scholar] [CrossRef]
- David, W.; Scott, M.; Krzysztof, S.; Dominic, J.; David, K.; James, T. Design and field experimentation of a prototype Lunar prospector. Int. J. Robot. Res. 2010, 29, 1550–1564. [Google Scholar] [CrossRef]
- Wiebke, B.; Leon, D.; Amrita, S.; Mehmed, Y.; Manuel, M.; Frank, K. Development strategies for multi-robot teams in context of planetary exploration. In Proceedings of the 2024 International Conference on Space Robotics (iSpaRo), Luxembourg, 24–27 June 2024; pp. 64–69. [Google Scholar] [CrossRef]
- Daisuke, F.; Naoki, T.; Tetsuya, O.; Kojiro, I. Analysis of a resistance force for the locked-wheel of push-pull locomotion rovers using large subsidence. J. TerraMech. 2021, 94, 1–12. [Google Scholar] [CrossRef]
- Kohei, I.; Kojiro, I. Proposal of a Planetary Exploration Rover with a Wheel using Sinking Performance for Crossing Slope. J. Robot. Soc. Jpn. 2021, 39, 958–965. (In Japanese) [Google Scholar] [CrossRef]
- Tatsuhiko, S.; Kojiro, I.; Daisuke, F. Study on the suppression of running skidding during slope contour movement using active subsidence on a steer angled wheel. Teramechanics 2023, 43, 41–46. (In Japanese) [Google Scholar]
- Bekker, M.G. Off-The-Road-Locomotion; University of Michigan Press: Ann Arbor, MI, USA, 1960. [Google Scholar]
- Bekker, M.G. Introduction to Terrain-Vehicle Systems; University of Michigan Press: Ann Arbor, MI, USA, 1969. [Google Scholar]
- Wong, J.Y. Theory of Ground Vehicles, 4th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2008. [Google Scholar]
- Genya, I.; Akiko, M.; Keiji, N.; Kazuya, Y. Terramechanics-based model for steering maneuvers of planetary exploration rovers on loose soil. J. Field Robot. 2007, 24, 233–250. [Google Scholar] [CrossRef]
- Wong, J.Y.; Reece, A.R. Prediction of rigid wheels performance based on analysis of soil-wheel stresses, Part I. performance of driven rigid wheels. J. Terramech. 1967, 4, 81–98. [Google Scholar] [CrossRef]
- Hiroshi, T.; Yutaka, S. Analysis on the Resistive Forces acting on the Bucket of Power Shovel in the Excavating Task of Piled Fragment Rocks. J. Appl. Mech. 2004, 7, 787–796. [Google Scholar] [CrossRef]
- Kenji, N.; Masatsugu, O.; Takashi, K.; Satoshi, T. Terramechanics-based Propulsive Characteristics of Mobile Robot Driven by Archimedean Screw Mechanism on Soft Soil. In Proceedings of the 2010 IEEE/RSJ International Conference on Intelligent Robots and Systems, Taipei, Taiwan, 18–22 October 2010; pp. 4946–4951. [Google Scholar] [CrossRef]
- Noriaki, M. Study on Development Locomotion Performance based on Terramechanics for Wheeled Rover on Soft Ground. Ph.D. Thesis, The Graduate University for Advanced Studies, SOKENDAI, Kanagawa, Japan, 2013. (In Japanese). [Google Scholar]
- Wong, J. Mechanics of Vehicle-Terrain Interaction: Terramechanics. In Theory of Ground Vehicles, 5th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2022; pp. 77–219. [Google Scholar] [CrossRef]
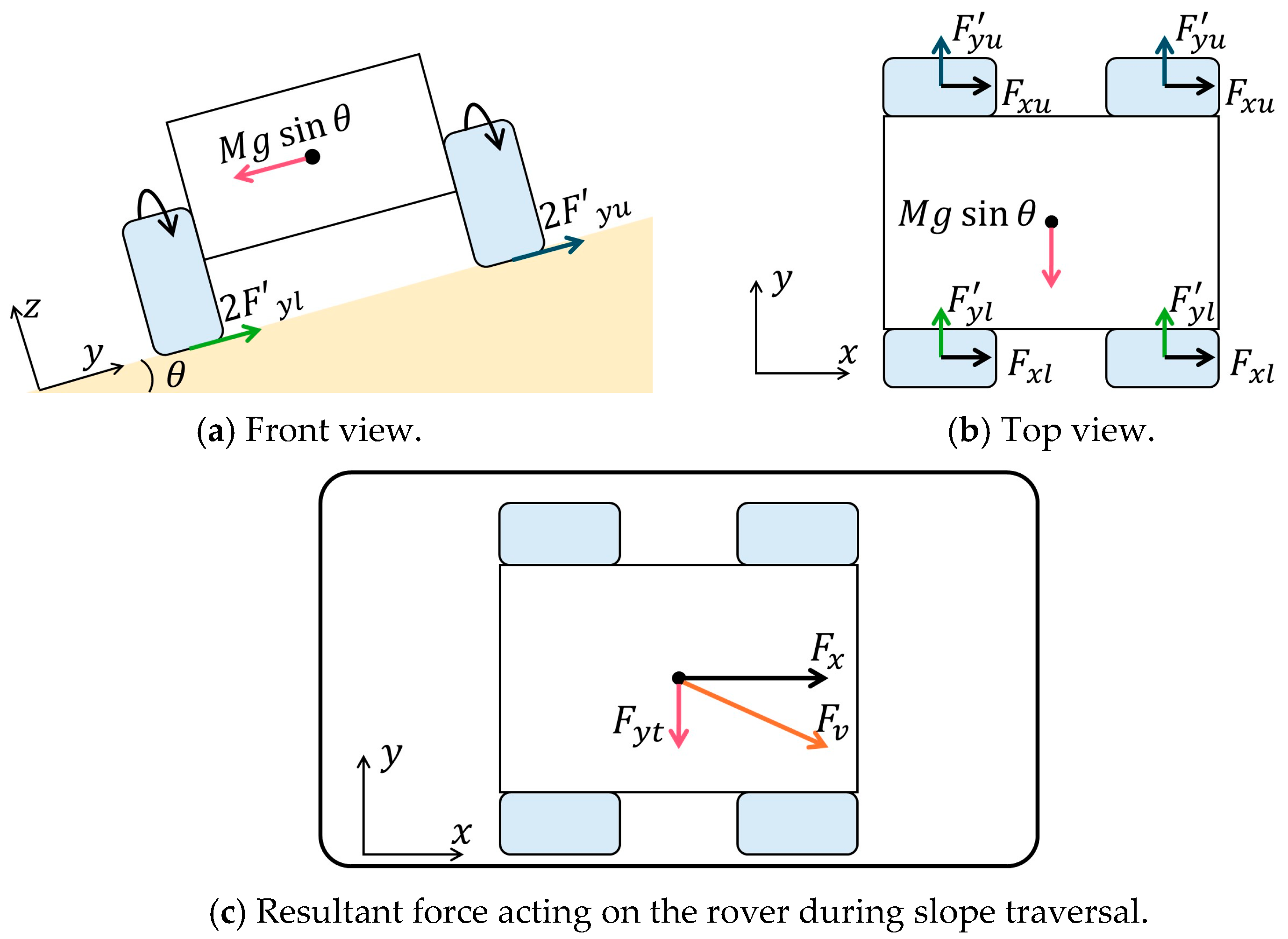
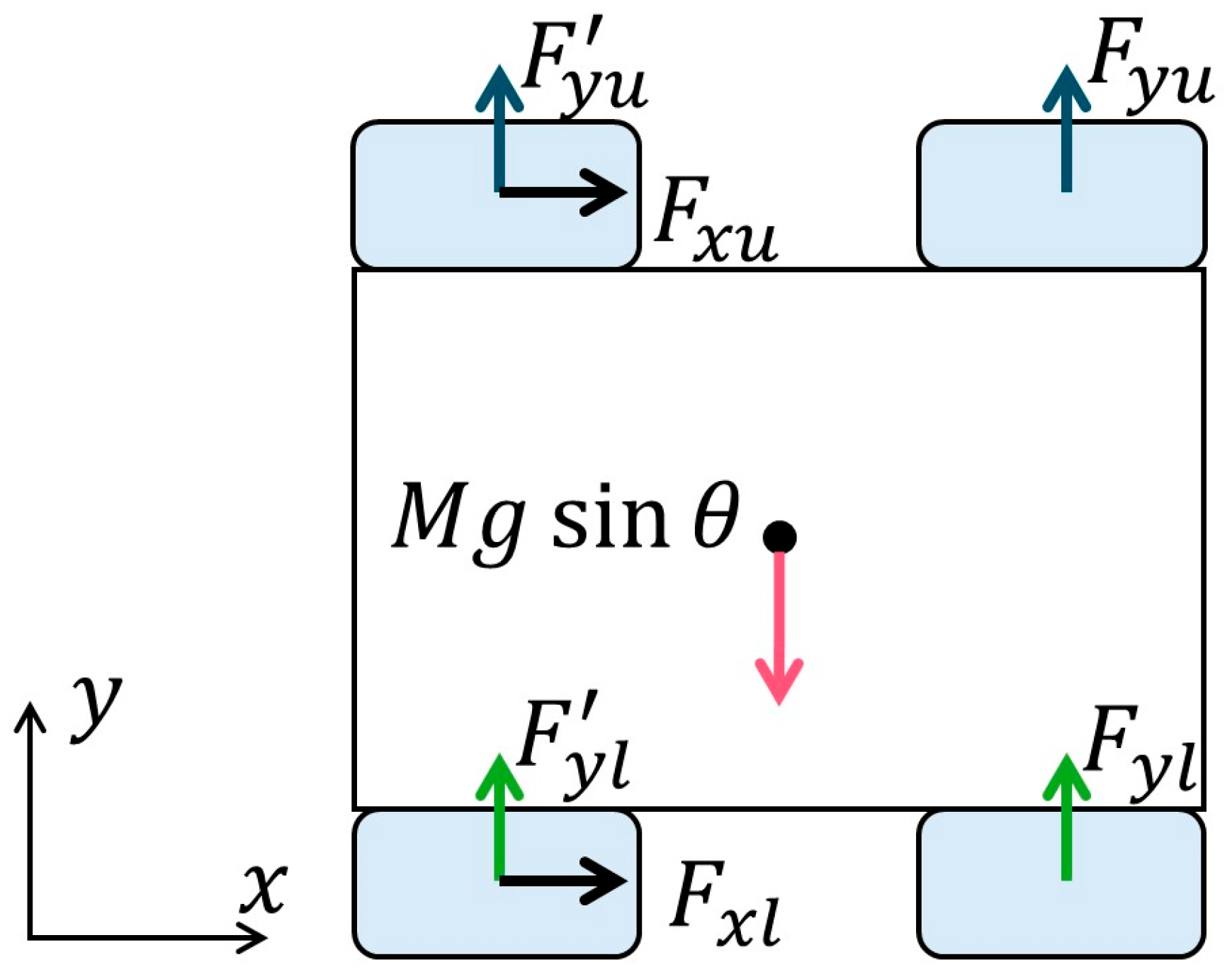
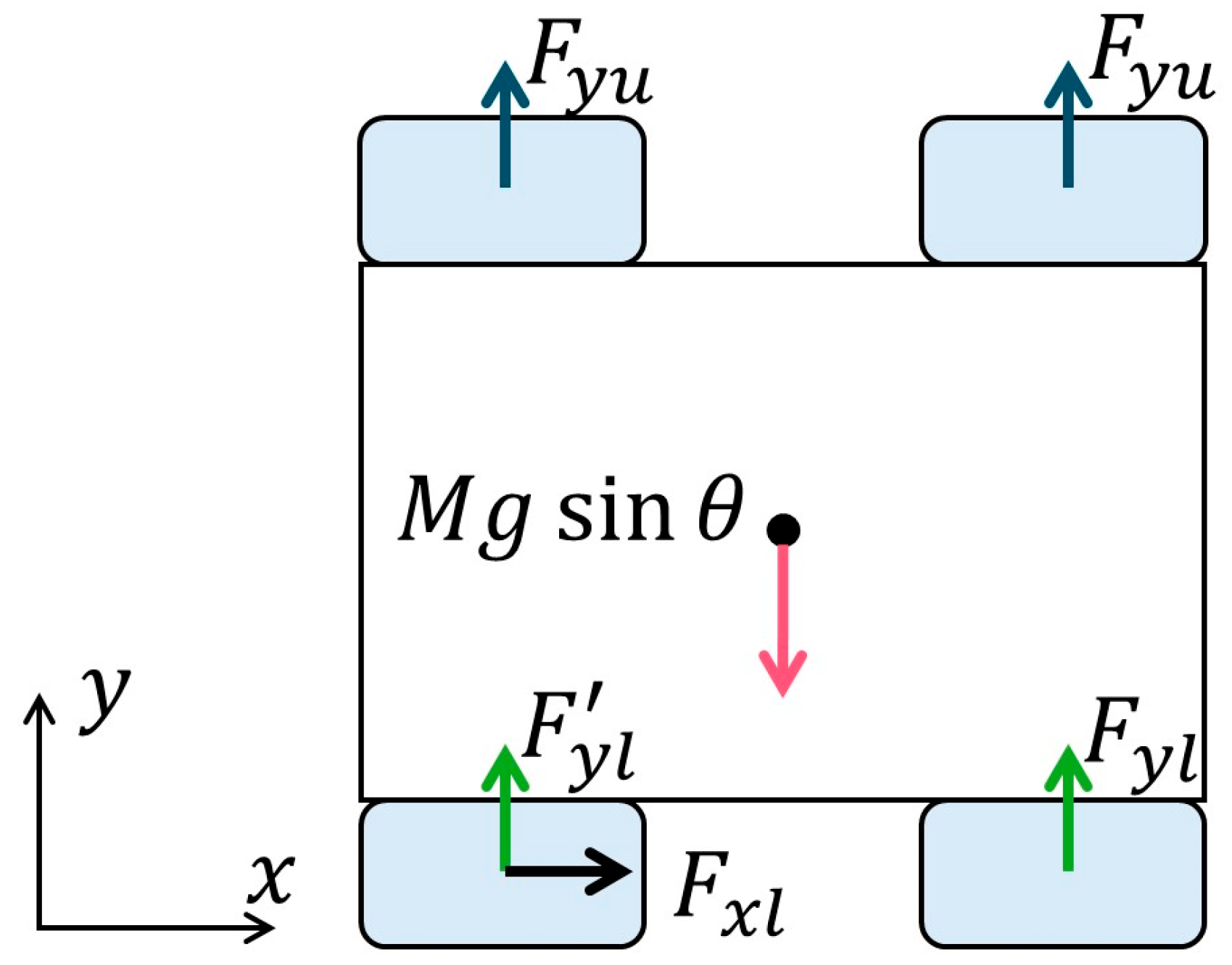



| Modulus | Value | Unit | Name of Parameters |
|---|---|---|---|
| (max) | 640 | mm | Maximum wheelbase length |
| (min) | 560 | mm | Minimum wheelbase length |
| (max) | 560 | mm | Maximum beam length |
| (min) | 480 | mm | Minimum beam length |
| - | 565 × 690 × 285 | mm | Rover width, length, and height |
| M | 120.5 | N | Weight |
| Modulus | Value | Unit | Parameter |
|---|---|---|---|
| 140 | mm | Diameter of wheel | |
| 80 | mm | Width of wheel | |
| 12.5 | mm | Height of lug | |
| 5 | mm | Width of lug | |
| 40 | mm | Pitch | |
| 4.6 | Lead Angle |
| Description | Value |
|---|---|
| Motion capture system | OptiTrack |
| Software | Motive 2.2.0 |
| Analysis software | SKYCOM 2.2.2 |
| Motive camera | Prime 13 (Acuity Inc., Tokyo, Japan) |
| Calibration wand | CW-500 (Acuity Inc., Tokyo, Japan) |
| Calibration Square | CS-200 (Acuity Inc., Tokyo, Japan) |
| Description | Unit | Value |
|---|---|---|
| Bulk density | g/cm3 | 1.29–1.31 |
| Angle of repose | 33 | |
| Internal friction angle | 22.3 [18] | |
| Cohesion | N/m3 | 761.8 |
| Shear deformation modulus | m | 0.001–0.025 [19] |
| Mean particle size | mm | 0.59 |
| Item | Unit | Value |
|---|---|---|
| Soil | - | Silica sand No. 5 |
| Slope angle | 20 | |
| Driving methods | - | Normal, APPL, 2DPPL |
| Traveling distance | mm | 500 |
| Trial | - | 5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sagara, K.; Fujiwara, D.; Iizuka, K. Development and Evaluation of a Two-Dimensional Extension/Contraction-Driven Rover for Sideslip Suppression During Slope Traversal. Aerospace 2025, 12, 699. https://doi.org/10.3390/aerospace12080699
Sagara K, Fujiwara D, Iizuka K. Development and Evaluation of a Two-Dimensional Extension/Contraction-Driven Rover for Sideslip Suppression During Slope Traversal. Aerospace. 2025; 12(8):699. https://doi.org/10.3390/aerospace12080699
Chicago/Turabian StyleSagara, Kenta, Daisuke Fujiwara, and Kojiro Iizuka. 2025. "Development and Evaluation of a Two-Dimensional Extension/Contraction-Driven Rover for Sideslip Suppression During Slope Traversal" Aerospace 12, no. 8: 699. https://doi.org/10.3390/aerospace12080699
APA StyleSagara, K., Fujiwara, D., & Iizuka, K. (2025). Development and Evaluation of a Two-Dimensional Extension/Contraction-Driven Rover for Sideslip Suppression During Slope Traversal. Aerospace, 12(8), 699. https://doi.org/10.3390/aerospace12080699







