Numerical Study of the Use of a Flapping Foil in Energy Harvesting with Suction- and Blower-Based Control

Abstract

The method of extracting energy from a fluid environment using flapping foils offers advantages such as structural simplicity and environmental friendliness. However, its low energy harvesting efficiency remains a significant factor limiting its development. This study employs suction and blower-based control (SBC) to enhance the energy harvesting efficiency of flapping foils. Using an orthogonal experimental design and numerical methods, 49 representative combinations of SBC geometries were selected for numerical simulation. The effects and priority rankings of geometric parameters on foil performance were statistically analyzed. It was found that under the optimal geometry (the suction slot position is 0.54c, the injection slot position is 0.79c, the width of the slot is 0.015c, the angle of the suction slot is −3°, and the angle of the injection slot is −9°), the energy harvesting efficiency can reach 40.7%. Furthermore, under laminar flow conditions, the benefit of SBC increases with higher Reynolds numbers (Re). At Re = 2200, SBC maximized the improvement in energy harvesting efficiency by 76%. No significant correlation was observed between the flapping amplitude and the SBC effect. However, the reduced frequency significantly influences the efficiency improvement generated by SBC. The SBC method shifts the foil’s optimal operating region towards lower reduced frequencies, which benefits energy harvesting efficiency. The research presented herein may have potential applications in the development of marine energy systems and bio-inspired propulsion.

1. Introduction

With the advancement of the times and the continuous improvement in social productivity, the demand for electricity driven by various human activities has been steadily increasing. In order to reduce the reliance on fossil fuel combustion for power generation and to mitigate the associated greenhouse gas emissions, the utilization of renewable energy sources—such as wind, biomass, and hydropower—has emerged as a crucial solution. Both terrestrial environments and the vast expanses of the ocean contain abundant hydropower resources. For hydropower extraction, turbines are generally used, with efficiencies typically exceeding 40% [1]. In some cases, the integration of auxiliary components—such as inlet nozzles—can provide additional pressure energy to the turbine, enabling the efficiency to surpass the Betz limit [2]. However, turbines also present certain limitations, including large spatial requirements and challenges in maintaining the operational stability of their rotating mechanisms.

Flapping foils can be employed for both propulsion and energy harvesting from the surrounding fluid environment. These foils typically feature simple structures, low noise levels, and strong adaptability to diverse environmental conditions. Wu [3] first proposed the concept of harnessing wave energy using oscillating foils in 1971. Since then, the application of oscillating foils for energy harvesting and propulsion in uniform flows has attracted considerable attention. Since the initial proposal and experimental demonstration by McKinney et al. [4], the development of flapping foil energy harvesting systems has progressed rapidly. 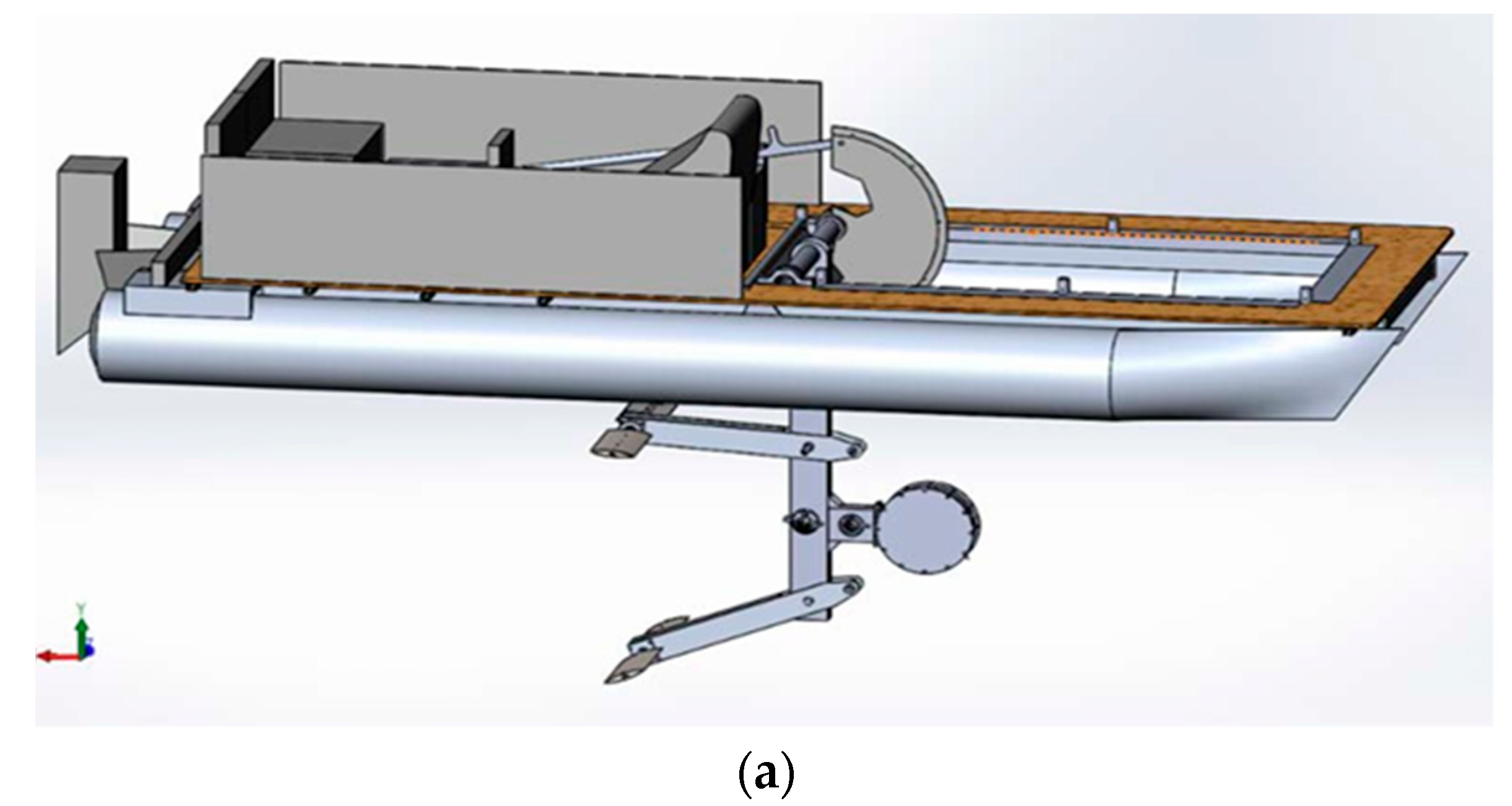In 2006, Kinsey and Dumas [5] discovered that energy could be extracted from oncoming flow using foils undergoing simultaneous heaving and pitching motions; under a Reynolds number of 1100, they achieved a maximum energy harvesting efficiency of 33.7%. The first commercial prototype of a flapping-based hydropower device was developed in 2002 by an engineering firm and was named “Stingray,” as shown in Figure 1. The entire system consists of a support frame, flapping foil, actuating arms, and hydraulic cylinders. The foil performs both pitching and heaving motions and is capable of generating 122 kW of power [6]. The Leading Edge research group at Brown University developed dual-foil energy harvesting systems with output capacities of 1.0 kW and 2.0 kW, as shown in Figure 2, achieving an energy harvesting efficiency of 28% [7]. Therefore, flapping foil energy harvesters can be installed in tidal current regions with large flow variability to generate electricity from water resources. However, the energy harvesting efficiency of flapping foils is generally not superior to that of traditional turbine-based systems, making the enhancement of flapping foil efficiency a key area of ongoing research.

In the pursuit of improving energy harvesting efficiency, researchers have extensively studied the motion trajectories of flapping foils. These foils typically undergo periodic coupled pitching and heaving motions. Various trajectories have been explored, including sinusoidal motion [8,9], non-sinusoidal motion [10,11], elliptical motion [12], and asymmetric sinusoidal motion [13]. Studies on motion parameters have revealed that the heaving amplitude significantly influences efficiency; as the amplitude increases, the efficiency initially rises and then declines [14]. Under different trajectory types, the pitching amplitude also exhibits an optimal value for maximizing efficiency. The pitching amplitude affects the formation of leading-edge vortices on the foil surface, which in turn impacts energy harvesting performance [14,15]. Kinsey et al. [15] and Zhu et al. [16] found that under sinusoidal motion at a Reynolds number of 1100, the reduced frequency plays a critical role in wake stability. The optimal energy harvesting efficiency occurs when the wake is most unstable, corresponding to a reduced frequency in the range of 0.1 to 0.15. The rotational axis of the pitching motion also plays a significant role in flapping foil performance. Variations in the axis location affect the flow velocity over the foil surface, thereby altering the pressure distribution and ultimately influencing the energy harvesting efficiency. When the rotational axis is positioned at one-third of the chord length, the synchronization between the generated lift and the heaving motion is enhanced, leading to improved energy harvesting performance [17]. In addition to rigid hydrofoils, researchers have investigated the use of flexible foils to further enhance energy harvesting efficiency. Leveraging the deformability of flexible foils, fluid–structure interaction (FSI) enables a combination of active and passive deformation modes. This coupling improves lift generation and reduces drag, thereby enhancing the overall energy harvesting performance of the flapping foil system [18,19,20].

Similarly to the approach of enhancing turbine performance through the addition of auxiliary devices, control mechanisms can be integrated into flapping foils to improve energy extraction efficiency. These mechanisms are generally categorized into passive and active control strategies. Traditional passive flow control methods require no external energy input and primarily involve additive or subtractive modifications to the foil surface to enhance flow characteristics. Such methods include surface protrusions, grooves, splitter plates, upstream rods, bleed, and dimpled surfaces, among others [21].

Active flow control methods require external energy input to manipulate the flow field. Low-power, high-efficiency active flow control strategies are particularly beneficial for enhancing the energy harvesting performance of flapping foils. These methods aim to mitigate periodic vortex shedding, reduce drag, and suppress fluctuations in lift forces [22]. For example, placing a bluff body upstream of the flapping foil can alter the direction of incoming flow, promote the formation of leading-edge vortices, and thereby improve foil performance—resulting in up to a 30% increase in efficiency [23]. In another strategy, two auxiliary foils are positioned on the upper and lower surfaces of the main flapping foil. When the main foil and auxiliary foils approach each other during motion, their respective induced vortices interact, leading to a redistribution of surface pressure and an enhancement in lift, thereby improving energy extraction [24]. Trailing-edge flaps have also been implemented on flapping foils to optimize energy harvesting performance [25,26]. Additionally, vortex generators mounted on the foil surface can generate secondary vortices that interact with those induced by the flapping motion, promoting energy exchange within the boundary layer and enhancing both lift and the synchronization between pitching and heaving motions [27]. Furthermore, jet slots installed at the trailing edge of the foil have been shown to increase energy harvesting efficiency by 21.6%, as reported in the literature [28].

Chen et al. [29] proposed the use of steady suction to modify boundary layer flow over a circular cylinder. Control strategies based on suction and blowing have been widely adopted for manipulating flow around cylinders. These steady suction and blowing control (SBC) devices can be easily installed on bluff bodies of various shapes and configurations [30,31]. The SBC approach has been demonstrated to be effective and energy efficient. Delaunay and Kaiktsis [32] conducted numerical simulations and stability analyses to investigate the effects of base suction and blowing on the flow around a cylinder at low Reynolds numbers. Their results indicated that for Re > 47, even mild blowing or sufficiently strong suction could stabilize the wake and reduce absolute instability in the near-wake region. Suction and blowing techniques have also been applied in aircraft slat design. For instance, a dual-slotted blown airfoil based on the NACA 23015 [33] profile was shown to achieve a significant increase in lift coefficient through optimization of configuration parameters [34]. Gao et al. [35] carried out an experimental study on the control effects and mechanisms of a bluff body subjected to windward-side suction combined with leeward-side blowing, as illustrated in Figure 3. Through active control, leeward-side blowing generated a pair of vortices in the cylinder’s wake, altering the conventional vortex shedding process. As these blowing-induced vortices shifted downstream, they facilitated the detachment of the unstable shear layers from the cylinder surface. The study demonstrated that steady and symmetric disturbances imposed on periodic flow over a circular cylinder could induce a symmetric mode of wake vortex shedding. Additionally, their research showed that when a circular cylinder exposed to transverse flow is allowed to oscillate, vortex-induced vibrations (VIVs) occur when the vortex shedding frequency matches the structural natural frequency. In engineering applications, effective control strategies are essential to mitigate the adverse effects caused by vortex shedding around bluff bodies.

The SBC method employed in this study differs from that used by Gao et al. [35]. Unlike their configuration, the present study adopts a reversed approach: suction is applied on the leeward side and blowing on the windward side, aiming to enhance the wake strength of the flapping foil. By synchronizing the timing of suction and blowing with different phases of the flapping motion, the control is coordinated as follows: at t/T = 0–0.5, when the foil moves downward, suction and blowing are applied on the lower surface; at t/T = 0.5–1, when the foil moves upward, they are applied on the upper surface. The generation and shedding of leading-edge vortices (LEVs) play a critical role in determining the energy harvesting efficiency of flapping foils. Therefore, the periodicity and spatial characteristics of vortex shedding must be carefully considered. In this study, the placement of SBC devices is aligned with the vortex formation regions induced by foil motion. This includes optimizing the slot position of SBC devices, as well as their slot length and depth and the angle of the blowing openings. The objective is to investigate the optimal installation positions and design parameters of SBC devices that can maximize energy harvesting efficiency and improve the overall performance of the flapping foil system.

It is well known that tidal flows are inherently slow. Due to the relatively low energy harvesting efficiency of flapping foils, their large-scale deployment has remained a challenge. This study introduces a suction and blowing control (SBC) strategy to enhance the energy harvesting performance of flapping foils. Compared with other flow control techniques, SBC offers distinct advantages, including strong environmental adaptability and low noise emission. This research quantitatively compares the energy harvesting efficiency of flapping foils equipped with SBC devices to that of baseline (uncontrolled) foils, aiming to overcome the efficiency bottleneck in low-speed flow conditions and enable the broader application of flapping foil technology. Through systematic numerical simulations, the effects of different SBC configurations—including installation positions and design parameters—on the energy harvesting performance of flapping foils are investigated. The study identifies the optimal SBC placement and geometry that maximize energy harvesting efficiency. Additionally, the influence of varying Reynolds numbers and pitching amplitudes on the effectiveness of SBC-enhanced energy harvesting is examined. The findings provide a valuable parametric basis for the optimized design and practical implementation of flapping foils integrated with SBC.

2. Motion Model and Kinematics

2.1. Foil Motion

Most studies on flapping foils have assumed that their movement was sinusoidal to control the experiment easily [36]. This motion was also used to perform numerical simulations.

As shown in Figure 4, the flapping foil exhibits periodic motion, and heave and pitch motions occur at the center of rotation. Here, $U_{\infty }$ represents the speed of uniform incoming flow. The airfoil has two degrees of freedom: rotational movement and translational heave displacement $h(t)$. $H_0$ is the amplitude of the heave motion, and $V_y(t)$ is the speed of the heave motion. The movement of the airfoil can be described as

$$\theta (t)={\theta }_0\mathit{sin}(\gamma t)$$

(1)

$$h(t)=H_0\mathit{sin}(\gamma t+\varphi )$$

(2)

where $\gamma$ represents the angular frequency, calculated using the formula $\gamma =2\pi f$; $f$ is the frequency of the movement of the flapping foils; and $\varphi$ is the phase difference between the pitch and heave motions. When the phase difference is 90°, the pitch motion is at the midpoint of its cycle when the heave motion reaches its maximum. At this phase relationship, the flapping foil sweeps through the smallest area while achieving the highest energy extraction. Since energy efficiency is positively correlated with the amount of harvested energy, this configuration yields optimal performance. The phase difference plays a critical role in modulating fluid dynamic effects, and a 90° phase difference has been shown to maximize the amount of energy that can be extracted from the flow. So, the energy harvesting efficiency of the flapping foils was ideal when the phase difference was 90° [37]. The pitch angular velocity and heave velocity can be calculated using Equations (1) and (2), respectively.

$$\omega (t)={\theta }_0\gamma \mathit{cos}(\gamma t)$$

(3)

$$V_y(t)=H_0\gamma \mathit{cos}(\gamma t+\varphi )$$

(4)

where $\omega (t)$ is the speed of pitch rotation, and ${\theta }_0$ is the pitch rotation angle amplitude. The airfoil pitch axis was set to 1/3 of the chord length to facilitate comparison with the results of [15].

2.2. SBC Parameters

In this study, an SBC model was designed inside a flapping foil that performed heave and pitch motions with an airfoil. For better comparison with [15], the airfoil profile curve used in this study was NACA0015 [38], as shown in Figure 3. In a uniform flow, the effective angle of attack $\alpha$, a physical quantity that changes with time, is defined as

$$\alpha (t)=\mathit{arctan}(-V_y(t)/U_{\infty })-\theta (t)$$

(5)

The corresponding drag and lift coefficients are expressed as

$$C_D={\displaystyle \frac{D}{0.5{\rho }_{\infty }{V}_{\infty }^{2}S}}$$

(6)

$$C_L={\displaystyle \frac{L}{0.5{\rho }_{\infty }{V}_{\infty }^{2}S}}$$

(7)

where ${\rho }_{\infty }$ and V_∞ denote the free-stream density and velocity, respectively, and S denotes the foil planform area.

In this study, the SBC airfoil was designed with an injection slot near the trailing edge and a suction slot near the center, as shown in Figure 5. The injection and suction slots were symmetrically arranged on both sides of the SBC-controlled airfoil. When the SBC on one side generated force, the SBC on the other side remained inactive. The inlet and outlet pipes of the pump were bifurcated, and control was implemented through simulation. The position of the fluid injection was controlled by a solenoid valve (keeping the suction and jet channels on the same side of the airfoil). The time step of the solenoid valve adjustment was 0.5T (where T is the movement period of the flapping foil). A simplified SBC calculation model was used in this study.

The active SBC time on the lower foil surface was 0.0T–0.5T (the first stroke of the flapping foil), and the active time on the upper foil surface was 0.5T–1.0T (the second stroke of the flapping foil). The SBC injection and suction exit speeds were 1.25 times the incoming flow. The injection slot sent a jet opposite to the main flow, and the suction slot was drawn in the same mass flow. Pumps and pipes were arranged inside the airfoil to send air from the suction slot to the injection slot. The SBC positions on the upper and lower foil surfaces were arranged symmetrically to take advantage of the symmetric trajectories of the flapping foil during the first and second strokes. The parameter design and optimization of the SBC are introduced in Section 4.1.

2.3. Efficiency Evaluation

The system energy capture efficiency can be expressed as the ratio of the energy captured by the airfoil motion in a period to the total energy contained in the motion area of the airfoil during the period, expressed as

$$\eta ={\displaystyle \frac{\overline{P}}{P_a}}$$

(8)

For flapping foil energy capture devices, without considering energy loss, the work conducted by the fluid on the system can be represented by the product of the force and displacement. For a fully active flapping foil, the system has two degrees of freedom and corresponding forces (lift corresponds to lifting motion and torque corresponds to rotating motion), as external excitation is not considered. The energy contribution of the lifting motion to the system is $P_y(t)=F_Y(t)V_y(t)$, and that of the pitching motion is $P_{\theta }(t)=M(t)\mathsf{\Omega }(t)$, where $F_Y(t)$ and $M(t)$ are the instantaneous lift and moment, respectively. Thus, the total energy extracted is $P(t)=P_y(t)+P_{\theta }(t)$ or $P(t)=F_Y(t)V_y(t)+M(t)\mathsf{\Omega }(t)$; the average value in a period is $\overline{P}=1/T{\int }_{t_0}^{t_0+T}Pdt$.

The instantaneous energy coefficient $C_{op}(t)$ is introduced as

$$C_{op}(t)={\displaystyle \frac{P(t)}{(1/2)\rho U_{\infty }^{3}c}}$$

(9)

The average value of the instantaneous energy coefficient in a period is expressed as

$${\overline{C}}_{op}={\overline{C}}_{py}+{\overline{C}}_{p\theta }={\displaystyle \frac{1}{T}}{\displaystyle {\int }_{t_0}^{t_0+T}\left\{C_y(t)\frac{V_y(t)}{U_{\infty }}\right.}+\left.C_m(t){\displaystyle \frac{\Omega (t)c}{U_{\infty }}}\right\} \mathrm{dt}$$

(10)

where $C_y(t)=F_Y(t)/((1/2)\rho U_{\infty }^{2}c)$ and $C_M(t)=M(t)/((1/2)\rho U_{\infty }^2{c}^2)$ are the instantaneous lift and moment coefficients, respectively; $U_{\infty }$ is the average velocity of the incoming flow. Similarly to Kinsey and Dumas [15], this study uses the following formula to calculate the system efficiency for fully activating flapping foils:

$$P_a={\displaystyle \frac{1}{2}}\rho U_{\infty }^{3}bd$$

(11)

Thus, to fully activate the flapping foil system, the energy harvesting efficiency can be expressed as the ratio of the energy captured by the airfoil movement in a period to the total energy contained in the airfoil movement area during the period.

$$\eta ={\displaystyle \frac{\overline{P}}{P_a}}={\displaystyle \frac{\overline{P_y}+\overline{P_{\theta }}}{(1/2)\rho U_{\infty }^{3}d}}={\overline{C}}_{op}{\displaystyle \frac{c}{d}},$$

(12)

where d is the overall vertical extent of the airfoil motion considering both heaving and pitching motions, as shown in Figure 2.

The input energy of a group of oscillating aspirators is considered as

$$P_b=\rho V_b^3{l}_{b}b$$

(13)

In Equation (13), $P_b$ is the instantaneous input power of a single oscillating aspirator, $V_b$ is the blowing speed of the oscillating aspirator, and $l_b$ is the length of the blowing surface of the oscillating aspirator. The average power of a single oscillating aspirator in a cycle is expressed as

$$\overline{P_b}={\displaystyle \frac{1}{T}}{\int }_{t_1}^{t_2}\rho V_b^3{l}_{b}b \mathrm{dt}$$

(14)

In Equation (14), t₁ represents the time node at which the oscillating aspirator starts to act in a single cycle, and t₂ represents the time node at which the oscillating aspirator ends. Thus, the net efficiency ${\eta }_{net}$ of the blower can be expressed as

$${\eta }_{net}={\displaystyle \frac{\overline{P}}{P_a+\overline{P_b}}}={\displaystyle \frac{\overline{P_y}+\overline{P_{\theta }}}{(1/2)\rho U_{\infty }^{3}d+\frac{2}{T}{\int }_{t_1}^{t_2}\rho V_b^3{l}_{b}d\mathrm{dt}}}$$

(15)

3. Numerical Method

3.1. Meshing

Fluent commercial software was used to simulate the 2D NACA0015 airfoil equipped with blowing and suction devices to perform pitching and lifting movements. The dynamic mesh and sliding mesh functions in Fluent were utilized to realize these motions. A specific calculation grid is shown in Figure 6. The size of the entire computational domain was $80c\times 70c$, where c is the chord length. The inlet and outlet boundaries were 35c from the rotation center; the upper and lower symmetric boundaries were both 40c from the rotation center; and the length of the side of the central square area was 5c. The radius of the inner circular area was 1.5c.

Two pairs of sliding interfaces were used to realize the lifting movement of the airfoil, and a circular sliding interface was used to realize the pitching movement of the airfoil. During movement, the grid in the central rectangular area traveled up and down as a rigid body. The dynamic layering model updated the horizontal solid line, and the circular area grid rotated around its axis while moving upward and downward.

High-resolution 2D unsteady computations were carried out using a Fluent finite-volume solver at low Reynolds numbers [5]. Unsteady laminar 2D numerical simulations were performed at Reynolds numbers of 550, 1100, and 2200. The one-equation Spalart–Allmaras turbulence model is very stable; the parameters selected were the same as those used in [15,39,40], with a Reynolds number of 10,000 being used in this study.

A second-order accurate upwind scheme and second-order central differencing scheme were used to discretize the convection and diffusion terms, respectively. To discretize time, a second-order accurate backward implicit scheme was used. The velocity–pressure coupling was based on the Semi-Implicit Method for Pressure-Linked Equations (SIMPLE) segregated algorithm. A velocity inlet was used for the suction and blowing slots with the user-defined function (UDF), and the movement of the hydrofoil was controlled using a UDF. We used CURRENT_TIME to control the time sequence, and the moment reference point was defined based on the time-varying heave displacement. The suction and blowing control method was implemented using a piecewise logic combined with periodic control.

3.2. Validation of Computation

Numerical simulations were conducted using the mesh distribution and boundary conditions shown in Figure 4, with variations in mesh density and time step size to assess the feasibility of the mesh configuration and the numerical scheme, as well as to evaluate the temporal independence of the results. The simulations employed a NACA0015 airfoil with the following flapping and flow parameters: Reynolds number Re = 1100, $f*=fC/U_{\infty }=0.14$, ${\theta }_0=76.33^{°}$, $H_0/c=1$, and $X_p/c=1/3$. These settings are consistent with those used by Kinsey and Dumas [5] and Cho and Zhu [41]. Three time step sizes were tested: $t=T/600$, $t=T/1000$, and $t=T/2000$. The numerical results and their comparisons with those reported by Kinsey and Dumas [5] and Cho and Zhu [41] are summarized in

Table 1. Comparison of results from this study with results from previous studies.

	Mesh	Time Step	$\mathit{\eta }$
Kinsey and Dumas [5]	72,000		0.337
Cho and Zhu [41]		t = T/1000	0.331
This study	36,046	t = T/1000	0.340
	100,911	t = T/600	0.338
		t = T/1000	0.339
		t = T/2000	0.340
	327,248	t = T/1000	0.341

. As shown, the simulations exhibit good independence with respect to both mesh density and time step. Compared to Kinsey and Dumas [5], the relative errors in all key parameters are within 1%, and they are within 3% when compared to Cho and Zhu [41]. The $C_x$, $C_y$, $C_M$, and the energy extraction efficiency $\eta$ at the fifth flapping cycle were also compared with the results of Kinsey and Dumas [5], as illustrated in Figure 7. The instantaneous values throughout the cycle demonstrate a high level of agreement with the reference data, further validating the reliability of the adopted mesh configuration and numerical methodology. Considering that active suction and blowing will be applied in subsequent studies, the mesh with 107,500 elements and a time step of $t=T/1000$ was selected for the following simulations. The names of each mesh subdomain are shown in Figure 8, and the corresponding mesh element counts are listed in

Table 2. A mesh resolution table showing the number of elements in each zone.

Zone	Center	Left	Right	Top	Bottom	Middle
Element	7000	31224	29747	11472	11472	9996

.

4. Results and Discussion

This study used the previously described methods to investigate the effect of the SBC method on the energy harvesting performance of the flapping foil. The results were compared to those of Kinsey and Dumas [15]. The NACA0015 airfoil was used in all simulations.

4.1. Geometric Design Influences Energy Extraction Efficiency

In this study, a reduced frequency of $f*=fC/U_{\infty }=0.14$, a pitch angle amplitude of ${\theta }_0=76.33^{°}$, and a Reynolds number of 1100 were employed for the SBC-equipped airfoil. The incoming flow velocity was set to 0.16 m/s (the airfoil chord length was set at 0.1 m) such that the Reynolds number was 1100 and the SBC injection and suction exit velocity was 0.2 m/s. The other parameters were controlled to observe the changes in the power coefficient of the flapping foils, as shown in Figure 9.

To explore the effects of geometric variations, the lift-based power coefficient and energy harvesting efficiency were numerically evaluated by altering the position, orientation, and width of the injection and suction slots, with the results summarized in

Table 3. Design parameters.

Factor Level	A. Suction Slot Position (Distance to Airfoil Leading Edge)	B. Injection Slot Position	C. Width of Slot	D. Angle of Suction Slot (Counter-Clockwise Is Positive)	E. Angle of Injection Slot
1	0.50c	0.71c	0.005c	−3	−9
2	0.54c	0.75c	0.007c	0	−6
3	0.58c	0.79c	0.009c	3	−3
4	0.62c	0.83c	0.011c	6	0
5	0.66c	0.87c	0.013c	9	3
6	0.70c	0.91c	0.015c

. The mathematical tool SPSS (IBM SPSS Statistics 26.0) [42] was used to establish an orthogonal table to simulate the lift power output coefficient and efficiency of the flapping foils with different parameters, as shown in

Table 4. Orthogonal optimization tests.

NO.	A	B	C	D	E	$\overline{{\mathit{C}}_{\mathit{p}\mathit{y}}}$	η
1	5	1	1	1	2	0.883	0.370
2	5	5	3	5	3	0.928	0.385
3	2	3	1	2	1	0.881	0.374
4	4	1	1	3	4	0.886	0.372
5	6	1	2	4	3	0.904	0.378
6	1	2	3	1	4	0.907	0.386
7	4	5	1	2	2	0.881	0.366
8	1	3	3	1	1	0.912	0.387
9	3	1	5	2	3	0.886	0.379
10	6	5	5	1	4	0.954	0.390
11	6	3	1	5	5	0.884	0.367
12	3	1	3	2	2	0.911	0.396
13	3	6	1	4	4	0.873	0.366
14	1	5	2	2	1	0.895	0.378
15	4	4	6	4	1	0.936	0.400
16	3	3	2	3	2	0.902	0.383
17	1	6	4	5	2	0.925	0.384
18	1	3	5	4	2	0.942	0.389
19	1	1	6	3	5	0.930	0.391
20	1	2	1	3	3	0.876	0.372
21	1	6	2	2	1	0.890	0.376
22	1	4	1	2	3	0.876	0.371
23	3	2	1	5	1	0.881	0.374
24	6	2	6	2	2	0.954	0.393
25	2	6	6	1	3	0.950	0.404
26	3	5	6	1	1	0.946	0.406
27	6	4	3	3	1	0.921	0.380
28	3	4	4	1	5	0.943	0.401
29	4	2	2	1	2	0.912	0.385
30	5	4	1	2	2	0.883	0.367
31	1	1	6	5	2	0.901	0.376
32	2	1	1	1	1	0.877	0.375
33	5	2	4	4	1	0.932	0.394
34	5	6	5	3	1	0.963	0.396
35	1	1	4	2	4	0.921	0.387
36	1	1	1	1	1	0.875	0.372
37	1	5	1	4	5	0.876	0.371
38	6	6	1	1	2	0.871	0.359
39	2	1	3	4	2	0.898	0.387
40	5	1	2	1	5	0.907	0.381
41	2	2	5	2	5	0.930	0.396
42	4	1	5	5	1	0.907	0.391
43	5	3	6	2	4	0.960	0.401
44	2	4	2	5	4	0.899	0.383
45	4	6	3	2	5	0.925	0.384
46	6	1	4	2	1	0.948	0.396
47	4	3	4	1	3	0.954	0.404
48	1	4	5	1	2	0.942	0.392
49	2	5	4	3	2	0.928	0.396

.

The effects of various geometric parameters on the average lift power coefficient and efficiency η of the flapping foil are shown in Figure 10 and Figure 11. The position of the suction slot (A), the position of the injection slot (B), the width of the slot (C), the angle of the suction slot (D), and the angle of injection slot E affect the average lift coefficient and energy harvesting efficiency of the flapping foil. Among these, the slot width (C) has the most pronounced impact, highlighting the crucial role of momentum variation induced by the SBC jet in enhancing performance. The sensitivities of the geometric parameters to the lift power coefficient were ranked as C > A > B > D > E; the sensitivities of the geometric parameters to efficiency were ranked as C > A > D > B > E. The variation trends of the position of the suction slot (A), the position of injection slot B, the angle of the suction slot (D), and the angle of injection slot E in the lift power coefficient and efficiency of a flapping foil are different and can be selected in actual engineering applications.

The parameter combination that created the largest lift power coefficient was A5B3C6D1E4; the combination leading to the highest efficiency was A2B3C6D1E1.

Table 5. The average lift power coefficients and efficiencies for the optimal parameter combinations and the original foil.

	$\overline{{\mathit{C}}_{\mathit{p}\mathit{y}}}$	η
Original NACA0015	0.820	0.338
A5B3C6D1E4	0.820	0.399
A2B3C6D1E1	0.956	0.407

presents the average lift power coefficients and efficiencies for the optimal parameter combinations. The maximum average lift power coefficient of the flapping foils was 0.956, and the maximum efficiency was 40.7%. The power coefficient of the lift can determine the optimal efficiency range of the flapping foil turbine, indicating that lift plays a decisive role in the efficiency contribution.

4.2. Potential Mechanism to Improve Flapping Foil Energy Harvesting Efficiency

The variation in the instantaneous power coefficient $C_p$ of the SBC flapping foil and original foil in a cycle are shown in Figure 12. The instantaneous power coefficient $C_p$ of the flapping foil exhibits two peaks in a half-cycle. The first and second strokes of the power coefficient of the flapping foil are symmetrical. The improvement due to the SBC reached its maximum when the power coefficient of the flapping foil was at its maximum.

Figure 13 presents the changes in lift coefficient $C_y$, moment coefficient $C_M$, and power coefficient of the flapping foil in one cycle. The lift of the SBC flapping foil was higher than that of the original flapping foil at different times, which improved the total lift power coefficient $C_{py}$ of the flapping foil (the lift force of the flapping foil was highly consistent with the heave motion). The peak torque power coefficient of the SBC flapping foil was improved compared to that of the original flapping foil; the torque performed more positive work over the cycle. This overall enhancement aligns with the expectations.

The vortex flow fields of the original and SBC airfoils at various time instants are shown in Figure 14. A comparison of the transient vortices reveals that the SBC airfoil generates stronger vortices that remain closer to the airfoil surface. This increased vortex strength significantly contributes to the lift enhancement of the flapping foil, as previously demonstrated in Figure 13 through the comparison of lift coefficients. Figure 14b,c were used to study the transient vortex at two instants, t/T = 0.48 and t/T = 0.50. The results indicate that the SBC method effectively delays flow separation and enhances vortex attachment along the airfoil surface. Figure 14a,d show two instants when the flapping foil reciprocates. The SBC operating mode (the lower surface of the airfoil activates the jet during the descending stroke of the flapping foil, and the upper surface of the airfoil activates the jet during the upward stroke of the flapping foil) adapted to the transient vortex changes. In addition, the jet direction strengthens the vortex at different times and positions, as shown in Figure 14e. As a result of the SBC mechanism, the vortex strength around the flapping foil increases, which is clearly evident from the vorticity peak values shown in Figure 14. Owing to the SBC mechanism, it is believed that the flapping foil vortex increased. This can be clearly observed from the specific vorticity peak values presented in

Table 6. The vorticity of each vortex.

Vortex Name	Vorticity
a	81.87
b	100.00
c	38.30
d	55.82
e	43.32
f	63.15
g	35.83
h	79.59
i	40.42
j	57.37
k	60.98
l	90.25
m	110.92
n	73.83
o	90.20

. Compared to the original airfoil, the airfoil equipped with the suction and blowing device exhibits a 20% increase in the vorticity magnitude of the corresponding vortex. As shown in Figure 14, the vortices that influence the pressure difference between the upper and lower surfaces of the airfoil are located closer to the surface in the controlled case, indicating a more pronounced effect on the flow characteristics near the upper surface of the airfoil.

A comparison of the surface pressure coefficients of the original and SBC airfoils at different moments is shown in Figure 15, indicating changes in the vortex and lift. The static pressure coefficient is defined as $C_{ps}=(p_s-p_0)/0.5\rho U_{\infty }^2$, where $p_s$ is the local static pressure and $p_0$ is the reference pressure. The SBC airfoil surface pressure gap was greater than that of the original airfoil; the surface pressure at different times revealed that the SBC airfoil lift was greater than that of the original airfoil.

At t/T = 0.28, the pressure coefficient on the lower surface of the SBC airfoil was higher than that of the original airfoil. This is also observed from the position and intensity of the leading-edge vortex, as shown in Figure 14a. At this time, there was no large pressure differential on the upper airfoil surface, and the SBC did not result in a significant pressure change for the upper airfoil surface (no vortex was generated).

The flapping foil was about to move to the horizontal position at t/T = 0.48, resulting in drastic changes in the pressure on the upper and lower surfaces of the airfoil, which required shedding of the vortex under the flap surface of the foil. At this time, the vortex reached the airfoil tail and was strengthened by the SBC such that the tail of the lower airfoil had greater surface pressure than the original airfoil (as illustrated in Figure 15). As shown in the lift coefficient plot over one cycle in Figure 13, at t/T = 0.48, both the original airfoil and the airfoil equipped with the suction and blowing device reach their maximum lift coefficient within the cycle. At this moment, two primary vortices are present on the lower surface of the airfoil. For the airfoil with suction and blowing, the vorticity of both vortices is higher than that of the original airfoil. Moreover, vortex f sheds more slowly compared to vortex d, remaining attached to the lower surface for a longer duration. This results in a larger and more sustained pressure difference between the upper and lower surfaces of the airfoil, thereby leading to a higher lift coefficient. At t/T = 0.82, the SBC impacted the upper airfoil surface such that it had greater surface pressure than the original airfoil. This feature is the reason for the increase in lift of the flapping foil in the 0.5T–1.0T period.

4.3. Effect of Reynolds Number on Energy Harvesting Efficiency

Figure 16 presents the energy harvesting efficiencies of the SBC and original airfoils at Reynolds numbers of 550, 1100, 2200, and 10,000. These represent the energy harvesting efficiencies of flapping foils in laminar and turbulent flows. It is evident that the SBC enhances the flapping foil energy harvesting efficiency (η) at low Reynolds numbers. The lifting performance of the SBC for flapping foils in laminar flows is higher than that in turbulent flows; thus, this study mainly focused on the energy harvesting efficiency for laminar flows.

The efficiency improvements of the SBC airfoil in laminar flow are shown in Figure 17. When the dimensionless reduced frequency ranges from 0.12 to 0.16, the energy harvesting efficiency of the SBC airfoil is promising. The optimal working area is the same as that of the original. The energy harvesting efficiency of the SBC airfoil also improved with an increase in the Reynolds number; the maximum efficiency was 42.6%. An increase in the Reynolds number can increase the energy harvesting efficiency of the SBC and original airfoils, but the efficiency improvement of the SBC is more pronounced.

As shown in the mappings, the efficiency enhancement achieved by the SBC becomes increasingly evident as the reduced frequency decreases. The improvement becomes more prominent with an increase in the Reynolds number. Compared with the original airfoil, the maximum increase in efficiency Δη reached 76.0%. Compared with other flow control methods, the efficiency gains obtained by SBC are notable. Given that real-world flow field conditions are often variable and difficult to control, the ability of the SBC to improve energy harvesting performance across a range of Reynolds numbers and reduced frequencies is particularly advantageous for practical applications.

Figure 18 shows a comparison of the energy harvesting characteristics of the SBC and original airfoils at Reynolds numbers of 550 and 2200 (the reduced frequency at which the flapping foil energy harvesting efficiency was at its maximum was selected). At various Reynolds numbers and time instants, the lift of the SBC airfoil was higher than that of the original lift. As the Reynolds number increased, the SBC increased the lift of the flapping foil. The envelope area of the lift power coefficient curve of the SBC airfoil at different Reynolds numbers was larger than that of the original airfoil. The SBC does not change the characteristics of the lift and lift power coefficients but increases their values at different times.

The SBC enhanced the moment coefficient of the airfoil at different times, significantly increasing the peak values. As the Reynolds number increased, the SBC increased the flapping foil torque. A comparison of the torque power coefficients indicated that the torque can perform both positive and negative functions. At different Reynolds numbers, the peak value of $C_{pM}$ can be improved by SBC.

As shown in Figure 19 and Figure 20, the instantaneous vorticity and pressure contours for the original airfoil and the airfoil with suction and blowing control (SBC) are presented at Re = 550 and Re = 2200. At the lower Reynolds number, the vortex on the lower surface of the SBC-controlled airfoil exhibits a higher vorticity compared to that of the original airfoil, as evidenced by the vorticity values listed in

Table 7. Vorticity of each vortex.

Vortex Name	Vorticity
a	26.79
b	20.82
c	31.62
d	22.89
e	186.26
f	130.51
g	236.95
h	141.77

. Furthermore, this vorticity increases with the Reynolds number, and the difference in vorticity between the SBC and original airfoils becomes more pronounced as the Re increases. From Figure 19, it can be observed that the vortices on the SBC-controlled airfoil remain closer to the foil surface. This increase in vorticity, combined with the proximity of the vortices to the airfoil surface, leads to a more substantial influence on the local flow field—an effect that is clearly reflected in the pressure distributions shown in Figure 20. In Figure 20, the low-pressure regions correspond to the areas where vortices are present. Compared to the original airfoil, the SBC-controlled airfoil exhibits a larger low-pressure region on the lower surface, with the core of the low-pressure zone being positioned closer to the surface. This results in a greater pressure difference between the upper and lower surfaces, thereby generating higher lift. Consequently, the SBC-controlled airfoil demonstrates improved energy harvesting performance at low Reynolds numbers. Additionally, by comparing the vortex dynamics at the two Reynolds numbers, it is evident that the vortices shed more slowly in the SBC case. This delayed vortex shedding extends the duration of vortex influence on the airfoil surface, which is particularly beneficial for flapping foils that rely on vortex-induced lift for energy harvesting.

4.4. Effect of Pitch Angle Amplitude on Energy Harvesting Efficiency

Figure 21 illustrates the power extraction efficiencies of the SBC airfoils and original NACA0015 at different pitch amplitudes. The flapping foil exhibited similar energy harvesting characteristics at different pitch amplitudes with and without SBC. However, the efficiency improvements provided by SBC varied depending on the pitch amplitude. The maximum energy harvesting efficiency of the SBC airfoil was achieved within the optimal pitch amplitude range of 70–90°.

The energy harvesting efficiencies of the SBC and original airfoils at different reduced frequency and pitch amplitudes are shown in Figure 22. Both the SBC and original airfoils exhibit optimal working areas, but the positions of these regions are slightly different. The optimal working region for the SBC-modified airfoil is shifted to the left of that for the original airfoil, indicating that a moderate reduction in the reduced frequency is favorable for the performance of the SBC.

In addition, the efficiency of the SBC airfoil is high, indicating that the SBC can significantly improve the energy harvesting efficiency of the flapping foil. When the pitch amplitude was 70–90°, both the SBC and original airfoils were in the optimal working area. In addition, the optimal pitch amplitude of the flapping foil was not affected by the change in Reynolds number. The SBC airfoil had the same characteristics as the original airfoil at different pitch amplitudes. The pitch amplitude of the flapping foil was not affected by SBC, and the use of suction and blowing did not alter the effective angle of attack of the flapping foil. However, the optimal reduced frequency range of the flapping foil was shifted to a lower value, suggesting an increase in the effective flow velocity achieved during operation. At a low Reynolds number, the flapping frequency is slower, and the flapping foil controlled by SBC takes advantage of the fact that the flapping foil is friendly to the flow field environment. In addition, the SBC can improve the energy harvesting efficiency of flapping foils for different pitch amplitudes and attenuation frequencies; thus, the application of the SBC method can deliver great benefits.

5. Conclusions

This study investigated the enhancement of energy harvesting efficiency in flapping foils at low Reynolds numbers through the application of suction and blowing control (SBC). The parameters of the SBC airfoil were compared with those of the same airfoil without SBC. For a given SBC outlet flow rate and operating condition, the optimal SBC position and placement angle explain the possible SBC mechanism.

An investigation of the energy harvesting efficiency of a flapping foil with SBC was conducted in laminar and turbulent flows. The results reveal that SBC performs better for flapping foils in laminar flows than in turbulent flows. Moreover, SBC was found to improve efficiency at low reduced frequencies, indicating that a proper reduction in the reduced frequency favors SBC performance. Overall, SBC contributed positively to energy harvesting efficiency across different attenuation frequencies and pitch amplitudes.

The conclusions of this study are summarized as follows:

(1)

The SBC position significantly influences the energy harvesting efficiency of the flapping foil. The SBC significantly increases both the lift force and torque, with the primary improvement mechanism being the enhancement of lift. Flow field analysis revealed that SBC strengthens vortex structures at various phases of the flapping cycle and brings them closer to the airfoil surface, thereby leveraging foil motion to improve energy extraction.

(2)

In laminar flows, the energy harvesting efficiency of the SBC airfoil increases with the Reynolds number and decreases with reduced frequency. At a Reynolds number of 2200, the maximum efficiency of the flapping foil with the SBC airfoil reached 42.6%, which is a 76.0% increase compared to that of the original airfoil.

(3)

SBC effectively enhances energy harvesting efficiency over a range of pitch amplitudes and attenuation frequencies. Both the SBC and original airfoils exhibited similar performance characteristics across different pitch amplitudes, with the optimal pitch amplitude range identified as 70–90°.