Investigation of the Effect of Vortex Generators on Flow Separation in a Supersonic Compressor Cascade
Abstract
1. Introduction
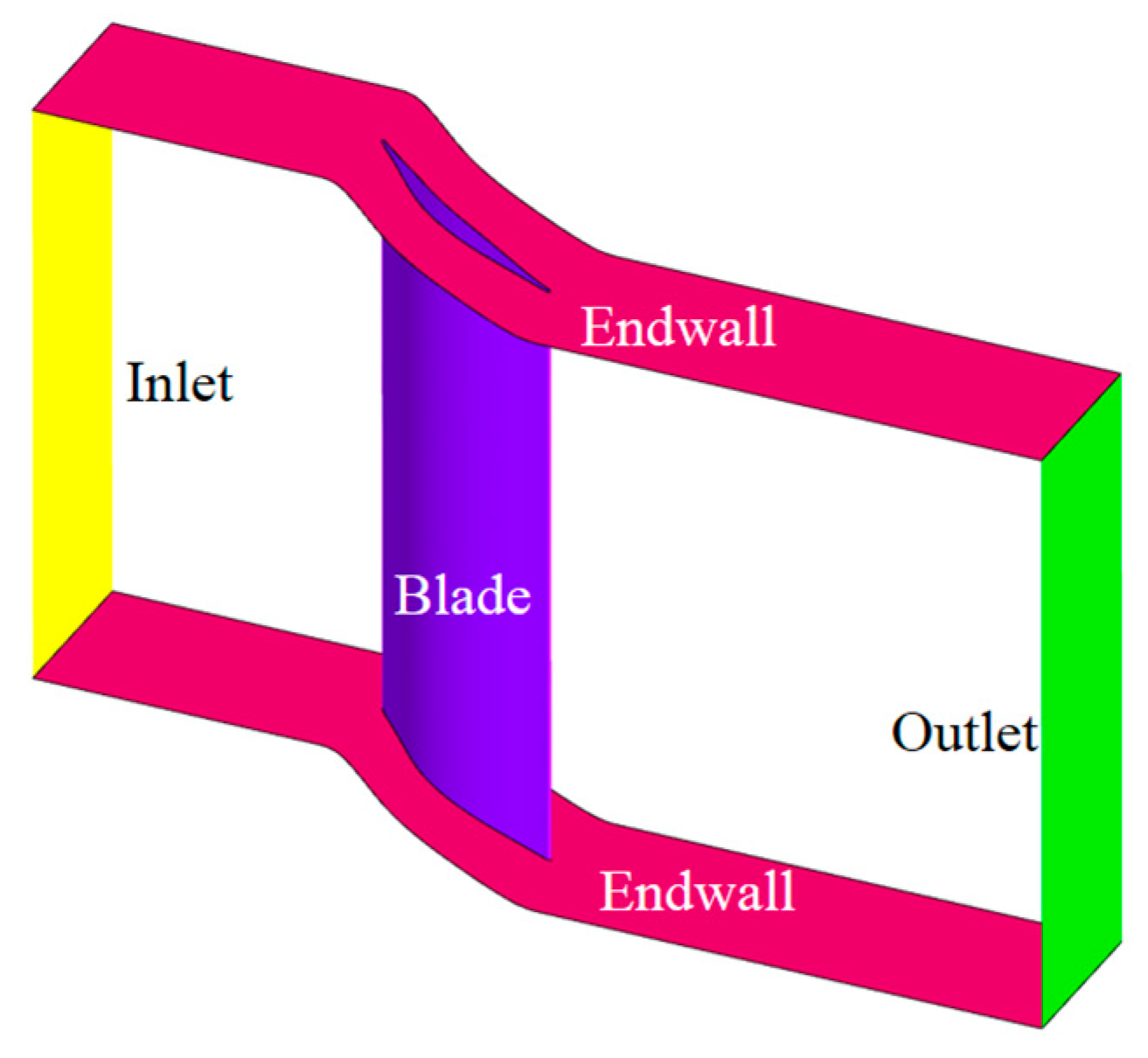
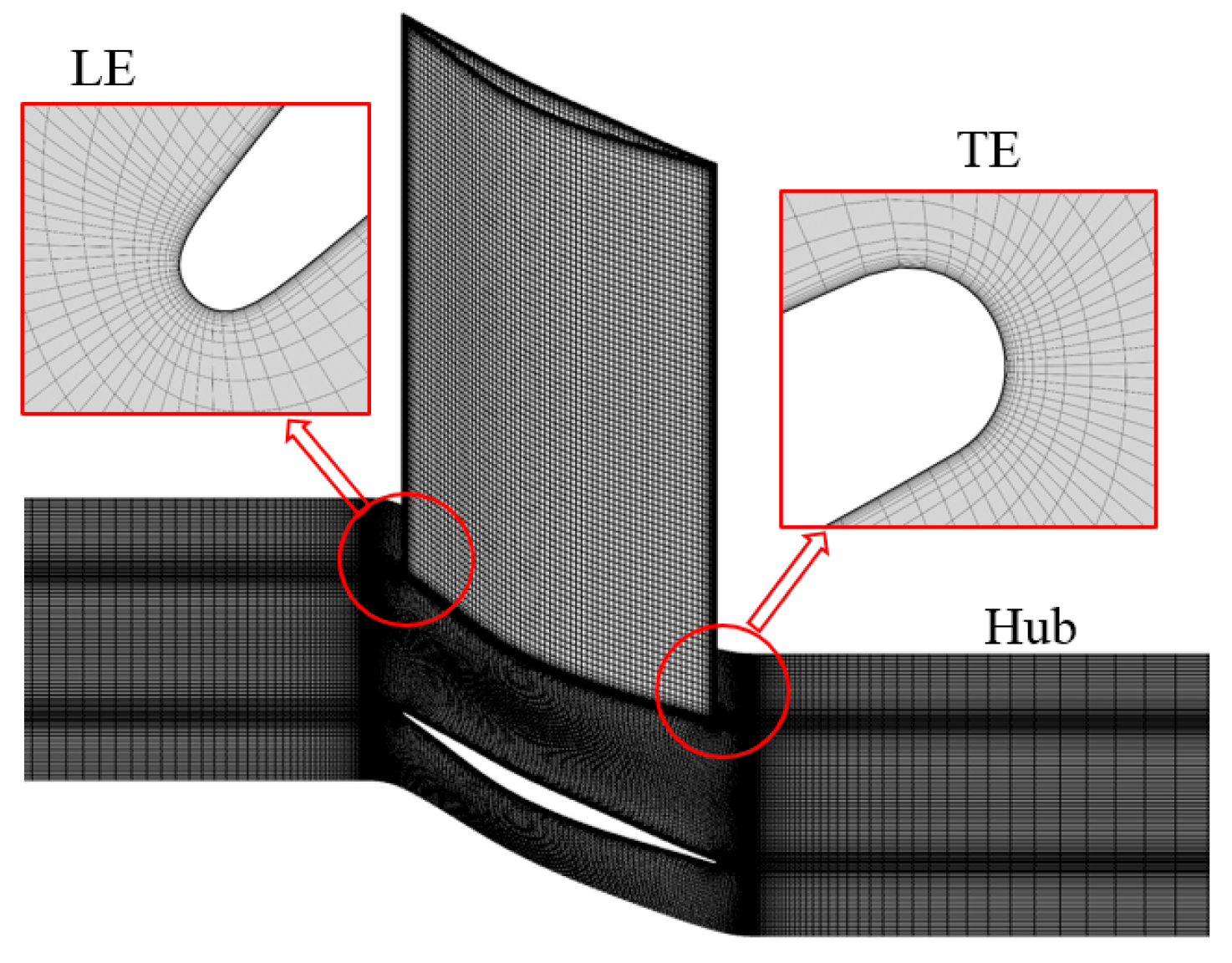
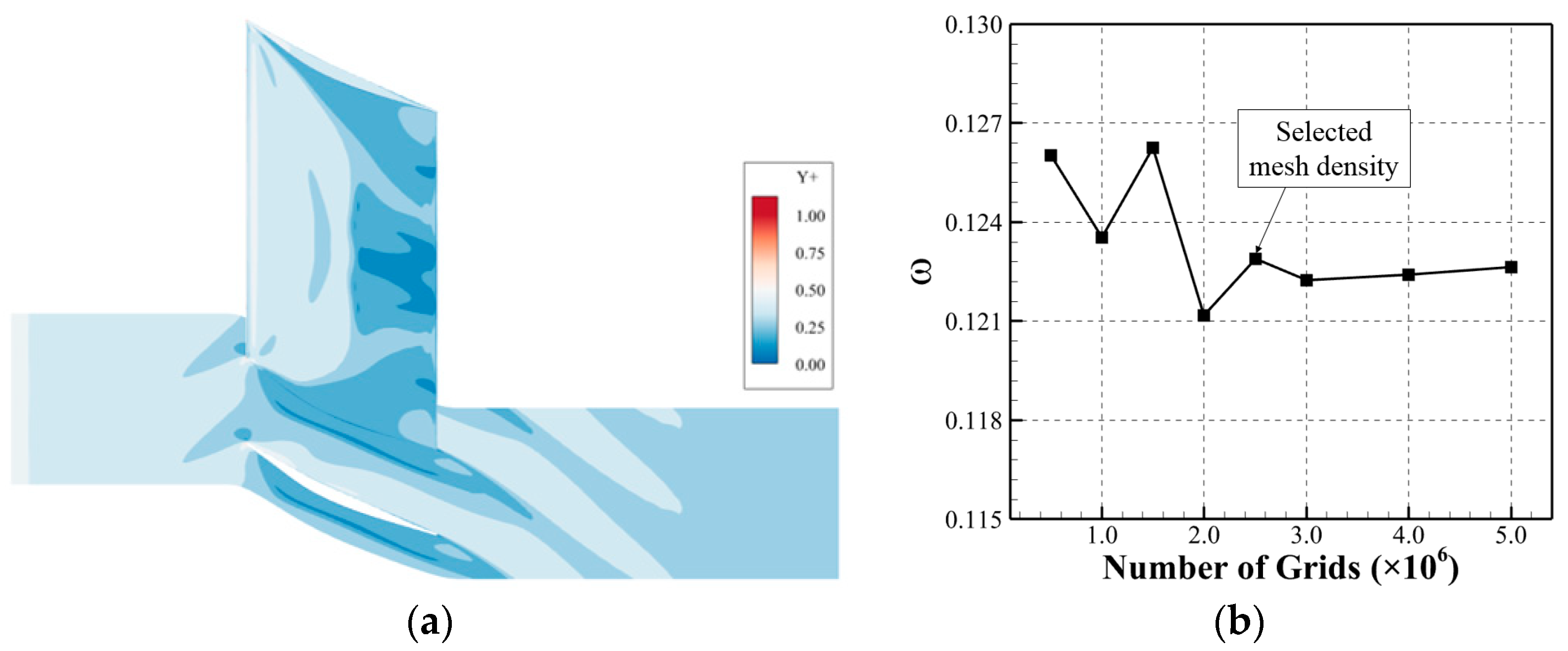
2. Geometrical and Aerodynamic Parameters
3. Geometrical and Aerodynamic Parameters
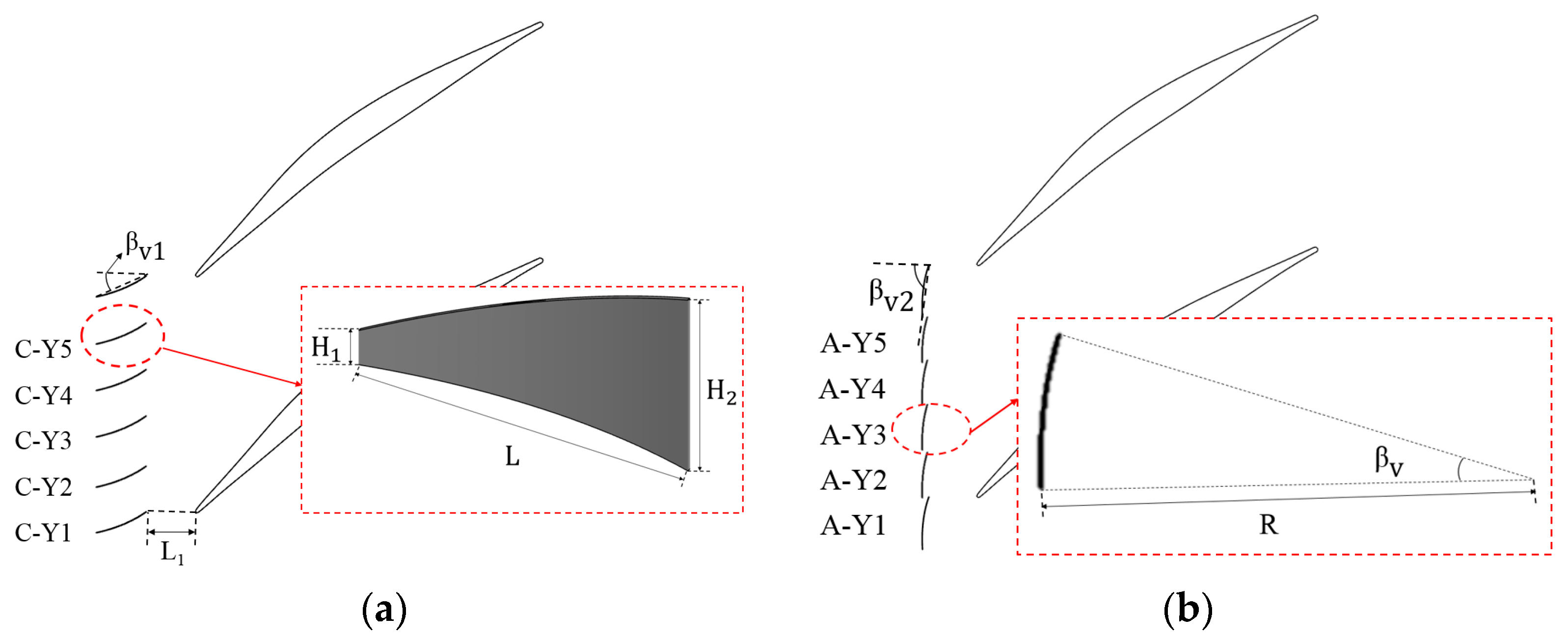
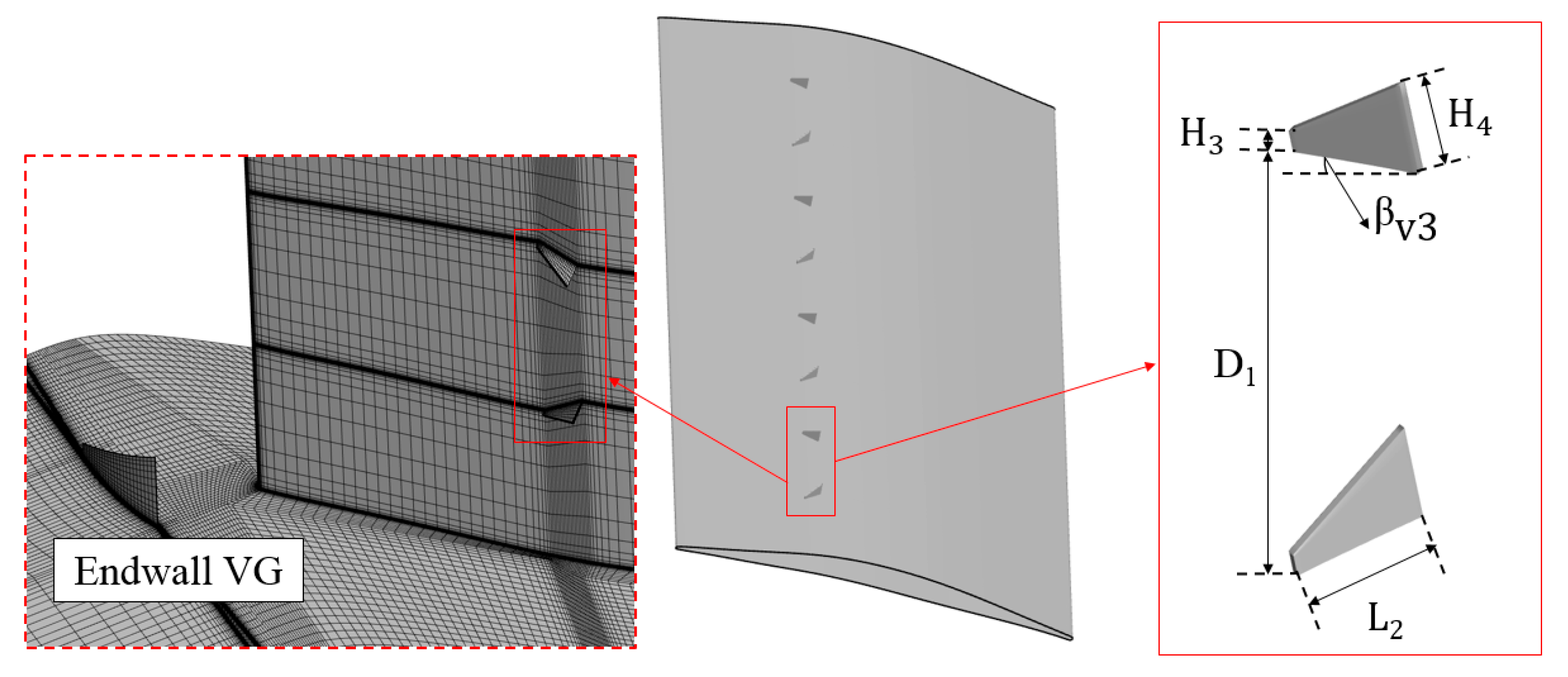
4. Design of Vortex Generator
5. Effect of Vortex Generator on the Corner Separation of the Supersonic Compressor Cascade
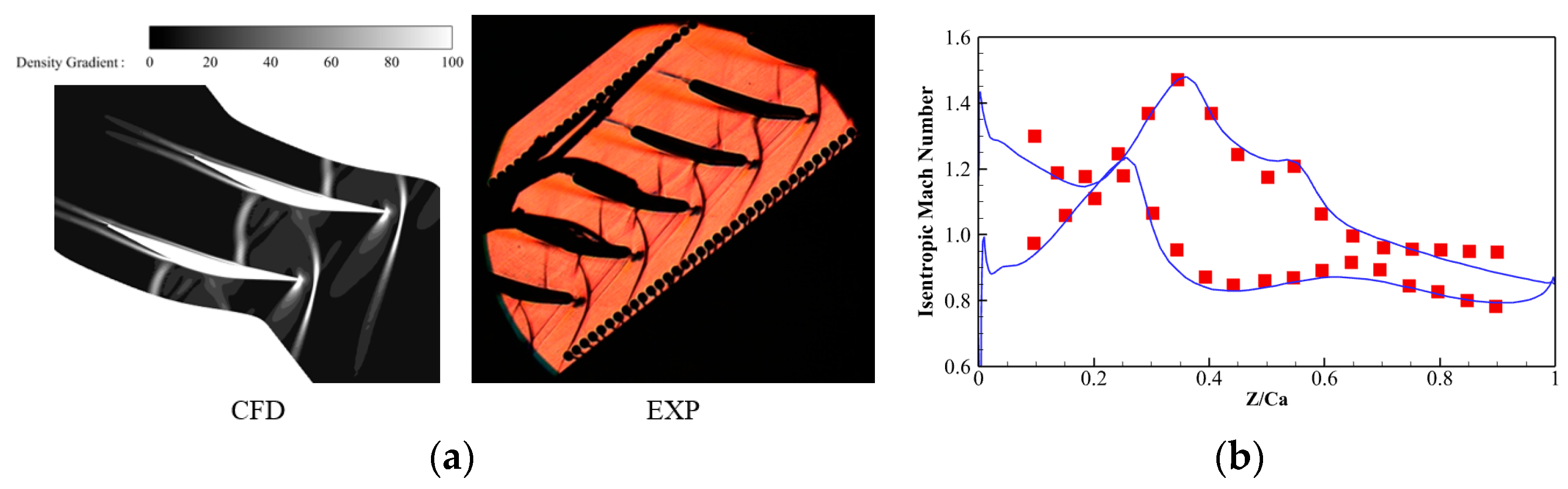
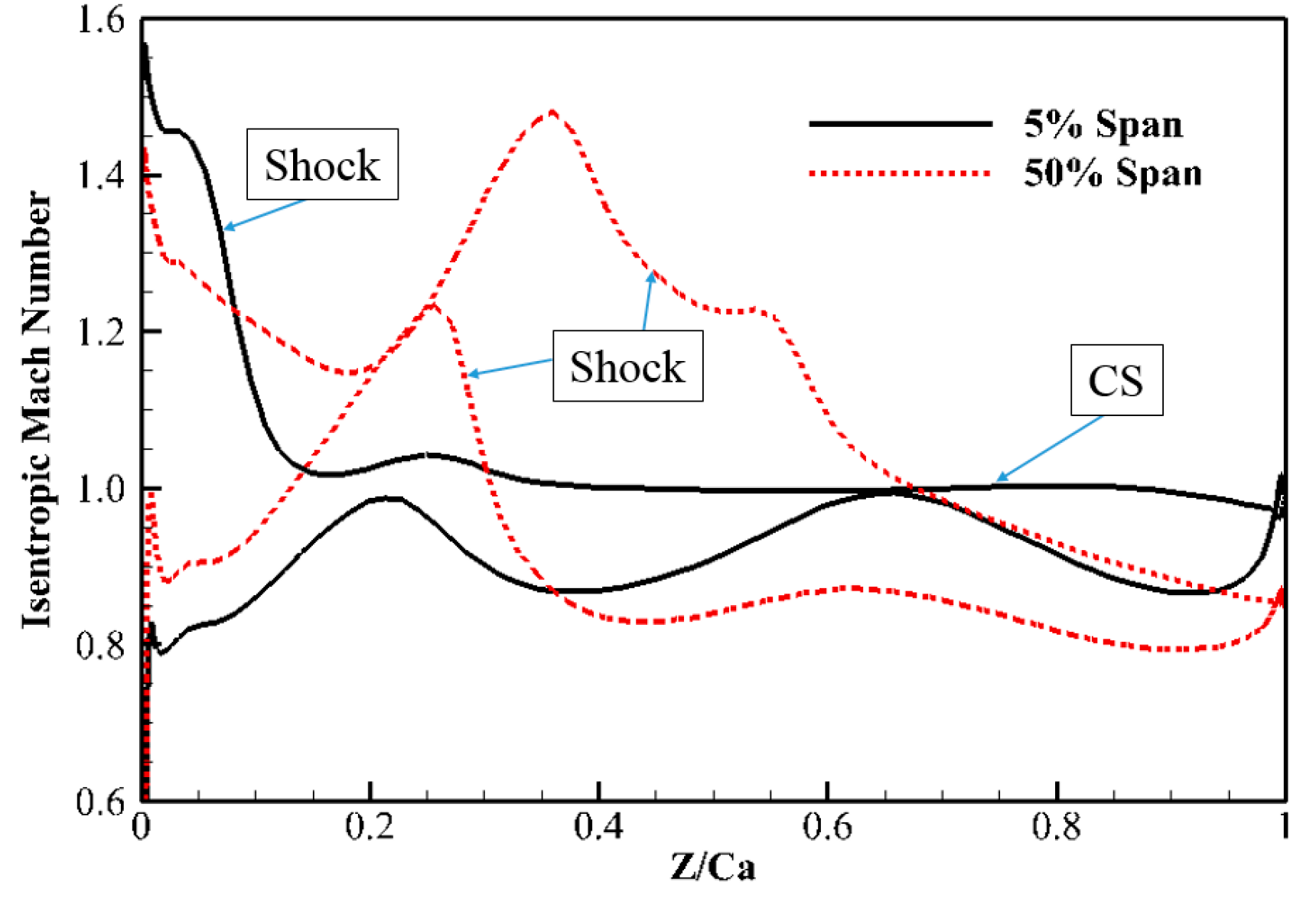
5.1. Flow Fields of Baseline Supersonic Compressor Cascade
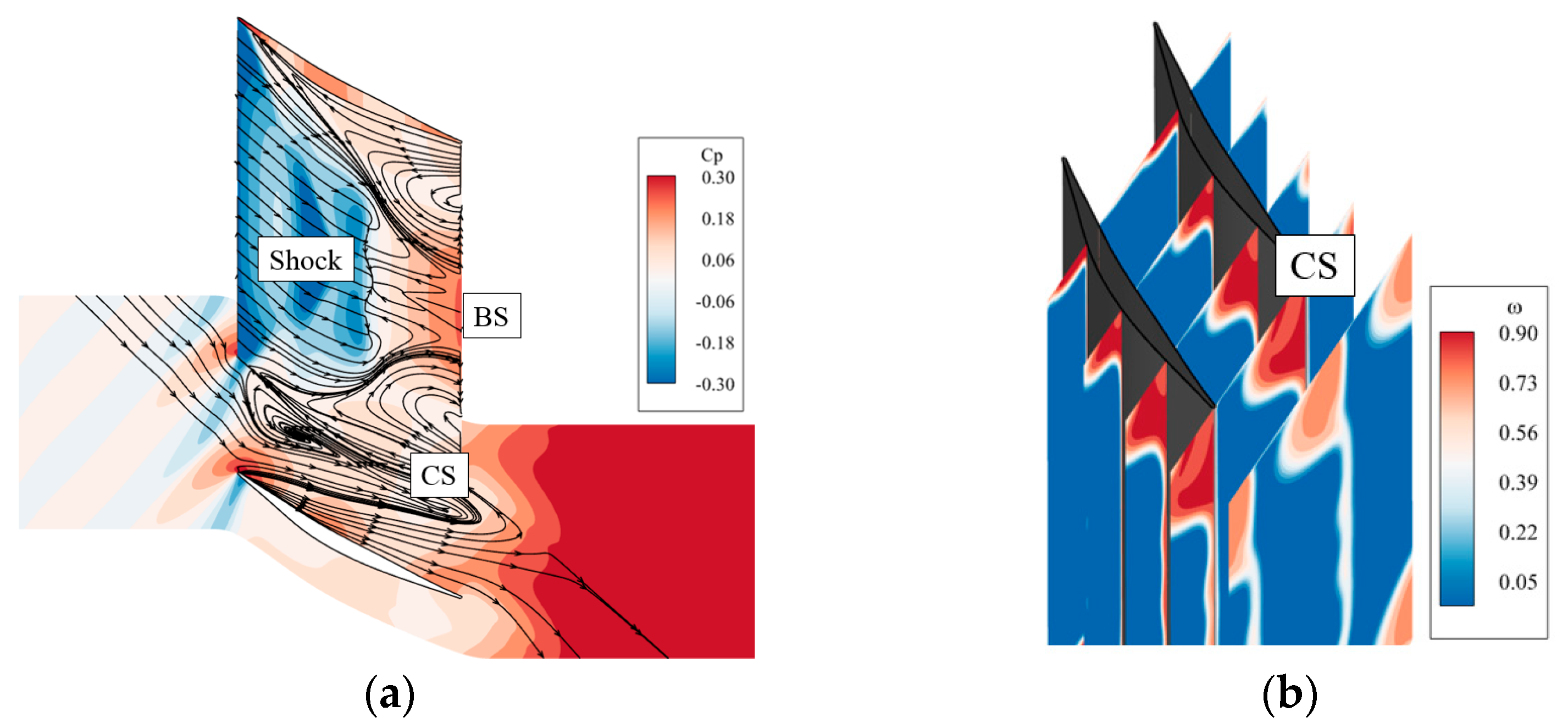
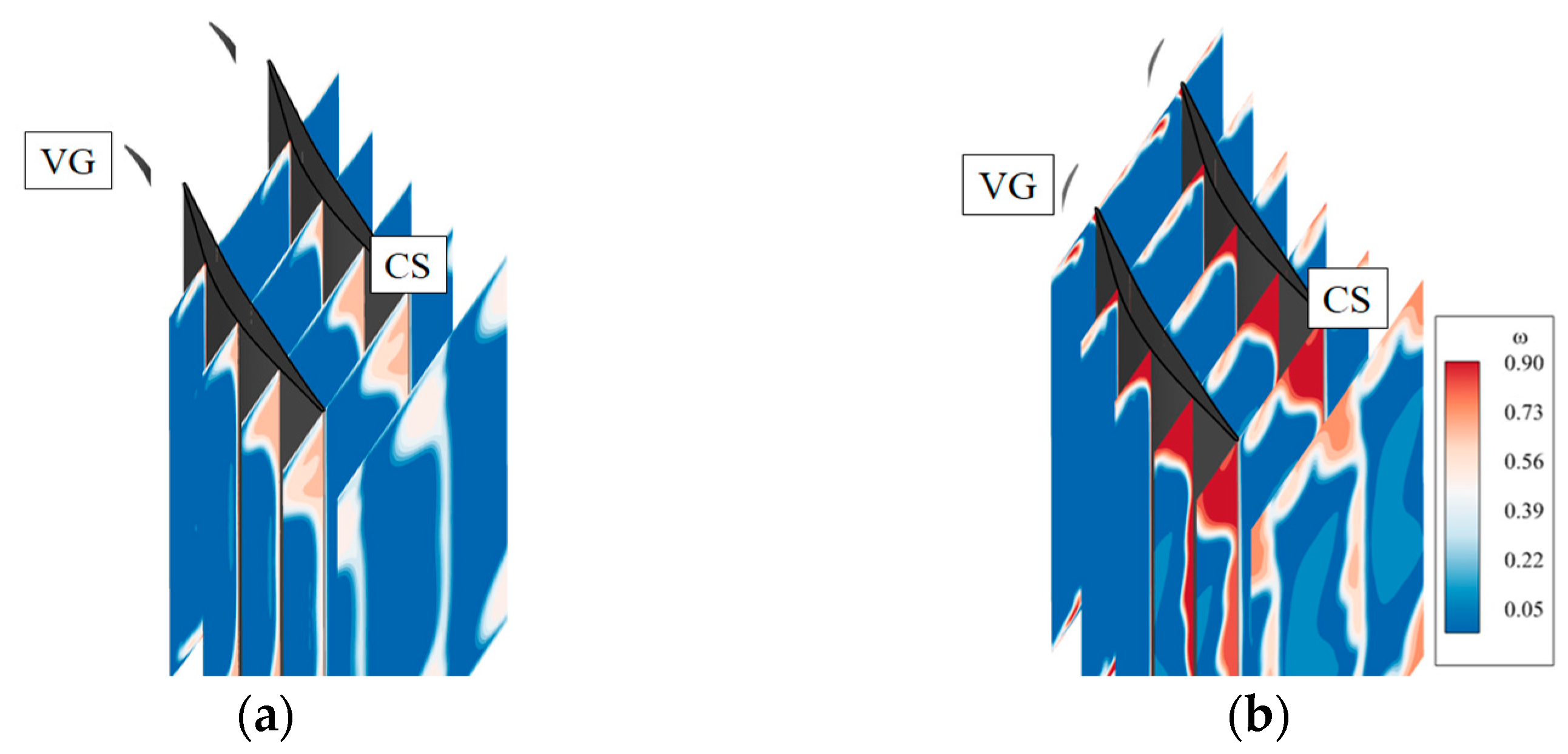
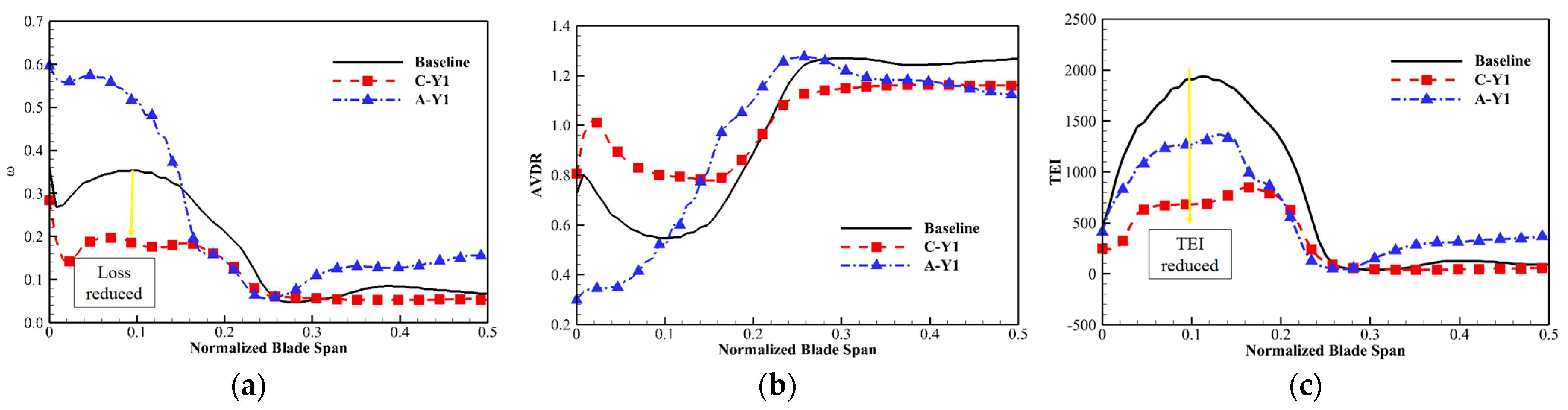
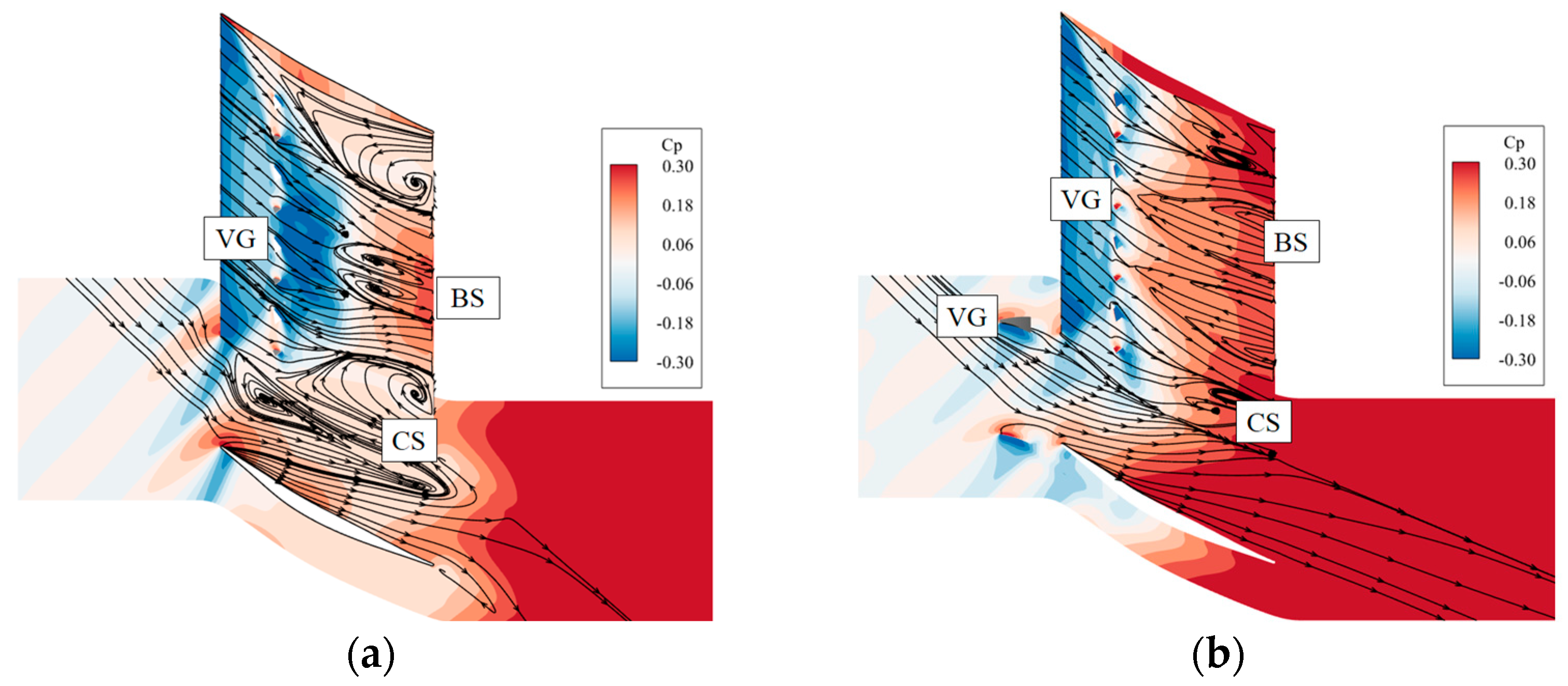
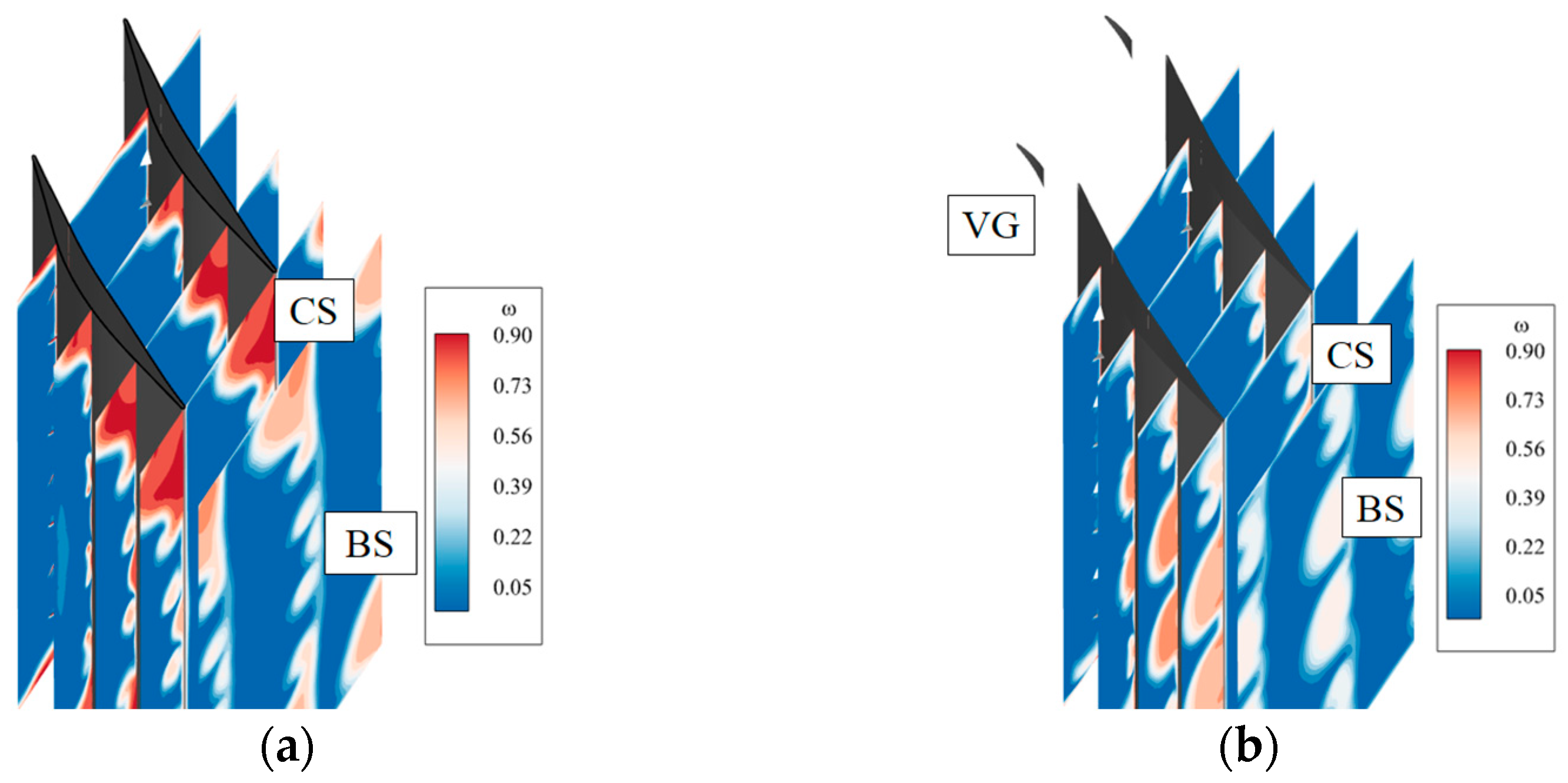
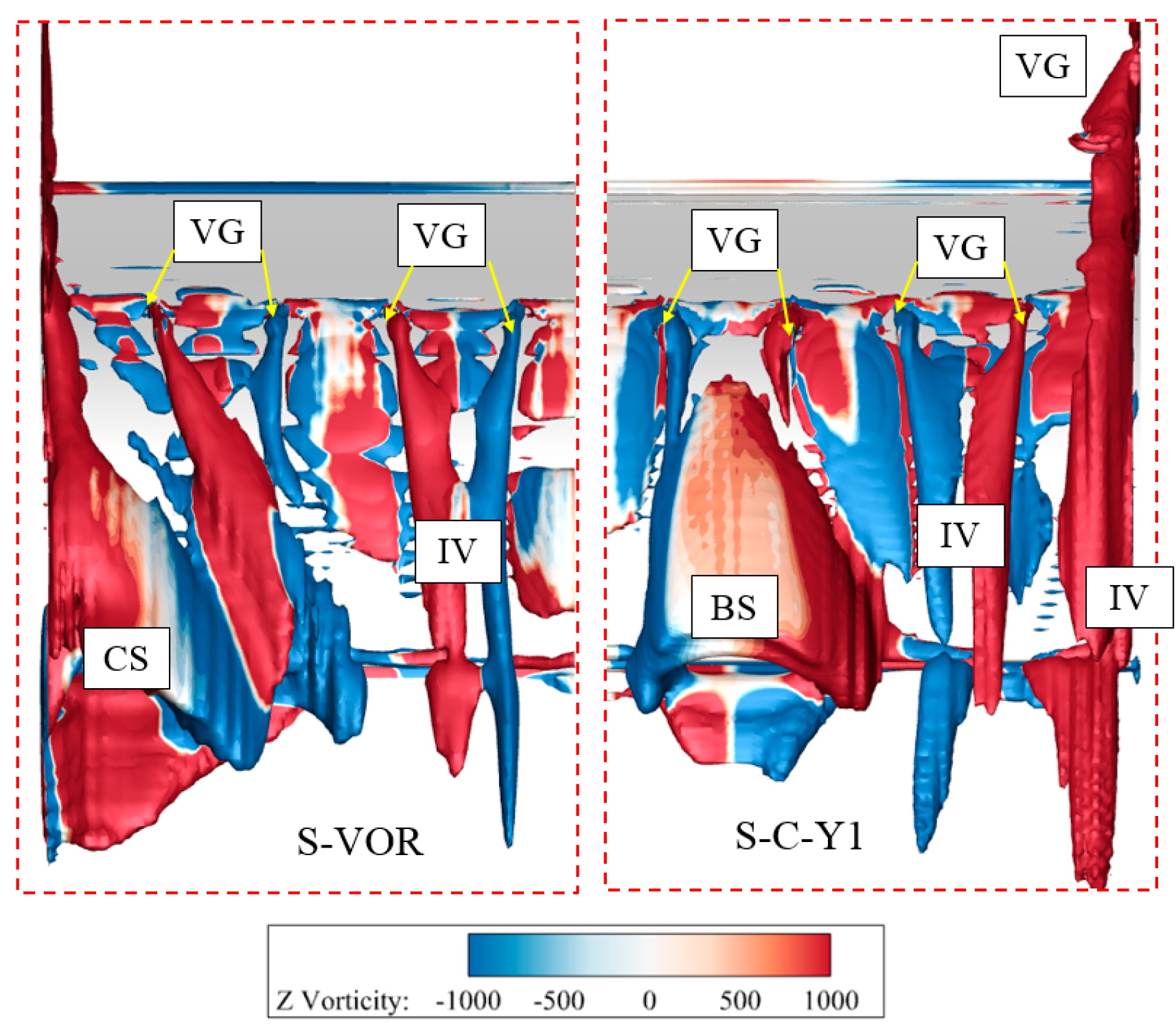
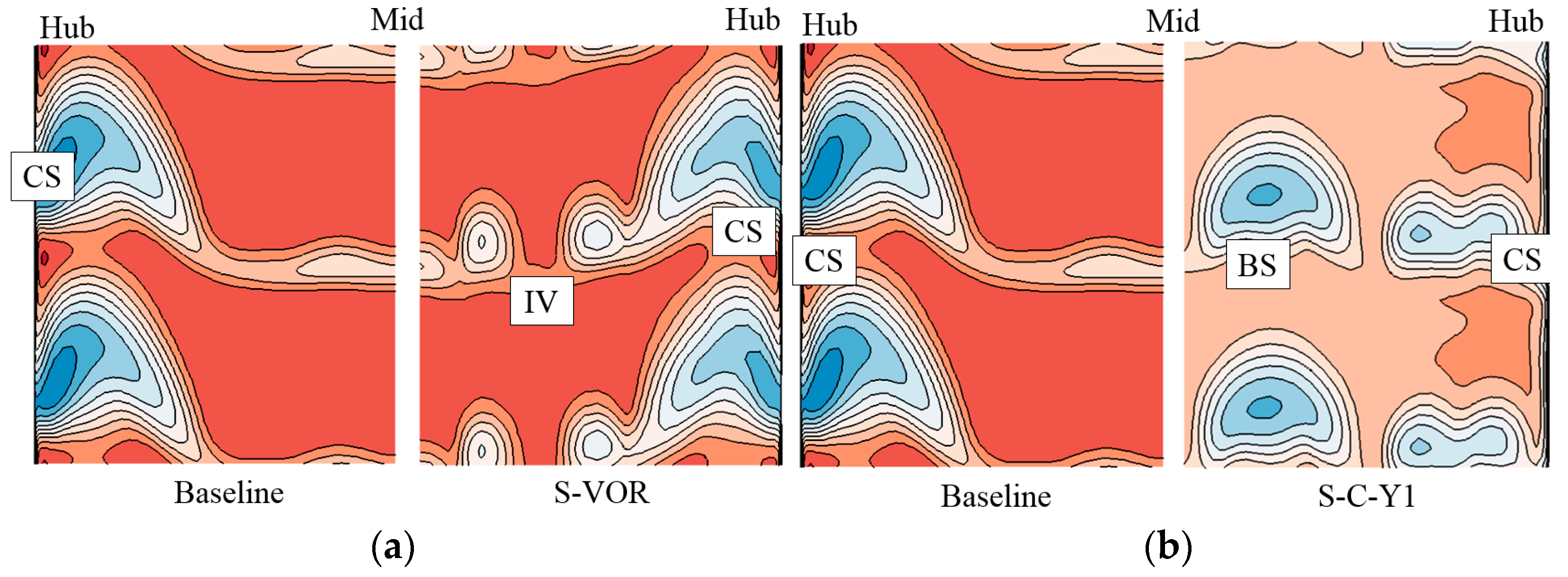
5.2. Effect of Endwall Vortex Generator on the Flow Field of the Supersonic Compressor Cascade
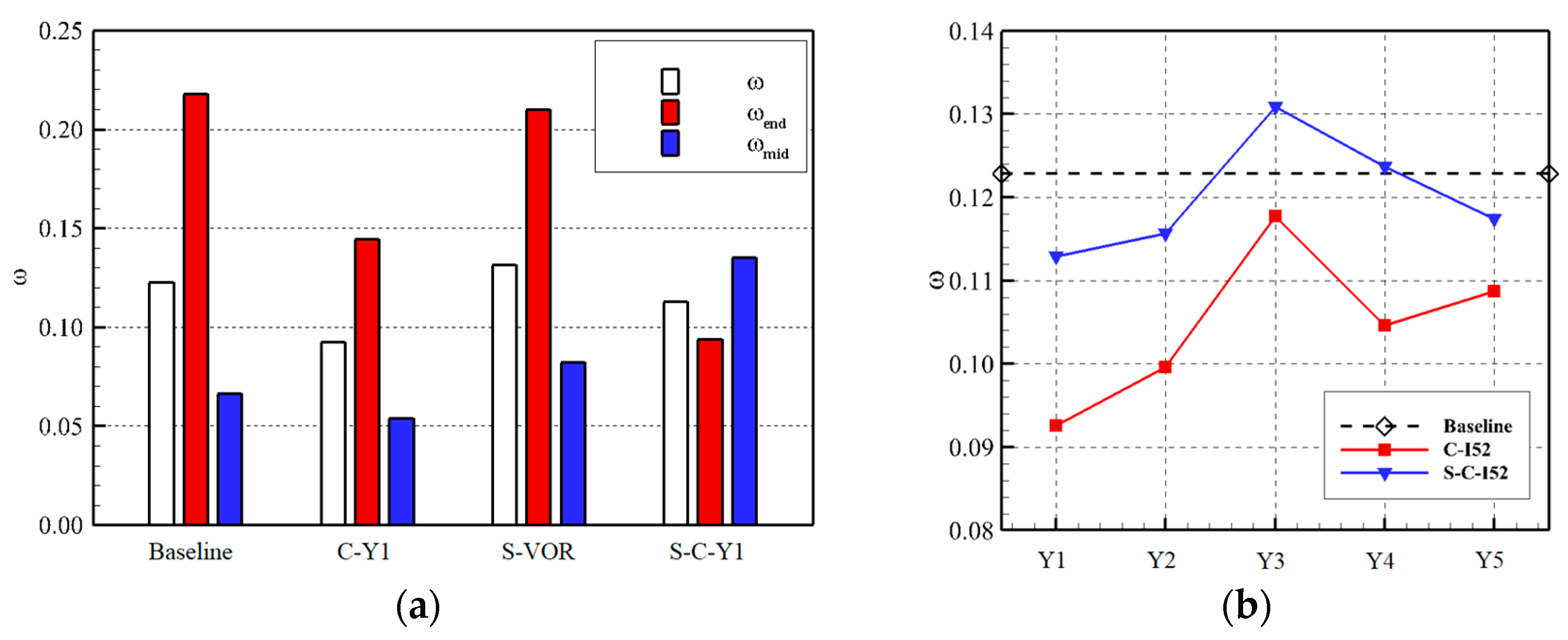
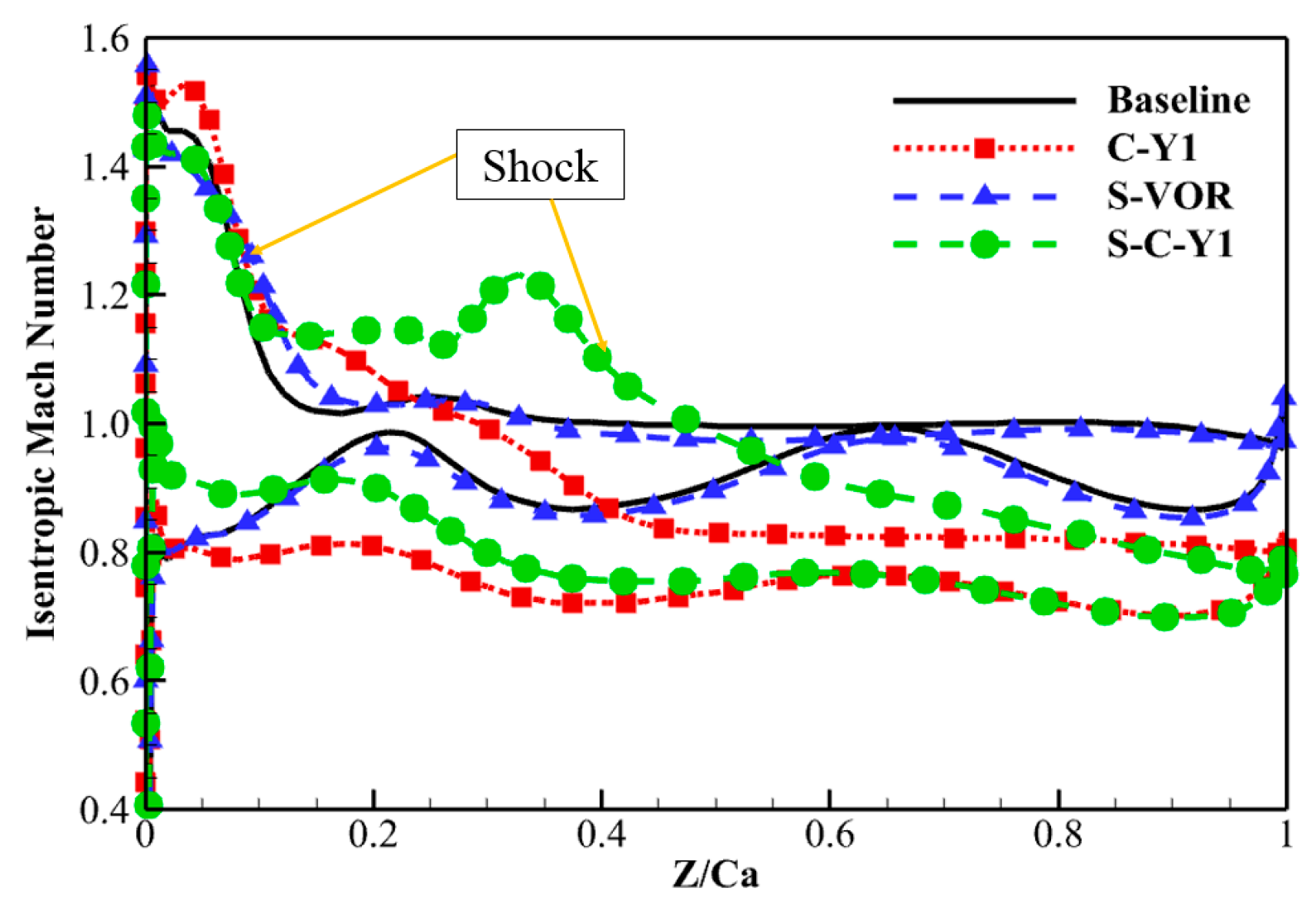
5.3. Effect of Endwall Vortex Generator Coupled with Suction Surface Vortex Generators on the Flow Field of the Supersonic Compressor Cascade
6. Conclusions
- (1)
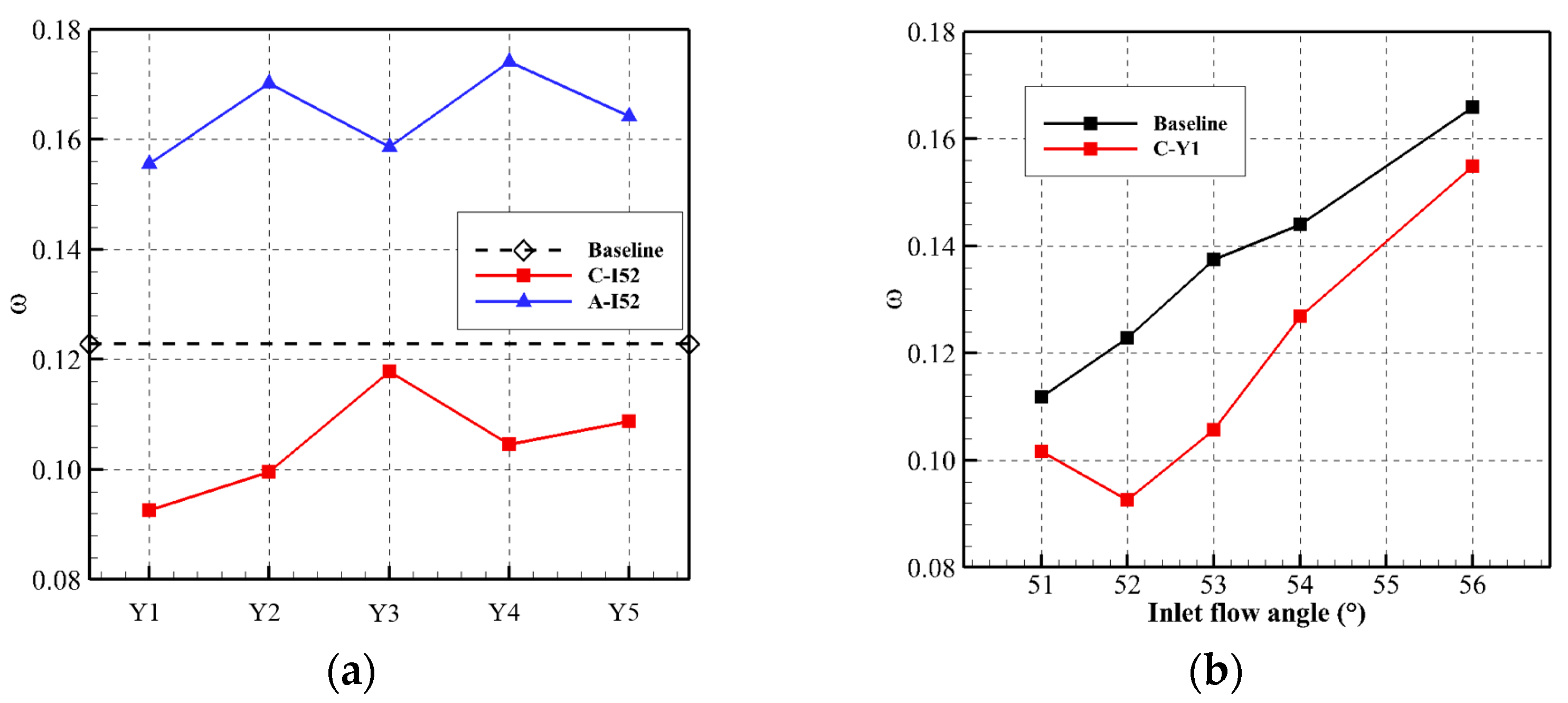
- The VG significantly reduced corner separation in the supersonic compressor cascade. Total pressure losses were reduced by as much as 24.6%, while endwall losses decreased by 33.6%. The optimal EVG design placed them near the suction surface and produced clockwise vortices. The coupled E-SVG design better controlled corner separation compared to the EVG only, with the endwall losses of the coupled design reduced by up to 56.9%.
- (2)
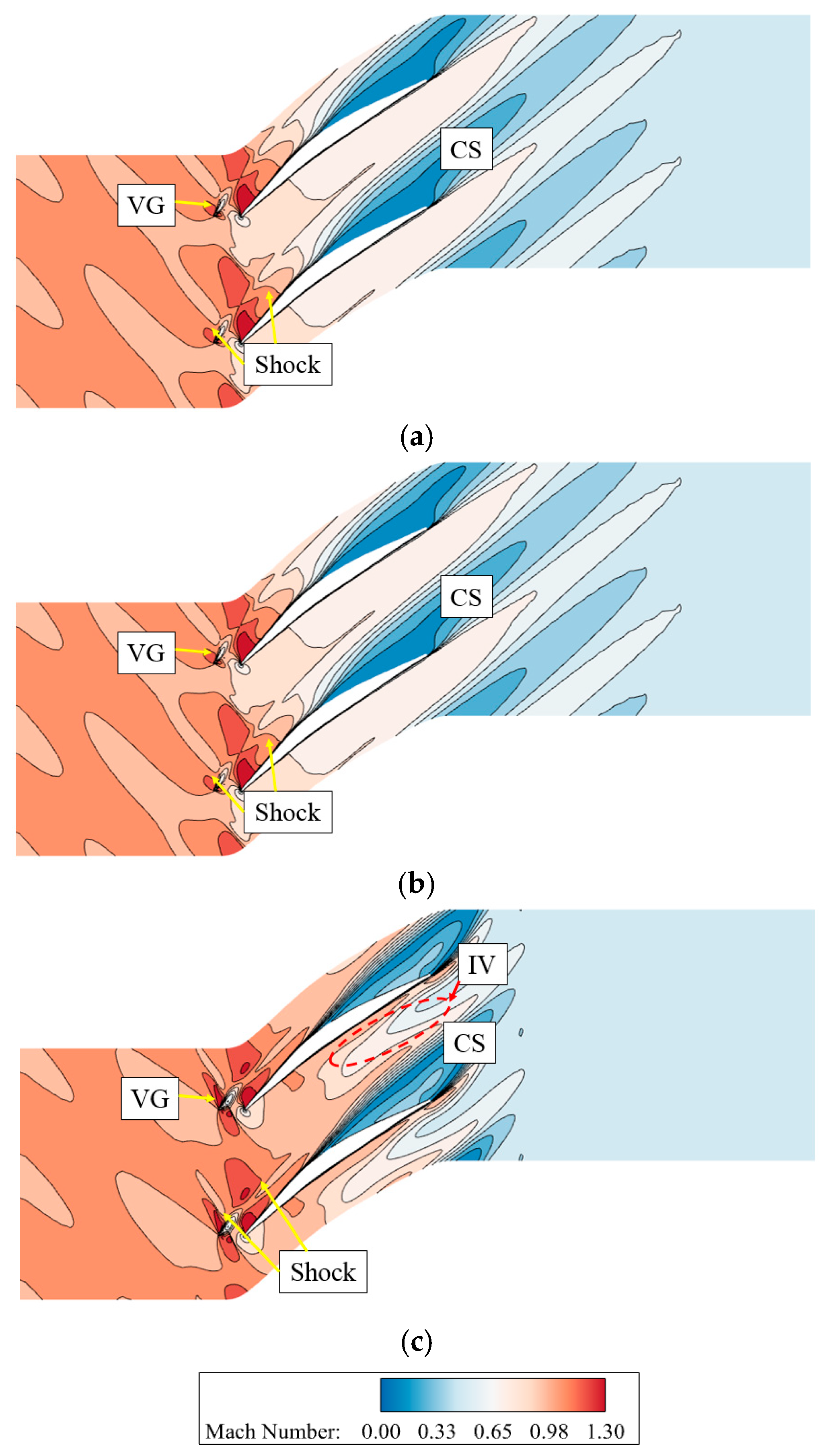
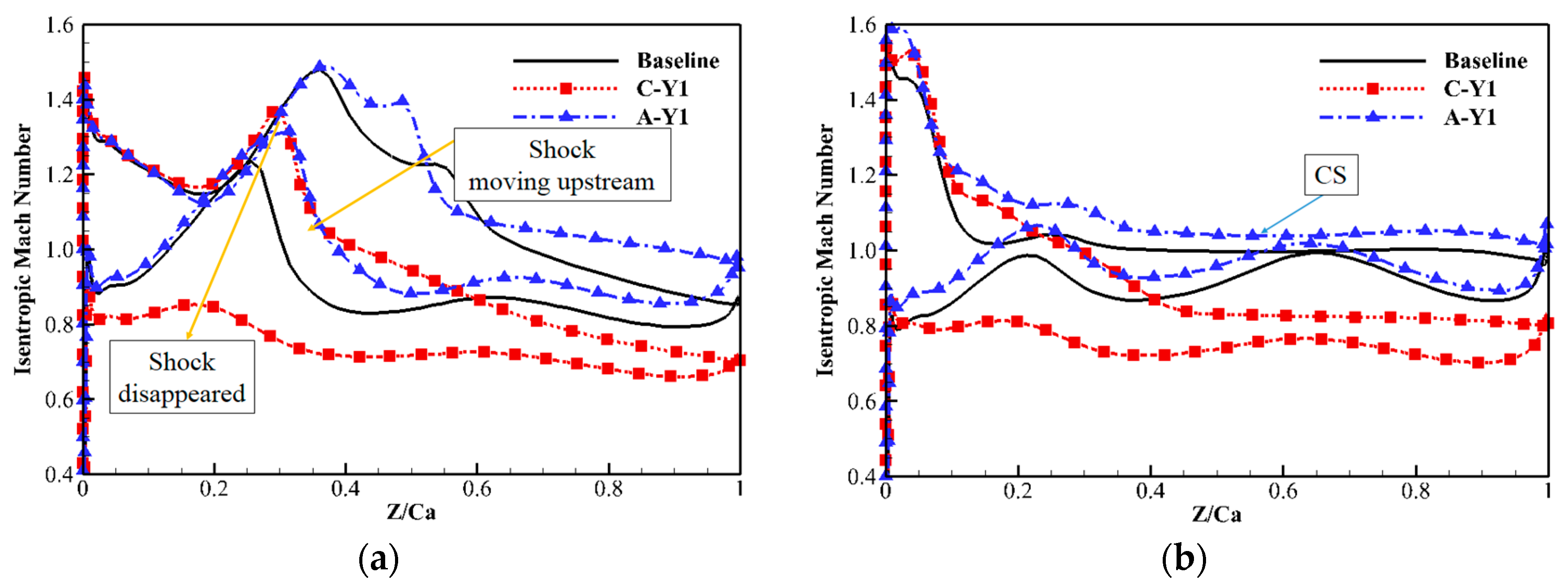
- The EVG reduced corner separation by changing the direction of the separation flow. Both clockwise and anticlockwise vortices reduced the high-loss region caused by corner separation. However, anticlockwise vortices induced new losses, increasing the total pressure losses. With clockwise vortices, the VG reduced losses at all pitchwise locations. The optimal design employed a VG located near the suction surface. An analysis of the shock structure near the endwall concluded that the VG of design C-Y1 had little effect on the shock structure, which made it suitable to control corner separation in a supersonic compressor cascade.
- (3)
- The coupled E-SVG design also reduced the total pressure losses in the supersonic compressor cascade. However, losses at mid-span increased due to the variation in AVDR. The SVG changed the shock structure. The isentropic Mach number near the endwall was first reduced and then increased in front of the SVG, and a new shock appeared behind the SVG. The variation in shock reduced the adverse pressure gradient induced by the shock, which was also beneficial for controlling corner separation.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| βin | Inlet flow angle |
| βout | Outlet flow angle |
| βs | Stagger angle |
| ρ | Density |
| ω | Total pressure loss coefficient |
| C | Chord of the compressor cascade |
| H | Height of the compressor cascade |
| P | Local static pressure |
| Pt | Total pressure |
| t | Pitch of the compressor cascade |
| Vz | Axial velocity |
| AVDR | Axial velocity density ratio |
| BS | Boundary-layer separation |
| CS | Corner separation |
| EVG | Endwall vortex generator |
| E-SVG | Endwall vortex generator coupled with suction surface vortex generator |
| IV | Vortex induced by vortex generator |
| LE | Blade leading edge |
| SVG | Suction surface vortex generator |
| TE | Blade trailing edge |
| VG | Vortex generator |
References
- Ma, Y.; Zhao, Q.; Zhang, K.; Xu, M.; Zhao, W. Analysis of Instantaneous Vibrational Energy Flow for an Aero-Engine Dual-Rotor–Support–Casing Coupling System. J. Eng. Gas. Turbines Power 2020, 142, 051011. [Google Scholar] [CrossRef]
- Shen, C.; Qiang, X.; Teng, J. Numerical and Experimental Investigation of an Axial Compressor Flow with Tandem Cascade. J. Therm. Sci. 2012, 21, 500–508. [Google Scholar] [CrossRef]
- Sun, S.; Hao, J.; Yang, J.; Zhou, L.; Ji, L. Impacts of Tandem Configurations on the Aerodynamic Performance of an Axial Supersonic Through-Flow Fan Cascade. J. Turbomach. 2022, 144, 041009. [Google Scholar] [CrossRef]
- Banjac, M.; Savanovic, T.; Petkovic, D.; Petrovic, M.V. A Comprehensive Analytical Shock Loss Model for Axial Compressor Cascades. J. Turbomach. 2022, 144, 091003. [Google Scholar] [CrossRef]
- Kusters, B.; Schreiber, H.A. Compressor Cascade Flow with Strong Shock-Wave/Boundary-Layer Interaction. AIAA J. 1998, 36, 2072–2078. [Google Scholar] [CrossRef]
- Prasad, A. Evolution of Upstream Propagating Shock Waves From a Transonic Compressor Rotor. J. Turbomach. 2003, 125, 133–140. [Google Scholar] [CrossRef]
- Li, Z.; Ju, Y.; Zhang, C. Parallel Large-Eddy Simulation of Subsonic and Transonic Flows with Transition in Compressor Cascade. J. Propuls. Power 2019, 35, 1163–1174. [Google Scholar] [CrossRef]
- Tweedt, D.L.; Schreiber, H.A.; Starken, H. Experimental Investigation of the Performance of a Supersonic Compressor Cascade. J. Turbomach. 1988, 110, 456–466. [Google Scholar] [CrossRef]
- Schreiber, H.A.; Starken, H. An investigation of a strong shock-wave turbulent boundary layer interaction in a supersonic compressor cascade. J. Turbomach. 1992, 114, 494–503. [Google Scholar] [CrossRef]
- Bloch, G.S.; Copenhaver, W.W.; O’Brien, W.F. A Shock loss model for supersonic compressor cascades. J. Turbomach. 1999, 121, 28–35. [Google Scholar] [CrossRef]
- Boudet, J.; Lévêque, E.; Touil, H. Unsteady Lattice Boltzmann Simulations of Corner Separation in a Compressor Cascade. J. Turbomach. 2022, 144, 011010. [Google Scholar] [CrossRef]
- Liu, Y.; Tang, Y.; Scillitoe, A.D.; Tucker, P.G. Modification of Shear Stress Transport Turbulence Model Using Helicity for Predicting Corner Separation Flow in a Linear Compressor Cascade. J. Turbomach. 2020, 142, 021004. [Google Scholar] [CrossRef]
- Ma, J.; Yang, G.; Zhou, L.; Ji, L.; Zhang, C. Effect of a Blade End Slot on Supersonic Compressor Cascade Hub-Corner Separation. Aerosp. Sci. Technol. 2021, 118, 107032. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, X.; Zhang, T.; Liu, B. Flow Mechanism and Aspiration Strategies in an Ultra-Highly Loaded Supersonic Compressor Cascade. Aerosp. Sci. Technol. 2020, 104, 105989. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, X.; Zhang, X.; Zhang, F.; Liu, B. Influence of Endwall Air Injection with Discrete Holes on Corner Separation of a Compressor Cascade. J. Therm. Sci. 2021, 30, 1684–1704. [Google Scholar] [CrossRef]
- Wang, Y.; Zhang, H.; Wu, Y.; Li, Y.; Zhu, Y. Supersonic Compressor Cascade Flow Control Using Plasma Actuation at Low Reynolds Number. Phys. Fluids 2022, 34, 027105. [Google Scholar] [CrossRef]
- Cao, Z.; Song, C.; Gao, X.; Zhang, X.; Liu, B. Computational Study on the Boundary Layer Suction Effects in the Supersonic Compressor Flow with a Bowed Blade. J. Therm. Sci. 2022, 31, 511–528. [Google Scholar] [CrossRef]
- Verma, S.B.; Manisankar, C. Separation and Flow Unsteadiness Control in a Compression Corner Induced Interaction Using Mechanical Vortex Generators: Effects of Vane Size and Inter-Device Spacing. Phys. Fluids 2022, 34, 096105. [Google Scholar] [CrossRef]
- Ma, S.; Chu, W.; Zhang, H.; Li, X.; Kuang, H. A Combined Application of Micro-Vortex Generator and Boundary Layer Suction in a High-Load Compressor Cascade. Chin. J. Aeronaut. 2019, 32, 1171–1183. [Google Scholar] [CrossRef]
- Ma, S.; Chu, W.; Zhang, H.; Yan, S.; Zhong, Y. Study of Combined Flow Control Strategies Based on a Quantitative Analysis in a High-Load Compressor Cascade. Aerosp. Sci. Technol. 2019, 93, 105346. [Google Scholar] [CrossRef]
- Şahin, F.C. Experimental Investigation on Flow Improvement in Compressor Cascades: Vortex Generators for Secondary Flow Improvement. Int. J. Energy Res. 2017, 41, 526–539. [Google Scholar] [CrossRef]
- Titchener, N.; Babinsky, H. Shock Wave/Boundary-Layer Interaction Control Using a Combination of Vortex Generators and Bleed. AIAA J. 2013, 51, 1221–1233. [Google Scholar] [CrossRef]
- Li, J.; Ji, L. Efficient Design Method for Applying Vortex Generators in Turbomachinery. J. Turbomach. 2019, 141, 081005. [Google Scholar] [CrossRef]
- Li, J.; Li, W.; Ji, L. Efficient Optimization Design of Vortex Generators in a Highly Loaded Compressor Stator. J. Eng. Gas. Turbines Power 2022, 144, 061002. [Google Scholar] [CrossRef]
- Fu, H.; Zhou, L.; Ji, L. Influence of Sub Boundary Layer Vortex Generator Height and Attack Angle on Cross-Flows in the Hub Region of Compressors. Chin. J. Aeronaut. 2022, 35, 30–44. [Google Scholar] [CrossRef]
- Hu, J.; Wang, R.; Huang, D. Flow Control Mechanisms of a Combined Approach Using Blade Slot and Vortex Generator in Compressor Cascade. Aerosp. Sci. Technol. 2018, 78, 320–331. [Google Scholar] [CrossRef]
- Hergt, A.; Meyer, R.; Engel, K. Effects of Vortex Generator Application on the Performance of a Compressor Cascade. J. Turbomach. 2013, 135, 021026. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, X.; Song, C.; Zhang, X.; Zhang, F.; Liu, B. Performance Enhancing for a Highly Loaded Tandem Cascade by Endwall Incoming Vortex–Corner Separation Interaction. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2021, 235, 6833–6846. [Google Scholar] [CrossRef]
- Cao, Z.; Gao, X.; Zhang, X.; Zhang, F.; Liu, B. Effect of Endwall Passage Vortex Generator on Corner Stall of a Tandem Compressor Cascade. Int. J. Heat. Fluid. Flow. 2022, 94, 108946. [Google Scholar] [CrossRef]



| Parameters | Value |
|---|---|
| Chord (C)/m | 0.1 |
| Solidity (C/t) | 1.815 |
| Aspect ratio (H/C) | 1.9 |
| Stagger angle (βS)/° | 38 |
| Inlet flow angle (βin)/° | 49.8 |
| Inlet flow Mach number (Ma1) | 1.05 |
| Reynolds number (Re) | 2.0 × 106 |
| Parameters | Value |
|---|---|
| D1 (mm) | 21.11 |
| L (mm) | 6.8 |
| L1 (mm) | 6.5 |
| L2 (mm) | 4.5 |
| H1 (mm) | 1.6 |
| H2 (mm) | 4 |
| H3 (mm) | 1 |
| H4 (mm) | 3 |
| βv1 (°) | 22 |
| βv2 (°) | 82 |
| βv3 (°) | 30 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, X.; Cao, Z.; Gu, Q.; Liu, B. Investigation of the Effect of Vortex Generators on Flow Separation in a Supersonic Compressor Cascade. Aerospace 2025, 12, 692. https://doi.org/10.3390/aerospace12080692
Gao X, Cao Z, Gu Q, Liu B. Investigation of the Effect of Vortex Generators on Flow Separation in a Supersonic Compressor Cascade. Aerospace. 2025; 12(8):692. https://doi.org/10.3390/aerospace12080692
Chicago/Turabian StyleGao, Xi, Zhiyuan Cao, Qinpeng Gu, and Bo Liu. 2025. "Investigation of the Effect of Vortex Generators on Flow Separation in a Supersonic Compressor Cascade" Aerospace 12, no. 8: 692. https://doi.org/10.3390/aerospace12080692
APA StyleGao, X., Cao, Z., Gu, Q., & Liu, B. (2025). Investigation of the Effect of Vortex Generators on Flow Separation in a Supersonic Compressor Cascade. Aerospace, 12(8), 692. https://doi.org/10.3390/aerospace12080692







