Abstract
The control stability and accuracy of quad tiltrotor UAVs is improved when encountering external disturbances during automatic flight by an active disturbance rejection control (ADRC) parameter self-tuning control strategy based on a radial basis function (RBF) neural network. Firstly, a nonlinear flight dynamics model of the quad tiltrotor UAV is established based on the approach of component-based mechanistic modeling. Secondly, the effects of internal uncertainties and external disturbances on the model are eliminated, whilst the online adaptive parameter tuning problem for the nonlinear active disturbance rejection controller is addressed. The superior nonlinear function approximation capability of the RBF neural network is then utilized by taking both the control inputs computed by the controller and the system outputs of the quad tiltrotor model as neural network inputs to implement adaptive parameter adjustments for the Extended State Observer (ESO) component responsible for disturbance estimation and the Nonlinear State Error Feedback (NLSEF) control law of the active disturbance rejection controller. Finally, an adaptive attitude control system for the quad tiltrotor UAV is constructed, centered on the ADRC-RBF controller. Subsequently, the efficacy of the attitude control system is validated through simulation, encompassing a range of flight conditions. The simulation results demonstrate that the Integral of Absolute Error (IAE) of the pitch angle response controlled by the ADRC-RBF controller is reduced to 37.4° in comparison to the ADRC controller in the absence of external disturbance in the full-states mode state of the quad tiltrotor UAV, and the oscillation amplitude of the pitch angle response controlled by the ADRC-RBF controller is generally reduced by approximately 50% in comparison to the ADRC controller in the presence of external disturbance. In comparison with the conventional ADRC controller, the proposed ADRC-RBF controller demonstrates superior performance with regard to anti-disturbance capability, adaptability, and tracking accuracy.
1. Introduction
With the rapid development of UAV technology, multi-rotor UAVs have gained extensive applications in military reconnaissance [1], disaster rescue [2], logistics transportation [3], and agricultural plant protection [4], owing to their vertical take-off and landing (VTOL) capability, hovering performance, and agile maneuverability. However, conventional multi-rotor UAVs are constrained by aerodynamic efficiency and endurance, making it challenging to meet the requirements of long-endurance and large-scale missions [5]. Meanwhile, fixed-wing UAVs demonstrate significant advantages in flight range and endurance owing to their high-speed performance and superior aerodynamic efficiency [6]. However, the absence of vertical take-off and landing capabilities and reliance on runways or catapult devices restrict their application in complex environments [7]. Therefore, the quad tiltrotor UAV with multi-rotor vertical take-off and landing capability and fixed-wing high-efficiency flight characteristics came into being [8]. By utilizing the tiltrotor mechanism, the UAV can achieve multimodal flight, thus balancing maneuverability, endurance and mission adaptability. These capabilities establish quad tiltrotor UAVs as a prominent research focus in the UAV domain [9].
The quad tiltrotor UAV is a time-varying multibody dynamics system featuring three flight modes: helicopter mode, transition mode, and airplane mode [10]. During the transition mode, continuous variation of the nacelle tilt angles induces intensified coupling interactions among aerodynamic characteristics, thrust vector direction, and airframe motion. This makes the system exhibit strong nonlinearity, time-varying, and multivariable coupling characteristics, which increases the design difficulty of the control system [11]. Due to the different flight characteristics of quad tiltrotor UAVs across different flight modes, conventional single-structure control strategy cannot adequately address the complex transient dynamics spanning helicopter-mode to airplane-mode transitions, resulting in a significant decrease in control performance during mode switching [12]. Therefore, research on the full-envelope flight control system for quad tiltrotor UAVs incorporating multiple flight modes has become a key focus in academic research.
Researchers have conducted extensive investigations into flight control systems for quad tiltrotor UAVs. In the field of linear control, El et al. proposed a proportional-derivative (PD) controller-based architecture, which effectively achieved the joint control of attitude and position for quad tiltrotor UAVs by integrating intelligent particle swarm optimization (PSO) for parameter tuning [13]. Wang et al. developed a novel approach to constructing the attitude control system of quadrotor and dual-rotor coaxial UAVs, utilizing a self-optimizing intelligent proportional-integral-derivative (PID) control method. This method was employed to ensure the maintenance of a stable attitude control of the aircraft [14]. Elshafei et al. introduced the tilt angle input variables around the X-axis and the Y-axis for each rotor separately for the quadrotor air vehicles (QRAV), thereby establishing a total of 12 control variables. It is on this basis, in conjunction with the PID control method, that the aircraft is capable of performing high-difficulty maneuvers with ease [15]. Cheng proposed a fuzzy adaptive control method with the objective of improving the response of the flight control of the tiltrotor UAV to different disturbances and realizing the stable control of the tiltrotor UAV’s attitude [16]. The proposed methodology is centered upon the implementation of a H-infinity control method for a quadrotor biplane tailsitter UAV, thereby ensuring the successful realization of the entire process of attitude robust control in the event of external wind disturbances [17]. Dharmawan et al. proposed a trajectory tracking control strategy combining an advanced error-state linear quadratic regulator (LQR) controller with a low-level controller, achieving full-mode flight control of tiltrotor aircraft [18]. Although control methods such as PD, PID, LQR, and H-infinity perform well in linear systems, they struggle to handle abrupt changes in dynamic properties caused by flight-mode switching in nonlinear systems. In contrast, the nonlinear control method shows superior adaptability. For example, Liu et al. proposed a height, speed, and attitude multi-loop control strategy for the transition mode of the tiltrotor aircraft, based on the Incremental Nonlinear Dynamic Inversion (INDI) theory. Experimental results demonstrated that the controller still maintains high control accuracy and strong robustness under complex disturbance conditions [19]. Bauersfeld et al. realized the nonlinear control for the full-states mode of the quad tiltrotor UAV based on model predictive control (MPC). Through numerical simulation and extensive outdoor flight tests, they demonstrated that the performance of the MPC controller is better than that of the PID controller [20]. Dalwadi et al. designed an enhanced backstepping controller incorporating a nonlinear observer to account for external disturbances in tiltrotor aircraft. Numerical simulations demonstrated that the nonlinear observer significantly improves the robustness and stability of the system [21]. The neural network-based control (NNC) proposed by Ducard et al. enables the NNC to approximate the MPC control performance by establishing an end-to-end mapping relationship between the input and output of MPC, enabling its application in the longitudinal control of the tiltrotor UAV [22]. These studies fully demonstrate the potential and advantages of nonlinear control in the flight control of quad tiltrotor UAVs.
The ADRC method transforms the nonlinear system into a series integral system by introducing an ESO to estimate and compensate the internal uncertainties and external disturbances of the system in real time, breaking the dependence of the traditional PID control on the linearized model. Therefore, it shows significant advantages in nonlinear control scenarios such as multi-mode switching of quad tiltrotor UAVs [23]. Gao et al. designed an adaptive disturbance rejection controller. When the tiltrotor UAV takes off and lands vertically in a windy environment, the controller makes the oscillation amplitude of each attitude response of the UAV significantly reduced and more stable [24]. Deng proposed an adaptive neural network active disturbance rejection controller (ANN-ADRC), which uses an adaptive neural network to estimate the total disturbance of the model, enhances the anti-disturbance performance of the ESO, and ensures the stable flight of the quad tiltrotor UAV in full mode [25]. The ADRC controller is characterized by a substantial number of parameters requiring adjustment. Consequently, the reliance on manual experience for the tuning of self-immunity controllers hinders their engineering applications. Ren et al. utilized an adaptive ant colony optimization-slime mold algorithm to optimize the parameters of the helicopter trajectory ADRC tracking controller, effectively reducing the complexity of parameter tuning [26]. Shen et al. proposed a genetic particle swarm optimization method for ADRC parameter tuning, but the offline tuning strategy struggles to meet the dynamic environment requirements [27]. Therefore, it is imperative that appropriate methodologies are adopted in order to facilitate the reduction of the complexity inherent in the parameter tuning of the active disturbance rejection attitude control system of the quad tiltrotor UAV. The feedforward neural network is an artificial neural network in which the connection between units does not form a loop. The feedforward neural network is considered to be the first artificial neural network. Furthermore, they are less complex than the corresponding RNN. The term ‘feedforward’ is employed to denote the process whereby information disseminates unidirectionally through the network, eschewing the formation of loops. This sequence of propagation commences at the input node, subsequently traversing the hidden node (if present) and culminating at the output node. The recurrent neural network (RNN) is distinguished from the conventional feedforward neural network by its capacity to establish cycles within the network. This property enables the RNN to receive a sequence of inputs, with each input exerting an influence on the subsequent output of the network. Consequently, RNN is particularly well suited for problems associated with data points preceding and following those previously mentioned, including language models and time series analysis. The RBF network is an artificial neural network that employs radial basis functions as its activation function. The network’s output is defined as a linear combination of the input radial basis function and the neuron parameters. The RBF neural network, leveraging its strong nonlinear approximation ability and rapid convergence properties, can identify the dynamic characteristics of the controlled system in real time through online training of input and output data [28]. In view of this, this paper integrates the dynamic identification capability of the RBF neural network with the disturbance rejection characteristics of ADRC, and constructs the ADRC-RBF adaptive control strategy. This strategy uses the RBF neural network to rapidly identify the dynamic characteristics of the quad tiltrotor UAV online, and dynamically adjusts the parameters of the ADRC controller based on the gradient descent algorithm to achieve real-time matching between the controller gain and the time-varying characteristics of the system, which significantly improves the disturbance rejection and environmental adaptability of the controller. The contributions of this paper are as follows:
- (1)
- Aiming at the problem of control redundancy of quad tiltrotor UAVs, the manipulation strategy under different flight modes is constructed, and the weight matrix is introduced to integrate the helicopter manipulation strategy with the aircraft manipulation strategy, and the control allocation under the transition mode is constructed to solve the problem of control redundancy during the flight of quad tiltrotor UAV.
- (2)
- The RBF neural network is applied to the identification process of the controlled system, and the Jacobi information of the controlled system is obtained. Combined with the parameter update rules, the parameters of the ADRC control module are dynamically updated, which enhances the robustness and anti-disturbance ability of the controller.
- (3)
- The attitude control system of the quad tiltrotor UAV is constructed by a combined ADRC-RBF controller. Under the condition of external disturbance, the attitude control system can stabilize the aircraft, and the anti-disturbance performance can be significantly improved. At the same time, it can realize the smooth transition and flight of the attitude in the full-flight mode.
The paper is organized as follows: Section 1 gives the introduction and the structure of the paper. Section 2 establishes the flight dynamics model of the quad tiltrotor UAV and presents the manipulation strategy and control allocation methodology. Section 3 presents the implementation of the ADRC controller for second-order nonlinear systems, utilizing RBF neural networks to dynamically adjust the ADRC parameters, and constructs the attitude control system for quad tiltrotor UAVs. Section 4 demonstrates simulation results under different flight modes, comparing the performance of the proposed ADRC-RBF controller with the ADRC controller. Section 5 draws the conclusion of the full text.
2. Quad Tiltrotor UAV Modeling
2.1. Flight Dynamics Model
The research object of this paper is a conventional quad tiltrotor UAV, the overall three-dimensional model structure of which is shown in Figure 1. The UAV is equipped with two pairs of rotors and a biplane configuration (front and rear wings). The airfoil of the wing is NACA63-415, and the installation angles of the front wing and the rear wing are 2.5° and 0.11°, respectively. The tilting mechanism integrated in the nacelle allows the nacelle and the rotor to tilt synchronously. Flaps and ailerons follow an integrated design approach to control roll and pitch movements in airplane mode. A rudder is mounted on the vertical tail to control yaw in airplane mode, and the vertical tail airfoil is NACA0012. The overall parameters of the quad tiltrotor UAV are shown in Table 1.
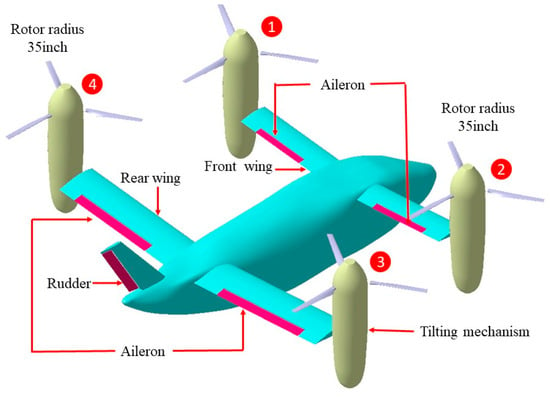
Figure 1.
Three-dimensional model of quad tiltrotor UAV.

Table 1.
Key parameters of the quad tiltrotor UAV.
This study adopts a component-based modeling approach, establishing a Cartesian coordinate system with the center of mass of the quad tiltrotor UAV as the coordinate origin. By calculating the aerodynamic forces and moments generated by the rotor, wing, fuselage, and vertical tail, and accounting for aerodynamic interference effects among the components, the forces and moments of individual components are summed to obtain the resultant force and moment acting on the entire aircraft. Combined with the rigid body kinematics equation and the Euler dynamics equation, a nonlinear full-state flight dynamics model of the quad tiltrotor UAV is constructed. The structure of the flight dynamics model is presented in Figure 2.
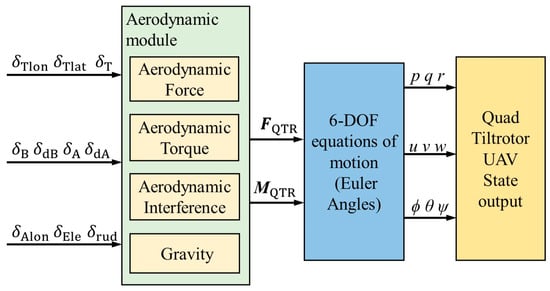
Figure 2.
Quad tiltrotor UAV flight dynamics model.
The aerodynamic components are modeled in the aerodynamic module. The aerodynamic force and moment of each component are calculated according to the control input and the flight state of the entire aircraft. The transfer of the aerodynamic force and moment of each component to the body coordinate system is achieved through the coordinate transformation matrix. Subsequently, numerical synthesis is conducted to derive the three-axis resultant force/resultant moment component of the quad tiltrotor UAV under body shafting [29], as delineated in Equation (1).
where and are the aerodynamic resultant force and resultant moment of the whole aircraft under the body coordinate system, respectively; subscripts , , , and are the abbreviations of rotor, fuselage, wing, and vertical tail, respectively.
In the kinematics module, the resultant force and resultant moment calculated by the aerodynamic module, in conjunction with the six-degree-of-freedom motion equation, are utilized to calculate the state quantity of the quad tiltrotor UAV under body shafting [30], as demonstrated in Equation (2).
and
where is the resultant external moment of the whole UAV; is the gravitational acceleration; is the inertia tensor matrix; is the resultant aerodynamic force vector; is the angular velocity anti-symmetric matrix; is the conversion matrix from airframe coordinates to ground coordinates; , , , etc., are the abbreviations of trigonometric functions such as , , , etc. is the linear velocity vector of the body coordinate system; is the Euler angle vector of roll, pitch, and yaw; is the angular rate vector; is longitudinal differential collective pitch; is longitudinal cyclic pitch coupling; is lateral differential collective pitch; is longitudinal differential cyclic pitch; is mean collective pitch; is lateral cyclic pitch coupling; is lateral differential cyclic pitch; is the front wing aileron differential; is rear wing aileron interconnection; is rudder deflection angle.
The complete nonlinear flight dynamics model of the quad tiltrotor UAV can be expressed in the following simplified form [31]:
and
where is the state variable of the quad tiltrotor UAV. This paper focuses on the rotational motion of the UAV, and designs the attitude flight control system for the full-state nonlinear flight dynamics model of the quad tiltrotor UAV.
2.2. Manipulation Strategy and Control Allocation
The quad tiltrotor UAV has multiple control inputs, exhibiting significant problems of control redundancy. Based on the kinematics and dynamics characteristics of the quad tiltrotor UAV, its flight mode of the quad tiltrotor UAV can be categorized into helicopter mode, transition mode, and airplane mode. During the hover and low-speed flight phase, the quad tiltrotor UAV utilizes the helicopter mode manipulation strategy. During the high-speed flight phase, the airplane mode manipulation strategy is utilized. In the transition phase, a hybrid manipulation strategy method combining helicopter manipulation strategy and airplane manipulation strategy is implemented to address control redundancy issues. The manipulation strategy of the quad tiltrotor UAV is presented in Figure 3.
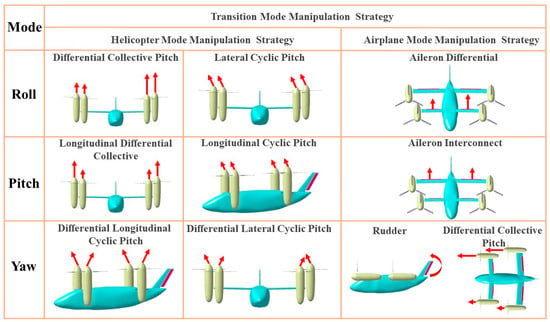
Figure 3.
Manipulation strategy for the quad tiltrotor UAV.
As can be seen from Figure 3, when the quad tiltrotor UAV is in helicopter mode, the roll channel can be operated by differential collective pitch and lateral cyclic pitch. The differential collective pitch means that the No. 1 and No. 4 rotors increase (decrease) the collective pitch, while the No. 2 and No. 3 rotors decrease (increase) the collective pitch. The lateral cyclic pitch means that the four rotors change the same lateral cyclic pitch at the same time. The pitch channel can be controlled by longitudinal differential collective and longitudinal cyclic pitch. The longitudinal differential collective is that the collective pitch of No. 1 and No. 2 rotors increases (decreases), while the collective pitch of No. 3 and No. 4 rotors decreases (increases). The longitudinal cyclic pitch is that four rotors change the same longitudinal cyclic variable pitch at the same time. The yaw channel can be operated by differential longitudinal cyclic pitch and differential lateral cyclic pitch. The differential longitudinal cyclic pitch is that the No. 1 and No. 4 rotors increase (decrease) the longitudinal cyclic variable pitch, while the No. 2 and No. 3 rotors decrease (increase) the longitudinal cyclic variable pitch. The differential lateral cyclic pitch is that the No. 1 and No. 2 rotors increase (decrease) the lateral cyclic variable pitch, while the No. 3 and No. 4 rotors increase (decrease) the lateral cyclic variable pitch. When the quad tiltrotor UAV is in airplane mode, the roll channel can be manipulated by aileron differential. The aileron differential is that the left aileron of the front wing deflects upward (downward), while the right aileron deflects downward (upward). The pitch channel can be manipulated by aileron interconnect, which means that the aileron on the rear wing deflects the same amount in the same direction. The yaw channel can be operated in two ways: rudder deflection and differential collective pitch. The rudder deflection refers to changing the yaw moment of the whole aircraft by rotating the rudder. When the helicopter is in transition mode, it is necessary to integrate the helicopter manipulation strategy with the airplane mode manipulation strategy.
The quad tiltrotor UAV contains four control loops: throttle control loop, lateral control loop, longitudinal control loop, and yaw control loop. A virtual control variable and a weighting coefficient matrix are introduced. By utilizing the weighting coefficient matrix to adjust the control authority distribution between helicopter mode and airplane mode operations, the transition process is ensured to be smooth and safe. The relationship between the control input variable, the virtual control variables, and the weighting coefficient matrix is shown in Equation (6):
and
where is the throttle channel virtual control input variable; is the lateral channel virtual control input variable; is the longitudinal channel virtual control input; is the yaw channel virtual control input variable; is the control weighting coefficient of with respect to ; , , and are the control weighting coefficients of , , and with respect to , respectively; , , and are the control weighting coefficients of , , and with respect to , respectively; , , and are the control weighting coefficients of , , and with respect to , respectively.
For a series of flight state equilibrium points, the Taylor series expansion is applied to analyze the control derivative matrix , and the weight coefficient matrix is obtained. As shown in Table 2, is the nacelle tilt angle, is the helicopter mode, is the airplane mode. In the transition flight mode, with the change of the flight mode of the nacelle inclination angle, the control surfaces of the helicopter and the fixed-wing aircraft have a certain control efficiency. The control energy is reduced by means of reasonably allocating the weight coefficient, and the control channels are guaranteed to have sufficient control efficiency.

Table 2.
Weighting matrix parameters.
Combining Equation (2) and Equation (6), the flight dynamics model expression for the quad tiltrotor UAV can be written as
3. ADRC-RBF Adaptive Controller
The ADRC-RBF adaptive controller is composed of three parts: an ADRC controller, a parameter update module, and an RBF neural network. The detailed internal architecture of the ADRC-RBF controller is shown in Figure 4.
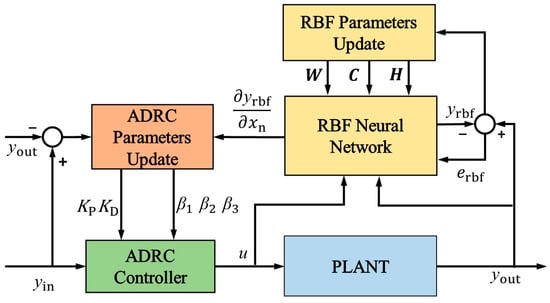
Figure 4.
Structure of the ADRC-RBF controller.
3.1. Structure of the ADRC Controller
The ADRC controller is composed of three components: a Tracking Differentiator (TD), an Extended State Observer (ESO), and a Nonlinear State Error Feedback (NLSEF) law, as shown in Figure 5. TD is used to arrange the transition process of the system, generate a smooth tracking signal, and resolve the contradiction between response speed and overshoot. ESO estimates the state variables and total disturbances (internal uncertainties and external disturbances) of the system in real time, and compensates the total disturbances through feedback. NLSEF calculates the control quantity through nonlinear combination based on the output signal of TD and the state estimation of ESO, achieving high precision control of the system.
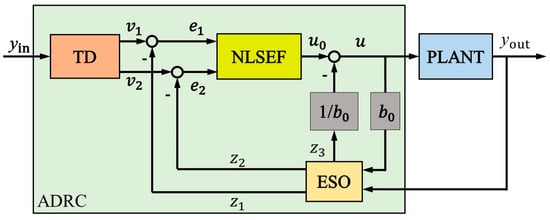
Figure 5.
Structure of the ADRC controller.
3.1.1. Tracking Differentiator (TD)
The discrete form of the nonlinear Tracking Differentiator for the second-order system is constructed [32], as shown in Equation (10).
where the specific expression of the fastest comprehensive function is
where is the input tracking signal of TD; is the tracking signal of ; is the differential signal of ; is the time discrete step size; is the fast factor (larger values improve response speed but may cause overshoot and oscillation); is the filtering factor (smaller values reduce initial overshoot but result in slower rise time).
3.1.2. Extended State Observer (ESO)
The extended observer can rapidly estimate the system state variables and total disturbances in real time [33]. Consider a second-order nonlinear system with both internal uncertainties and external disturbances:
is extended as a new state variable that incorporates both internal uncertainties and external disturbances, and the second-order nonlinear system is extended to the linear system shown in Equation (13).
Based on Equation (13), the discrete form of ESO is constructed as shown in Equation (14).
where are the observations of the state variables respectively; ; ; , . The expression of the filter function is
3.1.3. Nonlinear State Error Feedback (NLSEF)
The NLSEF obtains the control input for the controlled system through nonlinear combination of the error between the TD output and ESO observed values, with incorporation of the total disturbance estimate. The NLSEF control law expression for the second-order system is given in Equation (16):
where is the error signal; is the error differential signal; uses the same filter function as ESO; ; is the final control input variable.
3.2. RBF Neural Network
The RBF neural network is an artificial neural network. In comparison with feedforward neural networks and RNN, RBF neural networks exhibit certain advantages, including their simple structure, strong robustness, strong online learning ability, and high tolerance to external noise. It is evident that the aforementioned characteristics render the RBF network well suited for the online identification of the dynamic characteristics of quadrotor UAVs. The RBF network comprises three layers: the input layer, the hidden layer, and the output layer, as shown in Figure 6. The input layer and the hidden layer are directly connected, and the hidden layer and the output layer are connected by the weight vector. The number of neurons in the input layer is designated as m, the number of neurons in the hidden layer is denoted as n, and the number of neurons in the output layer is 1 [34].
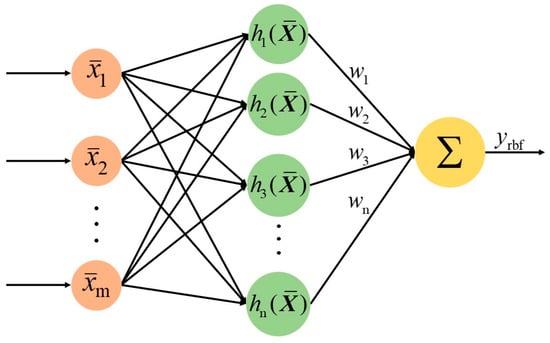
Figure 6.
Structure of the RBF neural network.
The output of the RBF neural network can be expressed as [35]
where is the input vector of the neural network; is the node weight matrix of the hidden layer; is the radial basis vector of the hidden layer. The Gaussian function is selected as the activation function to realize the nonlinear mapping from the input layer to the hidden layer. The specific calculation formula is
where is the center vector of the hidden layer neuron; ; is the radius width parameter of the Gaussian activation function of the hidden layer neuron.
The training process of the RBF neural network employs an online method in the context of supervised learning, with the adjustment of weights and radial basis function parameters being based on a single sample. The gradient descent method, which possesses excellent local search ability, is adopted in this study. The cost function is defined as . The parameters to be adjusted include output weight , radius width parameter , and center vector . The detailed parameter update rules are given in Equation (19).
where is the learning rate; is the momentum factor, ,.
The Jacobian information expression of the RBF neural network output variable with respect to the variable is
In the identification of unknown single input and output controlled systems, the radial basis function (RBF) neural network is utilized. The RBF neural network structure is set to 3-7-1. The input vector of the neural network is designated as , where is the control input variable of the controlled system, is the state output variable of the controlled system; is the output error of the RBF neural network. Combined with Equation (20), the Jacobian information of the radial basis function (RBF) neural network is utilized to substitute the Jacobian information of the output state variable of the controlled system with respect to the variable , as demonstrated in Equation (21). The process requires the RBF neural network to have the capacity for both rapid and accurate model identification for the controlled system.
Through numerical simulation, the capability of the RBF neural network to achieve fast and accurate identification of nonlinear unknown systems is verified. The number of hidden layer neurons in the RBF neural network is set to 7, with initial parameters configured as , , , , , where . The control input variable (periodic signal) of the unknown controlled system is given as shown in Figure 7a. The output state variable (random step signal) of the controlled system and the system identification result of the RBF neural network are shown in Figure 7b. Figure 7c displays the identification error of the neural network system. The results demonstrate that the RBF neural network can achieve rapid and accurate identification of the controlled system. When abrupt changes occur in the system’s output signals, the identification error initially surges but converges to zero within 0.02 s, enabling high-precision system identification.
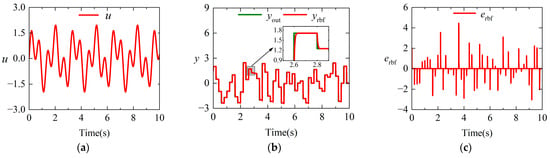
Figure 7.
RBF neural network-based system identification. (a) Input control variable of the unknown controlled system; (b) RBF neural network identification results; (c) system identification error of the RBF neural network.
3.3. ADRC Parameter Update
The conventional ADRC controller requires tuning multiple parameters, including NLSEF gain coefficients (,) and ESO gain coefficients (,,). Dynamic parameter adjustment of the ADRC controller is achieved through integration with the RBF neural network.
The loss function required for the controller parameter update is defined, is the expected output of the controlled system. By incorporating Equation (21), the increment expressions for ADRC parameters , , , , and to be updated are derived using the gradient descent algorithm [36], as given in Equation (22).
where ,,,, represent the updating coefficients. Finally, the ADRC parameter update formula is presented:
The variation range of ADRC parameters is bounded to ensure the stability of the whole system. Interested readers can refer to [37]. The steps for the dynamic parameters update of ADRC parameters during system operation are as follows:
- (a)
- Initialize the ADRC neural network parameters and RBF neural network parameters, set the simulation duration , start the system operation, and then proceed to step b.
- (b)
- At time , acquire the controlled system’s control input variable , state output variable , and RBF neural network identification error . Then, the RBF neural network carries out forward propagation to compute the neural network output variable and the controlled system’s Jacobian information , then proceeds to step c.
- (c)
- Determine whether the system operation time satisfies the condition . If the condition is satisfied, proceed to step d; otherwise execute step g.
- (d)
- The RBF neural network executes back propagation to compute increments for the updatable parameters, updates parameters , , and in the neural network based on Equation (19), then proceeds to step e.
- (e)
- Obtain the output response error of the controlled system, and determine whether the system’s output state error satisfies the condition . If the condition is satisfied, proceed to step b for the next iteration; if not satisfied, proceed to step f.
- (f)
- The output response error of the controlled system, the Jacobian information from the RBF neural network output, and the function of ESO and NLSEF. The ADRC controller parameters are then updated according to Equation (23), after which the process proceeds to step b for the next iteration cycle.
- (g)
- The simulation execution is terminated.
3.4. ADRC-RBF Attitude Control System for Quad Tiltrotor UAV
Define , , combined with Equation (9), the flight dynamics model for the attitude loop of the quad tiltrotor UAV is expressed as
The attitude model Equation (24) is transformed into a second-order nonlinear system:
where is the unknown function about the relevant state variables, is the unknown attitude gain matrix, . Incorporating the ADRC-RBF controller, an attitude control system is designed for the second-order nonlinear system given in Equation (25) with the detailed architecture shown in Figure 8. As illustrated in Figure 8, the attitude control system designs ADRC-RBF controllers for the roll, pitch, and yaw channels. The roll channel, for instance, has the following configuration: the input signal of the ADRC-RBF controller is the expected output signal of the controlled system. The RBF neural network in the roll channel ADRC-RBF controller is responsible for obtaining the actual roll angle output of the controlled system, the lateral channel virtual input control of the ADRC control module, and the RBF neural network identification error . The Jacobi information of the controlled system is calculated. Finally, the , , , , parameters are adjusted in accordance with the ADRC parameter adjustment rules. The principle of other attitude channels is analogous to that of the roll channel. The virtual input control quantity , , , obtained by the attitude control system, is calculated by the control allocation module to obtain the control quantity of each rudder surface. This process ultimately enables the tracking of the desired attitude signal.
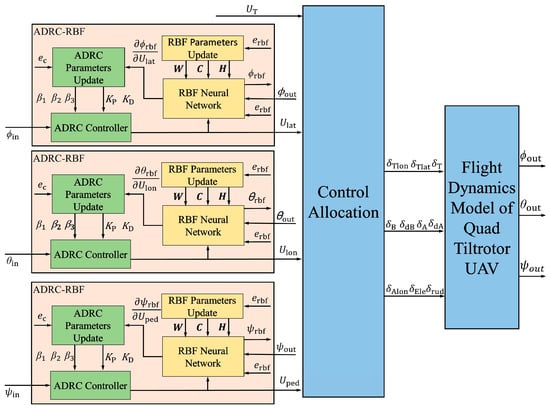
Figure 8.
ADRC-RBF attitude control system.
4. Simulation Results
Attitude control is performed for helicopter mode, airplane mode, and full-states mode. The structure of the attitude control system is shown in Figure 8. The control performance of the ADRC controller and ADRC-RBF controller is compared, with both controllers having the same initial parameters. Under the condition of no external disturbance, the initial values of the parameters to be updated for both ADRC controller and ADRC-RBF controller are randomly given within a reasonable parameter range. When external disturbances exist, parameters with good control effect under the condition of no disturbance are selected as the initial values of the parameters to be updated for both the ADRC controller and ADRC-RBF controller. The initial value of each parameter to be updated is given in the order of the roll control loop, the pitch control loop, and the yaw control loop. The RBF neural network in each ADRC-RBF controller module has a 3-7-1 structure and the same initial parameters, , , , , .
4.1. Helicopter Mode
The initial parameters of the ADRC controller and the ADRC-RBF controller in helicopter mode without disturbance and disturbance are given by the look-up table method [38], as demonstrated in Table 3. The initial roll angle, pitch angle, and yaw angle of the quad tiltrotor UAV are 0°.

Table 3.
ADRC/RBF-ADRC parameters in helicopter mode.
Under no disturbance conditions, the desired target values of three attitude angles are set to be square waves with an amplitude of 3°, period of 20 s, phase of 0°, and zero bias. The simulation running time is 25 s. Figure 9, Figure 10 and Figure 11, respectively, presents the dynamic processes of the three attitude angle responses, the Integral of Absolute Error (IAE) of the attitude angle responses, and the parameter updates of the ADRC-RBF controller in the pitch control channel. It is observed that the roll angle, pitch angle, and yaw angle response of the ADRC controller can effectively track the reference signals, but exhibit significant overshoot and oscillation at the switching points of the attitude angle reference signals, with the maximum overshoot of roll angle, pitch angle, and yaw angle reaching 20%, 22%, and 8%, respectively. The IAE of the response shows an increasing trend over time, with the IAE of roll angle, pitch angle, and yaw angle eventually reaching 26.7°, 27.9°, and 18.3°, respectively. In contrast, the ADRC-RBF controller shows better tracking performance of roll angle, pitch angle, and yaw angle response. The overshoot and oscillation at the switching points of the reference signals are smaller, with the maximum overshoot of roll angle, pitch angle, and yaw angle being only 2.7%, 6.5%, and 2%, respectively, and no obvious fluctuation. The IAE error is lower than that of the ADRC controller, with the IAE of roll angle, pitch angle, and yaw angle finally reaching 14.6°, 12.8°, and 14.7°, respectively, achieving higher tracking accuracy. The main reason is that when the attitude angle changes drastically, the ADRC controller with invariant control parameters has limited ESO estimation capability for internal uncertainties. The accuracy of the control signal output by NLSEF is limited, resulting in significant degradation of control stability and precision. The ADRC-RBF rapidly adjusts its parameters based on the UAV’s operational state during attitude changes, stabilizes them near appropriate values, enhances the performance of both ESO and NLSEF, and consequently demonstrates superior dynamic performance and control accuracy under significant attitude angle variations. The above analysis shows that when the quad tiltrotor UAV flies in helicopter mode under no external disturbance conditions, the ADRC-RBF controller can adjust parameters according to the aircraft’s real-time state, giving it stronger robustness, stability, control accuracy, and dynamic performance.
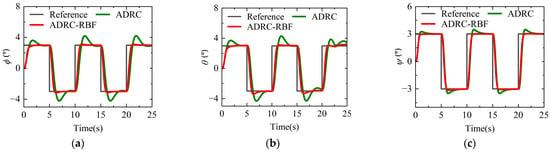
Figure 9.
Attitude angle response in helicopter mode under no disturbance conditions. (a) Roll angle response. (b) Pitch angle response. (c) Yaw angle response.
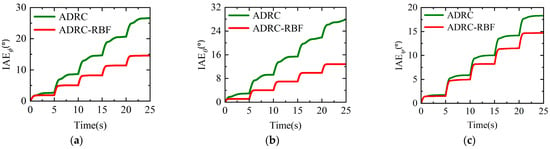
Figure 10.
IAE of attitude angle in helicopter mode under no disturbance conditions. (a) IAE of roll angle response. (b) IAE of pitch angle response. (c) IAE of yaw angle response.
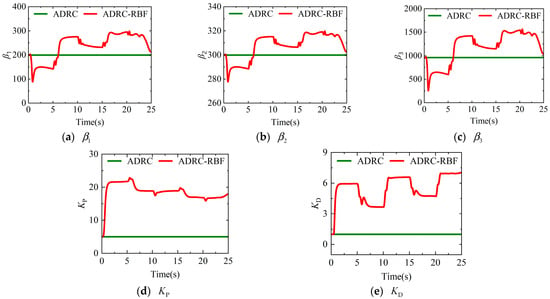
Figure 11.
Online parameter tuning process of ADRC-RBF controller in pitch control channel.
External disturbances will interfere with the flight of the quad tiltrotor UAV. Sinusoidal signals are used to simulate external attitude disturbances. The disturbance of ° is added to the roll, pitch, and yaw control loops. The desired target value of the attitude angle is set to a constant value of 3°, and the simulation run time is 10 s. Figure 12, Figure 13 and Figure 14, respectively, present the dynamic processes of the three attitude angle responses, attitude angle response errors, and the parameter updates of the ADRC-RBF controller in the roll control channel. The results indicate that after adding the attitude disturbance, the response curves of the roll angle, yaw angle, and pitch angle of the ADRC and ADRC-RBF controllers will show certain oscillations, but overall, they can follow the reference signal. The parameters of the ADRC-RBF controller in the roll channel are continuously and dynamically adjusted, with the adjustment process accompanied by minor fluctuations, thereby reducing the impact of external periodic attitude disturbances. From the local detail diagrams of the attitude response and error response, it can be seen that the ADRC controller with single parameter has limited anti-disturbance ability, and the attitude response and response error show a phenomenon of equal-amplitude oscillation. The oscillation amplitudes of the roll angle, pitch angle, and yaw angle responses are about 0.5°, 0.2°, and 0.4°, respectively. For the ADRC-RBF controller, due to the continuous dynamic update of the parameters, although the attitude response and attitude response error have the same initial oscillation amplitudes as the ADRC controller, the oscillation amplitudes will decrease with time, showing a convergent trend. This indicates that the update of the ESO module parameters gives it a stronger estimation ability for the external attitude disturbance of the quad tiltrotor UAV, so that the anti-disturbance ability and robustness of the controller are continuously enhanced with time. The above analysis shows that in helicopter mode, when there is external attitude disturbance, compared with ADRC controller, the ADRC-RBF controller shows stronger anti-external disturbance ability and robustness due to its ability to dynamically update parameters.
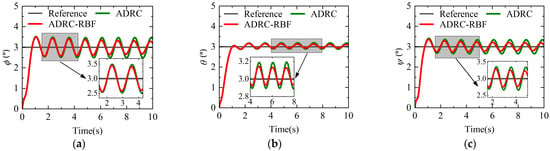
Figure 12.
Attitude angle response in helicopter mode under disturbance conditions. (a) Roll angle response. (b) Pitch angle response. (c) Yaw angle response.
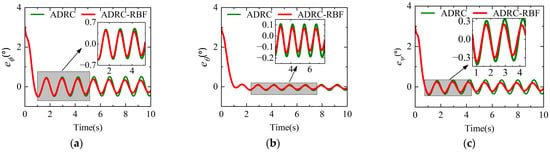
Figure 13.
Attitude angle response errors in helicopter mode under disturbance conditions. (a) Roll angle response error. (b) Pitch angle response error. (c) Yaw angle response error.
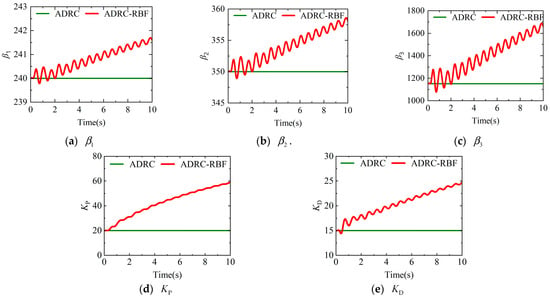
Figure 14.
Online parameter tuning process of ADRC-RBF controller in roll control channel.
4.2. Airplane Mode
The initial parameters of the ADRC controller and ADRC-RBF controller in airplane mode are given under the condition of no disturbance and disturbance [38], as shown in Table 4. The initial pitch angle is 3.42°, and the initial roll angle and the yaw angle are 0°.

Table 4.
ADRC/RBF-ADRC parameters in airplane mode.
Under no external disturbance conditions, the desired pitch angle reference is set as a square wave with 3° amplitude, 20 s period, 0° phase, and 3.42° bias, while the roll and yaw angle references are set as zero bias square waves with 3° amplitude, 20 s period, and 0° phase. The simulation run time is 50 s. Figure 15 and Figure 16, respectively, present the dynamic processes of the three attitude angle responses, IAE of the attitude angle responses. The results show that in airplane mode, when the roll angle, pitch angle, and yaw angle undergo multiple step changes, both the ADRC controller and ADRC-RBF controller can track the reference signals, demonstrating good control performance. The ADRC controller with fixed parameters exhibits limited anti-disturbance capability during periodic attitude changes. Its attitude angle dynamic response shows significant overshoot, with maximum overshoots of 2.6%, 4.9%, and 4.3% for roll, pitch, and yaw angles, respectively. Additionally, it has limited control capability and poor stability. In contrast, the ADRC-RBF controller shows superior performance. Its attitude angle response curves during periodic attitude changes are closer to the reference signals, with faster response speed and much smaller overshoot. The overshoot of the three attitude angles is all close to 0. The IAE values for roll, pitch, and yaw angles are ultimately 27.3°, 33.5°, and 26.9°, respectively, all lower than those of the ADRC controller. The reason is that the update of ESO module parameters enables it to have a stronger estimation capability for the internal uncertainties of the quad tiltrotor UAV, thereby enhancing the system’s stability and robustness. The update of NLSEF module parameters allows it to generate more accurate control inputs, thus improving the system’s control accuracy and dynamic performance. The above analysis demonstrates that in airplane mode, when the quad tiltrotor UAV is free from external attitude disturbances, the ADRC-RBF controller, by virtue of its adaptive parameter updating capability, exhibits superior tracking accuracy, enhanced stability, and greater robustness.
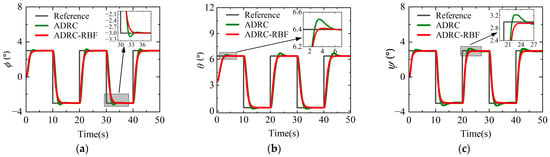
Figure 15.
Attitude angle response in airplane mode under no disturbance conditions. (a) Roll angle response. (b) Pitch angle response. (c) Yaw angle response.
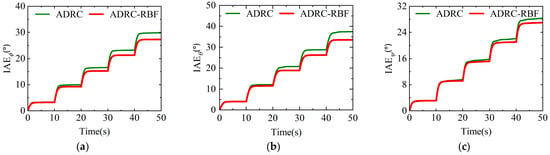
Figure 16.
IAE of attitude angle in airplane mode under no disturbance conditions. (a) IAE of roll angle response. (b) IAE of pitch angle response. (c) IAE of yaw angle response.
The sinusoidal disturbance of ° is applied to all three attitude control channels. The expected attitude command of roll angle and yaw angle are set to 3°, the expected attitude command of pitch angle is set to 6.42°, and the simulation time is 15 s. Figure 17 and Figure 18, respectively, present the dynamic processes of the three attitude angle responses, attitude angle response errors. It shows that under external attitude disturbances, both the ADRC controller and the ADRC-RBF controller can track the desired attitude commands. However, from the local detail diagram of the attitude response, compared with the ADRC controller, the roll angle and yaw angle of the ADRC-RBF controller have no significant fluctuation of the attitude during the rising process. Meanwhile, after the roll angle, pitch angle, and yaw angle track the attitude command, the oscillation amplitude of the attitude angle is smaller than that of the ADRC controller, and the amplitude of the roll angle response and the error amplitude show a trend of continuous convergence, indicating that the ability of the ADRC controller with fixed parameters to resist external attitude disturbance is limited. For the ADRC-RBF controller, due to the influence of its external disturbance, the controller parameters are constantly adjusted. The estimation ability of ESO to external disturbance is improved, and a more accurate input control quantity is obtained by combining NLSEF output with feedback compensation, so as to reduce the influence of external disturbance on the system. The above analysis shows that in airplane mode, there is attitude disturbance outside, and the ADRC-RBF controller has better anti-disturbance and robustness.
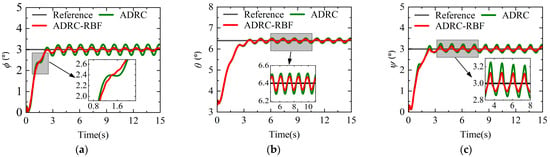
Figure 17.
Attitude angle response in airplane mode under disturbance conditions. (a) Roll angle response. (b) Pitch angle response. (c) Yaw angle response.
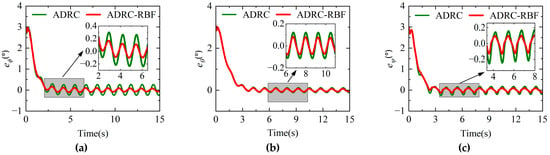
Figure 18.
Attitude angle response errors in airplane mode under disturbance conditions. (a) Roll angle response error. (b) Pitch angle response error. (c) Yaw angle response error.
4.3. Full-States Mode
The mission profile of the full-states mode is shown in Figure 19, which includes nine stages. Stage I: 0–40 s, helicopter mode, climbing vertically to 100 m; Stage II: 40–70 s, helicopter mode, accelerating to 35 m/s with a nose-down attitude; Stage III: 70–100 s, helicopter mode, maintaining level flight at 35 m/s with a nose-down attitude; Stage IV: 100–120 s, transition mode from helicopter to airplane mode, the nacelle tilts from 0° to 90° at a constant rate of 4.5°/s, and the speed increases from 35 m/s with a nose-up acceleration to 90 m/s; Stage V: 120–150 s, airplane mode, maintaining level flight at 90 m/s; Stage VI: 150–170 s, transition from airplane to helicopter mode, the nacelle tilts from 90° to 0° at 4.5°/s, and airspeed decelerates from 90 m/s to 35 m/s with initial nose-down and subsequent nose-up maneuvers; Stage VII: 170–200 s, helicopter mode, maintain level flight at 35 m/s with a nose-down attitude; Stage VIII: 200–230 s, helicopter mode, decelerates to 0 m/s with a nose-up attitude.; Stage IX: 230–285 s, helicopter mode, descending vertically to the ground.
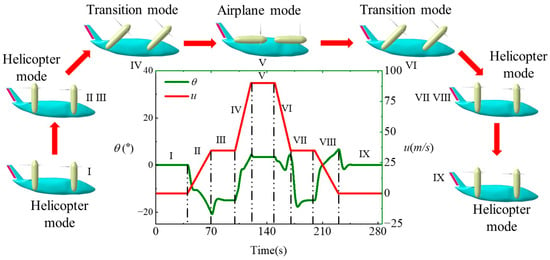
Figure 19.
Full-states mode mission profile.
Through the division of the above mission profile, when the quad tiltrotor UAV is simulated in full-states mode, only the pitch angle is greatly changed, while the roll angle and yaw angle are kept at 0°. The initial state of the quad tiltrotor UAV is set to hover, and the initial state of the roll angle, pitch angle, and yaw angle is set to 0°. The roll angle command is applied to it according to the flight profile shown in Figure 19, and the roll angle and yaw angle is set to 0°. The initial parameters of ADRC controller and ADRC-RBF controller under the condition of no disturbance and disturbance are given [38], as shown in Table 5.

Table 5.
ADRC/RBF-ADRC parameters in full-states mode.
When there is no attitude disturbance outside, Figure 20 shows the dynamic process of the pitch angle response and IAE of the pitch angle response in full-states mode, and Figure 21 shows the local details of pitch angle response in different flight stages. The results indicate that both the ADRC-RBF controller and the ADRC controller demonstrate the capacity to effectively track the pitch angle reference signal within the full-states mode. The IAE of the pitch angle response of the ADRC controller finally reached 78.2°, and the IAE of the pitch angle response of the ADRC-RBF controller finally decreased to 37.4°. The IAE demonstrated an overall upward trend, yet the IAE of the ADRC was generally higher than that of the ADRC-RBF controller. It can be seen from the details of Stage II (the helicopter mode nose-down acceleration) and Stage VIII (the helicopter mode nose-up deceleration) that due to the large change of the pitch angle, the internal uncertainty of the quad tiltrotor UAV changes drastically. The ESO module of the ADRC controller with fixed parameters has limited estimation for the internal disturbance, and it is difficult for the NLSEF to calculate precise control input variable. Therefore, the pitch angle response exhibits significant fluctuations, and the tracking accuracy becomes worse. From the pitch angle response details of transition Stage IV and VIII, it can be observed that the fixed-parameter ADRC controller fails to effectively accommodate the transformation of control surfaces (longitudinal differential collective pitch and rear wing aileron interconnection), nacelle tilt angle variations, and drastic flight state changes, consequently inducing significant pitch angle response fluctuations and oscillations that degrade both stability and robustness characteristics. In contrast, in full-flight mode, the ADRC-RBF controller continuously updates both ESO and NLSEF parameters according to flight state variations, achieving higher control precision while effectively addressing the severe internal uncertainty changes induced by flight mode transitions. This results in pitch angle responses without noticeable fluctuations and maintains superior stability and robustness. The above analysis results show that under the undisturbed flight conditions, the ADRC-RBF controller can maintain high control accuracy, stability, and robustness compared with the ADRC controller under the full-states mode control of the quad tiltrotor UAV.
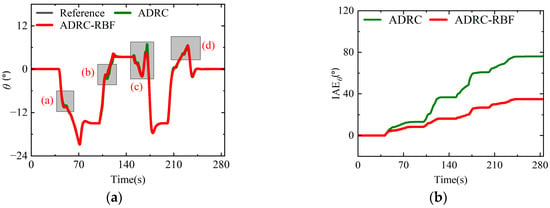
Figure 20.
Pitch angle response and IAE in full-states mode under no disturbance conditions. (a) Pitch angle response; (b) IAE of pitch angle response.
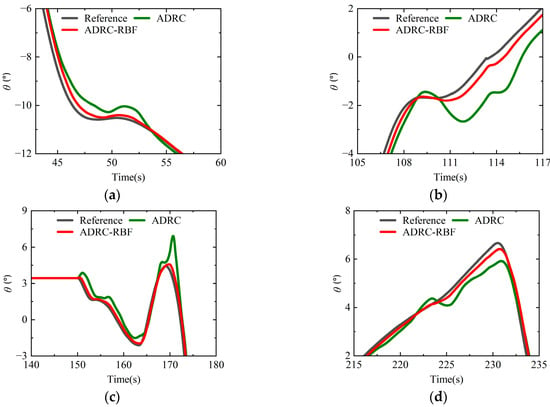
Figure 21.
Local details of pitch angle response in full-states mode under no disturbance conditions. (a) Local detail diagram of pitch angle response in Stage II. (b) Local detail diagram of pitch angle response in Stage IV. (c) Local detail diagram of pitch angle response in Stage VI. (d) Local details of pitch angle response in Stage VIII.
The external attitude disturbance of ° is applied to the pitch angle control loop. Figure 22 shows the dynamic process of the pitch angle response and IAE of the pitch angle response in full-states mode, and Figure 23 shows the local details of pitch angle response in different flight stages. It shows that under the disturbed flight conditions, the IAE of the ADRC-RBF controller is lower than that of the ADRC controller and has higher control accuracy. The local detail diagram of pitch angle response shows that in the acceleration and deceleration flight stage of the helicopter in Stage II and Stage VIII, the pitch angle attitude response of the ADRC controller with fixed parameter fluctuates in an obvious manner. By adjusting the parameters of ESO and NLSEF, the ADRC-RBF controller effectively reduces the influence of external attitude disturbance and large change of pitch attitude on pitch angle control, and reduces the overshoot and oscillation of the pitch angle dynamic response. In the transition mode of Stage IV and Stage VI, due to external attitude disturbances and internal disturbances caused by flight mode switching, the tracking accuracy of the ADRC controller decreases, and its pitch angle response exhibits significant fluctuations, resulting in poorer anti-disturbance capability. In contrast, the pitch angle response of the ADRC-RBF controller shows smaller fluctuations, indicating stronger compensation ability against disturbances. In the constant-speed flight stages of Stage V and Stage VII, the ADRC-RBF controller’s pitch angle oscillation amplitude is significantly smaller than that of the ADRC controller, demonstrating superior stability and disturbance rejection capability. The above analysis results show that compared with the ADRC controller, the ADRC-RBF controller can maintain higher control accuracy, while the amplitude of the attitude oscillation is reduced by about 50% as a whole, and has higher robustness and anti-disturbance ability under disturbed flight conditions. It is more suitable for full-states mode control in complex environments.
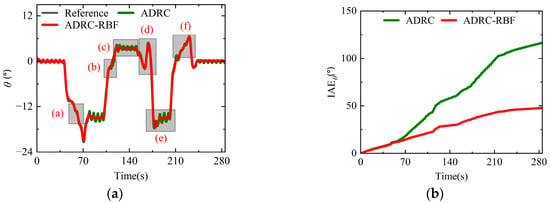
Figure 22.
Pitch angle response and IAE in full-states mode under disturbance conditions. (a) Pitch angle response; (b) IAE of pitch angle response.
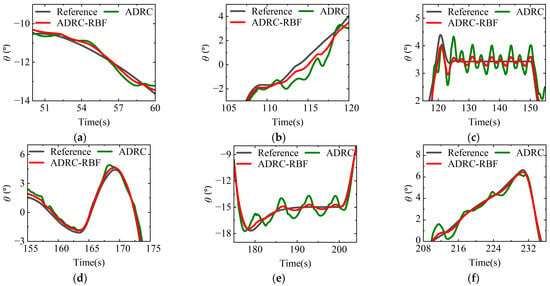
Figure 23.
Local details of pitch angle response in full-states mode under disturbance conditions. (a) Local detail diagram of pitch angle response in Stage II. (b) Local detail diagram of pitch angle response in Stage Ⅳ. (c) Local detail diagram of pitch angle response in Stage Ⅴ. (d) Local detail diagram of pitch angle response in Stage Ⅵ. (e) Local detail diagram of pitch angle response in Stage Ⅶ. (f) Local detail diagram of pitch angle response in Stage Ⅷ.
5. Conclusions
This paper sets out a control design method for ADRC parameter adaptive adjustment based on RBF neural networks. The RBF neural network is used to obtain the Jacobian information of the controlled system, and parameters of the Nonlinear State Error Feedback Control law and extended observer are adjusted using dynamic parameter adjustment rules. The attitude control system for quad tiltrotor UAVs based on this method is constructed, which overcomes the effects of internal and external disturbances and enables effective attitude control in different flight modes. The simulation results show that in helicopter mode, airplane mode, and full-states mode, the ADRC-RBF controller can adaptively adjust the ESO and NLSEF parameters according to the flight state. This effectively overcomes the effects of internal uncertainties and external disturbances in different flight modes, improves control accuracy, and ensures that the quad tiltrotor UAV maintains good dynamic performance and stability during large-angle attitude tracking control. It can also safely and stably complete flight mode switching and achieve high-precision attitude tracking control. The ADRC-RBF controller is more robust, more anti-disturbance, and more accurate than the ADRC controller. It also reduces the difficulty of parameter tuning for the ADRC controller and enhances the controller’s adaptive capability. The ADRC-RBF controller demonstrates superior control performance in full-states mode. Future research will concentrate on the design of an ADRC-RBF adaptive speed outer loop control system, full-states mode hardware-in-the-loop simulations, and door flight tests.
Author Contributions
Conceptualization, J.H. and B.R.; methodology, J.H., B.W., Y.X., Q.Z., S.D. and B.R.; software, J.H.; validation, B.R., Y.X. and S.D.; formal analysis, J.H. and S.D.; investigation, J.H., B.R. and S.D.; resources, Y.X., Q.Z., S.D. and B.W.; data curation, J.H., Y.X. and S.D.; writing—original draft preparation, J.H. and B.R.; writing—review and editing, Y.X., Q.Z., S.D. and B.W.; visualization, Y.X.; supervision, S.D. and B.W.; project administration, S.D. and B.W.; funding acquisition, Q.Z. All authors have read and agreed to the published version of the manuscript.
Funding
Thanks for the technical support from the National Key Laboratory of Helicopter Aeromechanics. This work is supported by the National Natural Science Foundation of China (no. 12032012) and the Priority Academic Program Development of Jiangsu Higher Education Institutions.
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
The research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest, and the authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| ADRC | Active Disturbance Rejection Control |
| RBF | Radial Basis Function |
| ESO | Extended State Observer |
| NLSEF | Nonlinear State Error Feedback |
| IAE | Integral Of Absolute Error |
| VTOL | Take-Off and Landing |
| UAV | Unmanned Aerial Vehicle |
| PD | Proportional-Derivative |
| PSO | Particle Swarm Optimization |
| PID | Proportional-Integral-Derivative |
| QRAV | Quadrotor Air Vehicles |
| LQR | Linear Quadratic Regulator |
| INDI | Incremental Nonlinear Dynamic Inversion |
| MPC | Model Predictive Control |
| NNC | Neural Network-Based Control |
| ANN | Adaptive Neural Network |
| RNN | Recurrent Neural Network |
| TD | Tracking Differentiator |
References
- Chen, Z.H. Based on intelligent attack and defense command technology system for multi-rotor tilting vertical takeoff and landing swarm uavs. In Proceedings of the 2023 IEEE International Conference on E-Business Engineering, Sydney, 4–6 November 2023; pp. 276–280. [Google Scholar]
- Hamrouni, A.; Ghazzai, H.; Menouar, H.; Massoud, Y. Multi-Rotor uavs in crowd management systems: Opportunities and challenges. IEEE Internet Things Mag. 2023, 6, 74–80. [Google Scholar] [CrossRef]
- Rejeb, A.; Rejeb, K.; Simske, S.J.; Treiblmaier, H. Drones for supply chain management and logistics: A review and research agenda. Int. J. Logist. Res. Appl. 2023, 26, 708–731. [Google Scholar] [CrossRef]
- Chen, H.; Lan, Y.; Fritz, B.K.; Hoffmann, W.C.; Liu, S. Review of agricultural spraying technologies for plant protection using unmanned aerial vehicle (UAV). Int. J. Agric. Biol. Eng. 2021, 14, 38–49. [Google Scholar] [CrossRef]
- Joo, S.; Kim, H.; Son, H. Multiobjective design optimization of hybrid-powered multirotors for enhanced endurance and payload capacity. IEEE/ASME Trans. Mechatron. 2024, 30, 1959–1970. [Google Scholar] [CrossRef]
- Sasane, A.; Borkar, S.; Majety, P. Optimizing endurance in fixed wing uavs. In International Conference on Smart Computing and Communication; Springer: Singapore, 2024; pp. 219–229. [Google Scholar]
- Liu, Y.; Wang, Y.; Li, H. Runway-free recovery methods for fixed-wing uavs: A comprehensive review. Drones 2024, 8, 463. [Google Scholar] [CrossRef]
- Rojo-Rodriguez, E.U.; Rojo-Rodriguez, E.G.; Araujo-Estrada, S.A. Design and performance of a novel tapered wing tiltrotor UAV for hover and cruise missions. Machines 2024, 12, 653. [Google Scholar] [CrossRef]
- Liu, Z.Q.; He, Y.; Yang, L. Control techniques of tilt rotor unmanned aerial vehicle systems: A review. Chin. J. Aeronaut. 2017, 30, 135–148. [Google Scholar] [CrossRef]
- Sheng, H.; Zhang, C.; Xiang, Y. Mathematical modeling and stability analysis of tiltrotor aircraft. Drones 2022, 6, 92. [Google Scholar] [CrossRef]
- Tran, S.A.; Lim, J.W. Interactional aerodynamics of the xv-15 tiltrotor aircraft during conversion maneuvers. J. Am. Helicopter Soc. 2022, 67, 56–68. [Google Scholar] [CrossRef]
- Lu, K.; Tian, H.; Zhen, P. Conversion flight control for tiltrotor aircraft via active disturbance rejection control. Aerospace 2022, 9, 155. [Google Scholar] [CrossRef]
- El, G.N.; Mjahed, M.; El, K.A. Particle swarm optimization based proportional-derivative parameters for unmanned tilt-rotor flight control and trajectory tracking. Automatika 2020, 61, 189–206. [Google Scholar]
- Wang, Z.; Yuan, Q.; Zhu, Y. Fast and intelligent Proportional—Integral—Derivative (PID) attitude control of quadrotor and dual-rotor coaxial unmanned aerial vehicles (UAVs) based on all-true composite motion. Drones 2024, 8, 747. [Google Scholar] [CrossRef]
- Elshafei, M.E.A.; Elfeky, M.A.; Saif, A.W.A.A. System and Method for Control of Quadrotor Air Vehicles with Tiltable Rotors. U.S. Patent Application No. 14/269,322, 5 May 2014. [Google Scholar]
- Cheng, X.; Wang, Y.; Zhao, J.; Liu, N. ESO-based fuzzy adaptive control of tiltrotor UAV against wind disturbance. Trans. Inst. Meas. Control. 2025. [Google Scholar] [CrossRef]
- Kumar, T.; Kothari, M.; Bhattacharya, R. H∞ Robust Control of a Quadrotor Biplane Tailsitter UAV. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024; p. 0318. [Google Scholar]
- Dharmawan, A.; Ashari, A.; Putra, A.E. Translation movement stability control of quad tiltrotor using LQR and LQG. Int. J. Intell. Syst. Appl. 2018, 10, 10–21. [Google Scholar] [CrossRef]
- Liu, S.X.; Lin, Z.H.; Liu, W. Control scheme for transition mode of tiltrotor UAV based on INDI. Acta Aeronaut. Astronaut. Sin. 2024, 45, 236–250. [Google Scholar]
- Bauersfeld, L.; Spannagl, L.; Ducard, G. MPC flight control for a tilt-rotor VTOL aircraft. IEEE Trans. Aerosp. Electron. Syst. 2021, 57, 2395–2409. [Google Scholar] [CrossRef]
- Dalwadi, N.; Deb, D.; Kothari, M. Disturbance observer-based backstepping control of tail-sitter UAVs. Actuators 2021, 10, 119. [Google Scholar] [CrossRef]
- Ducard, G.; Carughi, G. Neural network design and training for longitudinal flight control of a tilt-rotor hybrid vertical takeoff and landing unmanned aerial vehicle. Drones 2024, 8, 727. [Google Scholar] [CrossRef]
- Han, J.Q. From PID to active disturbance rejection control. IEEE Trans. Ind. Electron. 2009, 56, 900–906. [Google Scholar] [CrossRef]
- Gao, J.; Gao, S.; Chen, Y. Research on Anti-wind Disturbance Controller of Tiltrotor UAV Based on ADRC. In Proceedings of the 2024 IEEE 4th International Conference on Data Science and Computer Application (ICDSCA), Dalian, China, 22–24 November 2024; pp. 842–848. [Google Scholar]
- Deng, B.; Xu, J.; Yuan, X. Active disturbance rejection flight control and simulation of unmanned quad tilt rotor eVTOL based on adaptive neural network. Drones 2024, 8, 560. [Google Scholar] [CrossRef]
- Ren, B.W.; Du, S.L.; Cui, Z.Z. High-precision trajectory tracking control of helicopter based on ant colony optimization-slime mould algorithm. Chin. J. Aeronaut. 2025, 38, 103172. [Google Scholar] [CrossRef]
- Shen, S.; Xu, J. Attitude active disturbance rejection control of the quadrotor and its parameter tuning. Int. J. Aerosp. Eng. 2020, 2020, 8876177. [Google Scholar] [CrossRef]
- Liu, N.J.; Cai, Z.H.; Jiang, Z. Predictor-based model reference adaptive roll and yaw control of a quad-tiltrotor UAV. Chin. J. Aeronaut. 2020, 33, 282–295. [Google Scholar] [CrossRef]
- Saif, A.W.A. Feedback linearization control of quadrotor with tiltable rotors under wind gusts. Int. J. Adv. Appl. Sci. 2017, 4, 150–159. [Google Scholar] [CrossRef]
- Wang, Z.; Li, J.; Duan, D. Manipulation strategy of tilt quad rotor based on active disturbance rejection control. J. Aerosp. Eng. 2020, 234, 573–584. [Google Scholar] [CrossRef]
- Elfeky, M.; Elshafei, M.; Saif, A.W.A.; Al-Malki, M.F. Quadrotor with tiltable rotors for manned applications. In Proceedings of the 2014 IEEE 11th International Multi-Conference on Systems, Castelldefels, Spain, 11–14 February 2014; pp. 1–5. [Google Scholar]
- Hua, C.; Wang, K.; Chen, J.N. Tracking differentiator and extended state observer-based nonsingular fast terminal sliding mode attitude control for a quadrotor. Nonlinear Dyn. 2018, 94, 343–354. [Google Scholar] [CrossRef]
- Liang, Z.; Fan, L.; Wen, G.; Xu, Z. Design, modeling, and control of a composite tilt-rotor unmanned aerial vehicle. Drones 2024, 8, 102. [Google Scholar] [CrossRef]
- Sharkawy, A.N. Principle of neural network and its main types. J. Adv. Appl. Comput. Math. 2020, 7, 8–19. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Prentice Hall: Upper Saddle River, NJ, USA, 1994; pp. 409–412. [Google Scholar]
- Ding, H.; Liu, S.; Wang, Z. An ADRC parameters self-tuning controller based on RBF neural network for multi-color register system. Machines 2023, 11, 320. [Google Scholar] [CrossRef]
- Jie, L.; Yuanqing, X. On stability analysis of nonlinear ADRC-based control system with application to inverted pendulum problems. J. Syst. Eng. Electron. 2024, 35, 1563–1573. [Google Scholar]
- Li, J.; Qi, X.; Xia, Y. Research on linear/nonlinear active disturbance rejection switching control method. Acat Autom. Sin. 2016, 42, 202–212. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).