Low-Order Modelling of Extinction of Hydrogen Non-Premixed Swirl Flames
Abstract
1. Introduction
2. Methods
2.1. Governing Equation
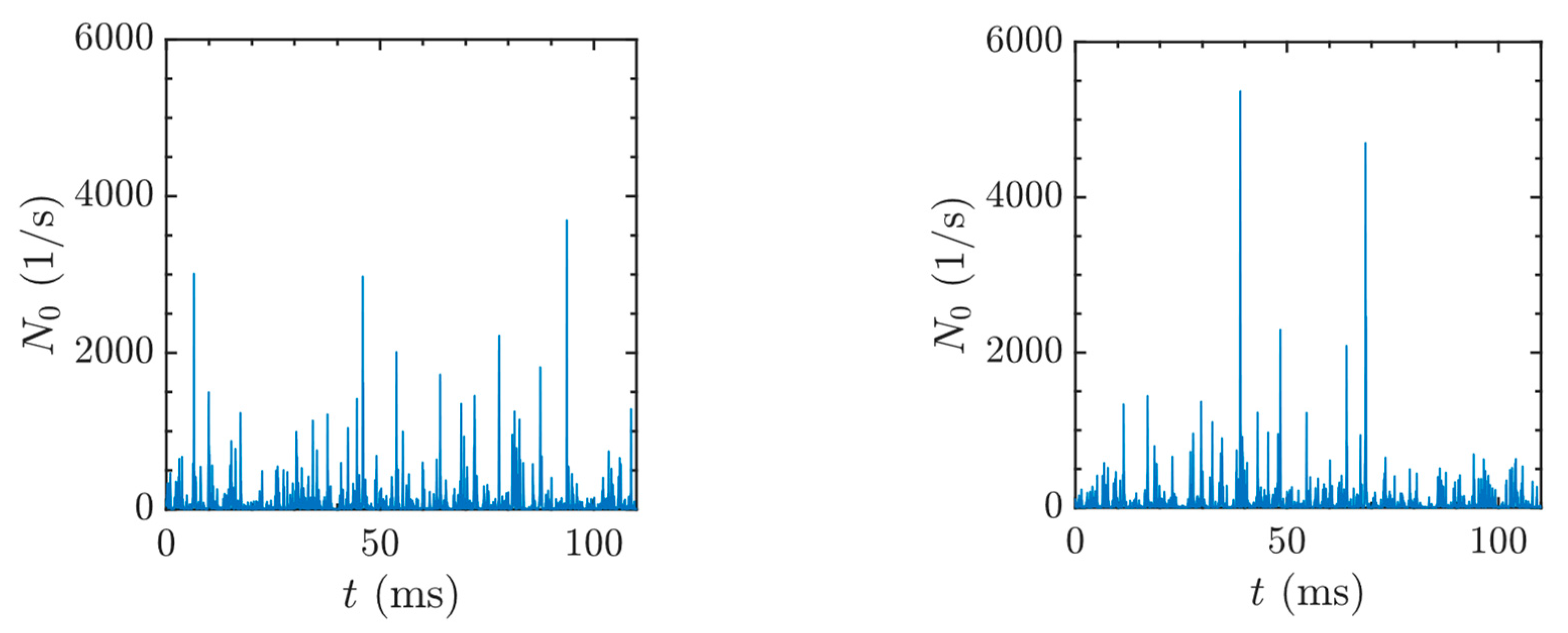
2.2. Extraction of sISR Parameters from CFD
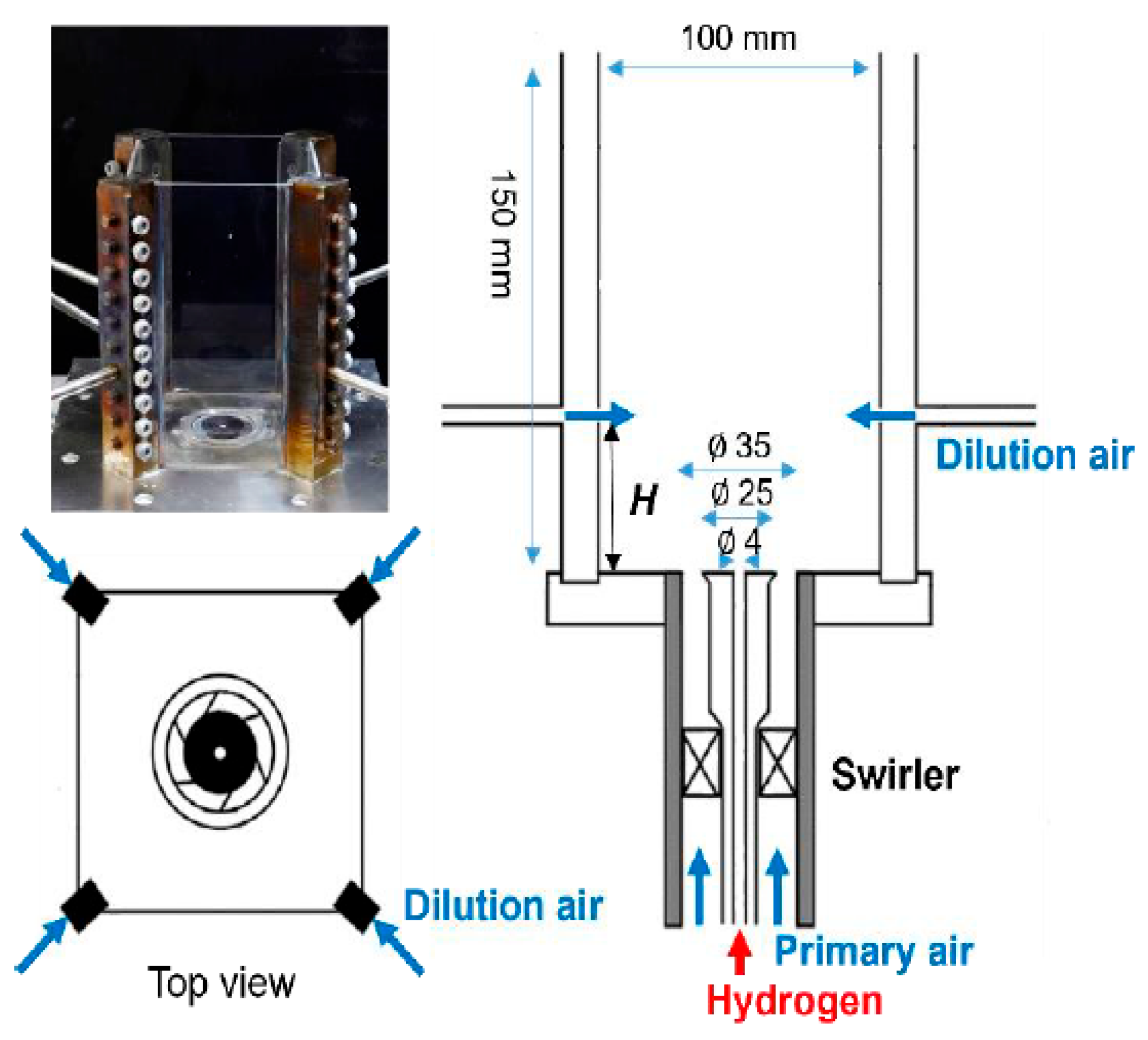
2.3. Investigated Combustor
2.4. Methodology and Numerical Implementation
- (1)
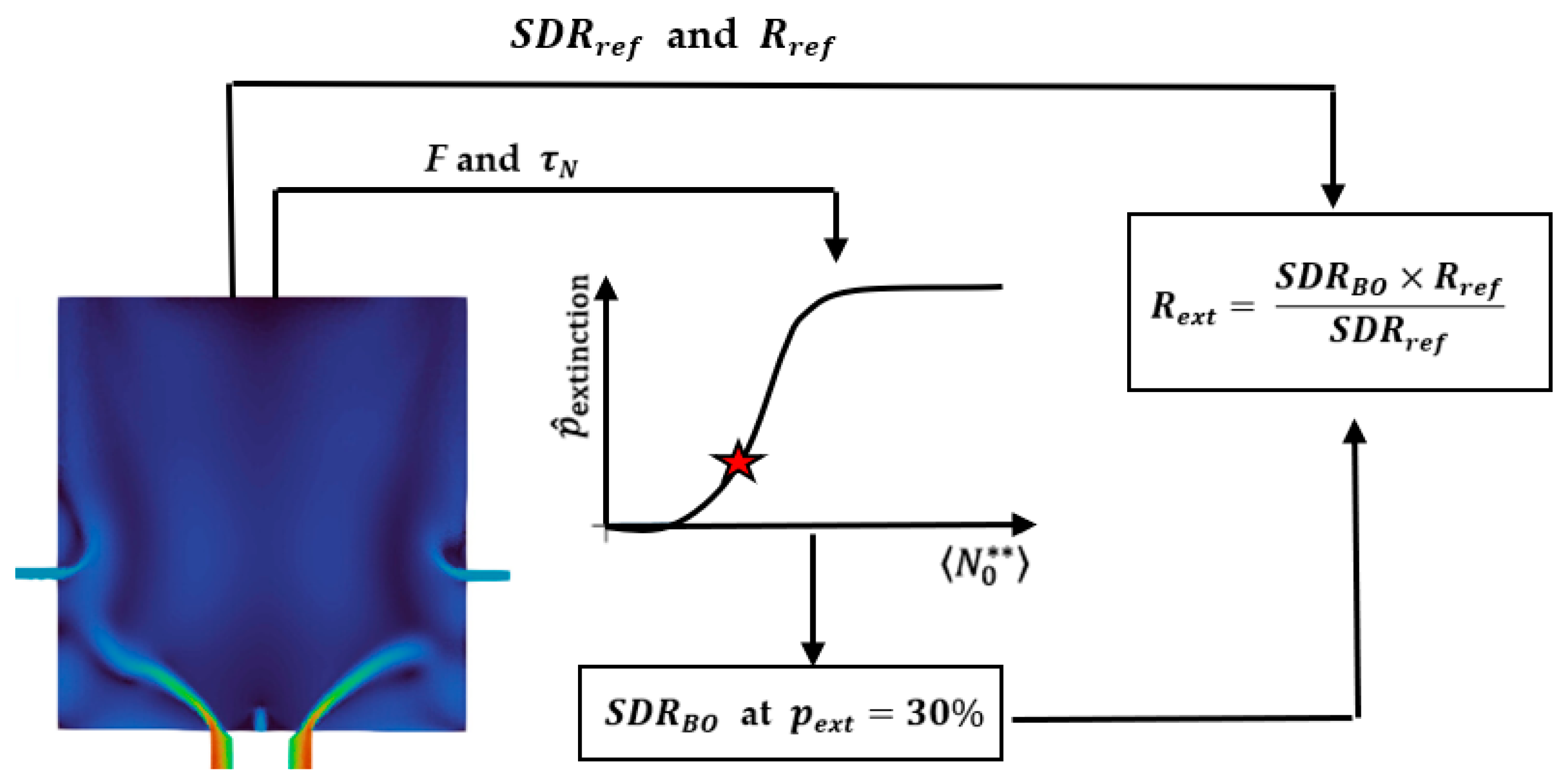
- Parameter Extraction from CFD: Key parameters—including SDR, fluctuation parameter , and a characteristic timescale —are extracted from a reference CFD simulation corresponding to a known operating condition.
- (2)
- The Construction of Extinction Probability Map: A series of sISR simulations is performed over a broad range of SDR values at the fixed values of and obtained in Step 1. These simulations yield extinction probabilities, from which an extinction probability map is constructed. The map is then refined by averaging the extinction probabilities over additional sets of and to ensure robustness. The extinction SDR is obtained at an extinction probability that corresponds to 30%.
- (3)
- The Identification of Extinction SDR: From the probability map, the critical SDR corresponding to an extinction probability of 30% is identified and defined as the extinction SDR.
- (4)
- Estimation of Extinction Dilution Ratio: Finally, the extinction dilution ratio is estimated by scaling the reference dilution ratio using the ratio of extinction SDR (step 3) to the reference SDR (step 1). A schematic of the sISR prediction methodology is shown in Figure 2 and more details can be found in Ref. [6].
3. Results
3.1. Cold-Flow Reference Simulations
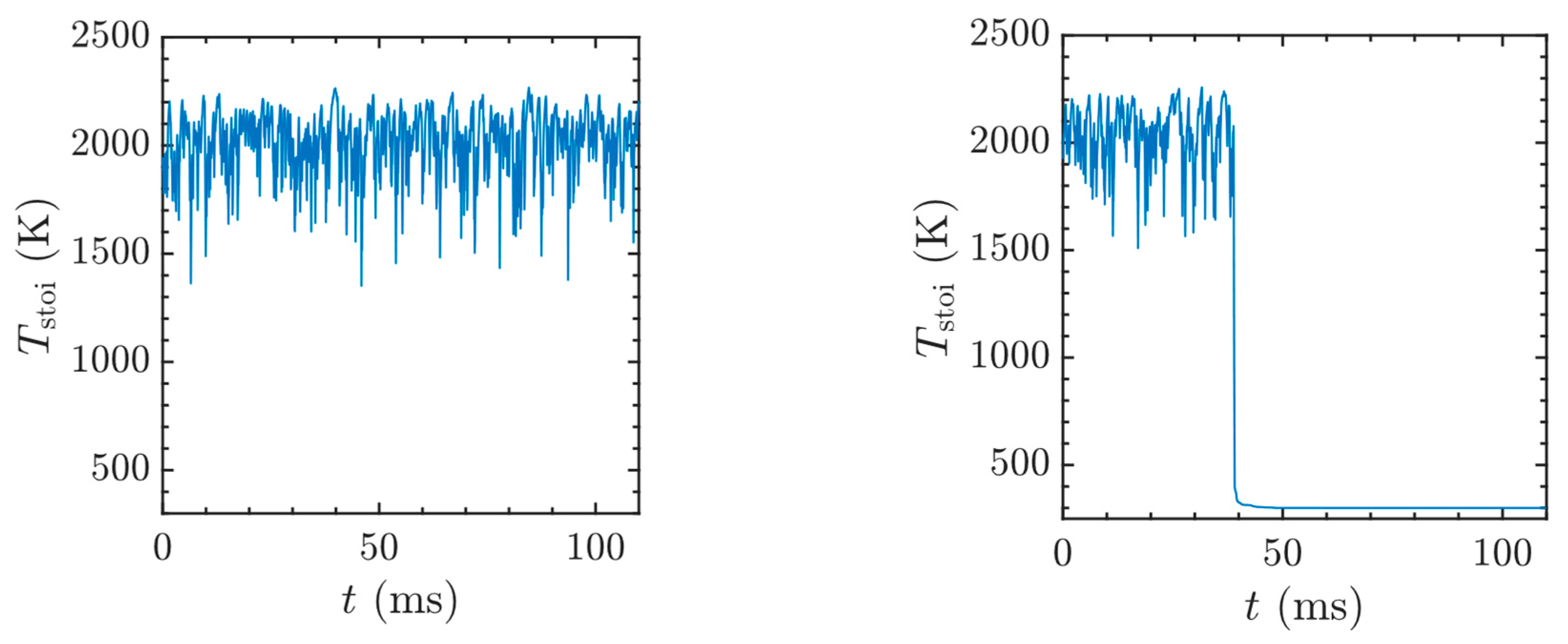
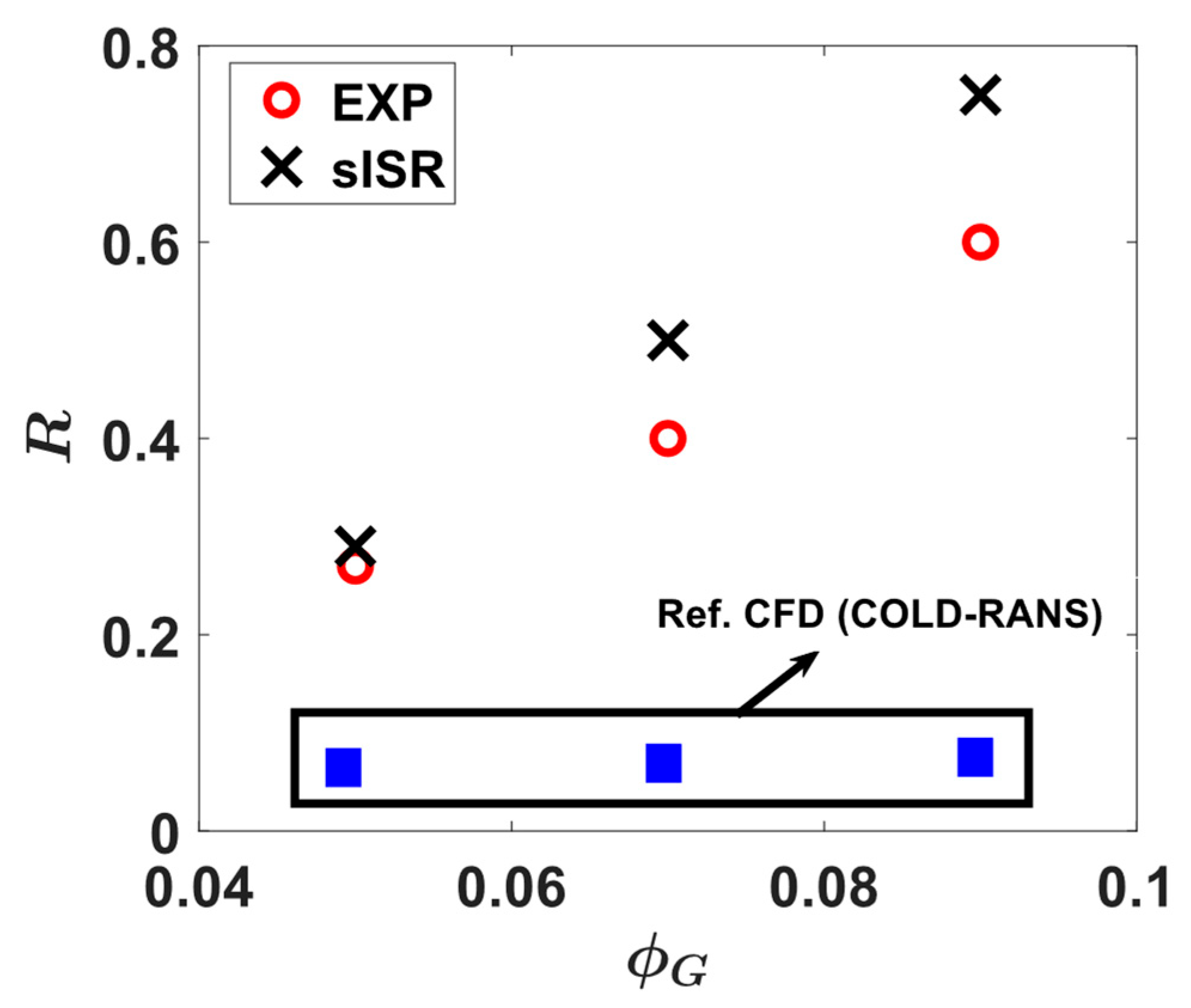
3.2. Extinction Probability
3.3. LBO Curve and Blow-Off Dilution Ratio Predictions
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Alhuyi Nazari, M.; Fahim Alavi, M.; Salem, M.; Assad, M.E.H. Utilization of hydrogen in gas turbines: A comprehensive review. Int. J. Low-Carbon Technol. 2022, 17, 513–519. [Google Scholar] [CrossRef]
- Straub, D.L.; Casleton, K.H.; Lewis, R.E.; Sidwell, T.G.; Maloney, D.J.; Richards, G.A. Assessment of rich-burn, quick-mix, lean-burn trapped vortex combustor for stationary gas turbines. J. Eng. Gas Turbines Power 2005, 127, 36–41. [Google Scholar] [CrossRef]
- Choe, J.; Mastorakos, E. Influence of side dilution jets on flame extinction and nitric oxide reduction in a hydrogen-fueled model gas turbine combustor. In Proceedings of the Mediterranean Combustion Symposium, Corfu, Greece, 1–5 June 2025. [Google Scholar]
- Awad, H.S.A.M.; Gkantonas, S.; Choe, J.; Mastorakos, E. The influence of side dilution jets on the flame stabilization mechanism and NOx emissions in a hydrogen-fuelled model gas turbine combustor. In Proceedings of the 12th European Combustion Meeting, Edinburgh, UK, 7–10 April 2025. [Google Scholar]
- Zhang, H.; Mastorakos, E. Prediction of global extinction conditions and dynamics in swirling non-premixed flames using LES/CMC modelling. Flow Turbul. Combust. 2016, 96, 863–889. [Google Scholar] [CrossRef]
- Gkantonas, S.; Mastorakos, E. Development of a low-order model of turbulent non-premixed flame global flow-off. Int. J. Spray Combust. Dyn. 2025. submitted. [Google Scholar]
- Mobini, K.; Bilger, R.W. Imperfectly Stirred Reactor Model Predictions of Reaction in a Burner with Strong Recirculation. Combust. Sci. Technol. 2004, 176, 45–70. [Google Scholar] [CrossRef]
- Gough, A.J.; Mobini, K.; Chen, Y.C.; Bilger, R.W. Measurements and Predictions in a Confined Bluff-Body Burner Modeled as an Imperfectly Stirred Reactor. Proc. Combust. Inst. 1998, 27, 3181–3188. [Google Scholar] [CrossRef]
- Klimenko, A.Y.; Bilger, R.W. Conditional moment closure for turbulent combustion. Prog. Energy Combust. Sci. 1999, 25, 595–687. [Google Scholar] [CrossRef]
- Sevault, A.; Dunn, M.; Barlow, R.S.; Ditaranto, M. On the structure of the near field of oxy-fuel jet flames using Raman/Rayleigh laser diagnostics. Combust. Flame 2012, 159, 3342–3352. [Google Scholar] [CrossRef]
- Barlow, R.S.; Frank, J.H. Effects of turbulence on species mass fractions in methane/air jet flames. Symp. Combust. 1998, 27, 1087–1095. [Google Scholar] [CrossRef]
- Ihme, M.; Pitsch, H. Modeling of radiation and nitric oxide formation in turbulent nonpremixed flames using a flamelet/progress variable formulation. Phys. Fluids 2008, 20, 055110. [Google Scholar] [CrossRef]
- Wandel, A.P.; Lindstedt, R.P. Hybrid multiple mapping conditioning modeling of local extinction. Proc. Combust. Inst. 2013, 34, 1365–1372. [Google Scholar] [CrossRef]
- Xu, J.; Pope, S.B. PDF Calculations of Turbulent Nonpremixed Flames with Local Extinction. Combust. Flame 2000, 123, 281–307. [Google Scholar] [CrossRef]
- Gkantonas, S. Predicting Soot Emissions with Advanced Turbulent Reacting Flow Modelling. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2021. [Google Scholar]
- Awad, H.S.A.M.; Gkantonas, S.; Mastorakos, E. A spark energy deposition model in mixture fraction space for simulations of turbulent non-premixed flame ignition. Appl. Energy Combust. Sci. 2025, 21, 100317. [Google Scholar] [CrossRef]
- O’Brien, E.E.; Jiang, T.L. The conditional dissipation rate of an initially binary scalar in homogeneous turbulence. Phys Fluids 1991, 12, 3121–3123. [Google Scholar] [CrossRef]
- Pitsch, H.; Fedotov, S. Investigation of scalar dissipation rate fluctuations in non-premixed turbulent combustion using a stochastic approach. Combust. Theory Model. 2001, 51, 41. [Google Scholar] [CrossRef]
- Gkantonas, S.; Mastorakos, E. Stochastic modelling for the effects of micromixing on soot in turbulent non-premixed flames. Combust. Theory Model. 2024, 28, 849–872. [Google Scholar] [CrossRef]
- Vedula, P.; Yeung, P.K.; Fox, R.O. Dynamics of scalar dissipation in isotropic turbulence: A numerical and modelling study. J. Fluid Mech. 2001, 433, 29–60. [Google Scholar] [CrossRef]
- Hong, Z.; Davidson, D.F.; Hanson, R.K. An improved H2/O2 mechanism based on recent shock tube/laser absorption measurements. Comb. Flame 2011, 158, 633–644. [Google Scholar] [CrossRef]
- Anand, M.S.; Eggels, R.L.G.M.; Staufer, M.; Zedda, M.; Zhu, J. An advanced unstructured-grid finite-volume design system for gas turbine combustion analysis. In Proceedings of the Gas Turbine India Conference, Bangalore, Karnataka, India, 5–6 December 2013; ASME: New York, NY, USA, 2013; Volume 35161, p. V001T03A003. [Google Scholar]
- Awad, H.S.A.M.; Gkantonas, S.; Mastorakos, E.; Eggels, R. Parametric analysis of hydrogen swirl combustors with incompletely stirred reactor network modelling. J. Propuls. Power 2025. submitted. [Google Scholar]
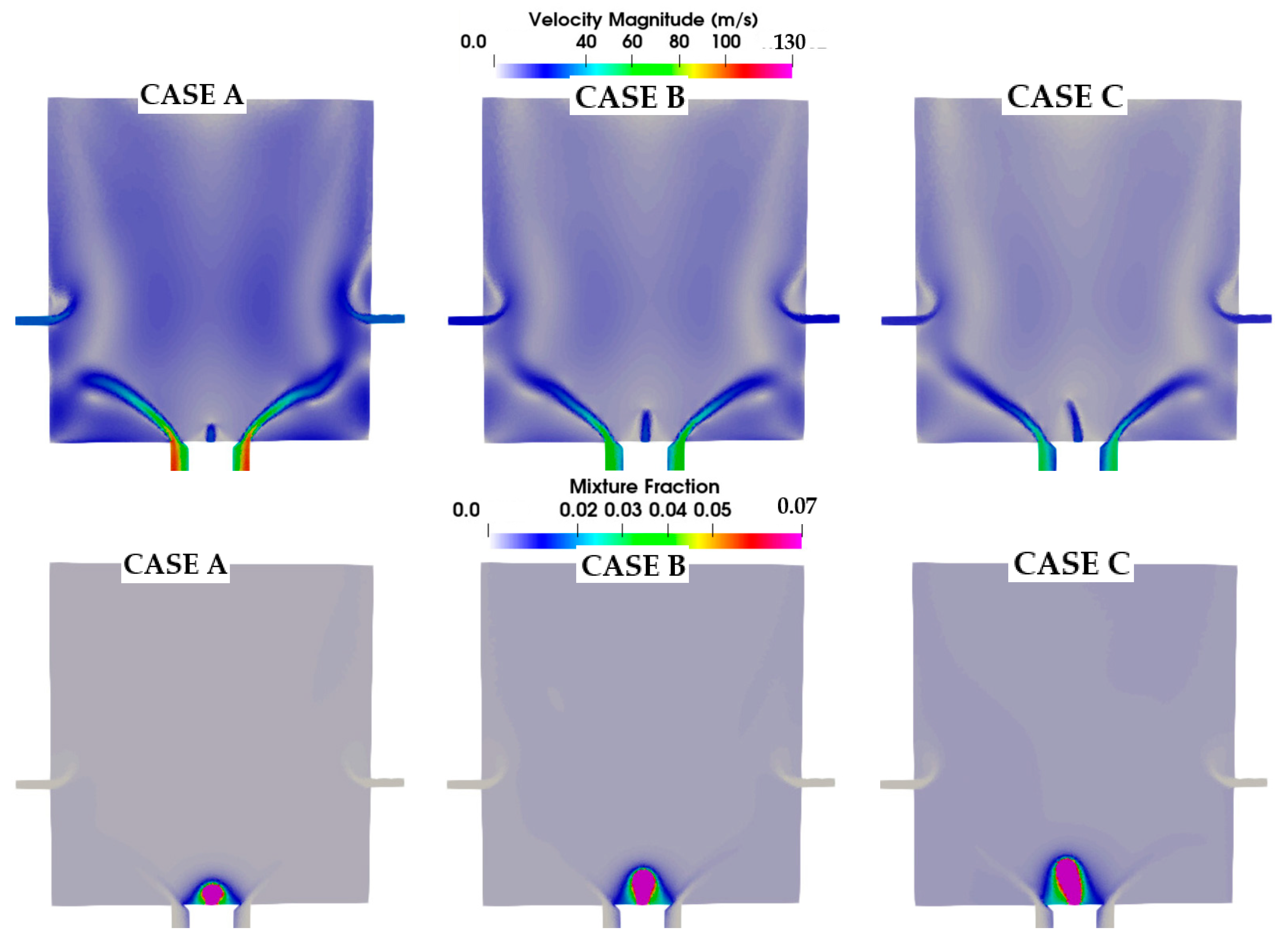


| Case | ||
|---|---|---|
| A | 0.05 | 0.1 |
| B | 0.07 | 0.1 |
| C | 0.09 | 0.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Awad, H.S.A.M.; Gkantonas, S.; Mastorakos, E. Low-Order Modelling of Extinction of Hydrogen Non-Premixed Swirl Flames. Aerospace 2025, 12, 676. https://doi.org/10.3390/aerospace12080676
Awad HSAM, Gkantonas S, Mastorakos E. Low-Order Modelling of Extinction of Hydrogen Non-Premixed Swirl Flames. Aerospace. 2025; 12(8):676. https://doi.org/10.3390/aerospace12080676
Chicago/Turabian StyleAwad, Hazem S. A. M., Savvas Gkantonas, and Epaminondas Mastorakos. 2025. "Low-Order Modelling of Extinction of Hydrogen Non-Premixed Swirl Flames" Aerospace 12, no. 8: 676. https://doi.org/10.3390/aerospace12080676
APA StyleAwad, H. S. A. M., Gkantonas, S., & Mastorakos, E. (2025). Low-Order Modelling of Extinction of Hydrogen Non-Premixed Swirl Flames. Aerospace, 12(8), 676. https://doi.org/10.3390/aerospace12080676