Numerical Study of the Late-Stage Flow Features and Stripping in Shock Liquid Drop Interaction
Abstract
1. Introduction
2. Numerical Models and Methods
2.1. Mathematical Formulation
- (1)
- Eulerian governing equations for the gas-phase blended with a turbulent model combined with the coupled level-set volume of fluid (CLSVOF) technique using the Ansys Fluent solver.
- (2)
- Discrete phase modelling (DPM) which employs a Lagrangian model for handling drop tracking and breakup. This model ensures that the location and speed of the drop are tracked promptly by taking into account the distortion of the drop. (1) and (2) are important because the SLDI is based on the simultaneous and consistent characterization of the gas and liquid phases.
- (3)
- The Kelvin–Helmholtz Rayleigh–Taylor (KHRT) breakup model for describing the disintegration of the liquid drop. The KHRT breakup model is activated in DPM in the Ansys Fluent solver to simulate the atomization process and to track the trajectory of the shed sub-droplets in the airflow.
2.1.1. Eulerian Governing Equations for the Supersonic Airflow
Turbulence Model
The CLSVOF Two-Phase Flow Model
2.1.2. Discrete Phase Modelling
Drop Trajectory Equations
Drop Trajectory Integration Schemes
KHRT Breakup Model
2.1.3. Discretization
2.2. Computational Details
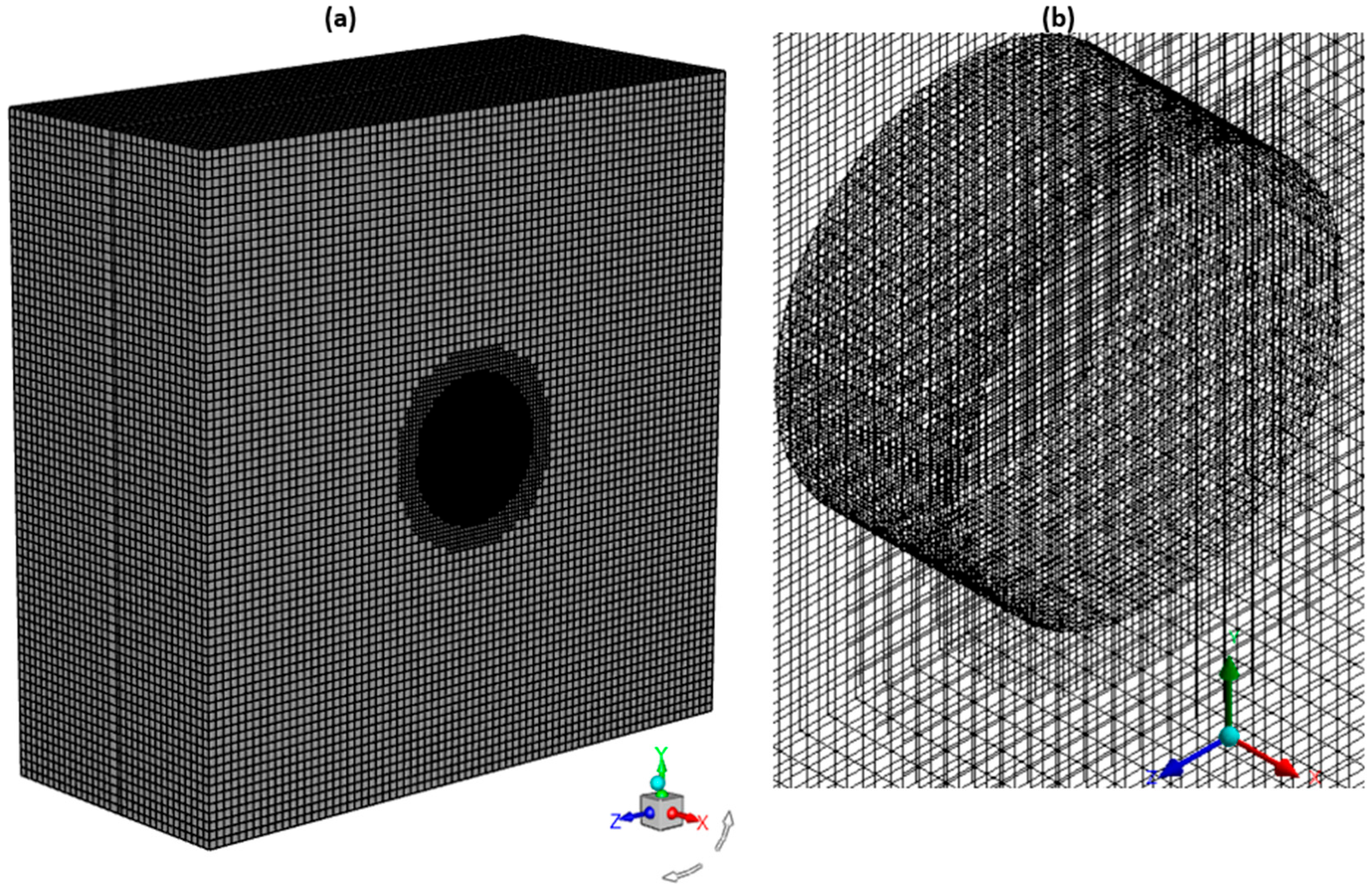
2.3. Mesh Independence Study
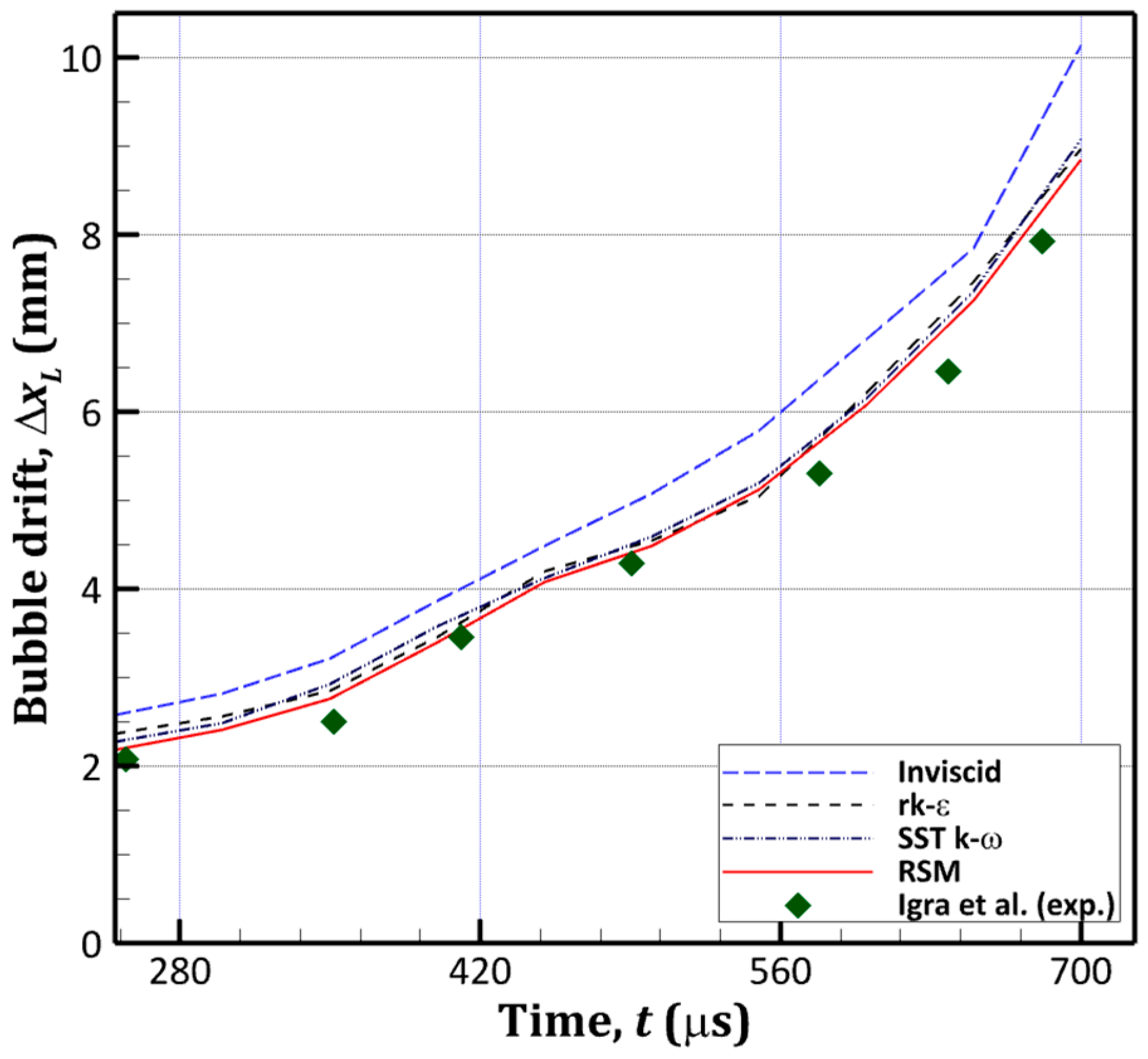
2.4. Turbulence Model Selection
3. Results and Discussions
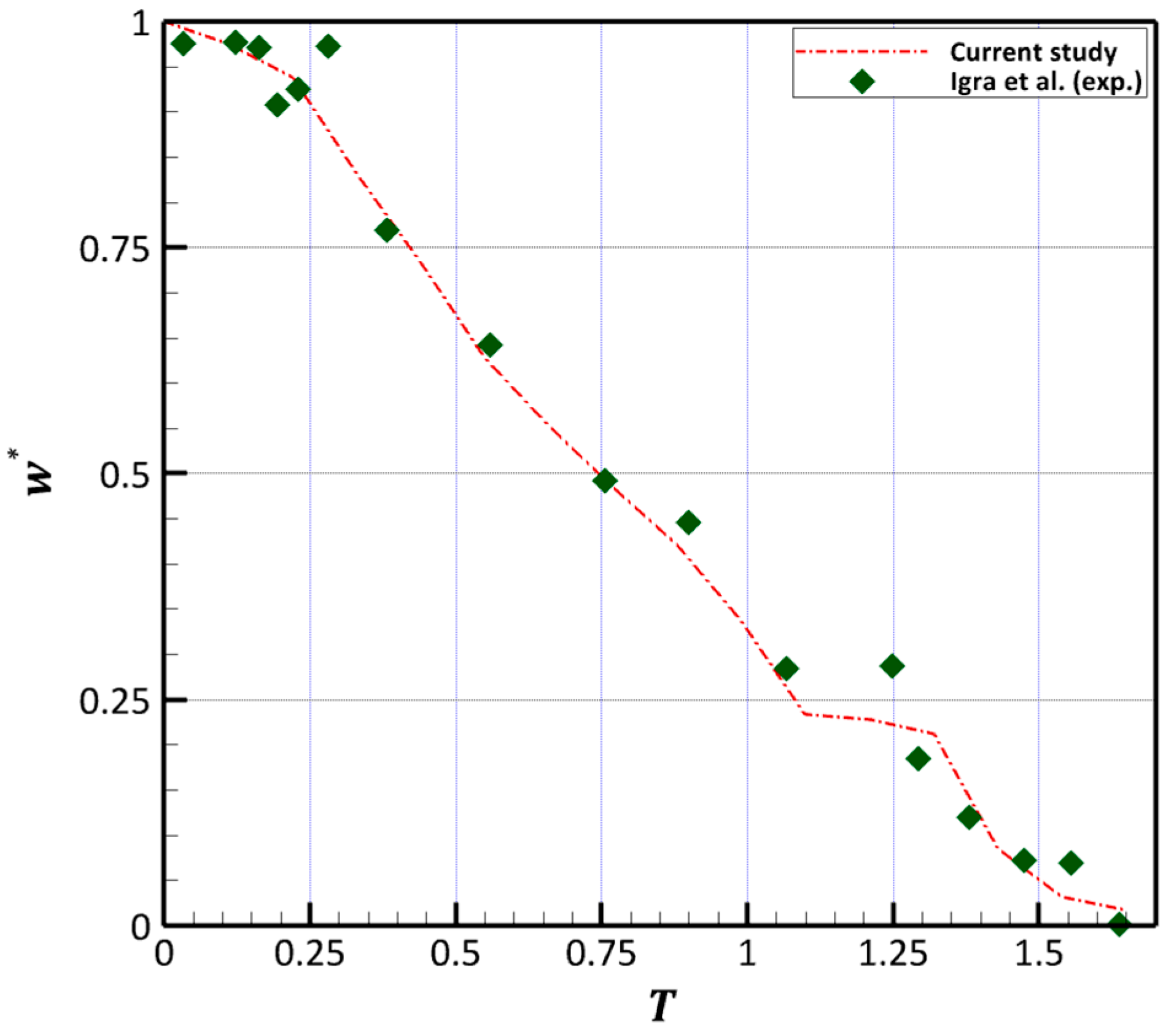
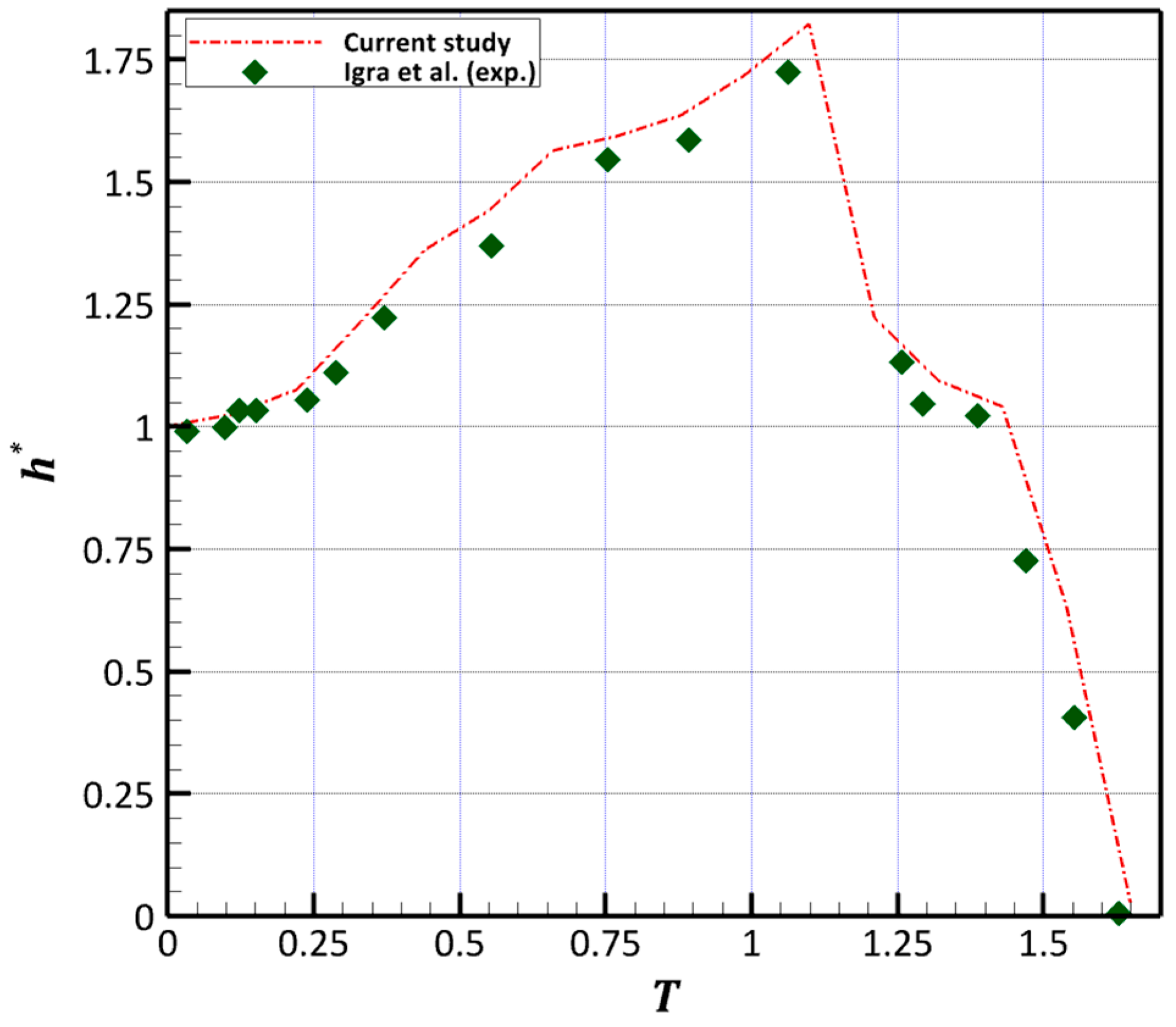
3.1. Predictions of the Temporal Changes of the Interfacial Characteristics Scales
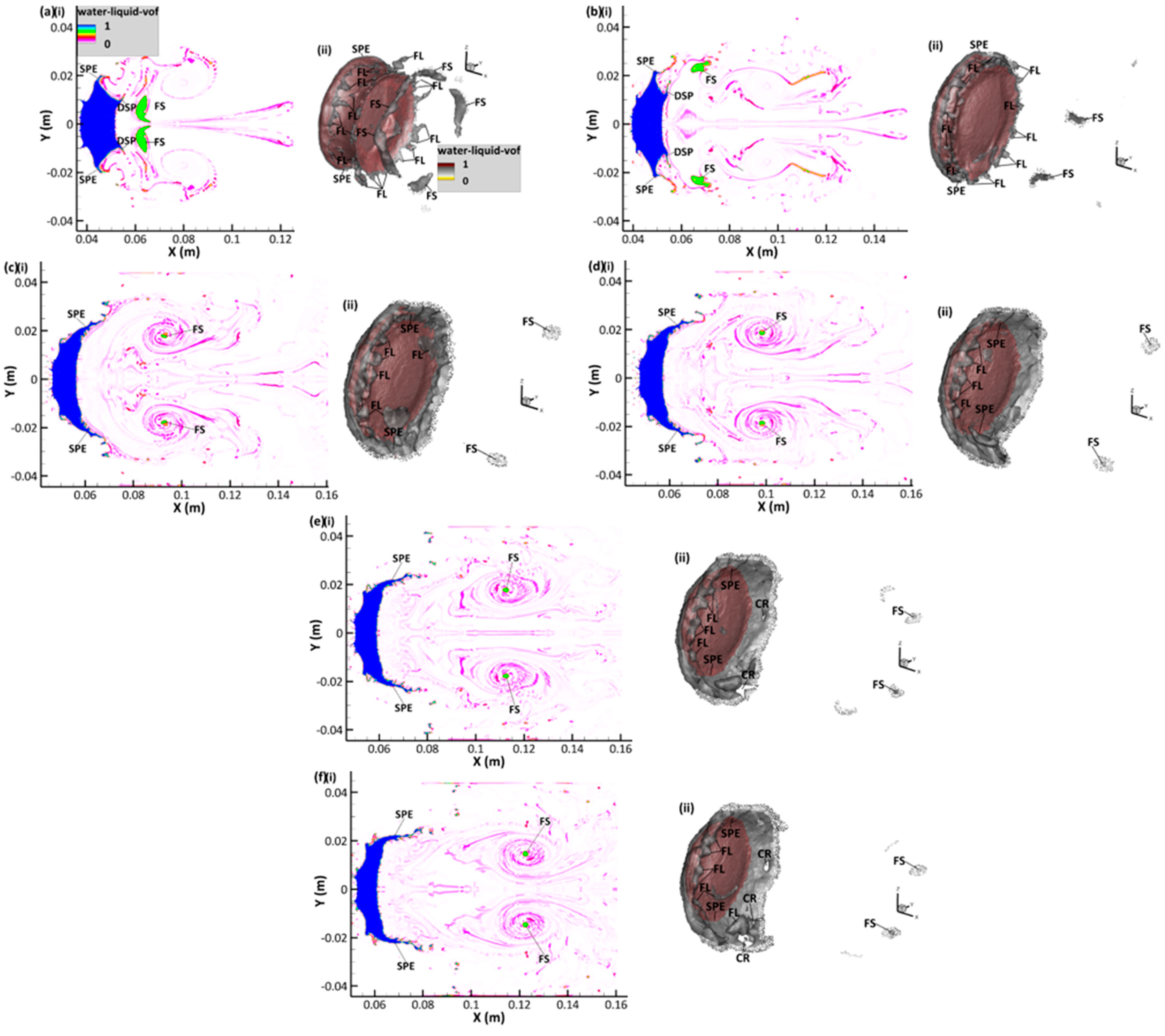
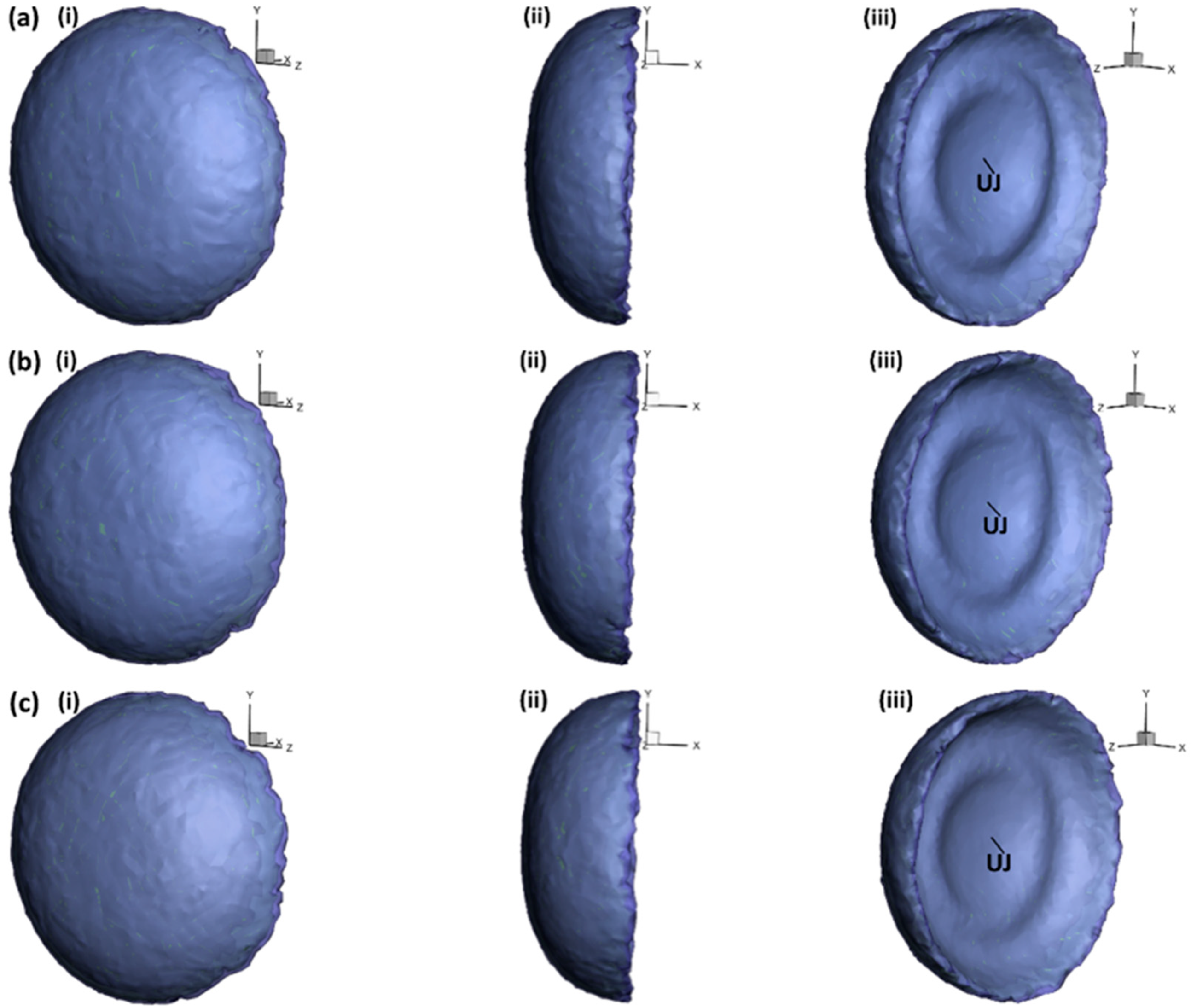
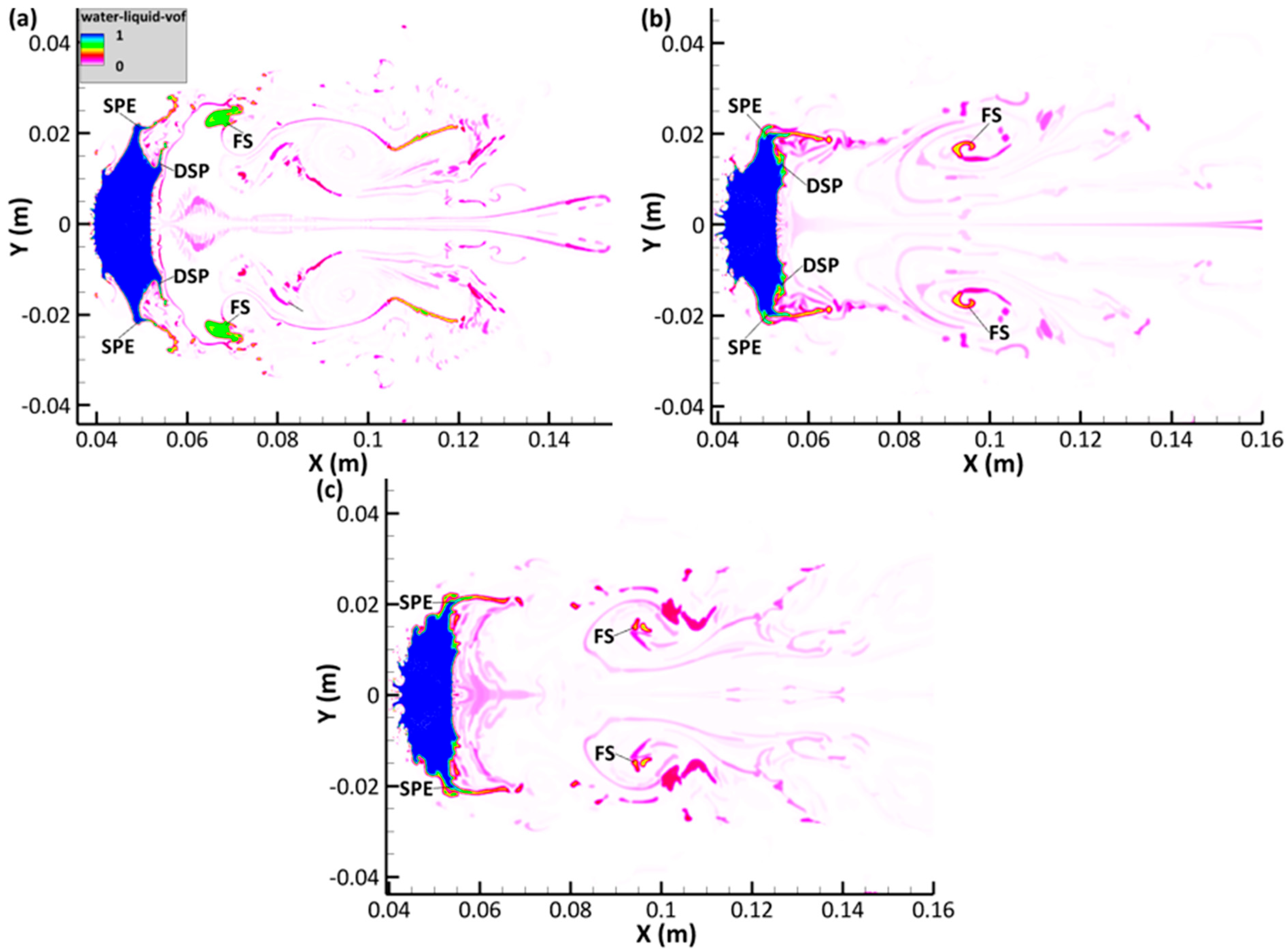
3.2. Stripping and Disintegration of the Liquid Drop
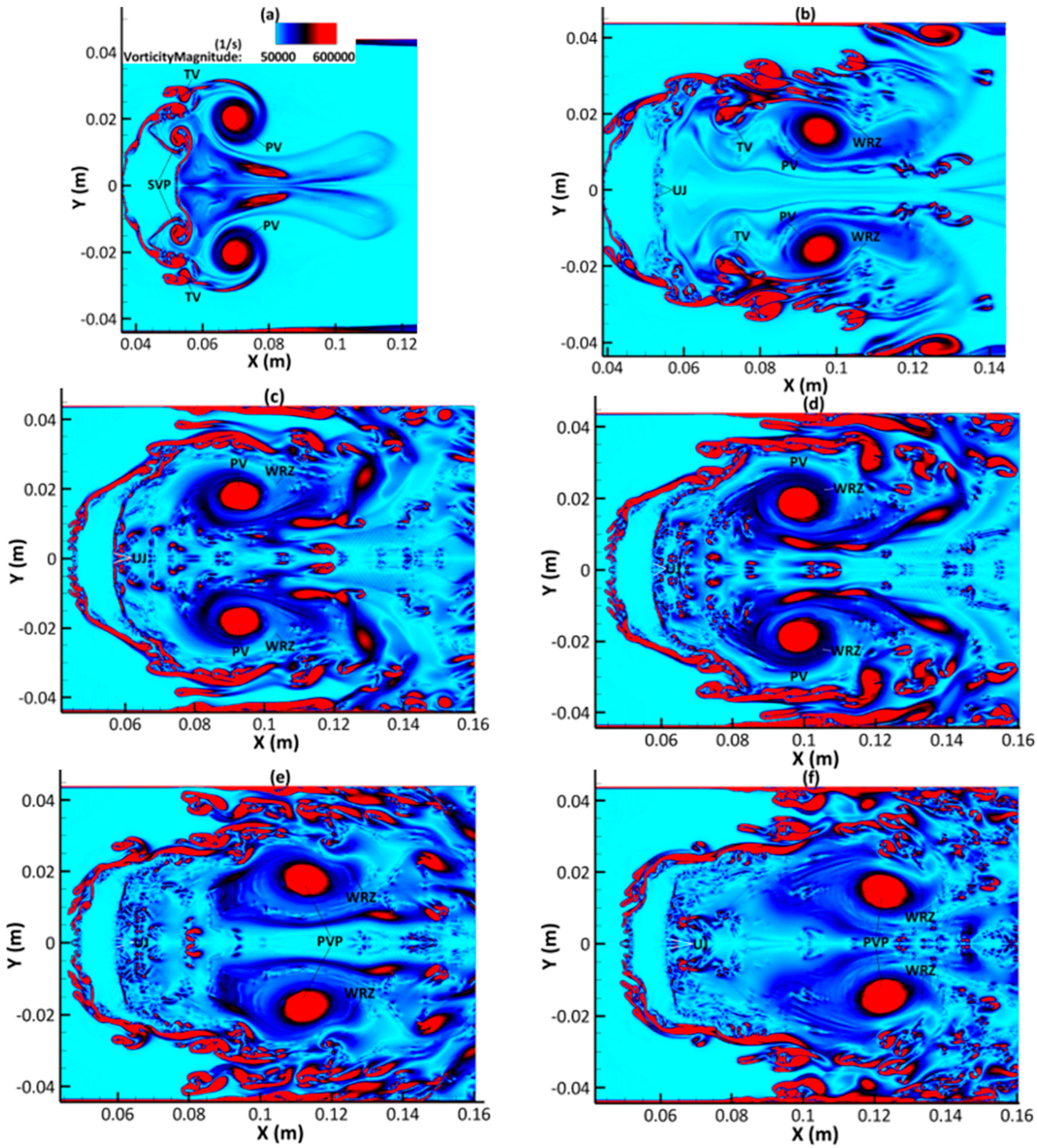
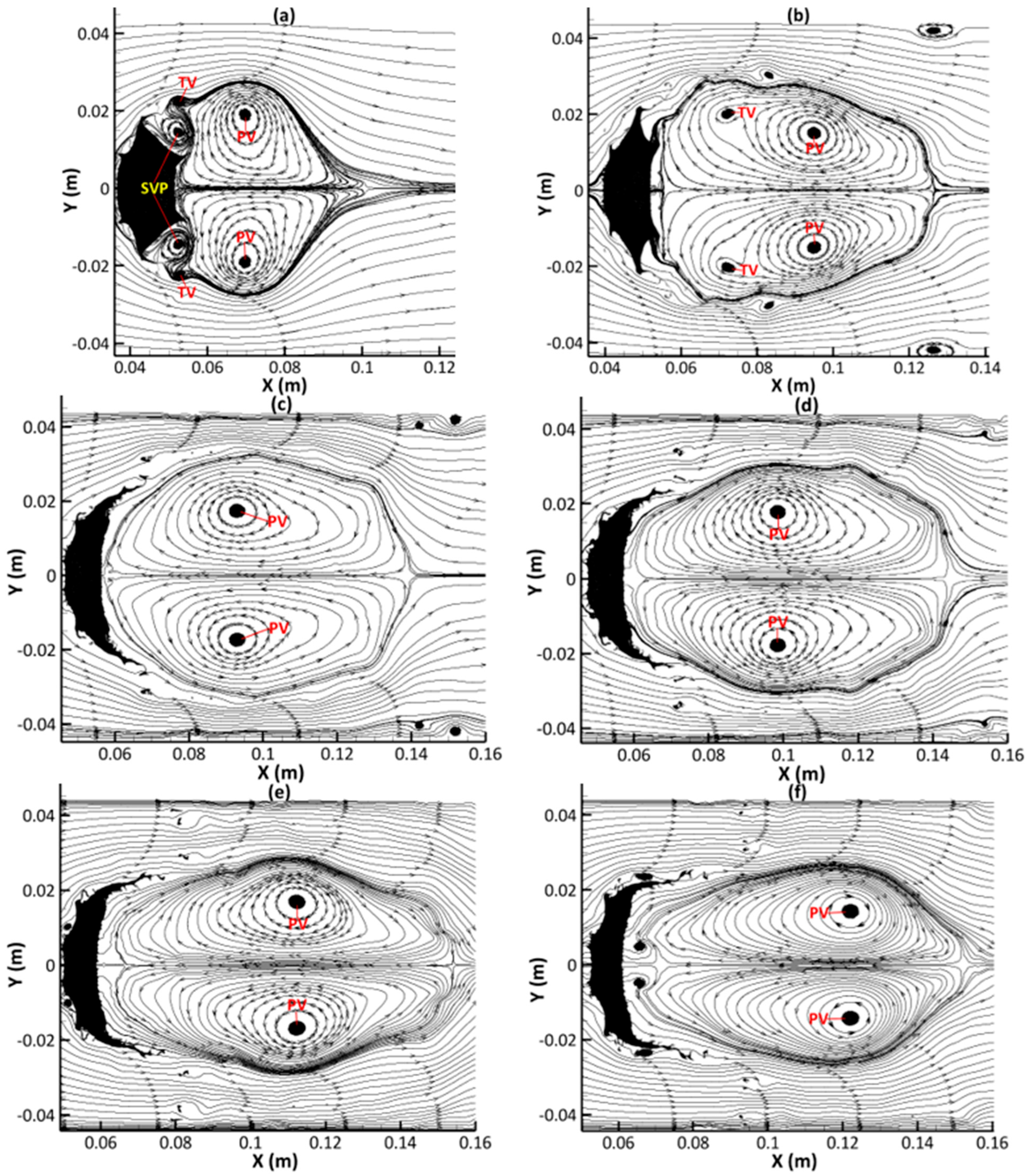
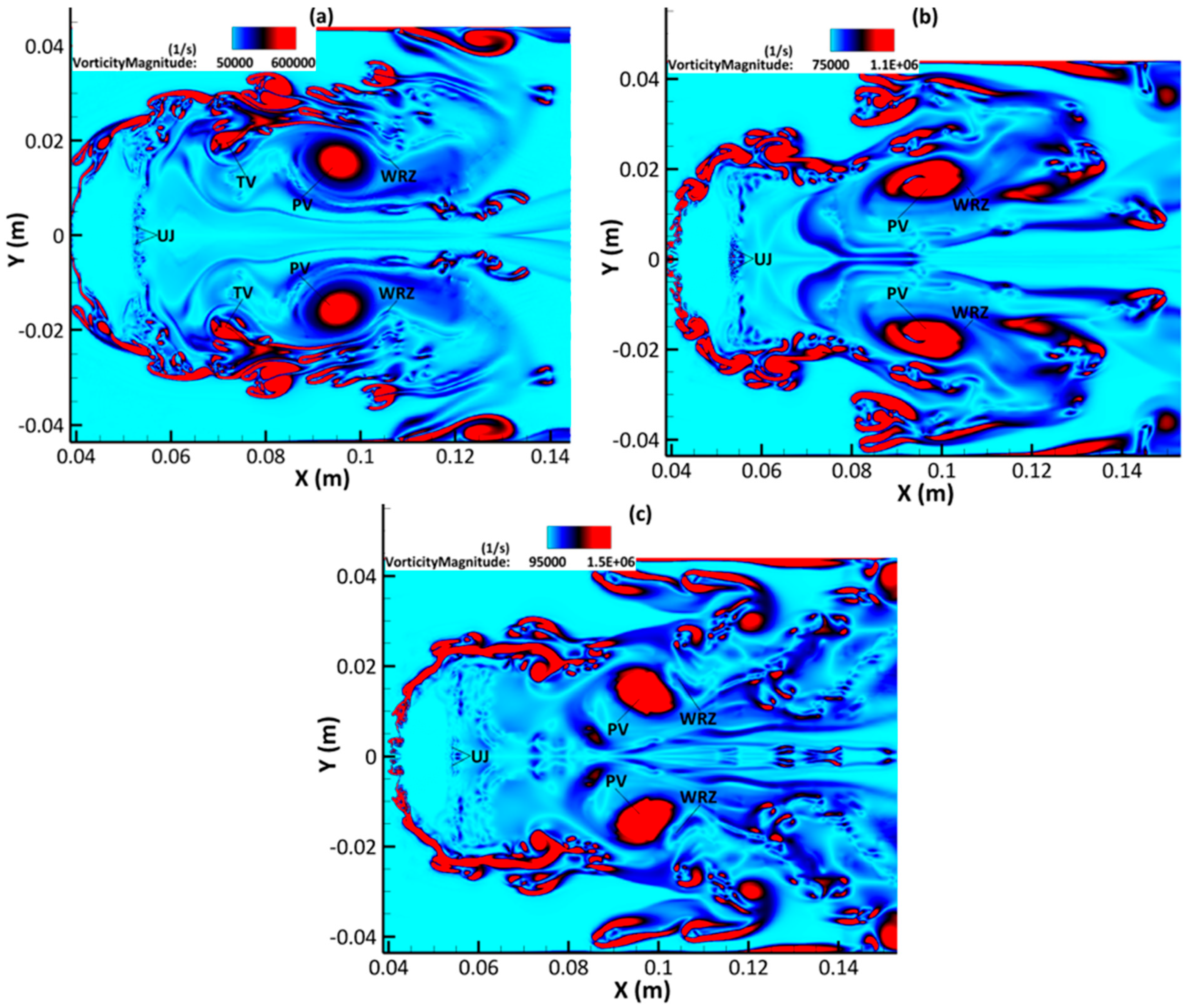
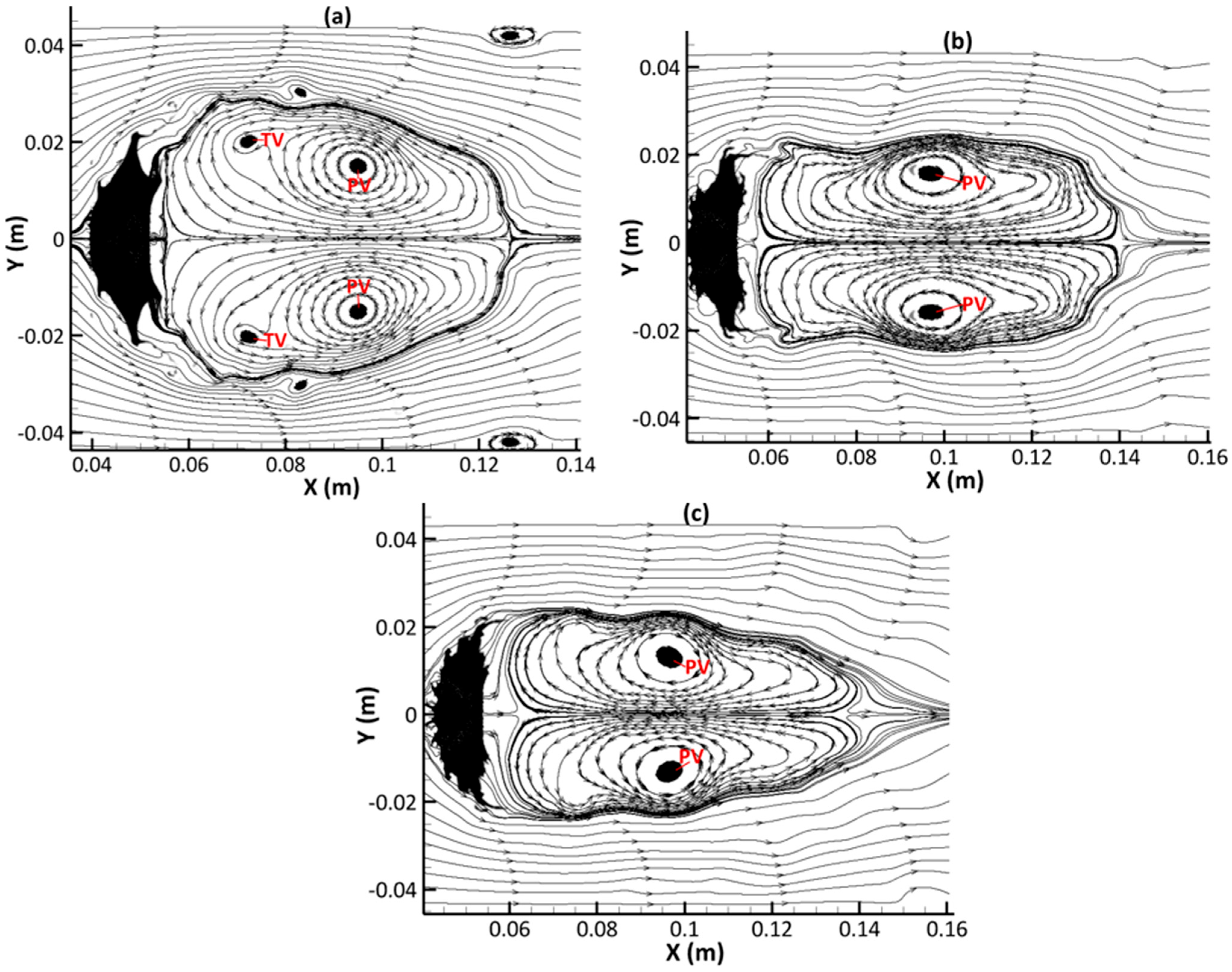
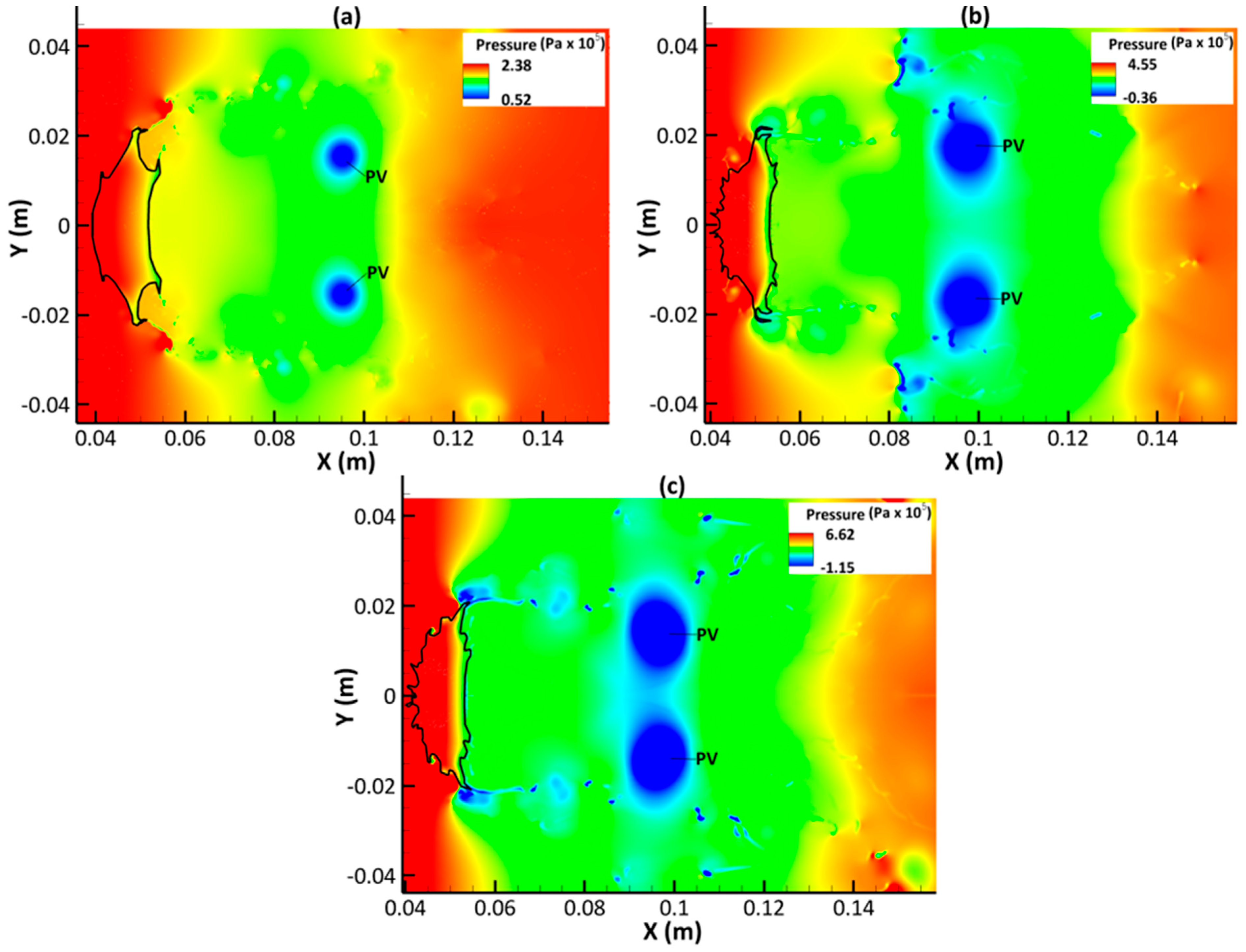
3.3. Dynamics of Vorticity Generation and Evolution
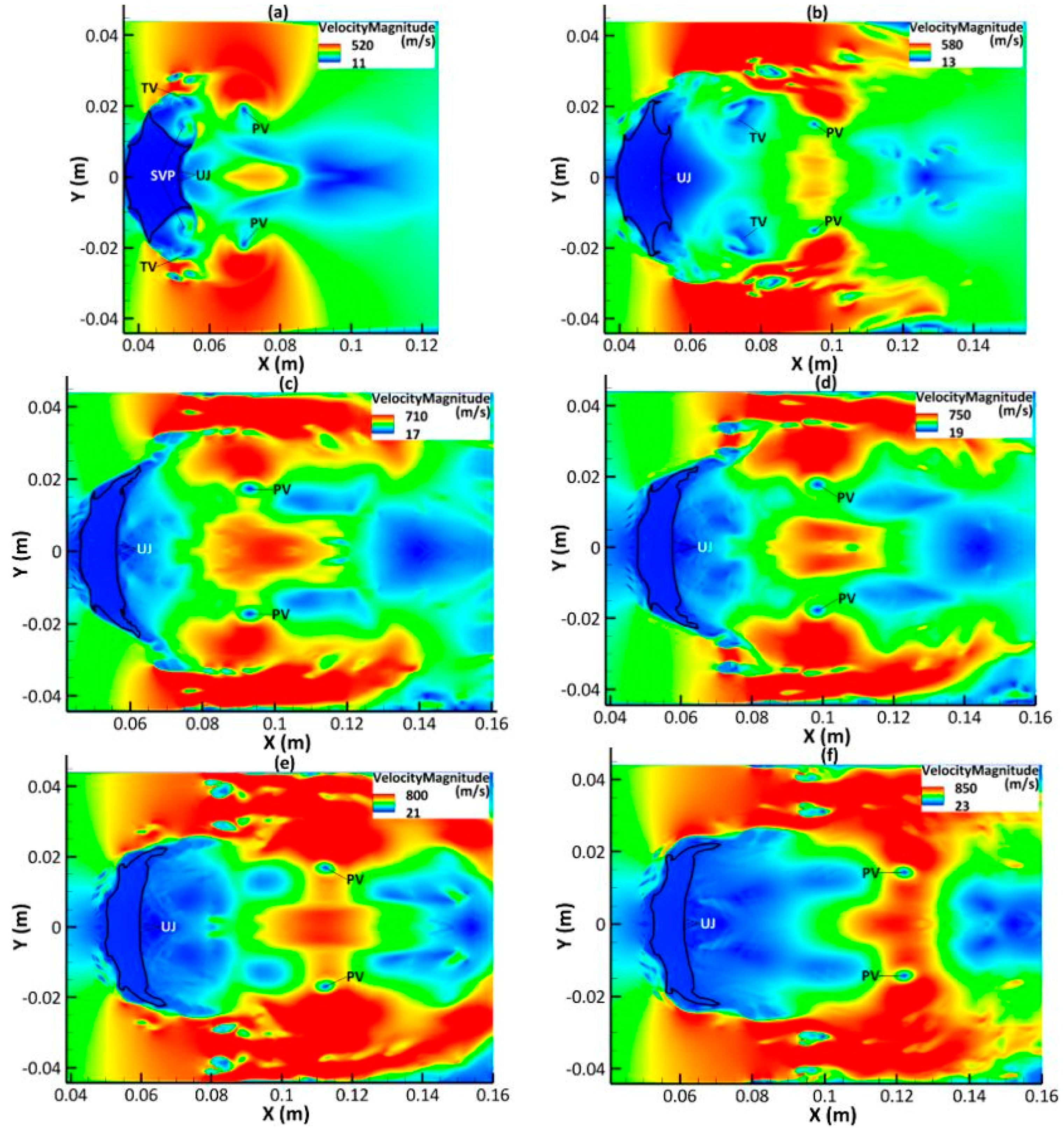
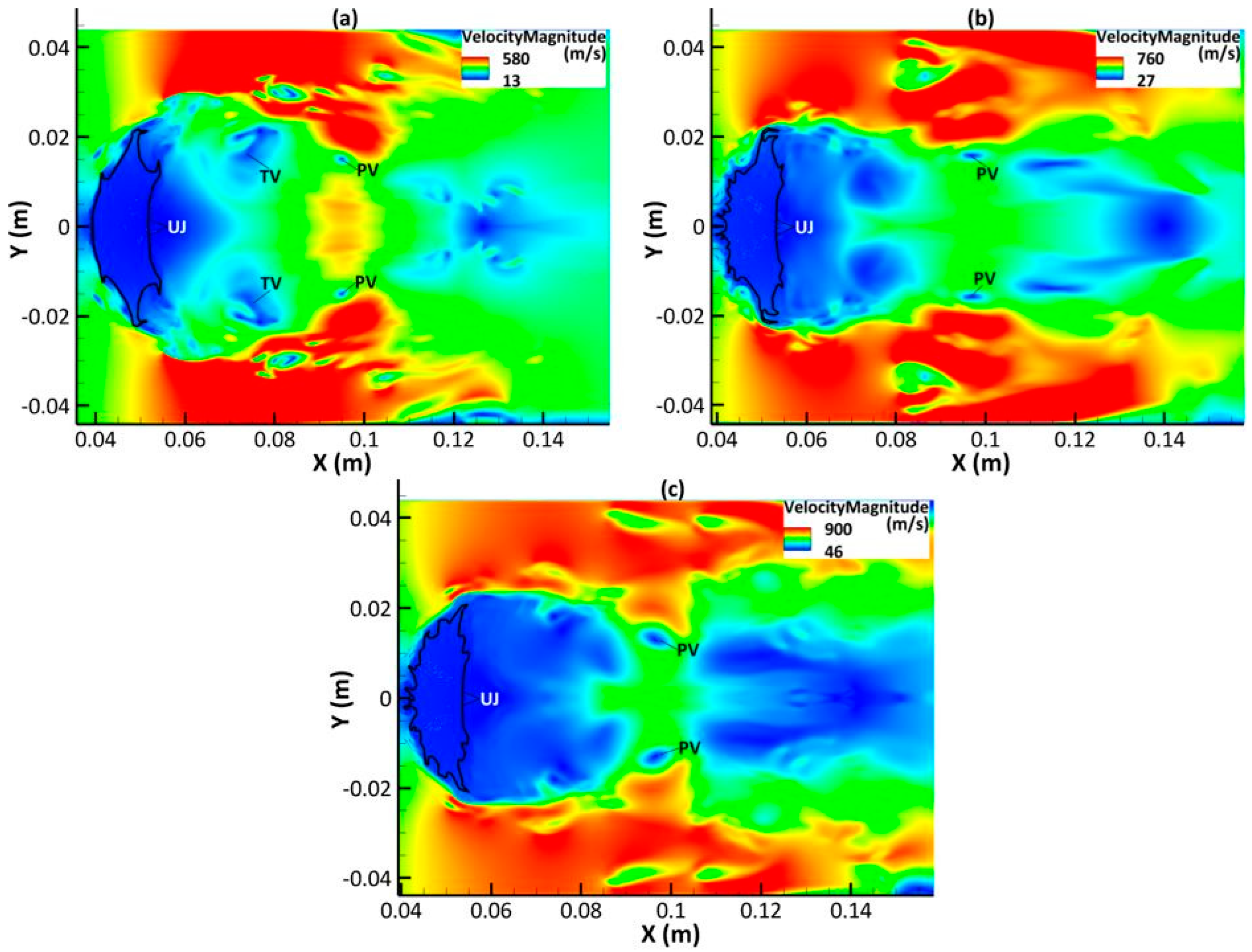
3.4. Velocity Distribution
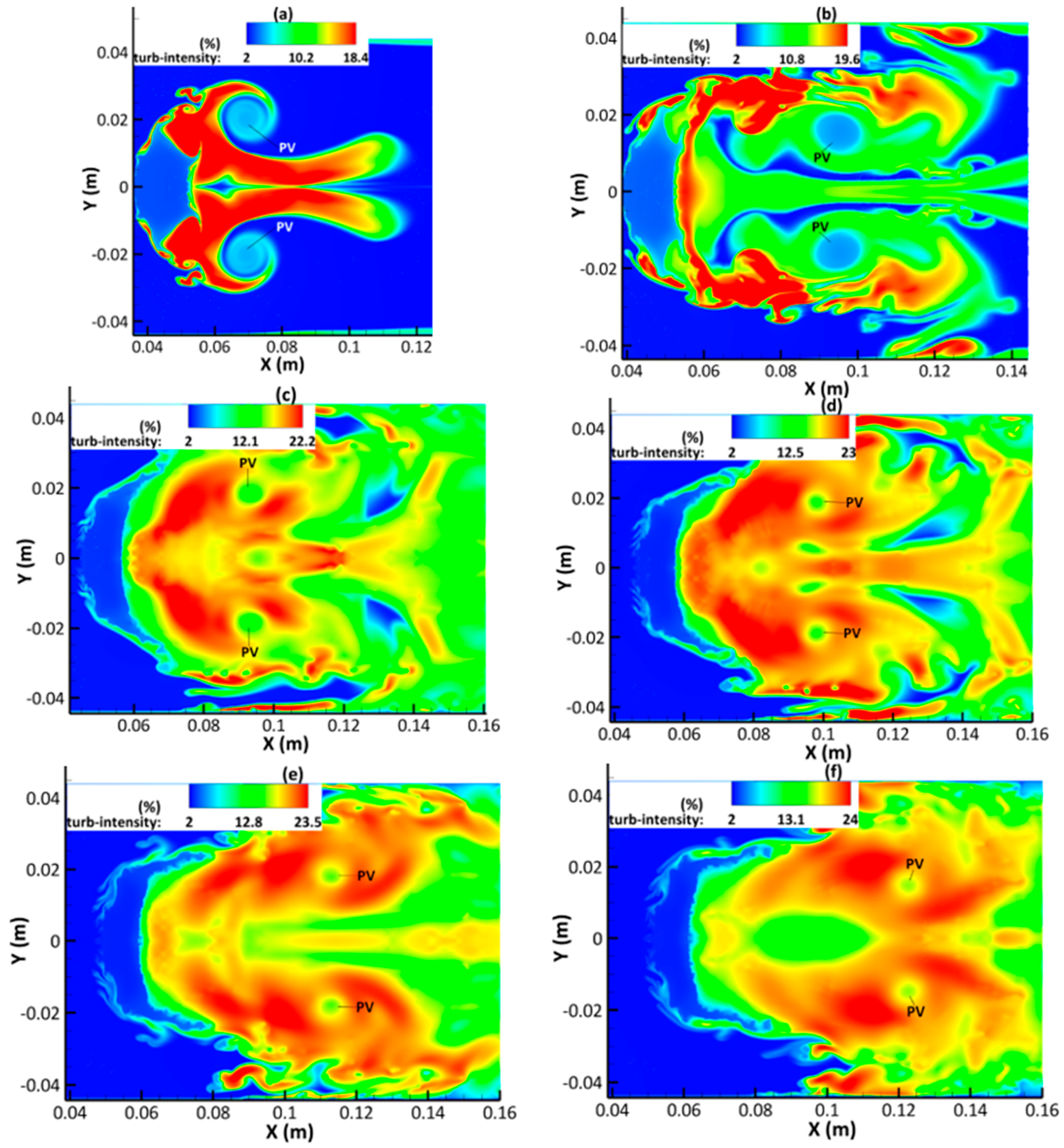
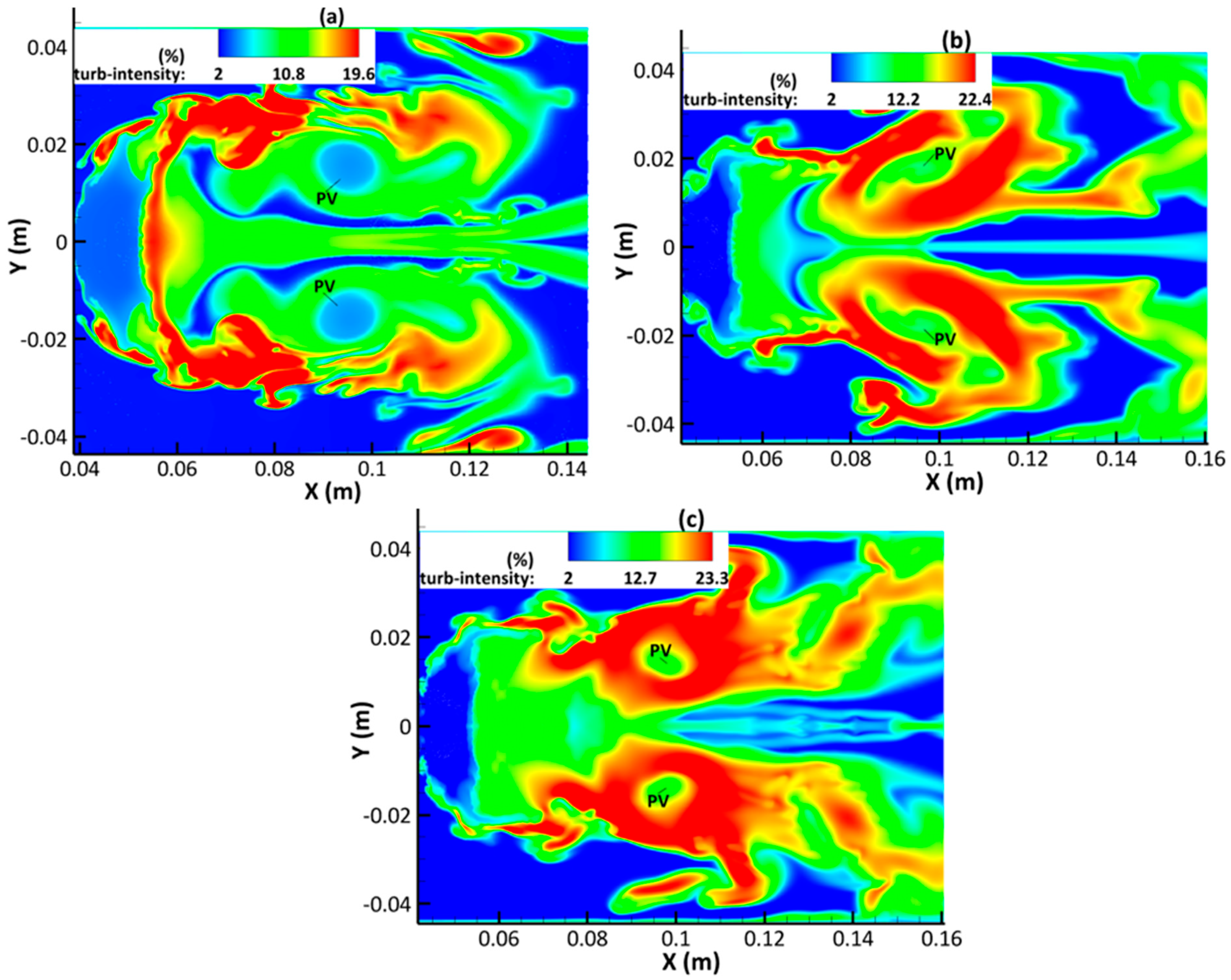
3.5. Turbulence Development
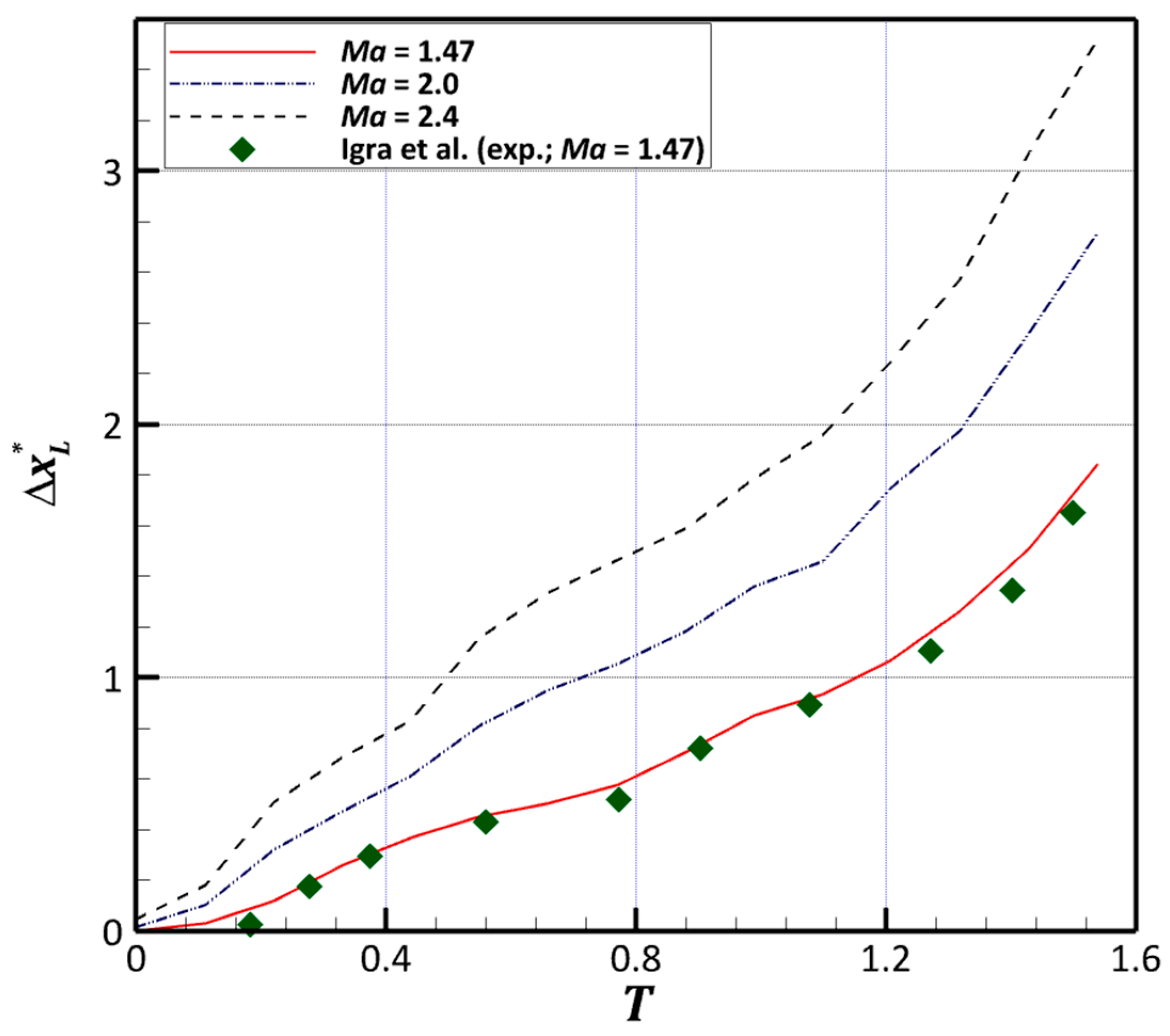
3.6. Effect of Mach Number on the Stripping Breakup of a Water Drop
4. Conclusions
- Fluid is mainly stripped from the deformed drop leeward side periphery as a result of strong inertial forces from the surrounding flow, leading to the formation of a discontinuous fluid sheet which eventually disintegrates into smaller sheets and micro-drops downstream.
- An upstream jet is formed as a result of the wake recirculation zone caused by the primary vortex pair. This upstream jet impinges on the drop leeward side, promoting the compression and hollowing of the deforming drop.
- The complex flow fields in the wake region are mainly due to the interaction of three vortex systems (primary, secondary, and tertiary) shedding from the deformed drop leeward side periphery. The secondary and tertiary vortices have a relatively short life span, whereas the primary vortices are still clearly observable further downstream towards the end of simulation time.
- The wake flow downstream from the severely deformed drop at the late-stage has become fully developed turbulent flow, with the maximum turbulence intensity reaching about 24%.
- The liquid sheet propagates faster in the downstream direction as increases. Also, the flattening of the leeward end, i.e., the extent of the flattened region bounded by downstream separation points, contracts as increases because of a reduction of the pressure imposed on the leeward side as well as a reduction in the velocity of the evolving upstream jet.
- Similarly, the stretching of the liquid sheet at the equator is weakened as increases, indicating that the liquid sheet grows less rapidly at higher . This is because the evolution of propagative waves induced by Kelvin–Helmholtz instabilities on the surface of the deformed drop are suppressed at higher . This suppression is due to the stabilizing effects of compressibility on the flow disturbance at these higher .
- With respect to the distribution of shed particles, fluid materials, and micro-drops, this study showed that, as increased, the shed fragments are constrained within a narrower area ahead of the distorted liquid sheet. This is because the stripping points at the equator have folded. As most of the material stripping now take place at these positions, the shed particles and micro-drops have a more confined spread.
- As rises, there is an increase in the amount of small-scale flow structures characterized by high vorticity, such that the turbulent flow in the far-field wake region is fully developed.
- Finally, as increases, the magnitude of turbulent intensity increases around and within the primary vortex, and the maximum value of turbulence intensity also increases across the flow field.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SLDI | Shock Liquid Drop Interaction |
| URANS | Unsteady Reynolds-averaged Navier–Stokes |
| KHRT | Kelvin–Helmholtz Rayleigh–Taylor |
| LSVOF | Level-Set coupled with Volume of Fluid |
| RTP | Rayleigh Taylor Piercing |
| SIE | Shear Induced Entrainment |
| SBI | Shock Bubble Interaction |
| RSM | Reynolds Stress Model |
| MUSCL | Monotonic Upstream-centered Scheme for Conservation Laws |
| AMR | Adaptive Mesh Refinement |
| SPE | Stripping Points at the Equator |
| FS | Fluid Sheet |
| DSP | Downstream Separation Points |
| FL | Fluid Ligaments |
| CR | Crevices |
| PV | Primary Vortex |
| SV | Secondary Vortex |
| TV | Tertiary Vortex |
| WRZ | Wake Recirculation Zone |
| UJ | Upstream Jet |
References
- Kaiser, J.W.J.; Winter, J.M.; Adami, S.; Adams, N.A. Investigation of interface deformation dynamics during high-weber number cylindrical droplet breakup. Int. J. Multiph. Flow 2020, 132, 103409. [Google Scholar] [CrossRef]
- Lee, C.H.; Reitz, R.D. An experimental study of the effect of gas density on the distortion and breakup mechanism of drops in high speed gas stream. Int. J. Multiph. Flow 2000, 26, 229–244. [Google Scholar] [CrossRef]
- Lebanoff, A.P.; Dickerson, A.K. Drop impact onto pine needle fibers with non-circular cross section. Phys. Fluids 2020, 32, 092113. [Google Scholar] [CrossRef]
- Agrawal, M.; Katiyar, R.K.; Karri, B.; Sahu, K.C. Experimental investigation of a nonspherical water droplet falling in air. Phys. Fluids 2020, 32, 112105. [Google Scholar] [CrossRef]
- Villermaux, E. Fragmentation. Annu. Rev. Fluid Mech. 2007, 39, 419–446. [Google Scholar] [CrossRef]
- Kumar, A.; Sahu, S. Liquid jet disintegration memory effect on downstream spray fluctuations in a coaxial twin-fluid injector. Phys. Fluids 2020, 32, 073302. [Google Scholar] [CrossRef]
- Liu, L.H.; Fu, Q.F.; Yang, L.J. Linear stability analysis of liquid jet exposed to subsonic crossflow with heat and mass transfer. Phys. Fluids 2021, 33, 034111. [Google Scholar] [CrossRef]
- Chou, W.H.; Gamboa, A.; Morales, J.O. Inkjet printing of small molecules, biologics, and nanoparticles. Int. J. Pharm. 2021, 600, 120462. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.Y.; Derby, B. Experimental study of the parameters for stable drop-on-demand inkjet performance. Phys. Fluids 2019, 31, 032004. [Google Scholar] [CrossRef]
- Antonopoulou, E.; Harlen, O.G.; Walkley, M.A.; Kapur, N. Jetting behavior in drop-on-demand printing: Laboratory experiments and numerical simulations. Phys. Rev. Fluids 2020, 5, 043603. [Google Scholar] [CrossRef]
- Sykes, T.C.; Castrejon-Pita, A.A.; Castrejon-Pita, J.R.; Harbottle, D.; Khatir, Z.; Thompson, H.M.; Wilson, M.C. Surface jets and internal mixing during the coalescence of impacting and sessile droplets. Phys. Rev. Fluids 2020, 5, 023602. [Google Scholar] [CrossRef]
- Wu, H.; Zhang, F.J.; Zhang, Z.Y. Droplet breakup and coalescence of an internal-mixing twin-fluid spray. Phys. Fluids 2021, 33, 013317. [Google Scholar] [CrossRef]
- Xu, M.H.; Li, X.R.; Riseman, A.; Frostad, J.M. Quantifying the effect of extensional rheology on the retention of agricultural sprays. Phys. Fluids 2021, 33, 032107. [Google Scholar] [CrossRef]
- Guildenbecher, D.R.; Lopez-Rivera, C.; Sojka, P.E. Secondary atomization. Exp. Fluids 2009, 46, 371–402. [Google Scholar] [CrossRef]
- Chen, H. Two-dimensional simulation of stripping breakup of a water droplet. AIAA J. 2008, 46, 1135–1143. [Google Scholar] [CrossRef]
- Zhu, W.; Zhao, N.; Jia, X.; Chen, X.; Zheng, H. Effect of airflow pressure on the droplet breakup in the shear breakup regime. Phys. Fluids 2021, 33, 053309. [Google Scholar] [CrossRef]
- Pilch, M.; Erdman, C.A. Use of breakup time data and velocity history data to predict the maximum size of stable fragments for acceleration-induced breakup of a liquid drop. Int. J. Multiph. Flow 1987, 13, 741–757. [Google Scholar] [CrossRef]
- Hsiang, L.-P.; Faeth, G.M. Drop deformation and breakup due to shock wave and steady disturbances. Int. J. Multiph. Flow 1995, 21, 545–560. [Google Scholar] [CrossRef]
- Hsiang, L.-P.; Faeth, G.M. Near-limit drop deformation and secondary breakup. Int. J. Multiph. Flow 1992, 18, 635–652. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Li, G.J.; Dinh, T.N. Aerobreakup in rarefied supersonic gas flows. J. Fluids Eng. 2004, 126, 516–527. [Google Scholar] [CrossRef]
- Nicholls, J.A.; Ranger, A.A. Aerodynamic shattering of liquid drops. AIAA J. 1969, 7, 285–290. [Google Scholar] [CrossRef]
- Dai, Z.; Faeth, G.M. Temporal properties of secondary drop breakup in the multimode breakup regime. Int. J. Multiph. Flow 2001, 27, 217–236. [Google Scholar] [CrossRef]
- Harper, E.Y.; Grube, G.W.; Chang, I.-D. On the breakup of accelerating liquid drops. J. Fluid Mech. 1972, 52, 565–591. [Google Scholar] [CrossRef]
- Theofanous, T.G. Aerobreakup of Newtonian and viscoelastic liquids. Annu. Rev. Fluid Mech. 2011, 43, 661–690. [Google Scholar] [CrossRef]
- Wierzba, A.; Takayama, K. Experimental investigation of the aerodynamic breakup of liquid drops. AIAA J. 1988, 26, 1329–1335. [Google Scholar] [CrossRef]
- Chou, W.H.; Hsiang, L.-P.; Faeth, G.M. Temporal properties of drop breakup in the shear breakup regime. Int. J. Multiph. Flow 1997, 23, 651–669. [Google Scholar] [CrossRef]
- Igra, D.; Ogawa, T.; Takayama, K. A parametric study of water column deformation resulting from shock wave loading. At. Sprays 2002, 12, 577–591. [Google Scholar] [CrossRef]
- Liu, Z.; Reitz, R.D. An analysis of the distortion and breakup mechanisms of high speed liquid drops. Int. J. Multiph. Flow 1997, 23, 631–650. [Google Scholar] [CrossRef]
- Joseph, D.D.; Belanger, J.; Beavers, G.S. Breakup of a liquid drop suddenly exposed to a high-speed airstream. Int. J. Multiph. Flow 1999, 25, 1263–1303. [Google Scholar] [CrossRef]
- Hirahara, H.; Kawahashi, M. Experimental investigation of viscous effects upon a breakup of droplets in high-speed air flow. Exp. Fluids 1992, 13, 423–428. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Li, G.J. On the physics of aerobreakup. Phys. Fluids 2008, 20, 052103. [Google Scholar] [CrossRef]
- Liu, N.; Wang, Z.; Sun, M.; Wang, H.; Wang, B. Numerical simulation of liquid droplet breakup in supersonic flows. Acta Astronaut. 2018, 145, 116–130. [Google Scholar] [CrossRef]
- Engel, O.G. Fragmentation of water drops in the zone behind an air shock. J. Res. Natl. Bur. Stand. 1958, 60, 245–280. [Google Scholar] [CrossRef]
- Waldman, G.D.; Reinecke, W. Raindrop breakup in the shock layer of a high-speed vehicle. AIAA J. 1972, 10, 1200–1204. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Mitkin, T.G.; Ng, C.L.; Chang, C.H.; Deng, X.; Sushchikh, S. The physics of aerobreakup. II. Viscous liquids. Phys. Fluids 2012, 24, 022104. [Google Scholar] [CrossRef]
- Theofanous, T.G.; Mitkin, T.G.; Ng, C.L. The physics of aerobreakup. III. Viscoelastic liquids. Phys. Fluids 2013, 25, 032101. [Google Scholar] [CrossRef]
- Gonor, A.L.; Zolotova, N.V. Spreading and break-up of a drop in a gas stream. Acta Astronaut. 1984, 11, 137–142. [Google Scholar] [CrossRef]
- Khosla, S.; Smith, C.E.; Throckmorton, R.P. Detailed understanding of drop atomization by gas crossflow using the volume of fluid method. In Proceedings of the Nineteenth Annual Conference on Liquid Atomization and Spray Systems, Toronto, ON, Canada, 23–26 May 2006; ILASS-Americas: Toronto, ON, Canada, 2006. [Google Scholar]
- Yang, W.; Jia, M.; Che, Z.; Sun, K.; Wang, T. Transitions of deformation to bag breakup and bag to bag-stamen breakup for droplets subjected to a continuous gas flow. Inter. J. Heat Mass Transf. 2017, 111, 884–894. [Google Scholar] [CrossRef]
- Meng, J.C.; Colonius, T. Numerical simulation of the aerobreakup of a water droplet. J. Fluid Mech. 2018, 835, 1108–1135. [Google Scholar] [CrossRef]
- Aslani, M.; Regele, J.D. A localized artificial diffusivity method to simulate compressible multiphase flows using the stiffened gas equation of state. Int. J. Numer. Meth. Fluids 2018, 88, 413–433. [Google Scholar] [CrossRef]
- Igra, D.; Takayama, K. A Study of Shock Wave Loading on a Cylindrical Water Column; Technical Report; Institute of Fluid Science, Tohoku University: Sendai, Japan, 2001. [Google Scholar]
- Meng, J.C.; Colonius, T. Numerical simulations of the early stages of high-speed droplet breakup. Shock Waves 2014, 25, 399–414. [Google Scholar] [CrossRef]
- ANSYS Academic Research, ANSYS Fluent Theory Guide; ANSYS Help System; ANSYS, Inc.: Southpointe/Canonsburg, PA, USA, 2020.
- Hinze, J.O. Turbulent Flow Regions with Shear Stress and Mean Velocity Gradient of Opposite Sign. Appl. Sci. Res. 1970, 22, 163–175. [Google Scholar] [CrossRef]
- Onwuegbu, S.; Yang, Z. Numerical analysis of shock interaction with a spherical bubble. AIP Adv. 2022, 12, 025215. [Google Scholar] [CrossRef]
- Onwuegbu, S.; Yang, Z.; Xie, J. Numerical simulation of the interaction between a planar shock wave and a cylindrical bubble. Modelling 2024, 5, 483–501. [Google Scholar] [CrossRef]
- Launder, B.E.; Reece, G.J.; Rodi, W. Progress in the Development of a Reynolds-Stress Turbulence Closure. J. Fluid Mech. 1975, 68, 537–566. [Google Scholar] [CrossRef]
- Gibson, M.M.; Launder, B.E. Ground Effects on Pressure Fluctuations in the Atmospheric Boundary Layer. J. Fluid Mech. 1978, 86, 491–511. [Google Scholar] [CrossRef]
- Launder, B.E. Second-Moment Closure: Present... and Future? Int. J. Heat Fluid Flow 1989, 10, 282–300. [Google Scholar] [CrossRef]
- Daly, B.J.; Harlow, F.H. Transport Equations in Turbulence. Phys. Fluids 1970, 13, 2634–2649. [Google Scholar] [CrossRef]
- Lien, F.S.; Leschziner, M.A. Assessment of Turbulent Transport Models Including Non-Linear RNG Eddy-Viscosity Formulation and Second-Moment Closure. Comput. Fluids 1994, 23, 983–1004. [Google Scholar] [CrossRef]
- Shyue, K.M. An efficient shock-capturing algorithm for compressible multicomponent problems. J. Comput. Phys. 1998, 142, 208–242. [Google Scholar] [CrossRef]
- Onwuegbu, S.; Yang, Z.; Xie, J. Numerical study of the shear stripping of a liquid drop under shock wave loading. Chin. J. Aeronaut. 2025; submitted. [Google Scholar]
- Serthian, J.A.; Smereka, P. Level set methods for fluid interfaces. Ann. Rev. Fluid Mech. 2003, 35, 341–372. [Google Scholar] [CrossRef]
- Olsson, E.; Kreiss, G.; Zahedi, S. A Conservative Level Set Method for Two Phase Flow II. J. Comput. Phys. 2007, 225, 785–807. [Google Scholar] [CrossRef]
- Jofre, L.; Lehmkuhl, O.; Castro, J.; Oliva, A. A 3-D volume-of-fluid advection method based on cell-vertex velocities. Comput. Fluids 2014, 94, 14–29. [Google Scholar] [CrossRef]
- Balcazar, N.; Lehmkuhl, O.; Jofre, L.; Rigola, J.; Olivia, A. A coupled volume-of-fluid/level-set method for simulation of two-phase flows on unstructured meshes. Comput. Fluids 2016, 124, 12–29. [Google Scholar] [CrossRef]
- Coralic, V.; Colonius, T. Finite-volume WENO scheme for viscous compressible multicomponent flows. J. Comput. Phys. 2014, 274, 95–121. [Google Scholar] [CrossRef] [PubMed]
- Ansari, M.R.; Azadi, R.; Salimi, E. Capturing of interface topological changes in two-phase gas-liquid flows using a coupled volume-of-fluid and level-set method (VOSET). Comput. Fluids 2016, 125, 82–100. [Google Scholar] [CrossRef]
- Sussman, M.; Fatemi, E.; Smereka, P.; Osher, S. An improved level set method for incompressible two-phase flows. Comput. Fluids 1998, 27, 663–680. [Google Scholar] [CrossRef]
- Luo, K.; Shao, C.; Yang, Y.; Fan, J. A mass conserving level set method for detailed numerical simulation of liquid atomization. J. Comput. Phys. 2015, 298, 495–519. [Google Scholar] [CrossRef]
- Wang, Z.; Li, S.; Chen, R.; Xun, Z.; Liao, Q.; Ye, D.; Zhang, B. Numerical study on dynamic behaviors of the coalescence between the advancing liquid meniscus and multi-droplets in a microchannel using CLSVOF method. Comput. Fluids 2018, 170, 341–348. [Google Scholar] [CrossRef]
- Cash, J.R.; Karp, A.H. A variable order Runge-Kutta method for initial value problems with rapidly varying right-hand sides. ACM Trans. Math. Software 1990, 16, 201–222. [Google Scholar] [CrossRef]
- Reitz, R.D. Mechanisms of atomization processes in high-pressure vaporizing sprays. At. Spray Technol. 1987, 3, 309–337. [Google Scholar]
- Liu, A.B.; Mather, D.; Reitz, R.D. Modeling the effects of drop drag and breakup on fuel sprays. J. Engines. 1993, 102, 83–95. [Google Scholar]
- Van Leer, B. Toward the Ultimate Conservative Difference Scheme. V. A Second Order Sequel to Godunov’s Method. J. Comput. Phys. 1979, 32, 101–136. [Google Scholar] [CrossRef]
- Sembian, S.; Liverts, M.; Tillmark, N.; Apazadis, N. Plane shock wave interaction with a cylindrical column. Phys. Fluids 2016, 28, 056102. [Google Scholar] [CrossRef]
- Houghton, E.L.; Brock, A.E. Table IV: Flow of dry air through a plane normal shock wave. In Tables for the Compressible Flow of Dry Air, 3rd ed.; Arnold, E., Ed.; Athenaeum Press Ltd.: Newcastle upon Tyne, UK, 1993; Volume 3, pp. 40–46. [Google Scholar]
- Hillier, R. Computation of shock wave diffraction at a ninety degrees convex edge. Shock Waves 1991, 1, 89–98. [Google Scholar] [CrossRef]
- Ingram, D.M.; Causon, D.M.; Mingham, C.G. Developments in Cartesian cut cell methods. Math. Comput. Simul. 2013, 61, 561–572. [Google Scholar] [CrossRef]
- Berger, M.; Aftosmis, M.J.; Allmaras, S.R. Progress towards a cartesian cut-cell methods for viscous compressible flow. In Proceedings of the 50th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Nashville, TN, USA, 9–12 January 2012; American Institute of Aeronautics and Astronautics: Nashville, TN, USA, 2012. [Google Scholar]
- Johnson, M.W. A novel Cartesian CFD cut cell approach. Comput. Fluids 2013, 79, 105–119. [Google Scholar] [CrossRef]
- Holleman, R.; Fringer, O.; Stacey, M. Numerical diffusion for flow-aligned unstructured grids with application to estuarine modelling. Int. J. Numer. Methods Fluids 2013, 72, 1117–1145. [Google Scholar] [CrossRef]
- Zubair, M.; Abdullah, M.Z.; Ahmad, K.A. Hybrid mesh for nasal airflow studies. Comput. Math. Methods Med. 2013, 1, 727362. [Google Scholar] [CrossRef] [PubMed]
- Lawlor, O.; Chakravorty, S.; Wilmarth, T.; Choudhury, N.; Dooley, I. Parfum: A parallel framework for unstructured meshes for scalable dynamic physics applications. Eng. Comput. 2006, 22, 215–235. [Google Scholar] [CrossRef]
- Jahangirian, A.; Shoraka, Y. Adaptive unstructured grid generation for engineering computation of aerodynamic flows. Math. Comput. Simulat. 2008, 78, 627–644. [Google Scholar] [CrossRef]
- Cant, R.S.; Ahmed, U.; Fang, J.; Chakarborty, N.; Nivarti, G.; Moulinec, C.; Emerson, D.R. An unstructured adaptive mesh refinement approach for computational fluid dynamics of reacting flows. J. Comput. Phys. 2022, 468, 111480. [Google Scholar] [CrossRef]
- Wang, Y.; Dong, G. A numerical study of shock-interface interaction and prediction of the mixing zone growth in inhomogeneous medium. Acta Mech. Sin. 2022, 38, 122163. [Google Scholar] [CrossRef]
- Yu, B.; Li, L.; Xu, H.; Zhang, B.; Liu, H. Effects of Reynolds number and Schmidt number on variable density mixing in shock bubble interaction. Acta Mech. Sin. 2022, 38, 121256. [Google Scholar] [CrossRef]
- Karyagin, V.P.; Lopatkin, A.I.; Shvets, A.I.; Shilin, N.M. Experimental investigation of the separation of flow around a sphere. Fluid Dyn. 1991, 26, 126–129. [Google Scholar] [CrossRef]
- Nagata, T.; Nonomura, T.; Takahashi, S.; Mizuno, Y.; Fukuda, K. Investigation on subsonic to supersonic flow around a sphere at low Reynolds number of between 50 and 300 by direct numerical simulation. Phys. Fluids 2016, 28, 056101. [Google Scholar] [CrossRef]
- Papamoschou, D.; Roshko, A. The compressible turbulent shear layer: An experimental study. J. Fluid Mech. 1988, 197, 453–477. [Google Scholar] [CrossRef]
- Jalaal, M.; Mehravaran, K. Transient growth of droplet instabilities in a stream. Phys. Fluids 2014, 26, 012101. [Google Scholar] [CrossRef]
- Wang, Z.; Hopfes, T.; Giglmaier, M.; Adams, N.K. Effect of Mach number on droplet aerobreakup in shear stripping regime. Exp. Fluids 2020, 61, 193. [Google Scholar] [CrossRef] [PubMed]
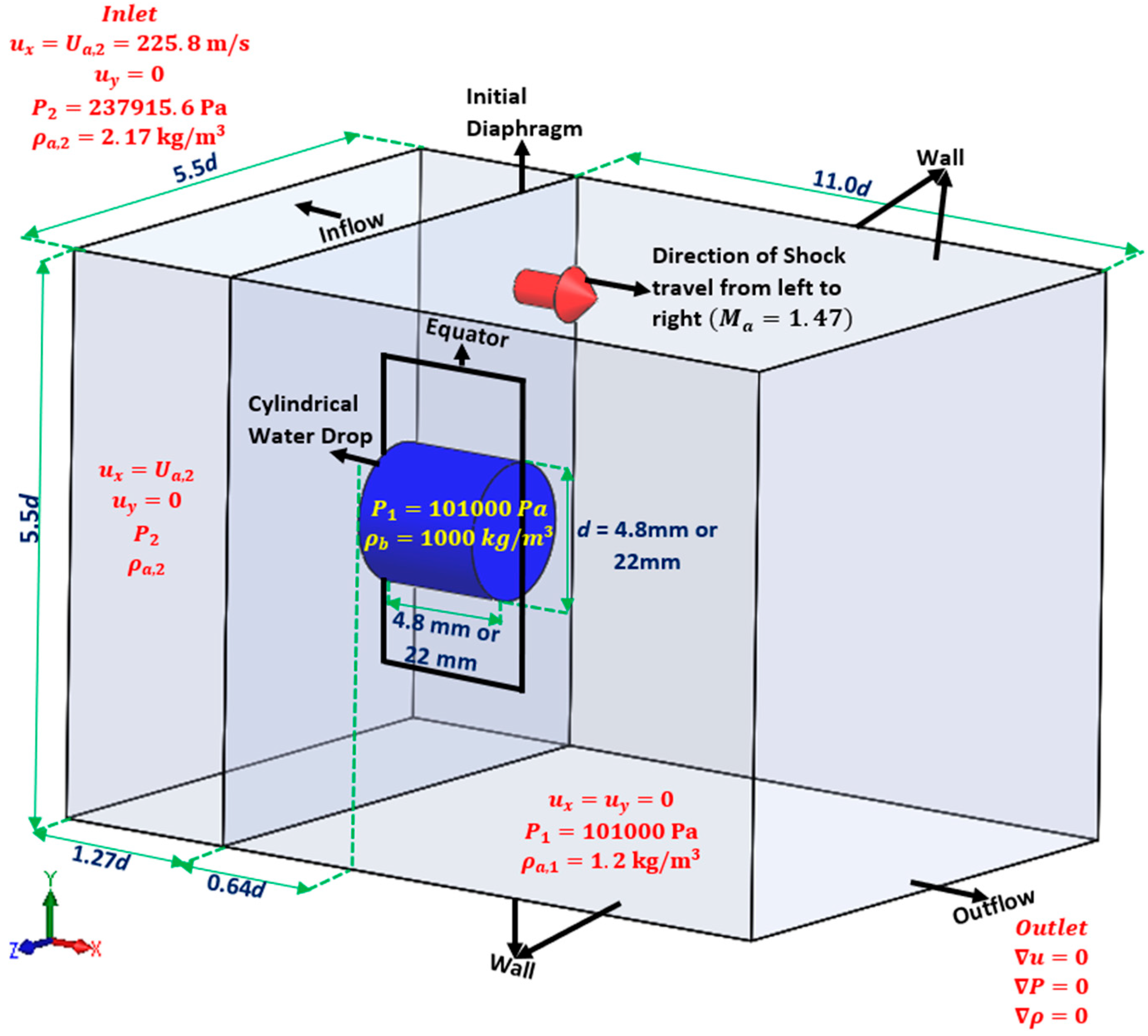

| Pre-Shock Air Properties | Post-Shock Air Properties | Water | |||
|---|---|---|---|---|---|
| 1.2 | 2.17 | 3.19 | 3.84 | 1000 | |
| 0 | 225.8 | 428.9 | 567.1 | 0 | |
| 0.101 | 0.24 | 0.45 | 0.66 | 0.101 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Onwuegbu, S.; Yang, Z.; Xie, J. Numerical Study of the Late-Stage Flow Features and Stripping in Shock Liquid Drop Interaction. Aerospace 2025, 12, 648. https://doi.org/10.3390/aerospace12080648
Onwuegbu S, Yang Z, Xie J. Numerical Study of the Late-Stage Flow Features and Stripping in Shock Liquid Drop Interaction. Aerospace. 2025; 12(8):648. https://doi.org/10.3390/aerospace12080648
Chicago/Turabian StyleOnwuegbu, Solomon, Zhiyin Yang, and Jianfei Xie. 2025. "Numerical Study of the Late-Stage Flow Features and Stripping in Shock Liquid Drop Interaction" Aerospace 12, no. 8: 648. https://doi.org/10.3390/aerospace12080648
APA StyleOnwuegbu, S., Yang, Z., & Xie, J. (2025). Numerical Study of the Late-Stage Flow Features and Stripping in Shock Liquid Drop Interaction. Aerospace, 12(8), 648. https://doi.org/10.3390/aerospace12080648





