Optimization of Biaxial Tensile Specimen Shapes on Aerospace Composite with Large Deformation
Abstract
1. Introduction
2. Material and Shape Parameters
2.1. Material
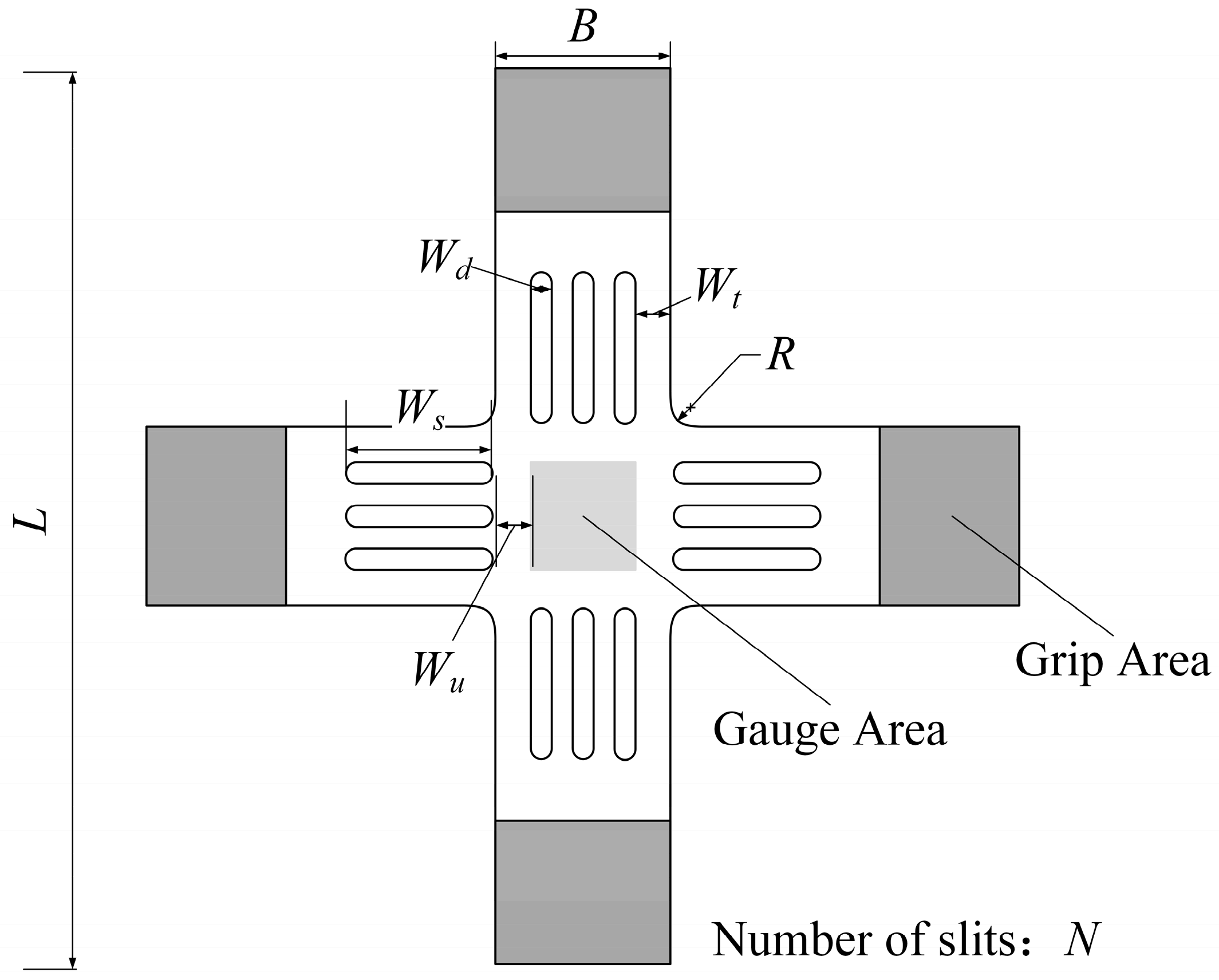
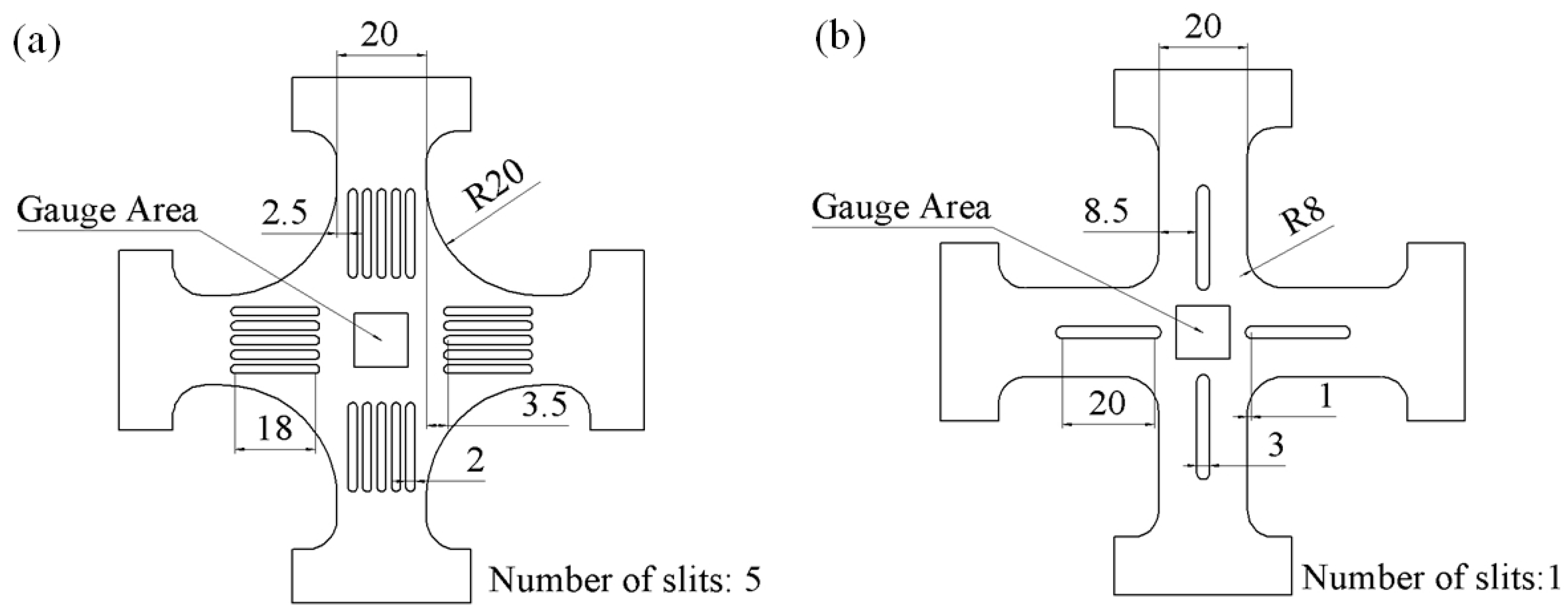
2.2. Parameters
3. Optimization Method
3.1. Multi-Objective Evaluation Indicator and Criterion
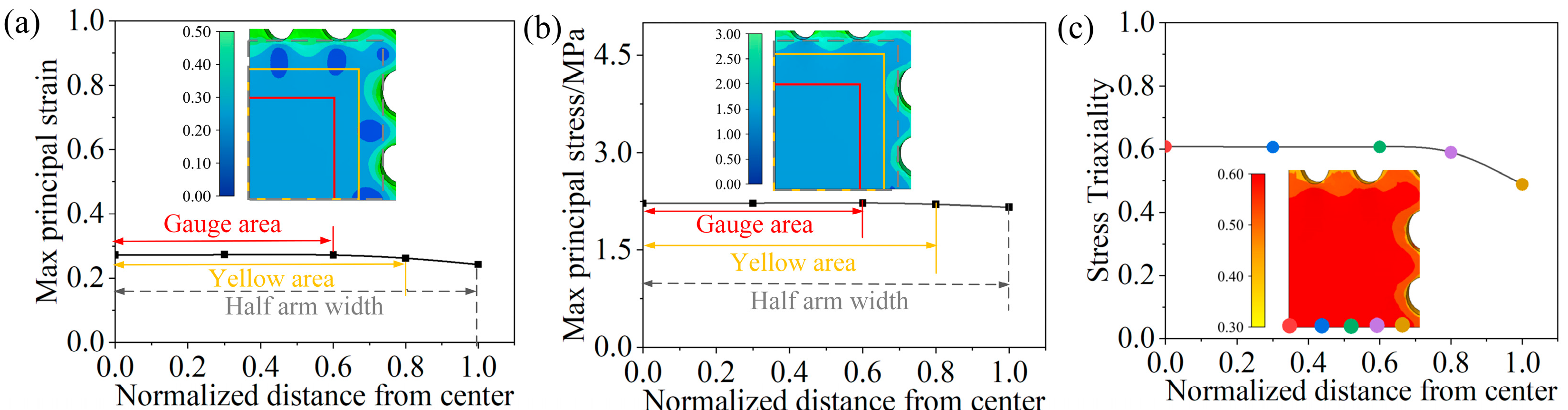
3.1.1. Uniformity of Stress and Strain
3.1.2. Load Transfer Efficiency
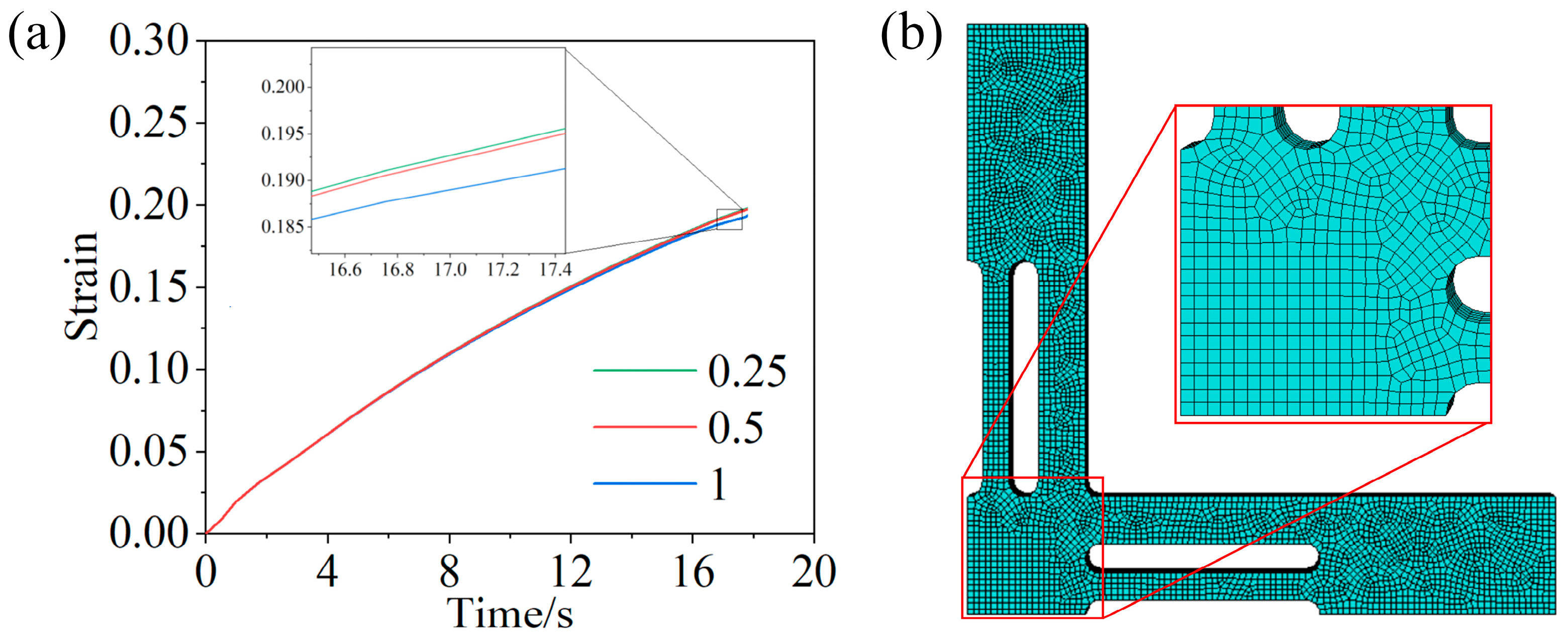
3.2. Multi-Parameter Analysis
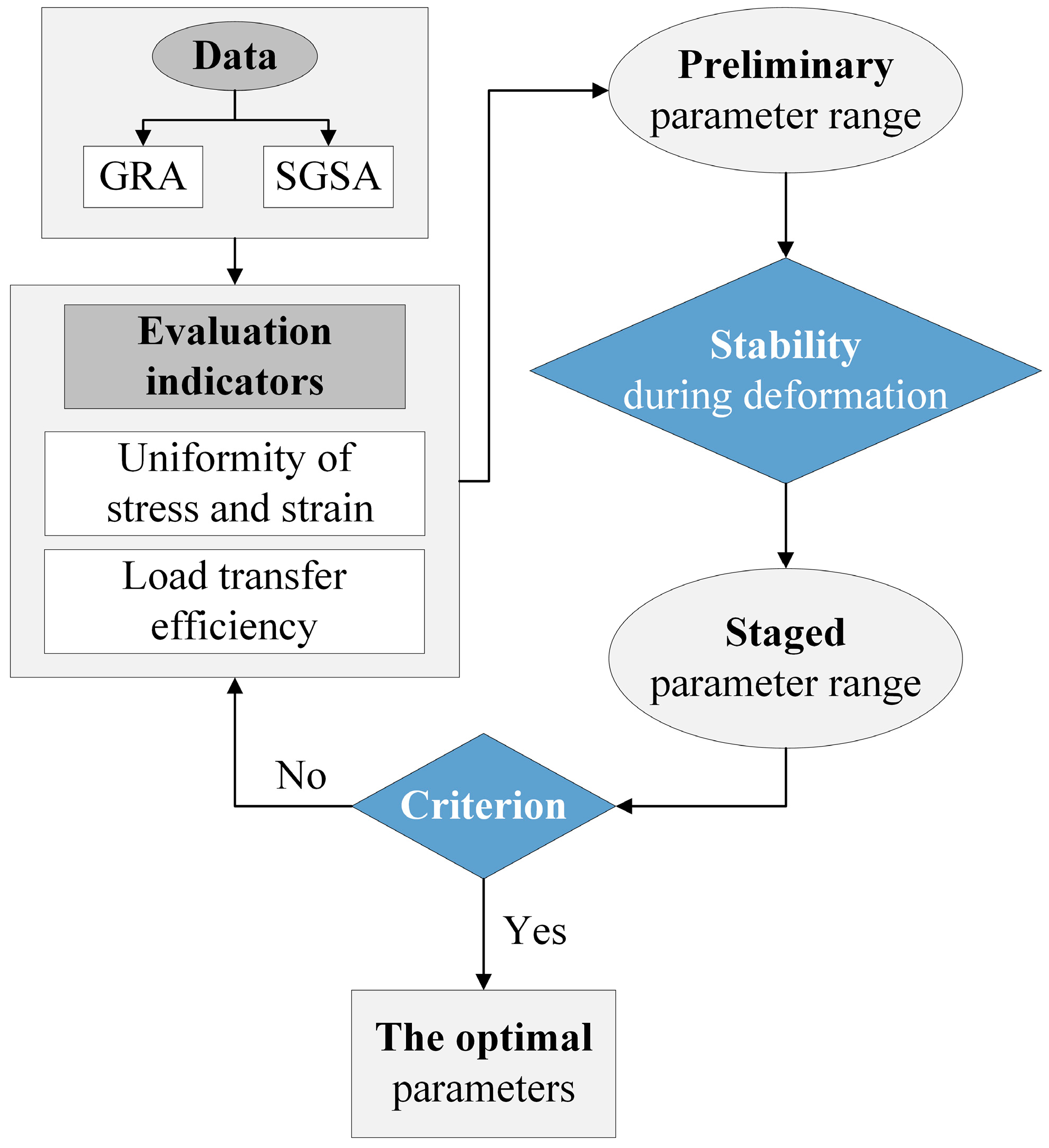
3.3. Optimization Process
4. Results and Discussion
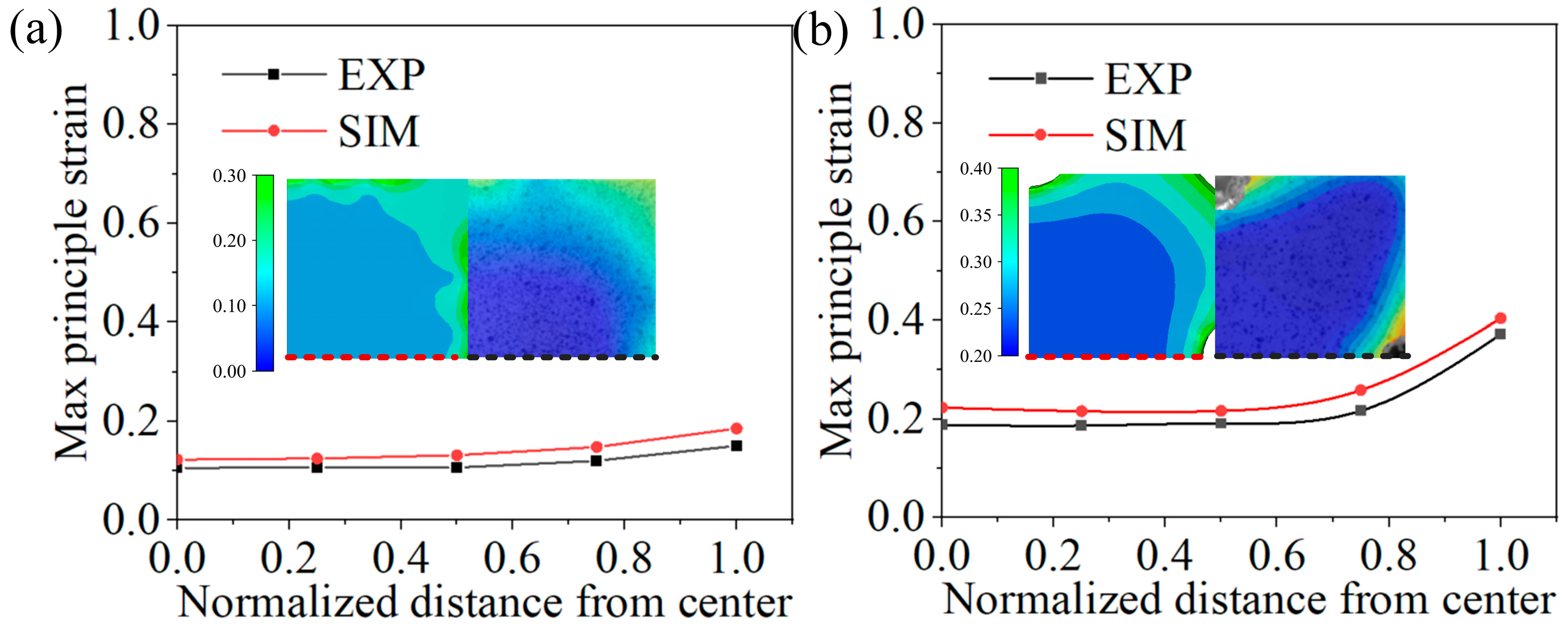
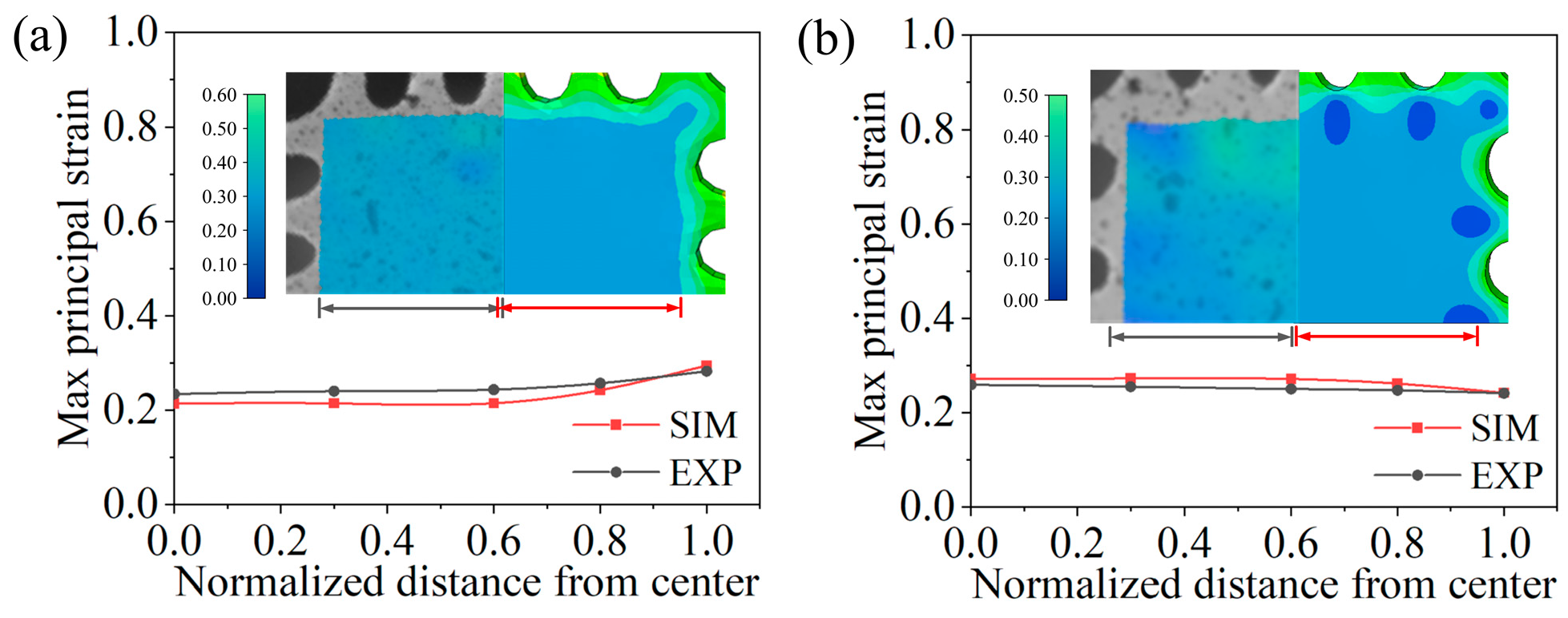
4.1. Validation of the Effectiveness of the Evaluation Program
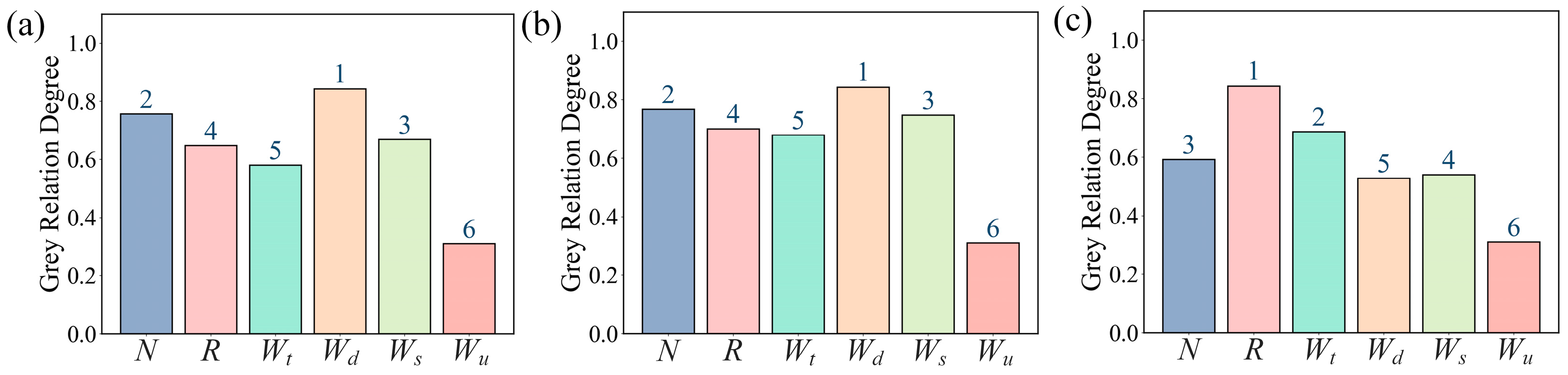
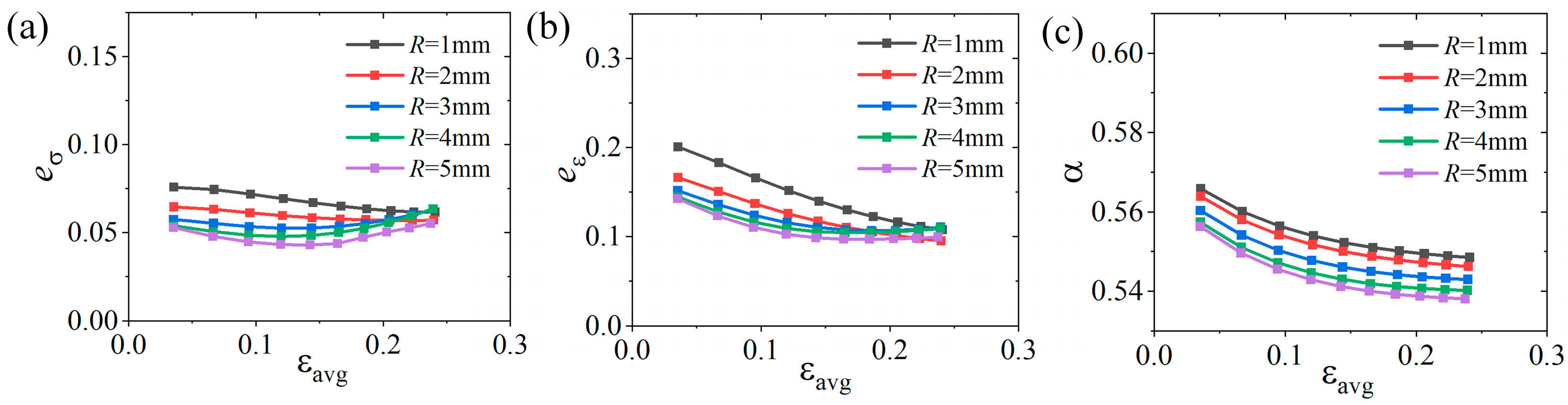
4.2. Parameter Correlation and Sensitivity Analysis
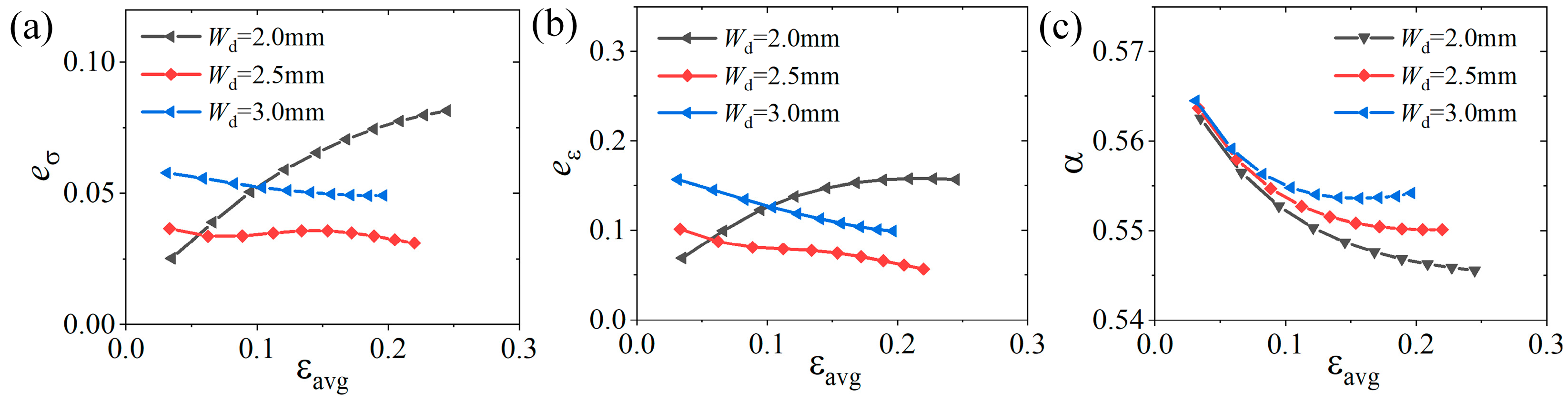
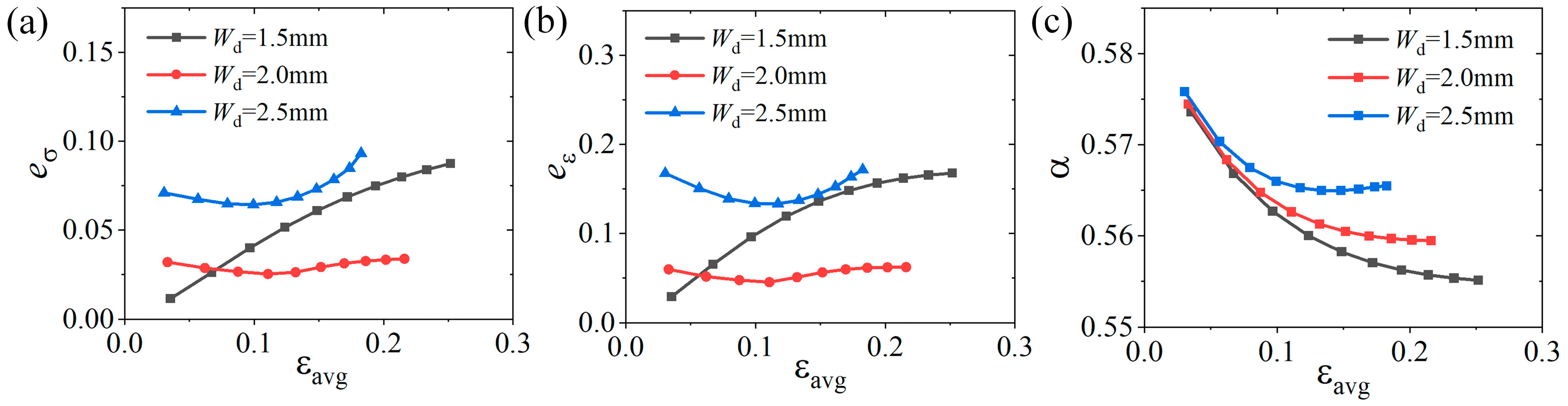
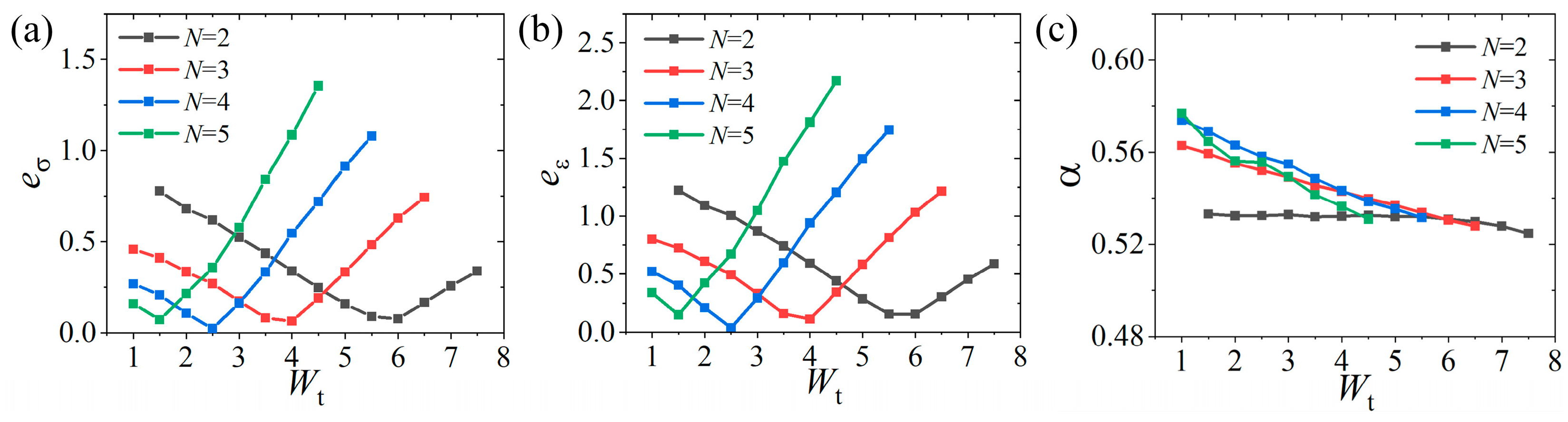
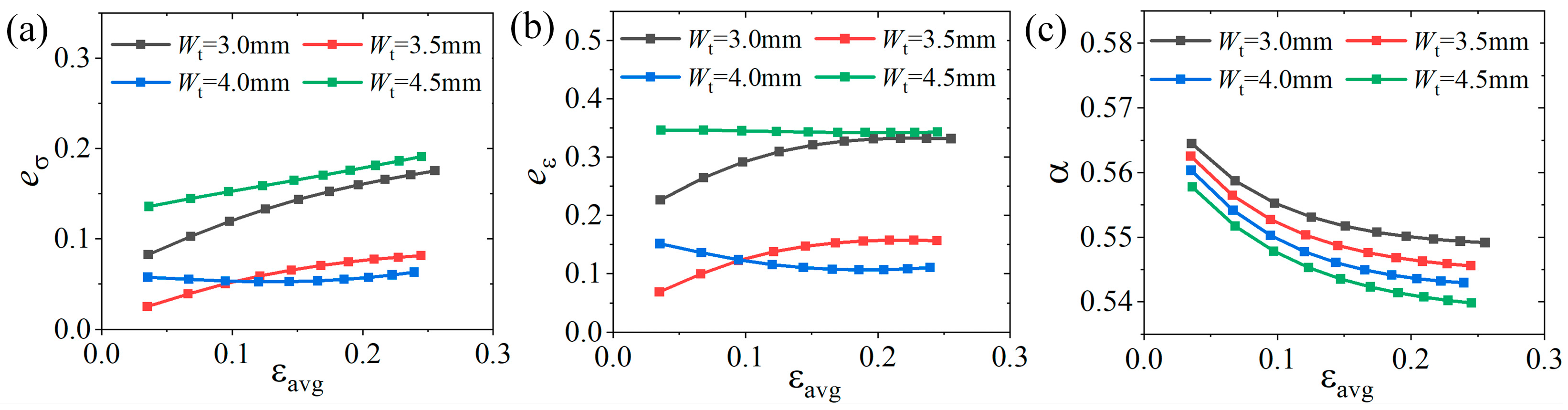
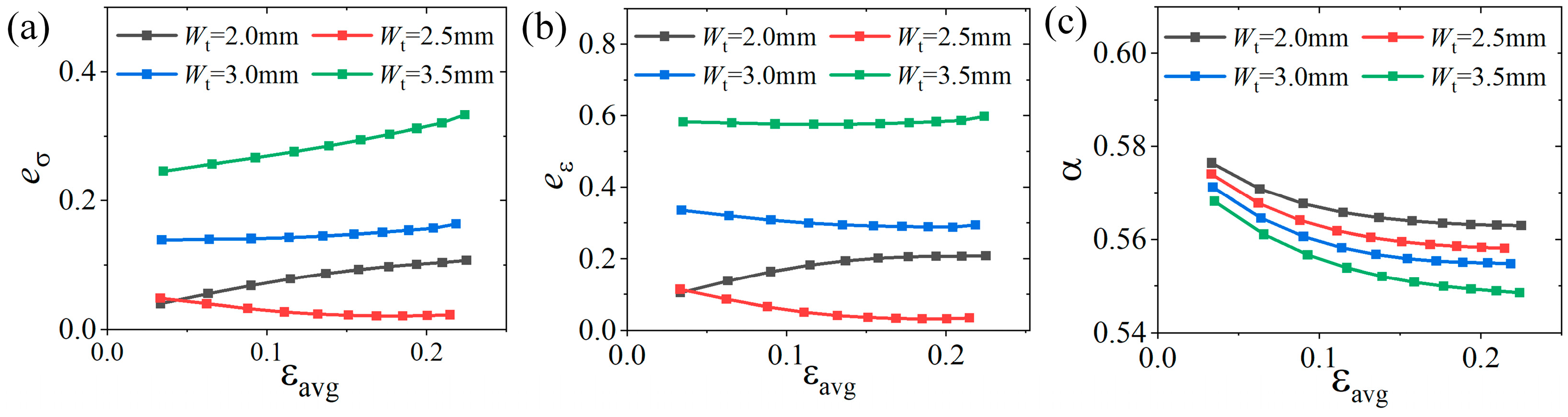
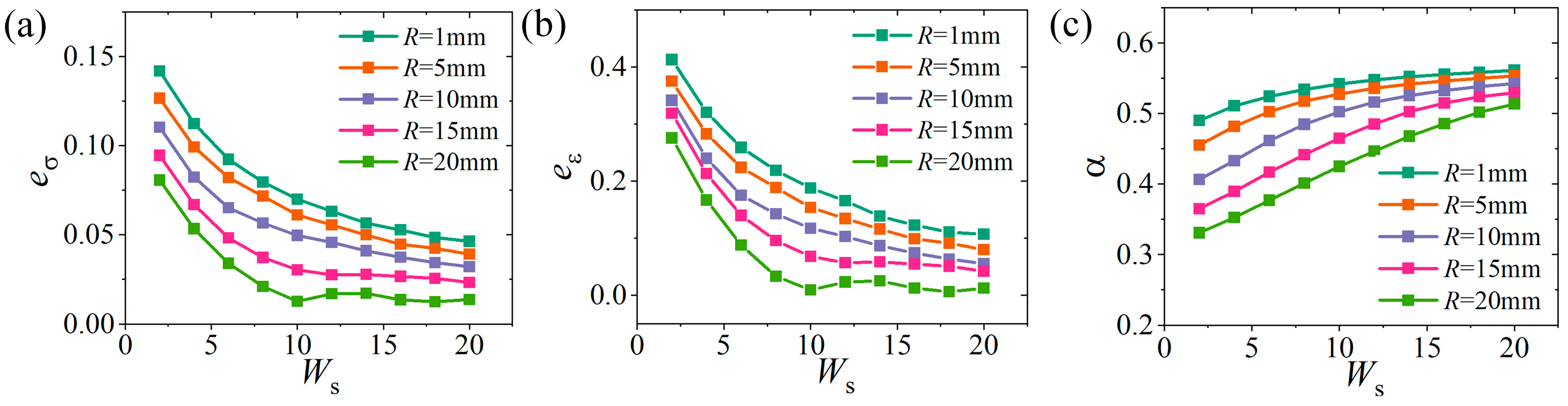
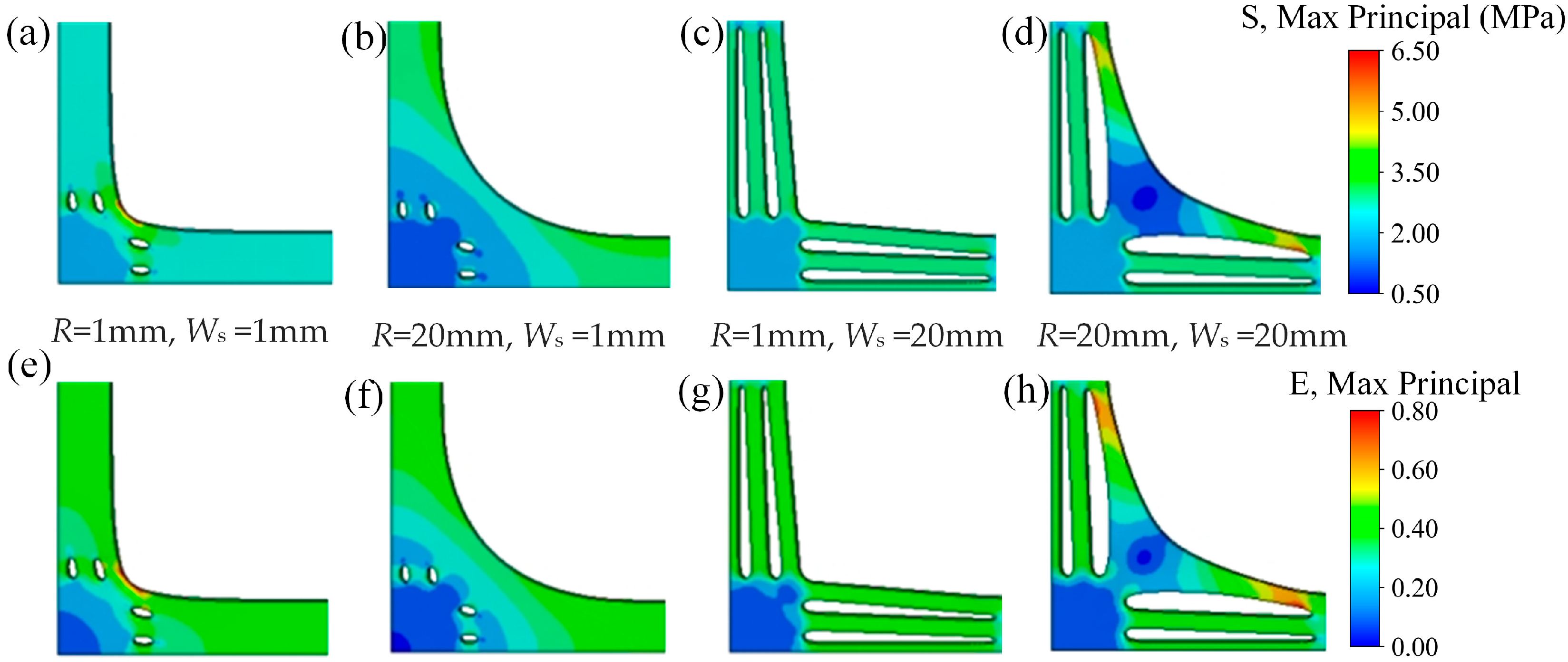
4.3. Influence of Parameters During Large Deformation
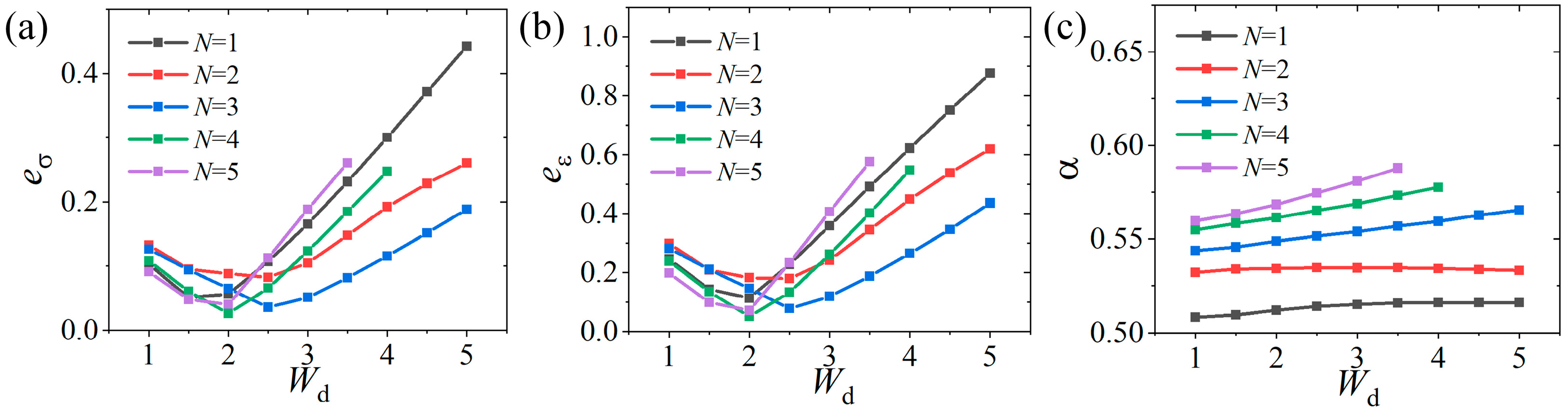
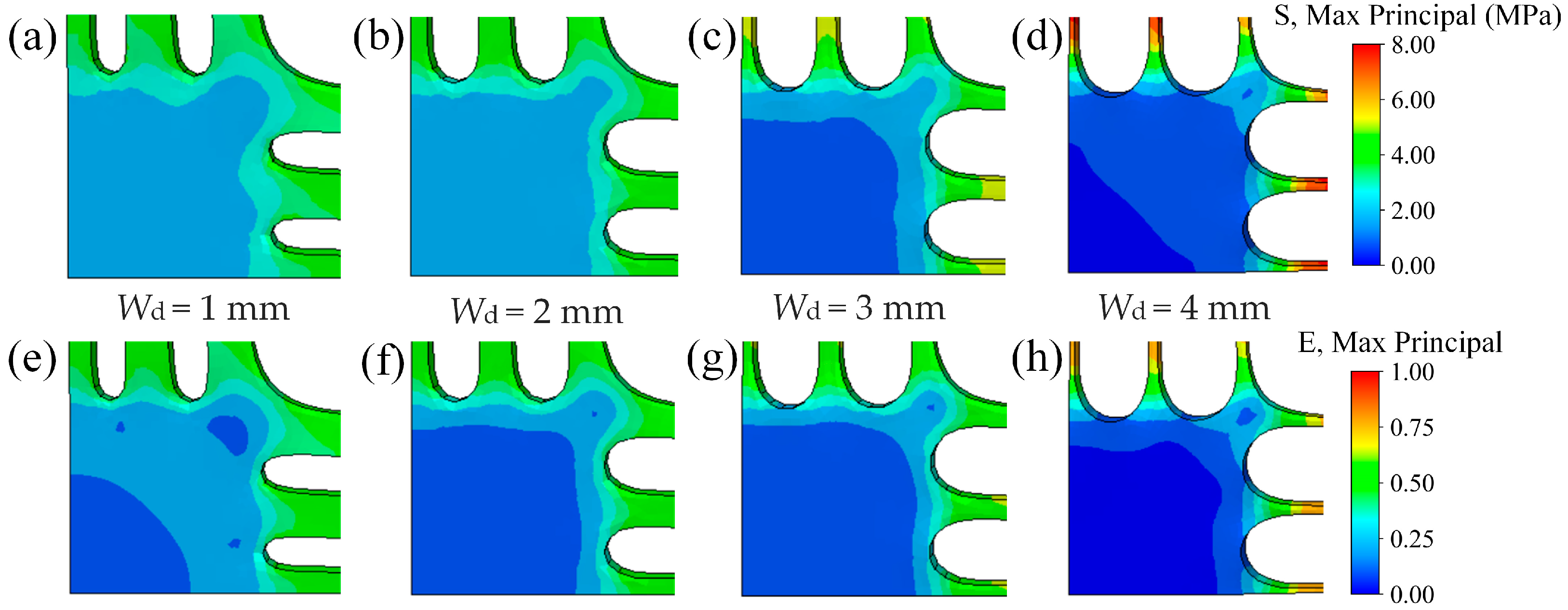
4.3.1. Influence of the Number and Width of Slits
4.3.2. Influence of Slit Edge Distance
4.3.3. Influence of Slit Length and Fillet Radius
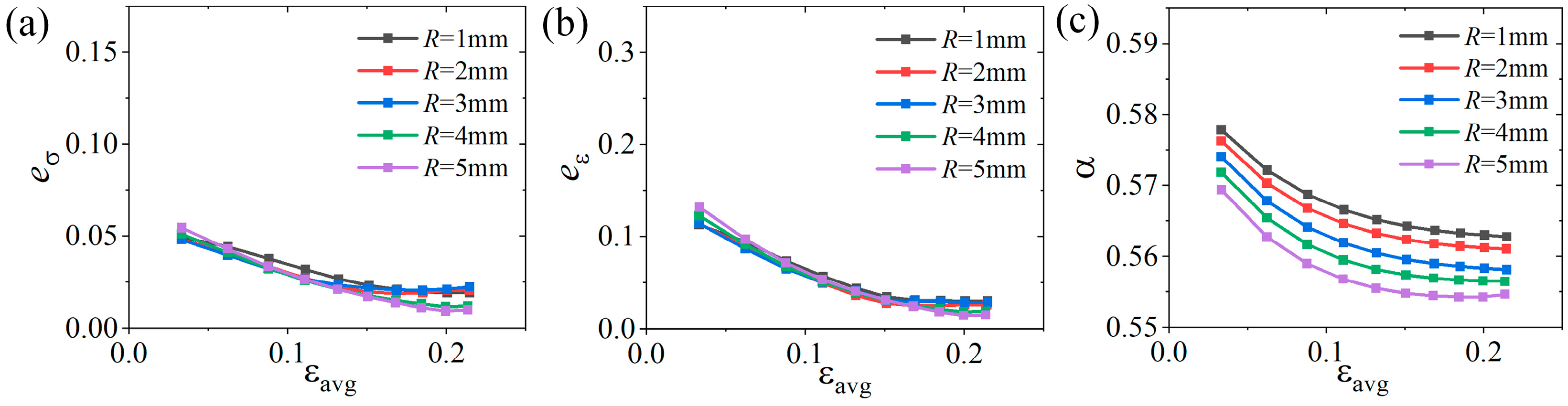
4.3.4. Optimal Parameters of the Cruciform Specimen
4.4. Further Discussion
5. Conclusions
- (1)
- An evaluation system for soft composites was developed, combining stress–strain uniformity in the gauge area and load transfer efficiency, with stability analysis during deformation as the novelty
- (2)
- The optimized specimen achieved high mechanical stability, with average stress and strain distribution errors during deformation of 5% and 3%, respectively, which decreased at 2.2% and 2.9%, respectively. The stable load transfer efficiency with the variation did not exceed 1.5%.
- (3)
- The dominant factors affecting the specimen performance are the slit width (Wd) and the number of slits (N), which are the most critical, and the influencing order is Wd > N > Ws ≈ Wt > R. Meanwhile, these parameters have a nonlinear effect on load transfer during the tensile process.
- (4)
- Slit placement enhanced gauge area uniformity but reduced load transfer efficiency by 50%, necessitating future improvements in clamping and efficiency.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| DIC | Digital Image Correlation |
| GRA | Grey Relational Analysis |
| SGSA | The Second-Order Sobol Global Sensitivity Analysis |
| OLHS | The Optimized Latin Hypercube Sampling |
References
- Jiang, S.; Yong, Z. Modulation of Mechanical Properties of Silica-Filled Silicone Rubber by Cross-Linked Network Structure. Polymers 2024, 16, 2304. [Google Scholar] [CrossRef] [PubMed]
- Porter, C.; Zaman, B.; Pazur, R. A Critical Examination of the Shelf Life of Nitrile Rubber O-Rings Used in Aerospace Sealing Applications. Polym. Degrad. Stab. 2022, 206, 110199. [Google Scholar] [CrossRef]
- Maurya, A.K.; De Souza, F.M.; Gupta, R.K. Polyurethane and Its Composites: Synthesis to Application. In ACS Symposium Series; Gupta, R.K., Ed.; American Chemical Society: Washington, DC, USA, 2023; Volume 1452, pp. 1–20. [Google Scholar] [CrossRef]
- Azoug, A.; Thorin, A.; Nevière, R.; Pradeilles-Duval, R.-M.; Constantinescu, A. Influence of Orthogonal Prestrain on the Viscoelastic Behaviour of Highly-Filled Elastomers. Polym. Test. 2013, 32, 375–384. [Google Scholar] [CrossRef][Green Version]
- Soni, R.; Verma, R.; Kumar Garg, R.; Sharma, V. A Critical Review of Recent Advances in the Aerospace Materials. Mater. Today Proc. 2024, 113, 180–184. [Google Scholar] [CrossRef]
- Zhou, L.-Y.; Fu, J.; He, Y. A Review of 3D Printing Technologies for Soft Polymer Materials. Adv. Funct. Mater. 2020, 30, 2000187. [Google Scholar] [CrossRef]
- Sasso, M.; Palmieri, G.; Chiappini, G.; Amodio, D. Characterization of Hyperelastic Rubber-like Materials by Biaxial and Uniaxial Stretching Tests Based on Optical Methods. Polym. Test. 2008, 27, 995–1004. [Google Scholar] [CrossRef]
- Destrade, M.; Saccomandi, G.; Sgura, I. Methodical Fitting for Mathematical Models of Rubber-like Materials. Proc. R. Soc. A 2017, 473, 20160811. [Google Scholar] [CrossRef]
- Large Deformation Isotropic Elasticity: On the Correlation of Theory and Experiment for Compressible Rubberlike Solids. Proc. R. Soc. Lond. A 1972, 328, 567–583. [CrossRef]
- Lu, Z.; Zhao, J.-Y.; Zhou, C.-Y.; He, X.-H. Optimization Design of a Small-Sized Cruciform Specimen for Biaxial Fatigue Testing. Metals 2020, 10, 1148. [Google Scholar] [CrossRef]
- Deng, N.; Kuwabara, T.; Korkolis, Y.P. Cruciform Specimen Design and Verification for Constitutive Identification of Anisotropic Sheets. Exp. Mech. 2015, 55, 1005–1022. [Google Scholar] [CrossRef]
- Demmerle, S.; Boehler, J.P. Optimal Design of Biaxial Tensile Cruciform Specimens. J. Mech. Phys. Solids 1993, 41, 143–181. [Google Scholar] [CrossRef]
- Baptista, R.; Infante, V.; Madeira, J.F.A. Optimization of a Cruciform Specimen for Fatigue Crack Growth under in and Out-of-Phase in-Plane Biaxial Loading Conditions. Mech. Adv. Mater. Struct. 2023, 30, 1649–1666. [Google Scholar] [CrossRef]
- Men, M.; Meng, B.; Wan, M. Investigation on the Biaxial Tensile Testing Method for Metal Foil Using Cruciform Specimen. Theor. Appl. Fract. Mech. 2024, 133, 104577. [Google Scholar] [CrossRef]
- Baptista, R.; Claudio, R.A.; Reis, L.; Madeira, J.F.A.; Guelho, I.; Freitas, M. Optimization of Cruciform Specimens for Biaxial Fatigue Loading with Direct Multi Search. Theor. Appl. Fract. Mech. 2015, 80, 65–72. [Google Scholar] [CrossRef]
- Jia, Y.; Zhang, W.; Zhang, W. Optimal design and examination study of biaxial tensile specimens for solid propellant. J. Propuls. Technol. 2011, 32, 737–740. [Google Scholar] [CrossRef]
- Yu, Y.; Wan, M.; Wu, X.-D.; Zhou, X.-B. Design of a Cruciform Biaxial Tensile Specimen for Limit Strain Analysis by FEM. J. Mater. Process. Technol. 2002, 123, 67–70. [Google Scholar] [CrossRef]
- Esmaeili, A.; George, D.; Masters, I.; Hossain, M. Biaxial Experimental Characterizations of Soft Polymers: A Review. Polym. Test. 2023, 128, 108246. [Google Scholar] [CrossRef]
- Lamkanfi, E.; Van Paepegem, W.; Degrieck, J. Shape Optimization of a Cruciform Geometry for Biaxial Testing of Polymers. Polym. Test. 2015, 41, 7–16. [Google Scholar] [CrossRef]
- Zhang, R.; Shao, Z.; Shi, Z.; Dean, T.A.; Lin, J. Effect of Cruciform Specimen Design on Strain Paths and Fracture Location in Equi-Biaxial Tension. J. Mater. Process. Technol. 2021, 289, 116932. [Google Scholar] [CrossRef]
- Yang, X.; Wu, Z.R.; Yang, Y.R.; Pan, Y.; Wang, S.Q.; Lei, H. Optimization Design of Cruciform Specimens for Biaxial Testing Based on Genetic Algorithm. J. Mater. Eng. Perform. 2023, 32, 2330–2343. [Google Scholar] [CrossRef]
- Cheng, C.; Wan, M.; Meng, B.; Zhao, R.; Han, W.P. Size Effect on the Yield Behavior of Metal Foil under Multiaxial Stress States: Experimental Investigation and Modelling. Int. J. Mech. Sci. 2019, 151, 760–771. [Google Scholar] [CrossRef]
- Helfenstein, J.; Hollenstein, M.; Mazza, E. Investigation on the Optimal Specimen Design for Planar-Biaxial Materials Testing of Soft Materials. In Constitutive Models for Rubber VI; CRC Press: Boca Raton, FL, USA, 2010; pp. 371–376. [Google Scholar] [CrossRef]
- Hanabusa, Y.; Takizawa, H.; Kuwabara, T. Numerical Verification of a Biaxial Tensile Test Method Using a Cruciform Specimen. J. Mater. Process. Technol. 2013, 213, 961–970. [Google Scholar] [CrossRef]
- Jin, L.; Fang, Q.; Yan, X.; Hu, Q. Biaxial Tensile Mechanical Properties of HTPB Solid Propellant. Int. J. Aerosp. Eng. 2023, 2023, 2407730. [Google Scholar] [CrossRef]
- Luo, Y.-M.; Nguyen, T.T.; Attar, H.; Chevalier, L.; Lesueur, F. A New Biaxial Apparatus for Tensile Tests on Poly Ethylene Terephthalate Optimized Specimen at Stretch Blow Molding Conditions. Polym. Test. 2022, 113, 107676. [Google Scholar] [CrossRef]
- Gerke, S.; Adulyasak, P.; Brünig, M. New Biaxially Loaded Specimens for the Analysis of Damage and Fracture in Sheet Metals. Int. J. Solids Struct. 2017, 110–111, 209–218. [Google Scholar] [CrossRef]
- Wei, Z.; Harting, M.; Gerke, S.; Brünig, M. Ductile Damage Analysis under Extreme Low-Cycle Biaxial Shear Loadings: Experiments and Simulations. Int. J. Solids Struct. 2025, 313, 113292. [Google Scholar] [CrossRef]
- Hou, Y.; Lee, M.-G.; Lin, J.; Min, J. Experimental Characterization and Modeling of Complex Anisotropic Hardening in Quenching and Partitioning (Q&P) Steel Subject to Biaxial Non-Proportional Loadings. Int. J. Plast. 2022, 156, 103347. [Google Scholar] [CrossRef]
- Zhao, X.; Berwick, Z.C.; Krieger, J.F.; Chen, H.; Chambers, S.; Kassab, G.S. Novel Design of Cruciform Specimens for Planar Biaxial Testing of Soft Materials. Exp. Mech. 2014, 54, 343–356. [Google Scholar] [CrossRef]
- Jalocha, D.; Constantinescu, A.; Nevière, R. Prestrained Biaxial DMA Investigation of Viscoelastic Nonlinearities in Highly Filled Elastomers. Polym. Test. 2015, 42, 37–44. [Google Scholar] [CrossRef]
- Seibert, H.; Scheffer, T.; Diebels, S. Biaxial Testing of Elastomers: Experimental Setup, Measurement and Experimental Optimisation of Specimen’s Shape. Tech. Mech. Eur. J. Eng. Mech. 2014, 34, 72–89. [Google Scholar] [CrossRef]
- GJB 771.107-93; Test Method for Performance of Propellant Tensile Strength Test of Solid Propellant. COSTIND: Beijing, China, 1993.
- Ranjan, R.; Murthy, H.; Bhowmik, D.; Sadavarte, V.S. Behaviour of Composite Solid Propellant under Biaxial Tensile Loading. Polym. Test. 2023, 124, 108054. [Google Scholar] [CrossRef]
- Deng, J.-L. Control Problems of Grey Systems. Syst. Control Lett. 1982, 1, 288–294. [Google Scholar] [CrossRef]
- Kahraman, H.; Haberstroh, E. Direction-Dependent and Multiaxial Stress-Softening Behavior of Carbon Black–Filled Rubber. Rubber Chem. Technol. 2014, 87, 139–151. [Google Scholar] [CrossRef]
- Wang, Q.; Wang, G.; Wang, Z.; Qiang, H.; Wang, X.; Li, S.; Zhu, Z. Biaxial Tensile Test and Meso Damage Numerical Simulation of HTPB Propellant. Sci. Rep. 2022, 12, 17635. [Google Scholar] [CrossRef]
- Siddiqui, A.H.; Tiwari, P.; Patil, J.P.; Tewari, A.; Mishra, S. Yield Locus and Texture Evolution of AA7475-T761 Aluminum Alloy under Planar Biaxial Loading: An Experimental and Analytical Study. J. Alloys Compd. 2024, 1000, 175115. [Google Scholar] [CrossRef]
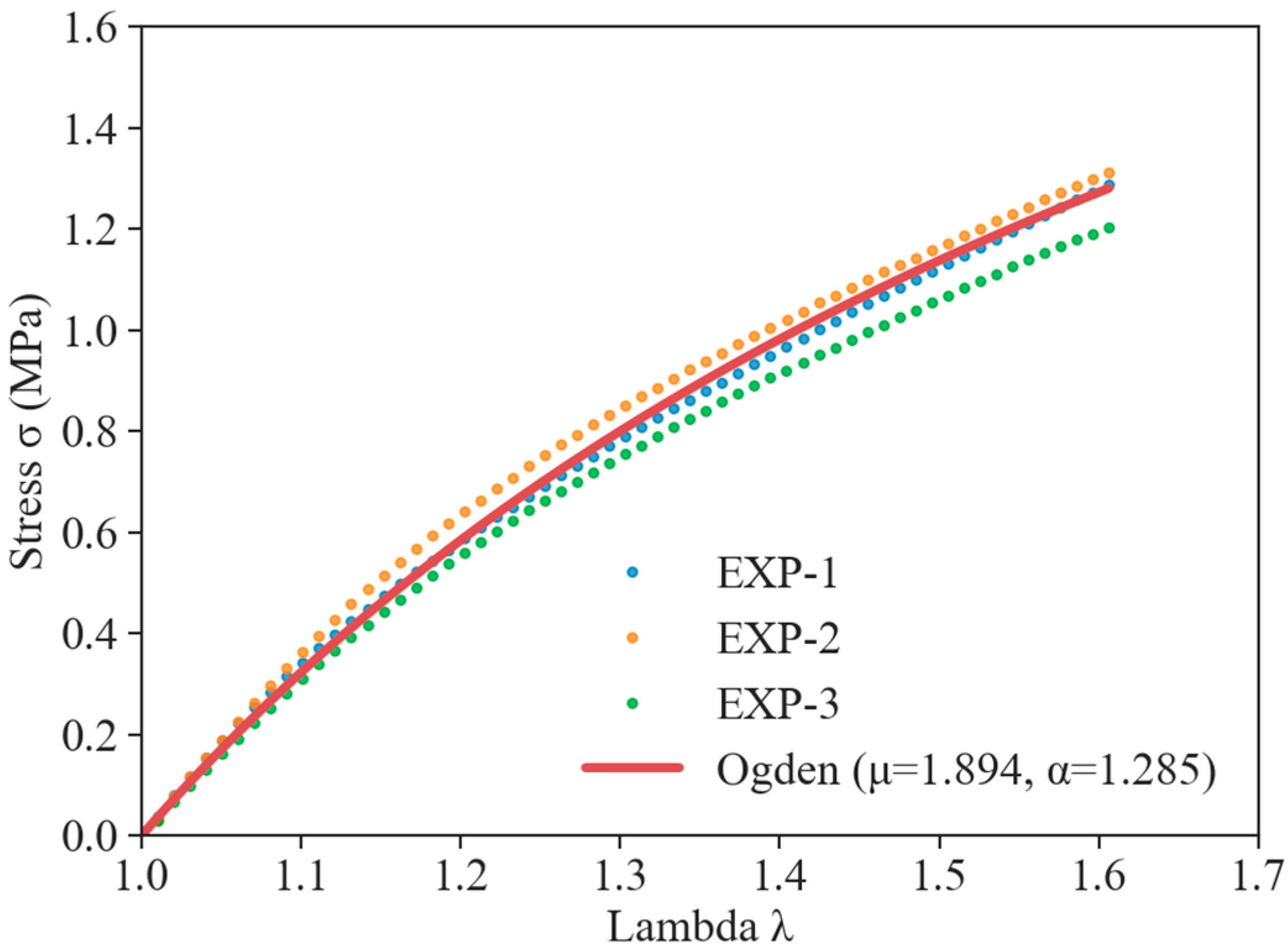





| Component | AP | Al | HTPB | Other |
|---|---|---|---|---|
| Content/% | 60.5 | 17 | 20 | 2.5 |
| Parameters | L | B | h | N | R | Wt | Wd | Ws | Wu |
|---|---|---|---|---|---|---|---|---|---|
| Value range/mm | 100 | 20 | 5 | ∈[1,5] | ∈[1,20] | ∈[1,10] | ∈[1,5] | ∈[1,20] | ∈[−2,2] |
| Parameters | L | B | h | N | R | Wt | Wd | Ws | Wu |
|---|---|---|---|---|---|---|---|---|---|
| Value range/mm | 100.0 | 20.0 | 5.0 | 4 | 3.0 | 2.5 | 2.0 | 15.0 | 0.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, H.; Wang, J.; Wang, X.; Liu, X. Optimization of Biaxial Tensile Specimen Shapes on Aerospace Composite with Large Deformation. Aerospace 2025, 12, 587. https://doi.org/10.3390/aerospace12070587
Luo H, Wang J, Wang X, Liu X. Optimization of Biaxial Tensile Specimen Shapes on Aerospace Composite with Large Deformation. Aerospace. 2025; 12(7):587. https://doi.org/10.3390/aerospace12070587
Chicago/Turabian StyleLuo, Haowen, Jiangtao Wang, Xueren Wang, and Xiangyang Liu. 2025. "Optimization of Biaxial Tensile Specimen Shapes on Aerospace Composite with Large Deformation" Aerospace 12, no. 7: 587. https://doi.org/10.3390/aerospace12070587
APA StyleLuo, H., Wang, J., Wang, X., & Liu, X. (2025). Optimization of Biaxial Tensile Specimen Shapes on Aerospace Composite with Large Deformation. Aerospace, 12(7), 587. https://doi.org/10.3390/aerospace12070587





