Shell-Stripping Mechanism of Red Sandstone Under Hypervelocity Impact with Aluminum Spheres
Abstract
1. Introduction
2. Experimental Methods
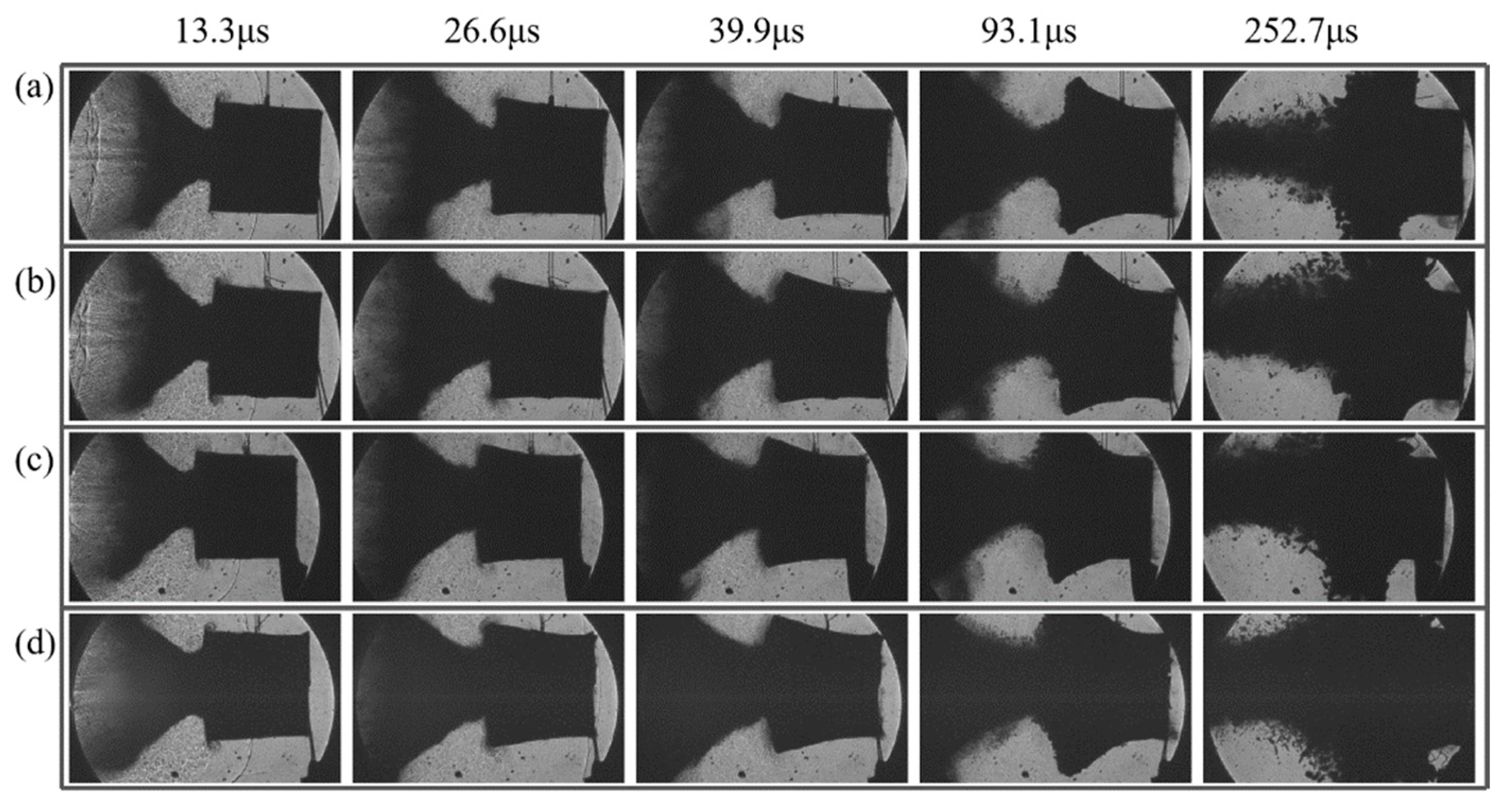
3. Experimental Results
4. Simulation Verification
4.1. Simulation Method
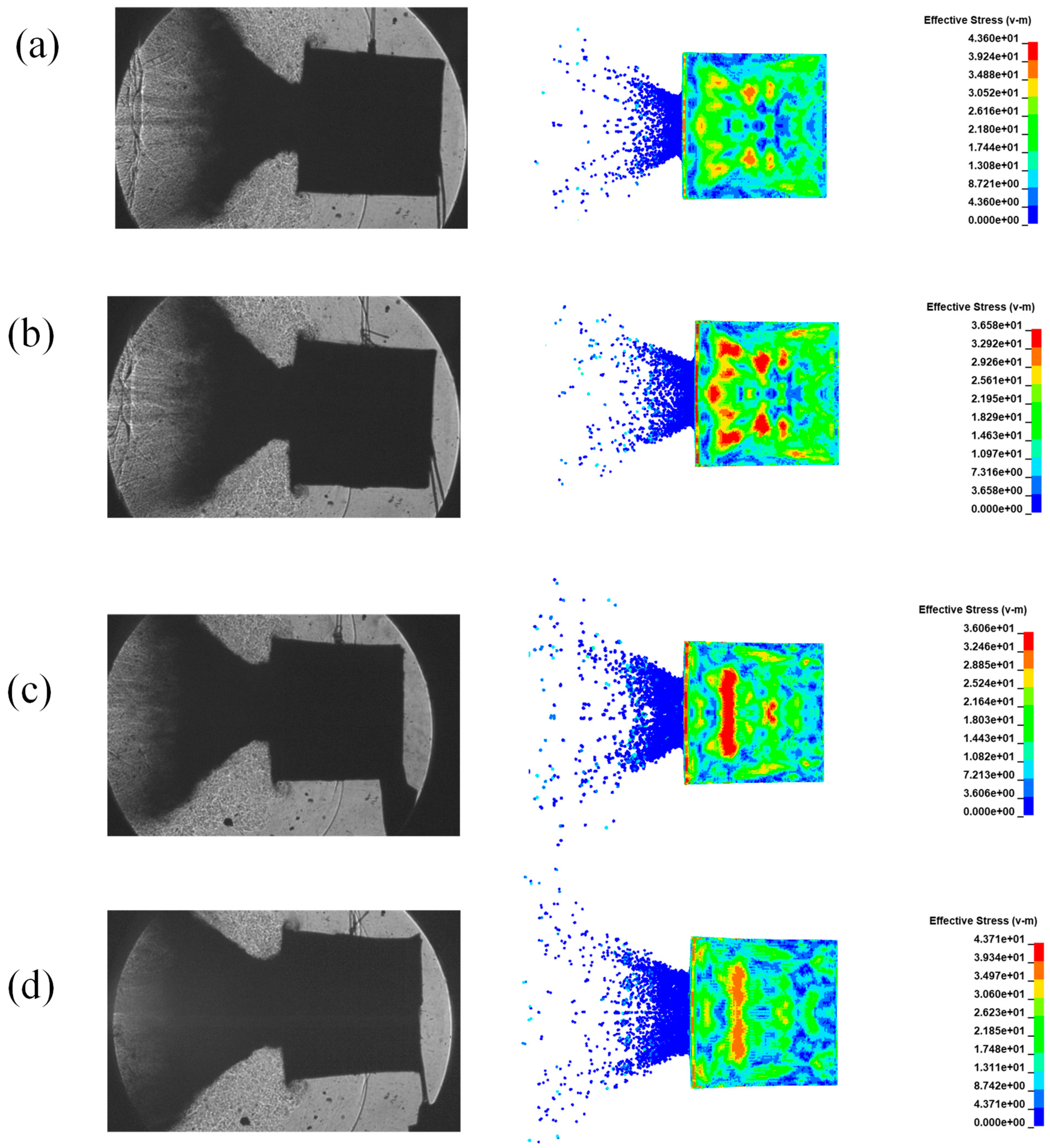
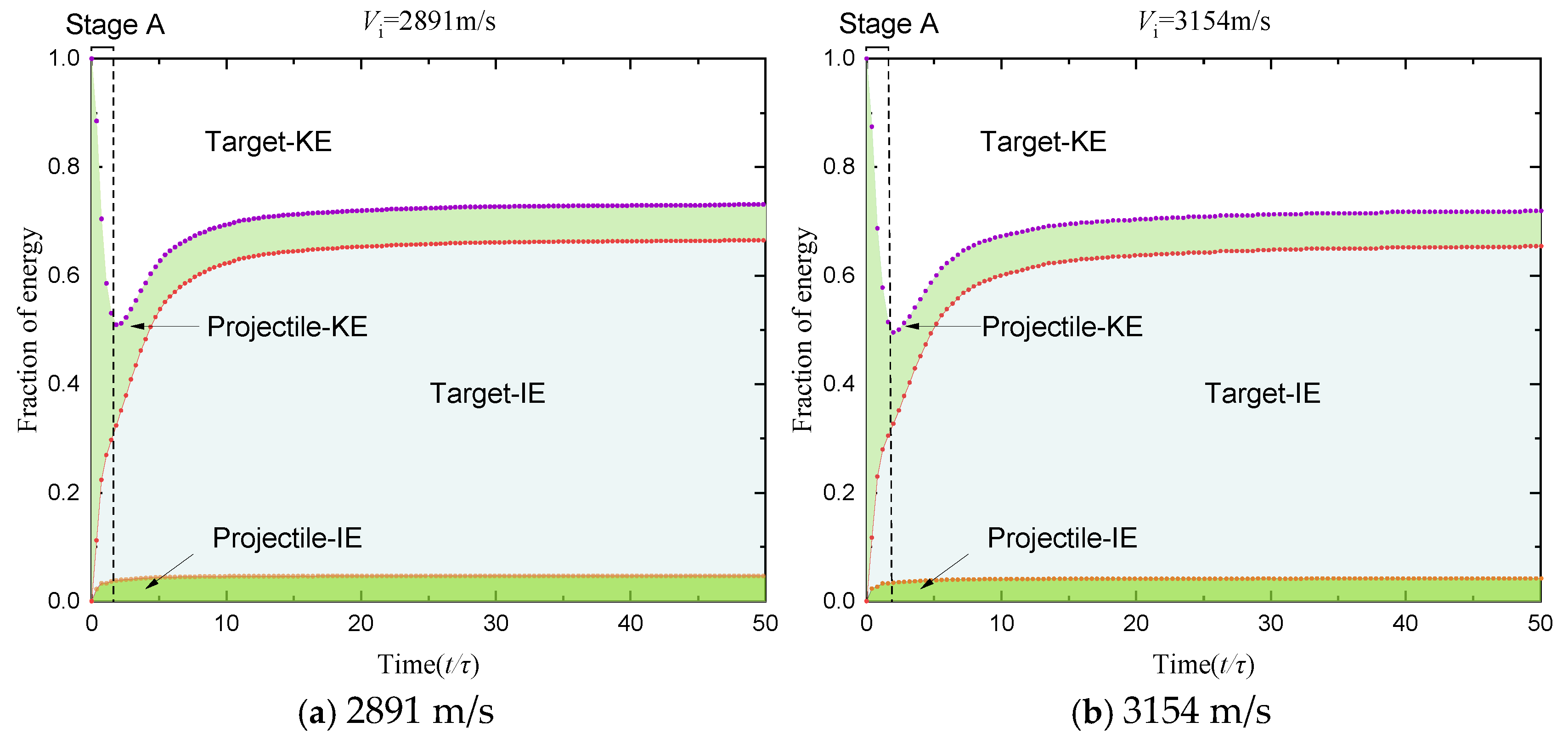
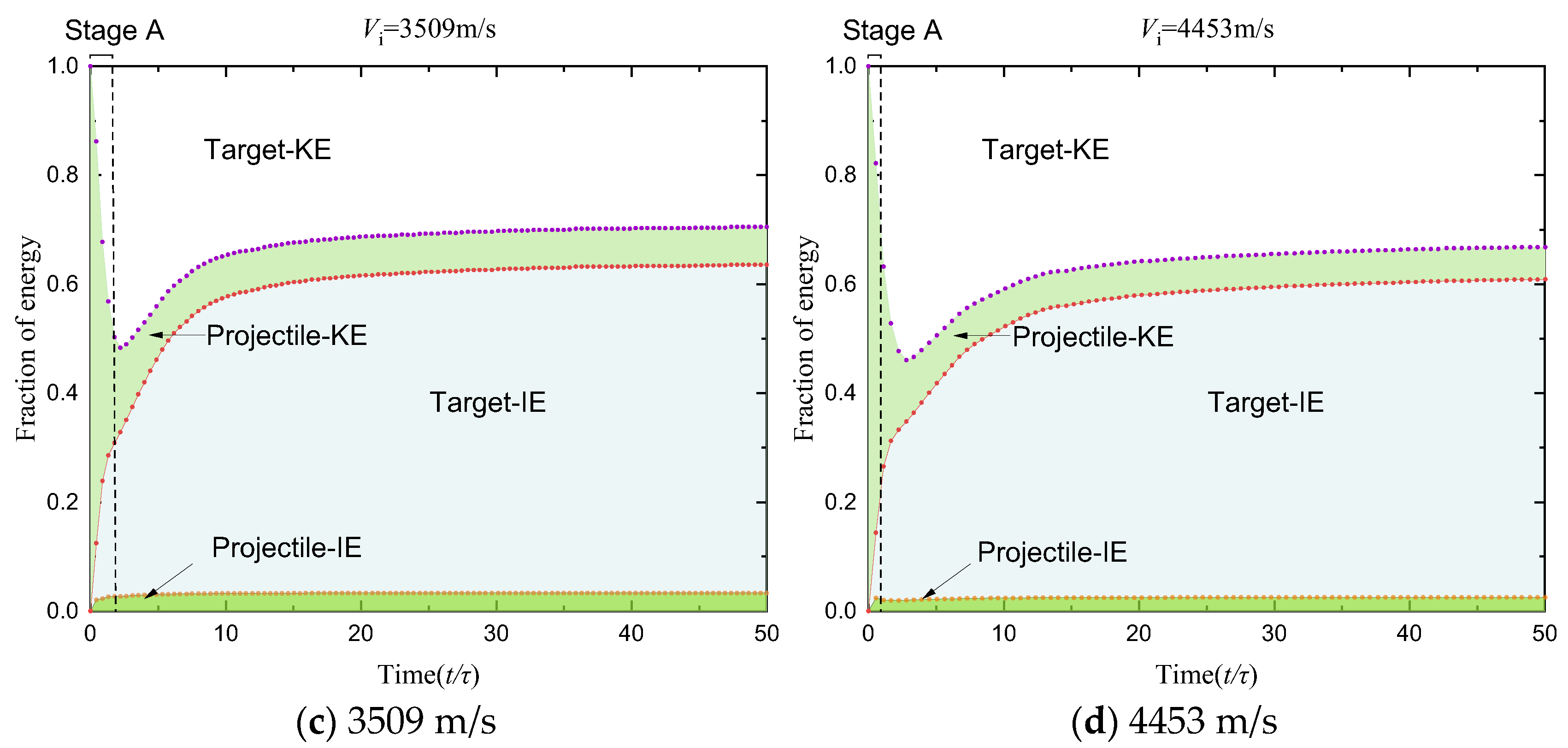
4.2. Simulation Results Analysis
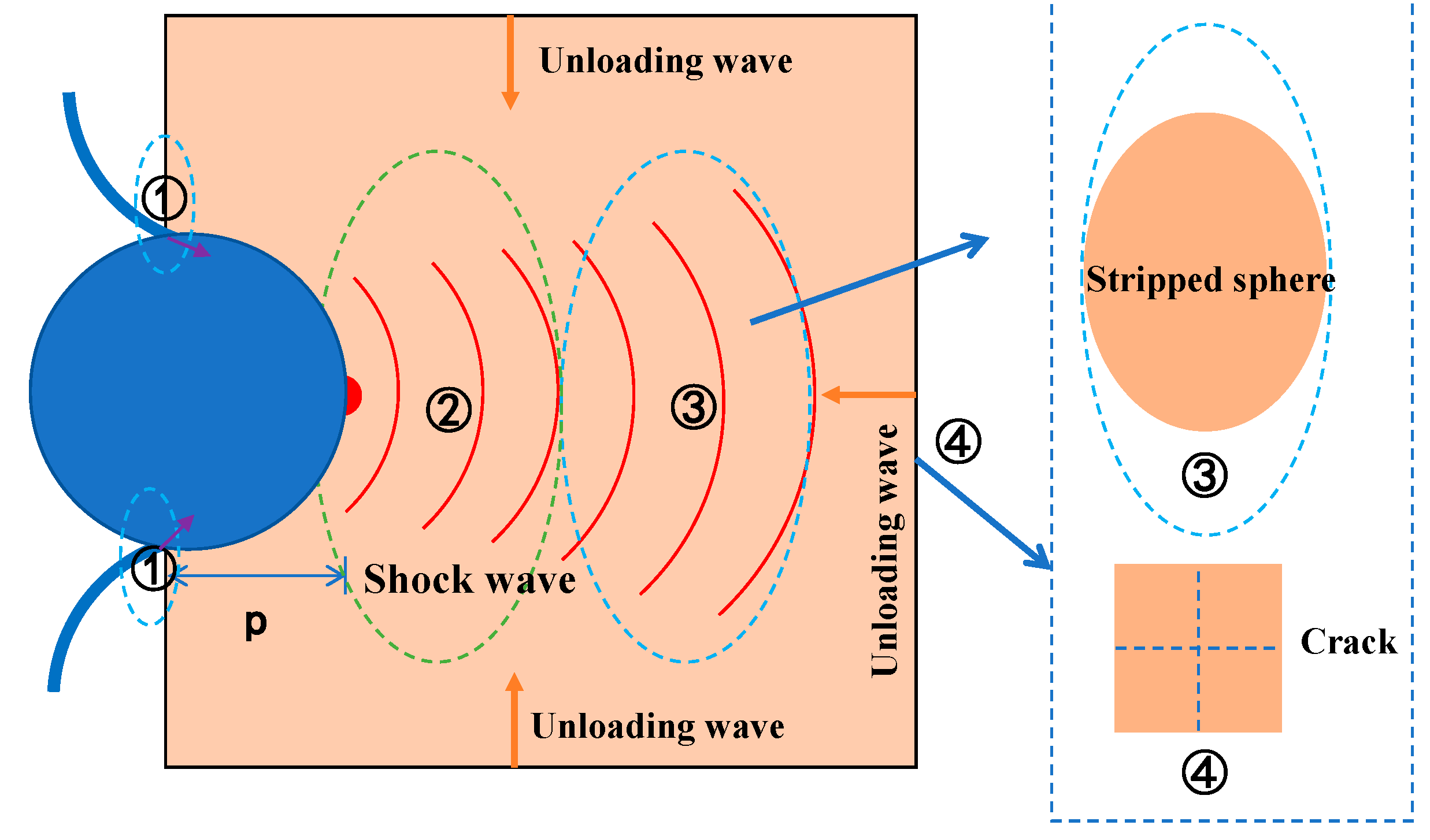
5. The Shell-Stripping Model
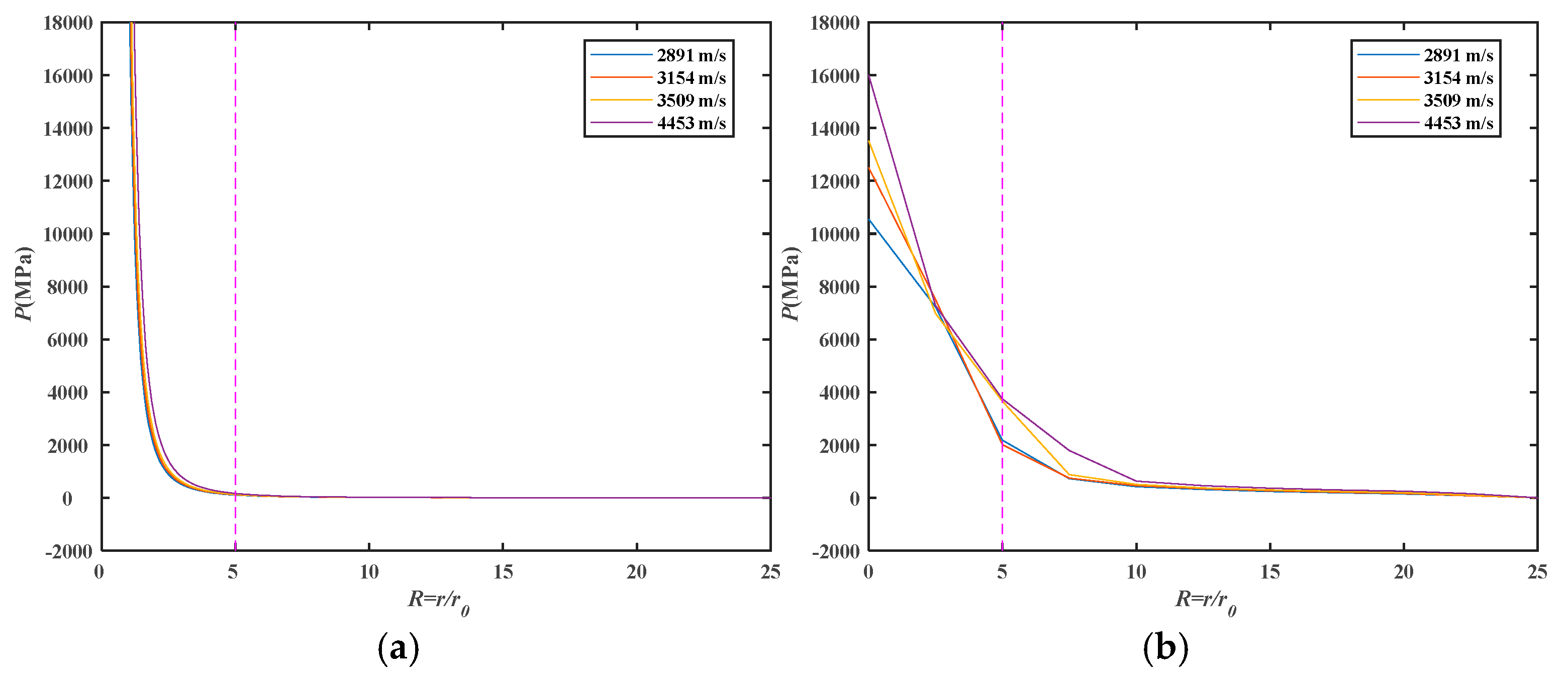
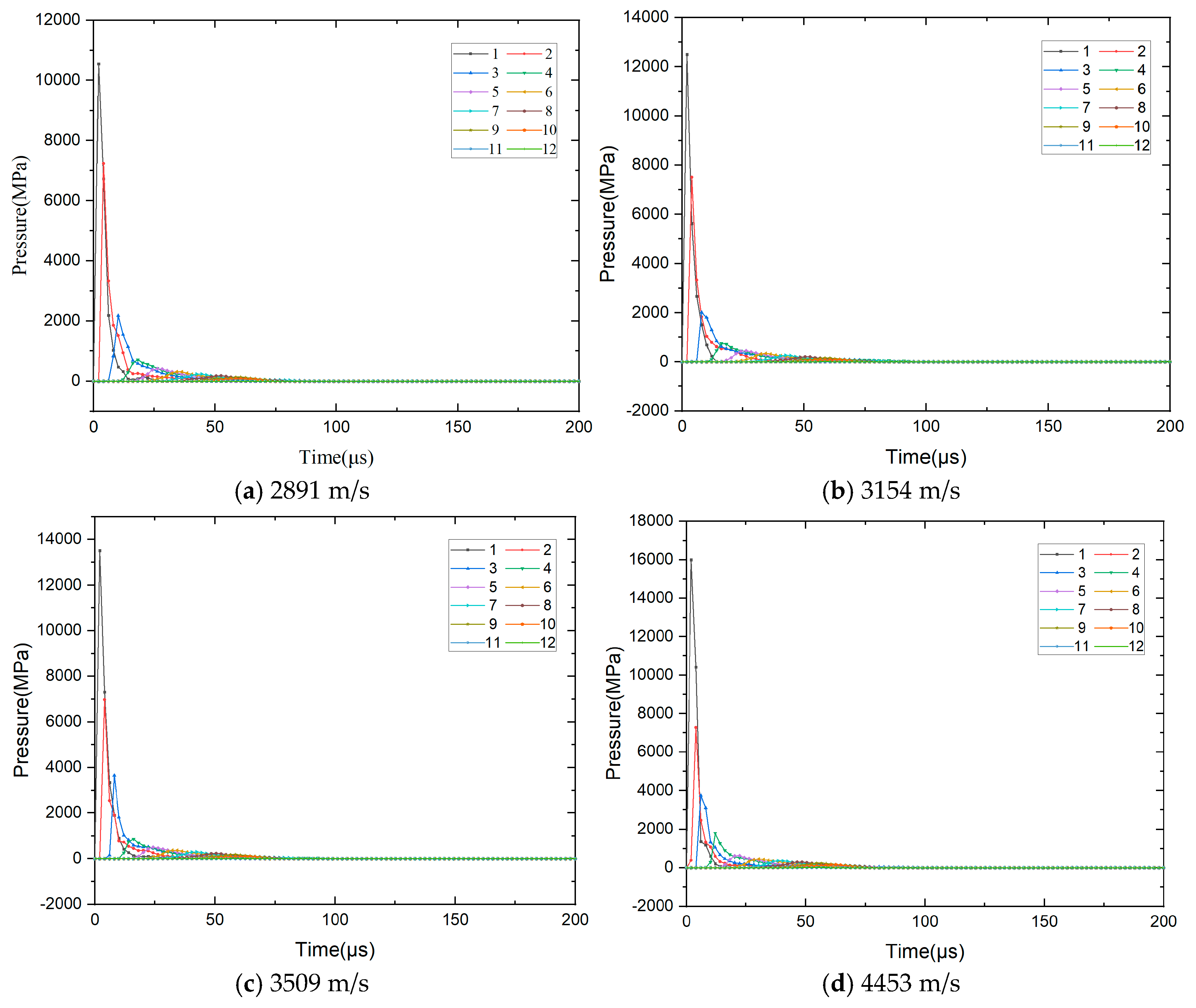
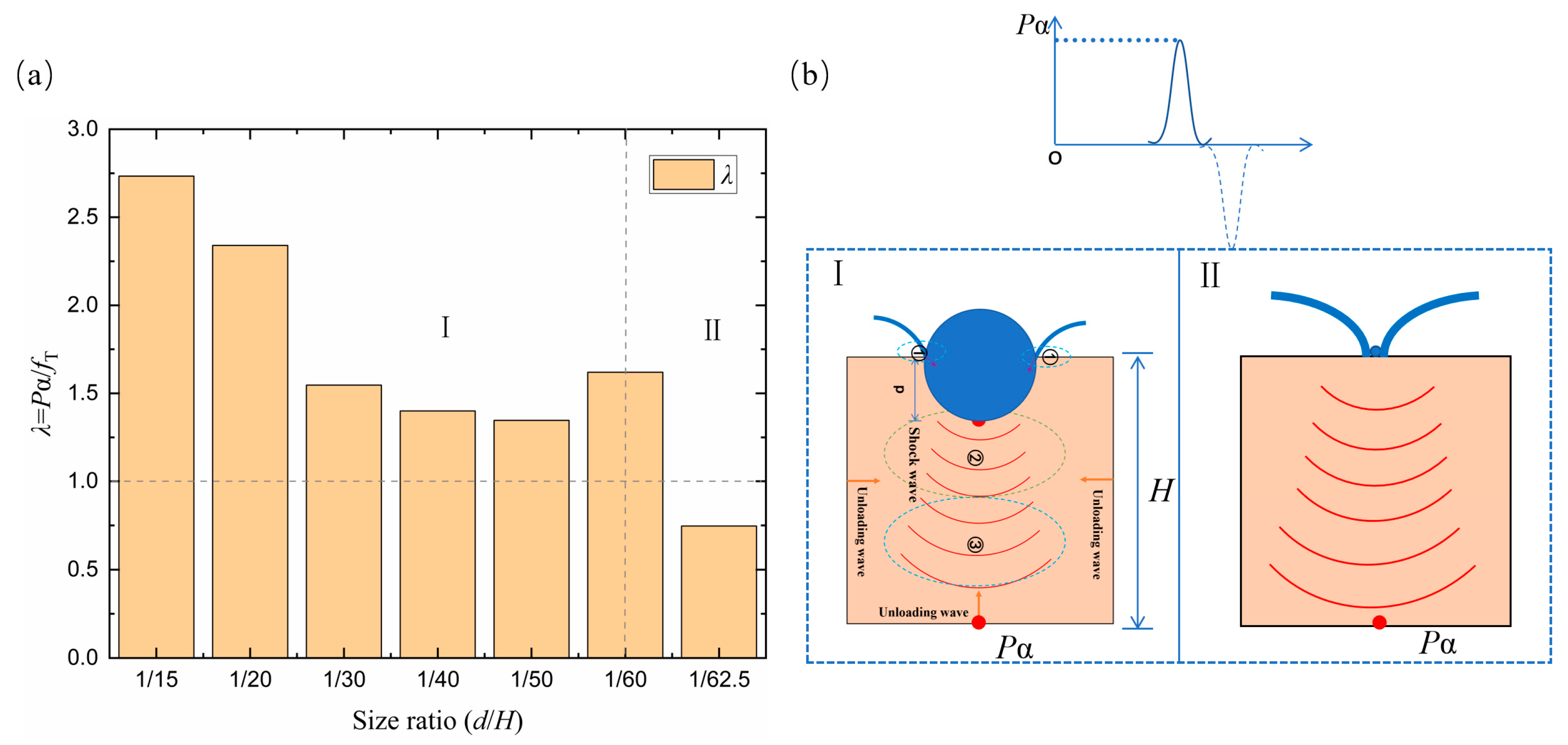
5.1. Shock Wave Attenuation Model
5.2. Shock Wave Stripping Model
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DART | Double asteroid redirection test |
| HVI | Hypervelocity impact |
| HJC | Holmquist–Johnson–Cook |
| JC | Johnson–Cook |
| MPC | Minor Planet Center |
| NEAs | Near-Earth asteroids |
| PHOs | Potentially hazardous objects |
| PVDF | Polyvinylidene fluoride |
| SPH | Smoothed particle hydrodynamics |
Appendix A. Initial Pressure Values for Theoretical Attenuation
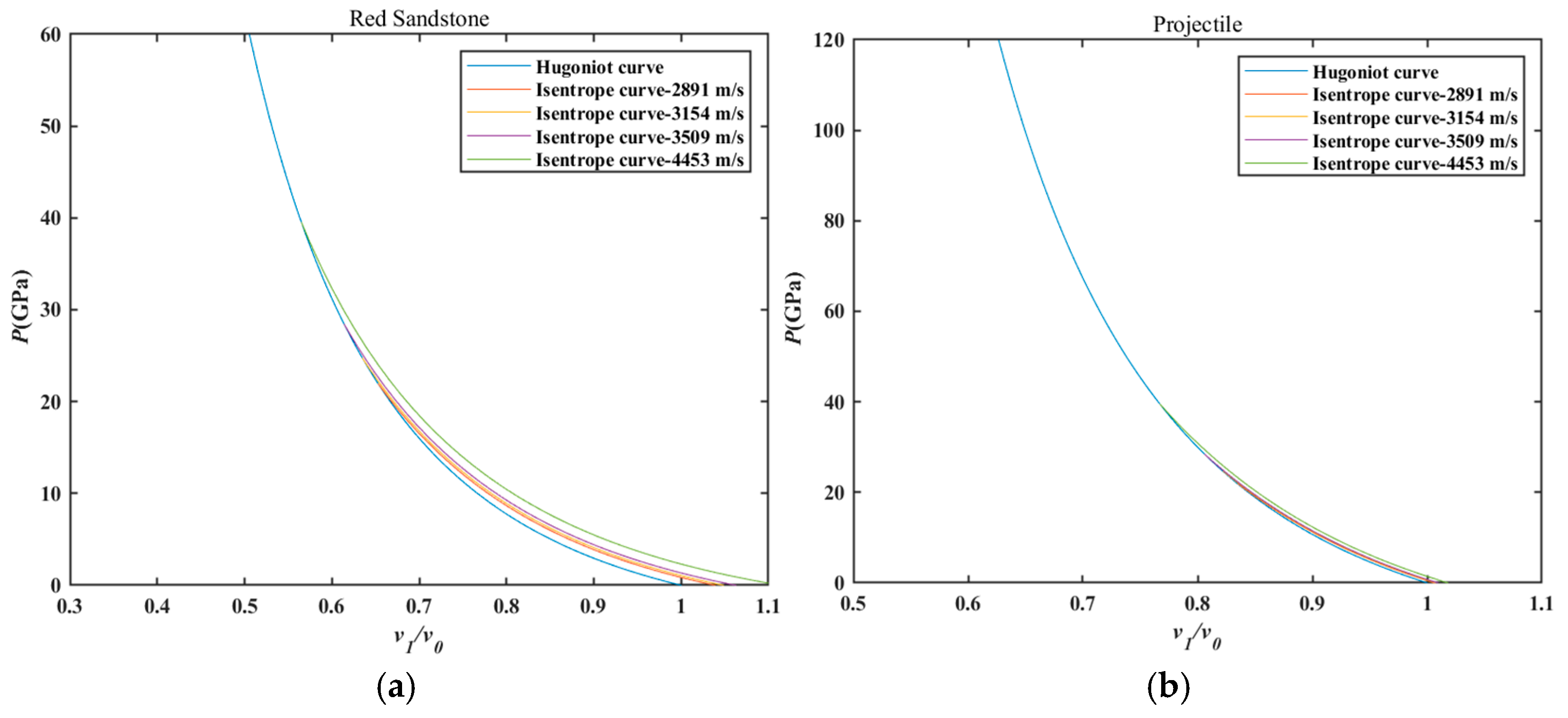
| Materials | ρ0 (g/cm3) | s1 | γ0 | K0 (GPa) | n |
| Al6061 | 2.77 | 5.386 | 1.97 | - | - |
| sandstone | 2.5 | 1.14 | 1 | 18.5 | 4.72 |
| vp (m/s) | pH (GPa) | UPp (km/s) | UPt (km/s) | URP (km/s) | URt (km/s) |
| 2891 | 21.95 | 1.15 | 1.75 | 1.13 | 1.64 |
| 3154 | 24.65 | 1.26 | 1.89 | 1.25 | 1.76 |
| 3509 | 28.47 | 1.41 | 2.10 | 1.36 | 1.94 |
| 4453 | 39.62 | 1.83 | 2.63 | 1.71 | 2.39 |
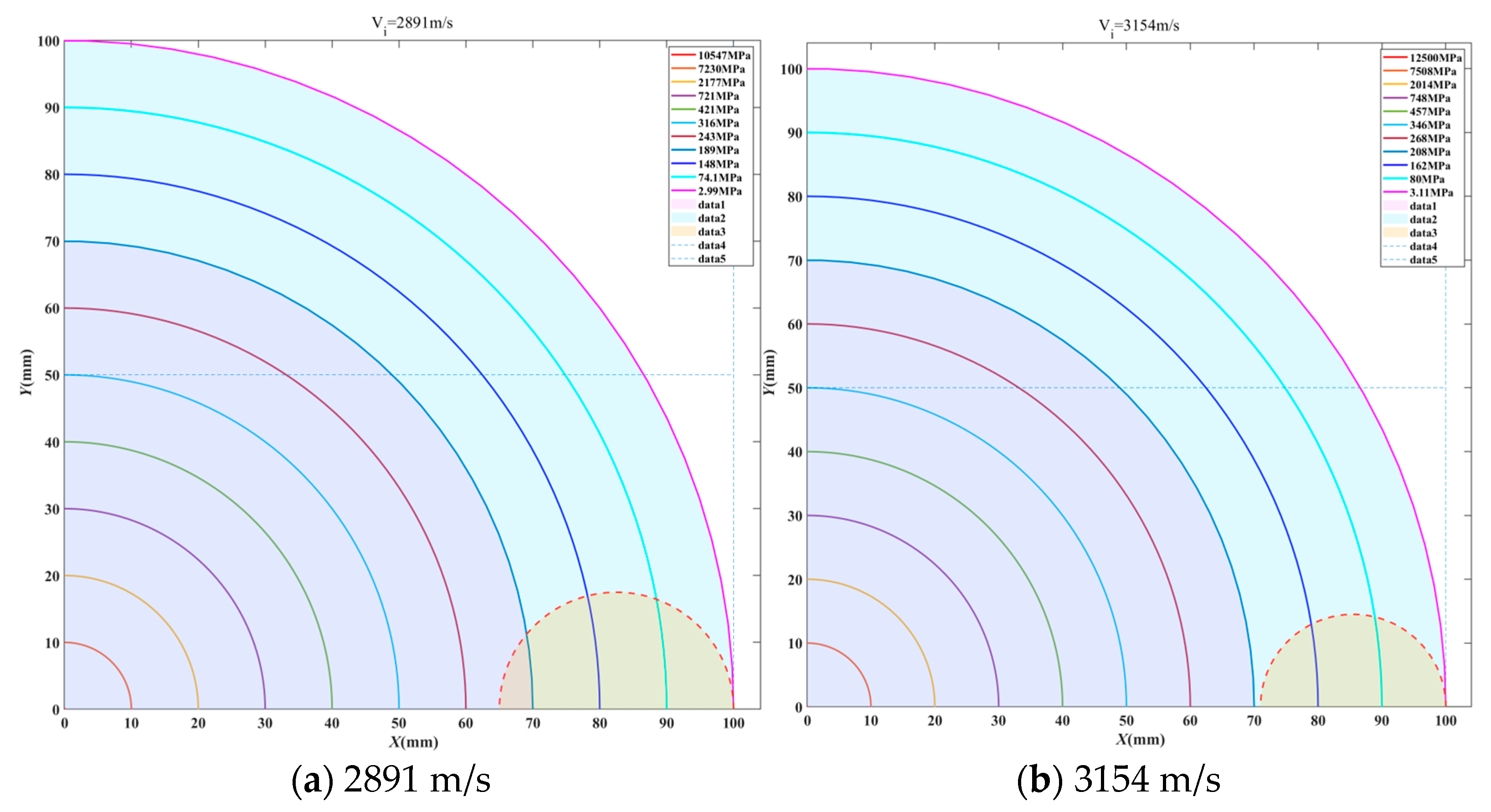
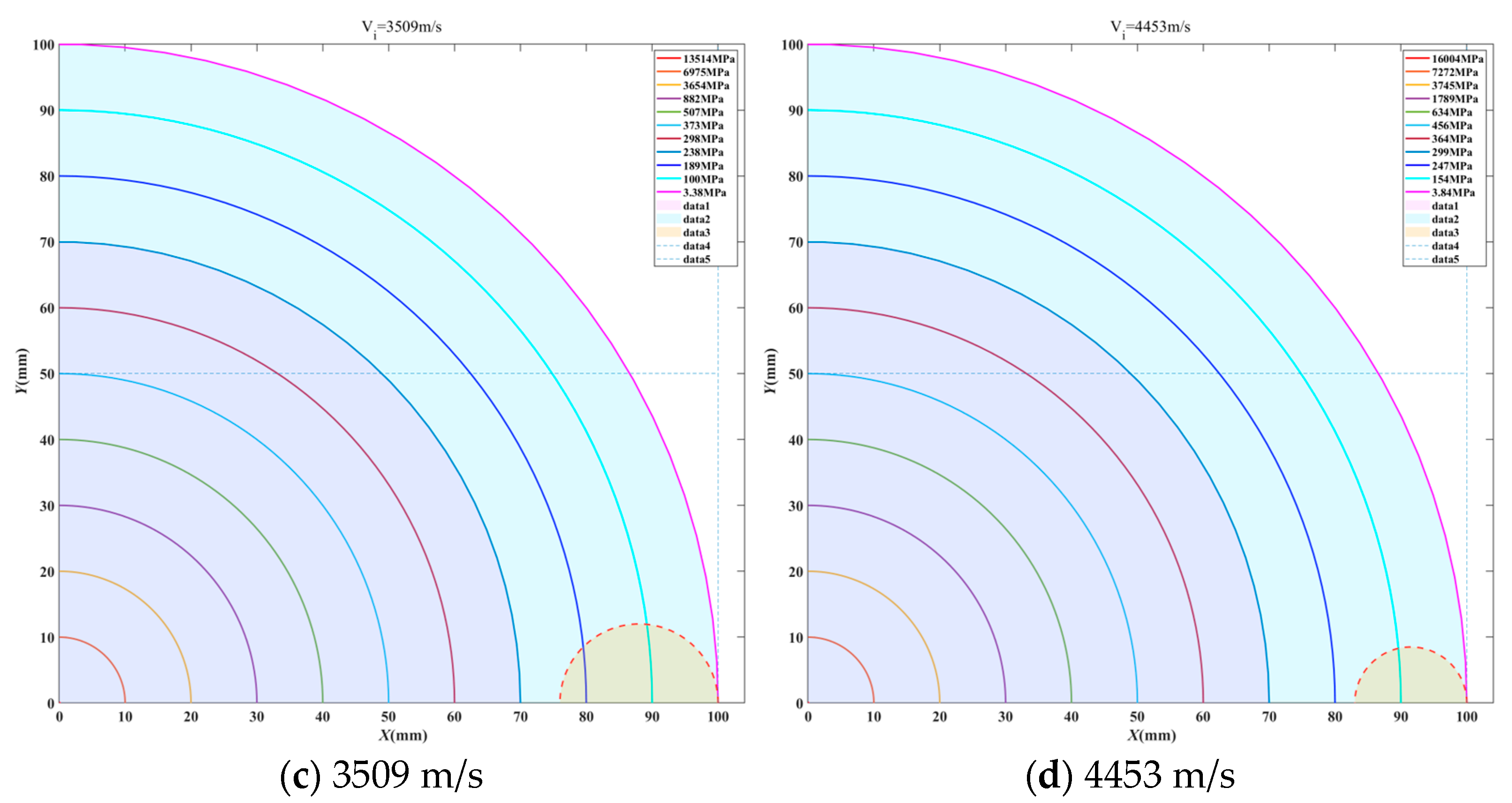
Appendix B. Grid Independence Verification
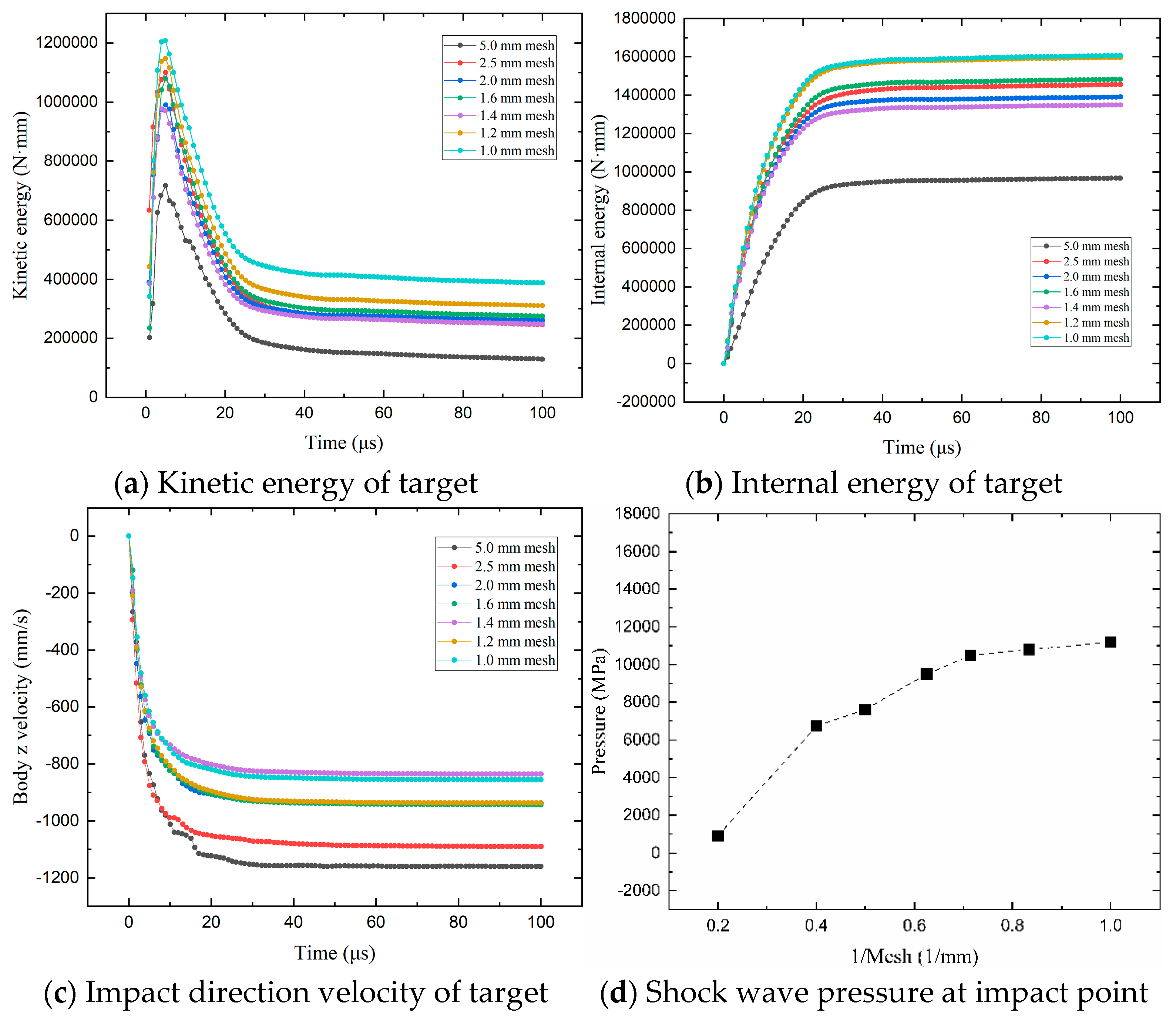
References
- Pengbin, M.A.; Hexi, B. Research Status of the Near-Earth Asteroids’ Hazard and Mitigation. J. Deep. Space Explor. 2016, 3, 10–17. [Google Scholar]
- Buys, M.; Squirini, R.M.; Wilson, C.M.; Gabriel, J.L.; Salehuddin, H.; Zimmerman, G.K.; Barbee, B.W. THEO & MUFN: Defending Earth against the 2023 PDC hypothetical asteroid impact. Acta Astronaut. 2024, 215, 217–233. [Google Scholar]
- NASA. Discovery Statistics [EB/OL]. Available online: https://cneos.jpl.nasa.gov/stats/ (accessed on 14 March 2018).
- Hergarten, S.; Kenkmann, T. The number of impact craters on Earth: Any room for further discoveries? Earth Planet. Sci. Lett. 2015, 425, 187–192. [Google Scholar] [CrossRef]
- Prinz, T. Multispectral remote sensing of the Gosses Bluff impact crater, central Australia (N.T.) by using Landsat-TM and ERS-1 data. ISPRS J. Photogramm. Remote Sens. 1996, 51, 137–149. [Google Scholar] [CrossRef]
- Hand, E. Updated: Drilling of Dinosaur-Killing Impact Crater Explains Buried Circular Hills. Available online: https://www.science.org/content/article/updated-drilling-dinosaur-killing-impact-crater-explains-buried-circular-hills (accessed on 27 November 2023).
- Kaplan, M. 11 Fascinating Impact Craters on Earth. Available online: https://www.touropia.com/impact-craters-on-earth/ (accessed on 27 November 2023).
- Puliti, L. Meteor Crater: Discover the Immense Crater of Arizona. Available online: https://www.travelinusa.us/meteor-crater-arizona/ (accessed on 27 November 2023).
- Carancas, H4-5. Available online: https://meteoritegallery.com/carancas-h4-5/ (accessed on 27 November 2023).
- Meteor Strikes Chelyabinsk, Russia. Available online: https://forum.nasaspaceflight.com/index.php?topic=31118.460 (accessed on 27 November 2023).
- Barbee, B.W.; Syal, M.B.; Dearborn, D.; Gisler, G.; Greenaugh, K.; Howley, K.M.; Leung, R.; Lyzhoft, J.; Miller, P.L.; Nuth, J.A.; et al. Options and uncertainties in planetary defense: Mission planning and vehicle design for flexible response. Acta Astronaut. 2018, 143, 37–61. [Google Scholar] [CrossRef]
- Cheng, A.F.; Agrusa, H.F.; Barbee, B.W.; Meyer, A.J.; Farnham, T.L.; Raducan, S.D.; Richardson, D.C.; Dotto, E.; Zinzi, A.; Della Corte, V.; et al. Momentum transfer from the DART mission kinetic impact on asteroid Dimorphos. Nature 2023, 616, 457–460. [Google Scholar] [CrossRef]
- Flynn, G.J.; Durda, D.D.; Molesky, M.J.; May, B.A.; Congram, S.N.; Loftus, C.L.; Reagan, J.R.; Strait, M.M.; Macke, R.J. Momentum transfer in hypervelocity cratering of meteorites and meteorite analogs: Implications for orbital evolution and kinetic impact deflection of asteroids. Int. J. Impact Eng. 2020, 136, 103437. [Google Scholar] [CrossRef]
- Gores, P.A.S.; Spray, J.G. Hypervelocity impact of anorthosite: Excavation, spallation and crater reconstruction. Int. J. Impact Eng. 2022, 160, 104078. [Google Scholar] [CrossRef]
- Hoerth, T.; Schäfer, F.; Thoma, K.; Kenkmann, T.; Poelchau, M.H.; Lexow, B.; Deutsch, A. Hypervelocity impacts on dry and wet sandstone: Observations of ejecta dynamics and crater growth. Meteorit. Planet. Sci. 2013, 48, 23–32. [Google Scholar] [CrossRef]
- Poelchau, M.H.; Kenkmann, T.; Hoerth, T.; Schäfer, F.; Rudolf, M.; Thoma, K. Impact cratering experiments into quartzite, sandstone and tuff: The effects of projectile size and target properties on spallation. Icarus 2014, 242, 211–224. [Google Scholar] [CrossRef]
- Chocron, S.; Walker, J.D.; Grosch, D.J.; Beissel, S.R.; Durda, D.D.; Housen, K.R. Momentum enhancement simulations for hypervelocity impacts on sandstone. Int. J. Impact Eng. 2021, 151, 103832. [Google Scholar] [CrossRef]
- Melosh, H.J. Impact Cratering: A Geologic Process; Oxford University Press: New York, NY, USA, 1989; pp. 1–240. [Google Scholar]
- Lockner, D.A. Rock Failure. In Rock Physics and Phase Relations: A Handbook of Physical Constants; Ahrens, T.J., Ed.; American Geophysical Union, AGU Reference Shelf: Washington, DC, USA, 1995; Volume 3, pp. 127–147. [Google Scholar]
- Lu, Z.; Wang, Z. Triaxial tests on dynamic properties of granite under intermediate and high strain rates. Chin. J. Geotech. Eng. 2016, 38, 1087–1094. [Google Scholar]
- Lv, H.; He, Q.; Chen, X.; Han, P. Numerical simulation of impact crater formation and distribution of high-pressure polymorphs. Acta Astronaut. 2023, 203, 169–186. [Google Scholar] [CrossRef]
- Liu, W.; Zhang, Q.; Long, R.; Gong, Z.; Wu, Q.; Siyuan, R.; Lu, Y.; Xu, J.; Zhong, X.; Jiankang, R. Ejecta velocity and motion model of spherical aluminum alloy projectile hypervelocity impact on basalt. Acta Astronaut. 2024, 224, 574–592. [Google Scholar] [CrossRef]
- Johnson, B.C.; Bowling, T.J.; Melosh, H.J. Jetting during vertical impacts of spherical projectiles. Icarus 2014, 238, 13–22. [Google Scholar] [CrossRef]
- Melosh, H.J. Impact ejection, spallation, and the origin of meteorites. Icarus 1984, 59, 234–260. [Google Scholar] [CrossRef]
- Nakamura, A.; Michel, P.; Setoh, M. Weibull parameters of Yakuno basalt targets used in documented high-velocity impact experiments. J. Geophys. Res. 2007, 112, E02001. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, Q.; Liu, Y.; Zhang, K.; Wei, Y.; Chen, T.; Guo, Y.; Lu, L.; Wei, B. Response characteristics and impact resistance of composite laminates with shear stiffening gel under hypervelocity impact. Acta Astronaut. 2024, 219, 858–870. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, K.; Chen, T.; Wang, Q.; Wei, B. Microstructural evolution and energetic characteristics of TiZrHfTa0.7W0.3 high-entropy alloy under high strain rates and its application in high-velocity penetration. J. Mater. Sci. Technol. 2023, 132, 144–153. [Google Scholar] [CrossRef]
- Wang, Y.; Zeng, X.; Chen, H.; Yang, X.; Wang, F.; Zeng, L. Modified Johnson-Cook constitutive model of metallic materials under a wide range of temperatures and strain rates. Results Phys. 2021, 27, 104498. [Google Scholar] [CrossRef]
- He, Q.; Chen, X.; Chen, J. Finite element-smoothed particle hydrodynamics adaptive method in simulating debris cloud. Acta Astronaut. 2020, 175, 99–117. [Google Scholar] [CrossRef]
- Sun, Y.; Wang, L.; Wang, J.; Tan, C.; Ye, Y.; Lin, K. A modified Holmquist–Johnson–Cook (HJC) constitutive model and its application to numerical simulations of explosions and impacts in rock materials. Simul. Modell. Pract. Theory 2025, 138, 103038. [Google Scholar] [CrossRef]
- Lu, S.; Wu, X. Finite element simulation of sandstone SHPB experiment under impact load. J. Hefei Univ. Technol. (Nat. Sci.) 2022, 45, 1517–1521. (In Chinese) [Google Scholar]
- Bagatin, A.C.; Alemañ, R.A.; Benavidez, P.G.; Pérez-Molina, M.; Richardson, D.C. Gravitational re-accumulation as the origin of most contact binaries and other small body shapes. Icarus 2020, 339, 113603. [Google Scholar] [CrossRef]
- Gault, D.E. The partition of energy for hypervelocity impact craters formed in rock. In Proceedings of the Sixth Hypervelocity Impact Symposium, Cleveland, OH, USA, 30 April–2 May 1963. [Google Scholar]
- Liu, K.; Zhao, J.; Wu, G.; Maksimenko, A.; Haque, A.; Zhang, Q.B. Dynamic strength and failure modes of sandstone under biaxial compression. Int. J. Rock. Mech. Min. Sci. 2020, 128, 104260. [Google Scholar] [CrossRef]
- Kubota, S.; Ogata, Y.; Wada, Y.; Simangunsong, G.; Shimada, H.; Matsui, K. Estimation of dynamic tensile strength of sandstone. Int. J. Rock. Mech. Min. Sci. 2008, 45, 397. [Google Scholar] [CrossRef]
- Padmanabha, V.; Schäfer, F.; Rae, A.S.P.; Kenkmann, T. Dynamic Split Tensile Strength of Basalt, Granite, Marble and Sandstone: Strain Rate Dependency and Fragmentation. Rock. Mech. Rock. Eng. 2023, 56, 109. [Google Scholar] [CrossRef]
- Tang, W.; Zhang, R.; Hu, J.; Jing, F. Approximation calculation methods of shock temperature. Adv. Mech. 1998, 28, 479–487. [Google Scholar]
- Kieffer, S.W.; Simonds, C.H. The role of volatiles and lithology in the impact cratering process. Rev. Geophys. 1980, 18, 143–181. [Google Scholar] [CrossRef]
- Zhang, J.J.; Bentley, L.R. Change of bulk and shear moduli of dry sandstone with effective pressure and temperature. CREWES Res. Rep. 1999, 11, 1–16. [Google Scholar]
- Qin, X.; Han, D.H.; Zhao, L. Measurement of grain bulk modulus on sandstone samples from the norwegian continental shelf. J. Geophys. Res. Solid Earth 2022, 127, e2022JB024550. [Google Scholar] [CrossRef]
- Kui, Z.; Xun, L.; Gang, Y. Study on planar impact experiment and state equation under high pressure of red sandstone. BLASTING 2024, 41, 69–74. [Google Scholar]
- McQueen, R.; Marsh, S.; Fritz, J. Hugoniot equation of state of twelve rocks. J. Geophys. Res. 1967, 72, 4999–5036. [Google Scholar] [CrossRef]




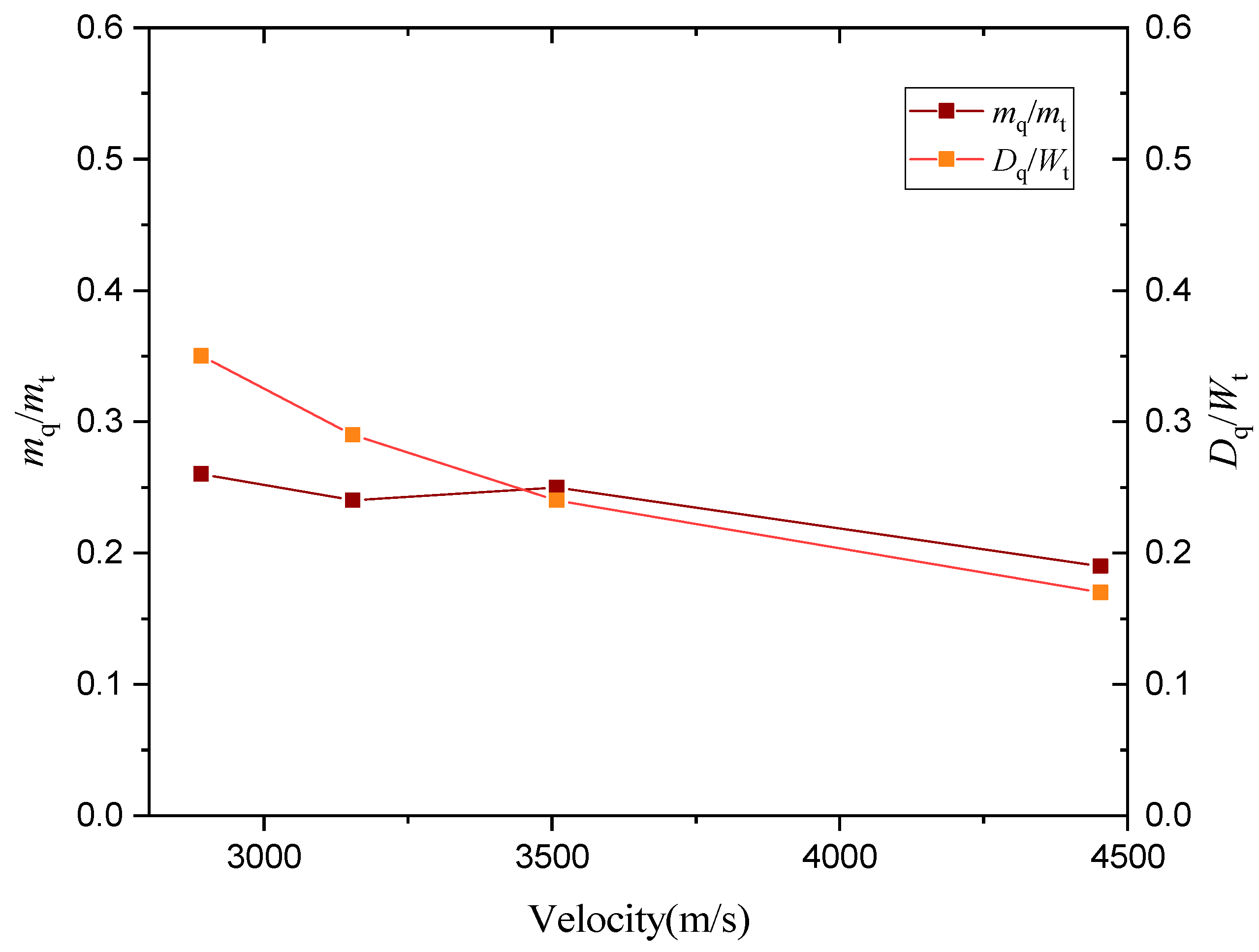
| vp (m/s) | ρp (g/cm3) | ρt (g/cm3) | mp (g) | mr (g) | mq (g) |
|---|---|---|---|---|---|
| 2891 | 2.700 | 2.518 | 19.0 | 1942 | 647 |
| 3154 | 2.700 | 2.504 | 19.0 | 1738 | 611 |
| 3509 | 2.700 | 2.498 | 19.0 | 1629 | 619 |
| 4453 | 2.700 | 2.498 | 19.0 | - | 485 |
| ρ0 (kg·m−3) | µ | G (GPa) | σs (MPa) | Nq (MPa) |
| 2773 | 0.33 | 27.6 | 290 | 203 |
| Ne | Q | Spall type | D0 | D2–5 |
| 0.35 | 0.011 | 3 | 1 | 0 |
| C (m·s−1) | S1 | γ |
| 5386 | 1.339 | 1.997 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Jiang, Q.; Liu, Z.; Jiang, M.; Li, Y.; Chang, Z.; Zhang, K.; Wei, B. Shell-Stripping Mechanism of Red Sandstone Under Hypervelocity Impact with Aluminum Spheres. Aerospace 2025, 12, 534. https://doi.org/10.3390/aerospace12060534
Liu Y, Jiang Q, Liu Z, Jiang M, Li Y, Chang Z, Zhang K, Wei B. Shell-Stripping Mechanism of Red Sandstone Under Hypervelocity Impact with Aluminum Spheres. Aerospace. 2025; 12(6):534. https://doi.org/10.3390/aerospace12060534
Chicago/Turabian StyleLiu, Yizhe, Quanyu Jiang, Zishang Liu, Minqiang Jiang, Yadong Li, Zhenghua Chang, Kun Zhang, and Bingchen Wei. 2025. "Shell-Stripping Mechanism of Red Sandstone Under Hypervelocity Impact with Aluminum Spheres" Aerospace 12, no. 6: 534. https://doi.org/10.3390/aerospace12060534
APA StyleLiu, Y., Jiang, Q., Liu, Z., Jiang, M., Li, Y., Chang, Z., Zhang, K., & Wei, B. (2025). Shell-Stripping Mechanism of Red Sandstone Under Hypervelocity Impact with Aluminum Spheres. Aerospace, 12(6), 534. https://doi.org/10.3390/aerospace12060534





