Porous Surface Design with Stability Analysis for Turbulent Transition Control in Hypersonic Boundary Layer
Abstract
1. Introduction
2. Methods
2.1. Linear Stability Theory
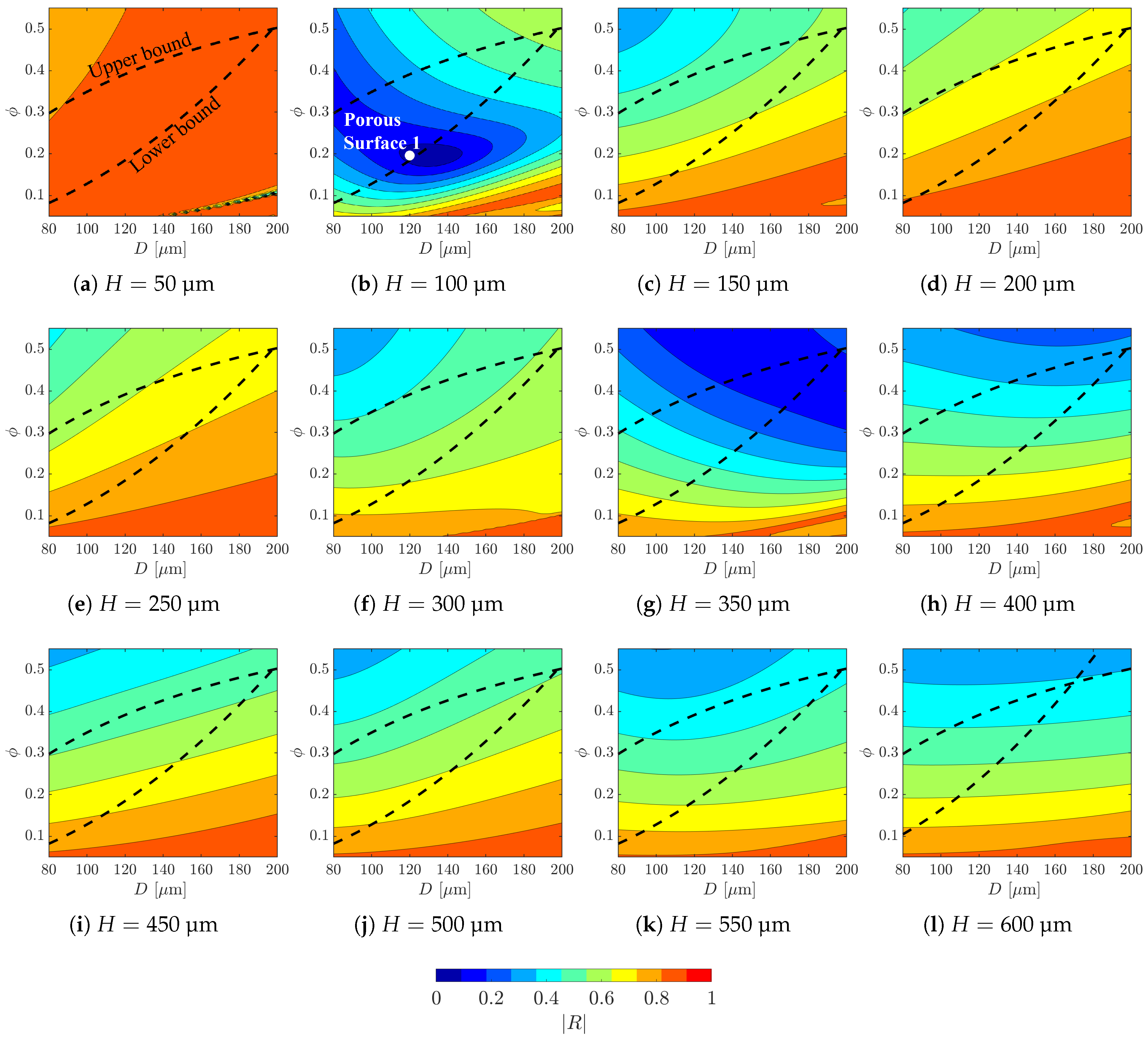
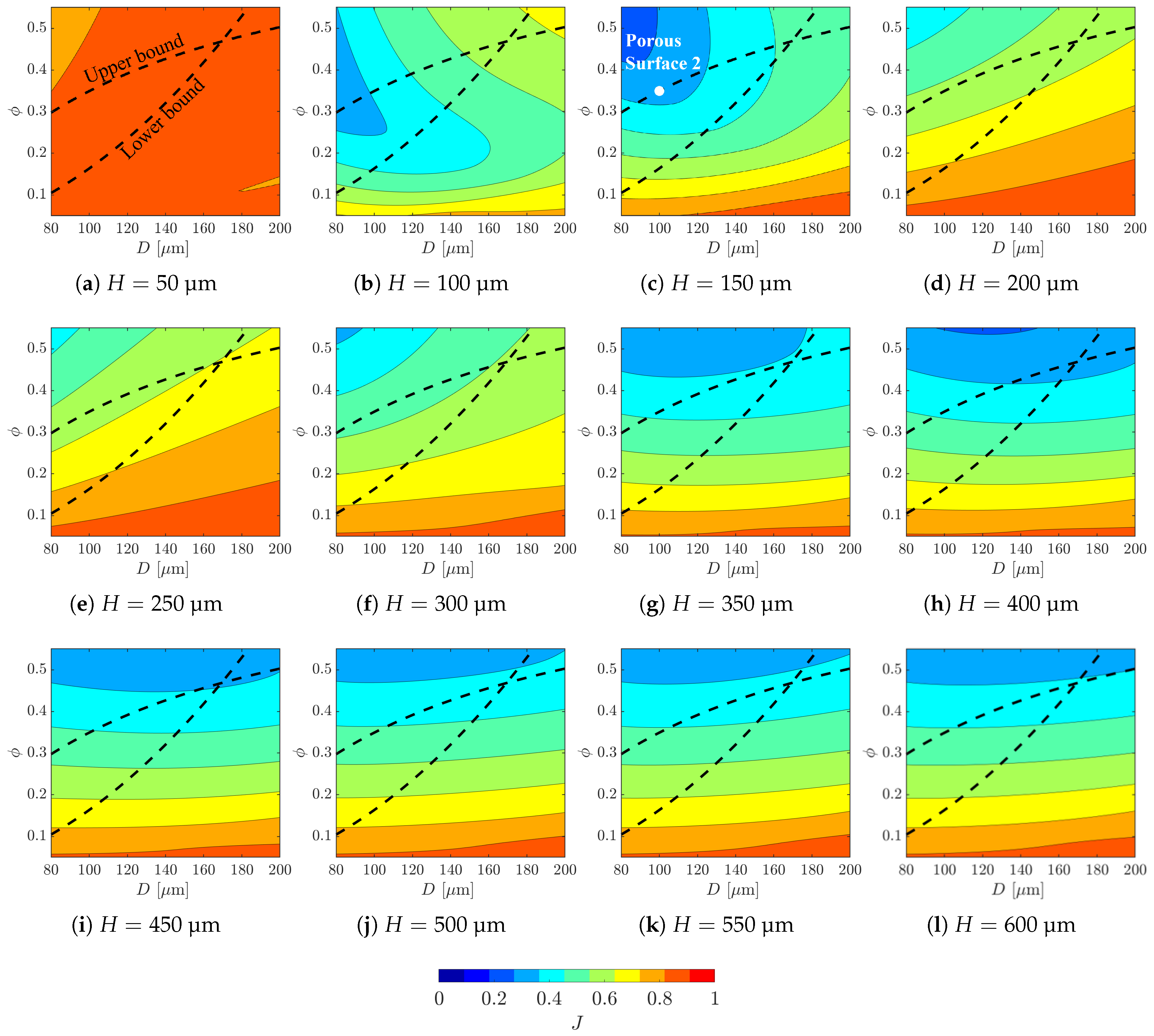
2.2. Design of Porous Surfaces
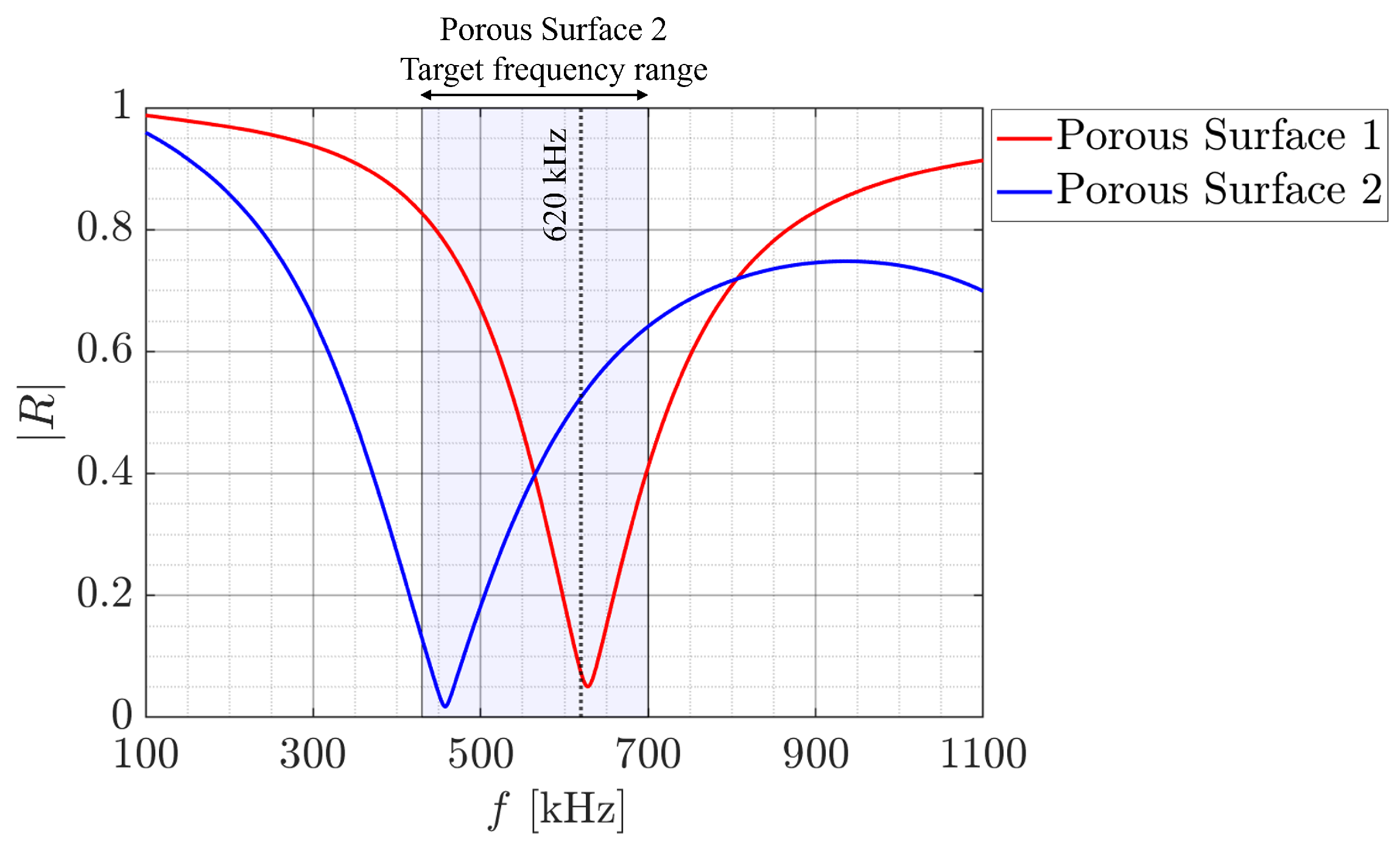
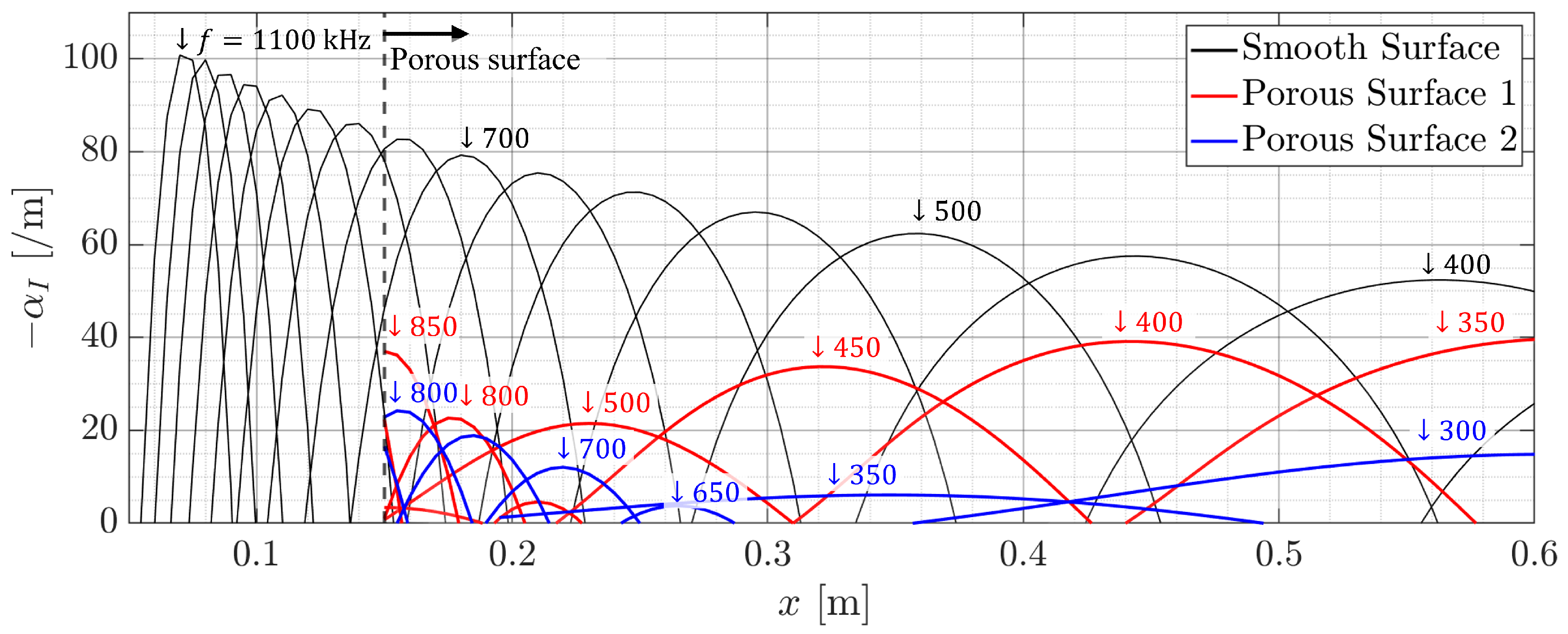
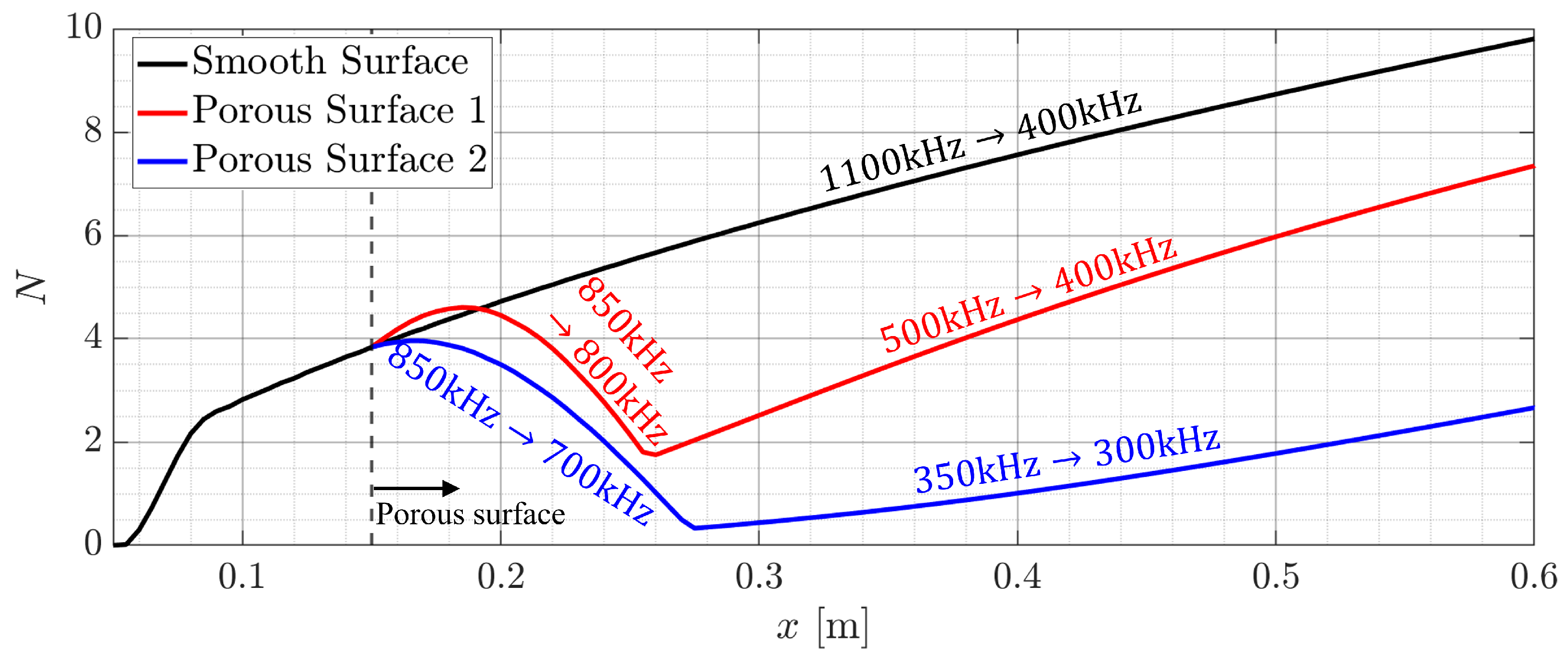
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Saric, W.S.; Reed, H.L.; Kerschen, E.J. Boundary-layer receptivity to freestream disturbances. Annu. Rev. Fluid Mech. 2002, 34, 291–319. [Google Scholar] [CrossRef]
- Fedorov, A. Transition and stability of high-speed boundary layers. Annu. Rev. Fluid Mech. 2011, 43, 79–95. [Google Scholar] [CrossRef]
- Zhong, X.; Wang, X. Direct numerical simulation on the receptivity, instability, and transition of hypersonic boundary layers. Annu. Rev. Fluid Mech. 2012, 44, 527–561. [Google Scholar] [CrossRef]
- Malik, M.; Zang, T.; Bushnell, D. Boundary Layer Transition in Hypersonic Flows. In Proceedings of the 2nd AIAA International Aerospace Planes Conference, Orlando, FL, USA, 29–31 October 1990. [Google Scholar] [CrossRef]
- Reshotko, E. Boundary Layer Instability, Transition and Control. In Proceedings of the 32nd AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 10–13 January 1994. [Google Scholar] [CrossRef]
- Yin, Y.; Lu, R.; Liu, J.; Huang, Z. Real gas effects on receptivity to roughness in hypersonic swept blunt flat-plate boundary layers. Aerospace 2024, 11, 58. [Google Scholar] [CrossRef]
- Mack, L.M. Boundary-layer linear stability theory. In Special Course on Stability and Transition of Laminar Flow; AGARD Report 709; Advisory Group for Aerospace Research and Development (AGARD): Neuilly sur Seine, France, 1984. [Google Scholar]
- Yang, H.s.; Liang, H.; Guo, S.g.; Tang, M.x.; Zhang, C.b.; Wu, Y.; Li, Y.h. Research progress of hypersonic boundary layer transition control experiments. Adv. Aerodyn. 2022, 4, 18. [Google Scholar] [CrossRef]
- Zhao, R.; Wen, C.; Zhou, Y.; Tu, G.; Lei, J. Review of acoustic metasurfaces for hypersonic boundary layer stabilization. Prog. Aerosp. Sci. 2022, 130, 100808. [Google Scholar] [CrossRef]
- Kimmel, R. Aspects of Hypersonic Boundary-Layer Transition Control. In Proceedings of the 41st AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 6–9 January 2003. [Google Scholar] [CrossRef]
- Fedorov, A.V. Prediction and control of laminar-turbulent transition in high-speed boundary-layer flows. Procedia IUTAM 2015, 14, 3–14. [Google Scholar] [CrossRef]
- Rasheed, A.; Hornung, H.G.; Fedorov, A.V.; Malmuth, N.D. Experiments on passive hypervelocity boundary-layer control using an ultrasonically absorptive surface. AIAA J. 2002, 40, 481–489. [Google Scholar] [CrossRef]
- Fedorov, A.; Shiplyuk, A.; Maslov, A.; Burov, E.; Malmuth, N. Stabilization of a hypersonic boundary layer using an ultrasonically absorptive coating. J. Fluid Mech. 2003, 479, 99–124; Corrigendum in J. Fluid Mech. 2015, 769, 725–728. [Google Scholar] [CrossRef]
- Lukashevich, S.; Morozov, S.; Shiplyuk, A. Passive porous coating effect on a hypersonic boundary layer on a sharp cone at small angle of attack. Exp. Fluids 2018, 59, 130. [Google Scholar] [CrossRef]
- Lim, J.; Kim, M.; Park, J.; Kim, T.; Jee, S.; Park, D. Simulation of hypersonic boundary layer on porous surfaces using OpenFOAM. Comput. Fluids 2022, 240, 105437. [Google Scholar] [CrossRef]
- Lim, J.; Kim, M.; Bae, H.; Lin, R.S.; Jee, S. Turbulent transition control using porous surfaces in hypersonic boundary layer. Int. J. Aeronaut. Space Sci. 2023, 24, 972–984. [Google Scholar] [CrossRef]
- Running, C.L.; Bemis, B.L.; Hill, J.L.; Borg, M.P.; Redmond, J.J.; Jantze, K.; Scalo, C. Attenuation of hypersonic second-mode boundary-layer instability with an ultrasonically absorptive silicon-carbide foam. Exp. Fluids 2023, 64, 79. [Google Scholar] [CrossRef]
- Holloway, P.F.; Sterrett, J.R. Effect of Controlled Surface Roughness on Boundary-Layer Transition and Heat Transfer at Mach Numbers of 4.8 and 6.0; Technical Report NASA-TN-D-2054; NASA Langley Research Center: Hampton, VA, USA, 1964. [Google Scholar]
- Duan, L.; Wang, X.; Zhong, X. Stabilization of a Mach 5.92 boundary layer by two-dimensional finite-height roughness. AIAA J. 2012, 51, 266–270. [Google Scholar] [CrossRef]
- Fong, K.D.; Wang, X.; Huang, Y.; Zhong, X.; McKiernan, G.R.; Fisher, R.A.; Schneider, S.P. Second mode suppression in hypersonic boundary layer by roughness: Design and experiments. AIAA J. 2015, 53, 3138–3144. [Google Scholar] [CrossRef]
- Fedorov, A.; Soudakov, V.; Egorov, I.; Sidorenko, A.; Gromyko, Y.; Bountin, D.; Polivanov, P.; Maslov, A. High-speed boundary-layer stability on a cone with localized wall heating or cooling. AIAA J. 2015, 53, 2512–2524. [Google Scholar] [CrossRef]
- Zhao, R.; Wen, C.; Tian, X.; Long, T.; Yuan, W. Numerical simulation of local wall heating and cooling effect on the stability of a hypersonic boundary layer. Int. J. Heat Mass Transf. 2018, 121, 986–998. [Google Scholar] [CrossRef]
- Oz, F.; Goebel, T.E.; Jewell, J.S.; Kara, K. Local wall cooling effects on hypersonic boundary-layer stability. J. Spacecr. Rocket. 2023, 60, 412–426. [Google Scholar] [CrossRef]
- Leyva, I.; Laurence, S.; Beierholm, A.; Hornung, H.; Wagnild, R.; Candler, G. Transition Delay in Hypervelocity Boundary Layers by Means of CO2/Acoustic Instability Interactions. In Proceedings of the 47th AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 5–8 January 2009. [Google Scholar] [CrossRef]
- Miró, F.M.; Pinna, F. Injection-gas-composition effects on hypersonic boundary-layer transition. J. Fluid Mech. 2020, 890, R4. [Google Scholar] [CrossRef]
- Shang, J.; Surzhikov, S.; Kimmel, R.; Gaitonde, D.; Menart, J.; Hayes, J. Mechanisms of plasma actuators for hypersonic flow control. Prog. Aerosp. Sci. 2005, 41, 642–668. [Google Scholar] [CrossRef]
- Yang, B.; Yang, H.; Zhao, N.; Liang, H.; Su, Z.; Zhang, D. Experimental study on hypersonic double-wedge induced flow based on plasma active actuation array. Aerospace 2024, 11, 60. [Google Scholar] [CrossRef]
- Liu, X.; Luo, Z.; Liu, Q.; Cheng, P.; Zhou, Y. Numerical investigation of hypersonic flat-plate boundary layer transition subjected to bi-frequency synthetic jet. Aerospace 2023, 10, 766. [Google Scholar] [CrossRef]
- Zhuang, G.H.; Wan, Z.H.; Ye, C.C.; Luo, Z.B.; Liu, N.S.; Sun, D.J.; Lu, X.Y. Active transition control by synthetic jets in a hypersonic boundary layer. Phys. Fluids 2023, 35, 034112. [Google Scholar] [CrossRef]
- Liu, J.; Xu, M.; Zhang, R.; Zhang, X.; Xi, W. Progress of porous/lattice structures applied in thermal management technology of aerospace applications. Aerospace 2022, 9, 827. [Google Scholar] [CrossRef]
- Malmuth, N.; Fedorov, A.; Shalaev, V.; Cole, J.; Hites, M.; Williams, D.; Khokhlov, A. Problems in High Speed Flow Prediction Relevant to Control. In Proceedings of the 2nd AIAA, Theoretical Fluid Mechanics Meeting, Albuquerque, NM, USA, 15–18 June 1998. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Malmuth, N.D.; Rasheed, A.; Hornung, H.G. Stabilization of hypersonic boundary layers by porous coatings. AIAA J. 2001, 39, 605–610. [Google Scholar] [CrossRef]
- Fedorov, A.; Malmuth, N. Parametric Studies of Hypersonic Laminar Flow Control Using a Porous Coating of Regular Microstructure. In Proceedings of the 46th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 7–10 January 2008. [Google Scholar] [CrossRef]
- Sandham, N.D.; Lüdeke, H. Numerical study of Mach 6 boundary-layer stabilization by means of a porous surface. AIAA J. 2009, 47, 2243–2252. [Google Scholar] [CrossRef]
- Lukashevich, S.V.; Maslov, A.A.; Shiplyuk, A.N.; Fedorov, A.V.; Soudakov, V.G. Stabilization of high-speed boundary layer using porous coatings of various thicknesses. AIAA J. 2012, 50, 1897–1904. [Google Scholar] [CrossRef]
- Zhao, R.; Zhang, X.X.; Wen, C.Y. Theoretical modeling of porous coatings with simple microstructures for hypersonic boundary-layer stabilization. AIAA J. 2020, 58, 981–986. [Google Scholar] [CrossRef]
- Wang, X.; Zhong, X. The stabilization of a hypersonic boundary layer using local sections of porous coating. Phys. Fluids 2012, 24, 034105. [Google Scholar] [CrossRef]
- Lukashevich, S.V.; Morozov, S.O.; Shiplyuk, A.N. Experimental study of the effect of a passive porous coating on disturbances in a hypersonic boundary layer. 1. Effect of the porous coating length. J. Appl. Mech. Tech. Phys. 2013, 54, 572–577. [Google Scholar] [CrossRef]
- Lukashevich, S.V.; Morozov, S.O.; Shiplyuk, A.N. Experimental study of the effect of a passive porous coating on disturbances in a hypersonic boundary layer 2. Effect of the porous coating location. J. Appl. Mech. Tech. Phys. 2016, 57, 873–878. [Google Scholar] [CrossRef]
- Brès, G.; Inkman, M.; Colonius, T.; Fedorov, A. Alternate Designs of Ultrasonic Absorptive Coatings for Hypersonic Boundary Layer Control. In Proceedings of the 39th AIAA Fluid Dynamics Conference, San Antonio, TX, USA, 22–25 June 2009. [Google Scholar] [CrossRef]
- Brès, G.A.; Colonius, T.; Fedorov, A.V. Acoustic properties of porous coatings for hypersonic boundary-layer control. AIAA J. 2010, 48, 267–274. [Google Scholar] [CrossRef]
- Tian, X.; Zhao, R.; Long, T.; Wen, C.Y. Reverse design of ultrasonic absorptive coating for the stabilization of Mack modes. AIAA J. 2019, 57, 2264–2269. [Google Scholar] [CrossRef]
- Zhao, R.; Fan, Y.; Liu, X.; Wen, C. Stabilization effect of acoustic metasurfaces on broadband disturbances in a Mach 6 boundary-layer flow. Phys. Fluids 2022, 34, 121706. [Google Scholar] [CrossRef]
- Maslov, A.; Shiplyuk, A.; Sidorenko, A.; Polivanov, P.; Fedorov, A.; Kozlov, V.; Malmuth, N. Hypersonic Laminar Flow Control Using a Porous Coating of Random Microstructure. In Proceedings of the 44th AIAA Aerospace Sciences Meeting and Exhibit, Reno, NV, USA, 9–12 January 2006. [Google Scholar] [CrossRef]
- Egorov, I.; Fedorov, A.; Soudakov, V. Receptivity of a hypersonic boundary layer over a flat plate with a porous coating. J. Fluid Mech. 2008, 601, 165–187. [Google Scholar] [CrossRef]
- Fedorov, A. Temporal Stability of Hypersonic Boundary Layer on Porous Wall: Comparison of Theory with DNS. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Zhao, R.; Wen, C.; Long, T.; Tian, X.; Zhou, L.; Wu, Y. Spatial direct numerical simulation of the hypersonic boundary-layer stabilization using porous coatings. AIAA J. 2019, 57, 5061–5065. [Google Scholar] [CrossRef]
- Xu, J.; Liu, J.; Mughal, S.; Yu, P.; Bai, J. Secondary instability of Mack mode disturbances in hypersonic boundary layers over micro-porous surface. Phys. Fluids 2020, 32, 044105. [Google Scholar] [CrossRef]
- Lim, J.; Kim, M.; Jeong, M.; Cho, S.; Jee, S. Computational Study on the Stability of Hypersonic Boundary Layer on a Porous Surface. In Proceedings of the AIAA SCITECH 2024 Forum, Orlando, FL, USA, 8–12 January 2024. [Google Scholar] [CrossRef]
- Kim, J.; Kim, J.; Hur, J.; Lee, B.J. Nozzle flow characterization of the SNU hypersonic shock tunnel. Int. J. Aeronaut. Space Sci. 2024, 26, 953–962. [Google Scholar] [CrossRef]
- Kim, D.M.; Lee, H.J. Experimental Visualization of Hypersonic Boundary Layer Transition. In Proceedings of the AIAA SCITECH 2025 Forum, Orlando, FL, USA, 6–10 January 2025. [Google Scholar] [CrossRef]
- White, F.M. Laminar boundary layers. In Viscous Fluid Flow, 3rd ed.; McGraw-Hill: New York, NY, USA, 2006; Chapter 4.10.2; pp. 293–294. [Google Scholar]
- Malik, M.R. Numerical methods for hypersonic boundary layer stability. J. Comput. Phys. 1990, 86, 376–413. [Google Scholar] [CrossRef]
- Park, D. Linear and Non-Linear Stability Analysis of Boundary Layers over a Hump by Using PSE. Ph.D. Thesis, Korea Advanced Institute of Science and Technology, Daejeon, Republic of Korea, 2013. [Google Scholar]
- Fedorov, A.; Tumin, A. High-speed boundary-layer instability: Old terminology and a new framework. AIAA J. 2011, 49, 1647–1657. [Google Scholar] [CrossRef]
- Bae, H.; Lim, J.; Kim, M.; Jee, S. Direct-numerical simulation with the stability theory for turbulent transition in hypersonic boundary layer. Int. J. Aeronaut. Space Sci. 2023, 24, 1004–1014. [Google Scholar] [CrossRef]
- Lim, J.; Jeong, M.; Kim, M.; Jee, S. Eddy-resolving simulation coupled with stability analysis for turbulent transition in compressible boundary layer. Flow Turbul. Combust. 2024, 115, 79–104. [Google Scholar] [CrossRef]
- Jeong, M.; Cho, S.; Kim, Y.; Park, J.; Jee, S. High-fidelity simulation of laminar-to-turbulent transition in hypersonic boundary layer on a sharp cone. Phys. Fluids 2025, 37, 034120. [Google Scholar] [CrossRef]
- Sivasubramanian, J.; Fasel, H.F. Direct numerical simulation of transition in a sharp cone boundary layer at Mach 6: Fundamental breakdown. J. Fluid Mech. 2015, 768, 175–218. [Google Scholar] [CrossRef]
- Brès, G.A.; Inkman, M.; Colonius, T.; Fedorov, A.V. Second-mode attenuation and cancellation by porous coatings in a high-speed boundary layer. J. Fluid Mech. 2013, 726, 312–337. [Google Scholar] [CrossRef]
- Köhler, M. Wet-chemical etching methods. In Etching in Microsystem Technology; WILEY-VCH: Weinheim, Germany, 1999; Chapter 3; pp. 73, 79, 100–101. [Google Scholar]
- Patel, D.; Jain, V.; Ramkumar, J. Micro texturing on metallic surfaces: State of the art. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2018, 232, 941–964. [Google Scholar] [CrossRef]
- Lee, J.; Hong, S. A Study on the Fabrication Process of Porous Surface and Experimental Model for Reducing Aerodynamic Heating of Hypersonic Boundary Layer Flow. In Proceedings of the Annual Conference of the Korean Society of Mechanical Engineering (KSME), Jeju Island, Republic of Korea, 6–9 November 2024. [Google Scholar]
- Jung, T.; Lee, J. A Study on the Design Process of Manufacturable Porous Microstructure for Reducing Aerodynamic Heating of Hypersonic Boundary Layer Flow. In Proceedings of the Annual Space Conference of the Korean Society for Aeronautical and Space Sciences (KSAS), Jeju, Republic of Korea, 19–21 April 2023. [Google Scholar]
- Marineau, E.C.; Grossir, G.; Wagner, A.; Leinemann, M.; Radespiel, R.; Tanno, H.; Chynoweth, B.C.; Schneider, S.P.; Wagnild, R.M.; Casper, K.M. Analysis of second-mode amplitudes on sharp cones in hypersonic wind tunnels. J. Spacecr. Rocket. 2018, 56, 307–318. [Google Scholar] [CrossRef]
- Ingen, J.V. The eN Method for Transition Prediction. Historical Review of Work at TU Delft. In Proceedings of the 38th AIAA Fluid Dynamics Conference and Exhibit, Seattle, WA, USA, 23–26 June 2008. [Google Scholar] [CrossRef]
- Schneider, S.P. Effects of high-speed tunnel noise on laminar-turbulent transition. J. Spacecr. Rocket. 2001, 38, 323–333. [Google Scholar] [CrossRef]
- Alba, C.; Casper, K.; Beresh, S.; Schneider, S. Comparison of Experimentally Measured and Computed Second-Mode Disturbances in Hypersonic Boundary-Layers. In Proceedings of the 48th AIAA Aerospace Sciences Meeting Including the New Horizons Forum and Aerospace Exposition, Orlando, FL, USA, 4–7 January 2010. [Google Scholar] [CrossRef]
- Berridge, D.; Casper, K.; Rufer, S.; Alba, C.; Lewis, D.; Beresh, S.; Schneider, S. Measurements and Computations of Second-Mode Instability Waves in Several Hypersonic Wind Tunnels. In Proceedings of the 40th AIAA Fluid Dynamics Conference and Exhibit, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar] [CrossRef][Green Version]
- Juliano, T.J.; Kimmel, R.L.; Willems, S.; Guelhan, A.; Wagnild, R. HIFiRE-1 Boundary-Layer Transition: Ground Test Results and Stability Analysis. In Proceedings of the 53rd AIAA Aerospace Sciences Meeting, Kissimmee, FL, USA, 5–9 January 2015. [Google Scholar] [CrossRef]
- Fedorov, A.V.; Khokhlov, A.P. Prehistory of instability in a hypersonic boundary layer. Theor. Comput. Fluid Dyn. 2001, 14, 359–375. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, T.; Wen, C.Y.; Zhu, J.; Cheng, L. Theoretical modeling and optimization of porous coating for hypersonic laminar flow control. AIAA J. 2018, 56, 2942–2946. [Google Scholar] [CrossRef]
- Zhao, R.; Liu, T.; Wen, C.y.; Zhu, J.; Cheng, L. Impedance-near-zero acoustic metasurface for hypersonic boundary-layer flow stabilization. Phys. Rev. Appl. 2019, 11, 044015. [Google Scholar] [CrossRef]
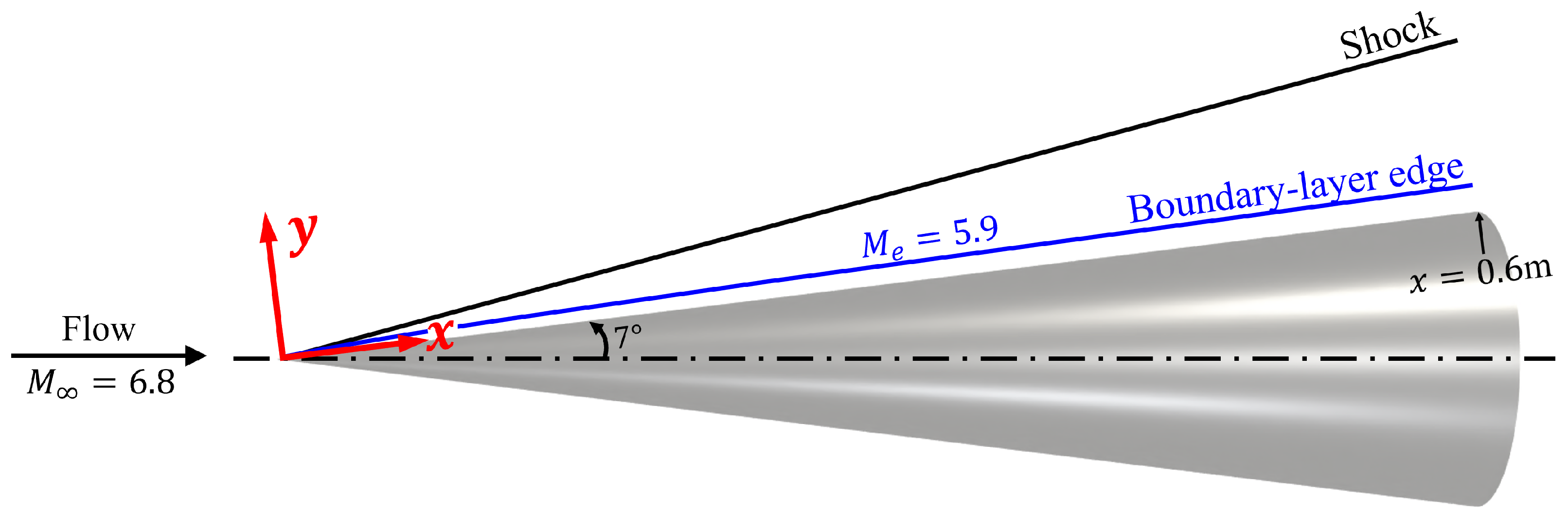
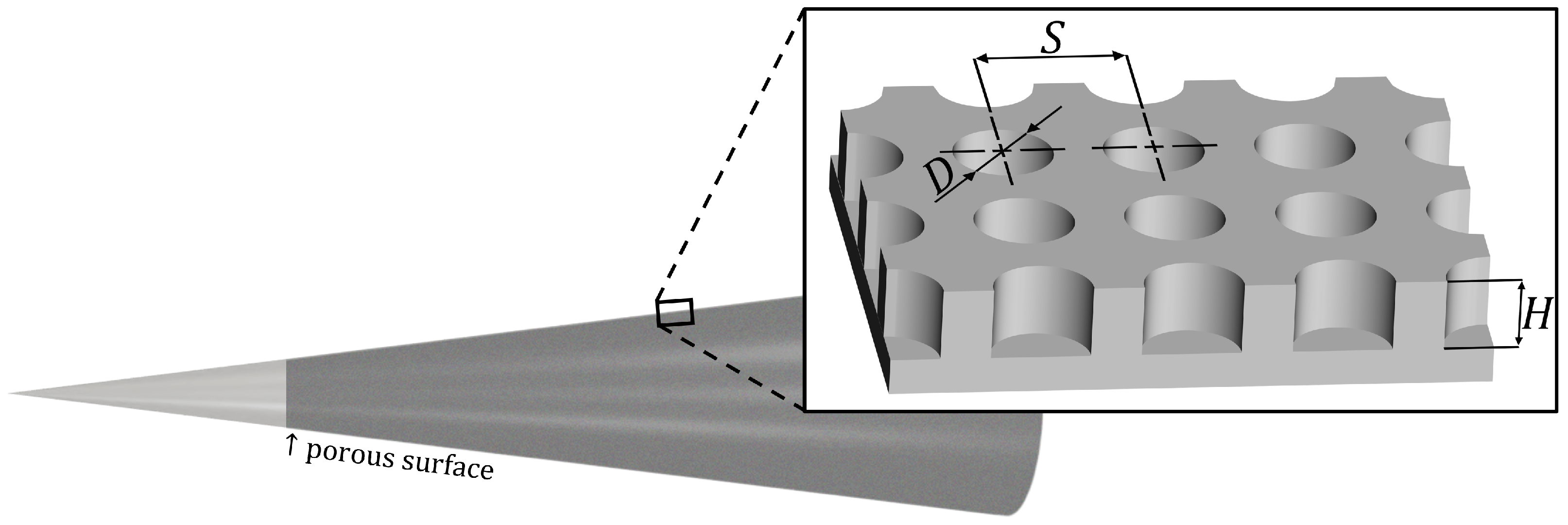

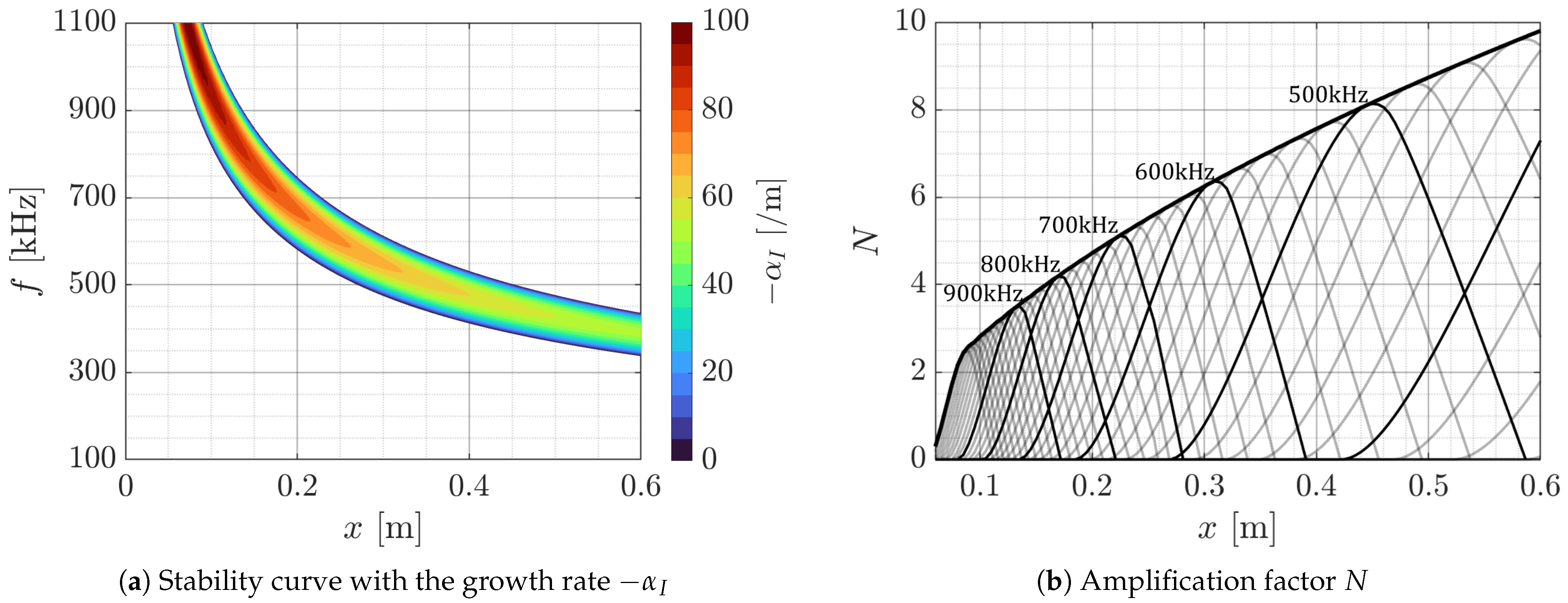
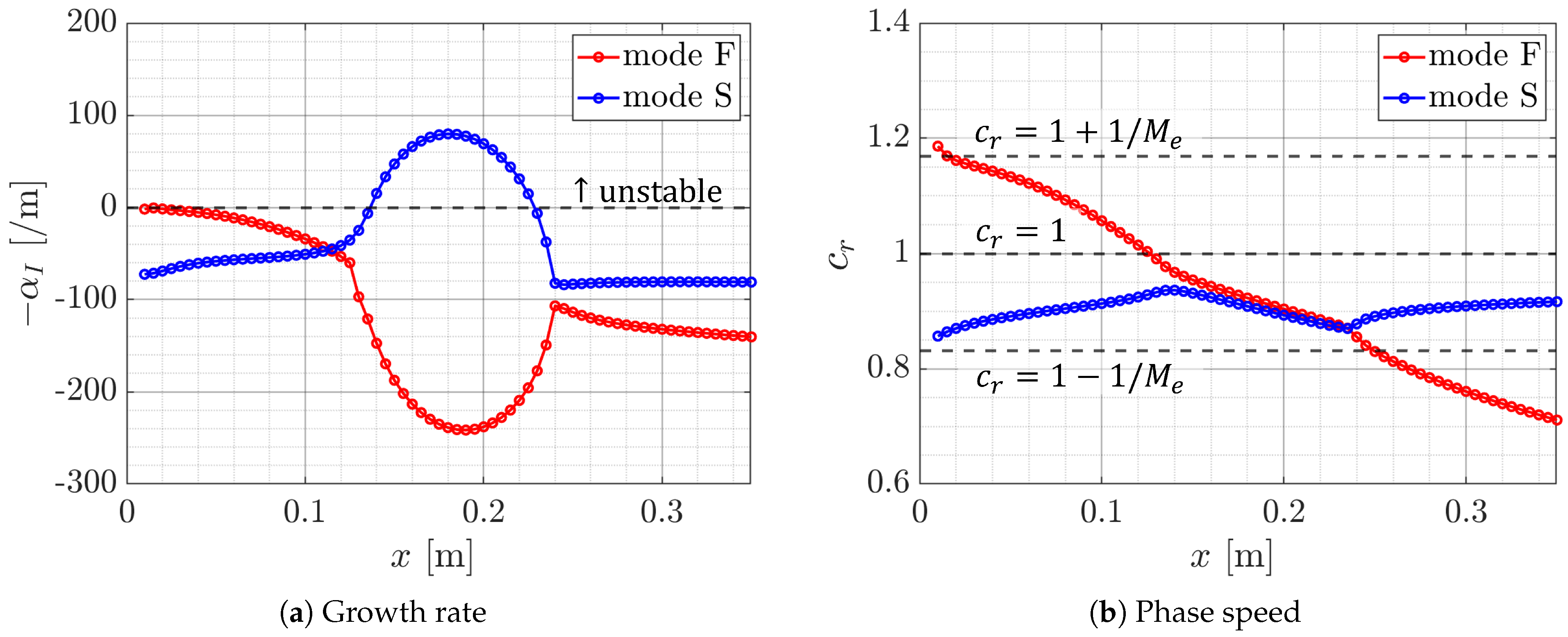

| Properties | Freestream | Boundary-Layer Edge | ||
|---|---|---|---|---|
| Mach number | 6.8 | 5.9 | ||
| Reynolds number [/m] | ||||
| Total enthalpy [MJ/Kg] | 1.7 | 1.7 | ||
| Pressure [kPa] | 2.12 | 4.67 | ||
| Temperature [K] | 163 | 206 | ||
| Porous Surface | Depth H [µm] | Diameter D [µm] | Unit Cell Size S [µm] | Porosity |
|---|---|---|---|---|
| Porous Surface 1 | 100 | 120 | 240 | 0.20 |
| Porous Surface 2 | 150 | 100 | 150 | 0.35 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, Y.; Jeong, M.; Cho, S.; Park, D.; Jee, S. Porous Surface Design with Stability Analysis for Turbulent Transition Control in Hypersonic Boundary Layer. Aerospace 2025, 12, 518. https://doi.org/10.3390/aerospace12060518
Kim Y, Jeong M, Cho S, Park D, Jee S. Porous Surface Design with Stability Analysis for Turbulent Transition Control in Hypersonic Boundary Layer. Aerospace. 2025; 12(6):518. https://doi.org/10.3390/aerospace12060518
Chicago/Turabian StyleKim, Youngwoo, Minjae Jeong, Suhun Cho, Donghun Park, and Solkeun Jee. 2025. "Porous Surface Design with Stability Analysis for Turbulent Transition Control in Hypersonic Boundary Layer" Aerospace 12, no. 6: 518. https://doi.org/10.3390/aerospace12060518
APA StyleKim, Y., Jeong, M., Cho, S., Park, D., & Jee, S. (2025). Porous Surface Design with Stability Analysis for Turbulent Transition Control in Hypersonic Boundary Layer. Aerospace, 12(6), 518. https://doi.org/10.3390/aerospace12060518






