Author Contributions
Conceptualization, B.Z. and C.H.; Methodology, B.Z., C.H., X.W., H.C., P.Y., Z.G. and S.Z.; Software, B.Z.; Validation, C.H., H.C. and Z.G.; Formal analysis, B.Z. and X.W.; Investigation, P.Y. and S.Z.; Resources, C.H., H.C., P.Y. and X.L. is not mentioned in author contribution part; Data curation, B.Z., X.W. and S.Z.; Writing – original draft, B.Z. and X.W.; Writing – review & editing, C.H. and H.C.; Visualization, X.W. and Z.G.; Supervision, C.H., H.C. and X.L. is not mentioned in author contribution part; Project administration, C.H. and P.Y.; Funding acquisition, C.H. All authors have read and agreed to the published version of the manuscript.
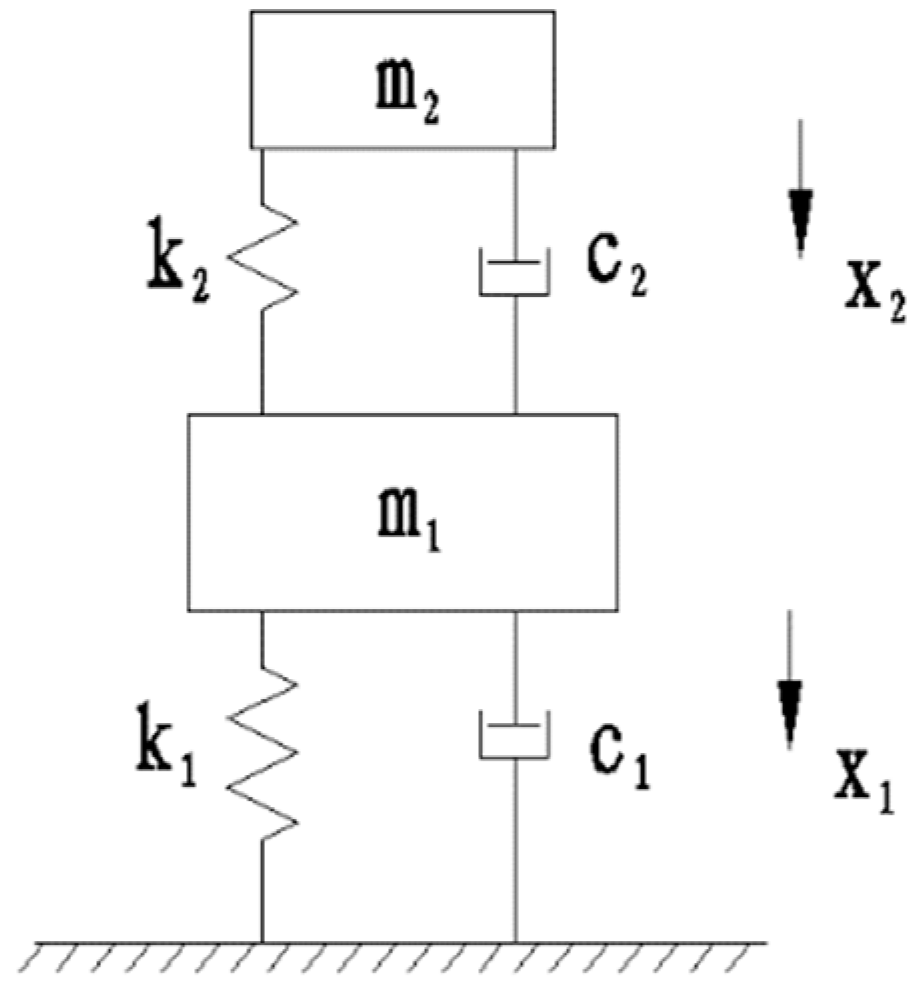
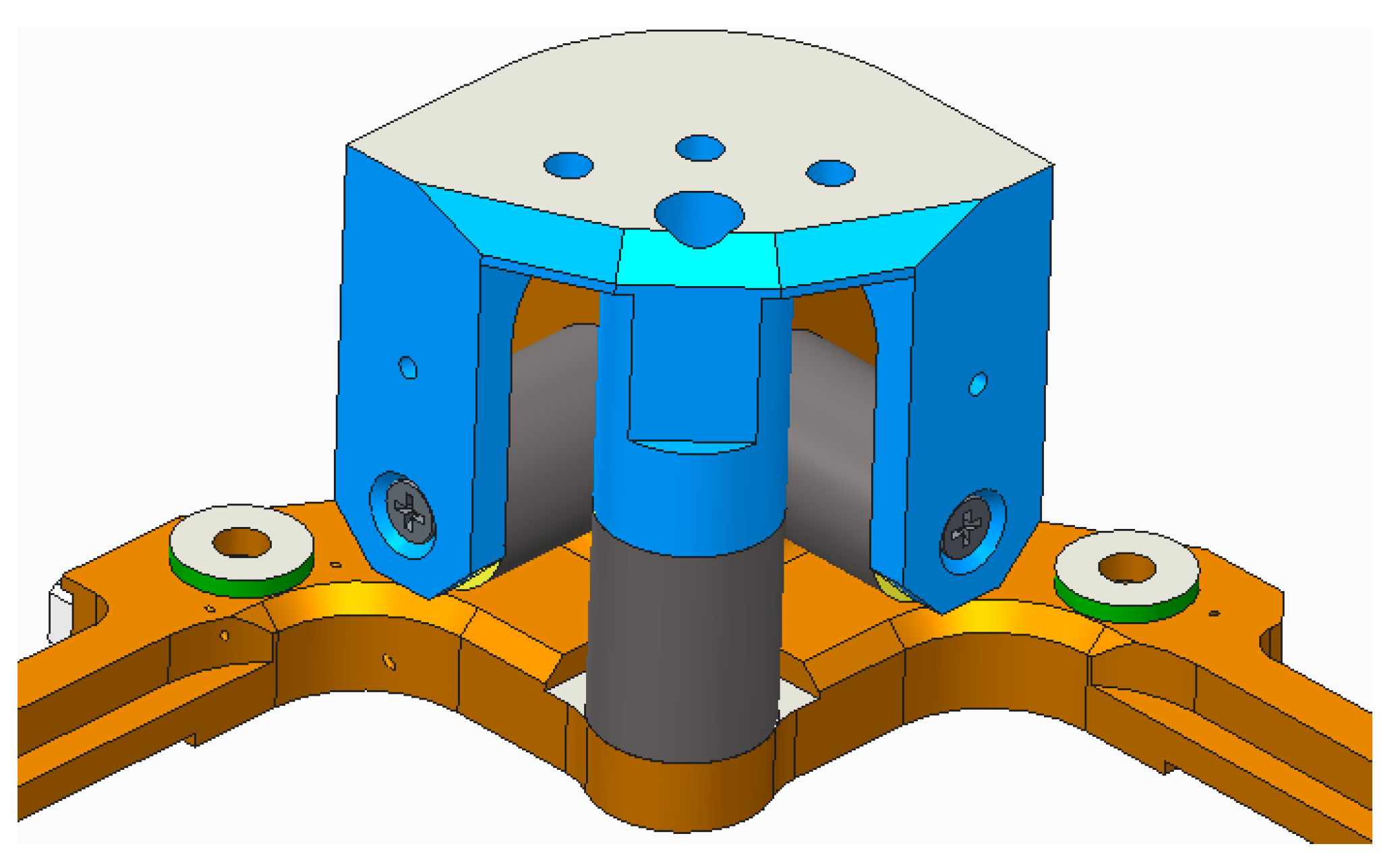
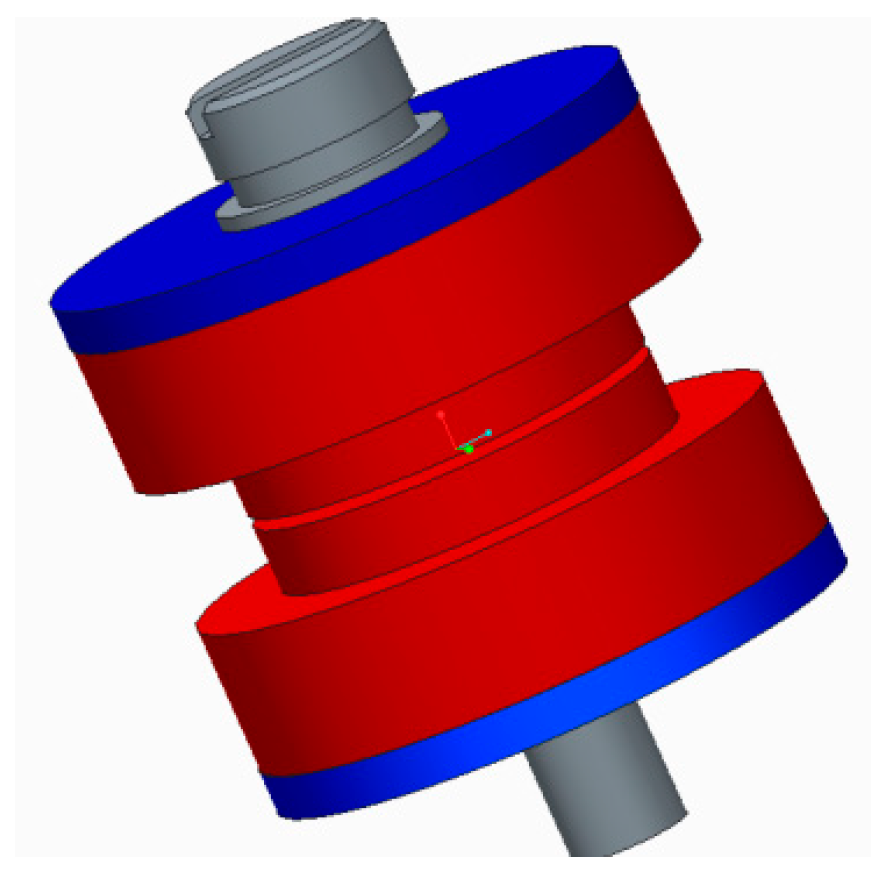
Figure 1.
Design parameter model of a dual-level vibration isolation system for a specific configuration.
Figure 1.
Design parameter model of a dual-level vibration isolation system for a specific configuration.
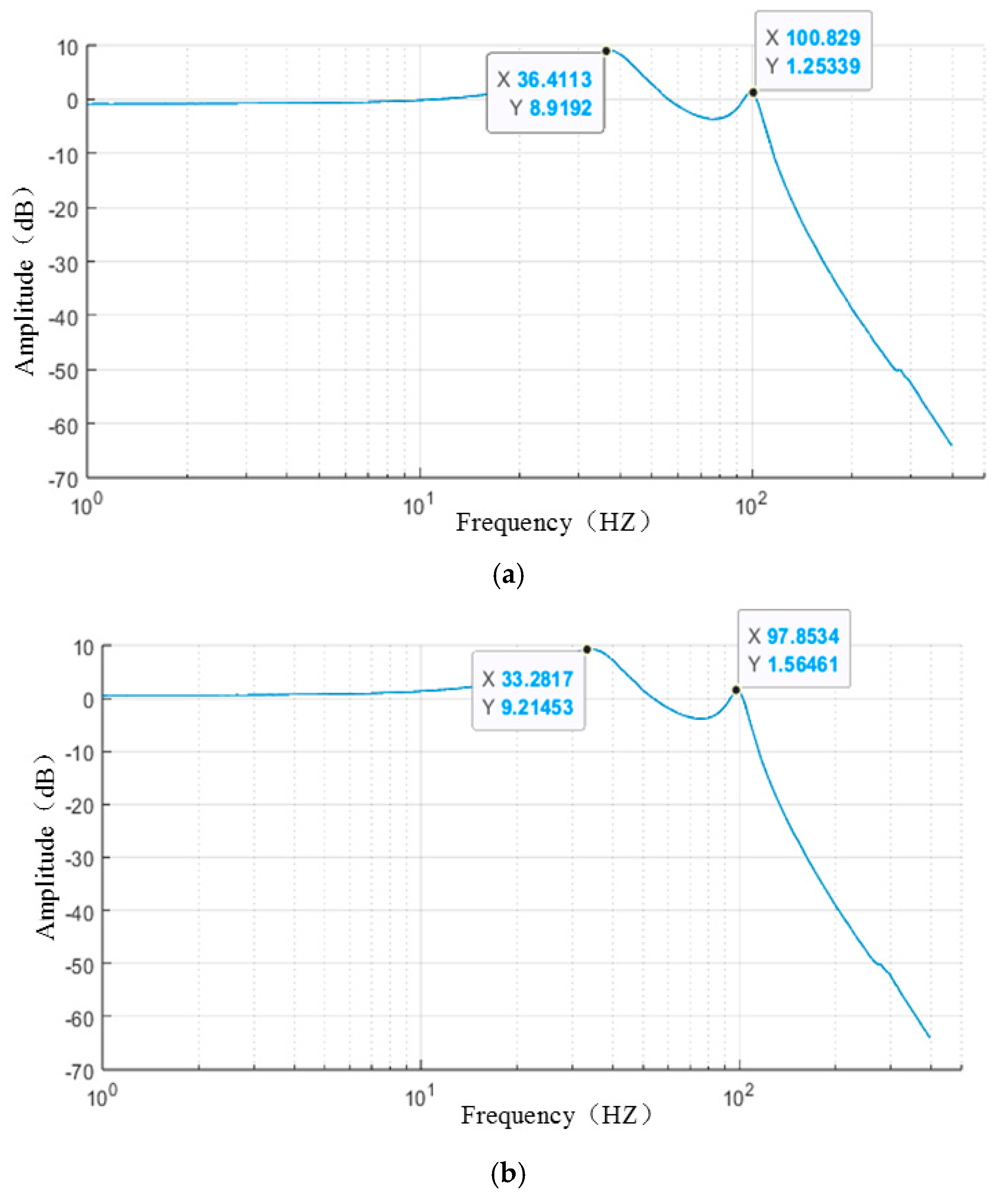
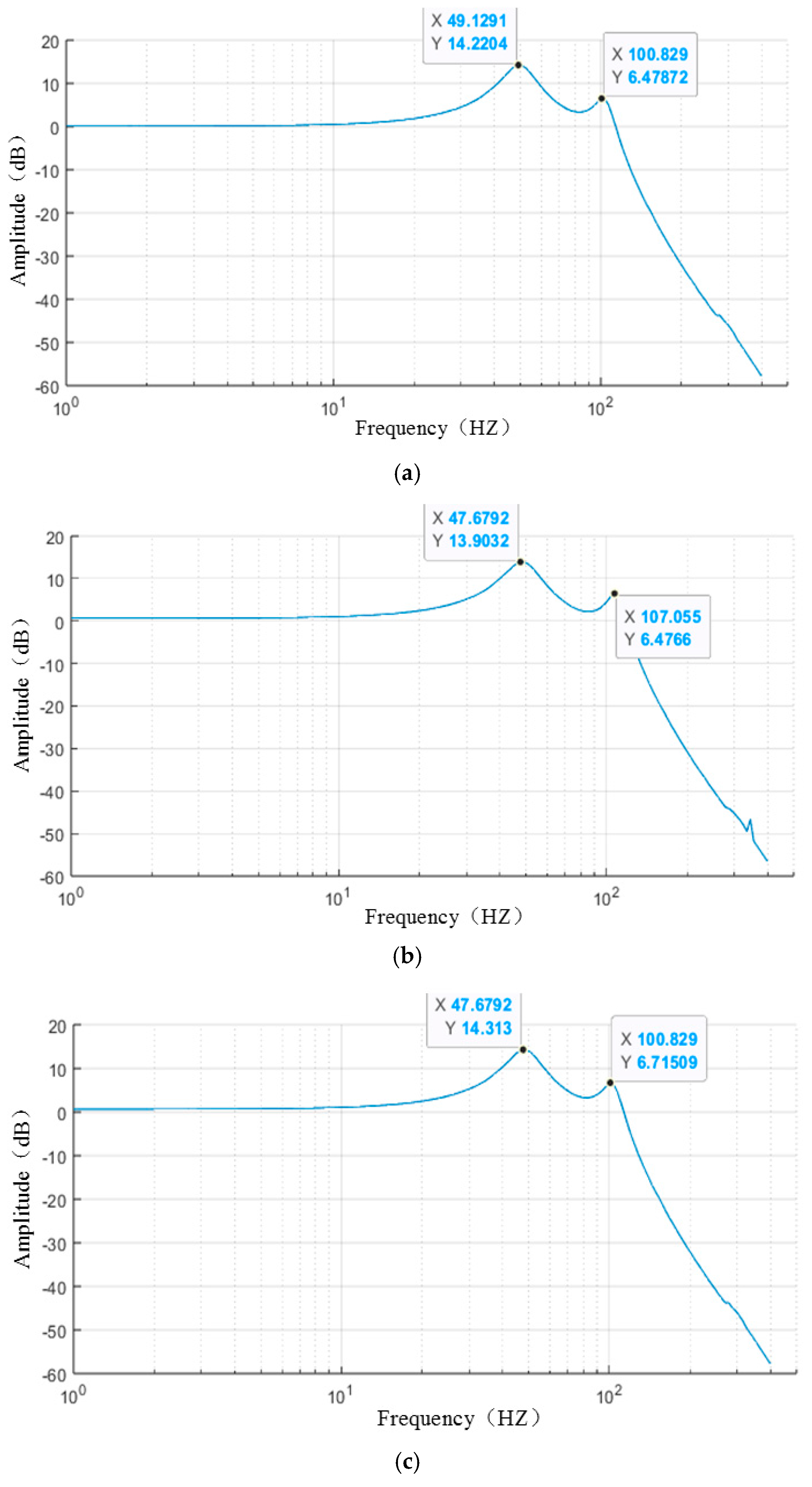
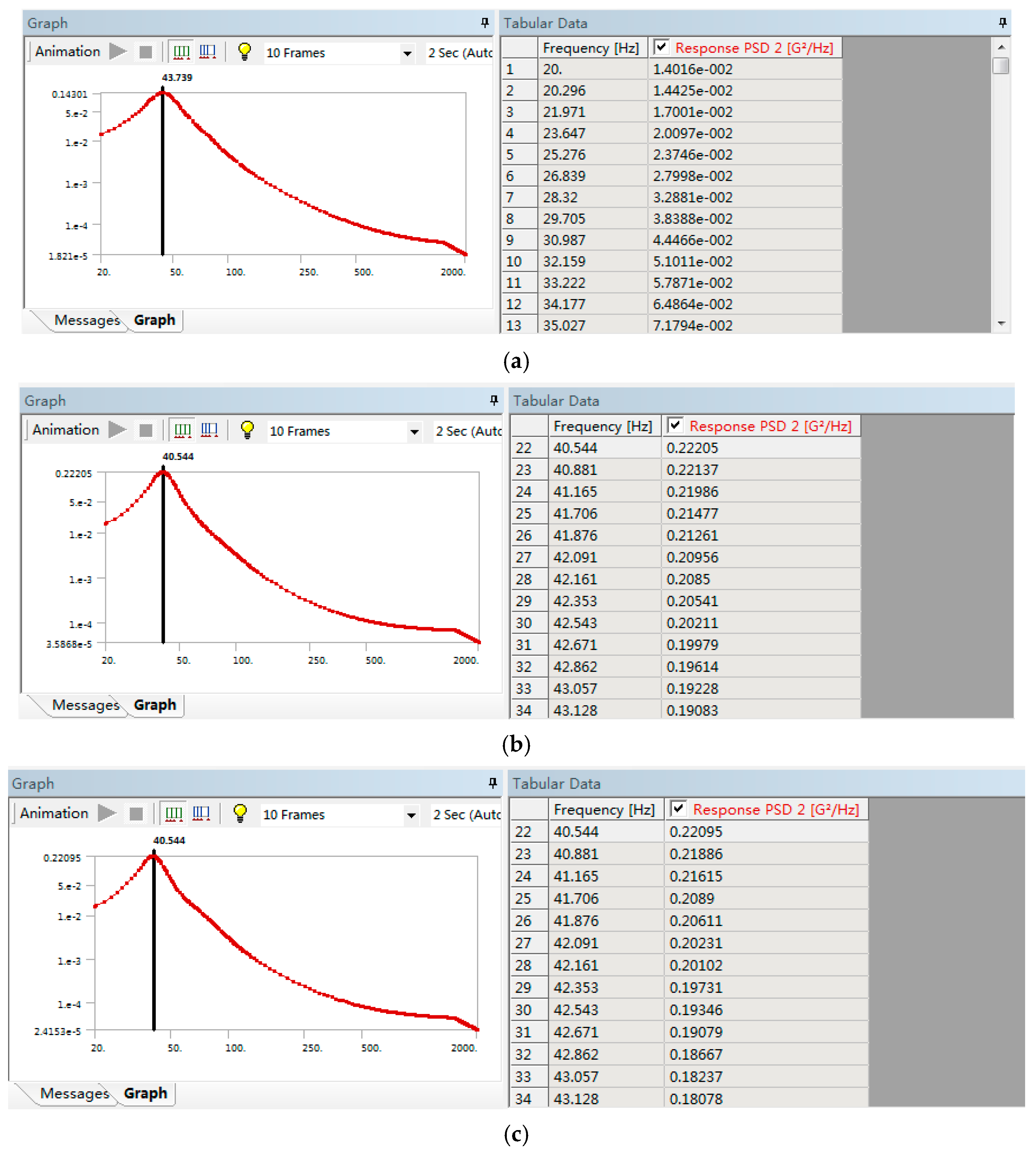
Figure 2.
Rigidity parameter 1 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
Figure 2.
Rigidity parameter 1 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
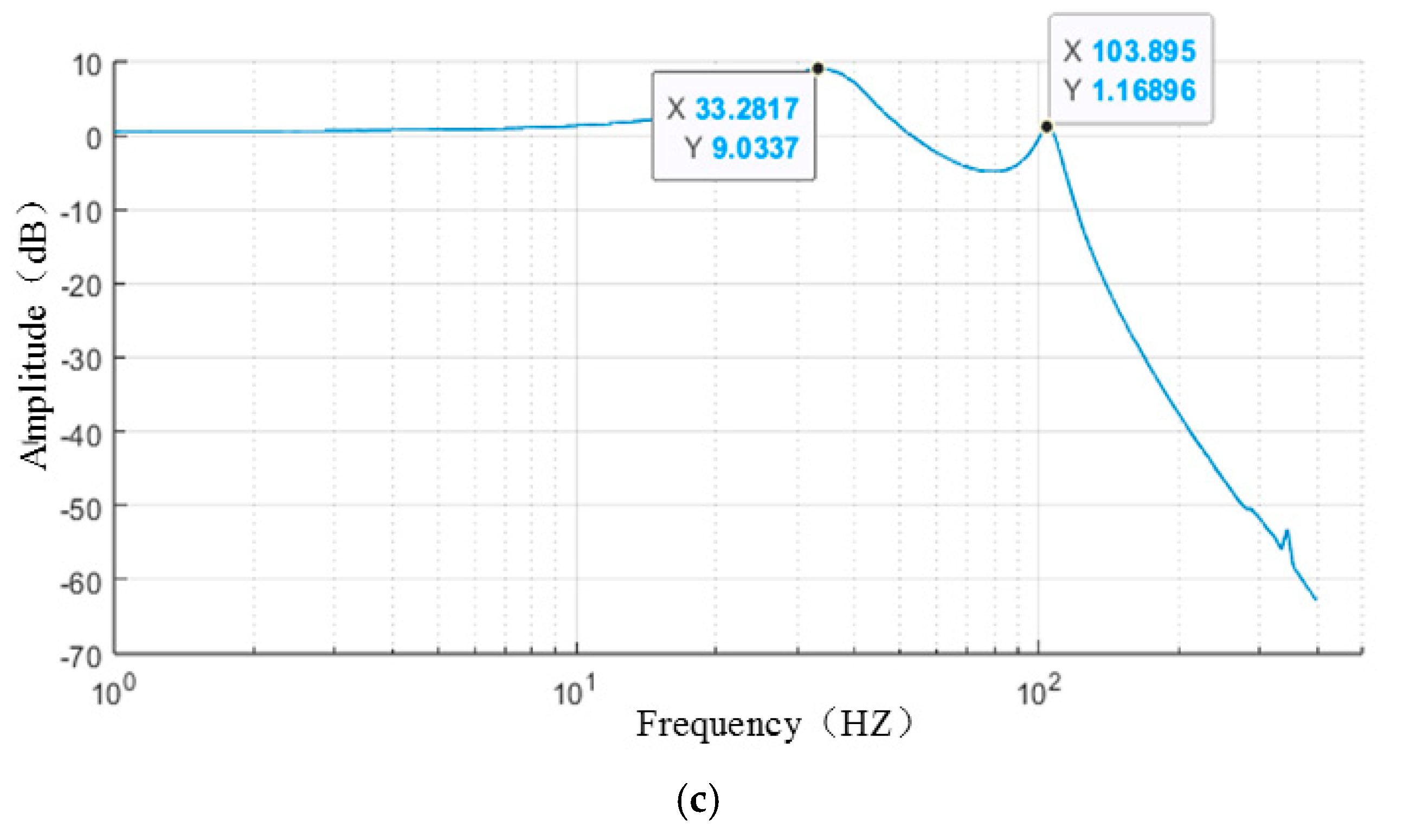
Figure 3.
Rigidity parameter 2 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
Figure 3.
Rigidity parameter 2 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
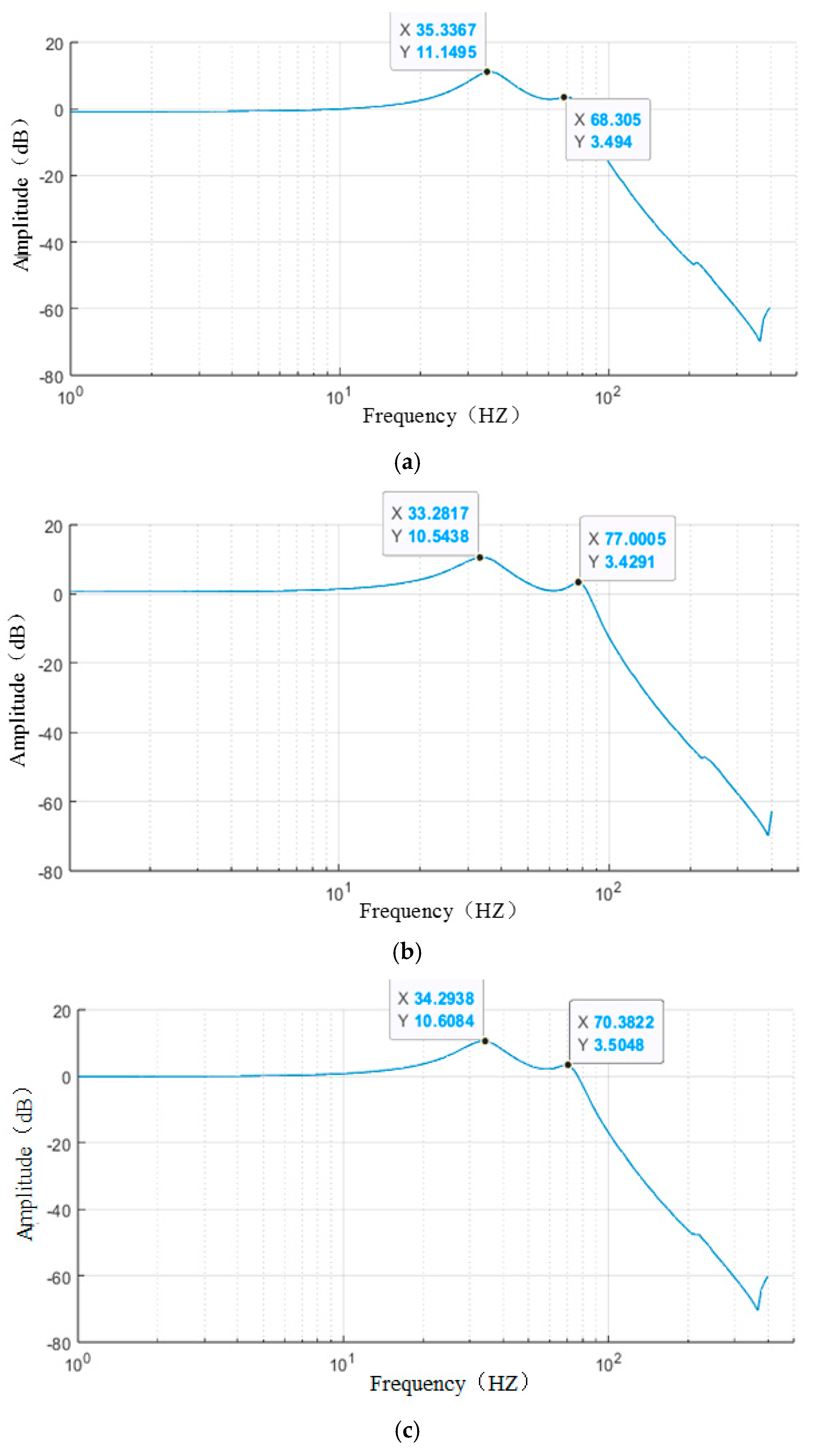
Figure 4.
Rigidity parameter 3 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
Figure 4.
Rigidity parameter 3 frequency response curve: (a) X direction; (b) Y direction; (c) Z direction.
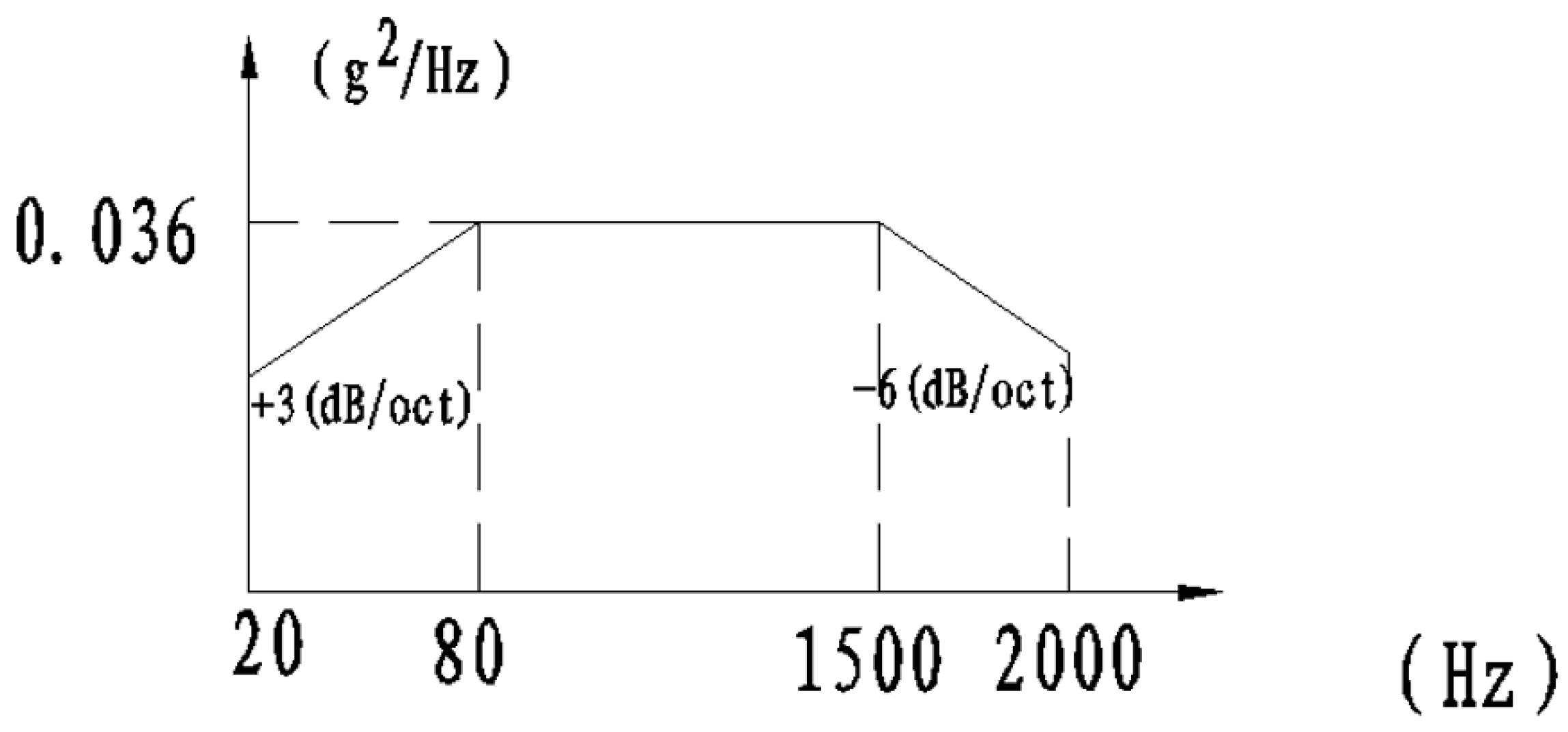
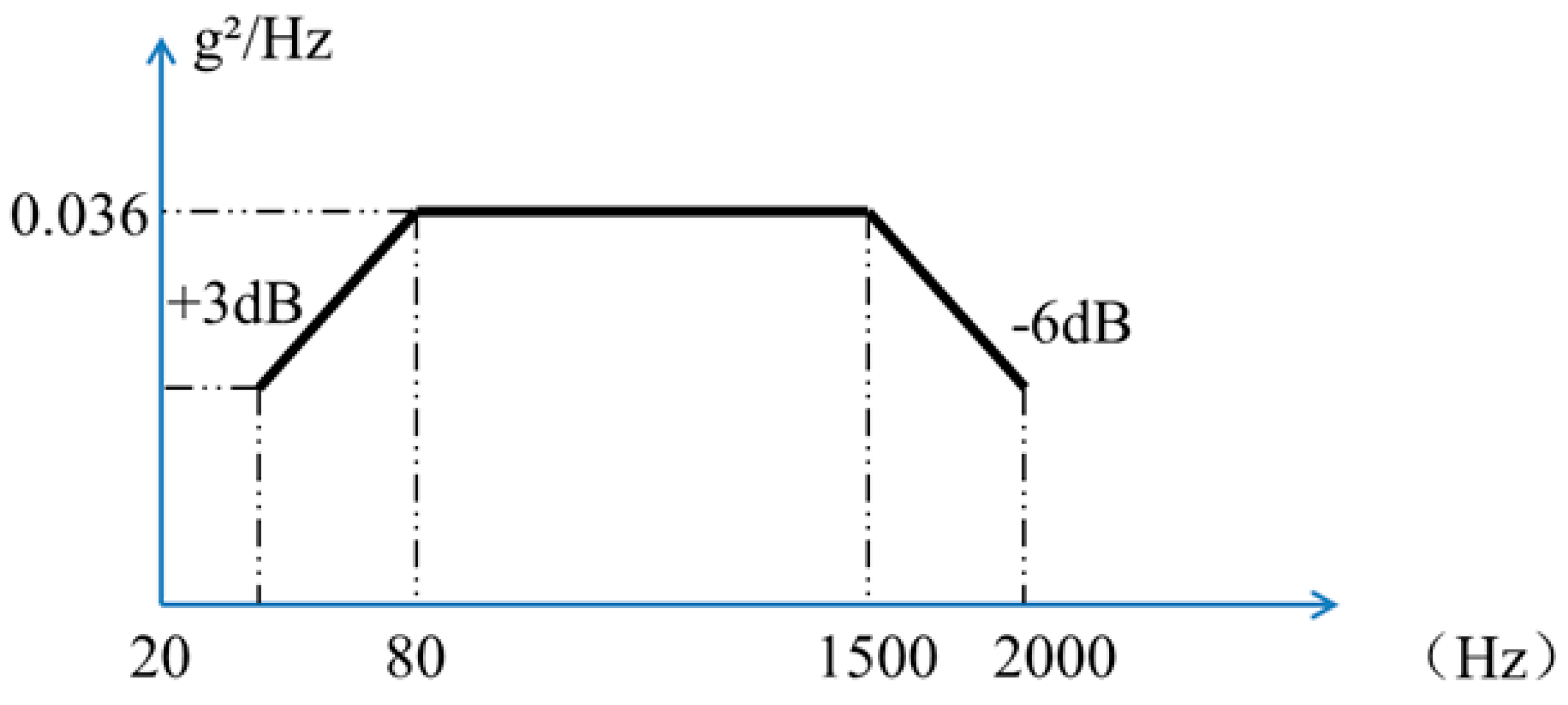
Figure 5.
External vibration spectrum type input conditions of inertial product-Simulation input.
Figure 5.
External vibration spectrum type input conditions of inertial product-Simulation input.
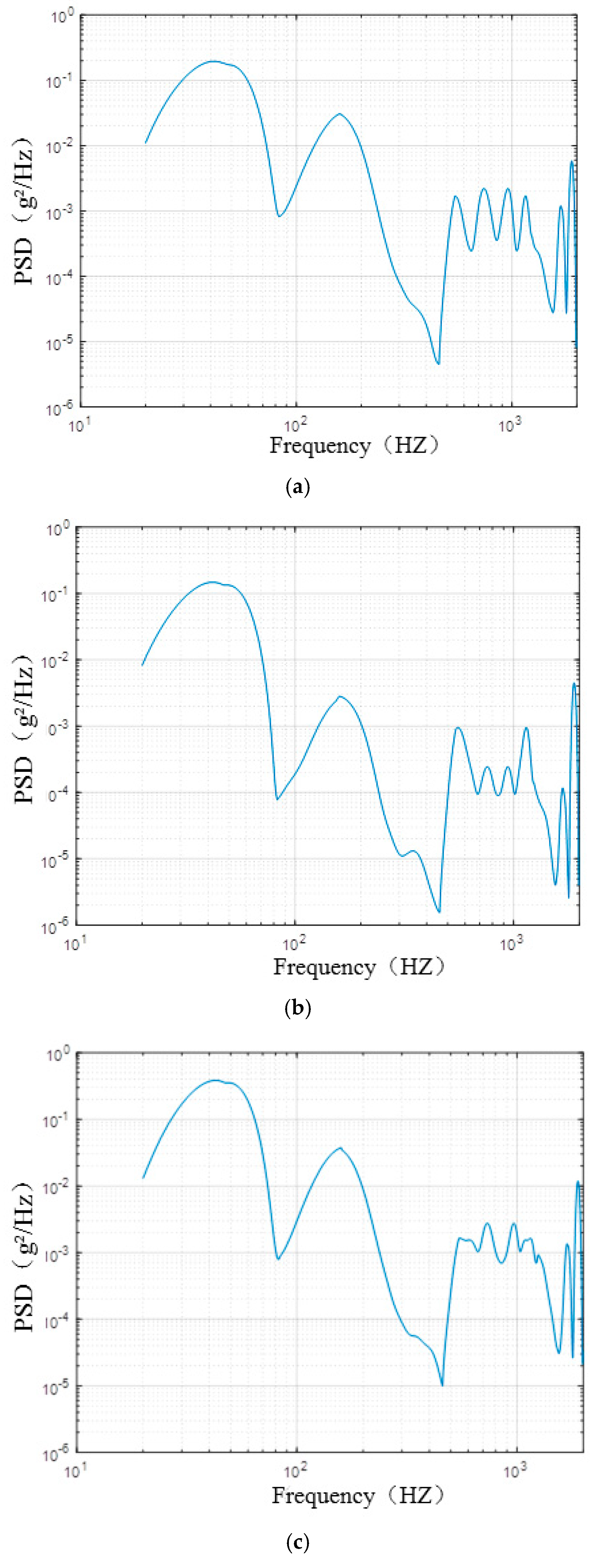
Figure 6.
Calculation curve of random vibration response of laser habit group: (a) X direction; (b) Y direction; (c) Z direction.
Figure 6.
Calculation curve of random vibration response of laser habit group: (a) X direction; (b) Y direction; (c) Z direction.
Figure 7.
External vibration reduction system.
Figure 7.
External vibration reduction system.
Figure 8.
Internal vibration reduction system.
Figure 8.
Internal vibration reduction system.
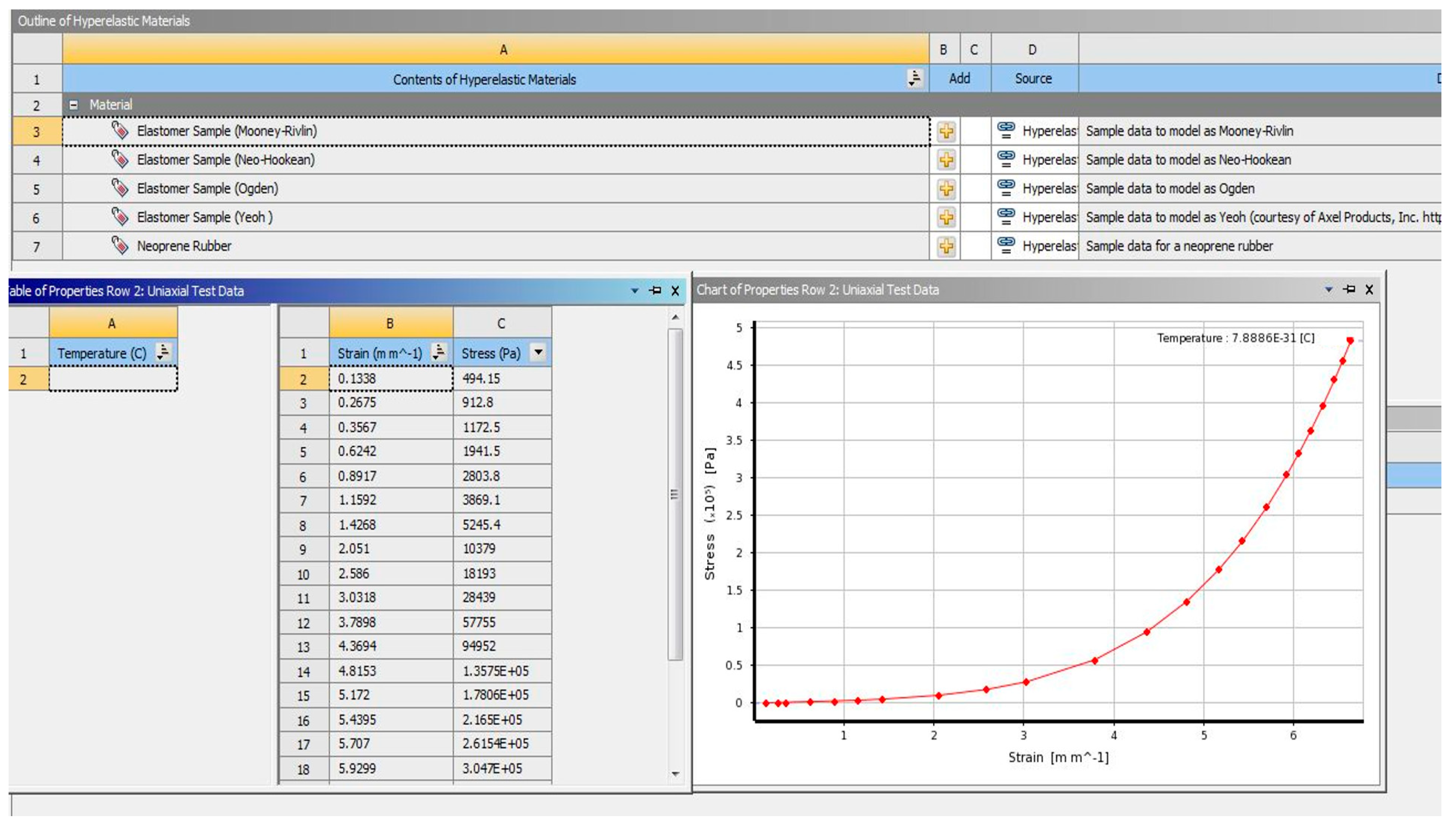
Figure 9.
Extract system material fitting curve.
Figure 9.
Extract system material fitting curve.
Figure 10.
Laser INS random vibration finite element response calculation curve: (a) X direction; (b) Y direction; (c) Z direction.
Figure 10.
Laser INS random vibration finite element response calculation curve: (a) X direction; (b) Y direction; (c) Z direction.
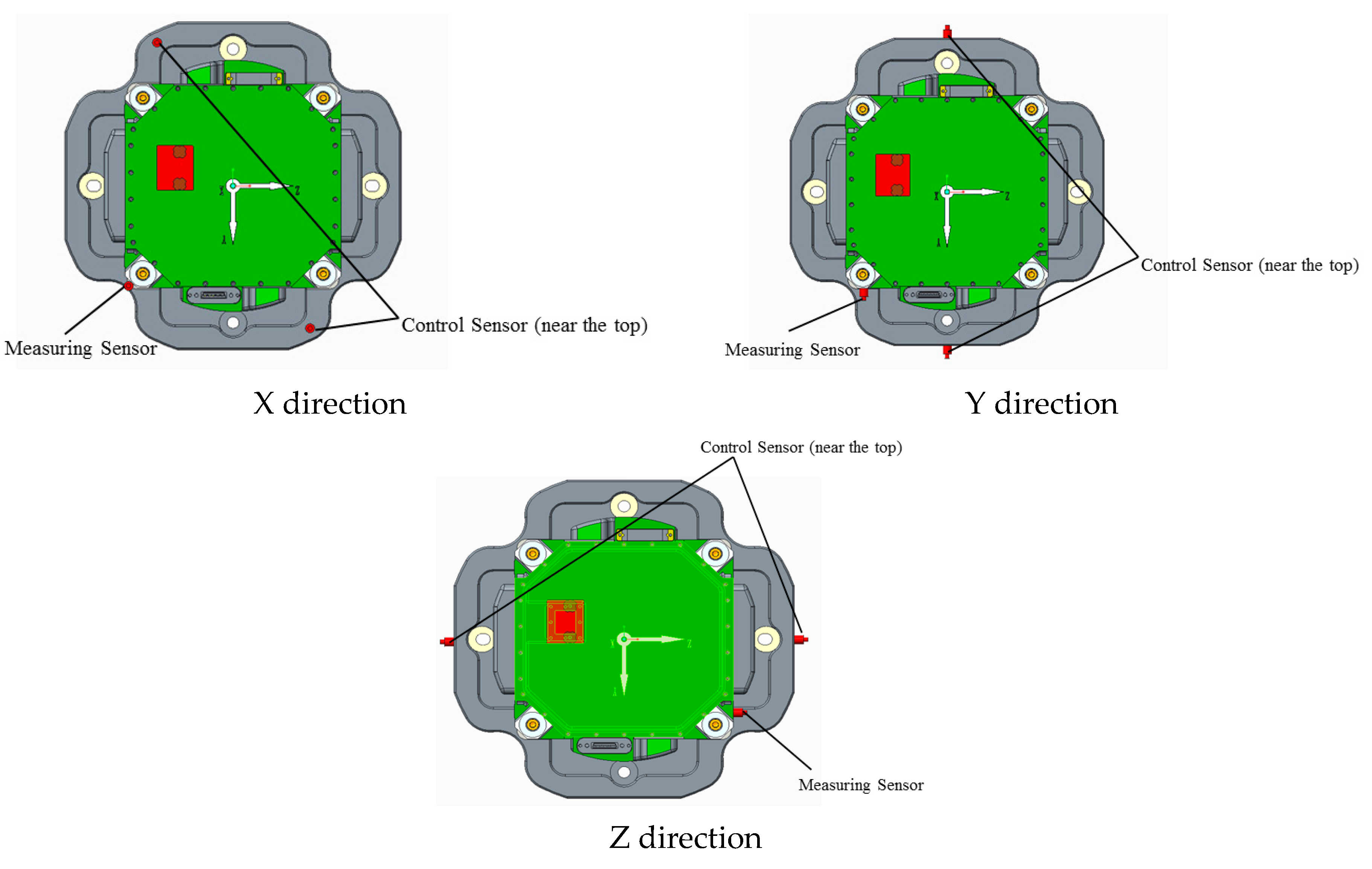
Figure 11.
Schematic diagram of sensor adhesion for three-axis vibration test of inertial measurement unit.
Figure 11.
Schematic diagram of sensor adhesion for three-axis vibration test of inertial measurement unit.
Figure 12.
External vibration spectrum type input conditions of inertial product-Experimental input.
Figure 12.
External vibration spectrum type input conditions of inertial product-Experimental input.
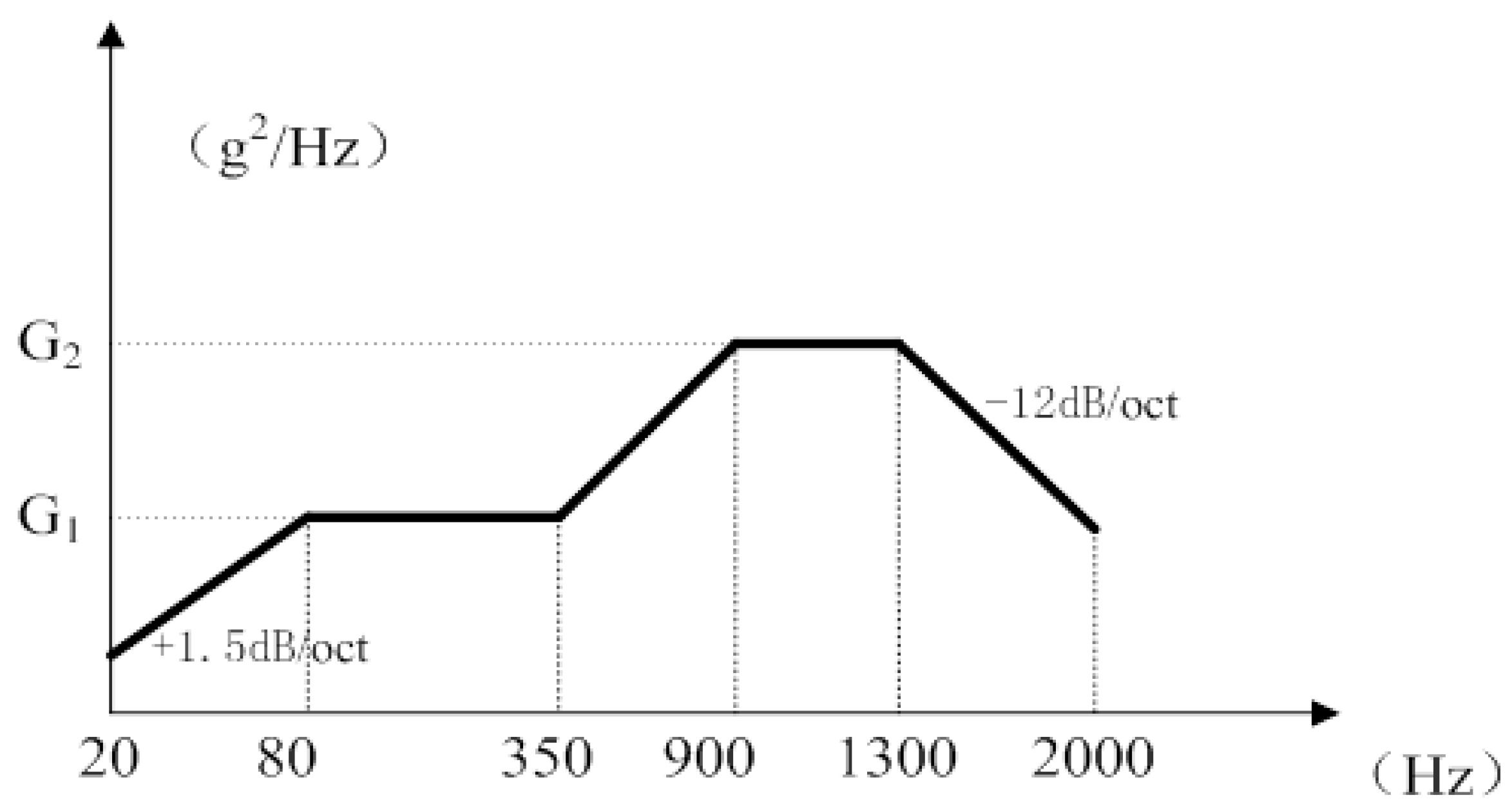
Figure 13.
External vibration spectrum type input conditions of inertial product.
Figure 13.
External vibration spectrum type input conditions of inertial product.
Figure 14.
Response results of the inertial measurement unit of the two-stage damping system. (a) X direction; (b) Y direction; (c) Z direction.
Figure 14.
Response results of the inertial measurement unit of the two-stage damping system. (a) X direction; (b) Y direction; (c) Z direction.
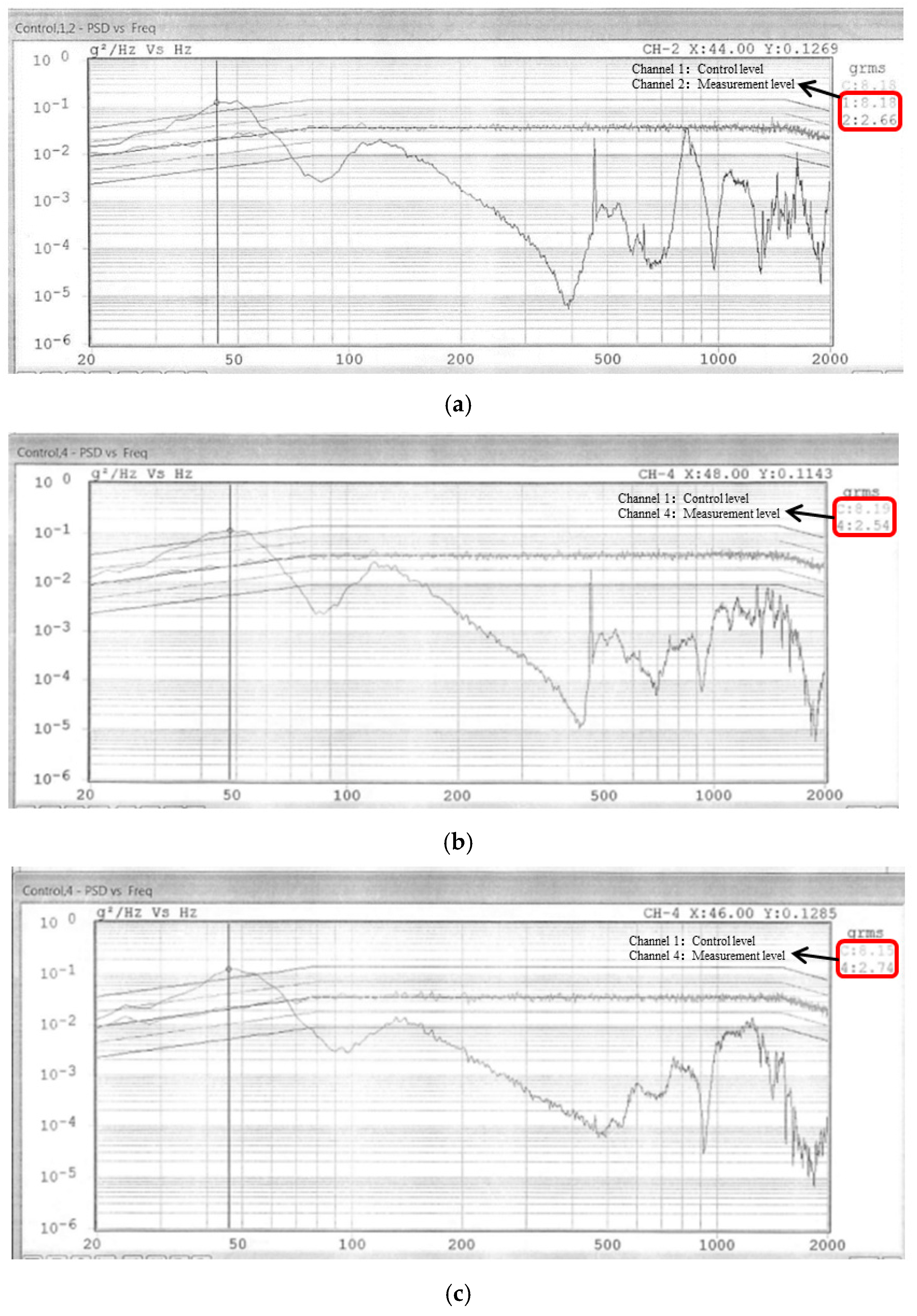
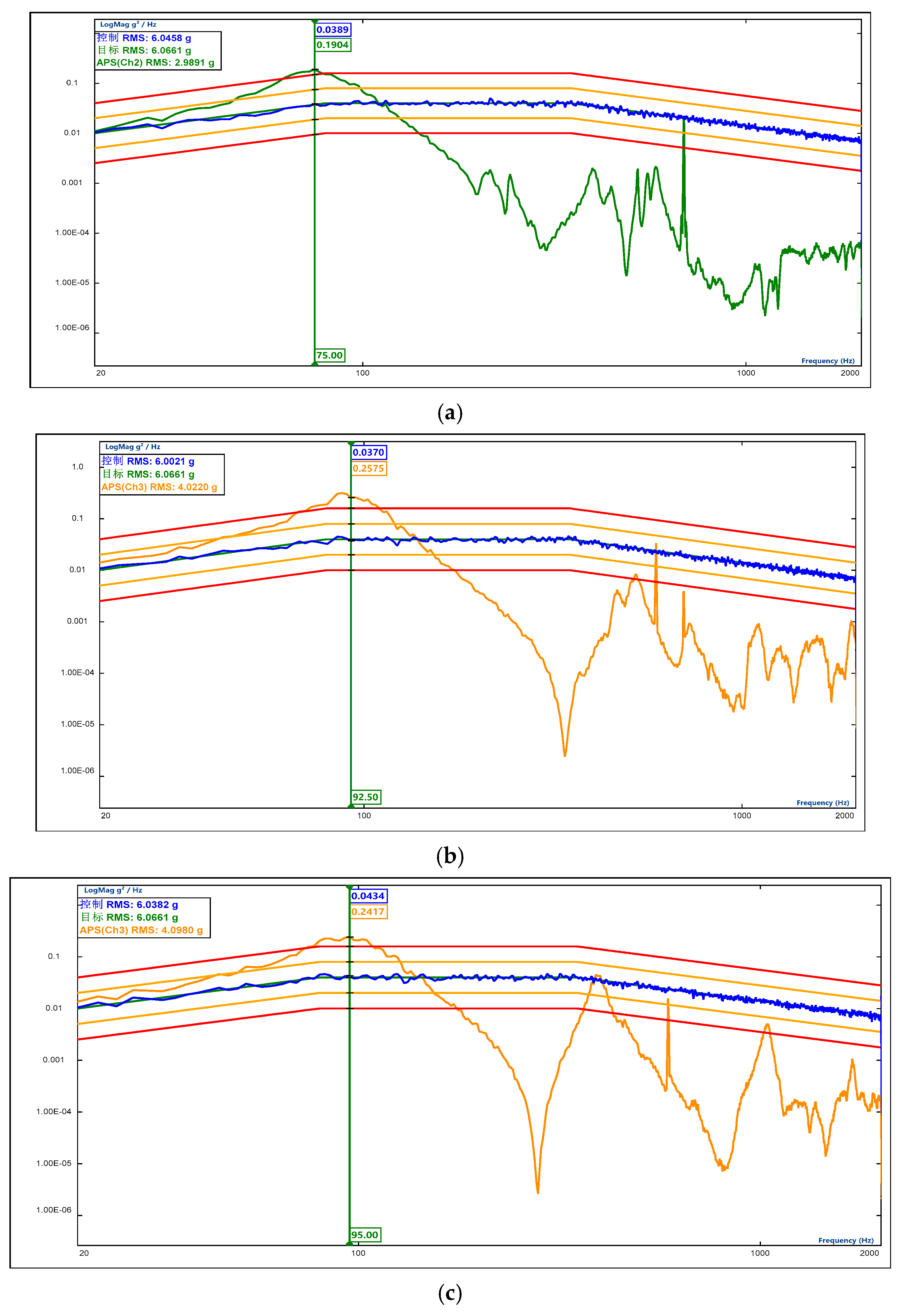
Figure 15.
Response results of inertial measurement unit in single-stage vibration reduction system. (a) X direction; (b) Y direction; (c) Z direction. The Chinese character ‘控制’ means control, and the Chinese character ‘目标’ means goal.
Figure 15.
Response results of inertial measurement unit in single-stage vibration reduction system. (a) X direction; (b) Y direction; (c) Z direction. The Chinese character ‘控制’ means control, and the Chinese character ‘目标’ means goal.
Figure 16.
Inertial measurement unit in X-direction additional angle curve.
Figure 16.
Inertial measurement unit in X-direction additional angle curve.
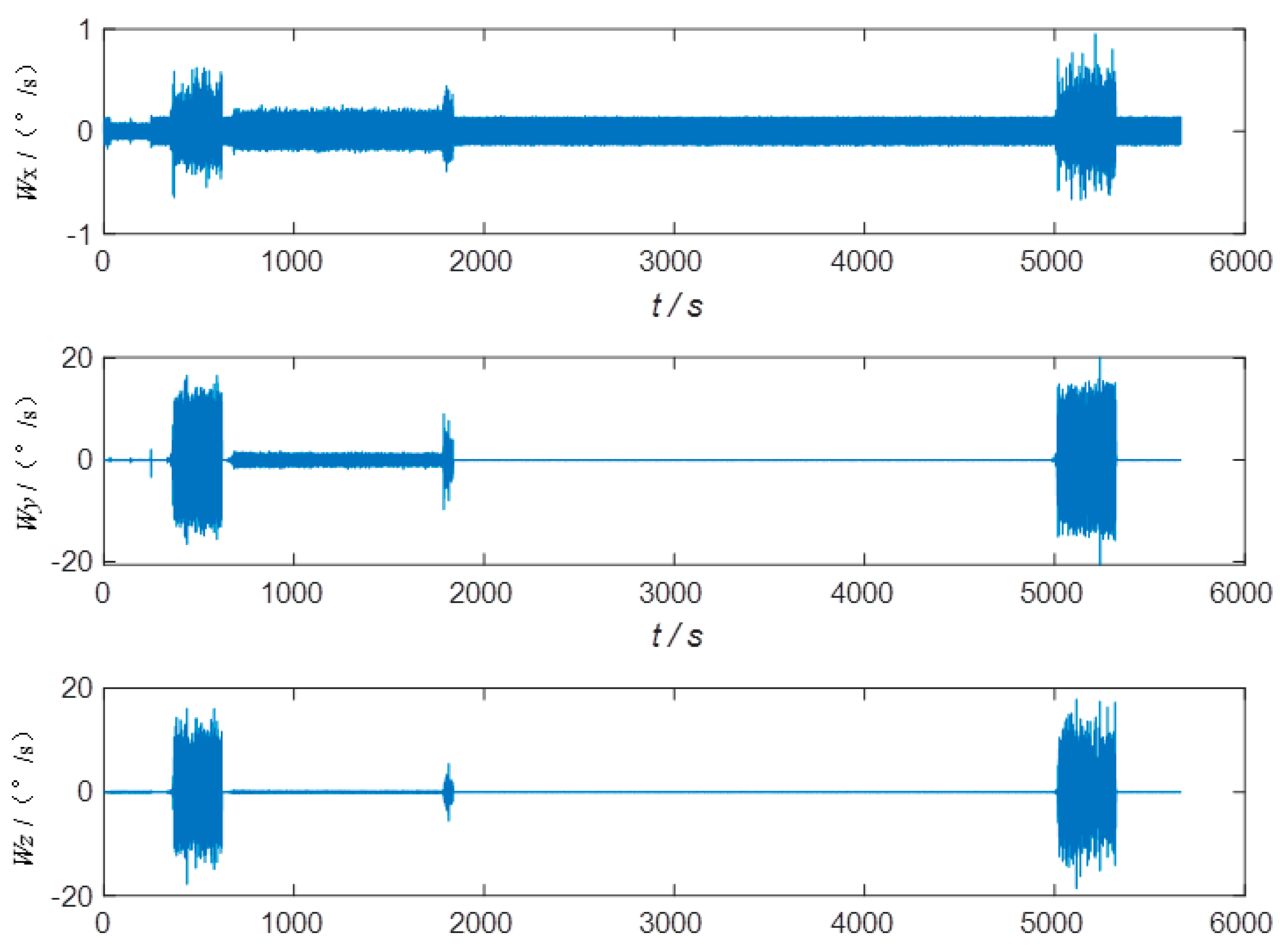
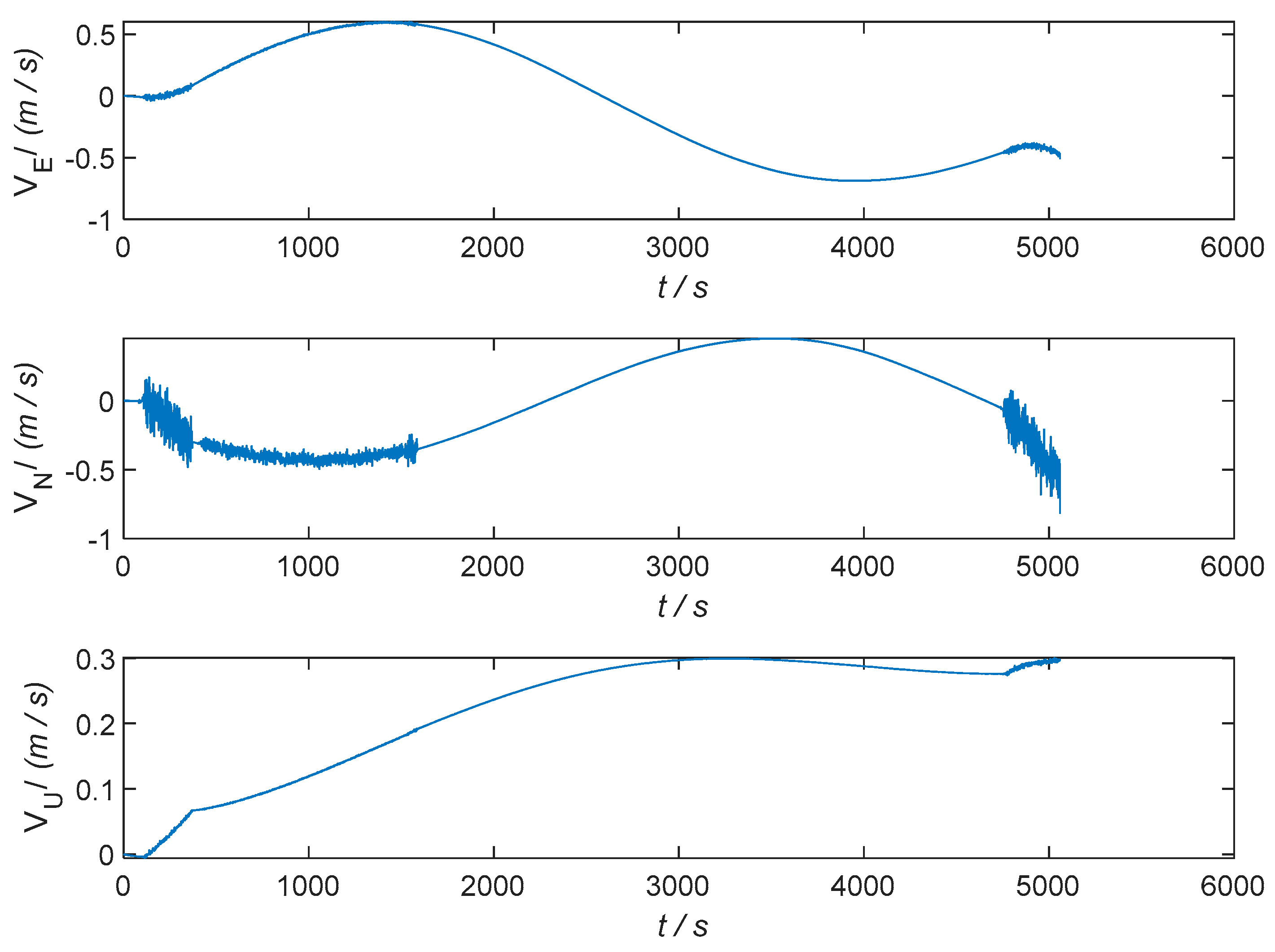
Figure 17.
Inertial measurement unit X-direction vibration navigation velocity error curve.
Figure 17.
Inertial measurement unit X-direction vibration navigation velocity error curve.
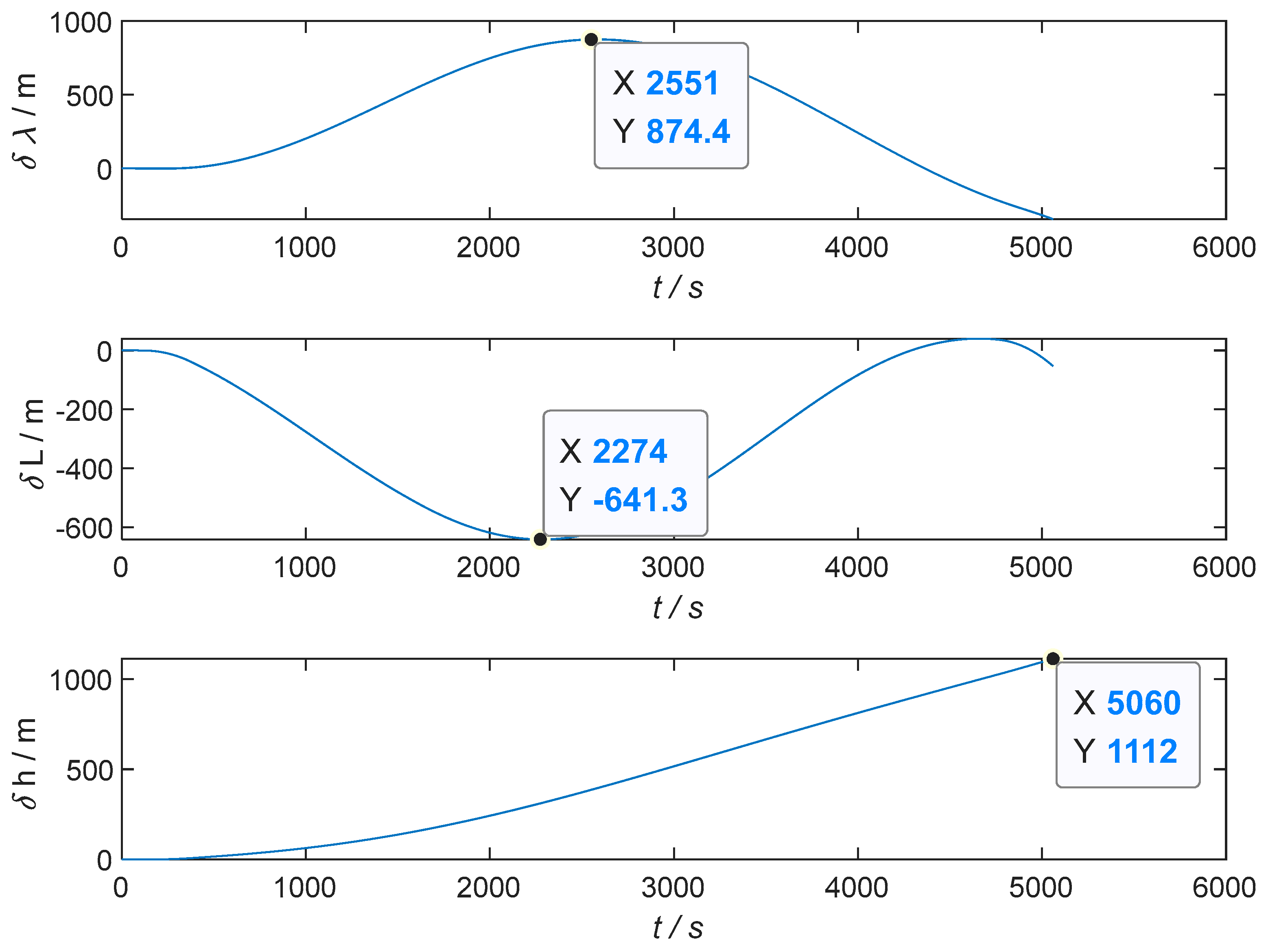
Figure 18.
Inertial measurement unit X-direction vibration navigation position error curve.
Figure 18.
Inertial measurement unit X-direction vibration navigation position error curve.
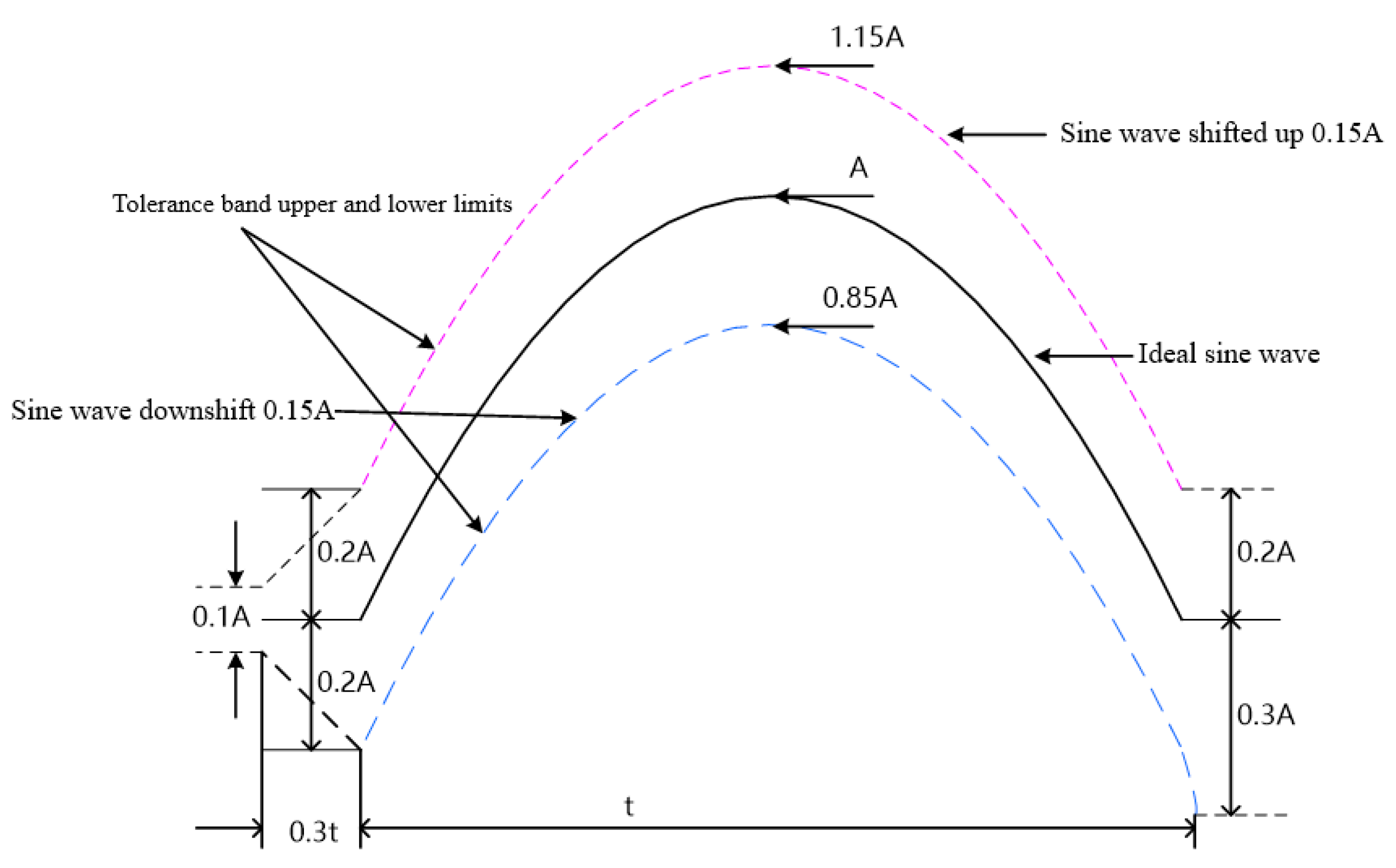
Figure 19.
Semi-sine shock pulse waveform and tolerance.
Figure 19.
Semi-sine shock pulse waveform and tolerance.
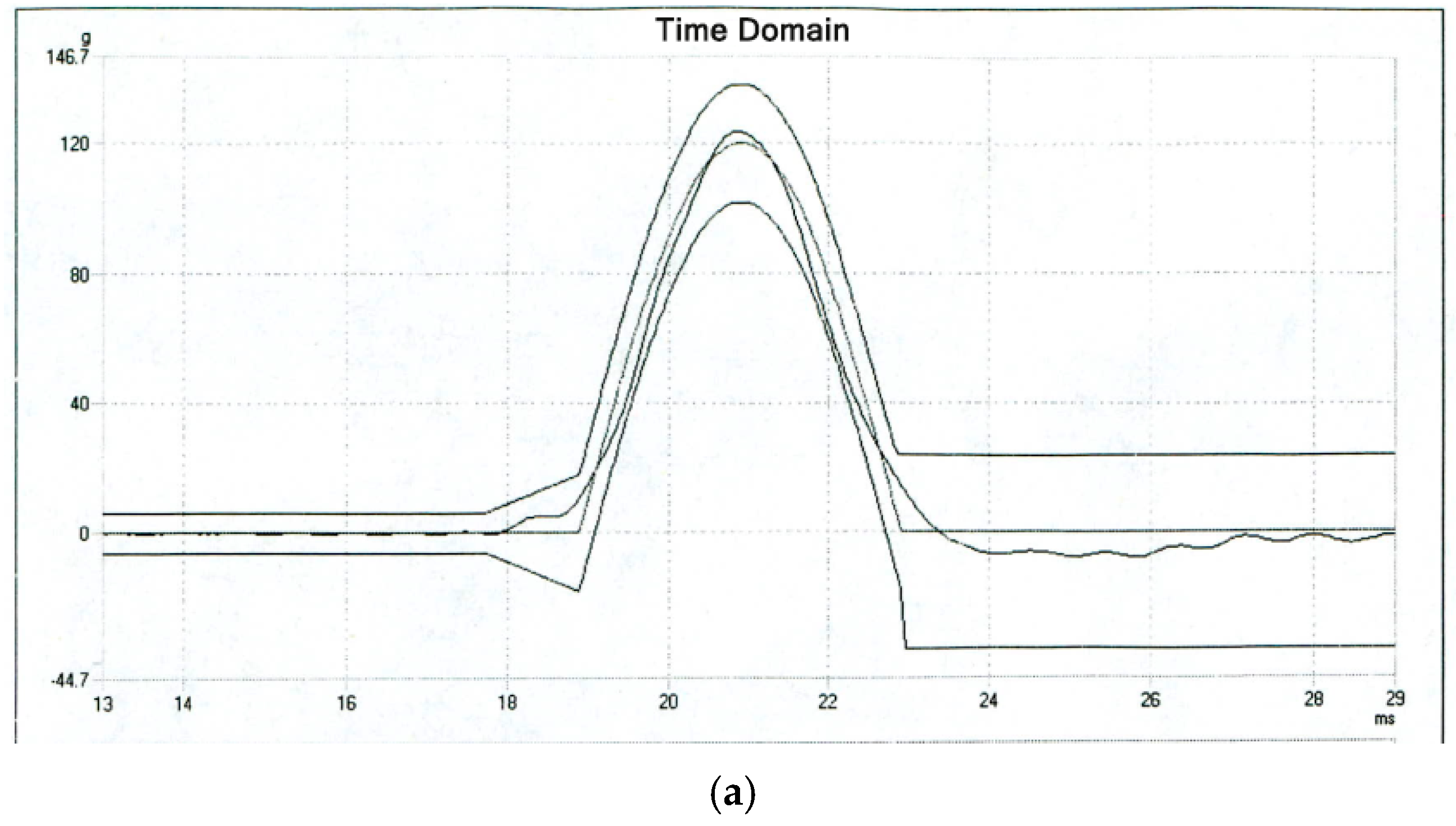
Figure 20.
(a) X-direction impact input; (b) X-direction impact table body response output.
Figure 20.
(a) X-direction impact input; (b) X-direction impact table body response output.
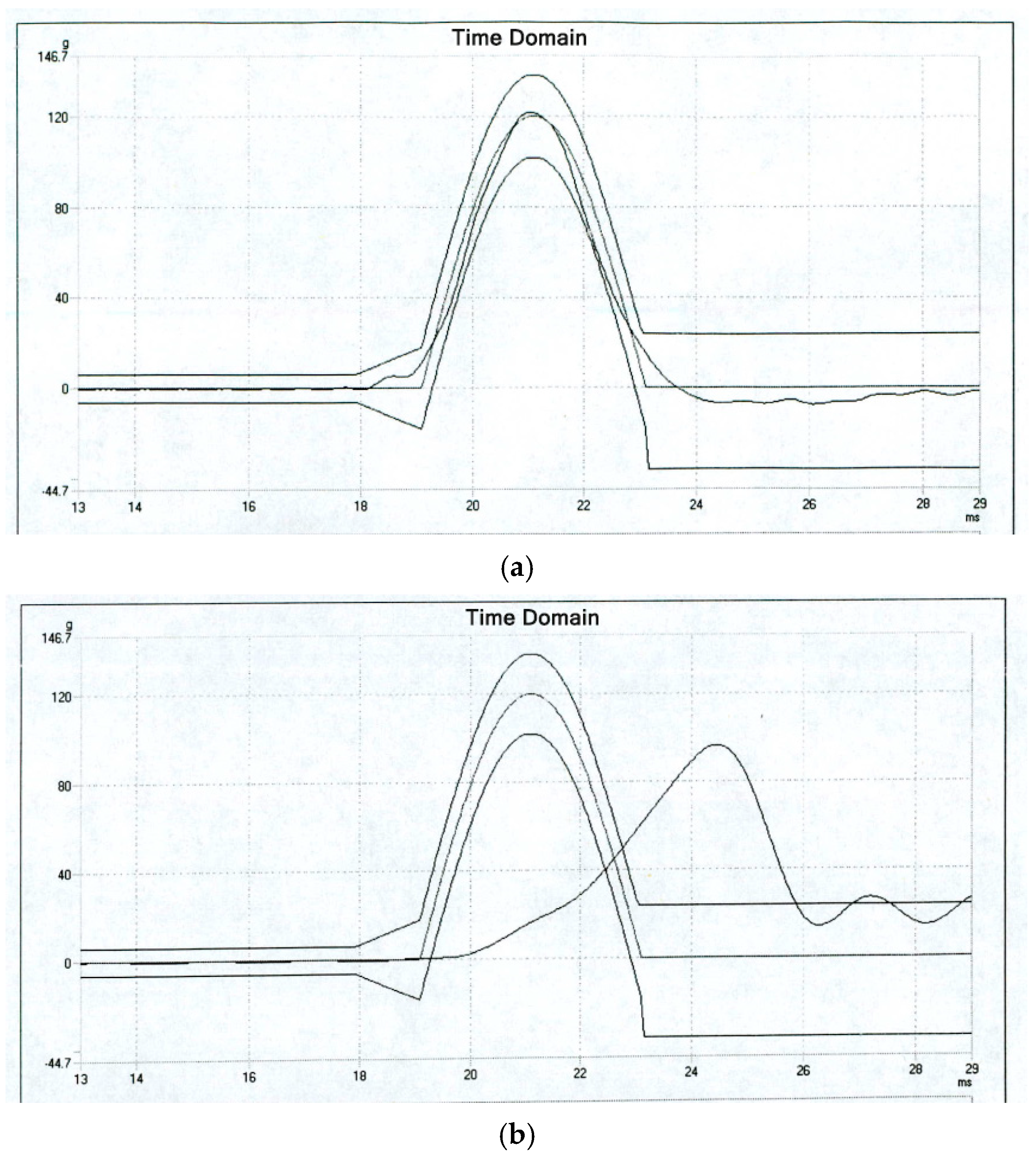
Figure 21.
(a) Y-direction impact input; (b) Y-direction impact table body response output.
Figure 21.
(a) Y-direction impact input; (b) Y-direction impact table body response output.
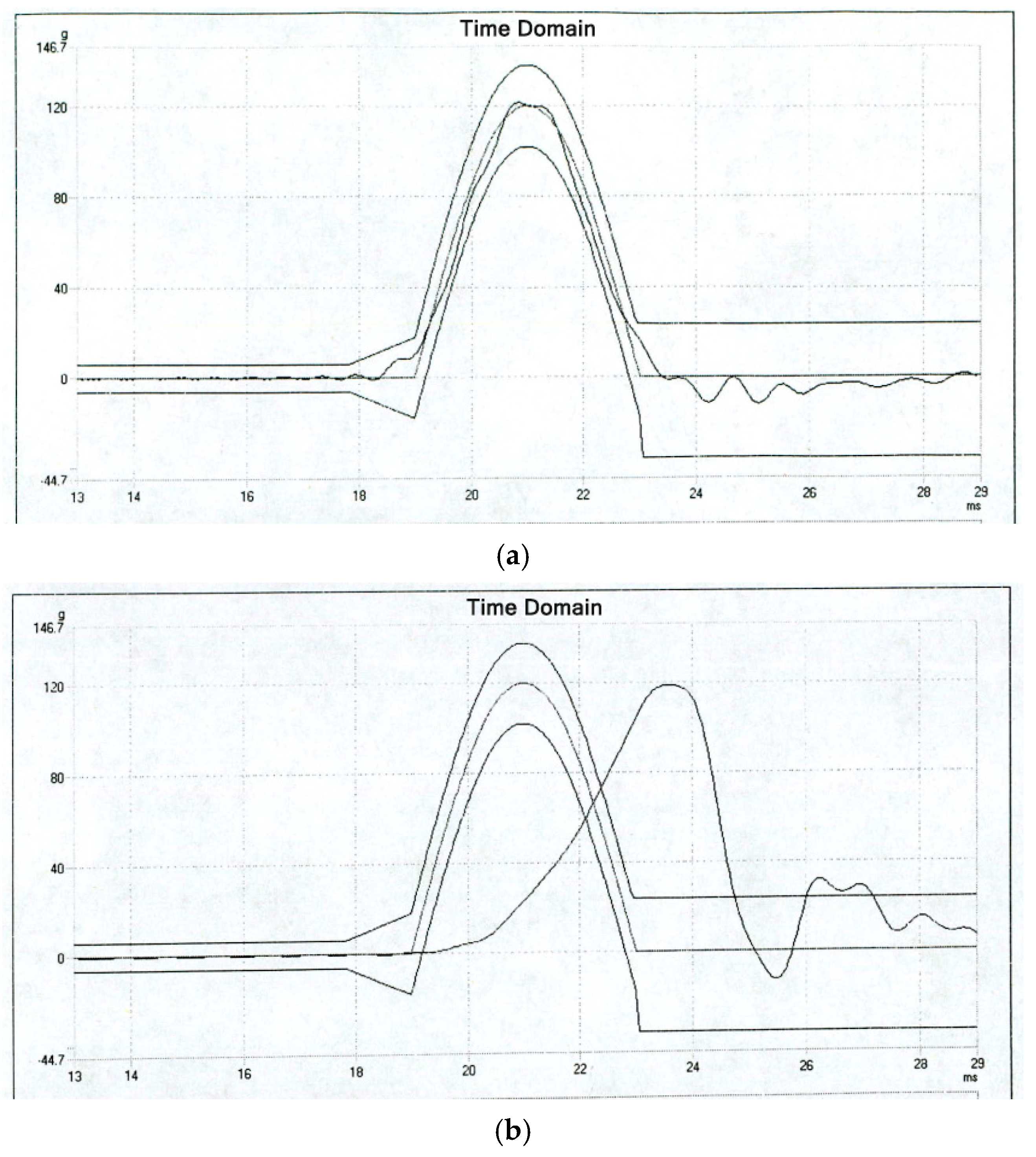
Figure 22.
(a) Z-direction impact input; (b) Z-direction impact table body response output.
Figure 22.
(a) Z-direction impact input; (b) Z-direction impact table body response output.
Table 1.
Parameters of the two-stage vibration isolation system.
Table 1.
Parameters of the two-stage vibration isolation system.
| Nomenclature | Designation | Stiffness Parameter 1 | Stiffness Parameter 2 | Stiffness Parameter 3 |
|---|
| Mass of outer vibration isolation assembly | | 17.2 kg |
| Mass of inner vibration isolation assembly | | 5.9 kg |
| External damping system stiffness (axial) | | 34,830 | 34,830 | 64,840 |
| External damping system stiffness (radial) | | 29,580 | 29,580 | 60,750 |
| Internal damping system stiffness (axial) | | 47,790 | 26,020 | 47,790 |
| Internal damping system stiffness (radial) | | 42,680 | 21,180 | 42,680 |
| External damping system damping (axial) | | 0.124 |
| External damping system damping (radial) | | 0.116 |
| Internal damping system damping (axial) | | 0.268 |
| Internal damping system damping (radial) | | 0.238 |
Table 2.
Three sets of rigidity parameters under the two-level vibration reduction system coupling coefficient.
Table 2.
Three sets of rigidity parameters under the two-level vibration reduction system coupling coefficient.
| Directional | Stiffness Parameter 1 | Stiffness Parameter 2 | Stiffness Parameter 3 |
|---|
| X | 2.00 | 4.98 | 8.19 |
| Y | 1.27 | 6.05 | 18.38 |
| Z | 1.50 | 25.84 | 17.39 |
Table 3.
Comparison of natural frequency differences between complete and simplified models.
Table 3.
Comparison of natural frequency differences between complete and simplified models.
| Modal Analysis (Under Constraint Conditions) | Simplified Model | Unsimplified Model | Natural Frequency Difference |
|---|
| 1st mode | 163.71 Hz | 149.32 Hz | 8.7% |
| 2nd order mode | 170.59 Hz | 158.67 Hz | 6.9% |
| 3rd order mode | 334.06 Hz | 316.88 Hz | 5.1% |
| 4th order mode | 336.32 Hz | 360.18 Hz | 7.1% |
| 5th order mode | 447.43 Hz | 463.98 Hz | 3.7% |
| 6th order mode | 476.26 Hz | 500.58 Hz | 5.1% |
Table 4.
Finite element simulation output results.
Table 4.
Finite element simulation output results.
| Direction | X | Y | Z |
|---|
| RMS Value | 1.9454 G | 2.0463 G | 2.0129 G |
| RMS Percentage | 100% | 100% | 100% |
| Expected Frequency | 73.497 Hz | 76.751 Hz | 68.039 Hz |
Table 6.
Comparison of attenuation levels after vibration between single-stage and two-stage vibration reduction systems.
Table 6.
Comparison of attenuation levels after vibration between single-stage and two-stage vibration reduction systems.
| Vibration Direction | Attenuation Level of Two-Stage Damping System After 8.1 g Input | Attenuation Level of Single-Stage Damping System After 6.06 g Input |
|---|
| X | 2.66 g | 2.99 g |
| Y | 2.54 g | 4.02 g |
| Z | 2.74 g | 4.09 g |
Table 7.
Vibration navigation results.
Table 7.
Vibration navigation results.
| Vibration Direction | Navigation Accuracy (m) | Additional Angular Motion (°/s) | Notes |
|---|
| Required Value | Actual Measurement Value | Required Value | Actual Measurement Value |
|---|
| Longitude | Latitude | Height | X | Y | Z |
|---|
| X | <3000 | 874.4 | −641.3 | 1112 | <25 | 0.95 | 20.6 | 18.5 | |
| Y | <3000 | −623.3 | 178 | −2647 | <25 | 1.84 | 1.72 | 2.0 | |
| Z | <3000 | −411.7 | 195.5 | 857.2 | <25 | 3.35 | 2.38 | 0.84 | |
Table 8.
Semi-sine shock test conditions.
Table 8.
Semi-sine shock test conditions.
| Project | Peak Acceleration A | Duration | Loading Direction |
|---|
| Half-sine wave shock | 120 g | 4 ms | X\Y\Z |
Table 9.
Data output of inertial measurement system for three-way impact test.
Table 9.
Data output of inertial measurement system for three-way impact test.
| | Gyroscope Output (°/s) | Angular Velocity of the Platform (°/s) | Inner Frame Variation (°) | Outer Frame Variation (°) |
|---|
| X | Y | Z | X | Y | Z | Before and After Impact | Before and After Impact |
|---|
| X impact | 4.8 | 43.8 | 64.2 | 5.5 | 22.8 | 40 | 0.011 | 0.035 |
| Y impact | 21.3 | 18.4 | 44.9 | 10.5 | 10.6 | 27 | 0.006 | 0.03 |
| Z impact | 42 | 44 | 5.9 | 36.6 | 32.1 | 5.9 | 0.107 | 0.027 |